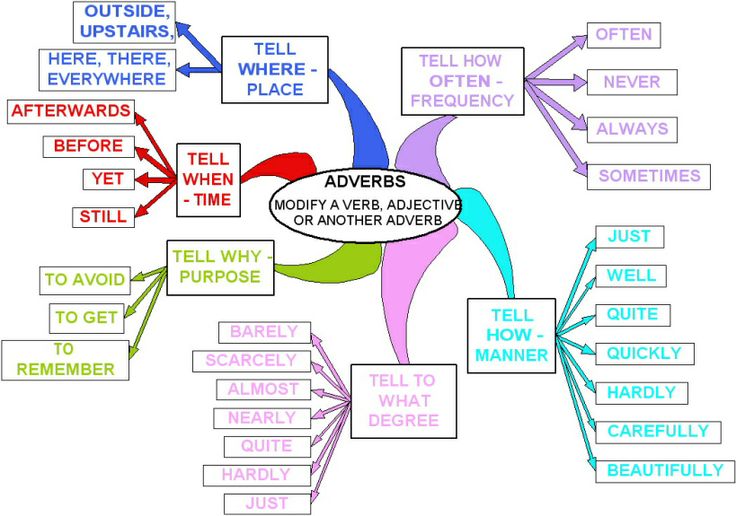
Mathematics

Multiple Choise
Medical Admission Preparation
দেশের সরকারী এবং বেসরকারী বিভিন মেডিকেল কলেজে ভর্তি পরীক্ষায় অংশগ্রহণ করে আশানুরূপ ফল অর্জনের ক্ষেত্রে সহায়ক সকল বিষয়ের প্রস্তুতি মূলক উপাদান এখানে রয়েছে।
BCS Preparation
দেশের ক্যাডার ভিত্তিক চাকুরীর পরীক্ষায় অংশগ্রহণ করে আশানুরূপ ফল অর্জনের ক্ষেত্রে সহায়ক সকল বিষয়ের প্রস্তুতি মূলক উপাদান এখানে রয়েছে।
বিগত সালের শিক্ষাবোর্ড ও বিশ্ববিদ্যালয়ের প্রশ্নপত্র



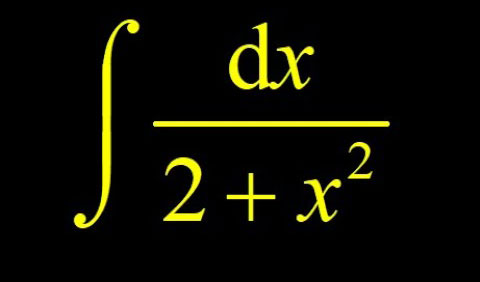













































- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004