এ অধ্যায়ের পাঠ্যসূচী।
- অসমান্তরাল সরলরেখা (Non-parallel straight lines)
- দুইটি অসমান্তরাল সরলরেখার মধ্যবর্তী কোণ (Angle between two non-parallel straight lines)
- দুইটি সরলরেখার পরস্পর লম্ব হওয়ার শর্ত (The condition of two straight lines being perpendicular to each other)
- দুইটি সরলরেখার পরস্পর সমান্তরাল হওয়ার শর্ত (The condition of two straight lines being parallel to each other)
- দুইটি সরলরেখার ছেদবিন্দুগামী যে কোনো সরলরেখার সমীকরণ (Equation of any straight line through the point of intersection of two straight lines)
- একটি নির্দিষ্ট বিন্দু এবং দুইটি সরলরেখার ছেদবিন্দুগামী সরলরেখার সমীকরণ (Equation of a straight line through a fixed point and the intersection of two straight lines)
- একটি নির্দিষ্ট সরলরেখার সমান্তরাল যে কোনো সরলরেখার সমীকরণ (Equation of any straight line parallel to a given straight line)
- একটি নির্দিষ্ট সরলরেখার উপর লম্ব যে কোনো সরলরেখার সমীকরণ (Equation of any straight line perpendicular to a given straight line)
- তিনটি সরলরেখার সমবিন্দু হওয়ার বা এক বিন্দুতে মিলিত হওয়ার শর্ত (The condition of three straight lines meeting at a point)
- শর্টকাট টেকনিক (Shortcut Technique)
- অধ্যায় \(3G\)-এর উদাহরণসমুহ
- অধ্যায় \(3G\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(3G\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3G\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3G\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
অসমান্তরাল সরলরেখা
Non-parallel straight lines
যদি একই সমতলে অবস্থিত দুই বা ততোধিক সরলরেখা চলার পথে কোনো একটি বিন্দুতে মিলিত হয় তবে তাদেরকে অসমান্তরাল সরলরেখা বলা হয়।
দুইটি অসমান্তরাল সরলরেখার মধ্যবর্তী কোণ
Angle between two non-parallel straight lines
দুইটি অসমান্তরাল সরলরেখা উভয়ই \(Y\) অক্ষের অসমান্তরাল হলে, তাদের মধ্যবর্তী কোণ
\(\theta=tan^{-1}\left(\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\right)\).
\(\theta=tan^{-1}\left(\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\right)\).
প্রমাণঃ
ধরি,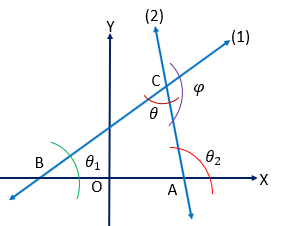
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণ \(\theta\).
\(BC\Rightarrow (1)\) ও \(AC\Rightarrow (2)\) রেখাদ্বয় পরস্পর \(C\) বিন্দুতে এবং অক্ষদ্বয়কে যথাক্রমে \(B\) ও \(A\) ছেদ করে ।
\((1)\) ও \((2)\) সরলরেখাদ্বয় অক্ষদ্বয়ের সহিত যথাক্রমে \(\theta_{1}\) ও \(\theta_{2}\) কোণ উৎপন্ন করে।
\(\therefore m_{1}=\tan\theta_{1}, \ m_{2}=\tan\theta_{2}\)
এখানে,
\(\angle ACB=\theta, \ \angle CBA=\theta_{1}, \ \angle CAX=\theta_{2},\)
\(\angle ACB+\angle CBA=\angle CAX\) ➜ ত্রিভুজের একবাহু বর্ধিত করায় উৎপন্ন বহিঃ কোণ, অন্তস্ত অপর দুই কোণের যোগফলের সমান।
\(\Rightarrow \theta+\theta_{1}=\theta_{2}\)
\(\Rightarrow \theta=\theta_{2}-\theta_{1}\)
\(\therefore \theta=-(\theta_{1}-\theta_{2}) ........(3)\)
আবার বিপরীতক্রমে,
\(BC\Rightarrow (2)\) ও \(AC\Rightarrow (1)\) বিবেচনা করে ।
\(\angle ACB+\angle CBA=\angle CAX\)
\(\Rightarrow \theta+\theta_{2}=\theta_{1}\)
\(\Rightarrow \theta=\theta_{1}-\theta_{2}\)
\(\therefore \theta=\theta_{1}-\theta_{2} ...........(4)\)
\((3)\) ও \((4)\) সমন্বয় করে,
\(\theta=\pm (\theta_{1}-\theta_{2}) ...........(5)\)
\(\Rightarrow \tan\theta=\tan\pm (\theta_{1}-\theta_{2})\) ➜ উভয় পার্শে \(\tan\) অনুপাত নিয়ে।
\(\Rightarrow \tan\theta=\pm \tan(\theta_{1}-\theta_{2})\)
\(\Rightarrow \tan\theta=\pm \frac{\tan\theta_{1}-\tan\theta_{2}}{1+\tan\theta_{1}\tan\theta_{2}}\)
\(\Rightarrow \tan\theta=\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\) ➜ \(\because m_{1}=\tan\theta_{1}, \ m_{2}=\tan\theta_{2}\)
\(\therefore \theta=\tan^{-1}(\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}})\)

\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণ \(\theta\).
\(BC\Rightarrow (1)\) ও \(AC\Rightarrow (2)\) রেখাদ্বয় পরস্পর \(C\) বিন্দুতে এবং অক্ষদ্বয়কে যথাক্রমে \(B\) ও \(A\) ছেদ করে ।
\((1)\) ও \((2)\) সরলরেখাদ্বয় অক্ষদ্বয়ের সহিত যথাক্রমে \(\theta_{1}\) ও \(\theta_{2}\) কোণ উৎপন্ন করে।
\(\therefore m_{1}=\tan\theta_{1}, \ m_{2}=\tan\theta_{2}\)
এখানে,
\(\angle ACB=\theta, \ \angle CBA=\theta_{1}, \ \angle CAX=\theta_{2},\)
\(\angle ACB+\angle CBA=\angle CAX\) ➜ ত্রিভুজের একবাহু বর্ধিত করায় উৎপন্ন বহিঃ কোণ, অন্তস্ত অপর দুই কোণের যোগফলের সমান।
\(\Rightarrow \theta+\theta_{1}=\theta_{2}\)
\(\Rightarrow \theta=\theta_{2}-\theta_{1}\)
\(\therefore \theta=-(\theta_{1}-\theta_{2}) ........(3)\)
আবার বিপরীতক্রমে,
\(BC\Rightarrow (2)\) ও \(AC\Rightarrow (1)\) বিবেচনা করে ।
\(\angle ACB+\angle CBA=\angle CAX\)
\(\Rightarrow \theta+\theta_{2}=\theta_{1}\)
\(\Rightarrow \theta=\theta_{1}-\theta_{2}\)
\(\therefore \theta=\theta_{1}-\theta_{2} ...........(4)\)
\((3)\) ও \((4)\) সমন্বয় করে,
\(\theta=\pm (\theta_{1}-\theta_{2}) ...........(5)\)
\(\Rightarrow \tan\theta=\tan\pm (\theta_{1}-\theta_{2})\) ➜ উভয় পার্শে \(\tan\) অনুপাত নিয়ে।
\(\Rightarrow \tan\theta=\pm \tan(\theta_{1}-\theta_{2})\)
\(\Rightarrow \tan\theta=\pm \frac{\tan\theta_{1}-\tan\theta_{2}}{1+\tan\theta_{1}\tan\theta_{2}}\)
\(\Rightarrow \tan\theta=\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\) ➜ \(\because m_{1}=\tan\theta_{1}, \ m_{2}=\tan\theta_{2}\)
\(\therefore \theta=\tan^{-1}(\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}})\)
সরলরেখাদ্বয়ের আকার সাধারণ হলে
অর্থাৎ রেখাদ্বয়,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণ
\(\theta=tan^{-1}\left(\pm \frac{a_{2}b_{1}-a_{1}b_{2}}{a_{1}a_{2}+b_{1}b_{2}}\right)\).
এখানে,
\((1)\) নং সরলরেখার ঢাল \(=-\frac{a_{1}}{b_{1}}\)
\((2)\) নং সরলরেখার ঢাল \(=-\frac{a_{2}}{b_{2}}\)
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণ
\(\theta=tan^{-1}\left(\pm \frac{a_{2}b_{1}-a_{1}b_{2}}{a_{1}a_{2}+b_{1}b_{2}}\right)\).
এখানে,
\((1)\) নং সরলরেখার ঢাল \(=-\frac{a_{1}}{b_{1}}\)
\((2)\) নং সরলরেখার ঢাল \(=-\frac{a_{2}}{b_{2}}\)
দুইটি সরলরেখার পরস্পর লম্ব হওয়ার শর্ত
The condition of two straight lines being perpendicular to each other
ধরি,
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখার পরস্পর লম্ব হওয়ার শর্ত
\(m_{1}\times m_{2}=-1\).
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখার পরস্পর লম্ব হওয়ার শর্ত
\(a_{1}a_{2}+ b_{1}b_{2}=0\).
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখার পরস্পর লম্ব হওয়ার শর্ত
\(m_{1}\times m_{2}=-1\).
প্রমাণঃ
ধরি,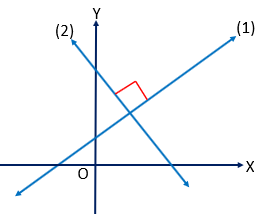
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখার ঢাল যথাক্রমে \(m_{1}\) ও \(m_{2}\)
সরলরেখাদ্বয় পরস্পর লম্ব হবে যদি তাদের মধ্যবর্তী কোণ \(\theta=90^{o}\) হয়।
\(\therefore \tan^{-1}(\frac{m_{1}-m_{2}}{1+m_{1}m_{2}})=90^{o}\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=\tan90^{o}\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=\infty\) ➜ \(\because \tan90^{o}=\infty\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=\frac{1}{0}\) ➜ \(\because \infty=\frac{1}{0}\)
\(\Rightarrow 1+m_{1}m_{2}=0\times (m_{1}-m_{2})\)
\(\Rightarrow 1+m_{1}m_{2}=0\)
\(\therefore m_{1}m_{2}=-1\) ইহাই লম্ব হওয়ার শর্ত।

\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখার ঢাল যথাক্রমে \(m_{1}\) ও \(m_{2}\)
সরলরেখাদ্বয় পরস্পর লম্ব হবে যদি তাদের মধ্যবর্তী কোণ \(\theta=90^{o}\) হয়।
\(\therefore \tan^{-1}(\frac{m_{1}-m_{2}}{1+m_{1}m_{2}})=90^{o}\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=\tan90^{o}\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=\infty\) ➜ \(\because \tan90^{o}=\infty\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=\frac{1}{0}\) ➜ \(\because \infty=\frac{1}{0}\)
\(\Rightarrow 1+m_{1}m_{2}=0\times (m_{1}-m_{2})\)
\(\Rightarrow 1+m_{1}m_{2}=0\)
\(\therefore m_{1}m_{2}=-1\) ইহাই লম্ব হওয়ার শর্ত।
সরলরেখাদ্বয়ের আকার সাধারণ হলে
রেখাদ্বয়,\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখার পরস্পর লম্ব হওয়ার শর্ত
\(a_{1}a_{2}+ b_{1}b_{2}=0\).
দুইটি সরলরেখার পরস্পর সমান্তরাল হওয়ার শর্ত
The condition of two straight lines being parallel to each other
ধরি,
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখার পরস্পর সমান্তরাল হওয়ার শর্ত
\(m_{1}=m_{2}\).
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখার পরস্পর সমান্তরাল হওয়ার শর্ত
\(a_{1}b_{2}=a_{2}b_{1}\).
অথবা,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\).
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখার পরস্পর সমান্তরাল হওয়ার শর্ত
\(m_{1}=m_{2}\).
প্রমাণঃ
ধরি,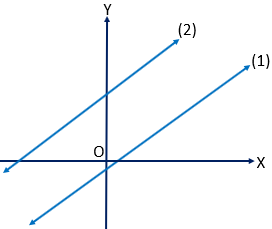
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\( (1)\) ও \((2)\) সরলরেখার ঢাল যথাক্রমে \(m_{1}\) ও \(m_{2}\)
সরলরেখাদ্বয় পরস্পর সমান্তরাল হবে যদি তাদের মধ্যবর্তী কোণ \(\theta=0\) হয়।
\(\therefore \tan^{-1}(\frac{m_{1}-m_{2}}{1+m_{1}m_{2}})=0\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=\tan0\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=0\) ➜ \(\because \tan0=0\)
\(\Rightarrow m_{1}-m_{2}=0\times (1+m_{1}m_{2})\)
\(\Rightarrow m_{1}-m_{2}=0\)
\(\therefore m_{1}=m_{2}\) ইহাই সমান্তরাল হওয়ার শর্ত।

\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\( (1)\) ও \((2)\) সরলরেখার ঢাল যথাক্রমে \(m_{1}\) ও \(m_{2}\)
সরলরেখাদ্বয় পরস্পর সমান্তরাল হবে যদি তাদের মধ্যবর্তী কোণ \(\theta=0\) হয়।
\(\therefore \tan^{-1}(\frac{m_{1}-m_{2}}{1+m_{1}m_{2}})=0\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=\tan0\)
\(\Rightarrow \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}=0\) ➜ \(\because \tan0=0\)
\(\Rightarrow m_{1}-m_{2}=0\times (1+m_{1}m_{2})\)
\(\Rightarrow m_{1}-m_{2}=0\)
\(\therefore m_{1}=m_{2}\) ইহাই সমান্তরাল হওয়ার শর্ত।
সরলরেখাদ্বয়ের আকার সাধারণ হলে
রেখাদ্বয়,\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখার পরস্পর সমান্তরাল হওয়ার শর্ত
\(a_{1}b_{2}=a_{2}b_{1}\).
অথবা,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\).
দুইটি সরলরেখার ছেদবিন্দুগামী যে কোনো সরলরেখার সমীকরণ
Equation of any straight line through the point of intersection of two straight lines
ধরি,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর ছেদবিন্দুগামী যে কোনো সরলরেখার সমীকরণ
\(a_{1}x+b_{1}y+c_{1}+k(a_{2}x+b_{2}y+c_{2})=0\).
এখানে,
\(k\) শুন্য ব্যাতীত যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর ছেদবিন্দুগামী যে কোনো সরলরেখার সমীকরণ
\(a_{1}x+b_{1}y+c_{1}+k(a_{2}x+b_{2}y+c_{2})=0\).
এখানে,
\(k\) শুন্য ব্যাতীত যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
প্রমাণঃ
ধরি,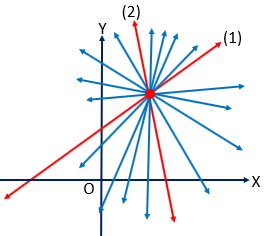
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর ছেদবিন্দু \((x_{1}, y_{1})\)
\(\therefore (1)\) ও \((2)\) হতে পাই,
\(a_{1}x_{1}+b_{1}y_{1}+c_{1}=0 ........(3)\)
\(a_{2}x_{1}+b_{2}y_{1}+c_{2}=0\)
\(\Rightarrow k(a_{2}x_{1}+b_{2}y_{1}+c_{2})=0........(4)\) ➜ \(\because \infty=\frac{1}{0}\)
এখানে,
\(k\) শুন্য ব্যাতীত যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
\((3)\) ও \((4)\) যোগ করে পাই,
\(a_{1}x_{1}+b_{1}y_{1}+c_{1}+k(a_{2}x_{1}+b_{2}y_{1}+c_{2})=0........(5)\)
\(\Rightarrow a_{1}x_{1}+b_{1}y_{1}+c_{1}+ka_{2}x_{1}+kb_{2}y_{1}+kc_{2}=0\)
\(\Rightarrow (a_{1}+ka_{2})x_{1}+(b_{1}+kb_{2})y_{1}+(c_{1}+kc_{2})=0\)
\(\Rightarrow (a_{1}+ka_{2})x+(b_{1}+kb_{2})y+(c_{1}+kc_{2})=0\)
ইহা স্পষ্ট যে \((x_{1}, y_{1})\) বিন্দুটি \((5)\) নং সমীকরণকে সিদ্ধ করে। সমীকরণটি \(x, \ y\) এর একঘাত সমীকরণ তাই ইহা একটি সরলরেখা নির্দেশ করে। অতএব, \((5)\) নং সরলরেখাটি \((1)\) ও \((2)\) এর ছেদবিন্দু দিয়ে অতিক্রান্ত একটি সরলরেখা। প্রকৃতপক্ষে \(k\) এর বিভিন্ন মানের \((k\neq 0)\) জন্য \((5)\) সরলরেখাটি বিভিন্ন সরলরেখা প্রকাশ করে; যাদের প্রত্যেকটি \((x_{1}, y_{1})\) বিন্দু দিয়ে যায়।

\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর ছেদবিন্দু \((x_{1}, y_{1})\)
\(\therefore (1)\) ও \((2)\) হতে পাই,
\(a_{1}x_{1}+b_{1}y_{1}+c_{1}=0 ........(3)\)
\(a_{2}x_{1}+b_{2}y_{1}+c_{2}=0\)
\(\Rightarrow k(a_{2}x_{1}+b_{2}y_{1}+c_{2})=0........(4)\) ➜ \(\because \infty=\frac{1}{0}\)
এখানে,
\(k\) শুন্য ব্যাতীত যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
\((3)\) ও \((4)\) যোগ করে পাই,
\(a_{1}x_{1}+b_{1}y_{1}+c_{1}+k(a_{2}x_{1}+b_{2}y_{1}+c_{2})=0........(5)\)
\(\Rightarrow a_{1}x_{1}+b_{1}y_{1}+c_{1}+ka_{2}x_{1}+kb_{2}y_{1}+kc_{2}=0\)
\(\Rightarrow (a_{1}+ka_{2})x_{1}+(b_{1}+kb_{2})y_{1}+(c_{1}+kc_{2})=0\)
\(\Rightarrow (a_{1}+ka_{2})x+(b_{1}+kb_{2})y+(c_{1}+kc_{2})=0\)
ইহা স্পষ্ট যে \((x_{1}, y_{1})\) বিন্দুটি \((5)\) নং সমীকরণকে সিদ্ধ করে। সমীকরণটি \(x, \ y\) এর একঘাত সমীকরণ তাই ইহা একটি সরলরেখা নির্দেশ করে। অতএব, \((5)\) নং সরলরেখাটি \((1)\) ও \((2)\) এর ছেদবিন্দু দিয়ে অতিক্রান্ত একটি সরলরেখা। প্রকৃতপক্ষে \(k\) এর বিভিন্ন মানের \((k\neq 0)\) জন্য \((5)\) সরলরেখাটি বিভিন্ন সরলরেখা প্রকাশ করে; যাদের প্রত্যেকটি \((x_{1}, y_{1})\) বিন্দু দিয়ে যায়।
একটি নির্দিষ্ট বিন্দু এবং দুইটি সরলরেখার ছেদবিন্দুগামী সরলরেখার সমীকরণ
Equation of a straight line through a fixed point and the intersection of two straight lines
ধরি,
নির্দিষ্ট বিন্দুটি \(P(x_{1}, y_{1})\) এবং সরলরেখাদ্বয়,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(P(x_{1}, y_{1})\) বিন্দু এবং \((1)\) ও \((2)\) এর ছেদবিন্দুগামী যে কোনো সরলরেখার সমীকরণ
\(\frac{a_{1}x+b_{1}y+c_{1}}{a_{1}x_{1}+b_{1}y_{1}+c_{1}}=\frac{a_{2}x+b_{2}y+c_{2}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}\).
নির্দিষ্ট বিন্দুটি \(P(x_{1}, y_{1})\) এবং সরলরেখাদ্বয়,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(P(x_{1}, y_{1})\) বিন্দু এবং \((1)\) ও \((2)\) এর ছেদবিন্দুগামী যে কোনো সরলরেখার সমীকরণ
\(\frac{a_{1}x+b_{1}y+c_{1}}{a_{1}x_{1}+b_{1}y_{1}+c_{1}}=\frac{a_{2}x+b_{2}y+c_{2}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}\).
প্রমাণঃ
ধরি,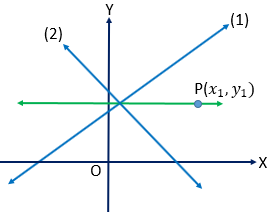
নির্দিষ্ট বিন্দুটি \(P(x_{1}, y_{1})\) এবং সরলরেখা দ্বয়,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর ছেদবিন্দুগামী যে কোনো সরলরেখার সমীকরণ
\(a_{1}x+b_{1}y+c_{1}+k(a_{2}x+b_{2}y+c_{2})=0 ........(3)\)
এখানে,
\(k\) শুন্য ব্যাতীত যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
\((3)\) নং সরলরেখাটি \(P(x_{1}, y_{1})\) বিন্দু দিয়ে যায়,
\(\therefore a_{1}x_{1}+b_{1}y_{1}+c_{1}+k(a_{2}x_{1}+b_{2}y_{1}+c_{2})=0\)
\(\Rightarrow k(a_{2}x_{1}+b_{2}y_{1}+c_{2})=-(a_{1}x_{1}+b_{1}y_{1}+c_{1})\)
\(\therefore k=-\frac{a_{1}x_{1}+b_{1}y_{1}+c_{1}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}\)
\(k\) এর এই মান \((3)\) সমীকরণে বসিয়ে পাই,
\(a_{1}x+b_{1}y+c_{1}+(-\frac{a_{1}x_{1}+b_{1}y_{1}+c_{1}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}})(a_{2}x+b_{2}y+c_{2})=0\)
\(\Rightarrow a_{1}x+b_{1}y+c_{1}-\frac{a_{1}x_{1}+b_{1}y_{1}+c_{1}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}(a_{2}x+b_{2}y+c_{2})=0\)
\(\Rightarrow a_{1}x+b_{1}y+c_{1}=\frac{a_{1}x_{1}+b_{1}y_{1}+c_{1}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}(a_{2}x+b_{2}y+c_{2})\)
\(\therefore \frac{a_{1}x+b_{1}y+c_{1}}{a_{1}x_{1}+b_{1}y_{1}+c_{1}}=\frac{a_{2}x+b_{2}y+c_{2}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}\)
ইহাই নির্ণেয় সরলরেখার সমীকরণ।

নির্দিষ্ট বিন্দুটি \(P(x_{1}, y_{1})\) এবং সরলরেখা দ্বয়,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর ছেদবিন্দুগামী যে কোনো সরলরেখার সমীকরণ
\(a_{1}x+b_{1}y+c_{1}+k(a_{2}x+b_{2}y+c_{2})=0 ........(3)\)
এখানে,
\(k\) শুন্য ব্যাতীত যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
\((3)\) নং সরলরেখাটি \(P(x_{1}, y_{1})\) বিন্দু দিয়ে যায়,
\(\therefore a_{1}x_{1}+b_{1}y_{1}+c_{1}+k(a_{2}x_{1}+b_{2}y_{1}+c_{2})=0\)
\(\Rightarrow k(a_{2}x_{1}+b_{2}y_{1}+c_{2})=-(a_{1}x_{1}+b_{1}y_{1}+c_{1})\)
\(\therefore k=-\frac{a_{1}x_{1}+b_{1}y_{1}+c_{1}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}\)
\(k\) এর এই মান \((3)\) সমীকরণে বসিয়ে পাই,
\(a_{1}x+b_{1}y+c_{1}+(-\frac{a_{1}x_{1}+b_{1}y_{1}+c_{1}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}})(a_{2}x+b_{2}y+c_{2})=0\)
\(\Rightarrow a_{1}x+b_{1}y+c_{1}-\frac{a_{1}x_{1}+b_{1}y_{1}+c_{1}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}(a_{2}x+b_{2}y+c_{2})=0\)
\(\Rightarrow a_{1}x+b_{1}y+c_{1}=\frac{a_{1}x_{1}+b_{1}y_{1}+c_{1}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}(a_{2}x+b_{2}y+c_{2})\)
\(\therefore \frac{a_{1}x+b_{1}y+c_{1}}{a_{1}x_{1}+b_{1}y_{1}+c_{1}}=\frac{a_{2}x+b_{2}y+c_{2}}{a_{2}x_{1}+b_{2}y_{1}+c_{2}}\)
ইহাই নির্ণেয় সরলরেখার সমীকরণ।
একটি নির্দিষ্ট সরলরেখার সমান্তরাল যে কোনো সরলরেখার সমীকরণ
Equation of any straight line parallel to a given straight line
ধরি,
নির্দিষ্ট সরলরেখাটি,
\(ax+by+c=0 ........(1)\)
\((1)\) নং সরলরেখার সমান্তরাল যে কোনো সরলরেখার সমীকরণ
\(ax+by+k=0\).
এখানে,
\(k\) যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
নির্দিষ্ট সরলরেখাটি,
\(ax+by+c=0 ........(1)\)
\((1)\) নং সরলরেখার সমান্তরাল যে কোনো সরলরেখার সমীকরণ
\(ax+by+k=0\).
এখানে,
\(k\) যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
প্রমাণঃ
ধরি,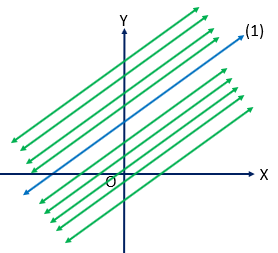
নির্দিষ্ট সরলরেখাটি,
\(ax+by+c=0 ........(1)\)
\(\Rightarrow by=-ax-c\)
\(\Rightarrow y=-\frac{a}{b}x-\frac{c}{b}\)
\(\therefore (1)\) এর ঢাল \(=-\frac{a}{b}\)
\(\therefore (1)\) এর সমান্তরাল সরলরেখার ঢাল \(=-\frac{a}{b}\) হবে।
ফলে \((1)\) নং সরলরেখার সমান্তরাল যে কোনো সরলরেখার সমীকরণ \(y=-\frac{a}{b}x+d\)
\(\Rightarrow y=-\frac{ax}{b}+d\)
\(\Rightarrow y=\frac{-ax+bd}{b}\)
\(\Rightarrow by=-ax+bd\)
\(\Rightarrow ax+by-bd=0\)
\(\Rightarrow ax+by+k=0\) যেখানে \(-bd=k\); \(k\) যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
\(\therefore ax+by+k=0, \ (1)\) নং সরলরেখার সমান্তরাল যে কোনো সরলরেখার সমীকরণ।

নির্দিষ্ট সরলরেখাটি,
\(ax+by+c=0 ........(1)\)
\(\Rightarrow by=-ax-c\)
\(\Rightarrow y=-\frac{a}{b}x-\frac{c}{b}\)
\(\therefore (1)\) এর ঢাল \(=-\frac{a}{b}\)
\(\therefore (1)\) এর সমান্তরাল সরলরেখার ঢাল \(=-\frac{a}{b}\) হবে।
ফলে \((1)\) নং সরলরেখার সমান্তরাল যে কোনো সরলরেখার সমীকরণ \(y=-\frac{a}{b}x+d\)
\(\Rightarrow y=-\frac{ax}{b}+d\)
\(\Rightarrow y=\frac{-ax+bd}{b}\)
\(\Rightarrow by=-ax+bd\)
\(\Rightarrow ax+by-bd=0\)
\(\Rightarrow ax+by+k=0\) যেখানে \(-bd=k\); \(k\) যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
\(\therefore ax+by+k=0, \ (1)\) নং সরলরেখার সমান্তরাল যে কোনো সরলরেখার সমীকরণ।
একটি নির্দিষ্ট সরলরেখার উপর লম্ব যে কোনো সরলরেখার সমীকরণ
Equation of any straight line perpendicular to a given straight line
ধরি,
নির্দিষ্ট সরলরেখাটি,
\(ax+by+c=0 ........(1)\)
\((1)\) নং সরলরেখার উপর লম্ব যে কোনো সরলরেখার সমীকরণ
\(bx-ay+k=0\).
এখানে,
\(k\) যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
নির্দিষ্ট সরলরেখাটি,
\(ax+by+c=0 ........(1)\)
\((1)\) নং সরলরেখার উপর লম্ব যে কোনো সরলরেখার সমীকরণ
\(bx-ay+k=0\).
এখানে,
\(k\) যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
প্রমাণঃ
ধরি,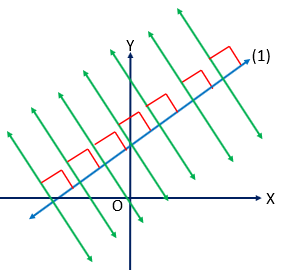
নির্দিষ্ট সরলরেখাটি,
\(ax+by+c=0 ........(1)\)
\(\Rightarrow by=-ax-c\)
\(\Rightarrow y=-\frac{a}{b}x-\frac{c}{b}\)
\(\therefore (1)\) এর ঢাল \(=-\frac{a}{b}\)
\(\therefore (1)\) এর উপর লম্ব সরলরেখার ঢাল \(=\frac{b}{a}\) হবে।
ফলে \((1)\) নং সরলরেখার উপর লম্ব যে কোনো সরলরেখার সমীকরণ \(y=\frac{b}{a}x+d\)
\(\Rightarrow y=\frac{bx}{a}+d\)
\(\Rightarrow y=\frac{bx+ad}{a}\)
\(\Rightarrow ay=bx+ad\)
\(\Rightarrow -bx+ay-ad=0\)
\(\Rightarrow bx-ay+ad=0\) ➜ উভয় পার্শে \(-1\) গুণ করে।
\(\Rightarrow bx-ay+k=0\) যেখানে \(ad=k\); \(k\) যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
\(\therefore bx-ay+k=0, \ (1)\) নং সরলরেখার উপর লম্ব যে কোনো সরলরেখার সমীকরণ।

নির্দিষ্ট সরলরেখাটি,
\(ax+by+c=0 ........(1)\)
\(\Rightarrow by=-ax-c\)
\(\Rightarrow y=-\frac{a}{b}x-\frac{c}{b}\)
\(\therefore (1)\) এর ঢাল \(=-\frac{a}{b}\)
\(\therefore (1)\) এর উপর লম্ব সরলরেখার ঢাল \(=\frac{b}{a}\) হবে।
ফলে \((1)\) নং সরলরেখার উপর লম্ব যে কোনো সরলরেখার সমীকরণ \(y=\frac{b}{a}x+d\)
\(\Rightarrow y=\frac{bx}{a}+d\)
\(\Rightarrow y=\frac{bx+ad}{a}\)
\(\Rightarrow ay=bx+ad\)
\(\Rightarrow -bx+ay-ad=0\)
\(\Rightarrow bx-ay+ad=0\) ➜ উভয় পার্শে \(-1\) গুণ করে।
\(\Rightarrow bx-ay+k=0\) যেখানে \(ad=k\); \(k\) যে কোনো বাস্তব সংখ্যা। ইহাকে ইচ্ছামূলক ধ্রুবক (Arbitrary Constant) ও বলা হয়ে থাকে।
\(\therefore bx-ay+k=0, \ (1)\) নং সরলরেখার উপর লম্ব যে কোনো সরলরেখার সমীকরণ।
তিনটি সরলরেখার সমবিন্দু হওয়ার বা এক বিন্দুতে মিলিত হওয়ার শর্ত
The condition of three straight lines meeting at a point
ধরি, সরলরেখা তিনটি,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
\((1)\) , \((2)\) , \((3)\) নং সরলরেখাত্রয় সমবিন্দু হবে যদি,
\(\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|=0\)
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
\((1)\) , \((2)\) , \((3)\) নং সরলরেখাত্রয় সমবিন্দু হবে যদি,
\(\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|=0\)
প্রমাণঃ
ধরি, সরলরেখা তিনটি , 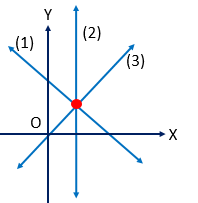
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
\((2)\) ও \((3)\) ( বজ্রগুণ পদ্ধতিতে ) সমাধান করি,
\(\frac{x}{b_{2}c_{3}-b_{3}c_{2}}=\frac{y}{a_{3}c_{2}-a_{2}c_{3}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\Rightarrow \frac{x}{b_{2}c_{3}-b_{3}c_{2}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}, \ \frac{y}{a_{3}c_{2}-a_{2}c_{3}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\Rightarrow x=\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}, \ y=\frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\therefore (2)\) ও \((3)\) এর ছেদবিন্দু \(P(\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}, \frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}})\)
শর্তমতে ,\(P\) বিন্দুটি \((1)\) নং সমীকরণকে সিদ্ধ করবে।
\(a_{1}\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}+b_{1}\frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}}+c_{1}=0\)
\(\Rightarrow \frac{a_{1}(b_{2}c_{3}-b_{3}c_{2})}{a_{2}b_{3}-a_{3}b_{2}}+\frac{b_{1}(a_{3}c_{2}-a_{2}c_{3})}{a_{2}b_{3}-a_{3}b_{2}}+c_{1}=0\)
\(\Rightarrow a_{1}(b_{2}c_{3}-b_{3}c_{2})+b_{1}(a_{3}c_{2}-a_{2}c_{3})+c_{1}(a_{2}b_{3}-a_{3}b_{2})=0\) ➜ উভয় পার্শে \(a_{2}b_{3}-a_{3}b_{2}\) গুণ করে
\(\Rightarrow \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত।

\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
\((2)\) ও \((3)\) ( বজ্রগুণ পদ্ধতিতে ) সমাধান করি,
\(\frac{x}{b_{2}c_{3}-b_{3}c_{2}}=\frac{y}{a_{3}c_{2}-a_{2}c_{3}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\Rightarrow \frac{x}{b_{2}c_{3}-b_{3}c_{2}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}, \ \frac{y}{a_{3}c_{2}-a_{2}c_{3}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\Rightarrow x=\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}, \ y=\frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\therefore (2)\) ও \((3)\) এর ছেদবিন্দু \(P(\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}, \frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}})\)
শর্তমতে ,\(P\) বিন্দুটি \((1)\) নং সমীকরণকে সিদ্ধ করবে।
\(a_{1}\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}+b_{1}\frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}}+c_{1}=0\)
\(\Rightarrow \frac{a_{1}(b_{2}c_{3}-b_{3}c_{2})}{a_{2}b_{3}-a_{3}b_{2}}+\frac{b_{1}(a_{3}c_{2}-a_{2}c_{3})}{a_{2}b_{3}-a_{3}b_{2}}+c_{1}=0\)
\(\Rightarrow a_{1}(b_{2}c_{3}-b_{3}c_{2})+b_{1}(a_{3}c_{2}-a_{2}c_{3})+c_{1}(a_{2}b_{3}-a_{3}b_{2})=0\) ➜ উভয় পার্শে \(a_{2}b_{3}-a_{3}b_{2}\) গুণ করে
\(\Rightarrow \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত।
শর্টকাট টেকনিক
Shortcut Technique
কোন সমতলে \(y=mx+c\) একটি সরলরেখার সমীকরণ-
সরলরেখাটির ঢাল বা নতি \(=m\)
সরলরেখাটি দ্বারা \(y\) অক্ষের খন্ডিতাংশ \(=c\)
\(y=mx+c\) সরলরেখার উপর লম্ব রেখার ঢাল বা নতি \(=-\frac{1}{m}\)
উদাহরণঃ \(y=-4x+2\) একটি সরলরেখার সমীকরণ-
সরলরেখাটির ঢাল \(=-4\)
সরলরেখাটি দ্বারা \(y\) অক্ষের খন্ডিতাংশ \(=2\)
\(y=-4x+2\) সরলরেখার উপর লম্ব রেখার ঢাল বা নতি \(=-\frac{1}{-4}\)
\(=\frac{1}{4}\)
কোন সমতলে \(ax+by+c=0\) একটি সরলরেখার সমীকরণ-
সরলরেখাটির ঢাল \(=-\frac{a}{b}\)
\(ax+by+c=0\) সরলরেখার উপর লম্ব রেখার ঢাল বা নতি \(=\frac{b}{a}\)
উদাহরণঃ \(3x-4y+7=0\) একটি সরলরেখার সমীকরণ-
সরলরেখাটির ঢাল \(=-\frac{3}{-4}\)
\(=\frac{3}{4}\)
\(3x-4y+7=0\) সরলরেখার উপর লম্ব রেখার ঢাল বা নতি \(=\frac{-4}{3}\)
\(=-\frac{4}{3}\)
\(ax+by+c=0\) সরলরেখার সমান্তরাল এবং \((\alpha, \beta)\) বিন্দুগামী সরলরেখার সমীকরণ,
\(ax+by=a\alpha+b\beta\)
উদাহরণঃ \(-5x+7y-9=0\) সরলরেখার সমান্তরাল এবং \((2, -1)\) বিন্দুগামী সরলরেখার সমীকরণ,
\(-5x+7y=-5\times2+7\times-1\)
\(\Rightarrow -5x+7y=-10-7\)
\(\Rightarrow -5x+7y=-17\)
\(\Rightarrow 5x-7y=17\)
\(\therefore 5x-7y-17=0\)
\(ax+by+c=0\) সরলরেখার উপর লম্ব এবং \((\alpha, \beta)\) বিন্দুগামী সরলরেখার সমীকরণ,
\(bx-ay=b\alpha-a\beta\)
উদাহরণঃ \(5x-3y-9=0\) সরলরেখার উপর লম্ব এবং \((-2, 3)\) বিন্দুগামী সরলরেখার সমীকরণ,
\(3x+5y=3\times-2+5\times3\)
\(\Rightarrow 3x+5y=-6+15\)
\(\Rightarrow 3x+5y=9\)
\(\therefore 3x+5y-9=0\)
\((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার সমীকরণ,
\((y_{1}-y_{2})x-(x_{1}-x_{2})y=(y_{1}-y_{2})x_{x}-(x_{1}-x_{2})y_{1}\)
\((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার লম্বসমদ্বিখন্ডকের সমীকরণ,
\((x_{1}-x_{2})x+(y_{1}-y_{2})y=\frac{1}{2}(x_{1}^2+y_{1}^2-x_{2}^2-y_{2}^2)\)
উদাহরণঃ \((5, -2)\) এবং \((-1, 3)\) বিন্দুদ্বয়ের সংযোগ সরলরেখার লম্বসমদ্বিখন্ডকের সমীকরণ,
\((5+1)x+(-2-3)y=\frac{1}{2}\{5^2+(-2)^2-(-1)^2-3^2\}\)
\(\Rightarrow 6x-5y=\frac{1}{2}\{25+4-1-9\}\)
\(\Rightarrow 6x-5y=\frac{1}{2}\{29-10\}\)
\(\Rightarrow 12x-10y=19\)
\(\therefore 12x-10y-19=0\)
\((x_{1}, y_{1})\) বিন্দুগামী এবং \((x_{2}, y_{2})\) ও \((x_{3}, y_{3})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার সমান্তরাল রেখার সমীকরণ,
\(y-y_{1}=\frac{y_{2}-y_{3}}{x_{2}-x_{3}}(x-x_{1})\)
উদাহরণঃ \((5, -2)\) বিন্দুগামী এবং \((-1, 3)\) ও \((4, 5)\) বিন্দুদ্বয়ের সংযোগ সরলরেখার সমান্তরাল রেখার সমীকরণ,
\(y+2=\frac{3-5}{-1-4}(x-5)\)
\(\Rightarrow y+2=\frac{-2}{-5}(x-5)\)
\(\Rightarrow -5y-10=-2x+10\)
\(\Rightarrow -5y-10+2x-10=0\)
\(\therefore 2x-5y-20=0\)
\((x_{1}, y_{1})\) বিন্দুগামী এবং \((x_{2}, y_{2})\) ও \((x_{3}, y_{3})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার উপর লম্বরেখার সমীকরণ,
\(y-y_{1}=-\frac{x_{2}-x_{3}}{y_{2}-y_{3}}(x-x_{1})\)
উদাহরণঃ \((5, -2)\) বিন্দুগামী এবং \((-1, 3)\) ও \((4, 5)\) বিন্দুদ্বয়ের সংযোগ সরলরেখার সমান্তরাল রেখার সমীকরণ,
\(y+2=-\frac{-1-4}{3-5}(x-5)\)
\(\Rightarrow y+2=-\frac{-5}{-2}(x-5)\)
\(\Rightarrow y+2=\frac{-5}{2}(x-5)\)
\(\Rightarrow 2y+4=-5x+25\)
\(\Rightarrow 5x-25+2y+4=0\)
\(\therefore 5x+2y-21=0\)
\((\alpha, \beta)\) বিন্দুগামী এবং \(a_{1}x+b_{1}y+c_{1}=0\) ও \(a_{2}x+b_{2}y+c_{2}=0\) এর ছেদবিন্দুগামী রেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{a_{1}\alpha+b_{1}\beta+c_{1}}=\frac{a_{2}x+b_{2}y+c_{2}}{a_{2}\alpha+b_{2}\beta+c_{2}}\)
উদাহরণঃ \((5, -2)\) বিন্দুগামী এবং \(4x+3y-5=0\) ও \(2x-5y+7=0\) এর ছেদবিন্দুগামী রেখার সমীকরণ,
\(\frac{4x+3y-5}{4\times5+3\times-2-5}=\frac{2x-5y+7}{2\times5-5\times-2+7}\)
\(\Rightarrow \frac{4x+3y-5}{20-6-5}=\frac{2x-5y+7}{10+10+7}\)
\(\Rightarrow \frac{4x+3y-5}{9}=\frac{2x-5y+7}{27}\)
\(\Rightarrow 4x+3y-5=\frac{2x-5y+7}{3}\)
\(\Rightarrow 12x+9y-15=2x-5y+7\)
\(\Rightarrow 12x+9y-15-2x+5y-7=0\)
\(\Rightarrow 10x+14y-22=0\)
\(\Rightarrow 2(5x+7y-11)=0\)
\(\therefore 5x+7y-11=0\)
সরলরেখাটির ঢাল বা নতি \(=m\)
সরলরেখাটি দ্বারা \(y\) অক্ষের খন্ডিতাংশ \(=c\)
\(y=mx+c\) সরলরেখার উপর লম্ব রেখার ঢাল বা নতি \(=-\frac{1}{m}\)
উদাহরণঃ \(y=-4x+2\) একটি সরলরেখার সমীকরণ-
সরলরেখাটির ঢাল \(=-4\)
সরলরেখাটি দ্বারা \(y\) অক্ষের খন্ডিতাংশ \(=2\)
\(y=-4x+2\) সরলরেখার উপর লম্ব রেখার ঢাল বা নতি \(=-\frac{1}{-4}\)
\(=\frac{1}{4}\)
কোন সমতলে \(ax+by+c=0\) একটি সরলরেখার সমীকরণ-
সরলরেখাটির ঢাল \(=-\frac{a}{b}\)
\(ax+by+c=0\) সরলরেখার উপর লম্ব রেখার ঢাল বা নতি \(=\frac{b}{a}\)
উদাহরণঃ \(3x-4y+7=0\) একটি সরলরেখার সমীকরণ-
সরলরেখাটির ঢাল \(=-\frac{3}{-4}\)
\(=\frac{3}{4}\)
\(3x-4y+7=0\) সরলরেখার উপর লম্ব রেখার ঢাল বা নতি \(=\frac{-4}{3}\)
\(=-\frac{4}{3}\)
\(ax+by+c=0\) সরলরেখার সমান্তরাল এবং \((\alpha, \beta)\) বিন্দুগামী সরলরেখার সমীকরণ,
\(ax+by=a\alpha+b\beta\)
উদাহরণঃ \(-5x+7y-9=0\) সরলরেখার সমান্তরাল এবং \((2, -1)\) বিন্দুগামী সরলরেখার সমীকরণ,
\(-5x+7y=-5\times2+7\times-1\)
\(\Rightarrow -5x+7y=-10-7\)
\(\Rightarrow -5x+7y=-17\)
\(\Rightarrow 5x-7y=17\)
\(\therefore 5x-7y-17=0\)
\(ax+by+c=0\) সরলরেখার উপর লম্ব এবং \((\alpha, \beta)\) বিন্দুগামী সরলরেখার সমীকরণ,
\(bx-ay=b\alpha-a\beta\)
উদাহরণঃ \(5x-3y-9=0\) সরলরেখার উপর লম্ব এবং \((-2, 3)\) বিন্দুগামী সরলরেখার সমীকরণ,
\(3x+5y=3\times-2+5\times3\)
\(\Rightarrow 3x+5y=-6+15\)
\(\Rightarrow 3x+5y=9\)
\(\therefore 3x+5y-9=0\)
\((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার সমীকরণ,
\((y_{1}-y_{2})x-(x_{1}-x_{2})y=(y_{1}-y_{2})x_{x}-(x_{1}-x_{2})y_{1}\)
\((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার লম্বসমদ্বিখন্ডকের সমীকরণ,
\((x_{1}-x_{2})x+(y_{1}-y_{2})y=\frac{1}{2}(x_{1}^2+y_{1}^2-x_{2}^2-y_{2}^2)\)
উদাহরণঃ \((5, -2)\) এবং \((-1, 3)\) বিন্দুদ্বয়ের সংযোগ সরলরেখার লম্বসমদ্বিখন্ডকের সমীকরণ,
\((5+1)x+(-2-3)y=\frac{1}{2}\{5^2+(-2)^2-(-1)^2-3^2\}\)
\(\Rightarrow 6x-5y=\frac{1}{2}\{25+4-1-9\}\)
\(\Rightarrow 6x-5y=\frac{1}{2}\{29-10\}\)
\(\Rightarrow 12x-10y=19\)
\(\therefore 12x-10y-19=0\)
\((x_{1}, y_{1})\) বিন্দুগামী এবং \((x_{2}, y_{2})\) ও \((x_{3}, y_{3})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার সমান্তরাল রেখার সমীকরণ,
\(y-y_{1}=\frac{y_{2}-y_{3}}{x_{2}-x_{3}}(x-x_{1})\)
উদাহরণঃ \((5, -2)\) বিন্দুগামী এবং \((-1, 3)\) ও \((4, 5)\) বিন্দুদ্বয়ের সংযোগ সরলরেখার সমান্তরাল রেখার সমীকরণ,
\(y+2=\frac{3-5}{-1-4}(x-5)\)
\(\Rightarrow y+2=\frac{-2}{-5}(x-5)\)
\(\Rightarrow -5y-10=-2x+10\)
\(\Rightarrow -5y-10+2x-10=0\)
\(\therefore 2x-5y-20=0\)
\((x_{1}, y_{1})\) বিন্দুগামী এবং \((x_{2}, y_{2})\) ও \((x_{3}, y_{3})\) বিন্দুদ্বয়ের সংযোগ সরলরেখার উপর লম্বরেখার সমীকরণ,
\(y-y_{1}=-\frac{x_{2}-x_{3}}{y_{2}-y_{3}}(x-x_{1})\)
উদাহরণঃ \((5, -2)\) বিন্দুগামী এবং \((-1, 3)\) ও \((4, 5)\) বিন্দুদ্বয়ের সংযোগ সরলরেখার সমান্তরাল রেখার সমীকরণ,
\(y+2=-\frac{-1-4}{3-5}(x-5)\)
\(\Rightarrow y+2=-\frac{-5}{-2}(x-5)\)
\(\Rightarrow y+2=\frac{-5}{2}(x-5)\)
\(\Rightarrow 2y+4=-5x+25\)
\(\Rightarrow 5x-25+2y+4=0\)
\(\therefore 5x+2y-21=0\)
\((\alpha, \beta)\) বিন্দুগামী এবং \(a_{1}x+b_{1}y+c_{1}=0\) ও \(a_{2}x+b_{2}y+c_{2}=0\) এর ছেদবিন্দুগামী রেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{a_{1}\alpha+b_{1}\beta+c_{1}}=\frac{a_{2}x+b_{2}y+c_{2}}{a_{2}\alpha+b_{2}\beta+c_{2}}\)
উদাহরণঃ \((5, -2)\) বিন্দুগামী এবং \(4x+3y-5=0\) ও \(2x-5y+7=0\) এর ছেদবিন্দুগামী রেখার সমীকরণ,
\(\frac{4x+3y-5}{4\times5+3\times-2-5}=\frac{2x-5y+7}{2\times5-5\times-2+7}\)
\(\Rightarrow \frac{4x+3y-5}{20-6-5}=\frac{2x-5y+7}{10+10+7}\)
\(\Rightarrow \frac{4x+3y-5}{9}=\frac{2x-5y+7}{27}\)
\(\Rightarrow 4x+3y-5=\frac{2x-5y+7}{3}\)
\(\Rightarrow 12x+9y-15=2x-5y+7\)
\(\Rightarrow 12x+9y-15-2x+5y-7=0\)
\(\Rightarrow 10x+14y-22=0\)
\(\Rightarrow 2(5x+7y-11)=0\)
\(\therefore 5x+7y-11=0\)

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004