এ অধ্যায়ের পাঠ্যসূচী।
- সমান্তরাল সরলরেখা (Parallel Straight lines)
- সরলরেখার ধনাত্মক ও ঋণাত্মক পার্শ (Positive and negative sides of a straight line with respect to the origin)
- কোনো সরলরেখার সাপেক্ষে মূলবিন্দুর অবস্থান (The position of the origin relative to a straight line)
- লম্ব দূরত্ব (Perpendicular Distance)
- মূলবিন্দু হতে একটি সরলরেখার লম্ব দূরত্ব (Perpendicular distance of a straight line from the origin)
- দুইটি সমান্তরাল সরলরেখার মধ্যবর্তী লম্ব দূরত্ব (Perpendicular distance between two parallel straight lines)
- দুইটি পরস্পরছেদী সরলরেখার অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ (Equation of the bisector of the angle included by two intersecting straight lines)
- ত্রিভুজের অন্তঃকেন্দ্র ও অন্তঃব্যাসার্ধ নির্ণয় (Finding incenter and inradius of a triangle)
- কোনো সরলরেখার সমান্তরাল এবং নির্দিষ্ট একক দূরবর্তী সরলরেখার সমীকরণ (Equation of a straight line parallel to and a given unit distance from a straight line)
- কোনো সরলরেখার উপরোস্থ নির্দিষ্ট বিন্দু হতে নির্দিষ্ট একক দূরবর্তী লম্ব রেখার সমীকরণ (The equation of a perpendicular line given a given unit distance from a given point on a straight line)
- দুইটি নির্দিষ্ট বিন্দুর একটি নির্দিষ্ট সরলরেখা সাপেক্ষে অবস্থান (The position of two fixed points relative to a fixed straight line)
- দুইটি পরস্পরছেদী সরলরেখার অন্তর্ভুক্ত স্থুলকোণের বা, সূক্ষ্মকোণের সমদ্বিখন্ডকসরলরেখাদ্বয়ের সমীকরণ (Equation of two straight lines bisector of the angle included by two straight lines)
- একটি নির্দিষ্ট বিন্দুধারী কোণ ও নির্দিষ্ট বিন্দুধারী কোণের সমদ্বিখন্ডিক সরলরেখারসমীকরণ (Equation of an isosceles straight line about a given acute angle)
- মূলবিন্দুধারী কোণ ও মূলবিন্দুধারী কোণের সমদ্বিখন্ডিক সরলরেখার সমীকরণ (Equations of isosceles straight lines of angles with focal points)
- সরলরেখার প্রতিচ্ছবি (The image of a straight line)
- দুইটি পরস্পরছেদী সরলরেখার সাপেক্ষে একটি নির্দিষ্ট বিন্দুর অবস্থান (The position of a fixed point relative to two intersecting straight lines)
- একটি ত্রিভুজের শীর্ষবিন্দুর সাপেক্ষে এর কোণগুলি সম্পর্কে ধারণা জ্ঞাপন (Conceptualize the angles of a triangle with respect to its vertices)
- একটি ত্রিভুজের বাহুরগুলির সাপেক্ষে এর কোণগুলি সম্পর্কে ধারণা জ্ঞাপন (Conceptualize the angles of a triangle with respect to its sides)
- অধ্যায় \(3H\)-এর উদাহরণসমুহ
- অধ্যায় \(3H\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(3H\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3H\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3H\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3H\) / \(Q.5\)-এর সৃজনশীল প্রশ্নসমূহ
- অধ্যায় \(3H\) / \(Q.6\)-এর ভর্তি পরীক্ষায় আসা প্রশ্নসমূহ
সমান্তরাল সরলরেখা
Parallel Straight lines
যদি একই সমতলে অবস্থিত দুই বা ততোধিক সরলরেখা চলার পথে পরস্পরকে কোথাও স্পর্শ না করে সর্বদা সমান দূরত্ব বজায় রেখে চলে তবে তাদেরকে সমান্তরাল সরলরেখা বলা হয়।
আবার, প্রত্যেক সরলরেখা তার নিজের সমান্তরাল। এক্ষেত্রে সমান্তরাল সরলরেখাগুলি মিলিত হয়।
সমান্তরাল রেখাগুলি নির্দিষ্ট পরিস্থিতিতে, দেখা করতে পারে।
 দৃষ্টান্তঃ একই সমতলে অবস্থিত দীর্ঘ্য সোজা দুইটি রেল-লাইন অসীম দূরত্বে মিলিত হয়েছে বলে দেখা যায়। অর্থাৎ কাল্পনিকভাবে সমান্তরাল সরলরেখাগুলি মিলিত হতে পারে।
দৃষ্টান্তঃ একই সমতলে অবস্থিত দীর্ঘ্য সোজা দুইটি রেল-লাইন অসীম দূরত্বে মিলিত হয়েছে বলে দেখা যায়। অর্থাৎ কাল্পনিকভাবে সমান্তরাল সরলরেখাগুলি মিলিত হতে পারে।
আবার, প্রত্যেক সরলরেখা তার নিজের সমান্তরাল। এক্ষেত্রে সমান্তরাল সরলরেখাগুলি মিলিত হয়।
সমান্তরাল রেখাগুলি নির্দিষ্ট পরিস্থিতিতে, দেখা করতে পারে।

মূলবিন্দু সাপেক্ষে সরলরেখার ধনাত্মক ও ঋণাত্মক পার্শ
Positive and negative sides of a straight line with respect to the origin
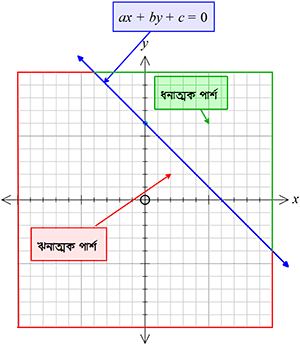
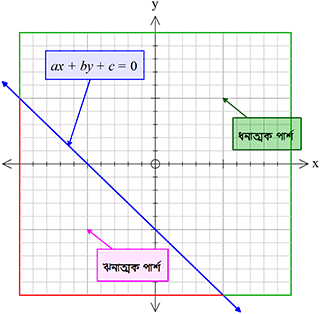 \(ax+by+c=0\) সরলরেখার যে কোনো পার্শের যে কোনো বিন্দু \((x_{1}, y_{1})\) এর জন্য যদি \(ax_{1}+by_{1}+c\) সর্বদা ধনাত্মক হয় তবে ঐ পার্শটিকে \((x_{1}, y_{1})\) বিন্দু সাপেক্ষে সরলরেখাটির ধনাত্মক পার্শ এবং তার বিপরীত পার্শটিকে ঋনাত্মক পার্শ বলা হয়।
\(ax+by+c=0\) সরলরেখার যে কোনো পার্শের যে কোনো বিন্দু \((x_{1}, y_{1})\) এর জন্য যদি \(ax_{1}+by_{1}+c\) সর্বদা ধনাত্মক হয় তবে ঐ পার্শটিকে \((x_{1}, y_{1})\) বিন্দু সাপেক্ষে সরলরেখাটির ধনাত্মক পার্শ এবং তার বিপরীত পার্শটিকে ঋনাত্মক পার্শ বলা হয়।
কোনো সরলরেখার সাপেক্ষে মূলবিন্দুর অবস্থান
The position of the origin relative to a straight line
যদি \(ax+by+c=0\) সমীকরণের \(c\) ধনাত্মক হয়, তবে মূলবিন্দু \(ax+by+c=0\) সরলরেখার ধনাত্মক পার্শে এবং \(c\) ঋনাত্মক হলে, মূলবিন্দু রেখাটির ঋনাত্মক পার্শে অবস্থিত হবে।
মূলবিন্দু ও অপর যে কোনো বিন্দুর অবস্থানঃ
\(ax+by+c=0\) সরলরেখার ক্ষেত্রে, যদি \(ax_{1}+by_{1}+c\) এবং \(c\) একই চিহ্নবিশিষ্ট হয় তবে মূলবিন্দু এবং \((x_{1}, y_{1})\) বিন্দু সরলরেখাটির একই পার্শে অবস্থিত হবে। আর যদি বিপরীত চিহ্নবিশিষ্ট হয় তবে মূলবিন্দু এবং \((x_{1}, y_{1})\) বিন্দু সরলরেখাটির বিপরীত পার্শে অবস্থিত হবে।
মূলবিন্দু ও অপর যে কোনো বিন্দুর অবস্থানঃ
\(ax+by+c=0\) সরলরেখার ক্ষেত্রে, যদি \(ax_{1}+by_{1}+c\) এবং \(c\) একই চিহ্নবিশিষ্ট হয় তবে মূলবিন্দু এবং \((x_{1}, y_{1})\) বিন্দু সরলরেখাটির একই পার্শে অবস্থিত হবে। আর যদি বিপরীত চিহ্নবিশিষ্ট হয় তবে মূলবিন্দু এবং \((x_{1}, y_{1})\) বিন্দু সরলরেখাটির বিপরীত পার্শে অবস্থিত হবে।
লম্ব দূরত্ব
Perpendicular Distance
\((x_{1}, y_{1})\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব,
\(d=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(d=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
প্রমাণঃ
ধরি,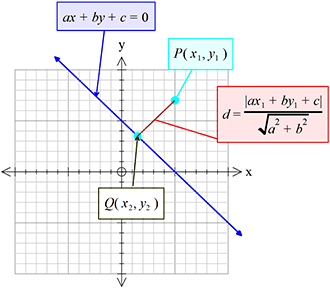
\(P(x_{1}, y_{1})\)
\(ax+by+c=0 ..............(1)\)
\((1)\) এর উপর যে কোনো বিন্দু \(Q(x_{2}, y_{2})\)
\((1)\) এর ঢাল \(m_{1}=-\frac{a}{b}\)
\(PQ\) এর ঢাল \(m_{2}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
শর্তমতে,
\((1)\) সরলরেখা এবং \(PQ\) রেখাংশ পরস্পর লম্ব।
\(\therefore m_{1}\times m_{2}=-1\)
\(\Rightarrow -\frac{a}{b}\times \frac{y_{1}-y_{2}}{x_{1}-x_{2}}=-1\)
\(\Rightarrow \frac{ay_{1}-ay_{2}}{bx_{1}-bx_{2}}=1\)
\(\Rightarrow ay_{1}-ay_{2}=bx_{1}-bx_{2}\)
\(\Rightarrow ay_{1}-ay_{2}-bx_{1}+bx_{2}=0\)
\(\Rightarrow bx_{2}-bx_{1}+ay_{1}-ay_{2}=0 ...........(2)\)
আবার,
\(Q\) বিন্দুটি \((1)\) এর উপর অবস্থিত।
\(\therefore ax_{2}+by_{2}+c=0 ......(3)\)
\((2)\) ও \((3)\) সমাধান করে \(x_{2}\) ও \(y_{2}\) এর মান নির্ণয় করি।
\((2)\times b+(3)\times a\) এর সাহায্যে,
\(b^{2}x_{2}-b^{2}x_{1}+aby_{1}-aby_{2}+a^{2}x_{2}+aby_{2}+ac=0\)
\(\Rightarrow b^{2}x_{2}-b^{2}x_{1}+aby_{1}+a^{2}x_{2}+ac=0\)
\(\Rightarrow x_{2}(b^{2}+a^{2})=b^{2}x_{1}-aby_{1}-ac\)
\(\therefore x_{2}=\frac{b^{2}x_{1}-aby_{1}-ac}{b^{2}+a^{2}}\)
\((2)\times a-(3)\times b\) এর সাহায্যে,
\(ab^{2}x_{2}-abx_{1}+a^{2}y_{1}-a^{2}y_{2}-abx_{2}-b^{2}y_{2}-bc=0\)
\(\Rightarrow -abx_{1}+a^{2}y_{1}-a^{2}y_{2}-b^{2}y_{2}-bc=0\)
\(\Rightarrow -y_{2}(a^{2}+b^{2})=abx_{1}-a^{2}y_{1}+bc\)
\(\therefore y_{2}=-\frac{abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}}\)
এখন,
লম্ব দূরত্ব
\(d=PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(x_{1}-\frac{b^{2}x_{1}-aby_{1}-ac}{b^{2}+a^{2}})^{2}+(y_{1}+\frac{abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}})^{2}}\)
\(=\sqrt{(\frac{b^{2}x_{1}+a^{2}x_{1}-b^{2}x_{1}+aby_{1}+ac}{a^{2}+b^{2}})^{2}+(\frac{a^{2}y_{1}+b^{2}y_{1}+abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}})^{2}}\)
\(=\sqrt{\frac{(a^{2}x_{1}+aby_{1}+ac)^{2}}{(a^{2}+b^{2})^{2}}+\frac{(b^{2}y_{1}+abx_{1}+bc)^{2}}{(a^{2}+b^{2})^{2}}}\)
\(=\sqrt{\frac{a^{2}(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}+\frac{b^{2}(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}}\)
\(=\sqrt{\frac{(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}\times (a^{2}+b^{2})}\)
\(=\sqrt{\frac{(ax_{1}+by_{1}+c)^{2}}{a^{2}+b^{2}}}\)
\(=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore \) লম্ব দূরত্ব \(d=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)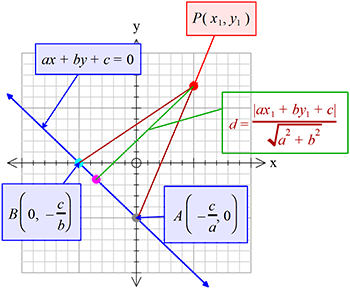
\(P(x_{1}, y_{1})\)
\(ax+by+c=0 .........(1)\)
\(P\) হতে \((1)\) এর লম্ব দূরত্ব \(d\).
\((1)\) হতে,
\(ax+by=-c\)
\(\Rightarrow \frac{ax}{-c}+\frac{by}{-c}=\frac{-c}{-c}\) ➜ উভয় পার্শে \(-c\) ভাগ করে
\(\Rightarrow \frac{x}{\frac{-c}{a}}+\frac{y}{\frac{-c}{b}}=1\)
\(\therefore (1)\) নং সরলরেখা অক্ষদ্বয়কে যথাক্রমে \(A(-\frac{c}{a}, 0)\) ও \(B(0, -\frac{c}{b})\) বিন্দুতে ছেদ করে।
এখন,
\(\triangle ABP=\frac{1}{2}\left|\begin{array}{c}-\frac{c}{a} \ \ \ \ 0 \ \ \ \ \ x_{1} \ \ \ -\frac{c}{a}\\ 0 \ -\frac{c}{b} \ \ \ \ \ y_{1} \ \ \ \ \ \ \ \ 0\end{array}\right|\)
\(=\frac{1}{2}\{(\frac{c^{2}}{ab}-0)+(0+\frac{cx_{1}}{b})+(0+\frac{cy_{1}}{a})\}\)
\(=\frac{1}{2}\{\frac{c^{2}}{ab}+\frac{cx_{1}}{b}+\frac{cy_{1}}{a}\}\)
\(=\frac{1}{2}\times \frac{c}{ab}\{c+ax_{1}+by_{1}\}\)
\(=\frac{c}{2ab}(ax_{1}+by_{1}+c)\)
\(AB=\sqrt{(-\frac{c}{a}-0)^{2}+(0+\frac{c}{b})^{2}}\)
\(=\sqrt{\frac{c^{2}}{a^{2}}+\frac{c^{2}}{b^{2}}}\)
\(=\sqrt{\frac{c^{2}(a^{2}+b^{2})}{a^{2}b^{2}}}\)
\(=\frac{c}{ab}\sqrt{a^{2}+b^{2}}\)
কিন্তু,
\(\frac{1}{2}\times AB\times d=\triangle ABP\)
\(\Rightarrow \frac{1}{2}\times \frac{c}{ab}\sqrt{a^{2}+b^{2}}\times d=\frac{c}{2ab}(ax_{1}+by_{1}+c)\)
\(\Rightarrow d=\frac{c}{2ab}(ax_{1}+by_{1}+c)\times 2\times \frac{ab}{c\sqrt{a^{2}+b^{2}}}\)
\(\Rightarrow d=\frac{\left| ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
ধরি,

\(P(x_{1}, y_{1})\)
\(ax+by+c=0 ..............(1)\)
\((1)\) এর উপর যে কোনো বিন্দু \(Q(x_{2}, y_{2})\)
\((1)\) এর ঢাল \(m_{1}=-\frac{a}{b}\)
\(PQ\) এর ঢাল \(m_{2}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
শর্তমতে,
\((1)\) সরলরেখা এবং \(PQ\) রেখাংশ পরস্পর লম্ব।
\(\therefore m_{1}\times m_{2}=-1\)
\(\Rightarrow -\frac{a}{b}\times \frac{y_{1}-y_{2}}{x_{1}-x_{2}}=-1\)
\(\Rightarrow \frac{ay_{1}-ay_{2}}{bx_{1}-bx_{2}}=1\)
\(\Rightarrow ay_{1}-ay_{2}=bx_{1}-bx_{2}\)
\(\Rightarrow ay_{1}-ay_{2}-bx_{1}+bx_{2}=0\)
\(\Rightarrow bx_{2}-bx_{1}+ay_{1}-ay_{2}=0 ...........(2)\)
আবার,
\(Q\) বিন্দুটি \((1)\) এর উপর অবস্থিত।
\(\therefore ax_{2}+by_{2}+c=0 ......(3)\)
\((2)\) ও \((3)\) সমাধান করে \(x_{2}\) ও \(y_{2}\) এর মান নির্ণয় করি।
\((2)\times b+(3)\times a\) এর সাহায্যে,
\(b^{2}x_{2}-b^{2}x_{1}+aby_{1}-aby_{2}+a^{2}x_{2}+aby_{2}+ac=0\)
\(\Rightarrow b^{2}x_{2}-b^{2}x_{1}+aby_{1}+a^{2}x_{2}+ac=0\)
\(\Rightarrow x_{2}(b^{2}+a^{2})=b^{2}x_{1}-aby_{1}-ac\)
\(\therefore x_{2}=\frac{b^{2}x_{1}-aby_{1}-ac}{b^{2}+a^{2}}\)
\((2)\times a-(3)\times b\) এর সাহায্যে,
\(ab^{2}x_{2}-abx_{1}+a^{2}y_{1}-a^{2}y_{2}-abx_{2}-b^{2}y_{2}-bc=0\)
\(\Rightarrow -abx_{1}+a^{2}y_{1}-a^{2}y_{2}-b^{2}y_{2}-bc=0\)
\(\Rightarrow -y_{2}(a^{2}+b^{2})=abx_{1}-a^{2}y_{1}+bc\)
\(\therefore y_{2}=-\frac{abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}}\)
এখন,
লম্ব দূরত্ব
\(d=PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(x_{1}-\frac{b^{2}x_{1}-aby_{1}-ac}{b^{2}+a^{2}})^{2}+(y_{1}+\frac{abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}})^{2}}\)
\(=\sqrt{(\frac{b^{2}x_{1}+a^{2}x_{1}-b^{2}x_{1}+aby_{1}+ac}{a^{2}+b^{2}})^{2}+(\frac{a^{2}y_{1}+b^{2}y_{1}+abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}})^{2}}\)
\(=\sqrt{\frac{(a^{2}x_{1}+aby_{1}+ac)^{2}}{(a^{2}+b^{2})^{2}}+\frac{(b^{2}y_{1}+abx_{1}+bc)^{2}}{(a^{2}+b^{2})^{2}}}\)
\(=\sqrt{\frac{a^{2}(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}+\frac{b^{2}(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}}\)
\(=\sqrt{\frac{(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}\times (a^{2}+b^{2})}\)
\(=\sqrt{\frac{(ax_{1}+by_{1}+c)^{2}}{a^{2}+b^{2}}}\)
\(=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore \) লম্ব দূরত্ব \(d=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
বিকল্প পদ্ধতিঃ
ধরি,
\(P(x_{1}, y_{1})\)
\(ax+by+c=0 .........(1)\)
\(P\) হতে \((1)\) এর লম্ব দূরত্ব \(d\).
\((1)\) হতে,
\(ax+by=-c\)
\(\Rightarrow \frac{ax}{-c}+\frac{by}{-c}=\frac{-c}{-c}\) ➜ উভয় পার্শে \(-c\) ভাগ করে
\(\Rightarrow \frac{x}{\frac{-c}{a}}+\frac{y}{\frac{-c}{b}}=1\)
\(\therefore (1)\) নং সরলরেখা অক্ষদ্বয়কে যথাক্রমে \(A(-\frac{c}{a}, 0)\) ও \(B(0, -\frac{c}{b})\) বিন্দুতে ছেদ করে।
এখন,
\(\triangle ABP=\frac{1}{2}\left|\begin{array}{c}-\frac{c}{a} \ \ \ \ 0 \ \ \ \ \ x_{1} \ \ \ -\frac{c}{a}\\ 0 \ -\frac{c}{b} \ \ \ \ \ y_{1} \ \ \ \ \ \ \ \ 0\end{array}\right|\)
\(=\frac{1}{2}\{(\frac{c^{2}}{ab}-0)+(0+\frac{cx_{1}}{b})+(0+\frac{cy_{1}}{a})\}\)
\(=\frac{1}{2}\{\frac{c^{2}}{ab}+\frac{cx_{1}}{b}+\frac{cy_{1}}{a}\}\)
\(=\frac{1}{2}\times \frac{c}{ab}\{c+ax_{1}+by_{1}\}\)
\(=\frac{c}{2ab}(ax_{1}+by_{1}+c)\)
\(AB=\sqrt{(-\frac{c}{a}-0)^{2}+(0+\frac{c}{b})^{2}}\)
\(=\sqrt{\frac{c^{2}}{a^{2}}+\frac{c^{2}}{b^{2}}}\)
\(=\sqrt{\frac{c^{2}(a^{2}+b^{2})}{a^{2}b^{2}}}\)
\(=\frac{c}{ab}\sqrt{a^{2}+b^{2}}\)
কিন্তু,
\(\frac{1}{2}\times AB\times d=\triangle ABP\)
\(\Rightarrow \frac{1}{2}\times \frac{c}{ab}\sqrt{a^{2}+b^{2}}\times d=\frac{c}{2ab}(ax_{1}+by_{1}+c)\)
\(\Rightarrow d=\frac{c}{2ab}(ax_{1}+by_{1}+c)\times 2\times \frac{ab}{c\sqrt{a^{2}+b^{2}}}\)
\(\Rightarrow d=\frac{\left| ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
মূলবিন্দু হতে একটি সরলরেখার লম্ব দূরত্ব
Perpendicular distance of a straight line from the origin
মূলবিন্দু তথা \(O(0, 0)\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব,
\(d=\frac{\left|c \right|}{\sqrt{a^{2}+b^{2}}}\)
\(d=\frac{\left|c \right|}{\sqrt{a^{2}+b^{2}}}\)
প্রমাণঃ
ধরি,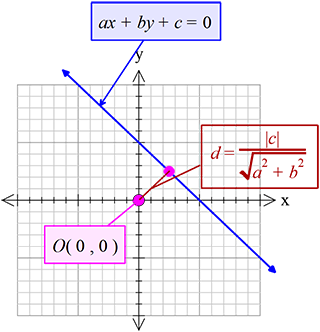
মূলবিন্দু তথা \(O(0, 0)\)
\(ax+by+c=0 ...........(1)\)
\(O(0, 0)\) হতে \((1)\) এর লম্ব দূরত্ব \(d=\frac{\left|a.0+b.0+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\Rightarrow d=\frac{\left|0+0+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore d=\frac{\left|c\right|}{\sqrt{a^{2}+b^{2}}}\)
ধরি,

মূলবিন্দু তথা \(O(0, 0)\)
\(ax+by+c=0 ...........(1)\)
\(O(0, 0)\) হতে \((1)\) এর লম্ব দূরত্ব \(d=\frac{\left|a.0+b.0+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\Rightarrow d=\frac{\left|0+0+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore d=\frac{\left|c\right|}{\sqrt{a^{2}+b^{2}}}\)
দুইটি সমান্তরাল সরলরেখার মধ্যবর্তী লম্ব দূরত্ব
Perpendicular distance between two parallel straight lines
\(ax+by+c_{1}=0\) ও \(ax+by+c_{2}=0\) সরলরেখাদ্বয়ের মধ্যবর্তী লম্ব দূরত্ব,
\(d=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
\(d=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
প্রমাণঃ
ধরি,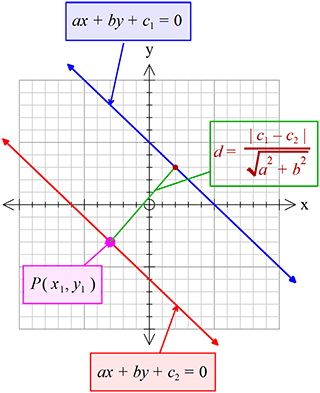
\(ax+by+c_{1}=0 ......(1)\)
\(ax+by+c_{2}=0 ......(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী লম্ব দূরত্ব \(d\)
\(p(x_{1}, y_{1})\) বিন্দুটি \((2)\) এর উপর অবস্থিত,
\(\therefore ax_{1}+by_{1}+c_{2}=0\)
\(\Rightarrow ax_{1}+by_{1}=-c_{2}...........(3)\)
আবার,
\(p(x_{1}, y_{1})\) বিন্দু হতে \((1)\) এর লম্ব দূরত্ব,
\(d=\frac{\left|ax_{1}+bx_{1}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}\)
\(=\frac{\left|-c_{2}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}\) ➜ \((3)\) এর সাহায্যে
\(=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore d=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
ধরি,

\(ax+by+c_{1}=0 ......(1)\)
\(ax+by+c_{2}=0 ......(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী লম্ব দূরত্ব \(d\)
\(p(x_{1}, y_{1})\) বিন্দুটি \((2)\) এর উপর অবস্থিত,
\(\therefore ax_{1}+by_{1}+c_{2}=0\)
\(\Rightarrow ax_{1}+by_{1}=-c_{2}...........(3)\)
আবার,
\(p(x_{1}, y_{1})\) বিন্দু হতে \((1)\) এর লম্ব দূরত্ব,
\(d=\frac{\left|ax_{1}+bx_{1}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}\)
\(=\frac{\left|-c_{2}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}\) ➜ \((3)\) এর সাহায্যে
\(=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore d=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
দুইটি পরস্পরছেদী সরলরেখার অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ
Equation of the bisector of the angle included by two intersecting straight lines
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=\pm \frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=\pm \frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).
প্রমাণঃ
ধরি,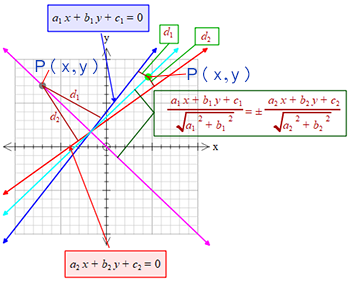
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের উপর যে কোনো বিন্দু \(P(x, y)\)।
\(P(x, y)\) হতে \((1)\) এর লম্ব দূরত্ব \(d_{1}=\frac{\left| a_{1}x+b_{1}y+c_{1} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}\)
\(P(x, y)\) হতে \((2)\) এর লম্ব দূরত্ব \(d_{2}=\frac{\left| a_{2}x+b_{2}y+c_{2} \right|}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
শর্তমতে,
\(d_{1}=d_{2}\)
\(\Rightarrow \frac{\left| a_{1}x+b_{1}y+c_{1} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\frac{\left| a_{2}x+b_{2}y+c_{2} \right|}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
\(\Rightarrow \frac{ a_{1}x+b_{1}y+c_{1} }{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\pm \frac{ a_{2}x+b_{2}y+c_{2} }{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
ইহাই নির্ণেয় সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ।
ধরি,

\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের উপর যে কোনো বিন্দু \(P(x, y)\)।
\(P(x, y)\) হতে \((1)\) এর লম্ব দূরত্ব \(d_{1}=\frac{\left| a_{1}x+b_{1}y+c_{1} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}\)
\(P(x, y)\) হতে \((2)\) এর লম্ব দূরত্ব \(d_{2}=\frac{\left| a_{2}x+b_{2}y+c_{2} \right|}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
শর্তমতে,
\(d_{1}=d_{2}\)
\(\Rightarrow \frac{\left| a_{1}x+b_{1}y+c_{1} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\frac{\left| a_{2}x+b_{2}y+c_{2} \right|}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
\(\Rightarrow \frac{ a_{1}x+b_{1}y+c_{1} }{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\pm \frac{ a_{2}x+b_{2}y+c_{2} }{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
ইহাই নির্ণেয় সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ।
ত্রিভুজের অন্তঃকেন্দ্র ও অন্তঃব্যাসার্ধ নির্ণয়
Finding incenter and inradius of a triangle
\(\triangle ABC\) এর শীর্ষবিন্দু তিনটি \((x_{1}, y_{1})\), \((x_{2}, y_{2})\) এবং \((x_{3}, y_{3})\) এবং বাহুগুলি \(BC=a, \ CA=b, \ AB=c \) হলে, এর অন্তঃকেন্দ্র,
\(I\left(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c}\right)\).
এবং অন্তঃব্যাসার্ধ
\(r=\frac{|\delta_{ABC}|}{a+b+c}\).
\(I\left(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c}\right)\).
এবং অন্তঃব্যাসার্ধ
\(r=\frac{|\delta_{ABC}|}{a+b+c}\).
প্রমাণঃ
ধরি,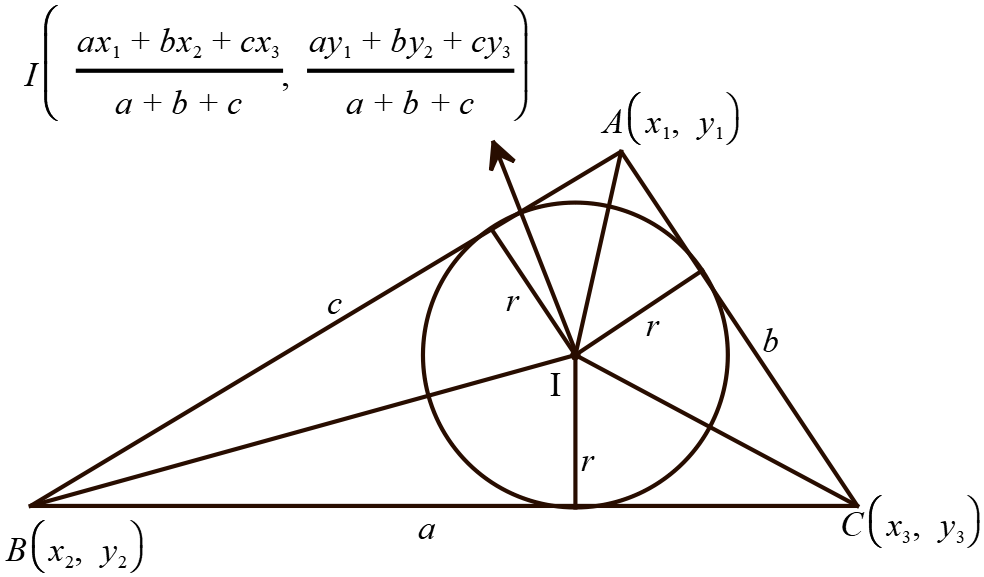
\(\triangle ABC\) এর \(\angle A\), \(\angle B\) কোণ দুইটির সমদ্বিখন্ডক \(AD\) ও \(BE\) পরস্পর \(I\) বিন্দুতে ছেদ করে যা ত্রিভুজের অন্তঃকেন্দ্র।
শর্তমতে,
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{c}{b}\)
\(\Rightarrow \frac{BD}{DC}=\frac{c}{b}\)
\(\Rightarrow BD:DC=c:b\)
\(\therefore D(\frac{bx_{2}+cx_{3}}{b+c}, \frac{by_{2}+cy_{3}}{b+c})\)
আবার,
\(\frac{AI}{ID}=\frac{AB}{BD}=\frac{AC}{CD}=\frac{AB+AC}{BD+CD}\)
\(\Rightarrow \frac{AI}{ID}=\frac{c+b}{BC}\)
\(\Rightarrow \frac{AI}{ID}=\frac{c+b}{a}\)
\(\Rightarrow AI:ID=(c+b):a\)
\(\therefore I(\frac{(b+c).\frac{bx_{2}+cx_{3}}{b+c}+a.x_{1}}{a+b+c}, \frac{(b+c).\frac{by_{2}+cy_{3}}{b+c}+a.y_{1}}{a+b+c})\)
\(\Rightarrow I(\frac{bx_{2}+cx_{3}+ax_{1}}{a+b+c}, \frac{by_{2}+cy_{3}+ay_{1}}{a+b+c})\)
\(\Rightarrow I(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c})\).
\(\therefore \triangle ABC \) এর অন্তঃকেন্দ্র \(I(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c})\). আবার,
\(\triangle{ABC}=\frac{1}{2}|\delta_{ABC}|=\frac{1}{2}\left|\begin{array}{c}x_{1}&x_{2}&x_{3}&x_{1}\\ y_{1}&y_{2}&y_{3}&y_{1}\end{array}\right|\)
যেখানে, \(\delta_{ABC}=\left|\begin{array}{c}x_{1}&x_{2}&x_{3}&x_{1}\\ y_{1}&y_{2}&y_{3}&y_{1}\end{array}\right|\)
এখন, \(\triangle{BIC}+\triangle{AIC}+\triangle{AIB}=\triangle{ABC}\)
\(\Rightarrow \frac{1}{2}BC\times{r}+\frac{1}{2}AC\times{r}+\frac{1}{2}AB\times{r}=\frac{1}{2}\delta_{ABC}\)
\(\Rightarrow \frac{1}{2}r(BC+AC+AB)=\frac{1}{2}|\delta_{ABC}|\)
\(\Rightarrow r(BC+AC+AB)=|\delta_{ABC}|\)
\(\Rightarrow r=\frac{|\delta_{ABC}|}{BC+AC+AB}\)
\(\therefore r=\frac{|\delta_{ABC}|}{a+b+c}\)
ধরি,

\(\triangle ABC\) এর \(\angle A\), \(\angle B\) কোণ দুইটির সমদ্বিখন্ডক \(AD\) ও \(BE\) পরস্পর \(I\) বিন্দুতে ছেদ করে যা ত্রিভুজের অন্তঃকেন্দ্র।
শর্তমতে,
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{c}{b}\)
\(\Rightarrow \frac{BD}{DC}=\frac{c}{b}\)
\(\Rightarrow BD:DC=c:b\)
\(\therefore D(\frac{bx_{2}+cx_{3}}{b+c}, \frac{by_{2}+cy_{3}}{b+c})\)
আবার,
\(\frac{AI}{ID}=\frac{AB}{BD}=\frac{AC}{CD}=\frac{AB+AC}{BD+CD}\)
\(\Rightarrow \frac{AI}{ID}=\frac{c+b}{BC}\)
\(\Rightarrow \frac{AI}{ID}=\frac{c+b}{a}\)
\(\Rightarrow AI:ID=(c+b):a\)
\(\therefore I(\frac{(b+c).\frac{bx_{2}+cx_{3}}{b+c}+a.x_{1}}{a+b+c}, \frac{(b+c).\frac{by_{2}+cy_{3}}{b+c}+a.y_{1}}{a+b+c})\)
\(\Rightarrow I(\frac{bx_{2}+cx_{3}+ax_{1}}{a+b+c}, \frac{by_{2}+cy_{3}+ay_{1}}{a+b+c})\)
\(\Rightarrow I(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c})\).
\(\therefore \triangle ABC \) এর অন্তঃকেন্দ্র \(I(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c})\). আবার,
\(\triangle{ABC}=\frac{1}{2}|\delta_{ABC}|=\frac{1}{2}\left|\begin{array}{c}x_{1}&x_{2}&x_{3}&x_{1}\\ y_{1}&y_{2}&y_{3}&y_{1}\end{array}\right|\)
যেখানে, \(\delta_{ABC}=\left|\begin{array}{c}x_{1}&x_{2}&x_{3}&x_{1}\\ y_{1}&y_{2}&y_{3}&y_{1}\end{array}\right|\)
এখন, \(\triangle{BIC}+\triangle{AIC}+\triangle{AIB}=\triangle{ABC}\)
\(\Rightarrow \frac{1}{2}BC\times{r}+\frac{1}{2}AC\times{r}+\frac{1}{2}AB\times{r}=\frac{1}{2}\delta_{ABC}\)
\(\Rightarrow \frac{1}{2}r(BC+AC+AB)=\frac{1}{2}|\delta_{ABC}|\)
\(\Rightarrow r(BC+AC+AB)=|\delta_{ABC}|\)
\(\Rightarrow r=\frac{|\delta_{ABC}|}{BC+AC+AB}\)
\(\therefore r=\frac{|\delta_{ABC}|}{a+b+c}\)
কোনো সরলরেখার সমান্তরাল এবং নির্দিষ্ট একক দূরবর্তী সরলরেখার সমীকরণ
Equation of a straight line parallel to and a given unit distance from a straight line
\(ax+by+c=0\) সরলরেখার সমান্তরাল এবং \(d\) একক দূরবর্তী সরলরেখার সমীকরণঃ
\(ax+by+c\pm d\sqrt{a^{2}+b^{2}}=0\).
\(ax+by+c\pm d\sqrt{a^{2}+b^{2}}=0\).
প্রমাণঃ
ধরি,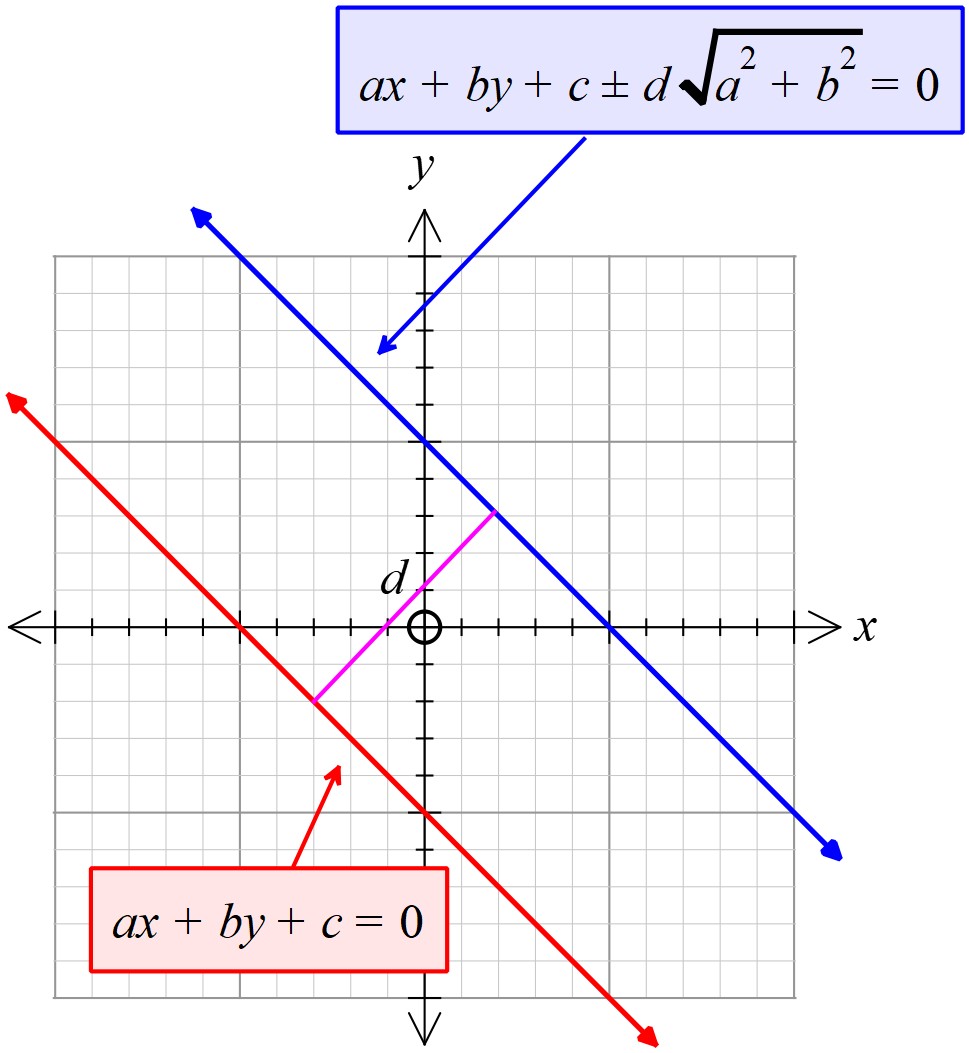
\(ax+by+c=0 ............(1)\)
\((1)\) এর সমান্তরাল যে কোনো সরলরেখার সমীকরণ,
\(ax+by+k=0 ............(2)\) ➜ \(k\) যে কোন বাস্তব সংখ্যা।
\((1)\) ও \((2)\) এর মধ্যবর্তী দূরত্ব \(=\frac{|k-c|}{\sqrt{a^{2}+b^{2}}}\)
শর্তমতে,
\(\frac{|k-c|}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow \pm \frac{k-c}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow \frac{k-c}{\sqrt{a^{2}+b^{2}}}=\pm d\)
\(\Rightarrow k-c=\pm d \sqrt{a^{2}+b^{2}}\)
\(\therefore k=c\pm d \sqrt{a^{2}+b^{2}}\)
\(k\) এর মান \((2)\) এ বসিয়ে,
\(ax+by+c\pm d \sqrt{a^{2}+b^{2}}=0\)
ইহাই নির্ণেয় সরলরেখার সমীকরণ।
ধরি,

\(ax+by+c=0 ............(1)\)
\((1)\) এর সমান্তরাল যে কোনো সরলরেখার সমীকরণ,
\(ax+by+k=0 ............(2)\) ➜ \(k\) যে কোন বাস্তব সংখ্যা।
\((1)\) ও \((2)\) এর মধ্যবর্তী দূরত্ব \(=\frac{|k-c|}{\sqrt{a^{2}+b^{2}}}\)
শর্তমতে,
\(\frac{|k-c|}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow \pm \frac{k-c}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow \frac{k-c}{\sqrt{a^{2}+b^{2}}}=\pm d\)
\(\Rightarrow k-c=\pm d \sqrt{a^{2}+b^{2}}\)
\(\therefore k=c\pm d \sqrt{a^{2}+b^{2}}\)
\(k\) এর মান \((2)\) এ বসিয়ে,
\(ax+by+c\pm d \sqrt{a^{2}+b^{2}}=0\)
ইহাই নির্ণেয় সরলরেখার সমীকরণ।
কোনো সরলরেখার উপরোস্থ নির্দিষ্ট বিন্দু হতে নির্দিষ্ট একক দূরবর্তী লম্ব রেখার সমীকরণ
The equation of a perpendicular line given a given unit distance from a given point on a straight line
\(ax+by+c=0\) সরলরেখার উপরোস্থ \((x_{1}, y_{1})\) বিন্দু হতে \(d\) একক দূরবর্তী লম্ব রেখার সমীকরণঃ
\(b(x-x_{1})-a(y-y_{1})\pm d\sqrt{a^{2}+b^{2}}=0\).
\(b(x-x_{1})-a(y-y_{1})\pm d\sqrt{a^{2}+b^{2}}=0\).
প্রমাণঃ
ধরি,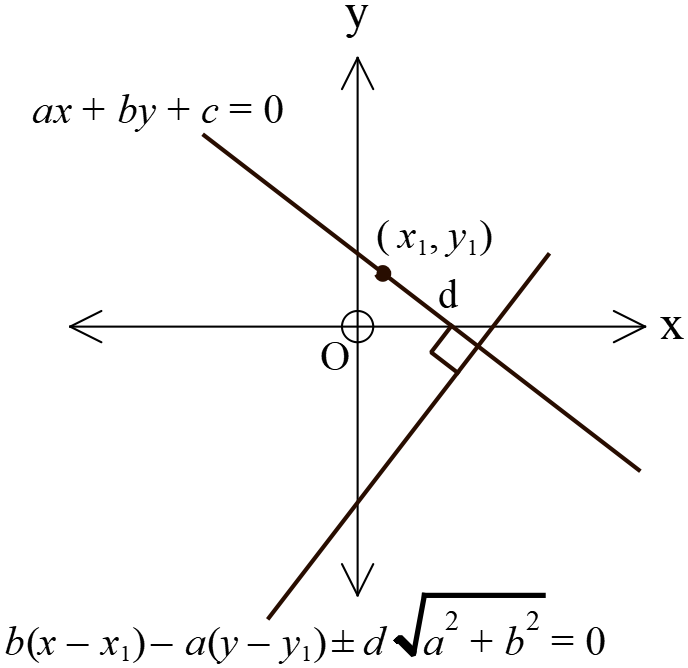
\(ax+by+c=0 ............(1)\)
\((1)\) এর উপর লম্ব যে কোনো সরলরেখার সমীকরণ,
\(bx-ay+k=0 ............(2)\) ➜ \(k\) যে কোন বাস্তব সংখ্যা।
\((x_{1}, y_{1})\) বিন্দু হতে \((2)\) এর লম্ব দূরত্ব \(=\frac{|bx_{1}-ay_{1}+k|}{\sqrt{a^{2}+b^{2}}}\)
শর্তমতে,
\(\frac{|bx_{1}-ay_{1}+k|}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow |bx_{1}-ay_{1}+k|=d\sqrt{a^{2}+b^{2}}\)
\(\Rightarrow bx_{1}-ay_{1}+k=\pm d\sqrt{a^{2}+b^{2}}\)
\(\therefore k=ay_{1}-bx_{1}\pm d\sqrt{a^{2}+b^{2}}\)
\(k\) এর মান \((2)\) এ বসিয়ে,
\(bx-ay+ay_{1}-bx_{1}\pm d\sqrt{a^{2}+b^{2}}=0\)
\(\therefore b(x-x_{1})-a(y-y_{1})\pm d\sqrt{a^{2}+b^{2}}=0\)
ইহাই নির্ণেয় সরলরেখার সমীকরণ।
ধরি,

\(ax+by+c=0 ............(1)\)
\((1)\) এর উপর লম্ব যে কোনো সরলরেখার সমীকরণ,
\(bx-ay+k=0 ............(2)\) ➜ \(k\) যে কোন বাস্তব সংখ্যা।
\((x_{1}, y_{1})\) বিন্দু হতে \((2)\) এর লম্ব দূরত্ব \(=\frac{|bx_{1}-ay_{1}+k|}{\sqrt{a^{2}+b^{2}}}\)
শর্তমতে,
\(\frac{|bx_{1}-ay_{1}+k|}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow |bx_{1}-ay_{1}+k|=d\sqrt{a^{2}+b^{2}}\)
\(\Rightarrow bx_{1}-ay_{1}+k=\pm d\sqrt{a^{2}+b^{2}}\)
\(\therefore k=ay_{1}-bx_{1}\pm d\sqrt{a^{2}+b^{2}}\)
\(k\) এর মান \((2)\) এ বসিয়ে,
\(bx-ay+ay_{1}-bx_{1}\pm d\sqrt{a^{2}+b^{2}}=0\)
\(\therefore b(x-x_{1})-a(y-y_{1})\pm d\sqrt{a^{2}+b^{2}}=0\)
ইহাই নির্ণেয় সরলরেখার সমীকরণ।
দুইটি নির্দিষ্ট বিন্দুর একটি নির্দিষ্ট সরলরেখা সাপেক্ষে অবস্থান
The position of two fixed points relative to a fixed straight line
\((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) বিন্দুদ্বয় \(ax+by+c=0\) সরলরেখার একই পার্শে অথবা বিপরীত পার্শে অবস্থিত কিনা তা নির্ণয়ঃ
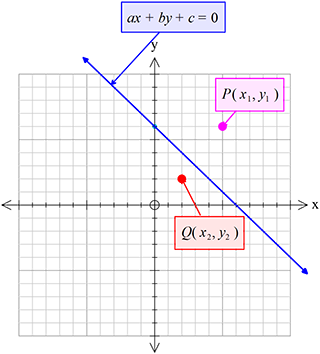 \(f(x_{1},y_{1})\) এবং \(f(x_{2},y_{2})\) রাশিদ্বয় বিপরীত চিহ্ন বিশিষ্ট হলে, \(P\) ও \(Q\) বিন্দুদ্বয় \((1)\) নং সরলরেখার বিপরীত পার্শে অবস্থান করবে।
\(f(x_{1},y_{1})\) এবং \(f(x_{2},y_{2})\) রাশিদ্বয় বিপরীত চিহ্ন বিশিষ্ট হলে, \(P\) ও \(Q\) বিন্দুদ্বয় \((1)\) নং সরলরেখার বিপরীত পার্শে অবস্থান করবে।
ধরি,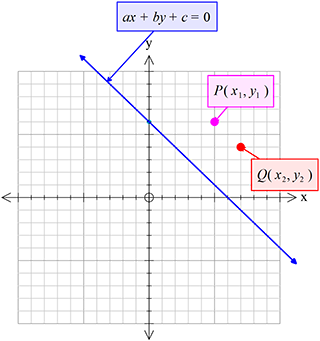
\(f(x,y)\equiv ax+by+c=0 ......(1)\)
\(P(x_{1}, y_{1})\)
\(Q(x_{2}, y_{2})\)
\(f(x_{1},y_{1})\) এবং \(f(x_{2},y_{2})\) রাশিদ্বয় একই চিহ্ন বিশিষ্ট হলে, \(P\) ও \(Q\) বিন্দুদ্বয় \((1)\) নং সরলরেখার একই পার্শে অবস্থান করবে।

\(f(x,y)\equiv ax+by+c=0 ......(1)\)
\(P(x_{1}, y_{1})\)
\(Q(x_{2}, y_{2})\)
\(f(x_{1},y_{1})\) এবং \(f(x_{2},y_{2})\) রাশিদ্বয় একই চিহ্ন বিশিষ্ট হলে, \(P\) ও \(Q\) বিন্দুদ্বয় \((1)\) নং সরলরেখার একই পার্শে অবস্থান করবে।
 \(f(x_{1},y_{1})\) এবং \(f(x_{2},y_{2})\) রাশিদ্বয় বিপরীত চিহ্ন বিশিষ্ট হলে, \(P\) ও \(Q\) বিন্দুদ্বয় \((1)\) নং সরলরেখার বিপরীত পার্শে অবস্থান করবে।
\(f(x_{1},y_{1})\) এবং \(f(x_{2},y_{2})\) রাশিদ্বয় বিপরীত চিহ্ন বিশিষ্ট হলে, \(P\) ও \(Q\) বিন্দুদ্বয় \((1)\) নং সরলরেখার বিপরীত পার্শে অবস্থান করবে।
দুইটি সরলরেখার অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ
Equation of two straight lines bisector of the angle included by two straight lines
দুইটি পরস্পরছেদী সরলরেখার অন্তর্ভুক্ত স্থুলকোণের বা, সূক্ষ্মকোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ।
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)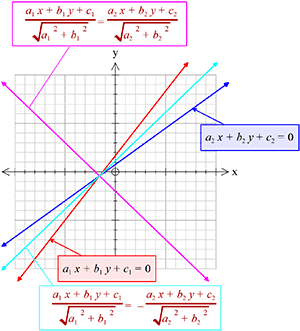
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
যদি,\( (a_{1}a_{2}+b_{1}b_{2})\gt{0}\) হয়, তবে
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত স্থুলকোণের সমদ্বিখন্ডক সরলরেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).
এবং
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত সূক্ষ্মকোণের সমদ্বিখন্ডক সরলরেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=-\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).

\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
যদি,\( (a_{1}a_{2}+b_{1}b_{2})\gt{0}\) হয়, তবে
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত স্থুলকোণের সমদ্বিখন্ডক সরলরেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).
এবং
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত সূক্ষ্মকোণের সমদ্বিখন্ডক সরলরেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=-\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).
যদি,\((a_{1}a_{2}+b_{1}b_{2})\lt{0}\) হয়, তবে
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত স্থুলকোণের সমদ্বিখন্ডক সরলরেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=-\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).
এবং
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত সূক্ষ্মকোণের সমদ্বিখন্ডক সরলরেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).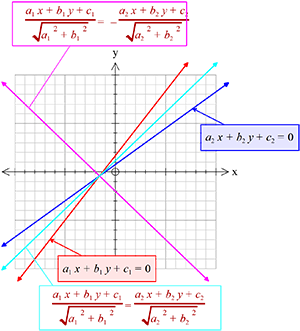
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত স্থুলকোণের সমদ্বিখন্ডক সরলরেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=-\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).
এবং
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত সূক্ষ্মকোণের সমদ্বিখন্ডক সরলরেখার সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).

একটি নির্দিষ্ট বিন্দুধারী কোণের সমদ্বিখন্ডিক সরলরেখার সমীকরণ
Equation of an isosceles straight line about a given acute angle
একটি নির্দিষ্ট বিন্দুধারী কোণ ও নির্দিষ্ট বিন্দুধারী কোণের সমদ্বিখন্ডিক সরলরেখার সমীকরণ।
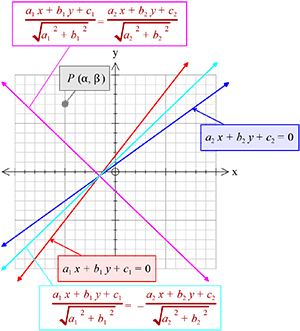 \(f(x,y)\equiv a_{1}x+b_{1}y+c_{1}=0\)
\(f(x,y)\equiv a_{1}x+b_{1}y+c_{1}=0\)\(g(x,y)\equiv a_{2}x+b_{2}y+c_{2}=0\)
যদি,\( f(\alpha,\beta)\times g(\alpha,\beta)\gt{0}\) হয়, তবে \(f(x,y)\) ও \(g(x,y)\) রেখাদ্বয়ের অন্তর্ভুক্ত কোণদ্বয়ের \(P(\alpha,\beta)\) বিন্দুধারী কোণটির সমদ্বিখন্ডকের সমীকরণ হবে,
যদি, \( f(\alpha,\beta)\times g(\alpha,\beta)\lt{0} \) হয়, তবে
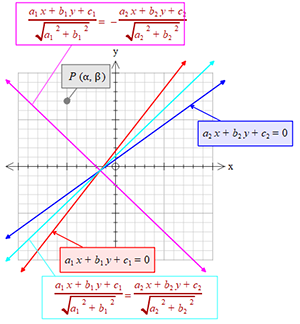 \(f(x,y)\) ও \(g(x,y)\) রেখাদ্বয়ের অন্তর্ভুক্ত কোণদ্বয়ের \(P(\alpha,\beta)\) বিন্দুধারী কোণটির সমদ্বিখন্ডকের সমীকরণ হবে,
\(f(x,y)\) ও \(g(x,y)\) রেখাদ্বয়ের অন্তর্ভুক্ত কোণদ্বয়ের \(P(\alpha,\beta)\) বিন্দুধারী কোণটির সমদ্বিখন্ডকের সমীকরণ হবে,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=-\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\)
 \(f(x,y)\) ও \(g(x,y)\) রেখাদ্বয়ের অন্তর্ভুক্ত কোণদ্বয়ের \(P(\alpha,\beta)\) বিন্দুধারী কোণটির সমদ্বিখন্ডকের সমীকরণ হবে,
\(f(x,y)\) ও \(g(x,y)\) রেখাদ্বয়ের অন্তর্ভুক্ত কোণদ্বয়ের \(P(\alpha,\beta)\) বিন্দুধারী কোণটির সমদ্বিখন্ডকের সমীকরণ হবে,\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=-\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\)
মূলবিন্দুধারী কোণের সমদ্বিখন্ডিক সরলরেখার সমীকরণ
Equations of isosceles straight lines of angles with focal points
মূলবিন্দুধারী কোণ ও মূলবিন্দুধারী কোণের সমদ্বিখন্ডিক সরলরেখার সমীকরণ।
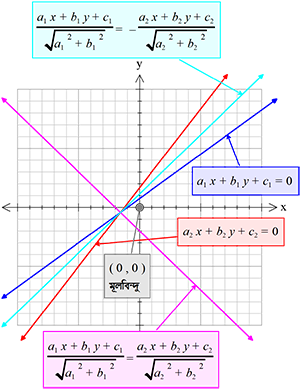 \(a_{1}x+b_{1}y+c_{1}=0 ......(1)\)
\(a_{1}x+b_{1}y+c_{1}=0 ......(1)\)\(a_{2}x+b_{2}y+c_{2}=0 .......(2)\)
যদি,\( c_{1}\) ও \( c_{2}\) সমচিহ্নযুক্ত হয়, তবে
\((1)\) ও \((2)\) রেখাদ্বয়ের অন্তর্ভুক্ত কোণদ্বয়ের মূলবিন্দুধারী কোণটির সমদ্বিখন্ডকের সমীকরণ হবে,
যদি, \( c_{1}\) ও \( c_{2}\) বিপরীত চিহ্নযুক্ত হয়, তবে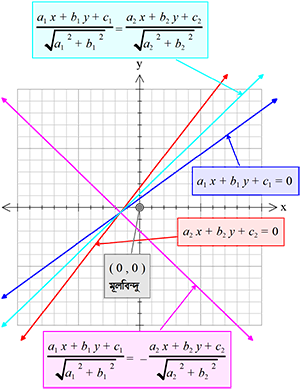
\((1)\) ও \((2)\) রেখাদ্বয়ের অন্তর্ভুক্ত কোণদ্বয়ের মূলবিন্দুধারী কোণটির সমদ্বিখন্ডকের সমীকরণ হবে,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=-\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\)

\((1)\) ও \((2)\) রেখাদ্বয়ের অন্তর্ভুক্ত কোণদ্বয়ের মূলবিন্দুধারী কোণটির সমদ্বিখন্ডকের সমীকরণ হবে,
সরলরেখার প্রতিচ্ছবি
The image of a straight line
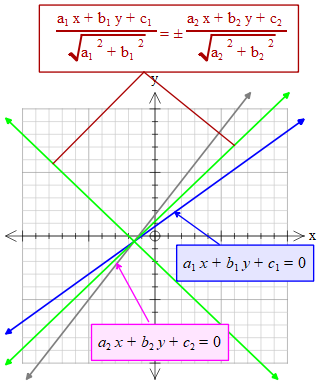 \(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=\pm \frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\) রেখাদ্বয়ের সাপেক্ষে \(a_{1}x+b_{1}y+c_{1}=0\) ও \(a_{2}x+b_{2}y+c_{2}=0\) রেখা দুইটি পরস্পর প্রতিচ্ছবি
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=\pm \frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\) রেখাদ্বয়ের সাপেক্ষে \(a_{1}x+b_{1}y+c_{1}=0\) ও \(a_{2}x+b_{2}y+c_{2}=0\) রেখা দুইটি পরস্পর প্রতিচ্ছবি
দুইটি পরস্পরছেদী সরলরেখার সাপেক্ষে একটি নির্দিষ্ট বিন্দুর অবস্থান
The position of a fixed point relative to two intersecting straight lines
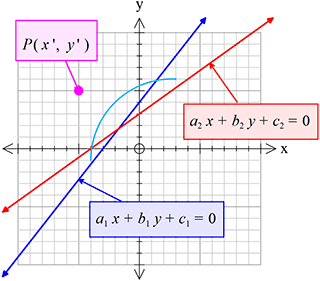 যদি,\((a_{1}\acute{x}+ b_{1}\acute{y}+c_{1})(a_{2}\acute{x}+ b_{2}\acute{y}+c_{2})(a_{1}a_{2}+b_{1}b_{2})\gt{0}\) হয়, তবে
যদি,\((a_{1}\acute{x}+ b_{1}\acute{y}+c_{1})(a_{2}\acute{x}+ b_{2}\acute{y}+c_{2})(a_{1}a_{2}+b_{1}b_{2})\gt{0}\) হয়, তবে\(P(\acute{x}, \acute{y})\) বিন্দুটি \(a_{1}x+b_{1}y+c_{1}=0\) ও \(a_{2}x+b_{2}y+c_{2}=0\) রেখাদ্বয়ের অন্তর্ভুক্ত স্থুলকোণের মধ্যে অবস্থিত হবে।
যদি,\((a_{1}\acute{x}+ b_{1}\acute{y}+c_{1})(a_{2}\acute{x}+ b_{2}\acute{y}+c_{2})(a_{1}a_{2}+b_{1}b_{2})\lt{0}\) হয়, তবে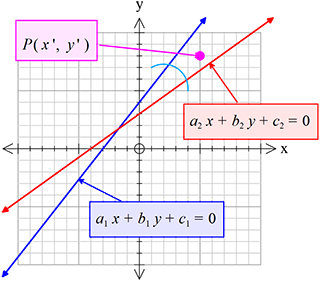
\(P(\acute{x}, \acute{y})\) বিন্দুটি \(a_{1}x+b_{1}y+c_{1}=0\) ও \(a_{2}x+b_{2}y+c_{2}=0\) রেখাদ্বয়ের অন্তর্ভুক্ত সূক্ষ্মকোণের মধ্যে অবস্থিত হবে।

\(P(\acute{x}, \acute{y})\) বিন্দুটি \(a_{1}x+b_{1}y+c_{1}=0\) ও \(a_{2}x+b_{2}y+c_{2}=0\) রেখাদ্বয়ের অন্তর্ভুক্ত সূক্ষ্মকোণের মধ্যে অবস্থিত হবে।
একটি ত্রিভুজের শীর্ষবিন্দুর সাপেক্ষে এর কোণগুলি সম্পর্কে ধারণা জ্ঞাপন
Conceptualize the angles of a triangle with respect to its vertices
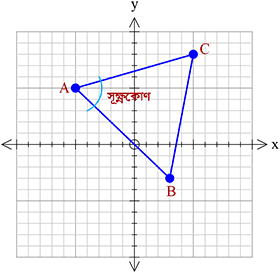 \(ABC\) ত্রিভুজের শীর্ষবিন্দু তিনটি \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\), \(C(x_{3}, y_{3})\)।
\(ABC\) ত্রিভুজের শীর্ষবিন্দু তিনটি \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\), \(C(x_{3}, y_{3})\)।যদি,\( (x_{1}-x_{2})(x_{1}-x_{3})+(y_{1}-y_{2})(y_{1}-y_{3})\gt{0}\) হয়, তবে \(\angle A\) হবে সূক্ষ্মকোণ।
যদি,\( (x_{1}-x_{2})(x_{1}-x_{3})+(y_{1}-y_{2})(y_{1}-y_{3})\lt{0}\) হয়, তবে \(\angle A\) হবে স্থুলকোণ।
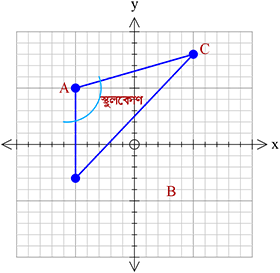

একটি ত্রিভুজের বাহুগুলির সাপেক্ষে এর কোণগুলি সম্পর্কে ধারণা জ্ঞাপন
Conceptualize the angles of a triangle with respect to its sides
 \(ABC\) ত্রিভুজের \(AB\), \(BC\), \(CA\) বাহু তিনটির সমীকরণ যথাক্রমে \(a_{1}x+b_{1}y+c_{1}=0,\) \(a_{2}x+b_{2}y+c_{2}=0,\) \(a_{3}x+b_{3}y+c_{3}=0\)।
\(ABC\) ত্রিভুজের \(AB\), \(BC\), \(CA\) বাহু তিনটির সমীকরণ যথাক্রমে \(a_{1}x+b_{1}y+c_{1}=0,\) \(a_{2}x+b_{2}y+c_{2}=0,\) \(a_{3}x+b_{3}y+c_{3}=0\)।যদি,\(\left|\begin{array}{c}a_{1}&b_{1}\\ a_{2}&b_{2}\end{array}\right|\times\left|\begin{array}{c}a_{2}&b_{2}\\ a_{3}&b_{3}\end{array}\right|\times(a_{1}a_{3}+b_{1}b_{3})\gt{0}\) হয়, তবে \(\angle{A}\) হবে স্থুলকোণ।
যদি,\(\left|\begin{array}{c}a_{1}&b_{1}\\ a_{2}&b_{2}\end{array}\right|\times\left|\begin{array}{c}a_{2}&b_{2}\\ a_{3}&b_{3}\end{array}\right|\times(a_{1}a_{3}+b_{1}b_{3})\lt{0}\) হয়, তবে \(\angle{A}\) হবে সূক্ষ্মকোণ।



- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000009