এ অধ্যায়ের পাঠ্যসূচী।
- ঐতিহাসিক পটভূমি
- কনিকের গঠনগত ব্যাখ্যা (Stractural explanation of Conics)
- সংজ্ঞাসমূহ (Definitions)
- বিভিন্ন প্রকৃতির কনিক (Different types of Conic)
- চিত্রের সাহায্যে কনিক উপস্থাপন (Representation of Conic by diagram)
- কোনোকের এবং সমতলের ছেদবিন্দুর সঞ্চারপথই যে কনিক তা চিত্রের সাহায্যে প্রকাশ (Conic which representing the locus of intersection of cone and a plane by diagram)
- সমতল দ্বারা কোণের ছেদন (Intersection of a Cone by a plane)
- পরাবৃত্তের সমীকরণ সনাক্তকরণ (Identifying the equation of the parabola)
- পরাবৃত্তের সমীকরণ \(y^2=4ax \ (a>0)\) এর বিবরণ
- পরাবৃত্তের সমীকরণ \(x^2=4ay \ (a>0)\) এর বিবরণ
- পরাবৃত্তের সমীকরণ \(y^2=-4ax \ (a>0)\) এর বিবরণ
- পরাবৃত্তের সমীকরণ \(x^2=-4ay \ (a>0)\) এর বিবরণ
- পরাবৃত্তের সমীকরণ \(y^2=4a(x+a) \ (a>0)\) এর বিবরণ
- পরাবৃত্তের সমীকরণ \(y^2=4a(x-a) \ (a>0)\)
- পরাবৃত্তের সমীকরণ \(x=ay^2+by+c\) এর বিবরণ
- পরাবৃত্তের সমীকরণ \(y=ax^2+bx+c\) এর বিবরণ
- পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য (Letus rectum of parabola)
- কনিকের সাধারণ সমীকরণ শনাক্তকরণ (Identification of Conic's general equation)
- কোনো সরলরেখা পরাবৃত্তের স্পর্শক হওয়ার শর্ত (Condition for a straight line to be tangent to a parabola)
- পরাবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুতে স্পর্শকের সমীকরণ (Equation of the tangent at a given point on the parabola)
- পরাবৃত্তের জ্যা এর সমীকরণ যার মধ্যবিন্দু দেয়া আছে (Equation of the chord of a parabola whose midpoint is given)
- অধ্যায় \(6A\)-এর উদাহরণসমুহ
- অধ্যায় \(6A\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(6A\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(6A\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(6A\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
ঐতিহাসিক পটভূমি
Historical Background

Manaechmus
(৩৮০-৩২০ খৃষ্টপুর্ব)
কোণক দ্বারা সমতলে বক্ররেখার ছেদাংশের বিভিন্ন অংশকে পরাবৃত্ত, উপবৃত্ত ও অধিবৃত্ত নামকরণ করেন।
একটি স্থির বিন্দু ও একটি সরলরেখা হতে যে সব বিন্দুর দূরত্বের অনুপাত একটি স্থির রাশি, তাদের সেটকে কনিক বলা হয়। স্থির বিন্দুটিকে উপকেন্দ্র বা ফোকাস, নির্দিষ্ট সরলরেখাকে নিয়ামক বা দিকাক্ষ এবং স্থির রাশিকে উৎকেন্দ্রিকতা (Eccentricity) বলা হয়। স্থির রাশিটিকে \(e\) দ্বারা সূচিত করা হয়। এই স্থির রাশির মানের উপর কনিকের আকৃতি নির্ভশীল।
কনিক পরস্পরছেদী এমন একটি বক্রতা, যা একটি সমতলের কৌণিকতা সৃষ্টি করে এবং যার আকৃতি মোচাকৃতি। সৃষ্টি জগতের অতি কৌতূহলী, আকর্ষণীয় ও দুর্বোধ্য ক্ষেত্র থেকেই মানুষ কনিকের ধারণা লাভ করে আসছে। বাস্তব ও জটিল সংখ্যার স্থানাঙ্ক এবং ম্যাট্রিক্স নির্ণয়ে কনিক ব্যবহৃত হয়। প্রাচীন জ্যামিতিক পদ্ধতিতে এর তিনটি গঠন প্রয়োগ করা হত। যেমনঃ পরাবৃত্ত, উপবৃত্ত এবং অধিবৃত্ত ।
প্রাচীন গণিতবিদ ম্যানাকমাস  ম্যানাকমাস (Manaechmus) (৩৮০-৩২০ খৃষ্টপুর্ব) । ও ইউডক্সাস
ম্যানাকমাস (Manaechmus) (৩৮০-৩২০ খৃষ্টপুর্ব) । ও ইউডক্সাস  ইউডক্সাস (Eudoxus) (৩৯০-৩৩৭ খৃষ্টপুর্ব) গ্রীক গণিতবিদ ও জ্যোতির্বিদ । (Manaechmus & Eudoxus) \(4^{th}\) century-তে প্লেটোর
ইউডক্সাস (Eudoxus) (৩৯০-৩৩৭ খৃষ্টপুর্ব) গ্রীক গণিতবিদ ও জ্যোতির্বিদ । (Manaechmus & Eudoxus) \(4^{th}\) century-তে প্লেটোর  প্লেটো (Plato) (খ্রিষ্টপূর্ব ৪২৭ - খ্রিষ্টপূর্ব ৩৪৭) বিশ্ববিখ্যাত গ্রিক দার্শনিক। তিনি দার্শনিক সক্রেটিসের ছাত্র ছিলেন এবং দার্শনিক এরিস্টটল তার ছাত্র ছিলেন। (Plato) স্কুলে কনিকের এ ত্রিগঠন সংযোজন করেন। Elements গ্রন্থে ইউক্লিড
প্লেটো (Plato) (খ্রিষ্টপূর্ব ৪২৭ - খ্রিষ্টপূর্ব ৩৪৭) বিশ্ববিখ্যাত গ্রিক দার্শনিক। তিনি দার্শনিক সক্রেটিসের ছাত্র ছিলেন এবং দার্শনিক এরিস্টটল তার ছাত্র ছিলেন। (Plato) স্কুলে কনিকের এ ত্রিগঠন সংযোজন করেন। Elements গ্রন্থে ইউক্লিড  ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। (৩০০-২৫০ খ্রিষ্টপূর্ব) কনিক সম্পর্কে বিস্তারিত আলোচনা করেন।এবং পরবর্তীতে "Quadrature of Parabola" গ্রন্থে আর্কিমিডিস
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। (৩০০-২৫০ খ্রিষ্টপূর্ব) কনিক সম্পর্কে বিস্তারিত আলোচনা করেন।এবং পরবর্তীতে "Quadrature of Parabola" গ্রন্থে আর্কিমিডিস  আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। (২৮৭-২১২ খ্রিষ্টপূর্ব) এবং অ্যাপোলোনিয়াস কনিকের প্রথম সিরিজ আকারে আটটি গ্রন্থে কনিক সম্পর্কে মৌলিক ও মূল্যবান তত্ত্ব ও তথ্যাবলির উপস্থাপন করেন। গ্রিক বিজ্ঞানীদের উদ্ভাবিত এসব তথ্য ও উপাত্তকে সপ্তদশ শতাব্দীতে জোহান ক্যাপলার
আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। (২৮৭-২১২ খ্রিষ্টপূর্ব) এবং অ্যাপোলোনিয়াস কনিকের প্রথম সিরিজ আকারে আটটি গ্রন্থে কনিক সম্পর্কে মৌলিক ও মূল্যবান তত্ত্ব ও তথ্যাবলির উপস্থাপন করেন। গ্রিক বিজ্ঞানীদের উদ্ভাবিত এসব তথ্য ও উপাত্তকে সপ্তদশ শতাব্দীতে জোহান ক্যাপলার  জোহান কেপলার (Johannes Kepler) (১৫৭১-১৬৩০) ছিলেন দক্ষিণ পশ্চিম জার্মানির গণিতবিদ ও জ্যোতির্বিদ। কেপলারের প্রিয় বিষয়গুলি ছিল গণিত ও জ্যোতির্বিদ্যা। কেপলারের সবচেয়ে উল্লেখযোগ্য পুস্তকটির নাম ‘নিউ অ্যাসট্রোনমি’, যা প্রকাশের পর বিজ্ঞানীরা জানতে পারলেন, সূর্যের চারদিকে গ্রহরা একটি উপবৃত্তাকার পথে পরিভ্রমণ করছে। (Johannes Kepler) (১৫৭১-১৬৩০) এবং রেনে দেকার্তে
জোহান কেপলার (Johannes Kepler) (১৫৭১-১৬৩০) ছিলেন দক্ষিণ পশ্চিম জার্মানির গণিতবিদ ও জ্যোতির্বিদ। কেপলারের প্রিয় বিষয়গুলি ছিল গণিত ও জ্যোতির্বিদ্যা। কেপলারের সবচেয়ে উল্লেখযোগ্য পুস্তকটির নাম ‘নিউ অ্যাসট্রোনমি’, যা প্রকাশের পর বিজ্ঞানীরা জানতে পারলেন, সূর্যের চারদিকে গ্রহরা একটি উপবৃত্তাকার পথে পরিভ্রমণ করছে। (Johannes Kepler) (১৫৭১-১৬৩০) এবং রেনে দেকার্তে  প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে আধুনিক ফাংশনের ধারণা দেন । (Rene Descartes) (১৫৯৬-১৬৫০) বৈজ্ঞানিকরূপে প্রতিষ্ঠিত করেন। আধুনিক বিজ্ঞানে কনিকের বিস্তার ও প্রয়োগ ব্যপকভাবে বৃদ্ধি পায়। গ্রহ, উপগ্রহ, ধূমকেতু, নৌকা চালনায়, শিল্পকারখানায় যন্ত্রপাতি ( গিয়ার), অ্যান্টেনা, আলোকবিজ্ঞান, দূরবিক্ষণ যন্ত্র ইত্যাদিতে কনিকের ব্যবহার পরিলক্ষিত হয়।
প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে আধুনিক ফাংশনের ধারণা দেন । (Rene Descartes) (১৫৯৬-১৬৫০) বৈজ্ঞানিকরূপে প্রতিষ্ঠিত করেন। আধুনিক বিজ্ঞানে কনিকের বিস্তার ও প্রয়োগ ব্যপকভাবে বৃদ্ধি পায়। গ্রহ, উপগ্রহ, ধূমকেতু, নৌকা চালনায়, শিল্পকারখানায় যন্ত্রপাতি ( গিয়ার), অ্যান্টেনা, আলোকবিজ্ঞান, দূরবিক্ষণ যন্ত্র ইত্যাদিতে কনিকের ব্যবহার পরিলক্ষিত হয়।
 ম্যানাকমাস (Manaechmus) (৩৮০-৩২০ খৃষ্টপুর্ব) । ও ইউডক্সাস
ম্যানাকমাস (Manaechmus) (৩৮০-৩২০ খৃষ্টপুর্ব) । ও ইউডক্সাস  ইউডক্সাস (Eudoxus) (৩৯০-৩৩৭ খৃষ্টপুর্ব) গ্রীক গণিতবিদ ও জ্যোতির্বিদ । (Manaechmus & Eudoxus) \(4^{th}\) century-তে প্লেটোর
ইউডক্সাস (Eudoxus) (৩৯০-৩৩৭ খৃষ্টপুর্ব) গ্রীক গণিতবিদ ও জ্যোতির্বিদ । (Manaechmus & Eudoxus) \(4^{th}\) century-তে প্লেটোর  প্লেটো (Plato) (খ্রিষ্টপূর্ব ৪২৭ - খ্রিষ্টপূর্ব ৩৪৭) বিশ্ববিখ্যাত গ্রিক দার্শনিক। তিনি দার্শনিক সক্রেটিসের ছাত্র ছিলেন এবং দার্শনিক এরিস্টটল তার ছাত্র ছিলেন। (Plato) স্কুলে কনিকের এ ত্রিগঠন সংযোজন করেন। Elements গ্রন্থে ইউক্লিড
প্লেটো (Plato) (খ্রিষ্টপূর্ব ৪২৭ - খ্রিষ্টপূর্ব ৩৪৭) বিশ্ববিখ্যাত গ্রিক দার্শনিক। তিনি দার্শনিক সক্রেটিসের ছাত্র ছিলেন এবং দার্শনিক এরিস্টটল তার ছাত্র ছিলেন। (Plato) স্কুলে কনিকের এ ত্রিগঠন সংযোজন করেন। Elements গ্রন্থে ইউক্লিড  ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। (৩০০-২৫০ খ্রিষ্টপূর্ব) কনিক সম্পর্কে বিস্তারিত আলোচনা করেন।এবং পরবর্তীতে "Quadrature of Parabola" গ্রন্থে আর্কিমিডিস
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। (৩০০-২৫০ খ্রিষ্টপূর্ব) কনিক সম্পর্কে বিস্তারিত আলোচনা করেন।এবং পরবর্তীতে "Quadrature of Parabola" গ্রন্থে আর্কিমিডিস  আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। (২৮৭-২১২ খ্রিষ্টপূর্ব) এবং অ্যাপোলোনিয়াস কনিকের প্রথম সিরিজ আকারে আটটি গ্রন্থে কনিক সম্পর্কে মৌলিক ও মূল্যবান তত্ত্ব ও তথ্যাবলির উপস্থাপন করেন। গ্রিক বিজ্ঞানীদের উদ্ভাবিত এসব তথ্য ও উপাত্তকে সপ্তদশ শতাব্দীতে জোহান ক্যাপলার
আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। (২৮৭-২১২ খ্রিষ্টপূর্ব) এবং অ্যাপোলোনিয়াস কনিকের প্রথম সিরিজ আকারে আটটি গ্রন্থে কনিক সম্পর্কে মৌলিক ও মূল্যবান তত্ত্ব ও তথ্যাবলির উপস্থাপন করেন। গ্রিক বিজ্ঞানীদের উদ্ভাবিত এসব তথ্য ও উপাত্তকে সপ্তদশ শতাব্দীতে জোহান ক্যাপলার  জোহান কেপলার (Johannes Kepler) (১৫৭১-১৬৩০) ছিলেন দক্ষিণ পশ্চিম জার্মানির গণিতবিদ ও জ্যোতির্বিদ। কেপলারের প্রিয় বিষয়গুলি ছিল গণিত ও জ্যোতির্বিদ্যা। কেপলারের সবচেয়ে উল্লেখযোগ্য পুস্তকটির নাম ‘নিউ অ্যাসট্রোনমি’, যা প্রকাশের পর বিজ্ঞানীরা জানতে পারলেন, সূর্যের চারদিকে গ্রহরা একটি উপবৃত্তাকার পথে পরিভ্রমণ করছে। (Johannes Kepler) (১৫৭১-১৬৩০) এবং রেনে দেকার্তে
জোহান কেপলার (Johannes Kepler) (১৫৭১-১৬৩০) ছিলেন দক্ষিণ পশ্চিম জার্মানির গণিতবিদ ও জ্যোতির্বিদ। কেপলারের প্রিয় বিষয়গুলি ছিল গণিত ও জ্যোতির্বিদ্যা। কেপলারের সবচেয়ে উল্লেখযোগ্য পুস্তকটির নাম ‘নিউ অ্যাসট্রোনমি’, যা প্রকাশের পর বিজ্ঞানীরা জানতে পারলেন, সূর্যের চারদিকে গ্রহরা একটি উপবৃত্তাকার পথে পরিভ্রমণ করছে। (Johannes Kepler) (১৫৭১-১৬৩০) এবং রেনে দেকার্তে  প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে আধুনিক ফাংশনের ধারণা দেন । (Rene Descartes) (১৫৯৬-১৬৫০) বৈজ্ঞানিকরূপে প্রতিষ্ঠিত করেন। আধুনিক বিজ্ঞানে কনিকের বিস্তার ও প্রয়োগ ব্যপকভাবে বৃদ্ধি পায়। গ্রহ, উপগ্রহ, ধূমকেতু, নৌকা চালনায়, শিল্পকারখানায় যন্ত্রপাতি ( গিয়ার), অ্যান্টেনা, আলোকবিজ্ঞান, দূরবিক্ষণ যন্ত্র ইত্যাদিতে কনিকের ব্যবহার পরিলক্ষিত হয়।
প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে আধুনিক ফাংশনের ধারণা দেন । (Rene Descartes) (১৫৯৬-১৬৫০) বৈজ্ঞানিকরূপে প্রতিষ্ঠিত করেন। আধুনিক বিজ্ঞানে কনিকের বিস্তার ও প্রয়োগ ব্যপকভাবে বৃদ্ধি পায়। গ্রহ, উপগ্রহ, ধূমকেতু, নৌকা চালনায়, শিল্পকারখানায় যন্ত্রপাতি ( গিয়ার), অ্যান্টেনা, আলোকবিজ্ঞান, দূরবিক্ষণ যন্ত্র ইত্যাদিতে কনিকের ব্যবহার পরিলক্ষিত হয়। কনিকের গঠনগত ব্যাখ্যা
Stractural explanation of Conics
 কনিক (Conics): কোন কার্তেসীয় সমতলে একটি বিন্দু যদি এমনভাবে চলে যে ঐ সমতলস্থিত একটি স্থির বিন্দু থেকে দূরত্ব এবং একটি নির্দিষ্ট রেখা থেকে লম্বদূরত্বের অনুপাত একটি স্থির রাশি , তবে ঐ বিন্দুর সঞ্চারপথকে কনিক বলা হয়।
স্থির বিন্দুটিকে কনিকের উপকেন্দ্র (Focus), নির্দিষ্ট সরলরেখাটিকে এর নিয়ামক রেখা (Directrix) এবং ঐ স্থির রাশিকে উৎকেন্দ্রিকতা বা বিকেন্দ্রিকতা (Eccentricity) বলা হয়।
কনিক (Conics): কোন কার্তেসীয় সমতলে একটি বিন্দু যদি এমনভাবে চলে যে ঐ সমতলস্থিত একটি স্থির বিন্দু থেকে দূরত্ব এবং একটি নির্দিষ্ট রেখা থেকে লম্বদূরত্বের অনুপাত একটি স্থির রাশি , তবে ঐ বিন্দুর সঞ্চারপথকে কনিক বলা হয়।
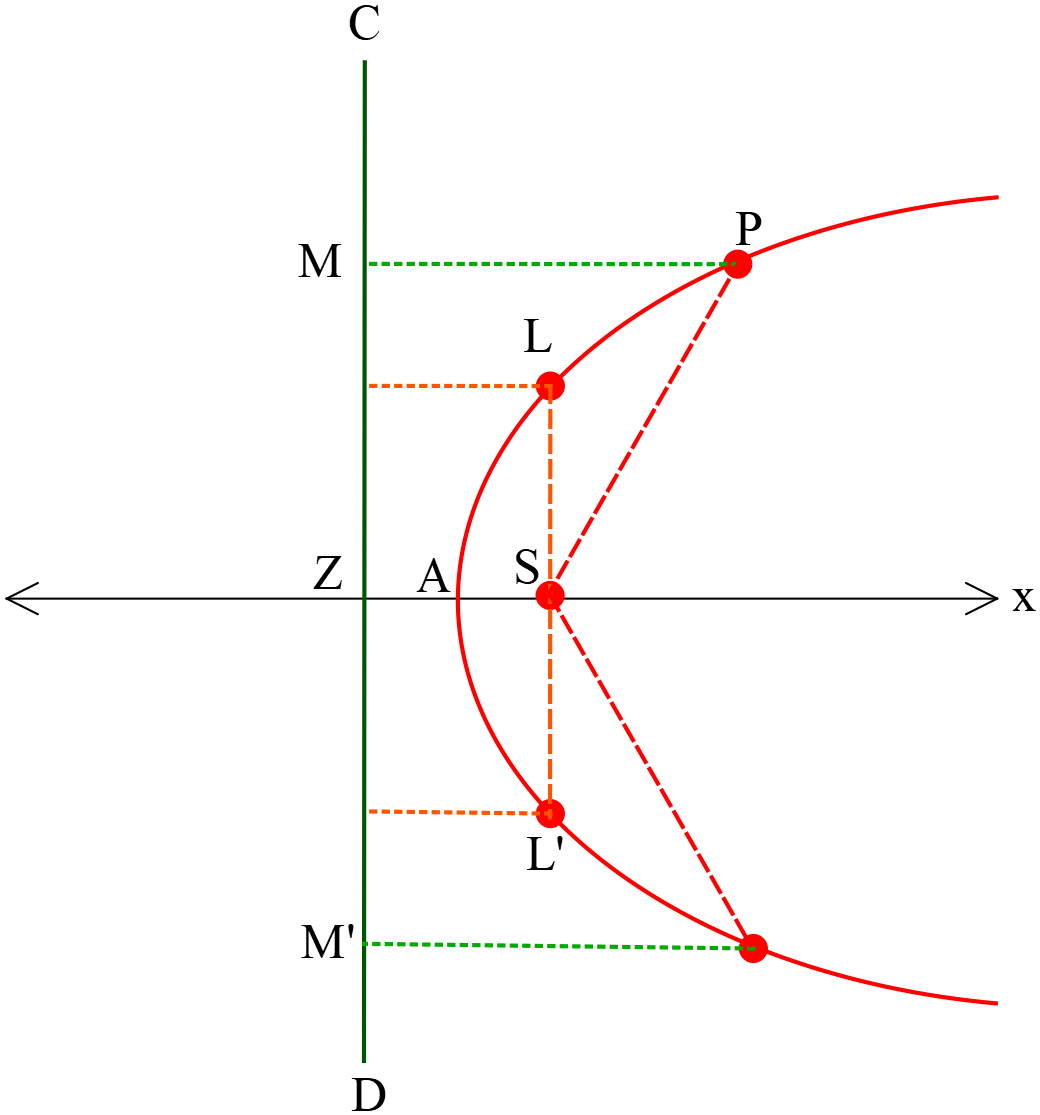
স্থির বিন্দুটিকে কনিকের উপকেন্দ্র (Focus), নির্দিষ্ট সরলরেখাটিকে এর নিয়ামক রেখা (Directrix) এবং ঐ স্থির রাশিকে উৎকেন্দ্রিকতা বা বিকেন্দ্রিকতা (Eccentricity) বলা হয়।জ্যামিতিক ব্যাখ্যাঃ মনে করি, কোন সমতলে \(S\) একটি স্থির বিন্দু এবং \(CD\) একটি স্থির সরলরেখা। একটি চলমান বিন্দু \(P(x, y)\) যা সমতলের উপর অবস্থিত। \(P\) বিন্দু হতে \(S\) বিন্দুর দূরত্ব \(PS\) এবং \(P\) বিন্দু হতে \(CD\) এর উপর লম্ব-দূরত্ব \(PM\) এর অনুপাত সর্বদা স্থির হয়, তাহলে \(P\) এর সঞ্চারপথকে কনিক বলে। স্থির রাশিটিকে \(e\) দ্বারা প্রকাশ করলে \(\frac{PS}{PM}=e\) হয়। এখানে \(e\) কে উৎকেন্দ্রিকতা (Eccentricity) বলে। সুতরাং \(PS=e.PM\) কনিকের সমীকরণ প্রকাশ করে।
সংজ্ঞাসমূহ
Definitions
অক্ষরেখা, শীর্ষবিন্দু, উপকেন্দ্র, নিয়ামকরেখা, উৎকেন্দ্রিকতা,নিয়ামকরেখার পাদবিন্দু , উপকেন্দ্রিক দূরত্ব, উপকেন্দ্রিক জ্যা ও উপকেন্দ্রিক লম্ব।
Axis, Vertex, Focus, Directrix, Eccentricity, Foot point, Focal distance, Focal chord and Latus rectum.
অক্ষরেখা (Axis): উপকেন্দ্রের মধ্যদিয়ে নিয়ামকরেখার উপর অঙ্কিত লম্ব রেখাটিকে (AX) পরাবৃত্তের অক্ষরেখা বা অক্ষ বলা হয়।
শীর্ষবিন্দু (Vertex): পরাবৃত্ত ও অক্ষরেখার ছেদবিন্দুকে (A) পরাবৃত্তের শীর্ষবিন্দু বলে।
উপকেন্দ্র (Focus): পরাবৃত্তের সংজ্ঞানুসারে নির্দিষ্ট বিন্দুটিকে (S) পরাবৃত্তের উপকেন্দ্র বলে।
নিয়ামকরেখা (Directrix): পরাবৃত্তের সংজ্ঞানুসারে নির্দিষ্ট সরলরেখাটিকে (CD) পরাবৃত্তের নিয়ামকরেখা বলে।
উৎকেন্দ্রিকতা (Eccentricity): পরাবৃত্তের সংজ্ঞানুসারে স্থির অনুপাতটিকে \((e)\) পরাবৃত্তের উৎকেন্দ্রিকতা বলে।
নিয়ামকরেখার পাদবিন্দু (Foot point): নিয়ামকরেখা ও অক্ষরেখার ছেদবিন্দুকে (Z) নিয়ামকরেখার পাদবিন্দু বলে।
উপকেন্দ্রিক দূরত্ব (Focal distance): উপকেন্দ্র থেকে পরাবৃত্তের যে কোন বিন্দুর দূরত্বকে উপকেন্দ্রিক দূরত্ব বলে।
উপকেন্দ্রিক জ্যা (Focal chord): পরাবৃত্তের যে জ্যা পরাবৃত্তের উপকেন্দ্র দিয়ে গমন করে তাকে উপকেন্দ্রিক জ্যা বলে।
উপকেন্দ্রিক লম্ব (Latus rectum): উপকেন্দ্রিক জ্যা অক্ষের উপর লম্ব হলে \(LL^{\prime}\) তাকে পরাবৃত্তের উপকেন্দ্রিক লম্ব বলে।
শীর্ষবিন্দু (Vertex): পরাবৃত্ত ও অক্ষরেখার ছেদবিন্দুকে (A) পরাবৃত্তের শীর্ষবিন্দু বলে।
উপকেন্দ্র (Focus): পরাবৃত্তের সংজ্ঞানুসারে নির্দিষ্ট বিন্দুটিকে (S) পরাবৃত্তের উপকেন্দ্র বলে।
নিয়ামকরেখা (Directrix): পরাবৃত্তের সংজ্ঞানুসারে নির্দিষ্ট সরলরেখাটিকে (CD) পরাবৃত্তের নিয়ামকরেখা বলে।
উৎকেন্দ্রিকতা (Eccentricity): পরাবৃত্তের সংজ্ঞানুসারে স্থির অনুপাতটিকে \((e)\) পরাবৃত্তের উৎকেন্দ্রিকতা বলে।
নিয়ামকরেখার পাদবিন্দু (Foot point): নিয়ামকরেখা ও অক্ষরেখার ছেদবিন্দুকে (Z) নিয়ামকরেখার পাদবিন্দু বলে।
উপকেন্দ্রিক দূরত্ব (Focal distance): উপকেন্দ্র থেকে পরাবৃত্তের যে কোন বিন্দুর দূরত্বকে উপকেন্দ্রিক দূরত্ব বলে।
উপকেন্দ্রিক জ্যা (Focal chord): পরাবৃত্তের যে জ্যা পরাবৃত্তের উপকেন্দ্র দিয়ে গমন করে তাকে উপকেন্দ্রিক জ্যা বলে।
উপকেন্দ্রিক লম্ব (Latus rectum): উপকেন্দ্রিক জ্যা অক্ষের উপর লম্ব হলে \(LL^{\prime}\) তাকে পরাবৃত্তের উপকেন্দ্রিক লম্ব বলে।
বিভিন্ন প্রকৃতির কনিক
Different types of Conic
বৃত্ত, পরাবৃত্ত, উপবৃত্ত, অধিবৃত্ত এবং যুগল সরলরেখা।
Circle, Parabola, Ellipse, Hyperbola and Pair of Straight Lines
\(e\) এর বিভিন্ন মানের জন্য সঞ্চারপথের আকৃতি বিভিন্ন হয়, যা নিম্নরূপঃ
বৃত্ত (Circle): \(e=0\) হলে, সঞ্চারপথকে বৃত্ত (Circle) বলা হয়। অতএব বৃত্ত হলো উপবৃত্তের একটি সীমায়িত অবস্থান যার বিকেন্দ্রিকতা শুন্য এবং যার নিয়ামক অসীমে থাকে। আবার একটি বৃত্ত বিন্দুতে পরিণত হতে পারে যখন এর ব্যাসার্ধ শুন্য হয়।
পরাবৃত্ত (Parabola): \(e=1\) হলে, সঞ্চারপথকে পরাবৃত্ত (Parabola) বলা হয়। অতএব, পরাবৃত্তস্থ প্রত্যেকটি বিন্দু উপকেন্দ্র ও নিয়ামকরেখা থেকে সমান দূরে অবস্থিত।
উপবৃত্ত (Ellipse): \(1>e>0\) হলে, সঞ্চারপথকে উপবৃত্ত (Ellipse) বলা হয়। উপবৃত্তস্থ প্রত্যেকটি বিন্দু থেকে উপকেন্দ্র ও নিয়ামকরেখার দূরত্বের অনুপাত একটি স্থির রাশি যার মাণ শুন্য অপেক্ষা বড় এবং \(1\) অপেক্ষা ছোট।
অধিবৃত্ত (Hyperbola): \(e>1\) হলে, সঞ্চারপথকে অধিবৃত্ত (Hyperbola) বলা হয়। অধিবৃত্তস্থ প্রত্যেকটি বিন্দু থেকে উপকেন্দ্র ও নিয়ামকরেখার দূরত্বের অনুপাত একটি স্থির রাশি যার মাণ \(1\) অপেক্ষা বড় ।
যুগল সরলরেখা (Pair of Straight Lines): \(e>1\) এবং উপকেন্দ্র নিয়ামকের উপর অবস্থিত হলে, সঞ্চারপথকে যুগল সরলরেখা (Pair of Straight Lines) বলা হয়। অতএব এক্ষেত্রে কনিকটি দুইটি বাস্তব ও ভিন্ন সরলরেখা নির্দেশ করে।
পরাবৃত্ত (Parabola): \(e=1\) হলে, সঞ্চারপথকে পরাবৃত্ত (Parabola) বলা হয়। অতএব, পরাবৃত্তস্থ প্রত্যেকটি বিন্দু উপকেন্দ্র ও নিয়ামকরেখা থেকে সমান দূরে অবস্থিত।
উপবৃত্ত (Ellipse): \(1>e>0\) হলে, সঞ্চারপথকে উপবৃত্ত (Ellipse) বলা হয়। উপবৃত্তস্থ প্রত্যেকটি বিন্দু থেকে উপকেন্দ্র ও নিয়ামকরেখার দূরত্বের অনুপাত একটি স্থির রাশি যার মাণ শুন্য অপেক্ষা বড় এবং \(1\) অপেক্ষা ছোট।
অধিবৃত্ত (Hyperbola): \(e>1\) হলে, সঞ্চারপথকে অধিবৃত্ত (Hyperbola) বলা হয়। অধিবৃত্তস্থ প্রত্যেকটি বিন্দু থেকে উপকেন্দ্র ও নিয়ামকরেখার দূরত্বের অনুপাত একটি স্থির রাশি যার মাণ \(1\) অপেক্ষা বড় ।
যুগল সরলরেখা (Pair of Straight Lines): \(e>1\) এবং উপকেন্দ্র নিয়ামকের উপর অবস্থিত হলে, সঞ্চারপথকে যুগল সরলরেখা (Pair of Straight Lines) বলা হয়। অতএব এক্ষেত্রে কনিকটি দুইটি বাস্তব ও ভিন্ন সরলরেখা নির্দেশ করে।
চিত্রের সাহায্যে কনিক উপস্থাপন
Representation of Conic by diagram
কোনো কনিকের উপকেন্দ্র \(S\) নিয়ামক রেখা \(MZ\acute M\) ( পরাবৃত্তের ক্ষেত্রে ) এবং \(MZ\) ও \(\acute M\acute Z\) ( উপবৃত্ত ও অধিবৃত্তের ক্ষেত্রে ) উৎকেন্দ্রিকতা \(e\) এবং উক্ত কনিকের উপরস্থ যে কোনো বিন্দু \(P(x, y)\) হলে উক্ত কনিকের সমীকরণ \(\frac{PS}{PM}=e\)।
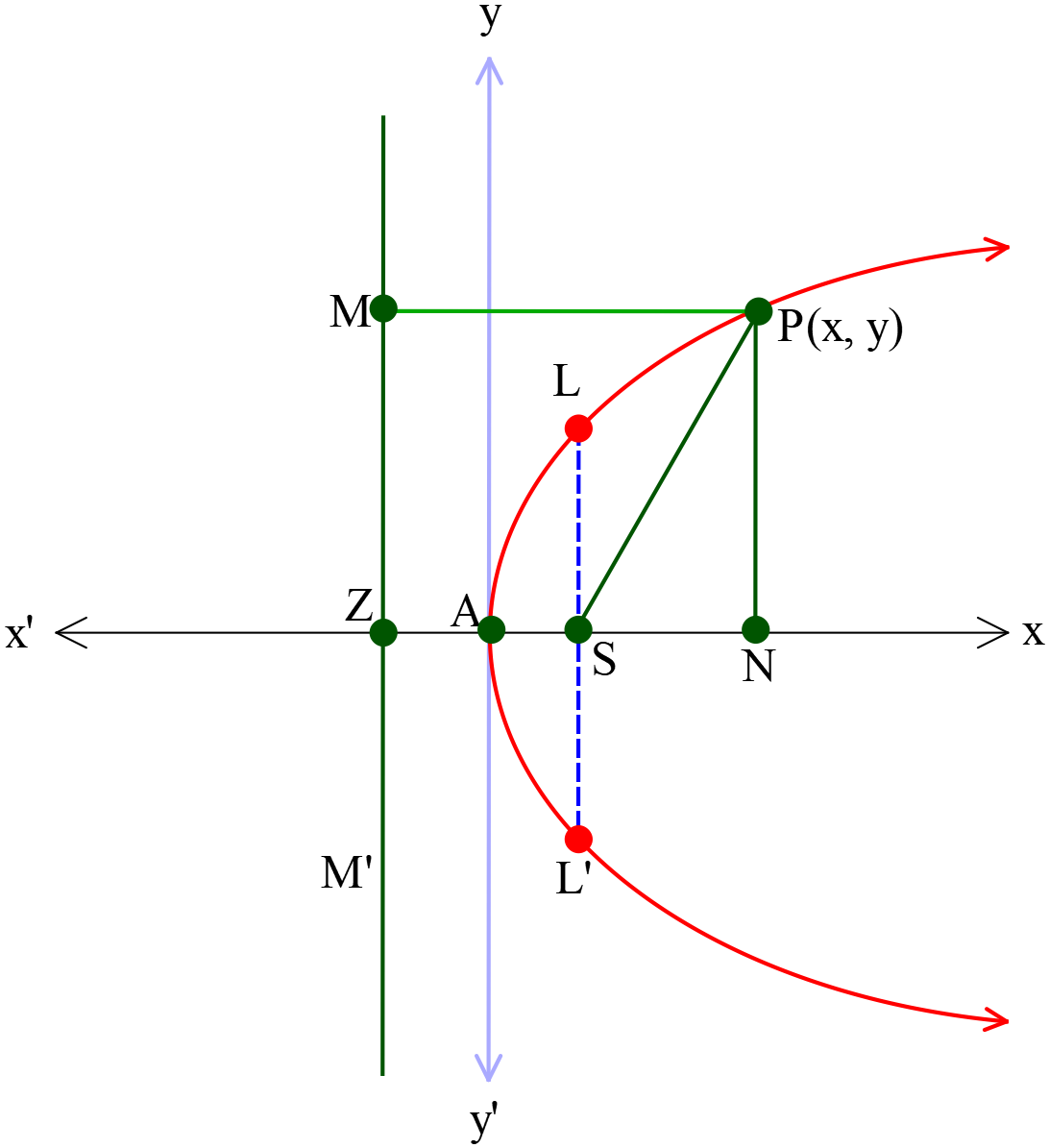
কনিকটি একটি পরাবৃত্ত (Parabola) প্রকাশ করে; যখন \(e=1\) এবং \(SP=PM\)।
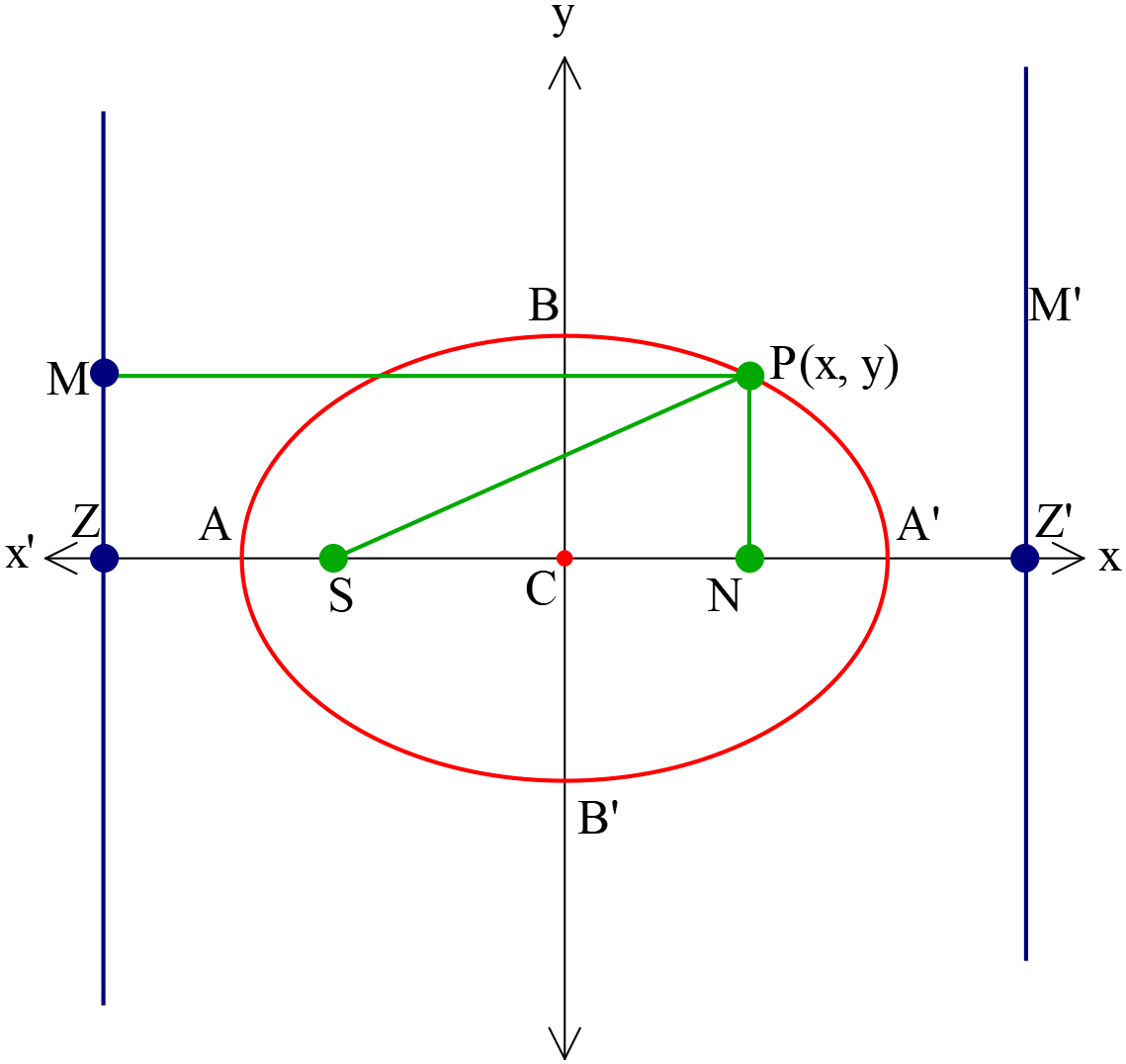
কনিকটি একটি উপবৃত্ত (Ellipse) প্রকাশ করে; যখন \(1 > e > 0\) এবং \(SP=e.PM\)।
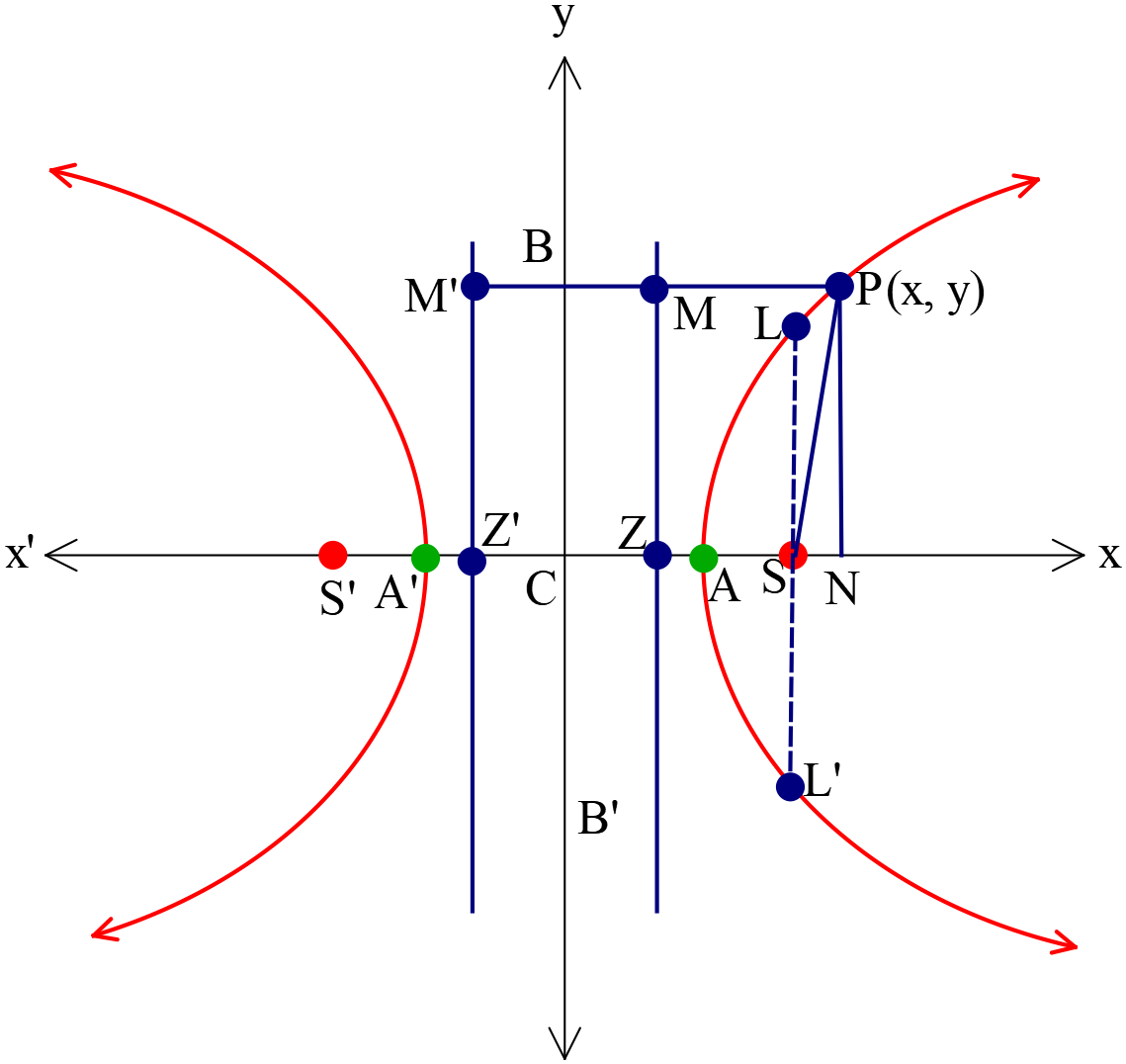
কনিকটি একটি অধিবৃত্ত (Hyperbola) প্রকাশ করে; যখন \(e>1\) এবং \(SP=e.PM\)।
কোনোকের এবং সমতলের ছেদবিন্দুর সঞ্চারপথই যে কনিক তা চিত্রের সাহায্যে প্রকাশ
Conic which representing the locus of intersection of cone and a plane by diagram
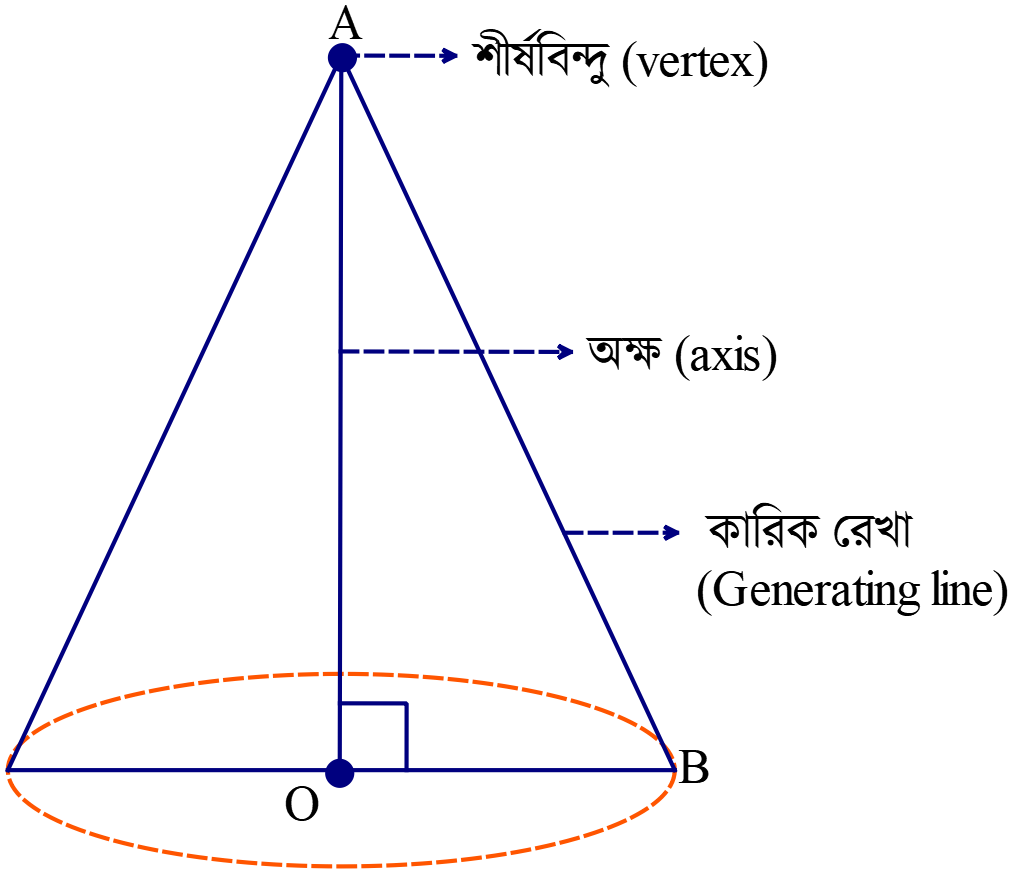 কোণ থেকে কনিকের উৎপত্তি। একটি নির্দিষ্ট সরলরেখা কোনো নির্দিষ্ট বিন্দুতে অপর একটি সরলরেখার এক প্রান্ত বেধে রেখে যদি রেখাটিকে ঐ নির্দিষ্ট রেখার চারিদিকে সূক্ষ্ণকোণে আবর্তন করানো হয়, তবে একটি বৃত্তীয় কোণ উৎপন্ন হয়। নির্দিষ্ট রেখাটি \((AO)\) ভূমির সহিত লম্ব অর্থাৎ \(\angle AOB=90^o\) হলে একটি সমবৃত্তীয় কোণ উৎপন্ন হয়। নির্দিষ্ট বিন্দুটিকে কোণের শীর্ষবিন্দু, নির্দিষ্ট সরলরেখাকে অক্ষ এবং ঘূর্নায়মান রেখাকে কারিক রেখা (Generating line) বলা হয়।
কোণ থেকে কনিকের উৎপত্তি। একটি নির্দিষ্ট সরলরেখা কোনো নির্দিষ্ট বিন্দুতে অপর একটি সরলরেখার এক প্রান্ত বেধে রেখে যদি রেখাটিকে ঐ নির্দিষ্ট রেখার চারিদিকে সূক্ষ্ণকোণে আবর্তন করানো হয়, তবে একটি বৃত্তীয় কোণ উৎপন্ন হয়। নির্দিষ্ট রেখাটি \((AO)\) ভূমির সহিত লম্ব অর্থাৎ \(\angle AOB=90^o\) হলে একটি সমবৃত্তীয় কোণ উৎপন্ন হয়। নির্দিষ্ট বিন্দুটিকে কোণের শীর্ষবিন্দু, নির্দিষ্ট সরলরেখাকে অক্ষ এবং ঘূর্নায়মান রেখাকে কারিক রেখা (Generating line) বলা হয়।চিত্রে, \(AO\) অক্ষ (Axis) \(AB\) কারিক রেখা (Generating line) এবং \(\angle OAB\) কে অর্ধশীর্ষ কোণ বলা হয়ে থাকে।
সমতল দ্বারা কোণের ছেদন
Intersection of a Cone by a plane
ভূমির সমান্তরাল কিন্তু শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একটি বৃত্ত (Circle) উৎপন্ন করে।
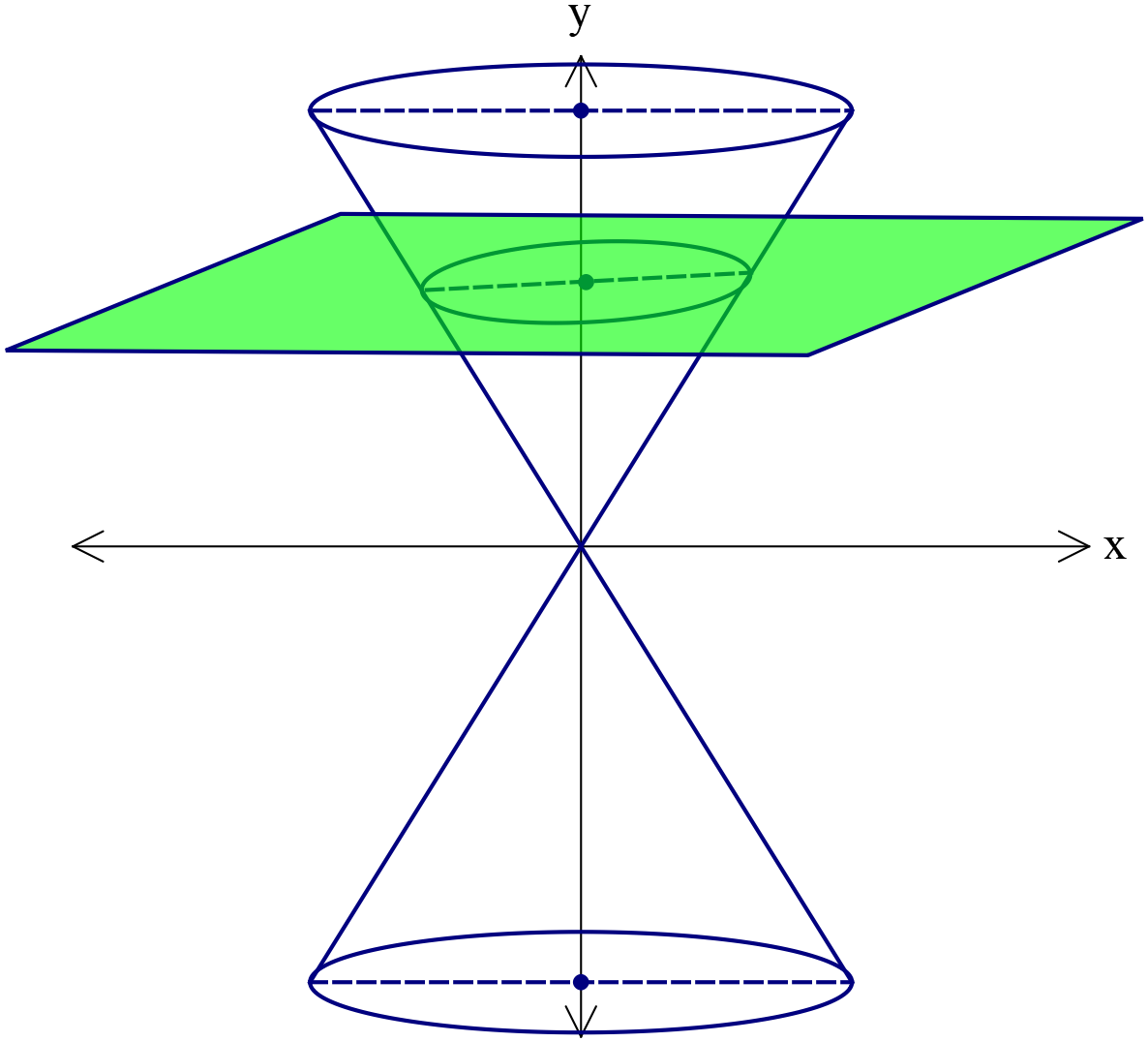
কারিক রেখার সমান্তরাল কিন্তু শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে ছেদ বা কর্তন করা হয়, তবে ছেদক রেখাটি একটি পরাবৃত্ত (parabola) উৎপন্ন করে।

কারিক রেখা ও ভূমির সমান্তরাল নয় এবং শীর্ষবিন্দুগামীও নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একটি উপবৃত্ত (Ellipse) উৎপন্ন করে।
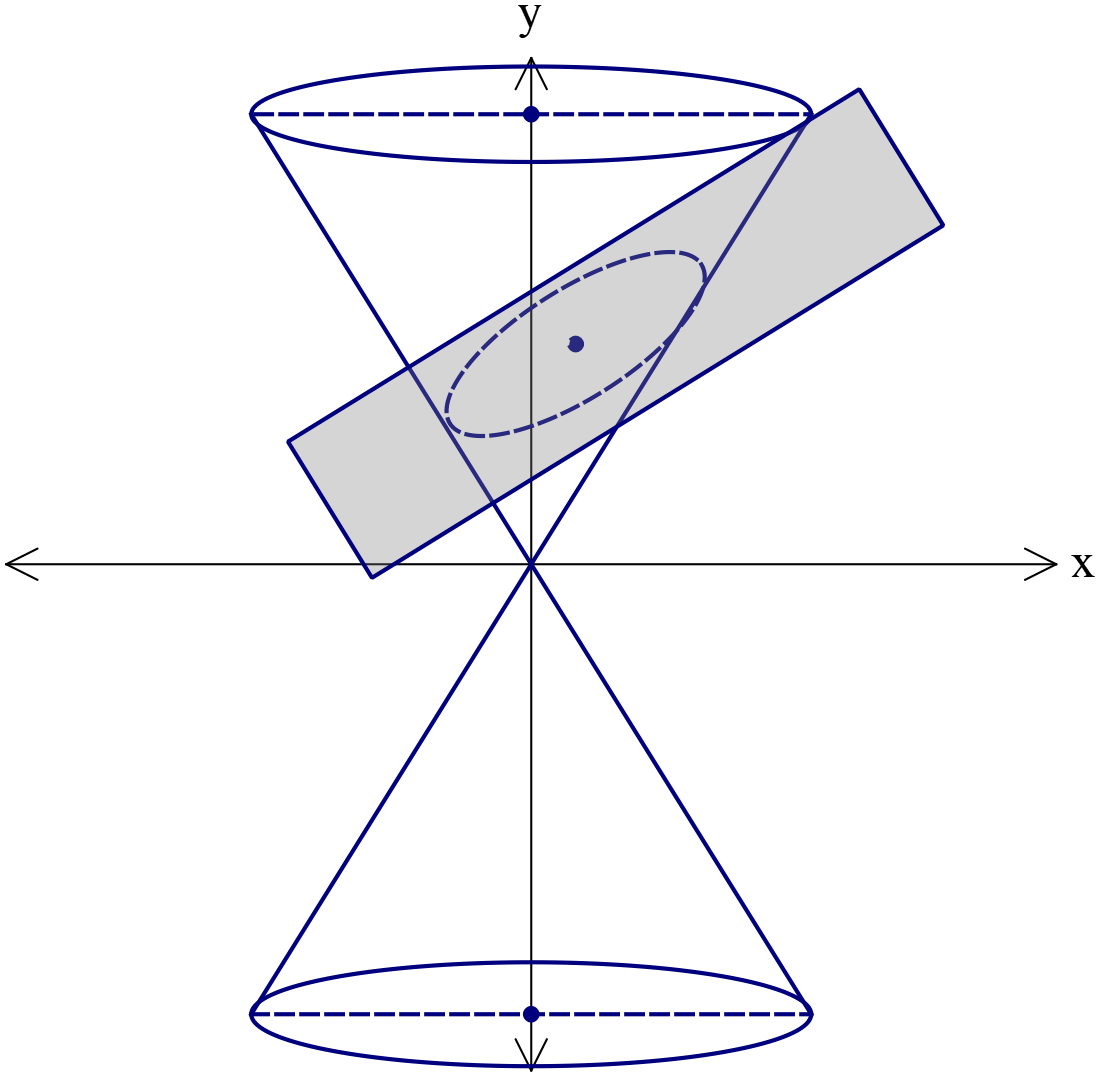
শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি কোনো দ্বিকোণকে এমনভাবে ছেদ করা হয় যেন তা উভয় কোণকে ছেদ করে, তবে ছেদক রেখাটি একটি অধিবৃত্ত (Hyperbola) উৎপন্ন করে।

শীর্ষবিন্দুগামী এবং ভূমির সহিত লম্ব এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একজোড়া সরলরেখা ( Pair of straight line) উৎপন্ন করে।
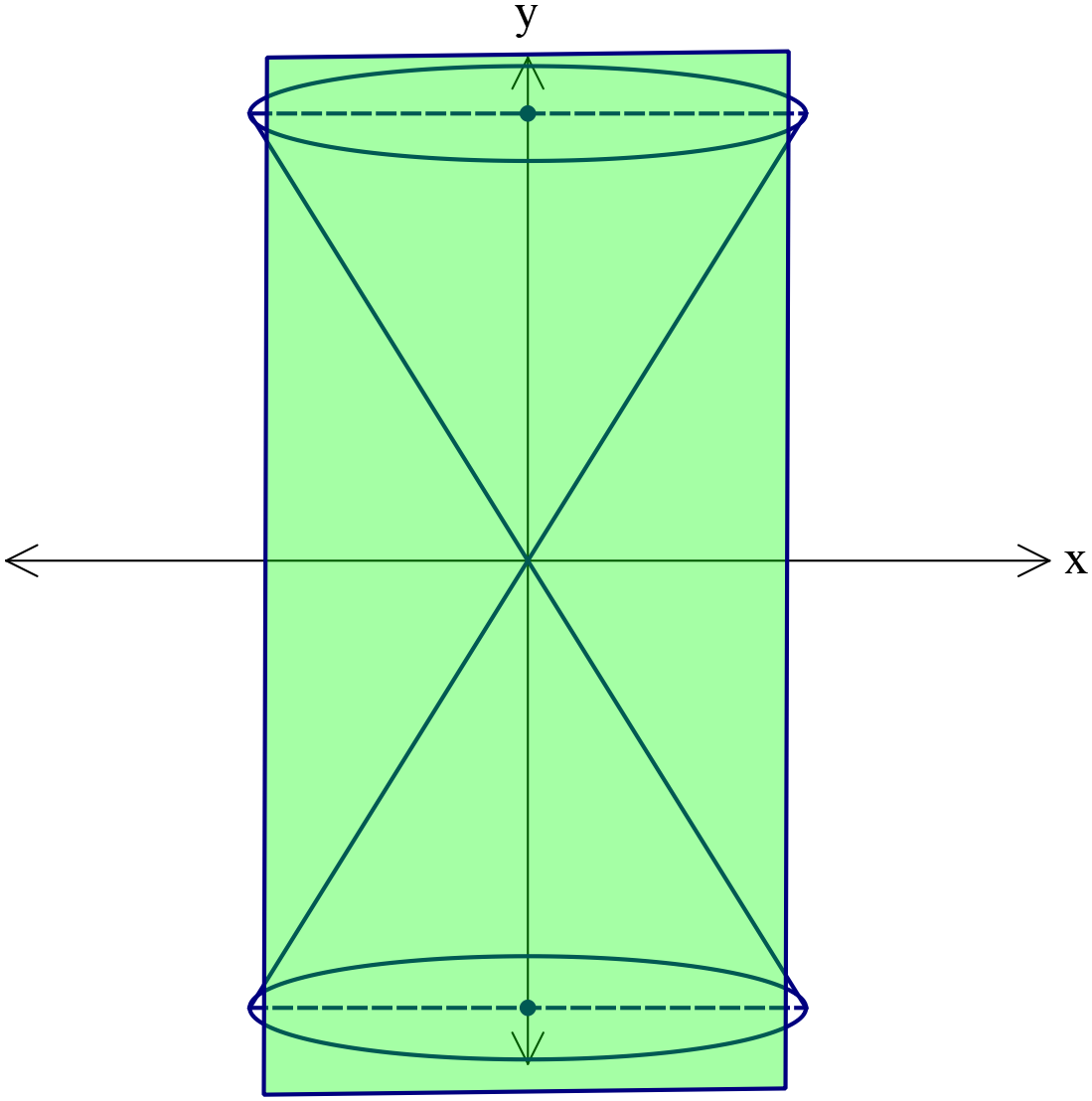
পরাবৃত্তের সমীকরণ সনাক্তকরণ
Identifying the equation of the parabola
পরাবৃত্তের সমীকরণে \(x^2\) অথবা, \(y^2\) যুক্ত পদ বিদ্যমান। \(x\) ও \(y\) যুক্ত পদ থাকতেও পারে নাও থাকতে পারে।
মূলবিন্দুগামী এবং \(x\) অক্ষের ধনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ
Equation of the parabola symmetrical about the origin and positive to the \(x\) axis
পরাবৃত্তের সমীকরণ \(y^2=4ax \ (a>0)\)
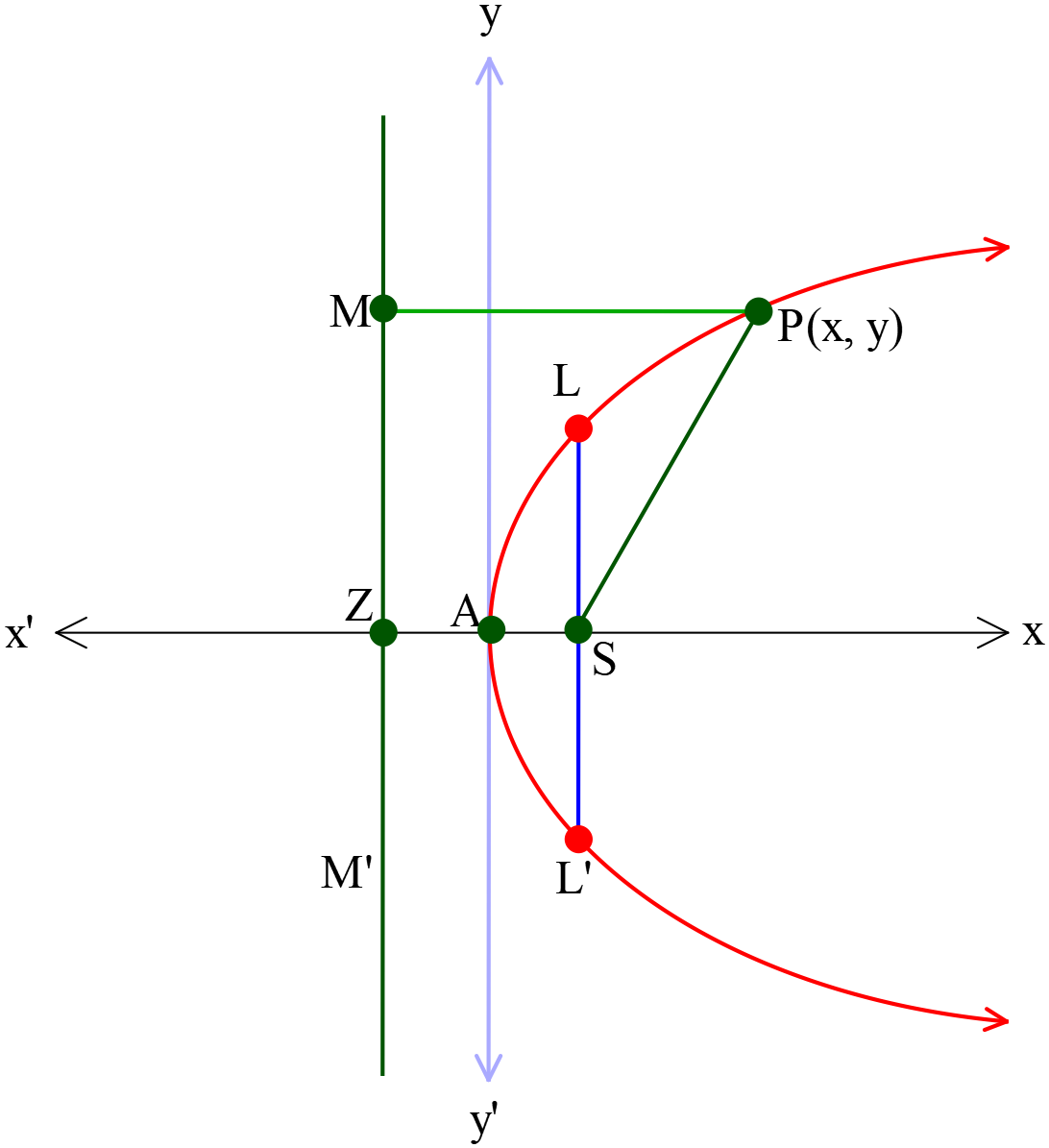
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(0, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(a, 0)\)
- নিয়ামক রেখার সমীকরণ \(x=-a\)
- অক্ষরেখার সমীকরণ \(y=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x=a\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(x=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(-a, 0)\)
- উপকেন্দ্রিক লম্বের প্রান্ত বিন্দুদ্বয়ের স্থানাংক \((a, \pm{2a})\)
- \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব \(=a+|x|\)
প্রমাণঃ
ধরি,
পরাবৃত্তের উপকেন্দ্র \(S\) এবং নিয়ামকরেখা \(MZ\acute M\)। উপকেন্দ্র \(S\) হতে নিয়ামকরেখার উপর \(SZ\) লম্ব আঁকি এবং \(SZ\) রেখা \(A\) বিন্দুতে সমদ্বিখণ্ডিত হয়। তাহলে \(SA=AZ\); সংজ্ঞানুসারে \(A\) শীর্ষবিন্দু এবং \(ZX\) পরাবৃত্তের অক্ষ। \(A\) বিন্দুকে মূলবিন্দু এবং \(AX\) ও \(AY\) রেখাকে যথাক্রমে \(X\)-অক্ষ ও \(Y\)-অক্ষ বিবেচনা করি।
আবার, \(AS=a=ZA\) এবং পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)। \(S,P\) যোগ করি এবং \(P\) বিন্দু হতে নিয়ামক রেখার উপর \(PM\) ও \(AX\)-এর উপর \(PN\) লম্ব আঁকি।
পরাবৃত্তের সংজ্ঞানুসারে,
\(SP=PM\)
\(\Rightarrow SP=ZN\) ➜ \(PM=ZN\)
\(\Rightarrow SP=ZA+AN\)
\(\Rightarrow SP=a+x\) ➜ \(AN=x, ZA=a\)
\(\Rightarrow SP^2=(a+x)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow SP^2=(a+x)^2\)
\(\Rightarrow SN^2+PN^2=(a+x)^2\) ➜ \(SPN\) সমকোণী ত্রিভুজে \(SP^2=SN^2+PN^2\)
\(\Rightarrow (x-a)^2+y^2=(a+x)^2\) ➜ \(\because SN=AN-AS=x-a\)
\(\Rightarrow y^2=(a+x)^2-(x-a)^2\)
\(\therefore y^2=4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
পরাবৃত্তের উপকেন্দ্র \(S(a, 0)\)
নিয়ামকের সমীকরণ \(x=-a \Rightarrow x+a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-a)^2+(y-0)^2}=\frac{|x+a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=\frac{|x+a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=\frac{|x+a|}{1}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=|x+a|\)
\(\Rightarrow (x-a)^2+y^2=(x+a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow y^2=(x+a)^2-(x-a)^2\)
\(\therefore y^2=4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
ধরি,
পরাবৃত্তের উপকেন্দ্র \(S\) এবং নিয়ামকরেখা \(MZ\acute M\)। উপকেন্দ্র \(S\) হতে নিয়ামকরেখার উপর \(SZ\) লম্ব আঁকি এবং \(SZ\) রেখা \(A\) বিন্দুতে সমদ্বিখণ্ডিত হয়। তাহলে \(SA=AZ\); সংজ্ঞানুসারে \(A\) শীর্ষবিন্দু এবং \(ZX\) পরাবৃত্তের অক্ষ। \(A\) বিন্দুকে মূলবিন্দু এবং \(AX\) ও \(AY\) রেখাকে যথাক্রমে \(X\)-অক্ষ ও \(Y\)-অক্ষ বিবেচনা করি।
আবার, \(AS=a=ZA\) এবং পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)। \(S,P\) যোগ করি এবং \(P\) বিন্দু হতে নিয়ামক রেখার উপর \(PM\) ও \(AX\)-এর উপর \(PN\) লম্ব আঁকি।
পরাবৃত্তের সংজ্ঞানুসারে,
\(SP=PM\)
\(\Rightarrow SP=ZN\) ➜ \(PM=ZN\)
\(\Rightarrow SP=ZA+AN\)
\(\Rightarrow SP=a+x\) ➜ \(AN=x, ZA=a\)
\(\Rightarrow SP^2=(a+x)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow SP^2=(a+x)^2\)
\(\Rightarrow SN^2+PN^2=(a+x)^2\) ➜ \(SPN\) সমকোণী ত্রিভুজে \(SP^2=SN^2+PN^2\)
\(\Rightarrow (x-a)^2+y^2=(a+x)^2\) ➜ \(\because SN=AN-AS=x-a\)
\(\Rightarrow y^2=(a+x)^2-(x-a)^2\)
\(\therefore y^2=4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
বিকল্প পদ্ধতিঃ
আমরা জানি,পরাবৃত্তের উপকেন্দ্র \(S(a, 0)\)
নিয়ামকের সমীকরণ \(x=-a \Rightarrow x+a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-a)^2+(y-0)^2}=\frac{|x+a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=\frac{|x+a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=\frac{|x+a|}{1}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=|x+a|\)
\(\Rightarrow (x-a)^2+y^2=(x+a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow y^2=(x+a)^2-(x-a)^2\)
\(\therefore y^2=4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
মূলবিন্দুগামী এবং \(y\) অক্ষের ধনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ
Equation of the parabola symmetrical about the origin and positive to the \(y\) axis
পরাবৃত্তের সমীকরণ \(x^2=4ay \ (a>0)\)
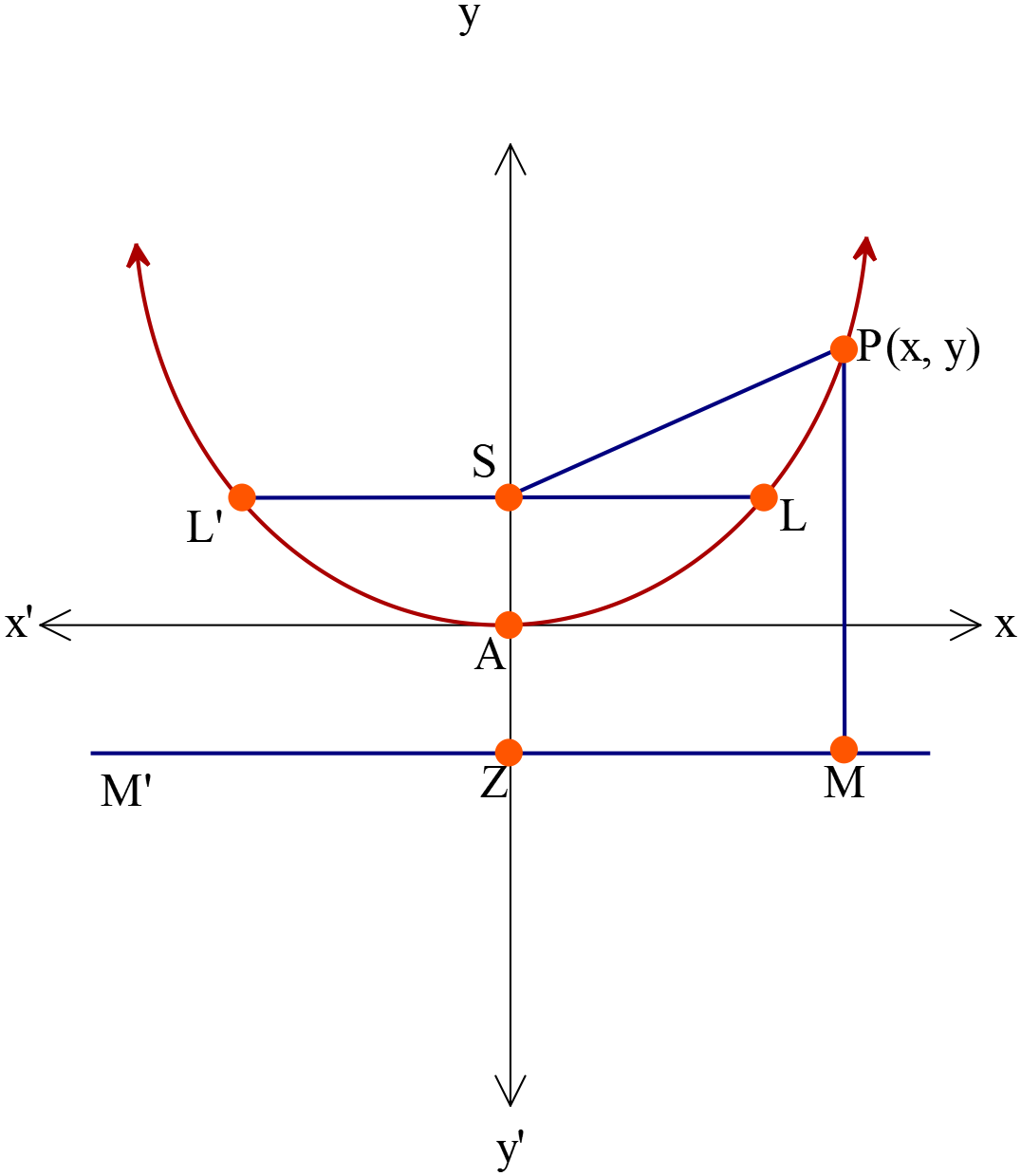
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(0, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(0, a)\)
- নিয়ামক রেখার সমীকরণ \(y=-a\)
- অক্ষরেখার সমীকরণ \(x=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y=a\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(y=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(0, -a)\)
- উপকেন্দ্রিক লম্বের প্রান্ত বিন্দুদ্বয়ের স্থানাংক \((\pm{2a}, a)\)
- \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব \(=a+|y|\)
প্রমাণঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(0, a)\)
নিয়ামকের সমীকরণ \(y=-a \Rightarrow y+a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y-a)^2}=\frac{|y+a|}{\sqrt{0^2+1^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-0)^2+(y-a)^2}=\frac{|y+a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+(y-a)^2}=\frac{|y+a|}{1}\)
\(\Rightarrow \sqrt{x^2+(y-a)^2}=|y+a|\)
\(\Rightarrow x^2+(y-a)^2=(y+a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2=(y+a)^2-(y-a)^2\)
\(\therefore x^2=4ay\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(0, a)\)
নিয়ামকের সমীকরণ \(y=-a \Rightarrow y+a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y-a)^2}=\frac{|y+a|}{\sqrt{0^2+1^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-0)^2+(y-a)^2}=\frac{|y+a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+(y-a)^2}=\frac{|y+a|}{1}\)
\(\Rightarrow \sqrt{x^2+(y-a)^2}=|y+a|\)
\(\Rightarrow x^2+(y-a)^2=(y+a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2=(y+a)^2-(y-a)^2\)
\(\therefore x^2=4ay\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
মূলবিন্দুগামী এবং \(x\) অক্ষের ঋনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ
Equation of the parabola symmetrical about the origin and negative to the \(x\) axis
পরাবৃত্তের সমীকরণ \(y^2=-4ax \ (a>0)\)
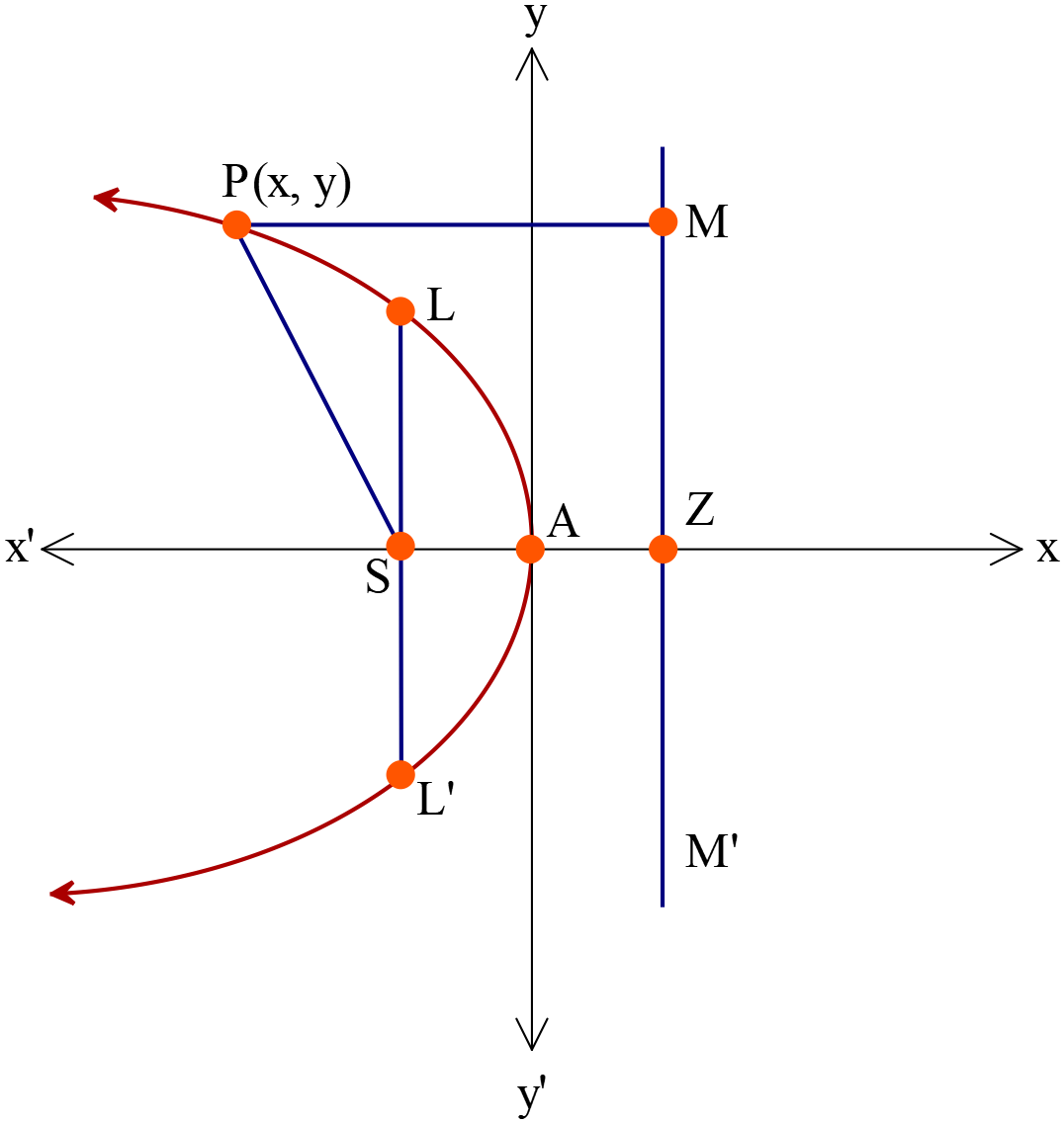
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(0, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(-a, 0)\)
- নিয়ামক রেখার সমীকরণ \(x=a\)
- অক্ষরেখার সমীকরণ \(y=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x=-a\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(x=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(a, 0)\)
- \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব \(=a+|x|\)
প্রমাণঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(-a, 0)\)
নিয়ামকের সমীকরণ \(x=a \Rightarrow x-a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x+a)^2+(y-0)^2}=\frac{|x-a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=\frac{|x-a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=\frac{|x-a|}{1}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=|x-a|\)
\(\Rightarrow (x+a)^2+y^2=(x-a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow y^2=(x-a)^2-(x+a)^2\)
\(\Rightarrow y^2=-\{(x+a)^2-(x-a)^2\}\)
\(\therefore y^2=-4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(-a, 0)\)
নিয়ামকের সমীকরণ \(x=a \Rightarrow x-a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x+a)^2+(y-0)^2}=\frac{|x-a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=\frac{|x-a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=\frac{|x-a|}{1}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=|x-a|\)
\(\Rightarrow (x+a)^2+y^2=(x-a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow y^2=(x-a)^2-(x+a)^2\)
\(\Rightarrow y^2=-\{(x+a)^2-(x-a)^2\}\)
\(\therefore y^2=-4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
মূলবিন্দুগামী এবং \(y\) অক্ষের ঋনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ
Equation of the parabola symmetrical about the origin and negative to the \(y\) axis
পরাবৃত্তের সমীকরণ \(x^2=-4ay \ (a>0)\)
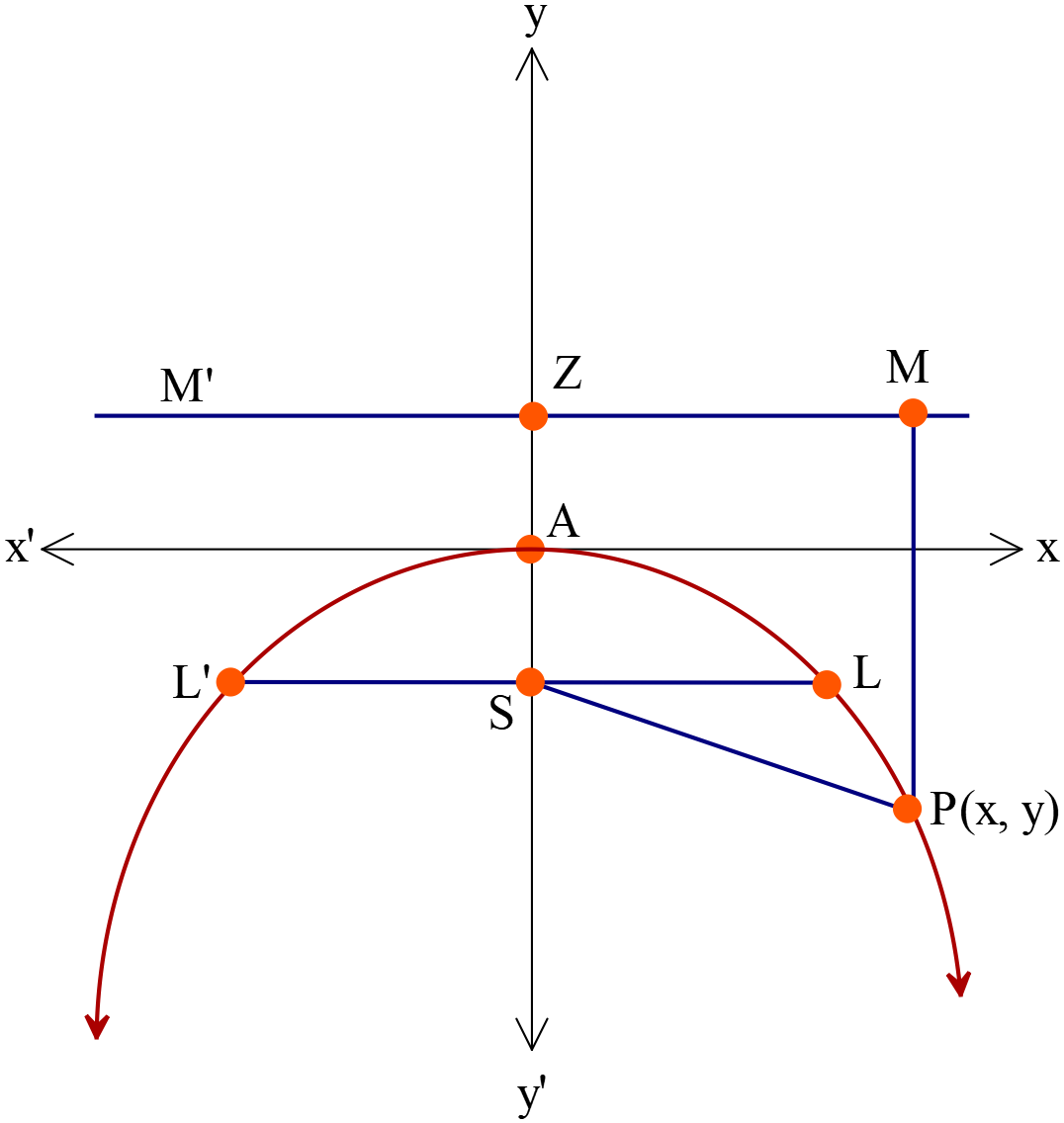
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(0, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(0, -a)\)
- নিয়ামক রেখার সমীকরণ \(y=a\)
- অক্ষরেখার সমীকরণ \(x=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y=-a\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(y=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(0, a)\)
- \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব \(=a+|y|\)
প্রমাণঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(0, -a)\)
নিয়ামকের সমীকরণ \(y=a \Rightarrow y-a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y+a)^2}=\frac{|y-a|}{\sqrt{0^2+1^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-0)^2+(y+a)^2}=\frac{|y-a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+(y+a)^2}=\frac{|y-a|}{1}\)
\(\Rightarrow \sqrt{x^2+(y+a)^2}=|y-a|\)
\(\Rightarrow x^2+(y+a)^2=(y-a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2=(y-a)^2-(y+a)^2\)
\(\Rightarrow x^2=-\{(y+a)^2-(y-a)^2\}\)
\(\therefore x^2=-4ay\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(0, -a)\)
নিয়ামকের সমীকরণ \(y=a \Rightarrow y-a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y+a)^2}=\frac{|y-a|}{\sqrt{0^2+1^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-0)^2+(y+a)^2}=\frac{|y-a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+(y+a)^2}=\frac{|y-a|}{1}\)
\(\Rightarrow \sqrt{x^2+(y+a)^2}=|y-a|\)
\(\Rightarrow x^2+(y+a)^2=(y-a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2=(y-a)^2-(y+a)^2\)
\(\Rightarrow x^2=-\{(y+a)^2-(y-a)^2\}\)
\(\therefore x^2=-4ay\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
মূলবিন্দুকে উপকেন্দ্রক ধরে পরাবৃত্তের সমীকরণ
Equation of a parabola with origin as epicenter
পরাবৃত্তের সমীকরণ \(y^2=4a(x+a) \ (a>0)\)
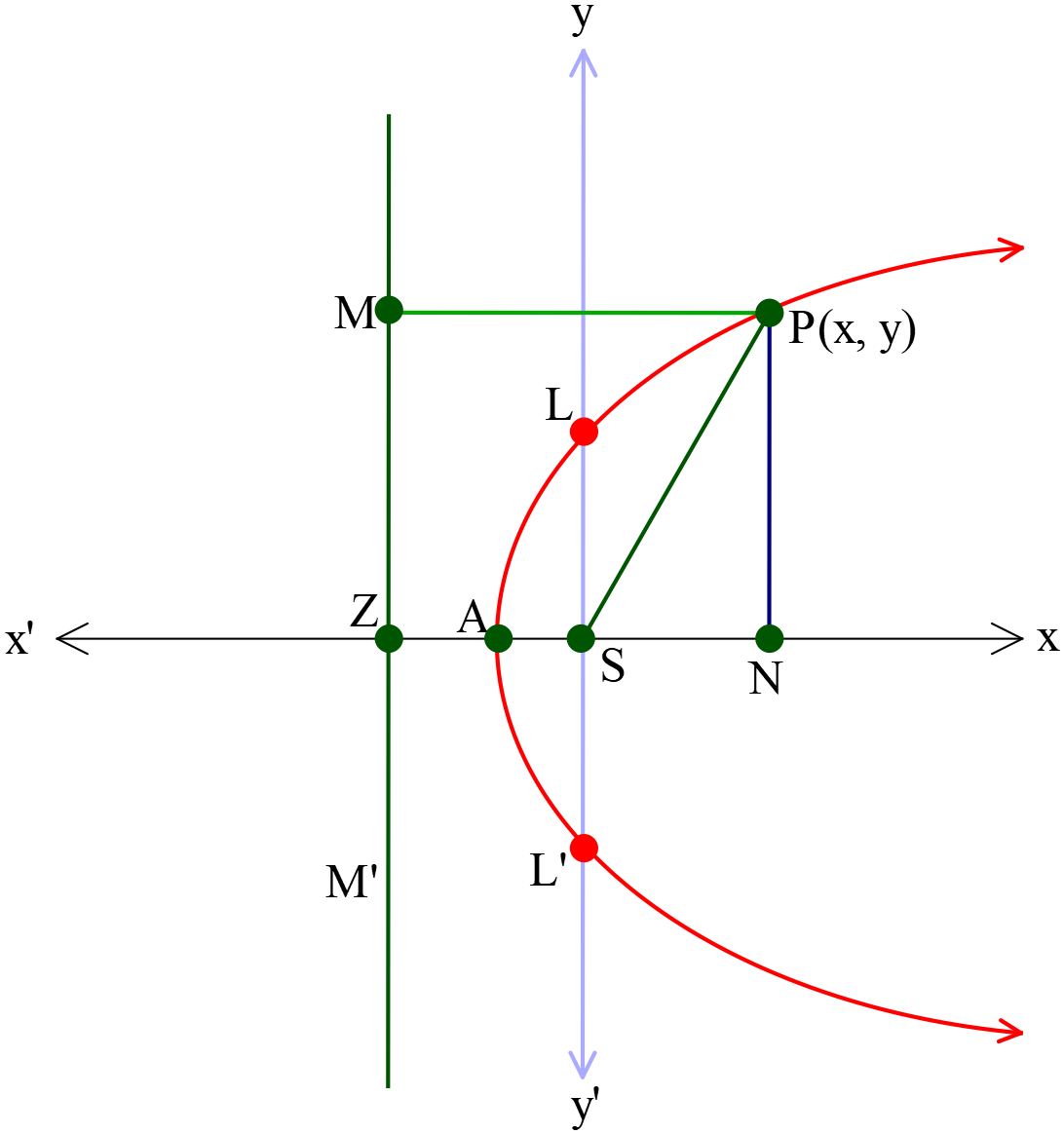
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(-a, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(0, 0)\)
- নিয়ামক রেখার সমীকরণ \(x+2a=0\)
- অক্ষরেখার সমীকরণ \(y=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x=0\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(x+a=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(-2a, 0)\)
প্রমাণঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(0, 0)\)
নিয়ামকের সমীকরণ \(x+2a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y-0)^2}=\frac{|x+2a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{x^2+x^2}=\frac{|x+2a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+y^2}=\frac{|x+2a|}{1}\)
\(\Rightarrow \sqrt{x^2+y^2}=|x+2a|\)
\(\Rightarrow x^2+y^2=(x+2a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2+y^2=x^2+4ax+4a^2\)
\(\Rightarrow x^2+y^2-x^2=4ax+4a^2\)
\(\Rightarrow y^2=4ax+4a^2\)
\(\therefore y^2=4a(x+a)\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(0, 0)\)
নিয়ামকের সমীকরণ \(x+2a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y-0)^2}=\frac{|x+2a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{x^2+x^2}=\frac{|x+2a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+y^2}=\frac{|x+2a|}{1}\)
\(\Rightarrow \sqrt{x^2+y^2}=|x+2a|\)
\(\Rightarrow x^2+y^2=(x+2a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2+y^2=x^2+4ax+4a^2\)
\(\Rightarrow x^2+y^2-x^2=4ax+4a^2\)
\(\Rightarrow y^2=4ax+4a^2\)
\(\therefore y^2=4a(x+a)\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
\(Y\)-অক্ষকে নিয়ামকরেখা এবং \(X\)-অক্ষকে অক্ষরেখা ধরে পরাবৃত্তের সমীকরণ
Equation of the parabola with the \(Y\)-axis as the directrix and the \(X\)-axis as the focus
পরাবৃত্তের সমীকরণ \(y^2=4a(x-a) \ (a>0)\)
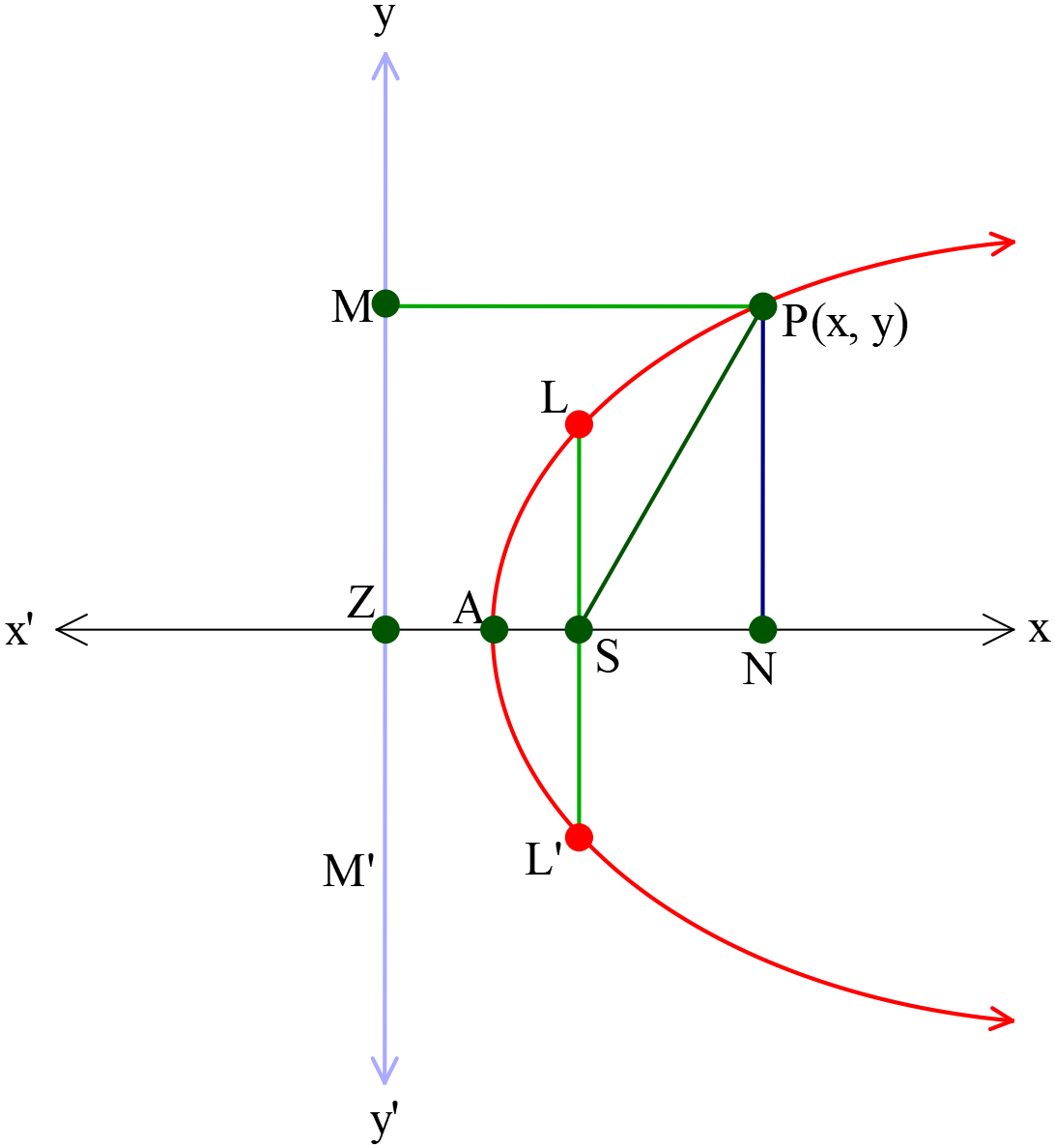
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(a, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(2a, 0)\)
- নিয়ামক রেখার সমীকরণ \(x=0\)
- অক্ষরেখার সমীকরণ \(y=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x-2a=0\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(x-a=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(0, 0)\)
প্রমাণঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(2a, 0)\)
নিয়ামকের সমীকরণ \(x=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-2a)^2+(y-0)^2}=\frac{|x|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-2a)^2+(y-0)^2}=\frac{|x|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x-2a)^2+y^2}=\frac{|x|}{1}\)
\(\Rightarrow \sqrt{x^2-4ax+4a^2+y^2}=|x|\)
\(\Rightarrow x^2-4ax+4a^2+y^2=x^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2+y^2-x^2=4ax-4a^2\)
\(\therefore y^2=4a(x-a)\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(2a, 0)\)
নিয়ামকের সমীকরণ \(x=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-2a)^2+(y-0)^2}=\frac{|x|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-2a)^2+(y-0)^2}=\frac{|x|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x-2a)^2+y^2}=\frac{|x|}{1}\)
\(\Rightarrow \sqrt{x^2-4ax+4a^2+y^2}=|x|\)
\(\Rightarrow x^2-4ax+4a^2+y^2=x^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2+y^2-x^2=4ax-4a^2\)
\(\therefore y^2=4a(x-a)\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
\(X\) অক্ষের সমান্তরাল অক্ষরেখা বিশিষ্ট পরাবৃত্তের সমীকর
Equation of the parabola with axis parallel to the \(X\) axis
পরাবৃত্তের সমীকরণ \(x=ay^2+by+c\)
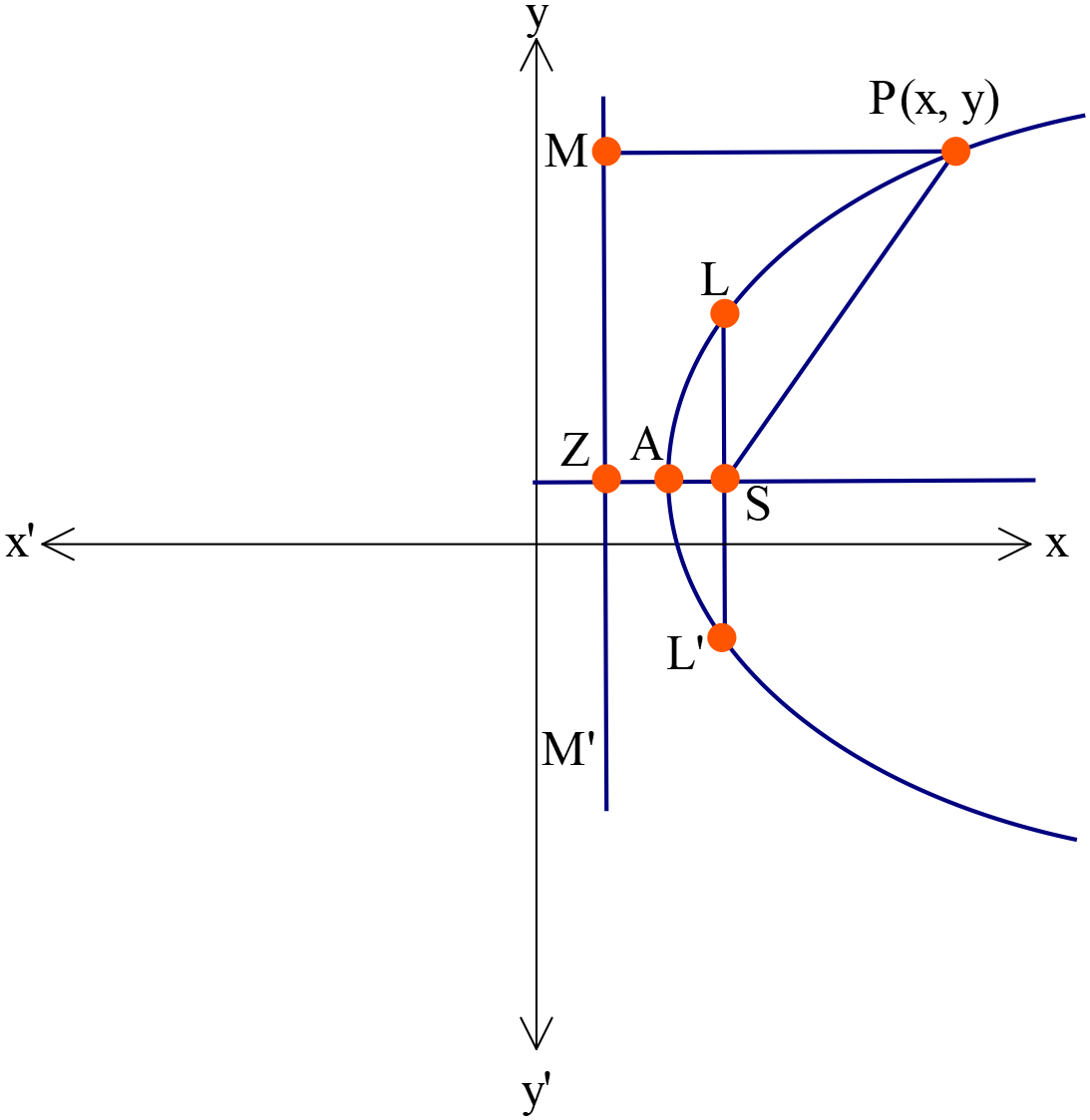
- অক্ষরেখা \(X\) অক্ষের সমান্তরাল।
- শীর্ষবিন্দুর স্থানাঙ্ক \(A\left(-\frac{b^2-4ac}{4a}, -\frac{b}{2a}\right)\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\)
উপরোক্ত পরাবৃত্তের সমীকরণের বিকল্পরূপ \((y-\beta)^2=4a(x-\alpha)\)
- অক্ষরেখা \(X\) অক্ষের সমান্তরাল।
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(\alpha, \beta)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(a+\alpha, \beta)\)
- উপকেন্দ্রিক লম্বের প্রান্ত বিন্দুদ্বয়ের স্থানাংক \((a+\alpha, \pm{2a}+\beta)\)
প্রমাণঃ
ধরি,
পরাবৃত্তের শীর্ষবিন্দু \(A(\alpha, \beta)\)
এবং \(AZ=AS=a\) পরাবৃত্তের অক্ষরেখা \(X\) অক্ষের সমান্তরাল।
পরবৃত্তের ফোকাস \(S(\alpha +a, \beta)\)
এবং নিয়ামকরেখার পাদবিন্দু \(Z(\alpha -a, \beta)\)
নিয়ামক রেখার সমীকরণ \(x=\alpha-a\)
\(\Rightarrow x-\alpha +a=0\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
পরাবৃত্তের সমীকরণ \(PS=PM\)
\(\Rightarrow PS=ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow PS^2=ZN^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow \{x-(\alpha +a)\}^2+(y-\beta)^2=\{x-(\alpha -a)\}^2\) ➜ \(\because ZN=x-(\alpha -a)\)
\(\Rightarrow \{x-\alpha -a\}^2+(y-\beta)^2=\{x-\alpha +a\}^2\)
\(\Rightarrow \{(x-\alpha)-a\}^2+(y-\beta)^2=\{(x-\alpha)+a\}^2\)
\(\Rightarrow (y-\beta)^2=\{(x-\alpha)+a\}^2-\{(x-\alpha)-a\}^2\)
\(\Rightarrow (y-\beta)^2=4(x-\alpha)a\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow (y-\beta)^2=4a(x-\alpha)\)
এখন,
\(4a(x-\alpha)=(y-\beta)^2\)
\(\Rightarrow 4ax-4a\alpha=y^2-2y\beta+\beta^2\)
\(\Rightarrow 4ax=y^2-2y\beta+\beta^2+4a\alpha\)
\(\Rightarrow x=\frac{1}{4a}y^2-\frac{2y\beta}{4a}+\frac{\beta^2+4a\alpha}{4a}\)
\(\Rightarrow x=\frac{1}{4a}y^2+\frac{-\beta}{2a}y+\frac{\beta^2+4a\alpha}{4a} ........(1)\)
ধরি,
\(\acute a=\frac{1}{4a}, b=\frac{-\beta}{2a}, c=\frac{\beta^2+4a\alpha}{4a}\)
তাহলে \((1)\) নং সমীকরণ দাঁড়ায়,
\(x=\acute ay^2+by+c \)
\(\therefore x=ay^2+by+c \) ➜ \(\acute a\) কে \(a\) দ্বারা প্রতিস্থাপন করে।
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
এখন,
\(x=ay^2+by+c \)
\(\Rightarrow ay^2+by+c=x \)
\(\Rightarrow ay^2+by=x-c \)
\(\Rightarrow y^2+\frac{by}{a}=\frac{x-c}{a} \)
\(\Rightarrow y^2+2\frac{b}{2a}y+(\frac{b}{2a})^2=\frac{x-c}{a}+(\frac{b}{2a})^2 \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{x-c}{a}+\frac{b^2}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax-4ac+b^2}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax+b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax}{4a^2}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{x}{a}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{1}{a}\left(x+\frac{b^2-4ac}{4a} \right) \)
\(\Rightarrow Y^2=\frac{1}{a}X ........(2)\) ➜ ধরি, \(X=x+\frac{b^2-4ac}{4a}, Y=y+\frac{b}{2a}\)
\((2)\) নং পরাবৃত্তের ক্ষেত্রে,
শীর্ষ বিন্দু \(A(0, 0 )\)
\(\Rightarrow X=0, Y=0 \)
\(\Rightarrow x+\frac{b^2-4ac}{4a}=0, y+\frac{b}{2a}=0 \) ➜ \(\because X=x+\frac{b^2-4ac}{4a}, Y=y+\frac{b}{2a}\)
\(\therefore x=-\frac{b^2-4ac}{4a}, y=-\frac{b}{2a} \)
\(\therefore \) শীর্ষ বিন্দু দাঁড়ায় \(A\left(-\frac{b^2-4ac}{4a}, -\frac{b}{2a} \right)\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\) ➜ \((2)\) নং পরাবৃত্তের ক্ষেত্রে, \(4a\Rightarrow \frac{1}{a}\)
ধরি,
পরাবৃত্তের শীর্ষবিন্দু \(A(\alpha, \beta)\)
এবং \(AZ=AS=a\) পরাবৃত্তের অক্ষরেখা \(X\) অক্ষের সমান্তরাল।
পরবৃত্তের ফোকাস \(S(\alpha +a, \beta)\)
এবং নিয়ামকরেখার পাদবিন্দু \(Z(\alpha -a, \beta)\)
নিয়ামক রেখার সমীকরণ \(x=\alpha-a\)
\(\Rightarrow x-\alpha +a=0\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
পরাবৃত্তের সমীকরণ \(PS=PM\)
\(\Rightarrow PS=ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow PS^2=ZN^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow \{x-(\alpha +a)\}^2+(y-\beta)^2=\{x-(\alpha -a)\}^2\) ➜ \(\because ZN=x-(\alpha -a)\)
\(\Rightarrow \{x-\alpha -a\}^2+(y-\beta)^2=\{x-\alpha +a\}^2\)
\(\Rightarrow \{(x-\alpha)-a\}^2+(y-\beta)^2=\{(x-\alpha)+a\}^2\)
\(\Rightarrow (y-\beta)^2=\{(x-\alpha)+a\}^2-\{(x-\alpha)-a\}^2\)
\(\Rightarrow (y-\beta)^2=4(x-\alpha)a\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow (y-\beta)^2=4a(x-\alpha)\)
এখন,
\(4a(x-\alpha)=(y-\beta)^2\)
\(\Rightarrow 4ax-4a\alpha=y^2-2y\beta+\beta^2\)
\(\Rightarrow 4ax=y^2-2y\beta+\beta^2+4a\alpha\)
\(\Rightarrow x=\frac{1}{4a}y^2-\frac{2y\beta}{4a}+\frac{\beta^2+4a\alpha}{4a}\)
\(\Rightarrow x=\frac{1}{4a}y^2+\frac{-\beta}{2a}y+\frac{\beta^2+4a\alpha}{4a} ........(1)\)
ধরি,
\(\acute a=\frac{1}{4a}, b=\frac{-\beta}{2a}, c=\frac{\beta^2+4a\alpha}{4a}\)
তাহলে \((1)\) নং সমীকরণ দাঁড়ায়,
\(x=\acute ay^2+by+c \)
\(\therefore x=ay^2+by+c \) ➜ \(\acute a\) কে \(a\) দ্বারা প্রতিস্থাপন করে।
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
এখন,
\(x=ay^2+by+c \)
\(\Rightarrow ay^2+by+c=x \)
\(\Rightarrow ay^2+by=x-c \)
\(\Rightarrow y^2+\frac{by}{a}=\frac{x-c}{a} \)
\(\Rightarrow y^2+2\frac{b}{2a}y+(\frac{b}{2a})^2=\frac{x-c}{a}+(\frac{b}{2a})^2 \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{x-c}{a}+\frac{b^2}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax-4ac+b^2}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax+b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax}{4a^2}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{x}{a}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{1}{a}\left(x+\frac{b^2-4ac}{4a} \right) \)
\(\Rightarrow Y^2=\frac{1}{a}X ........(2)\) ➜ ধরি, \(X=x+\frac{b^2-4ac}{4a}, Y=y+\frac{b}{2a}\)
\((2)\) নং পরাবৃত্তের ক্ষেত্রে,
শীর্ষ বিন্দু \(A(0, 0 )\)
\(\Rightarrow X=0, Y=0 \)
\(\Rightarrow x+\frac{b^2-4ac}{4a}=0, y+\frac{b}{2a}=0 \) ➜ \(\because X=x+\frac{b^2-4ac}{4a}, Y=y+\frac{b}{2a}\)
\(\therefore x=-\frac{b^2-4ac}{4a}, y=-\frac{b}{2a} \)
\(\therefore \) শীর্ষ বিন্দু দাঁড়ায় \(A\left(-\frac{b^2-4ac}{4a}, -\frac{b}{2a} \right)\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\) ➜ \((2)\) নং পরাবৃত্তের ক্ষেত্রে, \(4a\Rightarrow \frac{1}{a}\)
\(y\) অক্ষের সমান্তরাল অক্ষরেখা বিশিষ্ট পরাবৃত্তের সমীকর
Equation of the parabola with axis parallel to the \(y\) axis
পরাবৃত্তের সমীকরণ \(y=ax^2+bx+c\)
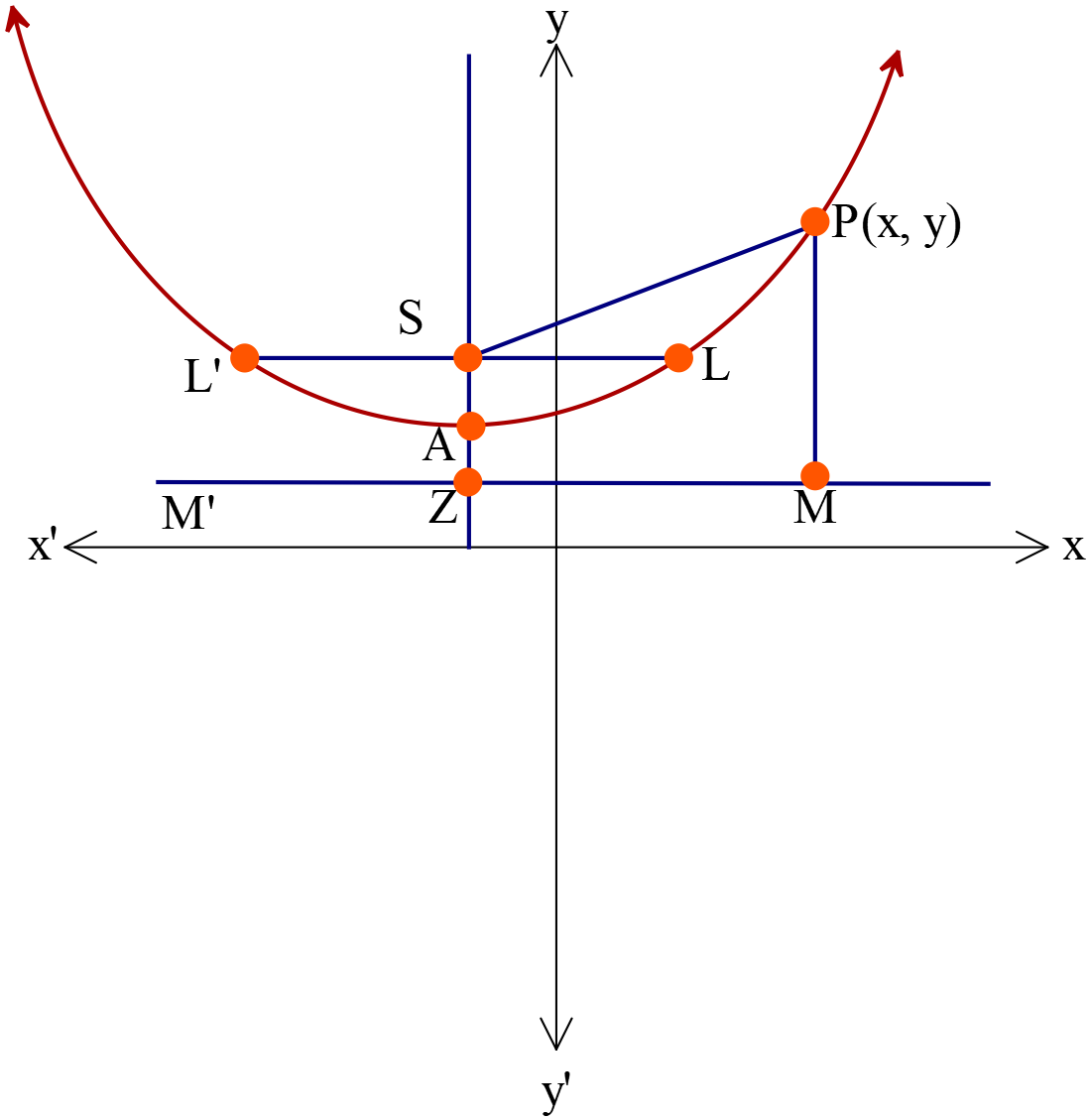
- অক্ষরেখা \(Y\) অক্ষের সমান্তরাল।
- শীর্ষবিন্দুর স্থানাঙ্ক \(A\left(-\frac{b}{2a}, -\frac{b^2-4ac}{4a}\right)\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\)
উপরোক্ত পরাবৃত্তের সমীকরণের বিকল্পরূপ \((x-\alpha)^2=4a(y-\beta)\)
- অক্ষরেখা \(Y\) অক্ষের সমান্তরাল।
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(\alpha, \beta)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(\alpha, a+\beta)\)
- উপকেন্দ্রিক লম্বের প্রান্ত বিন্দুদ্বয়ের স্থানাংক \((\pm{2a}+\alpha, a+\beta)\)
প্রমাণঃ
ধরি,
পরাবৃত্তের শীর্ষবিন্দু \(A(\alpha, \beta)\)
এবং \(AZ=AS=a\) পরাবৃত্তের অক্ষরেখা \(Y\) অক্ষের সমান্তরাল।
পরবৃত্তের ফোকাস \(S(\alpha, \beta +a)\)
এবং নিয়ামকরেখার পাদবিন্দু \(Z(\alpha, \beta -a)\)
নিয়ামক রেখার সমীকরণ \(y=\beta -a\)
\(\Rightarrow y-\beta +a=0\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
পরাবৃত্তের সমীকরণ \(PS=PM\)
\(\Rightarrow PS=ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow PS^2=ZN^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-\alpha)^2+\{y-(\beta +a)\}^2=\{y-(\beta -a)\}^2\) ➜ \(\because ZN=y-(\beta -a)\)
\(\Rightarrow (x-\alpha)^2+\{y-\beta -a\}^2=\{y-\beta +a\}^2\)
\(\Rightarrow (x-\alpha)^2+\{(y-\beta) -a\}^2=\{(y-\beta)+a\}^2\)
\(\Rightarrow (x-\alpha)^2=\{(y-\beta)+a\}^2-\{(y-\beta)-a\}^2\)
\(\Rightarrow (x-\alpha)^2=4(y-\beta)a\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow (x-\alpha)^2=4a(y-\beta)\)
এখন,
\(4a(y-\beta)=(x-\alpha)^2\)
\(\Rightarrow 4ay-4a\beta=x^2-2x\alpha+\alpha^2\)
\(\Rightarrow 4ay=x^2-2x\alpha+\alpha^2+4a\beta\)
\(\Rightarrow y=\frac{1}{4a}x^2-\frac{2x\alpha}{4a}+\frac{\alpha^2+4a\beta}{4a}\)
\(\Rightarrow x=\frac{1}{4a}x^2+\frac{-\alpha}{2a}x+\frac{\alpha^2+4a\beta}{4a} ........(1)\)
ধরি,
\(\acute a=\frac{1}{4a}, b=\frac{-\alpha}{2a}, c=\frac{\alpha^2+4a\beta}{4a}\)
তাহলে \((1)\) নং সমীকরণ দাঁড়ায়,
\(y=\acute ax^2+bx+c \)
\(\therefore y=ax^2+bx+c \) ➜ \(\acute a\) কে \(a\) দ্বারা প্রতিস্থাপন করে।
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
এখন,
\(y=ax^2+bx+c \)
\(\Rightarrow ax^2+bx+c=y \)
\(\Rightarrow ax^2+bx=y-c \)
\(\Rightarrow x^2+\frac{bx}{a}=\frac{y-c}{a} \)
\(\Rightarrow x^2+2\frac{b}{2a}x+(\frac{b}{2a})^2=\frac{y-c}{a}+(\frac{b}{2a})^2 \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{y-c}{a}+\frac{b^2}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay-4ac+b^2}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay+b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay}{4a^2}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{y}{a}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{1}{a}\left(y+\frac{b^2-4ac}{4a} \right) \)
\(\Rightarrow X^2=\frac{1}{a}Y ........(2)\) ➜ ধরি, \(X=x+\frac{b}{2a}, Y=y+\frac{b^2-4ac}{4a}, \)
\((2)\) নং পরাবৃত্তের ক্ষেত্রে,
শীর্ষ বিন্দু \(A(0, 0 )\)
\(\Rightarrow X=0, Y=0 \)
\(\Rightarrow x+\frac{b}{2a}=0, y+\frac{b^2-4ac}{4a}=0 \) ➜ \(\because X=x+\frac{b}{2a}, Y=y+\frac{b^2-4ac}{4a},\)
\(\therefore x=-\frac{b}{2a}, y=-\frac{b^2-4ac}{4a} \)
\(\therefore \) শীর্ষ বিন্দু দাঁড়ায় \(A\left(-\frac{b}{2a}, -\frac{b^2-4ac}{4a} \right)\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\) ➜ \((2)\) নং পরাবৃত্তের ক্ষেত্রে, \(4a\Rightarrow \frac{1}{a}\)
ধরি,
পরাবৃত্তের শীর্ষবিন্দু \(A(\alpha, \beta)\)
এবং \(AZ=AS=a\) পরাবৃত্তের অক্ষরেখা \(Y\) অক্ষের সমান্তরাল।
পরবৃত্তের ফোকাস \(S(\alpha, \beta +a)\)
এবং নিয়ামকরেখার পাদবিন্দু \(Z(\alpha, \beta -a)\)
নিয়ামক রেখার সমীকরণ \(y=\beta -a\)
\(\Rightarrow y-\beta +a=0\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
পরাবৃত্তের সমীকরণ \(PS=PM\)
\(\Rightarrow PS=ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow PS^2=ZN^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-\alpha)^2+\{y-(\beta +a)\}^2=\{y-(\beta -a)\}^2\) ➜ \(\because ZN=y-(\beta -a)\)
\(\Rightarrow (x-\alpha)^2+\{y-\beta -a\}^2=\{y-\beta +a\}^2\)
\(\Rightarrow (x-\alpha)^2+\{(y-\beta) -a\}^2=\{(y-\beta)+a\}^2\)
\(\Rightarrow (x-\alpha)^2=\{(y-\beta)+a\}^2-\{(y-\beta)-a\}^2\)
\(\Rightarrow (x-\alpha)^2=4(y-\beta)a\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow (x-\alpha)^2=4a(y-\beta)\)
এখন,
\(4a(y-\beta)=(x-\alpha)^2\)
\(\Rightarrow 4ay-4a\beta=x^2-2x\alpha+\alpha^2\)
\(\Rightarrow 4ay=x^2-2x\alpha+\alpha^2+4a\beta\)
\(\Rightarrow y=\frac{1}{4a}x^2-\frac{2x\alpha}{4a}+\frac{\alpha^2+4a\beta}{4a}\)
\(\Rightarrow x=\frac{1}{4a}x^2+\frac{-\alpha}{2a}x+\frac{\alpha^2+4a\beta}{4a} ........(1)\)
ধরি,
\(\acute a=\frac{1}{4a}, b=\frac{-\alpha}{2a}, c=\frac{\alpha^2+4a\beta}{4a}\)
তাহলে \((1)\) নং সমীকরণ দাঁড়ায়,
\(y=\acute ax^2+bx+c \)
\(\therefore y=ax^2+bx+c \) ➜ \(\acute a\) কে \(a\) দ্বারা প্রতিস্থাপন করে।
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
এখন,
\(y=ax^2+bx+c \)
\(\Rightarrow ax^2+bx+c=y \)
\(\Rightarrow ax^2+bx=y-c \)
\(\Rightarrow x^2+\frac{bx}{a}=\frac{y-c}{a} \)
\(\Rightarrow x^2+2\frac{b}{2a}x+(\frac{b}{2a})^2=\frac{y-c}{a}+(\frac{b}{2a})^2 \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{y-c}{a}+\frac{b^2}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay-4ac+b^2}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay+b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay}{4a^2}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{y}{a}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{1}{a}\left(y+\frac{b^2-4ac}{4a} \right) \)
\(\Rightarrow X^2=\frac{1}{a}Y ........(2)\) ➜ ধরি, \(X=x+\frac{b}{2a}, Y=y+\frac{b^2-4ac}{4a}, \)
\((2)\) নং পরাবৃত্তের ক্ষেত্রে,
শীর্ষ বিন্দু \(A(0, 0 )\)
\(\Rightarrow X=0, Y=0 \)
\(\Rightarrow x+\frac{b}{2a}=0, y+\frac{b^2-4ac}{4a}=0 \) ➜ \(\because X=x+\frac{b}{2a}, Y=y+\frac{b^2-4ac}{4a},\)
\(\therefore x=-\frac{b}{2a}, y=-\frac{b^2-4ac}{4a} \)
\(\therefore \) শীর্ষ বিন্দু দাঁড়ায় \(A\left(-\frac{b}{2a}, -\frac{b^2-4ac}{4a} \right)\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\) ➜ \((2)\) নং পরাবৃত্তের ক্ষেত্রে, \(4a\Rightarrow \frac{1}{a}\)
পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য
Letus rectum of parabola
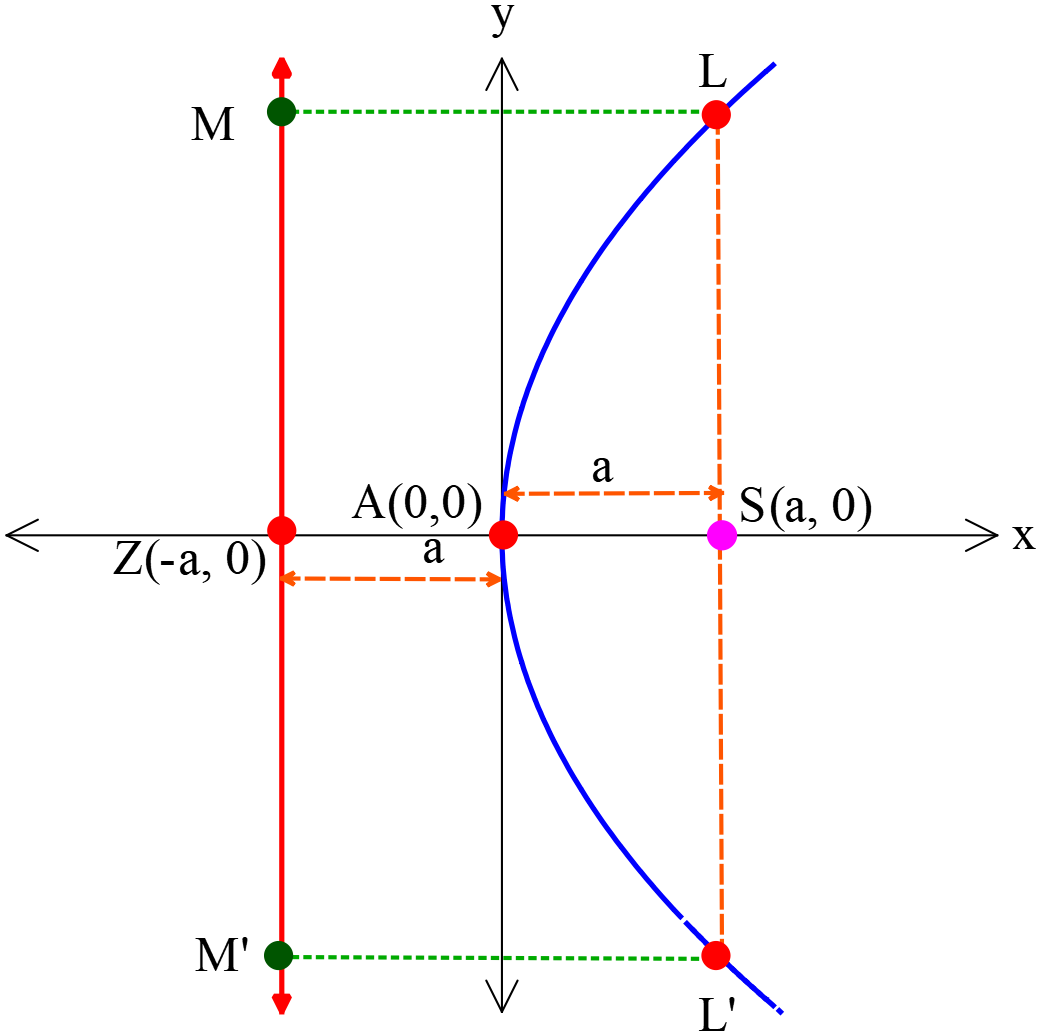 পরাবৃত্তের উপকেন্দ্র দিয়ে যার এবং এর অক্ষরেখার উপর লম্ব হয়, এরূপ জ্যাকে এর উপকেন্দ্রিক লম্ব (Letus rectum) বলা হয়। \(y^2=4ax\) পরাবৃত্তের \(AS\) অক্ষরেখার উপর \(L\acute{L}\) লম্ব আঁকি। সুতরাং \(L\acute{L}\) পরাবৃত্তটির উপকেন্দ্রিক লম্ব, এর উপকেন্দ্রের স্থানাঙ্ক \(S(a, 0)\) । \(L\acute{L}\) উপকেন্দ্রিক লম্বটি \(S\) বিন্দুতে সমদ্বিখণ্ডিত হয়। \(L\) বিন্দু থেকে \(MZ\acute{M}\)-এর উপর \(LM\) লম্ব আঁকি।
পরাবৃত্তের উপকেন্দ্র দিয়ে যার এবং এর অক্ষরেখার উপর লম্ব হয়, এরূপ জ্যাকে এর উপকেন্দ্রিক লম্ব (Letus rectum) বলা হয়। \(y^2=4ax\) পরাবৃত্তের \(AS\) অক্ষরেখার উপর \(L\acute{L}\) লম্ব আঁকি। সুতরাং \(L\acute{L}\) পরাবৃত্তটির উপকেন্দ্রিক লম্ব, এর উপকেন্দ্রের স্থানাঙ্ক \(S(a, 0)\) । \(L\acute{L}\) উপকেন্দ্রিক লম্বটি \(S\) বিন্দুতে সমদ্বিখণ্ডিত হয়। \(L\) বিন্দু থেকে \(MZ\acute{M}\)-এর উপর \(LM\) লম্ব আঁকি।পরাবৃত্তের সংজ্ঞানুসারে,
\(SL=ML\)
\(=ZS\)
\(=ZA+AS\)
\(=a+a\)
\(=2a\)
অনুরূপভাবে,
\(S\acute{L}=-2a\)
পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য্
\(L\acute{L}=|2a-(-2a)|=|2a+2a|=|4a|\)
আবার,
পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য,
\(L\acute{L}=SL+S\acute{L}\)
\(=SL+SL\)
\(=2SL\)
\(=2\times ML\)
\(=2\times SZ\)
\(=2\times \) উপকেন্দ্র হতে নিয়ামকরেখার লম্বদূরত্ব।
\(\therefore \) পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=2\times \) উপকেন্দ্র হতে নিয়ামকরেখার লম্বদূরত্ব।
কনিকের সাধারণ সমীকরণ শনাক্তকরণ
Identification of Conic's general equation
এখানে, \(\Delta \equiv abc+2fgh-af^2-bg^2-ch^2\)
- \(\Delta\ne{0},\) \(a=b\) এবং \(h=0\) হলে, কনিকটি একটি বৃত্ত নির্দেশ করবে।
- \(\Delta\ne{0}, \ ab-h^2=0\) এবং \(a+b\ne{0}\) হলে, কনিকটি একটি পরাবৃত্ত নির্দেশ করবে।
- \(\Delta\ne{0}, \ ab-h^2>0\) এবং \(a+b\ne{0}\) হলে, কনিকটি একটি উপবৃত্ত নির্দেশ করবে।
- \(\Delta\ne{0}, \ ab-h^2<0\) এবং \(a+b\ne{0}\) হলে, কনিকটি একটি অধিবৃত্ত নির্দেশ করবে।
- \(\Delta\ne{0}, \ ab-h^2<0 \) এবং \(a+b=0\) হলে, কনিকটি একটি আয়াতাকার অধিবৃত্ত নির্দেশ করবে।
- \(\Delta=0\) হলে, কনিকটি একজোড়া সরলরেখা নির্দেশ করবে।
কোনো সরলরেখা পরাবৃত্তের স্পর্শক হওয়ার শর্ত
Condition for a straight line to be tangent to a parabola
কোনো সরলরেখা পরাবৃত্তের স্পর্শক হওয়ার শর্ত, স্পর্শকের সমীকরণ এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও পরাবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(y^2=4ax ........(2) \)
সরলরেখা ও পরাবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(y^2=4ax ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং পরাবৃত্তকে স্পর্শ করার শর্তঃ \(c=\frac{a}{m}\)
স্পর্শকের সমীকরণঃ \(y=mx+\frac{a}{m}\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{a}{m^2}, \frac{2a}{m}\right)\)
প্রমাণঃ
ধরি,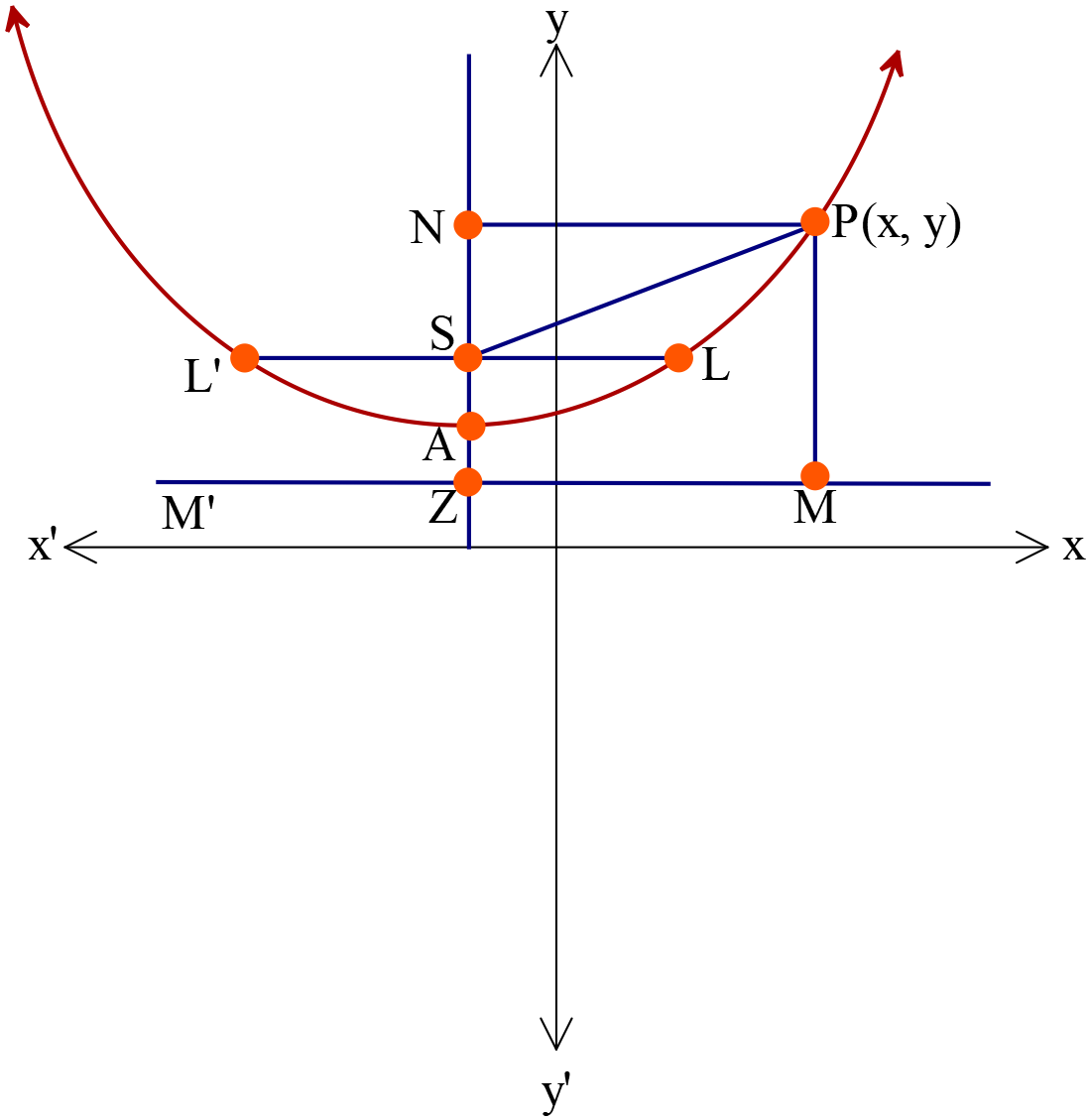
পরাবৃত্তের সমীকরণ \(y^2=4ax ....(1)\)
\(PQ\) সরলরেখার সমীকরণ \(y=mx+c ....(2)\)
পরাবৃত্তের উপর \(P\) একটি বিন্দু এবং \(PQ\) যে কোনো ছেদকরেখা। \(Q\) বিন্দু ক্রমশ \(P\) বিন্দুর দিকে অগ্রসর হয়ে \(P\) বিন্দুর উপর সমপতিত হলে ছেদকরেখাটি \(P\) বিন্দুতে উৎপন্ন পরাবৃত্তের একটি স্পর্শক হবে।
\((1)\) ও \((2)\) হতে,
\((mx+c)^2=4ax\)
\(\Rightarrow m^2x^2+2mcx+c^2=4ax\)
\(\Rightarrow m^2x^2+2mcx-4ax+c^2=0\)
\(\therefore m^2x^2+2(mc-2a)x+c^2=0 .......(3)\)
\(PQ\) সরলরেখাটি \((1)\) নং পরাবৃত্তের একটি স্পর্শক হবে যদি \((3)\) নং সমীকরণের মূলদ্বয় সমান হয়।
\(\therefore \{2(mc-2a)\}^2=4m^2c^2\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow 4(mc-2a)^2=4m^2c^2\)
\(\Rightarrow (mc-2a)^2=m^2c^2\)
\(\Rightarrow m^2c^2-4amc+4a^2=m^2c^2\)
\(\Rightarrow -4amc+4a^2=m^2c^2-m^2c^2\)
\(\Rightarrow -4amc+4a^2=0\)
\(\Rightarrow -4amc=-4a^2\)
\(\Rightarrow amc=a^2\)
\(\Rightarrow c=\frac{a^2}{am}\)
\(\therefore c=\frac{a}{m}\)
ইহাই নির্ণেয় স্পর্শক হওয়ার শর্ত।
আবার,
\((3)\) নং সমীকরণে \(c=\frac{a}{m}\) বসিয়ে,
\(m^2x^2+2\left(m\times \frac{a}{m}-2a\right)x+(\frac{a}{m})^2=0\)
\(\Rightarrow m^2x^2+2\left(a-2a\right)x+\frac{a^2}{m^2}=0\)
\(\Rightarrow m^2x^2-2ax+\frac{a^2}{m^2}=0\)
\(\Rightarrow \left(mx-\frac{a}{m}\right)^2=0\)
\(\Rightarrow mx-\frac{a}{m}=0\)
\(\Rightarrow mx=\frac{a}{m}\)
\(\therefore x=\frac{a}{m^2}\)
আবার,
\((3)\) নং সমীকরণ হতে,
\(y=m\times \frac{a}{m^2}+\frac{a}{m}\)
\(\Rightarrow y=\frac{a}{m}+\frac{a}{m}\)
\(\therefore y=\frac{2a}{m}\)
\(\therefore\) স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{a}{m^2},\frac{2a}{m}\right)\)
ধরি,

পরাবৃত্তের সমীকরণ \(y^2=4ax ....(1)\)
\(PQ\) সরলরেখার সমীকরণ \(y=mx+c ....(2)\)
পরাবৃত্তের উপর \(P\) একটি বিন্দু এবং \(PQ\) যে কোনো ছেদকরেখা। \(Q\) বিন্দু ক্রমশ \(P\) বিন্দুর দিকে অগ্রসর হয়ে \(P\) বিন্দুর উপর সমপতিত হলে ছেদকরেখাটি \(P\) বিন্দুতে উৎপন্ন পরাবৃত্তের একটি স্পর্শক হবে।
\((1)\) ও \((2)\) হতে,
\((mx+c)^2=4ax\)
\(\Rightarrow m^2x^2+2mcx+c^2=4ax\)
\(\Rightarrow m^2x^2+2mcx-4ax+c^2=0\)
\(\therefore m^2x^2+2(mc-2a)x+c^2=0 .......(3)\)
\(PQ\) সরলরেখাটি \((1)\) নং পরাবৃত্তের একটি স্পর্শক হবে যদি \((3)\) নং সমীকরণের মূলদ্বয় সমান হয়।
\(\therefore \{2(mc-2a)\}^2=4m^2c^2\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow 4(mc-2a)^2=4m^2c^2\)
\(\Rightarrow (mc-2a)^2=m^2c^2\)
\(\Rightarrow m^2c^2-4amc+4a^2=m^2c^2\)
\(\Rightarrow -4amc+4a^2=m^2c^2-m^2c^2\)
\(\Rightarrow -4amc+4a^2=0\)
\(\Rightarrow -4amc=-4a^2\)
\(\Rightarrow amc=a^2\)
\(\Rightarrow c=\frac{a^2}{am}\)
\(\therefore c=\frac{a}{m}\)
ইহাই নির্ণেয় স্পর্শক হওয়ার শর্ত।
আবার,
\((3)\) নং সমীকরণে \(c=\frac{a}{m}\) বসিয়ে,
\(m^2x^2+2\left(m\times \frac{a}{m}-2a\right)x+(\frac{a}{m})^2=0\)
\(\Rightarrow m^2x^2+2\left(a-2a\right)x+\frac{a^2}{m^2}=0\)
\(\Rightarrow m^2x^2-2ax+\frac{a^2}{m^2}=0\)
\(\Rightarrow \left(mx-\frac{a}{m}\right)^2=0\)
\(\Rightarrow mx-\frac{a}{m}=0\)
\(\Rightarrow mx=\frac{a}{m}\)
\(\therefore x=\frac{a}{m^2}\)
আবার,
\((3)\) নং সমীকরণ হতে,
\(y=m\times \frac{a}{m^2}+\frac{a}{m}\)
\(\Rightarrow y=\frac{a}{m}+\frac{a}{m}\)
\(\therefore y=\frac{2a}{m}\)
\(\therefore\) স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{a}{m^2},\frac{2a}{m}\right)\)
পরাবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুতে স্পর্শকের সমীকরণ
Equation of the tangent at a given point on the parabola
মনে করি,
একটি নির্দিষ্ট বিন্দু এবং একটি পরাবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(y^2=4ax ........(1) \)
একটি নির্দিষ্ট বিন্দু এবং একটি পরাবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(y^2=4ax ........(1) \)
\((1)\) নং পরাবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণ \(yy_1=2a(x+x_1)\)
\(y^2=4ax\) পরাবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণ \(yy_1=2a(x+x_1)\)
\(x^2=4ay\) পরাবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণ \(xx_1=2a(y+y_1)\)
পরাবৃত্তের জ্যা এর সমীকরণ যার মধ্যবিন্দু দেয়া আছে
Equation of the chord of a parabola whose midpoint is given
\(y^2=4ax\) পরাবৃত্তের জ্যা এর সমীকরণ, যার মধ্যবিন্দু \(P(x_1, y_1)\)
\(yy_1-2a(x+x_1)=y_{1}^2-4ax_{1}\)
\(yy_1-2a(x+x_1)=y_{1}^2-4ax_{1}\)

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004