এ অধ্যায়ের পাঠ্যসূচী
- ত্রিকোণমিতিক বা বৃত্তীয় ফাংশন (Trigonometric or Circular function)
- ত্রিকোণমিতিক বা বৃত্তীয় ফাংশনের ডোমেন ও রেঞ্জ (Domain and Range of Trigonometric or Circular function)
- ত্রিকোণমিতিক বা বৃত্তীয় ফাংশনের পর্যায়কাল (Period of Trigonometric or Circular function)
- যুক্ত ফাংশনের পর্যায়কাল (Period of added function)
- ত্রিকোণমিতিক বা বৃত্তীয় ফাংশনের মাণের পরিবর্তন (Change of the values of Trigonometric or Circular function)
- ত্রিকোণমিতিক বা বৃত্তীয় ফাংশনের লেখচিত্র (Graph of Trigonometric or Circular function)
- \(y=\sin{x}, \ -2\pi\leq{x}\leq{2\pi}\) ফাংশনের লেখচিত্র (Graph of \(y=\sin{x}, \ -2\pi\leq{x}\leq{2\pi}\) function)
- \(y=\cos{x}, \ -2\pi\leq{x}\leq{2\pi}\) ফাংশনের লেখচিত্র (Graph of \(y=\cos{x}, \ -2\pi\leq{x}\leq{2\pi}\) function)
- \(y=\tan{x}, \ -\frac{\pi}{2}\leq{x}\leq{\frac{\pi}{2}}\) ফাংশনের লেখচিত্র (Graph of \(y=\tan{x}, \ -\frac{\pi}{2}\leq{x}\leq{\frac{\pi}{2}}\) function)
- \(y=cosec \ {x}, \ -\pi\leq{x}\leq{\pi}\) ফাংশনের লেখচিত্র (Graph of \(y=cosec \ {x}, \ -\pi\leq{x}\leq{\pi}\) function)
- \(y=\sec{x}, \ -\pi\leq{x}\leq{\pi}\) ফাংশনের লেখচিত্র (Graph of \(y=\sec{x}, \ -\pi\leq{x}\leq{\pi}\) function)
- \(y=\cot{x}, \ -\pi\leq{x}\leq{\pi}\) ফাংশনের লেখচিত্র (Graph of \(y=\cot{x}, \ -\pi\leq{x}\leq{\pi}\) function)
- \(y=\tan{x}, \ -\frac{3\pi}{2}\leq{x}\leq{\frac{3\pi}{2}}\) ফাংশনের লেখচিত্র (Graph of \(y=\tan{x}, \ -\frac{3\pi}{2}\leq{x}\leq{\frac{3\pi}{2}}\) function)
- অধ্যায় \(vi.C\)-এর উদাহরণসমুহ
- অধ্যায় \(vi.C\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(vi.C\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(vi.C\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(vi.C\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
ত্রিকোণমিতিক বা বৃত্তীয় ফাংশন
Trigonometric or Circular function
কোণ পরিমাপের বৃত্তীয় একক হচ্ছে রেডিয়ান। ত্রিকোণমিতিক ফাংশনসমূহ যেমনঃ \(\sin{\theta}, \ \cos{\theta}, ....\) ইত্যাদির কোণ \(\theta\) কে সাধারণত রেডিয়ানে পরিমাপ করা হয়। এ জন্য এ ফাংশনগুলি বৃত্তীয় ফাংশন নামে পরিচিত।
ত্রিকোণমিতিক ফাংশনগুলির মধ্যে \(\tan{\theta}, \ cosec \ {\theta}, \ \sec{\theta}, \ \cot{\theta}\) ইত্যাদিকে \(\sin{\theta}, \ \cos{\theta}\) এর মাধ্যমে প্রকাশ করা যায়। আবার, যে কোনো বৃত্তের সমীকরণকে \(\sin{\theta}, \ \cos{\theta}\) এর মাধ্যমে প্রকাশ করা যায় বিধায় ফাংশনগুলিকে বৃত্তীয় ফাংশন বলা হয়ে থাকে।
যেমনঃ \(x^2+y^2=5^2\) বৃত্তকে \(x=5\cos{\theta}, \ y=5\sin{\theta}\) দ্বারা,
\(x^2+y^2=7^2\) বৃত্তকে \(x=7\cos{\theta}, \ y=7\sin{\theta}\) দ্বারা,
\((x-2)^2+(y-1)^2=2^2\) বৃত্তকে \(x-2=2\cos{\theta}, \ y-1=2\sin{\theta}\) দ্বারা প্রকাশ করা যায়।
ত্রিকোণমিতিক ফাংশনগুলির মধ্যে \(\tan{\theta}, \ cosec \ {\theta}, \ \sec{\theta}, \ \cot{\theta}\) ইত্যাদিকে \(\sin{\theta}, \ \cos{\theta}\) এর মাধ্যমে প্রকাশ করা যায়। আবার, যে কোনো বৃত্তের সমীকরণকে \(\sin{\theta}, \ \cos{\theta}\) এর মাধ্যমে প্রকাশ করা যায় বিধায় ফাংশনগুলিকে বৃত্তীয় ফাংশন বলা হয়ে থাকে।
যেমনঃ \(x^2+y^2=5^2\) বৃত্তকে \(x=5\cos{\theta}, \ y=5\sin{\theta}\) দ্বারা,
\(x^2+y^2=7^2\) বৃত্তকে \(x=7\cos{\theta}, \ y=7\sin{\theta}\) দ্বারা,
\((x-2)^2+(y-1)^2=2^2\) বৃত্তকে \(x-2=2\cos{\theta}, \ y-1=2\sin{\theta}\) দ্বারা প্রকাশ করা যায়।
ত্রিকোণমিতিক বা বৃত্তীয় ফাংশনের ডোমেন ও রেঞ্জ
Domain and Range of Trigonometric or Circular function
 বৃত্তীয় ফাংশনের ডোমেন ও রেঞ্জ নির্ণয়ের জন্য প্রথমে ফাংশনগুলিকে সংজ্ঞায়িত করা প্রয়োজন। যে কোনো \(\theta\) কোণের জন্য ঘূর্ণায়মান সরলরেখার শেষ অবস্থানের ওপর \(P(x,y)\) একটি বিন্দু হলে,
বৃত্তীয় ফাংশনের ডোমেন ও রেঞ্জ নির্ণয়ের জন্য প্রথমে ফাংশনগুলিকে সংজ্ঞায়িত করা প্রয়োজন। যে কোনো \(\theta\) কোণের জন্য ঘূর্ণায়মান সরলরেখার শেষ অবস্থানের ওপর \(P(x,y)\) একটি বিন্দু হলে,\(\sin{\theta}=\frac{y}{r}, \ \cos{\theta}=\frac{x}{r}, \ \tan{\theta}=\frac{y}{x}, \ cosec \ {\theta}=\frac{r}{y}, \ \sec{\theta}=\frac{r}{x}, \ \cot{\theta}=\frac{x}{y}\) যেখানে, \(r=\sqrt{x^2+y^2}\)
এখন, \(\theta\) কোণের অবস্থান যে কোনো চতুর্ভাগে হতে পারে বিধায় \(x\) ও \(y\) এর মাণ ধনাত্মক ও ঋণাত্মক হতে পারে। এমনকি ঘূর্ণায়মান সরলরেখা অক্ষের সাথে মিলিয়ে গেলে \(x\) অথবা \(y\) এর মাণ শূন্যও হতে পারে।
\(\theta\) এর যে কোনো বাস্তব মাণের জন্য \(\sin{\theta}\) ও \(\cos{\theta}\) এর বাস্তব মাণ পাওয়া যায়।
কাজেই
\(\sin{\theta}\) ও \(\cos{\theta}\) উভয়ের ডোমেন \(=\mathbb{R}\)
যখন \(x\) ও \(y\) উভয়ে ধণাত্মক, তখন \(\frac{x}{r}\lt{1}\) এবং \(\frac{y}{r}\lt{1}.\)
আবার, যখন \(x\) ও \(y\) উভয়ে ঋণাত্মক অথবা পরস্পর বিপরীত চিহ্নবিশিষ্ট, তখন \(\frac{x}{r}\gt{-1}\) এবং \(\frac{y}{r}\gt{-1}.\)
\(x\ne{0}\) এবং \(y\ne{0}\) হলে,
অর্থাৎ কোণ উৎপাদনকারী ঘূর্ণায়মান সরলরেখার অবস্থান যে কোনো চতুর্ভাগে হোক না কেন,
\(-1\lt{\sin{\theta}}\lt{1}\)
এবং
\(-1\lt{\cos{\theta}}\lt{1}\)
\(x=0\) এবং \(y\) ধনাত্মক বা ঋণাত্মক হলে, কোণ উৎপাদনকারী ঘূর্ণায়মান সরলরেখা আদিরেখার সাথে \(\frac{\pi}{2}\) বা \(\frac{3\pi}{2}\) কোণ উৎপন্ন করে।
সে ক্ষেত্রে \(\sin{\frac{\pi}{2}}=1, \ \sin{\frac{3\pi}{2}}=-1, \ \cos{\frac{\pi}{2}}=0, \ \cos{\frac{3\pi}{2}}=0\)
আবার, \(y=0\) এবং \(x\) ধনাত্মক বা ঋণাত্মক হলে, কোণ উৎপাদনকারী ঘূর্ণায়মান সরলরেখা আদিরেখার সাথে \(0, \ \pi\) বা \(2\pi\) কোণ উৎপন্ন করে।
সে ক্ষেত্রে \(\sin{0}=0, \ \sin{\pi}=0, \ \sin{2\pi}=0, \ \cos{0}=1, \ \cos{\pi}=-1, \ \cos{2\pi}=1\)
সুতরাং \(0\leq{\theta}\leq{2\pi}\) ব্যবধিতে যে কোনো কোণের জন্য
\(-1\leq{\sin{\theta}}\leq{1}\)
এবং
\(-1\leq{\cos{\theta}}\leq{1}\)
কাজেই
\(\sin{\theta}\) ও \(\cos{\theta}\) উভয়ের রেঞ্জ \(=[-1, 1]\)
\(\cos{\theta}=0\) অর্থাৎ \(\theta=\pm{(2n-1)\frac{\pi}{2}}, \ n\in{\mathbb{N}}\) এর জন্য
\(\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}=\infty\)
সুতরাং \(\theta=\pm{(2n-1)\frac{\pi}{2}}, \ n\in{\mathbb{N}}\) এর জন্য
\(\tan{\theta}\) এর ডোমেন \(=\mathbb{R}-\{\pm{(2n-1)\frac{\pi}{2}}, \ n\in{\mathbb{N}}\}\)
আবার, \(x\ne{0}, \ x\) ও \(y\) একই চিহ্নবিশিষ্ট হলে, এবং \(x\) কে স্থির রেখে \(y\) কে ক্রমাগতভানে বৃদ্ধি করলে
অর্থাৎ \(y\rightarrow{\infty}\) হলে, \(\tan{\theta}=\frac{y}{x}\rightarrow{\infty}\) হয়।
আবার, \(y\) কে স্থির রেখে \(x\) কে ক্রমাগতভানে হ্রাস করলেও
\(\tan{\theta}=\frac{y}{x}\rightarrow{\infty}\) হয়।
অন্যথায় \(x\) ও \(y\) বিপরীত চিহ্নবিশিষ্ট হলে, এবং \(x\) কে স্থির রেখে \(y\) কে ক্রমাগতভানে বৃদ্ধি
অথবা, \(y\) কে স্থির রেখে \(x\) কে ক্রমাগতভানে হ্রাস করলেও
\(\tan{\theta}=\frac{y}{x}\rightarrow{-\infty}\) হয়।
অর্থাৎ
\(-\infty\lt{\tan{\theta}}\lt{\infty}\)
কাজেই
\(\tan{\theta}\) এর রেঞ্জ \(=\mathbb{R}\)
যেহেতু \(\tan{\theta}=0\Rightarrow \cot{\theta}=\infty\)
অর্থাৎ \(\tan{\theta}=0\) অথবা, \(\theta=\pm{(n-1)\pi}, \ n\in{\mathbb{N}}\) এর জন্য
\(\cot{\theta}=\infty\) হয়।
কাজেই
\(\cot{\theta}\) এর ডোমেন \(=\mathbb{R}-\{\pm{(n-1)\pi}, \ n\in{\mathbb{N}}\}\)
এখন, \(-\infty\lt{\tan{\theta}}\lt{-0}\)
\(\Rightarrow -\frac{1}{0}\lt{\frac{1}{\cot{\theta}}}\lt{-0}\)
\(\Rightarrow -\frac{0}{1}\gt{\frac{\cot{\theta}}{1}}\gt{-\frac{1}{0}}\)
\(\therefore 0\gt{\cot{\theta}}\gt{-\infty}\)
আবার, \(+0\lt{\tan{\theta}}\lt{+\infty}\)
\(\Rightarrow +0\lt{\frac{1}{\cot{\theta}}}\lt{+\frac{1}{0}}\)
\(\Rightarrow +\frac{1}{0}\gt{\frac{\cot{\theta}}{1}}\gt{+\frac{0}{1}}\)
\(\therefore +\infty\gt{\cot{\theta}}\gt{0}\)
সতুরাং \(-\infty\lt{\cot{\theta}}\lt{+\infty}\)
কাজেই
\(\cot{\theta}\) এর রেঞ্জ \(=\mathbb{R}\)
যেহেতু \(\cos{\theta}=0\Rightarrow \sec{\theta}=\infty\)
অর্থাৎ \(\cos{\theta}=0\) অথবা, \(\theta=\pm{(2n-1)\frac{\pi}{2}}, \ n\in{\mathbb{N}}\) এর জন্য
\(\sec{\theta}=\infty\) হয়।
কাজেই
\(\sec{\theta}\) এর ডোমেন \(=\mathbb{R}-\{\pm{(2n-1)\frac{\pi}{2}}, \ n\in{\mathbb{N}}\}\)
এখন, \(\sec{\theta}=\frac{r}{x}\)
ফলে, \(x\) ও \(y\) ধনাত্মক হলে, \(\frac{r}{x}\gt{1}\)
এবং \(x\) ও \(y\) উভয়ে ঋণাত্মক বা পরস্পর বিপরীত চিহ্নবিশিষ্ট হলে , \(\frac{r}{x}\lt{-1}\)
অর্থাৎ \(\sec{\theta}\) এর মাণ \((-1, 1)\) ব্যবধিতে বিদ্যমান নেই।
কাজেই
\(\sec{\theta}\) এর রেঞ্জ \(=\mathbb{R}-(-1,1)\)
যেহেতু \(\sin{\theta}=0\Rightarrow cosec \ {\theta}=\infty\)
অর্থাৎ \(\sin{\theta}=0\) অথবা, \(\theta=\pm{(n-1)\pi}, \ n\in{\mathbb{N}}\) এর জন্য
\(cosec \ {\theta}=\infty\) হয়।
কাজেই
\(cosec \ {\theta}\) এর ডোমেন \(=\mathbb{R}-\{\pm{(n-1)\pi}, \ n\in{\mathbb{N}}\}\)
এখন, \(cosec \ {\theta}=\frac{r}{y}\)
ফলে, \(x\) ও \(y\) ধনাত্মক হলে, \(\frac{r}{y}\gt{1}\)
এবং \(x\) ও \(y\) উভয়ে ঋণাত্মক বা পরস্পর বিপরীত চিহ্নবিশিষ্ট হলে , \(\frac{r}{y}\lt{-1}\)
অর্থাৎ \(cosec \ {\theta}\) এর মাণ \((-1, 1)\) ব্যবধিতে বিদ্যমান নেই।
কাজেই
\(cosec \ {\theta}\) এর রেঞ্জ \(=\mathbb{R}-(-1,1)\)
ত্রিকোণমিতিক বা বৃত্তীয় ফাংশনের পর্যায়কাল
Pariod of Trigonometric or Circular function
\(f(\theta)\) ফাংশনকে পর্যায়ী বলা হয় যদি \(f(M+\theta)=f(\theta)\) হয় এবং \(M\) এর সর্বনিম্ন যে মাণের জন্য সম্পর্কটি সত্য হয় তাকে ফাংশনটির পর্যায়কাল বলে।
\(\sin{\theta}, \ \cos{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল \(2\pi\)
কেননা, \(\sin{\theta}=\sin{(2\pi+\theta)}=\sin{(4\pi+\theta)}=\sin{(6\pi+\theta)}=......\)
এবং \(\cos{\theta}=\cos{(2\pi+\theta)}=\cos{(4\pi+\theta)}=\cos{(6\pi+\theta)}=......\)
অনুরূপভাবে,
\(\sec{\theta}, \ cosec \ {\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল \(2\pi,\)
\(\tan{\theta}, \ \cot{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল \(\pi\)
কেননা, \(\tan{\theta}=\tan{(\pi+\theta)}=\tan{(2\pi+\theta)}=\tan{(3\pi+\theta)}=......\)
এবং \(\cot{\theta}=\cot{(\pi+\theta)}=\cot{(2\pi+\theta)}=\cot{(3\pi+\theta)}=......\)
কোনো পর্যায়ী মূল ফাংশনের পর্যায়কে প্রদত্ত ফাংশনের \(\theta\) এর সহগ দ্বারা ভাগ করে প্রদত্ত ফাংশনের পর্যায় পাওয়া যায়।
যেমনঃ \(\sin{\theta}\) এর পর্যায়কাল \(2\pi\)
\(\therefore \sin{(5\theta+2)}\) এর পর্যায়কাল \(=\frac{2\pi}{5}\)
\(\sin^2{(7\theta+1)}\) এর পর্যায়কাল \(=\frac{2\pi}{7}\)
এবং
\(\sin^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{2\pi}{P}\)
\(\cos{\theta}\) এর পর্যায়কাল \(2\pi\)
\(\therefore \cos{(8\theta+2)}\) এর পর্যায়কাল \(=\frac{2\pi}{8}=\frac{\pi}{4}\)
\(\cos^2{(9\theta+1)}\) এর পর্যায়কাল \(=\frac{2\pi}{9}\)
এবং
\(\cos^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{2\pi}{P}\)
\(\sec{\theta}\) এর পর্যায়কাল \(2\pi\)
\(\therefore \sec{(3\theta+2)}\) এর পর্যায়কাল \(=\frac{2\pi}{3}\)
\(\sec^2{(9\theta+1)}\) এর পর্যায়কাল \(=\frac{2\pi}{9}\)
এবং
\(\sec^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{2\pi}{P}\)
\(cosec \ {\theta}\) এর পর্যায়কাল \(2\pi\)
\(\therefore cosec \ {(3\theta+2)}\) এর পর্যায়কাল \(=\frac{2\pi}{3}\)
\(cosec^2{(9\theta+1)}\) এর পর্যায়কাল \(=\frac{2\pi}{9}\)
এবং
\(cosec^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{2\pi}{P}\)
\(\tan{\theta}\) এর পর্যায়কাল \(\pi\)
\(\therefore \tan{(3\theta+2)}\) এর পর্যায়কাল \(=\frac{\pi}{3}\)
\(\tan^2{(9\theta+1)}\) এর পর্যায়কাল \(=\frac{\pi}{9}\)
এবং
\(\tan^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{\pi}{P}\)
\(\cot{\theta}\) এর পর্যায়কাল \(\pi\)
\(\therefore \cot{(5\theta+2)}\) এর পর্যায়কাল \(=\frac{\pi}{5}\)
\(\cot^2{(6\theta+1)}\) এর পর্যায়কাল \(=\frac{\pi}{6}\)
এবং
\(\cot^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{\pi}{P}\)
\(\sin{\theta}, \ \cos{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল \(2\pi\)
কেননা, \(\sin{\theta}=\sin{(2\pi+\theta)}=\sin{(4\pi+\theta)}=\sin{(6\pi+\theta)}=......\)
এবং \(\cos{\theta}=\cos{(2\pi+\theta)}=\cos{(4\pi+\theta)}=\cos{(6\pi+\theta)}=......\)
অনুরূপভাবে,
\(\sec{\theta}, \ cosec \ {\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল \(2\pi,\)
\(\tan{\theta}, \ \cot{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল \(\pi\)
কেননা, \(\tan{\theta}=\tan{(\pi+\theta)}=\tan{(2\pi+\theta)}=\tan{(3\pi+\theta)}=......\)
এবং \(\cot{\theta}=\cot{(\pi+\theta)}=\cot{(2\pi+\theta)}=\cot{(3\pi+\theta)}=......\)
কোনো পর্যায়ী মূল ফাংশনের পর্যায়কে প্রদত্ত ফাংশনের \(\theta\) এর সহগ দ্বারা ভাগ করে প্রদত্ত ফাংশনের পর্যায় পাওয়া যায়।
যেমনঃ \(\sin{\theta}\) এর পর্যায়কাল \(2\pi\)
\(\therefore \sin{(5\theta+2)}\) এর পর্যায়কাল \(=\frac{2\pi}{5}\)
\(\sin^2{(7\theta+1)}\) এর পর্যায়কাল \(=\frac{2\pi}{7}\)
এবং
\(\sin^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{2\pi}{P}\)
\(\cos{\theta}\) এর পর্যায়কাল \(2\pi\)
\(\therefore \cos{(8\theta+2)}\) এর পর্যায়কাল \(=\frac{2\pi}{8}=\frac{\pi}{4}\)
\(\cos^2{(9\theta+1)}\) এর পর্যায়কাল \(=\frac{2\pi}{9}\)
এবং
\(\cos^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{2\pi}{P}\)
\(\sec{\theta}\) এর পর্যায়কাল \(2\pi\)
\(\therefore \sec{(3\theta+2)}\) এর পর্যায়কাল \(=\frac{2\pi}{3}\)
\(\sec^2{(9\theta+1)}\) এর পর্যায়কাল \(=\frac{2\pi}{9}\)
এবং
\(\sec^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{2\pi}{P}\)
\(cosec \ {\theta}\) এর পর্যায়কাল \(2\pi\)
\(\therefore cosec \ {(3\theta+2)}\) এর পর্যায়কাল \(=\frac{2\pi}{3}\)
\(cosec^2{(9\theta+1)}\) এর পর্যায়কাল \(=\frac{2\pi}{9}\)
এবং
\(cosec^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{2\pi}{P}\)
\(\tan{\theta}\) এর পর্যায়কাল \(\pi\)
\(\therefore \tan{(3\theta+2)}\) এর পর্যায়কাল \(=\frac{\pi}{3}\)
\(\tan^2{(9\theta+1)}\) এর পর্যায়কাল \(=\frac{\pi}{9}\)
এবং
\(\tan^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{\pi}{P}\)
\(\cot{\theta}\) এর পর্যায়কাল \(\pi\)
\(\therefore \cot{(5\theta+2)}\) এর পর্যায়কাল \(=\frac{\pi}{5}\)
\(\cot^2{(6\theta+1)}\) এর পর্যায়কাল \(=\frac{\pi}{6}\)
এবং
\(\cot^n{(P\theta+Q)}\) এর পর্যায়কাল \(=\frac{\pi}{P}\)
যুক্ত ফাংশনের পর্যায়কাল
Period of added function
\(\sin{\theta}, \ \cos{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল \(2\pi\)
এখন, \(f(\theta)=\sin{\theta}+\cos{\theta}\) ফাংশনটির পর্যায়কাল \(2\pi\) এবং \(2\pi\) এর ল.সা.গু \(2\pi\)
\(f(\theta)=\sin{(2\theta)}+\cos{\theta}\) ফাংশনটির পর্যায়কাল \(\frac{2\pi}{2}=\pi\) এবং \(2\pi\) এর ল.সা.গু \(2\pi\)
\(f(\theta)=\sin{(2\theta)}+\cos^2{(2\theta)}\) ফাংশনটির পর্যায়কাল \(\frac{2\pi}{2}=\pi\) এবং \(\frac{2\pi}{2}=\pi\) এর ল.সা.গু \(\pi\)
\(f(\theta)=\sin^2{(3\theta)}+\cos{(5\theta)}\) ফাংশনটির পর্যায়কাল \(\frac{2\pi}{3}\) এবং \(\frac{2\pi}{5}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{1}=2\pi\)
\(f(\theta)=\sin^3{(6\theta+2)}+\cos^4{(9\theta+3)}\) ফাংশনটির পর্যায়কাল \(\frac{2\pi}{6}=\frac{\pi}{3}\) এবং \(\frac{2\pi}{9}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{3}\)
\(f(\theta)=\sin^n{(P\theta+Q)}+\cos^n{(M\theta+N)}\) ফাংশনটির পর্যায়কাল,
\(\frac{2\pi}{P}\) এবং \(\frac{2\pi}{M}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M \ \text{এর গ.সা.গু}}\)
অনুরূপভাবে,
\(\sin{\theta}, \ \tan{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(2\pi\) এবং \(\pi\)
\(f(\theta)=\sin^n{(P\theta+Q)}+\tan^n{(M\theta+N)}\) ফাংশনটির পর্যায়কাল,
\(\frac{2\pi}{P}\) এবং \(\frac{\pi}{M}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M \ \text{এর গ.সা.গু}}\)
\(\cos{\theta}, \ \tan{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(2\pi\) এবং \(\pi\)
\(f(\theta)=\cos^n{(P\theta+Q)}+\tan^n{(M\theta+N)}\) ফাংশনটির পর্যায়কাল,
\(\frac{2\pi}{P}\) এবং \(\frac{\pi}{M}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M \ \text{এর গ.সা.গু}}\)
\(\cot{\theta}, \ \sec{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(\pi\) এবং \(2\pi\)
\(f(\theta)=\cot^n{(P\theta+Q)}+\sec^n{(M\theta+N)}\) ফাংশনটির পর্যায়কাল,
\(\frac{\pi}{P}\) এবং \(\frac{2\pi}{M}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M \ \text{এর গ.সা.গু}}\)
\(\cot{\theta}, \ \sec{\theta}, \ cosec \ {\theta}\) ফাংশনগুলি পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(\pi, \ 2\pi\) এবং \(2\pi\)
\(f(\theta)=\cot^n{(P\theta+Q)}+\sec^n{(M\theta+N)}+cosec^n{(R\theta+S)}\) ফাংশনটির পর্যায়কাল,
\(\frac{\pi}{P}, \ \frac{2\pi}{M}\) এবং \(\frac{2\pi}{R}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M, \ R \ \text{এর গ.সা.গু}}\)
\(\cos{\theta}, \ \tan{\theta}, \ \sin{\theta}\) ফাংশনগুলি পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(2\pi, \ \pi\) এবং \(2\pi\)
\(f(\theta)=\cos^n{(P\theta+Q)}+\tan^n{(M\theta+N)}+\sin^n{(R\theta+S)}\) ফাংশনটির পর্যায়কাল,
\(\frac{2\pi}{P}, \ \frac{\pi}{M}\) এবং \(\frac{2\pi}{R}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M, \ R \ \text{এর গ.সা.গু}}\)
\(------------------\)
\(------------------\)
এখন, \(f(\theta)=\sin{\theta}+\cos{\theta}\) ফাংশনটির পর্যায়কাল \(2\pi\) এবং \(2\pi\) এর ল.সা.গু \(2\pi\)
\(f(\theta)=\sin{(2\theta)}+\cos{\theta}\) ফাংশনটির পর্যায়কাল \(\frac{2\pi}{2}=\pi\) এবং \(2\pi\) এর ল.সা.গু \(2\pi\)
\(f(\theta)=\sin{(2\theta)}+\cos^2{(2\theta)}\) ফাংশনটির পর্যায়কাল \(\frac{2\pi}{2}=\pi\) এবং \(\frac{2\pi}{2}=\pi\) এর ল.সা.গু \(\pi\)
\(f(\theta)=\sin^2{(3\theta)}+\cos{(5\theta)}\) ফাংশনটির পর্যায়কাল \(\frac{2\pi}{3}\) এবং \(\frac{2\pi}{5}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{1}=2\pi\)
\(f(\theta)=\sin^3{(6\theta+2)}+\cos^4{(9\theta+3)}\) ফাংশনটির পর্যায়কাল \(\frac{2\pi}{6}=\frac{\pi}{3}\) এবং \(\frac{2\pi}{9}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{3}\)
\(f(\theta)=\sin^n{(P\theta+Q)}+\cos^n{(M\theta+N)}\) ফাংশনটির পর্যায়কাল,
\(\frac{2\pi}{P}\) এবং \(\frac{2\pi}{M}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M \ \text{এর গ.সা.গু}}\)
অনুরূপভাবে,
\(\sin{\theta}, \ \tan{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(2\pi\) এবং \(\pi\)
\(f(\theta)=\sin^n{(P\theta+Q)}+\tan^n{(M\theta+N)}\) ফাংশনটির পর্যায়কাল,
\(\frac{2\pi}{P}\) এবং \(\frac{\pi}{M}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M \ \text{এর গ.সা.গু}}\)
\(\cos{\theta}, \ \tan{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(2\pi\) এবং \(\pi\)
\(f(\theta)=\cos^n{(P\theta+Q)}+\tan^n{(M\theta+N)}\) ফাংশনটির পর্যায়কাল,
\(\frac{2\pi}{P}\) এবং \(\frac{\pi}{M}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M \ \text{এর গ.সা.গু}}\)
\(\cot{\theta}, \ \sec{\theta}\) ফাংশনদ্বয় পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(\pi\) এবং \(2\pi\)
\(f(\theta)=\cot^n{(P\theta+Q)}+\sec^n{(M\theta+N)}\) ফাংশনটির পর্যায়কাল,
\(\frac{\pi}{P}\) এবং \(\frac{2\pi}{M}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M \ \text{এর গ.সা.গু}}\)
\(\cot{\theta}, \ \sec{\theta}, \ cosec \ {\theta}\) ফাংশনগুলি পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(\pi, \ 2\pi\) এবং \(2\pi\)
\(f(\theta)=\cot^n{(P\theta+Q)}+\sec^n{(M\theta+N)}+cosec^n{(R\theta+S)}\) ফাংশনটির পর্যায়কাল,
\(\frac{\pi}{P}, \ \frac{2\pi}{M}\) এবং \(\frac{2\pi}{R}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M, \ R \ \text{এর গ.সা.গু}}\)
\(\cos{\theta}, \ \tan{\theta}, \ \sin{\theta}\) ফাংশনগুলি পর্যায়ী এবং এদের পর্যায়কাল যথাক্রমে \(2\pi, \ \pi\) এবং \(2\pi\)
\(f(\theta)=\cos^n{(P\theta+Q)}+\tan^n{(M\theta+N)}+\sin^n{(R\theta+S)}\) ফাংশনটির পর্যায়কাল,
\(\frac{2\pi}{P}, \ \frac{\pi}{M}\) এবং \(\frac{2\pi}{R}\) এর ল.সা.গু \(\frac{\text{লবগুলোর ল.সা.গু}}{\text{হরগুলোর গ.সা.গু}}=\frac{2\pi}{P, \ M, \ R \ \text{এর গ.সা.গু}}\)
\(------------------\)
\(------------------\)
ত্রিকোণমিতিক বা বৃত্তীয় ফাংশনের মাণের পরিবর্তন
Change of the values of Trigonometric or Circular function
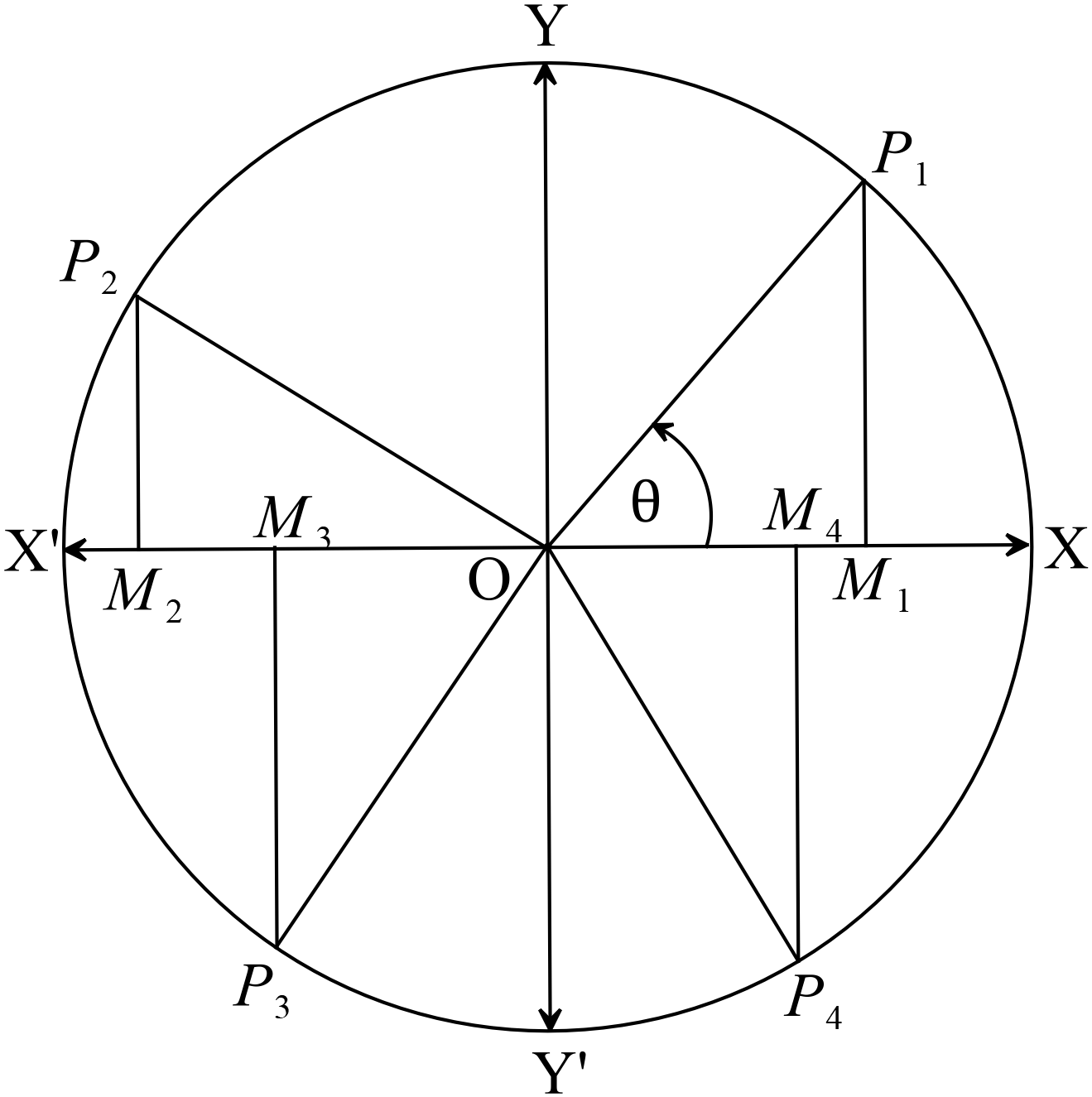 কোণের মাণের পরিবর্তনের সঙ্গে সঙ্গে ত্রিকোণমিতিক অনুপাত \(\sin{\theta}, \ \cos{\theta}, \ \tan{\theta}\) প্রভৃতির মাণের পরিবর্তন হয়।
কোণের মাণের পরিবর্তনের সঙ্গে সঙ্গে ত্রিকোণমিতিক অনুপাত \(\sin{\theta}, \ \cos{\theta}, \ \tan{\theta}\) প্রভৃতির মাণের পরিবর্তন হয়। ধরি, \(O\) বিন্দুকে কেন্দ্র করে যে কোনো ব্যাসার্ধ নিয়ে একটি বৃত্ত আঁকা হয়েছে এবং বৃত্তের \(XOX^{\prime}\) ও \(YOY^{\prime}\) ব্যাস দুইটি \(O\) বিন্দুতে পরস্পরকে সমকোণে ছেদ করেছে। আদি অবস্থান \(OX\) হতে একটি রেখাংশ ঘড়ির কাঁটার বিপরীত দিকে ঘুরে ক্রমশ \(0^{o}\) হতে শুরু করে \(360^{o}\) পরিমাণ কোণে ঘুরে আসলে তা পুনরায় আদি বা পূর্বাবস্থানে ফিরে আসে। রেখাংশের এই আবর্তনের বিভিন্ন অবস্থানে ত্রিকোণমিতিক অনুপাতগুলির মানও ভিন্ন ভিন্ন হয়।
 sine অনুপাতের পরিবর্তনঃ
sine অনুপাতের পরিবর্তনঃ চিত্রে হতে \(\sin{\theta}=\frac{y}{r}\)
চিত্রে, প্রথম চতুর্ভাগে \(\angle{MOP}=\theta=0^{o}\) হলে \(y=0\) হয়
এবং \(0^{o}\) কোণের সাইন অনুপাতের মাণ শূন্য হয়। অর্থাৎ \(\sin{0^{o}}=\frac{0}{r}=0\)
\(\theta=90^{o}\) হলে \(y=r\) হয়
সে ক্ষেত্রে \(\sin{90^{o}}=\frac{r}{r}=1\)
সুতরাং \(\theta\) এর মাণ যখন \(0^{o}\) থেকে ক্রমাগত বৃদ্ধি পেয়ে \(90^{o}\) হয় তখন \(\sin{\theta}\) এর মাণও ক্রমাগত বৃদ্ধি পেয়ে \(1\) হয়।
দ্বিতীয় চতুর্ভাগে \(\theta\) যতই বৃদ্ধি পায় \(y\) ততই ক্রমাগত হ্রাস পায় এবং \(\theta=180^{o}\) হলে, \(y=0\) হয় ।
সুতরাং \(\sin{180^{o}}=\frac{0}{r}=0\)
তৃতীয় চতুর্ভাগে \(y\) ঋণাত্মক এবং \(\theta\) এর মাণ বৃদ্ধির সাথে সাথে \(y=0\) এর পরিমাণ ক্রমাগত বৃদ্ধি পায় ফলে \(\frac{-y}{r}\) এর মাণ ক্রমাগত হ্রাস পায় এবং \(\theta=270^{o}\) হলে \(y=-r\) হয় ।
সুতরাং \(\sin{270^{o}}=\frac{-r}{r}=-1\)
চতুর্থ চতুর্ভাগে \(\theta\) বৃদ্ধির সাথে সাথে \(y\) ঋণাত্মক হতে থাকে এবং \(y\) এর মাণ ক্রমাগত হ্রাস পায়, ফলে \(\frac{-y}{r}\) এর মাণ বৃদ্ধি পায়। \(\theta=360^{o}\) হলে \(y=0\) হয় ।
সুতরাং \(\sin{360^{o}}=\frac{0}{r}=0\)
উপরোক্ত আলোচনা থেকে দেখা যায় যে, \(\theta\) এর মাণ \(0^{o}\) থেকে \(360^{o}\) পর্যন্ত পরিবর্তনের সঙ্গে সঙ্গে \(\sin{\theta}\) এর মাণ শূন্য থেকে বৃদ্ধি পেয়ে \(1\) হয়। আবার হ্রাস পেয়ে শূন্য হয় এবং আরও হ্রাস পেয়ে \(-1\) হয় এবং এর পর আবার বৃদ্ধি পেয়ে শূন্য হয়।
অর্থাৎ \(\sin{\theta}\) এর \(-1\) থেকে \(+1\) পর্যন্ত সকল বাস্তব সংখ্যা হতে পারে।
cosine অনুপাতের পরিবর্তনঃ
উপরোক্ত পদ্ধতিতে অগ্রসর হলে দেখা যায় \(\cos{0^{o}}=1\) এবং প্রথম চতুর্ভাগে \(\theta\) এর মাণ যখন \(0^{o}\) থেকে ক্রমাগত বৃদ্ধি পেয়ে \(90^{o}\) হয় তখন \(\cos{\theta}\) এর মাণ \(1\) থেকে হ্রাস পেয়ে শূন্য হয়। অতঃপর দ্বিতীয় ও তৃতীয় চতুর্ভাগে \(\cos{\theta}\) ঋণাত্মক এবং এর মাণ পর্যায়ক্রমে হ্রাস পেয়ে \(-1\) ও বৃদ্ধি পেয়ে শূন্য হয়ে যায় এবং চতুর্থ চতুর্ভাগে \(\cos{\theta}\) ধনাত্মক এবং বৃদ্ধি পেয়ে পূর্বাবস্থায় ফিরে আসে।
অর্থাৎ \(\cos{360^{o}}=1\) হয়।
tan অনুপাতের পরিবর্তনঃ
\(\theta=0^{o}\) হলে, \(\tan{\theta}\) এর মাণ শূন্য হয় এবং \(\theta\lt{90^{o}}\) অবস্থান হতে \(\theta\) এর মাণ \(0^{o}\) হতে যতই বৃদ্ধি পেয়ে \(90^{o}\) এর দিকে অগ্রসর হয় অথবা \(\theta\gt{90^{o}}\) অবস্থান হতে যতই হ্রাস পেয়ে \(90^{o}\) এর দিকে অগ্রসর হয় \(\tan{\theta}\) এর মাণ ততই সীমাহীনভাবে বৃদ্ধি পায়। \(\theta=90^{o}\) হলে \(\tan{\theta}\) অসংজ্ঞায়িত হয়। \(n\) এর সকল মানের জন্য \(\theta=(2n+1)\frac{\pi}{2}\) হলে \(\tan{\theta}\) অসংজ্ঞায়িত ।
দ্রষ্টব্যঃ ত্রিকোণমিতিক অনুপাতগুলি পর্যায়বৃত্ত ফাংশন। \(\sin{\theta}, \ \cos{\theta}, \ cosec \ {\theta}\) এবং \(\sec{\theta}\) এর পর্যায় \(2\pi\) বা \(360^{o}\)। সুতরাং এদের মাণের পরিবর্তন \(360^{o}\) পর পর একইভাবে পরিবর্তিত হবে। আবার, \(\tan{\theta}\) ও \( \cot{\theta}\) এর পর্যায় \(\pi\) বা \(180^{o}\) । সুতরাং এদের পরিবর্তনও \(180^{o}\) পর পর একই রকম হবে।
ত্রিকোণমিতিক বা বৃত্তীয় ফাংশনের লেখচিত্র
Graph of Trigonometric or Circular function
বৃত্তীয় বা ত্রিকোণমিতিক ফাংশনের লেখচিত্র অঙ্কনের জন্য বীজগণিতীয় ফাংশনের মত দুইটি পরস্পর লম্বভাবে ছেদকারী আনুভূমিক রেখা \(XOX^{\prime}\) কে \(x\) অক্ষ এবং উল্লম্ব \(YOY^{\prime}\) কে \(y\) অক্ষ বিবেচনা করা হয়। \(x\) অক্ষ বরাবর একটি নির্দিষ্ট স্কেলে কোণগুলিকে এবং একই স্কেলে অথবা পৃথক কোনো স্কেলে \(y\) অক্ষ বরাবর বৃত্তীয় বা ত্রিকোণমিতিক ফাংশনের মানগুলি উপস্থাপন করা হয়। এভাবে প্রতিটি কোণ এবং এদের সংশ্লিষ্ট ত্রিকোণমিতিক অনুপাত হতে ছক কাগজে এক একটি বিন্দু স্থাপন করা হয়। বিন্দুগুলি যোগ করে প্রদত্ত বৃত্তীয় বা ত্রিকোণমিতিক ফাংশনের লেখচিত্র পাওয়া যায় ।
\(y=\sin{x}, \ -2\pi\leq{x}\leq{2\pi}\) ফাংশনের লেখচিত্র
Graph of \(y=\sin{x}, \ -2\pi\leq{x}\leq{2\pi}\) function
\(y=\sin{x}, \ -2\pi\leq{x}\leq{2\pi}\) এর লেখচিত্র।
ঢাঃ ২০১১; দিঃ,চঃ,মাঃ ২০১৪ ।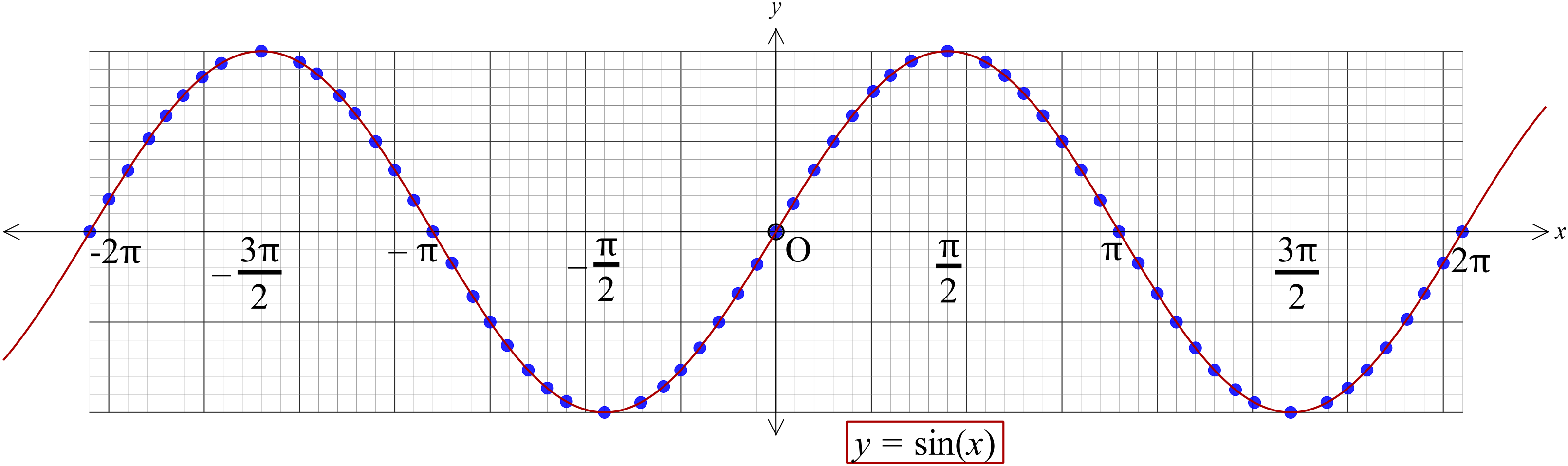
প্রমাণঃ
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে ক্যালকুলেটরের সাহায্যে \(x\) এর মানের জন্য \(y\) এর প্রতিসঙ্গী মানগুলি দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
এখন, ছক কাগজে পরস্পরছেদী দুইটি লম্ব রেখা দ্বারা \(x\) অক্ষ ও \(y\) অক্ষ নির্ধারণ করি। \(x\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের এক বাহু \(=\frac{\pi}{18}\) এবং \(y\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের \(10\) বাহু \(=1\) একক ধরে তালিকাভূক্ত বিন্দুগুলি ছক কাগজে স্থাপন করি। অতঃপর বিন্দুগুলি মসৃণ বক্ররেখা দ্বারা যুক্ত করলেই \(y=\sin{x}\) ফাংশনের লেখচিত্র পাওয়া যাবে।

সাইন লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রের কোথাও ছেদ বা বিচ্ছিন্নতা নেই। অর্থাৎ লেখচিত্রটি অবিচ্ছিন্ন।
\((ii)\) \(x\) এর সকল বাস্তব মানের জন্য ফাংশনটি সংজ্ঞায়িত। অর্থাৎ ডোমেন \(\mathbb{R}\)
\((iii)\) লেখচিত্রটির আকার ঢেউয়ের মতো এবং সর্বোচ্চ মান \(+1\) ও সর্বনিম্ন মান \(-1\) এর মধ্যে ভ্রাম্যমাণ। অর্থাৎ রেঞ্জ \([-1, 1]\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(360^{o}\) বা \(2\pi\)
\((v)\) \(x\) এর \(90^{o}\) এর বিজোড় গুণিতক মানগুলিতে সাইন ফাংশনের মান সর্বোচ্চ বা সর্বনম্ন।
\((vi)\) \(x\) এর \(90^{o}\) এর জোড় গুণিতক মানগুলিতে সাইন ফাংশনের মান শূন্য।
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে ক্যালকুলেটরের সাহায্যে \(x\) এর মানের জন্য \(y\) এর প্রতিসঙ্গী মানগুলি দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
| \(x\) | \(-\frac{36\pi}{18}\) | \(-\frac{33\pi}{18}\) | \(-\frac{30\pi}{18}\) | \(-\frac{27\pi}{18}\) | \(-\frac{24\pi}{18}\) | \(-\frac{21\pi}{18}\) | \(-\frac{18\pi}{18}\) | \(-\frac{15\pi}{18}\) | \(-\frac{12\pi}{18}\) | \(-\frac{9\pi}{18}\) | \(-\frac{6\pi}{18}\) | \(-\frac{3\pi}{18}\) | \(0\) |
| \(y=\sin{x}\) | \(0\) | \(0.5\) | \(0.87\) | \(1\) | \(0.87\) | \(0.5\) | \(0\) | \(-0.5\) | \(-0.87\) | \(-1\) | \(-0.87\) | \(-0.5\) | \(0\) |
| \((x, \ y)\) | \((-\frac{36\pi}{18}, 0)\) | \((-\frac{33\pi}{18}, 0.5)\) | \((-\frac{30\pi}{18}, 0.87)\) | \((-\frac{27\pi}{18}, 1)\) | \((-\frac{24\pi}{18}, 0.87)\) | \((-\frac{21\pi}{18}, 0.5)\) | \((-\frac{18\pi}{18}, 0)\) | \((-\frac{15\pi}{18}, -0.5)\) | \((-\frac{12\pi}{18}, -0.87)\) | \((-\frac{9\pi}{18}, -1)\) | \((-\frac{6\pi}{18}, -0.87)\) | \((-\frac{3\pi}{18}, -0.5)\) | \((0, 0)\) |
| \(x\) | \(\frac{3\pi}{18}\) | \(\frac{6\pi}{18}\) | \(\frac{9\pi}{18}\) | \(\frac{12\pi}{18}\) | \(\frac{15\pi}{18}\) | \(\frac{18\pi}{18}\) | \(\frac{21\pi}{18}\) | \(\frac{24\pi}{18}\) | \(\frac{27\pi}{18}\) | \(\frac{30\pi}{18}\) | \(\frac{33\pi}{18}\) | \(\frac{36\pi}{18}\) | |
| \(y=\sin{x}\) | \(0.5\) | \(0.87\) | \(1\) | \(0.87\) | \(0.5\) | \(0\) | \(0.5\) | \(0.87\) | \(1\) | \(0.87\) | \(0.5\) | \(0\) | |
| \((x, \ y)\) | \((\frac{3\pi}{18}, 0.5)\) | \((\frac{6\pi}{18}, 0.87)\) | \((\frac{9\pi}{18}, 1)\) | \((\frac{12\pi}{18}, 0.87)\) | \((\frac{15\pi}{18}, 0.5)\) | \((\frac{18\pi}{18}, 0)\) | \((\frac{21\pi}{18}, 0.5)\) | \((\frac{24\pi}{18}, 0.87)\) | \((\frac{27\pi}{18}, 1)\) | \((\frac{30\pi}{18}, 0.87)\) | \((\frac{33\pi}{18}, 0.5)\) | \((\frac{36\pi}{18}, 0)\) |

সাইন লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রের কোথাও ছেদ বা বিচ্ছিন্নতা নেই। অর্থাৎ লেখচিত্রটি অবিচ্ছিন্ন।
\((ii)\) \(x\) এর সকল বাস্তব মানের জন্য ফাংশনটি সংজ্ঞায়িত। অর্থাৎ ডোমেন \(\mathbb{R}\)
\((iii)\) লেখচিত্রটির আকার ঢেউয়ের মতো এবং সর্বোচ্চ মান \(+1\) ও সর্বনিম্ন মান \(-1\) এর মধ্যে ভ্রাম্যমাণ। অর্থাৎ রেঞ্জ \([-1, 1]\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(360^{o}\) বা \(2\pi\)
\((v)\) \(x\) এর \(90^{o}\) এর বিজোড় গুণিতক মানগুলিতে সাইন ফাংশনের মান সর্বোচ্চ বা সর্বনম্ন।
\((vi)\) \(x\) এর \(90^{o}\) এর জোড় গুণিতক মানগুলিতে সাইন ফাংশনের মান শূন্য।
\(y=\cos{x}, \ -2\pi\leq{x}\leq{2\pi}\) ফাংশনের লেখচিত্র
Graph of \(y=\cos{x}, \ -2\pi\leq{x}\leq{2\pi}\) function
\(y=\cos{x}, \ -2\pi\leq{x}\leq{2\pi}\) এর লেখচিত্র ।
যঃ ২০১৪,২০১০,২০০৪; কুঃ২০০৮; সিঃ২০১৪; মাঃ২০০৯ । 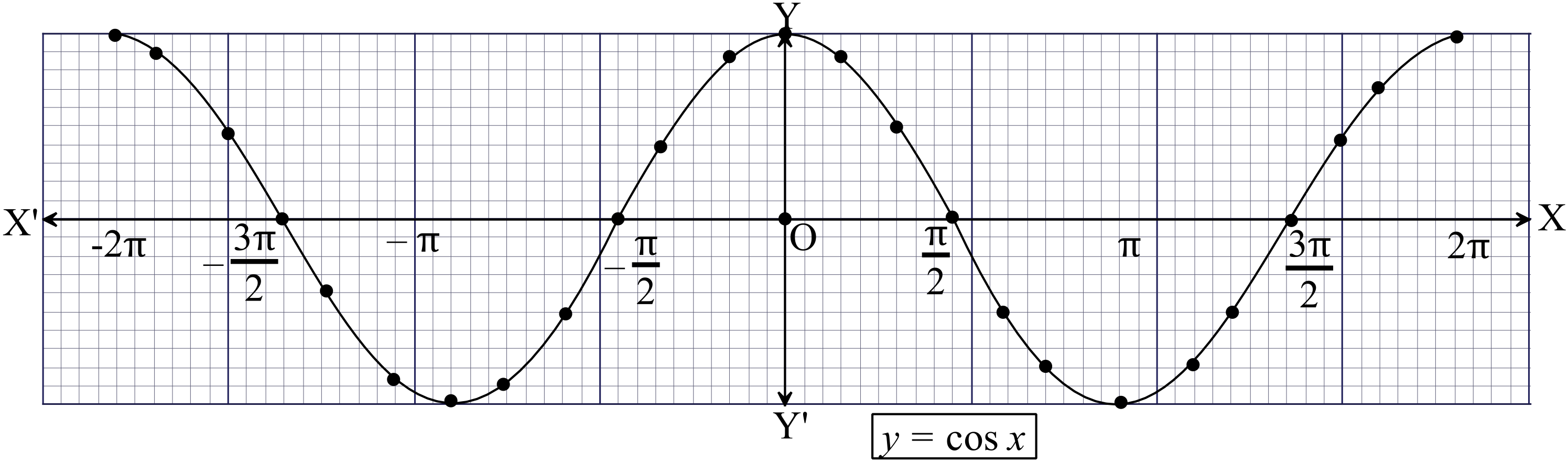
প্রমাণঃ
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\cos{x}\) এর মান সাইন সারণি বা ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
এখন, ছক কাগজে পরস্পরছেদী দুইটি লম্ব রেখা দ্বারা \(x\) অক্ষ ও \(y\) অক্ষ নির্ধারণ করি। \(x\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের তিন বাহু \(=\frac{\pi}{6}\) এবং \(y\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের \(10\) বাহু \(=1\) একক ধরে তালিকাভূক্ত বিন্দুগুলি ছক কাগজে স্থাপন করি। অতঃপর বিন্দুগুলি মসৃণ বক্ররেখা দ্বারা যুক্ত করলেই \(y=\cos{x}\) ফাংশনের লেখচিত্র পাওয়া যাবে।

কোসাইন লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রের কোথাও ছেদ বা বিচ্ছিন্নতা নেই। অর্থাৎ লেখচিত্রটি অবিচ্ছিন্ন।
\((ii)\) \(x\) এর সকল বাস্তব মানের জন্য ফাংশনটি সংজ্ঞায়িত। অর্থাৎ ডোমেন \(\mathbb{R}\)
\((iii)\) লেখচিত্রটির আকার ঢেউয়ের মতো এবং সর্বোচ্চ মান \(+1\) ও সর্বনিম্ন মান \(-1\) এর মধ্যে ভ্রাম্যমাণ। অর্থাৎ রেঞ্জ \([-1, 1]\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(360^{o}\) বা \(2\pi\)
\((v)\) \(x\) এর \(90^{o}\) এর জোড় গুণিতক মানগুলিতে কোসাইন ফাংশনের মান সর্বোচ্চ বা সর্বনম্ন।
\((vi)\) \(x\) এর \(90^{o}\) এর বিজোড় গুণিতক মানগুলিতে কোসাইন ফাংশনের মান শূন্য।
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\cos{x}\) এর মান সাইন সারণি বা ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
| \(x\) | \(-\frac{12\pi}{6}\) | \(-\frac{11\pi}{6}\) | \(-\frac{10\pi}{6}\) | \(-\frac{9\pi}{6}\) | \(-\frac{8\pi}{6}\) | \(-\frac{7\pi}{6}\) | \(-\frac{6\pi}{6}\) | \(-\frac{5\pi}{6}\) | \(-\frac{4\pi}{6}\) | \(-\frac{3\pi}{6}\) | \(-\frac{2\pi}{6}\) | \(-\frac{\pi}{6}\) | \(0^{o}\) |
| \(y=\cos{x}\) | \(1\) | \(0.87\) | \(0.5\) | \(0\) | \(-0.5\) | \(-0.87\) | \(-1\) | \(-0.87\) | \(-0.5\) | \(0\) | \(0.5\) | \(0.87\) | \(1\) |
| \((x, \ y)\) | \((-\frac{12\pi}{6}, 1)\) | \((-\frac{11\pi}{6}, 0.87)\) | \((-\frac{10\pi}{6}, 0.5)\) | \((-\frac{9\pi}{6}, 0)\) | \((-\frac{8\pi}{6}, -0.5)\) | \((-\frac{7\pi}{6}, -0.87)\) | \((-\frac{6\pi}{6}, -1)\) | \((-\frac{5\pi}{6}, -0.87)\) | \((-\frac{4\pi}{6}, -0.5)\) | \((-\frac{3\pi}{6}, 0)\) | \((-\frac{2\pi}{6}, 0.5)\) | \((-\frac{\pi}{6}, 0.87)\) | \((0^{o}, 1)\) |
| \(x\) | \(\frac{\pi}{6}\) | \(\frac{2\pi}{6}\) | \(\frac{3\pi}{6}\) | \(\frac{4\pi}{6}\) | \(\frac{5\pi}{6}\) | \(\frac{6\pi}{6}\) | \(\frac{7\pi}{6}\) | \(\frac{8\pi}{6}\) | \(\frac{9\pi}{6}\) | \(\frac{10\pi}{6}\) | \(\frac{11\pi}{6}\) | \(\frac{12\pi}{6}\) | |
| \(y=\cos{x}\) | \(0.87\) | \(0.5\) | \(0\) | \(-0.5\) | \(-0.87\) | \(-1\) | \(-0.87\) | \(-0.5\) | \(0\) | \(0.5\) | \(0.87\) | \(1\) | |
| \((x, \ y)\) | \((\frac{\pi}{6}, 0.87)\) | \((\frac{2\pi}{6}, 0.5)\) | \((\frac{3\pi}{6}, 0)\) | \((\frac{4\pi}{6}, -0.5)\) | \((\frac{5\pi}{6}, -0.87)\) | \((\frac{6\pi}{6}, -1)\) | \((\frac{7\pi}{6}, -0.87)\) | \((\frac{8\pi}{6}, -0.5)\) | \((\frac{9\pi}{6}, 0)\) | \((\frac{10\pi}{6}, 0.5)\) | \((\frac{11\pi}{6}, 0.87)\) | \((\frac{12\pi}{6}, 1)\) |

কোসাইন লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রের কোথাও ছেদ বা বিচ্ছিন্নতা নেই। অর্থাৎ লেখচিত্রটি অবিচ্ছিন্ন।
\((ii)\) \(x\) এর সকল বাস্তব মানের জন্য ফাংশনটি সংজ্ঞায়িত। অর্থাৎ ডোমেন \(\mathbb{R}\)
\((iii)\) লেখচিত্রটির আকার ঢেউয়ের মতো এবং সর্বোচ্চ মান \(+1\) ও সর্বনিম্ন মান \(-1\) এর মধ্যে ভ্রাম্যমাণ। অর্থাৎ রেঞ্জ \([-1, 1]\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(360^{o}\) বা \(2\pi\)
\((v)\) \(x\) এর \(90^{o}\) এর জোড় গুণিতক মানগুলিতে কোসাইন ফাংশনের মান সর্বোচ্চ বা সর্বনম্ন।
\((vi)\) \(x\) এর \(90^{o}\) এর বিজোড় গুণিতক মানগুলিতে কোসাইন ফাংশনের মান শূন্য।
\(y=\tan{x}, \ -\frac{\pi}{2}\leq{x}\leq{\frac{\pi}{2}}\) ফাংশনের লেখচিত্র
Graph of \(y=\tan{x}, \ -\frac{\pi}{2}\leq{x}\leq{\frac{\pi}{2}}\) function
\(y=\tan{x}, \ -\frac{\pi}{2}\leq{x}\leq{\frac{\pi}{2}}\) এর লেখচিত্র।
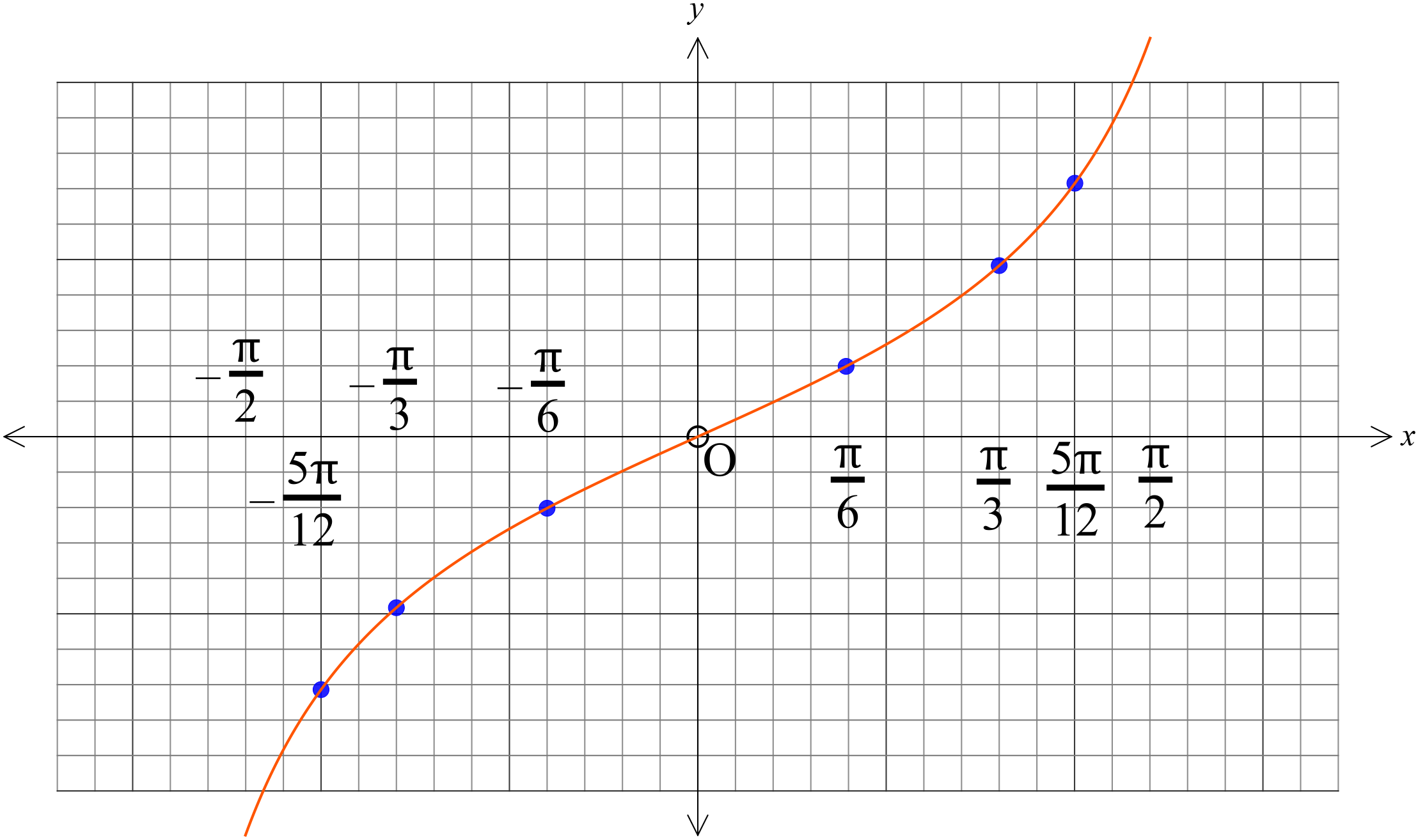
প্রমাণঃ
উপরোক্ত সীমায় \(x=\frac{\pi}{2}\) ও \(-\frac{\pi}{2}\) বিন্দুতে \(y=\tan{x}\) এর মান অসংজ্ঞায়িত ।
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\tan{x}\) এর লেখচিত্রের অংশ নির্ণয়ের জন্য ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
এখন, ছক কাগজে পরস্পরছেদী দুইটি লম্ব রেখা দ্বারা \(x\) অক্ষ ও \(y\) অক্ষ নির্ধারণ করি। \(x\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের এক বাহু \(=\frac{\pi}{24}\) এবং \(y\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের \(10\) বাহু \(=1\) একক ধরে তালিকাভূক্ত বিন্দুগুলি ছক কাগজে স্থাপন করি। অতঃপর বিন্দুগুলি মসৃণ বক্ররেখা দ্বারা যুক্ত করলেই \(y=\tan{x}\) ফাংশনের লেখচিত্র পাওয়া যাবে।

ট্যানজেন্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \(\frac{\pi}{2}\) এর বিজোড় গুণিতকের জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{(2n+1)\frac{\pi}{2}:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(180^{o}\) বা \(\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=(2n-1)\frac{\pi}{2}:n\in{\mathbb{Z}}\)
\((vi)\) যেহেতু \(\tan{(n\pi+x)}=\tan{x}\) লেখের প্রতিটি শাখা \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) সীমার মধ্যে আঁকা শাখাটির অনুরূপ।
উপরোক্ত সীমায় \(x=\frac{\pi}{2}\) ও \(-\frac{\pi}{2}\) বিন্দুতে \(y=\tan{x}\) এর মান অসংজ্ঞায়িত ।
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\tan{x}\) এর লেখচিত্রের অংশ নির্ণয়ের জন্য ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
| \(x\) | \(-\frac{12\pi}{24}\) | \(-\frac{8\pi}{24}\) | \(-\frac{6\pi}{24}\) | \(-\frac{4\pi}{24}\) | \(0\) | \(\frac{4\pi}{24}\) | \(\frac{6\pi}{24}\) | \(\frac{8\pi}{24}\) | \(\frac{12\pi}{24}\) |
| \(y=\tan{x}\) | \(-\infty\) | \(-1.73\) | \(-1\) | \(-0.58\) | \(0\) | \(0.58\) | \(1\) | \(1.73\) | \(+\infty\) |
| \((x, \ y)\) | \((-\frac{12\pi}{24},-\infty)\) | \((-\frac{8\pi}{24}, -1.73)\) | \((-\frac{6\pi}{24}, -1)\) | \((-\frac{4\pi}{24}, -0.58)\) | \((0, 0)\) | \((\frac{4\pi}{24}, 0.58)\) | \((\frac{6\pi}{24}, 1)\) | \((\frac{8\pi}{24}, 1.73)\) | \((\frac{12\pi}{24}, \infty)\) |

ট্যানজেন্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \(\frac{\pi}{2}\) এর বিজোড় গুণিতকের জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{(2n+1)\frac{\pi}{2}:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(180^{o}\) বা \(\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=(2n-1)\frac{\pi}{2}:n\in{\mathbb{Z}}\)
\((vi)\) যেহেতু \(\tan{(n\pi+x)}=\tan{x}\) লেখের প্রতিটি শাখা \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) সীমার মধ্যে আঁকা শাখাটির অনুরূপ।
\(y=cosec \ {x}, \ -\pi\leq{x}\leq{\pi}\) ফাংশনের লেখচিত্র
Graph of \(y=cosec \ {x}, \ -\pi\leq{x}\leq{\pi}\) function
\(y=cosec \ {x}, \ -\pi\leq{x}\leq{\pi}\) এর লেখচিত্র।
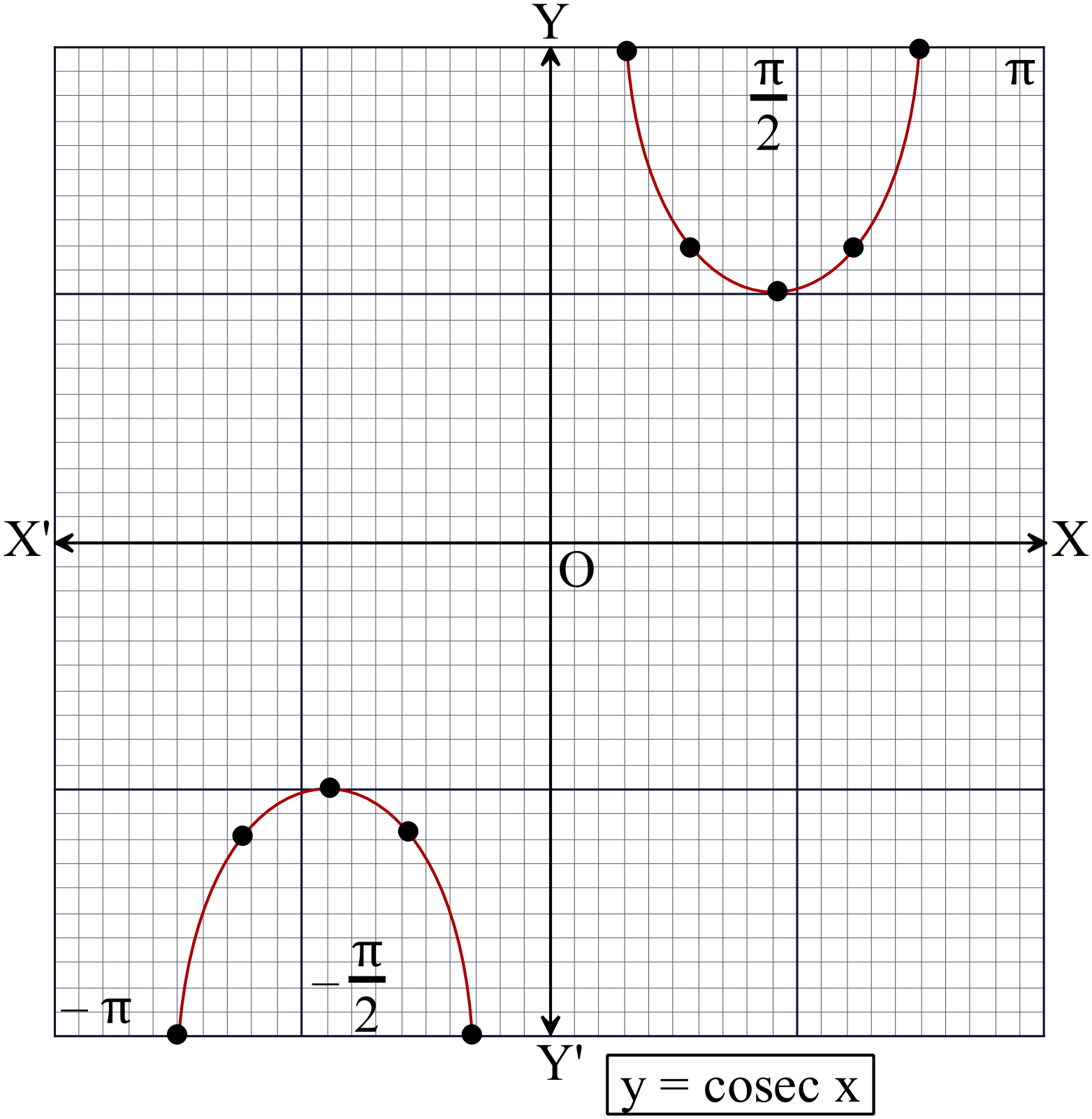
প্রমাণঃ
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=cosec \ {x}\) এর মান ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
এখন, ছক কাগজে পরস্পরছেদী দুইটি লম্ব রেখা দ্বারা \(x\) অক্ষ ও \(y\) অক্ষ নির্ধারণ করি। \(x\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের তিন বাহু \(=\frac{\pi}{6}\) এবং \(y\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের \(10\) বাহু \(=1\) একক ধরে তালিকাভূক্ত বিন্দুগুলি ছক কাগজে স্থাপন করি। অতঃপর বিন্দুগুলি মসৃণ বক্ররেখা দ্বারা যুক্ত করলেই \(y=cosec \ {x}\) ফাংশনের লেখচিত্র পাওয়া যাবে।

কোসেক্যান্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \(n\pi, \ n\in{\mathbb{Z}}\) এর জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{n\pi:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}-(-1,1)\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(360^{o}\) বা \(2\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=n\pi:n\in{\mathbb{Z}}\)
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=cosec \ {x}\) এর মান ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
| \(x\) | \(-\frac{6\pi}{6}\) | \(-\frac{5\pi}{6}\) | \(-\frac{4\pi}{6}\) | \(-\frac{3\pi}{6}\) | \(-\frac{2\pi}{6}\) | \(-\frac{\pi}{6}\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{2\pi}{6}\) | \(\frac{3\pi}{6}\) | \(\frac{4\pi}{6}\) | \(\frac{5\pi}{6}\) | \(\frac{6\pi}{6}\) |
| \(y=cosec \ {x}\) | \(\infty\) | \(-2\) | \(-1.15\) | \(-1\) | \(-1.15\) | \(-2\) | \(\infty\) | \(2\) | \(1.15\) | \(1\) | \(1.15\) | \(2\) | \(\infty\) |
| \((x, \ y)\) | \((-\frac{6\pi}{6},\infty)\) | \((-\frac{5\pi}{6}, -2)\) | \((-\frac{4\pi}{6}, -1.15)\) | \((--\frac{3\pi}{6}, -1)\) | \((-\frac{2\pi}{6}, -1.15)\) | \((-\frac{\pi}{6}, -2)\) | \((0, \infty)\) | \((\frac{\pi}{6}, 2)\) | \((\frac{2\pi}{6}, 1.15)\) | \((\frac{3\pi}{6}, 1)\) | \((\frac{4\pi}{6}, 1.15)\) | \((\frac{5\pi}{6}, 2)\) | \((\frac{6\pi}{6}, \infty)\) |

কোসেক্যান্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \(n\pi, \ n\in{\mathbb{Z}}\) এর জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{n\pi:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}-(-1,1)\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(360^{o}\) বা \(2\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=n\pi:n\in{\mathbb{Z}}\)
\(y=\sec{x}, \ -\pi\leq{x}\leq{\pi}\) ফাংশনের লেখচিত্র
Graph of \(y=\sec{x}, \ -\pi\leq{x}\leq{\pi}\) function
\(y=\sec{x}, \ -\pi\leq{x}\leq{\pi}\) এর লেখচিত্র।
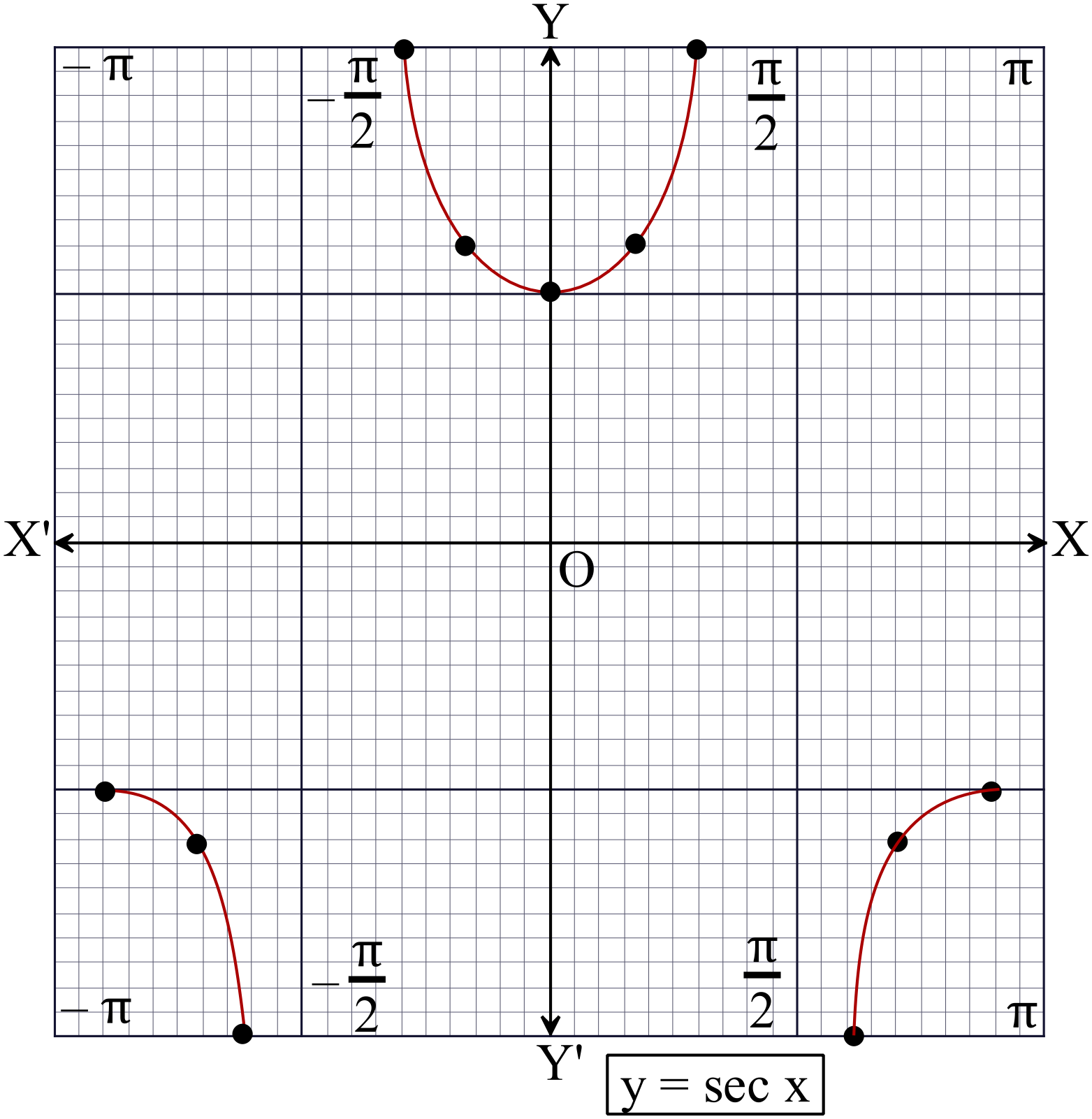
প্রমাণঃ
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\sec{x}\) এর মান ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
এখন, ছক কাগজে পরস্পরছেদী দুইটি লম্ব রেখা দ্বারা \(x\) অক্ষ ও \(y\) অক্ষ নির্ধারণ করি। \(x\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের তিন বাহু \(=\frac{\pi}{6}\) এবং \(y\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের \(10\) বাহু \(=1\) একক ধরে তালিকাভূক্ত বিন্দুগুলি ছক কাগজে স্থাপন করি। অতঃপর বিন্দুগুলি মসৃণ বক্ররেখা দ্বারা যুক্ত করলেই \(y=\sec{x}\) ফাংশনের লেখচিত্র পাওয়া যাবে।

সেক্যান্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \((2n-1)\pi, \ n\in{\mathbb{Z}}\) এর জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{(2n+1)\pi:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}-(-1,1)\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(360^{o}\) বা \(2\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=(2n-1)\pi:n\in{\mathbb{Z}}\)
\((vi)\) লেখচিত্রেটির \(y\) অক্ষের সাথে প্রতিসম।
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\sec{x}\) এর মান ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
| \(x\) | \(-\frac{6\pi}{6}\) | \(-\frac{5\pi}{6}\) | \(-\frac{4\pi}{6}\) | \(-\frac{3\pi}{6}\) | \(-\frac{2\pi}{6}\) | \(-\frac{\pi}{6}\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{2\pi}{6}\) | \(\frac{3\pi}{6}\) | \(\frac{4\pi}{6}\) | \(\frac{5\pi}{6}\) | \(\frac{6\pi}{6}\) |
| \(y=\sec{x}\) | \(-1\) | \(-1.15\) | \(-2\) | \(\infty\) | \(2\) | \(1.15\) | \(1\) | \(1.15\) | \(2\) | \(\infty\) | \(-2\) | \(-1.15\) | \(-1\) |
| \((x, \ y)\) | \((-\frac{6\pi}{6},-1)\) | \((-\frac{5\pi}{6}, -1.15)\) | \((-\frac{4\pi}{6}, -2)\) | \((-\frac{3\pi}{6}, \infty)\) | \((-\frac{2\pi}{6}, 2)\) | \((-\frac{\pi}{6}, 1.15)\) | \((0, 1)\) | \((\frac{\pi}{6}, 1.15)\) | \((\frac{2\pi}{6}, 2)\) | \((\frac{3\pi}{6}, \infty)\) | \((\frac{4\pi}{6}, -2)\) | \((\frac{5\pi}{6}, -1.15)\) | \((\frac{6\pi}{6}, -1)\) |

সেক্যান্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \((2n-1)\pi, \ n\in{\mathbb{Z}}\) এর জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{(2n+1)\pi:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}-(-1,1)\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(360^{o}\) বা \(2\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=(2n-1)\pi:n\in{\mathbb{Z}}\)
\((vi)\) লেখচিত্রেটির \(y\) অক্ষের সাথে প্রতিসম।
\(y=\cot{x}, \ -\pi\leq{x}\leq{\pi}\) ফাংশনের লেখচিত্র
Graph of \(y=\cot{x}, \ -\pi\leq{x}\leq{\pi}\) function
\(y=\cot{x}, \ -\pi\leq{x}\leq{\pi}\) এর লেখচিত্র।
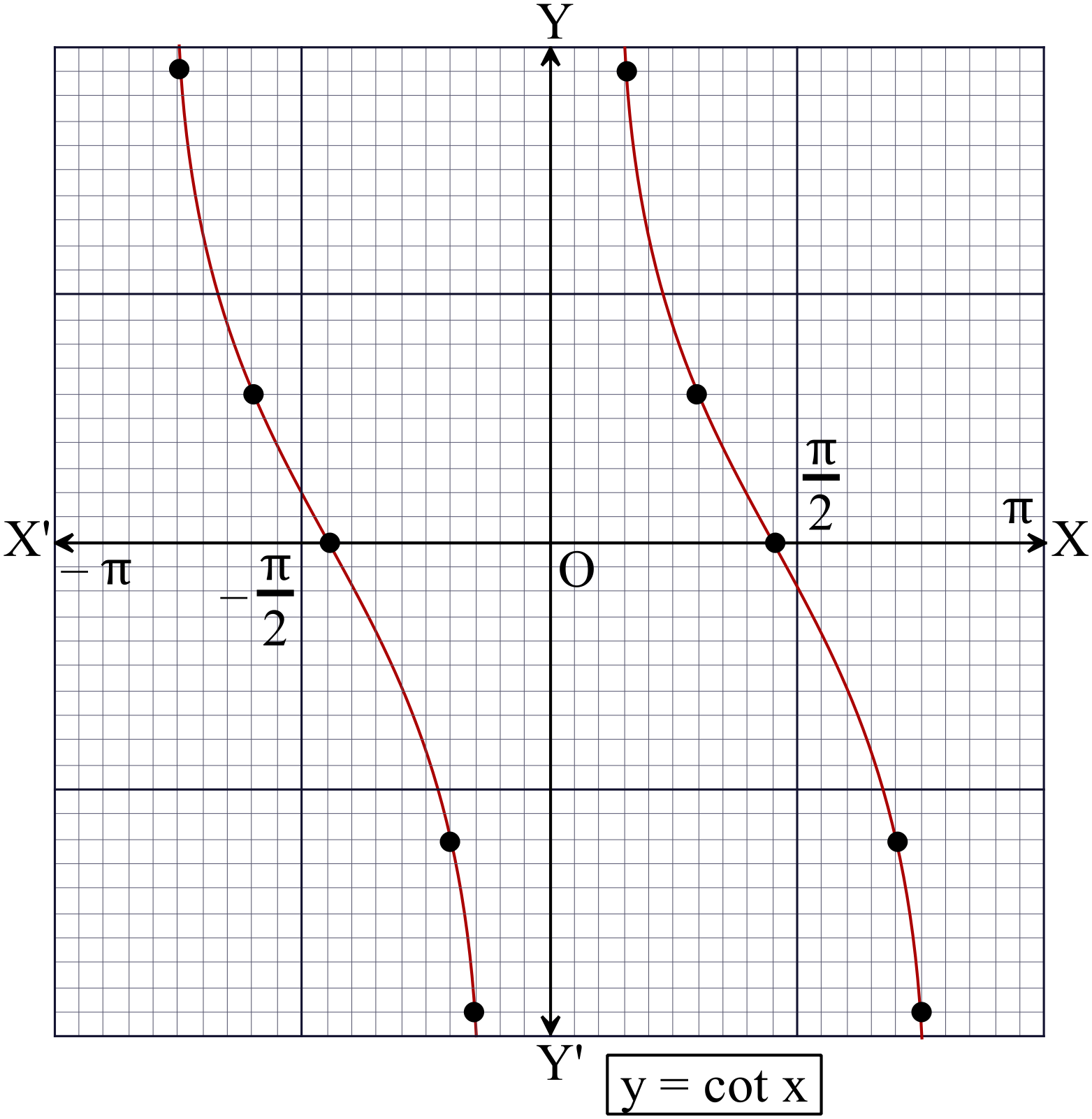
প্রমাণঃ
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\cot{x}\) এর মান ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
এখন, ছক কাগজে পরস্পরছেদী দুইটি লম্ব রেখা দ্বারা \(x\) অক্ষ ও \(y\) অক্ষ নির্ধারণ করি। \(x\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের তিন বাহু \(=\frac{\pi}{6}\) এবং \(y\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের \(10\) বাহু \(=1\) একক ধরে তালিকাভূক্ত বিন্দুগুলি ছক কাগজে স্থাপন করি। অতঃপর বিন্দুগুলি মসৃণ বক্ররেখা দ্বারা যুক্ত করলেই \(y=\cot{x}\) ফাংশনের লেখচিত্র পাওয়া যাবে।

কোট্যানজেন্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \(n\pi, \ n\in{\mathbb{Z}}\) এর জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{n\pi:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(180^{o}\) বা \(\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=n\pi:n\in{\mathbb{Z}}\)
\((vi)\) যেহেতু \(\cot{(n\pi+x)}=\cot{x}\) লেখের প্রতিটি শাখা \((0, \ \pi)\) সীমার মধ্যে আঁকা শাখাটির অনুরূপ।
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\cot{x}\) এর মান ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
| \(x\) | \(-\frac{6\pi}{6}\) | \(-\frac{5\pi}{6}\) | \(-\frac{4\pi}{6}\) | \(-\frac{3\pi}{6}\) | \(-\frac{2\pi}{6}\) | \(-\frac{\pi}{6}\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{2\pi}{6}\) | \(\frac{3\pi}{6}\) | \(\frac{4\pi}{6}\) | \(\frac{5\pi}{6}\) | \(\frac{6\pi}{6}\) |
| \(y=\cot{x}\) | \(\infty\) | \(1.73\) | \(0.58\) | \(0\) | \(-0.58\) | \(-1.73\) | \(\infty\) | \(1.73\) | \(0.58\) | \(0\) | \(-0.58\) | \(-1.73\) | \(\infty\) |
| \((x, \ y)\) | \((-\frac{6\pi}{6},\infty)\) | \((-\frac{5\pi}{6}, 1.73)\) | \((-\frac{4\pi}{6}, 0.58)\) | \((-\frac{3\pi}{6}, 0)\) | \((-\frac{2\pi}{6}, -0.58)\) | \((-\frac{\pi}{6}, -1.73)\) | \((0, \infty)\) | \((\frac{\pi}{6}, 1.73)\) | \((\frac{2\pi}{6}, 0.58)\) | \((\frac{3\pi}{6}, 0)\) | \((\frac{4\pi}{6}, -0.58)\) | \((\frac{5\pi}{6}, -1.73)\) | \((\frac{6\pi}{6}, \infty)\) |

কোট্যানজেন্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \(n\pi, \ n\in{\mathbb{Z}}\) এর জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{n\pi:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(180^{o}\) বা \(\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=n\pi:n\in{\mathbb{Z}}\)
\((vi)\) যেহেতু \(\cot{(n\pi+x)}=\cot{x}\) লেখের প্রতিটি শাখা \((0, \ \pi)\) সীমার মধ্যে আঁকা শাখাটির অনুরূপ।
\(y=\tan{x}, \ -\frac{3\pi}{2}\leq{x}\leq{\frac{3\pi}{2}}\) ফাংশনের লেখচিত্র
Graph of \(y=\tan{x}, \ -\frac{3\pi}{2}\leq{x}\leq{\frac{3\pi}{2}}\) function
\(y=\tan{x}, \ -\frac{3\pi}{2}\leq{x}\leq{\frac{3\pi}{2}}\) এর লেখচিত্র।
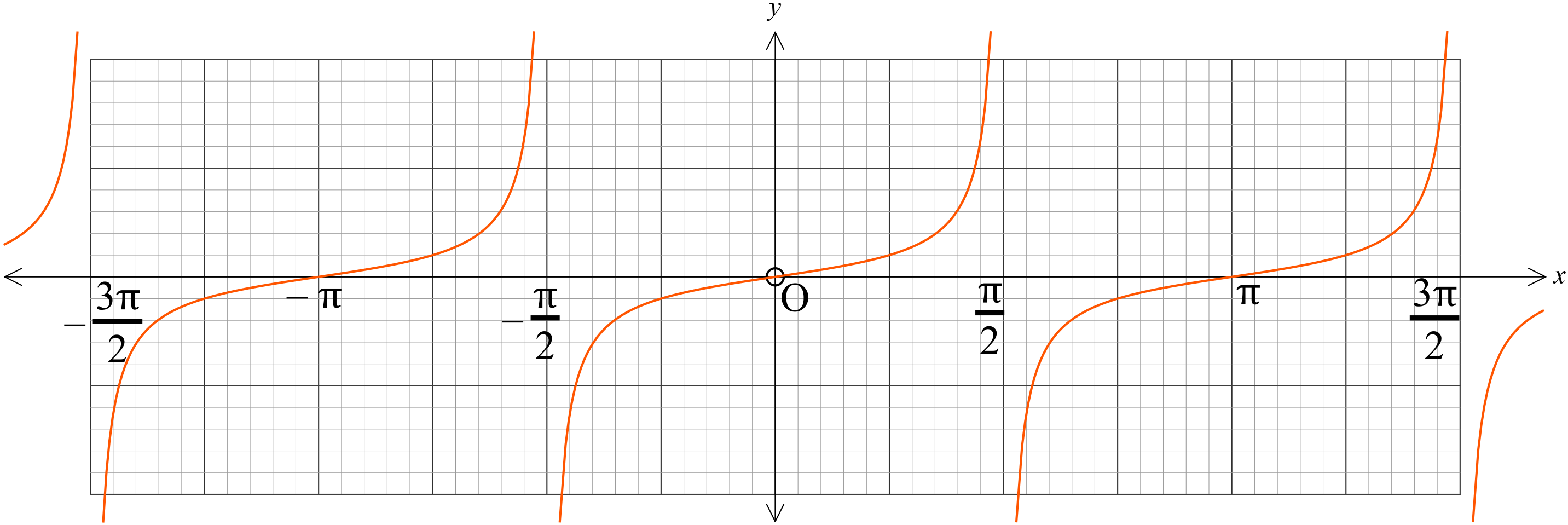
প্রমাণঃ
উপরোক্ত সীমায় \(x=-\pi, \ 0\) ও \(-\pi\) বিন্দুতে \(y=\tan{x}\) এর মান শূন্য।
আবার, \(x=\pm{\frac{\pi}{2}}, \ \pm{\frac{3\pi}{2}}\) বিন্দুগুলিতে \(y=\tan{x}\) এর মান বিশ্লেষন করলে দেখা যায়,
\(x\rightarrow \frac{\pi^{-}}{2} \ \left(\frac{\pi}{2} \text{ হতে সামান্য কম }\right)\) হলে \(y\rightarrow{\infty}\) হয়।
\(x\rightarrow{\frac{\pi^{+}}{2}} \ \left(\frac{\pi}{2} \text{ হতে সামান্য বেশি }\right)\) হলে \(y\rightarrow{-\infty}\) হয়।
অনুরূপভাবে,
\(x\rightarrow{\frac{3\pi^{-}}{2}} \) হলে, \(y\rightarrow{\infty}\) হয়।
\(x\rightarrow{-\frac{\pi^{+}}{2}} \) হলে, \(y\rightarrow{-\infty}\) হয়।
\(x\rightarrow{-\frac{\pi^{-}}{2}} \) হলে, \(y\rightarrow{\infty}\) হয়।
এবং \(x\rightarrow{-\frac{3\pi^{+}}{2}} \) হলে, \(y\rightarrow{-\infty}\) হয়।
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\tan{x}\) এর লেখচিত্রের অংশ নির্ণয়ের জন্য ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
\(-\frac{\pi}{2}\) হতে \(\frac{\pi}{2}\) সীমার মধ্য ফাংশনের লেখচিত্রের অংশ দেখতে যেমন, \(\frac{\pi}{2}\) হতে \(\frac{3\pi}{2}\) সীমার মধ্যে এবং \(-\frac{3\pi}{2}\) হতে \(-\frac{\pi}{2}\) সীমার মধ্যে একই রকম হবে।
এখন, ছক কাগজে পরস্পরছেদী দুইটি লম্ব রেখা দ্বারা \(x\) অক্ষ ও \(y\) অক্ষ নির্ধারণ করি। \(x\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের এক বাহু \(=\frac{\pi}{24}\) এবং \(y\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের \(10\) বাহু \(=1\) একক ধরে তালিকাভূক্ত বিন্দুগুলি ছক কাগজে স্থাপন করি। অতঃপর বিন্দুগুলি মসৃণ বক্ররেখা দ্বারা যুক্ত করলেই \(y=\tan{x}\) ফাংশনের লেখচিত্র পাওয়া যাবে।

ট্যানজেন্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \(\frac{\pi}{2}\) এর বিজোড় গুণিতকের জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{(2n+1)\frac{\pi}{2}:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(180^{o}\) বা \(2\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=(2n-1)\frac{\pi}{2}:n\in{\mathbb{Z}}\)
\((vi)\) যেহেতু \(\tan{(n\pi+x)}=\tan{x}\) লেখের প্রতিটি শাখা \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) সীমার মধ্যে আঁকা শাখাটির অনুরূপ।
উপরোক্ত সীমায় \(x=-\pi, \ 0\) ও \(-\pi\) বিন্দুতে \(y=\tan{x}\) এর মান শূন্য।
আবার, \(x=\pm{\frac{\pi}{2}}, \ \pm{\frac{3\pi}{2}}\) বিন্দুগুলিতে \(y=\tan{x}\) এর মান বিশ্লেষন করলে দেখা যায়,
\(x\rightarrow \frac{\pi^{-}}{2} \ \left(\frac{\pi}{2} \text{ হতে সামান্য কম }\right)\) হলে \(y\rightarrow{\infty}\) হয়।
\(x\rightarrow{\frac{\pi^{+}}{2}} \ \left(\frac{\pi}{2} \text{ হতে সামান্য বেশি }\right)\) হলে \(y\rightarrow{-\infty}\) হয়।
অনুরূপভাবে,
\(x\rightarrow{\frac{3\pi^{-}}{2}} \) হলে, \(y\rightarrow{\infty}\) হয়।
\(x\rightarrow{-\frac{\pi^{+}}{2}} \) হলে, \(y\rightarrow{-\infty}\) হয়।
\(x\rightarrow{-\frac{\pi^{-}}{2}} \) হলে, \(y\rightarrow{\infty}\) হয়।
এবং \(x\rightarrow{-\frac{3\pi^{+}}{2}} \) হলে, \(y\rightarrow{-\infty}\) হয়।
উক্ত সীমার মধ্যে \(\frac{\pi}{6}\) ব্যবধানে \(y=\tan{x}\) এর লেখচিত্রের অংশ নির্ণয়ের জন্য ক্যালকুলেটরের সাহায্যে দুই দশমিক স্থান পর্যন্ত নির্ণয় করে নিচে একটি তালিকা তৈরী করা হলো।
| \(x\) | \(-\frac{12\pi}{24}\) | \(-\frac{8\pi}{24}\) | \(-\frac{6\pi}{24}\) | \(-\frac{4\pi}{24}\) | \(0\) | \(\frac{4\pi}{24}\) | \(\frac{6\pi}{24}\) | \(\frac{8\pi}{24}\) | \(\frac{12\pi}{24}\) |
| \(y=\tan{x}\) | \(-\infty\) | \(-1.73\) | \(-1\) | \(-0.58\) | \(0\) | \(0.58\) | \(1\) | \(1.73\) | \(+\infty\) |
| \((x, \ y)\) | \((-\frac{12\pi}{24},-\infty)\) | \((-\frac{8\pi}{24}, -1.73)\) | \((-\frac{6\pi}{24}, -1)\) | \((-\frac{4\pi}{24}, -0.58)\) | \((0, 0)\) | \((\frac{4\pi}{24}, 0.58)\) | \((\frac{6\pi}{24}, 1)\) | \((\frac{8\pi}{24}, 1.73)\) | \((\frac{12\pi}{24}, \infty)\) |
এখন, ছক কাগজে পরস্পরছেদী দুইটি লম্ব রেখা দ্বারা \(x\) অক্ষ ও \(y\) অক্ষ নির্ধারণ করি। \(x\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের এক বাহু \(=\frac{\pi}{24}\) এবং \(y\) অক্ষ বরাবর ক্ষুদ্রতম বর্গের \(10\) বাহু \(=1\) একক ধরে তালিকাভূক্ত বিন্দুগুলি ছক কাগজে স্থাপন করি। অতঃপর বিন্দুগুলি মসৃণ বক্ররেখা দ্বারা যুক্ত করলেই \(y=\tan{x}\) ফাংশনের লেখচিত্র পাওয়া যাবে।

ট্যানজেন্ট লেখচিত্রের বৈশিষ্টঃ
\((i)\) লেখচিত্রেটি বিচ্ছিন্ন। অর্থাৎ \(x\) এর মান \(\frac{\pi}{2}\) এর বিজোড় গুণিতকের জন্য লেখচিত্রটি বিচ্ছিন্ন।
\((ii)\) ফাংশনটির ডোমেন \(\mathbb{R}-\{(2n+1)\frac{\pi}{2}:n\in{\mathbb{Z}}\}\)
\((iii)\) ফাংশনটির রেঞ্জ \(\mathbb{R}\)
\((iv)\) এটি একটি পর্যায় ভিত্তিক ফাংশন যার পর্যায়কাল \(180^{o}\) বা \(2\pi\)
\((v)\) লেখচিত্রটির আসীমতট \(x=(2n-1)\frac{\pi}{2}:n\in{\mathbb{Z}}\)
\((vi)\) যেহেতু \(\tan{(n\pi+x)}=\tan{x}\) লেখের প্রতিটি শাখা \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) সীমার মধ্যে আঁকা শাখাটির অনুরূপ।

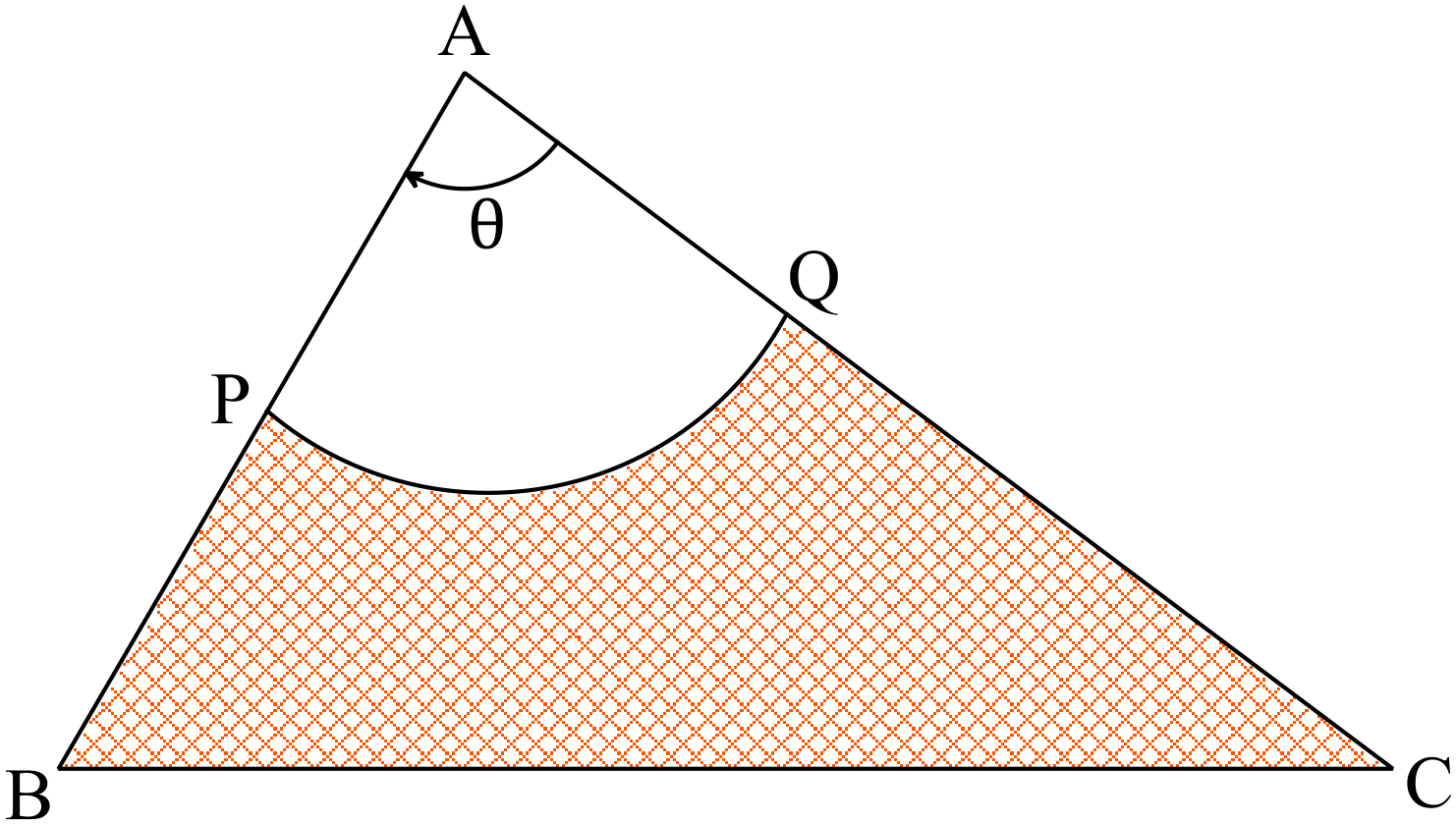 \(Ex.3.\) \(AP=7m, \ BP=3m,\) \(AC=14m, \ BC=18m,\) \(AP=AQ,\) চাপ \(PQ=10.5m\) এবং \(f(x)=\sin{x}\) একটি ত্রিকোণমিতিক ফাংশন।
\(Ex.3.\) \(AP=7m, \ BP=3m,\) \(AC=14m, \ BC=18m,\) \(AP=AQ,\) চাপ \(PQ=10.5m\) এবং \(f(x)=\sin{x}\) একটি ত্রিকোণমিতিক ফাংশন।
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004