এ অধ্যায়ের পাঠ্যসূচী
- ফাংশনের অন্তরীকরণ যোগ্যতা (Differentiability of functions)
- বিশেষ স্বরনীয় বিষয় (Special mention)
- রোলের উপপাদ্য (Rolle's theorem)
- টেলরের ধারা (Taylor's clause)
- গড়মান উপপাদ্য (Mean value theorem)
- মধ্যবর্তী মাণ উপপাদ্য (Intermediate value theorem)
- ক্রমবর্ধমান ও ক্রমহ্রাসমান ফাংশন (Increasing and Decreasing function)
- ফাংশনের চরম মাণ (Extreme values of function)
- ফাংশনের গরিষ্ঠমান (Maximum Values of a function)
- ফাংশনের লঘিষ্ঠমান (Minimum Values of a function)
- ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান বিদ্যমান থাকার প্রয়োজনীয় শর্ত (Necessary condition for existence of maximum and minimum of function)
- গরিষ্ঠমান ও লঘিষ্ঠমান নির্ণয় (Finding the maximum and minimum of a function)
- গরিষ্ঠমান ও লঘিষ্ঠমান নির্ণয়ের পদ্ধতি (Methods of finding maxima and minima of functions)
- খোলা ও বদ্ধ ব্যবধি (Open and Close Interval)
- অধ্যায় \(ix.I\)-এর উদাহরণসমুহ
- অধ্যায় \(ix.I\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(ix.I\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(ix.I\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(ix.I\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(ix.I\) / \(Q.5\)-এর সৃজনশীল প্রশ্নসমূহ
- অধ্যায় \(ix.I\) / \(Q.6\)-এর ভর্তি পরীক্ষায় আসা প্রশ্নসমূহ
ফাংশনের অন্তরীকরণ যোগ্যতা
Differentiability of functions
ধরি, \(f(x)\) ফাংশন \([a, b]\) ব্যবধিতে সংজ্ঞায়িত \(a>c>b\) হলে ফাংশনটি \(x=c\) বিন্দুতে অন্তরীকরণযোগ্য বলা হয় যদি
\[f^{\prime}(c)=\lim_{h \rightarrow 0}\frac{f(c+h)-f(c)}{h}\] বিদ্যমান থাকে এবং \[\lim_{h \rightarrow 0+}\frac{f(c+h)-f(c)}{h}\] ও \[\lim_{h \rightarrow 0-}\frac{f(c+h)-f(c)}{h}\] এর মাণ সসীম ও পরস্পর সমান হয়।
\[f^{\prime}(c)=\lim_{h \rightarrow 0}\frac{f(c+h)-f(c)}{h}\] বিদ্যমান থাকে এবং \[\lim_{h \rightarrow 0+}\frac{f(c+h)-f(c)}{h}\] ও \[\lim_{h \rightarrow 0-}\frac{f(c+h)-f(c)}{h}\] এর মাণ সসীম ও পরস্পর সমান হয়।
বিশেষ স্বরনীয় বিষয়
Special mention
\(x=c\) বিন্দুতে অন্তরীকরণযোগ্য ফাংশন \(x=c\) বিন্দুতে অবিচ্ছিন্ন হয়।
\(x=c\) বিন্দুতে অবিচ্ছিন্ন ফাংশন \(x=c\) বিন্দুতে অন্তরীকরণযোগ্য নাও হতে পারে।
ফাংশন \(f(x)\)-কে \((a, b)\) খোলা ব্যবধিতে অন্তরীকরণযোগ্য বলা হবে যদি সকল \(x\in(a, b)\) বিন্দুতে \(f(x)\) অন্তরীকরণযোগ্য হয়।
\(x=c\) বিন্দুতে অবিচ্ছিন্ন ফাংশন \(x=c\) বিন্দুতে অন্তরীকরণযোগ্য নাও হতে পারে।
ফাংশন \(f(x)\)-কে \((a, b)\) খোলা ব্যবধিতে অন্তরীকরণযোগ্য বলা হবে যদি সকল \(x\in(a, b)\) বিন্দুতে \(f(x)\) অন্তরীকরণযোগ্য হয়।
রোলের উপপাদ্য
Rolle's theorem
যদি \(f(x)\) ফাংশন
\([a, b]\) বদ্ধ ব্যবধিতে অবিচ্ছিন্ন হয়।
\((a, b)\) খোলা ব্যবধিতে অন্তরীকরণযোগ্য এবং
\(f(a)=f(b)\) হয়, তবে \(a\) ও \( b\) এর মধ্যে অন্ততঃপক্ষে \(x\)এর এমন একটি মান \(c\) পাওয়া যাবে যেখানে \(f^{\prime}(c)=0\) হবে।
অর্থাৎ \(a>c>b\) খোলা ব্যবধিতে \(f^{\prime}(c)=0\) হবে।
\([a, b]\) বদ্ধ ব্যবধিতে অবিচ্ছিন্ন হয়।
\((a, b)\) খোলা ব্যবধিতে অন্তরীকরণযোগ্য এবং
\(f(a)=f(b)\) হয়, তবে \(a\) ও \( b\) এর মধ্যে অন্ততঃপক্ষে \(x\)এর এমন একটি মান \(c\) পাওয়া যাবে যেখানে \(f^{\prime}(c)=0\) হবে।
অর্থাৎ \(a>c>b\) খোলা ব্যবধিতে \(f^{\prime}(c)=0\) হবে।
টেলরের ধারা
Taylor's clause
যদি \(f(x)\) ফাংশন এবং \(f^{\prime}(x), f^{\prime\prime}(x), f^{\prime\prime\prime}(x), .......f^{n-1}(x)\) ফাংশনগুলি \([a, a+h]\) বদ্ধ ব্যবধিতে অবিচ্ছিন্ন হয় এবং \(f^{n}(x)\) ফাংশনটি \((a, a+h)\) খোলা ব্যবধিতে বিদ্যমান থাকে, তবে,
\(f(a+h)=f(a)+hf^{\prime}(a)+\frac{h^2}{l^2}f^{\prime\prime}(a)+\frac{h^3}{l^3}f^{\prime\prime\prime}(a)+ ........\)
\(f(a+h)=f(a)+hf^{\prime}(a)+\frac{h^2}{l^2}f^{\prime\prime}(a)+\frac{h^3}{l^3}f^{\prime\prime\prime}(a)+ ........\)
গড়মান উপপাদ্য
Mean value theorem
যদি \(f(x)\) ফাংশন \([a, b]\) ব্যবধিতে অবিচ্ছিন্ন এবং \((a, b)\) ব্যবধিতে অন্তরীকরণযোগ্য হয় তবে \(a\) ও \( b\) এর মধ্যে অন্ততঃপক্ষে \(x\)এর এমন একটি মান \(c\) পাওয়া যাবে যাতে \(f(b)-f(a)=(b-a)f^{\prime}(c)\) হয়।
উদাহরণঃ
\((1, 3)\) ব্যবধিতে \(f(x)=x^2-2x+3\) ফাংশনের জন্য গড়মান উপপাদ্যটির সত্যতা নিরূপণ কর।
উদাহরণঃ
\((1, 3)\) ব্যবধিতে \(f(x)=x^2-2x+3\) ফাংশনের জন্য গড়মান উপপাদ্যটির সত্যতা নিরূপণ কর।
মধ্যবর্তী মান উপপাদ্য
Intermediate value theorem
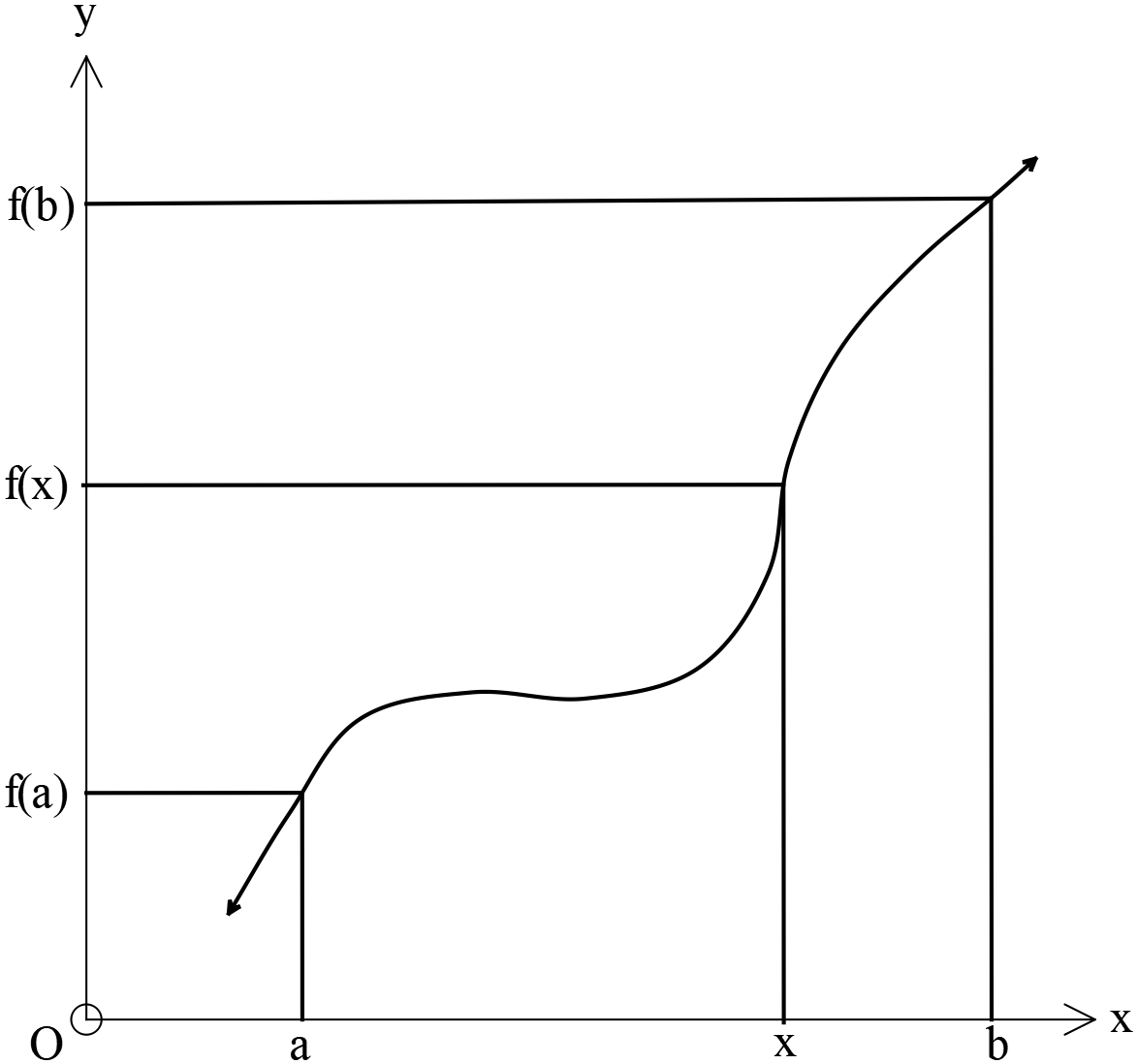
যদি \([a, b]\) বদ্ধ ব্যবধিতে \(f(x)\) অবিচ্ছিন্ন ফাংশন হয় এবং \(k\) যে কোনো একটি সংখ্যা \(f(a)\) ও \(f(b)\) এর মধ্যে অবস্থিত হয় তাহলে \([a, b]\) ব্যবধির মধ্যে কমপক্ষে একটি সংখ্যা থাকবে যেখানে \(f(x)=l\).
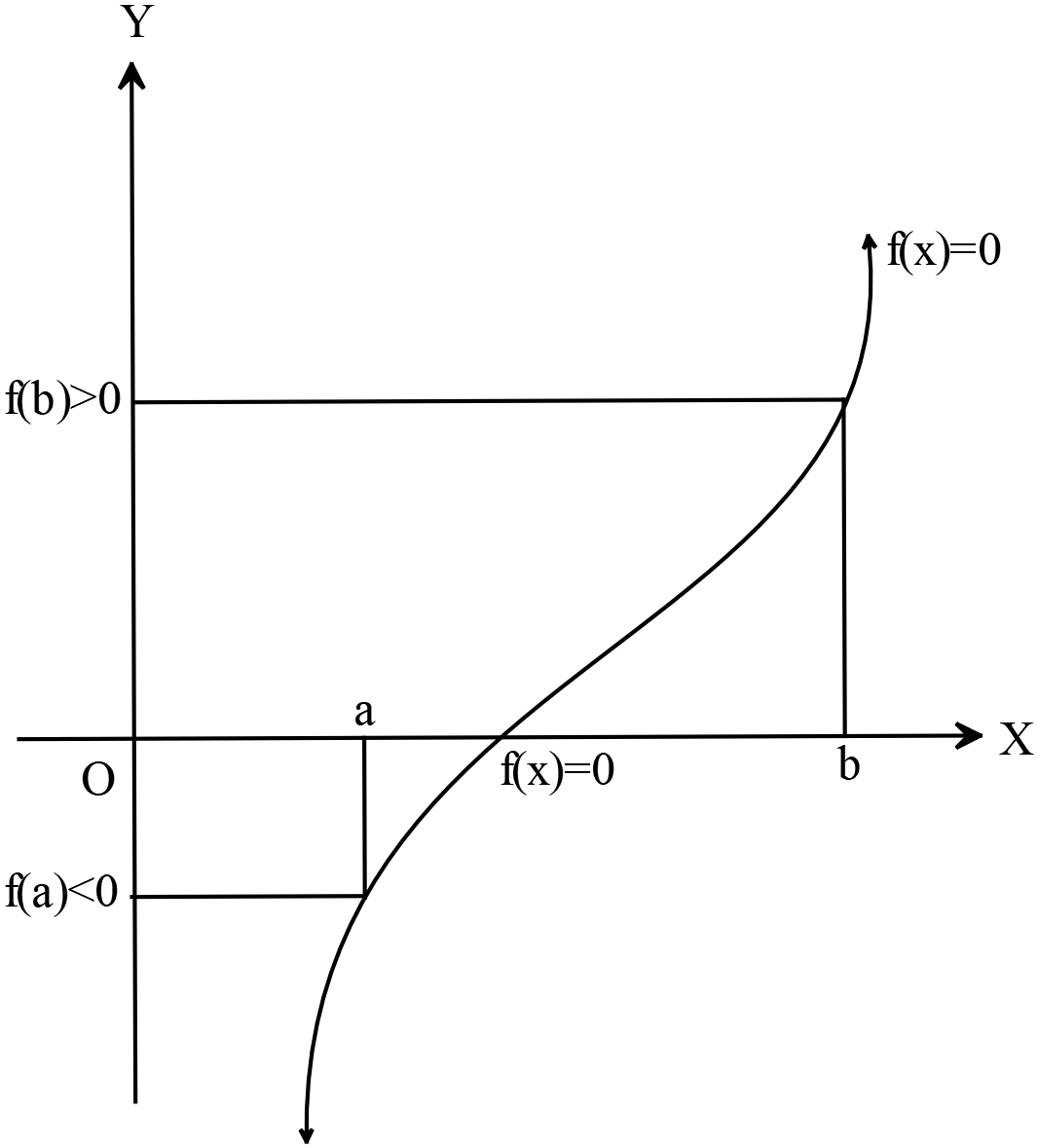প্রতিজ্ঞাঃযদি কোনো ফাংশন \(f(x), [a, b]\) বিন্দুতে অবিচ্ছিন্ন হয় এবং \(f(a)\) ও \(f(b)\) শূন্য না হয় এবং বিপরীত চিহ্ন বিশিষ্ট হয় তবে \(f(x)=0\) সমীকরণের \((a, b)\) ব্যবধিতে কমপক্ষে একটি সমাধান বিদ্যমান। উদাহরণঃ
মধ্যমান উপপাদ্য ব্যবহার করে দেখাও যে, \([-1, 0]\) ব্যবধিতে \(f(x)=x^3+x+1\) সমীকরণের সমাধান আছে।
ক্রমবর্ধমান ও ক্রমহ্রাসমান ফাংশন
Increasing and Decreasing function
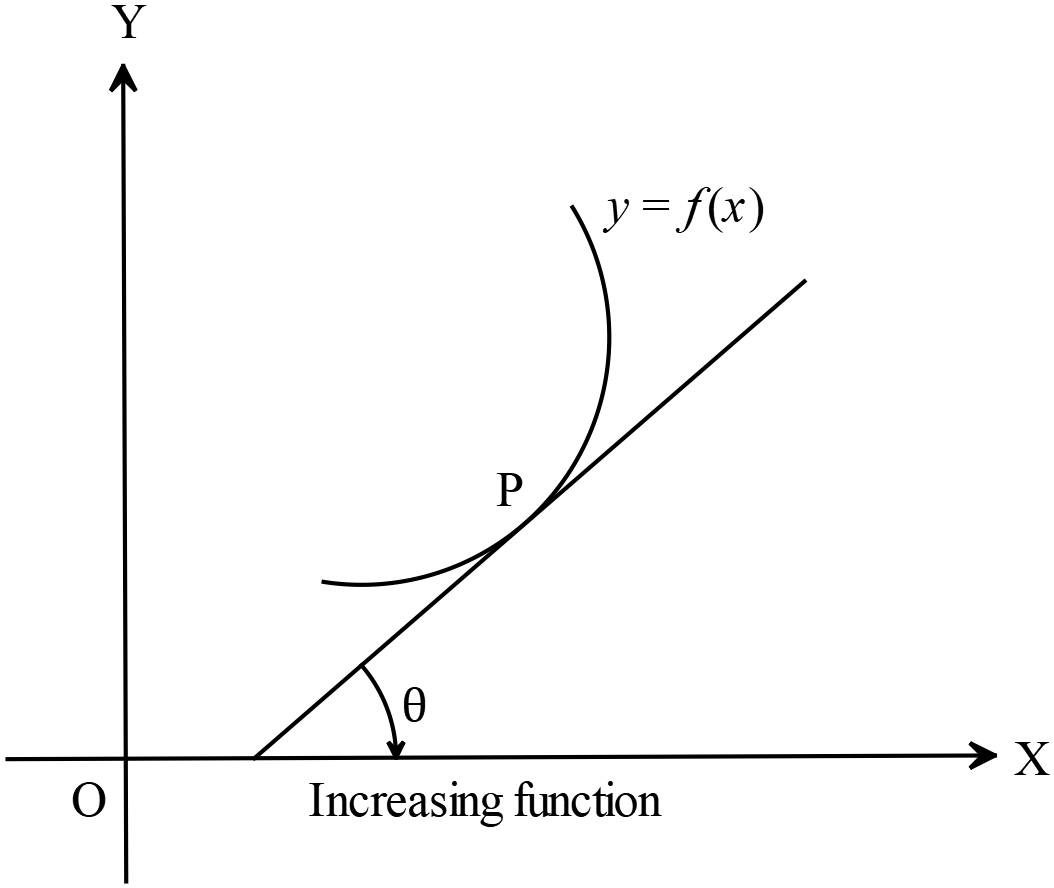ক্রমবর্ধমান ফাংশনঃযদি \(x\) এর মাণ বৃদ্ধির জন্য কোনো ফাংশন \(y=f(x)\) এর মাণ বৃদ্ধি পায় অর্থাৎ \(y=f(x)\) ফাংশনের উপরস্থ যে কোনো বিন্দুতে অঙ্কিত স্পর্শকের ঢাল ধনাত্মক হয়, তবে \(y=f(x)\) কে ক্রমবর্ধমান ফাংশন বলা হয়। ক্রমবর্ধমান ফাংশনের ক্ষেত্রে স্পর্শকের ঢাল ধনাত্মক।
অর্থাৎ, \(\frac{dy}{dx}>0\) এখানে \(\frac{dy}{dx}=\tan{\theta}\) এবং \(90^{o}>\theta\).
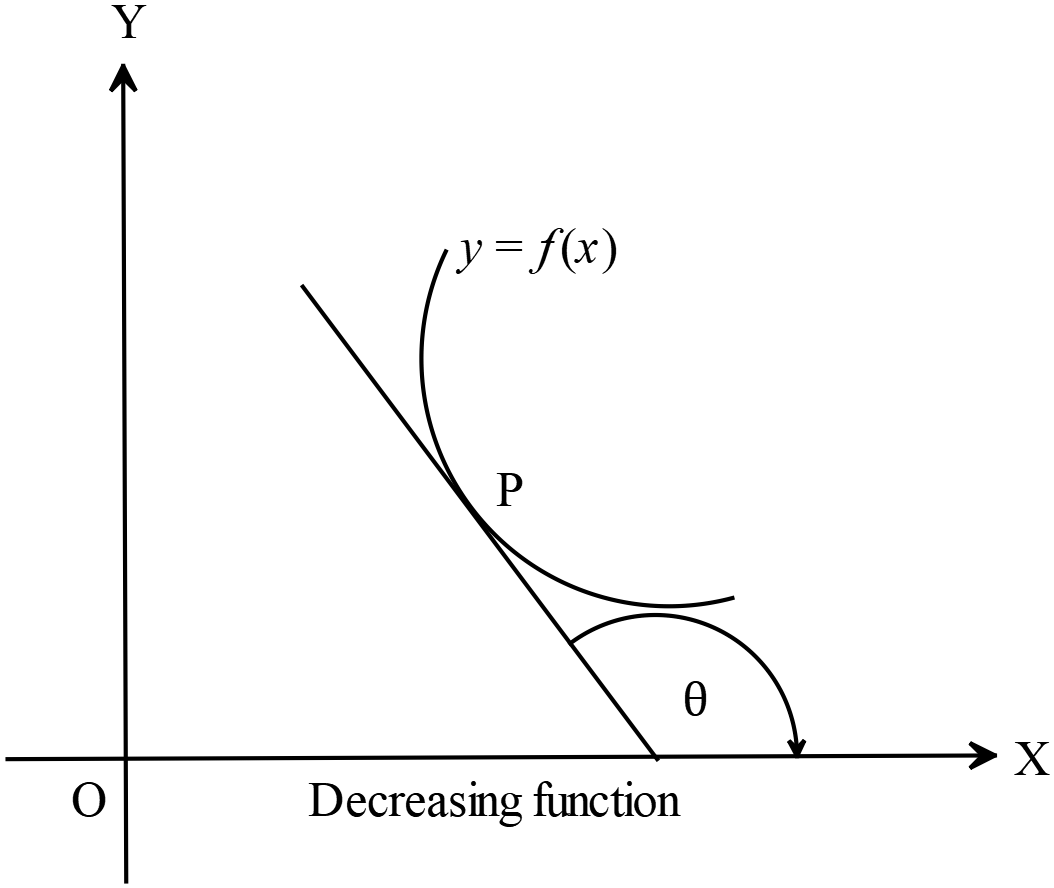ক্রমহ্রাসমান ফাংশনঃযদি \(x\) এর মাণ বৃদ্ধির জন্য কোনো ফাংশন \(y=f(x)\) এর মাণ হ্রাস পায় অর্থাৎ \(y=f(x)\) ফাংশনের উপরস্থ যে কোনো বিন্দুতে অঙ্কিত স্পর্শকের ঢাল ঋনাত্মক হয়, তবে \(y=f(x)\) কে ক্রমহ্রাসমান ফাংশন বলা হয়। ক্রমহ্রাসমান ফাংশনের ক্ষেত্রে স্পর্শকের ঢাল ঋনাত্মক।
অর্থাৎ, \(\frac{dy}{dx}<0\) এখানে \(\frac{dy}{dx}=\tan{\theta}\) এবং \(\theta>90^{o}\). মন্তব্যঃ
\(b>x>a\) এর সকল \(x\) এর জন্য \(f^{\prime}(x)>0\) হয়, তবে \(y=f(x)\) ফাংশন \((a, b)\) ব্যবধিতে ক্রমবর্ধমান হবে।
\(b>x>a\) এর সকল \(x\) এর জন্য \(f^{\prime}(x)<0\) হয়, তবে \(y=f(x)\) ফাংশন \((a, b)\) ব্যবধিতে ক্রমহ্রাসমান হবে।
ফাংশনের চরম মাণ
Extreme values of function
ফাংশনের চরম মাণঃ
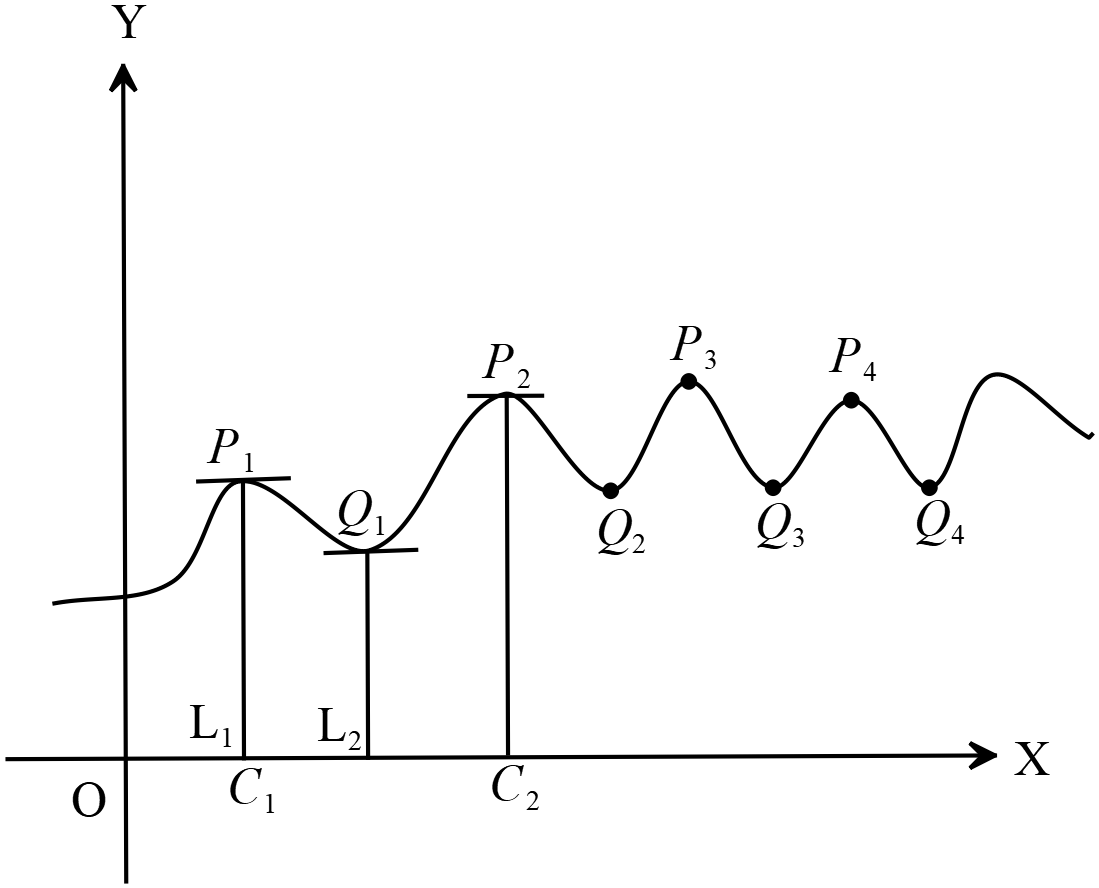
\(y=f(x)\) অবিচ্ছিন্ন ফাংশনটির লেখচিত্র থেকে আমরা দেখতে পাই যে, \(P_{1}\) বিন্দুর ডান ও বাম দিকে একটি ক্ষুদ্র ব্যবধি \(L_{1}L_{2}\) এর অন্তর্গত \(x\) এর সকল মানের মধ্যে \(x=OC_{1}=c\) এর জন্য \(f(x)=f(c)\) এর মাণ বৃহত্তম।
অনুরূপভাবে, \(P_{2}, P_{3}, P_{4}\) বিন্দুগুলিতেও বিন্দুগুলির উভয় দিকে \(x\) এর মাণসমূহের একটি ক্ষুদ্র ব্যবধির মধ্যে \(x\) এর একটি নির্দিষ্ট মানের জন্য \(f(x)\) এর মাণ বৃহত্তম।
অতএব, কোনো বিন্দুতে \(f(x)\) এর মাণ বৃহত্তমের অর্থ এই নয় যে, ফাংশনটির মাণ সে বিন্দুতে চুড়ান্তভাবে বৃহত্তম। ফাংশনটির ক্ষুদ্রতম মানও একইভাবে সংজ্ঞায়িত করা হয়। কোনো বিন্দুতে একটি ফাংশনের মাণ ক্ষুদ্রতম-এর অর্থ এই নয় যে, বিন্দুটিতে ফাংশনটির মাণ চুড়ান্তভাবে ক্ষুদ্রতম। লক্ষ করলে আরও দেখা যায় যে, কোনো বিন্দুতে ফাংশনটির ক্ষুদ্রতম মাণ আর একটি বিন্দুতে ফাংশনটির বৃহত্তম মানের চেয়ে বৃহত্তম। সুতরাং একটি ফাংশনের বৃহত্তম ও ক্ষুদ্রতম মানগুলি প্রকৃতপক্ষে আপেক্ষিকভাবে বৃহত্তম ও ক্ষুদ্রতম মাণ। ফাংশনের আপেক্ষিক বৃহত্তম ও ক্ষুদ্রতম মানগুলিকে ফাংশনের গুরুমান ও লঘুমান এবং এদের একত্রে ফাংশনের চরম মাণ বলা হয়। অর্থাৎ আপেক্ষিক বৃহত্তম মাণ ও আপেক্ষিক ক্ষুদ্রতম মাণ বুঝাতে আমরা 'গুরুমান' ও 'লঘুমান' ব্যবহার করব। মন্তব্যঃ
একটি ফাংশনের একাধিক গুরুমান ও লঘুমাণ থাকতে পারে।
কোনো বিন্দুতে ফাংশনের লঘুমান অন্য একটি বিন্দুতে ফাংশনটির গুরুমানের চেয়ে বড় হতে পারে।
ফাংশনের গরিষ্ঠমান
Maximum Value of a function
ফাংশনের গরিষ্ঠমানঃ
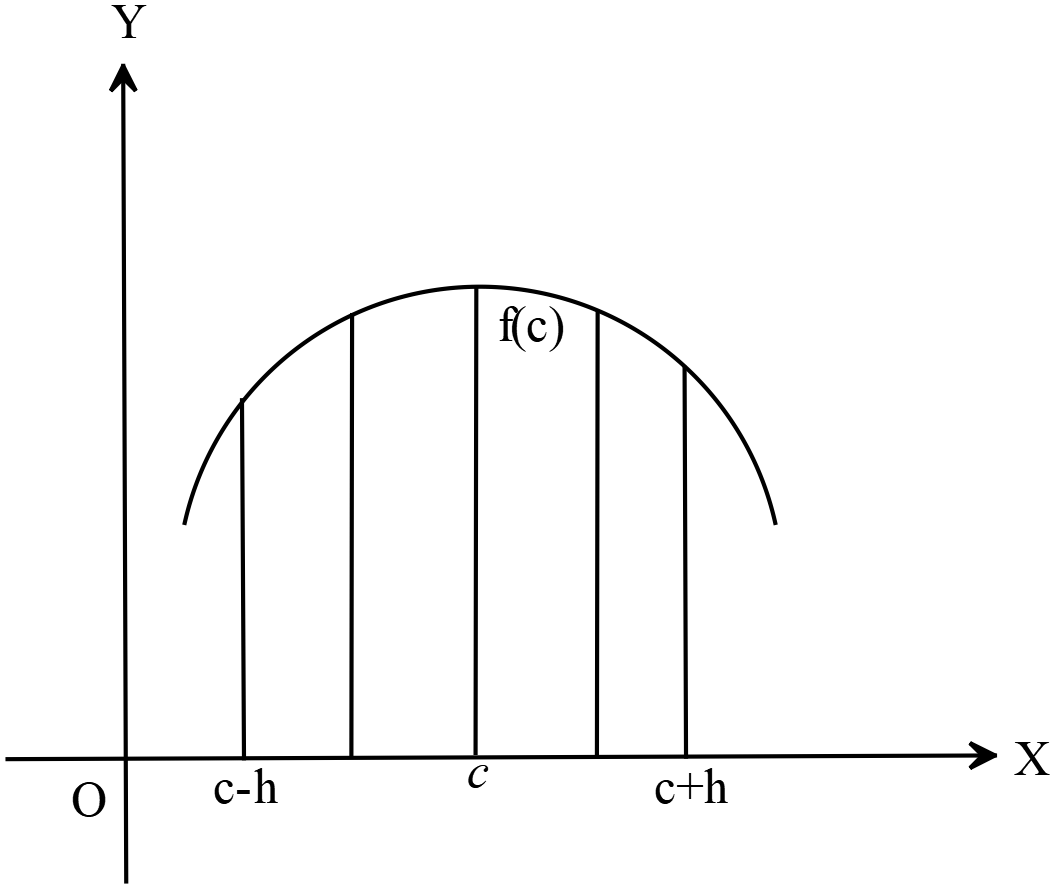\(f(c)\) কে \(f(x)\) ফাংশনের গরিষ্ঠমান বলা হবে যদি অতি ক্ষুদ্র \(h>0\) এর জন্য \((c-h, c+h)\) ব্যবধিতে \(x\)এর সকল মানের জন্য \(f(c)\) সর্বদাই \(f(x)\) এর অন্যান্য মাণ অপেক্ষা বৃহৎ থাকে।
অর্থাৎ \(f(c)>f(x)\) যেখানে \(x\in{(c-h, c+h)}\) কিন্তু \(x\ne{c}\)
তাহলে, \(f(c+h)-f(c)<0\)
অন্যভাবে, যদি \(x=c\) বিন্দুর নিকট প্রতিবেশীতে \(f(c)\) এর মাণ সর্দাই \(f(x)\) এর অন্যান্য মাণ অপেক্ষা বৃহৎ থাকে তবে, \(x=c\) বিন্দুতে \(f(x)\) এর গরিষ্ঠমান আছে এবং উহা \(f(c)\)
\(f(c)\) কে \(f(x)\) ফাংশনের গরিষ্ঠমান বলা হবে যদি অতি ক্ষুদ্র \(h>0\) এর জন্য \((c-h, c+h)\) ব্যবধিতে \(x\)এর সকল মানের জন্য \(f(c)\) সর্বদাই \(f(x)\) এর অন্যান্য মাণ অপেক্ষা বৃহৎ থাকে।অর্থাৎ \(f(c)>f(x)\) যেখানে \(x\in{(c-h, c+h)}\) কিন্তু \(x\ne{c}\)
তাহলে, \(f(c+h)-f(c)<0\)
অন্যভাবে, যদি \(x=c\) বিন্দুর নিকট প্রতিবেশীতে \(f(c)\) এর মাণ সর্দাই \(f(x)\) এর অন্যান্য মাণ অপেক্ষা বৃহৎ থাকে তবে, \(x=c\) বিন্দুতে \(f(x)\) এর গরিষ্ঠমান আছে এবং উহা \(f(c)\)
ফাংশনের লঘিষ্ঠমান
Minimum Value of a function
ফাংশনের লঘিষ্ঠমানঃ
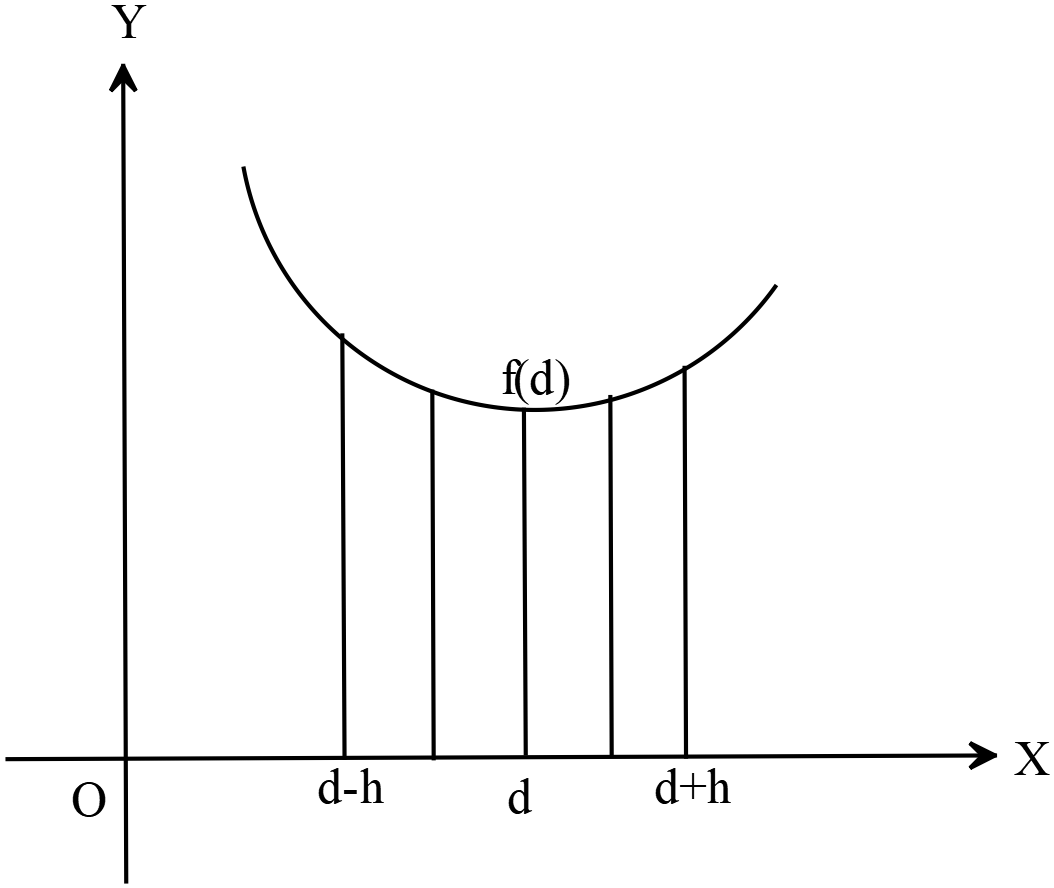\(f(d)\) কে \(f(x)\) ফাংশনের লঘিষ্ঠমান বলা হবে যদি অতি ক্ষুদ্র \(h>0\) এর জন্য \((d-h, d+h)\) ব্যবধিতে \(x\)এর সকল মানের জন্য \(f(d)\) সর্বদাই \(f(x)\) এর অন্যান্য মাণ অপেক্ষা ক্ষুদ্র থাকে।
অর্থাৎ \(f(d)>f(x)\) যেখানে \(x\in{(d-h, d+h)}\) কিন্তু \(x\ne{d}\)
তাহলে, \(f(d+h)-f(d)>0\)
অন্যভাবে, যদি \(x=d\) বিন্দুর নিকট প্রতিবেশীতে \(f(d)\) এর মাণ সর্দাই \(f(x)\) এর অন্যান্য মাণ অপেক্ষা ক্ষুদ্র থাকে তবে, \(x=d\) বিন্দুতে \(f(x)\) এর লঘিষ্ঠমান আছে এবং উহা \(f(d)\)
\(f(d)\) কে \(f(x)\) ফাংশনের লঘিষ্ঠমান বলা হবে যদি অতি ক্ষুদ্র \(h>0\) এর জন্য \((d-h, d+h)\) ব্যবধিতে \(x\)এর সকল মানের জন্য \(f(d)\) সর্বদাই \(f(x)\) এর অন্যান্য মাণ অপেক্ষা ক্ষুদ্র থাকে।অর্থাৎ \(f(d)>f(x)\) যেখানে \(x\in{(d-h, d+h)}\) কিন্তু \(x\ne{d}\)
তাহলে, \(f(d+h)-f(d)>0\)
অন্যভাবে, যদি \(x=d\) বিন্দুর নিকট প্রতিবেশীতে \(f(d)\) এর মাণ সর্দাই \(f(x)\) এর অন্যান্য মাণ অপেক্ষা ক্ষুদ্র থাকে তবে, \(x=d\) বিন্দুতে \(f(x)\) এর লঘিষ্ঠমান আছে এবং উহা \(f(d)\)
ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান বিদ্যমান থাকার প্রয়োজনীয় শর্ত
Necessary condition for existence of maximum and minimum of function
যদি \(x=c\) বিন্দুতে \(f(x)\) ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান থাকে এবং \(f^{\prime}(c)\) এর মাণ বিদ্যমান থাকে তবে \(f^{\prime}(c)=0\) হবে।
ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান নির্ণয়
Finding the maximum and minimum of a function
\(x=c\) বিন্দুতে \(f(x)\) ফাংশন অবিচ্ছিন্ন এবং \(f^{\prime}(c)=0\) ও \(f^{\prime\prime}(c)\ne{0}\) হলে,
\(x=c\) বিন্দুতে \(f(x)\) এর গরিষ্ঠমাণ থাকবে যদি \(f^{\prime\prime}(c)<0\) হয়।
বিন্দুতে \(f(x)\) এর লঘিষ্ঠমান থাকবে যদি \(f^{\prime\prime}(c)>0\) হয়।
\(x=c\) বিন্দুতে \(f(x)\) এর গরিষ্ঠমাণ থাকবে যদি \(f^{\prime\prime}(c)<0\) হয়।
বিন্দুতে \(f(x)\) এর লঘিষ্ঠমান থাকবে যদি \(f^{\prime\prime}(c)>0\) হয়।
ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান নির্ণয়ের পদ্ধতি
Methods of finding maxima and minima of functions
প্রদত্ত ফাংশনটিকে \(f(x)\) ধরতে হবে।
\(f^{\prime}(x)\) নির্ণয় করতে হবে।
ফাংশনটির গরিষ্ঠমাণ ও লঘিষ্ঠমানের জন্য \(f^{\prime}(x)=0\) ধরে \(x\) এর মান নির্ণয় করতে হবে।
ধরি, \(x=a, b, c\)
\(f^{\prime\prime}(x)\) নির্ণয় করতে হবে।
\(x=a\) মানের জন্য \(f^{\prime\prime}(x)\gt{0}\) হলে, বুঝতে হবে \(x=a\) বিন্দুতে ফাংশনটির লঘিষ্ঠমান আছে এবং ফাংশনটির লঘিষ্ঠমান \(=f(a)\)
\(x=b\) মানের জন্য \(f^{\prime\prime}(x)\lt{0}\) হলে, বুঝতে হবে \(x=b\) বিন্দুতে ফাংশনটির গরিষ্ঠমাণ আছে এবং ফাংশনটির গরিষ্ঠমাণ \(=f(b)\)
\(x=c\) মানের জন্য \(f^{\prime\prime}(x)=0\) হলে, বুঝতে হবে \(x=c\) বিন্দুতে ফাংশনটির লঘিষ্ঠমান ও গরিষ্ঠমাণ থাকতেও পারে আবার নাও থাকতে পারে। যা উচ্চতর পর্যায়ে শেখানো হবে।
\(f^{\prime}(x)\) নির্ণয় করতে হবে।
ফাংশনটির গরিষ্ঠমাণ ও লঘিষ্ঠমানের জন্য \(f^{\prime}(x)=0\) ধরে \(x\) এর মান নির্ণয় করতে হবে।
ধরি, \(x=a, b, c\)
\(f^{\prime\prime}(x)\) নির্ণয় করতে হবে।
\(x=a\) মানের জন্য \(f^{\prime\prime}(x)\gt{0}\) হলে, বুঝতে হবে \(x=a\) বিন্দুতে ফাংশনটির লঘিষ্ঠমান আছে এবং ফাংশনটির লঘিষ্ঠমান \(=f(a)\)
\(x=b\) মানের জন্য \(f^{\prime\prime}(x)\lt{0}\) হলে, বুঝতে হবে \(x=b\) বিন্দুতে ফাংশনটির গরিষ্ঠমাণ আছে এবং ফাংশনটির গরিষ্ঠমাণ \(=f(b)\)
\(x=c\) মানের জন্য \(f^{\prime\prime}(x)=0\) হলে, বুঝতে হবে \(x=c\) বিন্দুতে ফাংশনটির লঘিষ্ঠমান ও গরিষ্ঠমাণ থাকতেও পারে আবার নাও থাকতে পারে। যা উচ্চতর পর্যায়ে শেখানো হবে।
খোলা ও বদ্ধ ব্যবধি
Open and Close Interval
খোলা ব্যবধি \((a, b)\Rightarrow ]a, b[ \Rightarrow \{x\in{\mathbb{R}}: b\gt{x}\gt{a}\}\)
বদ্ধ খোলা ব্যবধি \([a, b) \Rightarrow [a, b[ \Rightarrow \{x\in{\mathbb{R}}: b\ge{x}\gt{a}\}\)
খোলা বদ্ধ ব্যবধি \((a, b]\Rightarrow ]a, b] \Rightarrow \{x\in{\mathbb{R}}: b\gt{x}\ge{a}\}\)
বদ্ধ ব্যবধি \([a, b]\Rightarrow [a, b] \Rightarrow \{x\in{\mathbb{R}}: b\ge{x}\ge{a}\}\)
বদ্ধ খোলা ব্যবধি \([a, b) \Rightarrow [a, b[ \Rightarrow \{x\in{\mathbb{R}}: b\ge{x}\gt{a}\}\)
খোলা বদ্ধ ব্যবধি \((a, b]\Rightarrow ]a, b] \Rightarrow \{x\in{\mathbb{R}}: b\gt{x}\ge{a}\}\)
বদ্ধ ব্যবধি \([a, b]\Rightarrow [a, b] \Rightarrow \{x\in{\mathbb{R}}: b\ge{x}\ge{a}\}\)
×
গড়মান উপপাদ্যঃ
যদি \(f(x)\) ফাংশন \([a, b]\) ব্যবধিতে অবিচ্ছিন্ন এবং \((a, b)\) ব্যবধিতে অন্তরীকরণযোগ্য হয় তবে \(a\) ও \( b\) এর মধ্যে অন্ততঃপক্ষে \(x\)এর এমন একটি মান \(c\) পাওয়া যাবে যাতে \(f(b)-f(a)=(b-a)f^{\prime}(c)\) হয়।
যদি \(f(x)\) ফাংশন \([a, b]\) ব্যবধিতে অবিচ্ছিন্ন এবং \((a, b)\) ব্যবধিতে অন্তরীকরণযোগ্য হয় তবে \(a\) ও \( b\) এর মধ্যে অন্ততঃপক্ষে \(x\)এর এমন একটি মান \(c\) পাওয়া যাবে যাতে \(f(b)-f(a)=(b-a)f^{\prime}(c)\) হয়।
Proof:
মনে করি,\(y=f(x)\) বক্ররেখার উপর \(P, Q, R\) তিনটি বিন্দু । এখন \(P, Q, R\) হতে \(X\) অক্ষের উপর \(PL, QM\) এবং \(RN\) লম্ব অঙ্কন করি।
ধরি, \(OL=a, OM=b\) এবং \(ON=c\)
তাহলে, \(PL=f(a), QM=f(b)\) এবং \(RN=f(c)\)
\(\therefore P\) ও \(Q\) বিন্দুর স্থানাঙ্ক যথাক্রমে \(P(a, f(a))\) এবং \(Q(b, f(b))\)
\(\therefore PQ\) ছেদকের ঢাল \(=\frac{f(b)-f(a)}{b-a} .....(1)\)
\(R\) বিন্দুতে স্পর্শকের ঢাল \(=f^{\prime}(c) .....(2)\)
যেহেতু \(f(x)\) ফাংশন \([a, b]\) বদ্ধ ব্যবধিতে অবিচ্ছিন্ন এবং \((a, b)\) খোলা ব্যবধিতে অন্তরীকরণযোগ্য, কাজেই \(c\) ভূজবিশিষ্ট \(P\) এবং \(Q\) এর মধ্যবর্তী রেখার অংশে এমন একটি বিন্দু \(R\) পাওয়া যাবে যেখানে \(R\) বিন্দুর স্পর্শক, \(PQ\) ছেদকের সমান্তরাল হবে।
\(\therefore R\) বিন্দুর স্পর্শকের ঢাল \(=PQ\) ছেদকের ঢাল
\(\Rightarrow f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}\) ➜ \((1)\) ও \((2)\) এর সাহায্যে।
\(\therefore f(b)-f(a)=(b-a)f^{\prime}(c)\); ইহাই গড়মান উপপাদ্য।
×
উদাহরণঃ \((1, 3)\) ব্যবধিতে \(f(x)=x^2-2x+3\) ফাংশনের জন্য গড়মান উপপাদ্যটির সত্যতা নিরূপণ কর।
সমাধানঃ
আমরা জানি,
গড়মান উপপাদ্য \(f(b)-f(a)=(b-a)f^{\prime}(c)\)
এখানে,
\(f(x)=x^2-2x+3\) একটি বহুপদী ফাংশন।
কাজেই \(x\) এর সকল মানের জন্য ফাংশনটি অবিচ্ছিন্ন এবং অন্তরীকরণযোগ্য।
যেখানে, \(b>c>a\)
\(f(x)=x^2-2x+3\)
\(\Rightarrow f^{\prime}(x)=2x-2.1+0\) ➜ \(x\) এর সাপেক্ষে অন্তরীকরণ করে।
\(\Rightarrow f^{\prime}(x)=2x-2\)
\(\therefore f^{\prime}(c)=2c-2 .....(1)\)
এখানে,
\(a=1, b=3, 3>c>1\)
\(f(1)=1^2-2.1+3\)
\(=1-2+3\)
\(=4-2\)
\(=2\)
এবং \(f(3)=3^2-2.3+3\)
\(=9-6+3\)
\(=12-6\)
\(=6\)
এখন, গড়মান উপপাদ্য \(f(b)-f(a)=(b-a)f^{\prime}(c)\)
\(\Rightarrow (b-a)f^{\prime}(c)=f(b)-f(a)\)
\(\Rightarrow (3-1)f^{\prime}(c)=6-2\)
\(\Rightarrow 2f^{\prime}(c)=4\)
\(\Rightarrow f^{\prime}(c)=\frac{4}{2}\)
\(\Rightarrow f^{\prime}(c)=2\)
\(\Rightarrow 2c-2=2\) ➜ \((1)\) হতে, \(\because f^{\prime}(c)=2c-2\)
\(\Rightarrow 2c=2+2\)
\(\Rightarrow 2c=4\)
\(\Rightarrow c=\frac{4}{2}\)
\(\therefore c=2\)
\(\therefore 3>2>1\)
\(\Rightarrow 3>c>1\)
অর্থাৎ \((1, 3)\) ব্যবধির মধ্যে অবস্থিত।
গড়মান উপপাদ্যটির সত্যতা প্রমাণিত হলো।
আমরা জানি,
গড়মান উপপাদ্য \(f(b)-f(a)=(b-a)f^{\prime}(c)\)
এখানে,
\(f(x)=x^2-2x+3\) একটি বহুপদী ফাংশন।
কাজেই \(x\) এর সকল মানের জন্য ফাংশনটি অবিচ্ছিন্ন এবং অন্তরীকরণযোগ্য।
যেখানে, \(b>c>a\)
\(f(x)=x^2-2x+3\)
\(\Rightarrow f^{\prime}(x)=2x-2.1+0\) ➜ \(x\) এর সাপেক্ষে অন্তরীকরণ করে।
\(\Rightarrow f^{\prime}(x)=2x-2\)
\(\therefore f^{\prime}(c)=2c-2 .....(1)\)
এখানে,
\(a=1, b=3, 3>c>1\)
\(f(1)=1^2-2.1+3\)
\(=1-2+3\)
\(=4-2\)
\(=2\)
এবং \(f(3)=3^2-2.3+3\)
\(=9-6+3\)
\(=12-6\)
\(=6\)
এখন, গড়মান উপপাদ্য \(f(b)-f(a)=(b-a)f^{\prime}(c)\)
\(\Rightarrow (b-a)f^{\prime}(c)=f(b)-f(a)\)
\(\Rightarrow (3-1)f^{\prime}(c)=6-2\)
\(\Rightarrow 2f^{\prime}(c)=4\)
\(\Rightarrow f^{\prime}(c)=\frac{4}{2}\)
\(\Rightarrow f^{\prime}(c)=2\)
\(\Rightarrow 2c-2=2\) ➜ \((1)\) হতে, \(\because f^{\prime}(c)=2c-2\)
\(\Rightarrow 2c=2+2\)
\(\Rightarrow 2c=4\)
\(\Rightarrow c=\frac{4}{2}\)
\(\therefore c=2\)
\(\therefore 3>2>1\)
\(\Rightarrow 3>c>1\)
অর্থাৎ \((1, 3)\) ব্যবধির মধ্যে অবস্থিত।
গড়মান উপপাদ্যটির সত্যতা প্রমাণিত হলো।
×
উদাহরণঃ মধ্যমান উপপাদ্য ব্যবহার করে দেখাও যে, \([-1, 0]\) ব্যবধিতে \(f(x)=x^3+x+1\) সমীকরণের সমাধান আছে।
সমাধানঃ
দেওয়া আছে,
\(f(x)=x^3+x+1\) একটি বহুপদী ফাংশন।
কাজেই \(x\) এর সকল মানের জন্য ফাংশনটি অবিচ্ছিন্ন ।
এখন,
\(f(-1)=(-1)^3+(-1)+1\)
\(=-1-1+1\)
\(=-2+1\)
\(=-1\)
\(\therefore f(-1)<0\)
আবার,
\(f(0)=(0)^3+0+1\)
\(=0+0+1\)
\(=1\)
\(\therefore f(0)>0\)
\(f(-1)\) এবং \(f(0)\) এর মাণ বিপরীত চিহ্ন বিশিষ্ট।
অতএব, \(f(x)\) এর সমাধান \([-1, 0]\) ব্যবধির অন্তর্ভুক্ত।
দেওয়া আছে,
\(f(x)=x^3+x+1\) একটি বহুপদী ফাংশন।
কাজেই \(x\) এর সকল মানের জন্য ফাংশনটি অবিচ্ছিন্ন ।
এখন,
\(f(-1)=(-1)^3+(-1)+1\)
\(=-1-1+1\)
\(=-2+1\)
\(=-1\)
\(\therefore f(-1)<0\)
আবার,
\(f(0)=(0)^3+0+1\)
\(=0+0+1\)
\(=1\)
\(\therefore f(0)>0\)
\(f(-1)\) এবং \(f(0)\) এর মাণ বিপরীত চিহ্ন বিশিষ্ট।
অতএব, \(f(x)\) এর সমাধান \([-1, 0]\) ব্যবধির অন্তর্ভুক্ত।
×
ফাংশনের লঘিষ্ঠমান ও গরিষ্ঠমান বিদ্যমান থাকার প্রয়োজনীয় শর্তঃ
যদি \(x=c\) বিন্দুতে \(f(x)\) ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান থাকে এবং \(f^{\prime}(c)\) এর মাণ বিদ্যমান থাকে তবে \(f^{\prime}(c)=0\) হবে।
যদি \(x=c\) বিন্দুতে \(f(x)\) ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান থাকে এবং \(f^{\prime}(c)\) এর মাণ বিদ্যমান থাকে তবে \(f^{\prime}(c)=0\) হবে।
proof:
\(x=c\) বিন্দুতে \(f(x)\) এর মাণ \(f(c)\) যদি \(x=c\) বিন্দুতে \(f(x)\) গরিষ্ঠমান হয়, তবে
\(f(c+h)-f(c)<0\) যদি \(h>0\) অথবা \(h<0\)
\(\frac{f(c+h)-f(c)}{h}<0\) যদি \(h>0\) এবং \(\frac{f(c+h)-f(c)}{h}>0\) যদি \(h<0\)
যেহেতু \(f^{\prime}(c)\) বিদ্যমান, কাজেই উভয় পক্ষে \[\lim_{h \rightarrow 0}\] সংযোগ করে পাই,
\[\lim_{h \rightarrow 0+}\frac{f(c+h)-f(c)}{h}\le{0}\] এবং \[\lim_{h \rightarrow 0-}\frac{f(c+h)-f(c)}{h}\ge{0}\]
\(\Rightarrow Rf^{\prime}(c)\le{0} ......(1)\) এবং \(Lf^{\prime}(c)\ge{0} ......(2)\)
যদি \(f^{\prime}(c)\) বিদ্যমান থাকে তবে \((1)\) নং ও \((2)\) নং হতে পাই,
\(Rf^{\prime}(c)=Lf^{\prime}(c)\) যেহেতু উভয় সীমার সাধারণ মাণ \(0\) সুতরাং \(f^{\prime}(c)=0\).
আবার যদি \(x=c\) বিন্দুতে \(f(x)\) ফাংশন লঘিষ্ঠ হয়,
তবে \(f(c+h)-f(c)>0\) যখন \(h>0\) অথবা \(h<0\) হয়।
\(\frac{f(c+h)-f(c)}{h}>0\) যদি \(h>0\) এবং \(\frac{f(c+h)-f(c)}{h}<0\) যদি \(h<0\)
যেহেতু \(f^{\prime}(c)\) বিদ্যমান, কাজেই উভয় পক্ষে \[\lim_{h \rightarrow 0}\] সংযোগ করে পাই,
\[\lim_{h \rightarrow 0+}\frac{f(c+h)-f(c)}{h}\ge{0}\] এবং \[\lim_{h \rightarrow 0-}\frac{f(c+h)-f(c)}{h}\le{0}\]
\(\Rightarrow Rf^{\prime}(c)\ge{0} ......(3)\) এবং \(Lf^{\prime}(c)\le{0} ......(4)\)
যদি \(f^{\prime}(c)\) বিদ্যমান থাকে তবে \((3)\) নং ও \((4)\) নং হতে পাই,
\(Rf^{\prime}(c)=Lf^{\prime}(c)\) যেহেতু উভয় সীমার সাধারণ মাণ \(0\) সুতরাং \(f^{\prime}(c)=0\)
সুতরাং \(x=c\) বিন্দুতে \(f(x)\) ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান হওয়ার শর্ত \(f^{\prime}(c)=0\).
\(x=c\) বিন্দুতে \(f(x)\) এর মাণ \(f(c)\) যদি \(x=c\) বিন্দুতে \(f(x)\) গরিষ্ঠমান হয়, তবে
\(f(c+h)-f(c)<0\) যদি \(h>0\) অথবা \(h<0\)
\(\frac{f(c+h)-f(c)}{h}<0\) যদি \(h>0\) এবং \(\frac{f(c+h)-f(c)}{h}>0\) যদি \(h<0\)
যেহেতু \(f^{\prime}(c)\) বিদ্যমান, কাজেই উভয় পক্ষে \[\lim_{h \rightarrow 0}\] সংযোগ করে পাই,
\[\lim_{h \rightarrow 0+}\frac{f(c+h)-f(c)}{h}\le{0}\] এবং \[\lim_{h \rightarrow 0-}\frac{f(c+h)-f(c)}{h}\ge{0}\]
\(\Rightarrow Rf^{\prime}(c)\le{0} ......(1)\) এবং \(Lf^{\prime}(c)\ge{0} ......(2)\)
যদি \(f^{\prime}(c)\) বিদ্যমান থাকে তবে \((1)\) নং ও \((2)\) নং হতে পাই,
\(Rf^{\prime}(c)=Lf^{\prime}(c)\) যেহেতু উভয় সীমার সাধারণ মাণ \(0\) সুতরাং \(f^{\prime}(c)=0\).
আবার যদি \(x=c\) বিন্দুতে \(f(x)\) ফাংশন লঘিষ্ঠ হয়,
তবে \(f(c+h)-f(c)>0\) যখন \(h>0\) অথবা \(h<0\) হয়।
\(\frac{f(c+h)-f(c)}{h}>0\) যদি \(h>0\) এবং \(\frac{f(c+h)-f(c)}{h}<0\) যদি \(h<0\)
যেহেতু \(f^{\prime}(c)\) বিদ্যমান, কাজেই উভয় পক্ষে \[\lim_{h \rightarrow 0}\] সংযোগ করে পাই,
\[\lim_{h \rightarrow 0+}\frac{f(c+h)-f(c)}{h}\ge{0}\] এবং \[\lim_{h \rightarrow 0-}\frac{f(c+h)-f(c)}{h}\le{0}\]
\(\Rightarrow Rf^{\prime}(c)\ge{0} ......(3)\) এবং \(Lf^{\prime}(c)\le{0} ......(4)\)
যদি \(f^{\prime}(c)\) বিদ্যমান থাকে তবে \((3)\) নং ও \((4)\) নং হতে পাই,
\(Rf^{\prime}(c)=Lf^{\prime}(c)\) যেহেতু উভয় সীমার সাধারণ মাণ \(0\) সুতরাং \(f^{\prime}(c)=0\)
সুতরাং \(x=c\) বিন্দুতে \(f(x)\) ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান হওয়ার শর্ত \(f^{\prime}(c)=0\).
×
ফাংশনের গরিষ্ঠমান ও লঘিষ্ঠমান নির্ণয়ঃ
\(x=c\) বিন্দুতে \(f(x)\) ফাংশন অবিচ্ছিন্ন এবং \(f^{\prime}(c)=0\) ও \(f^{\prime\prime}(c)\ne{0}\) হলে,
\(x=c\) বিন্দুতে \(f(x)\) এর গরিষ্ঠমাণ থাকবে যদি \(f^{\prime\prime}(c)<0\) হয়।
\(x=c\) বিন্দুতে \(f(x)\) এর লঘিষ্ঠমান থাকবে যদি \(f^{\prime\prime}(c)>0\) হয়।
\(x=c\) বিন্দুতে \(f(x)\) ফাংশন অবিচ্ছিন্ন এবং \(f^{\prime}(c)=0\) ও \(f^{\prime\prime}(c)\ne{0}\) হলে,
\(x=c\) বিন্দুতে \(f(x)\) এর গরিষ্ঠমাণ থাকবে যদি \(f^{\prime\prime}(c)<0\) হয়।
\(x=c\) বিন্দুতে \(f(x)\) এর লঘিষ্ঠমান থাকবে যদি \(f^{\prime\prime}(c)>0\) হয়।
proof:
\(x=c\) বিন্দুতে \(f(x)\) এর মাণ \(f(c)\).
যদি \(x=c\) বিন্দুতে \(f(x)\) এর গরিষ্ঠমান থাকে , তবে অতিক্ষুদ্র \(h\) এর জন্য
\(f(c+h)-f(c)<0\) যখন \(h>0\) অথবা \(h<0\)
এখন টেলর উপপাদ্যের সাহায্যে \(f(c+h)\) কে বিস্তার করে পাই,
\(f(c+h)=f(c)+hf^{\prime}(c)+\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ........\)
\(\Rightarrow f(c+h)-f(c)=hf^{\prime}(c)+\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ........\)
\(\Rightarrow f(c+h)-f(c)=\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ...\) ➜ \(\because f^{\prime}(c)=0\)
যেহেতু \(h\) অতিক্ষুদ্র, কাজেই \(h\) এর \(2\) মাত্রার উচ্চতর পদগুলিকে বাদ দিয়ে পাই,
\(f(c+h)-f(c)=\frac{h^2}{2!}f^{\prime\prime}(c)\)
যেহেতু \(h^2\) সর্বদা ধনাত্মক অর্থাৎ \(h^2>0\) , কাজেই \(f(c+h)-f(c)\) এর চিহ্ন, \(f^{\prime\prime}(c)\) এর চিহ্নের উপর নির্ভরশীল।
সুতরাং \(f(c+h)-f(c)\)এবং \(f^{\prime\prime}(c)\) এর চিহ্ন এক রকম হবে।
\(f^{\prime\prime}(c)<0\) হলে, \(h\) এর সকল মানের জন্য \(f(c+h)-f(c)<0\).
সুতরাং \(x=c\) বিন্দুতে \(f(x)\) গরিষ্ঠ হবে যদি \(f^{\prime}(c)=0\) এবং \(f^{\prime\prime}(c)<0\) হয়।
আবার,
\(x=c\) বিন্দুতে \(f(x)\) এর মাণ \(f(c)\).
যদি \(x=c\) বিন্দুতে \(f(x)\) এর লঘিষ্ঠমান থাকে , তবে অতিক্ষুদ্র \(h\) এর জন্য
\(f(c+h)-f(c)>0\) যখন \(h>0\) অথবা \(h<0\)
এখন টেলর উপপাদ্যের সাহায্যে \(f(c+h)\) কে বিস্তার করে পাই,
\(f(c+h)=f(c)+hf^{\prime}(c)+\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ........\)
\(\Rightarrow f(c+h)-f(c)=hf^{\prime}(c)+\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ........\)
\(\Rightarrow f(c+h)-f(c)=\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ...\) ➜ \(\because f^{\prime}(c)=0\)
যেহেতু \(h\) অতিক্ষুদ্র, কাজেই \(h\) এর \(2\) মাত্রার উচ্চতর পদগুলিকে বাদ দিয়ে পাই,
\(f(c+h)-f(c)=\frac{h^2}{2!}f^{\prime\prime}(c)\)
যেহেতু \(h^2\) সর্বদা ধনাত্মক অর্থাৎ \(h^2>0\) , কাজেই \(f(c+h)-f(c)\) এর চিহ্ন, \(f^{\prime\prime}(c)\) এর চিহ্নের উপর নির্ভরশীল।
সুতরাং \(f(c+h)-f(c)\)এবং \(f^{\prime\prime}(c)\) এর চিহ্ন এক রকম হবে।
\(f^{\prime\prime}(c)>0\) হলে, \(h\) এর সকল মানের জন্য \(f(c+h)-f(c)>0\).
সুতরাং \(x=c\) বিন্দুতে \(f(x)\) লঘিষ্ঠ হবে যদি \(f^{\prime}(c)=0\) এবং \(f^{\prime\prime}(c)>0\) হয়।
\(x=c\) বিন্দুতে \(f(x)\) এর মাণ \(f(c)\).
যদি \(x=c\) বিন্দুতে \(f(x)\) এর গরিষ্ঠমান থাকে , তবে অতিক্ষুদ্র \(h\) এর জন্য
\(f(c+h)-f(c)<0\) যখন \(h>0\) অথবা \(h<0\)
এখন টেলর উপপাদ্যের সাহায্যে \(f(c+h)\) কে বিস্তার করে পাই,
\(f(c+h)=f(c)+hf^{\prime}(c)+\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ........\)
\(\Rightarrow f(c+h)-f(c)=hf^{\prime}(c)+\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ........\)
\(\Rightarrow f(c+h)-f(c)=\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ...\) ➜ \(\because f^{\prime}(c)=0\)
যেহেতু \(h\) অতিক্ষুদ্র, কাজেই \(h\) এর \(2\) মাত্রার উচ্চতর পদগুলিকে বাদ দিয়ে পাই,
\(f(c+h)-f(c)=\frac{h^2}{2!}f^{\prime\prime}(c)\)
যেহেতু \(h^2\) সর্বদা ধনাত্মক অর্থাৎ \(h^2>0\) , কাজেই \(f(c+h)-f(c)\) এর চিহ্ন, \(f^{\prime\prime}(c)\) এর চিহ্নের উপর নির্ভরশীল।
সুতরাং \(f(c+h)-f(c)\)এবং \(f^{\prime\prime}(c)\) এর চিহ্ন এক রকম হবে।
\(f^{\prime\prime}(c)<0\) হলে, \(h\) এর সকল মানের জন্য \(f(c+h)-f(c)<0\).
সুতরাং \(x=c\) বিন্দুতে \(f(x)\) গরিষ্ঠ হবে যদি \(f^{\prime}(c)=0\) এবং \(f^{\prime\prime}(c)<0\) হয়।
আবার,
\(x=c\) বিন্দুতে \(f(x)\) এর মাণ \(f(c)\).
যদি \(x=c\) বিন্দুতে \(f(x)\) এর লঘিষ্ঠমান থাকে , তবে অতিক্ষুদ্র \(h\) এর জন্য
\(f(c+h)-f(c)>0\) যখন \(h>0\) অথবা \(h<0\)
এখন টেলর উপপাদ্যের সাহায্যে \(f(c+h)\) কে বিস্তার করে পাই,
\(f(c+h)=f(c)+hf^{\prime}(c)+\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ........\)
\(\Rightarrow f(c+h)-f(c)=hf^{\prime}(c)+\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ........\)
\(\Rightarrow f(c+h)-f(c)=\frac{h^2}{2!}f^{\prime\prime}(c)\)\(+\frac{h^3}{3!}f^{\prime\prime\prime}(c)+ ...\) ➜ \(\because f^{\prime}(c)=0\)
যেহেতু \(h\) অতিক্ষুদ্র, কাজেই \(h\) এর \(2\) মাত্রার উচ্চতর পদগুলিকে বাদ দিয়ে পাই,
\(f(c+h)-f(c)=\frac{h^2}{2!}f^{\prime\prime}(c)\)
যেহেতু \(h^2\) সর্বদা ধনাত্মক অর্থাৎ \(h^2>0\) , কাজেই \(f(c+h)-f(c)\) এর চিহ্ন, \(f^{\prime\prime}(c)\) এর চিহ্নের উপর নির্ভরশীল।
সুতরাং \(f(c+h)-f(c)\)এবং \(f^{\prime\prime}(c)\) এর চিহ্ন এক রকম হবে।
\(f^{\prime\prime}(c)>0\) হলে, \(h\) এর সকল মানের জন্য \(f(c+h)-f(c)>0\).
সুতরাং \(x=c\) বিন্দুতে \(f(x)\) লঘিষ্ঠ হবে যদি \(f^{\prime}(c)=0\) এবং \(f^{\prime\prime}(c)>0\) হয়।
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000002