এ অধ্যায়ের পাঠ্যসূচী
- নির্দিষ্ট যোগজীকরণ (Definite Integration)
- নির্দিষ্ট যোগজের বৈশিষ্ট্য (Characteristic of Definite Integration)
- নির্দিষ্ট যোগজীকরণের প্রয়োগ (Definite Integration and their applications)
- ক্ষেত্রফল থেকে যোগজের ধারণা (Concept of Integration from area)
- উর্ধসীমা ও নিম্নসীমা (Upper limit and Lower limit)
- নির্দিষ্ট যোগজীকরণে ধ্রুবক \( c\)-এর অপ্রয়োজনীয়তা (Redundancy of the constant \( c\) in definite summation)
- নির্দিষ্ট যোগজীকরণে জ্যামিতিক ব্যাখ্যা (Geometric interpretation of Definite Integration)
- নির্দিষ্ট যোগজ নির্ণয়ের ধাপসমুহ (Steps in determining the Definite Integration)
- প্রতিস্থাপন পদ্ধতিতে নির্দিষ্ট যোগজ নির্ণয়ের ধাপসমুহ (Steps in determining the Definite Integration in the substitution method)
- অধ্যায় \(x.G\)-এর উদাহরণসমুহ
- অধ্যায় \(x.G\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(x.G\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(x.G\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(x.G\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
নির্দিষ্ট যোগজীকরণ
Definite Integration
নির্দিষ্ট যোগজীকরণঃ আমরা জেনেছি, যোগজীকরণ হলো অন্তরীকরণের বিপরীত প্রক্রিয়া। এখন, আমরা একে সমষ্টিকরণের পদ্ধতি হিসেবে সংজ্ঞায়িত করব। প্রকৃতপক্ষে যোগজীকরণের উৎপত্তিই হলো বক্ররেখা দ্বারা আবদ্ধ ক্ষেত্রের ক্ষেত্রফল নির্ণয়ের উদ্দেশ্য নিয়ে। এক্ষেত্রে ক্ষেত্রটিকে ক্ষুদ্র ক্ষুদ্র অংশে বিভক্ত করে, ক্ষুদ্র ক্ষুদ্র ক্ষেত্রের সমষ্টি থেকেই মূল ক্ষেত্রের ক্ষেত্রফল নির্ণয় করা হয়।
নির্দিষ্ট যোগজের বৈশিষ্ট্য
Characteristic of Definite Integration
\(\int_{a}^{b}{f(x)dx}=\int_{a}^{b}{f(t)dt}\)
\(\int_{a}^{b}{f(x)dx}=-\int_{b}^{a}{f(x)dx}\)
যেহেতু,
\(\int_{0}^{\frac{\pi}{2}}{\sin{x}dx}\)
\(=\left[-\cos{x}\right]_{0}^{\frac{\pi}{2}}\)
\(=-\left[\cos{x}\right]_{0}^{\frac{\pi}{2}}\)
\(=-\left[\cos{\frac{\pi}{2}}-\cos{0}\right]\)
\(=-\left[0-1\right]\) ➜ \(\because \cos{\frac{\pi}{2}}=0, \cos{0}=1\)
\(=-\left[-1\right]\)
\(=1\)
এবং
\(-\int_{\frac{\pi}{2}}^{0}{\sin{x}dx}\)
\(=-\left[-\cos{x}\right]_{\frac{\pi}{2}}^{0}\)
\(=\left[\cos{x}\right]_{\frac{\pi}{2}}^{0}\)
\(=\left[\cos{0}-\cos{\frac{\pi}{2}}\right]\)
\(=\left[1-0\right]\) ➜ \(\because \cos{0}=1, \cos{\frac{\pi}{2}}=0\)
\(=1\)
\(\therefore \int_{0}^{\frac{\pi}{2}}{\sin{x}dx}=-\int_{\frac{\pi}{2}}^{0}{\sin{x}dx}\)
\(\int_{0}^{a}{f(x)dx}=\int_{0}^{a}{f(a-x)dx}\)
\(\int_{0}^{\frac{\pi}{2}}{\sin{x}dx}=\int_{0}^{\frac{\pi}{2}}{\sin{\left(\frac{\pi}{2}-x\right)}dx}\)
ইত্যাদি।
যেমনঃ
\(\int_{0}^{1}{x^2dx}=\int_{0}^{1}{t^2dt}\)\(\int_{a}^{b}{f(x)dx}=-\int_{b}^{a}{f(x)dx}\)
যেমনঃ
\(\int_{0}^{\frac{\pi}{2}}{\sin{x}dx}=-\int_{\frac{\pi}{2}}^{0}{\sin{x}dx}\)যেহেতু,
\(\int_{0}^{\frac{\pi}{2}}{\sin{x}dx}\)
\(=\left[-\cos{x}\right]_{0}^{\frac{\pi}{2}}\)
\(=-\left[\cos{x}\right]_{0}^{\frac{\pi}{2}}\)
\(=-\left[\cos{\frac{\pi}{2}}-\cos{0}\right]\)
\(=-\left[0-1\right]\) ➜ \(\because \cos{\frac{\pi}{2}}=0, \cos{0}=1\)
\(=-\left[-1\right]\)
\(=1\)
এবং
\(-\int_{\frac{\pi}{2}}^{0}{\sin{x}dx}\)
\(=-\left[-\cos{x}\right]_{\frac{\pi}{2}}^{0}\)
\(=\left[\cos{x}\right]_{\frac{\pi}{2}}^{0}\)
\(=\left[\cos{0}-\cos{\frac{\pi}{2}}\right]\)
\(=\left[1-0\right]\) ➜ \(\because \cos{0}=1, \cos{\frac{\pi}{2}}=0\)
\(=1\)
\(\therefore \int_{0}^{\frac{\pi}{2}}{\sin{x}dx}=-\int_{\frac{\pi}{2}}^{0}{\sin{x}dx}\)
\(\int_{0}^{a}{f(x)dx}=\int_{0}^{a}{f(a-x)dx}\)
যেমনঃ
\(\int_{0}^{2}{x^3dx}=\int_{0}^{2}{(2-x)^3dx}\);\(\int_{0}^{\frac{\pi}{2}}{\sin{x}dx}=\int_{0}^{\frac{\pi}{2}}{\sin{\left(\frac{\pi}{2}-x\right)}dx}\)
ইত্যাদি।
নির্দিষ্ট যোগজ ও এর প্রয়োগ
Definite Integration and their applications
নির্দিষ্ট যোগজের সাহায্যে আমরা কোনো সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল নির্ণয় করতে পারি। বক্ররেখার দৈর্ঘ্য, বক্ররেখা দ্বারা পরিবেষ্টিত ক্ষেত্রের ক্ষেত্রফল, কোনো বস্তুর আয়তন এবং গতিবেগ ইত্যাদি নির্ণয়ে নির্দিষ্ট যোগজ বিশেষ ভূমিকা পালন করে।
ক্ষেত্রফল থেকে যোগজের ধারণা
Concept of Integration from area
\(x=a, x=b, y=f(x)\) এবং \(y=0\) এ চারটি রেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে \(n\) সমানভাবে বিভক্ত করলে এবং প্রতিটি ভাগের দূরত্ব \(h\) হলে \(nh=b-a\) হবে। এখন \(nh=b-a\) হলে, \[\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)\]\[+ ..........+f(a+\overline{n-1}.h)\}\] কে নির্দিষ্ট যোগজ বলে। যাকে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা প্রকাশ করা হয়।
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)\]\[+ ..........+f(a+\overline{n-1}.h)\}\]
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)\]\[+ ..........+f(a+\overline{n-1}.h)\}\]
উর্ধসীমা ও নিম্নসীমা
Upper limit and Lower limit
উর্ধসীমা ও নিম্নসীমাঃ যদি \(f(x)\) ফাংশনের অনির্দিষ্ট যোগজ \(F(x)\) হয়, অর্থাৎ \(\int{f(x)dx}=F(x)\) হয়, তবে \([a, b]\) বদ্ধ ব্যবধিতে \(F(b)-F(a)\) কে \(f(x)\) ফাংশনের নির্দিষ্ট যোগজের মান বলা হয়, যাকে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা প্রকাশ করা হয় ।
গাণিতিকভাবে, যদি \(f(x)\) এর যোগজ \(F(x)\) হয়
অর্থাৎ \(\int{f(x)dx}=F(x)\) হয় তবে \(\int_{a}^{b}{f(x)dx}=\left[F(x)\right]_{a}^{b}=F(b)-F(a)\).
এখানে \(a\) কে নিম্নসীমা (lower limit) , \(b\) কে উর্ধসীমা (upper limit) এবং \([ a, b]\) ব্যবধিকে যোগজের রেঞ্জ বলে।
গাণিতিকভাবে, যদি \(f(x)\) এর যোগজ \(F(x)\) হয়
অর্থাৎ \(\int{f(x)dx}=F(x)\) হয় তবে \(\int_{a}^{b}{f(x)dx}=\left[F(x)\right]_{a}^{b}=F(b)-F(a)\).
এখানে \(a\) কে নিম্নসীমা (lower limit) , \(b\) কে উর্ধসীমা (upper limit) এবং \([ a, b]\) ব্যবধিকে যোগজের রেঞ্জ বলে।
মন্তব্যঃ
স্বাধীন চলরাশি \(x\) এর মান পরিবর্তিত হলে, অনির্দিষ্ট যোগজটির মান যে নির্দিষ্ট পরিমাণ পার্থক্য সৃষ্টি হয়, তা হলো নির্দিষ্ট যোজিতফল বা নির্দিষ্ট যোগজ।
নির্দিষ্ট যোগজীকরণে ধ্রুবক \( c\)-এর অপ্রয়োজনীয়তা
Redundancy of the constant \( c\) in definite summation
ব্যাখ্যাঃ \(\int{f(x)dx}=F(x)\) হয় তবে \(\int_{a}^{b}{f(x)dx}=\left[F(x)\right]_{a}^{b}=F(b)-F(a) ......(1)\)
আবার,
\(\int{f(x)dx}=F(x)+c\) হয় তবে \(\int_{a}^{b}{f(x)dx}=\left[F(x)+c\right]_{a}^{b}=F(b)+c-F(a)-c\)\(=F(b)-F(a) ......(2)\)
অর্থাৎ নির্দিষ্ট যোগজে ধ্রুবক \(c\) সংযুক্ত করলে উর্ধবপ্রান্ত এবং নিম্নপ্রান্ত প্রয়োগের ফলে তা অপসারিত হয়।
\((1)\) ও \((2)\) থেকে ইহা স্পষ্ট যে, \(\int_{a}^{b}{f(x)dx}\) এর যোজিতফল \(F(x)\) এর সাথে \(c\) ব্যবহার না করলেও ফলাফল যা, ব্যবহার করেও ফলাফল একই থাকে। কাজেই \(\int_{a}^{b}{f(x)dx}\) এর মান ধ্রুবক \(c\) এর উপর নির্ভরশীল নয়। তাই নির্দিষ্ট যোগজে ধ্রুবক \(c\) এর ব্যবহার অপ্রয়োজনীয়।
আবার,
\(\int{f(x)dx}=F(x)+c\) হয় তবে \(\int_{a}^{b}{f(x)dx}=\left[F(x)+c\right]_{a}^{b}=F(b)+c-F(a)-c\)\(=F(b)-F(a) ......(2)\)
অর্থাৎ নির্দিষ্ট যোগজে ধ্রুবক \(c\) সংযুক্ত করলে উর্ধবপ্রান্ত এবং নিম্নপ্রান্ত প্রয়োগের ফলে তা অপসারিত হয়।
\((1)\) ও \((2)\) থেকে ইহা স্পষ্ট যে, \(\int_{a}^{b}{f(x)dx}\) এর যোজিতফল \(F(x)\) এর সাথে \(c\) ব্যবহার না করলেও ফলাফল যা, ব্যবহার করেও ফলাফল একই থাকে। কাজেই \(\int_{a}^{b}{f(x)dx}\) এর মান ধ্রুবক \(c\) এর উপর নির্ভরশীল নয়। তাই নির্দিষ্ট যোগজে ধ্রুবক \(c\) এর ব্যবহার অপ্রয়োজনীয়।
নির্দিষ্ট যোগজীকরণে জ্যামিতিক ব্যাখ্যা
Geometric interpretation of Definite Integration
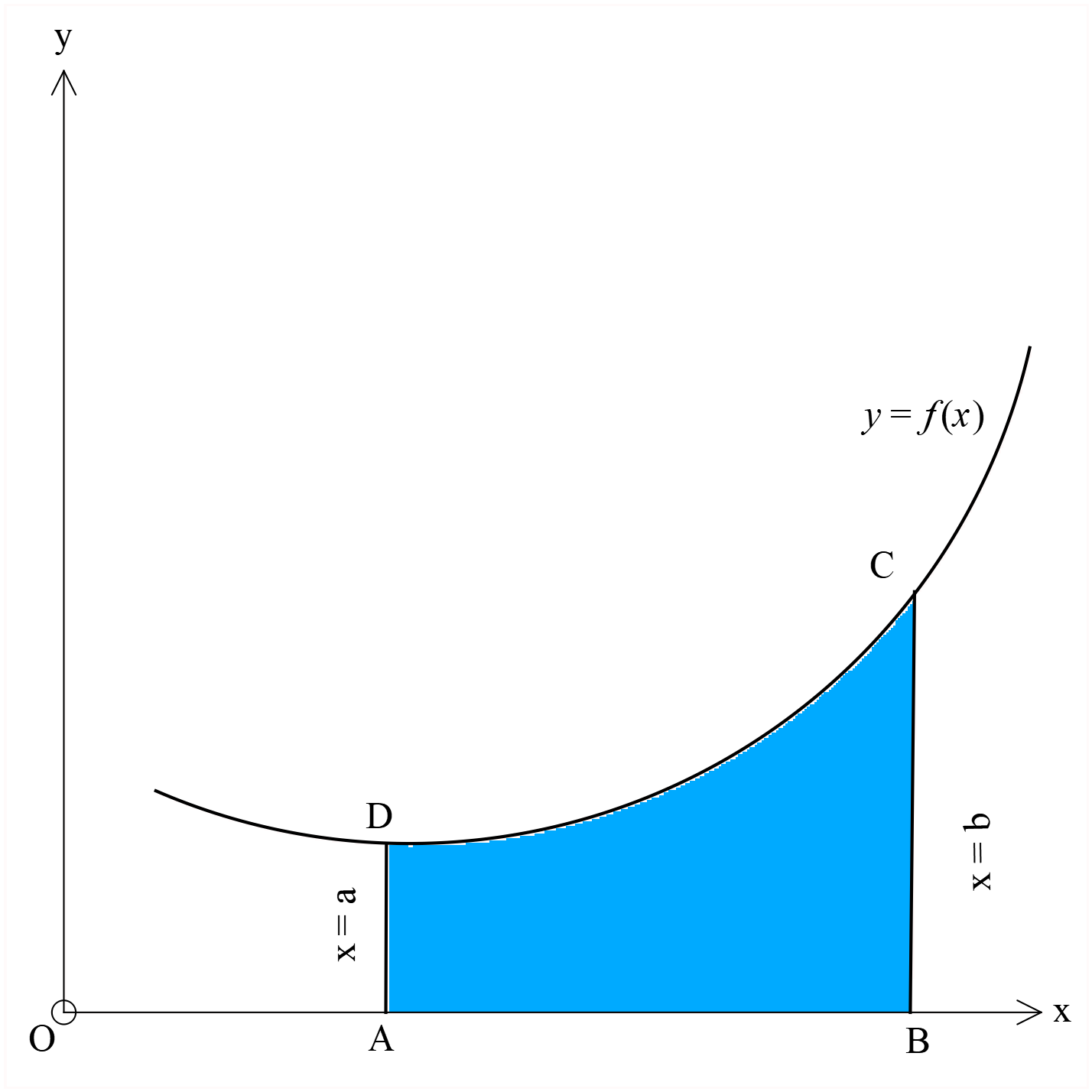 \(y=f(x)\) বক্ররেখা এবং \(y=0, x=a\) এবং \(x=b\) রেখত্রয় দ্বারা সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল \(ABCD\) কে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা প্রকাশ করা হয় ।
\(y=f(x)\) বক্ররেখা এবং \(y=0, x=a\) এবং \(x=b\) রেখত্রয় দ্বারা সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল \(ABCD\) কে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা প্রকাশ করা হয় ।অর্থাৎ \(ABCD\) এর ক্ষেত্রফল \(=\int_{a}^{b}{f(x)dx}\)
নির্দিষ্ট যোগজ নির্ণয়ের ধাপসমুহ
Steps in determining the Definite Integration
নির্দিষ্ট যোগজ নির্ণয়ের কতগুলি কৌশল অবলম্বন করা হয়। এই কৌশলের ধাপসমুহ নিম্নরূপঃ
প্রদত্ত ফাংশনের অনির্দিষ্ট যোগজ নির্ণয় করতে হয়। অর্থাৎ \(\int{f(x)dx}\) এর অনির্দিষ্ট যোগজ \(F(x)\) হলে, \(F(x)\) বের করতে হয়।
\(F(x)\) এ \(x\) এর পরিবর্তে যথাক্রমে উর্ধবপ্রান্ত \(b\) এবং নিম্নপ্রান্ত \(a\) বসিয়ে \(F(b)\) থেকে \(F(a)\) বিয়োগ করতে হয়। এ বিয়োগফলই অর্থাৎ \(F(b)-F(a)\) হচ্ছে \(a\) এবং \(b\) সীমার মধ্যে \(f(x)\) এর যোজিতফল অর্থাৎ \(\int_{a}^{b}{f(x)dx}\) এর মান।
প্রদত্ত ফাংশনের অনির্দিষ্ট যোগজ নির্ণয় করতে হয়। অর্থাৎ \(\int{f(x)dx}\) এর অনির্দিষ্ট যোগজ \(F(x)\) হলে, \(F(x)\) বের করতে হয়।
\(F(x)\) এ \(x\) এর পরিবর্তে যথাক্রমে উর্ধবপ্রান্ত \(b\) এবং নিম্নপ্রান্ত \(a\) বসিয়ে \(F(b)\) থেকে \(F(a)\) বিয়োগ করতে হয়। এ বিয়োগফলই অর্থাৎ \(F(b)-F(a)\) হচ্ছে \(a\) এবং \(b\) সীমার মধ্যে \(f(x)\) এর যোজিতফল অর্থাৎ \(\int_{a}^{b}{f(x)dx}\) এর মান।
প্রতিস্থাপন পদ্ধতিতে নির্দিষ্ট যোগজ নির্ণয়ের ধাপসমুহ
Steps in determining the Definite Integration in the substitution method
নির্দিষ্ট যোগজ নির্ণয়ের ক্ষেত্রে প্রতিস্থাপন পদ্ধতি একটি অত্যন্ত প্রয়োজনীয় প্রক্রিয়া। এর ধাপসমুহ নিম্নরূপঃ
যোজ্য ফাংশনকে নতুন চলরাশিতে প্রকাশ করা।
অন্তরজ \(dx\) কে নতুন চলরাশির অন্তরজে রূপান্তর করা।
নতুন চলরাশির সীমার মান নির্ণয় করা।
যোজ্য ফাংশনকে নতুন চলরাশিতে প্রকাশ করা।
অন্তরজ \(dx\) কে নতুন চলরাশির অন্তরজে রূপান্তর করা।
নতুন চলরাশির সীমার মান নির্ণয় করা।
×
\(x=a, x=b, y=f(x)\) এবং \(y=0\) এ চারটি রেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে \(n\) সমানভাবে বিভক্ত করলে এবং প্রতিটি ভাগের দূরত্ব \(h\) হলে \(nh=b-a\) হবে। এখন \(nh=b-a\) হলে, \[\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\] কে নির্দিষ্ট যোগজ বলে। যাকে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা প্রকাশ করা হয়।
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\]
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\]
Proof:
ধরি,
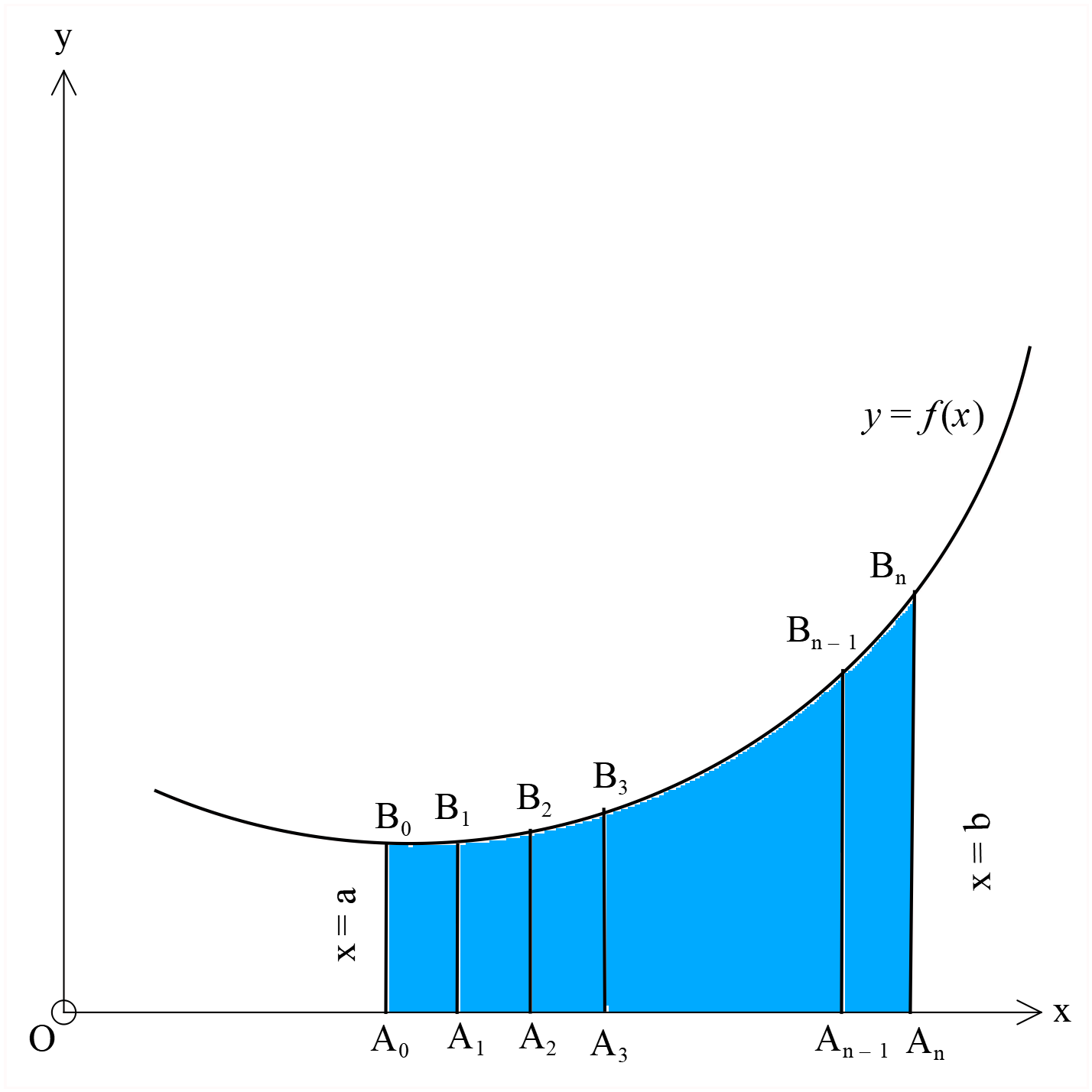
\(x=a\) সরলরেখা \(y=f(x)\) বক্ররেখাকে \(B_{0}\) বিন্দুতে এবং \(x\)-অক্ষরেখাকে \(A_{0}\) বিন্দুতে ছেদ করে। এবং \(x=b\) সরলরেখা উক্ত বক্ররেখা এবং \(x\)-অক্ষরেখাকে যথাক্রমে \(B_{n}\) এবং \(A_{n}\) বিন্দুতে ছেদ করে। অতএব, \(y=f(x)\) বক্ররেখা \(x=a, x=b\) এবং \(y=0\) কতৃক গঠিত ক্ষেত্র \(A_{0}A_{n}B_{n}B_{0}\) এবং মনে করি, এর ক্ষেত্রফল \(S\). এখন \(A_{0}A_{n}\) রেখাংশকে \(A_{1} A_{2} A_{3} ......... A_{n}\) বিন্দু দ্বারা সমান \(n\) ভাগে ভাগ করি যেন \(A_{0}A_{n}=nh\) হয়, অর্থাৎ \(b-a=nh\) হয়। \(x=a\) এর সমান্তরাল করে \(A_{1} A_{2} A_{3} ......... A_{n}\) বিন্দুগুলির মধ্যদিয়ে অঙ্কিত রেখাগুলি \(y=f(x)\) বক্ররেখাকে যথাক্রমে \(B_{1} B_{2} B_{3} ......... B_{n}\) বিন্দুতে ছেদ করে।
এখানে,
\(B_{0}\) বিন্দুর ভুজ \(=a\) এবং কটি \(=A_{0}B_{0}=f(a)\).
\(B_{1}\) বিন্দুর ভুজ \(=a+h\) এবং কটি \(A_{1}B_{1}=f(a+h)\).
\(B_{2}\) বিন্দুর ভুজ \(=a+2h\) এবং কটি \(A_{2}B_{2}=f(a+2h)\) ইত্যাদি।
আবার ধরি,
\(S_{n}= A_{0}B_{0}.A_{0}A_{1}+A_{1}B_{1}.A_{1}A_{2}+A_{2}B_{2}.A_{2}A_{3}+ ....... +A_{n-1}B_{n-1}.A_{n-1}A_{n}\)
\(= f(a).h+f(a+h).h+f(a+2h).h+ ....... +f(a+\overline{n-1}.h).h\)
\(=h\{f(a)+f(a+h)+f(a+2h)+ ....... +f(a+\overline{n-1}.h)\}\)
\(h\) অতি ক্ষুদ্র হলে, \(B_{0}A_{0}A_{1}B_{1}, B_{1}A_{1}A_{2}B_{2} ..... \) ক্ষেত্রগুলি আয়তক্ষেত্রের আকার ধারণ করে।
অতএব, \(n\rightarrow\infty\) হলে \(n\rightarrow 0\) হবে এবং এক্ষেত্রে
\(A_{0}A_{n}B_{n}B_{0}\) এর ক্ষেত্রফল \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\] হবে।
এ সীমাস্থ মানকে নির্দিষ্ট যোগজ বলে, যাকে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা সূচিত করা হয়।
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\]
(proved)
\(x=a\) সরলরেখা \(y=f(x)\) বক্ররেখাকে \(B_{0}\) বিন্দুতে এবং \(x\)-অক্ষরেখাকে \(A_{0}\) বিন্দুতে ছেদ করে। এবং \(x=b\) সরলরেখা উক্ত বক্ররেখা এবং \(x\)-অক্ষরেখাকে যথাক্রমে \(B_{n}\) এবং \(A_{n}\) বিন্দুতে ছেদ করে। অতএব, \(y=f(x)\) বক্ররেখা \(x=a, x=b\) এবং \(y=0\) কতৃক গঠিত ক্ষেত্র \(A_{0}A_{n}B_{n}B_{0}\) এবং মনে করি, এর ক্ষেত্রফল \(S\). এখন \(A_{0}A_{n}\) রেখাংশকে \(A_{1} A_{2} A_{3} ......... A_{n}\) বিন্দু দ্বারা সমান \(n\) ভাগে ভাগ করি যেন \(A_{0}A_{n}=nh\) হয়, অর্থাৎ \(b-a=nh\) হয়। \(x=a\) এর সমান্তরাল করে \(A_{1} A_{2} A_{3} ......... A_{n}\) বিন্দুগুলির মধ্যদিয়ে অঙ্কিত রেখাগুলি \(y=f(x)\) বক্ররেখাকে যথাক্রমে \(B_{1} B_{2} B_{3} ......... B_{n}\) বিন্দুতে ছেদ করে।

এখানে,
\(B_{0}\) বিন্দুর ভুজ \(=a\) এবং কটি \(=A_{0}B_{0}=f(a)\).
\(B_{1}\) বিন্দুর ভুজ \(=a+h\) এবং কটি \(A_{1}B_{1}=f(a+h)\).
\(B_{2}\) বিন্দুর ভুজ \(=a+2h\) এবং কটি \(A_{2}B_{2}=f(a+2h)\) ইত্যাদি।
আবার ধরি,
\(S_{n}= A_{0}B_{0}.A_{0}A_{1}+A_{1}B_{1}.A_{1}A_{2}+A_{2}B_{2}.A_{2}A_{3}+ ....... +A_{n-1}B_{n-1}.A_{n-1}A_{n}\)
\(= f(a).h+f(a+h).h+f(a+2h).h+ ....... +f(a+\overline{n-1}.h).h\)
\(=h\{f(a)+f(a+h)+f(a+2h)+ ....... +f(a+\overline{n-1}.h)\}\)
\(h\) অতি ক্ষুদ্র হলে, \(B_{0}A_{0}A_{1}B_{1}, B_{1}A_{1}A_{2}B_{2} ..... \) ক্ষেত্রগুলি আয়তক্ষেত্রের আকার ধারণ করে।
অতএব, \(n\rightarrow\infty\) হলে \(n\rightarrow 0\) হবে এবং এক্ষেত্রে
\(A_{0}A_{n}B_{n}B_{0}\) এর ক্ষেত্রফল \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\] হবে।
এ সীমাস্থ মানকে নির্দিষ্ট যোগজ বলে, যাকে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা সূচিত করা হয়।
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\]
(proved)
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004