এ অধ্যায়ের পাঠ্যসূচী
- নির্দিষ্ট যোগজএর সাহায্যে ক্ষেত্রফল (Area by Definite Integration)
- ক্ষেত্রফল নির্ণয় (Determine the area)
- দুইটি বক্ররেখা দ্বারা আবদ্ধ ক্ষেত্রের ক্ষেত্রফল (Area bounded by two curves)
- অধ্যায় \(x.H\)-এর উদাহরণসমুহ
- অধ্যায় \(x.H\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(x.H\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(x.H\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(x.H\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(x.H\) / \(Q.5\)-এর সৃজনশীল প্রশ্নসমূহ
- অধ্যায় \(x.H\) / \(Q.6\)-এর ভর্তি পরীক্ষায় আসা প্রশ্নসমূহ
নির্দিষ্ট যোগজএর সাহায্যে ক্ষেত্রফল
Area by Definite Integration
\(x=a, x=b, y=f(x)\) এবং \(y=0\) এ চারটি রেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে \(n\) সমানভাবে বিভক্ত করলে এবং প্রতিটি ভাগের দূরত্ব \(h\) হলে \(nh=b-a\) হবে। এখন \(nh=b-a\) হলে, \[\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)\]\[+..........+f(a+\overline{n-1}.h)\}\] কে নির্দিষ্ট যোগজ বলে। যাকে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা প্রকাশ করা হয়।
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)\]\[+..........+f(a+\overline{n-1}.h)\}\]
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)\]\[+..........+f(a+\overline{n-1}.h)\}\]
ক্ষেত্রফল নির্ণয়
Determine the area
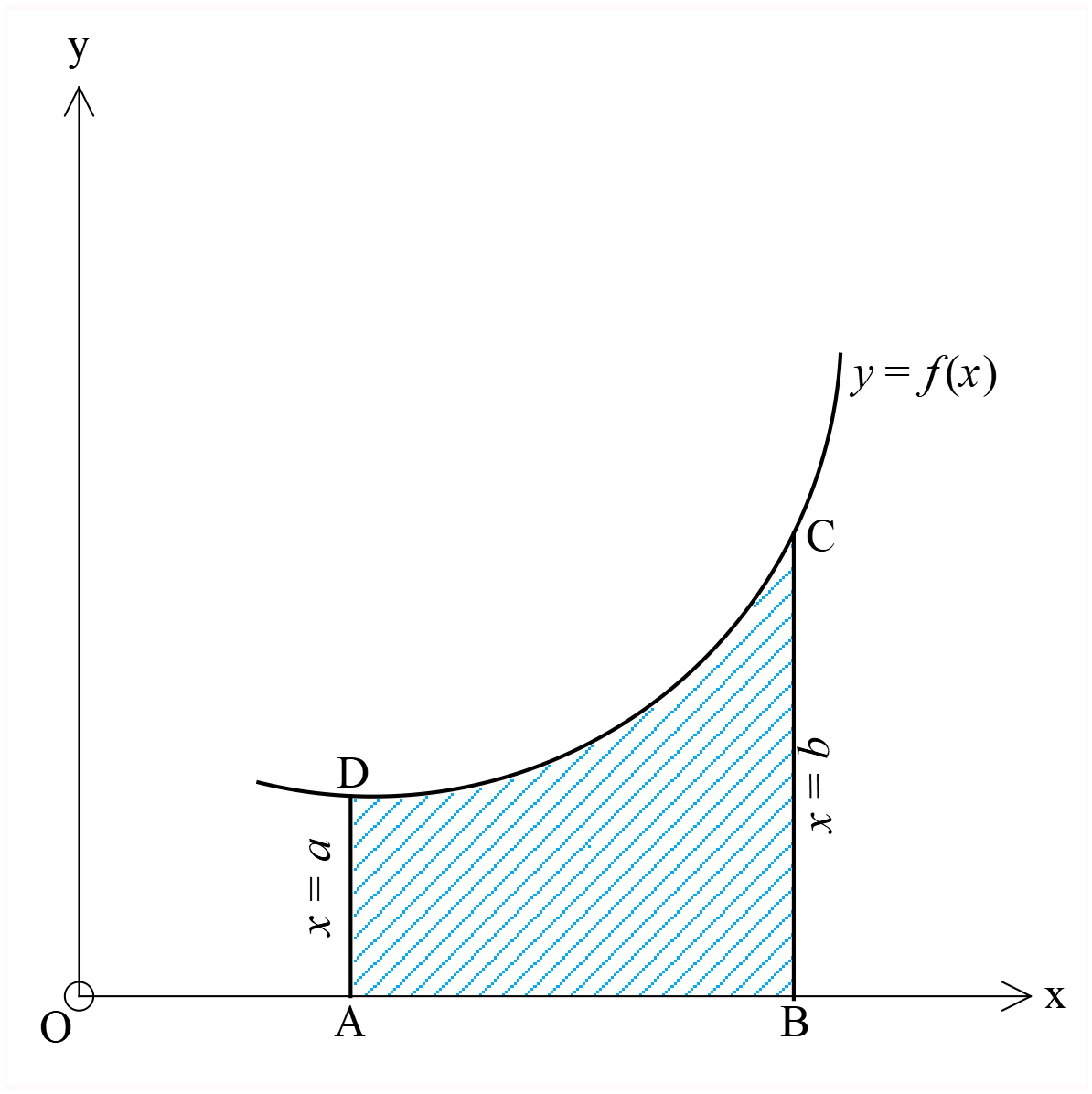
\(y=f(x)\) বক্ররেখা, \(x\) অক্ষরেখা এবং \(x=a, x=b\) রেখত্রয় দ্বারা সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল \(ABCD\) কে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা প্রকাশ করা হয় ।
অর্থাৎ \(ABCD\) এর ক্ষেত্রফল \(=\int_{a}^{b}{f(x)dx}\)
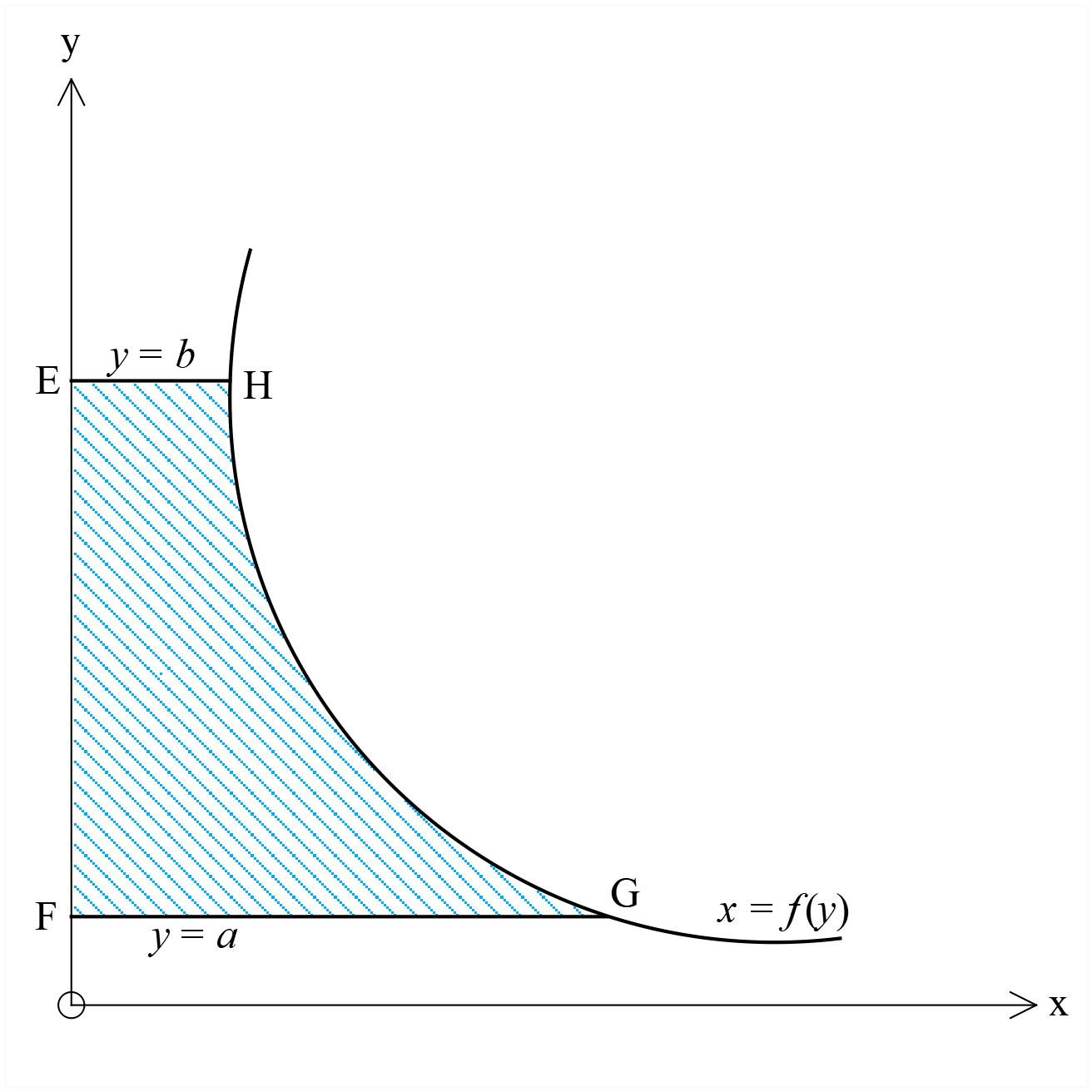
\(x=f(y)\) বক্ররেখা, \(y\) অক্ষরেখা এবং \(y=a, y=b\) রেখত্রয় দ্বারা সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল \(EFGH\) কে \(\int_{a}^{b}{f(y)dx}\) প্রতীক দ্বারা প্রকাশ করা হয় ।
অর্থাৎ \(EFGH\) এর ক্ষেত্রফল \(=\int_{a}^{b}{f(y)dx}\)
দুইটি বক্ররেখা দ্বারা আবদ্ধ ক্ষেত্রের ক্ষেত্রফল
Area bounded by two curves
দুইটি নির্দিষ্ট বক্ররেখা ও দুইটি নির্দিষ্ট কোটি দ্বারা আবদ্ধ ক্ষেত্রের ক্ষেত্রফলঃ
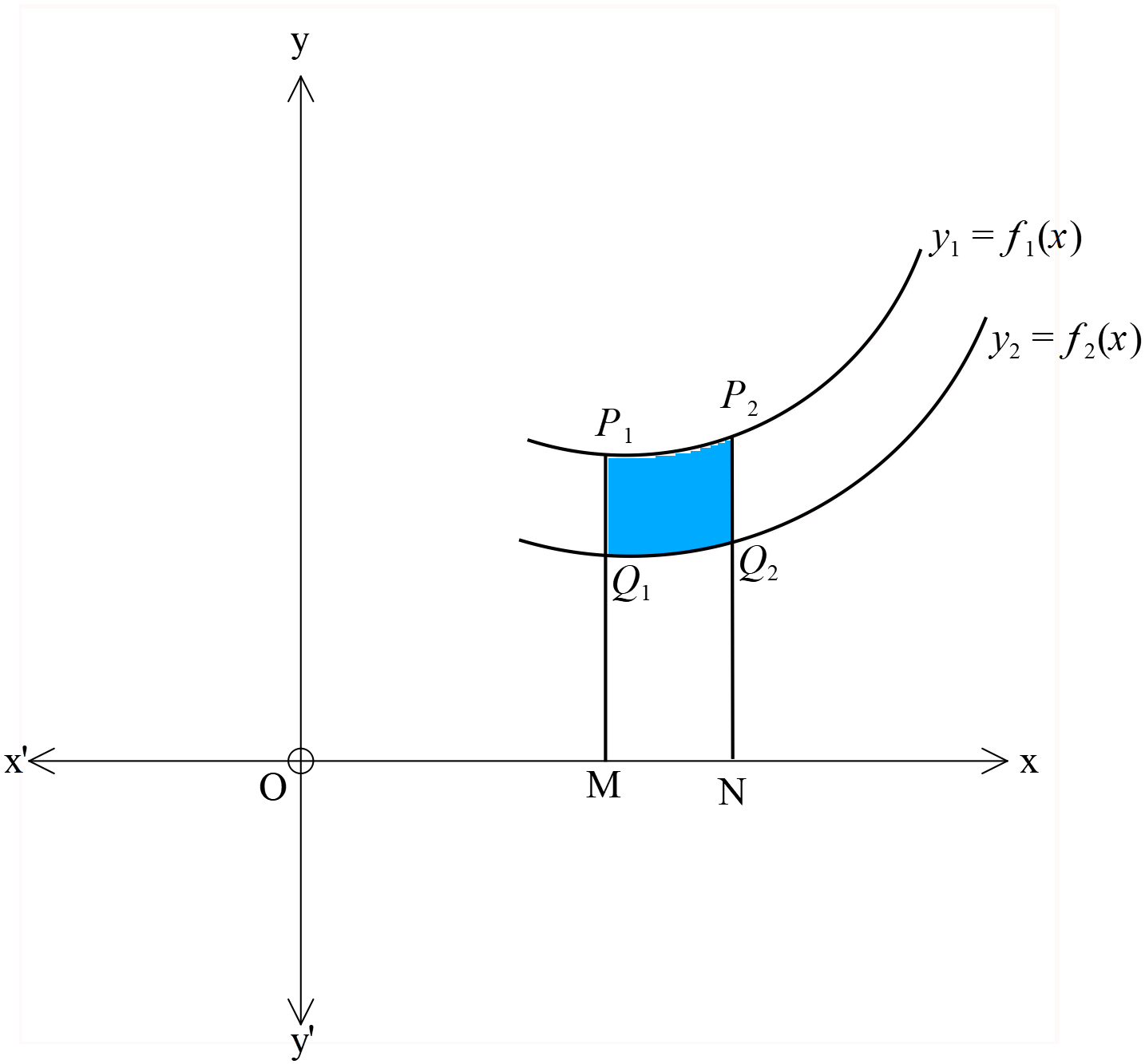
মনে করি, \(y_{1}=f_{1}(x)\) ও \(y_{2}=f_{2}(x)\) বক্ররেখাদ্বয় ও \(x=a, x=b\) দ্বারা বেষ্টিত ক্ষেত্র \(Q_{1}Q_{2}P_{2}P_{1}\) তাহলে, \(OM=a, ON=b\)
\(\therefore Q_{1}Q_{2}P_{2}P_{1}\) ক্ষেত্রের ক্ষেত্রফল
\(=P_{1}MNP_{2}\) ক্ষেত্রের ক্ষেত্রফল -\(Q_{1}MNQ_{2}\) ক্ষেত্রের ক্ষেত্রফল
\(=\int_{a}^{b}{f_{1}(x)dx}-\int_{a}^{b}{f_{2}(x)dx}\)
\(=\int_{a}^{b}{\{f_{1}(x)-f_{2}(x)\}dx}\)
\(=\int_{a}^{b}{(y_{1}-y_{2})dx}\)
এখানে, \(y_{1}\) এবং \(y_{2}\) যথাক্রমে \(P_{1}P_{2}\) ও \(Q_{1}Q_{2}\) বক্ররেখাদ্বয়ের কোটি নির্দেশ করে।

অনুরূপভাবে,
\(x_{1}=f_{1}(y)\) ও \(x_{2}=f_{2}(y)\) বক্ররেখাদ্বয় ও \(y=c, y=d\) দ্বারা বেষ্টিত ক্ষেত্র \(=\int_{c}^{d}{(x_{1}-x_{2})dy}\)

মনে করি, \(y_{1}=f_{1}(x)\) ও \(y_{2}=f_{2}(x)\) বক্ররেখাদ্বয় ও \(x=a, x=b\) দ্বারা বেষ্টিত ক্ষেত্র \(Q_{1}Q_{2}P_{2}P_{1}\) তাহলে, \(OM=a, ON=b\)
\(\therefore Q_{1}Q_{2}P_{2}P_{1}\) ক্ষেত্রের ক্ষেত্রফল
\(=P_{1}MNP_{2}\) ক্ষেত্রের ক্ষেত্রফল -\(Q_{1}MNQ_{2}\) ক্ষেত্রের ক্ষেত্রফল
\(=\int_{a}^{b}{f_{1}(x)dx}-\int_{a}^{b}{f_{2}(x)dx}\)
\(=\int_{a}^{b}{\{f_{1}(x)-f_{2}(x)\}dx}\)
\(=\int_{a}^{b}{(y_{1}-y_{2})dx}\)
এখানে, \(y_{1}\) এবং \(y_{2}\) যথাক্রমে \(P_{1}P_{2}\) ও \(Q_{1}Q_{2}\) বক্ররেখাদ্বয়ের কোটি নির্দেশ করে।

অনুরূপভাবে,
\(x_{1}=f_{1}(y)\) ও \(x_{2}=f_{2}(y)\) বক্ররেখাদ্বয় ও \(y=c, y=d\) দ্বারা বেষ্টিত ক্ষেত্র \(=\int_{c}^{d}{(x_{1}-x_{2})dy}\)
×
\(x=a, x=b, y=f(x)\) এবং \(y=0\) এ চারটি রেখা দ্বারা সীমাবদ্ধ ক্ষেত্রকে \(n\) সমানভাবে বিভক্ত করলে এবং প্রতিটি ভাগের দূরত্ব \(h\) হলে \(nh=b-a\) হবে। এখন \(nh=b-a\) হলে, \[\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+..\] \[........+f(a+\overline{n-1}.h)\}\] কে নির্দিষ্ট যোগজ বলে। যাকে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা প্রকাশ করা হয়।
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+..\] \[........+f(a+\overline{n-1}.h)\}\]
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+..\] \[........+f(a+\overline{n-1}.h)\}\]
Proof:
ধরি,
\(x=a\) সরলরেখা \(y=f(x)\) বক্ররেখাকে \(B_{0}\) বিন্দুতে এবং \(x\)-অক্ষরেখাকে \(A_{0}\) বিন্দুতে ছেদ করে। এবং \(x=b\) সরলরেখা উক্ত বক্ররেখা এবং \(x\)-অক্ষরেখাকে যথাক্রমে \(B_{n}\) এবং \(A_{n}\) বিন্দুতে ছেদ করে। অতএব, \(y=f(x)\) বক্ররেখা \(x=a, x=b\) এবং \(y=0\) কতৃক গঠিত ক্ষেত্র \(A_{0}A_{n}B_{n}B_{0}\) এবং মনে করি, এর ক্ষেত্রফল \(S\). এখন \(A_{0}A_{n}\) রেখাংশকে \(A_{1} A_{2} A_{3} ......... A_{n}\) বিন্দু দ্বারা সমান \(n\) ভাগে ভাগ করি যেন \(A_{0}A_{n}=nh\) হয়, অর্থাৎ \(b-a=nh\) হয়। \(x=a\) এর সমান্তরাল করে \(A_{1} A_{2} A_{3} ......... A_{n}\) বিন্দুগুলির মধ্যদিয়ে অঙ্কিত রেখাগুলি \(y=f(x)\) বক্ররেখাকে যথাক্রমে \(B_{1} B_{2} B_{3} ......... B_{n}\) বিন্দুতে ছেদ করে।
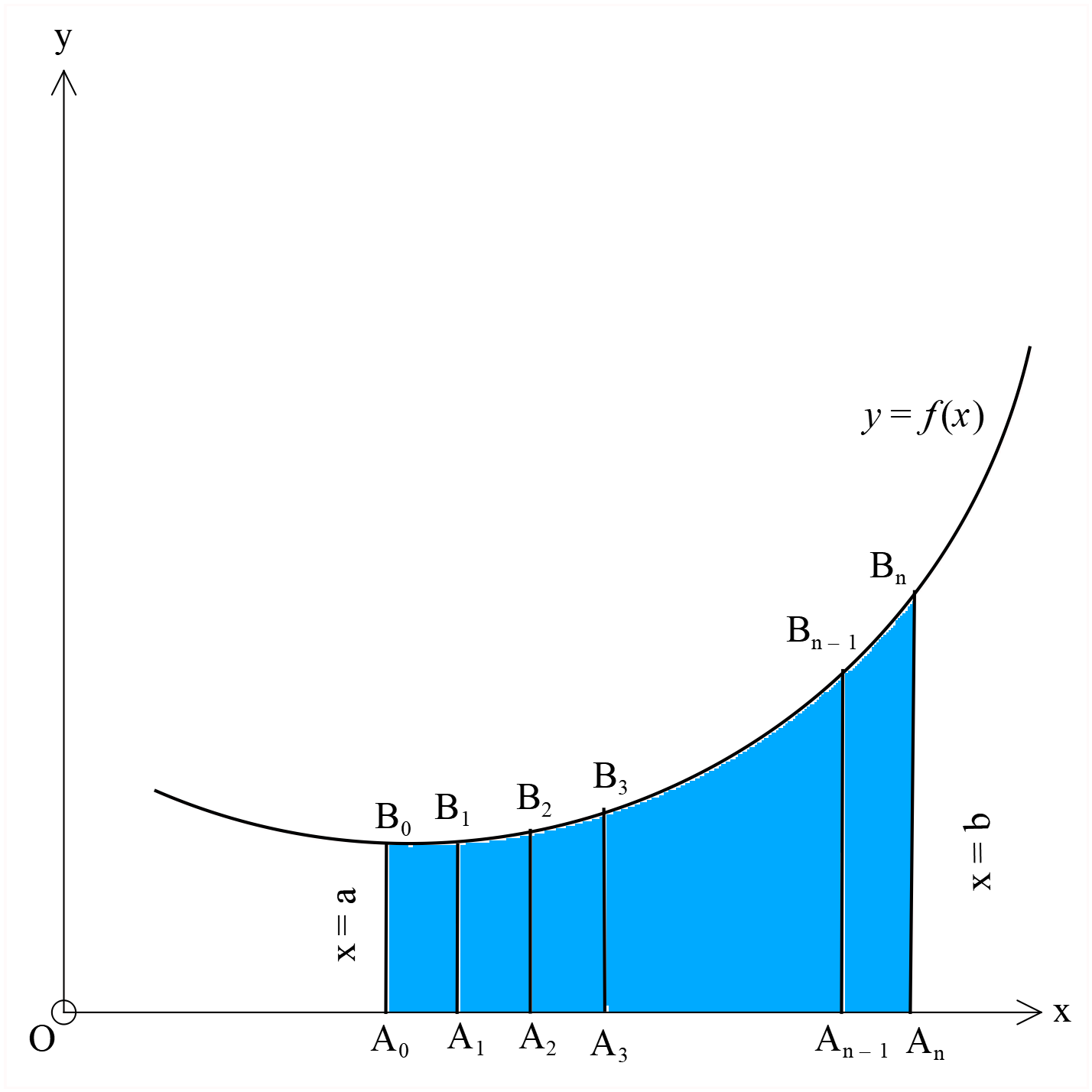
এখানে,
\(B_{0}\) বিন্দুর ভুজ \(=a\) এবং কটি \(=A_{0}B_{0}=f(a)\).
\(B_{1}\) বিন্দুর ভুজ \(=a+h\) এবং কটি \(A_{1}B_{1}=f(a+h)\).
\(B_{2}\) বিন্দুর ভুজ \(=a+2h\) এবং কটি \(A_{2}B_{2}=f(a+2h)\) ইত্যাদি।
আবার ধরি,
\(S_{n}= A_{0}B_{0}.A_{0}A_{1}+A_{1}B_{1}.A_{1}A_{2}+A_{2}B_{2}.A_{2}A_{3}+ ....... +A_{n-1}B_{n-1}.A_{n-1}A_{n}\)
\(= f(a).h+f(a+h).h+f(a+2h).h+ ....... +f(a+\overline{n-1}.h).h\)
\(=h\{f(a)+f(a+h)+f(a+2h)+ ....... +f(a+\overline{n-1}.h)\}\)
\(h\) অতি ক্ষুদ্র হলে, \(B_{0}A_{0}A_{1}B_{1}, B_{1}A_{1}A_{2}B_{2} ..... \) ক্ষেত্রগুলি আয়তক্ষেত্রের আকার ধারণ করে।
অতএব, \(n\rightarrow\infty\) হলে \(n\rightarrow 0\) হবে এবং এক্ষেত্রে
\(A_{0}A_{n}B_{n}B_{0}\) এর ক্ষেত্রফল \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\] হবে।
এ সীমাস্থ মানকে নির্দিষ্ট যোগজ বলে, যাকে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা সূচিত করা হয়।
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\]
(proved)
\(x=a\) সরলরেখা \(y=f(x)\) বক্ররেখাকে \(B_{0}\) বিন্দুতে এবং \(x\)-অক্ষরেখাকে \(A_{0}\) বিন্দুতে ছেদ করে। এবং \(x=b\) সরলরেখা উক্ত বক্ররেখা এবং \(x\)-অক্ষরেখাকে যথাক্রমে \(B_{n}\) এবং \(A_{n}\) বিন্দুতে ছেদ করে। অতএব, \(y=f(x)\) বক্ররেখা \(x=a, x=b\) এবং \(y=0\) কতৃক গঠিত ক্ষেত্র \(A_{0}A_{n}B_{n}B_{0}\) এবং মনে করি, এর ক্ষেত্রফল \(S\). এখন \(A_{0}A_{n}\) রেখাংশকে \(A_{1} A_{2} A_{3} ......... A_{n}\) বিন্দু দ্বারা সমান \(n\) ভাগে ভাগ করি যেন \(A_{0}A_{n}=nh\) হয়, অর্থাৎ \(b-a=nh\) হয়। \(x=a\) এর সমান্তরাল করে \(A_{1} A_{2} A_{3} ......... A_{n}\) বিন্দুগুলির মধ্যদিয়ে অঙ্কিত রেখাগুলি \(y=f(x)\) বক্ররেখাকে যথাক্রমে \(B_{1} B_{2} B_{3} ......... B_{n}\) বিন্দুতে ছেদ করে।

এখানে,
\(B_{0}\) বিন্দুর ভুজ \(=a\) এবং কটি \(=A_{0}B_{0}=f(a)\).
\(B_{1}\) বিন্দুর ভুজ \(=a+h\) এবং কটি \(A_{1}B_{1}=f(a+h)\).
\(B_{2}\) বিন্দুর ভুজ \(=a+2h\) এবং কটি \(A_{2}B_{2}=f(a+2h)\) ইত্যাদি।
আবার ধরি,
\(S_{n}= A_{0}B_{0}.A_{0}A_{1}+A_{1}B_{1}.A_{1}A_{2}+A_{2}B_{2}.A_{2}A_{3}+ ....... +A_{n-1}B_{n-1}.A_{n-1}A_{n}\)
\(= f(a).h+f(a+h).h+f(a+2h).h+ ....... +f(a+\overline{n-1}.h).h\)
\(=h\{f(a)+f(a+h)+f(a+2h)+ ....... +f(a+\overline{n-1}.h)\}\)
\(h\) অতি ক্ষুদ্র হলে, \(B_{0}A_{0}A_{1}B_{1}, B_{1}A_{1}A_{2}B_{2} ..... \) ক্ষেত্রগুলি আয়তক্ষেত্রের আকার ধারণ করে।
অতএব, \(n\rightarrow\infty\) হলে \(n\rightarrow 0\) হবে এবং এক্ষেত্রে
\(A_{0}A_{n}B_{n}B_{0}\) এর ক্ষেত্রফল \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\] হবে।
এ সীমাস্থ মানকে নির্দিষ্ট যোগজ বলে, যাকে \(\int_{a}^{b}{f(x)dx}\) প্রতীক দ্বারা সূচিত করা হয়।
\(\therefore \int_{a}^{b}{f(x)dx}\) \[=\lim_{a \rightarrow b}h\{f(a)+f(a+h)+f(a+2h)+f(a+3h)+ ..........+f(a+\overline{n-1}.h)\}\]
(proved)
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004