এ অধ্যায়ের পাঠ্যসূচী
- ঐতিহাসিক পটভূমি (Historical Background)
- সদিক রাশির প্রতিরূপ হিসেবে ভেক্টর (Vector as a counter part of directed line)
- ভেক্টরের ধারক রেখা (Line of support of Vector)
- ভেক্টরের মাণ (Magnitude of Vector)
- ভেক্টরের সমতা (Equality of Vector)
- বিপরীত ভেক্টর (Opposite Vector)
- শূন্য ভেক্টর বা নাল ভেক্টর (Zero Vector Or, Null Vector)
- একক ভেক্টর (Unite Vector)
- প্রকৃত ও অপ্রকৃত ভেক্টর (Proper and Improper Vector)
- সদৃশ ভেক্টর (Like Vector)
- অসদৃশ ভেক্টর (Unlike Vector)
- সমরৈখিক ভেক্টর (Collinear Vector)
- সমতলীয় ভেক্টর (Coplanar Vector)
- মুক্ত ভেক্টর (Free Vector)
- দুইটি ভেক্টরের অন্তরভুক্ত কোণ (The angle between two vectors)
- ভেক্টর যোগের ত্রিভুজ সূত্র (Triangle law of vector addition)
- ভেক্টর যোগের সামান্তরিক সূত্র (Parallelogram law of vector addition)
- ভেক্টর যোগের বহুভুজ সূত্র (Polygon law of vector addition)
- দুইটি ভেক্টরের বিয়োগ (Subtraction of two vectors)
- ভেক্টর রাশির স্কেলার গুণিতক (Scalar Multiple of Vector)
- দ্বিমাত্রিক ভেক্টরের যোগ, বিয়োগ ও স্কেলার গুণিতকের বিধি (Addition Subtraction and Scalar Multiple Law of two Dimensional Vector)
- দ্বিমাত্রিক ভেক্টরের বিশেষ বিধি (Special Law of two Dimensional Vector)
- সমতলে ভেক্টরের অংশক (Components of a Vector in a Plane)
- আয়ত একক ভেক্টর \(\hat{i}, \hat{j}\) (Unite Vector \(\hat{i}, \hat{j}\))
- কার্তেসীয় স্থানাংককে ভেক্টরে এবং ভেক্টরকে কার্তেসীয় স্থানাংকে প্রকাশ (Represention of Vector in Cartesian Co-ordinates and Cartesian Co-ordinates in Vector)
- অবস্থান ভেক্টর (Position Vector)
- কার্তেসীয় দ্বিমাত্রিক জগতে অবস্থান ভেক্টর (Position Vector in two Dimension Space)
- \(\overline{r}\) ভেক্টরের মাণ (Values of the vector \(\overline{r}\))
- দুইটি নির্দিষ্ট বিন্দুগামী ভেক্টর (Vector through two fixed points)
- ভেক্টর অন্তর্বিভক্তিকরণ সূত্র (Vector Interpolation Formula)
- ভেক্টর বহিঃর্বিভক্তিকরণ সূত্র (Vector extrinsic formula)
- অনুসিদ্ধান্ত-১ (Postulate-1)
- অনুসিদ্ধান্ত-২ (Postulate-2)
- অধ্যায় \(ii.A\)-এর উদাহরণসমুহ
- অধ্যায় \(ii.A\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(ii.A\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(ii.A\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(ii.A\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
ঐতিহাসিক পটভূমি
Historical Background
উইলইয়াম রোয়ান হ্যামিলটন ( ১৮০৫-১৮৬৫ )
আইরিশ গণিতবিদ, পদার্থবিদ, জ্যোতির্বিদ, উইলইয়াম রোয়ান হ্যামিলটন ( William Rowan Hamilton ) এর ১৮৪৩ সালে প্রদত্ত কোয়াটারনিয়ন সংখ্যার ধারনাই ভেক্টরের মূলভিত্তি।
ঊনবিংশ শতাব্দীর শেষ দিকে এবং বিংশ শতাব্দীর প্রথম দিকে জটিল সংখ্যার জ্যামিতিক উপস্থাপনের মধ্য দিয়ে পদ্ধতিগতভাবে ভেক্টরের ব্যবহার শুরু হলেও ভেক্টর ব্যবহারের ইতিহাস অনেক পুরনো। এরিষ্টটল 
দার্শনিক প্লেটোর শিষ্য ও প্রাণি বিজ্ঞানের জনক এরিস্টটল খ্রিষ্টপূর্ব ৩৮৪ সালে স্টাগিরাস নামের এক গ্রিক উপনিবেশে জন্ম নেন। শৈশবে তার বাবা মারা যান। ১৮ বছর বয়সে তিনি গ্রিসের রাজধানী এথেন্সে চলে আসেন এবং বিজ্ঞানী প্লেটোর একাডেমিতে ভর্তি হন। প্লেটোর অধীনে তিনি সেখানে ২০ বছর শিক্ষা গ্রহণ করেন। ( ৩৮৪-৩২২ খ্রীষ্টপূর্ব ) , গণিতবিদ হেরণ 
আলেকজান্দ্রিয়ার নায়ক হেরন হো আলেকজান্দ্রিয়াস; আলেকজান্দ্রিয়ার হেরন নামে পরিচিত । রোমান মিশরের তার আদি শহর আলেকজান্দ্রিয়াতে সক্রিয় ছিলেন। তাকে প্রায়শই প্রাচীনত্বের সর্বশ্রেষ্ঠ পরীক্ষক হিসাবে বিবেচনা করা হয় তাঁর সর্বাধিক বিখ্যাত আবিষ্কারগুলির মধ্যে একটি উইন্ড হুইল ছিল যা জমিতে বাতাসের সুরক্ষার প্রথম দিকের উদাহরণ তৈরি করেছিল। ( ১০-৭০ খ্রীষ্টপূর্ব ) , স্যার আইজ্যাক নিউটন 
১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। ( ১৬৪২-১৭২৭ খ্রীষ্টাব্দ ) প্রমুখ বিজ্ঞানীগণ ভেক্টর যোগের সামান্তরিক সূত্র ব্যবহার করেছেন। দেকার্ত, ফার্মাট, বলজানো, বিলাভিটিজ, ফার্দিনাদ মবিয়াস, ফেরিদ্রিচ, গাউস, গাব্রিয়াল স্টকস প্রমুখ গণিতবিদগণ ভেক্টর সম্পর্কিত তত্ত্ব ব্যাখ্যা করেন। গণিত ও বিজ্ঞানের বিভিন্ন সমস্যা উপস্থাপন এবং সমাধান করতে ভেক্টর ব্যবহৃত হয়।
ভেক্টর বিজ্ঞানের এমন একটি অংশ, যা জ্যামিতি ও বলবিদ্যার সকল শাখায় ব্যবহৃত হয়। যে রাশিকে সম্পূর্ণরূপে প্রকাশ করতে মাণ ও দিক উভয় নির্দেশ করতে হয়, তাকে ভেক্টর রাশি বলে। সরণ, ত্বরণ, বেগ প্রভৃতি ভেক্টর রাশি। ভেক্টর শব্দটির উৎপত্তি হয়েছে ল্যাটিন শব্দ 'Vehere'থেকে যার অর্থ - বহন করা।
বিংশ শতাব্দীর প্রথম দিকে জটিল সংখ্যার জ্যামিতিক পদ্ধতিতে ভেক্টরের ব্যবহার শুরু হলেও এর ইতিহাস প্রাচীন। দার্শনিক এরিষ্টটল ( ৩৮৪-৩২২ খ্রীষ্টপূর্ব ) ও গণিতবিদ হেরণ ভেক্টর ভাবনার সুত্রপাত করেন। ১৮৩১ সালের পর গণিতশাস্ত্রের তিনটি আবিষ্কার ভেক্টরের উদ্ভাবনকে ত্বরান্বিত করে -"গাউসের অবাস্তব সংখ্যার জ্যামিতিক ব্যাখ্যা," লিবনিজের "জ্যামিতিক অবস্থান নির্ণয় পদ্ধতি" এবং নিউটনের "সামান্তরিক ক্ষেত্রে বল বা গতি সম্পর্কিত বিদ্যা"। পরবর্তিতে অলিভার হ্যাকিসাইড ( Oliver Heakiside ) এবং জসিয়া উইলার্ড গিবস ( Jashia Willard Gibs ) একটি বিশেষ ভেক্টর পদ্ধতি আবিষ্কার করেন। টেন্সর ( Tensor ) ভেক্টরের অত্যাধুনিক রূপ তুলে ধরেন, যা গণিতশাস্ত্রের উচ্চতর পর্যায়ে আলোচনা করা হয়। গণিত, পদার্থবিদ্যা ও প্রকৌসল বিদ্যায় ভেক্টরের ব্যবহার বহুল। এছাড়া জ্যামিতিক প্রিমিটিভ যেমন বিন্দু, রেখা , বক্ররেখা ও বহুভুজের ভেক্টর গাণিতিক সমীকরণ ব্যবহার করে ভেক্টর গ্রাফিক্স পদ্ধতিতে কম্পিউটারে ছবি প্রদর্শন করা হয়। ভেক্টর গ্রাফিক্স পদ্ধতিতে ছবি বড় করলে তা বিটম্যাপ পদ্ধতির মতো ফেটে যায় না বরং আরও স্পষ্ট হয় এবং ফাইলের সাইজ অপরিবর্তিত থাকে।
দার্শনিক প্লেটোর শিষ্য ও প্রাণি বিজ্ঞানের জনক এরিস্টটল খ্রিষ্টপূর্ব ৩৮৪ সালে স্টাগিরাস নামের এক গ্রিক উপনিবেশে জন্ম নেন। শৈশবে তার বাবা মারা যান। ১৮ বছর বয়সে তিনি গ্রিসের রাজধানী এথেন্সে চলে আসেন এবং বিজ্ঞানী প্লেটোর একাডেমিতে ভর্তি হন। প্লেটোর অধীনে তিনি সেখানে ২০ বছর শিক্ষা গ্রহণ করেন। ( ৩৮৪-৩২২ খ্রীষ্টপূর্ব ) , গণিতবিদ হেরণ আলেকজান্দ্রিয়ার নায়ক হেরন হো আলেকজান্দ্রিয়াস; আলেকজান্দ্রিয়ার হেরন নামে পরিচিত । রোমান মিশরের তার আদি শহর আলেকজান্দ্রিয়াতে সক্রিয় ছিলেন। তাকে প্রায়শই প্রাচীনত্বের সর্বশ্রেষ্ঠ পরীক্ষক হিসাবে বিবেচনা করা হয় তাঁর সর্বাধিক বিখ্যাত আবিষ্কারগুলির মধ্যে একটি উইন্ড হুইল ছিল যা জমিতে বাতাসের সুরক্ষার প্রথম দিকের উদাহরণ তৈরি করেছিল। ( ১০-৭০ খ্রীষ্টপূর্ব ) , স্যার আইজ্যাক নিউটন ১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। ( ১৬৪২-১৭২৭ খ্রীষ্টাব্দ ) প্রমুখ বিজ্ঞানীগণ ভেক্টর যোগের সামান্তরিক সূত্র ব্যবহার করেছেন। দেকার্ত, ফার্মাট, বলজানো, বিলাভিটিজ, ফার্দিনাদ মবিয়াস, ফেরিদ্রিচ, গাউস, গাব্রিয়াল স্টকস প্রমুখ গণিতবিদগণ ভেক্টর সম্পর্কিত তত্ত্ব ব্যাখ্যা করেন। গণিত ও বিজ্ঞানের বিভিন্ন সমস্যা উপস্থাপন এবং সমাধান করতে ভেক্টর ব্যবহৃত হয়।
ভেক্টর বিজ্ঞানের এমন একটি অংশ, যা জ্যামিতি ও বলবিদ্যার সকল শাখায় ব্যবহৃত হয়। যে রাশিকে সম্পূর্ণরূপে প্রকাশ করতে মাণ ও দিক উভয় নির্দেশ করতে হয়, তাকে ভেক্টর রাশি বলে। সরণ, ত্বরণ, বেগ প্রভৃতি ভেক্টর রাশি। ভেক্টর শব্দটির উৎপত্তি হয়েছে ল্যাটিন শব্দ 'Vehere'থেকে যার অর্থ - বহন করা।
বিংশ শতাব্দীর প্রথম দিকে জটিল সংখ্যার জ্যামিতিক পদ্ধতিতে ভেক্টরের ব্যবহার শুরু হলেও এর ইতিহাস প্রাচীন। দার্শনিক এরিষ্টটল ( ৩৮৪-৩২২ খ্রীষ্টপূর্ব ) ও গণিতবিদ হেরণ ভেক্টর ভাবনার সুত্রপাত করেন। ১৮৩১ সালের পর গণিতশাস্ত্রের তিনটি আবিষ্কার ভেক্টরের উদ্ভাবনকে ত্বরান্বিত করে -"গাউসের অবাস্তব সংখ্যার জ্যামিতিক ব্যাখ্যা," লিবনিজের "জ্যামিতিক অবস্থান নির্ণয় পদ্ধতি" এবং নিউটনের "সামান্তরিক ক্ষেত্রে বল বা গতি সম্পর্কিত বিদ্যা"। পরবর্তিতে অলিভার হ্যাকিসাইড ( Oliver Heakiside ) এবং জসিয়া উইলার্ড গিবস ( Jashia Willard Gibs ) একটি বিশেষ ভেক্টর পদ্ধতি আবিষ্কার করেন। টেন্সর ( Tensor ) ভেক্টরের অত্যাধুনিক রূপ তুলে ধরেন, যা গণিতশাস্ত্রের উচ্চতর পর্যায়ে আলোচনা করা হয়। গণিত, পদার্থবিদ্যা ও প্রকৌসল বিদ্যায় ভেক্টরের ব্যবহার বহুল। এছাড়া জ্যামিতিক প্রিমিটিভ যেমন বিন্দু, রেখা , বক্ররেখা ও বহুভুজের ভেক্টর গাণিতিক সমীকরণ ব্যবহার করে ভেক্টর গ্রাফিক্স পদ্ধতিতে কম্পিউটারে ছবি প্রদর্শন করা হয়। ভেক্টর গ্রাফিক্স পদ্ধতিতে ছবি বড় করলে তা বিটম্যাপ পদ্ধতির মতো ফেটে যায় না বরং আরও স্পষ্ট হয় এবং ফাইলের সাইজ অপরিবর্তিত থাকে।
সদিক রাশির প্রতিরূপ হিসেবে ভেক্টর
Vector as a counter part of directed line
যে রাশির মাণ ও দিক উভয়ই আছে তাকে ভেক্টর রাশি বা সদিক রাশি বলে। যেমনঃ সরণ, ত্বরণ, বল, বেগ প্রভৃতি ভেক্টর রাশি।
সাধারণত একটি মাত্র বর্ণ বা প্রতীক দ্বারা \(( a, b, c, ... u, v, w )\) ভেক্টর বুঝানো হলে তার উপরে বা নিচে তীর চিহ্ন অথবা একটা টান \(( \overrightarrow{a}, \underline{b}, \overline{c} )\) ব্যবহার করা হয়। আবার একক ভেক্টরকে \(\hat{a}\) দ্বারা প্রকাশ করা হয়। অনেক সময় অক্ষর বোল্ড \(\bf{a}\) করেও ভেক্টর বুঝানো হয়।
\( \overrightarrow{a}\) ভেক্টরের মাণকে \(|a|\) দ্বারা প্রকাশ করা হয়। কোনো রেখাংশ \(OP\) কে ভেক্টর হিসেবে চিহ্নিত করার জন্য \( \overrightarrow{OP}\) লেখা হয়ে থাকে। উক্ত রেখাংশের দৈর্ঘ্যকে \( \overrightarrow{OP}\) ভেক্টরের মাণ হিসেবে বিবেচনা করা হয়। \(O\) বিন্দুকে মূলবিন্দু বা প্রারম্ভিক বিন্দু এবং \(P\) বিন্দুকে শীর্ষবিন্দু বা প্রান্তবিন্দু বলা হয়। প্রকৃতির সকল রাশিকে দুইভাগে ভাগ করা যায়। যেমনঃ অদিক রাশি বা স্কেলার রাশি অপরটি সদিক রাশি বা ভেক্টর রাশি। অদিক রাশি বা স্কেলার রাশিঃ যে সকল ভৌত রাশি প্রকাশ করতে দিকের প্রয়োজন হয় না শুধু মাণ দিয়ে সম্পূর্ণরূপে প্রকাশ করা যায় সেগুলিকে স্কেলার রাশি বা অদিক রাশি বলে। অর্থাৎ স্কেলার রাশির শুধু মাণ আছে দিক নেই। যেমনঃ দৈর্ঘ্য, ভর, সময়, আয়তন, তাপমাত্রা, দূরত্ব, দ্রুতি, কাজ, শক্তি , জনসংখ্যা, বাস্তব সংখ্যা ইত্যাদি। স্কেলার রাশিকে বীজগণিতের ন্যায় বর্ণ প্রতীক বা সংখ্যা দ্বারা প্রকাশ করা হয়। সদিক রাশি বা ভেক্টর রাশিঃ যে সকল ভৌত রাশিকে পূর্ণাঙ্গ প্রকাশের জন্য মাণ ও দিক উভয়েই প্রয়োজন হয় তাদেরকে ভেক্টর রাশি বা সদিক রাশি বলে। স্পষ্ট যে ভেক্টর রাশির মাণ ও দিক উভয়েই আছে। যেমনঃ সরণ, বেগ, ত্বরণ, মন্দন, ওজন, বল ইত্যাদি ভেক্টর রাশি।
সাধারণত একটি মাত্র বর্ণ বা প্রতীক দ্বারা \(( a, b, c, ... u, v, w )\) ভেক্টর বুঝানো হলে তার উপরে বা নিচে তীর চিহ্ন অথবা একটা টান \(( \overrightarrow{a}, \underline{b}, \overline{c} )\) ব্যবহার করা হয়। আবার একক ভেক্টরকে \(\hat{a}\) দ্বারা প্রকাশ করা হয়। অনেক সময় অক্ষর বোল্ড \(\bf{a}\) করেও ভেক্টর বুঝানো হয়।
\( \overrightarrow{a}\) ভেক্টরের মাণকে \(|a|\) দ্বারা প্রকাশ করা হয়। কোনো রেখাংশ \(OP\) কে ভেক্টর হিসেবে চিহ্নিত করার জন্য \( \overrightarrow{OP}\) লেখা হয়ে থাকে। উক্ত রেখাংশের দৈর্ঘ্যকে \( \overrightarrow{OP}\) ভেক্টরের মাণ হিসেবে বিবেচনা করা হয়। \(O\) বিন্দুকে মূলবিন্দু বা প্রারম্ভিক বিন্দু এবং \(P\) বিন্দুকে শীর্ষবিন্দু বা প্রান্তবিন্দু বলা হয়। প্রকৃতির সকল রাশিকে দুইভাগে ভাগ করা যায়। যেমনঃ অদিক রাশি বা স্কেলার রাশি অপরটি সদিক রাশি বা ভেক্টর রাশি। অদিক রাশি বা স্কেলার রাশিঃ যে সকল ভৌত রাশি প্রকাশ করতে দিকের প্রয়োজন হয় না শুধু মাণ দিয়ে সম্পূর্ণরূপে প্রকাশ করা যায় সেগুলিকে স্কেলার রাশি বা অদিক রাশি বলে। অর্থাৎ স্কেলার রাশির শুধু মাণ আছে দিক নেই। যেমনঃ দৈর্ঘ্য, ভর, সময়, আয়তন, তাপমাত্রা, দূরত্ব, দ্রুতি, কাজ, শক্তি , জনসংখ্যা, বাস্তব সংখ্যা ইত্যাদি। স্কেলার রাশিকে বীজগণিতের ন্যায় বর্ণ প্রতীক বা সংখ্যা দ্বারা প্রকাশ করা হয়। সদিক রাশি বা ভেক্টর রাশিঃ যে সকল ভৌত রাশিকে পূর্ণাঙ্গ প্রকাশের জন্য মাণ ও দিক উভয়েই প্রয়োজন হয় তাদেরকে ভেক্টর রাশি বা সদিক রাশি বলে। স্পষ্ট যে ভেক্টর রাশির মাণ ও দিক উভয়েই আছে। যেমনঃ সরণ, বেগ, ত্বরণ, মন্দন, ওজন, বল ইত্যাদি ভেক্টর রাশি।
ভেক্টরের ধারক রেখা
Line of support of Vector
যে দিক নির্দেশক রেখাংশ দ্বারা কোনো ভেক্টর রাশিকে সূচীত করা হয় তাকে ঐ ভেক্টরের ধারক রেখা বলা হয়। এখানে \(XY\) রেখার \(AB\) রেখাংশ দ্বারা \( \overrightarrow{V}\) ভেক্টরকে সূচিত করা হয়েছে তাই \( \overrightarrow{AB}\) কে \( \overrightarrow{V}\) ভেক্টরের ধারক রেখা বলে।
ভেক্টরের মাণ
Magnitude of Vector
ভেক্টর নির্দেশক রেখাংশের প্রারম্ভিক বিন্দু এবং প্রান্তবিন্দুর মধ্যবর্তী দূরত্বকে ভেক্টরের মাণ বলা হয়। \( \overrightarrow{V}\) ভেক্টরের মাণকে \(|\overrightarrow{V}|\) দ্বারা প্রকাশ করা হয়।
ভেক্টরের সমতা
Equality of Vector
দুইটি ভেক্টরকে সমান বলা হবে, যখন তাদের-
মাণ সমান হয়।
উভয়ের ধারক রেখা এক অথবা সমান্তরাল।
দিক অভিন্ন হয়।
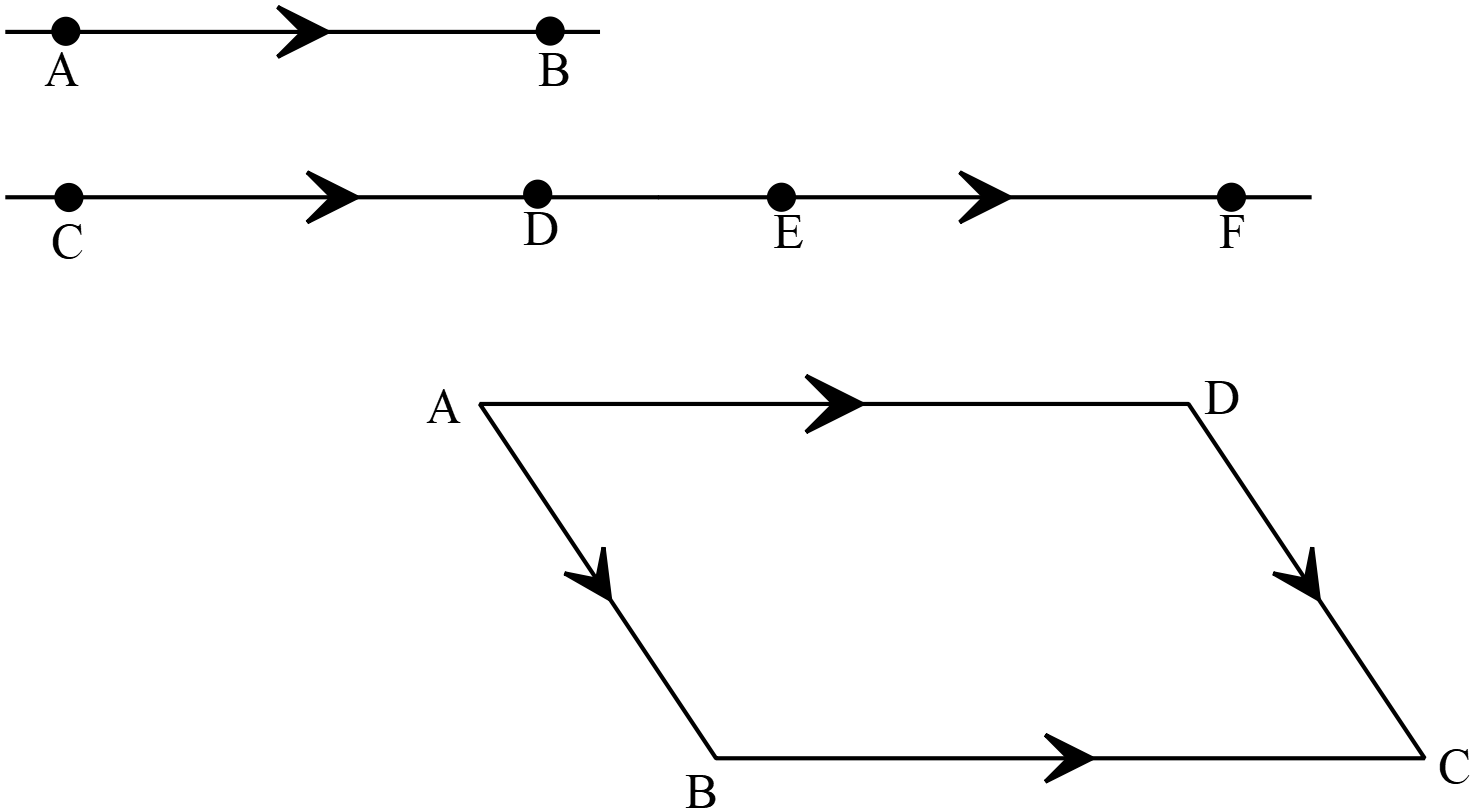দুইটি সদিক রেখাংশ একই ভেক্টর নির্দেশ করতে পারে।
যেমনঃ \(\overrightarrow{AB}, \ \overrightarrow{CD}, \ \overrightarrow{EF}\) রেখাংশগুলি সমান ভেক্টর নির্দেশ করে। কারণ তাদের ধারক রেখা একই অথবা সমান্তরাল এবং দৈর্ঘ্য সমান।
সামান্তরিকের বিপরীত বাহুগুলি দ্বারা সমান ভেক্টর নির্দেশ করা হয়।
যেমনঃ \(ABCD\) সামান্তরিকের ক্ষেত্রে \(\overrightarrow{AB}=\overrightarrow{DC}\) এবং \(\overrightarrow{AD}=\overrightarrow{BC}\)
মাণ সমান হয়।
উভয়ের ধারক রেখা এক অথবা সমান্তরাল।
দিক অভিন্ন হয়।
দুইটি সদিক রেখাংশ একই ভেক্টর নির্দেশ করতে পারে।যেমনঃ \(\overrightarrow{AB}, \ \overrightarrow{CD}, \ \overrightarrow{EF}\) রেখাংশগুলি সমান ভেক্টর নির্দেশ করে। কারণ তাদের ধারক রেখা একই অথবা সমান্তরাল এবং দৈর্ঘ্য সমান।
সামান্তরিকের বিপরীত বাহুগুলি দ্বারা সমান ভেক্টর নির্দেশ করা হয়।
যেমনঃ \(ABCD\) সামান্তরিকের ক্ষেত্রে \(\overrightarrow{AB}=\overrightarrow{DC}\) এবং \(\overrightarrow{AD}=\overrightarrow{BC}\)
বিপরীত ভেক্টর
Opposite Vector
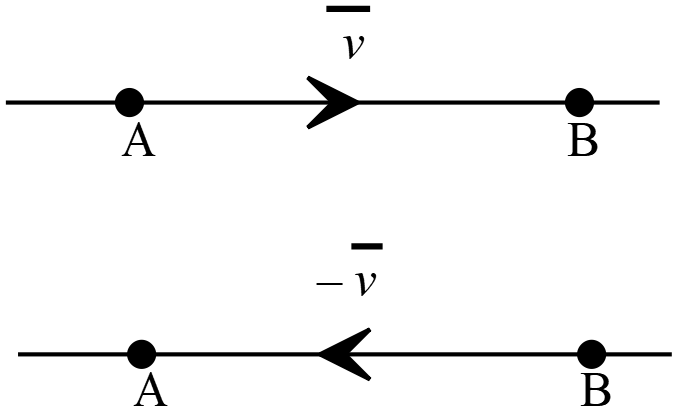দুইটি ভেক্টরের দৈর্ঘ্য বা মাণ সমান তাদের ধারক রেখা একই অথবা সমান্তরাল কিন্তু দিক বিপরীতমুখী এরূপ ভেক্টরকে একে অপরের বিপরীত ভেক্টর বলা হয়।যেমনঃ \(\overrightarrow{AB}=\overrightarrow{v}\) এবং বিপরীত ভেক্টর \(\overrightarrow{BA}=-\overrightarrow{v};\)
\(\overrightarrow{AB}\) এবং \(\overrightarrow{BA}\) এর দৈর্ঘ্য সমান কিন্তু এরা পরস্পর বিপরীতমুখী।
শূন্য ভেক্টর বা নাল ভেক্টর
Zero Vector Or, Null Vector
যে ভেক্টর রাশির দৈর্ঘ্য বা মাণ শূন্য, কোনো নির্দিষ্ট দিক নেই, তাকে শূন্য ভেক্টর বলে। এরূপ ভেক্টরের প্রারম্ভিক ও প্রান্তবিন্দু একই। এ ভেক্টরকে মোটা হরফে \(\bf{0}\) বা \(\underline{0}\) দ্বারা নির্দেশ করা হয়। এর বৈশিষ্ট স্কেলার রাশির মতই।
একক ভেক্টর
Unite Vector
কোনো ভেক্টরের দৈর্ঘ্য বা মাণ \(\) (এক) হলে তাকে একক ভেক্টর বলে। মাণ শন্য নয় এরূপ একটি ভেক্টরকে তার মাণ দ্বারা ভাগ করলে ঐ ভেক্টর রাশিটির দিক বরাবর অথবা তার সমান্তরাল বরাবর একটি একক ভেক্টর পাওয়া যায়। একক ভেক্টর প্রকাশের জন্য ভেক্টর প্রতীক হিসেবে হ্যাট \((\hat{})\) চিহ্ন ব্যবহার করা হয়।
যেমনঃ অক্ষ রেখা বরাবর একক ভেক্টরগুলি যথাক্রমে \(\hat{i}, \hat{j}, \hat{k}\)
আবার
\(\overline{a}\) একটি ভেক্টর রাশি যার মাণ \(|\overline{a}|,\) যেখানে \(|\overline{a}|\ne{0}\)
তাহলে,
\(\overline{a}\) এর একক ভেক্টর অথবা সমান্তরাল একক ভেক্টর, \(\hat{a}=\pm{\frac{\overline{a}}{|\overline{a}|}}\) \(\overline{a}\) এর দিক বরাবর একক ভেক্টর , \(\hat{a}=\frac{\overline{a}}{|\overline{a}|}\) \(\overline{a}\) এর বিপরিতদিক বরাবর একক ভেক্টর , \(\hat{a}=-\frac{\overline{a}}{|\overline{a}|}\)
যেমনঃ অক্ষ রেখা বরাবর একক ভেক্টরগুলি যথাক্রমে \(\hat{i}, \hat{j}, \hat{k}\)
আবার
\(\overline{a}\) একটি ভেক্টর রাশি যার মাণ \(|\overline{a}|,\) যেখানে \(|\overline{a}|\ne{0}\)
তাহলে,
\(\overline{a}\) এর একক ভেক্টর অথবা সমান্তরাল একক ভেক্টর, \(\hat{a}=\pm{\frac{\overline{a}}{|\overline{a}|}}\) \(\overline{a}\) এর দিক বরাবর একক ভেক্টর , \(\hat{a}=\frac{\overline{a}}{|\overline{a}|}\) \(\overline{a}\) এর বিপরিতদিক বরাবর একক ভেক্টর , \(\hat{a}=-\frac{\overline{a}}{|\overline{a}|}\)
প্রকৃত ও অপ্রকৃত ভেক্টর
Proper and Imporoper Vector
শূন্য ভেক্টর ব্যতীত সকল ভেক্টরকে প্রকৃত ভেক্টর এবং শূন্য ভেক্টরকে অপ্রকৃত ভেক্টর বলে।
সদৃশ ভেক্টর
Like Vector
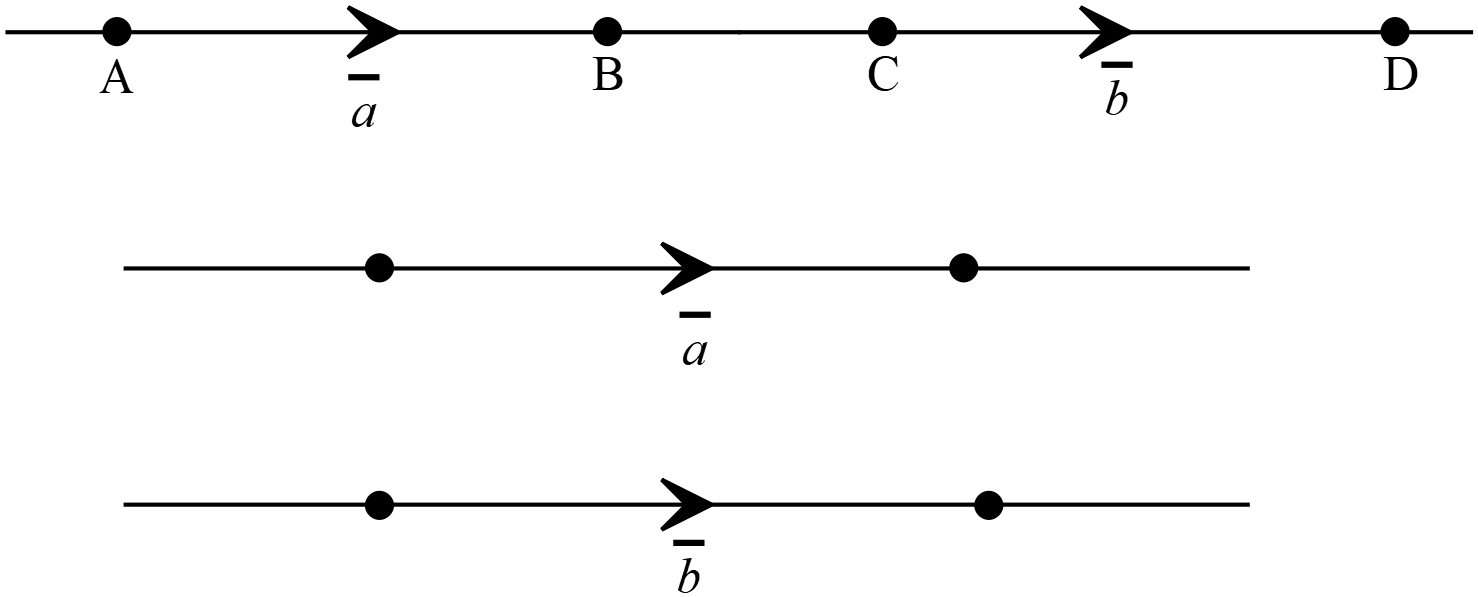যে সব ভেক্টরসমূহের দিক এবং ধারক রেখা একই অথবা পরস্পর সমান্তরাল তাদেরকে সদৃশ ভেক্টর বলে। সদৃশ ভেক্টরসমূহের মাণ সমান অথবা ভিন্ন হতে পারে।
অসদৃশ ভেক্টর
Unlike Vector
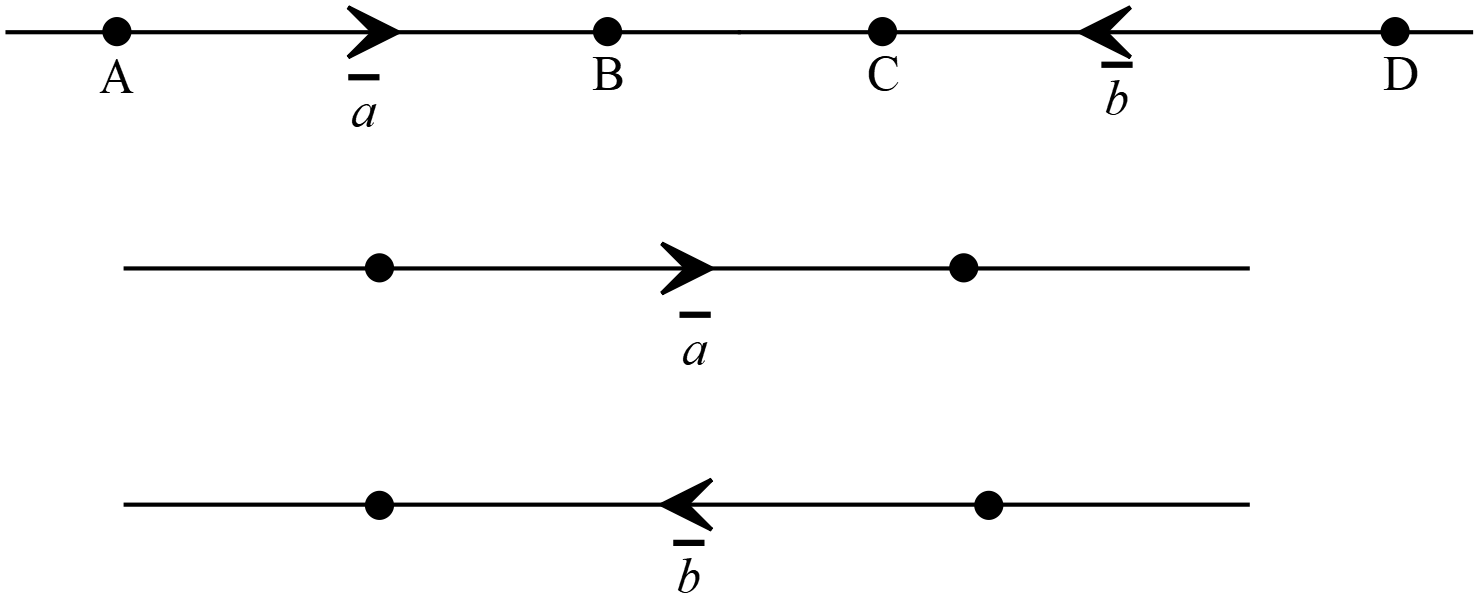দুইটি ভেক্টরের দিক বিপরীতমুখী কিন্তু ধারক রেখা একই অথবা পরস্পর সমান্তরাল তাদেরকে অসদৃশ ভেক্টর বলে। অসদৃশ ভেক্টরসমূহের মাণ সমান অথবা ভিন্ন হতে পারে।
সমরৈখিক ভেক্টর
Collinear Vector
দুই বা ততোধিক ভেক্টর একটি সরলরেখার সমান্তরাল হলে, তবে তাদেরকে সমরৈখিক বা সমান্তরাল ভেক্টর বলে।
যদি \(\overline{A}\) ও \(\overline{B}\) ভেক্টরদ্বয় সমরৈখিক হয় তবে \(\overline{A}=m\overline{B};\) যেখানে \(m\) একটি স্কেলার ।
যদি \(\overline{A}\) ও \(\overline{B}\) ভেক্টরদ্বয় সমরৈখিক হয় তবে \(\overline{A}=m\overline{B};\) যেখানে \(m\) একটি স্কেলার ।
সমতলীয় ভেক্টর
Coplanar Vector
দুই বা ততোধিক ভেক্টরের ধারক রেখা অভিন্ন হলে, তাদেরকে সমতলীয় ভেক্টর বলে।
মুক্ত ভেক্টর
Free Vector
যে ভেক্টরের মডুলাস ও দিক স্থির কিন্ত অবস্থান স্থির নয়, মডুলাস ও দিকের পরিবর্তন না করে যে ভেক্টরকে স্থানান্তর করা যায় তাকে মুক্ত ভেক্টর বলে।
দুইটি ভেক্টরের অন্তরভুক্ত কোণ
The angle between two vectors
ধরা যাক, \(\overline{P}\) ও \(\overline{Q}\) দুইটি ভেক্টর এদের ধারক রেখাদ্বয় পরস্পরকে \(O\) বিন্দুতে ছেদ করেছে। ছেদবিন্দুতে \(0<\theta<\pi\) কোণ উৎপন্ন হয়।
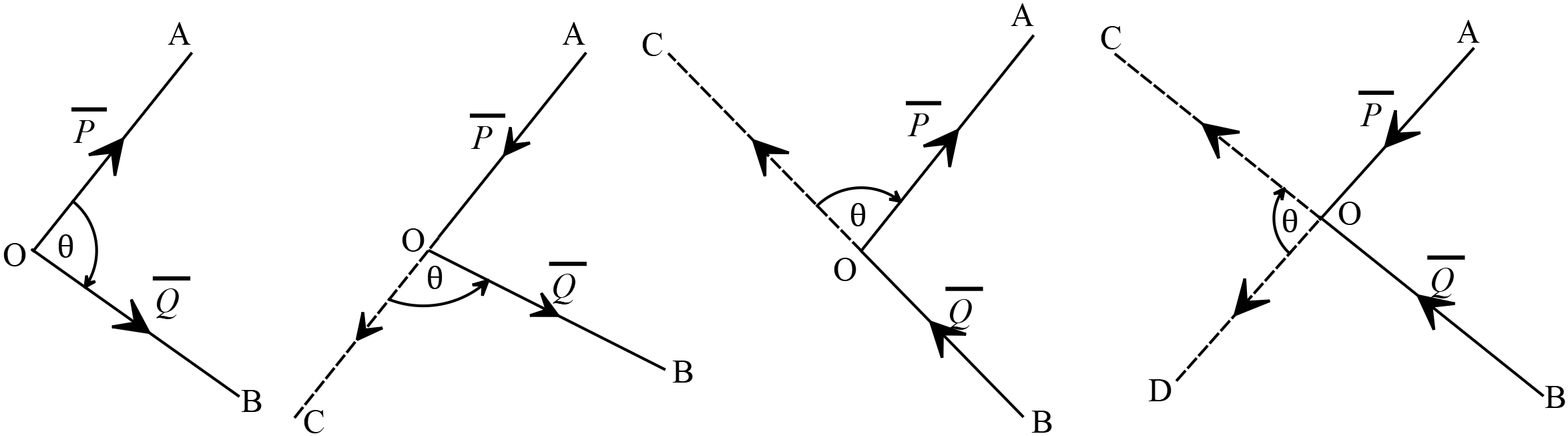
ভেক্টর যোগের ত্রিভুজ সূত্র
Triangle law of vector addition
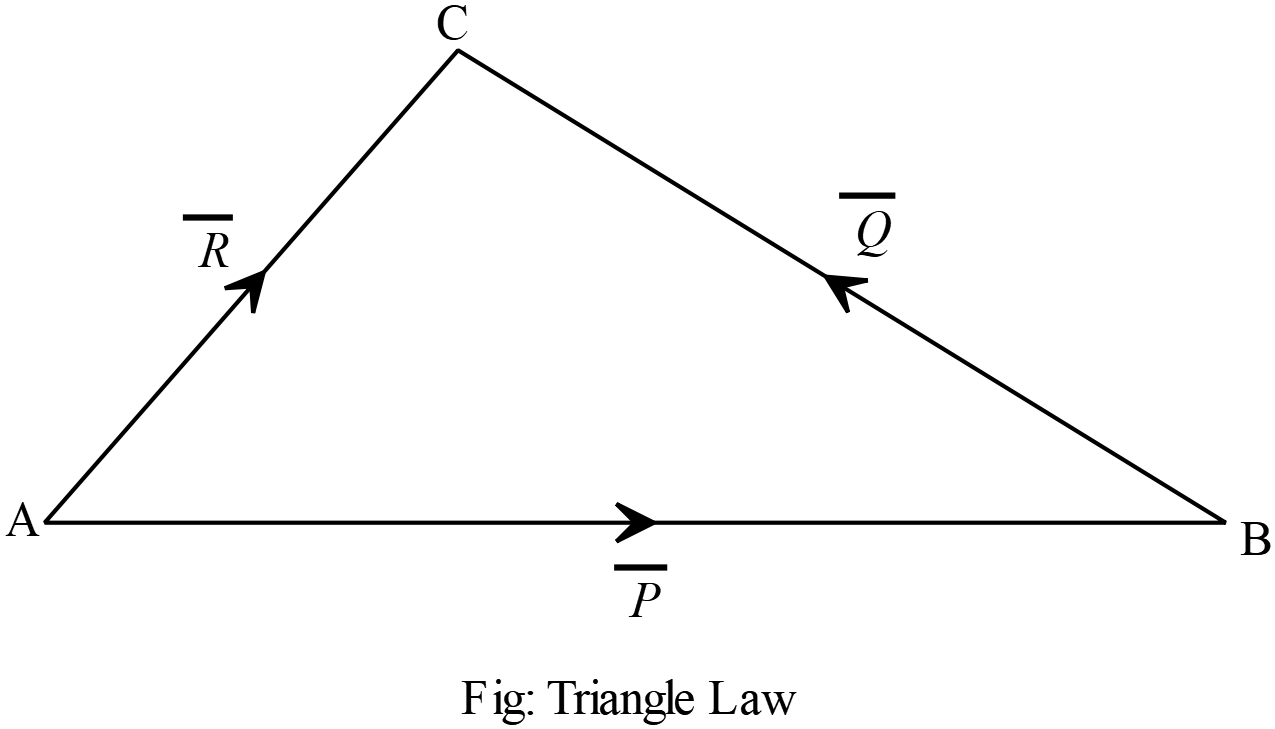যদি কোনো ত্রিভুজের দুইটি বাহু একই ক্রমে দিকে ও মাণে দুইটি ভেক্টর রাশিকে নির্দেশ করে, তাহলে ত্রিভুজের তৃতীয় বাহুটি বিপরীতক্রমে ভেক্টরদ্বয়ের লব্ধির মাণ ও দিক নির্দেশ করবে। এখানে, \(\overline{P}\) ও \(\overline{Q}\) ভেক্টর দুইটিকে \(\overrightarrow{AB}\) ও \(\overrightarrow{BC}\) দ্বারা সূচিত করা হলো। \(\overrightarrow{AB}\) এর প্রারম্ভিকবিন্দু \(A\) এবং \(\overrightarrow{BC}\) এর প্রান্তবিন্দু \(B\) এর সংযোগ রেখাংশ দ্বারা গঠিত ভেক্টর \(\overrightarrow{AC}\) পূর্বোক্ত ভেক্টরদ্বয়ের লব্ধি নির্দেশ করবে যাকে \(\overline{R}\) দ্বারা সূচীত করা হলো।
সুতরাং , \(\overline{P}+\overline{Q}=\overline{R}\)
\(\therefore \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
ভেক্টর যোগের সামান্তরিক সূত্র
Parallelogram law of vector addition
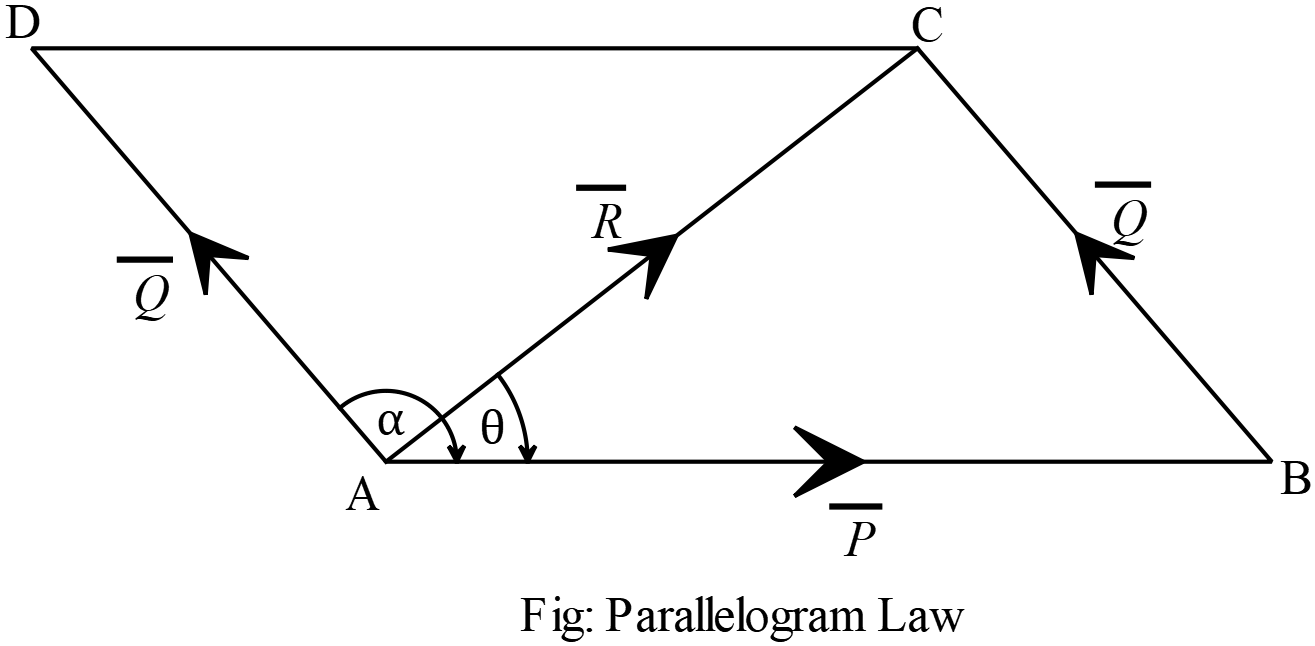কোনো সামান্তরিকের একটি কৌণিক বিন্দু থেকে অঙ্কিত সন্নিহিত বাহুদ্বয় যদি কোনো কণার উপর একই সময়ে ক্রিয়ারত দুইটি ভেক্টরের মাণ ও দিক নির্দেশ করে, তাহলে ঐ বিন্দু থেকে অঙ্কিত সামান্তরিকের কর্ণটি ভেক্টরদ্বয়ের লব্ধির মাণ ও দিক নির্দেশ করবে। অর্থাৎ, \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\)
দ্রঃ দুইটি ভেক্টর সমান্তরাল হলে তাদের যোগের ক্ষেত্রে সামান্তরিক বিধি প্রযোজ্য নয়, কিন্তু ত্রিভুজ বিধি সকল ক্ষেত্রেই প্রযোজ্য হবে।
ভেক্টর যোগের বহুভুজ সূত্র
Polygon law of vector addition
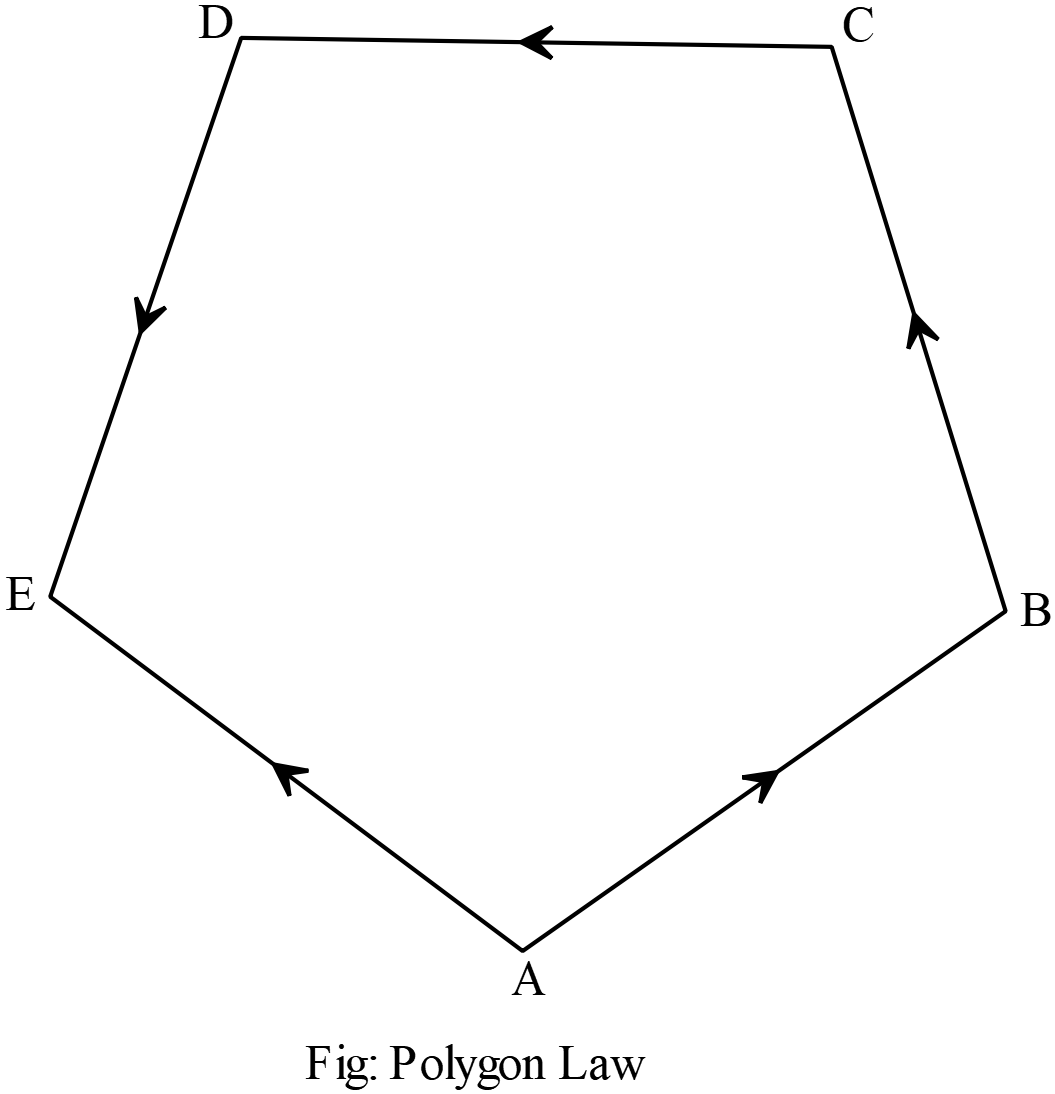দুইয়ের অধিক ভেক্টরের ক্ষেত্রে একই ক্রমে ভেক্টরগুলিকে সাজিয়ে প্রথম ভেক্টরের প্রারম্ভিকবিন্দু এবং শেষ ভেক্টরের প্রান্তবিন্দু যোগ করে একটি বহুভুজ অঙ্কন করলে বহুভুজের শেষ বাহুটি বিপরীতক্রমে ভেক্টরগুলির লব্ধির মাণ ও দিক নির্দেশ করবে। \(\therefore \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{AE}\)
দুইটি ভেক্টরের বিয়োগ
Subtraction of two vectors
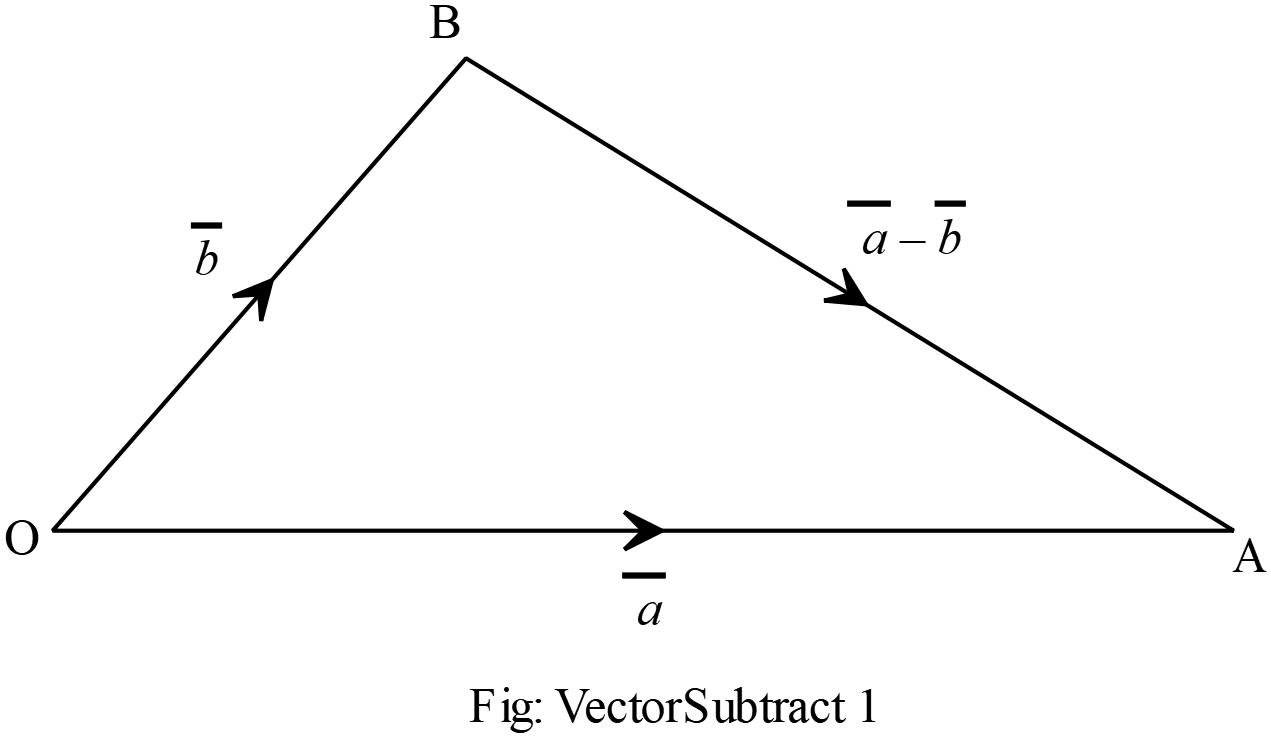ভেক্টরের বিয়োগের ক্ষেত্রে যে ভেক্টর বিয়োগ করতে হবে তার ঋণাত্মক ভেক্টরকে অপর ভেক্টরের সাথে যোগ করলেই বিয়োগফল পাওয়া যায়। \(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) দুইটি ভেক্টর।
এদের বিয়োগফল হবে,
\(\overrightarrow{BA}=\overline{a}-\overline{b}\)
অথবা,
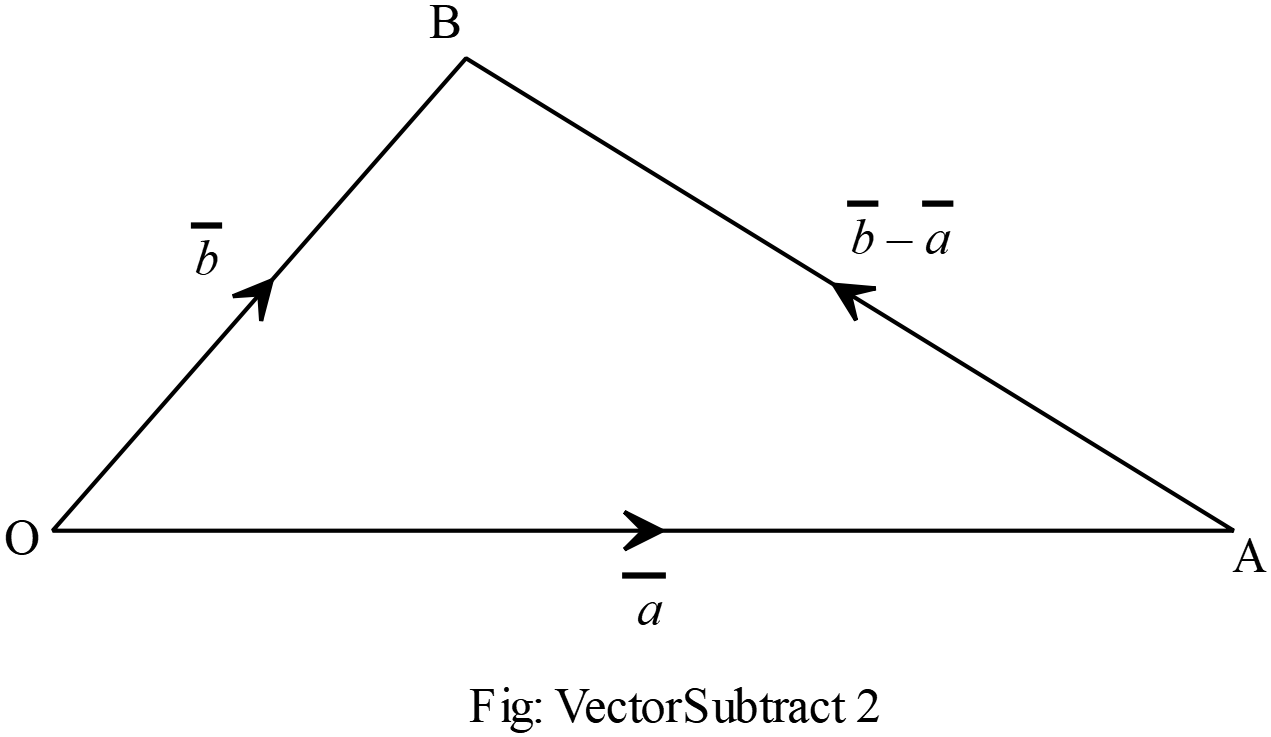
\(\overrightarrow{AB}=\overline{b}-\overline{a}\)
দ্রঃ ভেক্টরদ্বয়ের প্রান্তবিন্দুর সংযোগ রেখাংশ দ্বারা তাদের বিয়োগফল প্রকাশিত হয়। প্রথম ভেক্টরের প্রান্তবিন্দু পরে এবং দ্বিতীয় ভেক্টরের প্রান্তবিন্দু প্রথমে হয়।
ভেক্টর রাশির স্কেলার গুণিতক
Scalar Multiple of Vector
ধরি, \(\overline{a}\) একটি ভেক্টর এবং \(m\) একটি স্কেলার। \(m\overline{a}\) দ্বারা ভেক্টর \(\overline{a}\) এর \(m\) গুণিতক বোঝায়। \(m\) গুনিতকের বিবরণ নিম্নে দেওয়া হলো।
\(m\overline{a}\) এর দৈর্ঘ্য \(\overline{a}\) এর দৈর্ঘ্যের \(m\) গুণ হবে। অর্থাৎ, \(|m\overline{a}|=m|\overline{a}|\) হবে।
\(m\overline{a}\) এর দিক এবং \(\overline{a}\) এর দিক একই হবে যখন, \(m>0\)
\(m\overline{a}\) এর দিক এবং \(\overline{a}\) এর দিক পরস্পর বিপরীত হবে যখন, \(m<0\)
\(m(-\overline{a})=(-m)\overline{a}=-m\overline{a}\)
\((-1)\overline{a}=-\overline{a}\)
\(0\overline{a}=\underline{0}\) (এখানে, বামপক্ষের শূন্যটি স্কেলার কিন্তু ডানপক্ষের শূন্যটি ভেক্টর )
\(m=\frac{\overline{a}}{\overline{b}} \Rightarrow \overline{a}=m\overline{b}\)
দ্রঃ যদি দুইটি অশূণ্য ভেক্টরের ধারকরেখা একই অথবা সমান্তরাল হয়, তবে একটি ভেক্টরকে অন্যটির একটি স্কেলার গুণিতক হিসেবে বিবেচনা করা হয়।
\(\overline{a}=\underline{0}\) হলে,
\(m\overline{a}=\underline{0}\) \(\overline{a}\ne{\underline{0}}\) হলে,
\(m\overline{a}\) এবং \(\overline{a}\) এর ধারকরেখা একই অথবা সমান্তরাল হবে। \(m\overline{a}\) এর দৈর্ঘ্য \(\overline{a}\) এর দৈর্ঘ্যের \(m\) গুণ হবে। অর্থাৎ, \(|m\overline{a}|=m|\overline{a}|\) হবে।
\(m\overline{a}\) এর দিক এবং \(\overline{a}\) এর দিক একই হবে যখন, \(m>0\)
\(m\overline{a}\) এর দিক এবং \(\overline{a}\) এর দিক পরস্পর বিপরীত হবে যখন, \(m<0\)
\(m\) গুনিতকের বিশেষ বিধি
\((mn)\overline{a}=m(n)\overline{a}\)\(m(-\overline{a})=(-m)\overline{a}=-m\overline{a}\)
\((-1)\overline{a}=-\overline{a}\)
\(0\overline{a}=\underline{0}\) (এখানে, বামপক্ষের শূন্যটি স্কেলার কিন্তু ডানপক্ষের শূন্যটি ভেক্টর )
\(m=\frac{\overline{a}}{\overline{b}} \Rightarrow \overline{a}=m\overline{b}\)
দ্রঃ যদি দুইটি অশূণ্য ভেক্টরের ধারকরেখা একই অথবা সমান্তরাল হয়, তবে একটি ভেক্টরকে অন্যটির একটি স্কেলার গুণিতক হিসেবে বিবেচনা করা হয়।
দ্বিমাত্রিক ভেক্টরের যোগ, বিয়োগ ও স্কেলার গুণিতকের বিধি
Addition Subtraction and Scalar Multiple Law of two Dimensional Vector
ভেক্টর যোগের এবং স্কেলার গুণিতক গঠনের মৌলিক বিধিগুলো নিম্নে তালিকা আকারে দেওয়া হলো। এখানে, \(\overline{a}, \overline{b}, \overline{c}\) যে কোনো ভেক্টর এবং \(m, \ n\) কে স্কেলার হিসেবে বিবেচনা করা হয়েছে।
\(\overline{a}+\overline{b}=\overline{b}+\overline{a}\) ( যোগের বিনিময় বিধি )
\(\overline{a}+(\overline{b}+\overline{c})=(\overline{a}+\overline{b})+\overline{c}\) ( যোগের সংযোগ বিধি )
\(m\overline{a}=\overline{a}m\) ( গুণের বিনিময় বিধি )
\(m(n\overline{a})=(mn)\overline{a}\) ( গুণের সংযোগ বিধি )
\(m(\overline{a}+\overline{a})=m\overline{a}+m\overline{b}\) ( বন্টন বিধি )
\(\overline{a}+\overline{b}=\overline{b}+\overline{a}\) ( যোগের বিনিময় বিধি )
\(\overline{a}+(\overline{b}+\overline{c})=(\overline{a}+\overline{b})+\overline{c}\) ( যোগের সংযোগ বিধি )
\(m\overline{a}=\overline{a}m\) ( গুণের বিনিময় বিধি )
\(m(n\overline{a})=(mn)\overline{a}\) ( গুণের সংযোগ বিধি )
\(m(\overline{a}+\overline{a})=m\overline{a}+m\overline{b}\) ( বন্টন বিধি )
দ্বিমাত্রিক ভেক্টরের বিশেষ বিধি
Spacial Law of two Dimensional Vector
এখানে, \(\overline{a}\) যে কোনো ভেক্টর এবং \(m, \ n\) কে স্কেলার হিসেবে বিবেচনা করা হয়েছে।
\(\overline{a}+\underline{0}=\underline{0}+\overline{a}=\overline{a}\) ( যোগের অভেদক বিধি )
\(\overline{a}+(-\overline{a})=\underline{0}\) ( যোগের বিপরীতক বিধি )
\((m+n)\overline{a}=m\overline{a}+n\overline{a}\) ( বন্টন বিধি )
\(1(\overline{a})=\overline{a}\) ( গুণের অভেদক বিধি )
\(\overline{a}+\underline{0}=\underline{0}+\overline{a}=\overline{a}\) ( যোগের অভেদক বিধি )
\(\overline{a}+(-\overline{a})=\underline{0}\) ( যোগের বিপরীতক বিধি )
\((m+n)\overline{a}=m\overline{a}+n\overline{a}\) ( বন্টন বিধি )
\(1(\overline{a})=\overline{a}\) ( গুণের অভেদক বিধি )
সমতলে ভেক্টরের অংশক
Components of a Vector in a Plane
যদি, \(\overline{a}\) এবং \(\overline{b}\) দুইটি অসম ভেক্টর হয়, তবে \(\overline{a}\) ও \(\overline{b}\) এর সমতলে যে কোনো ভেক্টর \(\overline{r}\) কে \(\overline{a}\) ও \(\overline{b}\) এর যোগাশ্রয়ী সমাবেশ এককভাবে প্রকাশ করা যাবে।
অর্থাৎ,
\(\overline{r}=m\overline{a}+n\overline{b}\)
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=m\overline{a}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=n\overline{b}\)
অর্থাৎ,
\(\overline{r}=m\overline{a}+n\overline{b}\)
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=m\overline{a}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=n\overline{b}\)
আয়ত একক ভেক্টর \(\hat{i}, \hat{j}\)
Unite Vector \(\hat{i}, \hat{j}\)
কার্তেসীয় সমতলে \(x\) ও \(y\) অক্ষ বরাবর যথাক্রমে একক ভেক্টর \(\hat{i}\) ও \(\hat{j}\) কে আয়ত একক ভেক্টর বলা হয়। \(\hat{i}\) ও \(\hat{j}\) পরস্পর লম্ব দুইটি একক ভেক্টর।
এখানে,
\(|\hat{i}|=|\hat{j}|=1\)
এখানে,
\(|\hat{i}|=|\hat{j}|=1\)
কার্তেসীয় স্থানাংককে ভেক্টরে এবং ভেক্টরকে কার্তেসীয় স্থানাংকে প্রকাশ
Represention of Vector in Cartesian Co-ordinates and Cartesian Co-ordinates in Vector
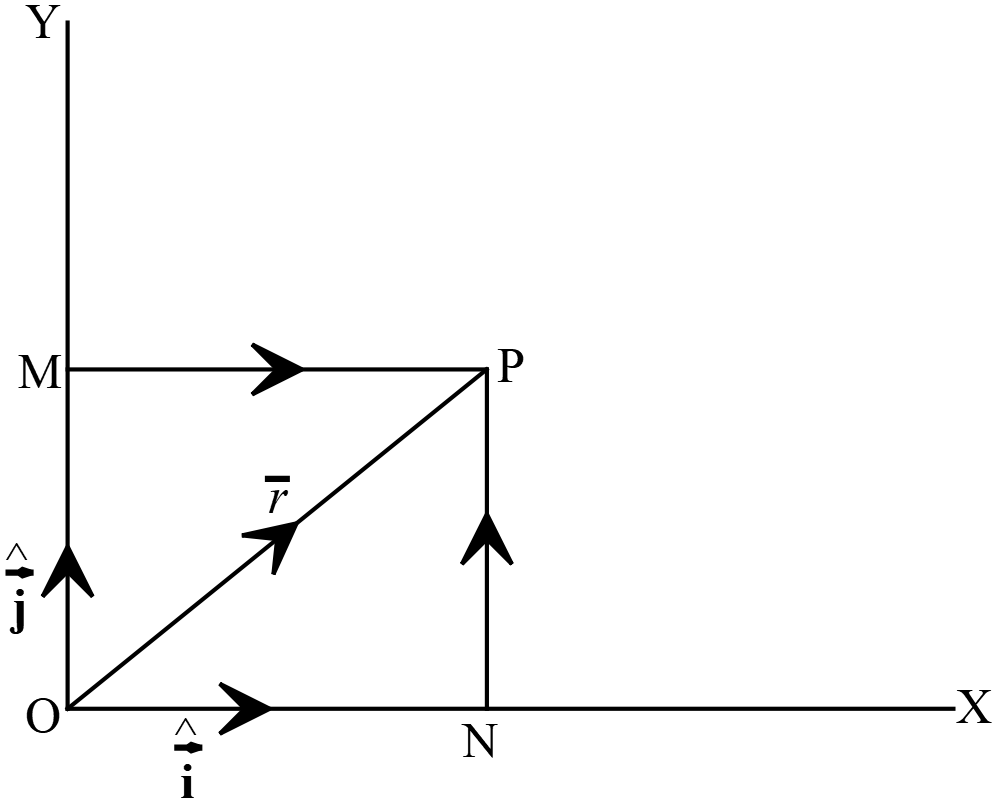ধরি, কার্তেসীয় সমতলে \(P\) বিন্দুর কার্তেসীয় স্থানাঙ্ক \((x, y)\) এবং মূলবিন্দু \((0, 0), x\) ও \(y\) অক্ষের ধনাত্মক দিকে একক ভেক্টর যথাক্রমে \(\hat{i}\) ও \(\hat{j}\)এবং \(\overrightarrow{OP}=\overline{r}\)
এখানে, \(PN\perp{OX}\) এবং \(PM\perp{OY}\)
তাহলে, \(\overrightarrow{ON}=x\hat{i}\) এবং \(\overrightarrow{NP}=\overrightarrow{OM}=y\hat{j}\)
এখন, \(\triangle{PON}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{ON}+\overrightarrow{NP}\)
\(\therefore\) \(\overline{r}=x\hat{i}+y\hat{j}\) আবার, \(\triangle{PON}\) সমকোণী
\(\therefore OP^2=ON^2+NP^2\)
\(\Rightarrow \overrightarrow{OP}.\overrightarrow{OP}=\overrightarrow{ON}.\overrightarrow{ON}+\overrightarrow{NP}.\overrightarrow{NP}\)
\(\Rightarrow \overline{r}.\overline{r}=x\hat{i}.x\hat{i}+y\hat{j}.y\hat{j}\)
\(\Rightarrow r^2=x^2\hat{i}.\hat{i}+y^2\hat{j}.\hat{j}\) ➜ \(\because \overline{r}.\overline{r}=r^2\)
\(\Rightarrow r^2=x^2.1+y^2.1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=1\)
\(\Rightarrow r^2=x^2+y^2\)
\(\Rightarrow r=\sqrt{x^2+y^2}\)
\(\therefore\) \(r=|\overline{r}|=\sqrt{x^2+y^2}\)
অবস্থান ভেক্টর
Position Vector
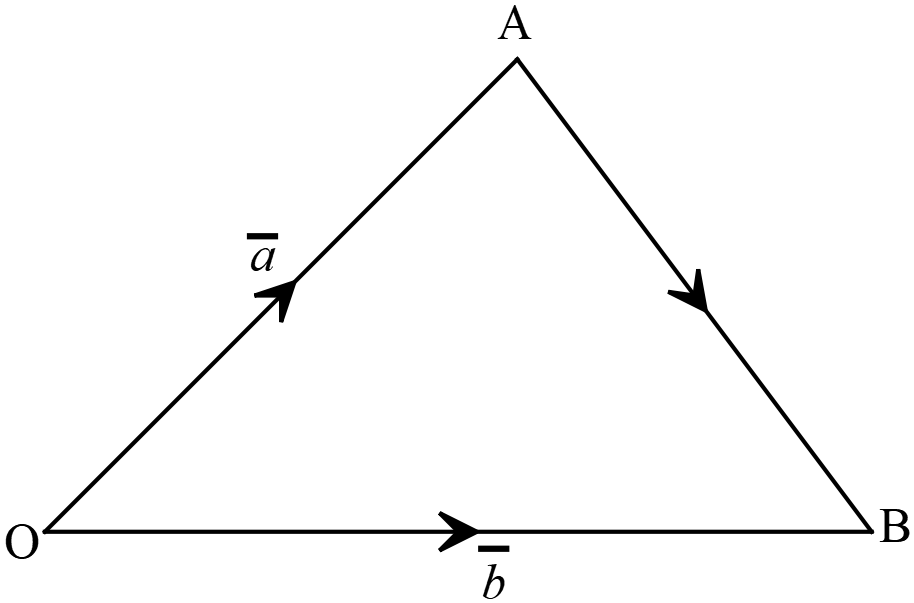অবস্থান ভেক্টরঃ প্রসঙ্গ কাঠামোর মূলবিন্দু সাপেক্ষে কোনো বিন্দুর অবস্থান যে ভেক্টরের মাধ্যমে প্রকাশ করা হয় তাকে ঐ বিন্দুর অবস্থান ভেক্টর বলে।ধরি, \(O\) মূলবিন্দু সাপেক্ষে \(A\) ও \(B\) এর অবস্থান ভেক্টর যথাক্রমে, \(\overline{a}\) ও \(\overline{b}\)
চিত্র হতে,
\(\overrightarrow{OA}=\overline{a}, \overrightarrow{OB}=\overline{b}\)
এখন, \(\triangle{OAB}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}\)
\(\Rightarrow \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\)
\(\therefore \overrightarrow{AB}=\overline{b}-\overline{a}\)
কার্তেসীয় দ্বিমাত্রিক জগতে অবস্থান ভেক্টর
Position Vector in two Dimension Space
কার্তেসীয় দ্বিমাত্রিক জগতে মূলবিন্দু \((0, 0)\) এর সাপেক্ষে \(P(x, y)\) এর অবস্থান ভেক্টর \(\overline{r}\) হলে, \(P\) বিন্দুর অবস্থান
\(\overline{r}=x\hat{i}+y\hat{j}\)
\(\overline{r}\) ভেক্টরের মাণ
Values of the vector \(\overline{r}\)
ধরি,\(P(x,y), \ M(0,y), \ N(x,0), \ \overrightarrow{OP}=\overline{r}\)
এবং অক্ষরেখাগুলি বরাবর একক ভেক্টর যথাক্রমে \(\hat{i}, \ \hat{j}\)
\(\therefore \overrightarrow{ON}=x\hat{i}, \overrightarrow{NP}=\overrightarrow{OM}=y\hat{j}\)
\(\triangle{OPN}\) সমকোণী
\(\therefore OP^2=ON^2+NP^2\)
\(\Rightarrow \overrightarrow{OP}.\overrightarrow{OP}=\overrightarrow{ON}.\overrightarrow{ON}+\overrightarrow{NP}.\overrightarrow{NP}\)
\(\Rightarrow \overline{r}.\overline{r}=x\hat{i}.x\hat{i}+y\hat{j}.y\hat{j}\)
\(\Rightarrow r^2=x^2\hat{i}.\hat{i}+y^2\hat{j}.\hat{j}\) ➜ \(\because \overline{r}.\overline{r}=r^2\)
\(\Rightarrow r^2=x^2.1+y^2.1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=1\)
\(\Rightarrow r^2=x^2+y^2\)
\(\Rightarrow r=\sqrt{x^2+y^2}\)
\(\therefore\) \(r=|\overline{r}|=\sqrt{x^2+y^2}\)
দুইটি নির্দিষ্ট বিন্দুগামী ভেক্টর
Vector through two fixed points
\(P(x_{1}, y_{1})\) \(Q(x_{2}, y_{2})\) হলে,
\(\overrightarrow{PQ}=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}\)
\(\overrightarrow{PQ}=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}\)
ভেক্টর অন্তর্বিভক্তিকরণ সূত্র
Vector Interpolation Formula
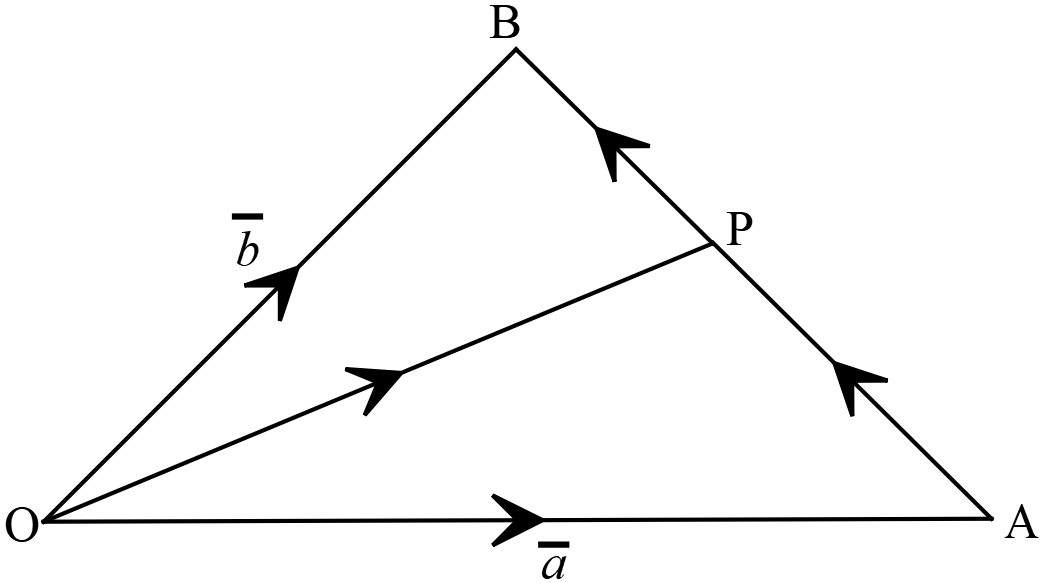\(O\) মূলবিন্দু এবং \(\overrightarrow{OA}\) ও \(\overrightarrow{OB}\) যথাক্রমে \(A\) ও \(B\) বিন্দুর অবস্থান ভেক্টর,যেখানে, \(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) এবং \(P\) বিন্দু \(AB\) রেখাংশকে \(m:n\) অনুপাতে অন্তর্বিভক্ত করে।
\(P\) বিন্দুর অবস্থান ভেক্টর,
\(\overrightarrow{OP}=\frac{m\overline{b}+n\overline{a}}{m+n}\)
ভেক্টর বহিঃর্বিভক্তিকরণ সূত্র
Vector extrinsic formula
\(O\) মূলবিন্দু এবং \(\overrightarrow{OA}\) ও \(\overrightarrow{OB}\) যথাক্রমে \(A\) ও \(B\) বিন্দুর অবস্থান ভেক্টর,
যেখানে, \(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) এবং \(P\) বিন্দু \(AB\) রেখাংশকে \(m:n\) অনুপাতে বহিঃর্বিভক্ত করে।
\(P\) বিন্দুর অবস্থান ভেক্টর,
\(\overrightarrow{OP}=\frac{m\overline{b}-n\overline{a}}{m-n}\)
যেখানে, \(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) এবং \(P\) বিন্দু \(AB\) রেখাংশকে \(m:n\) অনুপাতে বহিঃর্বিভক্ত করে।
\(P\) বিন্দুর অবস্থান ভেক্টর,
\(\overrightarrow{OP}=\frac{m\overline{b}-n\overline{a}}{m-n}\)
অনুসিদ্ধান্ত-১
Postulate-1
\(O\) মূলবিন্দু এবং \(\overrightarrow{OA}\) ও \(\overrightarrow{OB}\) যথাক্রমে \(A\) ও \(B\) বিন্দুর অবস্থান ভেক্টর,
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) এবং \(P, \ AB\) রেখাংশের মধ্যবিন্দু হলে,
\(P\) বিন্দুর অবস্থান ভেক্টর,
\(\overrightarrow{OP}=\frac{\overline{a}+\overline{b}}{2}\)
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) এবং \(P, \ AB\) রেখাংশের মধ্যবিন্দু হলে,
\(P\) বিন্দুর অবস্থান ভেক্টর,
\(\overrightarrow{OP}=\frac{\overline{a}+\overline{b}}{2}\)
অনুসিদ্ধান্ত-২
Postulate-2
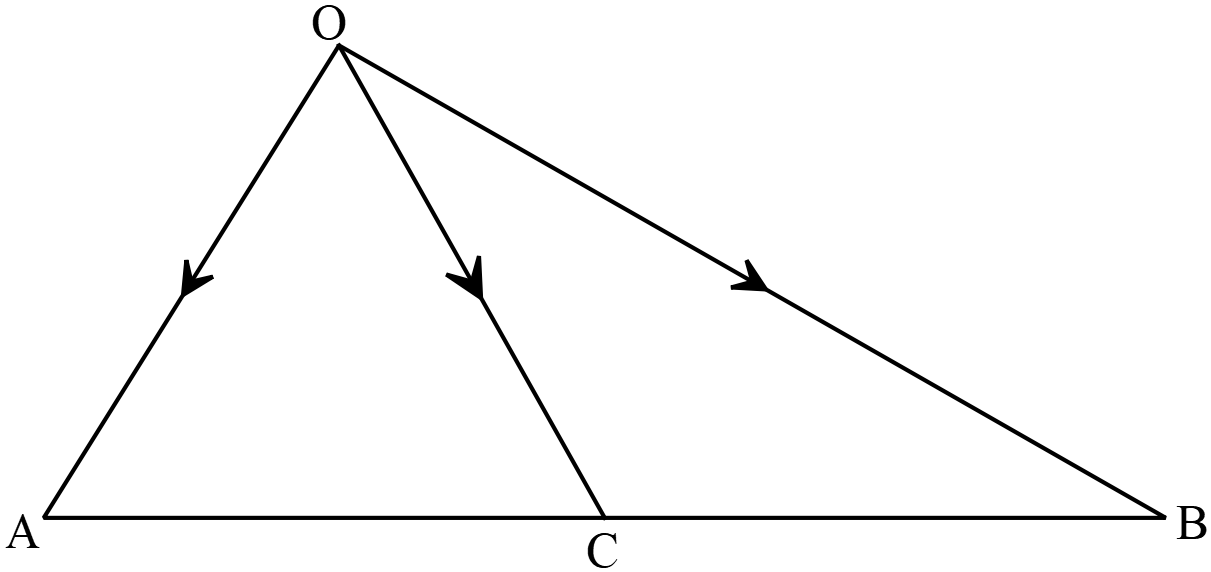\(O\) মূলবিন্দু এবং \(\overrightarrow{OA}\) ও \(\overrightarrow{OB}\) যথাক্রমে \(A\) ও \(B\) বিন্দুর অবস্থান ভেক্টর,\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) এবং \(C, \ AB\) রেখাংশের মধ্যবিন্দু হলে,
\(2\overrightarrow{OC}=(\overrightarrow{OA}+\overrightarrow{OB})\) \(\overrightarrow{OC}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})\)
ভেক্টর যোগের সামান্তরিক সূত্রঃ
কোনো সামান্তরিকের একটি কৌণিক বিন্দু থেকে অঙ্কিত সন্নিহিত বাহুদ্বয় যদি কোনো কণার উপর একই সময়ে ক্রিয়ারত দুইটি ভেক্টরের মাণ ও দিক নির্দেশ করে, তাহলে ঐ বিন্দু থেকে অঙ্কিত সামান্তরিকের কর্ণটি ভেক্টরদ্বয়ের লব্ধির মাণ ও দিক নির্দেশ করবে।
অর্থাৎ, \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\)
কোনো সামান্তরিকের একটি কৌণিক বিন্দু থেকে অঙ্কিত সন্নিহিত বাহুদ্বয় যদি কোনো কণার উপর একই সময়ে ক্রিয়ারত দুইটি ভেক্টরের মাণ ও দিক নির্দেশ করে, তাহলে ঐ বিন্দু থেকে অঙ্কিত সামান্তরিকের কর্ণটি ভেক্টরদ্বয়ের লব্ধির মাণ ও দিক নির্দেশ করবে।
অর্থাৎ, \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\)
প্রমাণঃ
ধরি,
একটি কণার উপর একই সময়ে \(\overline{P}\) ও \(\overline{Q}\) দুইটি ভেক্টর রাশি পরস্পর \(\alpha\) কোণে ক্রিয়ারত। \(AB\) এবং \(AD\) রেখাংশ দুইটি যথাক্রমে \(\overline{P}\) ও \(\overline{Q}\) এর মাণ এবং তীর চিহ্ন তাদের দিক নির্দেশ করছে।
অর্থাৎ, \(\overrightarrow{AB}=\overline{P}, \overrightarrow{AD}=\overline{Q}\)
এখানে, \(\angle{DAB}=\alpha\)
এই দুইটি ভেক্টর রাশির লব্ধি নির্ণয় করতে হবে।
\(ABCD\) সামান্তরিকটি অঙ্কন করি এবং \(A, C\) যুক্ত করি।
তাহলে \(AC\) কর্ণই ভেক্টর রাশি দুইটির লব্ধির মাণ ও দিক নির্দেশ করবে।
এখানে, \(\overrightarrow{AD}=\overrightarrow{BC}=\overline{Q}\)
এখান, \(\triangle{ABC}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
\(\Rightarrow \overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\)
\(\therefore\ \overline{R}=\overline{P}+\overline{Q}\)
\(\therefore AC\) কর্ণই ভেক্টর রাশি দুইটির লব্ধির মাণ ও দিক নির্দেশ করে।
একটি কণার উপর একই সময়ে \(\overline{P}\) ও \(\overline{Q}\) দুইটি ভেক্টর রাশি পরস্পর \(\alpha\) কোণে ক্রিয়ারত। \(AB\) এবং \(AD\) রেখাংশ দুইটি যথাক্রমে \(\overline{P}\) ও \(\overline{Q}\) এর মাণ এবং তীর চিহ্ন তাদের দিক নির্দেশ করছে।
অর্থাৎ, \(\overrightarrow{AB}=\overline{P}, \overrightarrow{AD}=\overline{Q}\)
এখানে, \(\angle{DAB}=\alpha\)
এই দুইটি ভেক্টর রাশির লব্ধি নির্ণয় করতে হবে।
\(ABCD\) সামান্তরিকটি অঙ্কন করি এবং \(A, C\) যুক্ত করি।
তাহলে \(AC\) কর্ণই ভেক্টর রাশি দুইটির লব্ধির মাণ ও দিক নির্দেশ করবে।
এখানে, \(\overrightarrow{AD}=\overrightarrow{BC}=\overline{Q}\)
এখান, \(\triangle{ABC}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
\(\Rightarrow \overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\)
\(\therefore\ \overline{R}=\overline{P}+\overline{Q}\)
\(\therefore AC\) কর্ণই ভেক্টর রাশি দুইটির লব্ধির মাণ ও দিক নির্দেশ করে।
ভেক্টর যোগের বহুভুজ সূত্রঃ
দুইয়ের অধিক ভেক্টরের ক্ষেত্রে একই ক্রমে ভেক্টরগুলিকে সাজিয়ে প্রথম ভেক্টরের প্রারম্ভিকবিন্দু এবং শেষ ভেক্টরের প্রান্তবিন্দু যোগ করে একটি বহুভুজ অঙ্কন করলে বহুভুজের শেষ বাহুটি বিপরীতক্রমে ভেক্টরগুলির লব্ধির মাণ ও দিক নির্দেশ করবে।
অর্থাৎ , \(\therefore \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{AE}\)
দুইয়ের অধিক ভেক্টরের ক্ষেত্রে একই ক্রমে ভেক্টরগুলিকে সাজিয়ে প্রথম ভেক্টরের প্রারম্ভিকবিন্দু এবং শেষ ভেক্টরের প্রান্তবিন্দু যোগ করে একটি বহুভুজ অঙ্কন করলে বহুভুজের শেষ বাহুটি বিপরীতক্রমে ভেক্টরগুলির লব্ধির মাণ ও দিক নির্দেশ করবে।
অর্থাৎ , \(\therefore \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{AE}\)
প্রমাণঃ
ধরি,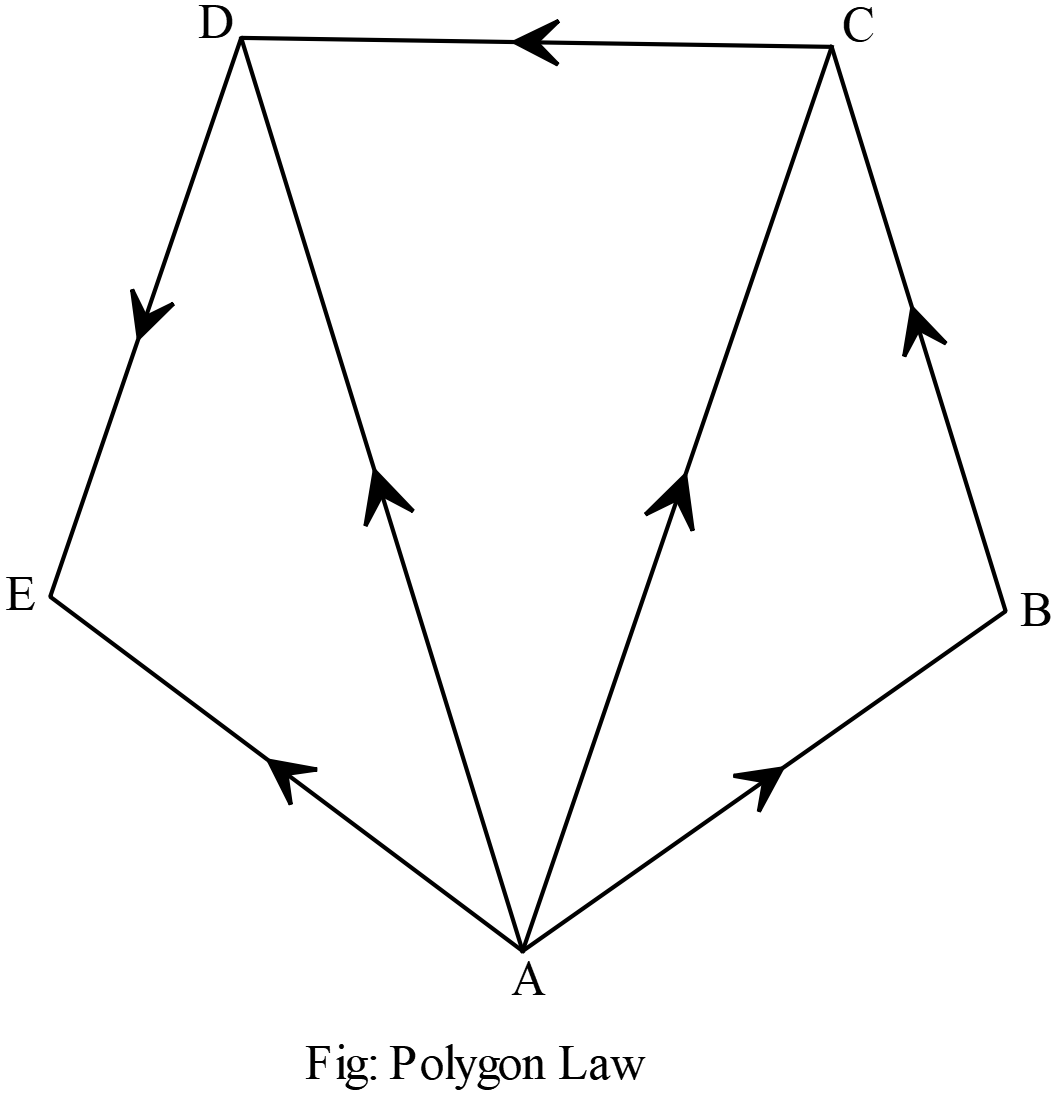
একটি কণার উপর একই সময়ে ক্রিয়ারত ভেক্টরগুলির মাণ ও দিক যথাক্রমে \(ABCDE\) বহুভুজের বাহু \(\overrightarrow{AB}, \overrightarrow{BC}, \overrightarrow{CD}\) ও \(\overrightarrow{DE}\) বরাবর নির্দেশ করে।
প্রমাণ করতে হবে যে,
\(\therefore \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{AE}\)
\(ABCDE\) বহুভুজে \(A, C\) এবং \(A, D\) যোগ করি,
এখন, \(\triangle{ABC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC} .........(1)\)
অনুরূপভাবে, \(\triangle{ACD}\) ও \(\triangle{ADE}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD} .........(2)\)
\(\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AE} .........(3)\)
\((1)\) হতে \(\overrightarrow{AC}\) এর মাণ \((2)\) এ বসিয়ে,
\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AD} .........(4)\)
\((4)\) হতে \(\overrightarrow{AD}\) এর মাণ \((3)\) এ বসিয়ে,
\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{AE}\)
( প্রমাণিত )
একটি কণার উপর একই সময়ে ক্রিয়ারত ভেক্টরগুলির মাণ ও দিক যথাক্রমে \(ABCDE\) বহুভুজের বাহু \(\overrightarrow{AB}, \overrightarrow{BC}, \overrightarrow{CD}\) ও \(\overrightarrow{DE}\) বরাবর নির্দেশ করে। প্রমাণ করতে হবে যে,
\(\therefore \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{AE}\)
\(ABCDE\) বহুভুজে \(A, C\) এবং \(A, D\) যোগ করি,
এখন, \(\triangle{ABC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC} .........(1)\)
অনুরূপভাবে, \(\triangle{ACD}\) ও \(\triangle{ADE}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD} .........(2)\)
\(\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AE} .........(3)\)
\((1)\) হতে \(\overrightarrow{AC}\) এর মাণ \((2)\) এ বসিয়ে,
\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AD} .........(4)\)
\((4)\) হতে \(\overrightarrow{AD}\) এর মাণ \((3)\) এ বসিয়ে,
\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{AE}\)
( প্রমাণিত )
দুইটি ভেক্টরের বিয়োগঃ
ভেক্টরের বিয়োগের ক্ষেত্রে যে ভেক্টর বিয়োগ করতে হবে তার ঋণাত্মক ভেক্টরকে অপর ভেক্টরের সাথে যোগ করলেই বিয়োগফল পাওয়া যায়।
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) দুইটি ভেক্টর।
এদের বিয়োগফল হবে,
\(\overrightarrow{BA}=\overline{a}-\overline{b}\)
অথবা,
\(\overrightarrow{AB}=\overline{b}-\overline{a}\)
ভেক্টরের বিয়োগের ক্ষেত্রে যে ভেক্টর বিয়োগ করতে হবে তার ঋণাত্মক ভেক্টরকে অপর ভেক্টরের সাথে যোগ করলেই বিয়োগফল পাওয়া যায়।
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) দুইটি ভেক্টর।
এদের বিয়োগফল হবে,
\(\overrightarrow{BA}=\overline{a}-\overline{b}\)
অথবা,
\(\overrightarrow{AB}=\overline{b}-\overline{a}\)
প্রমাণঃ
দেওয়া আছে,
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) দুইটি ভেক্টর।
\(A, B\) যোগ করি,
এখন, \(\triangle{OAB}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OB}+\overrightarrow{BA}=\overrightarrow{OA}\)
\(\Rightarrow \overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}\)
\(\therefore\ \overrightarrow{BA}=\overline{a}-\overline{b}\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{OB}=\overline{b}\)
আবার,
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) দুইটি ভেক্টর।
\(A, B\) যোগ করি,
এখন, \(\triangle{OAB}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}\)
\(\Rightarrow \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\)
\(\therefore\ \overrightarrow{AB}=\overline{b}-\overline{a}\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{OB}=\overline{b}\)
( প্রমাণিত )
দ্রঃ ভেক্টরদ্বয়ের প্রান্তবিন্দুর সংযোগ রেখাংশ দ্বারা তাদের বিয়োগফল প্রকাশিত হয়। প্রথম ভেক্টরের প্রান্তবিন্দু পরে এবং দ্বিতীয় ভেক্টরের প্রান্তবিন্দু প্রথমে হয়।
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) দুইটি ভেক্টর। \(A, B\) যোগ করি,
এখন, \(\triangle{OAB}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OB}+\overrightarrow{BA}=\overrightarrow{OA}\)
\(\Rightarrow \overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}\)
\(\therefore\ \overrightarrow{BA}=\overline{a}-\overline{b}\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{OB}=\overline{b}\)
আবার,
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) দুইটি ভেক্টর। \(A, B\) যোগ করি,
এখন, \(\triangle{OAB}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}\)
\(\Rightarrow \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\)
\(\therefore\ \overrightarrow{AB}=\overline{b}-\overline{a}\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{OB}=\overline{b}\)
( প্রমাণিত )
দ্রঃ ভেক্টরদ্বয়ের প্রান্তবিন্দুর সংযোগ রেখাংশ দ্বারা তাদের বিয়োগফল প্রকাশিত হয়। প্রথম ভেক্টরের প্রান্তবিন্দু পরে এবং দ্বিতীয় ভেক্টরের প্রান্তবিন্দু প্রথমে হয়।
ভেক্টর যোগের এবং স্কেলার গুণিতক গঠনের মৌলিক বিধিগুলো নিম্নে তালিকা আকারে দেওয়া হলো। এখানে, \(\overline{a}, \overline{b}, \ \overline{c}\) যে কোনো ভেক্টর এবং \(m, \ n\) কে স্কেলার হিসেবে বিবেচনা করা হয়েছে।
\(\overline{a}+\overline{b}=\overline{b}+\overline{a}\) ( যোগের বিনিময় বিধি )
\(\overline{a}+\overline{b}=\overline{b}+\overline{a}\) ( যোগের বিনিময় বিধি )
প্রমাণঃ
ধরি,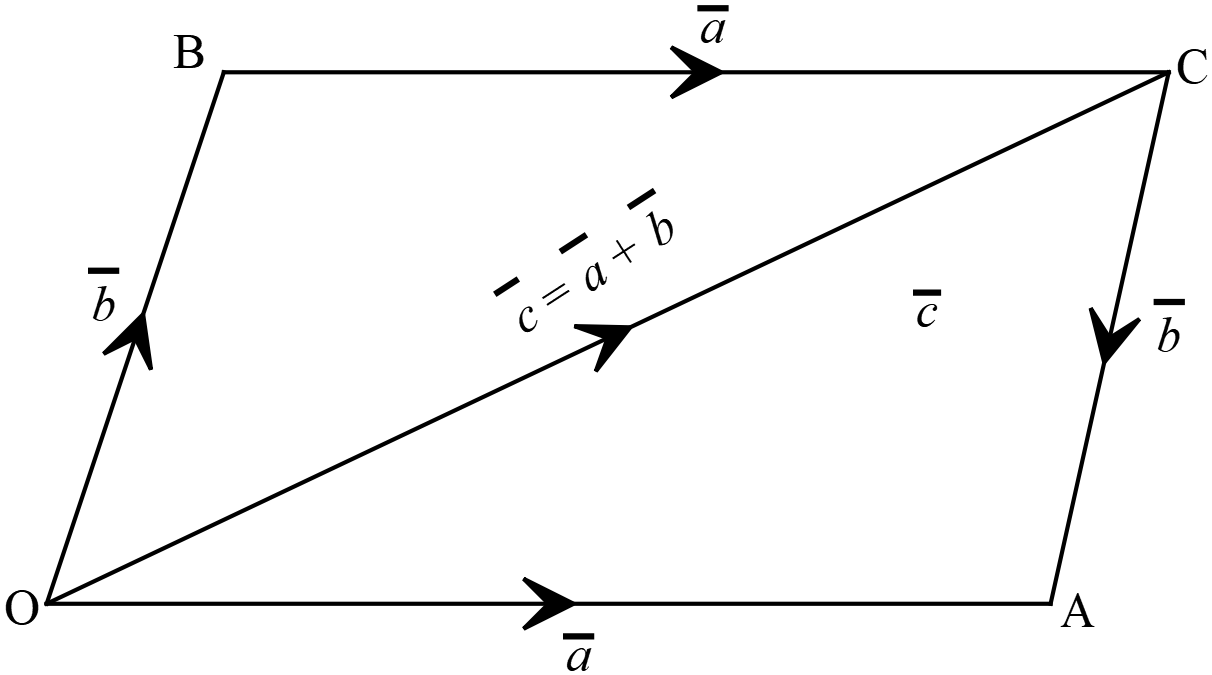
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) দুইটি ভেক্টর \(O\) বিন্দুতে ক্রিয়ারত।
\(OACB\) সামান্তরিকটি অঙ্কন করি,
\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}\) সামান্তরিক সূত্র মতে,
\(\therefore \overline{a}+\overline{b}=\overline{c}\)
\(OA\) এবং \(BC\) সামান এবং সমান্তরাল,
\(\therefore \overrightarrow{OA}=\overrightarrow{BC}=\overline{a}\)
আবার, \(OB\) এবং \(AC\) সামান এবং সমান্তরাল,
\(\therefore \overrightarrow{OB}=\overrightarrow{AC}=\overline{b}\)
এখন, \(\triangle{OAC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OC}\)
\(\therefore \overline{a}+\overline{b}=\overline{c} ....(1)\)
আবার, \(\triangle{OBC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OB}+\overrightarrow{BC}=\overrightarrow{OC}\)
\(\therefore \overline{b}+\overline{a}=\overline{c} ...(2)\)
\((1)\) ও \((2)\) হতে,
\(\overline{a}+\overline{b}=\overline{b}+\overline{a}\)
( প্রমাণিত )
\(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) দুইটি ভেক্টর \(O\) বিন্দুতে ক্রিয়ারত। \(OACB\) সামান্তরিকটি অঙ্কন করি,
\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}\) সামান্তরিক সূত্র মতে,
\(\therefore \overline{a}+\overline{b}=\overline{c}\)
\(OA\) এবং \(BC\) সামান এবং সমান্তরাল,
\(\therefore \overrightarrow{OA}=\overrightarrow{BC}=\overline{a}\)
আবার, \(OB\) এবং \(AC\) সামান এবং সমান্তরাল,
\(\therefore \overrightarrow{OB}=\overrightarrow{AC}=\overline{b}\)
এখন, \(\triangle{OAC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OC}\)
\(\therefore \overline{a}+\overline{b}=\overline{c} ....(1)\)
আবার, \(\triangle{OBC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OB}+\overrightarrow{BC}=\overrightarrow{OC}\)
\(\therefore \overline{b}+\overline{a}=\overline{c} ...(2)\)
\((1)\) ও \((2)\) হতে,
\(\overline{a}+\overline{b}=\overline{b}+\overline{a}\)
( প্রমাণিত )
ভেক্টর যোগের এবং স্কেলার গুণিতক গঠনের মৌলিক বিধিগুলো নিম্নে তালিকা আকারে দেওয়া হলো। এখানে, \(\overline{a}, \overline{b}, \ \overline{c}\) যে কোনো ভেক্টর এবং \(m, \ n\) কে স্কেলার হিসেবে বিবেচনা করা হয়েছে।
\(\overline{a}+(\overline{b}+\overline{c})=(\overline{a}+\overline{b})+\overline{c}\) ( যোগের সংযোগ বিধি )
\(\overline{a}+(\overline{b}+\overline{c})=(\overline{a}+\overline{b})+\overline{c}\) ( যোগের সংযোগ বিধি )
প্রমাণঃ
ধরি,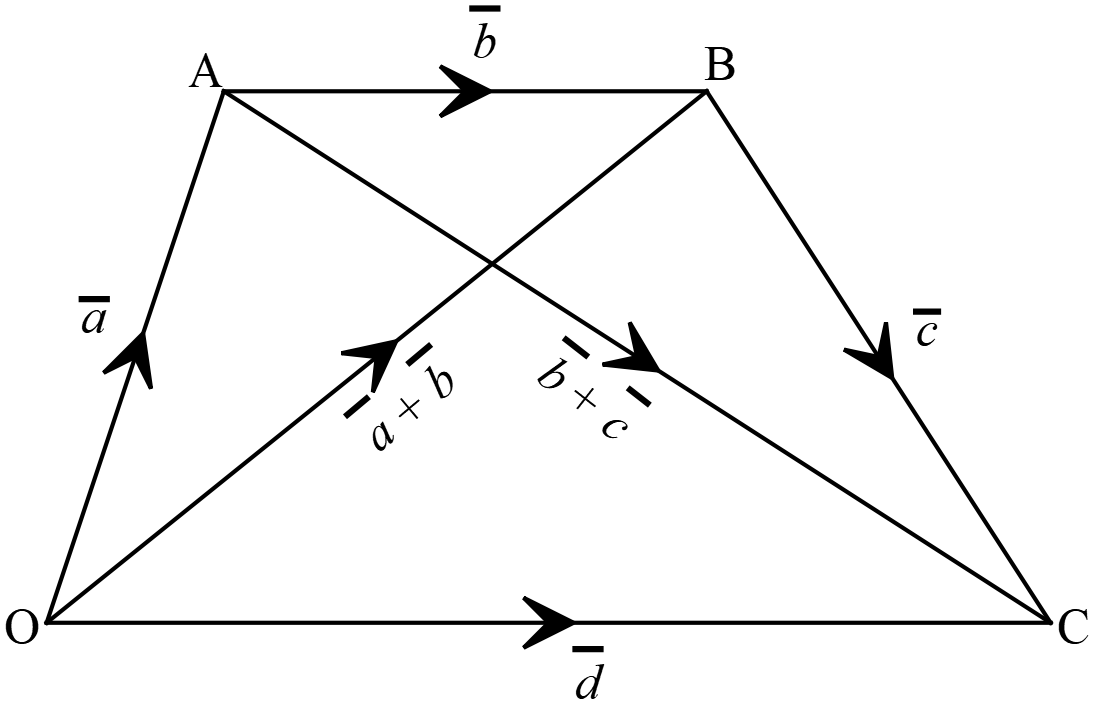
\(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{AB}=\overline{b}, \ \overrightarrow{BC}=\overline{c}\) এবং \(\overrightarrow{OC}=\overline{d}\)
\(OABC\) চতুর্ভুজটি অঙ্কন করি,
\(O, B\) এবং \(A, C\) সংযোগ করি,
এখন, \(\triangle{OAB}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}\)
\(\therefore \overrightarrow{OB}=\overline{a}+\overline{b} ....(1)\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{AB}=\overline{b}\)
আবার, \(\triangle{ABC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\)
\(\therefore \overrightarrow{AC}=\overline{b}+\overline{c} ...(2)\) ➜ \(\because \overrightarrow{AB}=\overline{b}\)
এবং \(\overrightarrow{BC}=\overline{c}\)
আবার, \(\triangle{OAC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}\)
\(\therefore \overline{d}=\overline{a}+(\overline{b}+\overline{c}) ...(3)\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{AC}=\overline{b}+\overline{c}\)
আবার, \(\triangle{OBC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{BC}\)
\(\therefore \overline{d}=(\overline{a}+\overline{b})+\overline{c} ...(4)\) ➜ \(\because \overrightarrow{OB}=\overline{a}+\overline{b}\)
এবং \(\overrightarrow{BC}=\overline{c}\)
\((3)\) ও \((4)\) হতে,
\(\overline{a}+(\overline{b}+\overline{c})=(\overline{a}+\overline{b})+\overline{c}\)
( প্রমাণিত )
\(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{AB}=\overline{b}, \ \overrightarrow{BC}=\overline{c}\) এবং \(\overrightarrow{OC}=\overline{d}\)\(OABC\) চতুর্ভুজটি অঙ্কন করি,
\(O, B\) এবং \(A, C\) সংযোগ করি,
এখন, \(\triangle{OAB}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}\)
\(\therefore \overrightarrow{OB}=\overline{a}+\overline{b} ....(1)\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{AB}=\overline{b}\)
আবার, \(\triangle{ABC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\)
\(\therefore \overrightarrow{AC}=\overline{b}+\overline{c} ...(2)\) ➜ \(\because \overrightarrow{AB}=\overline{b}\)
এবং \(\overrightarrow{BC}=\overline{c}\)
আবার, \(\triangle{OAC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}\)
\(\therefore \overline{d}=\overline{a}+(\overline{b}+\overline{c}) ...(3)\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{AC}=\overline{b}+\overline{c}\)
আবার, \(\triangle{OBC}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{BC}\)
\(\therefore \overline{d}=(\overline{a}+\overline{b})+\overline{c} ...(4)\) ➜ \(\because \overrightarrow{OB}=\overline{a}+\overline{b}\)
এবং \(\overrightarrow{BC}=\overline{c}\)
\((3)\) ও \((4)\) হতে,
\(\overline{a}+(\overline{b}+\overline{c})=(\overline{a}+\overline{b})+\overline{c}\)
( প্রমাণিত )
ভেক্টর যোগের এবং স্কেলার গুণিতক গঠনের মৌলিক বিধিগুলো নিম্নে তালিকা আকারে দেওয়া হলো। এখানে, \(\overline{a}, \overline{b}\) যে কোনো ভেক্টর এবং \(m\) কে স্কেলার হিসেবে বিবেচনা করা হয়েছে।
\(m\overline{a}=\overline{a}m\) ( গুণের বিনিময় বিধি )
\(m\overline{a}=\overline{a}m\) ( গুণের বিনিময় বিধি )
প্রমাণঃ
ধরি,
\(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(O, A, P\) একই সরলরেখায় অবস্থিত
এখন, \(OP=OA+AP\)
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}\) ভেক্টর চিহ্ন ব্যবহার করে।
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}+m_{1}\overrightarrow{OA}\) ➜ \(\because \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(\Rightarrow \overrightarrow{OP}=(1+m_{1})\overrightarrow{OA}\)
\(\therefore \overrightarrow{OP}=m\overline{a} .....(1)\) ➜ যেখানে, \(m=1+m_{1}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
আবার, \(OP=OA+AP\)
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}\) ভেক্টর চিহ্ন ব্যবহার করে।
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}+m_{1}\overrightarrow{OA}\) ➜ \(\because \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}(1+m_{1})\)
\(\therefore \overrightarrow{OP}=\overline{a}m .....(2)\) ➜ যেখানে, \(m=1+m_{1}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
\((1)\) ও \((2)\) হতে,
\(m\overline{a}=\overline{a}m\)
( প্রমাণিত )
\(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)\(O, A, P\) একই সরলরেখায় অবস্থিত
এখন, \(OP=OA+AP\)
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}\) ভেক্টর চিহ্ন ব্যবহার করে।
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}+m_{1}\overrightarrow{OA}\) ➜ \(\because \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(\Rightarrow \overrightarrow{OP}=(1+m_{1})\overrightarrow{OA}\)
\(\therefore \overrightarrow{OP}=m\overline{a} .....(1)\) ➜ যেখানে, \(m=1+m_{1}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
আবার, \(OP=OA+AP\)
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}\) ভেক্টর চিহ্ন ব্যবহার করে।
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}+m_{1}\overrightarrow{OA}\) ➜ \(\because \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(\Rightarrow \overrightarrow{OP}=\overrightarrow{OA}(1+m_{1})\)
\(\therefore \overrightarrow{OP}=\overline{a}m .....(2)\) ➜ যেখানে, \(m=1+m_{1}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
\((1)\) ও \((2)\) হতে,
\(m\overline{a}=\overline{a}m\)
( প্রমাণিত )
ভেক্টর যোগের এবং স্কেলার গুণিতক গঠনের মৌলিক বিধিগুলো নিম্নে তালিকা আকারে দেওয়া হলো। এখানে, \(\overline{a}, \overline{b}\) যে কোনো ভেক্টর এবং \(m, \ n\) কে স্কেলার হিসেবে বিবেচনা করা হয়েছে।
\(m(n\overline{a})=(mn)\overline{a}\) ( গুণের সংযোগ বিধি )
\(m(n\overline{a})=(mn)\overline{a}\) ( গুণের সংযোগ বিধি )
প্রমাণঃ
ধরি,
\(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(O, A, P\) একই সরলরেখায় অবস্থিত
এখন, \(OP=OA+AP\)
\(\Rightarrow nOP=nOA+nAP\)
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}+n\overrightarrow{AP}\) ভেক্টর চিহ্ন ব্যবহার করে।
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}+m_{1}n\overrightarrow{OA}\) ➜ \(\because \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(\Rightarrow n\overrightarrow{OP}=(1+m_{1})n\overrightarrow{OA}\)
\(\therefore n\overrightarrow{OP}=(mn)\overline{a} .....(1)\) ➜ যেখানে, \(m=1+m_{1}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
আবার, \(OP=OA+AP\)
\(\Rightarrow nOP=nOA+nAP\)
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}+n\overrightarrow{AP}\) ভেক্টর চিহ্ন ব্যবহার করে।
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}+m_{1}n\overrightarrow{OA}\) ➜ \(\because \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}(1+m_{1})\)
\(\Rightarrow n\overrightarrow{OP}=(n\overline{a})(1+m_{1})\)
\(\Rightarrow n\overrightarrow{OP}=(1+m_{1})(n\overline{a})\)
\(\therefore \overrightarrow{OP}=m(n\overline{a}) .....(2)\) ➜ যেখানে, \(m=1+m_{1}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
\((1)\) ও \((2)\) হতে,
\((mn)\overline{a}=m(n\overline{a})\)
( প্রমাণিত )
\(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)\(O, A, P\) একই সরলরেখায় অবস্থিত
এখন, \(OP=OA+AP\)
\(\Rightarrow nOP=nOA+nAP\)
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}+n\overrightarrow{AP}\) ভেক্টর চিহ্ন ব্যবহার করে।
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}+m_{1}n\overrightarrow{OA}\) ➜ \(\because \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(\Rightarrow n\overrightarrow{OP}=(1+m_{1})n\overrightarrow{OA}\)
\(\therefore n\overrightarrow{OP}=(mn)\overline{a} .....(1)\) ➜ যেখানে, \(m=1+m_{1}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
আবার, \(OP=OA+AP\)
\(\Rightarrow nOP=nOA+nAP\)
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}+n\overrightarrow{AP}\) ভেক্টর চিহ্ন ব্যবহার করে।
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}+m_{1}n\overrightarrow{OA}\) ➜ \(\because \overrightarrow{AP}=m_{1}\overrightarrow{OA}\)
\(\Rightarrow n\overrightarrow{OP}=n\overrightarrow{OA}(1+m_{1})\)
\(\Rightarrow n\overrightarrow{OP}=(n\overline{a})(1+m_{1})\)
\(\Rightarrow n\overrightarrow{OP}=(1+m_{1})(n\overline{a})\)
\(\therefore \overrightarrow{OP}=m(n\overline{a}) .....(2)\) ➜ যেখানে, \(m=1+m_{1}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
\((1)\) ও \((2)\) হতে,
\((mn)\overline{a}=m(n\overline{a})\)
( প্রমাণিত )
ভেক্টর যোগের এবং স্কেলার গুণিতক গঠনের মৌলিক বিধিগুলো নিম্নে তালিকা আকারে দেওয়া হলো। এখানে, \(\overline{a}, \overline{b}, \ \overline{c}\) যে কোনো ভেক্টর এবং \(m, \ n\) কে স্কেলার হিসেবে বিবেচনা করা হয়েছে।
\(m(\overline{a}+\overline{a})=m\overline{a}+m\overline{b}\) ( বন্টন বিধি )
\(m(\overline{a}+\overline{a})=m\overline{a}+m\overline{b}\) ( বন্টন বিধি )
প্রমাণঃ
ধরি,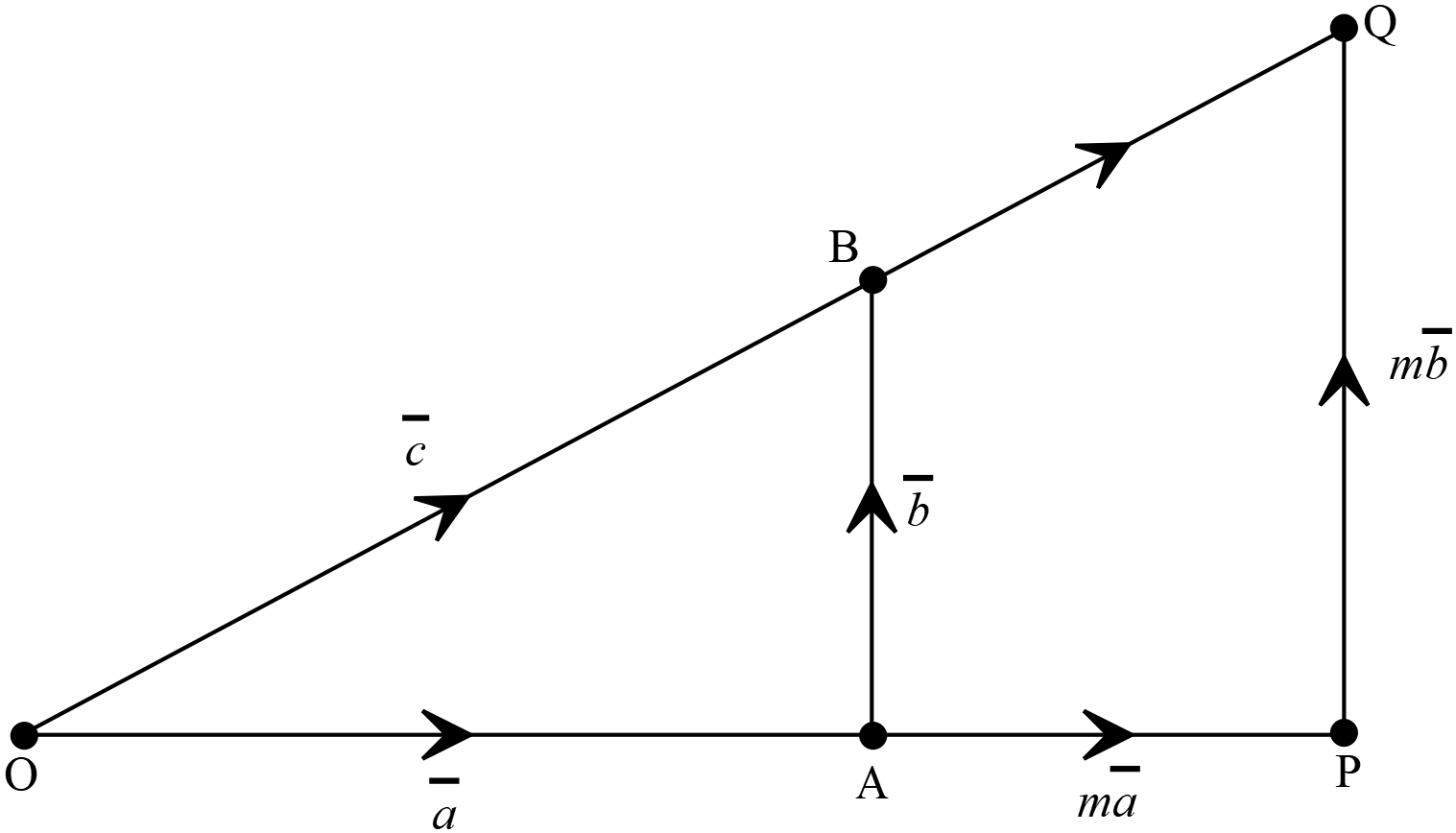
\(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{AB}=\overline{b}, \ \overrightarrow{OB}=\overline{c}\)
এখন, \(\triangle{OAB}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}\)
\(\therefore \overline{c}=\overline{a}+\overline{b} ....(1)\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
\(\overrightarrow{AB}=\overline{b}\)
এবং \(\overrightarrow{OB}=\overline{c}\)
আবার ধরি, \(\overrightarrow{OP}=m\overrightarrow{OA}=m\overline{a}\)
\(AB\parallel{PQ}\) আঁকি, যেন বর্ধিত \(OB\) রেখা \(PQ\) কে \(Q\) বিন্দুতে ছেদ করে।
\(O, B, Q\) একই সরলরেখা \(OQ\) তে অবস্থিত। সদৃশ \(\triangle{OAB}\) ও \(\triangle{OPQ}\) থেকে,
\(\frac{AB}{PQ}=\frac{OA}{OP}\)
\(\Rightarrow \frac{AB}{PQ}=\frac{OA}{mOA}\) ➜ \(\because \overrightarrow{OP}=m\overrightarrow{OA}\)
\(\Rightarrow \frac{AB}{PQ}=\frac{1}{m}\)
\(\Rightarrow PQ=mAB\)
\(\therefore \overrightarrow{PQ}=m\overrightarrow{AB}\)
অনুরূপভাবে, \(\overrightarrow{OQ}=m\overrightarrow{OB}\)
আবার, \(\triangle{OPQ}\) থেকে,
\(\overrightarrow{OQ}=\overrightarrow{OP}+\overrightarrow{PQ}\)
\(\Rightarrow m\overrightarrow{OB}=m\overrightarrow{OA}+m\overrightarrow{AB}\) ➜ \(\because \overrightarrow{OQ}=m\overrightarrow{OB}\)
এবং \(\overrightarrow{PQ}=m\overrightarrow{AB}\)
\(\Rightarrow m\overline{c}=m\overline{a}+m\overline{b}\)
\(\therefore m(\overline{a}+\overline{b})=m\overline{a}+m\overline{b}\) ➜ \(\because \overline{c}=\overline{a}+\overline{b}\)
( প্রমাণিত )
\(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{AB}=\overline{b}, \ \overrightarrow{OB}=\overline{c}\)এখন, \(\triangle{OAB}\) ত্রিভুজে ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}\)
\(\therefore \overline{c}=\overline{a}+\overline{b} ....(1)\) ➜ \(\because \overrightarrow{OA}=\overline{a}\)
\(\overrightarrow{AB}=\overline{b}\)
এবং \(\overrightarrow{OB}=\overline{c}\)
আবার ধরি, \(\overrightarrow{OP}=m\overrightarrow{OA}=m\overline{a}\)
\(AB\parallel{PQ}\) আঁকি, যেন বর্ধিত \(OB\) রেখা \(PQ\) কে \(Q\) বিন্দুতে ছেদ করে।
\(O, B, Q\) একই সরলরেখা \(OQ\) তে অবস্থিত। সদৃশ \(\triangle{OAB}\) ও \(\triangle{OPQ}\) থেকে,
\(\frac{AB}{PQ}=\frac{OA}{OP}\)
\(\Rightarrow \frac{AB}{PQ}=\frac{OA}{mOA}\) ➜ \(\because \overrightarrow{OP}=m\overrightarrow{OA}\)
\(\Rightarrow \frac{AB}{PQ}=\frac{1}{m}\)
\(\Rightarrow PQ=mAB\)
\(\therefore \overrightarrow{PQ}=m\overrightarrow{AB}\)
অনুরূপভাবে, \(\overrightarrow{OQ}=m\overrightarrow{OB}\)
আবার, \(\triangle{OPQ}\) থেকে,
\(\overrightarrow{OQ}=\overrightarrow{OP}+\overrightarrow{PQ}\)
\(\Rightarrow m\overrightarrow{OB}=m\overrightarrow{OA}+m\overrightarrow{AB}\) ➜ \(\because \overrightarrow{OQ}=m\overrightarrow{OB}\)
এবং \(\overrightarrow{PQ}=m\overrightarrow{AB}\)
\(\Rightarrow m\overline{c}=m\overline{a}+m\overline{b}\)
\(\therefore m(\overline{a}+\overline{b})=m\overline{a}+m\overline{b}\) ➜ \(\because \overline{c}=\overline{a}+\overline{b}\)
( প্রমাণিত )
যদি, \(\overline{a}\) এবং \(\overline{b}\) দুইটি অসম ভেক্টর হয়, তবে \(\overline{a}\) ও \(\overline{b}\) এর সমতলে যে কোনো ভেক্টর \(\overline{r}\) কে \(\overline{a}\) ও \(\overline{b}\) এর যোগাশ্রয়ী সমাবেশ এককভাবে প্রকাশ করা যাবে।
অর্থাৎ , \(\overline{r}=m\overline{a}+n\overline{b}\)
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=m\overline{a}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=n\overline{b}\)
অর্থাৎ , \(\overline{r}=m\overline{a}+n\overline{b}\)
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=m\overline{a}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=n\overline{b}\)
প্রমাণঃ
ধরি,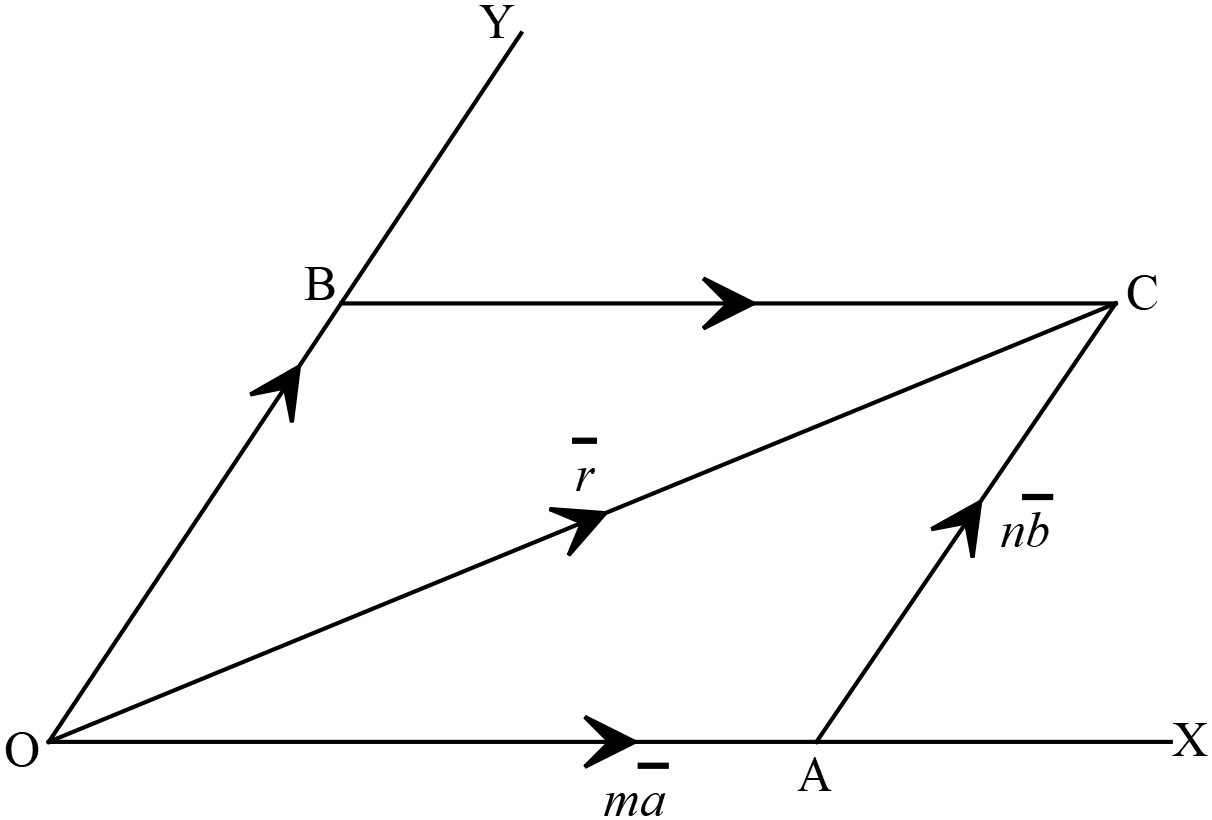
\(OA, OB, OC\) তিনটি রেখা একই সমতলে অবস্থান করে \(O\) বিন্দুতে ছেদ করে এবং \(OX\) বরাবর একটি ভেক্টর \(\overline{a}, \ OY\) বরাবর একটি ভেক্টর \(\overline{b}\) এবং \(\overrightarrow{OC}=\overline{r}\)
যেখানে, \(OACB\) সামান্তরিকের কর্ণ \(OC\) এবং \(OA\) ও \(OB\) সন্নিহিত দুইটি বাহু।
সুতরাং, দুইটি স্কেলার \(m\) ও \(n\) এর জন্য
\(\overrightarrow{OA}=m\overline{a}\) ও \(\overrightarrow{OB}=\overrightarrow{AC}=n\overline{b}\)
\(OACB\) সামান্তরিক হতে,
\(\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}\)
\(\therefore \overline{r}=m\overline{a}+n\overline{b}\)
( প্রমাণিত )
যেহেতু, \(\overline{a}\) ও \(\overline{b}\) বরাবর সন্নিহিত বাহু দ্বারা একটি মাত্র সামান্তরিক অঙ্কন করা যায়, যার কর্ণ \(\overrightarrow{OC},\) সুতরাং ইহা স্পষ্ট যে, \(\overline{r}\) কে এককভাবে বিশ্লেষণ করা যায়।
এখানে,
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=m\overline{a}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=n\overline{b}\)
\(OA, OB, OC\) তিনটি রেখা একই সমতলে অবস্থান করে \(O\) বিন্দুতে ছেদ করে এবং \(OX\) বরাবর একটি ভেক্টর \(\overline{a}, \ OY\) বরাবর একটি ভেক্টর \(\overline{b}\) এবং \(\overrightarrow{OC}=\overline{r}\)যেখানে, \(OACB\) সামান্তরিকের কর্ণ \(OC\) এবং \(OA\) ও \(OB\) সন্নিহিত দুইটি বাহু।
সুতরাং, দুইটি স্কেলার \(m\) ও \(n\) এর জন্য
\(\overrightarrow{OA}=m\overline{a}\) ও \(\overrightarrow{OB}=\overrightarrow{AC}=n\overline{b}\)
\(OACB\) সামান্তরিক হতে,
\(\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}\)
\(\therefore \overline{r}=m\overline{a}+n\overline{b}\)
( প্রমাণিত )
যেহেতু, \(\overline{a}\) ও \(\overline{b}\) বরাবর সন্নিহিত বাহু দ্বারা একটি মাত্র সামান্তরিক অঙ্কন করা যায়, যার কর্ণ \(\overrightarrow{OC},\) সুতরাং ইহা স্পষ্ট যে, \(\overline{r}\) কে এককভাবে বিশ্লেষণ করা যায়।
এখানে,
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=m\overline{a}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=n\overline{b}\)
কার্তেসীয় দ্বিমাত্রিক জগতে মূলবিন্দু \((0, 0)\) এর সাপেক্ষে \(P(x, y)\) এর অবস্থান ভেক্টর \(\overline{r}\) হলে,
\(P\) বিন্দুর অবস্থান ভেক্টর \(\overline{r}=x\hat{i}+y\hat{j}\)
\(P\) বিন্দুর অবস্থান ভেক্টর \(\overline{r}=x\hat{i}+y\hat{j}\)
প্রমাণঃ
ধরি,
কার্তেসীয় সমতলে \(P\) বিন্দুর কার্তেসীয় স্থানাঙ্ক \((x, y)\) এবং মূলবিন্দু \((0, 0), x\) ও \(y\) অক্ষের ধনাত্মক দিকে একক ভেক্টর যথাক্রমে \(\hat{i}\) ও \(\hat{j}\)
এবং \(\overrightarrow{OP}=\overline{r}\)
এখানে, \(PN\perp{OX}\) এবং \(PM\perp{OY}\)
তাহলে, \(\overrightarrow{ON}=x\hat{i}\) এবং \(\overrightarrow{NP}=\overrightarrow{OM}=y\hat{j}\)
এখন, \(\triangle{PON}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{ON}+\overrightarrow{NP}\)
\(\therefore\) \(\overline{r}=x\hat{i}+y\hat{j}\)
কার্তেসীয় সমতলে \(P\) বিন্দুর কার্তেসীয় স্থানাঙ্ক \((x, y)\) এবং মূলবিন্দু \((0, 0), x\) ও \(y\) অক্ষের ধনাত্মক দিকে একক ভেক্টর যথাক্রমে \(\hat{i}\) ও \(\hat{j}\)এবং \(\overrightarrow{OP}=\overline{r}\)
এখানে, \(PN\perp{OX}\) এবং \(PM\perp{OY}\)
তাহলে, \(\overrightarrow{ON}=x\hat{i}\) এবং \(\overrightarrow{NP}=\overrightarrow{OM}=y\hat{j}\)
এখন, \(\triangle{PON}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{ON}+\overrightarrow{NP}\)
\(\therefore\) \(\overline{r}=x\hat{i}+y\hat{j}\)
\(O\) মূলবিন্দু এবং \(\overrightarrow{OA}\) ও \(\overrightarrow{OB}\) যথাক্রমে \(A\) ও \(B\) বিন্দুর অবস্থান ভেক্টর,
যেখানে, \(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) এবং \(P\) বিন্দু \(AB\) রেখাংশকে \(m:n\) অনুপাতে অন্তর্বিভক্ত করে।
\(P\) বিন্দুর অবস্থান ভেক্টর, \(\overrightarrow{OP}=\frac{m\overline{b}+n\overline{a}}{m+n}\)
যেখানে, \(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) এবং \(P\) বিন্দু \(AB\) রেখাংশকে \(m:n\) অনুপাতে অন্তর্বিভক্ত করে।
\(P\) বিন্দুর অবস্থান ভেক্টর, \(\overrightarrow{OP}=\frac{m\overline{b}+n\overline{a}}{m+n}\)
প্রমাণঃ
\(\triangle{OAP}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OA}+\overrightarrow{AP}=\overrightarrow{OP}\)
\(\therefore \overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\)
আবার, \(\triangle{OBP}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}+\overrightarrow{PB}=\overrightarrow{OB}\)
\(\therefore \overrightarrow{PB}=\overrightarrow{OB}-\overrightarrow{OP}\)
প্রশ্ন মতে, \(AP:PB=m:n\)
\(\Rightarrow \frac{AP}{PB}=\frac{m}{n}\)
\(\Rightarrow nAP=mPB\)
\(\Rightarrow n\overrightarrow{AP}=m\overrightarrow{PB}\)
\(\Rightarrow n(\overrightarrow{OP}-\overrightarrow{OA})=m(\overrightarrow{OB}-\overrightarrow{OP})\) ➜ \(\because \overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\)
\(\overrightarrow{PB}=\overrightarrow{OB}-\overrightarrow{OP}\)
\(\Rightarrow n\overrightarrow{OP}-n\overrightarrow{OA}=m\overrightarrow{OB}-m\overrightarrow{OP}\)
\(\Rightarrow n\overrightarrow{OP}+m\overrightarrow{OP}=m\overrightarrow{OB}+n\overrightarrow{OA}\)
\(\Rightarrow \overrightarrow{OP}(m+n)=m\overline{b}+n\overline{a}\)
\(\therefore \overrightarrow{OP}=\frac{m\overline{b}+n\overline{a}}{m+n}\)
( প্রমাণিত )
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000003