এ অধ্যায়ের পাঠ্যসূচী
- ঐতিহাসিক পটভূমি
- কনিকের গঠনগত ব্যাখ্যা (Stractural explanation of Conics)
- বিভিন্ন প্রকৃতির কনিক (Different types of Conic)
- চিত্রের সাহায্যে কনিক উপস্থাপন (Representation of Conic by diagram)
- কোনোকের এবং সমতলের ছেদবিন্দুর সঞ্চারপথই যে কনিক তা চিত্রের সাহায্যে প্রকাশ (Conic which representing the locus of intersection of cone and a plane by diagram)
- কনিকের উৎস (Source of Conic)
- পরাবৃত্তের সমীকরণ সনাক্তকরণ (Identifying the equation of the parabola)
- মূলবিন্দুগামী এবং \(x\) অক্ষের ধনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ (Equation of the parabola symmetrical about the origin and positive to the \(x\) axis)
- মূলবিন্দুগামী এবং \(y\) অক্ষের ধনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ (Equation of the parabola symmetrical about the origin and positive to the \(y\) axis)
- মূলবিন্দুগামী এবং \(x\) অক্ষের ঋনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ (Equation of the parabola symmetrical about the origin and negative to the \(x\) axis)
- মূলবিন্দুগামী এবং \(y\) অক্ষের ঋনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ (Equation of the parabola symmetrical about the origin and negative to the \(y\) axis )
- মূলবিন্দুকে উপকেন্দ্রক ধরে পরাবৃত্তের সমীকরণ (Equation of a parabola with origin as epicenter)
- \(Y\) অক্ষকে নিয়ামকরেখা এবং \(X\) অক্ষকে অক্ষরেখা ধরে পরাবৃত্তের সমীকরণ (Equation of the parabola with the \(Y\) axis as the directrix and the \(X\) axis as the focus)
- \(X\) অক্ষের সমান্তরাল অক্ষরেখা বিশিষ্ট পরাবৃত্তের সমীকর (Equation of the parabola with axis parallel to the \(X\) axis)
- \(Y\) অক্ষের সমান্তরাল অক্ষরেখা বিশিষ্ট পরাবৃত্তের সমীকর (Equation of the parabola with axis parallel to the \(Y\) axis)
- পরাবৃত্তের স্পর্শক (Tangent of parabola)
- পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য (Letus rectum of parabola)
- উপবৃত্ত (Ellipse)
- উপবৃত্তের প্রমিত সমীকরণ (Standard equation of Ellipse)
- উপবৃত্তের আদর্শ সমীকরণ সনাক্তকরণ (Identifying the standard equation of an ellipse)
- উপবৃত্তের সমীকরণ সনাক্তকরণ (Identifying equation of an ellipse)
- উপবৃত্তের ক্ষেত্রফল (Area of ellipse)
- উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(x\) অক্ষ বরাবর (Equation of the ellipse whose Major axis along \(x\) axis)
- উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(y\) অক্ষ বরাবর (Equation of the ellipse whose Major axis along \(y\) axis)
- নির্দিষ্ট কেন্দ্রবিশিষ্ট উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(x\) অক্ষ বরাবর (Equation of an ellipse with fixed center whose major axis is along the \(x\) axis)
- নির্দিষ্ট কেন্দ্রবিশিষ্ট উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(y\) অক্ষ বরাবর (Equation of an ellipse with fixed center whose major axis is along the \(y\) axis)
- উপবৃত্তের স্পর্শক (Tangent of ellipse)
- উপবৃত্ত সাপেক্ষে কোনো বিন্দুর আপেক্ষিক অবস্থান (The relative position of a point with respect to the ellipse)
- উপবৃত্তের উপকেন্দ্র ও নিয়ামকরেখা (Focus and directrix of Ellipse)
- উপবৃত্তের বৃহদাক্ষ ও ক্ষুদ্রাক্ষ (Major and Minor axis of Ellipse)
- উপবৃত্তের সমীকরণ থেকে উৎকেন্দ্রতা (Eccentricity from the equation of ellipse)
- উপবৃত্তের সমীকরণ থেকে উপকেন্দ্রের স্থানাঙ্ক ও নিয়ামকের সমীকরণ (The co-ordinates of focus and the equation of directrix from the equation of ellipse)
- উপবৃত্তের সমীকরণ থেকে উপকেন্দ্রিক লম্ব ও এর দৈর্ঘ্য (From the equation of an ellipse Latus rectum and it's length)
- উপবৃত্তের উপরিস্থিত কোনো বিন্দুর উপকেন্দ্রিক দূরত্ব দুইটির সমষ্টি, বৃহদাক্ষের দৈর্ঘ্যের সমান (Sum of the two epicentral distance of a point on the ellipse is equal to the length of Major axis)
- কোনো নির্দিষ্ট বিন্দুতে উপবৃত্তের পরামিতিক স্থানাঙ্ক (Parametric coordinates of a given point on the ellipse)
- উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর লেখচিত্র (Graph of equation of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\))
- অধিবৃত্ত (Hyperbola)
- মূলবিন্দু কেন্দ্রবিশিষ্ট অধিবৃত্তের প্রমিত সমীকরণ (Standard equation of Hyperbola)
- অধিবৃত্তের আদর্শ সমীকরণ সনাক্তকরণ (Identifying the Standard equation of the hyperbola)
- অধিবৃত্তের সমীকরণ সনাক্তকরণ (Identifying the equation of the hyperbola)
- অধিবৃত্তের সমীকরণ যার প্রধান অক্ষ \(x\) অক্ষ বরাবর (Equation of the hyperbola whose major axis is along the \(x\) axis)
- অধিবৃত্তের সমীকরণ যার প্রধান অক্ষ \(y\) অক্ষ বরাবর (Equation of the hyperbola whose major axis is along the \(y\) axis)
- অধিবৃত্তের সমীকরণ যার কেন্দ্র \(C(\alpha, \beta)\) প্রধান অক্ষ \(x\) অক্ষ বরাবর (Equation of the hyperbola whose center \(C(\alpha, \beta)\) major axis is along the \(x\) axis)
- অধিবৃত্তের সমীকরণ যার কেন্দ্র \(C(\alpha, \beta)\) প্রধান অক্ষ \(y\) অক্ষ বরাবর (Equation of the hyperbola whose center \(C(\alpha, \beta)\) major axis is along the \(y\) axis)
- অধিবৃত্তের স্পর্শক (Tangent of hyperbola)
- অধিবৃত্ত সাপেক্ষে কোনো বিন্দুর আপেক্ষিক অবস্থান (The relative position of a point with respect to the hyperbola)
- অধিবৃত্তের উপরিস্থিত নির্দিষ্ট বিন্দুতে স্পর্শকের সমীকরণ (Equation of the tangent at a given point on the hyperbola)
- অধিবৃত্তের উপকেন্দ্র ও নিয়ামকরেখা (Focus and directrix of Hyperbola)
- অধিবৃত্তের আড় অক্ষ ও অনুবন্ধী অক্ষের দৈর্ঘ্য (Transverse and Conjugate axis of Hyperbola)
- অধিবৃত্তের সমীকরণ থেকে উৎকেন্দ্রতা (Eccentricity from the equation of Hyperbola)
- অধিবৃত্তের সমীকরণ থেকে উপকেন্দ্রের স্থানাঙ্ক ও নিয়ামকের সমীকরণ (The co-ordinates of focus and the equation of directrix from the equation of Hyperbola)
- উপকেন্দ্র ও নিয়ামকের সমীকরণ থেকে অধিবৃত্তের সমীকরণ নির্ণয় (Determination of the equation of Hyperbola from focus and equation of directrix)
- অধিবৃত্তের সমীকরণ থেকে উপকেন্দ্রিক লম্ব ও এর দৈর্ঘ্য (Latus rectum and it's length from the equation of Hyperbola)
- নির্দিষ্ট বিন্দুতে অধিবৃত্তের পরামিতিক স্থানাঙ্ক (Parametric coordinates of Hyperbola at fixed point)
- অধিবৃত্তের অসীমতটের অবস্থান নির্ণয় (Determination of the position of asymptotes of Hyperbola)
- অধিবৃত্তের অসীমতট রেখার সমীকরণ (Equation of asymptotes of Hyperbola)
- অধিবৃত্তের লেখচিত্র (Graph of Hyperbola)
- সাধারণ দ্বিঘাত সমীকরণ (General quadratic equation)
- কনিকের সমীকরণ শনাক্তকরণ (Identification of Conic's equation)
- স্পর্শ জ্য (Chord of Contact)
- পোল ও পোলার ( Poles and polars)
- ব্যাস, অনুবন্ধী ব্যাস এবং নির্দেশক (নিয়ত) বৃত্ত (Diameter, relative Diameter and Destiny circle)
- পরাবৃত্তে উপকেন্দ্রের অবস্থান (Location of Focus on parabola)
- কেন্দ্রীয় কণিকে উপকেন্দ্রের অবস্থান (Location of Focus on central conic)
- অসীমতট (Asymptote)
- কণিক শ্রেণী (System of conic)
- অনুবন্ধী অধিবৃত্ত (Conjugate Hyperbola)
- অসীমতট এবং অনুবন্ধী অধিবৃত্তের মধ্যে সম্পর্ক (Relation between Asymptote and Conjugate Hyperbola)
- অনুসিদ্ধান্ত (Postulate)
- সাধারণ দ্বিঘাত সমীকরণ সম্পর্কিত উপপাদ্য (Theorems relating to general quadratic equations)
- অধ্যায় \(C\)-এর উদাহরণসমুহ
- অধ্যায় \(C\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(C\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(C\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(C\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
ঐতিহাসিক পটভূমি
Historical Background

পিথাগোরাস
( ৫৭০ খ্রিষ্টপূর্ব-৪৯৫ খ্রিষ্টপূর্ব )
পিথাগোরাস ছিলেন একজন আয়োনীয় গ্রিক দার্শনিক, গণিতবিদ এবং পিথাগোরাসবাদী ভ্রাতৃত্বের জনক।
সিমন স্টেভিন  সিমন স্টেভিন (১৫৪৮-১৬২০) যাকে কখনও কখনও স্টেভিনাস বলা হত, তিনি ছিলেন ফ্লেমিশ গণিতবিদ, পদার্থবিদ এবং সামরিক প্রকৌশলী। তিনি তাত্ত্বিক এবং ব্যবহারিক উভয় ক্ষেত্রেই বিজ্ঞান এবং প্রকৌশল বিভাগের বিভিন্ন ক্ষেত্রে বিভিন্ন অবদান রেখেছিলেন। ১৫৯৫ সালে দ্বিঘাত সমীকরণ সমাধানের জন্য এমন একটি সূত্র প্রদান করেন যা সকল ক্ষেত্রে কার্যকরী। আধুনিক যুগে ব্যবহৃত দ্বিঘাত সমীকরণ সমাধানের সাধারণ সূত্রটি ১৮৯৬ সালে প্রকাশিত
হেনরি হিটনের (১৮৪৬-১৯২৭ )
সিমন স্টেভিন (১৫৪৮-১৬২০) যাকে কখনও কখনও স্টেভিনাস বলা হত, তিনি ছিলেন ফ্লেমিশ গণিতবিদ, পদার্থবিদ এবং সামরিক প্রকৌশলী। তিনি তাত্ত্বিক এবং ব্যবহারিক উভয় ক্ষেত্রেই বিজ্ঞান এবং প্রকৌশল বিভাগের বিভিন্ন ক্ষেত্রে বিভিন্ন অবদান রেখেছিলেন। ১৫৯৫ সালে দ্বিঘাত সমীকরণ সমাধানের জন্য এমন একটি সূত্র প্রদান করেন যা সকল ক্ষেত্রে কার্যকরী। আধুনিক যুগে ব্যবহৃত দ্বিঘাত সমীকরণ সমাধানের সাধারণ সূত্রটি ১৮৯৬ সালে প্রকাশিত
হেনরি হিটনের (১৮৪৬-১৯২৭ )  ১৮৭৪ থেকে ১৯১৮ সাল পর্যন্ত হিটন অ্যানালিস্ট এবং আমেরিকান ম্যাথমেটিক্যাল মাসিক পত্রিকায় গাণিতিক সমস্যার প্রায় একশত সমাধান প্রকাশ করেছিলেন। চতুর্ভুজ সমীকরণের সমাধানের পরিচিত রূপ হিসাবে 1896 সালে প্রথমবারের জন্য তাঁর সবচেয়ে গুরুত্বপূর্ণ এবং স্মরণীয় অবদান ছিল। একটি গবেষণাপত্র হতে উদ্ভূত হয়।
খ্রিষ্টপূর্ব ২০০০ অব্দের পূর্ব হতেই ব্যাবিলনীয় গণিতবিদ আয়তক্ষেত্রের ক্ষেত্রফল ও বাহুদ্বয় সংক্রান্ত গাণিতিক সমস্যা সমাধানের উপায় সম্পর্কে জ্ঞান রাখত। এই কাজে তারা যে পদ্ধতি ব্যবহার করত তা বর্তমান সময়ে প্রচলিত দ্বিঘাত সমীকরণ সমাধানের পদ্ধতির অনুরূপ না হলেও তাদের হাত ধরে দ্বিঘাত সমীকরণের যাত্রা শুরু হয়েছে বলে স্বীকার করে নেওয়া হয়েছে।
খ্রিষ্টপূর্ব অষ্টম শতাব্দীতে প্রাচীন ভারতীয়রা জ্যামিতিক পদ্ধতিতে \(ax^2=c\) এবং \(ax^2+bx+c=0\) আকারের দ্বিঘাত সমীকরণ সমসধান করেন। পরবর্তীতে খ্রিষ্টপূর্ব ৪০০ অব্দে ব্যবলনীয়রা এবং ২০০ অব্দে চৈনিক গণিতবিদগণ জ্যামিতিক উপায়ে দ্বিঘাত সমীকরণ সমাধানের চেষ্টা অব্যাহত রাখলেও দ্বিঘাত সমীকরণ সমাধানের কোনোরূপ ব্যক্ত সূত্র প্রতিষ্টা করতে পারেননি। এছাড়াও ইউক্লিড,
১৮৭৪ থেকে ১৯১৮ সাল পর্যন্ত হিটন অ্যানালিস্ট এবং আমেরিকান ম্যাথমেটিক্যাল মাসিক পত্রিকায় গাণিতিক সমস্যার প্রায় একশত সমাধান প্রকাশ করেছিলেন। চতুর্ভুজ সমীকরণের সমাধানের পরিচিত রূপ হিসাবে 1896 সালে প্রথমবারের জন্য তাঁর সবচেয়ে গুরুত্বপূর্ণ এবং স্মরণীয় অবদান ছিল। একটি গবেষণাপত্র হতে উদ্ভূত হয়।
খ্রিষ্টপূর্ব ২০০০ অব্দের পূর্ব হতেই ব্যাবিলনীয় গণিতবিদ আয়তক্ষেত্রের ক্ষেত্রফল ও বাহুদ্বয় সংক্রান্ত গাণিতিক সমস্যা সমাধানের উপায় সম্পর্কে জ্ঞান রাখত। এই কাজে তারা যে পদ্ধতি ব্যবহার করত তা বর্তমান সময়ে প্রচলিত দ্বিঘাত সমীকরণ সমাধানের পদ্ধতির অনুরূপ না হলেও তাদের হাত ধরে দ্বিঘাত সমীকরণের যাত্রা শুরু হয়েছে বলে স্বীকার করে নেওয়া হয়েছে।
খ্রিষ্টপূর্ব অষ্টম শতাব্দীতে প্রাচীন ভারতীয়রা জ্যামিতিক পদ্ধতিতে \(ax^2=c\) এবং \(ax^2+bx+c=0\) আকারের দ্বিঘাত সমীকরণ সমসধান করেন। পরবর্তীতে খ্রিষ্টপূর্ব ৪০০ অব্দে ব্যবলনীয়রা এবং ২০০ অব্দে চৈনিক গণিতবিদগণ জ্যামিতিক উপায়ে দ্বিঘাত সমীকরণ সমাধানের চেষ্টা অব্যাহত রাখলেও দ্বিঘাত সমীকরণ সমাধানের কোনোরূপ ব্যক্ত সূত্র প্রতিষ্টা করতে পারেননি। এছাড়াও ইউক্লিড,  ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। পিথাগোরাস
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। পিথাগোরাস  পিথাগোরাস ছিলেন একজন আয়োনীয় গ্রিক দার্শনিক, গণিতবিদ এবং পিথাগোরাসবাদী ভ্রাতৃত্বের জনক যার প্রকৃতি ধর্মীয় হলেও তা এমন সব নীতির উদ্ভব ঘটিয়েছিল যা পরবর্তীতে প্লেটো এবং এরিস্টটলের মত দার্শনিকদের প্রভাবিত করেছে। তিনি এজিয়ান সাগরের পূর্ব উপকূল অর্থাৎ বর্তমান তুরস্কের কাছাকাছি অবস্থিত সামোস দ্বীপে জন্মেছিলেন। ( ৫৭০ খ্রিষ্টপূর্ব-৪৯৫ খ্রিষ্টপূর্ব ), ডিওফ্যান্টাস
পিথাগোরাস ছিলেন একজন আয়োনীয় গ্রিক দার্শনিক, গণিতবিদ এবং পিথাগোরাসবাদী ভ্রাতৃত্বের জনক যার প্রকৃতি ধর্মীয় হলেও তা এমন সব নীতির উদ্ভব ঘটিয়েছিল যা পরবর্তীতে প্লেটো এবং এরিস্টটলের মত দার্শনিকদের প্রভাবিত করেছে। তিনি এজিয়ান সাগরের পূর্ব উপকূল অর্থাৎ বর্তমান তুরস্কের কাছাকাছি অবস্থিত সামোস দ্বীপে জন্মেছিলেন। ( ৫৭০ খ্রিষ্টপূর্ব-৪৯৫ খ্রিষ্টপূর্ব ), ডিওফ্যান্টাস  আলেকজান্দ্রিয়ার ডিওফ্যান্টাস ছিলেন আলেকজান্দ্রীয় হেলেনিস্টিক গণিতবিদ এবং অ্যারিথমেটিকা নামক একাধিক বইয়ের লেখক, যার অনেকগুলি এখন হারিয়ে গেছে। তাঁর পাঠ্য বইগুলিতে বীজগণিত সমীকরণগুলি সমাধান করার বিষয়ে আলোচনা করা হয়েছে। মত বিশিষ্ট গণিতবিদগণও জ্যামিতিক উপায়ে দ্বিঘাত সমীকরণ সমাধানের চেষ্টা অব্যাহত রাখেন। ৬২৮ খ্রিষ্টাব্দে ভারতীয় গণিতবিদ ব্রহ্মগুপ্ত
আলেকজান্দ্রিয়ার ডিওফ্যান্টাস ছিলেন আলেকজান্দ্রীয় হেলেনিস্টিক গণিতবিদ এবং অ্যারিথমেটিকা নামক একাধিক বইয়ের লেখক, যার অনেকগুলি এখন হারিয়ে গেছে। তাঁর পাঠ্য বইগুলিতে বীজগণিত সমীকরণগুলি সমাধান করার বিষয়ে আলোচনা করা হয়েছে। মত বিশিষ্ট গণিতবিদগণও জ্যামিতিক উপায়ে দ্বিঘাত সমীকরণ সমাধানের চেষ্টা অব্যাহত রাখেন। ৬২৮ খ্রিষ্টাব্দে ভারতীয় গণিতবিদ ব্রহ্মগুপ্ত  ব্রহ্মগুপ্ত ছিলেন একজন ভারতীয় গণিতবিদ এবং জ্যোতির্বিদ। তিনি গণিত ও জ্যোতির্বিদ্যার প্রথম তিনটি গ্রন্থের লেখক: ব্রহ্মসফুসিসিদ্ধন্ত, একটি তাত্ত্বিক গ্রন্থ এবং খড়খাদিক একটি আরও ব্যবহারিক গ্রন্থ। ব্রহ্মগুপ্ত প্রথম শূন্যের সাথে গণনা করার নিয়ম দিয়েছিলেন। সর্বপ্রথম দ্বিঘাত সমীকরণ সমাধানের ব্যক্ত সূত্র প্রদান করেন। তবে ব্রহ্মগুপ্তের এই সূত্র কিছু ক্ষেত্রে সমাধান নির্ণয়ে অকার্যকর বলে প্রতীয়মান হয়।
ব্রহ্মগুপ্ত ছিলেন একজন ভারতীয় গণিতবিদ এবং জ্যোতির্বিদ। তিনি গণিত ও জ্যোতির্বিদ্যার প্রথম তিনটি গ্রন্থের লেখক: ব্রহ্মসফুসিসিদ্ধন্ত, একটি তাত্ত্বিক গ্রন্থ এবং খড়খাদিক একটি আরও ব্যবহারিক গ্রন্থ। ব্রহ্মগুপ্ত প্রথম শূন্যের সাথে গণনা করার নিয়ম দিয়েছিলেন। সর্বপ্রথম দ্বিঘাত সমীকরণ সমাধানের ব্যক্ত সূত্র প্রদান করেন। তবে ব্রহ্মগুপ্তের এই সূত্র কিছু ক্ষেত্রে সমাধান নির্ণয়ে অকার্যকর বলে প্রতীয়মান হয়।
 সিমন স্টেভিন (১৫৪৮-১৬২০) যাকে কখনও কখনও স্টেভিনাস বলা হত, তিনি ছিলেন ফ্লেমিশ গণিতবিদ, পদার্থবিদ এবং সামরিক প্রকৌশলী। তিনি তাত্ত্বিক এবং ব্যবহারিক উভয় ক্ষেত্রেই বিজ্ঞান এবং প্রকৌশল বিভাগের বিভিন্ন ক্ষেত্রে বিভিন্ন অবদান রেখেছিলেন। ১৫৯৫ সালে দ্বিঘাত সমীকরণ সমাধানের জন্য এমন একটি সূত্র প্রদান করেন যা সকল ক্ষেত্রে কার্যকরী। আধুনিক যুগে ব্যবহৃত দ্বিঘাত সমীকরণ সমাধানের সাধারণ সূত্রটি ১৮৯৬ সালে প্রকাশিত
হেনরি হিটনের (১৮৪৬-১৯২৭ )
সিমন স্টেভিন (১৫৪৮-১৬২০) যাকে কখনও কখনও স্টেভিনাস বলা হত, তিনি ছিলেন ফ্লেমিশ গণিতবিদ, পদার্থবিদ এবং সামরিক প্রকৌশলী। তিনি তাত্ত্বিক এবং ব্যবহারিক উভয় ক্ষেত্রেই বিজ্ঞান এবং প্রকৌশল বিভাগের বিভিন্ন ক্ষেত্রে বিভিন্ন অবদান রেখেছিলেন। ১৫৯৫ সালে দ্বিঘাত সমীকরণ সমাধানের জন্য এমন একটি সূত্র প্রদান করেন যা সকল ক্ষেত্রে কার্যকরী। আধুনিক যুগে ব্যবহৃত দ্বিঘাত সমীকরণ সমাধানের সাধারণ সূত্রটি ১৮৯৬ সালে প্রকাশিত
হেনরি হিটনের (১৮৪৬-১৯২৭ )  ১৮৭৪ থেকে ১৯১৮ সাল পর্যন্ত হিটন অ্যানালিস্ট এবং আমেরিকান ম্যাথমেটিক্যাল মাসিক পত্রিকায় গাণিতিক সমস্যার প্রায় একশত সমাধান প্রকাশ করেছিলেন। চতুর্ভুজ সমীকরণের সমাধানের পরিচিত রূপ হিসাবে 1896 সালে প্রথমবারের জন্য তাঁর সবচেয়ে গুরুত্বপূর্ণ এবং স্মরণীয় অবদান ছিল। একটি গবেষণাপত্র হতে উদ্ভূত হয়।
খ্রিষ্টপূর্ব ২০০০ অব্দের পূর্ব হতেই ব্যাবিলনীয় গণিতবিদ আয়তক্ষেত্রের ক্ষেত্রফল ও বাহুদ্বয় সংক্রান্ত গাণিতিক সমস্যা সমাধানের উপায় সম্পর্কে জ্ঞান রাখত। এই কাজে তারা যে পদ্ধতি ব্যবহার করত তা বর্তমান সময়ে প্রচলিত দ্বিঘাত সমীকরণ সমাধানের পদ্ধতির অনুরূপ না হলেও তাদের হাত ধরে দ্বিঘাত সমীকরণের যাত্রা শুরু হয়েছে বলে স্বীকার করে নেওয়া হয়েছে।
খ্রিষ্টপূর্ব অষ্টম শতাব্দীতে প্রাচীন ভারতীয়রা জ্যামিতিক পদ্ধতিতে \(ax^2=c\) এবং \(ax^2+bx+c=0\) আকারের দ্বিঘাত সমীকরণ সমসধান করেন। পরবর্তীতে খ্রিষ্টপূর্ব ৪০০ অব্দে ব্যবলনীয়রা এবং ২০০ অব্দে চৈনিক গণিতবিদগণ জ্যামিতিক উপায়ে দ্বিঘাত সমীকরণ সমাধানের চেষ্টা অব্যাহত রাখলেও দ্বিঘাত সমীকরণ সমাধানের কোনোরূপ ব্যক্ত সূত্র প্রতিষ্টা করতে পারেননি। এছাড়াও ইউক্লিড,
১৮৭৪ থেকে ১৯১৮ সাল পর্যন্ত হিটন অ্যানালিস্ট এবং আমেরিকান ম্যাথমেটিক্যাল মাসিক পত্রিকায় গাণিতিক সমস্যার প্রায় একশত সমাধান প্রকাশ করেছিলেন। চতুর্ভুজ সমীকরণের সমাধানের পরিচিত রূপ হিসাবে 1896 সালে প্রথমবারের জন্য তাঁর সবচেয়ে গুরুত্বপূর্ণ এবং স্মরণীয় অবদান ছিল। একটি গবেষণাপত্র হতে উদ্ভূত হয়।
খ্রিষ্টপূর্ব ২০০০ অব্দের পূর্ব হতেই ব্যাবিলনীয় গণিতবিদ আয়তক্ষেত্রের ক্ষেত্রফল ও বাহুদ্বয় সংক্রান্ত গাণিতিক সমস্যা সমাধানের উপায় সম্পর্কে জ্ঞান রাখত। এই কাজে তারা যে পদ্ধতি ব্যবহার করত তা বর্তমান সময়ে প্রচলিত দ্বিঘাত সমীকরণ সমাধানের পদ্ধতির অনুরূপ না হলেও তাদের হাত ধরে দ্বিঘাত সমীকরণের যাত্রা শুরু হয়েছে বলে স্বীকার করে নেওয়া হয়েছে।
খ্রিষ্টপূর্ব অষ্টম শতাব্দীতে প্রাচীন ভারতীয়রা জ্যামিতিক পদ্ধতিতে \(ax^2=c\) এবং \(ax^2+bx+c=0\) আকারের দ্বিঘাত সমীকরণ সমসধান করেন। পরবর্তীতে খ্রিষ্টপূর্ব ৪০০ অব্দে ব্যবলনীয়রা এবং ২০০ অব্দে চৈনিক গণিতবিদগণ জ্যামিতিক উপায়ে দ্বিঘাত সমীকরণ সমাধানের চেষ্টা অব্যাহত রাখলেও দ্বিঘাত সমীকরণ সমাধানের কোনোরূপ ব্যক্ত সূত্র প্রতিষ্টা করতে পারেননি। এছাড়াও ইউক্লিড,  ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। পিথাগোরাস
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। পিথাগোরাস  পিথাগোরাস ছিলেন একজন আয়োনীয় গ্রিক দার্শনিক, গণিতবিদ এবং পিথাগোরাসবাদী ভ্রাতৃত্বের জনক যার প্রকৃতি ধর্মীয় হলেও তা এমন সব নীতির উদ্ভব ঘটিয়েছিল যা পরবর্তীতে প্লেটো এবং এরিস্টটলের মত দার্শনিকদের প্রভাবিত করেছে। তিনি এজিয়ান সাগরের পূর্ব উপকূল অর্থাৎ বর্তমান তুরস্কের কাছাকাছি অবস্থিত সামোস দ্বীপে জন্মেছিলেন। ( ৫৭০ খ্রিষ্টপূর্ব-৪৯৫ খ্রিষ্টপূর্ব ), ডিওফ্যান্টাস
পিথাগোরাস ছিলেন একজন আয়োনীয় গ্রিক দার্শনিক, গণিতবিদ এবং পিথাগোরাসবাদী ভ্রাতৃত্বের জনক যার প্রকৃতি ধর্মীয় হলেও তা এমন সব নীতির উদ্ভব ঘটিয়েছিল যা পরবর্তীতে প্লেটো এবং এরিস্টটলের মত দার্শনিকদের প্রভাবিত করেছে। তিনি এজিয়ান সাগরের পূর্ব উপকূল অর্থাৎ বর্তমান তুরস্কের কাছাকাছি অবস্থিত সামোস দ্বীপে জন্মেছিলেন। ( ৫৭০ খ্রিষ্টপূর্ব-৪৯৫ খ্রিষ্টপূর্ব ), ডিওফ্যান্টাস  আলেকজান্দ্রিয়ার ডিওফ্যান্টাস ছিলেন আলেকজান্দ্রীয় হেলেনিস্টিক গণিতবিদ এবং অ্যারিথমেটিকা নামক একাধিক বইয়ের লেখক, যার অনেকগুলি এখন হারিয়ে গেছে। তাঁর পাঠ্য বইগুলিতে বীজগণিত সমীকরণগুলি সমাধান করার বিষয়ে আলোচনা করা হয়েছে। মত বিশিষ্ট গণিতবিদগণও জ্যামিতিক উপায়ে দ্বিঘাত সমীকরণ সমাধানের চেষ্টা অব্যাহত রাখেন। ৬২৮ খ্রিষ্টাব্দে ভারতীয় গণিতবিদ ব্রহ্মগুপ্ত
আলেকজান্দ্রিয়ার ডিওফ্যান্টাস ছিলেন আলেকজান্দ্রীয় হেলেনিস্টিক গণিতবিদ এবং অ্যারিথমেটিকা নামক একাধিক বইয়ের লেখক, যার অনেকগুলি এখন হারিয়ে গেছে। তাঁর পাঠ্য বইগুলিতে বীজগণিত সমীকরণগুলি সমাধান করার বিষয়ে আলোচনা করা হয়েছে। মত বিশিষ্ট গণিতবিদগণও জ্যামিতিক উপায়ে দ্বিঘাত সমীকরণ সমাধানের চেষ্টা অব্যাহত রাখেন। ৬২৮ খ্রিষ্টাব্দে ভারতীয় গণিতবিদ ব্রহ্মগুপ্ত  ব্রহ্মগুপ্ত ছিলেন একজন ভারতীয় গণিতবিদ এবং জ্যোতির্বিদ। তিনি গণিত ও জ্যোতির্বিদ্যার প্রথম তিনটি গ্রন্থের লেখক: ব্রহ্মসফুসিসিদ্ধন্ত, একটি তাত্ত্বিক গ্রন্থ এবং খড়খাদিক একটি আরও ব্যবহারিক গ্রন্থ। ব্রহ্মগুপ্ত প্রথম শূন্যের সাথে গণনা করার নিয়ম দিয়েছিলেন। সর্বপ্রথম দ্বিঘাত সমীকরণ সমাধানের ব্যক্ত সূত্র প্রদান করেন। তবে ব্রহ্মগুপ্তের এই সূত্র কিছু ক্ষেত্রে সমাধান নির্ণয়ে অকার্যকর বলে প্রতীয়মান হয়।
ব্রহ্মগুপ্ত ছিলেন একজন ভারতীয় গণিতবিদ এবং জ্যোতির্বিদ। তিনি গণিত ও জ্যোতির্বিদ্যার প্রথম তিনটি গ্রন্থের লেখক: ব্রহ্মসফুসিসিদ্ধন্ত, একটি তাত্ত্বিক গ্রন্থ এবং খড়খাদিক একটি আরও ব্যবহারিক গ্রন্থ। ব্রহ্মগুপ্ত প্রথম শূন্যের সাথে গণনা করার নিয়ম দিয়েছিলেন। সর্বপ্রথম দ্বিঘাত সমীকরণ সমাধানের ব্যক্ত সূত্র প্রদান করেন। তবে ব্রহ্মগুপ্তের এই সূত্র কিছু ক্ষেত্রে সমাধান নির্ণয়ে অকার্যকর বলে প্রতীয়মান হয়।

অ্যাপোলোনিয়াস
(২৬২ খ্রিষ্টপূর্ব-১৯০ খ্রিষ্টপূর্ব)
পের্গার অ্যাপোলোনিয়াস ছিলেন গ্রীক জিওমিটার এবং জ্যোতির্বিজ্ঞানী, যেটি শঙ্কু বিভাগের বিষয়ে তত্ত্বগুলির জন্য পরিচিত ছিল।
খ্রিষ্টপূর্ব ৩২০ অব্দের নিকটবর্তী সময়ে কোণোক কর্তন করে বিভিন্ন প্রকার কণিক প্রাপ্তির ধারণার সূত্রপাত ঘটান প্রাচীন গ্রীক দার্শনিক ও জ্যমিতিবেত্তা ম্যানিসমিউস  ম্যানিসমিউস (৩৮০-৩২০ খ্রিষ্টপূর্ব) কোণক দ্বারা সমতলে বক্ররেখার ছেদাংশের বিভিন্ন অংশকে পরাবৃত্ত, উপবৃত্ত ও অধিবৃত্ত নামকরণ করেন। পরবর্তীতে ইউক্লিড
ম্যানিসমিউস (৩৮০-৩২০ খ্রিষ্টপূর্ব) কোণক দ্বারা সমতলে বক্ররেখার ছেদাংশের বিভিন্ন অংশকে পরাবৃত্ত, উপবৃত্ত ও অধিবৃত্ত নামকরণ করেন। পরবর্তীতে ইউক্লিড  ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। কণিক সংক্রান্ত চারটি পুস্তক রচনা করেন যার সবকটিই কালের অতল গর্ভে বিলিন হয়ে গেছে। আর্কিমিডিস
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। কণিক সংক্রান্ত চারটি পুস্তক রচনা করেন যার সবকটিই কালের অতল গর্ভে বিলিন হয়ে গেছে। আর্কিমিডিস  আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। কণিক নিয়ে গবেষ্ণা করেছিলেন বলে প্রমাণ পাওয়া যায়। তিনি পরাবৃত্ত ও উপবৃত্ত দ্বারা আবদ্ধ ক্ষেত্রের ক্ষেত্রফল নির্ণয়ের উপায় উদ্ভাবন করেন। গ্রীক দার্শনিক অ্যাপোলোনিয়াস
আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। কণিক নিয়ে গবেষ্ণা করেছিলেন বলে প্রমাণ পাওয়া যায়। তিনি পরাবৃত্ত ও উপবৃত্ত দ্বারা আবদ্ধ ক্ষেত্রের ক্ষেত্রফল নির্ণয়ের উপায় উদ্ভাবন করেন। গ্রীক দার্শনিক অ্যাপোলোনিয়াস  পের্গার অ্যাপোলোনিয়াস ছিলেন গ্রীক জিওমিটার এবং জ্যোতির্বিজ্ঞানী, যেটি শঙ্কু বিভাগের বিষয়ে তত্ত্বগুলির জন্য পরিচিত ছিল। এই বিষয়ে ইউক্লিড এবং আর্কিমিডিসের তত্ত্বগুলি থেকে শুরু করে, তিনি বিশ্লেষণাত্মক জ্যামিতির আবিষ্কারের ঠিক আগে তারা তাদের সেই অবস্থায় নিয়ে এসেছিলেন। তৎকালীন সময়ে প্রচলিত ধারণাসমূহ সংকলন করেন এবং তার প্রচলিত জ্ঞানসমূহের সম্প্রসারণ হিসেবে স্ব-উদ্ভাবিত কিছু ধারণা যুক্ত করেন। পাপ্পাস
পের্গার অ্যাপোলোনিয়াস ছিলেন গ্রীক জিওমিটার এবং জ্যোতির্বিজ্ঞানী, যেটি শঙ্কু বিভাগের বিষয়ে তত্ত্বগুলির জন্য পরিচিত ছিল। এই বিষয়ে ইউক্লিড এবং আর্কিমিডিসের তত্ত্বগুলি থেকে শুরু করে, তিনি বিশ্লেষণাত্মক জ্যামিতির আবিষ্কারের ঠিক আগে তারা তাদের সেই অবস্থায় নিয়ে এসেছিলেন। তৎকালীন সময়ে প্রচলিত ধারণাসমূহ সংকলন করেন এবং তার প্রচলিত জ্ঞানসমূহের সম্প্রসারণ হিসেবে স্ব-উদ্ভাবিত কিছু ধারণা যুক্ত করেন। পাপ্পাস  আলেকজান্দ্রিয়ার প্যাপস ছিলেন প্রাচীন প্রাচীন গ্রীক গণিতবিদদের মধ্যে অন্যতম, তিনি তাঁর সিনাগেজ বা সংগ্রহের জন্য এবং পাপ্পাসের ষড়ভুজ উপপাদ্যকে প্রজেক্টিভ জ্যামিতিতে জেনেছিলেন। কণিকের উপকেন্দ্রের গুরুত্ব অনুধাবন করেন। ১০০০ সালে আল-কুহি (940 AD-1000 AD)
আলেকজান্দ্রিয়ার প্যাপস ছিলেন প্রাচীন প্রাচীন গ্রীক গণিতবিদদের মধ্যে অন্যতম, তিনি তাঁর সিনাগেজ বা সংগ্রহের জন্য এবং পাপ্পাসের ষড়ভুজ উপপাদ্যকে প্রজেক্টিভ জ্যামিতিতে জেনেছিলেন। কণিকের উপকেন্দ্রের গুরুত্ব অনুধাবন করেন। ১০০০ সালে আল-কুহি (940 AD-1000 AD) আবাহ সাহল ওয়াজান ইবনে রুস্তম আল-কাহি ছিলেন একজন পার্সিয়ান গণিতবিদ, পদার্থবিদ এবং জ্যোতির্বিদ। তিনি আমোলের তাবারিস্তানের কুহ থেকে আগত এবং দশম শতাব্দীতে বাগদাদে বিকাশ লাভ করেছিলেন। তাঁকে গণিত ও জ্যোতির্বিজ্ঞান সংক্রান্ত অনেকগুলি লেখাই সর্বশ্রেষ্ঠ মুসলিম জিওমিটার হিসাবে বিবেচনা করা হয়। কণিকের চিত্র অঙ্কন করার সরঞ্জাম উদ্ভাবন করেন। পারস্যের বিখ্যাত কবি ও গণিতবিদ ওমর খৈয়াম
আবাহ সাহল ওয়াজান ইবনে রুস্তম আল-কাহি ছিলেন একজন পার্সিয়ান গণিতবিদ, পদার্থবিদ এবং জ্যোতির্বিদ। তিনি আমোলের তাবারিস্তানের কুহ থেকে আগত এবং দশম শতাব্দীতে বাগদাদে বিকাশ লাভ করেছিলেন। তাঁকে গণিত ও জ্যোতির্বিজ্ঞান সংক্রান্ত অনেকগুলি লেখাই সর্বশ্রেষ্ঠ মুসলিম জিওমিটার হিসাবে বিবেচনা করা হয়। কণিকের চিত্র অঙ্কন করার সরঞ্জাম উদ্ভাবন করেন। পারস্যের বিখ্যাত কবি ও গণিতবিদ ওমর খৈয়াম  ওমর খৈয়াম ছিলেন পার্সিয়ান গণিতবিদ, জ্যোতির্বিদ, দার্শনিক এবং কবি। তিনি উত্তর-পূর্ব ইরানের নীশাবরে জন্মগ্রহণ করেছিলেন এবং তাঁর বেশিরভাগ জীবন কারাখানিদ ও সেলজাক শাসকদের দরবারের নিকটে কাটিয়েছিলেন যা প্রথম ক্রুসেডের সাক্ষী ছিল। ( ১০৪৮-১১৩১ ) কণিক ব্যবহার করে বীজগাণিতিক সমীকরণ সমাধান করেন। রেনে দেকার্তে
ওমর খৈয়াম ছিলেন পার্সিয়ান গণিতবিদ, জ্যোতির্বিদ, দার্শনিক এবং কবি। তিনি উত্তর-পূর্ব ইরানের নীশাবরে জন্মগ্রহণ করেছিলেন এবং তাঁর বেশিরভাগ জীবন কারাখানিদ ও সেলজাক শাসকদের দরবারের নিকটে কাটিয়েছিলেন যা প্রথম ক্রুসেডের সাক্ষী ছিল। ( ১০৪৮-১১৩১ ) কণিক ব্যবহার করে বীজগাণিতিক সমীকরণ সমাধান করেন। রেনে দেকার্তে  প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে (১৫৯৬-১৬৫০) আধুনিক ফাংশনের ধারণা দেন । (১৫৯৬-১৬৫০) কণিকের ধর্ম ও বৈশিষ্ট নির্ণয়ে তার নব উদ্ভাবিত বৈশ্লেষিক জ্যামিতি ব্যবহার করেন। তার এই অবদানের ফলে কণিকের ধর্ম ও বৈশিষ্ট নির্ণয়ের জ্যামিতিক সমস্যাগুলো বীজগাণিতিক সমস্যায় রূপান্তরিত হয় যা অধিকতর সহজবোধ্য।
প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে (১৫৯৬-১৬৫০) আধুনিক ফাংশনের ধারণা দেন । (১৫৯৬-১৬৫০) কণিকের ধর্ম ও বৈশিষ্ট নির্ণয়ে তার নব উদ্ভাবিত বৈশ্লেষিক জ্যামিতি ব্যবহার করেন। তার এই অবদানের ফলে কণিকের ধর্ম ও বৈশিষ্ট নির্ণয়ের জ্যামিতিক সমস্যাগুলো বীজগাণিতিক সমস্যায় রূপান্তরিত হয় যা অধিকতর সহজবোধ্য।
 ম্যানিসমিউস (৩৮০-৩২০ খ্রিষ্টপূর্ব) কোণক দ্বারা সমতলে বক্ররেখার ছেদাংশের বিভিন্ন অংশকে পরাবৃত্ত, উপবৃত্ত ও অধিবৃত্ত নামকরণ করেন। পরবর্তীতে ইউক্লিড
ম্যানিসমিউস (৩৮০-৩২০ খ্রিষ্টপূর্ব) কোণক দ্বারা সমতলে বক্ররেখার ছেদাংশের বিভিন্ন অংশকে পরাবৃত্ত, উপবৃত্ত ও অধিবৃত্ত নামকরণ করেন। পরবর্তীতে ইউক্লিড  ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। কণিক সংক্রান্ত চারটি পুস্তক রচনা করেন যার সবকটিই কালের অতল গর্ভে বিলিন হয়ে গেছে। আর্কিমিডিস
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। কণিক সংক্রান্ত চারটি পুস্তক রচনা করেন যার সবকটিই কালের অতল গর্ভে বিলিন হয়ে গেছে। আর্কিমিডিস  আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। কণিক নিয়ে গবেষ্ণা করেছিলেন বলে প্রমাণ পাওয়া যায়। তিনি পরাবৃত্ত ও উপবৃত্ত দ্বারা আবদ্ধ ক্ষেত্রের ক্ষেত্রফল নির্ণয়ের উপায় উদ্ভাবন করেন। গ্রীক দার্শনিক অ্যাপোলোনিয়াস
আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। কণিক নিয়ে গবেষ্ণা করেছিলেন বলে প্রমাণ পাওয়া যায়। তিনি পরাবৃত্ত ও উপবৃত্ত দ্বারা আবদ্ধ ক্ষেত্রের ক্ষেত্রফল নির্ণয়ের উপায় উদ্ভাবন করেন। গ্রীক দার্শনিক অ্যাপোলোনিয়াস  পের্গার অ্যাপোলোনিয়াস ছিলেন গ্রীক জিওমিটার এবং জ্যোতির্বিজ্ঞানী, যেটি শঙ্কু বিভাগের বিষয়ে তত্ত্বগুলির জন্য পরিচিত ছিল। এই বিষয়ে ইউক্লিড এবং আর্কিমিডিসের তত্ত্বগুলি থেকে শুরু করে, তিনি বিশ্লেষণাত্মক জ্যামিতির আবিষ্কারের ঠিক আগে তারা তাদের সেই অবস্থায় নিয়ে এসেছিলেন। তৎকালীন সময়ে প্রচলিত ধারণাসমূহ সংকলন করেন এবং তার প্রচলিত জ্ঞানসমূহের সম্প্রসারণ হিসেবে স্ব-উদ্ভাবিত কিছু ধারণা যুক্ত করেন। পাপ্পাস
পের্গার অ্যাপোলোনিয়াস ছিলেন গ্রীক জিওমিটার এবং জ্যোতির্বিজ্ঞানী, যেটি শঙ্কু বিভাগের বিষয়ে তত্ত্বগুলির জন্য পরিচিত ছিল। এই বিষয়ে ইউক্লিড এবং আর্কিমিডিসের তত্ত্বগুলি থেকে শুরু করে, তিনি বিশ্লেষণাত্মক জ্যামিতির আবিষ্কারের ঠিক আগে তারা তাদের সেই অবস্থায় নিয়ে এসেছিলেন। তৎকালীন সময়ে প্রচলিত ধারণাসমূহ সংকলন করেন এবং তার প্রচলিত জ্ঞানসমূহের সম্প্রসারণ হিসেবে স্ব-উদ্ভাবিত কিছু ধারণা যুক্ত করেন। পাপ্পাস  আলেকজান্দ্রিয়ার প্যাপস ছিলেন প্রাচীন প্রাচীন গ্রীক গণিতবিদদের মধ্যে অন্যতম, তিনি তাঁর সিনাগেজ বা সংগ্রহের জন্য এবং পাপ্পাসের ষড়ভুজ উপপাদ্যকে প্রজেক্টিভ জ্যামিতিতে জেনেছিলেন। কণিকের উপকেন্দ্রের গুরুত্ব অনুধাবন করেন। ১০০০ সালে আল-কুহি (940 AD-1000 AD)
আলেকজান্দ্রিয়ার প্যাপস ছিলেন প্রাচীন প্রাচীন গ্রীক গণিতবিদদের মধ্যে অন্যতম, তিনি তাঁর সিনাগেজ বা সংগ্রহের জন্য এবং পাপ্পাসের ষড়ভুজ উপপাদ্যকে প্রজেক্টিভ জ্যামিতিতে জেনেছিলেন। কণিকের উপকেন্দ্রের গুরুত্ব অনুধাবন করেন। ১০০০ সালে আল-কুহি (940 AD-1000 AD) আবাহ সাহল ওয়াজান ইবনে রুস্তম আল-কাহি ছিলেন একজন পার্সিয়ান গণিতবিদ, পদার্থবিদ এবং জ্যোতির্বিদ। তিনি আমোলের তাবারিস্তানের কুহ থেকে আগত এবং দশম শতাব্দীতে বাগদাদে বিকাশ লাভ করেছিলেন। তাঁকে গণিত ও জ্যোতির্বিজ্ঞান সংক্রান্ত অনেকগুলি লেখাই সর্বশ্রেষ্ঠ মুসলিম জিওমিটার হিসাবে বিবেচনা করা হয়। কণিকের চিত্র অঙ্কন করার সরঞ্জাম উদ্ভাবন করেন। পারস্যের বিখ্যাত কবি ও গণিতবিদ ওমর খৈয়াম
আবাহ সাহল ওয়াজান ইবনে রুস্তম আল-কাহি ছিলেন একজন পার্সিয়ান গণিতবিদ, পদার্থবিদ এবং জ্যোতির্বিদ। তিনি আমোলের তাবারিস্তানের কুহ থেকে আগত এবং দশম শতাব্দীতে বাগদাদে বিকাশ লাভ করেছিলেন। তাঁকে গণিত ও জ্যোতির্বিজ্ঞান সংক্রান্ত অনেকগুলি লেখাই সর্বশ্রেষ্ঠ মুসলিম জিওমিটার হিসাবে বিবেচনা করা হয়। কণিকের চিত্র অঙ্কন করার সরঞ্জাম উদ্ভাবন করেন। পারস্যের বিখ্যাত কবি ও গণিতবিদ ওমর খৈয়াম  ওমর খৈয়াম ছিলেন পার্সিয়ান গণিতবিদ, জ্যোতির্বিদ, দার্শনিক এবং কবি। তিনি উত্তর-পূর্ব ইরানের নীশাবরে জন্মগ্রহণ করেছিলেন এবং তাঁর বেশিরভাগ জীবন কারাখানিদ ও সেলজাক শাসকদের দরবারের নিকটে কাটিয়েছিলেন যা প্রথম ক্রুসেডের সাক্ষী ছিল। ( ১০৪৮-১১৩১ ) কণিক ব্যবহার করে বীজগাণিতিক সমীকরণ সমাধান করেন। রেনে দেকার্তে
ওমর খৈয়াম ছিলেন পার্সিয়ান গণিতবিদ, জ্যোতির্বিদ, দার্শনিক এবং কবি। তিনি উত্তর-পূর্ব ইরানের নীশাবরে জন্মগ্রহণ করেছিলেন এবং তাঁর বেশিরভাগ জীবন কারাখানিদ ও সেলজাক শাসকদের দরবারের নিকটে কাটিয়েছিলেন যা প্রথম ক্রুসেডের সাক্ষী ছিল। ( ১০৪৮-১১৩১ ) কণিক ব্যবহার করে বীজগাণিতিক সমীকরণ সমাধান করেন। রেনে দেকার্তে  প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে (১৫৯৬-১৬৫০) আধুনিক ফাংশনের ধারণা দেন । (১৫৯৬-১৬৫০) কণিকের ধর্ম ও বৈশিষ্ট নির্ণয়ে তার নব উদ্ভাবিত বৈশ্লেষিক জ্যামিতি ব্যবহার করেন। তার এই অবদানের ফলে কণিকের ধর্ম ও বৈশিষ্ট নির্ণয়ের জ্যামিতিক সমস্যাগুলো বীজগাণিতিক সমস্যায় রূপান্তরিত হয় যা অধিকতর সহজবোধ্য।
প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে (১৫৯৬-১৬৫০) আধুনিক ফাংশনের ধারণা দেন । (১৫৯৬-১৬৫০) কণিকের ধর্ম ও বৈশিষ্ট নির্ণয়ে তার নব উদ্ভাবিত বৈশ্লেষিক জ্যামিতি ব্যবহার করেন। তার এই অবদানের ফলে কণিকের ধর্ম ও বৈশিষ্ট নির্ণয়ের জ্যামিতিক সমস্যাগুলো বীজগাণিতিক সমস্যায় রূপান্তরিত হয় যা অধিকতর সহজবোধ্য।
কনিকের গঠনগত ব্যাখ্যা
Stractural explanation of Conics
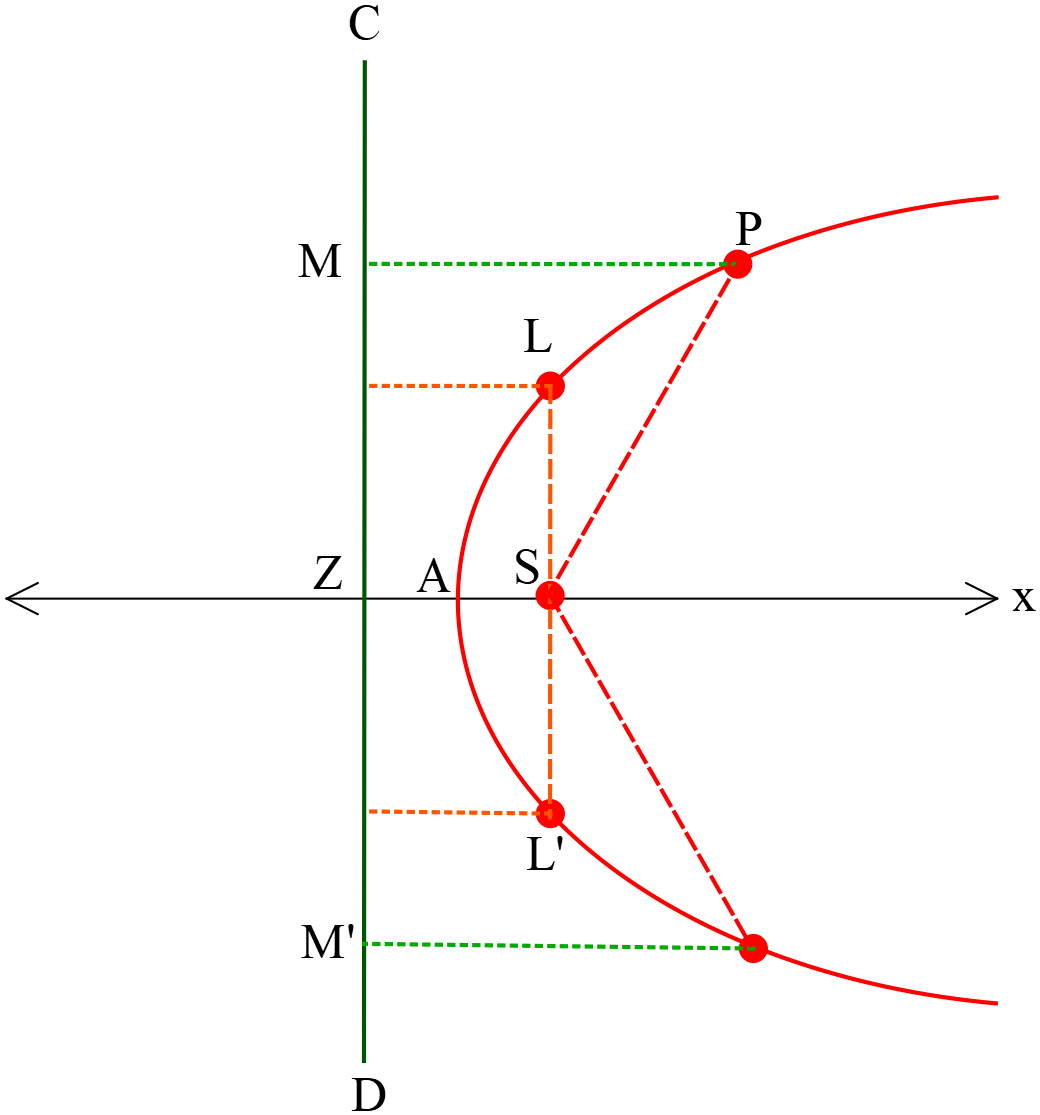 কনিক (Conics): কোন কার্তেসীয় সমতলে একটি বিন্দু যদি এমনভাবে চলে যে ঐ সমতলস্থিত একটি স্থির বিন্দু থেকে দূরত্ব এবং একটি নির্দিষ্ট রেখা থেকে লম্বদূরত্বের অনুপাত একটি স্থির রাশি , তবে ঐ বিন্দুর সঞ্চারপথকে কনিক বলা হয়।
স্থির বিন্দুটিকে কনিকের উপকেন্দ্র (Focus), নির্দিষ্ট সরলরেখাটিকে এর নিয়ামক রেখা (Directrix) এবং ঐ স্থির রাশিকে উৎকেন্দ্রিকতা বা বিকেন্দ্রিকতা (Eccentricity) বলাহয়।
জ্যামিতিক ব্যাখ্যাঃ মনে করি, কোন সমতলে \(S\) একটি স্থির বিন্দু এবং \(CD\) একটি স্থির সরলরেখা। একটি চলমান বিন্দু \(P(x, y)\) যা সমতলের উপর অবস্থিত। \(P\) বিন্দু হতে \(S\) বিন্দুর দূরত্ব \(PS\) এবং \(P\) বিন্দু হতে \(CD\) এর উপর লম্ব-দূরত্ব \(PM\) এর অনুপাত সর্বদা স্থির হয়, তাহলে \(P\) এর সঞ্চারপথকে কনিক বলে। স্থির রাশিটিকে \(e\) দ্বারা প্রকাশ করলে \(\frac{PS}{PM}=e\) হয়। এখানে \(e\) কে উৎকেন্দ্রিকতা (Eccentricity) বলে। সুতরাং \(PS=e.PM\) কনিকের সমীকরণ প্রকাশ করে।
কনিক (Conics): কোন কার্তেসীয় সমতলে একটি বিন্দু যদি এমনভাবে চলে যে ঐ সমতলস্থিত একটি স্থির বিন্দু থেকে দূরত্ব এবং একটি নির্দিষ্ট রেখা থেকে লম্বদূরত্বের অনুপাত একটি স্থির রাশি , তবে ঐ বিন্দুর সঞ্চারপথকে কনিক বলা হয়।
স্থির বিন্দুটিকে কনিকের উপকেন্দ্র (Focus), নির্দিষ্ট সরলরেখাটিকে এর নিয়ামক রেখা (Directrix) এবং ঐ স্থির রাশিকে উৎকেন্দ্রিকতা বা বিকেন্দ্রিকতা (Eccentricity) বলাহয়।
জ্যামিতিক ব্যাখ্যাঃ মনে করি, কোন সমতলে \(S\) একটি স্থির বিন্দু এবং \(CD\) একটি স্থির সরলরেখা। একটি চলমান বিন্দু \(P(x, y)\) যা সমতলের উপর অবস্থিত। \(P\) বিন্দু হতে \(S\) বিন্দুর দূরত্ব \(PS\) এবং \(P\) বিন্দু হতে \(CD\) এর উপর লম্ব-দূরত্ব \(PM\) এর অনুপাত সর্বদা স্থির হয়, তাহলে \(P\) এর সঞ্চারপথকে কনিক বলে। স্থির রাশিটিকে \(e\) দ্বারা প্রকাশ করলে \(\frac{PS}{PM}=e\) হয়। এখানে \(e\) কে উৎকেন্দ্রিকতা (Eccentricity) বলে। সুতরাং \(PS=e.PM\) কনিকের সমীকরণ প্রকাশ করে।
সংজ্ঞাসমূহ
Definitions
অক্ষরেখাঃ উপকেন্দ্রের মধ্যদিয়ে নিয়ামকরেখার উপর অঙ্কিত লম্ব রেখাটিকে (AX) পরাবৃত্তের অক্ষরেখা বা অক্ষ (Axis) বলা হয়।
শীর্ষবিন্দুঃ পরাবৃত্ত ও অক্ষরেখার ছেদবিন্দুকে (A) পরাবৃত্তের শীর্ষবিন্দু (Vertex) বলে।
উপকেন্দ্রঃ পরাবৃত্তের সংজ্ঞানুসারে নির্দিষ্ট বিন্দুটিকে (S) পরাবৃত্তের উপকেন্দ্র (Focus) বলে।
নিয়ামকরেখাঃ পরাবৃত্তের সংজ্ঞানুসারে নির্দিষ্ট সরলরেখাটিকে (CD) পরাবৃত্তের নিয়ামকরেখা (Directrix) বলে।
উৎকেন্দ্রিকতাঃ পরাবৃত্তের সংজ্ঞানুসারে স্থির অনুপাতটিকে \((e)\) পরাবৃত্তের উৎকেন্দ্রিকতা (Eccentricity) বলে।
নিয়ামকরেখার পাদবিন্দুঃ নিয়ামকরেখা ও অক্ষরেখার ছেদবিন্দুকে (Z) নিয়ামকরেখার পাদবিন্দু (Foot point) বলে।
উপকেন্দ্রিক দূরত্বঃ উপকেন্দ্র থেকে পরাবৃত্তের যে কোন বিন্দুর দূরত্বকে উপকেন্দ্রিক দূরত্ব (Focal distance) বলে।
উপকেন্দ্রিক জ্যাঃ পরাবৃত্তের যে জ্যা পরাবৃত্তের উপকেন্দ্র দিয়ে গমন করে তাকে উপকেন্দ্রিক জ্যা (Focal chord) বলে।
উপকেন্দ্রিক লম্বঃ উপকেন্দ্রিক জ্যা অক্ষের উপর লম্ব হলে \(L\acute L\) তাকে পরাবৃত্তের উপকেন্দ্রিক লম্ব (Latus rectum) বলে।
শীর্ষবিন্দুঃ পরাবৃত্ত ও অক্ষরেখার ছেদবিন্দুকে (A) পরাবৃত্তের শীর্ষবিন্দু (Vertex) বলে।
উপকেন্দ্রঃ পরাবৃত্তের সংজ্ঞানুসারে নির্দিষ্ট বিন্দুটিকে (S) পরাবৃত্তের উপকেন্দ্র (Focus) বলে।
নিয়ামকরেখাঃ পরাবৃত্তের সংজ্ঞানুসারে নির্দিষ্ট সরলরেখাটিকে (CD) পরাবৃত্তের নিয়ামকরেখা (Directrix) বলে।
উৎকেন্দ্রিকতাঃ পরাবৃত্তের সংজ্ঞানুসারে স্থির অনুপাতটিকে \((e)\) পরাবৃত্তের উৎকেন্দ্রিকতা (Eccentricity) বলে।
নিয়ামকরেখার পাদবিন্দুঃ নিয়ামকরেখা ও অক্ষরেখার ছেদবিন্দুকে (Z) নিয়ামকরেখার পাদবিন্দু (Foot point) বলে।
উপকেন্দ্রিক দূরত্বঃ উপকেন্দ্র থেকে পরাবৃত্তের যে কোন বিন্দুর দূরত্বকে উপকেন্দ্রিক দূরত্ব (Focal distance) বলে।
উপকেন্দ্রিক জ্যাঃ পরাবৃত্তের যে জ্যা পরাবৃত্তের উপকেন্দ্র দিয়ে গমন করে তাকে উপকেন্দ্রিক জ্যা (Focal chord) বলে।
উপকেন্দ্রিক লম্বঃ উপকেন্দ্রিক জ্যা অক্ষের উপর লম্ব হলে \(L\acute L\) তাকে পরাবৃত্তের উপকেন্দ্রিক লম্ব (Latus rectum) বলে।
বিভিন্ন প্রকৃতির কনিক
Different types of Conic
\(e\) এর বিভিন্ন মানের জন্য সঞ্চারপথের আকৃতি বিভিন্ন হয়, যা নিম্নরূপঃ
বৃত্তঃ \(e=0\) হলে, সঞ্চারপথকে বৃত্ত (Circle) বলা হয়। অতএব বৃত্ত হলো উপবৃত্তের একটি সীমায়িত অবস্থান যার বিকেন্দ্রিকতা শুন্য এবং যার নিয়ামক অসীমে থাকে। আবার একটি বৃত্ত বিন্দুতে পরিণত হতে পারে যখন এর ব্যাসার্ধ শুন্য হয়।
পরাবৃত্তঃ \(e=1\) হলে, সঞ্চারপথকে পরাবৃত্ত (Parabola) বলা হয়। অতএব, পরাবৃত্তস্থ প্রত্যেকটি বিন্দু উপকেন্দ্র ও নিয়ামকরেখা থেকে সমান দূরে অবস্থিত।
উপবৃত্তঃ \(1>e>0\) হলে, সঞ্চারপথকে উপবৃত্ত (Ellipse) বলা হয়। উপবৃত্তস্থ প্রত্যেকটি বিন্দু থেকে উপকেন্দ্র ও নিয়ামকরেখার দূরত্বের অনুপাত একটি স্থির রাশি যার মাণ শুন্য অপেক্ষা বড় এবং \(1\) অপেক্ষা ছোট।
অধিবৃত্তঃ \(e>1\) হলে, সঞ্চারপথকে অধিবৃত্ত (Hyperbola) বলা হয়। অধিবৃত্তস্থ প্রত্যেকটি বিন্দু থেকে উপকেন্দ্র ও নিয়ামকরেখার দূরত্বের অনুপাত একটি স্থির রাশি যার মাণ \(1\) অপেক্ষা বড় ।
যুগল সরলরেখাঃ \(e>1\) এবং উপকেন্দ্র নিয়ামকের উপর অবস্থিত হলে, সঞ্চারপথকে যুগল সরলরেখা (Pair of Straight Lines) বলা হয়। অতএব এক্ষেত্রে কনিকটি দুইটি বাস্তব ও ভিন্ন সরলরেখা নির্দেশ করেন।
বৃত্তঃ \(e=0\) হলে, সঞ্চারপথকে বৃত্ত (Circle) বলা হয়। অতএব বৃত্ত হলো উপবৃত্তের একটি সীমায়িত অবস্থান যার বিকেন্দ্রিকতা শুন্য এবং যার নিয়ামক অসীমে থাকে। আবার একটি বৃত্ত বিন্দুতে পরিণত হতে পারে যখন এর ব্যাসার্ধ শুন্য হয়।
পরাবৃত্তঃ \(e=1\) হলে, সঞ্চারপথকে পরাবৃত্ত (Parabola) বলা হয়। অতএব, পরাবৃত্তস্থ প্রত্যেকটি বিন্দু উপকেন্দ্র ও নিয়ামকরেখা থেকে সমান দূরে অবস্থিত।
উপবৃত্তঃ \(1>e>0\) হলে, সঞ্চারপথকে উপবৃত্ত (Ellipse) বলা হয়। উপবৃত্তস্থ প্রত্যেকটি বিন্দু থেকে উপকেন্দ্র ও নিয়ামকরেখার দূরত্বের অনুপাত একটি স্থির রাশি যার মাণ শুন্য অপেক্ষা বড় এবং \(1\) অপেক্ষা ছোট।
অধিবৃত্তঃ \(e>1\) হলে, সঞ্চারপথকে অধিবৃত্ত (Hyperbola) বলা হয়। অধিবৃত্তস্থ প্রত্যেকটি বিন্দু থেকে উপকেন্দ্র ও নিয়ামকরেখার দূরত্বের অনুপাত একটি স্থির রাশি যার মাণ \(1\) অপেক্ষা বড় ।
যুগল সরলরেখাঃ \(e>1\) এবং উপকেন্দ্র নিয়ামকের উপর অবস্থিত হলে, সঞ্চারপথকে যুগল সরলরেখা (Pair of Straight Lines) বলা হয়। অতএব এক্ষেত্রে কনিকটি দুইটি বাস্তব ও ভিন্ন সরলরেখা নির্দেশ করেন।
চিত্রের সাহায্যে কনিক উপস্থাপন
Representation of Conic by diagram
কোনো কনিকের উপকেন্দ্র \(S\) নিয়ামক রেখা \(MZ\acute M\) ( পরাবৃত্তের ক্ষেত্রে ) এবং \(MZ\) ও \(\acute M\acute Z\) ( উপবৃত্ত ও অধিবৃত্তের ক্ষেত্রে ) উৎকেন্দ্রিকতা \(e\) এবং উক্ত কনিকের উপরস্থ যে কোনো বিন্দু \(P(x, y)\) হলে উক্ত কনিকের সমীকরণ \(\frac{PS}{PM}=e\)।
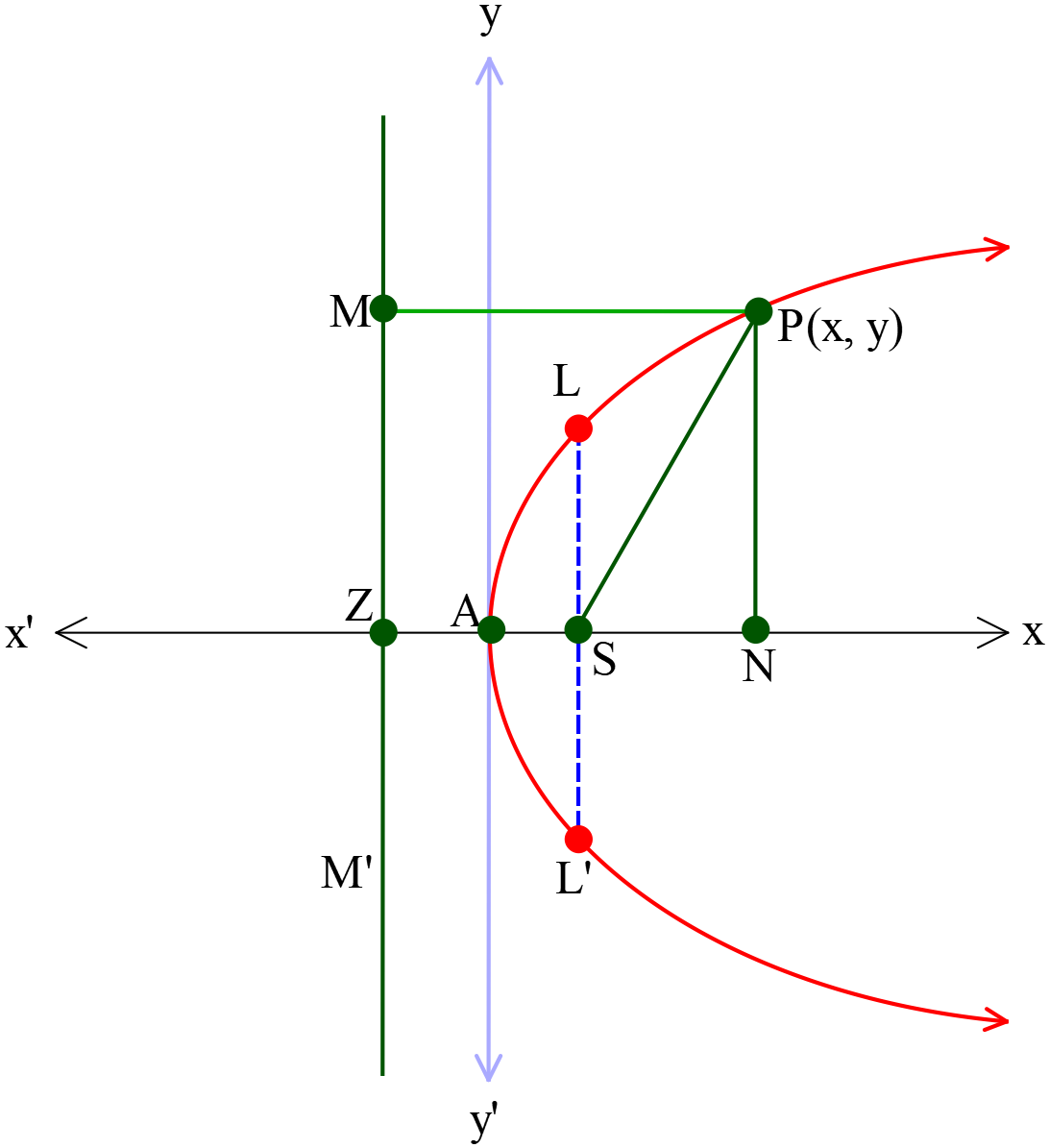 কনিকটি একটি পরাবৃত্ত (Parabola) প্রকাশ করে; যখন \(e=1\) এবং \(SP=PM\)।
কনিকটি একটি পরাবৃত্ত (Parabola) প্রকাশ করে; যখন \(e=1\) এবং \(SP=PM\)।
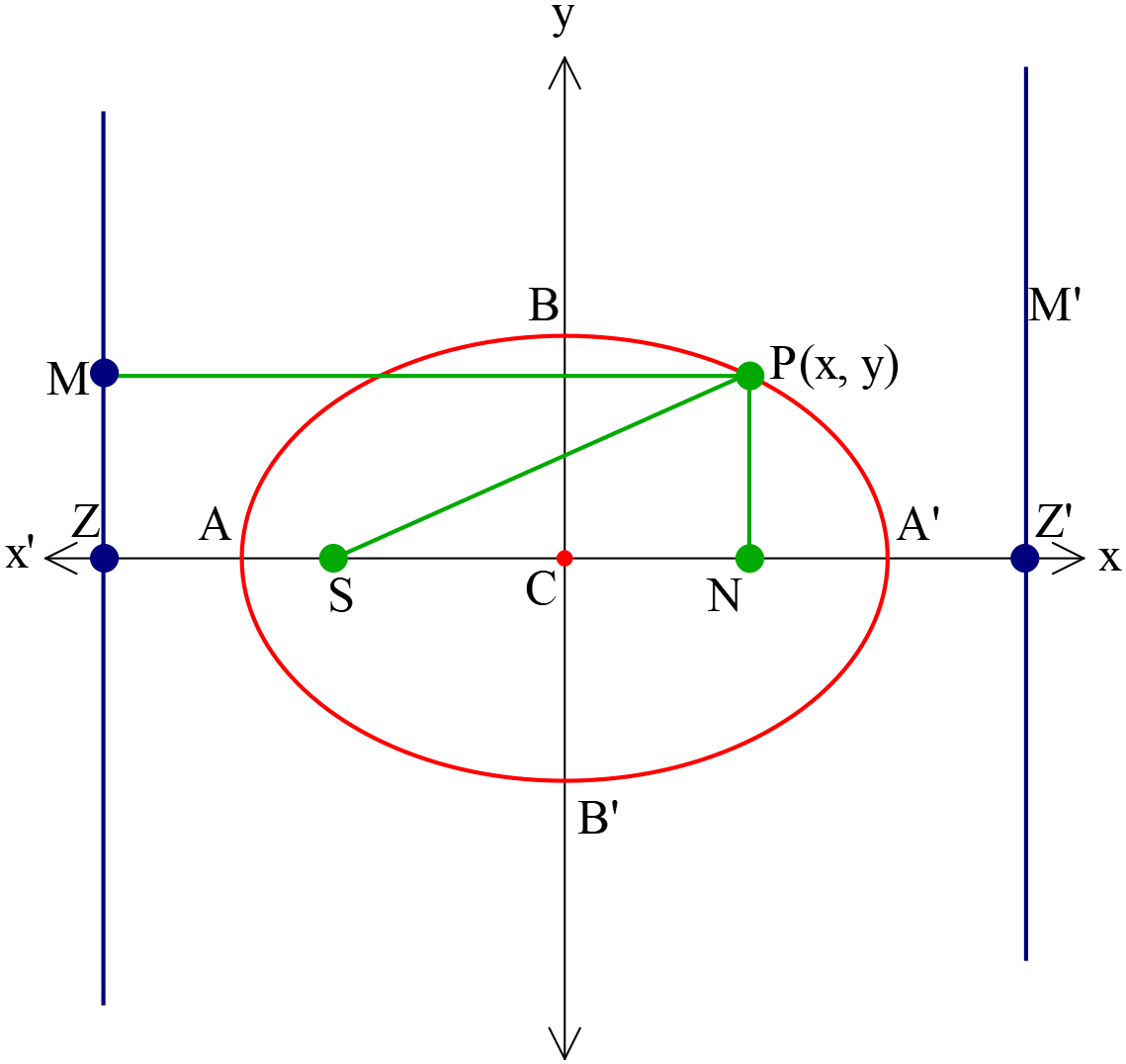 কনিকটি একটি উপবৃত্ত (Ellipse) প্রকাশ করে; যখন \(1 > e > 0\) এবং \(SP=e.PM\)।
কনিকটি একটি উপবৃত্ত (Ellipse) প্রকাশ করে; যখন \(1 > e > 0\) এবং \(SP=e.PM\)।
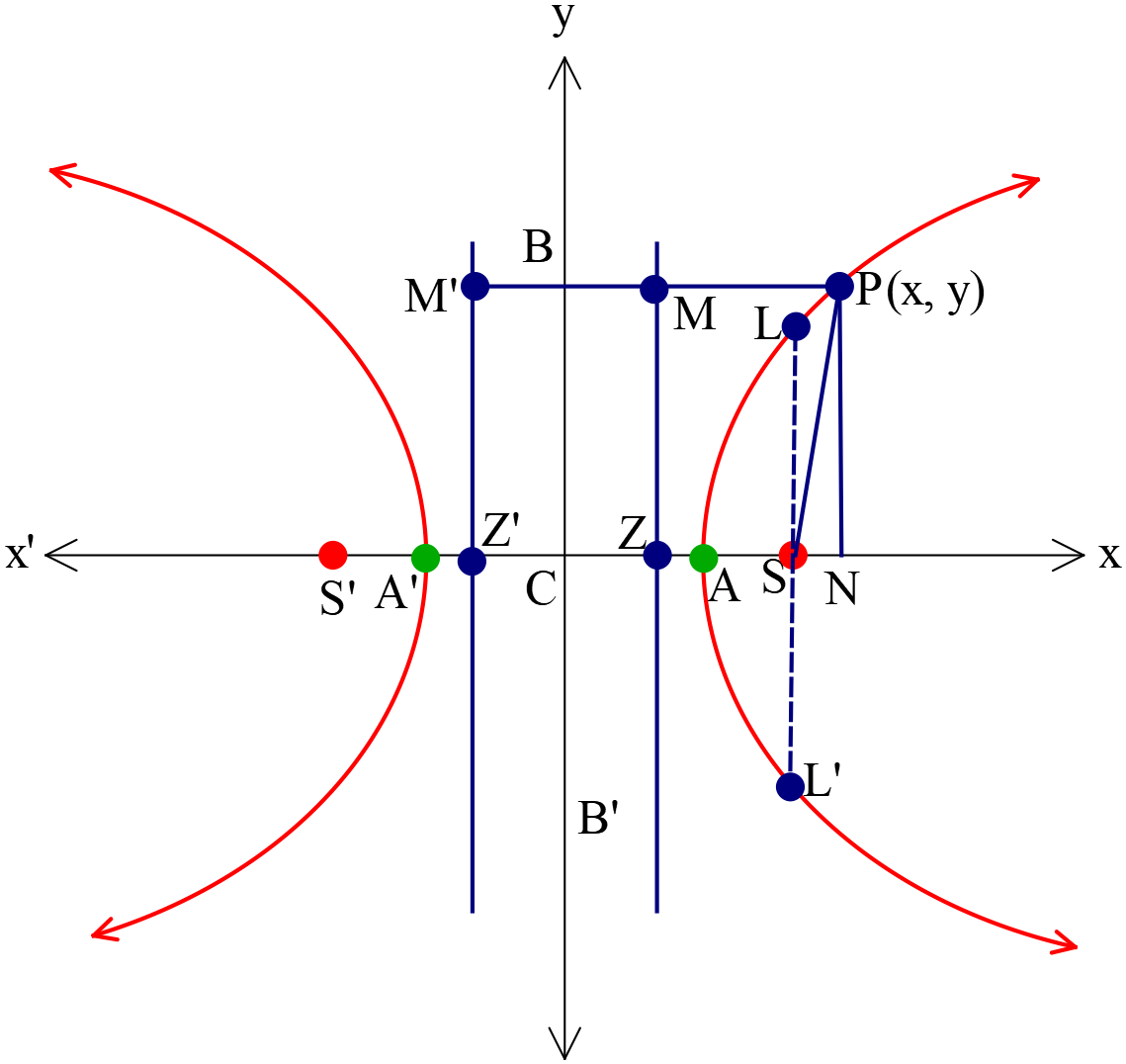 কনিকটি একটি অধিবৃত্ত (Hyperbola) প্রকাশ করে; যখন \(e>1\) এবং \(SP=e.PM\)।
কনিকটি একটি অধিবৃত্ত (Hyperbola) প্রকাশ করে; যখন \(e>1\) এবং \(SP=e.PM\)।
 কনিকটি একটি পরাবৃত্ত (Parabola) প্রকাশ করে; যখন \(e=1\) এবং \(SP=PM\)।
কনিকটি একটি পরাবৃত্ত (Parabola) প্রকাশ করে; যখন \(e=1\) এবং \(SP=PM\)। কনিকটি একটি উপবৃত্ত (Ellipse) প্রকাশ করে; যখন \(1 > e > 0\) এবং \(SP=e.PM\)।
কনিকটি একটি উপবৃত্ত (Ellipse) প্রকাশ করে; যখন \(1 > e > 0\) এবং \(SP=e.PM\)। কনিকটি একটি অধিবৃত্ত (Hyperbola) প্রকাশ করে; যখন \(e>1\) এবং \(SP=e.PM\)।
কনিকটি একটি অধিবৃত্ত (Hyperbola) প্রকাশ করে; যখন \(e>1\) এবং \(SP=e.PM\)। কোনোকের এবং সমতলের ছেদবিন্দুর সঞ্চারপথই যে কনিক তা চিত্রের সাহায্যে প্রকাশ
Conic which representing the locus of intersection of cone and a plane by diagram
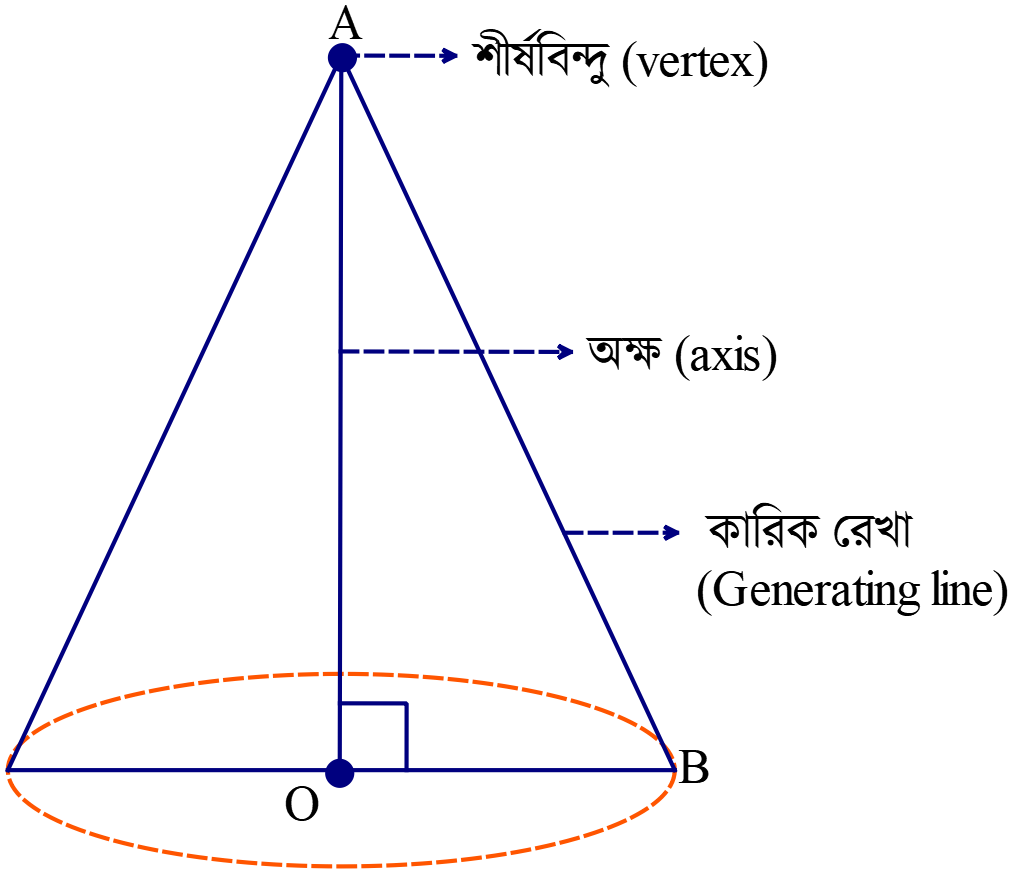 কোণ থেকে কনিকের উৎপত্তি। একটি নির্দিষ্ট সরলরেখা কোনো নির্দিষ্ট বিন্দুতে অপর একটি সরলরেখার এক প্রান্ত বেধে রেখে যদি রেখাটিকে ঐ নির্দিষ্ট রেখার চারিদিকে সূক্ষ্ণকোণে আবর্তন করানো হয়, তবে একটি বৃত্তীয় কোণ উৎপন্ন হয়। নির্দিষ্ট রেখাটি \((AO)\) ভূমির সহিত লম্ব অর্থাৎ \(\angle AOB=90^o\) হলে একটি সমবৃত্তীয় কোণ উৎপন্ন হয়। নির্দিষ্ট বিন্দুটিকে কোণের শীর্ষবিন্দু, নির্দিষ্ট সরলরেখাকে অক্ষ এবং ঘূর্নায়মান রেখাকে কারিক রেখা (Generating line) বলা হয়।
কোণ থেকে কনিকের উৎপত্তি। একটি নির্দিষ্ট সরলরেখা কোনো নির্দিষ্ট বিন্দুতে অপর একটি সরলরেখার এক প্রান্ত বেধে রেখে যদি রেখাটিকে ঐ নির্দিষ্ট রেখার চারিদিকে সূক্ষ্ণকোণে আবর্তন করানো হয়, তবে একটি বৃত্তীয় কোণ উৎপন্ন হয়। নির্দিষ্ট রেখাটি \((AO)\) ভূমির সহিত লম্ব অর্থাৎ \(\angle AOB=90^o\) হলে একটি সমবৃত্তীয় কোণ উৎপন্ন হয়। নির্দিষ্ট বিন্দুটিকে কোণের শীর্ষবিন্দু, নির্দিষ্ট সরলরেখাকে অক্ষ এবং ঘূর্নায়মান রেখাকে কারিক রেখা (Generating line) বলা হয়।চিত্রে, \(AO\) অক্ষ (Axis) \(AB\) কারিক রেখা (Generating line) এবং \(\angle OAB\) কে অর্ধশীর্ষ কোণ বলা হয়ে থাকে।
কনিকের উৎস
Source of Conic
সমতল দ্বারা কোণের ছেদন বা কর্তনের ফলে কনিক উৎপন্ন হয়।
ভূমির সমান্তরাল কিন্তু শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একটি বৃত্ত (Circle) উৎপন্ন করে।
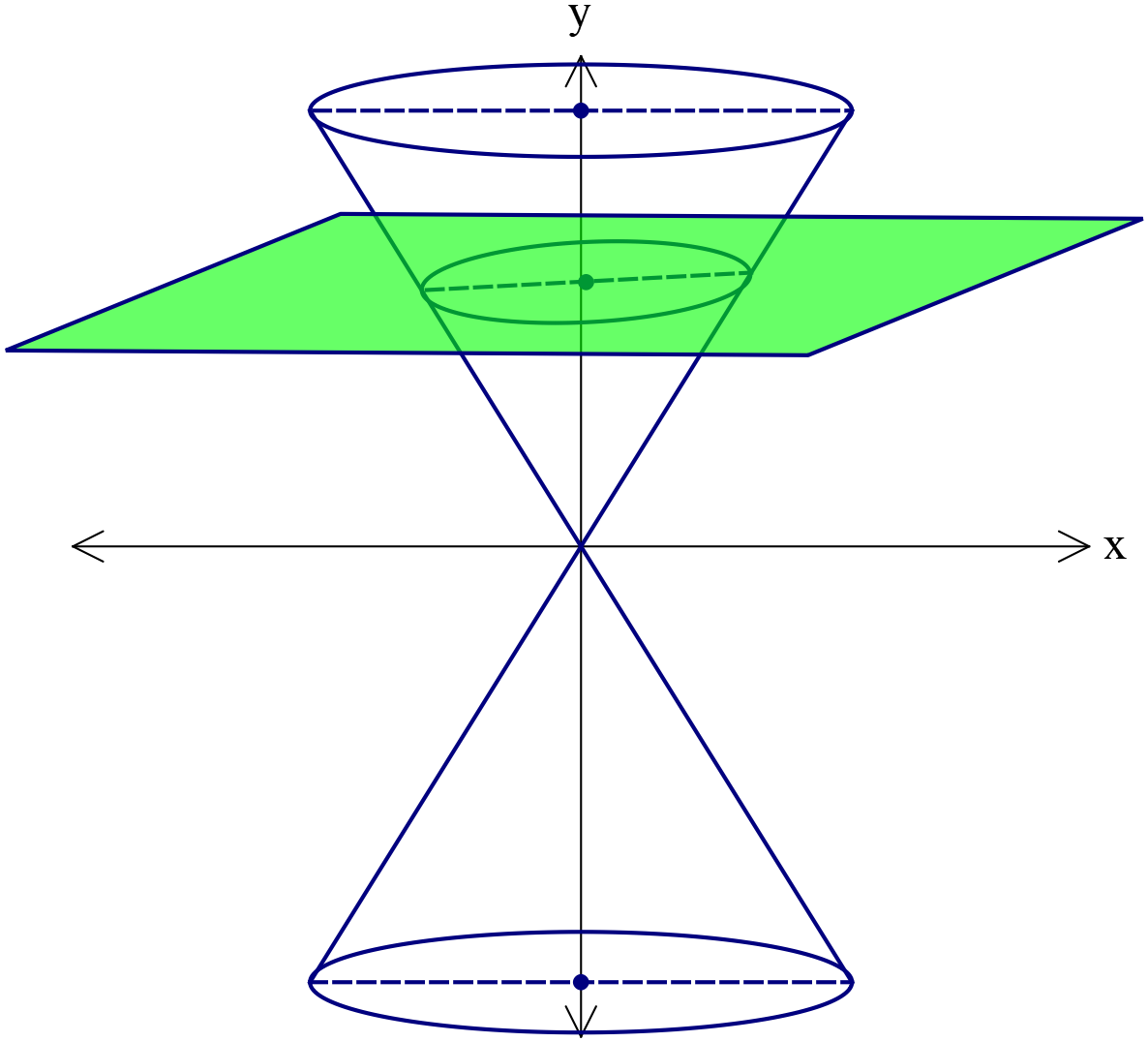 কারিক রেখার সমান্তরাল কিন্তু শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে ছেদ বা কর্তন করা হয়, তবে ছেদক রেখাটি একটি পরাবৃত্ত (parabola) উৎপন্ন করে।
কারিক রেখার সমান্তরাল কিন্তু শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে ছেদ বা কর্তন করা হয়, তবে ছেদক রেখাটি একটি পরাবৃত্ত (parabola) উৎপন্ন করে।
 কারিক রেখা ও ভূমির সমান্তরাল নয় এবং শীর্ষবিন্দুগামীও নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একটি উপবৃত্ত (Ellipse) উৎপন্ন করে।
কারিক রেখা ও ভূমির সমান্তরাল নয় এবং শীর্ষবিন্দুগামীও নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একটি উপবৃত্ত (Ellipse) উৎপন্ন করে।
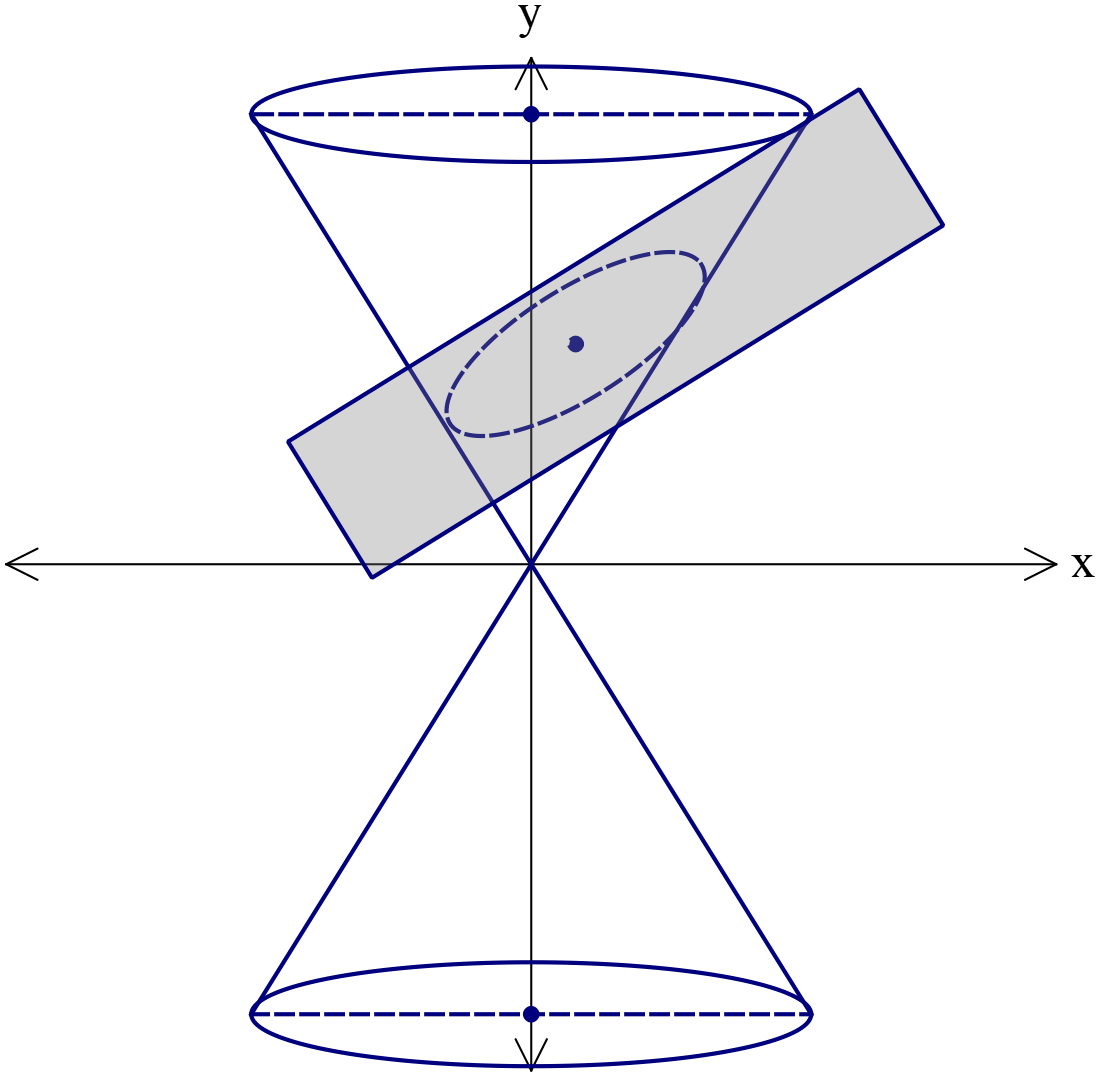 শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি কোনো দ্বিকোণকে এমনভাবে ছেদ করা হয় যেন তা উভয় কোণকে ছেদ করে, তবে ছেদক রেখাটি একটি অধিবৃত্ত (Hyperbola) উৎপন্ন করে।
শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি কোনো দ্বিকোণকে এমনভাবে ছেদ করা হয় যেন তা উভয় কোণকে ছেদ করে, তবে ছেদক রেখাটি একটি অধিবৃত্ত (Hyperbola) উৎপন্ন করে।
 শীর্ষবিন্দুগামী এবং ভূমির সহিত লম্ব এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একজোড়া সরলরেখা ( Pair of straight line) উৎপন্ন করে।
শীর্ষবিন্দুগামী এবং ভূমির সহিত লম্ব এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একজোড়া সরলরেখা ( Pair of straight line) উৎপন্ন করে।
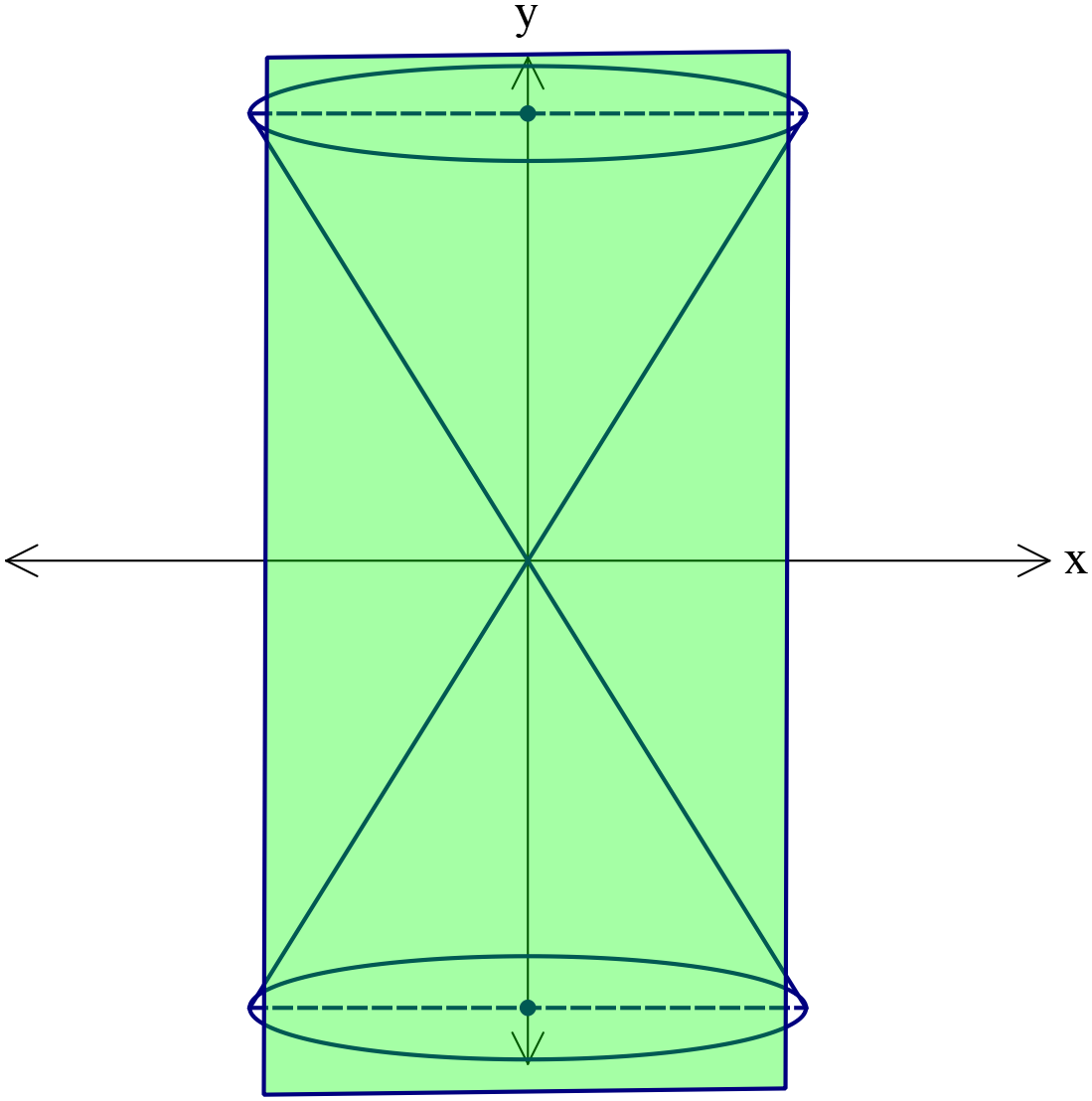
যেমনঃ
বৃত্ত, পরাবৃত্ত, উপবৃত্ত, অধিবৃত্ত এবং যুগল সরলরেখা।ভূমির সমান্তরাল কিন্তু শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একটি বৃত্ত (Circle) উৎপন্ন করে।
 কারিক রেখার সমান্তরাল কিন্তু শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে ছেদ বা কর্তন করা হয়, তবে ছেদক রেখাটি একটি পরাবৃত্ত (parabola) উৎপন্ন করে।
কারিক রেখার সমান্তরাল কিন্তু শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে ছেদ বা কর্তন করা হয়, তবে ছেদক রেখাটি একটি পরাবৃত্ত (parabola) উৎপন্ন করে। কারিক রেখা ও ভূমির সমান্তরাল নয় এবং শীর্ষবিন্দুগামীও নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একটি উপবৃত্ত (Ellipse) উৎপন্ন করে।
কারিক রেখা ও ভূমির সমান্তরাল নয় এবং শীর্ষবিন্দুগামীও নয় এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একটি উপবৃত্ত (Ellipse) উৎপন্ন করে। শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি কোনো দ্বিকোণকে এমনভাবে ছেদ করা হয় যেন তা উভয় কোণকে ছেদ করে, তবে ছেদক রেখাটি একটি অধিবৃত্ত (Hyperbola) উৎপন্ন করে।
শীর্ষবিন্দুগামী নয় এরূপ কোনো সমতল দ্বারা যদি কোনো দ্বিকোণকে এমনভাবে ছেদ করা হয় যেন তা উভয় কোণকে ছেদ করে, তবে ছেদক রেখাটি একটি অধিবৃত্ত (Hyperbola) উৎপন্ন করে। শীর্ষবিন্দুগামী এবং ভূমির সহিত লম্ব এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একজোড়া সরলরেখা ( Pair of straight line) উৎপন্ন করে।
শীর্ষবিন্দুগামী এবং ভূমির সহিত লম্ব এরূপ কোনো সমতল দ্বারা যদি সমবৃত্তীয় কোনোককে সম্পূর্ণরূপে ছেদ করা হয় তবে ছেদক রেখাটি একজোড়া সরলরেখা ( Pair of straight line) উৎপন্ন করে।
পরাবৃত্তের সমীকরণ সনাক্তকরণ
Identifying the equation of the parabola
পরাবৃত্তের সমীকরণে \(x^2\) অথবা, \(y^2\) যুক্ত পদ বিদ্যমান। \(x\) ও \(y\) যুক্ত পদ থাকতেও পারে নাও থাকতে পারে।
মূলবিন্দুগামী এবং \(x\) অক্ষের ধনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ
Equation of the parabola symmetrical about the origin and positive to the \(x\) axis
পরাবৃত্তের সমীকরণ \(y^2=4ax \ (a\gt{0})\)
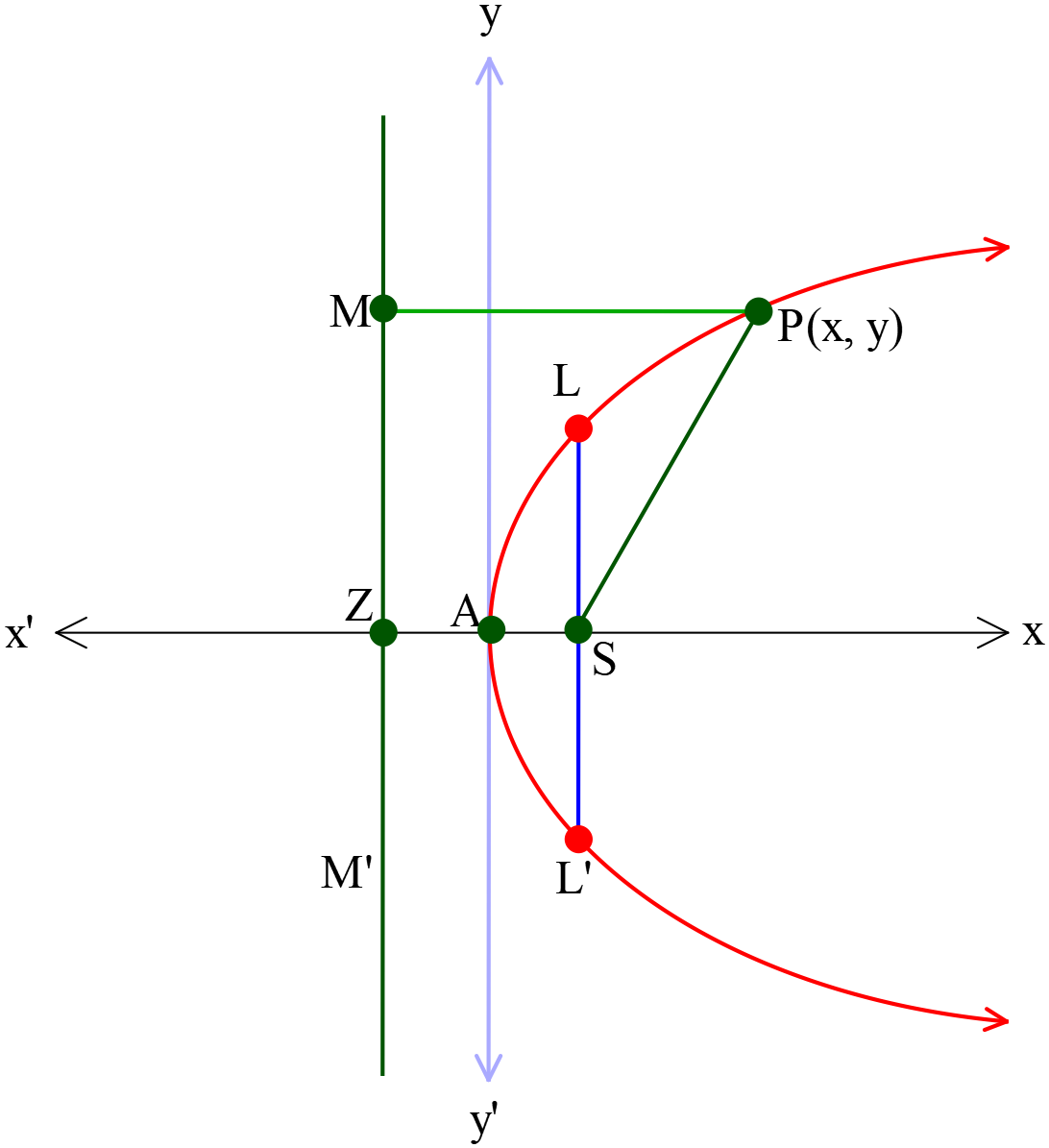

- শীর্ষবিন্দুর স্থানাঙ্ক \(A(0, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(a, 0)\)
- নিয়ামক রেখার সমীকরণ \(x=-a\)
- অক্ষরেখার সমীকরণ \(y=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x=a\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(x=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(-a, 0)\)
- \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব \(=a+|x|\)
মূলবিন্দুগামী এবং \(y\) অক্ষের ধনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ
Equation of the parabola symmetrical about the origin and positive to the \(y\) axis
পরাবৃত্তের সমীকরণ \(x^2=4ay \ (a\gt{0})\)
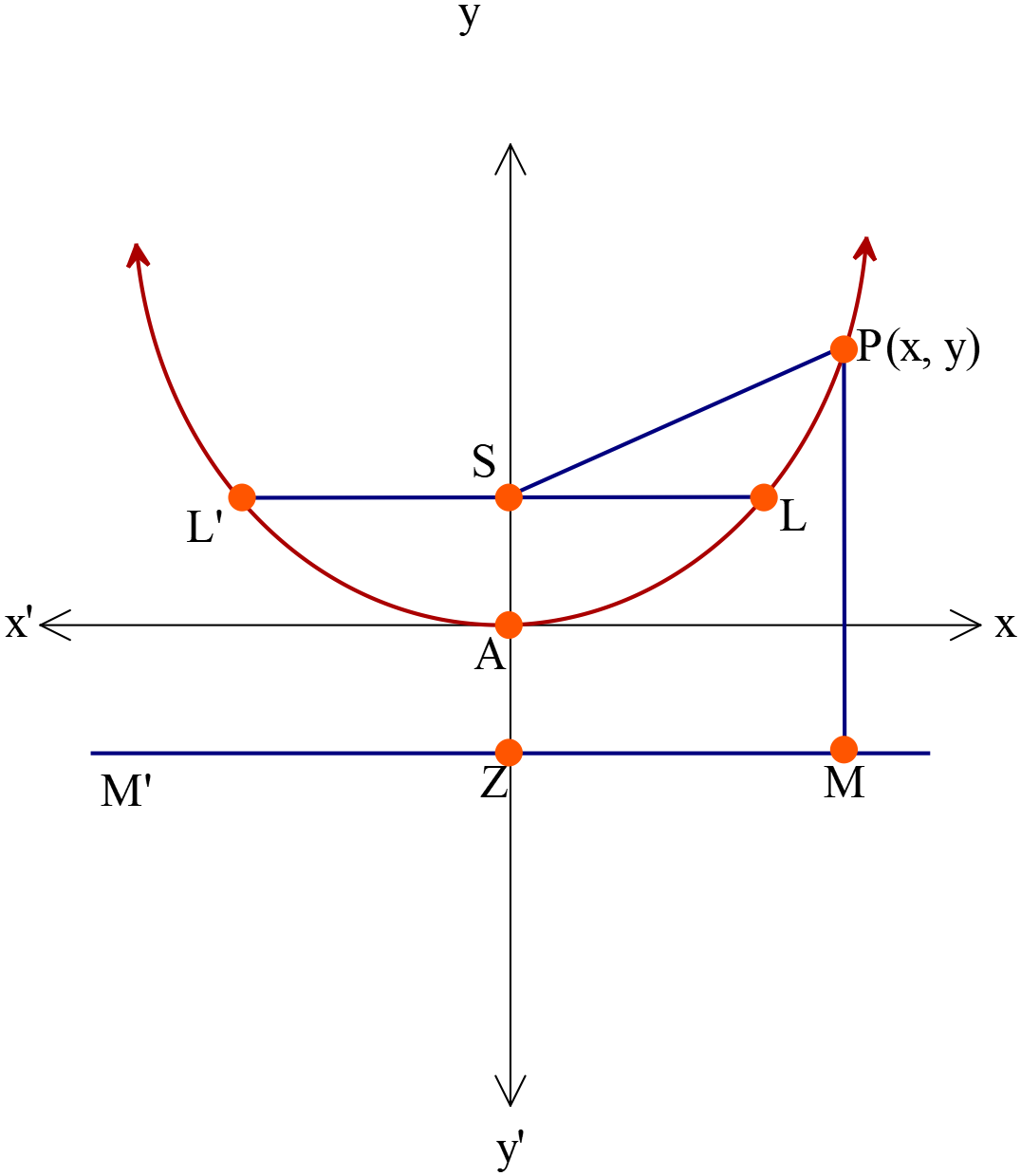

- শীর্ষবিন্দুর স্থানাঙ্ক \(A(0, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(0, a)\)
- নিয়ামক রেখার সমীকরণ \(y=-a\)
- অক্ষরেখার সমীকরণ \(x=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y=a\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(y=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(0, -a)\)
- \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব \(=a+|y|\)
মূলবিন্দুগামী এবং \(x\) অক্ষের ঋনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ
Equation of the parabola symmetrical about the origin and negative to the \(x\) axis
পরাবৃত্তের সমীকরণ \(y^2=-4ax \ (a\gt{0})\)
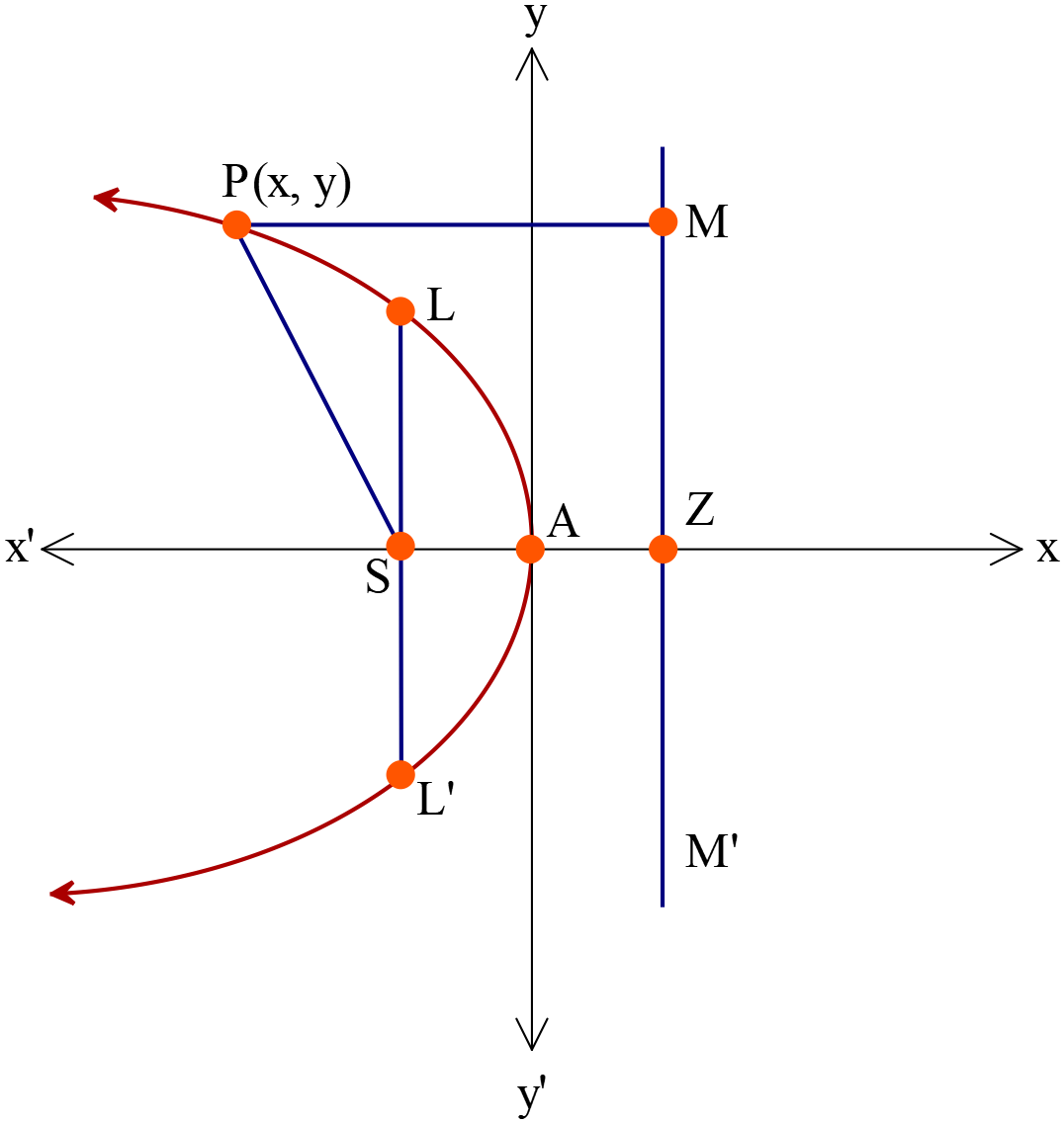

- শীর্ষবিন্দুর স্থানাঙ্ক \(A(0, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(-a, 0)\)
- নিয়ামক রেখার সমীকরণ \(x=a\)
- অক্ষরেখার সমীকরণ \(y=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x=-a\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(x=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(a, 0)\)
- \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব \(=a+|x|\)
মূলবিন্দুগামী এবং \(y\) অক্ষের ঋনাত্মক দিকে প্রতিসম পরাবৃত্তের সমীকরণ
Equation of the parabola symmetrical about the origin and negative to the \(y\) axis
পরাবৃত্তের সমীকরণ \(x^2=-4ay \ (a\gt{0})\)
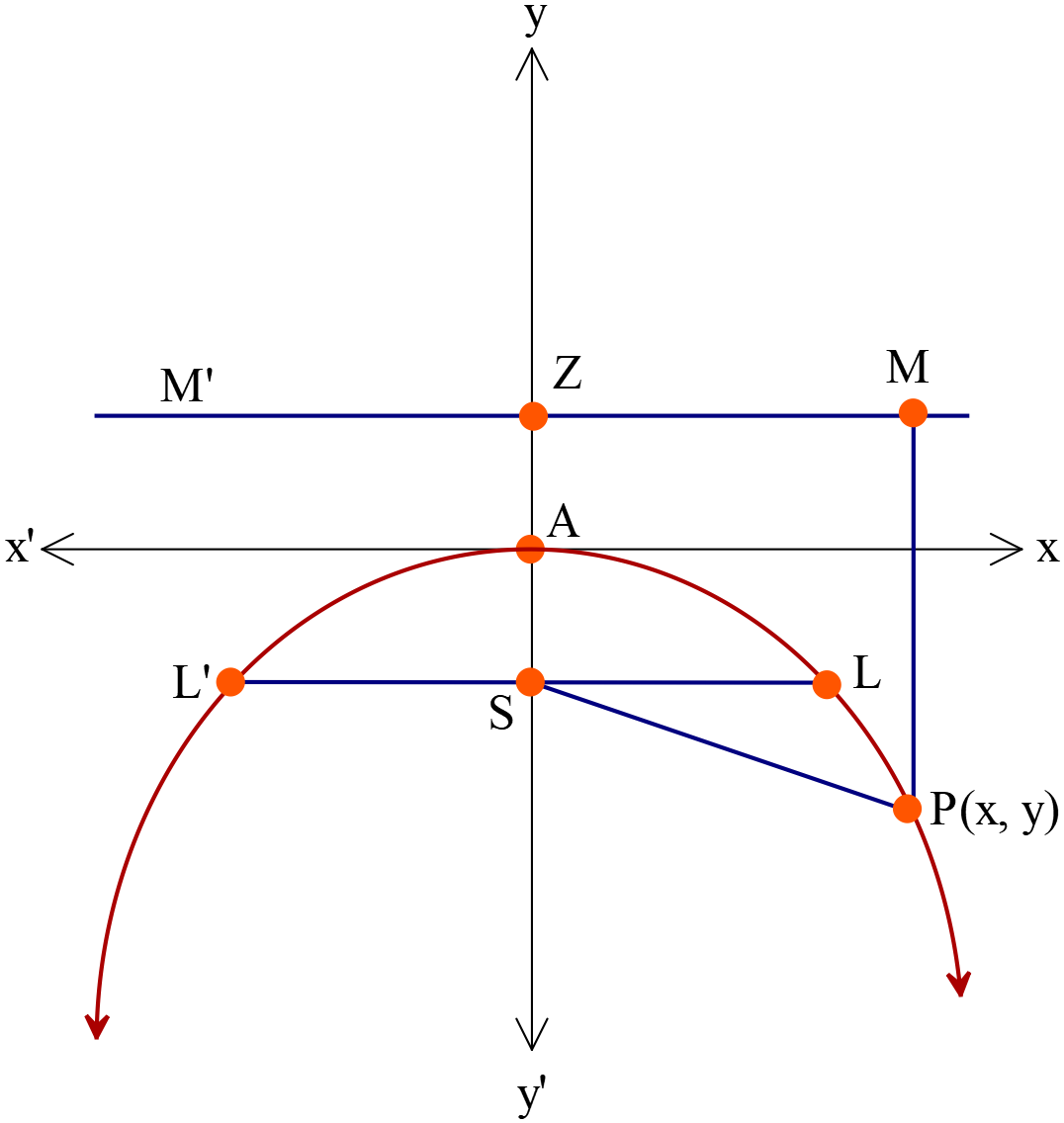

- শীর্ষবিন্দুর স্থানাঙ্ক \(A(0, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(0, -a)\)
- নিয়ামক রেখার সমীকরণ \(y=a\)
- অক্ষরেখার সমীকরণ \(x=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y=-a\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(y=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(0, a)\)
- \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব \(=a+|y|\)
মূলবিন্দুকে উপকেন্দ্রক ধরে পরাবৃত্তের সমীকরণ
Equation of a parabola with origin as epicenter
মূলবিন্দুকে উপকেন্দ্রক ধরে পরাবৃত্তের সমীকরণ \(y^2=4a(x+a) \ (a\gt{0})\)
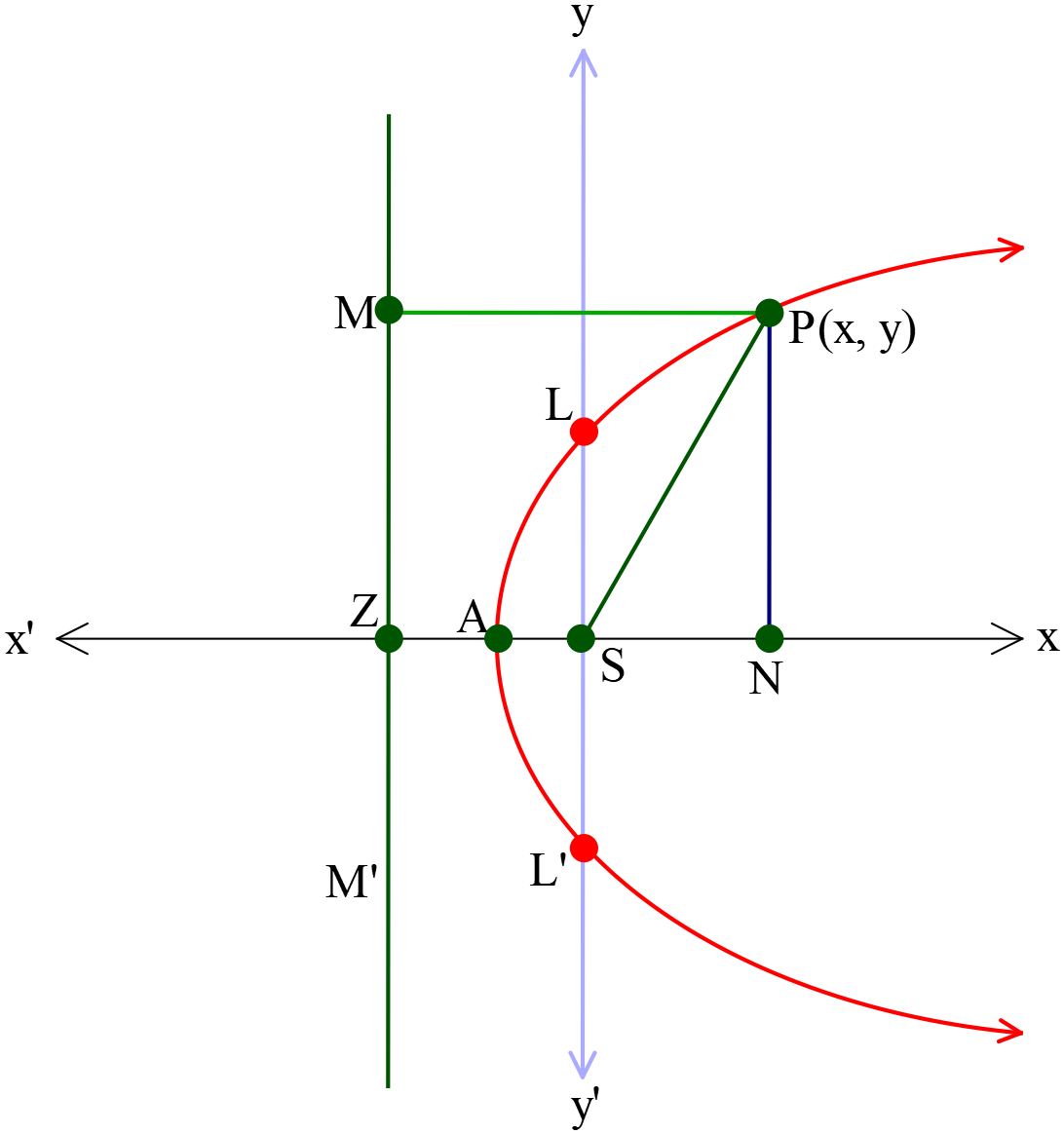

- শীর্ষবিন্দুর স্থানাঙ্ক \(A(-a, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(0, 0)\)
- নিয়ামক রেখার সমীকরণ \(x+2a=0\)
- অক্ষরেখার সমীকরণ \(y=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x=0\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(x+a=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(-2a, 0)\)
\(Y\) অক্ষকে নিয়ামকরেখা এবং \(X\) অক্ষকে অক্ষরেখা ধরে পরাবৃত্তের সমীকরণ
Equation of the parabola with the \(Y\) axis as the directrix and the \(X\) axis as the focus
\(Y\)-অক্ষকে নিয়ামকরেখা এবং \(X\)-অক্ষকে অক্ষরেখা ধরে পরাবৃত্তের সমীকরণ \(y^2=4a(x-a) \ (a\gt{0})\)
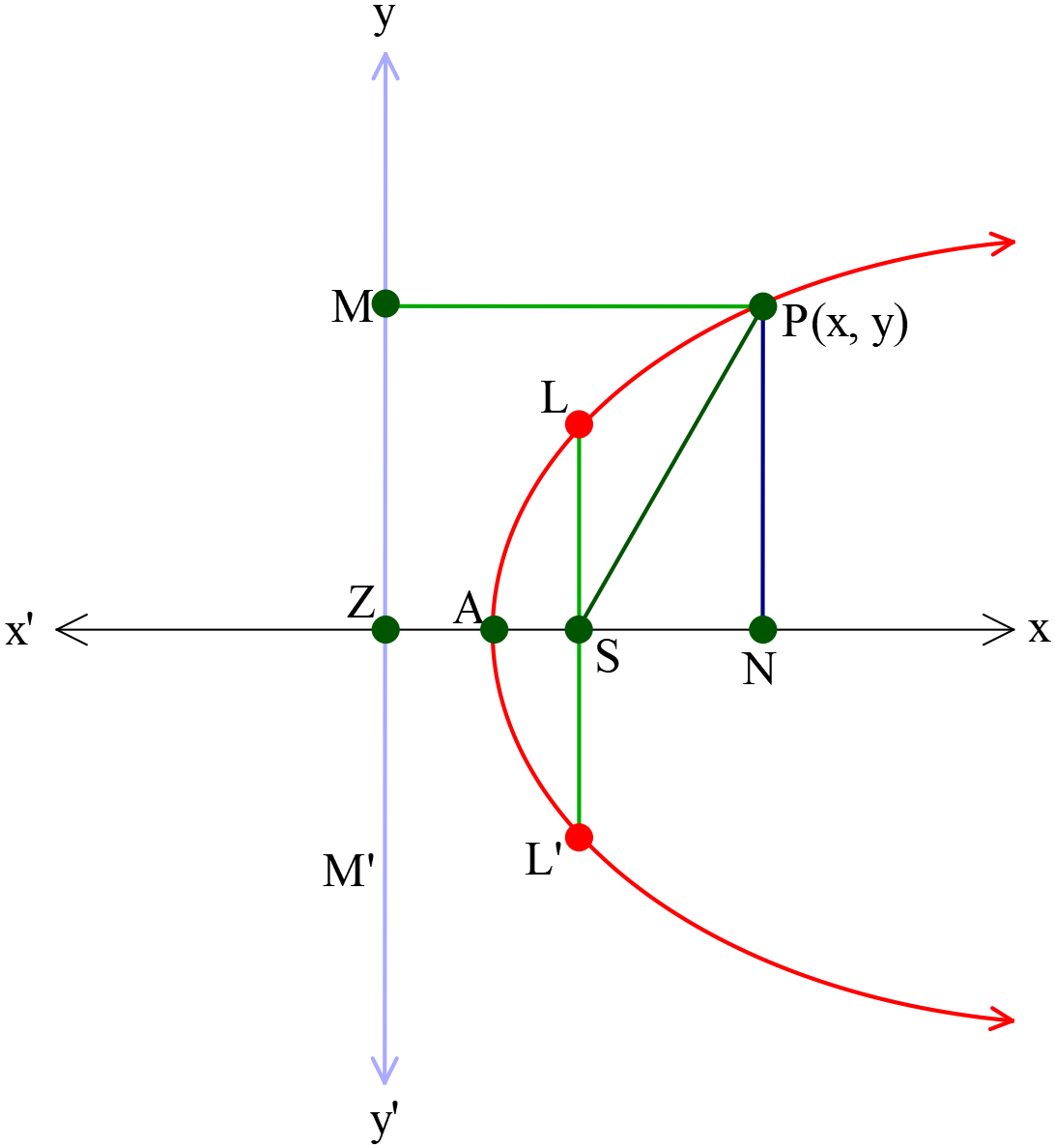

- শীর্ষবিন্দুর স্থানাঙ্ক \(A(a, 0)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(2a, 0)\)
- নিয়ামক রেখার সমীকরণ \(x=0\)
- অক্ষরেখার সমীকরণ \(y=0\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x-2a=0\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
- শীর্ষবিন্দুতে স্পর্শকের সমীকরণ \(x-a=0\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \(Z(0, 0)\)
\(X\) অক্ষের সমান্তরাল অক্ষরেখা বিশিষ্ট পরাবৃত্তের সমীকর
Equation of the parabola with axis parallel to the \(X\) axis
পরাবৃত্তের সমীকরণ \(x=ay^2+by+c\)
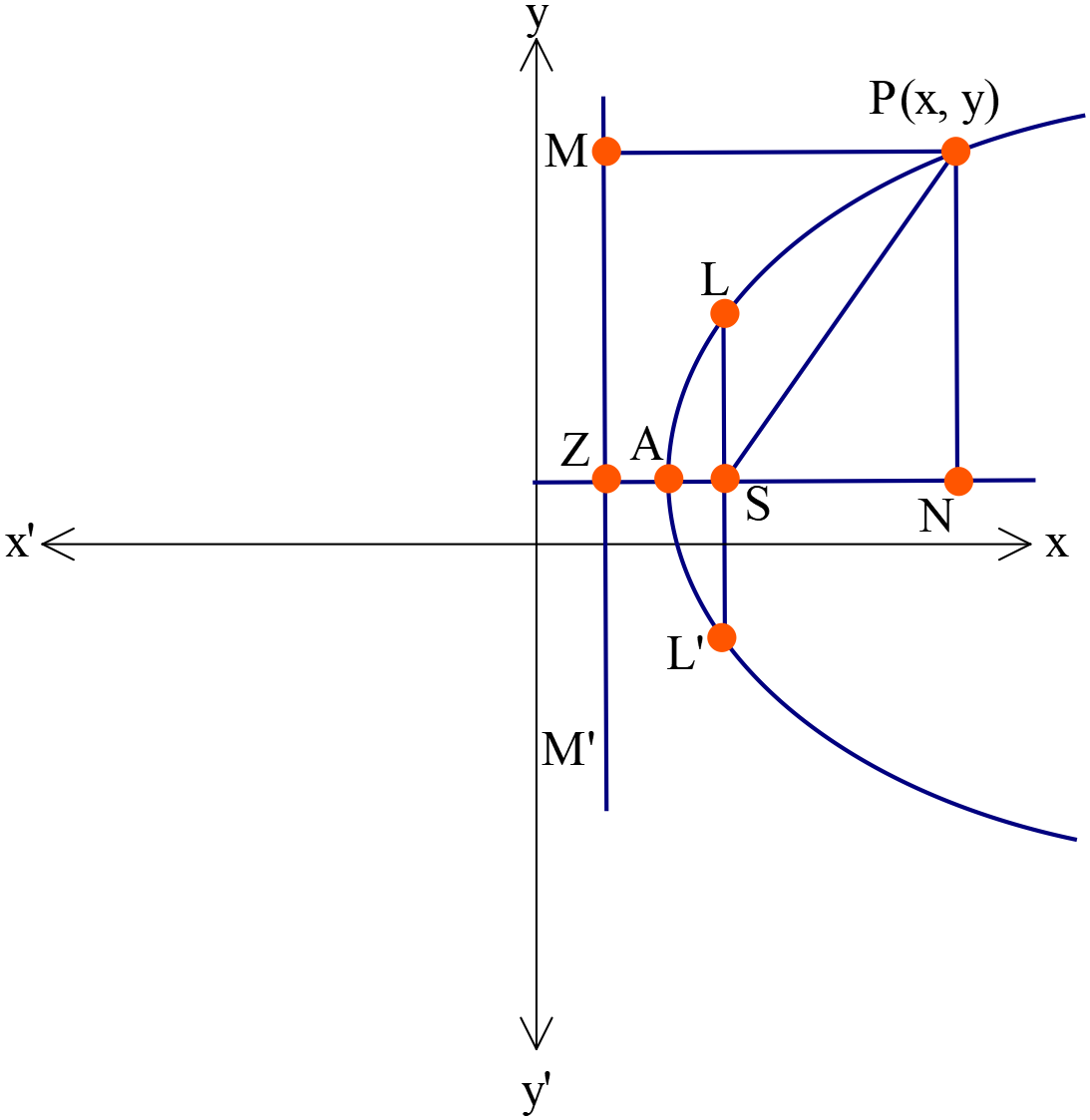

- অক্ষরেখা \(X\) অক্ষের সমান্তরাল।
- শীর্ষবিন্দুর স্থানাঙ্ক \(A\left(-\frac{b^2-4ac}{4a}, -\frac{b}{2a}\right)\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\)
উপরোক্ত পরাবৃত্তের সমীকরণের বিকল্পরূপ \((y-\beta)^2=4a(x-\alpha)\)
- অক্ষরেখা \(X\) অক্ষের সমান্তরাল।
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(\alpha, \beta)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(a+\alpha, \beta)\)
\(Y\) অক্ষের সমান্তরাল অক্ষরেখা বিশিষ্ট পরাবৃত্তের সমীকর
Equation of the parabola with axis parallel to the \(Y\) axis
পরাবৃত্তের সমীকরণ \(y=ax^2+bx+c\)
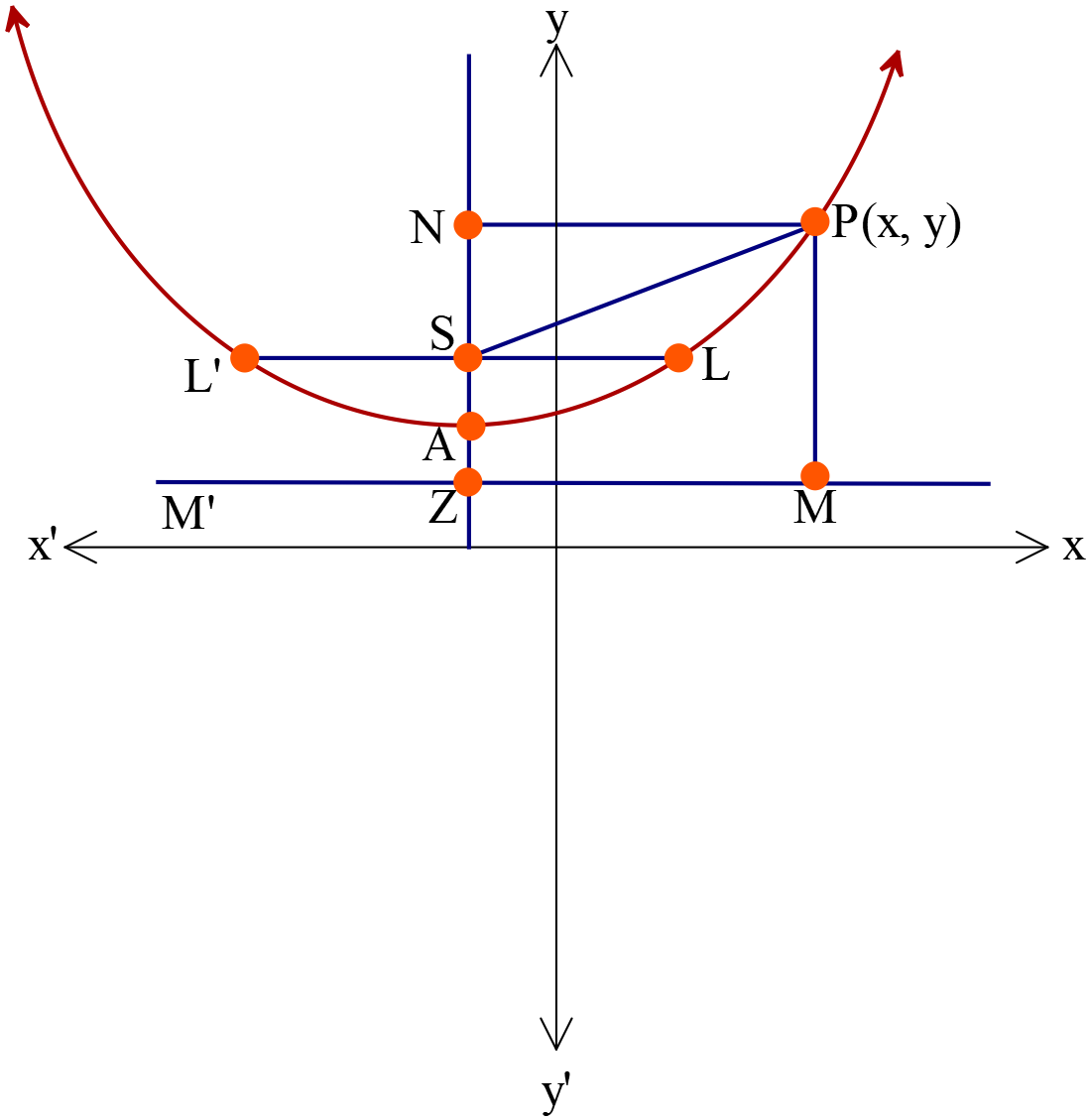

- অক্ষরেখা \(Y\) অক্ষের সমান্তরাল।
- শীর্ষবিন্দুর স্থানাঙ্ক \(A\left(-\frac{b}{2a}, -\frac{b^2-4ac}{4a}\right)\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\)
উপরোক্ত পরাবৃত্তের সমীকরণের বিকল্পরূপ \((x-\alpha)^2=4a(y-\beta)\)
- অক্ষরেখা \(Y\) অক্ষের সমান্তরাল।
- শীর্ষবিন্দুর স্থানাঙ্ক \(A(\alpha, \beta)\)
- উপকেন্দ্রের স্থানাঙ্ক \(S(\alpha, a+\beta)\)
পরাবৃত্তের স্পর্শক
Tangent of parabola
কোনো সরলরেখা পরাবৃত্তের স্পর্শক হওয়ার শর্ত, স্পর্শকের সমীকরণ এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও পরাবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(y^2=4ax ........(2) \)
সরলরেখা \((2)\) নং পরাবৃত্তকে স্পর্শ করার শর্তঃ \(c=\frac{a}{m}\)
স্পর্শকের সমীকরণঃ \(y=mx+\frac{a}{m}\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{a}{m^2}, \frac{2a}{m}\right)\)
\(y^2=4ax\) পরাবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণ \(yy_1=2a(x+x_1)\)
\(x^2=4ay\) পরাবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণ \(xx_1=2a(y+y_1)\)
মনে করি,
সরলরেখা ও পরাবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(y^2=4ax ........(2) \)
সরলরেখা \((2)\) নং পরাবৃত্তকে স্পর্শ করার শর্তঃ \(c=\frac{a}{m}\)
স্পর্শকের সমীকরণঃ \(y=mx+\frac{a}{m}\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{a}{m^2}, \frac{2a}{m}\right)\)
\(y^2=4ax\) পরাবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণ \(yy_1=2a(x+x_1)\)
\(x^2=4ay\) পরাবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণ \(xx_1=2a(y+y_1)\)
পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য
Letus rectum of parabola
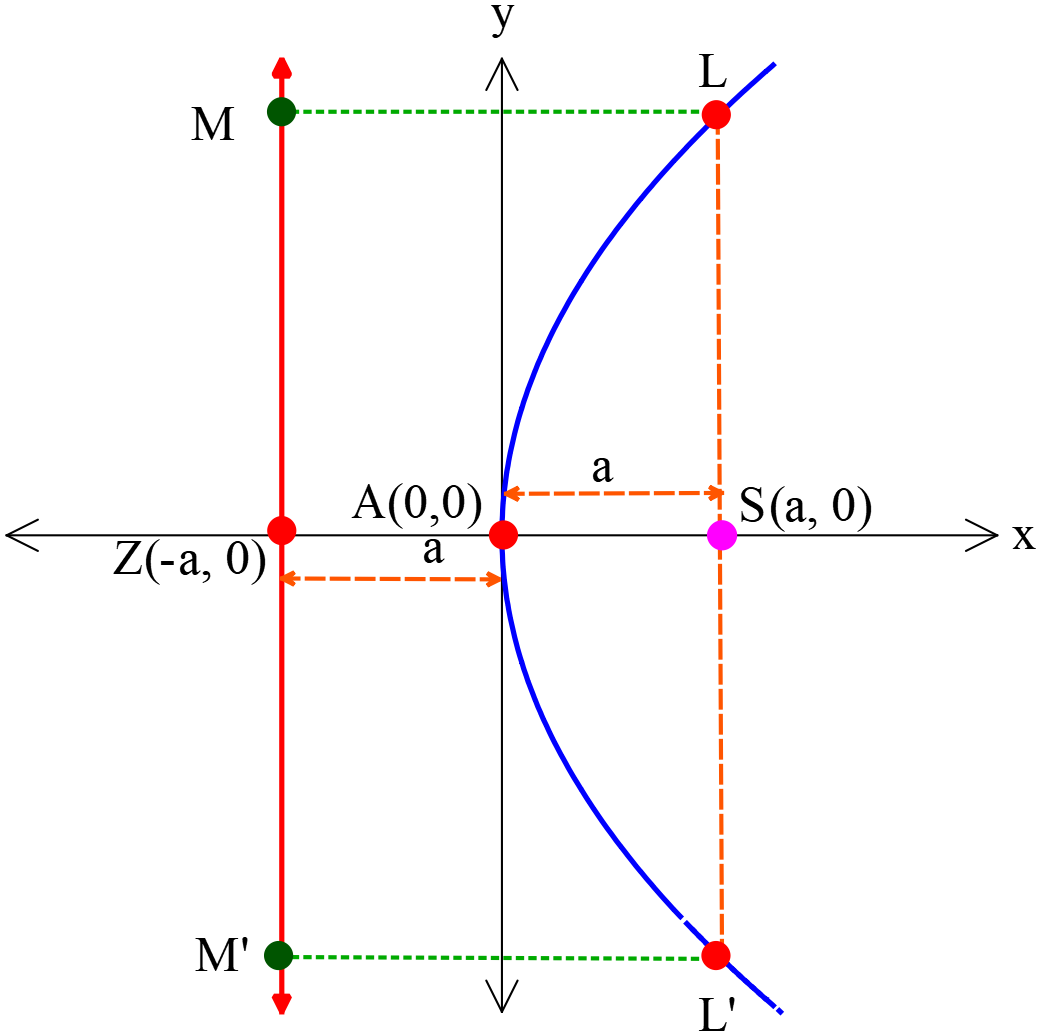 পরাবৃত্তের উপকেন্দ্র দিয়ে যার এবং এর অক্ষরেখার উপর লম্ব হয়, এরূপ জ্যাকে এর উপকেন্দ্রিক লম্ব (Letus rectum) বলা হয়। \(y^2=4ax\) পরাবৃত্তের \(AS\) অক্ষরেখার উপর \(L\acute{L}\) লম্ব আঁকি। সুতরাং \(L\acute{L}\) পরাবৃত্তটির উপকেন্দ্রিক লম্ব, এর উপকেন্দ্রের স্থানাঙ্ক \(S(a, 0)\) । \(L\acute{L}\) উপকেন্দ্রিক লম্বটি \(S\) বিন্দুতে সমদ্বিখণ্ডিত হয়। \(L\) বিন্দু থেকে \(MZ\acute{M}\)-এর উপর \(LM\) লম্ব আঁকি।
পরাবৃত্তের উপকেন্দ্র দিয়ে যার এবং এর অক্ষরেখার উপর লম্ব হয়, এরূপ জ্যাকে এর উপকেন্দ্রিক লম্ব (Letus rectum) বলা হয়। \(y^2=4ax\) পরাবৃত্তের \(AS\) অক্ষরেখার উপর \(L\acute{L}\) লম্ব আঁকি। সুতরাং \(L\acute{L}\) পরাবৃত্তটির উপকেন্দ্রিক লম্ব, এর উপকেন্দ্রের স্থানাঙ্ক \(S(a, 0)\) । \(L\acute{L}\) উপকেন্দ্রিক লম্বটি \(S\) বিন্দুতে সমদ্বিখণ্ডিত হয়। \(L\) বিন্দু থেকে \(MZ\acute{M}\)-এর উপর \(LM\) লম্ব আঁকি।পরাবৃত্তের সংজ্ঞানুসারে,
\(SL=ML\)
\(=ZS\)
\(=ZA+AS\)
\(=a+a\)
\(=2a\)
অনুরূপভাবে,
\(S\acute{L}=-2a\)
পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য্
\(L\acute{L}=|2a-(-2a)|=|2a+2a|=|4a|\)
আবার,
পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য,
\(L\acute{L}=SL+S\acute{L}\)
\(=SL+SL\)
\(=2SL\)
\(=2\times ML\)
\(=2\times SZ\)
\(=2\times \) উপকেন্দ্র হতে নিয়ামকরেখার লম্বদূরত্ব।
\(\therefore \) পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=2\times \) উপকেন্দ্র হতে নিয়ামকরেখার লম্বদূরত্ব।
×
মূলবিন্দুগামী পরাবৃত্তের আদর্শ সমীকরণ \(y^2=4ax \ (a\gt{0})\) নির্ণয়ঃ
ধরি,
পরাবৃত্তের উপকেন্দ্র \(S\) এবং নিয়ামকরেখা \(MZ\acute M\)। উপকেন্দ্র \(S\) হতে নিয়ামকরেখার উপর \(SZ\) লম্ব আঁকি এবং \(SZ\) রেখা \(A\) বিন্দুতে সমদ্বিখণ্ডিত হয়। তাহলে \(SA=AZ\); সংজ্ঞানুসারে \(A\) শীর্ষবিন্দু এবং \(ZX\) পরাবৃত্তের অক্ষ। \(A\) বিন্দুকে মূলবিন্দু এবং \(AX\) ও \(AY\) রেখাকে যথাক্রমে \(X\)-অক্ষ ও \(Y\)-অক্ষ বিবেচনা করি।
আবার, \(AS=a=ZA\) এবং পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)। \(S,P\) যোগ করি এবং \(P\) বিন্দু হতে নিয়ামক রেখার উপর \(PM\) ও \(AX\)-এর উপর \(PN\) লম্ব আঁকি।
পরাবৃত্তের সংজ্ঞানুসারে,
\(SP=PM\)
\(\Rightarrow SP=ZN\) ➜ \(PM=ZN\)
\(\Rightarrow SP=ZA+AN\)
\(\Rightarrow SP=a+x\) ➜ \(AN=x, ZA=a\)
\(\Rightarrow SP^2=(a+x)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow SP^2=(a+x)^2\)
\(\Rightarrow SN^2+PN^2=(a+x)^2\) ➜ \(SPN\) সমকোণী ত্রিভুজে \(SP^2=SN^2+PN^2\)
\(\Rightarrow (x-a)^2+y^2=(a+x)^2\) ➜ \(\because SN=AN-AS=x-a\)
\(\Rightarrow y^2=(a+x)^2-(x-a)^2\)
\(\therefore y^2=4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
পরাবৃত্তের উপকেন্দ্র \(S(a, 0)\)
নিয়ামকের সমীকরণ \(x=-a \Rightarrow x+a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-a)^2+(y-0)^2}=\frac{|x+a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=\frac{|x+a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=\frac{|x+a|}{1}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=|x+a|\)
\(\Rightarrow (x-a)^2+y^2=(x+a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow y^2=(x+a)^2-(x-a)^2\)
\(\therefore y^2=4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
ধরি,

পরাবৃত্তের উপকেন্দ্র \(S\) এবং নিয়ামকরেখা \(MZ\acute M\)। উপকেন্দ্র \(S\) হতে নিয়ামকরেখার উপর \(SZ\) লম্ব আঁকি এবং \(SZ\) রেখা \(A\) বিন্দুতে সমদ্বিখণ্ডিত হয়। তাহলে \(SA=AZ\); সংজ্ঞানুসারে \(A\) শীর্ষবিন্দু এবং \(ZX\) পরাবৃত্তের অক্ষ। \(A\) বিন্দুকে মূলবিন্দু এবং \(AX\) ও \(AY\) রেখাকে যথাক্রমে \(X\)-অক্ষ ও \(Y\)-অক্ষ বিবেচনা করি।
আবার, \(AS=a=ZA\) এবং পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)। \(S,P\) যোগ করি এবং \(P\) বিন্দু হতে নিয়ামক রেখার উপর \(PM\) ও \(AX\)-এর উপর \(PN\) লম্ব আঁকি।
পরাবৃত্তের সংজ্ঞানুসারে,
\(SP=PM\)
\(\Rightarrow SP=ZN\) ➜ \(PM=ZN\)
\(\Rightarrow SP=ZA+AN\)
\(\Rightarrow SP=a+x\) ➜ \(AN=x, ZA=a\)
\(\Rightarrow SP^2=(a+x)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow SP^2=(a+x)^2\)
\(\Rightarrow SN^2+PN^2=(a+x)^2\) ➜ \(SPN\) সমকোণী ত্রিভুজে \(SP^2=SN^2+PN^2\)
\(\Rightarrow (x-a)^2+y^2=(a+x)^2\) ➜ \(\because SN=AN-AS=x-a\)
\(\Rightarrow y^2=(a+x)^2-(x-a)^2\)
\(\therefore y^2=4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
বিকল্প পদ্ধতিঃ
আমরা জানি,পরাবৃত্তের উপকেন্দ্র \(S(a, 0)\)
নিয়ামকের সমীকরণ \(x=-a \Rightarrow x+a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-a)^2+(y-0)^2}=\frac{|x+a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=\frac{|x+a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=\frac{|x+a|}{1}\)
\(\Rightarrow \sqrt{(x-a)^2+y^2}=|x+a|\)
\(\Rightarrow (x-a)^2+y^2=(x+a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow y^2=(x+a)^2-(x-a)^2\)
\(\therefore y^2=4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
×
মূলবিন্দুগামী পরাবৃত্তের আদর্শ সমীকরণ \(x^2=4ay \ (a\gt{0})\) নির্ণয়ঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(0, a)\)
নিয়ামকের সমীকরণ \(y=-a \Rightarrow y+a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y-a)^2}=\frac{|y+a|}{\sqrt{0^2+1^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-0)^2+(y-a)^2}=\frac{|y+a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+(y-a)^2}=\frac{|y+a|}{1}\)
\(\Rightarrow \sqrt{x^2+(y-a)^2}=|y+a|\)
\(\Rightarrow x^2+(y-a)^2=(y+a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2=(y+a)^2-(y-a)^2\)
\(\therefore x^2=4ay\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,

পরাবৃত্তের উপকেন্দ্র \(S(0, a)\)
নিয়ামকের সমীকরণ \(y=-a \Rightarrow y+a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y-a)^2}=\frac{|y+a|}{\sqrt{0^2+1^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-0)^2+(y-a)^2}=\frac{|y+a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+(y-a)^2}=\frac{|y+a|}{1}\)
\(\Rightarrow \sqrt{x^2+(y-a)^2}=|y+a|\)
\(\Rightarrow x^2+(y-a)^2=(y+a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2=(y+a)^2-(y-a)^2\)
\(\therefore x^2=4ay\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
×
মূলবিন্দুগামী পরাবৃত্তের আদর্শ সমীকরণ \(y^2=-4ax \ (a\gt{0})\) নির্ণয়ঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(-a, 0)\)
নিয়ামকের সমীকরণ \(x=a \Rightarrow x-a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x+a)^2+(y-0)^2}=\frac{|x-a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=\frac{|x-a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=\frac{|x-a|}{1}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=|x-a|\)
\(\Rightarrow (x+a)^2+y^2=(x-a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow y^2=(x-a)^2-(x+a)^2\)
\(\Rightarrow y^2=-\{(x+a)^2-(x-a)^2\}\)
\(\therefore y^2=-4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,

পরাবৃত্তের উপকেন্দ্র \(S(-a, 0)\)
নিয়ামকের সমীকরণ \(x=a \Rightarrow x-a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x+a)^2+(y-0)^2}=\frac{|x-a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=\frac{|x-a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=\frac{|x-a|}{1}\)
\(\Rightarrow \sqrt{(x+a)^2+y^2}=|x-a|\)
\(\Rightarrow (x+a)^2+y^2=(x-a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow y^2=(x-a)^2-(x+a)^2\)
\(\Rightarrow y^2=-\{(x+a)^2-(x-a)^2\}\)
\(\therefore y^2=-4ax\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
×
মূলবিন্দুগামী পরাবৃত্তের আদর্শ সমীকরণ \(x^2=-4ay \ (a\gt{0})\) নির্ণয়ঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(0, -a)\)
নিয়ামকের সমীকরণ \(y=a \Rightarrow y-a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y+a)^2}=\frac{|y-a|}{\sqrt{0^2+1^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-0)^2+(y+a)^2}=\frac{|y-a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+(y+a)^2}=\frac{|y-a|}{1}\)
\(\Rightarrow \sqrt{x^2+(y+a)^2}=|y-a|\)
\(\Rightarrow x^2+(y+a)^2=(y-a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2=(y-a)^2-(y+a)^2\)
\(\Rightarrow x^2=-\{(y+a)^2-(y-a)^2\}\)
\(\therefore x^2=-4ay\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,

পরাবৃত্তের উপকেন্দ্র \(S(0, -a)\)
নিয়ামকের সমীকরণ \(y=a \Rightarrow y-a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y+a)^2}=\frac{|y-a|}{\sqrt{0^2+1^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-0)^2+(y+a)^2}=\frac{|y-a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+(y+a)^2}=\frac{|y-a|}{1}\)
\(\Rightarrow \sqrt{x^2+(y+a)^2}=|y-a|\)
\(\Rightarrow x^2+(y+a)^2=(y-a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2=(y-a)^2-(y+a)^2\)
\(\Rightarrow x^2=-\{(y+a)^2-(y-a)^2\}\)
\(\therefore x^2=-4ay\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
×
মূলবিন্দুকে উপকেন্দ্রক ধরে পরাবৃত্তের সমীকরণ \(y^2=4a(x+a) \ (a\gt{0})\) নির্ণয়ঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(0, 0)\)
নিয়ামকের সমীকরণ \(x+2a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y-0)^2}=\frac{|x+2a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{x^2+x^2}=\frac{|x+2a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+y^2}=\frac{|x+2a|}{1}\)
\(\Rightarrow \sqrt{x^2+y^2}=|x+2a|\)
\(\Rightarrow x^2+y^2=(x+2a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2+y^2=x^2+4ax+4a^2\)
\(\Rightarrow x^2+y^2-x^2=4ax+4a^2\)
\(\Rightarrow y^2=4ax+4a^2\)
\(\therefore y^2=4a(x+a)\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,

পরাবৃত্তের উপকেন্দ্র \(S(0, 0)\)
নিয়ামকের সমীকরণ \(x+2a=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-0)^2+(y-0)^2}=\frac{|x+2a|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{x^2+x^2}=\frac{|x+2a|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{x^2+y^2}=\frac{|x+2a|}{1}\)
\(\Rightarrow \sqrt{x^2+y^2}=|x+2a|\)
\(\Rightarrow x^2+y^2=(x+2a)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2+y^2=x^2+4ax+4a^2\)
\(\Rightarrow x^2+y^2-x^2=4ax+4a^2\)
\(\Rightarrow y^2=4ax+4a^2\)
\(\therefore y^2=4a(x+a)\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
×
\(Y\)-অক্ষকে নিয়ামকরেখা এবং \(X\)-অক্ষকে অক্ষরেখা ধরে পরাবৃত্তের সমীকরণ \(y^2=4a(x-a) \ (a\gt{0})\) নির্ণয়ঃ
আমরা জানি,
পরাবৃত্তের উপকেন্দ্র \(S(2a, 0)\)
নিয়ামকের সমীকরণ \(x=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-2a)^2+(y-0)^2}=\frac{|x|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-2a)^2+(y-0)^2}=\frac{|x|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x-2a)^2+y^2}=\frac{|x|}{1}\)
\(\Rightarrow \sqrt{x^2-4ax+4a^2+y^2}=|x|\)
\(\Rightarrow x^2-4ax+4a^2+y^2=x^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2+y^2-x^2=4ax-4a^2\)
\(\therefore y^2=4a(x-a)\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
আমরা জানি,

পরাবৃত্তের উপকেন্দ্র \(S(2a, 0)\)
নিয়ামকের সমীকরণ \(x=0 \)
উৎকেন্দ্রিকতা \(e=1\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
সংজ্ঞানুসারে, \(PS=PM\)
\(\Rightarrow \sqrt{(x-2a)^2+(y-0)^2}=\frac{|x|}{\sqrt{1^2+0^2}}\) ➜ \((x_1, y_1)\) বিন্দু হতে \(ax+by+c=0\) এর লম্ব দূরত্ব \(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
\(\Rightarrow \sqrt{(x-2a)^2+(y-0)^2}=\frac{|x|}{\sqrt{1}}\)
\(\Rightarrow \sqrt{(x-2a)^2+y^2}=\frac{|x|}{1}\)
\(\Rightarrow \sqrt{x^2-4ax+4a^2+y^2}=|x|\)
\(\Rightarrow x^2-4ax+4a^2+y^2=x^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow x^2+y^2-x^2=4ax-4a^2\)
\(\therefore y^2=4a(x-a)\)
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
×
পরাবৃত্তের সমীকরণ \(x=ay^2+by+c\) নির্ণয়ঃ
ধরি,
পরাবৃত্তের শীর্ষবিন্দু \(A(\alpha, \beta)\)
এবং \(AZ=AS=a\) পরাবৃত্তের অক্ষরেখা \(X\) অক্ষের সমান্তরাল।
পরবৃত্তের ফোকাস \(S(\alpha +a, \beta)\)
এবং নিয়ামকরেখার পাদবিন্দু \(Z(\alpha -a, \beta)\)
নিয়ামকরেখার সমীকরণ \(x=\alpha-a\)
\(\Rightarrow x-\alpha +a=0\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
পরাবৃত্তের সমীকরণ \(PS=PM\)
\(\Rightarrow PS=ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow PS^2=ZN^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow \{x-(\alpha +a)\}^2+(y-\beta)^2=\{x-(\alpha -a)\}^2\) ➜ \(\because ZN=x-(\alpha -a)\)
\(\Rightarrow \{x-\alpha -a\}^2+(y-\beta)^2=\{x-\alpha +a\}^2\)
\(\Rightarrow \{(x-\alpha)-a\}^2+(y-\beta)^2=\{(x-\alpha)+a\}^2\)
\(\Rightarrow (y-\beta)^2=\{(x-\alpha)+a\}^2-\{(x-\alpha)-a\}^2\)
\(\Rightarrow (y-\beta)^2=4(x-\alpha)a\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow (y-\beta)^2=4a(x-\alpha)\)
এখন,
\(4a(x-\alpha)=(y-\beta)^2\)
\(\Rightarrow 4ax-4a\alpha=y^2-2y\beta+\beta^2\)
\(\Rightarrow 4ax=y^2-2y\beta+\beta^2+4a\alpha\)
\(\Rightarrow x=\frac{1}{4a}y^2-\frac{2y\beta}{4a}+\frac{\beta^2+4a\alpha}{4a}\)
\(\Rightarrow x=\frac{1}{4a}y^2+\frac{-\beta}{2a}y+\frac{\beta^2+4a\alpha}{4a} ........(1)\)
ধরি,
\(\acute a=\frac{1}{4a}, b=\frac{-\beta}{2a}, c=\frac{\beta^2+4a\alpha}{4a}\)
তাহলে \((1)\) নং সমীকরণ দাঁড়ায়,
\(x=\acute ay^2+by+c \)
\(\therefore x=ay^2+by+c \) ➜ \(\acute a\) কে \(a\) দ্বারা প্রতিস্থাপন করে।
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
এখন,
\(x=ay^2+by+c \)
\(\Rightarrow ay^2+by+c=x \)
\(\Rightarrow ay^2+by=x-c \)
\(\Rightarrow y^2+\frac{by}{a}=\frac{x-c}{a} \)
\(\Rightarrow y^2+2\frac{b}{2a}y+(\frac{b}{2a})^2=\frac{x-c}{a}+(\frac{b}{2a})^2 \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{x-c}{a}+\frac{b^2}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax-4ac+b^2}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax+b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax}{4a^2}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{x}{a}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{1}{a}\left(x+\frac{b^2-4ac}{4a} \right) \)
\(\Rightarrow Y^2=\frac{1}{a}X ........(2)\) ➜ ধরি, \(X=x+\frac{b^2-4ac}{4a}, Y=y+\frac{b}{2a}\)
\((2)\) নং পরাবৃত্তের ক্ষেত্রে,
শীর্ষ বিন্দু \(A(0, 0 )\)
\(\Rightarrow X=0, Y=0 \)
\(\Rightarrow x+\frac{b^2-4ac}{4a}=0, y+\frac{b}{2a}=0 \) ➜ \(\because X=x+\frac{b^2-4ac}{4a}, Y=y+\frac{b}{2a}\)
\(\therefore x=-\frac{b^2-4ac}{4a}, y=-\frac{b}{2a} \)
\(\therefore \) শীর্ষ বিন্দু দাঁড়ায় \(A\left(-\frac{b^2-4ac}{4a}, -\frac{b}{2a} \right)\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\) ➜ \((2)\) নং পরাবৃত্তের ক্ষেত্রে, \(4a\Rightarrow \frac{1}{a}\)
ধরি,

পরাবৃত্তের শীর্ষবিন্দু \(A(\alpha, \beta)\)
এবং \(AZ=AS=a\) পরাবৃত্তের অক্ষরেখা \(X\) অক্ষের সমান্তরাল।
পরবৃত্তের ফোকাস \(S(\alpha +a, \beta)\)
এবং নিয়ামকরেখার পাদবিন্দু \(Z(\alpha -a, \beta)\)
নিয়ামকরেখার সমীকরণ \(x=\alpha-a\)
\(\Rightarrow x-\alpha +a=0\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
পরাবৃত্তের সমীকরণ \(PS=PM\)
\(\Rightarrow PS=ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow PS^2=ZN^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow \{x-(\alpha +a)\}^2+(y-\beta)^2=\{x-(\alpha -a)\}^2\) ➜ \(\because ZN=x-(\alpha -a)\)
\(\Rightarrow \{x-\alpha -a\}^2+(y-\beta)^2=\{x-\alpha +a\}^2\)
\(\Rightarrow \{(x-\alpha)-a\}^2+(y-\beta)^2=\{(x-\alpha)+a\}^2\)
\(\Rightarrow (y-\beta)^2=\{(x-\alpha)+a\}^2-\{(x-\alpha)-a\}^2\)
\(\Rightarrow (y-\beta)^2=4(x-\alpha)a\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow (y-\beta)^2=4a(x-\alpha)\)
এখন,
\(4a(x-\alpha)=(y-\beta)^2\)
\(\Rightarrow 4ax-4a\alpha=y^2-2y\beta+\beta^2\)
\(\Rightarrow 4ax=y^2-2y\beta+\beta^2+4a\alpha\)
\(\Rightarrow x=\frac{1}{4a}y^2-\frac{2y\beta}{4a}+\frac{\beta^2+4a\alpha}{4a}\)
\(\Rightarrow x=\frac{1}{4a}y^2+\frac{-\beta}{2a}y+\frac{\beta^2+4a\alpha}{4a} ........(1)\)
ধরি,
\(\acute a=\frac{1}{4a}, b=\frac{-\beta}{2a}, c=\frac{\beta^2+4a\alpha}{4a}\)
তাহলে \((1)\) নং সমীকরণ দাঁড়ায়,
\(x=\acute ay^2+by+c \)
\(\therefore x=ay^2+by+c \) ➜ \(\acute a\) কে \(a\) দ্বারা প্রতিস্থাপন করে।
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
এখন,
\(x=ay^2+by+c \)
\(\Rightarrow ay^2+by+c=x \)
\(\Rightarrow ay^2+by=x-c \)
\(\Rightarrow y^2+\frac{by}{a}=\frac{x-c}{a} \)
\(\Rightarrow y^2+2\frac{b}{2a}y+(\frac{b}{2a})^2=\frac{x-c}{a}+(\frac{b}{2a})^2 \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{x-c}{a}+\frac{b^2}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax-4ac+b^2}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax+b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{4ax}{4a^2}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{x}{a}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (y+\frac{b}{2a})^2=\frac{1}{a}\left(x+\frac{b^2-4ac}{4a} \right) \)
\(\Rightarrow Y^2=\frac{1}{a}X ........(2)\) ➜ ধরি, \(X=x+\frac{b^2-4ac}{4a}, Y=y+\frac{b}{2a}\)
\((2)\) নং পরাবৃত্তের ক্ষেত্রে,
শীর্ষ বিন্দু \(A(0, 0 )\)
\(\Rightarrow X=0, Y=0 \)
\(\Rightarrow x+\frac{b^2-4ac}{4a}=0, y+\frac{b}{2a}=0 \) ➜ \(\because X=x+\frac{b^2-4ac}{4a}, Y=y+\frac{b}{2a}\)
\(\therefore x=-\frac{b^2-4ac}{4a}, y=-\frac{b}{2a} \)
\(\therefore \) শীর্ষ বিন্দু দাঁড়ায় \(A\left(-\frac{b^2-4ac}{4a}, -\frac{b}{2a} \right)\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\) ➜ \((2)\) নং পরাবৃত্তের ক্ষেত্রে, \(4a\Rightarrow \frac{1}{a}\)
×
পরাবৃত্তের সমীকরণ \(y=ax^2+bx+c\) নির্ণয়ঃ
ধরি,
পরাবৃত্তের শীর্ষবিন্দু \(A(\alpha, \beta)\)
এবং \(AZ=AS=a\) পরাবৃত্তের অক্ষরেখা \(Y\) অক্ষের সমান্তরাল।
পরবৃত্তের ফোকাস \(S(\alpha, \beta +a)\)
এবং নিয়ামকরেখার পাদবিন্দু \(Z(\alpha, \beta -a)\)
নিয়ামকরেখার সমীকরণ \(y=\beta -a\)
\(\Rightarrow y-\beta +a=0\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
পরাবৃত্তের সমীকরণ \(PS=PM\)
\(\Rightarrow PS=ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow PS^2=ZN^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-\alpha)^2+\{y-(\beta +a)\}^2=\{y-(\beta -a)\}^2\) ➜ \(\because ZN=y-(\beta -a)\)
\(\Rightarrow (x-\alpha)^2+\{y-\beta -a\}^2=\{y-\beta +a\}^2\)
\(\Rightarrow (x-\alpha)^2+\{(y-\beta) -a\}^2=\{(y-\beta)+a\}^2\)
\(\Rightarrow (x-\alpha)^2=\{(y-\beta)+a\}^2-\{(y-\beta)-a\}^2\)
\(\Rightarrow (x-\alpha)^2=4(y-\beta)a\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow (x-\alpha)^2=4a(y-\beta)\)
এখন,
\(4a(y-\beta)=(x-\alpha)^2\)
\(\Rightarrow 4ay-4a\beta=x^2-2x\alpha+\alpha^2\)
\(\Rightarrow 4ay=x^2-2x\alpha+\alpha^2+4a\beta\)
\(\Rightarrow y=\frac{1}{4a}x^2-\frac{2x\alpha}{4a}+\frac{\alpha^2+4a\beta}{4a}\)
\(\Rightarrow x=\frac{1}{4a}x^2+\frac{-\alpha}{2a}x+\frac{\alpha^2+4a\beta}{4a} ........(1)\)
ধরি,
\(\acute a=\frac{1}{4a}, b=\frac{-\alpha}{2a}, c=\frac{\alpha^2+4a\beta}{4a}\)
তাহলে \((1)\) নং সমীকরণ দাঁড়ায়,
\(y=\acute ax^2+bx+c \)
\(\therefore y=ax^2+bx+c \) ➜ \(\acute a\) কে \(a\) দ্বারা প্রতিস্থাপন করে।
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
এখন,
\(y=ax^2+bx+c \)
\(\Rightarrow ax^2+bx+c=y \)
\(\Rightarrow ax^2+bx=y-c \)
\(\Rightarrow x^2+\frac{bx}{a}=\frac{y-c}{a} \)
\(\Rightarrow x^2+2\frac{b}{2a}x+(\frac{b}{2a})^2=\frac{y-c}{a}+(\frac{b}{2a})^2 \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{y-c}{a}+\frac{b^2}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay-4ac+b^2}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay+b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay}{4a^2}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{y}{a}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{1}{a}\left(y+\frac{b^2-4ac}{4a} \right) \)
\(\Rightarrow X^2=\frac{1}{a}Y ........(2)\) ➜ ধরি, \(X=x+\frac{b}{2a}, Y=y+\frac{b^2-4ac}{4a}, \)
\((2)\) নং পরাবৃত্তের ক্ষেত্রে,
শীর্ষ বিন্দু \(A(0, 0 )\)
\(\Rightarrow X=0, Y=0 \)
\(\Rightarrow x+\frac{b}{2a}=0, y+\frac{b^2-4ac}{4a}=0 \) ➜ \(\because X=x+\frac{b}{2a}, Y=y+\frac{b^2-4ac}{4a},\)
\(\therefore x=-\frac{b}{2a}, y=-\frac{b^2-4ac}{4a} \)
\(\therefore \) শীর্ষ বিন্দু দাঁড়ায় \(A\left(-\frac{b}{2a}, -\frac{b^2-4ac}{4a} \right)\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\) ➜ \((2)\) নং পরাবৃত্তের ক্ষেত্রে, \(4a\Rightarrow \frac{1}{a}\)
ধরি,

পরাবৃত্তের শীর্ষবিন্দু \(A(\alpha, \beta)\)
এবং \(AZ=AS=a\) পরাবৃত্তের অক্ষরেখা \(Y\) অক্ষের সমান্তরাল।
পরবৃত্তের ফোকাস \(S(\alpha, \beta +a)\)
এবং নিয়ামকরেখার পাদবিন্দু \(Z(\alpha, \beta -a)\)
নিয়ামকরেখার সমীকরণ \(y=\beta -a\)
\(\Rightarrow y-\beta +a=0\)
পরাবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)
পরাবৃত্তের সমীকরণ \(PS=PM\)
\(\Rightarrow PS=ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow PS^2=ZN^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-\alpha)^2+\{y-(\beta +a)\}^2=\{y-(\beta -a)\}^2\) ➜ \(\because ZN=y-(\beta -a)\)
\(\Rightarrow (x-\alpha)^2+\{y-\beta -a\}^2=\{y-\beta +a\}^2\)
\(\Rightarrow (x-\alpha)^2+\{(y-\beta) -a\}^2=\{(y-\beta)+a\}^2\)
\(\Rightarrow (x-\alpha)^2=\{(y-\beta)+a\}^2-\{(y-\beta)-a\}^2\)
\(\Rightarrow (x-\alpha)^2=4(y-\beta)a\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow (x-\alpha)^2=4a(y-\beta)\)
এখন,
\(4a(y-\beta)=(x-\alpha)^2\)
\(\Rightarrow 4ay-4a\beta=x^2-2x\alpha+\alpha^2\)
\(\Rightarrow 4ay=x^2-2x\alpha+\alpha^2+4a\beta\)
\(\Rightarrow y=\frac{1}{4a}x^2-\frac{2x\alpha}{4a}+\frac{\alpha^2+4a\beta}{4a}\)
\(\Rightarrow x=\frac{1}{4a}x^2+\frac{-\alpha}{2a}x+\frac{\alpha^2+4a\beta}{4a} ........(1)\)
ধরি,
\(\acute a=\frac{1}{4a}, b=\frac{-\alpha}{2a}, c=\frac{\alpha^2+4a\beta}{4a}\)
তাহলে \((1)\) নং সমীকরণ দাঁড়ায়,
\(y=\acute ax^2+bx+c \)
\(\therefore y=ax^2+bx+c \) ➜ \(\acute a\) কে \(a\) দ্বারা প্রতিস্থাপন করে।
ইহাই নির্ণেয় পরাবৃত্তের সমীকরণ।
এখন,
\(y=ax^2+bx+c \)
\(\Rightarrow ax^2+bx+c=y \)
\(\Rightarrow ax^2+bx=y-c \)
\(\Rightarrow x^2+\frac{bx}{a}=\frac{y-c}{a} \)
\(\Rightarrow x^2+2\frac{b}{2a}x+(\frac{b}{2a})^2=\frac{y-c}{a}+(\frac{b}{2a})^2 \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{y-c}{a}+\frac{b^2}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay-4ac+b^2}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay+b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{4ay}{4a^2}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{y}{a}+\frac{b^2-4ac}{4a^2} \)
\(\Rightarrow (x+\frac{b}{2a})^2=\frac{1}{a}\left(y+\frac{b^2-4ac}{4a} \right) \)
\(\Rightarrow X^2=\frac{1}{a}Y ........(2)\) ➜ ধরি, \(X=x+\frac{b}{2a}, Y=y+\frac{b^2-4ac}{4a}, \)
\((2)\) নং পরাবৃত্তের ক্ষেত্রে,
শীর্ষ বিন্দু \(A(0, 0 )\)
\(\Rightarrow X=0, Y=0 \)
\(\Rightarrow x+\frac{b}{2a}=0, y+\frac{b^2-4ac}{4a}=0 \) ➜ \(\because X=x+\frac{b}{2a}, Y=y+\frac{b^2-4ac}{4a},\)
\(\therefore x=-\frac{b}{2a}, y=-\frac{b^2-4ac}{4a} \)
\(\therefore \) শীর্ষ বিন্দু দাঁড়ায় \(A\left(-\frac{b}{2a}, -\frac{b^2-4ac}{4a} \right)\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{1}{a}|\) ➜ \((2)\) নং পরাবৃত্তের ক্ষেত্রে, \(4a\Rightarrow \frac{1}{a}\)
×
কোনো সরলরেখা পরাবৃত্তের স্পর্শক হওয়ার শর্ত, স্পর্শকের সমীকরণ এবং স্পর্শবিন্দুর স্থানাঙ্ক নির্ণয়ঃ
ধরি,
পরাবৃত্তের সমীকরণ \(y^2=4ax ....(1)\)
\(PQ\) সরলরেখার সমীকরণ \(y=mx+c ....(2)\)
পরাবৃত্তের উপর \(P\) একটি বিন্দু এবং \(PQ\) যে কোনো ছেদকরেখা। \(Q\) বিন্দু ক্রমশ \(P\) বিন্দুর দিকে অগ্রসর হয়ে \(P\) বিন্দুর উপর সমপতিত হলে ছেদকরেখাটি \(P\) বিন্দুতে উৎপন্ন পরাবৃত্তের একটি স্পর্শক হবে।
\((1)\) ও \((2)\) হতে,
\((mx+c)^2=4ax\)
\(\Rightarrow m^2x^2+2mcx+c^2=4ax\)
\(\Rightarrow m^2x^2+2mcx-4ax+c^2=0\)
\(\therefore m^2x^2+2(mc-2a)x+c^2=0 .......(3)\)
\(PQ\) সরলরেখাটি \((1)\) নং পরাবৃত্তের একটি স্পর্শক হবে যদি \((3)\) নং সমীকরণের মূলদ্বয় সমান হয়।
\(\therefore \{2(mc-2a)\}^2=4m^2c^2\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow 4(mc-2a)^2=4m^2c^2\)
\(\Rightarrow (mc-2a)^2=m^2c^2\)
\(\Rightarrow m^2c^2-4amc+4a^2=m^2c^2\)
\(\Rightarrow -4amc+4a^2=m^2c^2-m^2c^2\)
\(\Rightarrow -4amc+4a^2=0\)
\(\Rightarrow -4amc=-4a^2\)
\(\Rightarrow amc=a^2\)
\(\Rightarrow c=\frac{a^2}{am}\)
\(\therefore c=\frac{a}{m}\)
ইহাই নির্ণেয় স্পর্শক হওয়ার শর্ত।
আবার,
\((3)\) নং সমীকরণে \(c=\frac{a}{m}\) বসিয়ে,
\(m^2x^2+2\left(m\times \frac{a}{m}-2a\right)x+(\frac{a}{m})^2=0\)
\(\Rightarrow m^2x^2+2\left(a-2a\right)x+\frac{a^2}{m^2}=0\)
\(\Rightarrow m^2x^2-2ax+\frac{a^2}{m^2}=0\)
\(\Rightarrow \left(mx-\frac{a}{m}\right)^2=0\)
\(\Rightarrow mx-\frac{a}{m}=0\)
\(\Rightarrow mx=\frac{a}{m}\)
\(\therefore x=\frac{a}{m^2}\)
আবার,
\((3)\) নং সমীকরণ হতে,
\(y=m\times \frac{a}{m^2}+\frac{a}{m}\)
\(\Rightarrow y=\frac{a}{m}+\frac{a}{m}\)
\(\therefore y=\frac{2a}{m}\)
\(\therefore\) স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{a}{m^2},\frac{2a}{m}\right)\)
ধরি,

পরাবৃত্তের সমীকরণ \(y^2=4ax ....(1)\)
\(PQ\) সরলরেখার সমীকরণ \(y=mx+c ....(2)\)
পরাবৃত্তের উপর \(P\) একটি বিন্দু এবং \(PQ\) যে কোনো ছেদকরেখা। \(Q\) বিন্দু ক্রমশ \(P\) বিন্দুর দিকে অগ্রসর হয়ে \(P\) বিন্দুর উপর সমপতিত হলে ছেদকরেখাটি \(P\) বিন্দুতে উৎপন্ন পরাবৃত্তের একটি স্পর্শক হবে।
\((1)\) ও \((2)\) হতে,
\((mx+c)^2=4ax\)
\(\Rightarrow m^2x^2+2mcx+c^2=4ax\)
\(\Rightarrow m^2x^2+2mcx-4ax+c^2=0\)
\(\therefore m^2x^2+2(mc-2a)x+c^2=0 .......(3)\)
\(PQ\) সরলরেখাটি \((1)\) নং পরাবৃত্তের একটি স্পর্শক হবে যদি \((3)\) নং সমীকরণের মূলদ্বয় সমান হয়।
\(\therefore \{2(mc-2a)\}^2=4m^2c^2\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow 4(mc-2a)^2=4m^2c^2\)
\(\Rightarrow (mc-2a)^2=m^2c^2\)
\(\Rightarrow m^2c^2-4amc+4a^2=m^2c^2\)
\(\Rightarrow -4amc+4a^2=m^2c^2-m^2c^2\)
\(\Rightarrow -4amc+4a^2=0\)
\(\Rightarrow -4amc=-4a^2\)
\(\Rightarrow amc=a^2\)
\(\Rightarrow c=\frac{a^2}{am}\)
\(\therefore c=\frac{a}{m}\)
ইহাই নির্ণেয় স্পর্শক হওয়ার শর্ত।
আবার,
\((3)\) নং সমীকরণে \(c=\frac{a}{m}\) বসিয়ে,
\(m^2x^2+2\left(m\times \frac{a}{m}-2a\right)x+(\frac{a}{m})^2=0\)
\(\Rightarrow m^2x^2+2\left(a-2a\right)x+\frac{a^2}{m^2}=0\)
\(\Rightarrow m^2x^2-2ax+\frac{a^2}{m^2}=0\)
\(\Rightarrow \left(mx-\frac{a}{m}\right)^2=0\)
\(\Rightarrow mx-\frac{a}{m}=0\)
\(\Rightarrow mx=\frac{a}{m}\)
\(\therefore x=\frac{a}{m^2}\)
আবার,
\((3)\) নং সমীকরণ হতে,
\(y=m\times \frac{a}{m^2}+\frac{a}{m}\)
\(\Rightarrow y=\frac{a}{m}+\frac{a}{m}\)
\(\therefore y=\frac{2a}{m}\)
\(\therefore\) স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{a}{m^2},\frac{2a}{m}\right)\)
উপবৃত্ত
Ellipse
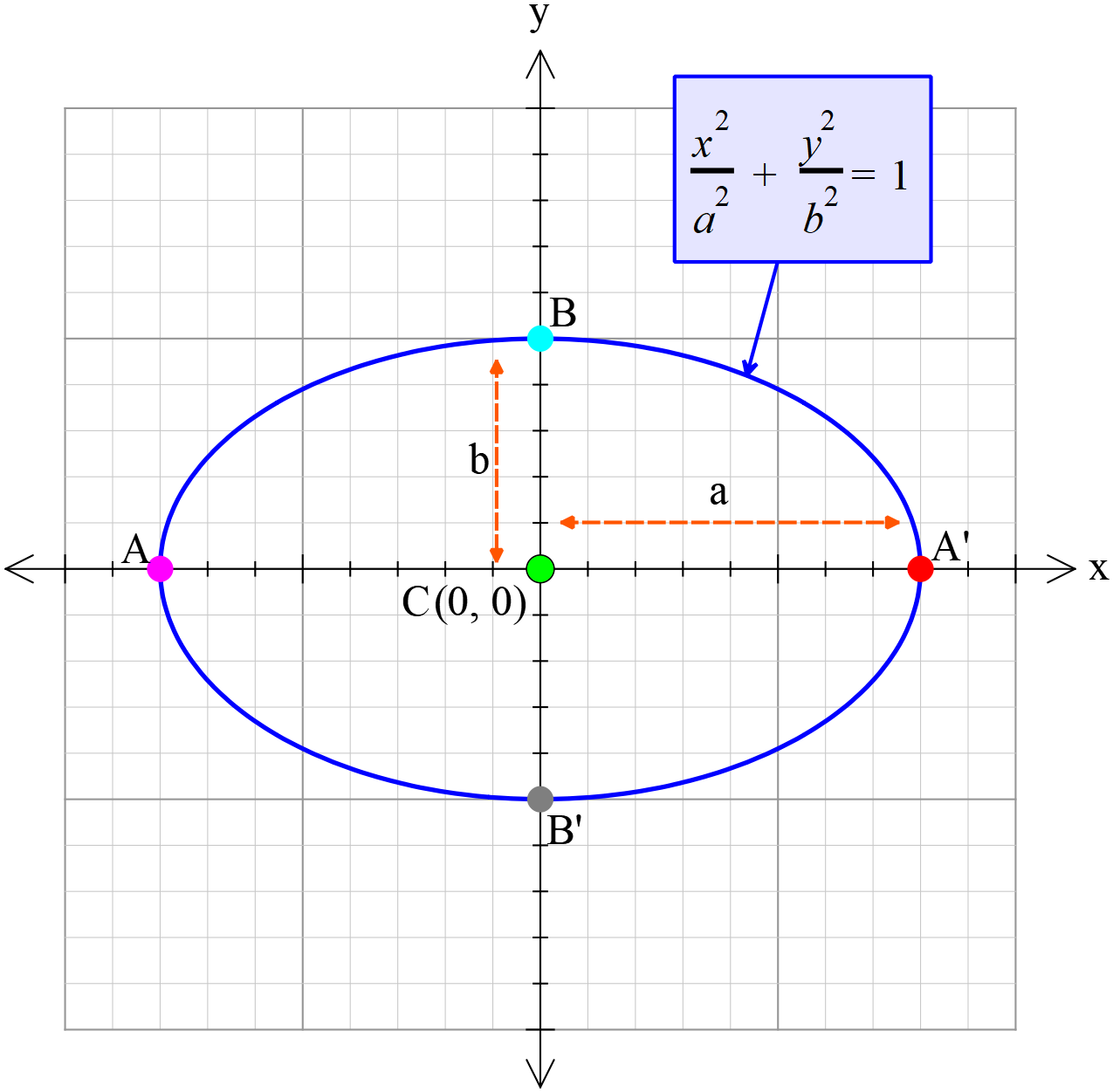 উপবৃত্তঃ কোনো কার্তেসীয় সমতলে একটি বিন্দু যদি এমনভাবে চলে যে ঐ সমতলস্থিত একটি স্থির বিন্দু থেকে দূরত্ব এবং একটি নির্দিষ্ট রেখা থেকে লম্ব দূরত্বের অনুপাত একটি স্থির রাশি এবং ঐ স্থির রাশিটির মান \(1\) অপেক্ষা ক্ষুদ্রতর, তবে ঐ বিন্দুর সঞ্চারপথকে উপবৃত্ত বলা হয়। উক্ত স্থির রাশিকে উৎকেন্দ্রতা (Eccentricity) বলা হয়, এবং ইহাকে \(e\) দ্বারা সূচিত করা হয়,যেখানে \(1 > e > 0\) হবে ।
উপকেন্দ্র দুইটির মধ্যদিয়ে অঙ্কিত উপবৃত্তের সর্ববৃহত রেখাংশ \(A\acute A\) কে বৃহৎ অক্ষ (Major axis) বলা হয়। বৃহদাক্ষের লম্ব দ্বিখন্ডক রেখাংশ \(B\acute B\) কে ক্ষুদ্র অক্ষ (Minor axis) বলা হয়। অক্ষদ্বয়ের মিলিত বিন্দু \(C\) কে কেন্দ্র এবং বৃহদাক্ষের প্রান্ত বিন্দু দুইটিকে শীর্ষবিন্দু বলা হয়।
উপবৃত্তঃ কোনো কার্তেসীয় সমতলে একটি বিন্দু যদি এমনভাবে চলে যে ঐ সমতলস্থিত একটি স্থির বিন্দু থেকে দূরত্ব এবং একটি নির্দিষ্ট রেখা থেকে লম্ব দূরত্বের অনুপাত একটি স্থির রাশি এবং ঐ স্থির রাশিটির মান \(1\) অপেক্ষা ক্ষুদ্রতর, তবে ঐ বিন্দুর সঞ্চারপথকে উপবৃত্ত বলা হয়। উক্ত স্থির রাশিকে উৎকেন্দ্রতা (Eccentricity) বলা হয়, এবং ইহাকে \(e\) দ্বারা সূচিত করা হয়,যেখানে \(1 > e > 0\) হবে ।
উপকেন্দ্র দুইটির মধ্যদিয়ে অঙ্কিত উপবৃত্তের সর্ববৃহত রেখাংশ \(A\acute A\) কে বৃহৎ অক্ষ (Major axis) বলা হয়। বৃহদাক্ষের লম্ব দ্বিখন্ডক রেখাংশ \(B\acute B\) কে ক্ষুদ্র অক্ষ (Minor axis) বলা হয়। অক্ষদ্বয়ের মিলিত বিন্দু \(C\) কে কেন্দ্র এবং বৃহদাক্ষের প্রান্ত বিন্দু দুইটিকে শীর্ষবিন্দু বলা হয়।
উপবৃত্তের প্রমিত সমীকরণ
Standard equation of Ellipse
ধরি,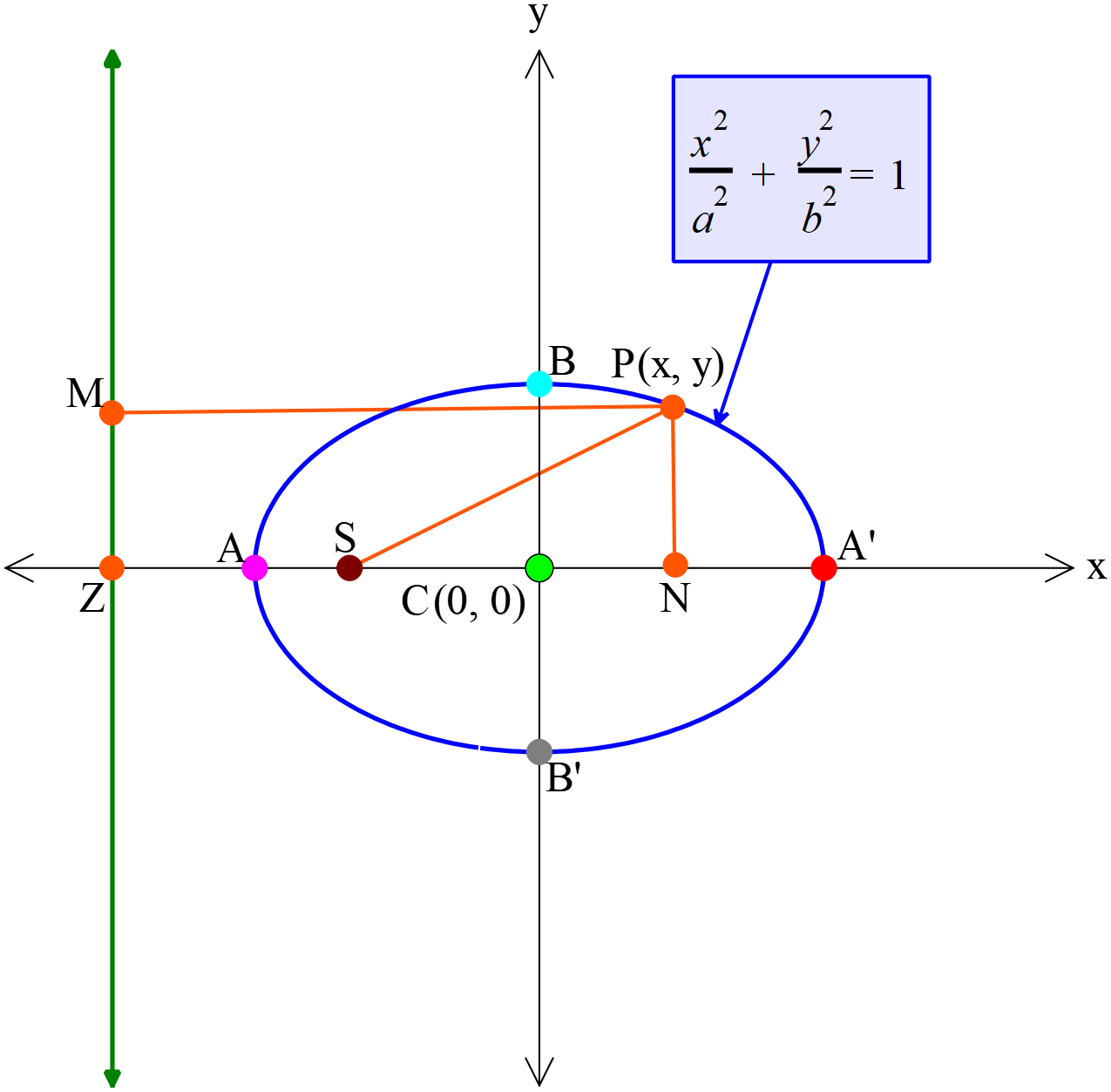
উপবৃত্তের উপকেন্দ্র \(S\) নিয়ামকরেখা \(MZ\) এবং উৎকেন্দ্রিকতা \(e (0 < e < 1)\), নিয়ামকরেখার উপর \(SZ\) লম্ব আঁকি। \(SZ\) রেখাকে \(A\) ও \(\acute A\) বিন্দুদ্বয় \(e:1\) অনুপাতে যথাক্রমে অন্তর্বিভক্ত ও বহিঃর্বিভক্ত করে, যেন \(SA=e.AZ\) এবং \(S\acute A=e.\acute AZ\)।
তাহলে, \(A\) ও \(\acute A\) উপবৃত্তের উপর দুইটি বিন্দু অর্থাৎ শীর্ষবিন্দু।
মনে করি \(A\acute A\)-এর মধ্যবিন্দু \(C\) এবং \(A\acute A=2a\)
তাহলে, \(CA=C\acute A=a\)
এখন,
\(SA=e.AZ\)
\(\therefore a-CS=e(CZ-a) .......(1)\) ➜ \(\because SA=CA-CS=a-CS; AZ=CZ-CA=CZ-a\)
এবং \(S\acute A=e.\acute AZ\)
\(\therefore a+CS=e(CZ+a) ........(2)\) ➜ \(\because S\acute A=C\acute A+CS=a+CS; \acute AZ=CZ+CA=CZ+a\)
\((1)\) ও \((2)\) যোগ করে,
\(a-CS+a+CS=e(CZ-a)+e(CZ+a)\)
\(\Rightarrow 2a=e(CZ-a+CZ+a)\)
\(\Rightarrow 2a=e.2CZ\)
\(\Rightarrow a=e.CZ\)
\(\Rightarrow e.CZ=a\)
\(\therefore CZ=\frac{a}{e}\)
\((2)\) - \((1)\)-এর সাহায্যে,
\(a+CS-a+CS=e(CZ+a)-e(CZ-a)\)
\(\Rightarrow 2CS=e(CZ+a-CZ+a)\)
\(\Rightarrow 2CS=e.2a\)
\(\Rightarrow CS=e.a\)
\(\therefore CS=ae\)
\(C\)-কে মূলবিন্দু , \(CX\) ও \(CY\)-কে যথাক্রমে \(x\)-অক্ষ ও \(y\)-অক্ষ বিবেচনা করি। উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)। \(P\) বিন্দু হতে \(A\acute A\)-এর উপর \(PN\) ও নিয়ামকরেখার উপর \(PM\) লম্ব আঁকি।
সুতরাং উপবৃত্তের সংজ্ঞানুসারে, \(SP=e.PM\)
\(\Rightarrow SP=e.NZ\) ➜ \(\because PM=NZ\)
\(\Rightarrow SP^2=e^2.NZ^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow SN^2+PN^2=e^2(CN+CZ)^2\) ➜ \(\because SP^2=SN^2+PN^2; NZ=CN+CZ\)
\(\Rightarrow (ae+x)^2+y^2=e^2\left(x+\frac{a}{e}\right)^2\) ➜ \(\because SN=CS+CN=ae+x; NZ=x+\frac{a}{e}\)
\(\Rightarrow (ae+x)^2+y^2=e^2\left(\frac{ex+a}{e}\right)^2\)
\(\Rightarrow (ae+x)^2+y^2=e^2.\frac{(ex+a)^2}{e^2}\)
\(\Rightarrow (ae+x)^2+y^2=(ex+a)^2\)
\(\Rightarrow a^2e^2+2aex+x^2+y^2=e^2x^2+2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex+a^2-a^2e^2-2aex\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2-a^2e^2\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2(1-e^2)\)
\(\Rightarrow \frac{x^2(1-e^2)}{a^2(1-e^2)}+\frac{y^2}{a^2(1-e^2)}=1\) ➜ উভয় পার্শে \(a^2(1-e^2)\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{a^2(1-e^2)}=1 .......(3)\)
\((3)\) নং সমীকরণে \(x=0\) বসিয়ে,
\(\frac{0^2}{a^2}+\frac{y^2}{a^2(1-e^2)}=1\)
\(\Rightarrow \frac{0}{a^2}+\frac{y^2}{a^2(1-e^2)}=1\)
\(\Rightarrow 0+\frac{y^2}{a^2(1-e^2)}=1\)
\(\Rightarrow y^2=a^2(1-e^2)\)
\(\Rightarrow y=\pm \sqrt{a^2(1-e^2)}\)
\(\therefore y=\pm a\sqrt{(1-e^2)}\); ইহা স্পষ্ট যে \(Y\)-অক্ষ উপবৃত্তকে দুইটি বাস্তব বিন্দুতে (যেহেতু \(1>e \)) ছেদ করে।
ধরি,
\(B\) ও \(\acute B\) বিন্দু দুইটি \(C\)-এর বিপরীত দিকে এমনভাবে অবস্থিত যে,
\(CB=C\acute B=a\sqrt{(1-e^2)}\)।
ধরি,
\(CB=C\acute B=b\)
তাহলে, \(b=a\sqrt{(1-e^2)}\)
\(\therefore b^2=a^2(1-e^2) ........(4)\) ➜ উভয় পার্শে বর্গ করে।
\((4)\)-এর সাহায্য নিয়ে \((3)\) হতে পাই,
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই উপবৃত্তের আদর্শ সমীকরণ।

উপবৃত্তের উপকেন্দ্র \(S\) নিয়ামকরেখা \(MZ\) এবং উৎকেন্দ্রিকতা \(e (0 < e < 1)\), নিয়ামকরেখার উপর \(SZ\) লম্ব আঁকি। \(SZ\) রেখাকে \(A\) ও \(\acute A\) বিন্দুদ্বয় \(e:1\) অনুপাতে যথাক্রমে অন্তর্বিভক্ত ও বহিঃর্বিভক্ত করে, যেন \(SA=e.AZ\) এবং \(S\acute A=e.\acute AZ\)।
তাহলে, \(A\) ও \(\acute A\) উপবৃত্তের উপর দুইটি বিন্দু অর্থাৎ শীর্ষবিন্দু।
মনে করি \(A\acute A\)-এর মধ্যবিন্দু \(C\) এবং \(A\acute A=2a\)
তাহলে, \(CA=C\acute A=a\)
এখন,
\(SA=e.AZ\)
\(\therefore a-CS=e(CZ-a) .......(1)\) ➜ \(\because SA=CA-CS=a-CS; AZ=CZ-CA=CZ-a\)
এবং \(S\acute A=e.\acute AZ\)
\(\therefore a+CS=e(CZ+a) ........(2)\) ➜ \(\because S\acute A=C\acute A+CS=a+CS; \acute AZ=CZ+CA=CZ+a\)
\((1)\) ও \((2)\) যোগ করে,
\(a-CS+a+CS=e(CZ-a)+e(CZ+a)\)
\(\Rightarrow 2a=e(CZ-a+CZ+a)\)
\(\Rightarrow 2a=e.2CZ\)
\(\Rightarrow a=e.CZ\)
\(\Rightarrow e.CZ=a\)
\(\therefore CZ=\frac{a}{e}\)
\((2)\) - \((1)\)-এর সাহায্যে,
\(a+CS-a+CS=e(CZ+a)-e(CZ-a)\)
\(\Rightarrow 2CS=e(CZ+a-CZ+a)\)
\(\Rightarrow 2CS=e.2a\)
\(\Rightarrow CS=e.a\)
\(\therefore CS=ae\)
\(C\)-কে মূলবিন্দু , \(CX\) ও \(CY\)-কে যথাক্রমে \(x\)-অক্ষ ও \(y\)-অক্ষ বিবেচনা করি। উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)। \(P\) বিন্দু হতে \(A\acute A\)-এর উপর \(PN\) ও নিয়ামকরেখার উপর \(PM\) লম্ব আঁকি।
সুতরাং উপবৃত্তের সংজ্ঞানুসারে, \(SP=e.PM\)
\(\Rightarrow SP=e.NZ\) ➜ \(\because PM=NZ\)
\(\Rightarrow SP^2=e^2.NZ^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow SN^2+PN^2=e^2(CN+CZ)^2\) ➜ \(\because SP^2=SN^2+PN^2; NZ=CN+CZ\)
\(\Rightarrow (ae+x)^2+y^2=e^2\left(x+\frac{a}{e}\right)^2\) ➜ \(\because SN=CS+CN=ae+x; NZ=x+\frac{a}{e}\)
\(\Rightarrow (ae+x)^2+y^2=e^2\left(\frac{ex+a}{e}\right)^2\)
\(\Rightarrow (ae+x)^2+y^2=e^2.\frac{(ex+a)^2}{e^2}\)
\(\Rightarrow (ae+x)^2+y^2=(ex+a)^2\)
\(\Rightarrow a^2e^2+2aex+x^2+y^2=e^2x^2+2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex+a^2-a^2e^2-2aex\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2-a^2e^2\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2(1-e^2)\)
\(\Rightarrow \frac{x^2(1-e^2)}{a^2(1-e^2)}+\frac{y^2}{a^2(1-e^2)}=1\) ➜ উভয় পার্শে \(a^2(1-e^2)\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{a^2(1-e^2)}=1 .......(3)\)
\((3)\) নং সমীকরণে \(x=0\) বসিয়ে,
\(\frac{0^2}{a^2}+\frac{y^2}{a^2(1-e^2)}=1\)
\(\Rightarrow \frac{0}{a^2}+\frac{y^2}{a^2(1-e^2)}=1\)
\(\Rightarrow 0+\frac{y^2}{a^2(1-e^2)}=1\)
\(\Rightarrow y^2=a^2(1-e^2)\)
\(\Rightarrow y=\pm \sqrt{a^2(1-e^2)}\)
\(\therefore y=\pm a\sqrt{(1-e^2)}\); ইহা স্পষ্ট যে \(Y\)-অক্ষ উপবৃত্তকে দুইটি বাস্তব বিন্দুতে (যেহেতু \(1>e \)) ছেদ করে।
ধরি,
\(B\) ও \(\acute B\) বিন্দু দুইটি \(C\)-এর বিপরীত দিকে এমনভাবে অবস্থিত যে,
\(CB=C\acute B=a\sqrt{(1-e^2)}\)।
ধরি,
\(CB=C\acute B=b\)
তাহলে, \(b=a\sqrt{(1-e^2)}\)
\(\therefore b^2=a^2(1-e^2) ........(4)\) ➜ উভয় পার্শে বর্গ করে।
\((4)\)-এর সাহায্য নিয়ে \((3)\) হতে পাই,
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই উপবৃত্তের আদর্শ সমীকরণ।
উপবৃত্তের আদর্শ সমীকরণ সনাক্তকরণ
Identifying the standard equation of an ellipse
মূলবিন্দু কেন্দ্রবিশিষ্ট উপবৃত্তের প্রমিত সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এ \(x\) বা \(y\) যুক্ত পদ থাকবে না। শুধু \(x^2\) ও \(y^2\) যুক্ত পদ বিদ্যমান। \(x^2\)-এর সহগ \(\frac{1}{a^2}\) এবং \(y^2\)-এর সহগ \(\frac{1}{b^2}\) অসমান ও অভিন্ন চিহ্নযুক্ত।
উপবৃত্তের সমীকরণ সনাক্তকরণ
Identifying equation of an ellipse
উপবৃত্তের সমীকরণে \(x^2\) ও \(y^2\) যুক্ত পদ বিদ্যমান। \(x^2\)-এর সহগ এবং \(y^2\)-এর সহগ অসমান ও অভিন্ন চিহ্নযুক্ত। \(x\) ও \(y\) যুক্ত পদ থাকতেও পারে নাও থাকতে পারে।
উপবৃত্তের ক্ষেত্রফল
Area of ellipse
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের ক্ষেত্রফল \(=\pi ab\)
উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(x\) অক্ষ বরাবর
Equation of the ellipse whose Major axis along \(x\) axis
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \ (a>b)\)
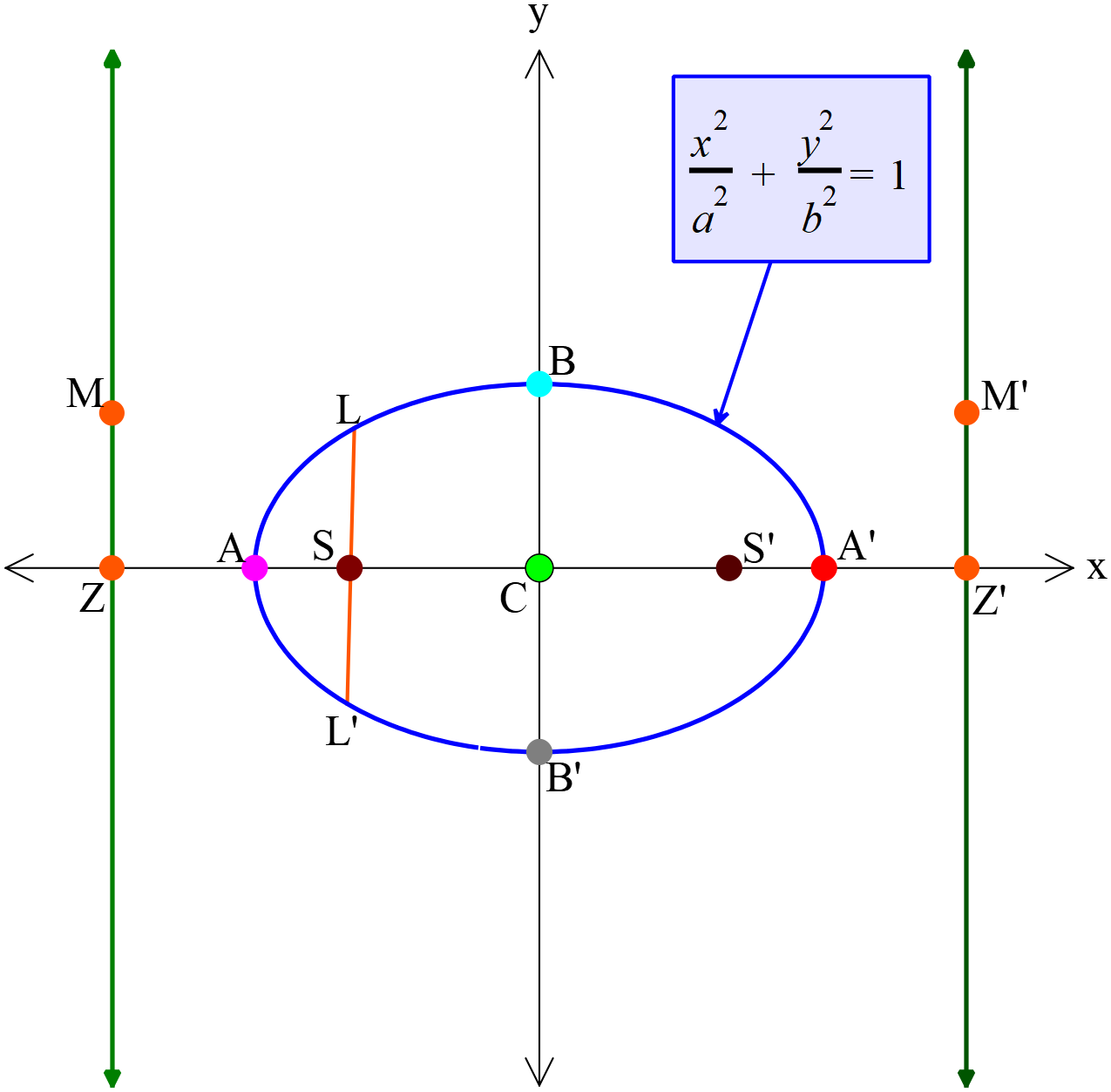

- উপবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(0, 0)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
- বৃহদাক্ষের দৈর্ঘ্য \(=|2a|\)
- ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2b|\)
- বৃহদাক্ষের সমীকরণ \(y=0\)
- ক্ষুদ্রাক্ষের সমীকরণ \(x=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((\pm ae, 0)\)
- নিয়ামকরেখার সমীকরণ \(x=\pm \frac{a}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2b^2}{a}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x=\pm ae\)
- শীর্ষবিন্দুর স্থানাঙ্ক \((\pm a, 0)\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \((\pm \frac{a}{e}, 0)\)
- উপকেন্দ্রের মধ্যকার দূরত্ব \(=|2ae|\)
- নিয়ামকদ্বয়ের মধ্যকার দূরত্ব \(=|\frac{2a}{e}|\)
- একই দিকের উপকেন্দ্র ও অনুরূপ নিয়ামকরেখার মধ্যকার দূরত্ব \(|\frac{a}{e}-ae|\)
উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(y\) অক্ষ বরাবর
Equation of the ellipse whose Major axis along \(y\) axis
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \ (b > a)\)
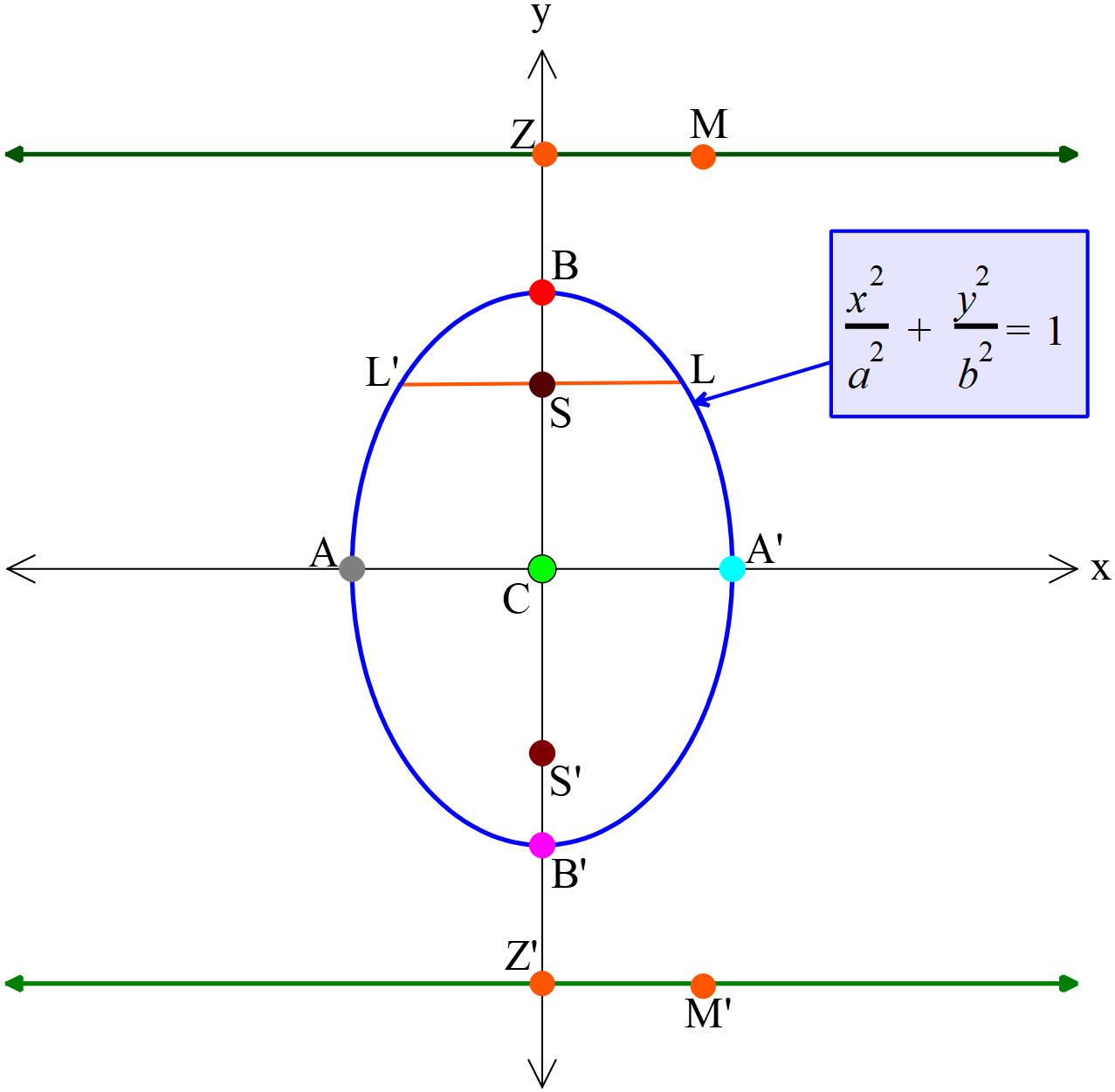

- উপবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(0, 0)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{a^2}{b^2}}\)
- বৃহদাক্ষের দৈর্ঘ্য \(=|2b|\)
- ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2a|\)
- বৃহদাক্ষের সমীকরণ \(x=0\)
- ক্ষুদ্রাক্ষের সমীকরণ \(y=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((0, \pm be)\)
- নিয়ামকরেখার সমীকরণ \(y=\pm \frac{b}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2a^2}{b}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y=\pm be\)
- শীর্ষবিন্দুর স্থানাঙ্ক \((0, \pm b)\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \((0, \pm \frac{b}{e})\)
- উপকেন্দ্রের মধ্যকার দূরত্ব \(=|2be|\)
- নিয়ামকদ্বয়ের মধ্যকার দূরত্ব \(=|\frac{2b}{e}|\)
- একই দিকের উপকেন্দ্র ও অনুরূপ নিয়ামকরেখার মধ্যকার দূরত্ব \(=|\frac{b}{e}-be|\)
নির্দিষ্ট কেন্দ্রবিশিষ্ট উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(x\) অক্ষ বরাবর
Equation of an ellipse with fixed center whose major axis is along the \(x\) axis
উপবৃত্তের সমীকরণ \(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1 \ (a\gt{b})\)
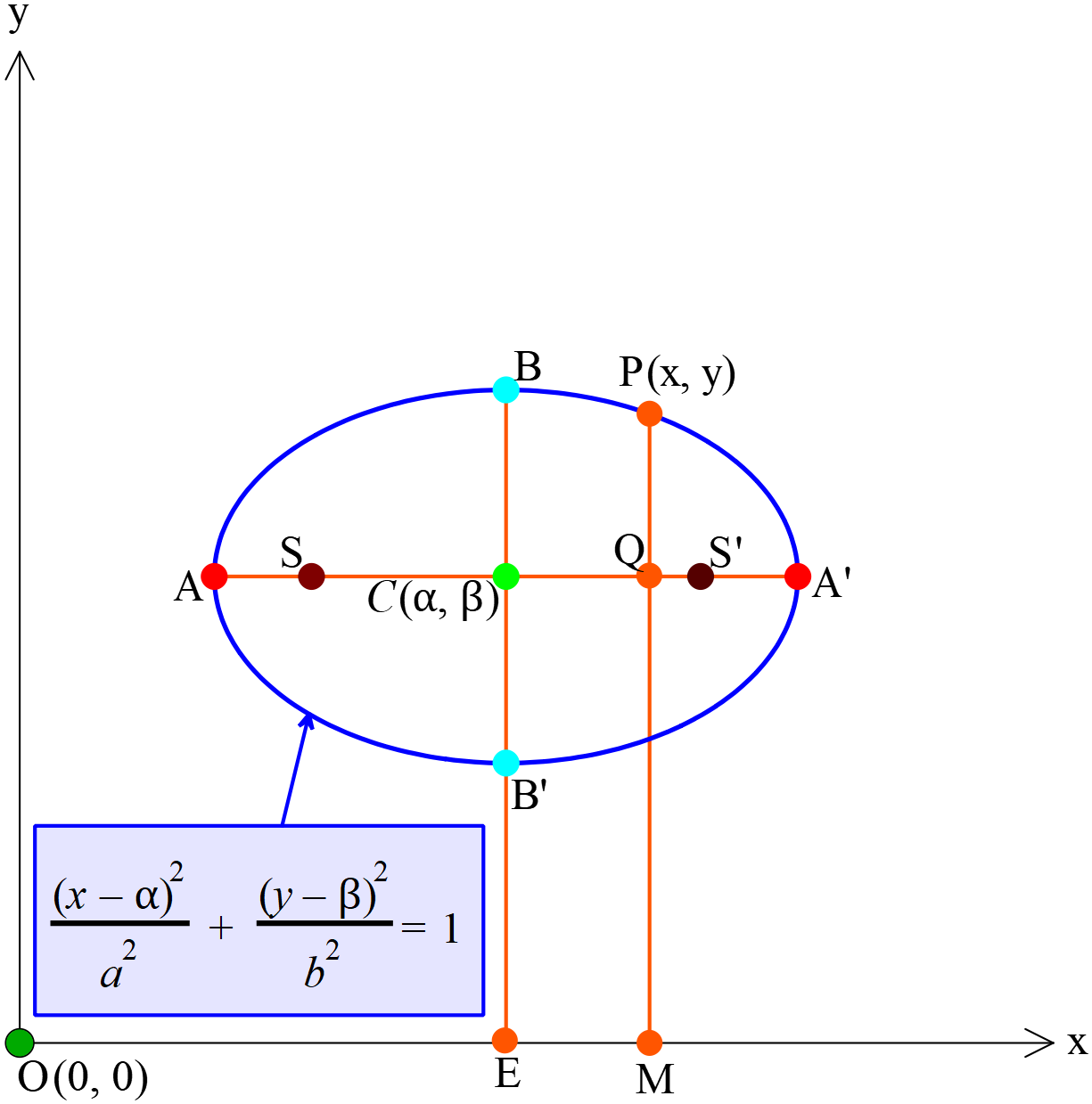

- শীর্ষবিন্দুর স্থানাঙ্ক \((\pm a+\alpha, 0)\)
- উপবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(\alpha, \beta)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
- বৃহদাক্ষের দৈর্ঘ্য \(=|2a|\)
- ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2b|\)
- বৃহদাক্ষের সমীকরণ \(y-\beta=0\)
- ক্ষুদ্রাক্ষের সমীকরণ \(x-\alpha=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((\pm ae+\alpha, \beta)\)
- নিয়ামকরেখার সমীকরণ \(x-\alpha=\pm \frac{a}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2b^2}{a}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x-\alpha=\pm ae\)
নির্দিষ্ট কেন্দ্রবিশিষ্ট উপবৃত্তের সমীকরণ যার বৃহৎ অক্ষ \(y\) অক্ষ বরাবর
Equation of an ellipse with fixed center whose major axis is along the \(y\) axis
উপবৃত্তের সমীকরণ \(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1 \ (a\lt{b})\)
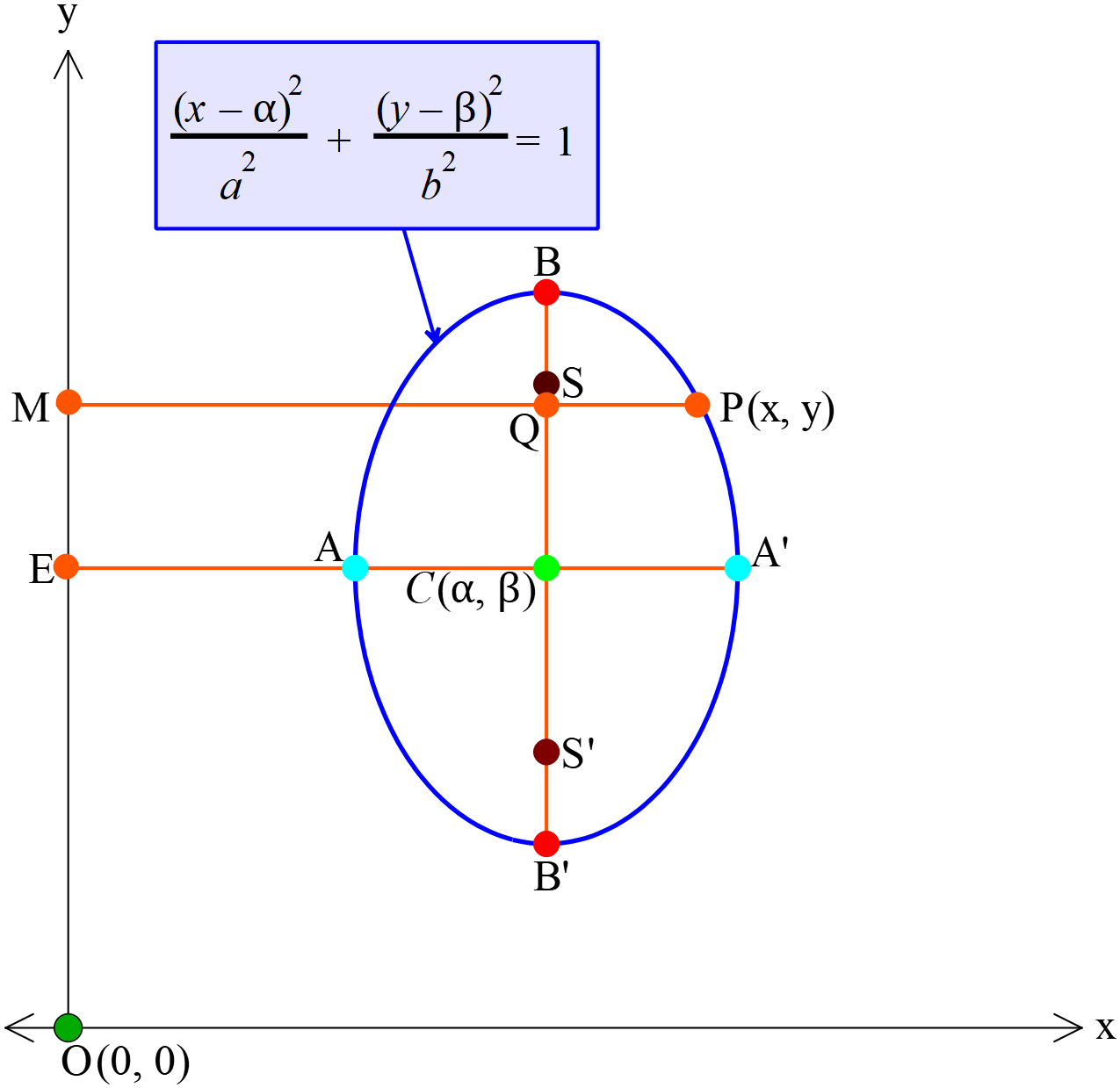
- শীর্ষবিন্দুর স্থানাঙ্ক \((\alpha, \pm b+\beta)\)
- উপবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(\alpha, \beta)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{a^2}{b^2}}\)
- বৃহদাক্ষের দৈর্ঘ্য \(=|2b|\)
- ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2a|\)
- বৃহদাক্ষের সমীকরণ \(x-\alpha=0\)
- ক্ষুদ্রাক্ষের সমীকরণ \(y-\beta=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((\alpha, \pm be+\beta)\)
- নিয়ামকরেখার সমীকরণ \(y-\beta=\pm \frac{b}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2a^2}{b}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y-\beta=\pm be\)
উপবৃত্তের স্পর্শক
Tangent of ellipse
কোনো সরলরেখা উপবৃত্তের স্পর্শক হওয়ার শর্ত, স্পর্শকের সমীকরণ এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং উপবৃত্তকে স্পর্শ করার শর্তঃ \(c=\pm \sqrt{(a^2m^2+b^2)}\)
স্পর্শকের সমীকরণঃ \(y=mx\pm \sqrt{(a^2m^2+b^2)}\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\right)\)
কোনো সরলরেখা উপবৃত্তের স্পর্শক হওয়ার শর্ত এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(x\cos\alpha + y\sin\alpha=p.............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং উপবৃত্তকে স্পর্শ করার শর্তঃ \(p^2=a^2\cos^2\alpha+b^2\sin^2\alpha\)
স্পর্শকের সমীকরণঃ \(x\cos\alpha + y\sin\alpha \pm \sqrt{(a^2\cos^2\alpha+b^2\sin^2\alpha)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{a^2\cos\alpha}{p}, \frac{b^2\sin\alpha}{p}\right)\)
কোনো সরলরেখা উপবৃত্তের স্পর্শক হওয়ার শর্ত এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(lx+my+n=0.............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং উপবৃত্তকে স্পর্শ করার শর্তঃ \(a^2l^2+b^2m^2=n^2\)
স্পর্শকের সমীকরণঃ \(lx+my \pm \sqrt{(a^2l^2+b^2m^2)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{-a^2l}{n}, \frac{-b^2m}{n}\right)\)
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং উপবৃত্তকে স্পর্শ করার শর্তঃ \(c=\pm \sqrt{(a^2m^2+b^2)}\)
স্পর্শকের সমীকরণঃ \(y=mx\pm \sqrt{(a^2m^2+b^2)}\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\right)\)
কোনো সরলরেখা উপবৃত্তের স্পর্শক হওয়ার শর্ত এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(x\cos\alpha + y\sin\alpha=p.............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং উপবৃত্তকে স্পর্শ করার শর্তঃ \(p^2=a^2\cos^2\alpha+b^2\sin^2\alpha\)
স্পর্শকের সমীকরণঃ \(x\cos\alpha + y\sin\alpha \pm \sqrt{(a^2\cos^2\alpha+b^2\sin^2\alpha)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{a^2\cos\alpha}{p}, \frac{b^2\sin\alpha}{p}\right)\)
কোনো সরলরেখা উপবৃত্তের স্পর্শক হওয়ার শর্ত এবং স্পর্শবিন্দুর স্থানাঙ্ক।
মনে করি,
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(lx+my+n=0.............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং উপবৃত্তকে স্পর্শ করার শর্তঃ \(a^2l^2+b^2m^2=n^2\)
স্পর্শকের সমীকরণঃ \(lx+my \pm \sqrt{(a^2l^2+b^2m^2)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{-a^2l}{n}, \frac{-b^2m}{n}\right)\)
উপবৃত্ত সাপেক্ষে কোনো বিন্দুর আপেক্ষিক অবস্থান
The relative position of a point with respect to the ellipse
মনে করি,
একটি নির্দিষ্ট বিন্দু এবং একটি উপবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1) \)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের উপরে অবস্থান করার শর্তঃ \(\frac{x^2_1}{a^2}+\frac{y^2_1}{b^2}=0\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের ভিতরে অবস্থান করার শর্তঃ \(0>\frac{x^2_1}{a^2}+\frac{y^2_1}{b^2}\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের বাহিরে অবস্থান করার শর্তঃ \(\frac{x^2_1}{a^2}+\frac{y^2_1}{b^2} > 0\)
উপবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুতে স্পর্শকের সমীকরণ।
মনে করি,
একটি নির্দিষ্ট বিন্দু এবং একটি উপবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1) \)
\((1)\) নং উপবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণঃ \(\frac{xx_1}{a^2}+\frac{yy_1}{b^2}=1\)
একটি নির্দিষ্ট বিন্দু এবং একটি উপবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1) \)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের উপরে অবস্থান করার শর্তঃ \(\frac{x^2_1}{a^2}+\frac{y^2_1}{b^2}=0\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের ভিতরে অবস্থান করার শর্তঃ \(0>\frac{x^2_1}{a^2}+\frac{y^2_1}{b^2}\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের বাহিরে অবস্থান করার শর্তঃ \(\frac{x^2_1}{a^2}+\frac{y^2_1}{b^2} > 0\)
উপবৃত্তের উপরিস্থিত কোনো নির্দিষ্ট বিন্দুতে স্পর্শকের সমীকরণ।
মনে করি,
একটি নির্দিষ্ট বিন্দু এবং একটি উপবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1) \)
\((1)\) নং উপবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণঃ \(\frac{xx_1}{a^2}+\frac{yy_1}{b^2}=1\)
উপবৃত্তের উপকেন্দ্র ও নিয়ামকরেখা
Focus and directrix of Ellipse
 একটি উপবৃত্তের দুইটি উপকেন্দ্র ও নিয়ামকরেখা আছে। যেহেতু, উপবৃত্তটি \(y\) অক্ষ বরাবর প্রতিসম তাই তাকে \(B\acute B\) বরাবর ভাঁজ করা হলে উপবৃত্তের ডান ও বাম পক্ষ দুইটি পরস্পরের সাথে সমাপতিত হয়। এখন \(x\) অক্ষের উপর \(\acute S\) ও \(\acute Z\) দুইটি বিন্দু এমনভাবে নেওয়া হয়, যেন \(C\acute S=CS=ae \) এবং \(C\acute Z=CZ=\frac{a}{e}\) হয়। \(Z\acute Z\)-এর উপর \(\acute M\acute Z\) লম্ব আঁকি। তাহলে প্রতিসাম্য অনুযায়ী, এটি স্পষ্ট যে, \(\acute S\)-কে উপকেন্দ্র এবং \(\acute M\acute Z\)-কে নিয়ামকরেখা ধরে আমরা একই উপবৃত্ত পাই। অতএব, উপবৃত্তের দুইটি উপকেন্দ্র এবং দুইটি নিয়ামকরেখা আছে।
একটি উপবৃত্তের দুইটি উপকেন্দ্র ও নিয়ামকরেখা আছে। যেহেতু, উপবৃত্তটি \(y\) অক্ষ বরাবর প্রতিসম তাই তাকে \(B\acute B\) বরাবর ভাঁজ করা হলে উপবৃত্তের ডান ও বাম পক্ষ দুইটি পরস্পরের সাথে সমাপতিত হয়। এখন \(x\) অক্ষের উপর \(\acute S\) ও \(\acute Z\) দুইটি বিন্দু এমনভাবে নেওয়া হয়, যেন \(C\acute S=CS=ae \) এবং \(C\acute Z=CZ=\frac{a}{e}\) হয়। \(Z\acute Z\)-এর উপর \(\acute M\acute Z\) লম্ব আঁকি। তাহলে প্রতিসাম্য অনুযায়ী, এটি স্পষ্ট যে, \(\acute S\)-কে উপকেন্দ্র এবং \(\acute M\acute Z\)-কে নিয়ামকরেখা ধরে আমরা একই উপবৃত্ত পাই। অতএব, উপবৃত্তের দুইটি উপকেন্দ্র এবং দুইটি নিয়ামকরেখা আছে।
উপবৃত্তের বৃহদাক্ষ ও ক্ষুদ্রাক্ষ
Major and Minor axis of Ellipse
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ........(1)\)
\(a>b\) ধরে \(C(0, 0)\) বিন্দু উপবৃত্তের কেন্দ্র।
\((1)\) নং সমীকরণে \(y=0\) বসিয়ে পাই \(\frac{x^2}{a^2}+\frac{0^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{0}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+0=1\)
\(\Rightarrow \frac{x^2}{a^2}=1\)
\(\Rightarrow x^2=a^2\)
\(\therefore x=\pm a\) সুতরাং উপবৃত্ত \(X\)-অক্ষকে \(A(a, 0)\) এবং \(\acute A(-a, 0)\) বিন্দুতে ছেদ করে।
\(A\acute A\) বৃহদাক্ষ এবং এর দৈর্ঘ্য
\(A\acute A=AC+C\acute A=a+a=2a\)
\(\therefore \) বৃহদাক্ষের দৈর্ঘ্য \(=|2a|\)।
আবার,
\((1)\) নং সমীকরণে \(x=0\) বসিয়ে পাই \(\frac{0^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{0}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow 0+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}=1\)
\(\Rightarrow y^2=b^2\)
\(\therefore y=\pm b\)
সুতরাং উপবৃত্ত \(Y\)-অক্ষকে \(B(0, b)\) এবং \(\acute B(0, -b)\) বিন্দুতে ছেদ করে।
\(B\acute B\) ক্ষুদ্রাক্ষ এবং এর দৈর্ঘ্য \(B\acute B=BC+C\acute B=b+b=2b\)
\(\therefore \) ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2b|\)।

\(a>b\) ধরে \(C(0, 0)\) বিন্দু উপবৃত্তের কেন্দ্র।
\((1)\) নং সমীকরণে \(y=0\) বসিয়ে পাই \(\frac{x^2}{a^2}+\frac{0^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{0}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+0=1\)
\(\Rightarrow \frac{x^2}{a^2}=1\)
\(\Rightarrow x^2=a^2\)
\(\therefore x=\pm a\) সুতরাং উপবৃত্ত \(X\)-অক্ষকে \(A(a, 0)\) এবং \(\acute A(-a, 0)\) বিন্দুতে ছেদ করে।
\(A\acute A\) বৃহদাক্ষ এবং এর দৈর্ঘ্য
\(A\acute A=AC+C\acute A=a+a=2a\)
\(\therefore \) বৃহদাক্ষের দৈর্ঘ্য \(=|2a|\)।
আবার,
\((1)\) নং সমীকরণে \(x=0\) বসিয়ে পাই \(\frac{0^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{0}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow 0+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}=1\)
\(\Rightarrow y^2=b^2\)
\(\therefore y=\pm b\)
সুতরাং উপবৃত্ত \(Y\)-অক্ষকে \(B(0, b)\) এবং \(\acute B(0, -b)\) বিন্দুতে ছেদ করে।
\(B\acute B\) ক্ষুদ্রাক্ষ এবং এর দৈর্ঘ্য \(B\acute B=BC+C\acute B=b+b=2b\)
\(\therefore \) ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=|2b|\)।
উপবৃত্তের সমীকরণ থেকে উৎকেন্দ্রতা
Eccentricity from the equation of ellipse
আমরা জানি,
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)
এবং
\(b^2=a^2(1-e^2)\)
\(\Rightarrow \frac{b^2}{a^2}=1-e^2\)
\(\Rightarrow e^2=1-\frac{b^2}{a^2}\)
\(\therefore e=\sqrt{1-\frac{b^2}{a^2}}\)
যেহেতু, উপবৃত্তের \(e\)-এর মান \(1 > e > 0\)
সুতরাং \(e\)-কে ধনাত্মক হিসাবে বিবেচনা করা হয়েছে।
উপবৃত্তের বৃহদাক্ষ হতে \(a\)-এর মান এবং ক্ষুদ্রাক্ষ হতে \(b\)-এর মান জানা থাকলে উৎকেন্দ্রতা \(e\)-এর মান নির্ণয় করা যায়।

উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)
এবং
\(b^2=a^2(1-e^2)\)
\(\Rightarrow \frac{b^2}{a^2}=1-e^2\)
\(\Rightarrow e^2=1-\frac{b^2}{a^2}\)
\(\therefore e=\sqrt{1-\frac{b^2}{a^2}}\)
যেহেতু, উপবৃত্তের \(e\)-এর মান \(1 > e > 0\)
সুতরাং \(e\)-কে ধনাত্মক হিসাবে বিবেচনা করা হয়েছে।
উপবৃত্তের বৃহদাক্ষ হতে \(a\)-এর মান এবং ক্ষুদ্রাক্ষ হতে \(b\)-এর মান জানা থাকলে উৎকেন্দ্রতা \(e\)-এর মান নির্ণয় করা যায়।
উপবৃত্তের সমীকরণ থেকে উপকেন্দ্রের স্থানাঙ্ক ও নিয়ামকের সমীকরণ
The co-ordinates of focus and the equation of directrix from the equation of ellipse
মনে করি,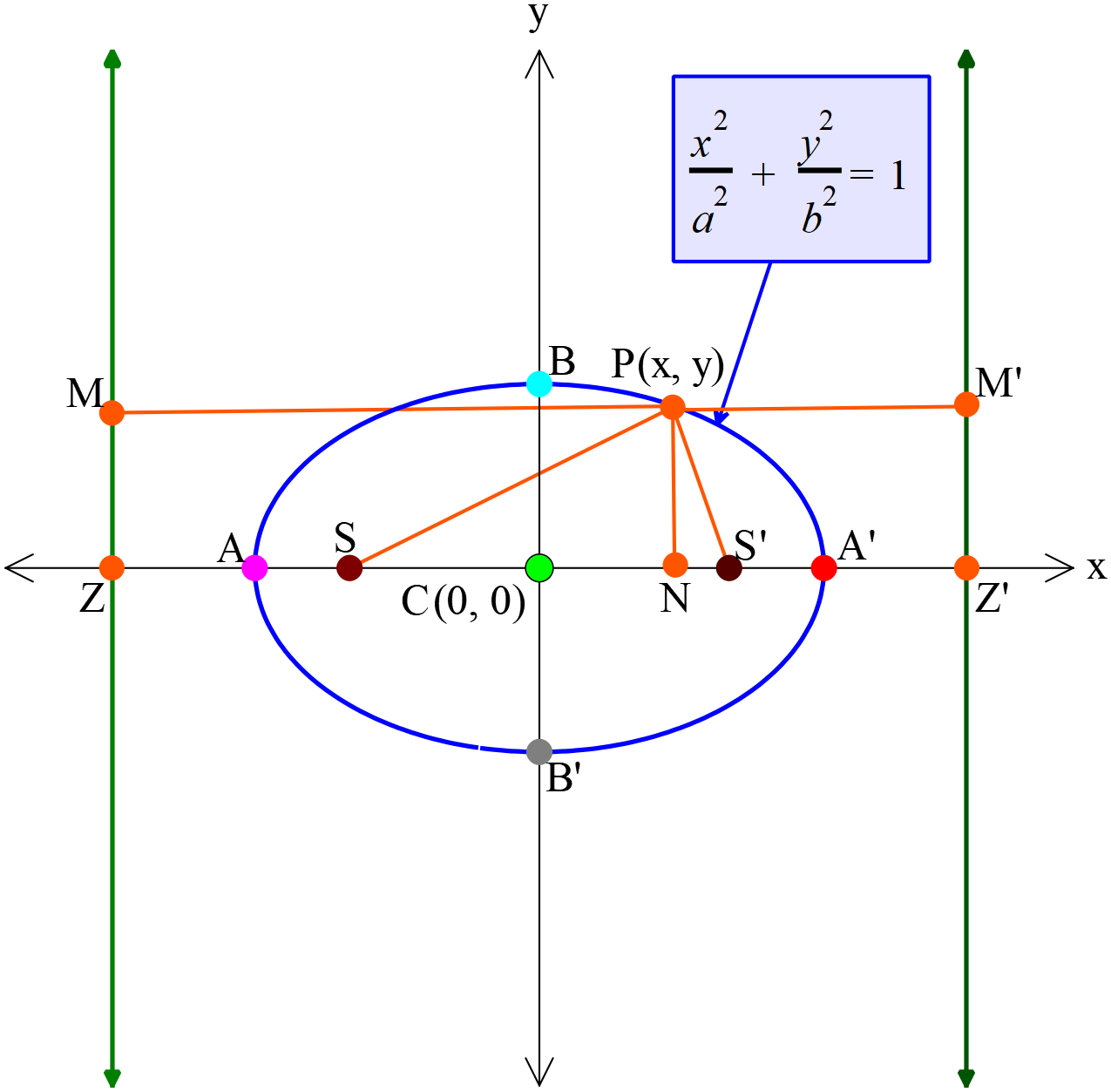
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)
এবং
\(b^2=a^2(1-e^2)\) ➜ এখানে \(e\) উৎকেন্দ্রিকতা।
আবার,
উপবৃত্তের উপকেন্দ্র \(S\) ও \(\acute S\) এবং নিয়ামক রেখা \(MZ\) ও \(\acute M\acute Z\)।
\(Z\acute Z\) রেখা \(S\) এবং \(\acute S\) বিন্দুগামী। \(Z\acute Z\) রেখা নিয়ামকদ্বয়ের উপর লম্ব।
\(SZ\)-এর উপর \(A\) এমন একটি বিন্দু নেওয়া হল যেন \(SA=eAZ ........(1)\)
আবার,
\(SZ\)-এর বর্দ্ধিতাংশের উপর \(\acute A\) এমন একটি বিন্দু নেওয়া হল যেন \(S\acute A=e\acute AZ\)
ধরি,
\(A\acute A=2a\) এবং \(C\) হল \(A\acute A\)-এর মধ্যবিন্দু। \(C\)-কে কেন্দ্র বিন্দু বলা হয় যার স্থানাঙ্ক \(C(0, 0)\)।
\((1)\) ও \((2)\) যোগ করে পাই
\(SA+S\acute A=eAZ+e\acute AZ\)
\(\Rightarrow A\acute A=e(AZ+\acute AZ)\)
\(\Rightarrow 2a=e(AZ+A\acute A+AZ)\) ➜ \(\because \acute AZ=A\acute A+AZ\)
\(\Rightarrow 2a=e(A\acute A+2AZ)\)
\(\Rightarrow 2a=e(2a+2AZ)\)
\(\Rightarrow 2a=2e(a+AZ)\)
\(\Rightarrow a=e(a+AZ)\)
\(\Rightarrow a=eCZ\) ➜ \(\because CZ=CA+AZ=a+AZ\)
\(\Rightarrow eCZ=a\)
\(\therefore CZ=\frac{a}{e} ......(3)\)
আবার,
\(CS=CA-AS\)
\(\Rightarrow CS=CA-eAZ\) ➜ \(\because AS=eAZ\)
\(\Rightarrow CS=CA-e(CZ-CA)\)
\(\Rightarrow CS=a-e\left(\frac{a}{e}-a\right)\)
\(\Rightarrow CS=a-a+ae\)
\(\therefore CS=ae .........(4)\)
\(C\) বিন্দুকে মূলবিন্দু ধরে \(CX\)-কে \(x\)অক্ষ এবং \(CY\)-কে \(y\)অক্ষ বিবেচনা করি। যেহেতু \(S\) বিন্দু \(x\)অক্ষের উপর অবস্থিত ।
অতএব, \(S\)-এর স্থানাঙ্ক \((ae, 0)\) এখানে \(S\)-কে উপকেন্দ্র বলে। যেহেতু উপকেন্দ্র \(S\) ও \(\acute S\) সুতরাং এদের স্থানাঙ্ক লেখা হয় \((\pm ae, 0)\)।
এবং নিয়ামক রেখা \(\acute M\acute Z\)-এর সমীকরণ \(x=CZ=\frac{a}{e}\)
\(\therefore x=\frac{a}{e}\)
অনুরূপভাবে, নিয়ামক রেখা \(MZ\)-এর সমীকরণ \(x=-\frac{a}{e}\)
সুতরাং উপবৃত্তের নিয়ামক রেখার সমীকরণ \(x=\pm \frac{a}{e}\)

উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)
এবং
\(b^2=a^2(1-e^2)\) ➜ এখানে \(e\) উৎকেন্দ্রিকতা।
আবার,
উপবৃত্তের উপকেন্দ্র \(S\) ও \(\acute S\) এবং নিয়ামক রেখা \(MZ\) ও \(\acute M\acute Z\)।
\(Z\acute Z\) রেখা \(S\) এবং \(\acute S\) বিন্দুগামী। \(Z\acute Z\) রেখা নিয়ামকদ্বয়ের উপর লম্ব।
\(SZ\)-এর উপর \(A\) এমন একটি বিন্দু নেওয়া হল যেন \(SA=eAZ ........(1)\)
আবার,
\(SZ\)-এর বর্দ্ধিতাংশের উপর \(\acute A\) এমন একটি বিন্দু নেওয়া হল যেন \(S\acute A=e\acute AZ\)
ধরি,
\(A\acute A=2a\) এবং \(C\) হল \(A\acute A\)-এর মধ্যবিন্দু। \(C\)-কে কেন্দ্র বিন্দু বলা হয় যার স্থানাঙ্ক \(C(0, 0)\)।
\((1)\) ও \((2)\) যোগ করে পাই
\(SA+S\acute A=eAZ+e\acute AZ\)
\(\Rightarrow A\acute A=e(AZ+\acute AZ)\)
\(\Rightarrow 2a=e(AZ+A\acute A+AZ)\) ➜ \(\because \acute AZ=A\acute A+AZ\)
\(\Rightarrow 2a=e(A\acute A+2AZ)\)
\(\Rightarrow 2a=e(2a+2AZ)\)
\(\Rightarrow 2a=2e(a+AZ)\)
\(\Rightarrow a=e(a+AZ)\)
\(\Rightarrow a=eCZ\) ➜ \(\because CZ=CA+AZ=a+AZ\)
\(\Rightarrow eCZ=a\)
\(\therefore CZ=\frac{a}{e} ......(3)\)
আবার,
\(CS=CA-AS\)
\(\Rightarrow CS=CA-eAZ\) ➜ \(\because AS=eAZ\)
\(\Rightarrow CS=CA-e(CZ-CA)\)
\(\Rightarrow CS=a-e\left(\frac{a}{e}-a\right)\)
\(\Rightarrow CS=a-a+ae\)
\(\therefore CS=ae .........(4)\)
\(C\) বিন্দুকে মূলবিন্দু ধরে \(CX\)-কে \(x\)অক্ষ এবং \(CY\)-কে \(y\)অক্ষ বিবেচনা করি। যেহেতু \(S\) বিন্দু \(x\)অক্ষের উপর অবস্থিত ।
অতএব, \(S\)-এর স্থানাঙ্ক \((ae, 0)\) এখানে \(S\)-কে উপকেন্দ্র বলে। যেহেতু উপকেন্দ্র \(S\) ও \(\acute S\) সুতরাং এদের স্থানাঙ্ক লেখা হয় \((\pm ae, 0)\)।
এবং নিয়ামক রেখা \(\acute M\acute Z\)-এর সমীকরণ \(x=CZ=\frac{a}{e}\)
\(\therefore x=\frac{a}{e}\)
অনুরূপভাবে, নিয়ামক রেখা \(MZ\)-এর সমীকরণ \(x=-\frac{a}{e}\)
সুতরাং উপবৃত্তের নিয়ামক রেখার সমীকরণ \(x=\pm \frac{a}{e}\)
উপবৃত্তের সমীকরণ থেকে উপকেন্দ্রিক লম্ব ও এর দৈর্ঘ্য
From the equation of an ellipse Latus rectum and it's length
উপবৃত্তের যে কোনো উপকেন্দ্রের মধ্য দিয়ে অঙ্কিত বৃহদাক্ষের উপর লম্ব রেখার উপবৃত্তের অন্তর্গত অংশই উপকেন্দ্রিক লম্ব। যদি \(L\acute L\) উপকেন্দ্রিক লম্ব হয়, তবে \(SL=S\acute L\) এবং \(\acute L\)-এর স্থানাঙ্ক \((-ae, SL)\) ।
\(\acute L(-ae, SL)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)-এর উপর অবস্থিত।
\(\Rightarrow \frac{(-ae)^2}{a^2}+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{a^2e^2}{a^2}+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow e^2+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{SL^2}{b^2}=1-e^2 \)
\(\Rightarrow SL^2=b^2(1-e^2) \)
\(\Rightarrow SL^2=b^2\times \frac{b^2}{a^2} \) ➜ \(\because 1-e^2=\frac{b^2}{a^2}\)
\(\Rightarrow SL^2=\frac{b^4}{a^2} \)
\(\therefore SL=\frac{b^2}{a} \)
\(\therefore L\acute L=2SL=\frac{2b^2}{a} \)

\(\acute L(-ae, SL)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a > b)\)-এর উপর অবস্থিত।
\(\Rightarrow \frac{(-ae)^2}{a^2}+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{a^2e^2}{a^2}+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow e^2+\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{SL^2}{b^2}=1-e^2 \)
\(\Rightarrow SL^2=b^2(1-e^2) \)
\(\Rightarrow SL^2=b^2\times \frac{b^2}{a^2} \) ➜ \(\because 1-e^2=\frac{b^2}{a^2}\)
\(\Rightarrow SL^2=\frac{b^4}{a^2} \)
\(\therefore SL=\frac{b^2}{a} \)
\(\therefore L\acute L=2SL=\frac{2b^2}{a} \)
উপবৃত্তের উপরিস্থিত কোনো বিন্দুর উপকেন্দ্রিক দূরত্ব দুইটির সমষ্টি, বৃহদাক্ষের দৈর্ঘ্যের সমান
Sum of the two epicentral distance of a point on the ellipse is equal to the length of Major axis
ধরি,
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের উপরিস্থিত কোনো বিন্দু \(P(x, y)\)।
উপবৃত্তের উপকেন্দ্র দুইটি \(S\) ও \(\acute S\) এবং নিয়ামক রেখা দুইটি যথাক্রমে \(MZ\) ও \(\acute M\acute Z\) ।
\(SP\) এবং \(\acute SP\) যোগ করি এবং নিয়ামক রেখা দইটির উপর \(MP\acute M\) লম্ব আঁকি।
এখন,
উপবৃত্তের সংজ্ঞানুসারে,
\(SP=e.PM .......(1)\)
এবং \(\acute SP=e.P\acute M .......(2)\)
\((1)\) ও \((2)\) যোগ করে,
\(SP+\acute SP=e.PM+e.P\acute M\)
\(\Rightarrow SP+\acute SP=e(PM+P\acute M)\)
\(\Rightarrow SP+\acute SP=e\{(CZ+CN)+(C\acute Z-CN)\}\) ➜ \(\because PM=CZ+CN; P\acute M=C\acute Z-CN\)
\(\Rightarrow SP+\acute SP=e\{CZ+CN+C\acute Z-CN\}\)
\(\Rightarrow SP+\acute SP=e\{CZ+C\acute Z\}\)
\(\Rightarrow SP+\acute SP=e\{CZ+CZ\}\) ➜ \(\because CZ=C\acute Z\)
\(\Rightarrow SP+\acute SP=e.2CZ\)
\(\Rightarrow SP+\acute SP=2.e.CZ\)
\(\Rightarrow SP+\acute SP=2.CA\) ➜ \(\because e.CZ=CA\)
\(\Rightarrow SP+\acute SP=A\acute A\) ➜ \(\because 2.CA=A\acute A\)
\(\therefore SP+\acute SP=2a\) ➜ \(\because A\acute A=2a\)
\(\therefore \) উপবৃত্তের উপরিস্থিত \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব দুইটির সমষ্টি, বৃহদাক্ষের দৈর্ঘ্যের সমান। ইহা অতি গুরুত্বপূর্ণ।

\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের উপরিস্থিত কোনো বিন্দু \(P(x, y)\)।
উপবৃত্তের উপকেন্দ্র দুইটি \(S\) ও \(\acute S\) এবং নিয়ামক রেখা দুইটি যথাক্রমে \(MZ\) ও \(\acute M\acute Z\) ।
\(SP\) এবং \(\acute SP\) যোগ করি এবং নিয়ামক রেখা দইটির উপর \(MP\acute M\) লম্ব আঁকি।
এখন,
উপবৃত্তের সংজ্ঞানুসারে,
\(SP=e.PM .......(1)\)
এবং \(\acute SP=e.P\acute M .......(2)\)
\((1)\) ও \((2)\) যোগ করে,
\(SP+\acute SP=e.PM+e.P\acute M\)
\(\Rightarrow SP+\acute SP=e(PM+P\acute M)\)
\(\Rightarrow SP+\acute SP=e\{(CZ+CN)+(C\acute Z-CN)\}\) ➜ \(\because PM=CZ+CN; P\acute M=C\acute Z-CN\)
\(\Rightarrow SP+\acute SP=e\{CZ+CN+C\acute Z-CN\}\)
\(\Rightarrow SP+\acute SP=e\{CZ+C\acute Z\}\)
\(\Rightarrow SP+\acute SP=e\{CZ+CZ\}\) ➜ \(\because CZ=C\acute Z\)
\(\Rightarrow SP+\acute SP=e.2CZ\)
\(\Rightarrow SP+\acute SP=2.e.CZ\)
\(\Rightarrow SP+\acute SP=2.CA\) ➜ \(\because e.CZ=CA\)
\(\Rightarrow SP+\acute SP=A\acute A\) ➜ \(\because 2.CA=A\acute A\)
\(\therefore SP+\acute SP=2a\) ➜ \(\because A\acute A=2a\)
\(\therefore \) উপবৃত্তের উপরিস্থিত \(P(x, y)\) বিন্দুর উপকেন্দ্রিক দূরত্ব দুইটির সমষ্টি, বৃহদাক্ষের দৈর্ঘ্যের সমান। ইহা অতি গুরুত্বপূর্ণ।
কোনো সমতলে, কোনো সেটের বিন্দুসমুহ যদি এমনভাবে অবস্থিত হয় যে, ঐ সমতলে অবস্থিত দুইটি নির্দিষ্ট বিন্দু হতে এর দূরত্ব দুইটির সমষ্টি সর্বদা স্থীর হয় তাহলে উক্ত বিন্দু সেটের সঞ্চারপথ উপবৃত্ত হবে।
দ্রঃ উপবৃত্তের বৃহৎ অক্ষ এর বৃহত্তম জ্যা। কোনো নির্দিষ্ট বিন্দুতে উপবৃত্তের পরামিতিক স্থানাঙ্ক যখন \((a\gt{b})\)
Parametric coordinates of a given point on the ellipse when \((a\gt{b})\)
ধরি,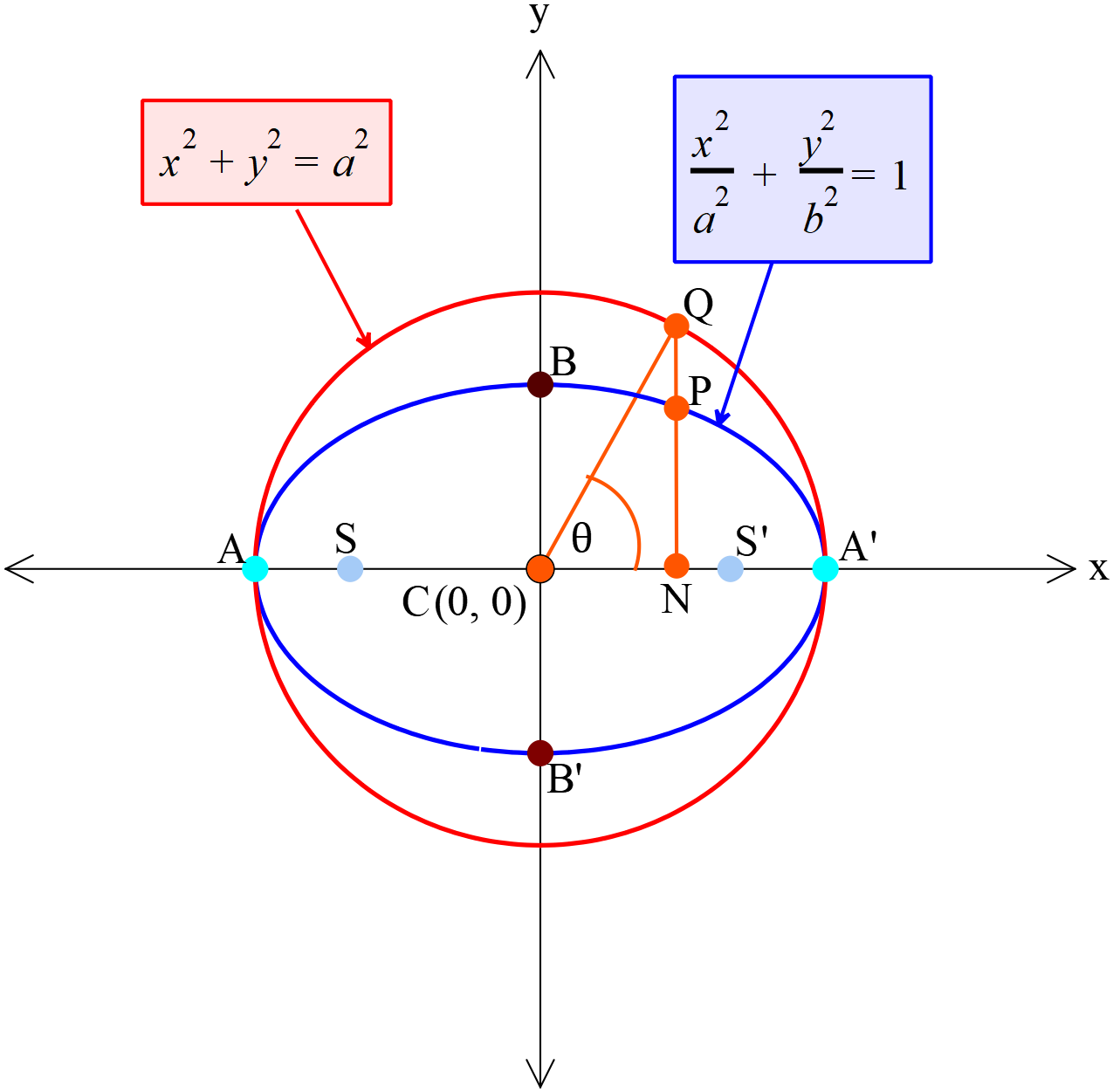
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a>b) ........(1)\)
এবং উপবৃত্তের উপরিস্থিত একটি বিন্দু \(P(x, y)\)
উপবৃত্তের বৃহদাক্ষকে ব্যাস ধরে সহায়ক বৃত্ত অঙ্কন করি, যার সমীকরণ \(x^2+y^2=a^2 .......(2)\)
\(P(x, y)\) বিন্দু থেকে বৃহদাক্ষের উপর একটি লম্ব অঙ্কন করে বর্ধিত করি যা বৃহদাক্ষকে \(N\) এবং বৃত্তকে \(Q\) বিন্দুতে ছেদ করে। \(C\) ও \(Q\) যোগ করি।
মনে করি,
\(\angle QCN=\theta\), এখানে \(\theta\)-কে উপকেন্দ্র কোণ বলা হয়।
\(P\) বিন্দুর স্থানাঙ্ক \((x, y)\) হওয়ায়, \(CN=x\) এবং \(PN=y\)
এখন, \(QCN\) সমকোণী ত্রিভুজে \(\cos\theta=\frac{CN}{CQ}\)
\(\Rightarrow CN=CQ\cos\theta\)
\(\therefore x=a\cos\theta ........(3)\) ➜ \(\because CQ=a=\)বৃত্তের ব্যাসার্ধ।
\(x=a\cos\theta\)-এর এই মান \((1)\)-এ বসিয়ে,
\(\frac{(a\cos\theta)^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{a^2\cos^2\theta}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \cos^2\theta+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}=1-\cos^2\theta\)
\(\Rightarrow \frac{y^2}{b^2}=\sin^2\theta\)
\(\Rightarrow y^2=b^2\sin^2\theta\)
\(\therefore y=b\sin\theta ......(4)\)
সুতরাং, \(P(a\cos\theta, b\sin\theta)\)
\(\theta\)-এর যে কোনো মানের জন্য \(P(a\cos\theta, b\sin\theta)\) বিন্দুটি উপবৃত্তের উপর অবস্থিত, যাকে উপবৃত্তের পরামিতিক স্থানাঙ্ক বলা হয় এবং \(\theta\)-কে পরামিতি (parameter) বলা হয়।
আবার,
\((3)\) ও \((4)\) হতে যথাক্রমে,
\(\cos\theta=\frac{x}{a} ........(5)\)
\(\sin\theta=\frac{y}{b} ........(6)\)
\(\frac{\sin\theta}{\cos\theta}=\frac{\frac{y}{b}}{\frac{x}{a}}\) ➜ \((6)\)-কে \((5)\) দিয়ে ভাগ করে।
\(\Rightarrow \tan\theta=\frac{ay}{bx}\)
\(\therefore \theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)
\(\theta \)-এর এই মাণ নির্ণয়ের সময় বিন্দুটি কোন চতুর্ভাগে অবস্থিত তা লক্ষনীয়।
\(x=a\cos\theta\) এবং \(y=b\sin\theta\)-কে একত্রে \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের পরামিতিক সমীকরণ বলে।
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a>b) \) উপবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\cos\theta, b\sin\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)।
দ্রঃ ইহা স্পষ্ট যে উপবৃত্তের আকার যাই হউকনা কেন ইহার উপরোস্থ যে কোনো বিন্দুর পরামিতিক স্থানাঙ্ক হবে \(P(a\cos\theta, b\sin\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{ay}{bx}\right)\). এবং উপবৃত্তের পরামিতিক সমীকরণ হবে
\(x=a\cos\theta\),\(y=b\sin\theta\).

উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a>b) ........(1)\)
এবং উপবৃত্তের উপরিস্থিত একটি বিন্দু \(P(x, y)\)
উপবৃত্তের বৃহদাক্ষকে ব্যাস ধরে সহায়ক বৃত্ত অঙ্কন করি, যার সমীকরণ \(x^2+y^2=a^2 .......(2)\)
\(P(x, y)\) বিন্দু থেকে বৃহদাক্ষের উপর একটি লম্ব অঙ্কন করে বর্ধিত করি যা বৃহদাক্ষকে \(N\) এবং বৃত্তকে \(Q\) বিন্দুতে ছেদ করে। \(C\) ও \(Q\) যোগ করি।
মনে করি,
\(\angle QCN=\theta\), এখানে \(\theta\)-কে উপকেন্দ্র কোণ বলা হয়।
\(P\) বিন্দুর স্থানাঙ্ক \((x, y)\) হওয়ায়, \(CN=x\) এবং \(PN=y\)
এখন, \(QCN\) সমকোণী ত্রিভুজে \(\cos\theta=\frac{CN}{CQ}\)
\(\Rightarrow CN=CQ\cos\theta\)
\(\therefore x=a\cos\theta ........(3)\) ➜ \(\because CQ=a=\)বৃত্তের ব্যাসার্ধ।
\(x=a\cos\theta\)-এর এই মান \((1)\)-এ বসিয়ে,
\(\frac{(a\cos\theta)^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{a^2\cos^2\theta}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \cos^2\theta+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}=1-\cos^2\theta\)
\(\Rightarrow \frac{y^2}{b^2}=\sin^2\theta\)
\(\Rightarrow y^2=b^2\sin^2\theta\)
\(\therefore y=b\sin\theta ......(4)\)
সুতরাং, \(P(a\cos\theta, b\sin\theta)\)
\(\theta\)-এর যে কোনো মানের জন্য \(P(a\cos\theta, b\sin\theta)\) বিন্দুটি উপবৃত্তের উপর অবস্থিত, যাকে উপবৃত্তের পরামিতিক স্থানাঙ্ক বলা হয় এবং \(\theta\)-কে পরামিতি (parameter) বলা হয়।
আবার,
\((3)\) ও \((4)\) হতে যথাক্রমে,
\(\cos\theta=\frac{x}{a} ........(5)\)
\(\sin\theta=\frac{y}{b} ........(6)\)
\(\frac{\sin\theta}{\cos\theta}=\frac{\frac{y}{b}}{\frac{x}{a}}\) ➜ \((6)\)-কে \((5)\) দিয়ে ভাগ করে।
\(\Rightarrow \tan\theta=\frac{ay}{bx}\)
\(\therefore \theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)
\(\theta \)-এর এই মাণ নির্ণয়ের সময় বিন্দুটি কোন চতুর্ভাগে অবস্থিত তা লক্ষনীয়।
\(x=a\cos\theta\) এবং \(y=b\sin\theta\)-কে একত্রে \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তের পরামিতিক সমীকরণ বলে।
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1; (a>b) \) উপবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\cos\theta, b\sin\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{ay}{bx}\right)\)।
দ্রঃ ইহা স্পষ্ট যে উপবৃত্তের আকার যাই হউকনা কেন ইহার উপরোস্থ যে কোনো বিন্দুর পরামিতিক স্থানাঙ্ক হবে \(P(a\cos\theta, b\sin\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{ay}{bx}\right)\). এবং উপবৃত্তের পরামিতিক সমীকরণ হবে
\(x=a\cos\theta\),\(y=b\sin\theta\).
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর লেখচিত্র
Graph of equation of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)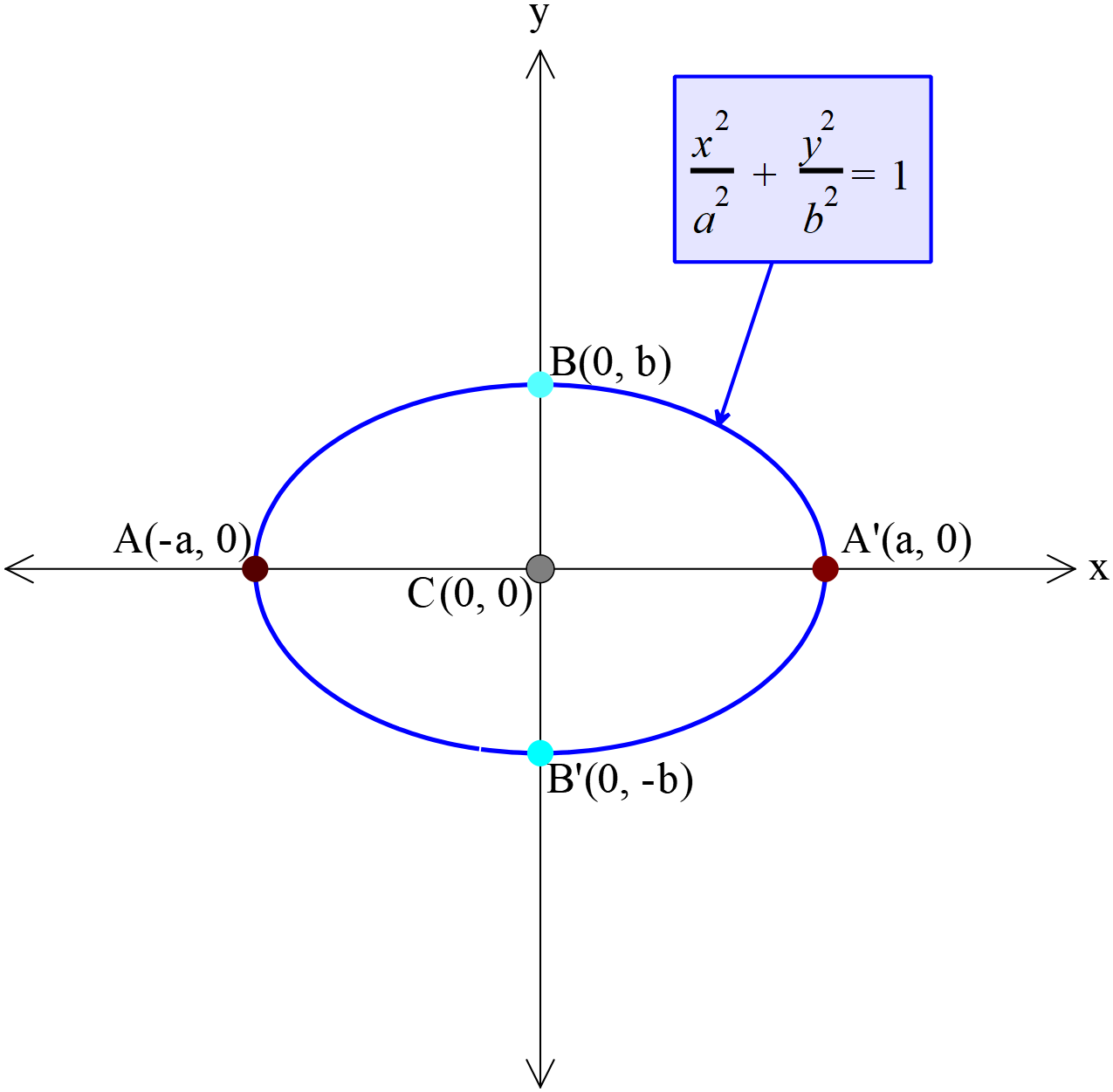
\(\Rightarrow \frac{y^2}{b^2}=1-\frac{x^2}{a^2}\)
\(\Rightarrow \frac{y^2}{b^2}=\frac{a^2-x^2}{a^2}\)
\(\Rightarrow y^2=\frac{b^2(a^2-x^2)}{a^2}\)
\(\Rightarrow y=\pm \sqrt{\frac{b^2(a^2-x^2)}{a^2}}\)
\(\therefore y=\pm b\sqrt{\frac{(a^2-x^2)}{a^2}}\)
\(\therefore a>x\)-এর যে কোনো মানের জন্য \(y\)-এর দুইটি মান পাওয়া যায়। মান দুইটি সমান কিন্তু বিপরীত চিহ্নবিশিষ্ট। অতএব, ইহা স্পষ্ট যে,উপবৃত্তটি \(X\)-অক্ষ ( বৃহৎ অক্ষ ) বরাবর প্রতিসম।
আবার,
\(x\)-এর সর্বোচ্চ মান \(a\) এবং সর্বনিম্ন মান \(-a\) কারণ, যদি \(x > a\) বা \(-a>x\) হয়, তবে,
\(\frac{a^2-x^2}{a^2}\) ঋনাত্মক হয় এবং \(y\)-এর মান দুইটি অবাস্তব হয়।
অতএব, উপবৃত্তের কোনো অংশই \(x\)-অক্ষের উপর \(A\) ও \(\acute A\) বিন্দু দুইটির বাইরে অবস্থিত হবে না।
উপবৃত্তের সমীকরণটিকে নিম্নোক্তভাবেও লেখা যায়,\(\therefore x=\pm a\sqrt{\frac{(b^2-y^2)}{b^2}}\)
\(\therefore b > y\)-এর যে কোনো মানের জন্য \(x\)-এর দুইটি মান পাওয়া যায়। মান দুইটি সমান কিন্তু বিপরীত চিহ্নবিশিষ্ট। অতএব, ইহা স্পষ্ট যে,উপবৃত্তটি \(Y\)-অক্ষ (ক্ষুদ্র অক্ষ ) বরাবর প্রতিসম।
\(y\)-এর সর্বোচ্চ মান \(b\) এবং সর্বনিম্ন মান \(-b\) কারণ, যদি \(y > b\) বা \(-b > y\) হয়, তবে,
\(\frac{b^2-y^2}{b^2}\) ঋনাত্মক হয় এবং \(x\)-এর মান দুইটি অবাস্তব হয়।
অতএব, উপবৃত্তের কোনো অংশই \(y\)-অক্ষের উপর \(B\) ও \(\acute B\) বিন্দু দুইটির বাইরে অবস্থিত হবে না।
অতএব , উপবৃত্ত একটি সীমাবদ্ধ বক্ররেখা, যা, পুরাপুরি \(x=\pm a, y=\pm b\) সরলরেখা চতুষ্টয় দ্বারা সীমিত আয়তের মধ্যে অবস্থিত।
অক্ষদ্বয়ের দৈর্ঘ্য \(2a\) ও \(2b\) এবং তাদের সমীকরণ যথাক্রমে \(a_{1}x+b_{1}y+c_{1}=0\) ও \(a_{2}x+b_{2}y+c_{2}=0\) উপবৃত্তের সমীকরণ,
\(\frac{1}{a^2}\left(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_{1}^2+b_{1}^2}}\right)^2+\frac{1}{b^2}\left(\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_{2}^2+b_{2}^2}}\right)^2=1\)

\(\Rightarrow \frac{y^2}{b^2}=1-\frac{x^2}{a^2}\)
\(\Rightarrow \frac{y^2}{b^2}=\frac{a^2-x^2}{a^2}\)
\(\Rightarrow y^2=\frac{b^2(a^2-x^2)}{a^2}\)
\(\Rightarrow y=\pm \sqrt{\frac{b^2(a^2-x^2)}{a^2}}\)
\(\therefore y=\pm b\sqrt{\frac{(a^2-x^2)}{a^2}}\)
\(\therefore a>x\)-এর যে কোনো মানের জন্য \(y\)-এর দুইটি মান পাওয়া যায়। মান দুইটি সমান কিন্তু বিপরীত চিহ্নবিশিষ্ট। অতএব, ইহা স্পষ্ট যে,উপবৃত্তটি \(X\)-অক্ষ ( বৃহৎ অক্ষ ) বরাবর প্রতিসম।
আবার,
\(x\)-এর সর্বোচ্চ মান \(a\) এবং সর্বনিম্ন মান \(-a\) কারণ, যদি \(x > a\) বা \(-a>x\) হয়, তবে,
\(\frac{a^2-x^2}{a^2}\) ঋনাত্মক হয় এবং \(y\)-এর মান দুইটি অবাস্তব হয়।
অতএব, উপবৃত্তের কোনো অংশই \(x\)-অক্ষের উপর \(A\) ও \(\acute A\) বিন্দু দুইটির বাইরে অবস্থিত হবে না।
উপবৃত্তের সমীকরণটিকে নিম্নোক্তভাবেও লেখা যায়,\(\therefore x=\pm a\sqrt{\frac{(b^2-y^2)}{b^2}}\)
\(\therefore b > y\)-এর যে কোনো মানের জন্য \(x\)-এর দুইটি মান পাওয়া যায়। মান দুইটি সমান কিন্তু বিপরীত চিহ্নবিশিষ্ট। অতএব, ইহা স্পষ্ট যে,উপবৃত্তটি \(Y\)-অক্ষ (ক্ষুদ্র অক্ষ ) বরাবর প্রতিসম।
\(y\)-এর সর্বোচ্চ মান \(b\) এবং সর্বনিম্ন মান \(-b\) কারণ, যদি \(y > b\) বা \(-b > y\) হয়, তবে,
\(\frac{b^2-y^2}{b^2}\) ঋনাত্মক হয় এবং \(x\)-এর মান দুইটি অবাস্তব হয়।
অতএব, উপবৃত্তের কোনো অংশই \(y\)-অক্ষের উপর \(B\) ও \(\acute B\) বিন্দু দুইটির বাইরে অবস্থিত হবে না।
অতএব , উপবৃত্ত একটি সীমাবদ্ধ বক্ররেখা, যা, পুরাপুরি \(x=\pm a, y=\pm b\) সরলরেখা চতুষ্টয় দ্বারা সীমিত আয়তের মধ্যে অবস্থিত।
অক্ষদ্বয়ের দৈর্ঘ্য \(2a\) ও \(2b\) এবং তাদের সমীকরণ যথাক্রমে \(a_{1}x+b_{1}y+c_{1}=0\) ও \(a_{2}x+b_{2}y+c_{2}=0\) উপবৃত্তের সমীকরণ,
\(\frac{1}{a^2}\left(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_{1}^2+b_{1}^2}}\right)^2+\frac{1}{b^2}\left(\frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_{2}^2+b_{2}^2}}\right)^2=1\)
×
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \ (a>b)\) নির্ণয়।
আমরা জানি,
উপবৃত্তের উপকেন্দ্র \(S(ae, 0)\)
উপবৃত্তের দিকাক্ষের সমীকরণ \(x-\frac{a}{e}=0\)
উপবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(\Rightarrow e^2=1-\frac{b^2}{a^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow \frac{b^2}{a^2}=1-e^2\)
\(\therefore b^2=a^2(1-e^2) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-ae)^2+(y-0)^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1^2+0^2}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1+0}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(|x-\frac{a}{e}|\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(x-\frac{a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{ex-a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\frac{(ex-a)^2}{e^2}\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=(ex-a)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2x^2-2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex-a^2e^2-2aex+a^2\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2-a^2e^2\)
\(\Rightarrow \frac{x^2}{a^2}.a^2(1-e^2)+y^2=a^2(1-e^2)\)
\(\Rightarrow \frac{x^2}{a^2}.b^2+y^2=b^2\) ➜ \((1)\)-এর সাহায্যে \(\because b^2=a^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}.\frac{b^2}{b^2}+\frac{y^2}{b^2}=\frac{b^2}{b^2}\) ➜ উভয় পার্শে \(b^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।

উপবৃত্তের উপকেন্দ্র \(S(ae, 0)\)
উপবৃত্তের দিকাক্ষের সমীকরণ \(x-\frac{a}{e}=0\)
উপবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(\Rightarrow e^2=1-\frac{b^2}{a^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow \frac{b^2}{a^2}=1-e^2\)
\(\therefore b^2=a^2(1-e^2) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-ae)^2+(y-0)^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1^2+0^2}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1+0}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(|x-\frac{a}{e}|\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(x-\frac{a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{ex-a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\frac{(ex-a)^2}{e^2}\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=(ex-a)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2x^2-2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex-a^2e^2-2aex+a^2\)
\(\Rightarrow x^2(1-e^2)+y^2=a^2-a^2e^2\)
\(\Rightarrow \frac{x^2}{a^2}.a^2(1-e^2)+y^2=a^2(1-e^2)\)
\(\Rightarrow \frac{x^2}{a^2}.b^2+y^2=b^2\) ➜ \((1)\)-এর সাহায্যে \(\because b^2=a^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}.\frac{b^2}{b^2}+\frac{y^2}{b^2}=\frac{b^2}{b^2}\) ➜ উভয় পার্শে \(b^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
×
উপবৃত্তের সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \ (b > a)\) নির্ণয়।
আমরা জানি,
 উপবৃত্তের উপকেন্দ্র \(S(0, be)\)
উপবৃত্তের উপকেন্দ্র \(S(0, be)\)
উপবৃত্তের দিকাক্ষের সমীকরণ \(y-\frac{b}{e}=0\)
উপবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{a^2}{b^2}}\)
\(\Rightarrow e^2=1-\frac{a^2}{b^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow \frac{a^2}{b^2}=1-e^2\)
\(\therefore a^2=b^2(1-e^2) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-0)^2+(y-be)^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0^2+1^2}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0+1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(|y-\frac{b}{e}|\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(y-\frac{b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{ey-b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\frac{(ey-b)^2}{e^2}\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=(ey-b)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2y^2-2bey+b^2\)
\(\Rightarrow x^2+y^2-e^2y^2=2bey-b^2e^2-2bey+b^2\)
\(\Rightarrow x^2+y^2(1-e^2)=b^2-b^2e^2\)
\(\Rightarrow x^2+\frac{y^2}{b^2}.b^2(1-e^2)=b^2(1-e^2)\)
\(\Rightarrow x^2+\frac{y^2}{b^2}.a^2=a^2\) ➜ \((1)\)-এর সাহায্যে \(\because a^2=b^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}.\frac{a^2}{a^2}=\frac{a^2}{a^2}\) ➜ উভয় পার্শে \(a^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
 উপবৃত্তের উপকেন্দ্র \(S(0, be)\)
উপবৃত্তের উপকেন্দ্র \(S(0, be)\)উপবৃত্তের দিকাক্ষের সমীকরণ \(y-\frac{b}{e}=0\)
উপবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{a^2}{b^2}}\)
\(\Rightarrow e^2=1-\frac{a^2}{b^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow \frac{a^2}{b^2}=1-e^2\)
\(\therefore a^2=b^2(1-e^2) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-0)^2+(y-be)^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0^2+1^2}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0+1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(|y-\frac{b}{e}|\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(y-\frac{b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{ey-b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\frac{(ey-b)^2}{e^2}\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=(ey-b)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2y^2-2bey+b^2\)
\(\Rightarrow x^2+y^2-e^2y^2=2bey-b^2e^2-2bey+b^2\)
\(\Rightarrow x^2+y^2(1-e^2)=b^2-b^2e^2\)
\(\Rightarrow x^2+\frac{y^2}{b^2}.b^2(1-e^2)=b^2(1-e^2)\)
\(\Rightarrow x^2+\frac{y^2}{b^2}.a^2=a^2\) ➜ \((1)\)-এর সাহায্যে \(\because a^2=b^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}.\frac{a^2}{a^2}=\frac{a^2}{a^2}\) ➜ উভয় পার্শে \(a^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
×
উপবৃত্তের সমীকরণ \(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1 \ (a > b)\) নির্ণয়।
ধরি,
 উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
বৃহদাক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
ক্ষুদ্রাক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(X\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(X=CQ=EM=OM-OE=x-\alpha\)
এবং \(Y=PQ=PM-QM=PM-CE=y-\beta\)
\(P(X, Y)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}+\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
 উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)বৃহদাক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
ক্ষুদ্রাক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(X\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(X=CQ=EM=OM-OE=x-\alpha\)
এবং \(Y=PQ=PM-QM=PM-CE=y-\beta\)
\(P(X, Y)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}+\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
×
উপবৃত্তের সমীকরণ \(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1 \ (b>a)\) নির্ণয়।
ধরি,
উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
বৃহদাক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
ক্ষুদ্রাক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(Y\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(Y=CQ=EM=OM-OE=y-\beta\)
এবং \(X=PQ=PM-QM=PM-CE=x-\alpha\)
\(P(X, Y)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}+\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।

উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
বৃহদাক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
ক্ষুদ্রাক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
উপবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(Y\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(Y=CQ=EM=OM-OE=y-\beta\)
এবং \(X=PQ=PM-QM=PM-CE=x-\alpha\)
\(P(X, Y)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}+\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}+\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় উপবৃত্তের সমীকরণ।
×
কোনো সরলরেখা উপবৃত্তের স্পর্শক হওয়ার শর্ত, স্পর্শকের সমীকরণ এবং স্পর্শবিন্দুর স্থানাঙ্ক নির্ণয়।
মনে করি,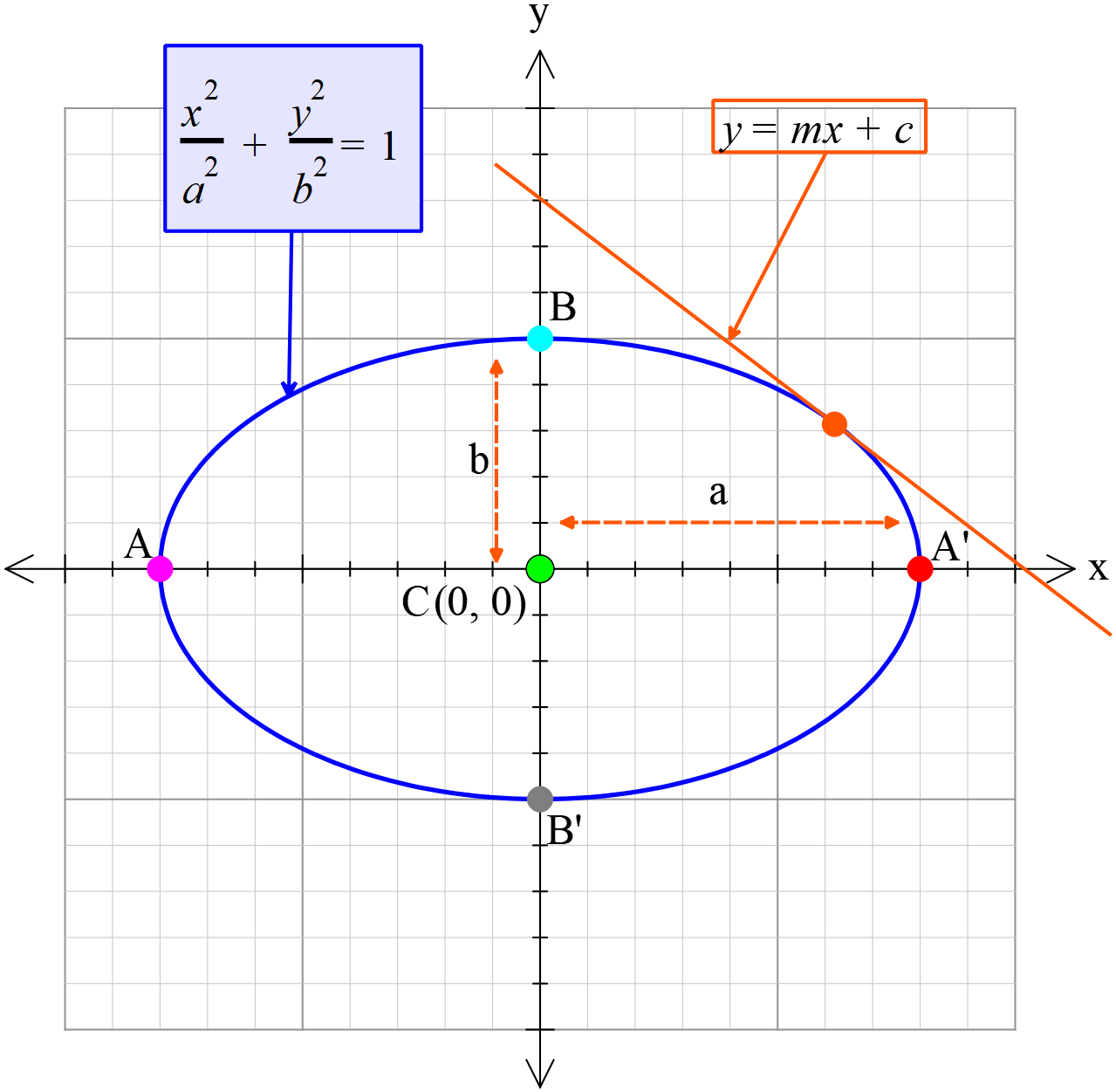
সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ...(2)\)
\((1) \) ও \((2) \) নং হতে,
\(\frac{x^2}{a^2}+\frac{(mx+c)^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{m^2x^2+2mcx+c^2}{b^2}=1\)
\(\Rightarrow b^2x^2+a^2(m^2x^2+2mcx+c^2)=a^2b^2\) ➜ উভয় পার্শে \(a^2b^2\) গুণ করে।
\(\Rightarrow b^2x^2+a^2m^2x^2+2a^2mcx+a^2c^2-a^2b^2=0\)
\(\Rightarrow (a^2m^2+b^2)x^2+2a^2mcx+a^2(c^2-b^2)=0...(3)\)
\((3)\) নং \(x\)-এর একটি দ্বিঘাত সমীকরণ। সুতরাং এর মূল দুইটি বাস্তব ও অসমান, বাস্তব ও সমান, অথবা কাল্পনিক হতে পারে। মূলদ্বয় \(x_1\) ও \(x_2\) হলে, \((1)\) নং সমীকরণ হতে \(y_1\) ও \(y_2\) পাওয়া যাবে। \(x_1\) ও \(x_2\)-এর মানের উপর ভিত্তি করে তিনটি ঘটনা ঘটতে পারে,
\((ii)\) \(x_1\) ও \(x_2\) বাস্তব ও সমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে স্পর্শ করবে।
\((iii)\) \(x_1\) ও \(x_2\) কাল্পনিক হলে, \((1)\) নং রেখা উপবৃত্তটিকে আদৌ স্পর্শ করবে না।
এখন,
\((ii)\) ঘটনা সত্য হলে, \((3)\) নং হতে \((2a^2mc)^2=4.(a^2m^2+b^2).a^2(c^2-b^2)\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow a^4m^2c^2=(a^2m^2+b^2).a^2(c^2-b^2)\)
\(\Rightarrow a^4m^2c^2=(a^2m^2+b^2)(a^2c^2-a^2b^2)\)
\(\Rightarrow a^4m^2c^2=(a^2c^2-a^2b^2)(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2=a^2c^2(a^2m^2+b^2)-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2=a^4c^2m^2+a^2b^2c^2-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2-a^4m^2c^2-a^2b^2c^2=-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow -a^2b^2c^2=-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow c^2=(a^2m^2+b^2)\) ➜ উভয় পার্শে \(-a^2b^2\) ভাগ করে।
\(\therefore c=\pm \sqrt{(a^2m^2+b^2)}\) ইহাই নির্ণেয় শর্ত।
আবার,
\(c=\pm \sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=mx \pm \sqrt{(a^2m^2+b^2)}\) ইহাই নির্ণেয় স্পর্শকের সমীকরণ।
আবার,
\((3)\) নং সমীকরণ হতে সমান মূলদ্বয়ের মান \(x=\frac{-2a^2mc}{2(a^2m^2+b^2)}\) ➜ \(ax^2+bx+c=0\) সমীকরণের সমাণ মূলদ্বয়ের মাণ \(\frac{-b}{2a}\)
\(\Rightarrow x=\frac{-a^2mc}{a^2m^2+b^2}\)
\(\Rightarrow x=\frac{-a^2m\times \pm \sqrt{(a^2m^2+b^2)}}{a^2m^2+b^2}\) ➜ \(\because c=\pm \sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow x=\frac{\pm a^2m\sqrt{(a^2m^2+b^2)}}{\sqrt{(a^2m^2+b^2)}\times \sqrt{(a^2m^2+b^2)}}\)
\(\therefore x=\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}\)
আবার,
\(x=\frac{a^2m}{\sqrt{(a^2m^2+b^2)}}\) এবং \(c=-\sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{a^2m}{\sqrt{(a^2m^2+b^2)}}-\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{a^2m^2}{\sqrt{(a^2m^2+b^2)}}-\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{a^2m^2-a^2m^2-b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y=\frac{-b^2}{\sqrt{(a^2m^2+b^2)}}\)
আবার,
\(x=\frac{-a^2m}{\sqrt{(a^2m^2+b^2)}}\) এবং \(c=\sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{-a^2m}{\sqrt{(a^2m^2+b^2)}}+\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2}{\sqrt{(a^2m^2+b^2)}}+\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2+a^2m^2+b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y=\frac{b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y\)-এর এই দুই মাণ সমন্বয় করে পাই,
\(y=\frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\)
অতএব, স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\right)\)

সরলরেখা ও উপবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ...(2)\)
\((1) \) ও \((2) \) নং হতে,
\(\frac{x^2}{a^2}+\frac{(mx+c)^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}+\frac{m^2x^2+2mcx+c^2}{b^2}=1\)
\(\Rightarrow b^2x^2+a^2(m^2x^2+2mcx+c^2)=a^2b^2\) ➜ উভয় পার্শে \(a^2b^2\) গুণ করে।
\(\Rightarrow b^2x^2+a^2m^2x^2+2a^2mcx+a^2c^2-a^2b^2=0\)
\(\Rightarrow (a^2m^2+b^2)x^2+2a^2mcx+a^2(c^2-b^2)=0...(3)\)
\((3)\) নং \(x\)-এর একটি দ্বিঘাত সমীকরণ। সুতরাং এর মূল দুইটি বাস্তব ও অসমান, বাস্তব ও সমান, অথবা কাল্পনিক হতে পারে। মূলদ্বয় \(x_1\) ও \(x_2\) হলে, \((1)\) নং সমীকরণ হতে \(y_1\) ও \(y_2\) পাওয়া যাবে। \(x_1\) ও \(x_2\)-এর মানের উপর ভিত্তি করে তিনটি ঘটনা ঘটতে পারে,
যেমনঃ
\((i)\) \(x_1\) ও \(x_2\) বাস্তব ও অসমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে দুইটি ভিন্ন বিন্দুতে ছেদ করবে।\((ii)\) \(x_1\) ও \(x_2\) বাস্তব ও সমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে স্পর্শ করবে।
\((iii)\) \(x_1\) ও \(x_2\) কাল্পনিক হলে, \((1)\) নং রেখা উপবৃত্তটিকে আদৌ স্পর্শ করবে না।
এখন,
\((ii)\) ঘটনা সত্য হলে, \((3)\) নং হতে \((2a^2mc)^2=4.(a^2m^2+b^2).a^2(c^2-b^2)\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow a^4m^2c^2=(a^2m^2+b^2).a^2(c^2-b^2)\)
\(\Rightarrow a^4m^2c^2=(a^2m^2+b^2)(a^2c^2-a^2b^2)\)
\(\Rightarrow a^4m^2c^2=(a^2c^2-a^2b^2)(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2=a^2c^2(a^2m^2+b^2)-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2=a^4c^2m^2+a^2b^2c^2-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow a^4m^2c^2-a^4m^2c^2-a^2b^2c^2=-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow -a^2b^2c^2=-a^2b^2(a^2m^2+b^2)\)
\(\Rightarrow c^2=(a^2m^2+b^2)\) ➜ উভয় পার্শে \(-a^2b^2\) ভাগ করে।
\(\therefore c=\pm \sqrt{(a^2m^2+b^2)}\) ইহাই নির্ণেয় শর্ত।
আবার,
\(c=\pm \sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=mx \pm \sqrt{(a^2m^2+b^2)}\) ইহাই নির্ণেয় স্পর্শকের সমীকরণ।
আবার,
\((3)\) নং সমীকরণ হতে সমান মূলদ্বয়ের মান \(x=\frac{-2a^2mc}{2(a^2m^2+b^2)}\) ➜ \(ax^2+bx+c=0\) সমীকরণের সমাণ মূলদ্বয়ের মাণ \(\frac{-b}{2a}\)
\(\Rightarrow x=\frac{-a^2mc}{a^2m^2+b^2}\)
\(\Rightarrow x=\frac{-a^2m\times \pm \sqrt{(a^2m^2+b^2)}}{a^2m^2+b^2}\) ➜ \(\because c=\pm \sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow x=\frac{\pm a^2m\sqrt{(a^2m^2+b^2)}}{\sqrt{(a^2m^2+b^2)}\times \sqrt{(a^2m^2+b^2)}}\)
\(\therefore x=\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}\)
আবার,
\(x=\frac{a^2m}{\sqrt{(a^2m^2+b^2)}}\) এবং \(c=-\sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{a^2m}{\sqrt{(a^2m^2+b^2)}}-\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{a^2m^2}{\sqrt{(a^2m^2+b^2)}}-\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{a^2m^2-a^2m^2-b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y=\frac{-b^2}{\sqrt{(a^2m^2+b^2)}}\)
আবার,
\(x=\frac{-a^2m}{\sqrt{(a^2m^2+b^2)}}\) এবং \(c=\sqrt{(a^2m^2+b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{-a^2m}{\sqrt{(a^2m^2+b^2)}}+\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2}{\sqrt{(a^2m^2+b^2)}}+\sqrt{(a^2m^2+b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2+a^2m^2+b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y=\frac{b^2}{\sqrt{(a^2m^2+b^2)}}\)
\(\therefore y\)-এর এই দুই মাণ সমন্বয় করে পাই,
\(y=\frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\)
অতএব, স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2+b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2+b^2)}}\right)\)
অধিবৃত্ত
Hyperbola
অধিবৃত্তঃ কোনো কার্তেসীয় সমতলে একটি বিন্দু যদি এমনভাবে চলে যে ঐ সমতলস্থিত একটি স্থির বিন্দু থেকে দূরত্ব এবং একটি নির্দিষ্ট রেখা থেকে লম্ব দূরত্বের অনুপাত একটি স্থির রাশি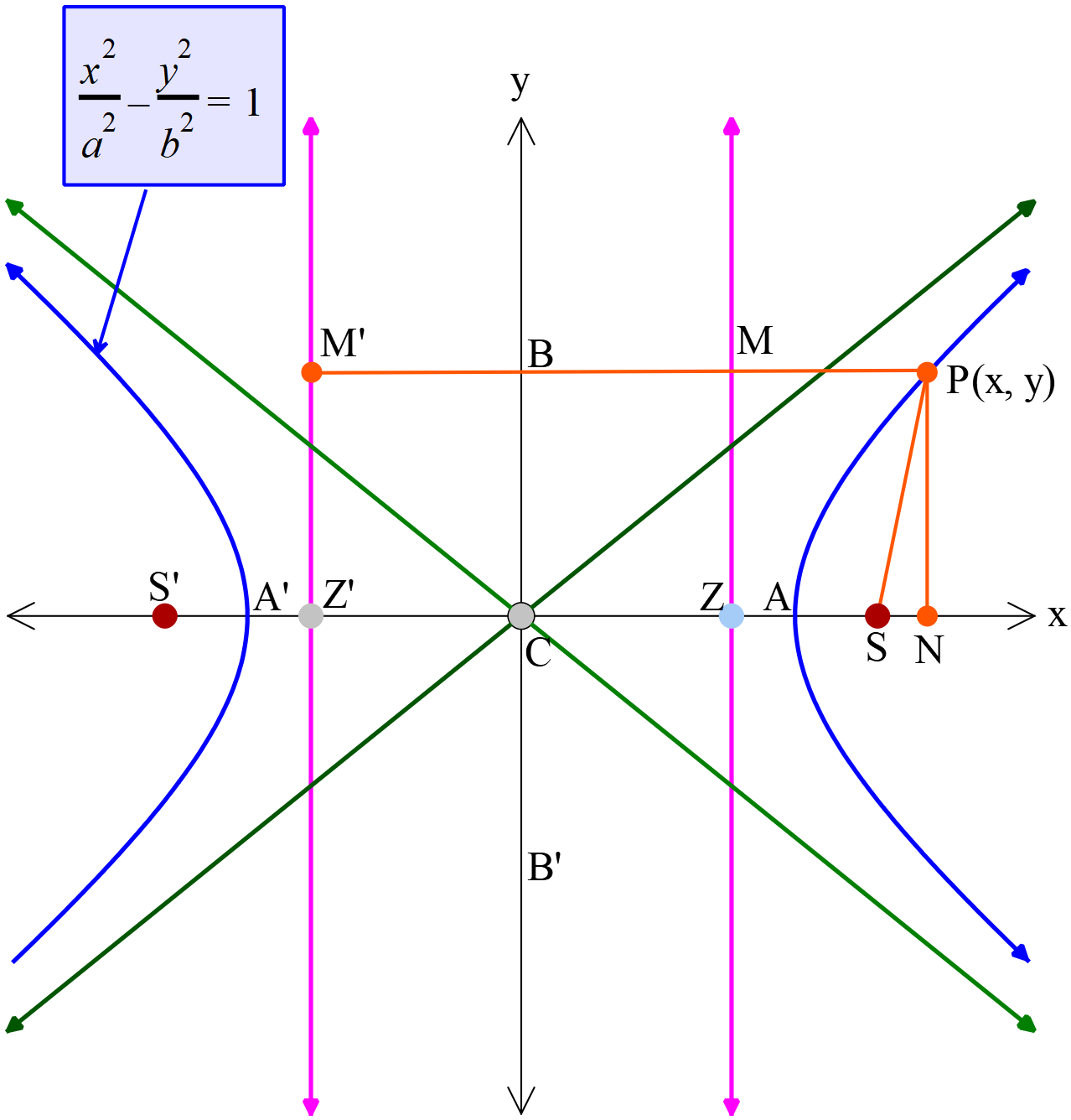 এবং ঐ স্থির রাশিটির মান \(1\) অপেক্ষা বৃহত্তর, তবে ঐ বিন্দুর সঞ্চারপথকে অধিবৃত্ত বলা হয়। উক্ত স্থির রাশিকে উৎকেন্দ্রতা (Eccentricity) বলা হয়, এবং ইহাকে \(e\) দ্বারা সূচিত করা হয়,যেখানে \( e > 1\) হবে ।
উপকেন্দ্র দুইটির মধ্যদিয়ে অঙ্কিত অধিবৃত্তের সর্ববৃহত রেখাংশ \(A\acute A\) কে প্রধান বা আড় অক্ষ ( Transverse axis) বলা হয়। প্রধান অক্ষের লম্ব দ্বিখন্ডক রেখাংশ \(B\acute B\) কে অনুবন্ধী অক্ষ ( Conjugate axis) বলা হয়। অক্ষদ্বয়ের মিলিত বিন্দু \(C\) কে কেন্দ্র বলা হয়।
এবং ঐ স্থির রাশিটির মান \(1\) অপেক্ষা বৃহত্তর, তবে ঐ বিন্দুর সঞ্চারপথকে অধিবৃত্ত বলা হয়। উক্ত স্থির রাশিকে উৎকেন্দ্রতা (Eccentricity) বলা হয়, এবং ইহাকে \(e\) দ্বারা সূচিত করা হয়,যেখানে \( e > 1\) হবে ।
উপকেন্দ্র দুইটির মধ্যদিয়ে অঙ্কিত অধিবৃত্তের সর্ববৃহত রেখাংশ \(A\acute A\) কে প্রধান বা আড় অক্ষ ( Transverse axis) বলা হয়। প্রধান অক্ষের লম্ব দ্বিখন্ডক রেখাংশ \(B\acute B\) কে অনুবন্ধী অক্ষ ( Conjugate axis) বলা হয়। অক্ষদ্বয়ের মিলিত বিন্দু \(C\) কে কেন্দ্র বলা হয়।
 এবং ঐ স্থির রাশিটির মান \(1\) অপেক্ষা বৃহত্তর, তবে ঐ বিন্দুর সঞ্চারপথকে অধিবৃত্ত বলা হয়। উক্ত স্থির রাশিকে উৎকেন্দ্রতা (Eccentricity) বলা হয়, এবং ইহাকে \(e\) দ্বারা সূচিত করা হয়,যেখানে \( e > 1\) হবে ।
উপকেন্দ্র দুইটির মধ্যদিয়ে অঙ্কিত অধিবৃত্তের সর্ববৃহত রেখাংশ \(A\acute A\) কে প্রধান বা আড় অক্ষ ( Transverse axis) বলা হয়। প্রধান অক্ষের লম্ব দ্বিখন্ডক রেখাংশ \(B\acute B\) কে অনুবন্ধী অক্ষ ( Conjugate axis) বলা হয়। অক্ষদ্বয়ের মিলিত বিন্দু \(C\) কে কেন্দ্র বলা হয়।
এবং ঐ স্থির রাশিটির মান \(1\) অপেক্ষা বৃহত্তর, তবে ঐ বিন্দুর সঞ্চারপথকে অধিবৃত্ত বলা হয়। উক্ত স্থির রাশিকে উৎকেন্দ্রতা (Eccentricity) বলা হয়, এবং ইহাকে \(e\) দ্বারা সূচিত করা হয়,যেখানে \( e > 1\) হবে ।
উপকেন্দ্র দুইটির মধ্যদিয়ে অঙ্কিত অধিবৃত্তের সর্ববৃহত রেখাংশ \(A\acute A\) কে প্রধান বা আড় অক্ষ ( Transverse axis) বলা হয়। প্রধান অক্ষের লম্ব দ্বিখন্ডক রেখাংশ \(B\acute B\) কে অনুবন্ধী অক্ষ ( Conjugate axis) বলা হয়। অক্ষদ্বয়ের মিলিত বিন্দু \(C\) কে কেন্দ্র বলা হয়।
মূলবিন্দু কেন্দ্রবিশিষ্ট অধিবৃত্তের প্রমিত সমীকরণ
Standard equation of Hyperbola
ধরি,
অধিবৃত্তের উপকেন্দ্র \(S\) নিয়ামকরেখা \(MZ\) এবং উৎকেন্দ্রিকতা \(e, (e > 1)\), নিয়ামকরেখার উপর \(SZ\) লম্ব আঁকি। \(SZ\) রেখাকে \(A\) ও \(\acute A\) বিন্দুদ্বয় \(e:1\) অনুপাতে যথাক্রমে অন্তর্বিভক্ত ও বহিঃর্বিভক্ত করে, যেন \(SA=e.AZ\) এবং \(S\acute A=e.\acute AZ\)।
তাহলে, \(A\) ও \(\acute A\) অধিবৃত্তের উপর দুইটি বিন্দু।
মনে করি \(A\acute A\)-এর মধ্যবিন্দু \(C\) এবং \(A\acute A=2a\)
তাহলে, \(CA=C\acute A=a\)
এখন,
\(SA=e.AZ\)
\(\therefore CS-a=e(a-CZ) .......(1)\) ➜ \(\because SA=CA-CS=CS-a; AZ=CZ-CA=a-CZ\)
এবং \(S\acute A=e.\acute AZ\)
\(\therefore CS+a=e(a+CZ) ........(2)\) ➜ \(\because S\acute A=C\acute A+CS=CS+a; \acute AZ=CZ+CA=a+CZ\)
\((1)\) ও \((2)\) যোগ করে,
\(CS-a+CS+a=e(a-CZ)+e(a+CZ)\)
\(\Rightarrow 2CS=e(a-CZ+a+CZ)\)
\(\Rightarrow 2CS=e.2a\)
\(\therefore CS=ae\)
\((2)\) - \((1)\)-এর সাহায্যে,
\(CS+a-CS+a=e(a+CZ)-e(a-CZ)\)
\(\Rightarrow 2a=e(a+CZ-a+CZ)\)
\(\Rightarrow 2a=e.2CZ\)
\(\Rightarrow a=eCZ\)
\(\Rightarrow eCZ=a\)
\(\therefore CZ=\frac{a}{e}\)
\(C\)-কে মূলবিন্দু , \(CX\) ও \(CY\)-কে যথাক্রমে \(x\)-অক্ষ ও \(y\)-অক্ষ বিবেচনা করি। অধিবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)। \(P\) বিন্দু হতে \(A\acute A\)-এর উপর \(PN\) ও নিয়ামকরেখার উপর \(PM\) লম্ব আঁকি।
সুতরাং অধিবৃত্তের সংজ্ঞানুসারে, \(SP=e.PM\)
\(\Rightarrow SP=e.NZ\) ➜ \(\because PM=NZ\)
\(\Rightarrow SP^2=e^2.NZ^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow SN^2+PN^2=e^2(CN-CZ)^2\) ➜ \(\because SP^2=SN^2+PN^2; NZ=CN-CZ\)
\(\Rightarrow (x-ae)^2+y^2=e^2\left(x-\frac{a}{e}\right)^2\) ➜ \(\because SN=CS+CN=x-ae; NZ=x-\frac{a}{e}\)
\(\Rightarrow (x-ae)^2+y^2=e^2\left(\frac{ex-a}{e}\right)^2\)
\(\Rightarrow (x-ae)^2+y^2=e^2.\frac{(ex-a)^2}{e^2}\)
\(\Rightarrow (x-ae)^2+y^2=(ex-a)^2\)
\(\Rightarrow x^2+a^2e^2-2aex+y^2=e^2x^2-2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex+a^2-a^2e^2-2aex\)
\(\Rightarrow -x^2(e^2-1)+y^2=a^2-a^2e^2\)
\(\Rightarrow -x^2(e^2-1)+y^2=-a^2(e^2-1)\)
\(\Rightarrow x^2(e^2-1)-y^2=a^2(e^2-1)\) ➜ উভয় পার্শে \(-1\) গুণ করে।
\(\Rightarrow \frac{x^2(e^2-1)}{a^2(e^2-1)}-\frac{y^2}{a^2(e^2-1)}=1\) ➜ উভয় পার্শে \(a^2(e^2-1)\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}-\frac{y^2}{a^2(e^2-1)}=1 .......(3)\)
যেহেতু \(e>1, a^2(e^2-1)\) ধনাত্মক।
অতএব, লিখা যায় \(b^2=a^2(e^2-1)\) ➜ \(b\) একটি ধনাত্মক বাস্তব সংখ্যা।
\(\therefore b^2=a^2(e^2-1) ........(4)\)
\((4)\)-এর সাহায্য নিয়ে \((3)\) হতে পাই,
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
ইহাই অধিবৃত্তের আদর্শ সমীকরণ।

অধিবৃত্তের উপকেন্দ্র \(S\) নিয়ামকরেখা \(MZ\) এবং উৎকেন্দ্রিকতা \(e, (e > 1)\), নিয়ামকরেখার উপর \(SZ\) লম্ব আঁকি। \(SZ\) রেখাকে \(A\) ও \(\acute A\) বিন্দুদ্বয় \(e:1\) অনুপাতে যথাক্রমে অন্তর্বিভক্ত ও বহিঃর্বিভক্ত করে, যেন \(SA=e.AZ\) এবং \(S\acute A=e.\acute AZ\)।
তাহলে, \(A\) ও \(\acute A\) অধিবৃত্তের উপর দুইটি বিন্দু।
মনে করি \(A\acute A\)-এর মধ্যবিন্দু \(C\) এবং \(A\acute A=2a\)
তাহলে, \(CA=C\acute A=a\)
এখন,
\(SA=e.AZ\)
\(\therefore CS-a=e(a-CZ) .......(1)\) ➜ \(\because SA=CA-CS=CS-a; AZ=CZ-CA=a-CZ\)
এবং \(S\acute A=e.\acute AZ\)
\(\therefore CS+a=e(a+CZ) ........(2)\) ➜ \(\because S\acute A=C\acute A+CS=CS+a; \acute AZ=CZ+CA=a+CZ\)
\((1)\) ও \((2)\) যোগ করে,
\(CS-a+CS+a=e(a-CZ)+e(a+CZ)\)
\(\Rightarrow 2CS=e(a-CZ+a+CZ)\)
\(\Rightarrow 2CS=e.2a\)
\(\therefore CS=ae\)
\((2)\) - \((1)\)-এর সাহায্যে,
\(CS+a-CS+a=e(a+CZ)-e(a-CZ)\)
\(\Rightarrow 2a=e(a+CZ-a+CZ)\)
\(\Rightarrow 2a=e.2CZ\)
\(\Rightarrow a=eCZ\)
\(\Rightarrow eCZ=a\)
\(\therefore CZ=\frac{a}{e}\)
\(C\)-কে মূলবিন্দু , \(CX\) ও \(CY\)-কে যথাক্রমে \(x\)-অক্ষ ও \(y\)-অক্ষ বিবেচনা করি। অধিবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\)। \(P\) বিন্দু হতে \(A\acute A\)-এর উপর \(PN\) ও নিয়ামকরেখার উপর \(PM\) লম্ব আঁকি।
সুতরাং অধিবৃত্তের সংজ্ঞানুসারে, \(SP=e.PM\)
\(\Rightarrow SP=e.NZ\) ➜ \(\because PM=NZ\)
\(\Rightarrow SP^2=e^2.NZ^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow SN^2+PN^2=e^2(CN-CZ)^2\) ➜ \(\because SP^2=SN^2+PN^2; NZ=CN-CZ\)
\(\Rightarrow (x-ae)^2+y^2=e^2\left(x-\frac{a}{e}\right)^2\) ➜ \(\because SN=CS+CN=x-ae; NZ=x-\frac{a}{e}\)
\(\Rightarrow (x-ae)^2+y^2=e^2\left(\frac{ex-a}{e}\right)^2\)
\(\Rightarrow (x-ae)^2+y^2=e^2.\frac{(ex-a)^2}{e^2}\)
\(\Rightarrow (x-ae)^2+y^2=(ex-a)^2\)
\(\Rightarrow x^2+a^2e^2-2aex+y^2=e^2x^2-2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex+a^2-a^2e^2-2aex\)
\(\Rightarrow -x^2(e^2-1)+y^2=a^2-a^2e^2\)
\(\Rightarrow -x^2(e^2-1)+y^2=-a^2(e^2-1)\)
\(\Rightarrow x^2(e^2-1)-y^2=a^2(e^2-1)\) ➜ উভয় পার্শে \(-1\) গুণ করে।
\(\Rightarrow \frac{x^2(e^2-1)}{a^2(e^2-1)}-\frac{y^2}{a^2(e^2-1)}=1\) ➜ উভয় পার্শে \(a^2(e^2-1)\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}-\frac{y^2}{a^2(e^2-1)}=1 .......(3)\)
যেহেতু \(e>1, a^2(e^2-1)\) ধনাত্মক।
অতএব, লিখা যায় \(b^2=a^2(e^2-1)\) ➜ \(b\) একটি ধনাত্মক বাস্তব সংখ্যা।
\(\therefore b^2=a^2(e^2-1) ........(4)\)
\((4)\)-এর সাহায্য নিয়ে \((3)\) হতে পাই,
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
ইহাই অধিবৃত্তের আদর্শ সমীকরণ।
অধিবৃত্তের আদর্শ সমীকরণ সনাক্তকরণ
Identifying the Standard equation of the hyperbola
মূলবিন্দু কেন্দ্রবিশিষ্ট অধিবৃত্তের প্রমিত সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1; \frac{y^2}{b^2}-\frac{x^2}{a^2}=1\)-এ \(x\) বা \(y\) যুক্ত পদ থাকবে না। শুধু \(x^2\) ও \(y^2\) যুক্ত পদ বিদ্যমান। \(x^2\)-এর সহগ \(\frac{1}{a^2}\) এবং \(y^2\)-এর সহগ \(-\frac{1}{b^2}\) অসমান ও ভিন্ন চিহ্নযুক্ত।
অধিবৃত্তের সমীকরণ সনাক্তকরণ
Identifying the equation of the hyperbola
অধিবৃত্তের সমীকরণে \(x^2\) ও \(y^2\) যুক্ত পদ বিদ্যমান। \(x^2\)-এর সহগ এবং \(y^2\)-এর সহগ অসমান ও ভিন্ন চিহ্নযুক্ত। \(x\) ও \(y\) যুক্ত পদ থাকতেও পারে নাও থাকতে পারে।
অধিবৃত্তের সমীকরণ যার প্রধান অক্ষ \(x\) অক্ষ বরাবর
Equation of the hyperbola whose major axis is along the \(x\) axis
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \)
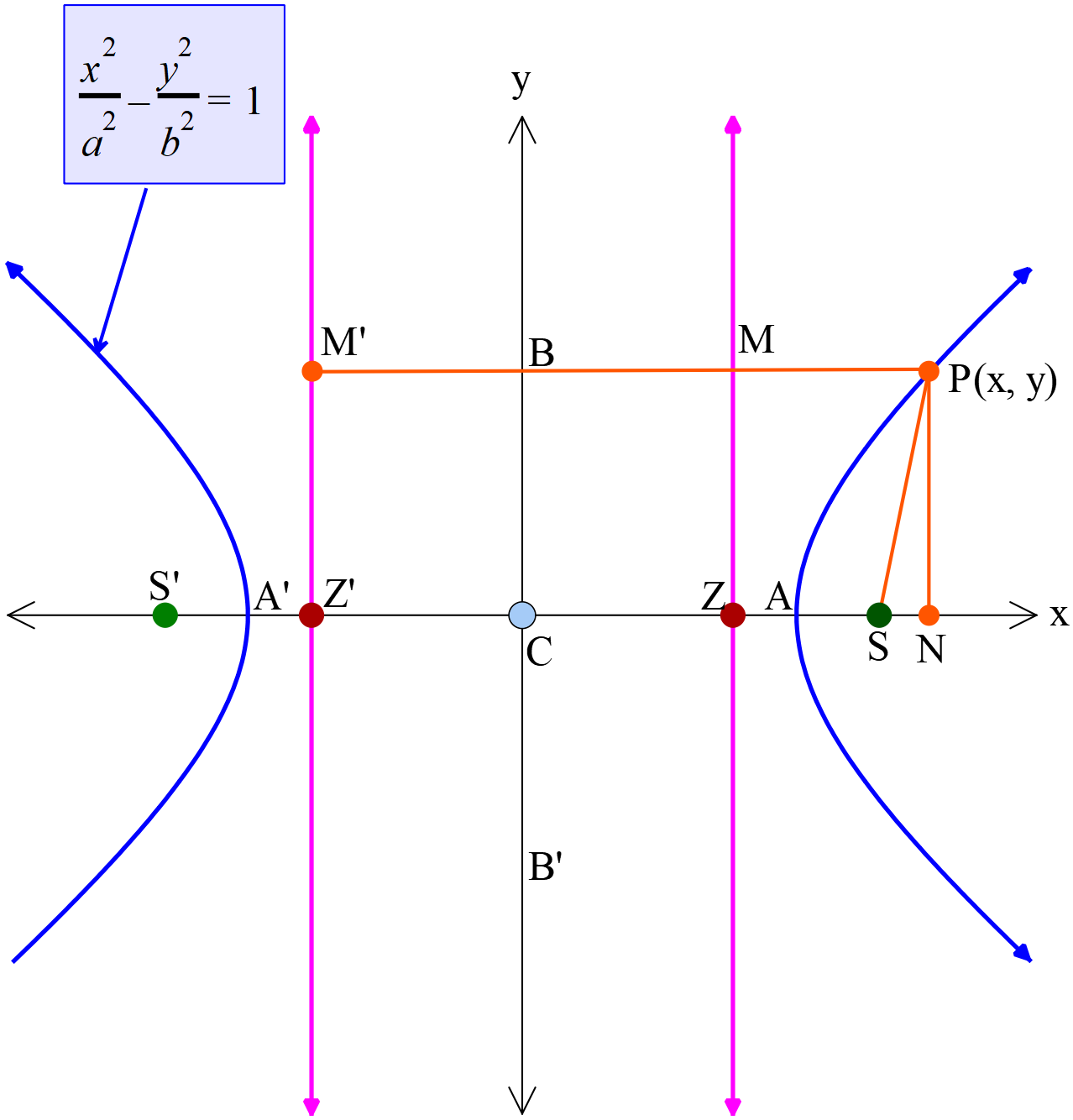

- অধিবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(0, 0)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1+\frac{b^2}{a^2}}\)
- আড় অক্ষের দৈর্ঘ্য \(=|2a|\)
- অনুবন্ধী অক্ষের দৈর্ঘ্য \(=|2b|\)
- আড় অক্ষের সমীকরণ \(y=0\)
- অনুবন্ধী অক্ষের সমীকরণ \(x=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((\pm ae, 0)\)
- নিয়ামকরেখার সমীকরণ \(x=\pm \frac{a}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2b^2}{a}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x=\pm ae\)
- শীর্ষবিন্দুর স্থানাঙ্ক \((\pm a, 0)\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \((\pm \frac{a}{e}, 0)\)
- উপকেন্দ্রের মধ্যকার দূরত্ব \(=|2ae|\)
- নিয়ামকদ্বয়ের মধ্যকার দূরত্ব \(=|\frac{2a}{e}|\)
- একই দিকের উপকেন্দ্র ও অনুরূপ নিয়ামকরেখার মধ্যকার দূরত্ব \(|\frac{a}{e}-ae|\)
- অসীমতটের সমীকরণ \( y=\pm \frac{b}{a}x\)
অধিবৃত্তের সমীকরণ যার প্রধান অক্ষ \(y\) অক্ষ বরাবর
Equation of the hyperbola whose major axis is along the \(y\) axis
অধিবৃত্তের সমীকরণ \(\frac{y^2}{b^2}-\frac{x^2}{a^2}=1 \)
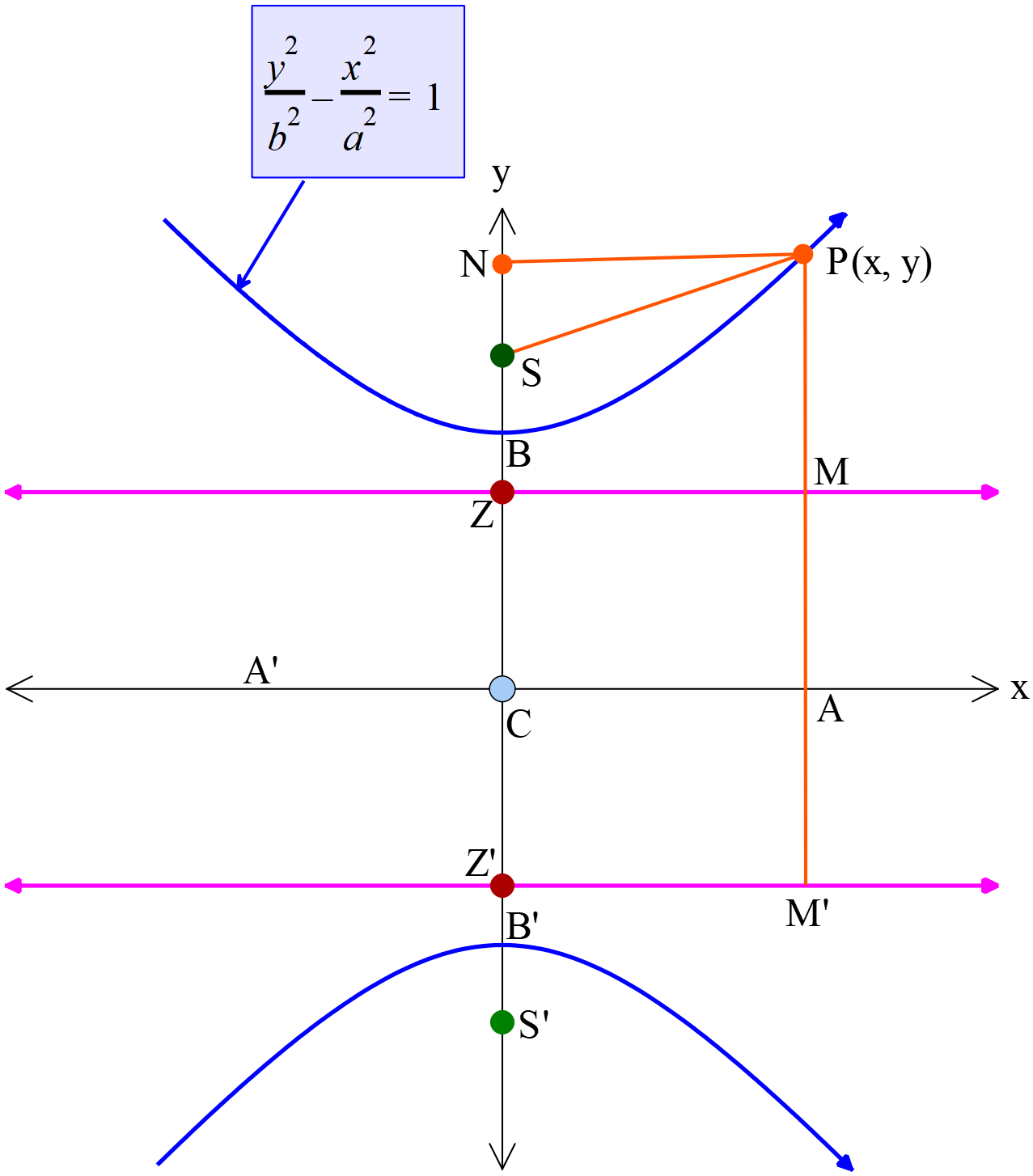

- অধিবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(0, 0)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1+\frac{a^2}{b^2}}\)
- আড় অক্ষের দৈর্ঘ্য \(=|2b|\)
- অনুবন্ধী অক্ষের দৈর্ঘ্য \(=|2a|\)
- আড় অক্ষের সমীকরণ \(x=0\)
- অনুবন্ধী অক্ষের সমীকরণ \(y=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((0, \pm be)\)
- নিয়ামকরেখার সমীকরণ \(y=\pm \frac{b}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2a^2}{b}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y=\pm be\)
- শীর্ষবিন্দুর স্থানাঙ্ক \((0, \pm b)\)
- নিয়ামকরেখার পাদবিন্দুর স্থানাঙ্ক \((0, \pm \frac{b}{e})\)
- উপকেন্দ্রের মধ্যকার দূরত্ব \(=|2be|\)
- নিয়ামকদ্বয়ের মধ্যকার দূরত্ব \(=|\frac{2b}{e}|\)
- একই দিকের উপকেন্দ্র ও অনুরূপ নিয়ামকরেখার মধ্যকার দূরত্ব \(|\frac{b}{e}-be|\)
- অসীমতটের সমীকরণ \( y=\pm \frac{b}{a}x\)
অধিবৃত্তের সমীকরণ যার কেন্দ্র \(C(\alpha, \beta)\) প্রধান অক্ষ \(x\) অক্ষ বরাবর
Equation of the hyperbola whose center \(C(\alpha, \beta)\) major axis is along the \(x\) axis
অধিবৃত্তের সমীকরণ \(\frac{(x-\alpha)^2}{a^2}-\frac{(y-\beta)^2}{b^2}=1\)
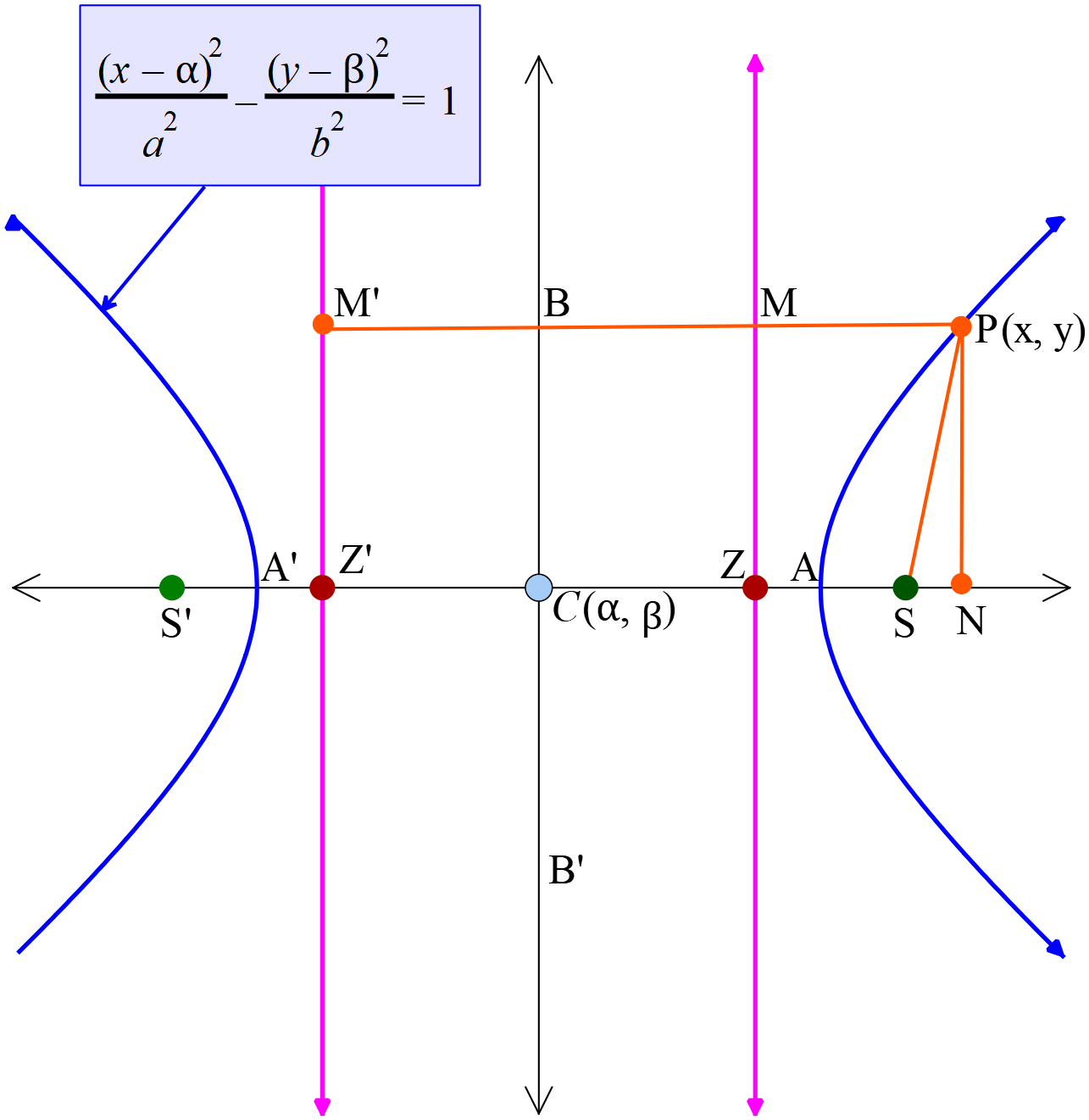

- অধিবৃত্তের শীর্ষবিন্দুর স্থানাঙ্ক \((\pm a+\alpha, 0)\)
- অধিবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(\alpha, \beta)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1+\frac{b^2}{a^2}}\)
- আড় অক্ষের দৈর্ঘ্য \(=|2a|\)
- অনুবন্ধী অক্ষের দৈর্ঘ্য \(=|2b|\)
- আড় অক্ষের সমীকরণ \(y-\beta=0\)
- অনুবন্ধী অক্ষের সমীকরণ \(x-\alpha=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((\pm ae+\alpha, \beta)\)
- নিয়ামকরেখার সমীকরণ \(x-\alpha=\pm \frac{a}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2b^2}{a}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(x-\alpha=\pm ae\)
- অসীমতটের সমীকরণ \( y-\beta=\pm \frac{b}{a}(x-\alpha)\)
অধিবৃত্তের সমীকরণ যার কেন্দ্র \(C(\alpha, \beta)\) প্রধান অক্ষ \(y\) অক্ষ বরাবর
Equation of the hyperbola whose center \(C(\alpha, \beta)\) major axis is along the \(y\) axis
অধিবৃত্তের সমীকরণ \(\frac{(y-\beta)^2}{b^2}-\frac{(x-\alpha)^2}{a^2}=1\)
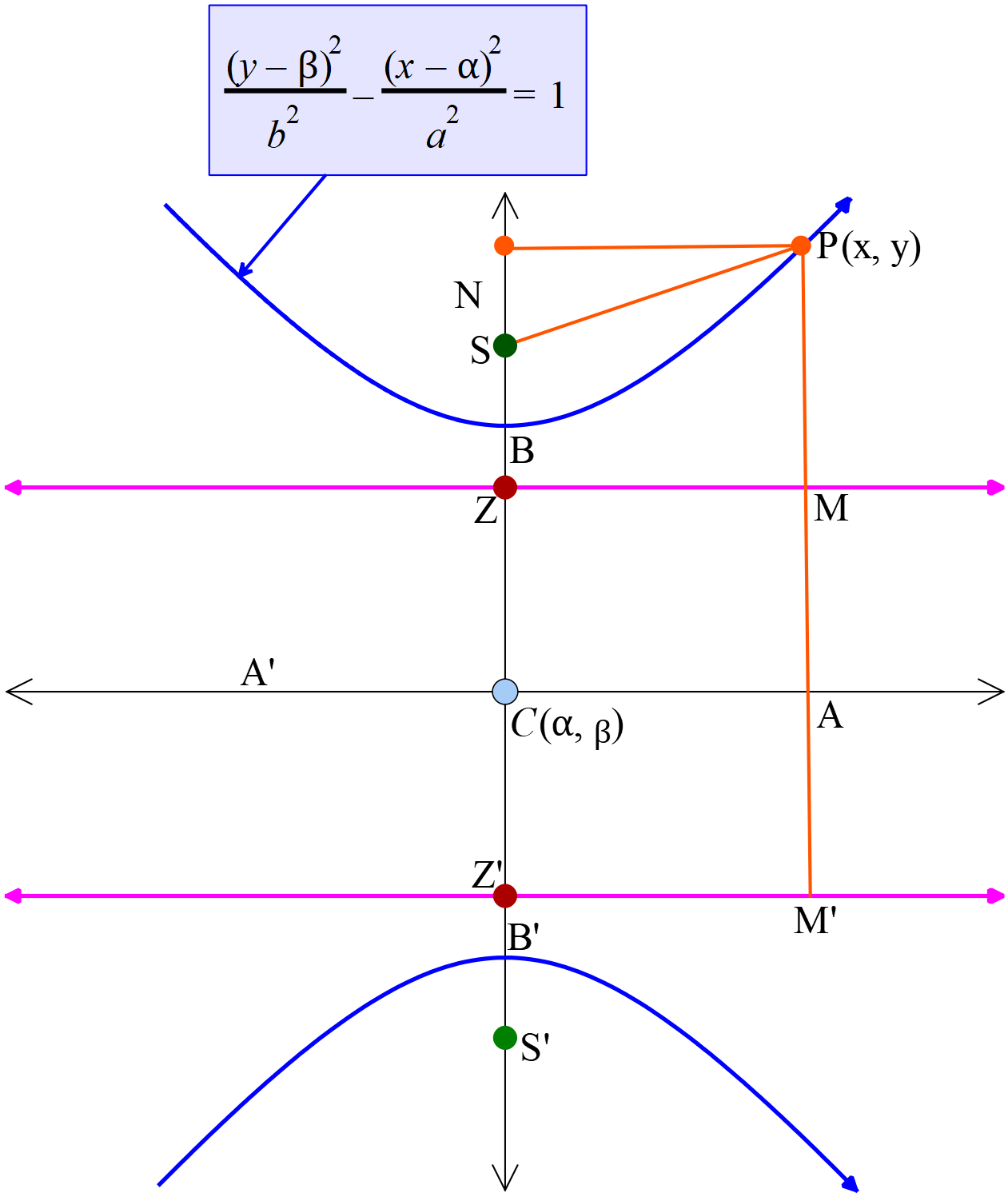

- অধিবৃত্তের শীর্ষবিন্দুর স্থানাঙ্ক \((0, \pm b+\beta)\)
- অধিবৃত্তের কেন্দ্রের স্থানাঙ্ক \(C(\alpha, \beta)\)
- উৎকেন্দ্রিকতা \(e=\sqrt{1+\frac{a^2}{b^2}}\)
- আড় অক্ষের দৈর্ঘ্য \(=|2b|\)
- অনুবন্ধী অক্ষের দৈর্ঘ্য \(=|2a|\)
- আড় অক্ষের সমীকরণ \(x-\alpha=0\)
- অনুবন্ধী অক্ষের সমীকরণ \(y-\beta=0\)
- উপকেন্দ্রের স্থানাঙ্ক \((\alpha, \pm be+\beta)\)
- নিয়ামকরেখার সমীকরণ \(y-\beta=\pm \frac{b}{e}\)
- উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|\frac{2a^2}{b}|\)
- উপকেন্দ্রিক লম্বের সমীকরণ \(y-\beta=\pm be\)
- অসীমতটের সমীকরণ \( y-\beta=\pm \frac{b}{a}(x-\alpha)\)
অধিবৃত্তের স্পর্শক
Tangent of hyperbola
মনে করি,
সরলরেখা ও অধিবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং অধিবৃত্তকে স্পর্শ করার শর্তঃ \(c=\pm \sqrt{(a^2m^2-b^2)}\)
স্পর্শকের সমীকরণঃ \(y=mx\pm \sqrt{(a^2m^2-b^2)}\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2-b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2-b^2)}}\right)\)
মনে করি,
সরলরেখা ও অধিবৃত্তটির সমীকরণ যথাক্রমে
\(x\cos\alpha + y\sin\alpha=p.............(1) \)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং অধিবৃত্তকে স্পর্শ করার শর্তঃ \(p^2=a^2\cos^2\alpha-b^2\sin^2\alpha\)
স্পর্শকের সমীকরণঃ \(x\cos\alpha + y\sin\alpha \pm \sqrt{(a^2\cos^2\alpha-b^2\sin^2\alpha)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{a^2\cos\alpha}{p}, \frac{b^2\sin\alpha}{p}\right)\)
মনে করি,
সরলরেখা ও অধিবৃত্তটির সমীকরণ যথাক্রমে
\(lx+my+n=0.............(1) \)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং অধিবৃত্তকে স্পর্শ করার শর্তঃ \(a^2l^2-b^2m^2=n^2\)
স্পর্শকের সমীকরণঃ \(lx+my \pm \sqrt{(a^2l^2-b^2m^2)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{-a^2l}{n}, \frac{b^2m}{n}\right)\)
সরলরেখা ও অধিবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .............(1) \)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং অধিবৃত্তকে স্পর্শ করার শর্তঃ \(c=\pm \sqrt{(a^2m^2-b^2)}\)
স্পর্শকের সমীকরণঃ \(y=mx\pm \sqrt{(a^2m^2-b^2)}\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2-b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2-b^2)}}\right)\)
মনে করি,
সরলরেখা ও অধিবৃত্তটির সমীকরণ যথাক্রমে
\(x\cos\alpha + y\sin\alpha=p.............(1) \)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং অধিবৃত্তকে স্পর্শ করার শর্তঃ \(p^2=a^2\cos^2\alpha-b^2\sin^2\alpha\)
স্পর্শকের সমীকরণঃ \(x\cos\alpha + y\sin\alpha \pm \sqrt{(a^2\cos^2\alpha-b^2\sin^2\alpha)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{a^2\cos\alpha}{p}, \frac{b^2\sin\alpha}{p}\right)\)
মনে করি,
সরলরেখা ও অধিবৃত্তটির সমীকরণ যথাক্রমে
\(lx+my+n=0.............(1) \)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(2) \)
\((1)\) নং সরলরেখা \((2)\) নং অধিবৃত্তকে স্পর্শ করার শর্তঃ \(a^2l^2-b^2m^2=n^2\)
স্পর্শকের সমীকরণঃ \(lx+my \pm \sqrt{(a^2l^2-b^2m^2)}=0\)
স্পর্শবিন্দুর স্থানাঙ্কঃ \(\left(\frac{-a^2l}{n}, \frac{b^2m}{n}\right)\)
অধিবৃত্ত সাপেক্ষে কোনো বিন্দুর আপেক্ষিক অবস্থান
The relative position of a point with respect to the hyperbola
মনে করি,
একটি নির্দিষ্ট বিন্দু এবং একটি অধিবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(1) \)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং অধিবৃত্তের উপরে অবস্থান করার শর্তঃ \(\frac{x^2_1}{a^2}-\frac{y^2_1}{b^2}=0\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং অধিবৃত্তের ভিতরে অবস্থান করার শর্তঃ \(\frac{y^2_1}{b^2}>\frac{x^2_1}{a^2}\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের বাহিরে অবস্থান করার শর্তঃ \(\frac{x^2_1}{a^2}>\frac{y^2_1}{b^2}\)
একটি নির্দিষ্ট বিন্দু এবং একটি অধিবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(1) \)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং অধিবৃত্তের উপরে অবস্থান করার শর্তঃ \(\frac{x^2_1}{a^2}-\frac{y^2_1}{b^2}=0\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং অধিবৃত্তের ভিতরে অবস্থান করার শর্তঃ \(\frac{y^2_1}{b^2}>\frac{x^2_1}{a^2}\)
\(P(x_1, y_1)\) বিন্দুটি \((1)\) নং উপবৃত্তের বাহিরে অবস্থান করার শর্তঃ \(\frac{x^2_1}{a^2}>\frac{y^2_1}{b^2}\)
অধিবৃত্তের উপরিস্থিত নির্দিষ্ট বিন্দুতে স্পর্শকের সমীকরণ
Equation of the tangent at a given point on the hyperbola
মনে করি,
একটি নির্দিষ্ট বিন্দু এবং একটি অধিবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(1) \)
\((1)\) নং উপবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণঃ \(\frac{xx_1}{a^2}-\frac{yy_1}{b^2}=1\)
একটি নির্দিষ্ট বিন্দু এবং একটি অধিবৃত্ত যথাক্রমে \(P(x_1, y_1)\)
এবং \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(1) \)
\((1)\) নং উপবৃত্তের উপরিস্থিত \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণঃ \(\frac{xx_1}{a^2}-\frac{yy_1}{b^2}=1\)
অধিবৃত্তের উপকেন্দ্র ও নিয়ামকরেখা
Focus and directrix of Hyperbola
 একটি অধিবৃত্তের দুইটি উপকেন্দ্র ও নিয়ামকরেখা আছে। যেহেতু, অধিবৃত্তটি \(y\) অক্ষ বরাবর প্রতিসম তাই তাকে \(B\acute B\) বরাবর ভাঁজ করা হলে অধিবৃত্তের ডান ও বাম পক্ষ দুইটি পরস্পরের সাথে সমাপতিত হয়। এখন \(x\) অক্ষের উপর \(\acute S\) ও \(\acute Z\) দুইটি বিন্দু এমনভাবে নেওয়া হয়, যেন \(C\acute S=CS=ae \) এবং \(C\acute Z=CZ=\frac{a}{e}\) হয়। \(Z\acute Z\)-এর উপর \(\acute M\acute Z\) লম্ব আঁকি। তাহলে প্রতিসাম্য অনুযায়ী, এটি স্পষ্ট যে, \(\acute S\)-কে উপকেন্দ্র এবং \(\acute M\acute Z\)-কে নিয়ামকরেখা ধরে আমরা একই অধিবৃত্ত পাই। অতএব, অধিবৃত্তের দুইটি উপকেন্দ্র এবং দুইটি নিয়ামকরেখা আছে।
একটি অধিবৃত্তের দুইটি উপকেন্দ্র ও নিয়ামকরেখা আছে। যেহেতু, অধিবৃত্তটি \(y\) অক্ষ বরাবর প্রতিসম তাই তাকে \(B\acute B\) বরাবর ভাঁজ করা হলে অধিবৃত্তের ডান ও বাম পক্ষ দুইটি পরস্পরের সাথে সমাপতিত হয়। এখন \(x\) অক্ষের উপর \(\acute S\) ও \(\acute Z\) দুইটি বিন্দু এমনভাবে নেওয়া হয়, যেন \(C\acute S=CS=ae \) এবং \(C\acute Z=CZ=\frac{a}{e}\) হয়। \(Z\acute Z\)-এর উপর \(\acute M\acute Z\) লম্ব আঁকি। তাহলে প্রতিসাম্য অনুযায়ী, এটি স্পষ্ট যে, \(\acute S\)-কে উপকেন্দ্র এবং \(\acute M\acute Z\)-কে নিয়ামকরেখা ধরে আমরা একই অধিবৃত্ত পাই। অতএব, অধিবৃত্তের দুইটি উপকেন্দ্র এবং দুইটি নিয়ামকরেখা আছে।
অধিবৃত্তের আড় অক্ষ ও অনুবন্ধী অক্ষের দৈর্ঘ্য
Transverse and Conjugate axis of Hyperbola
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ........(1)\)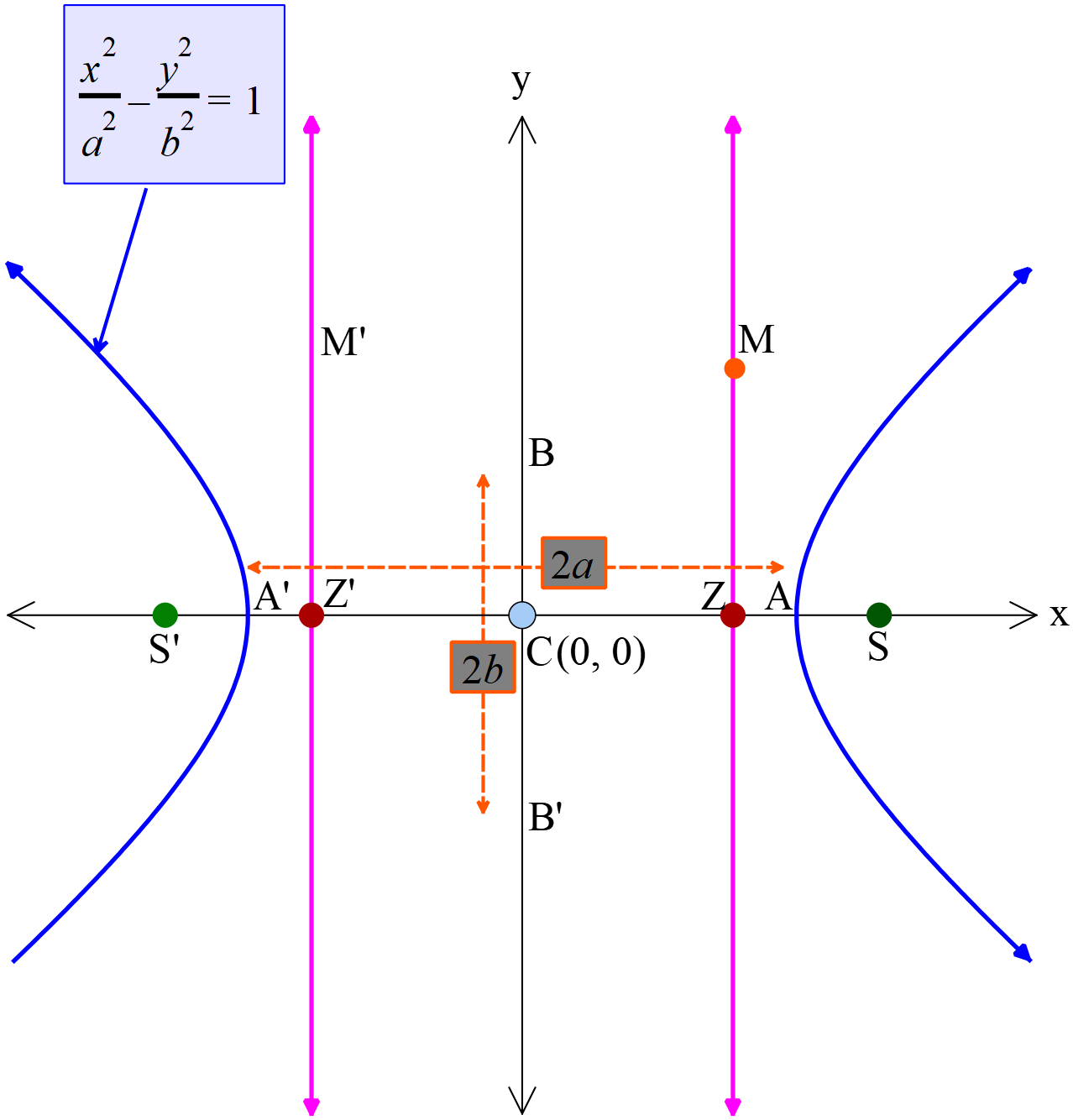
\(C(0, 0)\) বিন্দু উপবৃত্তের কেন্দ্র।
\((1)\) নং সমীকরণে \(y=0\) বসিয়ে পাই \(\frac{x^2}{a^2}+\frac{0^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}-\frac{0}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}-0=1\)
\(\Rightarrow \frac{x^2}{a^2}=1\)
\(\Rightarrow x^2=a^2\)
\(\therefore x=\pm a\)
সুতরাং অধিবৃত্ত \(X\)-অক্ষকে \(A(a, 0)\) এবং \(\acute A(-a, 0)\) বিন্দুতে ছেদ করে।
\(A\acute A\) আড় অক্ষ এবং এর দৈর্ঘ্য
\(A\acute A=AC+C\acute A=a+a=2a\)
\(\therefore \) আড় অক্ষের দৈর্ঘ্য \(=|2a|\)।
আবার,
\((1)\) নং সমীকরণে \(x=0\) বসিয়ে পাই \(\frac{0^2}{a^2}-\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{0}{a^2}-\frac{y^2}{b^2}=1\)
\(\Rightarrow 0-\frac{y^2}{b^2}=1\)
\(\Rightarrow -\frac{y^2}{b^2}=1\)
\(\Rightarrow y^2=-b^2\)
\(\Rightarrow y=\sqrt{-b^2}\)
\(\Rightarrow y=b\sqrt{-1}\)
\(\therefore y=\pm ib\) ➜ \(\because i=\sqrt{-1}\)
সুতরাং অধিবৃত্ত \(Y\)-অক্ষকে কাল্পনিকভাবে \(B(0, ib)\) এবং \(\acute B(0, -ib)\) ( কাল্পনিক ) বিন্দুতে ছেদ করে।
\(B\acute B\) অনুবন্ধী অক্ষ এবং এর দৈর্ঘ্য \(B\acute B=BC+C\acute B=b+b=2b\)
\(\therefore \) অনুবন্ধী অক্ষের দৈর্ঘ্য \(=|2b|\)।

\(C(0, 0)\) বিন্দু উপবৃত্তের কেন্দ্র।
\((1)\) নং সমীকরণে \(y=0\) বসিয়ে পাই \(\frac{x^2}{a^2}+\frac{0^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}-\frac{0}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}-0=1\)
\(\Rightarrow \frac{x^2}{a^2}=1\)
\(\Rightarrow x^2=a^2\)
\(\therefore x=\pm a\)
সুতরাং অধিবৃত্ত \(X\)-অক্ষকে \(A(a, 0)\) এবং \(\acute A(-a, 0)\) বিন্দুতে ছেদ করে।
\(A\acute A\) আড় অক্ষ এবং এর দৈর্ঘ্য
\(A\acute A=AC+C\acute A=a+a=2a\)
\(\therefore \) আড় অক্ষের দৈর্ঘ্য \(=|2a|\)।
আবার,
\((1)\) নং সমীকরণে \(x=0\) বসিয়ে পাই \(\frac{0^2}{a^2}-\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{0}{a^2}-\frac{y^2}{b^2}=1\)
\(\Rightarrow 0-\frac{y^2}{b^2}=1\)
\(\Rightarrow -\frac{y^2}{b^2}=1\)
\(\Rightarrow y^2=-b^2\)
\(\Rightarrow y=\sqrt{-b^2}\)
\(\Rightarrow y=b\sqrt{-1}\)
\(\therefore y=\pm ib\) ➜ \(\because i=\sqrt{-1}\)
সুতরাং অধিবৃত্ত \(Y\)-অক্ষকে কাল্পনিকভাবে \(B(0, ib)\) এবং \(\acute B(0, -ib)\) ( কাল্পনিক ) বিন্দুতে ছেদ করে।
\(B\acute B\) অনুবন্ধী অক্ষ এবং এর দৈর্ঘ্য \(B\acute B=BC+C\acute B=b+b=2b\)
\(\therefore \) অনুবন্ধী অক্ষের দৈর্ঘ্য \(=|2b|\)।
অধিবৃত্তের সমীকরণ থেকে উৎকেন্দ্রতা
Eccentricity from the equation of Hyperbola
আমরা জানি,
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
এবং
\(b^2=a^2(e^2-1)\)
\(\Rightarrow \frac{b^2}{a^2}=e^2-1\)
\(\Rightarrow \frac{b^2}{a^2}+1=e^2\)
\(\Rightarrow e^2=1+\frac{b^2}{a^2}\)
\(\therefore e=\sqrt{1+\frac{b^2}{a^2}}\)
যেহেতু, অধিবৃত্তের \(e\)-এর মান \(e > 1\)
সুতরাং \(e\)-কে ধনাত্মক হিসাবে বিবেচনা করা হয়েছে।
অধিবৃত্তের আড় অক্ষ হতে \(a\)-এর মান এবং অনুবন্ধী অক্ষ হতে \(b\)-এর মান জানা থাকলে উৎকেন্দ্রতা \(e\)-এর মান নির্ণয় করা যায়।
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
এবং
\(b^2=a^2(e^2-1)\)
\(\Rightarrow \frac{b^2}{a^2}=e^2-1\)
\(\Rightarrow \frac{b^2}{a^2}+1=e^2\)
\(\Rightarrow e^2=1+\frac{b^2}{a^2}\)
\(\therefore e=\sqrt{1+\frac{b^2}{a^2}}\)
যেহেতু, অধিবৃত্তের \(e\)-এর মান \(e > 1\)
সুতরাং \(e\)-কে ধনাত্মক হিসাবে বিবেচনা করা হয়েছে।
অধিবৃত্তের আড় অক্ষ হতে \(a\)-এর মান এবং অনুবন্ধী অক্ষ হতে \(b\)-এর মান জানা থাকলে উৎকেন্দ্রতা \(e\)-এর মান নির্ণয় করা যায়।
অধিবৃত্তের সমীকরণ থেকে উপকেন্দ্রের স্থানাঙ্ক ও নিয়ামকের সমীকরণ
The co-ordinates of focus and the equation of directrix from the equation of Hyperbola
মনে করি,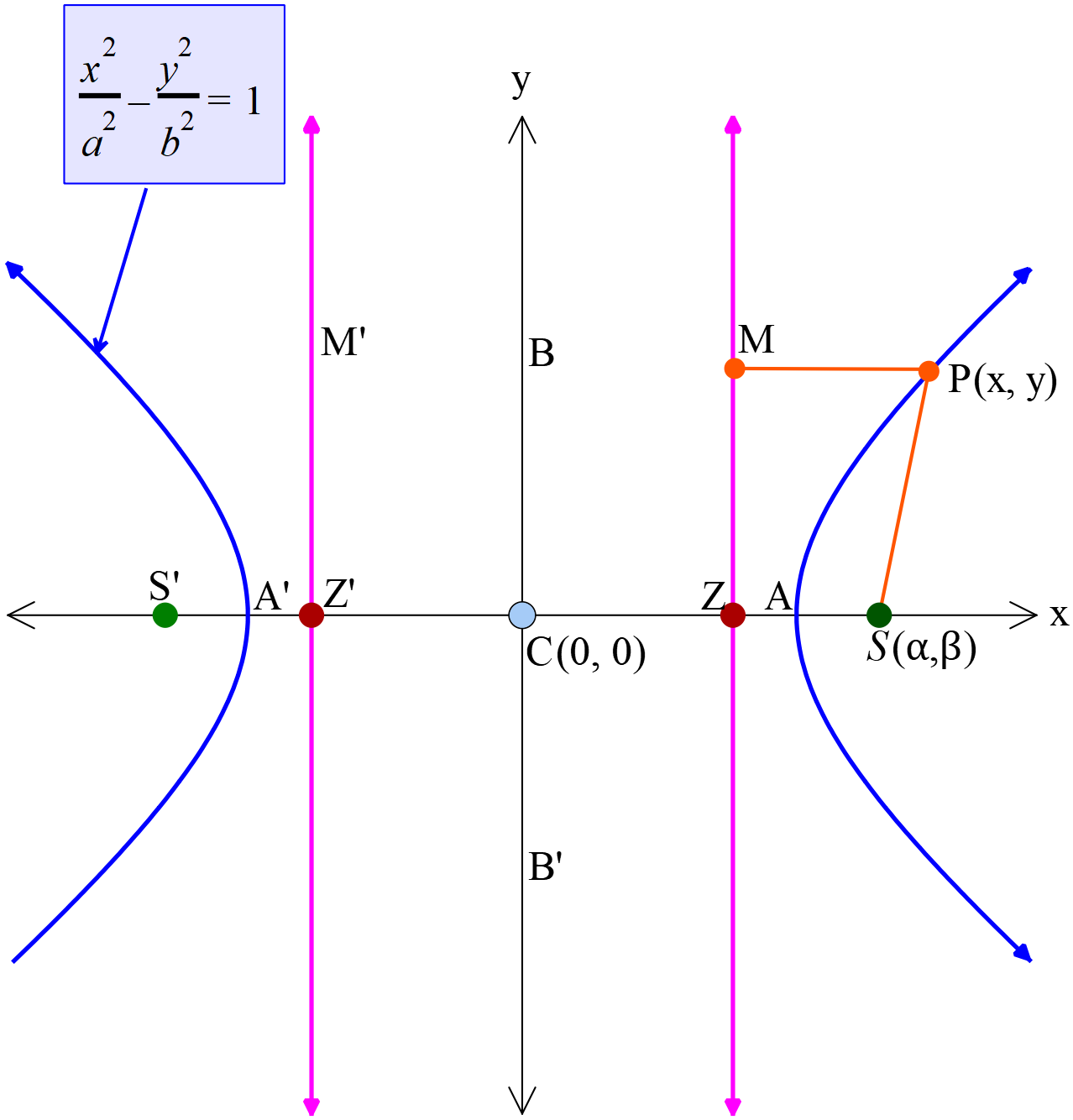
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
এবং
\(b^2=a^2(e^2-1)\) ➜ এখানে \(e\) উৎকেন্দ্রিকতা।
আবার,
উপবৃত্তের উপকেন্দ্র \(S\) ও \(\acute S\) এবং নিয়ামক রেখা \(MZ\) ও \(\acute M\acute Z\)।
\(Z\acute Z\) রেখা \(S\) এবং \(\acute S\) বিন্দুগামী। \(Z\acute Z\) রেখা নিয়ামকদ্বয়ের উপর লম্ব।
\(SZ\)-এর উপর \(A\) এমন একটি বিন্দু নেওয়া হল যেন \(SA=eAZ ........(1)\)
আবার,
\(SZ\)-এর বর্দ্ধিতাংশের উপর \(\acute A\) এমন একটি বিন্দু নেওয়া হল যেন \(S\acute A=e\acute AZ\)
ধরি,
\(A\acute A=2a\) এবং \(C\) হল \(A\acute A\)-এর মধ্যবিন্দু। \(C\)-কে কেন্দ্র বিন্দু বলা হয় যার স্থানাঙ্ক \(C(0, 0)\)।
\((1)\) ও \((2)\) যোগ করে পাই
\(SA+S\acute A=eAZ+e\acute AZ\)
\(\Rightarrow A\acute A=e(AZ+\acute AZ)\)
\(\Rightarrow 2a=e(AZ+A\acute A+AZ)\) ➜ \(\because \acute AZ=A\acute A+AZ\)
\(\Rightarrow 2a=e(A\acute A+2AZ)\)
\(\Rightarrow 2a=e(2a+2AZ)\)
\(\Rightarrow 2a=2e(a+AZ)\)
\(\Rightarrow a=e(a+AZ)\)
\(\Rightarrow a=eCZ\) ➜ \(\because CZ=CA+AZ=a+AZ\)
\(\Rightarrow eCZ=a\)
\(\therefore CZ=\frac{a}{e} ......(3)\)
আবার,
\(CS=CA-AS\)
\(\Rightarrow CS=CA-eAZ\) ➜ \(\because AS=eAZ\)
\(\Rightarrow CS=CA-e(CZ-CA)\)
\(\Rightarrow CS=a-e\left(\frac{a}{e}-a\right)\)
\(\Rightarrow CS=a-a+ae\)
\(\therefore CS=ae .........(4)\)
\(C\) বিন্দুকে মূলবিন্দু ধরে \(CX\)-কে \(x\) অক্ষ এবং \(CY\)-কে \(y\) অক্ষ বিবেচনা করি। যেহেতু \(S\) বিন্দু \(x\) অক্ষের উপর অবস্থিত ।
অতএব, \(S\)-এর স্থানাঙ্ক \((ae, 0)\) এখানে \(S\)-কে উপকেন্দ্র বলে। যেহেতু উপকেন্দ্র \(S\) ও \(\acute S\) সুতরাং এদের স্থানাঙ্ক লেখা হয় \((\pm ae, 0)\)।
এবং নিয়ামক রেখা \(\acute M\acute Z\)-এর সমীকরণ \(x=CZ=\frac{a}{e}\)
\(\therefore x=\frac{a}{e}\)
অনুরূপভাবে, নিয়ামক রেখা \(MZ\)-এর সমীকরণ \(x=-\frac{a}{e}\)
সুতরাং উপবৃত্তের নিয়ামক রেখার সমীকরণ \(x=\pm \frac{a}{e}\)

অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
এবং
\(b^2=a^2(e^2-1)\) ➜ এখানে \(e\) উৎকেন্দ্রিকতা।
আবার,
উপবৃত্তের উপকেন্দ্র \(S\) ও \(\acute S\) এবং নিয়ামক রেখা \(MZ\) ও \(\acute M\acute Z\)।
\(Z\acute Z\) রেখা \(S\) এবং \(\acute S\) বিন্দুগামী। \(Z\acute Z\) রেখা নিয়ামকদ্বয়ের উপর লম্ব।
\(SZ\)-এর উপর \(A\) এমন একটি বিন্দু নেওয়া হল যেন \(SA=eAZ ........(1)\)
আবার,
\(SZ\)-এর বর্দ্ধিতাংশের উপর \(\acute A\) এমন একটি বিন্দু নেওয়া হল যেন \(S\acute A=e\acute AZ\)
ধরি,
\(A\acute A=2a\) এবং \(C\) হল \(A\acute A\)-এর মধ্যবিন্দু। \(C\)-কে কেন্দ্র বিন্দু বলা হয় যার স্থানাঙ্ক \(C(0, 0)\)।
\((1)\) ও \((2)\) যোগ করে পাই
\(SA+S\acute A=eAZ+e\acute AZ\)
\(\Rightarrow A\acute A=e(AZ+\acute AZ)\)
\(\Rightarrow 2a=e(AZ+A\acute A+AZ)\) ➜ \(\because \acute AZ=A\acute A+AZ\)
\(\Rightarrow 2a=e(A\acute A+2AZ)\)
\(\Rightarrow 2a=e(2a+2AZ)\)
\(\Rightarrow 2a=2e(a+AZ)\)
\(\Rightarrow a=e(a+AZ)\)
\(\Rightarrow a=eCZ\) ➜ \(\because CZ=CA+AZ=a+AZ\)
\(\Rightarrow eCZ=a\)
\(\therefore CZ=\frac{a}{e} ......(3)\)
আবার,
\(CS=CA-AS\)
\(\Rightarrow CS=CA-eAZ\) ➜ \(\because AS=eAZ\)
\(\Rightarrow CS=CA-e(CZ-CA)\)
\(\Rightarrow CS=a-e\left(\frac{a}{e}-a\right)\)
\(\Rightarrow CS=a-a+ae\)
\(\therefore CS=ae .........(4)\)
\(C\) বিন্দুকে মূলবিন্দু ধরে \(CX\)-কে \(x\) অক্ষ এবং \(CY\)-কে \(y\) অক্ষ বিবেচনা করি। যেহেতু \(S\) বিন্দু \(x\) অক্ষের উপর অবস্থিত ।
অতএব, \(S\)-এর স্থানাঙ্ক \((ae, 0)\) এখানে \(S\)-কে উপকেন্দ্র বলে। যেহেতু উপকেন্দ্র \(S\) ও \(\acute S\) সুতরাং এদের স্থানাঙ্ক লেখা হয় \((\pm ae, 0)\)।
এবং নিয়ামক রেখা \(\acute M\acute Z\)-এর সমীকরণ \(x=CZ=\frac{a}{e}\)
\(\therefore x=\frac{a}{e}\)
অনুরূপভাবে, নিয়ামক রেখা \(MZ\)-এর সমীকরণ \(x=-\frac{a}{e}\)
সুতরাং উপবৃত্তের নিয়ামক রেখার সমীকরণ \(x=\pm \frac{a}{e}\)
উপকেন্দ্র ও নিয়ামকের সমীকরণ থেকে অধিবৃত্তের সমীকরণ নির্ণয়
Determination of the equation of Hyperbola from focus and equation of directrix
ধরি,
অধিবৃত্তের উপকেন্দ্র \(S(\alpha, \beta)\), নিয়ামকরেখার সমীকরণ, \(ax+by+c=0\) এবং উৎকেন্দ্রিকতা \(e; (e>1)\)।
অধিবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(P\) বিন্দু থেকে নিয়ামকরেখার উপর \(PM\) লম্ব আঁকি এবং \(S, p\) যোগ করি।
এখন,
\(P(x, y)\) ও \(S(\alpha, \beta)\) বিন্দুদ্বয়ের দূরত্ব \(PS=\sqrt{(x-\alpha)^2+(y-\beta)^2}\)
এবং \(P(x, y)\) হতে নিয়ামকরেখার লম্ব দূরত্ব \(PM=\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
অধিবৃত্তের সংজ্ঞানুসারে, \(PS=e.PM\)
\(\Rightarrow \sqrt{(x-\alpha)^2+(y-\beta)^2}=e.\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
\(\Rightarrow (x-\alpha)^2+(y-\beta)^2=e^2.\frac{(ax+by+c)^2}{a^2+b^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\therefore (a^2+b^2)\{(x-\alpha)^2+(y-\beta)^2\}=e^2(ax+by+c)^2\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।

অধিবৃত্তের উপকেন্দ্র \(S(\alpha, \beta)\), নিয়ামকরেখার সমীকরণ, \(ax+by+c=0\) এবং উৎকেন্দ্রিকতা \(e; (e>1)\)।
অধিবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(P\) বিন্দু থেকে নিয়ামকরেখার উপর \(PM\) লম্ব আঁকি এবং \(S, p\) যোগ করি।
এখন,
\(P(x, y)\) ও \(S(\alpha, \beta)\) বিন্দুদ্বয়ের দূরত্ব \(PS=\sqrt{(x-\alpha)^2+(y-\beta)^2}\)
এবং \(P(x, y)\) হতে নিয়ামকরেখার লম্ব দূরত্ব \(PM=\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
অধিবৃত্তের সংজ্ঞানুসারে, \(PS=e.PM\)
\(\Rightarrow \sqrt{(x-\alpha)^2+(y-\beta)^2}=e.\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
\(\Rightarrow (x-\alpha)^2+(y-\beta)^2=e^2.\frac{(ax+by+c)^2}{a^2+b^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\therefore (a^2+b^2)\{(x-\alpha)^2+(y-\beta)^2\}=e^2(ax+by+c)^2\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।
অধিবৃত্তের সমীকরণ থেকে উপকেন্দ্রিক লম্ব ও এর দৈর্ঘ্য
Latus rectum and it's length from the equation of Hyperbola
অধিবৃত্তের যে কোনো উপকেন্দ্রের মধ্য দিয়ে অঙ্কিত আড় অক্ষের উপর লম্ব রেখার অধিবৃত্তের অন্তর্গত অংশই উপকেন্দ্রিক লম্ব। যদি \(L\acute L\) উপকেন্দ্রিক লম্ব হয়, তবে \(SL=S\acute L\) এবং \(\acute L\)-এর স্থানাঙ্ক \((-ae, SL)\) ।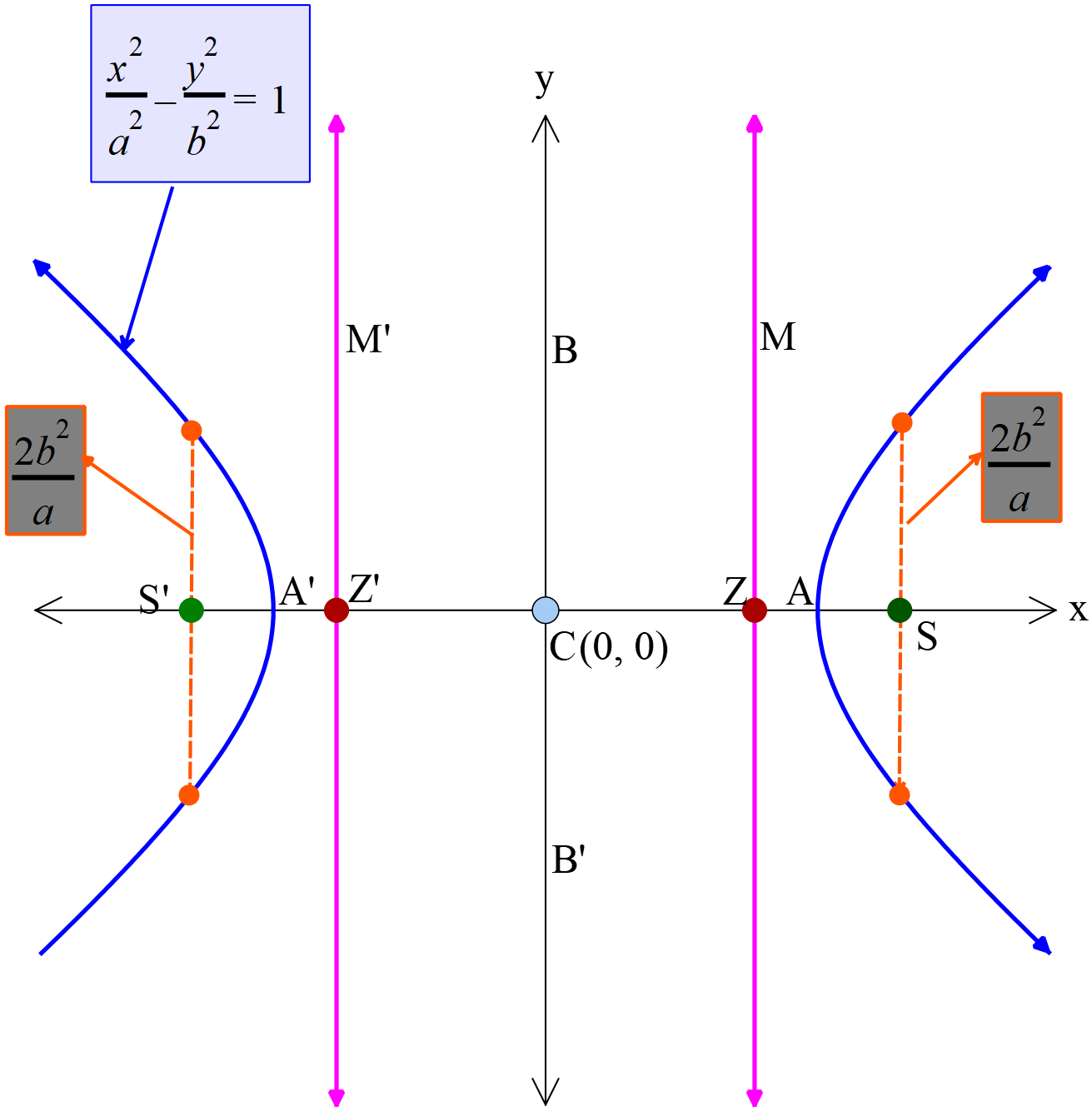
\(\acute L(-ae, SL)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত।
\(\Rightarrow \frac{(-ae)^2}{a^2}-\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{a^2e^2}{a^2}-\frac{SL^2}{b^2}=1 \)
\(\Rightarrow e^2-\frac{SL^2}{b^2}=1 \)
\(\Rightarrow e^2-1=\frac{SL^2}{b^2} \)
\(\Rightarrow \frac{SL^2}{b^2}=e^2-1 \)
\(\Rightarrow SL^2=b^2(e^2-1) \)
\(\Rightarrow SL^2=b^2\times \frac{b^2}{a^2} \) ➜ \(\because e^2-1=\frac{b^2}{a^2}\)
\(\Rightarrow SL^2=\frac{b^4}{a^2} \)
\(\therefore SL=\frac{b^2}{a} \)
\(\therefore L\acute L=2SL=\frac{2b^2}{a} \)

\(\acute L(-ae, SL)\) বিন্দুটি উপবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত।
\(\Rightarrow \frac{(-ae)^2}{a^2}-\frac{SL^2}{b^2}=1 \)
\(\Rightarrow \frac{a^2e^2}{a^2}-\frac{SL^2}{b^2}=1 \)
\(\Rightarrow e^2-\frac{SL^2}{b^2}=1 \)
\(\Rightarrow e^2-1=\frac{SL^2}{b^2} \)
\(\Rightarrow \frac{SL^2}{b^2}=e^2-1 \)
\(\Rightarrow SL^2=b^2(e^2-1) \)
\(\Rightarrow SL^2=b^2\times \frac{b^2}{a^2} \) ➜ \(\because e^2-1=\frac{b^2}{a^2}\)
\(\Rightarrow SL^2=\frac{b^4}{a^2} \)
\(\therefore SL=\frac{b^2}{a} \)
\(\therefore L\acute L=2SL=\frac{2b^2}{a} \)
নির্দিষ্ট বিন্দুতে অধিবৃত্তের পরামিতিক স্থানাঙ্ক
Parametric coordinates of Hyperbola at fixed point
ধরি,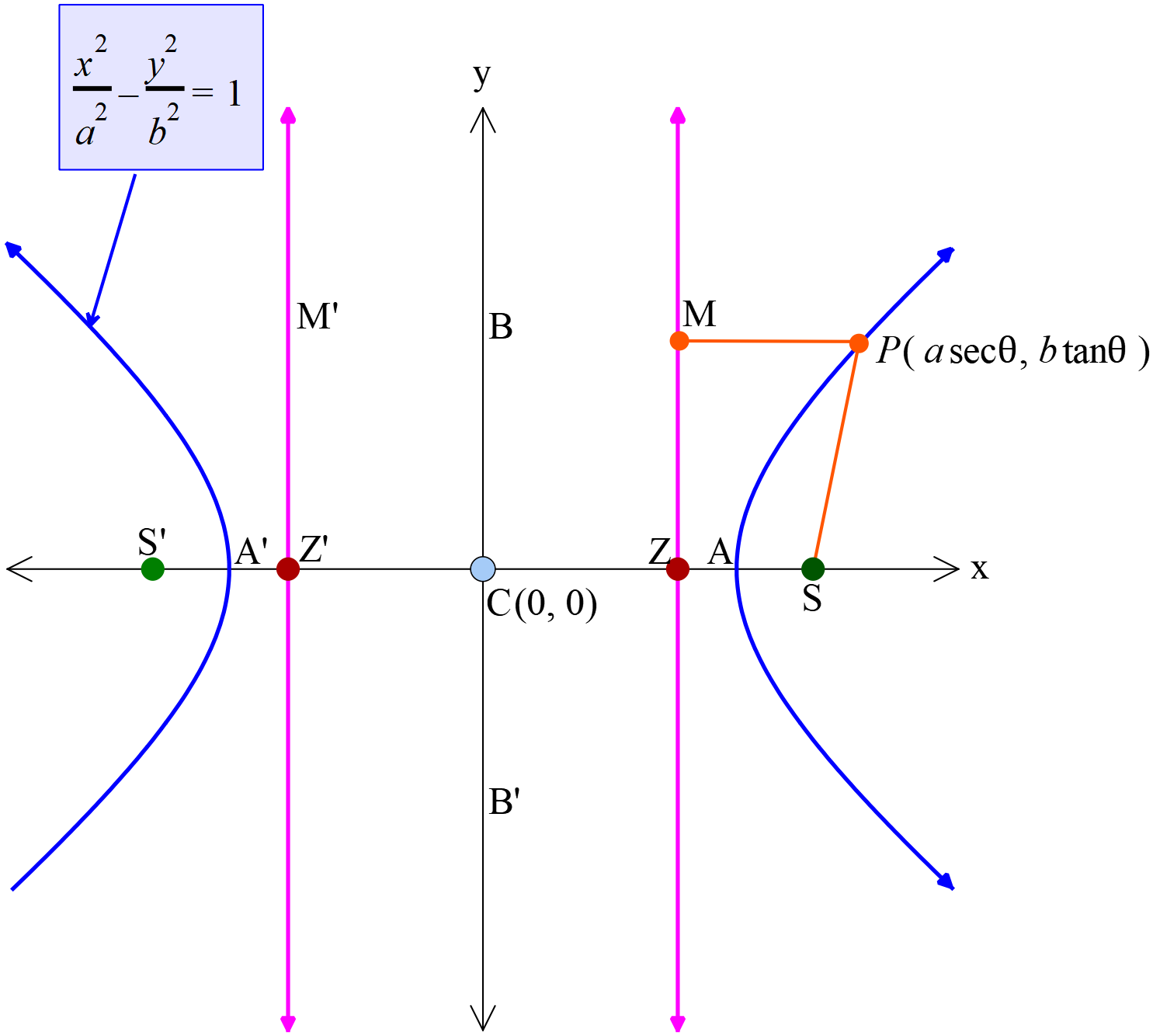
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1........(1)\)
এবং অধিবৃত্তের উপরিস্থিত একটি বিন্দু \(P(x, y)\)
অধিবৃত্তের আড় অক্ষকে ব্যাস ধরে সহায়ক বৃত্ত অঙ্কন করি, যার সমীকরণ \(x^2+y^2=a^2 .......(2)\)
\(P(x, y)\) বিন্দু থেকে আড় অক্ষের উপর \(PN\) লম্ব অঙ্কন করি। \(N\) থেকে সহায়ক বৃত্তে \(NQ\) স্পর্শক আঁকি এবং \(C\) ও \(Q\) যোগ করি।
মনে করি,
\(\angle QCN=\theta\), এখানে \(\theta\)-কে উপকেন্দ্র কোণ বলা হয়। \(C(0, 0)\) অধিবৃত্তের কেন্দ্র।
\(\therefore \angle QCN=90^{o}\)
\(P\) বিন্দুর স্থানাঙ্ক \((x, y)\) হওয়ায়, \(CN=x\) এবং \(PN=y\)
এখন, \(CQN\) সমকোণী ত্রিভুজ থেকে পাই,
\(\cos \theta=\frac{CQ}{CN}\)
\(\Rightarrow \frac{1}{\cos \theta}=\frac{CN}{CQ}\)
\(\Rightarrow \sec \theta=\frac{CN}{CQ}\)
\(\Rightarrow CN=CQ\sec \theta\)
\(\therefore x=a\sec\theta ........(3)\) ➜ \(\because CQ=a=\)বৃত্তের ব্যাসার্ধ।
\(x=a\sec\theta\)-এর এই মান \((1)\)-এ বসিয়ে,
\(\frac{(a\sec\theta)^2}{a^2}-\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{a^2\sec^2\theta}{a^2}-\frac{y^2}{b^2}=1\)
\(\Rightarrow \sec^2\theta-\frac{y^2}{b^2}=1\)
\(\Rightarrow \sec^2\theta-1=\frac{y^2}{b^2}\)
\(\Rightarrow \frac{y^2}{b^2}=1+\sec^2\theta\)
\(\Rightarrow \frac{y^2}{b^2}=\tan^2\theta\)
\(\Rightarrow y^2=b^2\tan^2\theta\)
\(\therefore y=b\tan\theta ......(4)\)
সুতরাং, \(P(a\sec\theta, b\tan\theta)\)
\(\theta\)-এর যে কোনো মানের জন্য \(P(a\sec\theta, b\tan\theta)\) বিন্দুটি অধিবৃত্তের উপর অবস্থিত, যাকে অধিবৃত্তের পরামিতিক স্থানাঙ্ক বলা হয় এবং \(\theta\)-কে পরামিতি (parameter) বলা হয়।
আবার,
\((4)\) হতে যথাক্রমে,
\(b\tan\theta=y\)
\(\Rightarrow \tan\theta=\frac{y}{b}\)
\(\Rightarrow \theta=\tan^{-1}\left(\frac{y}{b}\right)\)
\(\therefore \theta=\tan^{-1}\left(\frac{y}{b}\right)\)
\(\theta \)-এর এই মাণ নির্ণয়ের সময় বিন্দুটি কোন চতুর্ভাগে অবস্থিত তা লক্ষনীয়।
\(x=a\sec\theta\) এবং \(y=b\tan\theta\)-কে একত্রে \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) অধিবৃত্তের পরামিতিক সমীকরণ বলে।
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \) অধিবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\sec\theta, b\tan\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{y}{b}\right)\)।
\(\frac{y^2}{b^2}-\frac{x^2}{a^2}=1 \) অধিবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\tan\theta, b\sec\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{x}{a}\right)\)।

অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1........(1)\)
এবং অধিবৃত্তের উপরিস্থিত একটি বিন্দু \(P(x, y)\)
অধিবৃত্তের আড় অক্ষকে ব্যাস ধরে সহায়ক বৃত্ত অঙ্কন করি, যার সমীকরণ \(x^2+y^2=a^2 .......(2)\)
\(P(x, y)\) বিন্দু থেকে আড় অক্ষের উপর \(PN\) লম্ব অঙ্কন করি। \(N\) থেকে সহায়ক বৃত্তে \(NQ\) স্পর্শক আঁকি এবং \(C\) ও \(Q\) যোগ করি।
মনে করি,
\(\angle QCN=\theta\), এখানে \(\theta\)-কে উপকেন্দ্র কোণ বলা হয়। \(C(0, 0)\) অধিবৃত্তের কেন্দ্র।
\(\therefore \angle QCN=90^{o}\)
\(P\) বিন্দুর স্থানাঙ্ক \((x, y)\) হওয়ায়, \(CN=x\) এবং \(PN=y\)
এখন, \(CQN\) সমকোণী ত্রিভুজ থেকে পাই,
\(\cos \theta=\frac{CQ}{CN}\)
\(\Rightarrow \frac{1}{\cos \theta}=\frac{CN}{CQ}\)
\(\Rightarrow \sec \theta=\frac{CN}{CQ}\)
\(\Rightarrow CN=CQ\sec \theta\)
\(\therefore x=a\sec\theta ........(3)\) ➜ \(\because CQ=a=\)বৃত্তের ব্যাসার্ধ।
\(x=a\sec\theta\)-এর এই মান \((1)\)-এ বসিয়ে,
\(\frac{(a\sec\theta)^2}{a^2}-\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{a^2\sec^2\theta}{a^2}-\frac{y^2}{b^2}=1\)
\(\Rightarrow \sec^2\theta-\frac{y^2}{b^2}=1\)
\(\Rightarrow \sec^2\theta-1=\frac{y^2}{b^2}\)
\(\Rightarrow \frac{y^2}{b^2}=1+\sec^2\theta\)
\(\Rightarrow \frac{y^2}{b^2}=\tan^2\theta\)
\(\Rightarrow y^2=b^2\tan^2\theta\)
\(\therefore y=b\tan\theta ......(4)\)
সুতরাং, \(P(a\sec\theta, b\tan\theta)\)
\(\theta\)-এর যে কোনো মানের জন্য \(P(a\sec\theta, b\tan\theta)\) বিন্দুটি অধিবৃত্তের উপর অবস্থিত, যাকে অধিবৃত্তের পরামিতিক স্থানাঙ্ক বলা হয় এবং \(\theta\)-কে পরামিতি (parameter) বলা হয়।
আবার,
\((4)\) হতে যথাক্রমে,
\(b\tan\theta=y\)
\(\Rightarrow \tan\theta=\frac{y}{b}\)
\(\Rightarrow \theta=\tan^{-1}\left(\frac{y}{b}\right)\)
\(\therefore \theta=\tan^{-1}\left(\frac{y}{b}\right)\)
\(\theta \)-এর এই মাণ নির্ণয়ের সময় বিন্দুটি কোন চতুর্ভাগে অবস্থিত তা লক্ষনীয়।
\(x=a\sec\theta\) এবং \(y=b\tan\theta\)-কে একত্রে \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) অধিবৃত্তের পরামিতিক সমীকরণ বলে।
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \) অধিবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\sec\theta, b\tan\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{y}{b}\right)\)।
\(\frac{y^2}{b^2}-\frac{x^2}{a^2}=1 \) অধিবৃত্তের উপর \(P(x, y)\) বিন্দুর পরামিতিক স্থানাংক \(P(a\tan\theta, b\sec\theta)\), যেখানে \(\theta=\tan^{-1}\left(\frac{x}{a}\right)\)।
অধিবৃত্তের অসীমতটের অবস্থান নির্ণয়
Determination of the position of asymptotes of Hyperbola
অসীমতটঃ একটি সরলরেখা কোনো বক্ররেখার সহিত অসীম দূরে অবস্থিত দুইটি সমাপতিত বিন্দুতে ছেদ করলে, ঐ সরলরেখা নিজে সম্পুর্ণ অসীমে অবস্থিত নয়, তবে ঐ সরলরেখাকে বক্ররেখাটির অসীমতট বলে।
অধিবৃত্তের অসীমতটঃ কোনো রেখাকে বর্ধিত করলে যদি অধিবৃত্তকে অসীমে ছেদ করে কিন্তু রেখা নিজে অসীমে অবস্থিত নয় তবে ঐ রেখাকে অধিবৃত্তের অসীমতট বলা হয়। অধিবৃত্তের সমীকরণের ডান পক্ষে \(1\)-এর পরিবর্তে \(0\) প্রতিস্থাপন করলে এর দইটি অসীমতট পাওয়া যায়।
ধরি,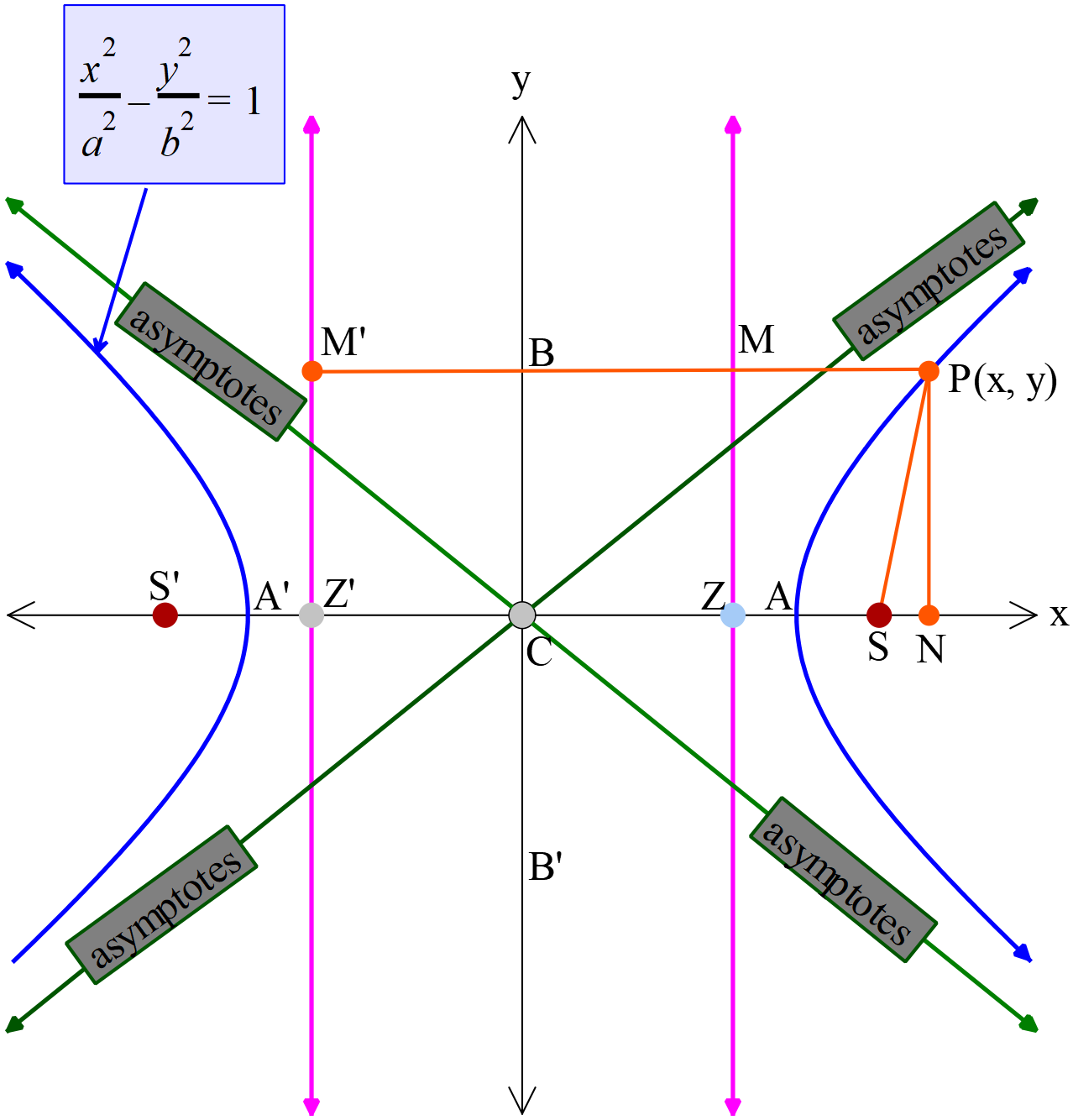
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1........(1)\)
এবং সরলরেখার সমীকরণ, \(y=mx+c ....(2)\)
\((2)\) হতে \(y\)-এর মাণ \((1)\)-এ বসিয়ে,
\(\frac{x^2}{a^2}-\frac{(mx+c)^2}{b^2}=1\)
\(\Rightarrow \frac{b^2x^2-a^2(mx+c)^2}{a^2b^2}=1\)
\(\Rightarrow b^2x^2-a^2(mx+c)^2=a^2b^2\)
\(\Rightarrow b^2x^2-a^2(m^2x^2+2mcx+c^2)=a^2b^2\)
\(\Rightarrow b^2x^2-a^2m^2x^2-2a^2mcx-a^2c^2=a^2b^2\)
\(\Rightarrow x^2(b^2-a^2m^2)-2a^2mcx-a^2c^2-a^2b^2=0\)
\(\therefore x^2(b^2-a^2m^2)-2a^2mcx-a^2(c^2+b^2)=0 ....(3)\)
\((1)\) নং অধিবৃত্তকে \((2)\) নং সরলরেখা অসীমে ছেদ করলে সেক্ষেত্রে \((3)\) নং দ্বিঘাত সমীকরনের \(x^2\) ও \(x\)-এর সহগ শুন্য হবে। অর্থাৎ \((3)\) নং দ্বিঘাত সমীকরনের উভয় মূলই অসীম হবে।
\(\therefore b^2-a^2m^2=0; -2a^2mc=0\)
\(\Rightarrow -a^2m^2=-b^2; c=0; -2a^2m\ne 0\)
\(\Rightarrow m^2=\frac{b^2}{a^2}; c=0\)
\(\therefore m=\pm \frac{b}{a}; c=0\)
\(m\) ও \(c\)-এর মাণ \((2)\) -এ বসিয়ে,
\(y=\pm \frac{b}{a}x+0 \)
\(\therefore y=\pm \frac{b}{a}x \)
ইহাই নির্ণেয় অসীমতটের সমীকরণ।
অধিবৃত্তের অসীমতটঃ কোনো রেখাকে বর্ধিত করলে যদি অধিবৃত্তকে অসীমে ছেদ করে কিন্তু রেখা নিজে অসীমে অবস্থিত নয় তবে ঐ রেখাকে অধিবৃত্তের অসীমতট বলা হয়। অধিবৃত্তের সমীকরণের ডান পক্ষে \(1\)-এর পরিবর্তে \(0\) প্রতিস্থাপন করলে এর দইটি অসীমতট পাওয়া যায়।
ধরি,

অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1........(1)\)
এবং সরলরেখার সমীকরণ, \(y=mx+c ....(2)\)
\((2)\) হতে \(y\)-এর মাণ \((1)\)-এ বসিয়ে,
\(\frac{x^2}{a^2}-\frac{(mx+c)^2}{b^2}=1\)
\(\Rightarrow \frac{b^2x^2-a^2(mx+c)^2}{a^2b^2}=1\)
\(\Rightarrow b^2x^2-a^2(mx+c)^2=a^2b^2\)
\(\Rightarrow b^2x^2-a^2(m^2x^2+2mcx+c^2)=a^2b^2\)
\(\Rightarrow b^2x^2-a^2m^2x^2-2a^2mcx-a^2c^2=a^2b^2\)
\(\Rightarrow x^2(b^2-a^2m^2)-2a^2mcx-a^2c^2-a^2b^2=0\)
\(\therefore x^2(b^2-a^2m^2)-2a^2mcx-a^2(c^2+b^2)=0 ....(3)\)
\((1)\) নং অধিবৃত্তকে \((2)\) নং সরলরেখা অসীমে ছেদ করলে সেক্ষেত্রে \((3)\) নং দ্বিঘাত সমীকরনের \(x^2\) ও \(x\)-এর সহগ শুন্য হবে। অর্থাৎ \((3)\) নং দ্বিঘাত সমীকরনের উভয় মূলই অসীম হবে।
\(\therefore b^2-a^2m^2=0; -2a^2mc=0\)
\(\Rightarrow -a^2m^2=-b^2; c=0; -2a^2m\ne 0\)
\(\Rightarrow m^2=\frac{b^2}{a^2}; c=0\)
\(\therefore m=\pm \frac{b}{a}; c=0\)
\(m\) ও \(c\)-এর মাণ \((2)\) -এ বসিয়ে,
\(y=\pm \frac{b}{a}x+0 \)
\(\therefore y=\pm \frac{b}{a}x \)
ইহাই নির্ণেয় অসীমতটের সমীকরণ।
অধিবৃত্তের অসীমতট রেখার সমীকরণ
Equation of asymptotes of Hyperbola
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) অধিবৃত্তের অসীমতট রেখার সমীকরণঃ \( y=\pm \frac{b}{a}x\)
\(\frac{y^2}{b^2}-\frac{x^2}{a^2}=1\) অধিবৃত্তের অসীমতট রেখার সমীকরণঃ \( y=\pm \frac{b}{a}x\)
\(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\) অধিবৃত্তের অসীমতট রেখার সমীকরণঃ \( y-k=\pm \frac{b}{a}(x-h)\)
\(\frac{(y-k)^2}{b^2}-\frac{(x-h)^2}{a^2}=1\) অধিবৃত্তের অসীমতট রেখার সমীকরণঃ \( y-k=\pm \frac{b}{a}(x-h)\)
অধিবৃত্তের লেখচিত্র
Graph of Hyperbola
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)-এর লেখচিত্র ।

অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) থেকে দেখা যাচ্ছে যে, যখন \(y=0; x=\pm a\) অতএব অধিবৃত্ত \(X\) অক্ষকে \(A(a, 0)\) এবং \(\acute{A}(-a, 0)\) বিন্দু দইটিতে ছেদ করে। \(A\) ও \(\acute{A}\) বিন্দু দুইটি অধিবৃত্তের শীর্ষবিন্দু এবং \(A\acute{A}\) অধিবৃত্তের আড় অক্ষ।
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) এ যখন \(x=0; y^2=-b^2\) এ ক্ষেত্রে \(y\)-এর কোনো বাস্তব মাণ পাওয়া যায় না। \(Y\) অক্ষের উপর \(B(0, b)\) এবং \(\acute{B}(0, -b)\) বিন্দু দুইটি নেই। উল্লেখ্য যে, \(B\acute{B}\) অধিবৃত্তের অনুবন্ধী অক্ষ।
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) থেকে পাই, \(\frac{x^2}{a^2}=1+\frac{y^2}{b^2}\geq 1\)
অতএব, \(|x|\leq a\) অর্থাৎ \(x\leq +a\) এবং \(x\geq -a\) সুতরাং \(x=a\) এবং \(x=-a\) রেখা দুইটির মধ্যে লেখের কোনো বিন্দু নেই। প্রত্যেক অধিবৃত্তের তাই দুইটি শাখা রয়েছে। যদি \((x, y)\) লেখের উপর কোনো বিন্দু হয় তবে \((-x, y)\) বিন্দুটিও লেখের উপর অবস্থিত। অর্থাৎ, লেখটি \(Y\) অক্ষের সাপেক্ষে প্রতিসম। অনুরূপভাবে এটি দেখানো যায় যে, লেখটি \(X\) অক্ষের সাপেক্ষেও প্রতিসম। \(x\) এর মাণ বৃদ্ধির সাথে সাথে \(y\) এর মাণ অসীম পর্যন্ত বৃদ্ধি পায়। অতএব, অধিবৃত্ত দুইদিকে অসীমে বিস্তৃত হয়।

অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) থেকে দেখা যাচ্ছে যে, যখন \(y=0; x=\pm a\) অতএব অধিবৃত্ত \(X\) অক্ষকে \(A(a, 0)\) এবং \(\acute{A}(-a, 0)\) বিন্দু দইটিতে ছেদ করে। \(A\) ও \(\acute{A}\) বিন্দু দুইটি অধিবৃত্তের শীর্ষবিন্দু এবং \(A\acute{A}\) অধিবৃত্তের আড় অক্ষ।
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) এ যখন \(x=0; y^2=-b^2\) এ ক্ষেত্রে \(y\)-এর কোনো বাস্তব মাণ পাওয়া যায় না। \(Y\) অক্ষের উপর \(B(0, b)\) এবং \(\acute{B}(0, -b)\) বিন্দু দুইটি নেই। উল্লেখ্য যে, \(B\acute{B}\) অধিবৃত্তের অনুবন্ধী অক্ষ।
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) থেকে পাই, \(\frac{x^2}{a^2}=1+\frac{y^2}{b^2}\geq 1\)
অতএব, \(|x|\leq a\) অর্থাৎ \(x\leq +a\) এবং \(x\geq -a\) সুতরাং \(x=a\) এবং \(x=-a\) রেখা দুইটির মধ্যে লেখের কোনো বিন্দু নেই। প্রত্যেক অধিবৃত্তের তাই দুইটি শাখা রয়েছে। যদি \((x, y)\) লেখের উপর কোনো বিন্দু হয় তবে \((-x, y)\) বিন্দুটিও লেখের উপর অবস্থিত। অর্থাৎ, লেখটি \(Y\) অক্ষের সাপেক্ষে প্রতিসম। অনুরূপভাবে এটি দেখানো যায় যে, লেখটি \(X\) অক্ষের সাপেক্ষেও প্রতিসম। \(x\) এর মাণ বৃদ্ধির সাথে সাথে \(y\) এর মাণ অসীম পর্যন্ত বৃদ্ধি পায়। অতএব, অধিবৃত্ত দুইদিকে অসীমে বিস্তৃত হয়।
×
অধিবৃত্তের সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \) নির্ণয়।
আমরা জানি,
অধিবৃত্তের উপকেন্দ্র \(S(ae, 0)\)
অধিবৃত্তের দিকাক্ষের সমীকরণ \(x-\frac{a}{e}=0\)
অধিবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1+\frac{b^2}{a^2}}\)
\(\Rightarrow e^2=1+\frac{b^2}{a^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow e^2-1=\frac{b^2}{a^2}\)
\(\Rightarrow \frac{b^2}{a^2}=e^2-1\)
\(\therefore b^2=a^2(e^2-1) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-ae)^2+(y-0)^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1^2+0^2}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1+0}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(|x-\frac{a}{e}|\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(x-\frac{a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{ex-a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\frac{(ex-a)^2}{e^2}\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=(ex-a)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2x^2-2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex-a^2e^2-2aex+a^2\)
\(\Rightarrow -x^2(e^2-1)+y^2=a^2-a^2e^2\)
\(\Rightarrow -x^2(e^2-1)+y^2=-a^2(e^2-1)\)
\(\Rightarrow x^2(e^2-1)-y^2=a^2(e^2-1)\)
\(\Rightarrow \frac{x^2}{a^2}.a^2(e^2-1)-y^2=a^2(e^2-1)\)
\(\Rightarrow \frac{x^2}{a^2}.b^2-y^2=b^2\) ➜ \((1)\)-এর সাহায্যে \(\because b^2=a^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}.\frac{b^2}{b^2}-\frac{y^2}{b^2}=\frac{b^2}{b^2}\) ➜ উভয় পার্শে \(b^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।

অধিবৃত্তের উপকেন্দ্র \(S(ae, 0)\)
অধিবৃত্তের দিকাক্ষের সমীকরণ \(x-\frac{a}{e}=0\)
অধিবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1+\frac{b^2}{a^2}}\)
\(\Rightarrow e^2=1+\frac{b^2}{a^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow e^2-1=\frac{b^2}{a^2}\)
\(\Rightarrow \frac{b^2}{a^2}=e^2-1\)
\(\therefore b^2=a^2(e^2-1) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-ae)^2+(y-0)^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1^2+0^2}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1+0}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{|x-\frac{a}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(|x-\frac{a}{e}|\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(x-\frac{a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\left(\frac{ex-a}{e}\right)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2.\frac{(ex-a)^2}{e^2}\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=(ex-a)^2\)
\(\Rightarrow x^2-2aex+a^2e^2+y^2=e^2x^2-2aex+a^2\)
\(\Rightarrow x^2-e^2x^2+y^2=2aex-a^2e^2-2aex+a^2\)
\(\Rightarrow -x^2(e^2-1)+y^2=a^2-a^2e^2\)
\(\Rightarrow -x^2(e^2-1)+y^2=-a^2(e^2-1)\)
\(\Rightarrow x^2(e^2-1)-y^2=a^2(e^2-1)\)
\(\Rightarrow \frac{x^2}{a^2}.a^2(e^2-1)-y^2=a^2(e^2-1)\)
\(\Rightarrow \frac{x^2}{a^2}.b^2-y^2=b^2\) ➜ \((1)\)-এর সাহায্যে \(\because b^2=a^2(1-e^2) \)
\(\Rightarrow \frac{x^2}{a^2}.\frac{b^2}{b^2}-\frac{y^2}{b^2}=\frac{b^2}{b^2}\) ➜ উভয় পার্শে \(b^2\) ভাগ করে।
\(\therefore \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।
×
অধিবৃত্তের সমীকরণ \(\frac{y^2}{b^2}-\frac{x^2}{a^2}=1 \) নির্ণয়।
আমরা জানি,
অধিবৃত্তের উপকেন্দ্র \(S(0, be)\)
অধিবৃত্তের দিকাক্ষের সমীকরণ \(y-\frac{b}{e}=0\)
অধিবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1+\frac{a^2}{b^2}}\)
\(\Rightarrow e^2=1+\frac{a^2}{b^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow e^2-1=\frac{a^2}{b^2}\)
\(\Rightarrow \frac{a^2}{b^2}=e^2-1\)
\(\therefore a^2=b^2(e^2-1) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-0)^2+(y-be)^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0^2+1^2}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0+1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(|y-\frac{b}{e}|\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(y-\frac{b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{ey-b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\frac{(ey-b)^2}{e^2}\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=(ey-b)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2y^2-2bey+b^2\)
\(\Rightarrow x^2+y^2-e^2y^2=2bey-b^2e^2-2bey+b^2\)
\(\Rightarrow x^2-y^2(e^2-1)=b^2-b^2e^2\)
\(\Rightarrow x^2-\frac{y^2}{b^2}.b^2(e^2-1)=-b^2(e^2-1)\)
\(\Rightarrow x^2-\frac{y^2}{b^2}.a^2=-a^2\) ➜ \((1)\)-এর সাহায্যে \(\because a^2=b^2(e^2-1) \)
\(\Rightarrow \frac{x^2}{-a^2}-\frac{y^2}{b^2}.\frac{a^2}{-a^2}=\frac{-a^2}{-a^2}\) ➜ উভয় পার্শে \(-a^2\) ভাগ করে।
\(\Rightarrow -\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}-\frac{x^2}{a^2}=1\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।

অধিবৃত্তের উপকেন্দ্র \(S(0, be)\)
অধিবৃত্তের দিকাক্ষের সমীকরণ \(y-\frac{b}{e}=0\)
অধিবৃত্তের উপরিস্থিত যে কোনো বিন্দু \(P(x, y)\)
উৎকেন্দ্রিকতা \(e=\sqrt{1+\frac{a^2}{b^2}}\)
\(\Rightarrow e^2=1+\frac{a^2}{b^2}\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow e^2-1=\frac{a^2}{b^2}\)
\(\Rightarrow \frac{a^2}{b^2}=e^2-1\)
\(\therefore a^2=b^2(e^2-1) ........(1)\)
সংজ্ঞানুসারে,
\(PS=e.PM\)
\(\Rightarrow PS^2=e^2.PM^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow (x-0)^2+(y-be)^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0^2+1^2}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{0+1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{|y-\frac{b}{e}|}{\sqrt{1}}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(|y-\frac{b}{e}|\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(y-\frac{b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\left(\frac{ey-b}{e}\right)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2.\frac{(ey-b)^2}{e^2}\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=(ey-b)^2\)
\(\Rightarrow x^2+y^2-2bey+b^2e^2=e^2y^2-2bey+b^2\)
\(\Rightarrow x^2+y^2-e^2y^2=2bey-b^2e^2-2bey+b^2\)
\(\Rightarrow x^2-y^2(e^2-1)=b^2-b^2e^2\)
\(\Rightarrow x^2-\frac{y^2}{b^2}.b^2(e^2-1)=-b^2(e^2-1)\)
\(\Rightarrow x^2-\frac{y^2}{b^2}.a^2=-a^2\) ➜ \((1)\)-এর সাহায্যে \(\because a^2=b^2(e^2-1) \)
\(\Rightarrow \frac{x^2}{-a^2}-\frac{y^2}{b^2}.\frac{a^2}{-a^2}=\frac{-a^2}{-a^2}\) ➜ উভয় পার্শে \(-a^2\) ভাগ করে।
\(\Rightarrow -\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow \frac{y^2}{b^2}-\frac{x^2}{a^2}=1\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।
×
অধিবৃত্তের সমীকরণ \(\frac{(x-\alpha)^2}{a^2}-\frac{(y-\beta)^2}{b^2}=1\) নির্ণয়।
ধরি,
উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
আড় অক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
কনুবন্ধী অক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
অধিবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(X\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(X=CQ=EM=OM-OE=x-\alpha\)
এবং \(Y=PQ=PM-QM=PM-CE=y-\beta\)
\(P(X, Y)\) বিন্দুটি অধিবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}-\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}-\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।

উপবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
আড় অক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
কনুবন্ধী অক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
অধিবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(X\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(X=CQ=EM=OM-OE=x-\alpha\)
এবং \(Y=PQ=PM-QM=PM-CE=y-\beta\)
\(P(X, Y)\) বিন্দুটি অধিবৃত্তের আদর্শ সমীকরণ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{X^2}{a^2}-\frac{Y^2}{b^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(x-\alpha)^2}{a^2}-\frac{(y-\beta)^2}{b^2}=1\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।
×
অধিবৃত্তের সমীকরণ \(\frac{(y-\beta)^2}{b^2}-\frac{(x-\alpha)^2}{a^2}=1\) নির্ণয়।
ধরি,
অধিবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
আড় অক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
কনুবন্ধী অক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
অধিবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(Y\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(Y=CQ=EM=OM-OE=y-\beta\)
এবং \(X=PQ=PM-QM=PM-CE=x-\alpha\)
\(P(X, Y)\) বিন্দুটি অধিবৃত্তের আদর্শ সমীকরণ \(\frac{y^2}{b^2}-\frac{x^2}{a^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{Y^2}{b^2}-\frac{X^2}{a^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(y-\beta)^2}{b^2}-\frac{(x-\alpha)^2}{a^2}=1\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।

অধিবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
আড় অক্ষ \(B\acute B\), যা \(Y\) অক্ষের সমান্তরাল এবং \(B\acute B=2b\)।
কনুবন্ধী অক্ষ \(A\acute A\), যা \(X\) অক্ষের সমান্তরাল এবং \(A\acute A=2a\)।
অধিবৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) । \(Y\)-অক্ষের উপর \(PM\) লম্ব অঙ্কন করি যা বৃহদাক্ষকে \(Q\) বিন্দুতে ছেদ করে। \(C\)-কে মূলবিন্দু ধরে \(C\)-এর প্রেক্ষিতে \(P\) বিন্দুর স্থানাঙ্ক \((X, Y)\)
যখন, \(Y=CQ=EM=OM-OE=y-\beta\)
এবং \(X=PQ=PM-QM=PM-CE=x-\alpha\)
\(P(X, Y)\) বিন্দুটি অধিবৃত্তের আদর্শ সমীকরণ \(\frac{y^2}{b^2}-\frac{x^2}{a^2}=1\)-এর উপর অবস্থিত,
সুতরাং \(\frac{Y^2}{b^2}-\frac{X^2}{a^2}=1 .....(1)\)
\((1)\) নং সমীকরণে \(X\) ও \(Y\)-এর মান বসিয়ে,
\(\frac{(y-\beta)^2}{b^2}-\frac{(x-\alpha)^2}{a^2}=1\)
ইহাই নির্ণেয় অধিবৃত্তের সমীকরণ।
×
কোনো সরলরেখা অধিবৃত্তের স্পর্শক হওয়ার শর্ত, স্পর্শকের সমীকরণ এবং স্পর্শবিন্দুর স্থানাঙ্ক নির্ণয়।
মনে করি,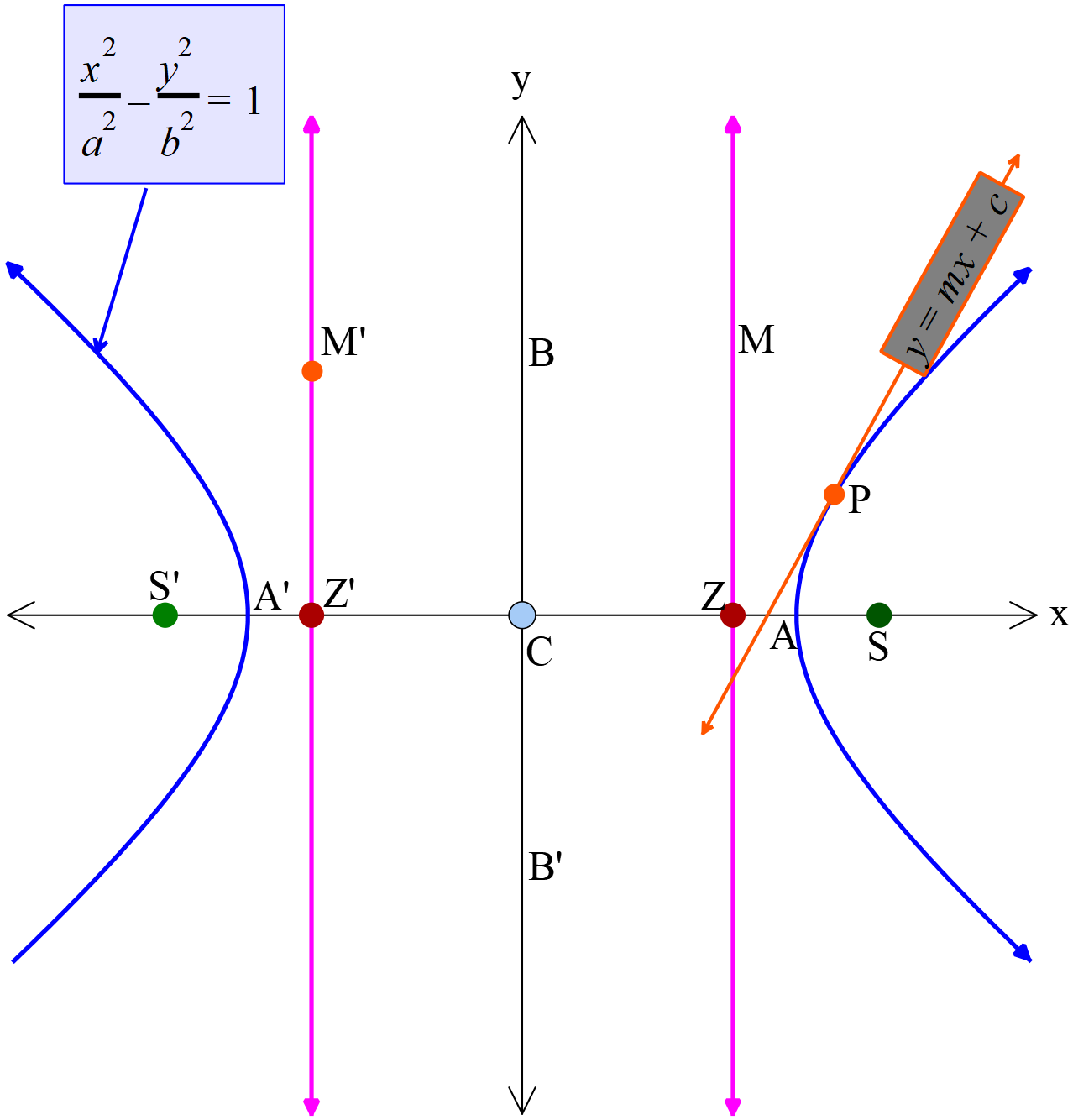
সরলরেখা ও অধিবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .........(1) \)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 .....(2) \)
\((1) \) ও \((2) \) নং হতে,
\(\frac{x^2}{a^2}-\frac{(mx+c)^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}-\frac{m^2x^2+2mcx+c^2}{b^2}=1\)
\(\Rightarrow b^2x^2-a^2(m^2x^2+2mcx+c^2)=a^2b^2\) ➜ উভয় পার্শে \(a^2b^2\) গুণ করে।
\(\Rightarrow b^2x^2-a^2m^2x^2-2a^2mcx-a^2c^2-a^2b^2=0\)
\(\Rightarrow (b^2-a^2m^2)x^2-2a^2mcx-a^2(b^2+c^2)=0 ...(3)\)
\((3)\) নং \(x\)-এর একটি দ্বিঘাত সমীকরণ। সুতরাং এর মূল দুইটি বাস্তব ও অসমান, বাস্তব ও সমান, অথবা কাল্পনিক হতে পারে। মূলদ্বয় \(x_1\) ও \(x_2\) হলে, \((1)\) নং সমীকরণ হতে \(y_1\) ও \(y_2\) পাওয়া যাবে। \(x_1\) ও \(x_2\)-এর মানের উপর ভিত্তি করে তিনটি ঘটনা ঘটতে পারে,
\((ii)\) \(x_1\) ও \(x_2\) বাস্তব ও সমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে স্পর্শ করবে।
\((iii)\) \(x_1\) ও \(x_2\) কাল্পনিক হলে, \((1)\) নং রেখা উপবৃত্তটিকে আদৌ স্পর্শ করবে না।
এখন,
\((ii)\) ঘটনা সত্য হলে, \((3)\) নং হতে \((-2a^2mc)^2=4.(b^2-a^2m^2)\times -a^2(b^2+c^2)\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow 4a^4m^2c^2=4(b^2-a^2m^2)\times -a^2(b^2+c^2)\)
\(\Rightarrow a^4m^2c^2=(b^2-a^2m^2)(-a^2b^2-a^2c^2)\)
\(\Rightarrow a^4m^2c^2=(-a^2b^2-a^2c^2)(b^2-a^2m^2)\)
\(\Rightarrow a^4m^2c^2=-a^2b^2(b^2-a^2m^2)-a^2c^2(b^2-a^2m^2)\)
\(\Rightarrow a^4m^2c^2=-a^2b^2(b^2-a^2m^2)-a^2c^2b^2+a^4c^2m^2\)
\(\Rightarrow a^4m^2c^2+a^2c^2b^2-a^4c^2m^2=-a^2b^2(b^2-a^2m^2)\)
\(\Rightarrow a^2c^2b^2=-a^2b^2(b^2-a^2m^2)\)
\(\Rightarrow c^2=-(b^2-a^2m^2)\) ➜ উভয় পার্শে \(a^2b^2\) ভাগ করে।
\(\Rightarrow c^2=a^2m^2-b^2\)
\(\therefore c=\pm \sqrt{(a^2m^2-b^2)}\) ইহাই নির্ণেয় শর্ত।
আবার,
\(c=\pm \sqrt{(a^2m^2-b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=mx \pm \sqrt{(a^2m^2-b^2)}\) ইহাই নির্ণেয় স্পর্শকের সমীকরণ।
আবার,
\((3)\) নং সমীকরণ হতে সমান মূলদ্বয়ের মান \(x=\frac{2a^2mc}{2(a^2m^2-b^2)}\) ➜ \(ax^2+bx+c=0\) সমীকরণের সমাণ মূলদ্বয়ের মাণ \(\frac{-b}{2a}\)
\(\Rightarrow x=\frac{a^2mc}{a^2m^2-b^2}\)
\(\Rightarrow x=\frac{a^2m\times \pm \sqrt{(a^2m^2-b^2)}}{a^2m^2-b^2}\) ➜ \(\because c=\pm \sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow x=\frac{\pm a^2m\sqrt{(a^2m^2-b^2)}}{\sqrt{(a^2m^2-b^2)}\times \sqrt{(a^2m^2-b^2)}}\)
\(\therefore x=\frac{\pm a^2m}{\sqrt{(a^2m^2-b^2)}}\)
আবার,
\(x=\frac{a^2m}{\sqrt{(a^2m^2-b^2)}}\) এবং \(c=-\sqrt{(a^2m^2-b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{a^2m}{\sqrt{(a^2m^2-b^2)}}-\sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow y=\frac{a^2m^2}{\sqrt{(a^2m^2-b^2)}}-\sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow y=\frac{a^2m^2-a^2m^2+b^2}{\sqrt{(a^2m^2-b^2)}}\)
\(\therefore y=\frac{b^2}{\sqrt{(a^2m^2-b^2)}}\)
আবার,
\(x=\frac{-a^2m}{\sqrt{(a^2m^2-b^2)}}\) এবং \(c=\sqrt{(a^2m^2-b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{-a^2m}{\sqrt{(a^2m^2-b^2)}}+\sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2}{\sqrt{(a^2m^2-b^2)}}+\sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2+a^2m^2-b^2}{\sqrt{(a^2m^2-b^2)}}\)
\(\therefore y=\frac{-b^2}{\sqrt{(a^2m^2-b^2)}}\)
\(\therefore y\)-এর এই দুই মাণ সমন্বয় করে পাই,
\(y=\frac{\pm b^2}{\sqrt{(a^2m^2-b^2)}}\)
অতএব, স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2-b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2-b^2)}}\right)\)

সরলরেখা ও অধিবৃত্তটির সমীকরণ যথাক্রমে
\(y=mx+c .........(1) \)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 .....(2) \)
\((1) \) ও \((2) \) নং হতে,
\(\frac{x^2}{a^2}-\frac{(mx+c)^2}{b^2}=1\)
\(\Rightarrow \frac{x^2}{a^2}-\frac{m^2x^2+2mcx+c^2}{b^2}=1\)
\(\Rightarrow b^2x^2-a^2(m^2x^2+2mcx+c^2)=a^2b^2\) ➜ উভয় পার্শে \(a^2b^2\) গুণ করে।
\(\Rightarrow b^2x^2-a^2m^2x^2-2a^2mcx-a^2c^2-a^2b^2=0\)
\(\Rightarrow (b^2-a^2m^2)x^2-2a^2mcx-a^2(b^2+c^2)=0 ...(3)\)
\((3)\) নং \(x\)-এর একটি দ্বিঘাত সমীকরণ। সুতরাং এর মূল দুইটি বাস্তব ও অসমান, বাস্তব ও সমান, অথবা কাল্পনিক হতে পারে। মূলদ্বয় \(x_1\) ও \(x_2\) হলে, \((1)\) নং সমীকরণ হতে \(y_1\) ও \(y_2\) পাওয়া যাবে। \(x_1\) ও \(x_2\)-এর মানের উপর ভিত্তি করে তিনটি ঘটনা ঘটতে পারে,
যেমনঃ
\((i)\) \(x_1\) ও \(x_2\) বাস্তব ও অসমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে দুইটি ভিন্ন বিন্দুতে ছেদ করবে।\((ii)\) \(x_1\) ও \(x_2\) বাস্তব ও সমান হলে, \((1)\) নং রেখা উপবৃত্তটিকে স্পর্শ করবে।
\((iii)\) \(x_1\) ও \(x_2\) কাল্পনিক হলে, \((1)\) নং রেখা উপবৃত্তটিকে আদৌ স্পর্শ করবে না।
এখন,
\((ii)\) ঘটনা সত্য হলে, \((3)\) নং হতে \((-2a^2mc)^2=4.(b^2-a^2m^2)\times -a^2(b^2+c^2)\) ➜ \(ax^2+bx+c=0\) সমীকরণের মূলদ্বয় সমাণ হওয়ার শর্ত, \(b^2=4ac\)
\(\Rightarrow 4a^4m^2c^2=4(b^2-a^2m^2)\times -a^2(b^2+c^2)\)
\(\Rightarrow a^4m^2c^2=(b^2-a^2m^2)(-a^2b^2-a^2c^2)\)
\(\Rightarrow a^4m^2c^2=(-a^2b^2-a^2c^2)(b^2-a^2m^2)\)
\(\Rightarrow a^4m^2c^2=-a^2b^2(b^2-a^2m^2)-a^2c^2(b^2-a^2m^2)\)
\(\Rightarrow a^4m^2c^2=-a^2b^2(b^2-a^2m^2)-a^2c^2b^2+a^4c^2m^2\)
\(\Rightarrow a^4m^2c^2+a^2c^2b^2-a^4c^2m^2=-a^2b^2(b^2-a^2m^2)\)
\(\Rightarrow a^2c^2b^2=-a^2b^2(b^2-a^2m^2)\)
\(\Rightarrow c^2=-(b^2-a^2m^2)\) ➜ উভয় পার্শে \(a^2b^2\) ভাগ করে।
\(\Rightarrow c^2=a^2m^2-b^2\)
\(\therefore c=\pm \sqrt{(a^2m^2-b^2)}\) ইহাই নির্ণেয় শর্ত।
আবার,
\(c=\pm \sqrt{(a^2m^2-b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=mx \pm \sqrt{(a^2m^2-b^2)}\) ইহাই নির্ণেয় স্পর্শকের সমীকরণ।
আবার,
\((3)\) নং সমীকরণ হতে সমান মূলদ্বয়ের মান \(x=\frac{2a^2mc}{2(a^2m^2-b^2)}\) ➜ \(ax^2+bx+c=0\) সমীকরণের সমাণ মূলদ্বয়ের মাণ \(\frac{-b}{2a}\)
\(\Rightarrow x=\frac{a^2mc}{a^2m^2-b^2}\)
\(\Rightarrow x=\frac{a^2m\times \pm \sqrt{(a^2m^2-b^2)}}{a^2m^2-b^2}\) ➜ \(\because c=\pm \sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow x=\frac{\pm a^2m\sqrt{(a^2m^2-b^2)}}{\sqrt{(a^2m^2-b^2)}\times \sqrt{(a^2m^2-b^2)}}\)
\(\therefore x=\frac{\pm a^2m}{\sqrt{(a^2m^2-b^2)}}\)
আবার,
\(x=\frac{a^2m}{\sqrt{(a^2m^2-b^2)}}\) এবং \(c=-\sqrt{(a^2m^2-b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{a^2m}{\sqrt{(a^2m^2-b^2)}}-\sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow y=\frac{a^2m^2}{\sqrt{(a^2m^2-b^2)}}-\sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow y=\frac{a^2m^2-a^2m^2+b^2}{\sqrt{(a^2m^2-b^2)}}\)
\(\therefore y=\frac{b^2}{\sqrt{(a^2m^2-b^2)}}\)
আবার,
\(x=\frac{-a^2m}{\sqrt{(a^2m^2-b^2)}}\) এবং \(c=\sqrt{(a^2m^2-b^2)}\), \((1)\) নং সমীকরণে বসিয়ে
\(y=m\frac{-a^2m}{\sqrt{(a^2m^2-b^2)}}+\sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2}{\sqrt{(a^2m^2-b^2)}}+\sqrt{(a^2m^2-b^2)}\)
\(\Rightarrow y=\frac{-a^2m^2+a^2m^2-b^2}{\sqrt{(a^2m^2-b^2)}}\)
\(\therefore y=\frac{-b^2}{\sqrt{(a^2m^2-b^2)}}\)
\(\therefore y\)-এর এই দুই মাণ সমন্বয় করে পাই,
\(y=\frac{\pm b^2}{\sqrt{(a^2m^2-b^2)}}\)
অতএব, স্পর্শবিন্দুর স্থানাঙ্ক \(\left(\frac{\pm a^2m}{\sqrt{(a^2m^2-b^2)}}, \frac{\pm b^2}{\sqrt{(a^2m^2-b^2)}}\right)\)
সাধারণ দ্বিঘাত সমীকরণ
General quadratic equation
\(a, \ h\) ও \(b\) এর প্রত্যেকটির মাণ শূন্য না হলে \(ax^2+2hxy+by^2+2gx+2fy+c=0\) সমীকরণটিকে সাধারণ দ্বিঘাত সমীকরণ বলা হয়। এই সাধারণ দ্বিঘাত সমীকরণটি ভিন্ন ভিন্ন নির্দিষ্ট শর্ত সাপেক্ষে যুগল সরলরেখা, বৃত্ত ও কণিক সূচিত করে।
কনিকের সমীকরণ শনাক্তকরণ
Identification of Conic's equation
কনিকের সাধারণ সমীকরণ হতে বৃত্ত, পরাবৃত্ত, উপবৃত্ত, অধিবৃত্ত এবং যুগল সরলরেখা শনাক্তকরণ।
কনিকের সাধারণ সমীকরণ \(ax^2+2hxy+by^2+2gx+2fy+c=0\)
এখানে, \(\Delta \equiv abc+2fgh-af^2-bg^2-ch^2\)
কনিকের সাধারণ সমীকরণ \(ax^2+2hxy+by^2+2gx+2fy+c=0\)
এখানে, \(\Delta \equiv abc+2fgh-af^2-bg^2-ch^2\)
- \(\Delta\ne{0},\) \(a=b\) এবং \(h=0\) হলে, কনিকটি একটি বৃত্ত নির্দেশ করবে।
- \(\Delta\ne{0}, \ ab-h^2=0\) এবং \(a+b\ne{0}\) হলে, কনিকটি একটি পরাবৃত্ত নির্দেশ করবে।
- \(\Delta\ne{0}, \ ab-h^2\gt{0}\) এবং \(a+b\ne{0}\) হলে, কনিকটি একটি উপবৃত্ত নির্দেশ করবে।
- \(\Delta\ne{0}, \ ab-h^2\lt{0}\) এবং \(a+b\ne{0}\) হলে, কনিকটি একটি অধিবৃত্ত নির্দেশ করবে।
- \(\Delta\ne{0}, \ ab-h^2\lt{0}\) এবং \(a+b=0\) হলে, কনিকটি একটি আয়াতাকার অধিবৃত্ত নির্দেশ করবে।
- \(\Delta=0\) হলে, কনিকটি একজোড়া সরলরেখা নির্দেশ করবে।
স্পর্শ জ্য
Chord of Contact
কোনো কণিকের বহিঃস্থ একটি বিন্দু \(P(x_{1}, y_{1})\) হতে উহার উপর দুইটি স্পর্শক অঙ্কন করা যায়। স্পর্শক দুইটির স্পর্শবিন্দুদ্বয়ের সংযোগ সরলরেখাকে স্পর্শ জ্যা (Chord of Contact) বলা হয়।
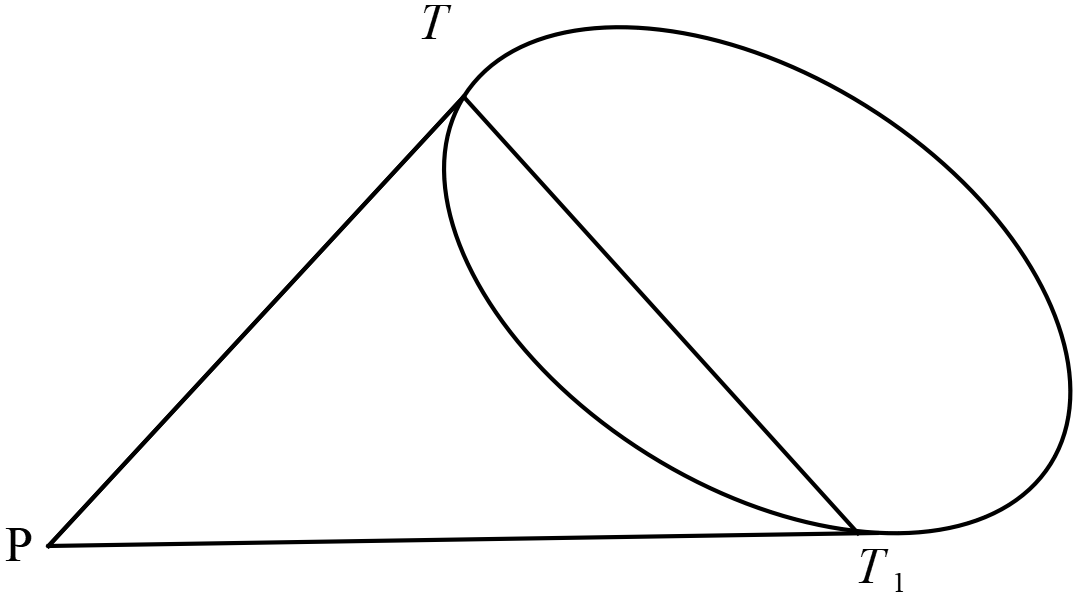
মনে করি,
স্পর্শকদ্বয় \(PT\) এবং \(PT^{\prime}\) যারা প্রদত্ত কণিককে \(T\) ও \(T^{\prime}\) বিন্দুতে স্পর্শ করে। স্পর্শ বিন্দুদ্বয়ের সংযোগ সরলরেখা \(TT^{\prime}\) কে \(P\) হতে কণিকের উপর অঙ্কিত স্পর্শকের স্পর্শ জ্যা বলা হয়।

মনে করি,
স্পর্শকদ্বয় \(PT\) এবং \(PT^{\prime}\) যারা প্রদত্ত কণিককে \(T\) ও \(T^{\prime}\) বিন্দুতে স্পর্শ করে। স্পর্শ বিন্দুদ্বয়ের সংযোগ সরলরেখা \(TT^{\prime}\) কে \(P\) হতে কণিকের উপর অঙ্কিত স্পর্শকের স্পর্শ জ্যা বলা হয়।
পোল ও পোলার
Poles and polars
পোল ও পোলারঃ একটি নির্দিষ্ট বিন্দু দিয়ে কোনো কণিকের যে সব জ্যা অতিক্রম করে তাদের প্রান্তবিন্দুতে অঙ্কিত যুগল স্পর্শকগুলোর ছেদবিন্দুর সঞ্চারপথকে কণিকটির প্রেক্ষিতে ঐ বিন্দুর পোলার বলা হয়। প্রদত্ত বিন্দুটিকে এই পোলারের পোল বলে।
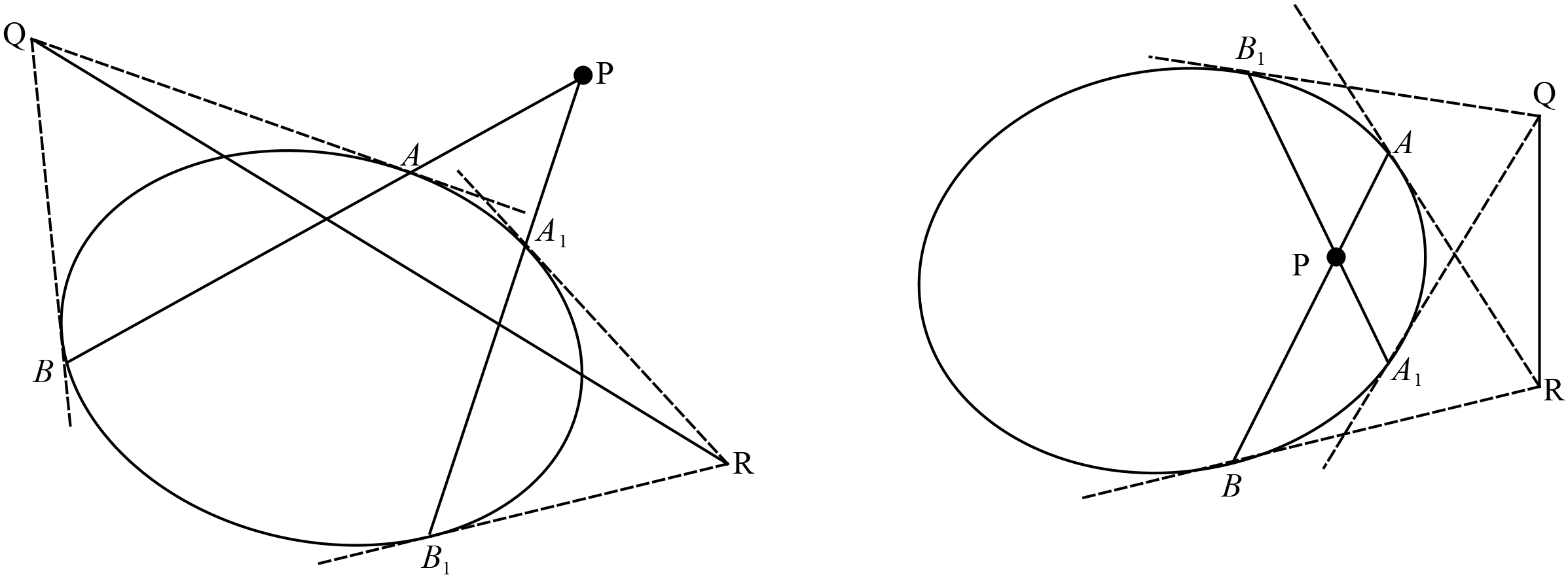
দ্রষ্টব্যঃ কণিকের পোলার ও স্পর্শকের সমীকরণের আকার একই হলেও ইহারা মূলত ভিন্ন। স্পর্শকের জন্য \((x_{1}, y_{1})\) বিন্দুটি অবশ্যই কণিকের উপর অবস্থিত কিন্তু পোলার রেখার জন্য \((x_{1}, y_{1})\) বিন্দুটি কণিকের উপর হতে হবে এমন নয়, কণিকের বাইরে এবং ভিতরে অবস্থান করতে পারে। তবে বিন্দুটি কণিকের উপর অবস্থিত হলে স্পর্শক ও পোলার সমপতিত হয়।

দ্রষ্টব্যঃ কণিকের পোলার ও স্পর্শকের সমীকরণের আকার একই হলেও ইহারা মূলত ভিন্ন। স্পর্শকের জন্য \((x_{1}, y_{1})\) বিন্দুটি অবশ্যই কণিকের উপর অবস্থিত কিন্তু পোলার রেখার জন্য \((x_{1}, y_{1})\) বিন্দুটি কণিকের উপর হতে হবে এমন নয়, কণিকের বাইরে এবং ভিতরে অবস্থান করতে পারে। তবে বিন্দুটি কণিকের উপর অবস্থিত হলে স্পর্শক ও পোলার সমপতিত হয়।
ব্যাস, অনুবন্ধী ব্যাস এবং নির্দেশক (নিয়ত) বৃত্ত
Diameter, relative Diameter and Destiny circle
ব্যাসঃ একটি কণিকের একশ্রেণী সমান্তরাল জ্যা-এর মধ্যবিন্দুসমূহের সঞ্চার পথকে কণিকের একটি ব্যাস বলে।
অনুবন্ধী ব্যাসঃ একটি কণিকের দুইটি ব্যাস যদি এরূপ হয় যে ওদের প্রত্যেকে অপরের সমান্তরাল জ্যাসমূহকে সমদ্বিখণ্ডিত করে তবে তাদেরকে ঐ কণিকের অনুবন্ধী ব্যাস বলে।
অনুবন্ধী রেখাঃ দুইটি সরলরেখা যদি এরূপ হয় যে প্রত্যেকের পোল অপরের ওপর থাকে তবে তাদেরকে অনুবন্ধী রেখা বলে।
নির্দেশক (নিয়ত) বৃত্তঃ কোনো কণিকের পরস্পর লম্ব দুইটি স্পর্শকের ছেদবিন্দুর সঞ্চার পথকে কণিকটির নির্দেশক (নিয়ত) বৃত্ত বলা হয়। এটিকে চালক বৃত্ত ও বলা হয়ে থাকে।
অনুবন্ধী ব্যাসঃ একটি কণিকের দুইটি ব্যাস যদি এরূপ হয় যে ওদের প্রত্যেকে অপরের সমান্তরাল জ্যাসমূহকে সমদ্বিখণ্ডিত করে তবে তাদেরকে ঐ কণিকের অনুবন্ধী ব্যাস বলে।
অনুবন্ধী রেখাঃ দুইটি সরলরেখা যদি এরূপ হয় যে প্রত্যেকের পোল অপরের ওপর থাকে তবে তাদেরকে অনুবন্ধী রেখা বলে।
নির্দেশক (নিয়ত) বৃত্তঃ কোনো কণিকের পরস্পর লম্ব দুইটি স্পর্শকের ছেদবিন্দুর সঞ্চার পথকে কণিকটির নির্দেশক (নিয়ত) বৃত্ত বলা হয়। এটিকে চালক বৃত্ত ও বলা হয়ে থাকে।
পরাবৃত্তে উপকেন্দ্রের অবস্থান
Location of Focus on parabola
চালক বৃত্তের সমীকরণ \((ab-h^2)(x^2+y^2)+2(bg-hf)x+2(af-hg)y+\) \((a+b)c-g^2-f^2=0\) কে নিম্নলিখিতভাবে প্রকাশ করা যায়
\((ab-h^2)(x^2+y^2)-2(hf-bg)x-2(hg-af)y+\) \((bc-f^2)+(ca-g^2)=0\)
\(\therefore C(x^2+y^2)-2Gx-2Fy+A+B=0 .........(1)\)
যেখানে, \(A, \ B, \ C, \ F, \ G \) হলো
\(\Delta=\left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c \end{array}\right|\) নির্ণায়কের যথাক্রমে
\(a, \ b, \ c, \ f, \ g \) এর সহগূণক।
অর্থাৎ, \(A=bc-f^2, \ B=ca-g^2, \ C=ab-h^2, \ F=gh-af,\) \(G=hf-bg \)
এখন, \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকটি যদি একটি পরাবৃত্ত নির্দেশ করে তবে,
\(C=ab-h^2=0\) হয়।
ফলে, \((1)\) নং সমীকরণটি দাঁড়ায়
\(-2Gx-2Fy+A+B=0\)
\(\therefore 2Gx+2Fy-(A+B)=0\)
যা, পরাবৃত্তটির নিয়ামক নির্দেশ করে।
আবার, পরাবৃত্তটির ফোকাস \(S(x_{1}, y_{1})\)
\(\frac{ax_{1}+hy_{1}+g}{2G}=\frac{hx_{1}+by_{1}+f}{2F}=\frac{gx_{1}+fy_{1}+c}{-(A+B)}\)
এর উপর অবস্থান করে।
\((ab-h^2)(x^2+y^2)-2(hf-bg)x-2(hg-af)y+\) \((bc-f^2)+(ca-g^2)=0\)
\(\therefore C(x^2+y^2)-2Gx-2Fy+A+B=0 .........(1)\)
যেখানে, \(A, \ B, \ C, \ F, \ G \) হলো
\(\Delta=\left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c \end{array}\right|\) নির্ণায়কের যথাক্রমে
\(a, \ b, \ c, \ f, \ g \) এর সহগূণক।
অর্থাৎ, \(A=bc-f^2, \ B=ca-g^2, \ C=ab-h^2, \ F=gh-af,\) \(G=hf-bg \)
এখন, \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকটি যদি একটি পরাবৃত্ত নির্দেশ করে তবে,
\(C=ab-h^2=0\) হয়।
ফলে, \((1)\) নং সমীকরণটি দাঁড়ায়
\(-2Gx-2Fy+A+B=0\)
\(\therefore 2Gx+2Fy-(A+B)=0\)
যা, পরাবৃত্তটির নিয়ামক নির্দেশ করে।
আবার, পরাবৃত্তটির ফোকাস \(S(x_{1}, y_{1})\)
\(\frac{ax_{1}+hy_{1}+g}{2G}=\frac{hx_{1}+by_{1}+f}{2F}=\frac{gx_{1}+fy_{1}+c}{-(A+B)}\)
এর উপর অবস্থান করে।
কেন্দ্রীয় কণিকে উপকেন্দ্রের অবস্থান
Location of Focus on central conic
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) একটি কেন্দ্রীয় কনিক যার ফোকাস \(S(x_{1}, y_{1})\)
এই ক্ষেত্রে ফোকাস \(S(x_{1}, y_{1})\)
\(\frac{(ax_{1}+hy_{1}+g)^2-(hx_{1}+by_{1}+f)^2}{a-b}=\frac{(ax_{1}+hy_{1}+g)(hx_{1}+by_{1}+f)}{h}=\) \(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
এর উপর অবস্থান করে।
এই ক্ষেত্রে ফোকাস \(S(x_{1}, y_{1})\)
\(\frac{(ax_{1}+hy_{1}+g)^2-(hx_{1}+by_{1}+f)^2}{a-b}=\frac{(ax_{1}+hy_{1}+g)(hx_{1}+by_{1}+f)}{h}=\) \(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
এর উপর অবস্থান করে।
অসীমতট
Asymptote
অসীমতটঃ যদি কোনো সরলরেখা একটি অধিবৃত্তের অসীমে অবস্থিত একটি বিন্দুতে মিলিত হয় কিন্তু সরলরেখাটি সম্পূর্ণ অসীমে অবস্থান করে না, তবে এরূপ সরলরেখাকে অধিবৃত্তের অসীমতট বলা হয়।
কণিক শ্রেণী
System of conic
কণিক শ্রেণীঃ যদি \(S=0\) ও \(S^{\prime}\) দুইটি কণিকের সমীকরণ হয় তবে ধ্রুবক \(\lambda\) এর যে কোনো মানের জন্য \(S+\lambda{S^{\prime}}=0\) সমীকরণটি একটি কণিক নির্দেশ করবে।
\(S=0\) এবং \(S^{\prime}\) এর উভয়কে সিদ্ধ করে এরূপ প্রতিটি বিন্দুই \(S+\lambda{S^{\prime}}=0\) সমীকরণকে সিদ্ধ করবে। কাজেই \(\lambda\) এর যেকোনো মানের জন্য \(S+\lambda{S^{\prime}}=0\) সমীকরণটি \(S=0\) ও \(S^{\prime}\) কণিক দুইটির ছেদবিন্দুগামী একটি কণিক নির্দেশ করে। \(\lambda\) এর বিভিন্ন মানের জন্য এটা বিভিন্ন কণিক নির্দেশ করে।
\(\therefore S=0\) ও \(S^{\prime}\) এর দ্বারা নির্ণীত কণিক শ্রেণীর সমীকরণ,
\(S+\lambda{S^{\prime}}=0\)
\(S=0\) এবং \(S^{\prime}\) এর উভয়কে সিদ্ধ করে এরূপ প্রতিটি বিন্দুই \(S+\lambda{S^{\prime}}=0\) সমীকরণকে সিদ্ধ করবে। কাজেই \(\lambda\) এর যেকোনো মানের জন্য \(S+\lambda{S^{\prime}}=0\) সমীকরণটি \(S=0\) ও \(S^{\prime}\) কণিক দুইটির ছেদবিন্দুগামী একটি কণিক নির্দেশ করে। \(\lambda\) এর বিভিন্ন মানের জন্য এটা বিভিন্ন কণিক নির্দেশ করে।
\(\therefore S=0\) ও \(S^{\prime}\) এর দ্বারা নির্ণীত কণিক শ্রেণীর সমীকরণ,
\(S+\lambda{S^{\prime}}=0\)
অনুবন্ধী অধিবৃত্ত
Conjugate Hyperbola
অনুবন্ধী অধিবৃত্তঃ একটি অধিবৃত্তের আড় অক্ষ ও অনুবন্ধী অক্ষ যথাক্রমে \(x\) ও \(y\) অক্ষ বরাবর বা এদের সমান্তরাল আবার, অপর একটি অধিবৃত্তের আড় অক্ষ ও অনুবন্ধী অক্ষ যথাক্রমে \(y\) ও \(x\) অক্ষ বরাবর বা এদের সমান্তরাল হয় তবে অধিবৃত্তদ্বয় পরস্পরের অনুবন্ধী হবে।
অধিবৃত্তের সমীকরণঃ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) অনুবন্ধী অধিবৃত্তের সমীকরণঃ \(\frac{y^2}{b^2}-\frac{x^2}{a^2}=1\)
অধিবৃত্তের সমীকরণঃ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) অনুবন্ধী অধিবৃত্তের সমীকরণঃ \(\frac{y^2}{b^2}-\frac{x^2}{a^2}=1\)
অসীমতট এবং অনুবন্ধী অধিবৃত্তের মধ্যে সম্পর্ক
Relation between Asymptote and Conjugate Hyperbola
অধিবৃত্তের সমীকরণঃ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ......(1)\)
অসীমতটের সমীকরণঃ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=0 .......(2)\)
অনুবন্ধী অধিবৃত্তের সমীকরণঃ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1 .......(3)\)
ইহা স্পষ্ট যে \((1)\) ও \((2)\) নং সমীকরণের মধ্যে যে ধ্রুবকের পার্থক্য, \((2)\) ও \((3)\) নং সমীকরণের মধ্যে সেই একই ধ্রুবকের পার্থক্য। মূলবিন্দু স্থানান্তর বা অক্ষদ্বয়কে আবর্তন করলে উপরোক্ত তিনটি সমীকরণের বামপক্ষ একই আকারে রূপান্তরিত হবে এবং ডানপক্ষের ধ্রুবক গুলির এরূপ পরিবর্তন হবে, যাতে এদের সম্পর্ক পূর্বের ন্যায় থাকে। সুতরাং অধিবৃত্তের সমীকরণ যাই হোক না কেন, এর অসীমতটের সমীকরণের সহিত কেবলমাত্র একটি ধ্রুবকের পার্থক্য থাকবে এবং অসীমতটের সমীকরণের সহিত অনুবন্ধী অধিবৃত্তের সমীকরণেরও একই পার্থক্য থাকবে।
ইহা স্পষ্ট যে \((1)\) ও \((2)\) নং সমীকরণের মধ্যে যে ধ্রুবকের পার্থক্য, \((2)\) ও \((3)\) নং সমীকরণের মধ্যে সেই একই ধ্রুবকের পার্থক্য। মূলবিন্দু স্থানান্তর বা অক্ষদ্বয়কে আবর্তন করলে উপরোক্ত তিনটি সমীকরণের বামপক্ষ একই আকারে রূপান্তরিত হবে এবং ডানপক্ষের ধ্রুবক গুলির এরূপ পরিবর্তন হবে, যাতে এদের সম্পর্ক পূর্বের ন্যায় থাকে। সুতরাং অধিবৃত্তের সমীকরণ যাই হোক না কেন, এর অসীমতটের সমীকরণের সহিত কেবলমাত্র একটি ধ্রুবকের পার্থক্য থাকবে এবং অসীমতটের সমীকরণের সহিত অনুবন্ধী অধিবৃত্তের সমীকরণেরও একই পার্থক্য থাকবে।
অনুসিদ্ধান্ত
Postulate
অধিবৃত্তের সমীকরণঃ \(ax^2+2hxy+by^2+2gx+2fy+k_{1}=0 ....(1)\)
অসীমতটের সমীকরণঃ \(ax^2+2hxy+by^2+2gx+2fy+k_{2}=0 ....(2)\)
অনুবন্ধী অধিবৃত্তের সমীকরণঃ \(ax^2+2hxy+by^2+2gx+2fy+k_{3}=0 ....(3)\)
\((1)\) ও \((2)\) নং সমীকরণের মধ্যে ধ্রুবকের পার্থক্য \(=k_{1}-k_{2}\)
\((2)\) ও \((3)\) নং সমীকরণের মধ্যে ধ্রুবকের পার্থক্য \(=k_{2}-k_{3}\)
\(\therefore k_{1}-k_{2}=k_{2}-k_{3}\)
\(\Rightarrow k_{1}+k_{3}=2k_{2}\)
\(\therefore 2k_{2}=k_{1}+k_{3}\)
\(k_{1}=2k_{2}-k_{3}\) \(k_{2}=\frac{1}{2}(k_{1}+k_{3})\) \(k_{3}=2k_{2}-k_{1}\) অনুবন্ধী অধিবৃত্তের সমীকরণ, \(2\times\)( অসীমতটের সমীকরণ ) - অধিবৃত্তের সমীকরণ \(=0\)
\((1)\) ও \((2)\) নং সমীকরণের মধ্যে ধ্রুবকের পার্থক্য \(=k_{1}-k_{2}\)
\((2)\) ও \((3)\) নং সমীকরণের মধ্যে ধ্রুবকের পার্থক্য \(=k_{2}-k_{3}\)
\(\therefore k_{1}-k_{2}=k_{2}-k_{3}\)
\(\Rightarrow k_{1}+k_{3}=2k_{2}\)
\(\therefore 2k_{2}=k_{1}+k_{3}\)
\(k_{1}=2k_{2}-k_{3}\) \(k_{2}=\frac{1}{2}(k_{1}+k_{3})\) \(k_{3}=2k_{2}-k_{1}\) অনুবন্ধী অধিবৃত্তের সমীকরণ, \(2\times\)( অসীমতটের সমীকরণ ) - অধিবৃত্তের সমীকরণ \(=0\)
সাধারণ দ্বিঘাত সমীকরণ সম্পর্কিত উপপাদ্য
Theorems relating to general quadratic equations
প্রমাণ কর যে, একটি কণিকের সমীকরণ সর্বদাই একটি দ্বিঘাত সমীকরণ কিন্তু বিপরীতক্রমে এটি সর্বদা সত্য নয়।
কোনো কণিকের উৎকেন্দ্রতা \(e\) উপকেন্দ্র \(S(\alpha, \beta)\) এবং নিয়ামক রেখার সমীকরণ \(lx+my+n=0\) হলে কণিকের সমীকরণ নির্ণয় কর।
উত্তরঃ\((l^2+m^2-e^2l^2)x^2-2lme^2xy+(l^2+m^2-e^2m^2)y^2-\) \(2\{\alpha(l^2+m^2)+e^2ln\}x-2\{\beta(l^2+m^2)+e^2mn\}y+\) \((l^2+m^2)(\alpha^2+\beta^2)-e^2n^2=0\)
যে শর্তে সাধারণ দ্বিঘাত সমীকরণ কণিক প্রকাশ করে তা নির্ণয় কর।
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের কেন্দ্র
\(\left(\frac{hf-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কেন্দ্রিক কণিকের প্রমাণ আকার
\(a^{\prime}x^2+b^{\prime}y^2+\frac{\Delta}{ab-h^2}=0\)
\(Ax^2+2Hxy+By^2=1\) কণিকের ক্ষেত্রেঃ
যদি কণিকের অর্ধাক্ষের দৈর্ঘ্য \(r\) হয় তবে, \((AB-H^2)r^4-(A+B)r^2+1=0\) \(r_{1}\) এবং \(r_{2}\) উভয়ে ধনাত্মক হলে কণিকটি উপবৃত্ত হবে সেক্ষেত্রেঃ
বৃহৎ অক্ষের দৈর্ঘ্য \(=2r_{1}, \ \ r_{1}>r_{2}\).png)
ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=2r_{2}, \ \ r_{1}>r_{2}\)
\(r_{1}\) এবং \(r_{2}\) এর একটি ধনাত্মক এবং অপরটি ঋণাত্মক হলে কণিকটি অধিবৃত্ত হবে সেক্ষেত্রেঃ
আড় অক্ষের দৈর্ঘ্য \(=2r_{1}\)
অনুবন্ধী অক্ষের দৈর্ঘ্য \(=2\sqrt{|r_{2}^2|}\)
উভয় ক্ষেত্রে উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2r_{2}^2}{r_{1}}\right|\)
উভয় ক্ষেত্রে বিকেন্দ্রিকতা \(e=\sqrt{1-\frac{r_{2}^2}{r_{1}^2}}, \ \ r_{1}>r_{2}\)
বৃহৎ অক্ষের সমীকরণ \(\left(A-\frac{1}{r_{1}^2}\right)x+Hy=0\) ক্ষুদ্রাক্ষের সমীকরণ \(\left(A-\frac{1}{r_{2}^2}\right)x+Hy=0\) শীর্ষদ্বয়ের স্থানাঙ্ক \(A(\alpha+r_{1}\cos{\theta}, \beta+r_{1}\sin{\theta})\) এবং \(A^{\prime}(\alpha-r_{1}\cos{\theta}, \beta-r_{1}\sin{\theta})\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\) ফোকাসদ্বয়ের স্থানাঙ্ক \(S(\alpha+r_{1}e\cos{\theta}, \beta+r_{1}e\sin{\theta})\) এবং \(S^{\prime}(\alpha-r_{1}e\cos{\theta}, \beta-r_{1}e\sin{\theta})\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\) নিয়ামকদ্বয়ের পাদবিন্দুর স্থানাঙ্ক
\(Z\left(\alpha+\frac{r_{1}}{e}\cos{\theta}, \beta+\frac{r_{1}}{e}\sin{\theta}\right)\) এবং \(Z^{\prime}\left(\alpha-\frac{r_{1}}{e}\cos{\theta}, \beta-\frac{r_{1}}{e}\sin{\theta}\right)\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কেন্দ্রবিহীন কণিকের প্রমাণ আকার
\(y^2=4a^{\prime}x\)
যেখানে, \(a^{\prime}=\frac{\sqrt{(k\sqrt{a}-g)^2+(k\sqrt{b}-f)^2}}{2(a+b)}\)
এবং \(k=\frac{g\sqrt{a}+f\sqrt{b}}{a+b}\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের উপরস্থ \((x_{1}, y_{1})\) বিন্দুতে এর স্পর্শকের সমীকরণ
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+\) \(f(y+y_{1})+c=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের উপরস্থ \((x_{1}, y_{1})\) বিন্দুতে এর অভিলম্বের সমীকরণ
\(\frac{x-x_{1}}{ax_{1}+hy_{1}+g}=\frac{y-y_{1}}{hx_{1}+by_{1}+f}\)
\((x_{1}, y_{1})\) বিন্দু হতে \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকে অঙ্কিত স্পর্শক যুগলের সমীকরণ
\(T^2=SS_{1}\)
যেখানে, \(S=ax^2+2hxy+by^2+2gx+2fy+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})\) \(+c\)
কণিকের উপরে অবস্থিত নয় এরূপ কোনো বিন্দু হতে কণিকে কেবলমাত্র দুইটি স্পর্শক অঙ্কন করা যায়।
\((x_{1}, y_{1})\) বিন্দু হতে \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের স্পর্শ জ্যা এর সমীকরণ
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+\) \(f(y+y_{1})+c=0\)
\(lx+my+n=0\) সরলরেখাটি \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের একটি স্পর্শক হওয়ার শর্ত
\(\left|\begin{array}{c}a & h & g & l\\ h & b & f & m\\ g & f & c & n\\ l & m & n & 0\end{array}\right|=0\)
একটি কণিকের কোনো জ্যা এর মধ্যবিন্দু জানা থাকলে এর সমীকরণ
\(T=S_{1}\).
যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})\) \(+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিক সাপেক্ষে \((x_{1}, y_{1})\) বিন্দুর পোলারের সমীকরণ
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+\) \(f(y+y_{1})+c=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিক সাপেক্ষে কোনো সরলরেখার পোল নির্ণয় কর।
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের ব্যাসের সমীকরণ
\(ax+hy+g+m(hx_{1}+by_{1}+f)=0\).
এবং এটি কণিকের কেন্দ্রগামী
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের দুইটি ব্যাস যথাক্রমে \(y=m_{1}x+c_{1}\) ও \(y=m_{2}x+c_{2}\) পরস্পর অনুবন্ধী হওয়ার শর্ত
\(a+h(m_{1}+m_{2})+bm_{1}m_{2}=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকে সাপেক্ষে \(P(x_{1}, y_{1})\) বিন্দুর পোলার যদি \(Q(x_{2}, y_{2})\) বিন্দুগামী হয়, তবে \(Q(x_{2}, y_{2})\) বিন্দুর পোলারও \(P(x_{1}, y_{1})\) বিন্দুগামী হবে।
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকে সাপেক্ষে \(l_{1}x+m_{1}y+n_{1}=0\) ও \(l_{2}x+m_{2}y+n_{2}=0\) সরলরেখাদ্বয়ের পরস্পর অনুবন্ধী হওয়ার শর্ত
\(\left|\begin{array}{c}a & h & g & l_{1}\\ h & b & f & m_{1}\\ g & f & c & n_{1}\\ l_{2} & m_{2} & n_{2} & 0\end{array}\right|=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের নির্দেশক (নিয়ত) বৃত্ত বা চালক বৃত্তের সমীকরণ
\((ab-h^2)(x^2+y^2)+2(bg-hf)x+2(af-hg)y+\) \((a+b)c-g^2-f^2=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) অধিবৃত্তে অসীমতটের সমীকরণ
\(ax^2+2hxy+by^2+2gx+2fy+c=\frac{\Delta}{ab-h^2}\)
অথবা,
\(ax^2+2hxy+by^2+2gx+2fy-g\alpha-f\beta=0\)
অথবা,
\(ax^2+2hxy+by^2+2gx+2fy+c+k=0\)
যেখানে, অধিবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
দ্রষ্টব্যঃ \(l_{1}x+m_{1}y+n_{1}=0\) ও \(l_{2}x+m_{2}y+n_{2}=0\) অসীমতট বিশিষ্ট অধিবৃত্তের সমীকরণ
\((l_{1}x+m_{1}y+n_{1})(l_{2}x+m_{2}y+n_{2})+k=0\)
এখানে, \(k\) যে কোনো বাস্তব সংখ্যা।
দ্রষ্টব্যঃ উপবৃত্ত অসীম পদ পর্যন্ত বিস্তৃত নয় তাই ইহার অসীমতট নেই। পরাবৃত্তের অসীমতট অসীমে অবস্থান করে সুতরাং ইহার বাস্তব অসীমতট নেই। শুধুমাত্র অধিবৃত্তের অসীমতট বাস্তবে নির্ণয় করা যায়।
দ্রষ্টব্যঃ দুইটি সমউপকেন্দ্রিক কণিকের অভিন্ন কেন্দ্র ও অক্ষ থাকে।
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 .........(1), \ (a\gt{b})\)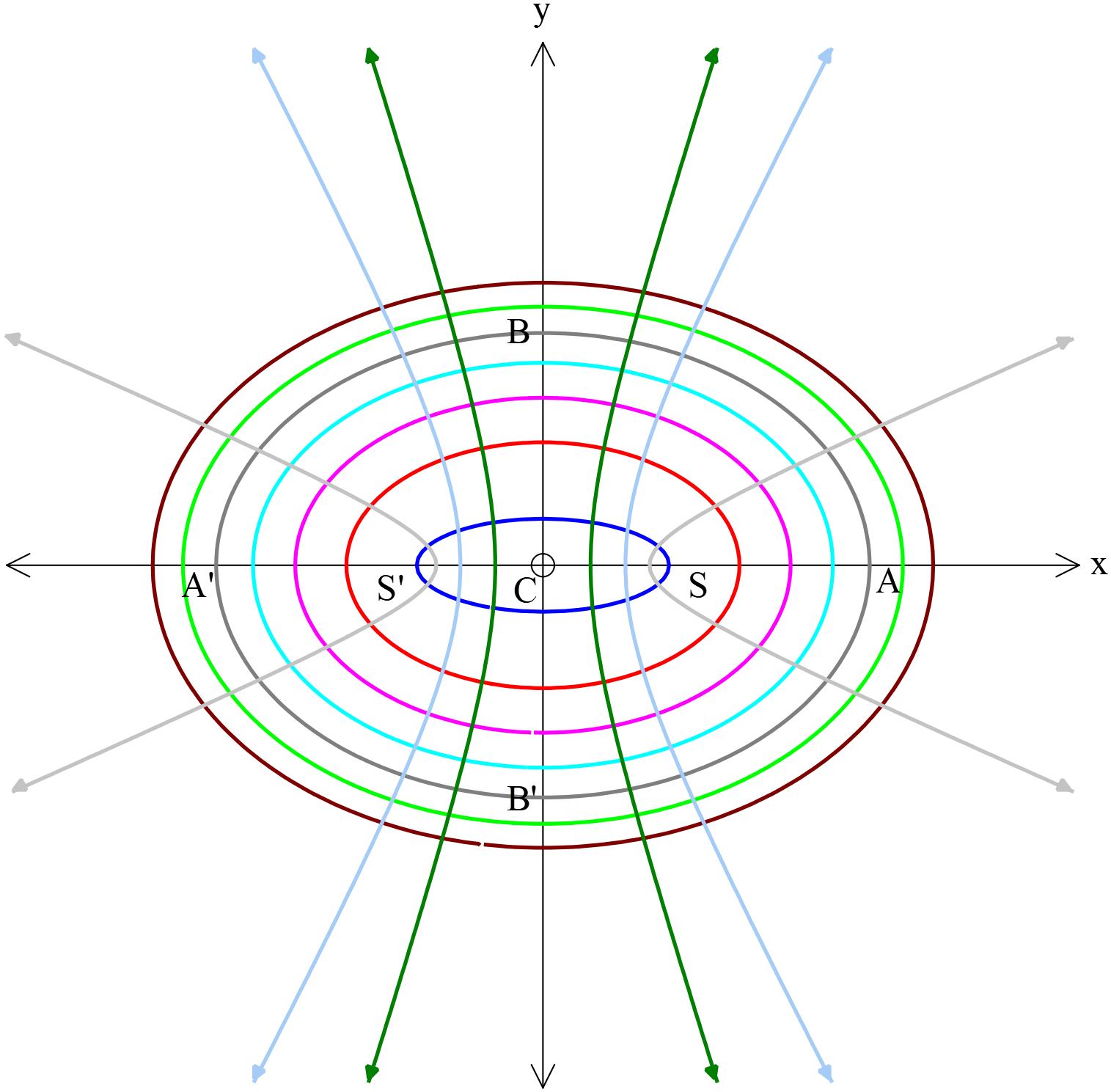
\((1)\) নং উপবৃত্তের ফোকাস দুইটি \((\pm{ae}, 0)\)
\(\Rightarrow \left(\pm{a\times{\frac{\sqrt{a^2-b^2}}{a}}}, 0\right)\)
\(\therefore (\pm{\sqrt{a^2-b^2}}, 0)\) ➜ \(\because e=\frac{\sqrt{a^2-b^2}}{a}\)
এখন ধ্রুবক \(k\) এর যেকোনো মানের জন্য
\(\frac{x^2}{a^2+k}+\frac{y^2}{b^2+k}=1 .........(2)\)
\((2)\) নং সমীকরণ দ্বারা নির্দেশিত উপবৃত্তের ফোকাস দুইটি
\((\pm{\sqrt{(a^2+k)-(b^2+k)}}, 0)\)
\(\Rightarrow (\pm{\sqrt{a^2+k-b^2-k}}, 0)\)
\(\therefore (\pm{\sqrt{a^2-b^2}}, 0)\)
যারা \((1)\) নং উপবৃত্তের ফোকাস দুইটির অনুরূপ।
কাজেই \((2)\) নং উপবৃত্তটি \((1)\) নং উপবৃত্তের সাথে সমউপকেন্দ্রিক কনিক শ্রেণী প্রকাশ করে।
যদি \(k>0\) এবং \(k\) এর মাণ ক্রমশ বৃদ্ধি পেতে থাকে তবে, \(a^2+k\) ও \(b^2+k\) উভয়ে বৃদ্ধি পেতে থাকবে অর্থাৎ \((2)\) নং সমীকরণ দ্বারা প্রকাশিত উপবৃত্তটি ক্রমশ স্ফীত হয়ে গোলাকৃতি হতে থাকবে এবং \(k\) এর মাণ যখন অসীমে পৌঁছাবে তখন এটা একটি অসীম ব্যাসার্ধ বিশিষ্ট বৃত্তে পরিণত হবে।
কোনো কণিকের উপকেন্দ্র পোল হলে কণিকটির পোলার সমীকরণ ও দিকাক্ষের পোলার সমীকরণ
কণিকের পোলার সমীকরণঃ \(\frac{l}{r}=1-e\cos{\theta}\)
দিকাক্ষের পোলার সমীকরণঃ \(\frac{l}{r}=e\cos{\theta}\)
কোনো কণিকের অক্ষরেখা আদি রেখার সহিত \(\alpha\) কোণ উৎপন্ন করলে এবং এটির উপকেন্দ্র পোল হলে কণিকটির পোলার সমীকরণ ও দিকাক্ষের পোলার সমীকরণ
কণিকের পোলার সমীকরণঃ \(\frac{l}{r}=1-e\cos{(\theta-\alpha)}\)
দিকাক্ষের পোলার সমীকরণঃ \(\frac{l}{r}=e\cos{(\theta-\alpha)}\)
\(\frac{l}{r}=1-e\cos{\theta}\) কণিকের ক্ষেত্রে
জ্যা এর সমীকরণঃ \(\frac{l}{r}=\sec{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}-e\cos{\theta}\)
যেখানে, \(\alpha\) এবং \(\beta\) জ্যা এর প্রান্ত বিন্দুর ভেক্টর কোণ।
\(\alpha\) বিন্দুতে স্পর্শকের সমীকরণঃ \(\frac{l}{r}=\cos{(\theta-\alpha)}-e\cos{\theta}\)
কেন্দ্রীয় কনিক \(ax^2+2hxy+by^2+2gx+2fy+c=0\) এর বিকেন্দ্রিকতা \(e\) হলে,
\(e^4+\frac{(a-b)^2+4h^2}{ab-h^2}(e^2-1)=0\)
জাতীঃসঃ ২০১২, ২০১৬
কোনো কণিকের উৎকেন্দ্রতা \(e\) উপকেন্দ্র \(S(\alpha, \beta)\) এবং নিয়ামক রেখার সমীকরণ \(lx+my+n=0\) হলে কণিকের সমীকরণ নির্ণয় কর।
উত্তরঃ\((l^2+m^2-e^2l^2)x^2-2lme^2xy+(l^2+m^2-e^2m^2)y^2-\) \(2\{\alpha(l^2+m^2)+e^2ln\}x-2\{\beta(l^2+m^2)+e^2mn\}y+\) \((l^2+m^2)(\alpha^2+\beta^2)-e^2n^2=0\)
যে শর্তে সাধারণ দ্বিঘাত সমীকরণ কণিক প্রকাশ করে তা নির্ণয় কর।
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের কেন্দ্র
\(\left(\frac{hf-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কেন্দ্রিক কণিকের প্রমাণ আকার
\(a^{\prime}x^2+b^{\prime}y^2+\frac{\Delta}{ab-h^2}=0\)
\(Ax^2+2Hxy+By^2=1\) কণিকের ক্ষেত্রেঃ
যদি কণিকের অর্ধাক্ষের দৈর্ঘ্য \(r\) হয় তবে, \((AB-H^2)r^4-(A+B)r^2+1=0\) \(r_{1}\) এবং \(r_{2}\) উভয়ে ধনাত্মক হলে কণিকটি উপবৃত্ত হবে সেক্ষেত্রেঃ
বৃহৎ অক্ষের দৈর্ঘ্য \(=2r_{1}, \ \ r_{1}>r_{2}\)
.png)
ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=2r_{2}, \ \ r_{1}>r_{2}\)
\(r_{1}\) এবং \(r_{2}\) এর একটি ধনাত্মক এবং অপরটি ঋণাত্মক হলে কণিকটি অধিবৃত্ত হবে সেক্ষেত্রেঃ
আড় অক্ষের দৈর্ঘ্য \(=2r_{1}\)
অনুবন্ধী অক্ষের দৈর্ঘ্য \(=2\sqrt{|r_{2}^2|}\)
উভয় ক্ষেত্রে উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2r_{2}^2}{r_{1}}\right|\)
উভয় ক্ষেত্রে বিকেন্দ্রিকতা \(e=\sqrt{1-\frac{r_{2}^2}{r_{1}^2}}, \ \ r_{1}>r_{2}\)
বৃহৎ অক্ষের সমীকরণ \(\left(A-\frac{1}{r_{1}^2}\right)x+Hy=0\) ক্ষুদ্রাক্ষের সমীকরণ \(\left(A-\frac{1}{r_{2}^2}\right)x+Hy=0\) শীর্ষদ্বয়ের স্থানাঙ্ক \(A(\alpha+r_{1}\cos{\theta}, \beta+r_{1}\sin{\theta})\) এবং \(A^{\prime}(\alpha-r_{1}\cos{\theta}, \beta-r_{1}\sin{\theta})\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\) ফোকাসদ্বয়ের স্থানাঙ্ক \(S(\alpha+r_{1}e\cos{\theta}, \beta+r_{1}e\sin{\theta})\) এবং \(S^{\prime}(\alpha-r_{1}e\cos{\theta}, \beta-r_{1}e\sin{\theta})\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\) নিয়ামকদ্বয়ের পাদবিন্দুর স্থানাঙ্ক
\(Z\left(\alpha+\frac{r_{1}}{e}\cos{\theta}, \beta+\frac{r_{1}}{e}\sin{\theta}\right)\) এবং \(Z^{\prime}\left(\alpha-\frac{r_{1}}{e}\cos{\theta}, \beta-\frac{r_{1}}{e}\sin{\theta}\right)\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কেন্দ্রবিহীন কণিকের প্রমাণ আকার
\(y^2=4a^{\prime}x\)
যেখানে, \(a^{\prime}=\frac{\sqrt{(k\sqrt{a}-g)^2+(k\sqrt{b}-f)^2}}{2(a+b)}\)
এবং \(k=\frac{g\sqrt{a}+f\sqrt{b}}{a+b}\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের উপরস্থ \((x_{1}, y_{1})\) বিন্দুতে এর স্পর্শকের সমীকরণ
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+\) \(f(y+y_{1})+c=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের উপরস্থ \((x_{1}, y_{1})\) বিন্দুতে এর অভিলম্বের সমীকরণ
\(\frac{x-x_{1}}{ax_{1}+hy_{1}+g}=\frac{y-y_{1}}{hx_{1}+by_{1}+f}\)
\((x_{1}, y_{1})\) বিন্দু হতে \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকে অঙ্কিত স্পর্শক যুগলের সমীকরণ
\(T^2=SS_{1}\)
যেখানে, \(S=ax^2+2hxy+by^2+2gx+2fy+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})\) \(+c\)
কণিকের উপরে অবস্থিত নয় এরূপ কোনো বিন্দু হতে কণিকে কেবলমাত্র দুইটি স্পর্শক অঙ্কন করা যায়।
\((x_{1}, y_{1})\) বিন্দু হতে \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের স্পর্শ জ্যা এর সমীকরণ
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+\) \(f(y+y_{1})+c=0\)
\(lx+my+n=0\) সরলরেখাটি \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের একটি স্পর্শক হওয়ার শর্ত
\(\left|\begin{array}{c}a & h & g & l\\ h & b & f & m\\ g & f & c & n\\ l & m & n & 0\end{array}\right|=0\)
একটি কণিকের কোনো জ্যা এর মধ্যবিন্দু জানা থাকলে এর সমীকরণ
\(T=S_{1}\).
যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})\) \(+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিক সাপেক্ষে \((x_{1}, y_{1})\) বিন্দুর পোলারের সমীকরণ
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+\) \(f(y+y_{1})+c=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিক সাপেক্ষে কোনো সরলরেখার পোল নির্ণয় কর।
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের ব্যাসের সমীকরণ
\(ax+hy+g+m(hx_{1}+by_{1}+f)=0\).
এবং এটি কণিকের কেন্দ্রগামী
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের দুইটি ব্যাস যথাক্রমে \(y=m_{1}x+c_{1}\) ও \(y=m_{2}x+c_{2}\) পরস্পর অনুবন্ধী হওয়ার শর্ত
\(a+h(m_{1}+m_{2})+bm_{1}m_{2}=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকে সাপেক্ষে \(P(x_{1}, y_{1})\) বিন্দুর পোলার যদি \(Q(x_{2}, y_{2})\) বিন্দুগামী হয়, তবে \(Q(x_{2}, y_{2})\) বিন্দুর পোলারও \(P(x_{1}, y_{1})\) বিন্দুগামী হবে।
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকে সাপেক্ষে \(l_{1}x+m_{1}y+n_{1}=0\) ও \(l_{2}x+m_{2}y+n_{2}=0\) সরলরেখাদ্বয়ের পরস্পর অনুবন্ধী হওয়ার শর্ত
\(\left|\begin{array}{c}a & h & g & l_{1}\\ h & b & f & m_{1}\\ g & f & c & n_{1}\\ l_{2} & m_{2} & n_{2} & 0\end{array}\right|=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের নির্দেশক (নিয়ত) বৃত্ত বা চালক বৃত্তের সমীকরণ
\((ab-h^2)(x^2+y^2)+2(bg-hf)x+2(af-hg)y+\) \((a+b)c-g^2-f^2=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) অধিবৃত্তে অসীমতটের সমীকরণ
\(ax^2+2hxy+by^2+2gx+2fy+c=\frac{\Delta}{ab-h^2}\)
অথবা,
\(ax^2+2hxy+by^2+2gx+2fy-g\alpha-f\beta=0\)
অথবা,
\(ax^2+2hxy+by^2+2gx+2fy+c+k=0\)
যেখানে, অধিবৃত্তের কেন্দ্র \(C(\alpha, \beta)\)
দ্রষ্টব্যঃ \(l_{1}x+m_{1}y+n_{1}=0\) ও \(l_{2}x+m_{2}y+n_{2}=0\) অসীমতট বিশিষ্ট অধিবৃত্তের সমীকরণ
\((l_{1}x+m_{1}y+n_{1})(l_{2}x+m_{2}y+n_{2})+k=0\)
এখানে, \(k\) যে কোনো বাস্তব সংখ্যা।
দ্রষ্টব্যঃ উপবৃত্ত অসীম পদ পর্যন্ত বিস্তৃত নয় তাই ইহার অসীমতট নেই। পরাবৃত্তের অসীমতট অসীমে অবস্থান করে সুতরাং ইহার বাস্তব অসীমতট নেই। শুধুমাত্র অধিবৃত্তের অসীমতট বাস্তবে নির্ণয় করা যায়।
সম-উপকেন্দ্রিক কণিক শ্রেণীঃ দুইটি কণিকের উপকেন্দ্র অভিন্ন হলে এদেরকে সম-উপকেন্দ্রিক কণিক বলা হয়। যেহেতু উপকেন্দ্রসমূহ অক্ষ রেখার উপর থাকে, সুতরাং দুইটি সম-উপকেন্দ্রিক কণিকের অক্ষদ্বয়ও অভিন্ন হবে।
দুইটি সমউপকেন্দ্রিক কনিক পরস্পরকে সমকোণে ছেদ করে।দ্রষ্টব্যঃ দুইটি সমউপকেন্দ্রিক কণিকের অভিন্ন কেন্দ্র ও অক্ষ থাকে।
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 .........(1), \ (a\gt{b})\)

\((1)\) নং উপবৃত্তের ফোকাস দুইটি \((\pm{ae}, 0)\)
\(\Rightarrow \left(\pm{a\times{\frac{\sqrt{a^2-b^2}}{a}}}, 0\right)\)
\(\therefore (\pm{\sqrt{a^2-b^2}}, 0)\) ➜ \(\because e=\frac{\sqrt{a^2-b^2}}{a}\)
এখন ধ্রুবক \(k\) এর যেকোনো মানের জন্য
\(\frac{x^2}{a^2+k}+\frac{y^2}{b^2+k}=1 .........(2)\)
\((2)\) নং সমীকরণ দ্বারা নির্দেশিত উপবৃত্তের ফোকাস দুইটি
\((\pm{\sqrt{(a^2+k)-(b^2+k)}}, 0)\)
\(\Rightarrow (\pm{\sqrt{a^2+k-b^2-k}}, 0)\)
\(\therefore (\pm{\sqrt{a^2-b^2}}, 0)\)
যারা \((1)\) নং উপবৃত্তের ফোকাস দুইটির অনুরূপ।
কাজেই \((2)\) নং উপবৃত্তটি \((1)\) নং উপবৃত্তের সাথে সমউপকেন্দ্রিক কনিক শ্রেণী প্রকাশ করে।
যদি \(k>0\) এবং \(k\) এর মাণ ক্রমশ বৃদ্ধি পেতে থাকে তবে, \(a^2+k\) ও \(b^2+k\) উভয়ে বৃদ্ধি পেতে থাকবে অর্থাৎ \((2)\) নং সমীকরণ দ্বারা প্রকাশিত উপবৃত্তটি ক্রমশ স্ফীত হয়ে গোলাকৃতি হতে থাকবে এবং \(k\) এর মাণ যখন অসীমে পৌঁছাবে তখন এটা একটি অসীম ব্যাসার্ধ বিশিষ্ট বৃত্তে পরিণত হবে।
কোনো কণিকের উপকেন্দ্র পোল হলে কণিকটির পোলার সমীকরণ ও দিকাক্ষের পোলার সমীকরণ
কণিকের পোলার সমীকরণঃ \(\frac{l}{r}=1-e\cos{\theta}\)
দিকাক্ষের পোলার সমীকরণঃ \(\frac{l}{r}=e\cos{\theta}\)
কোনো কণিকের অক্ষরেখা আদি রেখার সহিত \(\alpha\) কোণ উৎপন্ন করলে এবং এটির উপকেন্দ্র পোল হলে কণিকটির পোলার সমীকরণ ও দিকাক্ষের পোলার সমীকরণ
কণিকের পোলার সমীকরণঃ \(\frac{l}{r}=1-e\cos{(\theta-\alpha)}\)
দিকাক্ষের পোলার সমীকরণঃ \(\frac{l}{r}=e\cos{(\theta-\alpha)}\)
\(\frac{l}{r}=1-e\cos{\theta}\) কণিকের ক্ষেত্রে
জ্যা এর সমীকরণঃ \(\frac{l}{r}=\sec{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}-e\cos{\theta}\)
যেখানে, \(\alpha\) এবং \(\beta\) জ্যা এর প্রান্ত বিন্দুর ভেক্টর কোণ।
\(\alpha\) বিন্দুতে স্পর্শকের সমীকরণঃ \(\frac{l}{r}=\cos{(\theta-\alpha)}-e\cos{\theta}\)
কেন্দ্রীয় কনিক \(ax^2+2hxy+by^2+2gx+2fy+c=0\) এর বিকেন্দ্রিকতা \(e\) হলে,
\(e^4+\frac{(a-b)^2+4h^2}{ab-h^2}(e^2-1)=0\)
×
প্রমাণ কর যে, একটি কণিকের সমীকরণ সর্বদাই একটি দ্বিঘাত সমীকরণ কিন্তু বিপরীতক্রমে এটি সর্বদা সত্য নয়।
জাতীঃসঃ ২০১২, ২০১৬
Proof:
মনে করি,
কণিকটির উপকেন্দ্র \(S(\alpha, \beta)\)
উৎকেন্দ্রতা \(e\)
নিয়ামক রেখা \(AB\)
নিয়ামক রেখার সমীকরণ \(lx+my+n=0 ........(1)\)
কণিকটির উপর যে কোনো বিন্দু \(P(x, y)\)
\(\therefore PS=\sqrt{(x-\alpha)^2+(y-\beta)^2}\) ➜ \(\because (x_{1}, y_{1})\) ও \((x_{2}, y_{2})\) বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}\)
\(P\) হতে দিকাক্ষ \(AB\) এর উপর লম্ব দূরত্ব,
\(PM=\frac{lx+my+n}{\sqrt{l^2+m^2}}\) ➜ \(\because (x_{1}, y_{1})\) বিন্দু হতে
\(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব
\(=\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
কণিকের সংজ্ঞানুসারে,
\(\frac{PS}{PM}=e\)
\(\Rightarrow PS=ePM\)
\(\Rightarrow \sqrt{(x-\alpha)^2+(y-\beta)^2}=e\frac{lx+my+n}{\sqrt{l^2+m^2}}\)
\(\Rightarrow (x-\alpha)^2+(y-\beta)^2=e^2\frac{(lx+my+n)^2}{l^2+m^2}\)
\(\Rightarrow (l^2+m^2)(x-\alpha)^2+(l^2+m^2)(y-\beta)^2=e^2(l^2x^2+m^2y^2+n^2+2lmxy+2lnx+2mny)\) ➜ উভয় পার্শে \(l^2+m^2\) গুণ করে।
\(\Rightarrow (l^2+m^2)(x^2-2x\alpha+\alpha^2)+(l^2+m^2)(y^2-2y\beta+\beta^2)-e^2(l^2x^2+m^2y^2+n^2+2lmxy+2lnx+2mny)=0\)
\(\Rightarrow (l^2+m^2-e^2l^2)x^2-2lme^2xy+(l^2+m^2-e^2m^2)y^2-2\{\alpha(l^2+m^2)+e^2ln\}x-2\{\beta(l^2+m^2)+e^2mn\}y+(l^2+m^2)(\alpha^2+\beta^2)-e^2n^2=0\)
\(\therefore ax^2+2hxy+by^2+2gx+2fy+c=0\)
যেখানে, \(a=l^2+m^2-e^2l^2\)
\(b=l^2+m^2-e^2m^2\)
\(h=-lme^2\)
\(g=-\{\alpha(l^2+m^2)+e^2ln\}\)
\(f=-\{\beta(l^2+m^2)+e^2mn\}\)
\(c=(l^2+m^2)(\alpha^2+\beta^2)-e^2n^2\)
\(\therefore \) কণিকের সমীকরণ সর্বদাই একটি দ্বিঘাত সমীকরণ
বিপরীতক্রমে,
সাধারণ দ্বিঘাত সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(2)\)
\((2)\) নং সমীকরণের \(a, \ b, \ c, \ h, \ g\) ও \(f\) এর মাণ
যদি এরূপ হয় যে,
\(\Delta=abc+2fgh-af^2-bg^2-ch^2=\left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c\end{array}\right|=0\)
তবে সে ক্ষেত্রে \((2)\) নং সমীকরণ কণিক প্রকাশ না করে যুগল সরলরেখা প্রকাশ করে।
অতএব ইহা স্পষ্ট যে সাধারণ দ্বিঘাত সমীকরণ সর্বদা কণিক প্রকাশ করে না।

কণিকটির উপকেন্দ্র \(S(\alpha, \beta)\)
উৎকেন্দ্রতা \(e\)
নিয়ামক রেখা \(AB\)
নিয়ামক রেখার সমীকরণ \(lx+my+n=0 ........(1)\)
কণিকটির উপর যে কোনো বিন্দু \(P(x, y)\)
\(\therefore PS=\sqrt{(x-\alpha)^2+(y-\beta)^2}\) ➜ \(\because (x_{1}, y_{1})\) ও \((x_{2}, y_{2})\) বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}\)
\(P\) হতে দিকাক্ষ \(AB\) এর উপর লম্ব দূরত্ব,
\(PM=\frac{lx+my+n}{\sqrt{l^2+m^2}}\) ➜ \(\because (x_{1}, y_{1})\) বিন্দু হতে
\(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব
\(=\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
কণিকের সংজ্ঞানুসারে,
\(\frac{PS}{PM}=e\)
\(\Rightarrow PS=ePM\)
\(\Rightarrow \sqrt{(x-\alpha)^2+(y-\beta)^2}=e\frac{lx+my+n}{\sqrt{l^2+m^2}}\)
\(\Rightarrow (x-\alpha)^2+(y-\beta)^2=e^2\frac{(lx+my+n)^2}{l^2+m^2}\)
\(\Rightarrow (l^2+m^2)(x-\alpha)^2+(l^2+m^2)(y-\beta)^2=e^2(l^2x^2+m^2y^2+n^2+2lmxy+2lnx+2mny)\) ➜ উভয় পার্শে \(l^2+m^2\) গুণ করে।
\(\Rightarrow (l^2+m^2)(x^2-2x\alpha+\alpha^2)+(l^2+m^2)(y^2-2y\beta+\beta^2)-e^2(l^2x^2+m^2y^2+n^2+2lmxy+2lnx+2mny)=0\)
\(\Rightarrow (l^2+m^2-e^2l^2)x^2-2lme^2xy+(l^2+m^2-e^2m^2)y^2-2\{\alpha(l^2+m^2)+e^2ln\}x-2\{\beta(l^2+m^2)+e^2mn\}y+(l^2+m^2)(\alpha^2+\beta^2)-e^2n^2=0\)
\(\therefore ax^2+2hxy+by^2+2gx+2fy+c=0\)
যেখানে, \(a=l^2+m^2-e^2l^2\)
\(b=l^2+m^2-e^2m^2\)
\(h=-lme^2\)
\(g=-\{\alpha(l^2+m^2)+e^2ln\}\)
\(f=-\{\beta(l^2+m^2)+e^2mn\}\)
\(c=(l^2+m^2)(\alpha^2+\beta^2)-e^2n^2\)
\(\therefore \) কণিকের সমীকরণ সর্বদাই একটি দ্বিঘাত সমীকরণ
বিপরীতক্রমে,
সাধারণ দ্বিঘাত সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(2)\)
\((2)\) নং সমীকরণের \(a, \ b, \ c, \ h, \ g\) ও \(f\) এর মাণ
যদি এরূপ হয় যে,
\(\Delta=abc+2fgh-af^2-bg^2-ch^2=\left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c\end{array}\right|=0\)
তবে সে ক্ষেত্রে \((2)\) নং সমীকরণ কণিক প্রকাশ না করে যুগল সরলরেখা প্রকাশ করে।
অতএব ইহা স্পষ্ট যে সাধারণ দ্বিঘাত সমীকরণ সর্বদা কণিক প্রকাশ করে না।
×
কোনো কণিকের উৎকেন্দ্রতা \(e\) উপকেন্দ্র \(S(\alpha, \beta)\) এবং নিয়ামক রেখার সমীকরণ \(lx+my+n=0\) হলে কণিকের সমীকরণ নির্ণয় কর।
উত্তরঃ \((l^2+m^2-e^2l^2)x^2-2lme^2xy+(l^2+m^2-e^2m^2)y^2-2\{\alpha(l^2+m^2)+e^2ln\}x-\)\(2\{\beta(l^2+m^2)+e^2mn\}y+(l^2+m^2)(\alpha^2+\beta^2)-e^2n^2=0\) সমাধানঃ
দেওয়া আছে,
উৎকেন্দ্রতা \(e\)
কণিকটির উপকেন্দ্র \(S(\alpha, \beta)\)
নিয়ামক রেখার সমীকরণ \(lx+my+n=0 ........(1)\)
ধরি,
নিয়ামক রেখা \(AB\)
কণিকটির উপর যে কোনো বিন্দু \(P(x, y)\)
\(\therefore PS=\sqrt{(x-\alpha)^2+(y-\beta)^2}\) ➜ \(\because (x_{1}, y_{1})\) ও \((x_{2}, y_{2})\) বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}\)
\(P\) হতে দিকাক্ষ \(AB\) এর উপর লম্ব দূরত্ব,
\(PM=\frac{lx+my+n}{\sqrt{l^2+m^2}}\) ➜ \(\because (x_{1}, y_{1})\) বিন্দু হতে
\(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব
\(=\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
কণিকের সংজ্ঞানুসারে,
\(\frac{PS}{PM}=e\)
\(\Rightarrow PS=ePM\)
\(\Rightarrow \sqrt{(x-\alpha)^2+(y-\beta)^2}=e\frac{lx+my+n}{\sqrt{l^2+m^2}}\)
\(\Rightarrow (x-\alpha)^2+(y-\beta)^2=e^2\frac{(lx+my+n)^2}{l^2+m^2}\)
\(\Rightarrow (l^2+m^2)(x-\alpha)^2+(l^2+m^2)(y-\beta)^2=e^2(l^2x^2+m^2y^2+n^2+2lmxy+2lnx+2mny)\) ➜ উভয় পার্শে \(l^2+m^2\) গুণ করে।
\(\Rightarrow (l^2+m^2)(x^2-2x\alpha+\alpha^2)+(l^2+m^2)(y^2-2y\beta+\beta^2)-e^2(l^2x^2+m^2y^2+n^2+2lmxy+2lnx+2mny)=0\)
\(\therefore (l^2+m^2-e^2l^2)x^2-2lme^2xy+(l^2+m^2-e^2m^2)y^2-2\{\alpha(l^2+m^2)+e^2ln\}x-2\{\beta(l^2+m^2)+e^2mn\}y+(l^2+m^2)(\alpha^2+\beta^2)-e^2n^2=0\)
ইহাই নির্ণেয় কণিকের সমীকরণ।

উৎকেন্দ্রতা \(e\)
কণিকটির উপকেন্দ্র \(S(\alpha, \beta)\)
নিয়ামক রেখার সমীকরণ \(lx+my+n=0 ........(1)\)
ধরি,
নিয়ামক রেখা \(AB\)
কণিকটির উপর যে কোনো বিন্দু \(P(x, y)\)
\(\therefore PS=\sqrt{(x-\alpha)^2+(y-\beta)^2}\) ➜ \(\because (x_{1}, y_{1})\) ও \((x_{2}, y_{2})\) বিন্দুদ্বয়ের মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}\)
\(P\) হতে দিকাক্ষ \(AB\) এর উপর লম্ব দূরত্ব,
\(PM=\frac{lx+my+n}{\sqrt{l^2+m^2}}\) ➜ \(\because (x_{1}, y_{1})\) বিন্দু হতে
\(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব
\(=\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
কণিকের সংজ্ঞানুসারে,
\(\frac{PS}{PM}=e\)
\(\Rightarrow PS=ePM\)
\(\Rightarrow \sqrt{(x-\alpha)^2+(y-\beta)^2}=e\frac{lx+my+n}{\sqrt{l^2+m^2}}\)
\(\Rightarrow (x-\alpha)^2+(y-\beta)^2=e^2\frac{(lx+my+n)^2}{l^2+m^2}\)
\(\Rightarrow (l^2+m^2)(x-\alpha)^2+(l^2+m^2)(y-\beta)^2=e^2(l^2x^2+m^2y^2+n^2+2lmxy+2lnx+2mny)\) ➜ উভয় পার্শে \(l^2+m^2\) গুণ করে।
\(\Rightarrow (l^2+m^2)(x^2-2x\alpha+\alpha^2)+(l^2+m^2)(y^2-2y\beta+\beta^2)-e^2(l^2x^2+m^2y^2+n^2+2lmxy+2lnx+2mny)=0\)
\(\therefore (l^2+m^2-e^2l^2)x^2-2lme^2xy+(l^2+m^2-e^2m^2)y^2-2\{\alpha(l^2+m^2)+e^2ln\}x-2\{\beta(l^2+m^2)+e^2mn\}y+(l^2+m^2)(\alpha^2+\beta^2)-e^2n^2=0\)
ইহাই নির্ণেয় কণিকের সমীকরণ।
×
যে শর্তে সাধারণ দ্বিঘাত সমীকরণ কণিক প্রকাশ করে তা নির্ণয় কর।
সমাধানঃ
সাধারণ দ্বিঘাত সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 ........(1)\)
ধরি, স্থানাঙ্কের অক্ষদ্বয় আয়তাকার। মূলবিন্দু অপরিবর্তিত রেখে অক্ষদ্বয়কে \(\theta\) কোণে আবর্তন করা হল যেখানে \(\tan{\theta}=\frac{2h}{a-b}\) । তাহলে \((1)\) নং সমীকরণ থেকে \(xy\) যুক্ত পদ অপসারিত হবে এবং সমীকরণটির পরিবর্তিত রূপ হবে,
\(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0 ........(2)\)
যেখানে \(ax^2+2hxy+by^2\) রাশিটির পরিবর্তিত রূপ \(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2\)
\(\therefore\) অপরিবর্তী রাশির সূত্র হতে,
\(a+b=a^{\prime}+b^{\prime}\)
এবং \(ab-h^2=a^{\prime}b^{\prime}\)
\((i)\) যদি \(ab-h^2=0\) হয় তবে, \(a^{\prime}b^{\prime}=0\)
সুতরাং হয় \(a^{\prime}=0,\) অথবা, \(b^{\prime}=0\) কিন্তু \(a^{\prime}\) ও \(b^{\prime}\) একত্রে শূন্য হতে পারে না কারণ সেক্ষেত্রে \((2)\) নং সমীকরণটি একঘাত সমীকরণে পরিণত হয় যা অসম্ভব।
ধরা যাক \(a^{\prime}=0,\) তাহলে \((2)\) নং সমীকরণটি দাঁড়াবে।
\(b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0\)
\(\Rightarrow {y^{\prime}}^2+2\frac{g^{\prime}x^{\prime}}{b^{\prime}}+2\frac{f^{\prime}y^{\prime}}{b^{\prime}}+\frac{c}{b^{\prime}}=0\)
\(\Rightarrow \left(y^{\prime}+\frac{f^{\prime}}{b^{\prime}}\right)^2-\frac{{f^{\prime}}^2}{{b^{\prime}}^2}+2\frac{g^{\prime}x^{\prime}}{b^{\prime}}+\frac{c}{b^{\prime}}=0\)
\(\therefore \left(y^{\prime}+\frac{f^{\prime}}{b^{\prime}}\right)^2=-2\frac{g^{\prime}x^{\prime}}{b^{\prime}}-\frac{c}{b^{\prime}}+\frac{{f^{\prime}}^2}{{b^{\prime}}^2} .......(3)\)
যদি \(g^{\prime}\ne{0}\) হয় তবে \((3)\) নং সমীকরণটি একটি প্যারাবোলা প্রকাশ করে যার অক্ষরেখা নতুন \(x\) অক্ষের সমান্তরাল।
যদি \(g^{\prime}=0\) হয় তবে \((3)\) নং সমীকরণটি একজোড়া ( বাস্তব অথবা কাল্পনিক ) সরলরেখা প্রকাশ করে।
অনুরূপভাবে, যদি \(b^{\prime}=0\) হয় তবে \((2)\) নং সমীকরণটি একটি প্যারাবোলা প্রকাশ করে যার অক্ষরেখা নতুন \(y\) অক্ষের সমান্তরাল, অথবা একজোড়া ( বাস্তব অথবা কাল্পনিক ) সরলরেখা প্রকাশ করবে।
\((ii)\) যদি \(ab-h^2\ne{0}\) হয় তবে, \(a^{\prime}b^{\prime}\ne{0}\)
\(\therefore a^{\prime}\ne{0}, \ b^{\prime}\ne{0}\)
সুতরাং \((2)\) নং সমীকরণটি দাঁড়াবে।
\(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0\)
\(\Rightarrow a^{\prime}\left({x^{\prime}}^2+2\frac{g^{\prime}}{a^{\prime}}x^{\prime}\right)+b^{\prime}\left({y^{\prime}}^2+2\frac{f^{\prime}}{b^{\prime}}y^{\prime}\right)+c=0\)
\(\Rightarrow a^{\prime}\left({x^{\prime}}^2+2\frac{g^{\prime}}{a^{\prime}}x^{\prime}+\frac{{g^{\prime}}^2}{{a^{\prime}}^2}\right)+b^{\prime}\left({y^{\prime}}^2+2\frac{f^{\prime}}{b^{\prime}}y^{\prime}+\frac{{f^{\prime}}^2}{{b^{\prime}}^2}\right)+c-\frac{{g^{\prime}}^2}{{a^{\prime}}^2}-\frac{{f^{\prime}}^2}{{b^{\prime}}^2}=0\)
\(\Rightarrow a^{\prime}\left(x^{\prime}+\frac{g^{\prime}}{a^{\prime}}\right)^2+b^{\prime}\left(y^{\prime}+\frac{f^{\prime}}{b^{\prime}}\right)^2=\frac{{g^{\prime}}^2}{{a^{\prime}}^2}+\frac{{f^{\prime}}^2}{{b^{\prime}}^2}-c\)
\(\therefore a^{\prime}\left(x^{\prime}+\frac{g^{\prime}}{a^{\prime}}\right)^2+b^{\prime}\left(y^{\prime}+\frac{f^{\prime}}{b^{\prime}}\right)^2=k .........(4)\)
যেখানে, \(k=\frac{{g^{\prime}}^2}{{a^{\prime}}^2}+\frac{{f^{\prime}}^2}{{b^{\prime}}^2}-c\)
যদি, \(k=0\) হয় তবে \((4)\) নং সমীকরণটি একজোড়া ( বাস্তব অথবা কাল্পনিক ) সরলরেখা প্রকাশ করবে।
যদি, \(k\ne{0}, \ a^{\prime}\ne{b^{\prime}}\) এবং \(a^{\prime}, \ b^{\prime}\) একই চিহ্নবিশিষ্ট হয় তবে \((4)\) নং সমীকরণটি একটি ( বাস্তব অথবা কাল্পনিক ) উপবৃত্ত প্রকাশ করবে।
যদি, \(k\ne{0}, \ a^{\prime}+b^{\prime}=0\) এবং \(a^{\prime}, \ b^{\prime}\) বিপরীত চিহ্নবিশিষ্ট হয় তবে \((4)\) নং সমীকরণটি একটি অধিবৃত্ত প্রকাশ করবে।
যদি, \(k\ne{0}\) এবং \(a^{\prime}=b^{\prime}\) হয় তবে \((4)\) নং সমীকরণটি একটি বৃত্ত প্রকাশ করবে।
এখন, \(a^{\prime}\) ও \(b^{\prime}\) এর চিহ্ন একই হলে
\(a^{\prime}b^{\prime}>0\) হয়।
\(\therefore ab-h^2\gt{0}\)
আবার, \(a^{\prime}\) ও \(b^{\prime}\) এর চিহ্ন বিপরীত হলে
\(a^{\prime}b^{\prime}<0\) হয়।
\(\therefore ab-h^2\lt{0}\)
আবার, \(a^{\prime}+b^{\prime}=0\) হলে
\(a+b=0\) হয়।
এবং \(a^{\prime}b^{\prime}=0\) হলে
\(ab-h^2=0\) হয়।
আমরা জানি,
\(\Delta=\left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c\end{array}\right|=0\) হলে
\((1)\) নং সমীকরণটি একজোড়া সরলরেখা প্রকাশ করে।
সুতরাং \((1)\) নং সমীকরণটি ( স্থানাঙ্কের অক্ষদ্বয় আয়তাকার হলে )
\((i)\) একটি পরাবৃত্ত প্রকাশ করবে যদি \(\Delta\ne{0}\) এবং \(ab-h^2=0\) হয়।
\((ii)\) একটি উপবৃত্ত প্রকাশ করবে যদি \(\Delta\ne{0}\) এবং \(ab-h^2\gt{0}\) হয়।
\((iii)\) একটি অধিবৃত্ত প্রকাশ করবে যদি \(\Delta\ne{0}\) এবং \(ab-h^2\lt{0} \) হয়।
আর এই অধিবৃত্তটি আয়াতাকার হবে যদি \(a+b=0\) হয়।
ইহাই নির্ণেয় শর্ত।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 ........(1)\)
ধরি, স্থানাঙ্কের অক্ষদ্বয় আয়তাকার। মূলবিন্দু অপরিবর্তিত রেখে অক্ষদ্বয়কে \(\theta\) কোণে আবর্তন করা হল যেখানে \(\tan{\theta}=\frac{2h}{a-b}\) । তাহলে \((1)\) নং সমীকরণ থেকে \(xy\) যুক্ত পদ অপসারিত হবে এবং সমীকরণটির পরিবর্তিত রূপ হবে,
\(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0 ........(2)\)
যেখানে \(ax^2+2hxy+by^2\) রাশিটির পরিবর্তিত রূপ \(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2\)
\(\therefore\) অপরিবর্তী রাশির সূত্র হতে,
\(a+b=a^{\prime}+b^{\prime}\)
এবং \(ab-h^2=a^{\prime}b^{\prime}\)
\((i)\) যদি \(ab-h^2=0\) হয় তবে, \(a^{\prime}b^{\prime}=0\)
সুতরাং হয় \(a^{\prime}=0,\) অথবা, \(b^{\prime}=0\) কিন্তু \(a^{\prime}\) ও \(b^{\prime}\) একত্রে শূন্য হতে পারে না কারণ সেক্ষেত্রে \((2)\) নং সমীকরণটি একঘাত সমীকরণে পরিণত হয় যা অসম্ভব।
ধরা যাক \(a^{\prime}=0,\) তাহলে \((2)\) নং সমীকরণটি দাঁড়াবে।
\(b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0\)
\(\Rightarrow {y^{\prime}}^2+2\frac{g^{\prime}x^{\prime}}{b^{\prime}}+2\frac{f^{\prime}y^{\prime}}{b^{\prime}}+\frac{c}{b^{\prime}}=0\)
\(\Rightarrow \left(y^{\prime}+\frac{f^{\prime}}{b^{\prime}}\right)^2-\frac{{f^{\prime}}^2}{{b^{\prime}}^2}+2\frac{g^{\prime}x^{\prime}}{b^{\prime}}+\frac{c}{b^{\prime}}=0\)
\(\therefore \left(y^{\prime}+\frac{f^{\prime}}{b^{\prime}}\right)^2=-2\frac{g^{\prime}x^{\prime}}{b^{\prime}}-\frac{c}{b^{\prime}}+\frac{{f^{\prime}}^2}{{b^{\prime}}^2} .......(3)\)
যদি \(g^{\prime}\ne{0}\) হয় তবে \((3)\) নং সমীকরণটি একটি প্যারাবোলা প্রকাশ করে যার অক্ষরেখা নতুন \(x\) অক্ষের সমান্তরাল।
যদি \(g^{\prime}=0\) হয় তবে \((3)\) নং সমীকরণটি একজোড়া ( বাস্তব অথবা কাল্পনিক ) সরলরেখা প্রকাশ করে।
অনুরূপভাবে, যদি \(b^{\prime}=0\) হয় তবে \((2)\) নং সমীকরণটি একটি প্যারাবোলা প্রকাশ করে যার অক্ষরেখা নতুন \(y\) অক্ষের সমান্তরাল, অথবা একজোড়া ( বাস্তব অথবা কাল্পনিক ) সরলরেখা প্রকাশ করবে।
\((ii)\) যদি \(ab-h^2\ne{0}\) হয় তবে, \(a^{\prime}b^{\prime}\ne{0}\)
\(\therefore a^{\prime}\ne{0}, \ b^{\prime}\ne{0}\)
সুতরাং \((2)\) নং সমীকরণটি দাঁড়াবে।
\(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0\)
\(\Rightarrow a^{\prime}\left({x^{\prime}}^2+2\frac{g^{\prime}}{a^{\prime}}x^{\prime}\right)+b^{\prime}\left({y^{\prime}}^2+2\frac{f^{\prime}}{b^{\prime}}y^{\prime}\right)+c=0\)
\(\Rightarrow a^{\prime}\left({x^{\prime}}^2+2\frac{g^{\prime}}{a^{\prime}}x^{\prime}+\frac{{g^{\prime}}^2}{{a^{\prime}}^2}\right)+b^{\prime}\left({y^{\prime}}^2+2\frac{f^{\prime}}{b^{\prime}}y^{\prime}+\frac{{f^{\prime}}^2}{{b^{\prime}}^2}\right)+c-\frac{{g^{\prime}}^2}{{a^{\prime}}^2}-\frac{{f^{\prime}}^2}{{b^{\prime}}^2}=0\)
\(\Rightarrow a^{\prime}\left(x^{\prime}+\frac{g^{\prime}}{a^{\prime}}\right)^2+b^{\prime}\left(y^{\prime}+\frac{f^{\prime}}{b^{\prime}}\right)^2=\frac{{g^{\prime}}^2}{{a^{\prime}}^2}+\frac{{f^{\prime}}^2}{{b^{\prime}}^2}-c\)
\(\therefore a^{\prime}\left(x^{\prime}+\frac{g^{\prime}}{a^{\prime}}\right)^2+b^{\prime}\left(y^{\prime}+\frac{f^{\prime}}{b^{\prime}}\right)^2=k .........(4)\)
যেখানে, \(k=\frac{{g^{\prime}}^2}{{a^{\prime}}^2}+\frac{{f^{\prime}}^2}{{b^{\prime}}^2}-c\)
যদি, \(k=0\) হয় তবে \((4)\) নং সমীকরণটি একজোড়া ( বাস্তব অথবা কাল্পনিক ) সরলরেখা প্রকাশ করবে।
যদি, \(k\ne{0}, \ a^{\prime}\ne{b^{\prime}}\) এবং \(a^{\prime}, \ b^{\prime}\) একই চিহ্নবিশিষ্ট হয় তবে \((4)\) নং সমীকরণটি একটি ( বাস্তব অথবা কাল্পনিক ) উপবৃত্ত প্রকাশ করবে।
যদি, \(k\ne{0}, \ a^{\prime}+b^{\prime}=0\) এবং \(a^{\prime}, \ b^{\prime}\) বিপরীত চিহ্নবিশিষ্ট হয় তবে \((4)\) নং সমীকরণটি একটি অধিবৃত্ত প্রকাশ করবে।
যদি, \(k\ne{0}\) এবং \(a^{\prime}=b^{\prime}\) হয় তবে \((4)\) নং সমীকরণটি একটি বৃত্ত প্রকাশ করবে।
এখন, \(a^{\prime}\) ও \(b^{\prime}\) এর চিহ্ন একই হলে
\(a^{\prime}b^{\prime}>0\) হয়।
\(\therefore ab-h^2\gt{0}\)
আবার, \(a^{\prime}\) ও \(b^{\prime}\) এর চিহ্ন বিপরীত হলে
\(a^{\prime}b^{\prime}<0\) হয়।
\(\therefore ab-h^2\lt{0}\)
আবার, \(a^{\prime}+b^{\prime}=0\) হলে
\(a+b=0\) হয়।
এবং \(a^{\prime}b^{\prime}=0\) হলে
\(ab-h^2=0\) হয়।
আমরা জানি,
\(\Delta=\left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c\end{array}\right|=0\) হলে
\((1)\) নং সমীকরণটি একজোড়া সরলরেখা প্রকাশ করে।
সুতরাং \((1)\) নং সমীকরণটি ( স্থানাঙ্কের অক্ষদ্বয় আয়তাকার হলে )
\((i)\) একটি পরাবৃত্ত প্রকাশ করবে যদি \(\Delta\ne{0}\) এবং \(ab-h^2=0\) হয়।
\((ii)\) একটি উপবৃত্ত প্রকাশ করবে যদি \(\Delta\ne{0}\) এবং \(ab-h^2\gt{0}\) হয়।
\((iii)\) একটি অধিবৃত্ত প্রকাশ করবে যদি \(\Delta\ne{0}\) এবং \(ab-h^2\lt{0} \) হয়।
আর এই অধিবৃত্তটি আয়াতাকার হবে যদি \(a+b=0\) হয়।
ইহাই নির্ণেয় শর্ত।
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের কেন্দ্রঃ
\(\left(\frac{hf-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)সমাধানঃ
মনে করি,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
\((1)\) নং সমীকরণকে যথাক্রমে \(x\) ও \(y\) এর সাপেক্ষে আংশিক অন্তরীকরণ করে,
\(\frac{\partial}{\partial{x}}(ax^2+2hxy+by^2+2gx+2fy+c)=0\)
\(\Rightarrow a.2x+2hy.1+0+2g.1+0+0=0\)
\(\Rightarrow 2ax+2hy+2g=0\)
\(\Rightarrow 2(ax+hy+g)=0\)
\(\therefore ax+hy+g=0 .....(2)\)
আবার,
\(\frac{\partial}{\partial{y}}(ax^2+2hxy+by^2+2gx+2fy+c)=0\)
\(\Rightarrow 0+2hx.1+b.2y+0+2f.1+0=0\)
\(\Rightarrow 2hx+2by+2f=0\)
\(\Rightarrow 2(hx+by+f)=0\)
\(\therefore hx+by+f=0 .....(3)\)
\((2)\) ও \((3)\) বজ্রগুণ করে,
\(ax+hy+g=0\)
\(hx+by+f=0\)
\(\frac{x}{hf-bg}=\frac{y}{hg-ab}=\frac{1}{ab-h^2}\)
\(\Rightarrow \frac{x}{hf-bg}=\frac{1}{ab-h^2}, \ \frac{y}{hg-ab}=\frac{1}{ab-h^2}\)
\(\therefore x=\frac{hf-bg}{ab-h^2}, \ y=\frac{hg-ab}{ab-h^2}\)
\(\therefore\) নির্ণেয় কণিকের কেন্দ্র \(\left(\frac{hf-bg}{ab-h^2}, \frac{hg-af}{ab-h^2}\right)\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
\((1)\) নং সমীকরণকে যথাক্রমে \(x\) ও \(y\) এর সাপেক্ষে আংশিক অন্তরীকরণ করে,
\(\frac{\partial}{\partial{x}}(ax^2+2hxy+by^2+2gx+2fy+c)=0\)
\(\Rightarrow a.2x+2hy.1+0+2g.1+0+0=0\)
\(\Rightarrow 2ax+2hy+2g=0\)
\(\Rightarrow 2(ax+hy+g)=0\)
\(\therefore ax+hy+g=0 .....(2)\)
আবার,
\(\frac{\partial}{\partial{y}}(ax^2+2hxy+by^2+2gx+2fy+c)=0\)
\(\Rightarrow 0+2hx.1+b.2y+0+2f.1+0=0\)
\(\Rightarrow 2hx+2by+2f=0\)
\(\Rightarrow 2(hx+by+f)=0\)
\(\therefore hx+by+f=0 .....(3)\)
\((2)\) ও \((3)\) বজ্রগুণ করে,
\(ax+hy+g=0\)
\(hx+by+f=0\)
\(\frac{x}{hf-bg}=\frac{y}{hg-ab}=\frac{1}{ab-h^2}\)
\(\Rightarrow \frac{x}{hf-bg}=\frac{1}{ab-h^2}, \ \frac{y}{hg-ab}=\frac{1}{ab-h^2}\)
\(\therefore x=\frac{hf-bg}{ab-h^2}, \ y=\frac{hg-ab}{ab-h^2}\)
\(\therefore\) নির্ণেয় কণিকের কেন্দ্র \(\left(\frac{hf-bg}{ab-h^2}, \frac{hg-af}{ab-h^2}\right)\)
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কেন্দ্রিক কণিকের প্রমাণ আকারঃ
\(a^{\prime}x^2+b^{\prime}y^2+\frac{\Delta}{ab-h^2}=0\)সমাধানঃ
মনে করি,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
সমীকরণটি একটি কেন্দ্রিক কণিক প্রকাশ করে এবং এর কেন্দ্র \((\alpha, \beta)\)
তাহলে, \(\Delta=abc+2fgh-af^2-bg^2-ch^2\ne{0}, \ ab-h^2\ne{0}\)
এখন, অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুকে \((\alpha, \beta)\) বিন্দুতে স্থানান্তরিত করা হলে স্থানান্তর সূত্রঃ
\(x=x^{\prime}+\alpha\)
\(y=y^{\prime}+\beta\)
ফলে, \((1)\) সমীকরণটির পরিবর্তিত রূপ দাঁড়াবে
\(a(x^{\prime}+\alpha)^2+2h(x^{\prime}+\alpha)(y^{\prime}+\beta)+b(y^{\prime}+\beta)^2+2g(x^{\prime}+\alpha)+2f(y^{\prime}+\beta)+c=0\) ➜ \(x=x^{\prime}+\alpha\)
\(y=y^{\prime}+\beta\)
বসিয়ে
\(\therefore a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+2(a\alpha+h\beta+g)x^{\prime}+2(h\alpha+b\beta+f)y^{\prime}+\)\(a\alpha^2+2h\alpha\beta+b\beta^2+2g\alpha+2f\beta+c=0 ........(2)\)
\((1)\) নং সমীকরণ থেকে \(x^{\prime}\) ও \(y^{\prime}\) যুক্ত পদ অপসারিত হবে যদি \(x^{\prime}\) ও \(y^{\prime}\) এর সহগ দুইটি শূন্য হয়।
অর্থাৎ যদি
\(a\alpha+h\beta+g=0 .........(3)\)
এবং \(h\alpha+b\beta+f=0 .........(4)\)
পদ দুইটি অপসারণের পর \((2)\) এর রূপ দাঁড়াবে
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0 .......(5)\)
যেখানে, \(c^{\prime}=a\alpha^2+2h\alpha\beta+b\beta^2+2g\alpha+2f\beta+c\)
\(=a\alpha^2+h\alpha\beta+g\alpha+h\alpha\beta+b\beta^2+f\beta+g\alpha+f\beta+c\)
\(=\alpha(a\alpha+h\beta+g)+\beta(h\alpha+b\beta+f)+g\alpha+f\beta+c\)
\(=\alpha(0)+\beta(0)+g\alpha+f\beta+c\) ➜ \(\because a\alpha+h\beta+g=0\)
\(h\alpha+b\beta+f=0\)
\((3)\) ও \((4)\) হতে,
\(=0+0+g\alpha+f\beta+c\)
\(\therefore c^{\prime}=g\alpha+f\beta+c\)
আবার
\((3)\) ও \((4)\) সমাধান করি
\(a\alpha+h\beta+g=0\)
\(h\alpha+b\beta+f=0\)
\(\frac{\alpha}{hf-bg}=\frac{\beta}{hg-af}=\frac{1}{ab-h^2}\)
\(\Rightarrow \frac{\alpha}{hf-bg}=\frac{1}{ab-h^2}, \ \frac{\beta}{hg-af}=\frac{1}{ab-h^2}\)
\(\therefore \alpha=\frac{hf-bg}{ab-h^2}, \ \beta=\frac{hg-af}{ab-h^2}\)
\(\therefore (\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
এখন, \(c^{\prime}=g\alpha+f\beta+c\)
\(=g\frac{fh-bg}{ab-h^2}+f\frac{gh-af}{ab-h^2}+c\)
\(=\frac{fgh-bg^2}{ab-h^2}+\frac{fgh-af^2}{ab-h^2}+c\)
\(=\frac{fgh-bg^2+fgh-af^2+abc-ch^2}{ab-h^2}\)
\(=\frac{abc+2fgh-af^2-bg^2-ch^2}{ab-h^2}\)
\(\therefore c^{\prime}=\frac{\Delta}{ab-h^2}\)
ধরা যাক, স্থানাঙ্কের অক্ষদ্বয় আয়াতাকার। নতুন মূলবিন্দুতে অক্ষদ্বয়কে \(\theta=\frac{1}{2}\tan^{-1}{\frac{2h}{a-b}}\) কোণে ঘুরানো হলো।
তাহলে, \((5)\) নং সমীকরণ থেকে \(x^{\prime}y^{\prime}\) যুক্ত পদ অপসারিত হবে এবং সমীকরণটির পরিবর্তিত রূপ হবে,
\(a^{\prime}x^2+b^{\prime}y^2+c^{\prime}=0\) ➜ যেখানে, স্থানাঙ্কের রূপান্তর সূত্র
\(x^{\prime}=x\cos{\theta}-y\sin{\theta}\)
এবং \(y^{\prime}=x\sin{\theta}+y\cos{\theta}\)
\(\therefore a^{\prime}x^2+b^{\prime}y^2+\frac{\Delta}{ab-h^2}=0\) ➜ \(\because c^{\prime}=\frac{\Delta}{ab-h^2}\)
ইহাই নির্ণেয় কেন্দ্রিক কণিকের প্রমাণ আকার।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
সমীকরণটি একটি কেন্দ্রিক কণিক প্রকাশ করে এবং এর কেন্দ্র \((\alpha, \beta)\)
তাহলে, \(\Delta=abc+2fgh-af^2-bg^2-ch^2\ne{0}, \ ab-h^2\ne{0}\)
এখন, অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুকে \((\alpha, \beta)\) বিন্দুতে স্থানান্তরিত করা হলে স্থানান্তর সূত্রঃ
\(x=x^{\prime}+\alpha\)
\(y=y^{\prime}+\beta\)
ফলে, \((1)\) সমীকরণটির পরিবর্তিত রূপ দাঁড়াবে
\(a(x^{\prime}+\alpha)^2+2h(x^{\prime}+\alpha)(y^{\prime}+\beta)+b(y^{\prime}+\beta)^2+2g(x^{\prime}+\alpha)+2f(y^{\prime}+\beta)+c=0\) ➜ \(x=x^{\prime}+\alpha\)
\(y=y^{\prime}+\beta\)
বসিয়ে
\(\therefore a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+2(a\alpha+h\beta+g)x^{\prime}+2(h\alpha+b\beta+f)y^{\prime}+\)\(a\alpha^2+2h\alpha\beta+b\beta^2+2g\alpha+2f\beta+c=0 ........(2)\)
\((1)\) নং সমীকরণ থেকে \(x^{\prime}\) ও \(y^{\prime}\) যুক্ত পদ অপসারিত হবে যদি \(x^{\prime}\) ও \(y^{\prime}\) এর সহগ দুইটি শূন্য হয়।
অর্থাৎ যদি
\(a\alpha+h\beta+g=0 .........(3)\)
এবং \(h\alpha+b\beta+f=0 .........(4)\)
পদ দুইটি অপসারণের পর \((2)\) এর রূপ দাঁড়াবে
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0 .......(5)\)
যেখানে, \(c^{\prime}=a\alpha^2+2h\alpha\beta+b\beta^2+2g\alpha+2f\beta+c\)
\(=a\alpha^2+h\alpha\beta+g\alpha+h\alpha\beta+b\beta^2+f\beta+g\alpha+f\beta+c\)
\(=\alpha(a\alpha+h\beta+g)+\beta(h\alpha+b\beta+f)+g\alpha+f\beta+c\)
\(=\alpha(0)+\beta(0)+g\alpha+f\beta+c\) ➜ \(\because a\alpha+h\beta+g=0\)
\(h\alpha+b\beta+f=0\)
\((3)\) ও \((4)\) হতে,
\(=0+0+g\alpha+f\beta+c\)
\(\therefore c^{\prime}=g\alpha+f\beta+c\)
আবার
\((3)\) ও \((4)\) সমাধান করি
\(a\alpha+h\beta+g=0\)
\(h\alpha+b\beta+f=0\)
\(\frac{\alpha}{hf-bg}=\frac{\beta}{hg-af}=\frac{1}{ab-h^2}\)
\(\Rightarrow \frac{\alpha}{hf-bg}=\frac{1}{ab-h^2}, \ \frac{\beta}{hg-af}=\frac{1}{ab-h^2}\)
\(\therefore \alpha=\frac{hf-bg}{ab-h^2}, \ \beta=\frac{hg-af}{ab-h^2}\)
\(\therefore (\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
এখন, \(c^{\prime}=g\alpha+f\beta+c\)
\(=g\frac{fh-bg}{ab-h^2}+f\frac{gh-af}{ab-h^2}+c\)
\(=\frac{fgh-bg^2}{ab-h^2}+\frac{fgh-af^2}{ab-h^2}+c\)
\(=\frac{fgh-bg^2+fgh-af^2+abc-ch^2}{ab-h^2}\)
\(=\frac{abc+2fgh-af^2-bg^2-ch^2}{ab-h^2}\)
\(\therefore c^{\prime}=\frac{\Delta}{ab-h^2}\)
ধরা যাক, স্থানাঙ্কের অক্ষদ্বয় আয়াতাকার। নতুন মূলবিন্দুতে অক্ষদ্বয়কে \(\theta=\frac{1}{2}\tan^{-1}{\frac{2h}{a-b}}\) কোণে ঘুরানো হলো।
তাহলে, \((5)\) নং সমীকরণ থেকে \(x^{\prime}y^{\prime}\) যুক্ত পদ অপসারিত হবে এবং সমীকরণটির পরিবর্তিত রূপ হবে,
\(a^{\prime}x^2+b^{\prime}y^2+c^{\prime}=0\) ➜ যেখানে, স্থানাঙ্কের রূপান্তর সূত্র
\(x^{\prime}=x\cos{\theta}-y\sin{\theta}\)
এবং \(y^{\prime}=x\sin{\theta}+y\cos{\theta}\)
\(\therefore a^{\prime}x^2+b^{\prime}y^2+\frac{\Delta}{ab-h^2}=0\) ➜ \(\because c^{\prime}=\frac{\Delta}{ab-h^2}\)
ইহাই নির্ণেয় কেন্দ্রিক কণিকের প্রমাণ আকার।
×
\(Ax^2+2Hxy+By^2=1\) কণিকের ক্ষেত্রেঃ
যদি কণিকের অর্ধাক্ষের দৈর্ঘ্য \(r\) হয় তবে, \((AB-H^2)r^4-(A+B)r^2+1=0\) \(r_{1}\) এবং \(r_{2}\) উভয়ে ধনাত্মক হলে কণিকটি উপবৃত্ত হবে সেক্ষেত্রেঃ
বৃহৎ অক্ষের দৈর্ঘ্য \(=2r_{1}, \ \ r_{1}>r_{2}\).png)
ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=2r_{2}, \ \ r_{1}>r_{2}\)
\(r_{1}\) এবং \(r_{2}\) এর একটি ধনাত্মক এবং অপরটি ঋণাত্মক হলে কণিকটি অধিবৃত্ত হবে সেক্ষেত্রেঃ
আড় অক্ষের দৈর্ঘ্য \(=2r_{1}\)
অনুবন্ধী অক্ষের দৈর্ঘ্য \(=2\sqrt{|r_{2}^2|}\)
উভয় ক্ষেত্রে উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2r_{2}^2}{r_{1}}\right|\)
উভয় ক্ষেত্রে বিকেন্দ্রিকতা \(e=\sqrt{1-\frac{r_{2}^2}{r_{1}^2}}\)
বৃহৎ অক্ষের সমীকরণ \(\left(A-\frac{1}{r_{1}^2}\right)x+Hy=0\) ক্ষুদ্রাক্ষের সমীকরণ \(\left(A-\frac{1}{r_{2}^2}\right)x+Hy=0\) শীর্ষদ্বয়ের স্থানাঙ্ক \(A(\alpha+r_{1}\cos{\theta}, \beta+r_{1}\sin{\theta})\) এবং \(A^{\prime}(\alpha-r_{1}\cos{\theta}, \beta-r_{1}\sin{\theta})\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\) ফোকাসদ্বয়ের স্থানাঙ্ক \(S(\alpha+r_{1}e\cos{\theta}, \beta+r_{1}e\sin{\theta})\) এবং \(S^{\prime}(\alpha-r_{1}e\cos{\theta}, \beta-r_{1}e\sin{\theta})\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\) নিয়ামকদ্বয়ের পাদবিন্দুর স্থানাঙ্ক \(Z\left(\alpha+\frac{r_{1}}{e}\cos{\theta}, \beta+\frac{r_{1}}{e}\sin{\theta}\right)\) এবং \(Z^{\prime}\left(\alpha-\frac{r_{1}}{e}\cos{\theta}, \beta-\frac{r_{1}}{e}\sin{\theta}\right)\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\)
যদি কণিকের অর্ধাক্ষের দৈর্ঘ্য \(r\) হয় তবে, \((AB-H^2)r^4-(A+B)r^2+1=0\) \(r_{1}\) এবং \(r_{2}\) উভয়ে ধনাত্মক হলে কণিকটি উপবৃত্ত হবে সেক্ষেত্রেঃ
বৃহৎ অক্ষের দৈর্ঘ্য \(=2r_{1}, \ \ r_{1}>r_{2}\)
.png)
ক্ষুদ্রাক্ষের দৈর্ঘ্য \(=2r_{2}, \ \ r_{1}>r_{2}\)
\(r_{1}\) এবং \(r_{2}\) এর একটি ধনাত্মক এবং অপরটি ঋণাত্মক হলে কণিকটি অধিবৃত্ত হবে সেক্ষেত্রেঃ
আড় অক্ষের দৈর্ঘ্য \(=2r_{1}\)
অনুবন্ধী অক্ষের দৈর্ঘ্য \(=2\sqrt{|r_{2}^2|}\)
উভয় ক্ষেত্রে উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2r_{2}^2}{r_{1}}\right|\)
উভয় ক্ষেত্রে বিকেন্দ্রিকতা \(e=\sqrt{1-\frac{r_{2}^2}{r_{1}^2}}\)
বৃহৎ অক্ষের সমীকরণ \(\left(A-\frac{1}{r_{1}^2}\right)x+Hy=0\) ক্ষুদ্রাক্ষের সমীকরণ \(\left(A-\frac{1}{r_{2}^2}\right)x+Hy=0\) শীর্ষদ্বয়ের স্থানাঙ্ক \(A(\alpha+r_{1}\cos{\theta}, \beta+r_{1}\sin{\theta})\) এবং \(A^{\prime}(\alpha-r_{1}\cos{\theta}, \beta-r_{1}\sin{\theta})\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\) ফোকাসদ্বয়ের স্থানাঙ্ক \(S(\alpha+r_{1}e\cos{\theta}, \beta+r_{1}e\sin{\theta})\) এবং \(S^{\prime}(\alpha-r_{1}e\cos{\theta}, \beta-r_{1}e\sin{\theta})\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\) নিয়ামকদ্বয়ের পাদবিন্দুর স্থানাঙ্ক \(Z\left(\alpha+\frac{r_{1}}{e}\cos{\theta}, \beta+\frac{r_{1}}{e}\sin{\theta}\right)\) এবং \(Z^{\prime}\left(\alpha-\frac{r_{1}}{e}\cos{\theta}, \beta-\frac{r_{1}}{e}\sin{\theta}\right)\) যেখানে, কেন্দ্র \(C(\alpha, \beta)\)
সমাধানঃ
ধরি,
\(Ax^2+2Hxy+By^2=1 ..........(1)\).png)
কণিকটির সাথে সমকেন্দ্রিক এবং \(r\) ব্যাসার্ধ বিশিষ্ট বৃত্তের সমীকরণ,
\(x^2+y^2=r^2\)
\(\Rightarrow \frac{x^2+y^2}{r^2}=1 .......(2)\)
\((1)\) কে \((2)\) এর সাহায্যে সমমাত্রিক করি,
\(Ax^2+2Hxy+By^2=\frac{x^2+y^2}{r^2}\)
\(\Rightarrow Ax^2+2Hxy+By^2-\frac{x^2+y^2}{r^2}=0\)
\(\Rightarrow Ax^2+2Hxy+By^2-\frac{x^2}{r^2}-\frac{y^2}{r^2}=0\)
\(\Rightarrow Ax^2-\frac{x^2}{r^2}+2Hxy+By^2-\frac{y^2}{r^2}=0\)
\(\therefore \left(A-\frac{1}{r^2}\right)x^2+2Hxy+\left(B-\frac{1}{r^2}\right)y^2=0 .......(3)\)
এটি দুইটি সরলরেখা নির্দেশ করে যারা মূলবিন্দু তথা কণিকের কেন্দ্র এবং কনিক ও বৃত্তের ছেদবিন্দু দিয়ে অতিক্রম করে। এই রেখা দুইটি সমাপতিত হয় যখন এবং কেবল যখন এরা কণিকটির কোনো অক্ষ বরাবর অবস্থান করে।
আর রেখা দুইটির সমাপতিত হওয়ার শর্ত হল,
\(\left(A-\frac{1}{r^2}\right)\left(B-\frac{1}{r^2}\right)=H^2\)
\(\Rightarrow AB-\frac{A}{r^2}-\frac{B}{r^2}+\frac{1}{r^4}=H^2\)
\(\Rightarrow ABr^4-Ar^2-Br^2+1=H^2r^4\)
\(\Rightarrow ABr^4-H^2r^4-Ar^2-Br^2+1=0\)
\(\therefore (AB-H^2)r^4-(A+B)r^2+1=0 .......(4)\)
এটি \(r^2\) এর দ্বিঘাত সমীকরণ। ধরা যাক \(r^2\) এর মাণ দুইটি \(r_{1}^2\) এবং \(r_{2}^2\)
যদি কণিকটি একটি উপবৃত্ত হয় তবে, \(r_{1}, \ r_{2}\) উভয়ে ধনাত্মক হবে এবং উপবৃত্তটির অক্ষ দুইটির দৈর্ঘ্য হবে \(2r_{1}\) এবং \(2r_{2}\) ।
যদি কণিকটি একটি অধিবৃত্ত হয় তবে, \(r_{1}, \ r_{2}\) এর একটি ধনাত্মক এবং অপরটি ঋণাত্মক হবে।
ধরা যাক \(r_{1}^2>0\) এবং \(r_{2}^2<0\).
অতএব অধিবৃত্তটির আড় অক্ষের দৈর্ঘ্য \(2r_{1}\)
এবং অনুবন্ধী অক্ষের দৈর্ঘ্য \(2\sqrt{|r_{2}^2|}\).
\((3)\) নং সমীকরণকে \(\left(A-\frac{1}{r^2}\right)\) দ্বারা গুণ করে।
\(\left(A-\frac{1}{r^2}\right)^2x^2+2H\left(A-\frac{1}{r^2}\right)xy+\left(A-\frac{1}{r^2}\right)\left(B-\frac{1}{r^2}\right)y^2=0\)
\(\Rightarrow \left(A-\frac{1}{r^2}\right)^2x^2+2H\left(A-\frac{1}{r^2}\right)xy+H^2y^2=0\) ➜ \(\because \left(A-\frac{1}{r^2}\right)\left(B-\frac{1}{r^2}\right)=H^2\)
\(\Rightarrow \left\{\left(A-\frac{1}{r^2}\right)x\right\}^2+2\left(A-\frac{1}{r^2}\right)x.Hy+(Hy)^2=0\)
\(\Rightarrow \left\{\left(A-\frac{1}{r^2}\right)x+Hy\right\}^2=0\)
\(\therefore \left(A-\frac{1}{r^2}\right)x+Hy=0 .........(5)\)
উপবৃত্তের ক্ষেত্রে \(r_{1}^2>r_{2}^2\) হলে,
উপবৃত্তের বৃহৎ অক্ষের সমীকরণ, \(\left(A-\frac{1}{r_{1}^2}\right)x+Hy=0 .........(6)\)
উপবৃত্তের ক্ষুদ্রাক্ষের সমীকরণ, \(\left(A-\frac{1}{r_{2}^2}\right)x+Hy=0 .........(7)\)
যেখানে \(r_{1}\) ও \(r_{2}\) যথাক্রমে বৃহৎ অর্ধাক্ষ ও ক্ষুদ্র অর্ধাক্ষ সূচিত করে।
অধিবৃত্তের ক্ষেত্রে \(r_{2}^2<0\) হলে,
অধিবৃত্তের আড় অক্ষের সমীকরণ, \(\left(A-\frac{1}{r_{1}^2}\right)x+Hy=0 .........(8)\)
অধিবৃত্তের অনুবন্ধী অক্ষের সমীকরণ, \(\left(A-\frac{1}{r_{2}^2}\right)x+Hy=0 .........(9)\)
যেখানে \(r_{1}\) ও \(r_{2}\) যথাক্রমে আড় অর্ধাক্ষ ও অনুবন্ধী অর্ধাক্ষ সূচিত করে।
উভয় ক্ষেত্রে বিকেন্দ্রিকতা, \(e=\sqrt{1-\frac{r_{2}^2}{r_{1}^2}}\).png)
\((6)\) নং সমীকরণটির ঢাল \(=\frac{\left(A-\frac{1}{r_{2}^2}\right)}{H}\) থেকে \(\sin{\theta}\) ও \(\cos{\theta}\) এর মাণ পাওয়া যায়।
চিত্রে, \(AA^{\prime}\) রেখাটি বৃহৎ অক্ষ ও আড় অক্ষ নির্দেশ করেছে যা নতুন ও আদি \(x\) অক্ষের উভয়ের ধনাত্মক দিকের সাথে \(\theta\) কোণ উৎপন্ন করে।
ফোকাস দুইটি \(S, \ S^{\prime},\) শীর্ষ দুইটি \(A, \ A^{\prime}\) এবং নিয়ামকদ্বয়ের পাদবিন্দু দুইটি \(Z, \ Z^{\prime}\) বিন্দু দ্বারা সূচিত।
\(\therefore CA=r_{1}, \ CS=r_{1}e, CZ=\frac{r_{1}}{e}\)
যেহেতু \(C\) এর স্থানাঙ্ক \((\alpha, \beta)\) কাজেই আদি অক্ষের প্রেক্ষিতে
শীর্ষ \(A\) ও \(A^{\prime}\) এর স্থানাঙ্ক \((\alpha+r_{1}\cos{\theta}, \beta+r_{1}\sin{\theta})\) ও \((\alpha-r_{1}\cos{\theta}, \beta-r_{1}\sin{\theta})\)
ফোকাস \(S\) ও \(S^{\prime}\) এর স্থানাঙ্ক \((\alpha+r_{1}e\cos{\theta}, \beta+r_{1}e\sin{\theta})\) ও \((\alpha-r_{1}e\cos{\theta}, \beta-r_{1}e\sin{\theta})\)
নিয়ামকদ্বয়ের পাদবিন্দু \(Z\) ও \(Z^{\prime}\) এর স্থানাঙ্ক \((\alpha+\frac{r_{1}}{e}\cos{\theta}, \beta+\frac{r_{1}}{e}\sin{\theta})\) ও \((\alpha-\frac{r_{1}}{e}\cos{\theta}, \beta-\frac{r_{1}}{e}\sin{\theta})\)
এখন ক্ষুদ্রাক্ষ বা অনুবন্ধী অক্ষের সমান্তরাল এবং ফোকাস \(S\) ও \(S^{\prime}\) গামী সরলরেখাই কণিকটির ফোকাস লম্ব।
ক্ষুদ্রাক্ষ বা অনুবন্ধী অক্ষের সমান্তরাল এবং নিয়ামকদ্বয়ের পাদবিন্দু \(Z\) ও \(Z^{\prime}\) গামী সরলরেখাই কণিকটির নিয়ামক।
ক্ষুদ্রাক্ষ বা অনুবন্ধী অক্ষের সমান্তরাল এবং শীর্ষ \(A\) ও \(A^{\prime}\) গামী সরলরেখাই কণিকটির শীর্ষবিন্দুতে স্পর্শক হবে।
\(Ax^2+2Hxy+By^2=1 ..........(1)\)
.png)
কণিকটির সাথে সমকেন্দ্রিক এবং \(r\) ব্যাসার্ধ বিশিষ্ট বৃত্তের সমীকরণ,
\(x^2+y^2=r^2\)
\(\Rightarrow \frac{x^2+y^2}{r^2}=1 .......(2)\)
\((1)\) কে \((2)\) এর সাহায্যে সমমাত্রিক করি,
\(Ax^2+2Hxy+By^2=\frac{x^2+y^2}{r^2}\)
\(\Rightarrow Ax^2+2Hxy+By^2-\frac{x^2+y^2}{r^2}=0\)
\(\Rightarrow Ax^2+2Hxy+By^2-\frac{x^2}{r^2}-\frac{y^2}{r^2}=0\)
\(\Rightarrow Ax^2-\frac{x^2}{r^2}+2Hxy+By^2-\frac{y^2}{r^2}=0\)
\(\therefore \left(A-\frac{1}{r^2}\right)x^2+2Hxy+\left(B-\frac{1}{r^2}\right)y^2=0 .......(3)\)
এটি দুইটি সরলরেখা নির্দেশ করে যারা মূলবিন্দু তথা কণিকের কেন্দ্র এবং কনিক ও বৃত্তের ছেদবিন্দু দিয়ে অতিক্রম করে। এই রেখা দুইটি সমাপতিত হয় যখন এবং কেবল যখন এরা কণিকটির কোনো অক্ষ বরাবর অবস্থান করে।
আর রেখা দুইটির সমাপতিত হওয়ার শর্ত হল,
\(\left(A-\frac{1}{r^2}\right)\left(B-\frac{1}{r^2}\right)=H^2\)
\(\Rightarrow AB-\frac{A}{r^2}-\frac{B}{r^2}+\frac{1}{r^4}=H^2\)
\(\Rightarrow ABr^4-Ar^2-Br^2+1=H^2r^4\)
\(\Rightarrow ABr^4-H^2r^4-Ar^2-Br^2+1=0\)
\(\therefore (AB-H^2)r^4-(A+B)r^2+1=0 .......(4)\)
এটি \(r^2\) এর দ্বিঘাত সমীকরণ। ধরা যাক \(r^2\) এর মাণ দুইটি \(r_{1}^2\) এবং \(r_{2}^2\)
যদি কণিকটি একটি উপবৃত্ত হয় তবে, \(r_{1}, \ r_{2}\) উভয়ে ধনাত্মক হবে এবং উপবৃত্তটির অক্ষ দুইটির দৈর্ঘ্য হবে \(2r_{1}\) এবং \(2r_{2}\) ।
যদি কণিকটি একটি অধিবৃত্ত হয় তবে, \(r_{1}, \ r_{2}\) এর একটি ধনাত্মক এবং অপরটি ঋণাত্মক হবে।
ধরা যাক \(r_{1}^2>0\) এবং \(r_{2}^2<0\).
অতএব অধিবৃত্তটির আড় অক্ষের দৈর্ঘ্য \(2r_{1}\)
এবং অনুবন্ধী অক্ষের দৈর্ঘ্য \(2\sqrt{|r_{2}^2|}\).
\((3)\) নং সমীকরণকে \(\left(A-\frac{1}{r^2}\right)\) দ্বারা গুণ করে।
\(\left(A-\frac{1}{r^2}\right)^2x^2+2H\left(A-\frac{1}{r^2}\right)xy+\left(A-\frac{1}{r^2}\right)\left(B-\frac{1}{r^2}\right)y^2=0\)
\(\Rightarrow \left(A-\frac{1}{r^2}\right)^2x^2+2H\left(A-\frac{1}{r^2}\right)xy+H^2y^2=0\) ➜ \(\because \left(A-\frac{1}{r^2}\right)\left(B-\frac{1}{r^2}\right)=H^2\)
\(\Rightarrow \left\{\left(A-\frac{1}{r^2}\right)x\right\}^2+2\left(A-\frac{1}{r^2}\right)x.Hy+(Hy)^2=0\)
\(\Rightarrow \left\{\left(A-\frac{1}{r^2}\right)x+Hy\right\}^2=0\)
\(\therefore \left(A-\frac{1}{r^2}\right)x+Hy=0 .........(5)\)
উপবৃত্তের ক্ষেত্রে \(r_{1}^2>r_{2}^2\) হলে,
উপবৃত্তের বৃহৎ অক্ষের সমীকরণ, \(\left(A-\frac{1}{r_{1}^2}\right)x+Hy=0 .........(6)\)
উপবৃত্তের ক্ষুদ্রাক্ষের সমীকরণ, \(\left(A-\frac{1}{r_{2}^2}\right)x+Hy=0 .........(7)\)
যেখানে \(r_{1}\) ও \(r_{2}\) যথাক্রমে বৃহৎ অর্ধাক্ষ ও ক্ষুদ্র অর্ধাক্ষ সূচিত করে।
অধিবৃত্তের ক্ষেত্রে \(r_{2}^2<0\) হলে,
অধিবৃত্তের আড় অক্ষের সমীকরণ, \(\left(A-\frac{1}{r_{1}^2}\right)x+Hy=0 .........(8)\)
অধিবৃত্তের অনুবন্ধী অক্ষের সমীকরণ, \(\left(A-\frac{1}{r_{2}^2}\right)x+Hy=0 .........(9)\)
যেখানে \(r_{1}\) ও \(r_{2}\) যথাক্রমে আড় অর্ধাক্ষ ও অনুবন্ধী অর্ধাক্ষ সূচিত করে।
উভয় ক্ষেত্রে বিকেন্দ্রিকতা, \(e=\sqrt{1-\frac{r_{2}^2}{r_{1}^2}}\)
.png)
\((6)\) নং সমীকরণটির ঢাল \(=\frac{\left(A-\frac{1}{r_{2}^2}\right)}{H}\) থেকে \(\sin{\theta}\) ও \(\cos{\theta}\) এর মাণ পাওয়া যায়।
চিত্রে, \(AA^{\prime}\) রেখাটি বৃহৎ অক্ষ ও আড় অক্ষ নির্দেশ করেছে যা নতুন ও আদি \(x\) অক্ষের উভয়ের ধনাত্মক দিকের সাথে \(\theta\) কোণ উৎপন্ন করে।
ফোকাস দুইটি \(S, \ S^{\prime},\) শীর্ষ দুইটি \(A, \ A^{\prime}\) এবং নিয়ামকদ্বয়ের পাদবিন্দু দুইটি \(Z, \ Z^{\prime}\) বিন্দু দ্বারা সূচিত।
\(\therefore CA=r_{1}, \ CS=r_{1}e, CZ=\frac{r_{1}}{e}\)
যেহেতু \(C\) এর স্থানাঙ্ক \((\alpha, \beta)\) কাজেই আদি অক্ষের প্রেক্ষিতে
শীর্ষ \(A\) ও \(A^{\prime}\) এর স্থানাঙ্ক \((\alpha+r_{1}\cos{\theta}, \beta+r_{1}\sin{\theta})\) ও \((\alpha-r_{1}\cos{\theta}, \beta-r_{1}\sin{\theta})\)
ফোকাস \(S\) ও \(S^{\prime}\) এর স্থানাঙ্ক \((\alpha+r_{1}e\cos{\theta}, \beta+r_{1}e\sin{\theta})\) ও \((\alpha-r_{1}e\cos{\theta}, \beta-r_{1}e\sin{\theta})\)
নিয়ামকদ্বয়ের পাদবিন্দু \(Z\) ও \(Z^{\prime}\) এর স্থানাঙ্ক \((\alpha+\frac{r_{1}}{e}\cos{\theta}, \beta+\frac{r_{1}}{e}\sin{\theta})\) ও \((\alpha-\frac{r_{1}}{e}\cos{\theta}, \beta-\frac{r_{1}}{e}\sin{\theta})\)
এখন ক্ষুদ্রাক্ষ বা অনুবন্ধী অক্ষের সমান্তরাল এবং ফোকাস \(S\) ও \(S^{\prime}\) গামী সরলরেখাই কণিকটির ফোকাস লম্ব।
ক্ষুদ্রাক্ষ বা অনুবন্ধী অক্ষের সমান্তরাল এবং নিয়ামকদ্বয়ের পাদবিন্দু \(Z\) ও \(Z^{\prime}\) গামী সরলরেখাই কণিকটির নিয়ামক।
ক্ষুদ্রাক্ষ বা অনুবন্ধী অক্ষের সমান্তরাল এবং শীর্ষ \(A\) ও \(A^{\prime}\) গামী সরলরেখাই কণিকটির শীর্ষবিন্দুতে স্পর্শক হবে।
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কেন্দ্রবিহীন কণিকের প্রমাণ আকারঃ
\(y^2=4a^{\prime}x\)যেখানে, \(a^{\prime}=\frac{\sqrt{(k\sqrt{a}-g)^2+(k\sqrt{b}-f)^2}}{2(a+b)}\)
এবং \(k=\frac{g\sqrt{a}+f\sqrt{b}}{a+b}\)
সমাধানঃ
মনে করি,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
সমীকরণটি একটি কেন্দ্রবিহীন কণিক অর্থাৎ পরাবৃত্ত প্রকাশ করে।
তাহলে, \(\Delta=abc+2fgh-af^2-bg^2-ch^2\ne{0}\)
এবং \(ab-h^2=0\)
\(\Rightarrow h^2=ab\)
\(\therefore h=\sqrt{ab}\)
এখন, \((1)\) সমীকরণটিকে লিখা যায়
\(ax^2+2\sqrt{ab}xy+by^2+2gx+2fy+c=0\)
\(\Rightarrow (\sqrt{a}x)^2+2\sqrt{a}x\sqrt{b}y+(\sqrt{b}y)^2+2gx+2fy+c=0\)
\(\Rightarrow (\sqrt{a}x+\sqrt{b}y)^2+2gx+2fy+c=0\)
\(\Rightarrow (\sqrt{a}x+\sqrt{b}y+k)^2-2k\sqrt{a}x-2k\sqrt{b}y-k^2+2gx+2fy+c=0\)
\(\Rightarrow (\sqrt{a}x+\sqrt{b}y+k)^2=2k\sqrt{a}x+2k\sqrt{b}y+k^2-2gx-2fy-c\)
\(\therefore (\sqrt{a}x+\sqrt{b}y+k)^2=2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c .....(2)\)
যেখানে ধ্রুবক \(k\) নেয়া হয়েছে এই শর্তে যে
\(\sqrt{a}x+\sqrt{b}y+k=0 ........(3)\)
এবং \(2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c=0 ........(4)\)
\((3)\) ও \((4)\) সরলরেখাদ্বয় পরস্পর লম্ব হয়।
\(\therefore \sqrt{a}.2(k\sqrt{a}-g)+\sqrt{b}.2(k\sqrt{b}-f)=0\) ➜ \(\because a_{1}x+b_{1}y+c_{1}=0\)
এবং \(a_{2}x+b_{2}y+c_{2}=0\)
সরলরেখাদ্বয়ের পরস্পর লম্ব হওয়ার শর্তঃ
\(a_{1}a_{2}+b_{1}b_{2}=0\)
\(\Rightarrow 2ak-2g\sqrt{a}+2bk-2f\sqrt{b}=0\)
\(\Rightarrow 2k(a+b)-2(g\sqrt{a}+f\sqrt{b})=0\)
\(\Rightarrow 2k(a+b)=2(g\sqrt{a}+f\sqrt{b})\)
\(\Rightarrow k=\frac{2(g\sqrt{a}+f\sqrt{b})}{2(a+b)}\)
\(\therefore k=\frac{g\sqrt{a}+f\sqrt{b}}{a+b} ......(5)\)
\(k\) এর এই মানের জন্য সরলরেখা দুইটি পরস্পর লম্ব হবে।
\((3)\) ও \((4)\) নং সরলরেখা দুইটি যথাক্রমে \((2)\) নং পরাবৃত্তটির অক্ষরেখা ও শীর্ষবিন্দুতে স্পর্শক নির্দেশ করে। আর এদের ছেদবিন্দুই শীর্ষবিন্দু।
\((3)\) ও \((4)\) নং সরলরেখা দুইটিকে যথাক্রমে স্থানাঙ্কের নতুন \(x\) অক্ষ ও \(y\) অক্ষ ধরা যাক। যদি \(P(x, y)\) আদি অক্ষদ্বয় অনুসারে পরাবৃত্তটির ওপর যে কোনো বিন্দু হয় এবং নতুন অক্ষদ্বয় অনুসারে এর স্থানাঙ্ক \((x^{\prime}, x^{\prime})\) হয় তবে,
\(x^{\prime}=\frac{2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c}{\sqrt{4(k\sqrt{a}-g)^2+4(k\sqrt{b}-f)^2}}\) ➜ \(ax+by+c=0\) ও \(bx-ay+d=0\) রেখা দুইটিকে যথাক্রমে নুতন আয়তাকার \(x\) অক্ষ ও \(y\) অক্ষ ধরে
রূপান্তর সূত্র
\(x=\frac{bx-ay+d}{\sqrt{a^2+b^2}}\)
\(y=\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
এবং \(y^{\prime}=\frac{\sqrt{a}x+\sqrt{b}y+k}{\sqrt{a+b}}\)
সমীকরণ \((2)\) কে লিখা যায়
\(\frac{(\sqrt{a}x+\sqrt{b}y+k)^2}{a+b}=\frac{2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c}{a+b}\)
\(\Rightarrow \left(\frac{\sqrt{a}x+\sqrt{b}y+k}{\sqrt{a+b}}\right)^2=\frac{\sqrt{4(k\sqrt{a}-g)^2+4(k\sqrt{b}-f)^2}}{a+b}\times{\frac{2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c}{\sqrt{4(k\sqrt{a}-g)^2+4(k\sqrt{b}-f)^2}}}\)
\(\Rightarrow {y^{\prime}}^2=\frac{2\sqrt{(k\sqrt{a}-g)^2+(k\sqrt{b}-f)^2}}{a+b}x^{\prime}\) ➜ \(\because x^{\prime}=\frac{2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c}{\sqrt{4(k\sqrt{a}-g)^2+4(k\sqrt{b}-f)^2}}\)
এবং \(y^{\prime}=\frac{\sqrt{a}x+\sqrt{b}y+k}{\sqrt{a+b}}\)
\(\Rightarrow {y^{\prime}}^2=4a^{\prime}x^{\prime}\)
যেখানে, \(a^{\prime}=\frac{\sqrt{(k\sqrt{a}-g)^2+(k\sqrt{b}-f)^2}}{2(a+b)}\)
\(\therefore y^2=4a^{\prime}x\) ➜ \(x^{\prime}\) কে \(x\) দ্বারা
এবং \(y^{\prime}\) কে \(y\) দ্বারা প্রতিস্থাপিত করে,
ইহাই নির্ণেয় কেন্দ্রবিহীন কণিকের প্রমাণ আকার।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
সমীকরণটি একটি কেন্দ্রবিহীন কণিক অর্থাৎ পরাবৃত্ত প্রকাশ করে।
তাহলে, \(\Delta=abc+2fgh-af^2-bg^2-ch^2\ne{0}\)
এবং \(ab-h^2=0\)
\(\Rightarrow h^2=ab\)
\(\therefore h=\sqrt{ab}\)
এখন, \((1)\) সমীকরণটিকে লিখা যায়
\(ax^2+2\sqrt{ab}xy+by^2+2gx+2fy+c=0\)
\(\Rightarrow (\sqrt{a}x)^2+2\sqrt{a}x\sqrt{b}y+(\sqrt{b}y)^2+2gx+2fy+c=0\)
\(\Rightarrow (\sqrt{a}x+\sqrt{b}y)^2+2gx+2fy+c=0\)
\(\Rightarrow (\sqrt{a}x+\sqrt{b}y+k)^2-2k\sqrt{a}x-2k\sqrt{b}y-k^2+2gx+2fy+c=0\)
\(\Rightarrow (\sqrt{a}x+\sqrt{b}y+k)^2=2k\sqrt{a}x+2k\sqrt{b}y+k^2-2gx-2fy-c\)
\(\therefore (\sqrt{a}x+\sqrt{b}y+k)^2=2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c .....(2)\)
যেখানে ধ্রুবক \(k\) নেয়া হয়েছে এই শর্তে যে
\(\sqrt{a}x+\sqrt{b}y+k=0 ........(3)\)
এবং \(2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c=0 ........(4)\)
\((3)\) ও \((4)\) সরলরেখাদ্বয় পরস্পর লম্ব হয়।
\(\therefore \sqrt{a}.2(k\sqrt{a}-g)+\sqrt{b}.2(k\sqrt{b}-f)=0\) ➜ \(\because a_{1}x+b_{1}y+c_{1}=0\)
এবং \(a_{2}x+b_{2}y+c_{2}=0\)
সরলরেখাদ্বয়ের পরস্পর লম্ব হওয়ার শর্তঃ
\(a_{1}a_{2}+b_{1}b_{2}=0\)
\(\Rightarrow 2ak-2g\sqrt{a}+2bk-2f\sqrt{b}=0\)
\(\Rightarrow 2k(a+b)-2(g\sqrt{a}+f\sqrt{b})=0\)
\(\Rightarrow 2k(a+b)=2(g\sqrt{a}+f\sqrt{b})\)
\(\Rightarrow k=\frac{2(g\sqrt{a}+f\sqrt{b})}{2(a+b)}\)
\(\therefore k=\frac{g\sqrt{a}+f\sqrt{b}}{a+b} ......(5)\)
\(k\) এর এই মানের জন্য সরলরেখা দুইটি পরস্পর লম্ব হবে।
\((3)\) ও \((4)\) নং সরলরেখা দুইটি যথাক্রমে \((2)\) নং পরাবৃত্তটির অক্ষরেখা ও শীর্ষবিন্দুতে স্পর্শক নির্দেশ করে। আর এদের ছেদবিন্দুই শীর্ষবিন্দু।
\((3)\) ও \((4)\) নং সরলরেখা দুইটিকে যথাক্রমে স্থানাঙ্কের নতুন \(x\) অক্ষ ও \(y\) অক্ষ ধরা যাক। যদি \(P(x, y)\) আদি অক্ষদ্বয় অনুসারে পরাবৃত্তটির ওপর যে কোনো বিন্দু হয় এবং নতুন অক্ষদ্বয় অনুসারে এর স্থানাঙ্ক \((x^{\prime}, x^{\prime})\) হয় তবে,
\(x^{\prime}=\frac{2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c}{\sqrt{4(k\sqrt{a}-g)^2+4(k\sqrt{b}-f)^2}}\) ➜ \(ax+by+c=0\) ও \(bx-ay+d=0\) রেখা দুইটিকে যথাক্রমে নুতন আয়তাকার \(x\) অক্ষ ও \(y\) অক্ষ ধরে
রূপান্তর সূত্র
\(x=\frac{bx-ay+d}{\sqrt{a^2+b^2}}\)
\(y=\frac{ax+by+c}{\sqrt{a^2+b^2}}\)
এবং \(y^{\prime}=\frac{\sqrt{a}x+\sqrt{b}y+k}{\sqrt{a+b}}\)
সমীকরণ \((2)\) কে লিখা যায়
\(\frac{(\sqrt{a}x+\sqrt{b}y+k)^2}{a+b}=\frac{2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c}{a+b}\)
\(\Rightarrow \left(\frac{\sqrt{a}x+\sqrt{b}y+k}{\sqrt{a+b}}\right)^2=\frac{\sqrt{4(k\sqrt{a}-g)^2+4(k\sqrt{b}-f)^2}}{a+b}\times{\frac{2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c}{\sqrt{4(k\sqrt{a}-g)^2+4(k\sqrt{b}-f)^2}}}\)
\(\Rightarrow {y^{\prime}}^2=\frac{2\sqrt{(k\sqrt{a}-g)^2+(k\sqrt{b}-f)^2}}{a+b}x^{\prime}\) ➜ \(\because x^{\prime}=\frac{2(k\sqrt{a}-g)x+2(k\sqrt{b}-f)y+k^2-c}{\sqrt{4(k\sqrt{a}-g)^2+4(k\sqrt{b}-f)^2}}\)
এবং \(y^{\prime}=\frac{\sqrt{a}x+\sqrt{b}y+k}{\sqrt{a+b}}\)
\(\Rightarrow {y^{\prime}}^2=4a^{\prime}x^{\prime}\)
যেখানে, \(a^{\prime}=\frac{\sqrt{(k\sqrt{a}-g)^2+(k\sqrt{b}-f)^2}}{2(a+b)}\)
\(\therefore y^2=4a^{\prime}x\) ➜ \(x^{\prime}\) কে \(x\) দ্বারা
এবং \(y^{\prime}\) কে \(y\) দ্বারা প্রতিস্থাপিত করে,
ইহাই নির্ণেয় কেন্দ্রবিহীন কণিকের প্রমাণ আকার।
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের উপরস্থ \((x_{1}, y_{1})\) বিন্দুতে এর স্পর্শকের সমীকরণঃ
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c=0\)সমাধানঃ
মনে করি,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((1)\) নং সমীকরণটিকে \(x\) এর সাপেক্ষে অন্তরীকরণ করে।
\(a\frac{d}{dx}(x^2)+2h\frac{d}{dx}(xy)+b\frac{d}{dx}(y^2)+2g\frac{d}{dx}(x)+2f\frac{d}{dx}(y)+\frac{d}{dx}(c)=0\)
\(\Rightarrow a.2x+2hx\frac{dy}{dx}+2hy.1+b2y\frac{dy}{dx}+2g.1+2f\frac{dy}{dx}+0=0\)
\(\Rightarrow 2ax+2hx\frac{dy}{dx}+2hy+2by\frac{dy}{dx}+2g+2f\frac{dy}{dx}=0\)
\(\Rightarrow 2(hx+by+f)\frac{dy}{dx}+2(ax+hy+g)=0\)
\(\Rightarrow 2(hx+by+f)\frac{dy}{dx}=-2(ax+hy+g)\)
\(\Rightarrow \frac{dy}{dx}=-\frac{2(ax+hy+g)}{2(hx+by+f)}\)
\(\Rightarrow \frac{dy}{dx}=-\frac{ax+hy+g}{hx+by+f}\)
\(\therefore (x_{1}, y_{1})\) বিন্দুতে স্পর্শকের ঢাল \(m=-\frac{ax_{1}+hy_{1}+g}{hx_{1}+by_{1}+f}\)
এখন, \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ,
\(y-y_{1}=m(x-x_{1})\)
\(\Rightarrow y-y_{1}=-\frac{ax_{1}+hy_{1}+g}{hx_{1}+by_{1}+f}(x-x_{1})\)
\(\Rightarrow (y-y_{1})(hx_{1}+by_{1}+f)=-(x-x_{1})(ax_{1}+hy_{1}+g)\)
\(\Rightarrow hx_{1}y+byy_{1}+fy-hx_{1}y_{1}-by_{1}^2-fy_{1}=-axx_{1}-hxy_{1}-gx+ax_{1}^2+hx_{1}y_{1}+gx_{1}\)
\(\Rightarrow axx_{1}+hx_{1}y+hxy_{1}+byy_{1}+gx+fy=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+gx_{1}+fy_{1}\)
\(\Rightarrow axx_{1}+h(x_{1}y+xy_{1})+byy_{1}+gx+gx_{1}+fy+fy_{1}+c=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\therefore axx_{1}+h(x_{1}y+xy_{1})+byy_{1}+g(x+x_{1})+f(y+fy_{1})+c=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c .....(2)\)
যেহেতু \((x_{1}, y_{1})\) বিন্দুটি \((1)\) নং কণিকের উপর অবস্থিত,
\(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(\therefore (2)\) হতে,
\(axx_{1}+h(x_{1}y+xy_{1})+byy_{1}+g(x+x_{1})+f(y+fy_{1})+c=0\)
ইহাই নির্ণেয় স্পর্শকের সমীকরণ।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((1)\) নং সমীকরণটিকে \(x\) এর সাপেক্ষে অন্তরীকরণ করে।
\(a\frac{d}{dx}(x^2)+2h\frac{d}{dx}(xy)+b\frac{d}{dx}(y^2)+2g\frac{d}{dx}(x)+2f\frac{d}{dx}(y)+\frac{d}{dx}(c)=0\)
\(\Rightarrow a.2x+2hx\frac{dy}{dx}+2hy.1+b2y\frac{dy}{dx}+2g.1+2f\frac{dy}{dx}+0=0\)
\(\Rightarrow 2ax+2hx\frac{dy}{dx}+2hy+2by\frac{dy}{dx}+2g+2f\frac{dy}{dx}=0\)
\(\Rightarrow 2(hx+by+f)\frac{dy}{dx}+2(ax+hy+g)=0\)
\(\Rightarrow 2(hx+by+f)\frac{dy}{dx}=-2(ax+hy+g)\)
\(\Rightarrow \frac{dy}{dx}=-\frac{2(ax+hy+g)}{2(hx+by+f)}\)
\(\Rightarrow \frac{dy}{dx}=-\frac{ax+hy+g}{hx+by+f}\)
\(\therefore (x_{1}, y_{1})\) বিন্দুতে স্পর্শকের ঢাল \(m=-\frac{ax_{1}+hy_{1}+g}{hx_{1}+by_{1}+f}\)
এখন, \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ,
\(y-y_{1}=m(x-x_{1})\)
\(\Rightarrow y-y_{1}=-\frac{ax_{1}+hy_{1}+g}{hx_{1}+by_{1}+f}(x-x_{1})\)
\(\Rightarrow (y-y_{1})(hx_{1}+by_{1}+f)=-(x-x_{1})(ax_{1}+hy_{1}+g)\)
\(\Rightarrow hx_{1}y+byy_{1}+fy-hx_{1}y_{1}-by_{1}^2-fy_{1}=-axx_{1}-hxy_{1}-gx+ax_{1}^2+hx_{1}y_{1}+gx_{1}\)
\(\Rightarrow axx_{1}+hx_{1}y+hxy_{1}+byy_{1}+gx+fy=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+gx_{1}+fy_{1}\)
\(\Rightarrow axx_{1}+h(x_{1}y+xy_{1})+byy_{1}+gx+gx_{1}+fy+fy_{1}+c=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\therefore axx_{1}+h(x_{1}y+xy_{1})+byy_{1}+g(x+x_{1})+f(y+fy_{1})+c=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c .....(2)\)
যেহেতু \((x_{1}, y_{1})\) বিন্দুটি \((1)\) নং কণিকের উপর অবস্থিত,
\(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(\therefore (2)\) হতে,
\(axx_{1}+h(x_{1}y+xy_{1})+byy_{1}+g(x+x_{1})+f(y+fy_{1})+c=0\)
ইহাই নির্ণেয় স্পর্শকের সমীকরণ।
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের উপরস্থ \((x_{1}, y_{1})\) বিন্দুতে এর অভিলম্বের সমীকরণঃ
\(\frac{x-x_{1}}{ax_{1}+hy_{1}+g}=\frac{y-y_{1}}{hx_{1}+by_{1}+f}\)সমাধানঃ
মনে করি,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((1)\) নং সমীকরণটিকে \(x\) এর সাপেক্ষে অন্তরীকরণ করে।
\(a\frac{d}{dx}(x^2)+2h\frac{d}{dx}(xy)+b\frac{d}{dx}(y^2)+2g\frac{d}{dx}(x)+2f\frac{d}{dx}(y)+\frac{d}{dx}(c)=0\)
\(\Rightarrow a.2x+2hx\frac{dy}{dx}+2hy.1+b2y\frac{dy}{dx}+2g.1+2f\frac{dy}{dx}+0=0\)
\(\Rightarrow 2ax+2hx\frac{dy}{dx}+2hy+2by\frac{dy}{dx}+2g+2f\frac{dy}{dx}=0\)
\(\Rightarrow 2(hx+by+f)\frac{dy}{dx}+2(ax+hy+g)=0\)
\(\Rightarrow 2(hx+by+f)\frac{dy}{dx}=-2(ax+hy+g)\)
\(\Rightarrow \frac{dy}{dx}=-\frac{2(ax+hy+g)}{2(hx+by+f)}\)
\(\Rightarrow \frac{dy}{dx}=-\frac{ax+hy+g}{hx+by+f}\)
\(\therefore (x_{1}, y_{1})\) বিন্দুতে স্পর্শকের ঢাল \(m=-\frac{ax_{1}+hy_{1}+g}{hx_{1}+by_{1}+f}\)
আবার, \((x_{1}, y_{1})\) বিন্দুতে অভিলম্বের ঢাল \(m_{1}=-\frac{1}{m}\)
\(=\frac{hx_{1}+by_{1}+f}{ax_{1}+hy_{1}+g}\)
এখন, \((x_{1}, y_{1})\) বিন্দুতে অভিলম্বের সমীকরণ,
\(y-y_{1}=m_{1}(x-x_{1})\)
\(\Rightarrow y-y_{1}=\frac{hx_{1}+by_{1}+f}{ax_{1}+hy_{1}+g}(x-x_{1})\)
\(\Rightarrow \frac{y-y_{1}}{hx_{1}+by_{1}+f}=\frac{x-x_{1}}{ax_{1}+hy_{1}+g}\)
\(\therefore \frac{x-x_{1}}{ax_{1}+hy_{1}+g}=\frac{y-y_{1}}{hx_{1}+by_{1}+f}\)
ইহাই নির্ণেয় অভিলম্বের সমীকরণ।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((1)\) নং সমীকরণটিকে \(x\) এর সাপেক্ষে অন্তরীকরণ করে।
\(a\frac{d}{dx}(x^2)+2h\frac{d}{dx}(xy)+b\frac{d}{dx}(y^2)+2g\frac{d}{dx}(x)+2f\frac{d}{dx}(y)+\frac{d}{dx}(c)=0\)
\(\Rightarrow a.2x+2hx\frac{dy}{dx}+2hy.1+b2y\frac{dy}{dx}+2g.1+2f\frac{dy}{dx}+0=0\)
\(\Rightarrow 2ax+2hx\frac{dy}{dx}+2hy+2by\frac{dy}{dx}+2g+2f\frac{dy}{dx}=0\)
\(\Rightarrow 2(hx+by+f)\frac{dy}{dx}+2(ax+hy+g)=0\)
\(\Rightarrow 2(hx+by+f)\frac{dy}{dx}=-2(ax+hy+g)\)
\(\Rightarrow \frac{dy}{dx}=-\frac{2(ax+hy+g)}{2(hx+by+f)}\)
\(\Rightarrow \frac{dy}{dx}=-\frac{ax+hy+g}{hx+by+f}\)
\(\therefore (x_{1}, y_{1})\) বিন্দুতে স্পর্শকের ঢাল \(m=-\frac{ax_{1}+hy_{1}+g}{hx_{1}+by_{1}+f}\)
আবার, \((x_{1}, y_{1})\) বিন্দুতে অভিলম্বের ঢাল \(m_{1}=-\frac{1}{m}\)
\(=\frac{hx_{1}+by_{1}+f}{ax_{1}+hy_{1}+g}\)
এখন, \((x_{1}, y_{1})\) বিন্দুতে অভিলম্বের সমীকরণ,
\(y-y_{1}=m_{1}(x-x_{1})\)
\(\Rightarrow y-y_{1}=\frac{hx_{1}+by_{1}+f}{ax_{1}+hy_{1}+g}(x-x_{1})\)
\(\Rightarrow \frac{y-y_{1}}{hx_{1}+by_{1}+f}=\frac{x-x_{1}}{ax_{1}+hy_{1}+g}\)
\(\therefore \frac{x-x_{1}}{ax_{1}+hy_{1}+g}=\frac{y-y_{1}}{hx_{1}+by_{1}+f}\)
ইহাই নির্ণেয় অভিলম্বের সমীকরণ।
×
\((x_{1}, y_{1})\) বিন্দু হতে \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকে অঙ্কিত স্পর্শক যুগলের সমীকরণঃ
\(T^2=SS_{1}\)যেখানে, \(S=ax^2+2hxy+by^2+2gx+2fy+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c\)
সমাধানঃ
মনে করি,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((x_{1}, y_{1})\) বিন্দুগামী যেকোনো সরলরেখার সমীকরণ,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=r .......(2)\)
\((2)\) হতে,
\(\frac{x-x_{1}}{l}=r, \ \frac{y-y_{1}}{m}=r\)
\(\Rightarrow x-x_{1}=rl, \ y-y_{1}=rm\)
\(\therefore x=x_{1}+rl, \ y=y_{1}+rm\)
যদি \((2)\) নং সরলরেখা \((1)\) নং কণিককে স্পর্শ করে,
তাহলে, \(x=x_{1}+rl, \ y=y_{1}+rm\) এই মাণগুলো \((1)\) নং কণিককে সিদ্ধ করবে,
\(a(x_{1}+rl)^2+2h(x_{1}+rl)(y_{1}+rm)+b(y_{1}+rm)^2+2g(x_{1}+rl)+2f(y_{1}+rm)+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+S_{1}=0\) ➜ যেখানে, \(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
ইহা \(r\) এর দ্বিঘাত সমীকরণ। অতএব, এখানে \(r\) এর দুইটি মাণ আছে।
শর্তমতে \(r\) এর এই মাণ দুইটি সমান।
\(\therefore 4\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}^2=4(al^2+2hlm+bm^2)S_{1}\) ➜ \(\because ax^2+bx+c=0\) সমীকরণে,
\(x\) এর মাণদ্বয়ের সমান হওয়ার শর্তঃ
\(b^2=4ac\)
\(\Rightarrow \{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}^2=(al^2+2hlm+bm^2)S_{1}\)
\(\Rightarrow m^2\left\{\frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=m^2\left\{a\left(\frac{l}{m}\right)^2+2h\frac{l}{m}+b\right\}S_{1}\)
\(\Rightarrow \left\{\frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=\left\{a\left(\frac{l}{m}\right)^2+2h\frac{l}{m}+b\right\}S_{1} .....(3)\)
আবার, \((2)\) হতে,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}\)
\(\therefore \frac{l}{m}=\frac{x-x_{1}}{y-y_{1}} ......(4)\)
\((4)\) এর সাহায্য নিয়ে \((3)\) হতে,
\(\left\{\frac{x-x_{1}}{y-y_{1}}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=\left\{a\frac{(x-x_{1})^2}{(y-y_{1})^2}+2h\frac{x-x_{1}}{y-y_{1}}+b\right\}S_{1} \)
\(\Rightarrow \frac{\{(x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)\}^2}{(y-y_{1})^2}=\frac{a(x-x_{1})^2+2h(x-x_{1})(y-y_{1})+b(y-y_{1})^2}{(y-y_{1})^2}S_{1} \)
\(\Rightarrow \{(x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)\}^2=\{a(x-x_{1})^2+2h(x-x_{1})(y-y_{1})+b(y-y_{1})^2\}S_{1} \)
\(\Rightarrow \{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c-(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)\}^2=\)\([(ax^2+2hxy+by^2+2gx+2fy+c)+(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)-2\{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c\}]S_{1} \)
\(\Rightarrow \{T-S_{1}\}^2=[S+S_{1}-2T]S_{1} \) ➜ যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S=ax^2+2hxy+by^2+2gx+2fy+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\Rightarrow T^2-2TS_{1}+S_{1}^2=SS_{1}+S_{1}^2-2TS_{1} \)
\(\therefore T^2=SS_{1}\)
ইহাই নির্ণেয় স্পর্শক যুগলের সমীকরণ।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((x_{1}, y_{1})\) বিন্দুগামী যেকোনো সরলরেখার সমীকরণ,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=r .......(2)\)
\((2)\) হতে,
\(\frac{x-x_{1}}{l}=r, \ \frac{y-y_{1}}{m}=r\)
\(\Rightarrow x-x_{1}=rl, \ y-y_{1}=rm\)
\(\therefore x=x_{1}+rl, \ y=y_{1}+rm\)
যদি \((2)\) নং সরলরেখা \((1)\) নং কণিককে স্পর্শ করে,
তাহলে, \(x=x_{1}+rl, \ y=y_{1}+rm\) এই মাণগুলো \((1)\) নং কণিককে সিদ্ধ করবে,
\(a(x_{1}+rl)^2+2h(x_{1}+rl)(y_{1}+rm)+b(y_{1}+rm)^2+2g(x_{1}+rl)+2f(y_{1}+rm)+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+S_{1}=0\) ➜ যেখানে, \(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
ইহা \(r\) এর দ্বিঘাত সমীকরণ। অতএব, এখানে \(r\) এর দুইটি মাণ আছে।
শর্তমতে \(r\) এর এই মাণ দুইটি সমান।
\(\therefore 4\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}^2=4(al^2+2hlm+bm^2)S_{1}\) ➜ \(\because ax^2+bx+c=0\) সমীকরণে,
\(x\) এর মাণদ্বয়ের সমান হওয়ার শর্তঃ
\(b^2=4ac\)
\(\Rightarrow \{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}^2=(al^2+2hlm+bm^2)S_{1}\)
\(\Rightarrow m^2\left\{\frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=m^2\left\{a\left(\frac{l}{m}\right)^2+2h\frac{l}{m}+b\right\}S_{1}\)
\(\Rightarrow \left\{\frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=\left\{a\left(\frac{l}{m}\right)^2+2h\frac{l}{m}+b\right\}S_{1} .....(3)\)
আবার, \((2)\) হতে,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}\)
\(\therefore \frac{l}{m}=\frac{x-x_{1}}{y-y_{1}} ......(4)\)
\((4)\) এর সাহায্য নিয়ে \((3)\) হতে,
\(\left\{\frac{x-x_{1}}{y-y_{1}}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=\left\{a\frac{(x-x_{1})^2}{(y-y_{1})^2}+2h\frac{x-x_{1}}{y-y_{1}}+b\right\}S_{1} \)
\(\Rightarrow \frac{\{(x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)\}^2}{(y-y_{1})^2}=\frac{a(x-x_{1})^2+2h(x-x_{1})(y-y_{1})+b(y-y_{1})^2}{(y-y_{1})^2}S_{1} \)
\(\Rightarrow \{(x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)\}^2=\{a(x-x_{1})^2+2h(x-x_{1})(y-y_{1})+b(y-y_{1})^2\}S_{1} \)
\(\Rightarrow \{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c-(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)\}^2=\)\([(ax^2+2hxy+by^2+2gx+2fy+c)+(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)-2\{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c\}]S_{1} \)
\(\Rightarrow \{T-S_{1}\}^2=[S+S_{1}-2T]S_{1} \) ➜ যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S=ax^2+2hxy+by^2+2gx+2fy+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\Rightarrow T^2-2TS_{1}+S_{1}^2=SS_{1}+S_{1}^2-2TS_{1} \)
\(\therefore T^2=SS_{1}\)
ইহাই নির্ণেয় স্পর্শক যুগলের সমীকরণ।
×
কণিকের উপরে অবস্থিত নয় এরূপ কোনো বিন্দু হতে কণিকে কেবলমাত্র দুইটি স্পর্শক অঙ্কন করা যায়।
সমাধানঃ
মনে করি, কণিকের সমীকরণ
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
কণিকের উপরে অবস্থিত নয় \((x_{1}, y_{1})\) বিন্দুগামী যেকোনো সরলরেখার সমীকরণ,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=r .......(2)\)
\((2)\) হতে,
\(\frac{x-x_{1}}{l}=r, \ \frac{y-y_{1}}{m}=r\)
\(\Rightarrow x-x_{1}=rl, \ y-y_{1}=rm\)
\(\therefore x=x_{1}+rl, \ y=y_{1}+rm\)
যদি \((2)\) নং সরলরেখা \((1)\) নং কণিককে স্পর্শ করে,
তাহলে, \(x=x_{1}+rl, \ y=y_{1}+rm\) এই মাণগুলো \((1)\) নং কণিককে সিদ্ধ করবে,
\(a(x_{1}+rl)^2+2h(x_{1}+rl)(y_{1}+rm)+b(y_{1}+rm)^2+2g(x_{1}+rl)+2f(y_{1}+rm)+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+S_{1}=0\) ➜ যেখানে, \(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
ইহা \(r\) এর দ্বিঘাত সমীকরণ। অতএব, এখানে \(r\) এর দুইটি মাণ আছে।
শর্তমতে \(r\) এর এই মাণ দুইটি সমান।
\(\therefore 4\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}^2=4(al^2+2hlm+bm^2)S_{1}\) ➜ \(\because ax^2+bx+c=0\) সমীকরণে,
\(x\) এর মাণদ্বয়ের সমান হওয়ার শর্তঃ
\(b^2=4ac\)
\(\Rightarrow \{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}^2=(al^2+2hlm+bm^2)S_{1}\)
\(\Rightarrow m^2\left\{\frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=m^2\left\{a\left(\frac{l}{m}\right)^2+2h\frac{l}{m}+b\right\}S_{1}\)
\(\Rightarrow \left\{\frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=\left\{a\left(\frac{l}{m}\right)^2+2h\frac{l}{m}+b\right\}S_{1} .....(3)\)
আবার, \((2)\) হতে,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}\)
\(\therefore \frac{l}{m}=\frac{x-x_{1}}{y-y_{1}} ......(4)\)
\((4)\) এর সাহায্য নিয়ে \((3)\) হতে,
\(\left\{\frac{x-x_{1}}{y-y_{1}}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=\left\{a\frac{(x-x_{1})^2}{(y-y_{1})^2}+2h\frac{x-x_{1}}{y-y_{1}}+b\right\}S_{1} \)
\(\Rightarrow \frac{\{(x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)\}^2}{(y-y_{1})^2}=\frac{a(x-x_{1})^2+2h(x-x_{1})(y-y_{1})+b(y-y_{1})^2}{(y-y_{1})^2}S_{1} \)
\(\Rightarrow \{(x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)\}^2=\{a(x-x_{1})^2+2h(x-x_{1})(y-y_{1})+b(y-y_{1})^2\}S_{1} \)
\(\Rightarrow \{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c-(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)\}^2=\)\([(ax^2+2hxy+by^2+2gx+2fy+c)+(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)-2\{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c\}]S_{1} \)
\(\Rightarrow \{T-S_{1}\}^2=[S+S_{1}-2T]S_{1} \) ➜ যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S=ax^2+2hxy+by^2+2gx+2fy+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\Rightarrow T^2-2TS_{1}+S_{1}^2=SS_{1}+S_{1}^2-2TS_{1} \)
\(\therefore T^2=SS_{1}\)
যা দুইটি স্পর্শকের সমীকরণ নির্দেশ করে।
তাহলে স্পষ্ট যে কণিকের উপরে অবস্থিত নয় এরূপ কোনো বিন্দু হতে কণিকে কেবলমাত্র দুইটি স্পর্শক অঙ্কন করা যায়।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
কণিকের উপরে অবস্থিত নয় \((x_{1}, y_{1})\) বিন্দুগামী যেকোনো সরলরেখার সমীকরণ,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=r .......(2)\)
\((2)\) হতে,
\(\frac{x-x_{1}}{l}=r, \ \frac{y-y_{1}}{m}=r\)
\(\Rightarrow x-x_{1}=rl, \ y-y_{1}=rm\)
\(\therefore x=x_{1}+rl, \ y=y_{1}+rm\)
যদি \((2)\) নং সরলরেখা \((1)\) নং কণিককে স্পর্শ করে,
তাহলে, \(x=x_{1}+rl, \ y=y_{1}+rm\) এই মাণগুলো \((1)\) নং কণিককে সিদ্ধ করবে,
\(a(x_{1}+rl)^2+2h(x_{1}+rl)(y_{1}+rm)+b(y_{1}+rm)^2+2g(x_{1}+rl)+2f(y_{1}+rm)+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+S_{1}=0\) ➜ যেখানে, \(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
ইহা \(r\) এর দ্বিঘাত সমীকরণ। অতএব, এখানে \(r\) এর দুইটি মাণ আছে।
শর্তমতে \(r\) এর এই মাণ দুইটি সমান।
\(\therefore 4\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}^2=4(al^2+2hlm+bm^2)S_{1}\) ➜ \(\because ax^2+bx+c=0\) সমীকরণে,
\(x\) এর মাণদ্বয়ের সমান হওয়ার শর্তঃ
\(b^2=4ac\)
\(\Rightarrow \{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}^2=(al^2+2hlm+bm^2)S_{1}\)
\(\Rightarrow m^2\left\{\frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=m^2\left\{a\left(\frac{l}{m}\right)^2+2h\frac{l}{m}+b\right\}S_{1}\)
\(\Rightarrow \left\{\frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=\left\{a\left(\frac{l}{m}\right)^2+2h\frac{l}{m}+b\right\}S_{1} .....(3)\)
আবার, \((2)\) হতে,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}\)
\(\therefore \frac{l}{m}=\frac{x-x_{1}}{y-y_{1}} ......(4)\)
\((4)\) এর সাহায্য নিয়ে \((3)\) হতে,
\(\left\{\frac{x-x_{1}}{y-y_{1}}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)\right\}^2=\left\{a\frac{(x-x_{1})^2}{(y-y_{1})^2}+2h\frac{x-x_{1}}{y-y_{1}}+b\right\}S_{1} \)
\(\Rightarrow \frac{\{(x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)\}^2}{(y-y_{1})^2}=\frac{a(x-x_{1})^2+2h(x-x_{1})(y-y_{1})+b(y-y_{1})^2}{(y-y_{1})^2}S_{1} \)
\(\Rightarrow \{(x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)\}^2=\{a(x-x_{1})^2+2h(x-x_{1})(y-y_{1})+b(y-y_{1})^2\}S_{1} \)
\(\Rightarrow \{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c-(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)\}^2=\)\([(ax^2+2hxy+by^2+2gx+2fy+c)+(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)-2\{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c\}]S_{1} \)
\(\Rightarrow \{T-S_{1}\}^2=[S+S_{1}-2T]S_{1} \) ➜ যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S=ax^2+2hxy+by^2+2gx+2fy+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\Rightarrow T^2-2TS_{1}+S_{1}^2=SS_{1}+S_{1}^2-2TS_{1} \)
\(\therefore T^2=SS_{1}\)
যা দুইটি স্পর্শকের সমীকরণ নির্দেশ করে।
তাহলে স্পষ্ট যে কণিকের উপরে অবস্থিত নয় এরূপ কোনো বিন্দু হতে কণিকে কেবলমাত্র দুইটি স্পর্শক অঙ্কন করা যায়।
×
\((x_{1}, y_{1})\) বিন্দু হতে \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের স্পর্শ জ্যা এর সমীকরণঃ
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c=0\)সমাধানঃ
মনে করি, কণিকের সমীকরণ
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((1)\) নং কণিকের বহিঃস্থ একটি বিন্দু \(P(x_1, y_1)\)। \(P\) হতে \((1)\) নং কণিকে অঙ্কিত স্পর্শকদ্বয় যথাক্রমে \(PA\) ও \(PB\)।
ধরি,
স্পর্শবিন্দুদ্বয় যথাক্রমে \(A(x_2, y_2)\) ও \(B(x_3, y_3)\) ।
এখন,
\((1)\) নং কণিকের উপরোস্থ \(A(x_2, y_2)\) ও \(B(x_3, y_3)\) বিন্দুতে স্পর্শকদ্বয়ের সমীকরণ,
\(axx_2+h(xy_{2}+x_{2}y)+byy_2+g(x+x_2)+f(y+y_2)+c=0 ..........(2)\)
\(axx_3+h(xy_{3}+x_{3}y)+byy_3+g(x+x_3)+f(y+y_3)+c=0 ..........(3)\)
যেহেতু স্পর্শকদ্বয় \(P(x_1, y_1)\) বিন্দুগামী,
\(ax_1x_2+h(x_{1}y_{2}+x_{2}y_{1})+by_1y_2+g(x_1+x_2)+f(y_1+y_2)+c=0 ..........(4)\)
\(ax_1x_3+h(x_{1}y_{3}+x_{3}y_{1})+by_1y_3+g(x_1+x_3)+f(y_1+y_3)+c=0 ..........(5)\)
\((4)\) ও \((5)\) সমীকরণ দুইটি হতে প্রমাণিত হয় যে, \(A(x_2, y_2)\) ও \(B(x_3, y_3)\) বিন্দুদ্বয়ের স্থানাঙ্ক দ্বারা নিম্নলিখিত সমীকরণটি সিদ্ধ হয়।
\(axx_1+h(xy_{1}+x_{1}y)+byy_1+g(x+x_1)+f(y+y_1)+c=0 ..........(6)\)
\((6)\) নং সমীকরণটি একটি সরলরেখা সূচিত করে।
অতএব, ইহাই নির্ণেয় স্পর্শ জ্যা-এর সমীকরণ।

\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((1)\) নং কণিকের বহিঃস্থ একটি বিন্দু \(P(x_1, y_1)\)। \(P\) হতে \((1)\) নং কণিকে অঙ্কিত স্পর্শকদ্বয় যথাক্রমে \(PA\) ও \(PB\)।
ধরি,
স্পর্শবিন্দুদ্বয় যথাক্রমে \(A(x_2, y_2)\) ও \(B(x_3, y_3)\) ।
এখন,
\((1)\) নং কণিকের উপরোস্থ \(A(x_2, y_2)\) ও \(B(x_3, y_3)\) বিন্দুতে স্পর্শকদ্বয়ের সমীকরণ,
\(axx_2+h(xy_{2}+x_{2}y)+byy_2+g(x+x_2)+f(y+y_2)+c=0 ..........(2)\)
\(axx_3+h(xy_{3}+x_{3}y)+byy_3+g(x+x_3)+f(y+y_3)+c=0 ..........(3)\)
যেহেতু স্পর্শকদ্বয় \(P(x_1, y_1)\) বিন্দুগামী,
\(ax_1x_2+h(x_{1}y_{2}+x_{2}y_{1})+by_1y_2+g(x_1+x_2)+f(y_1+y_2)+c=0 ..........(4)\)
\(ax_1x_3+h(x_{1}y_{3}+x_{3}y_{1})+by_1y_3+g(x_1+x_3)+f(y_1+y_3)+c=0 ..........(5)\)
\((4)\) ও \((5)\) সমীকরণ দুইটি হতে প্রমাণিত হয় যে, \(A(x_2, y_2)\) ও \(B(x_3, y_3)\) বিন্দুদ্বয়ের স্থানাঙ্ক দ্বারা নিম্নলিখিত সমীকরণটি সিদ্ধ হয়।
\(axx_1+h(xy_{1}+x_{1}y)+byy_1+g(x+x_1)+f(y+y_1)+c=0 ..........(6)\)
\((6)\) নং সমীকরণটি একটি সরলরেখা সূচিত করে।
অতএব, ইহাই নির্ণেয় স্পর্শ জ্যা-এর সমীকরণ।
×
\(lx+my+n=0\) সরলরেখাটি \(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের একটি স্পর্শক হওয়ার শর্তঃ
\(\left|\begin{array}{c}a & h & g & l\\ h & b & f & m\\ g & f & c & n\\ l & m & n & 0\end{array}\right|=0\)
সমাধানঃ
মনে করি,
\(lx+my+n=0 .........(1)\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(2)\)
ধরি, \((1)\) নং সরলরেখাটি \((2)\) নং কণিককে \(P(x_1, y_1)\) বিন্দুতে স্পর্শ করে।
এখন, \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণ,
\(axx_1+h(xy_{1}+x_{1}y)+byy_1+g(x+x_1)+f(y+y_1)+c=0\)
\(\therefore (ax_1+hy_{1}+g)x+(hx_{1}+by_1+f)y+gx_1+fy_1+c=0 .......(3)\)
শর্তমতে \((3)\) ও \((1)\) নং সমীকরণ অভিন্ন
\(\therefore \frac{ax_1+hy_{1}+g}{l}=\frac{hx_{1}+by_1+f}{m}=\frac{gx_1+fy_1+c}{n}\) ➜ \(\because a_{1}x+b_{1}y+c_{1}=0\)
\(a_{2}x+b_{2}y+c_{2}=0\) সমীকরণদ্বয়ের অভিন্ন হওয়ার শর্তঃ
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
ধরি, \(\frac{ax_1+hy_{1}+g}{l}=\frac{hx_{1}+by_1+f}{m}=\frac{gx_1+fy_1+c}{n}=k\)
\(\Rightarrow \frac{ax_1+hy_{1}+g}{l}=k, \ \frac{hx_{1}+by_1+f}{m}=k, \ \frac{gx_1+fy_1+c}{n}=k\)
\(\Rightarrow ax_1+hy_{1}+g=kl, \ hx_{1}+by_1+f=mk, \ gx_1+fy_1+c=nk\)
\(\Rightarrow ax_1+hy_{1}+g-kl=0, \ hx_{1}+by_1+f-mk=0, \ gx_1+fy_1+c-nk=0\)
\(\therefore ax_1+hy_{1}+g-kl=0 .....(4)\)
\(hx_{1}+by_1+f-mk=0 .....(5)\)
\(gx_1+fy_1+c-nk=0 ......(6)\)
যেহেতু \(P(x_1, y_1)\) বিন্দুটি \((1)\) নং সরলরেখাটির উপর অবস্থিত।
\(\therefore lx_{1}+my_{1}+n=0 .........(7)\)
এখন, \((4), (5), (6), (7)\) হতে \(x_{1}, y_{1}\) এবং \(k\) অপনয়ন করে,
\(\left|\begin{array}{c}a & h & g & -l\\ h & b & f & -m\\ g & f & c & -n\\ l & m & n & 0\end{array}\right|=0\)
\(\Rightarrow (-1)\left|\begin{array}{c}a & h & g & l\\ h & b & f & m\\ g & f & c & n\\ l & m & n & 0\end{array}\right|=0\)
\(\therefore \left|\begin{array}{c}a & h & g & l\\ h & b & f & m\\ g & f & c & n\\ l & m & n & 0\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত।
\(lx+my+n=0 .........(1)\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(2)\)
ধরি, \((1)\) নং সরলরেখাটি \((2)\) নং কণিককে \(P(x_1, y_1)\) বিন্দুতে স্পর্শ করে।
এখন, \(P(x_1, y_1)\) বিন্দুতে স্পর্শকের সমীকরণ,
\(axx_1+h(xy_{1}+x_{1}y)+byy_1+g(x+x_1)+f(y+y_1)+c=0\)
\(\therefore (ax_1+hy_{1}+g)x+(hx_{1}+by_1+f)y+gx_1+fy_1+c=0 .......(3)\)
শর্তমতে \((3)\) ও \((1)\) নং সমীকরণ অভিন্ন
\(\therefore \frac{ax_1+hy_{1}+g}{l}=\frac{hx_{1}+by_1+f}{m}=\frac{gx_1+fy_1+c}{n}\) ➜ \(\because a_{1}x+b_{1}y+c_{1}=0\)
\(a_{2}x+b_{2}y+c_{2}=0\) সমীকরণদ্বয়ের অভিন্ন হওয়ার শর্তঃ
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
ধরি, \(\frac{ax_1+hy_{1}+g}{l}=\frac{hx_{1}+by_1+f}{m}=\frac{gx_1+fy_1+c}{n}=k\)
\(\Rightarrow \frac{ax_1+hy_{1}+g}{l}=k, \ \frac{hx_{1}+by_1+f}{m}=k, \ \frac{gx_1+fy_1+c}{n}=k\)
\(\Rightarrow ax_1+hy_{1}+g=kl, \ hx_{1}+by_1+f=mk, \ gx_1+fy_1+c=nk\)
\(\Rightarrow ax_1+hy_{1}+g-kl=0, \ hx_{1}+by_1+f-mk=0, \ gx_1+fy_1+c-nk=0\)
\(\therefore ax_1+hy_{1}+g-kl=0 .....(4)\)
\(hx_{1}+by_1+f-mk=0 .....(5)\)
\(gx_1+fy_1+c-nk=0 ......(6)\)
যেহেতু \(P(x_1, y_1)\) বিন্দুটি \((1)\) নং সরলরেখাটির উপর অবস্থিত।
\(\therefore lx_{1}+my_{1}+n=0 .........(7)\)
এখন, \((4), (5), (6), (7)\) হতে \(x_{1}, y_{1}\) এবং \(k\) অপনয়ন করে,
\(\left|\begin{array}{c}a & h & g & -l\\ h & b & f & -m\\ g & f & c & -n\\ l & m & n & 0\end{array}\right|=0\)
\(\Rightarrow (-1)\left|\begin{array}{c}a & h & g & l\\ h & b & f & m\\ g & f & c & n\\ l & m & n & 0\end{array}\right|=0\)
\(\therefore \left|\begin{array}{c}a & h & g & l\\ h & b & f & m\\ g & f & c & n\\ l & m & n & 0\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত।
×
একটি কণিকের কোনো জ্যা এর মধ্যবিন্দু জানা থাকলে এর সমীকরণঃ
\(T=S_{1}\).যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
সমাধানঃ
মনে করি, কণিকের সমীকরণ
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((1)\) নং কণিকের একটি জ্যা এর মধ্যবিন্দু \((x_{1}, y_{1})\)
\((x_{1}, y_{1})\) বিন্দুগামী যে কোনো সরলরেখার সমীকরণ,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=r .......(2)\)
\((2)\) হতে,
\(\frac{x-x_{1}}{l}=r, \ \frac{y-y_{1}}{m}=r\)
\(\Rightarrow x-x_{1}=rl, \ y-y_{1}=rm\)
\(\therefore x=x_{1}+rl, \ y=y_{1}+rm\)
যদি \((2)\) নং সরলরেখা \((1)\) নং কণিককে ছেদ করে,
তাহলে, \(x=x_{1}+rl, \ y=y_{1}+rm\) এই মাণগুলো \((1)\) নং কণিককে সিদ্ধ করবে,
\(a(x_{1}+rl)^2+2h(x_{1}+rl)(y_{1}+rm)+b(y_{1}+rm)^2+2g(x_{1}+rl)+2f(y_{1}+rm)+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
ইহা \(r\) এর দ্বিঘাত সমীকরণ। অতএব, এখানে \(r\) এর দুইটি মাণ আছে।
শর্তমতে \(r\) এর এই মাণ দুইটি \((x_{1}, y_{1})\) বিন্দু হতে কণিক ও রেখাটির ছেদবিন্দুদ্বয় তথা জ্যাটির প্রান্তবিন্দুদ্বয়ের বীজগাণিতিক দূরত্ব সূচিত করে। যেহেতু \((x_{1}, y_{1})\) জ্যাটির মধ্যবিন্দু কাজেই \(r\) এর মাণ দুইটির যোগফল শূন্য হবে।
\(\therefore -\frac{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)}{al^2+2hlm+bm^2}=0\) ➜ \(\because ax^2+bx+c=0\) সমীকরণে,
\(x\) এর মাণদ্বয়ের যোগফল শূন্য হওয়ার শর্তঃ
\(-\frac{b}{a}=0\)
\(\Rightarrow l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)=0\)
\(\therefore \frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)=0 ........(3)\)
আবার, \((2)\) হতে,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}\)
\(\therefore \frac{l}{m}=\frac{x-x_{1}}{y-y_{1}} ......(4)\)
\((4)\) এর সাহায্য নিয়ে \((3)\) হতে,
\(\therefore \frac{x-x_{1}}{y-y_{1}}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)=0\)
\(\Rightarrow (x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)=0\)
\(\Rightarrow axx_{1}+hxy_{1}+gx-ax_{1}^2-hx_{1}y_{1}-gx_{1}+hx_{1}y+byy_{1}+fy-hx_{1}y_{1}-by_{1}^2-fy_{1}=0\)
\(\Rightarrow axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c-(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)=0\)
\(\Rightarrow T-S_{1}=0\) ➜ যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\therefore T=S_{1}\)
ইহাই নির্ণেয় জ্যা এর সমীকরণ।
যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
\((1)\) নং কণিকের একটি জ্যা এর মধ্যবিন্দু \((x_{1}, y_{1})\)
\((x_{1}, y_{1})\) বিন্দুগামী যে কোনো সরলরেখার সমীকরণ,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=r .......(2)\)
\((2)\) হতে,
\(\frac{x-x_{1}}{l}=r, \ \frac{y-y_{1}}{m}=r\)
\(\Rightarrow x-x_{1}=rl, \ y-y_{1}=rm\)
\(\therefore x=x_{1}+rl, \ y=y_{1}+rm\)
যদি \((2)\) নং সরলরেখা \((1)\) নং কণিককে ছেদ করে,
তাহলে, \(x=x_{1}+rl, \ y=y_{1}+rm\) এই মাণগুলো \((1)\) নং কণিককে সিদ্ধ করবে,
\(a(x_{1}+rl)^2+2h(x_{1}+rl)(y_{1}+rm)+b(y_{1}+rm)^2+2g(x_{1}+rl)+2f(y_{1}+rm)+c=0\)
\(\Rightarrow r^2(al^2+2hlm+bm^2)+2r\{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)\}+ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c=0\)
ইহা \(r\) এর দ্বিঘাত সমীকরণ। অতএব, এখানে \(r\) এর দুইটি মাণ আছে।
শর্তমতে \(r\) এর এই মাণ দুইটি \((x_{1}, y_{1})\) বিন্দু হতে কণিক ও রেখাটির ছেদবিন্দুদ্বয় তথা জ্যাটির প্রান্তবিন্দুদ্বয়ের বীজগাণিতিক দূরত্ব সূচিত করে। যেহেতু \((x_{1}, y_{1})\) জ্যাটির মধ্যবিন্দু কাজেই \(r\) এর মাণ দুইটির যোগফল শূন্য হবে।
\(\therefore -\frac{l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)}{al^2+2hlm+bm^2}=0\) ➜ \(\because ax^2+bx+c=0\) সমীকরণে,
\(x\) এর মাণদ্বয়ের যোগফল শূন্য হওয়ার শর্তঃ
\(-\frac{b}{a}=0\)
\(\Rightarrow l(ax_{1}+hy_{1}+g)+m(hx_{1}+by_{1}+f)=0\)
\(\therefore \frac{l}{m}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)=0 ........(3)\)
আবার, \((2)\) হতে,
\(\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}\)
\(\therefore \frac{l}{m}=\frac{x-x_{1}}{y-y_{1}} ......(4)\)
\((4)\) এর সাহায্য নিয়ে \((3)\) হতে,
\(\therefore \frac{x-x_{1}}{y-y_{1}}(ax_{1}+hy_{1}+g)+(hx_{1}+by_{1}+f)=0\)
\(\Rightarrow (x-x_{1})(ax_{1}+hy_{1}+g)+(y-y_{1})(hx_{1}+by_{1}+f)=0\)
\(\Rightarrow axx_{1}+hxy_{1}+gx-ax_{1}^2-hx_{1}y_{1}-gx_{1}+hx_{1}y+byy_{1}+fy-hx_{1}y_{1}-by_{1}^2-fy_{1}=0\)
\(\Rightarrow axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c-(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)=0\)
\(\Rightarrow T-S_{1}=0\) ➜ যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\therefore T=S_{1}\)
ইহাই নির্ণেয় জ্যা এর সমীকরণ।
যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিক সাপেক্ষে \((x_{1}, y_{1})\) বিন্দুর পোলারের সমীকরণঃ
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c=0\) সমাধানঃ
মনে করি,
\(S=ax^2+2hxy+by^2+2gx+2fy+c .......(1)\) এর প্রেক্ষিতে
\((x_{1}, y_{1})\) বিন্দুর পোলার নির্ণয় করতে হবে।
ধরি, \((x_{1}, y_{1})\) বিন্দুগামী কোনো জ্যা এর প্রান্তদ্বয় \(A\) ও \(B\) এবং কণিক \(S=0\) এর \(A\) ও \(B\) অঙ্কিত স্পর্শক দুইটি \((x^{\prime}, y^{\prime})\) বিন্দুতে ছেদ করেছে। \((x^{\prime}, y^{\prime})\) বিন্দুর সঞ্চার পথটিই নির্ণেয় পোলার।
এখন \((x^{\prime}, y^{\prime})\) বিন্দু থেকে কণিক \(S=0\) এ অঙ্কিত স্পর্শকদ্বয়ের স্পর্শ জ্যা হলো \(AB\) জ্যা।
অতএব \(AB\) জ্যা এর সমীকরণ,
\(axx^{\prime}+h(xy^{\prime}+x^{\prime}y)+byy^{\prime}+g(x+x^{\prime})+f(y+y^{\prime})+c=0\)
এই জ্যাটি \((x_{1}, y_{1})\) বিন্দু দিয়ে অতিক্রম করে বলে,
\(ax_{1}x^{\prime}+h(x_{1}y^{\prime}+x^{\prime}y_{1})+by_{1}y^{\prime}+g(x_{1}+x^{\prime})+f(y_{1}+y^{\prime})+c=0 ......(2)\)
\(\therefore (x^{\prime}, y^{\prime})\) বিন্দুর সঞ্চারপথ তথা নির্ণেয় পোলারের সমীকরণ,
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c=0\) ➜ \((2)\) নং সমীকরণে,
\(x^{\prime}, \ y^{\prime}\) কে যথাক্রমে
\(x, \ y\) দ্বারা প্রতিস্থাপিত করে
\(S=ax^2+2hxy+by^2+2gx+2fy+c .......(1)\) এর প্রেক্ষিতে
\((x_{1}, y_{1})\) বিন্দুর পোলার নির্ণয় করতে হবে।
ধরি, \((x_{1}, y_{1})\) বিন্দুগামী কোনো জ্যা এর প্রান্তদ্বয় \(A\) ও \(B\) এবং কণিক \(S=0\) এর \(A\) ও \(B\) অঙ্কিত স্পর্শক দুইটি \((x^{\prime}, y^{\prime})\) বিন্দুতে ছেদ করেছে। \((x^{\prime}, y^{\prime})\) বিন্দুর সঞ্চার পথটিই নির্ণেয় পোলার।
এখন \((x^{\prime}, y^{\prime})\) বিন্দু থেকে কণিক \(S=0\) এ অঙ্কিত স্পর্শকদ্বয়ের স্পর্শ জ্যা হলো \(AB\) জ্যা।
অতএব \(AB\) জ্যা এর সমীকরণ,
\(axx^{\prime}+h(xy^{\prime}+x^{\prime}y)+byy^{\prime}+g(x+x^{\prime})+f(y+y^{\prime})+c=0\)
এই জ্যাটি \((x_{1}, y_{1})\) বিন্দু দিয়ে অতিক্রম করে বলে,
\(ax_{1}x^{\prime}+h(x_{1}y^{\prime}+x^{\prime}y_{1})+by_{1}y^{\prime}+g(x_{1}+x^{\prime})+f(y_{1}+y^{\prime})+c=0 ......(2)\)
\(\therefore (x^{\prime}, y^{\prime})\) বিন্দুর সঞ্চারপথ তথা নির্ণেয় পোলারের সমীকরণ,
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c=0\) ➜ \((2)\) নং সমীকরণে,
\(x^{\prime}, \ y^{\prime}\) কে যথাক্রমে
\(x, \ y\) দ্বারা প্রতিস্থাপিত করে
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিক সাপেক্ষে কোনো সরলরেখার পোল নির্ণয় কর।
সমাধানঃ
প্রদত্ত কণিকের সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
মনে করি, সরলরেখার সমীকরণ
\(lx+my+n=0 .......(2)\)
সরলরেখাটির পোল \((x_{1}, y_{1})\)
\((1)\) এর সাপেক্ষে \((x_{1}, y_{1})\) এর পোলার সমীকরণ,
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c=0\)
\(\therefore (ax_{1}+hy_{1}+g)x+(hx_{1}+by_{1}+f)y+gx_{1}+fy_{1}+c=0 .......(3)\)
যেহেতু \((2)\) ও \((3)\) একই রেখাকে সূচিত করে,
\(\frac{ax_{1}+hy_{1}+g}{l}=\frac{hx_{1}+by_{1}+f}{m}=\frac{gx_{1}+fy_{1}+c}{n}\)
\(\Rightarrow \frac{ax_{1}+hy_{1}+g}{l}=\frac{gx_{1}+fy_{1}+c}{n}, \ \frac{hx_{1}+by_{1}+f}{m}=\frac{gx_{1}+fy_{1}+c}{n}\)
\(\Rightarrow anx_{1}+hny_{1}+gn=glx_{1}+fly_{1}+cl, \ hnx_{1}+bny_{1}+fn=gmx_{1}+fmy_{1}+cm\)
\(\Rightarrow (an-gl)x_{1}+(hn-fl)y_{1}=cl-gn, \ (hn-gm)x_{1}+(bn-fm)y_{1}=cm-fn\)
\(\therefore (an-gl)x_{1}+(hn-fl)y_{1}=cl-gn .......(4)\)
\((hn-gm)x_{1}+(bn-fm)y_{1}=cm-fn .......(5)\)
\((4)\) ও \((5)\) সমাধান করে \((2)\) নং সরলরেখার পোল পাওয়া যাবে।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
মনে করি, সরলরেখার সমীকরণ
\(lx+my+n=0 .......(2)\)
সরলরেখাটির পোল \((x_{1}, y_{1})\)
\((1)\) এর সাপেক্ষে \((x_{1}, y_{1})\) এর পোলার সমীকরণ,
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c=0\)
\(\therefore (ax_{1}+hy_{1}+g)x+(hx_{1}+by_{1}+f)y+gx_{1}+fy_{1}+c=0 .......(3)\)
যেহেতু \((2)\) ও \((3)\) একই রেখাকে সূচিত করে,
\(\frac{ax_{1}+hy_{1}+g}{l}=\frac{hx_{1}+by_{1}+f}{m}=\frac{gx_{1}+fy_{1}+c}{n}\)
\(\Rightarrow \frac{ax_{1}+hy_{1}+g}{l}=\frac{gx_{1}+fy_{1}+c}{n}, \ \frac{hx_{1}+by_{1}+f}{m}=\frac{gx_{1}+fy_{1}+c}{n}\)
\(\Rightarrow anx_{1}+hny_{1}+gn=glx_{1}+fly_{1}+cl, \ hnx_{1}+bny_{1}+fn=gmx_{1}+fmy_{1}+cm\)
\(\Rightarrow (an-gl)x_{1}+(hn-fl)y_{1}=cl-gn, \ (hn-gm)x_{1}+(bn-fm)y_{1}=cm-fn\)
\(\therefore (an-gl)x_{1}+(hn-fl)y_{1}=cl-gn .......(4)\)
\((hn-gm)x_{1}+(bn-fm)y_{1}=cm-fn .......(5)\)
\((4)\) ও \((5)\) সমাধান করে \((2)\) নং সরলরেখার পোল পাওয়া যাবে।
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের ব্যাসের সমীকরণঃ
\(ax+hy+g+m(hx_{1}+by_{1}+f)=0\).এবং এটি কণিকের কেন্দ্রগামী
সমাধানঃ
প্রদত্ত কণিকের সমীকরণ,
\(S\equiv{ax^2+2hxy+by^2+2gx+2fy+c}=0 .......(1)\)
কণিকের \(m\) ঢাল বিশিষ্ট এক শ্রেণীর সমান্তরাল জ্যা এর অন্তর্ভুক্ত কোনো একটি জ্যা এর মধ্যবিন্দু \((x_{1}, y_{1})\)
\(\therefore \) ঐ জ্যা এর সমীকরণ,
\(T=S_{1}\) ➜ যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\Rightarrow axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\therefore (ax_{1}+hy_{1}+g)x+(hx_{1}+by_{1}+f)y=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+gx_{1}+fy_{1}\)
এটির ঢাল,
\(m=-\frac{ax_{1}+hy_{1}+g}{hx_{1}+by_{1}+f}\) ➜ \(\because ax+by+c=0\)
সমীকরণের ঢাল,
\(m=-\frac{a}{b}\)
\(\Rightarrow ax_{1}+hy_{1}+g=-m(hx_{1}+by_{1}+f)\)
\(\therefore ax_{1}+hy_{1}+g+m(hx_{1}+by_{1}+f)=0\)
সুতরাং \((x_{1}, y_{1})\) বিন্দুর সঞ্চারপথ,
\(ax+hy+g+m(hx+by+f)=0\)
এটিই কণিক \(S=0\) এর সে সকল সমান্তরাল জ্যা এর মধ্যবিন্দুর সঞ্চারপথ, যে জ্যা গুলি \(y=mx\) সরলরেখার সমান্তরাল। এটা একটি সরলরেখা যা \(ax+hy+g=0\) ও \(hx+by+f=0\) সরলরেখাদ্বয়ের ছেদবিন্দু তথা কণিক \(S=0\) এর কেন্দ্র দিয়ে যায়।
সুতরাং এটি কণিক \(S=0\) এর একটি ব্যাস।
\(S\equiv{ax^2+2hxy+by^2+2gx+2fy+c}=0 .......(1)\)
কণিকের \(m\) ঢাল বিশিষ্ট এক শ্রেণীর সমান্তরাল জ্যা এর অন্তর্ভুক্ত কোনো একটি জ্যা এর মধ্যবিন্দু \((x_{1}, y_{1})\)
\(\therefore \) ঐ জ্যা এর সমীকরণ,
\(T=S_{1}\) ➜ যেখানে, \(T=axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c\)
\(S_{1}=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\Rightarrow axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c\)
\(\therefore (ax_{1}+hy_{1}+g)x+(hx_{1}+by_{1}+f)y=ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+gx_{1}+fy_{1}\)
এটির ঢাল,
\(m=-\frac{ax_{1}+hy_{1}+g}{hx_{1}+by_{1}+f}\) ➜ \(\because ax+by+c=0\)
সমীকরণের ঢাল,
\(m=-\frac{a}{b}\)
\(\Rightarrow ax_{1}+hy_{1}+g=-m(hx_{1}+by_{1}+f)\)
\(\therefore ax_{1}+hy_{1}+g+m(hx_{1}+by_{1}+f)=0\)
সুতরাং \((x_{1}, y_{1})\) বিন্দুর সঞ্চারপথ,
\(ax+hy+g+m(hx+by+f)=0\)
এটিই কণিক \(S=0\) এর সে সকল সমান্তরাল জ্যা এর মধ্যবিন্দুর সঞ্চারপথ, যে জ্যা গুলি \(y=mx\) সরলরেখার সমান্তরাল। এটা একটি সরলরেখা যা \(ax+hy+g=0\) ও \(hx+by+f=0\) সরলরেখাদ্বয়ের ছেদবিন্দু তথা কণিক \(S=0\) এর কেন্দ্র দিয়ে যায়।
সুতরাং এটি কণিক \(S=0\) এর একটি ব্যাস।
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের দুইটি ব্যাস যথাক্রমে \(y=m_{1}x+c_{1}\) ও \(y=m_{2}x+c_{2}\) পরস্পর অনুবন্ধী হওয়ার শর্তঃ
\(a+h(m_{1}+m_{2})+bm_{1}m_{2}=0\).সমাধানঃ
প্রদত্ত কণিকের সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
কণিকের দুইটি ব্যাস যথাক্রমে
\(y=m_{1}x+c_{1} ....(2)\)
\(y=m_{2}x+c_{2} ....(3)\)
শর্তমতে \((3)\) নং ব্যসটি \((2)\) নং ব্যসের সমান্তরাল জ্যা সমূহকে সমন্ডিখণ্ডিত করে।
সুতরাং \((3)\) নং ব্যসের সমীকরণ হবে,
\(ax+hy+g+m_{1}(hx+by+f)=0\)
\(\Rightarrow (a+m_{1}h)x+(h+m_{1}b)y+(g+m_{1}f)=0\)
\(\therefore \) এর ঢাল \(=-\frac{a+m_{1}h}{h+m_{1}b}\)
শর্তমতে, \(m_{2}=-\frac{a+m_{1}h}{h+m_{1}b}\)
\(\Rightarrow a+m_{1}h=-m_{2}(h+m_{1}b)\)
\(\Rightarrow a+m_{1}h=-hm_{2}-bm_{1}m_{2}\)
\(\Rightarrow a+m_{1}h+hm_{2}+bm_{1}m_{2}=0\)
\(\therefore a+h(m_{1}+m_{2})+bm_{1}m_{2}=0\)
ইহাই নির্ণেয় শর্ত।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
কণিকের দুইটি ব্যাস যথাক্রমে
\(y=m_{1}x+c_{1} ....(2)\)
\(y=m_{2}x+c_{2} ....(3)\)
শর্তমতে \((3)\) নং ব্যসটি \((2)\) নং ব্যসের সমান্তরাল জ্যা সমূহকে সমন্ডিখণ্ডিত করে।
সুতরাং \((3)\) নং ব্যসের সমীকরণ হবে,
\(ax+hy+g+m_{1}(hx+by+f)=0\)
\(\Rightarrow (a+m_{1}h)x+(h+m_{1}b)y+(g+m_{1}f)=0\)
\(\therefore \) এর ঢাল \(=-\frac{a+m_{1}h}{h+m_{1}b}\)
শর্তমতে, \(m_{2}=-\frac{a+m_{1}h}{h+m_{1}b}\)
\(\Rightarrow a+m_{1}h=-m_{2}(h+m_{1}b)\)
\(\Rightarrow a+m_{1}h=-hm_{2}-bm_{1}m_{2}\)
\(\Rightarrow a+m_{1}h+hm_{2}+bm_{1}m_{2}=0\)
\(\therefore a+h(m_{1}+m_{2})+bm_{1}m_{2}=0\)
ইহাই নির্ণেয় শর্ত।
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকে সাপেক্ষে \(P(x_{1}, y_{1})\) বিন্দুর পোলার যদি \(Q(x_{2}, y_{2})\) বিন্দুগামী হয়, তবে \(Q(x_{2}, y_{2})\) বিন্দুর পোলারও \(P(x_{1}, y_{1})\) বিন্দুগামী হবে।
সমাধানঃ
প্রদত্ত কণিকের সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
\((1)\) নং কণিক সাপেক্ষে \(P(x_{1}, y_{1})\) বিন্দুর পোলার
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c=0 ....(2)\)
এবং \(P(x_{2}, y_{2})\) বিন্দুর পোলার
\(axx_{2}+h(xy_{2}+x_{2}y)+byy_{2}+\)\(g(x+x_{2})+f(y+y_{2})+c=0 ....(3)\)
যদি \((2)\) নং রেখাটি \(P(x_{2}, y_{2})\) বিন্দু দিয়ে যায় তাহলে,
\(ax_{2}x_{1}+h(x_{2}y_{1}+x_{1}y_{2})+by_{2}y_{1}+\)\(g(x_{2}+x_{1})+f(y_{2}+y_{1})+c=0\)
\(\therefore ax_{1}x_{2}+h(x_{1}y_{2}+x_{2}y_{1})+by_{1}y_{2}+\)\(g(x_{1}+x_{2})+f(y_{1}+y_{2})+c=0 ....(4)\)
আবার, যদি \((3)\) নং রেখাটি \(P(x_{1}, y_{1})\) বিন্দু দিয়ে যায় তাহলে,
\(ax_{1}x_{2}+h(x_{1}y_{2}+x_{2}y_{1})+by_{1}y_{2}+\)\(g(x_{1}+x_{2})+f(y_{1}+y_{2})+c=0 ....(5)\)
যেহেতু \((4)\) নং ও \((5)\) নং সমীকরণ অভিন্ন,
( প্রমাণিত )
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
\((1)\) নং কণিক সাপেক্ষে \(P(x_{1}, y_{1})\) বিন্দুর পোলার
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c=0 ....(2)\)
এবং \(P(x_{2}, y_{2})\) বিন্দুর পোলার
\(axx_{2}+h(xy_{2}+x_{2}y)+byy_{2}+\)\(g(x+x_{2})+f(y+y_{2})+c=0 ....(3)\)
যদি \((2)\) নং রেখাটি \(P(x_{2}, y_{2})\) বিন্দু দিয়ে যায় তাহলে,
\(ax_{2}x_{1}+h(x_{2}y_{1}+x_{1}y_{2})+by_{2}y_{1}+\)\(g(x_{2}+x_{1})+f(y_{2}+y_{1})+c=0\)
\(\therefore ax_{1}x_{2}+h(x_{1}y_{2}+x_{2}y_{1})+by_{1}y_{2}+\)\(g(x_{1}+x_{2})+f(y_{1}+y_{2})+c=0 ....(4)\)
আবার, যদি \((3)\) নং রেখাটি \(P(x_{1}, y_{1})\) বিন্দু দিয়ে যায় তাহলে,
\(ax_{1}x_{2}+h(x_{1}y_{2}+x_{2}y_{1})+by_{1}y_{2}+\)\(g(x_{1}+x_{2})+f(y_{1}+y_{2})+c=0 ....(5)\)
যেহেতু \((4)\) নং ও \((5)\) নং সমীকরণ অভিন্ন,
( প্রমাণিত )
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকে সাপেক্ষে \(l_{1}x+m_{1}y+n_{1}=0\) ও \(l_{2}x+m_{2}y+n_{2}=0\) সরলরেখাদ্বয়ের পরস্পর অনুবন্ধী হওয়ার শর্তঃ
\(\left|\begin{array}{c}a & h & g & l_{1}\\ h & b & f & m_{1}\\ g & f & c & n_{1}\\ l_{2} & m_{2} & n_{2} & 0\end{array}\right|=0\)সমাধানঃ
প্রদত্ত কণিক ও সরলরেখাদ্বয়ের সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
\(l_{1}x+m_{1}y+n_{1}=0 .......(2)\)
\(l_{2}x+m_{2}y+n_{2}=0 .......(3)\)
ধরি, \((1)\) নং কণিক সাপেক্ষে \((2)\) নং সরলরেখার পোল \(P(x_{1}, y_{1})\)
\((1)\) নং কণিক সাপেক্ষে \(P(x_{1}, y_{1})\) বিন্দুর পোলার
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c=0\)
\(\therefore (ax_1+hy_{1}+g)x+(hx_{1}+by_1+f)y+gx_1+fy_1+c=0 ....(4)\)
শর্তমতে \((4)\) নং ও \((2)\) নং সমীকরণ অভিন্ন
\(\therefore \frac{ax_1+hy_{1}+g}{l_{1}}=\frac{hx_{1}+by_1+f}{m_{1}}=\frac{gx_1+fy_1+c}{n_{1}}\) ➜ \(\because a_{1}x+b_{1}y+c_{1}=0\)
\(a_{2}x+b_{2}y+c_{2}=0\) সমীকরণদ্বয়ের অভিন্ন হওয়ার শর্তঃ
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
ধরি, \(\frac{ax_1+hy_{1}+g}{l_{1}}=\frac{hx_{1}+by_1+f}{m_{1}}=\frac{gx_1+fy_1+c}{n_{1}}=k\)
\(\Rightarrow \frac{ax_1+hy_{1}+g}{l_{1}}=k, \ \frac{hx_{1}+by_1+f}{m_{1}}=k, \ \frac{gx_1+fy_1+c}{n_{1}}=k\)
\(\Rightarrow ax_1+hy_{1}+g=l_{1}k, \ hx_{1}+by_1+f=m_{1}k, \ gx_1+fy_1+c=n_{1}k\)
\(\Rightarrow ax_1+hy_{1}+g-l_{1}k=0, \ hx_{1}+by_1+f-m_{1}k=0, \ gx_1+fy_1+c-n_{1}k=0\)
\(\therefore ax_1+hy_{1}+g-l_{1}k=0 .....(4)\)
\(hx_{1}+by_1+f-m_{1}k=0 .....(5)\)
\(gx_1+fy_1+c-n_{1}k=0 ......(6)\)
যেহেতু \((2)\) ও \((3)\) নং রেখাদ্বয় পরস্পর অনুবন্ধী, সুতরাং \(P(x_1, y_1)\) বিন্দুটি \((3)\) নং সরলরেখাটিকে সিদ্ধ করবে।
\(l_{2}x_1+m_{2}y_1+n_{2}=0 .......(7)\)
এখন, \((4), (5), (6), (7)\) হতে \(x_{1}, y_{1}\) এবং \(k\) অপনয়ন করে,
\(\left|\begin{array}{c}a & h & g & -l_1\\ h & b & f & -m_1\\ g & f & c & -n_1\\ l_{2} & m_{2} & n_{2} & 0\end{array}\right|=0\)
\(\Rightarrow (-1)\left|\begin{array}{c}a & h & g & l_1\\ h & b & f & m_1\\ g & f & c & n_1\\ l_{2} & m_{2} & n_{2} & 0\end{array}\right|=0\)
\(\therefore \left|\begin{array}{c}a & h & g & l_1\\ h & b & f & m_1\\ g & f & c & n_1\\ l_{2} & m_{2} & n_{2} & 0\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
\(l_{1}x+m_{1}y+n_{1}=0 .......(2)\)
\(l_{2}x+m_{2}y+n_{2}=0 .......(3)\)
ধরি, \((1)\) নং কণিক সাপেক্ষে \((2)\) নং সরলরেখার পোল \(P(x_{1}, y_{1})\)
\((1)\) নং কণিক সাপেক্ষে \(P(x_{1}, y_{1})\) বিন্দুর পোলার
\(axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+\)\(g(x+x_{1})+f(y+y_{1})+c=0\)
\(\therefore (ax_1+hy_{1}+g)x+(hx_{1}+by_1+f)y+gx_1+fy_1+c=0 ....(4)\)
শর্তমতে \((4)\) নং ও \((2)\) নং সমীকরণ অভিন্ন
\(\therefore \frac{ax_1+hy_{1}+g}{l_{1}}=\frac{hx_{1}+by_1+f}{m_{1}}=\frac{gx_1+fy_1+c}{n_{1}}\) ➜ \(\because a_{1}x+b_{1}y+c_{1}=0\)
\(a_{2}x+b_{2}y+c_{2}=0\) সমীকরণদ্বয়ের অভিন্ন হওয়ার শর্তঃ
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
ধরি, \(\frac{ax_1+hy_{1}+g}{l_{1}}=\frac{hx_{1}+by_1+f}{m_{1}}=\frac{gx_1+fy_1+c}{n_{1}}=k\)
\(\Rightarrow \frac{ax_1+hy_{1}+g}{l_{1}}=k, \ \frac{hx_{1}+by_1+f}{m_{1}}=k, \ \frac{gx_1+fy_1+c}{n_{1}}=k\)
\(\Rightarrow ax_1+hy_{1}+g=l_{1}k, \ hx_{1}+by_1+f=m_{1}k, \ gx_1+fy_1+c=n_{1}k\)
\(\Rightarrow ax_1+hy_{1}+g-l_{1}k=0, \ hx_{1}+by_1+f-m_{1}k=0, \ gx_1+fy_1+c-n_{1}k=0\)
\(\therefore ax_1+hy_{1}+g-l_{1}k=0 .....(4)\)
\(hx_{1}+by_1+f-m_{1}k=0 .....(5)\)
\(gx_1+fy_1+c-n_{1}k=0 ......(6)\)
যেহেতু \((2)\) ও \((3)\) নং রেখাদ্বয় পরস্পর অনুবন্ধী, সুতরাং \(P(x_1, y_1)\) বিন্দুটি \((3)\) নং সরলরেখাটিকে সিদ্ধ করবে।
\(l_{2}x_1+m_{2}y_1+n_{2}=0 .......(7)\)
এখন, \((4), (5), (6), (7)\) হতে \(x_{1}, y_{1}\) এবং \(k\) অপনয়ন করে,
\(\left|\begin{array}{c}a & h & g & -l_1\\ h & b & f & -m_1\\ g & f & c & -n_1\\ l_{2} & m_{2} & n_{2} & 0\end{array}\right|=0\)
\(\Rightarrow (-1)\left|\begin{array}{c}a & h & g & l_1\\ h & b & f & m_1\\ g & f & c & n_1\\ l_{2} & m_{2} & n_{2} & 0\end{array}\right|=0\)
\(\therefore \left|\begin{array}{c}a & h & g & l_1\\ h & b & f & m_1\\ g & f & c & n_1\\ l_{2} & m_{2} & n_{2} & 0\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত।
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের নির্দেশক (নিয়ত) বৃত্ত বা চালক বৃত্তের সমীকরণঃ
\((ab-h^2)(x^2+y^2)+2(bg-hf)x+2(af-hg)y+(a+b)c-g^2-f^2=0\)সমাধানঃ
প্রদত্ত কণিক ও সরলরেখাদ্বয়ের সমীকরণ,
\(S\equiv{ax^2+2hxy+by^2+2gx+2fy+c}=0 .......(1)\)
ধরি, \((1)\) নং কণিকের কোনো যুগল স্পর্শকের ছেদবিন্দু \((x_{1}, y_{1})\), তাহলে এই স্পর্শ দ্বয়ের সমীকরণ,
\(T^2=SS_{1}\)
\(\Rightarrow SS_{1}=T^2\)
\(\Rightarrow (ax^2+2hxy+by^2+2gx+2fy+c)(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)=\{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c\}^2\)
\(\therefore (ax^2+2hxy+by^2+2gx+2fy+c)(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)=\{(ax_1+hy_{1}+g)x+(hx_{1}+by_1+f)y+gx_1+fy_1+c\}^2\)
যদি, স্পর্শকদ্বয় পরস্পরের সহিত লম্ব হয় তবে এই সমীকরণটির \(x^2\) ও \(y^2\) এর সহগের সমষ্টি শূন্য হবে।
\(\therefore (a+b)(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)-(ax_1+hy_{1}+g)^2-(hx_{1}+by_1+f)^2=0\)
\(\Rightarrow (a^2+ab-a^2-h^2)x_{1}^2+(ab+b^2-b^2-h^2)y_{1}^2+\{2g(a+b)-2ag-2hf\}x_{1}+\{2f(a+b)-2hg-2bf\}y_{1}+(a+b)c-g^2-f^2=0\)
\(\Rightarrow (ab-h^2)x_{1}^2+(ab-h^2)y_{1}^2+\{2ag+2bg-2ag-2hf\}x_{1}+\{2af+2bf-2hg-2bf\}y_{1}+(a+b)c-g^2-f^2=0\)
\(\Rightarrow (ab-h^2)(x_{1}^2+y_{1}^2)+\{2bg-2hf\}x_{1}+\{2af-2hg\}y_{1}+(a+b)c-g^2-f^2=0\)
\(\Rightarrow (ab-h^2)(x_{1}^2+y_{1}^2)+2(bg-hf)x_{1}+2(af-hg)y_{1}+(a+b)c-g^2-f^2=0\)
\(\therefore (x_{1}, y_{1})\) বিন্দুর সঞ্চারপথ তথা নির্ণেয় চালক বৃত্তের সমীকরণ,
\(\therefore (ab-h^2)(x^2+y^2)+2(bg-hf)x+2(af-hg)y+(a+b)c-g^2-f^2=0\) ➜ \(x_{1}, \ y_{1}\) কে যথাক্রমে
\(x, \ y\) দ্বারা প্রতিস্থাপিত করে
\(S\equiv{ax^2+2hxy+by^2+2gx+2fy+c}=0 .......(1)\)
ধরি, \((1)\) নং কণিকের কোনো যুগল স্পর্শকের ছেদবিন্দু \((x_{1}, y_{1})\), তাহলে এই স্পর্শ দ্বয়ের সমীকরণ,
\(T^2=SS_{1}\)
\(\Rightarrow SS_{1}=T^2\)
\(\Rightarrow (ax^2+2hxy+by^2+2gx+2fy+c)(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)=\{axx_{1}+h(xy_{1}+x_{1}y)+byy_{1}+g(x+x_{1})+f(y+y_{1})+c\}^2\)
\(\therefore (ax^2+2hxy+by^2+2gx+2fy+c)(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)=\{(ax_1+hy_{1}+g)x+(hx_{1}+by_1+f)y+gx_1+fy_1+c\}^2\)
যদি, স্পর্শকদ্বয় পরস্পরের সহিত লম্ব হয় তবে এই সমীকরণটির \(x^2\) ও \(y^2\) এর সহগের সমষ্টি শূন্য হবে।
\(\therefore (a+b)(ax_{1}^2+2hx_{1}y_{1}+by_{1}^2+2gx_{1}+2fy_{1}+c)-(ax_1+hy_{1}+g)^2-(hx_{1}+by_1+f)^2=0\)
\(\Rightarrow (a^2+ab-a^2-h^2)x_{1}^2+(ab+b^2-b^2-h^2)y_{1}^2+\{2g(a+b)-2ag-2hf\}x_{1}+\{2f(a+b)-2hg-2bf\}y_{1}+(a+b)c-g^2-f^2=0\)
\(\Rightarrow (ab-h^2)x_{1}^2+(ab-h^2)y_{1}^2+\{2ag+2bg-2ag-2hf\}x_{1}+\{2af+2bf-2hg-2bf\}y_{1}+(a+b)c-g^2-f^2=0\)
\(\Rightarrow (ab-h^2)(x_{1}^2+y_{1}^2)+\{2bg-2hf\}x_{1}+\{2af-2hg\}y_{1}+(a+b)c-g^2-f^2=0\)
\(\Rightarrow (ab-h^2)(x_{1}^2+y_{1}^2)+2(bg-hf)x_{1}+2(af-hg)y_{1}+(a+b)c-g^2-f^2=0\)
\(\therefore (x_{1}, y_{1})\) বিন্দুর সঞ্চারপথ তথা নির্ণেয় চালক বৃত্তের সমীকরণ,
\(\therefore (ab-h^2)(x^2+y^2)+2(bg-hf)x+2(af-hg)y+(a+b)c-g^2-f^2=0\) ➜ \(x_{1}, \ y_{1}\) কে যথাক্রমে
\(x, \ y\) দ্বারা প্রতিস্থাপিত করে
×
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) কণিকের অসীমতটের সমীকরণঃ
\(ax^2+2hxy+by^2+2gx+2fy-g\alpha-f\beta=0\)সমাধানঃ
ধরি,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
যেহেতু অসীমতটদ্বয়ের সমীকরণ ও কণিকের সমীকরণের মধ্যে কেবলমাত্র একটি ধ্রুবকের পার্থক্য সুতরাং অসীমতটদ্বয়ের সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c+\lambda=0 .......(2)\)
যেখানে, \(\lambda\) একটি ধ্রুবক
\(\lambda\) এর সকল মানের জন্য \((2)\) নং সমীকরণ একজোড়া সরলরেখা সূচিত করবে।
\(\left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c+\lambda\end{array}\right|=0\)
\(\Rightarrow \left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c\end{array}\right|+\left|\begin{array}{c}a & h & 0\\ h & b & 0\\ g & f & \lambda\end{array}\right|=0\)
\(\Rightarrow \Delta+\lambda(ab-h^2)=0\)
\(\Rightarrow \lambda(ab-h^2)=-\Delta\)
\(\therefore \lambda=-\frac{\Delta}{ab-h^2}\)
এখন, \(\lambda\) এর মাণ \((2)\) এ বসিয়ে,
\(ax^2+2hxy+by^2+2gx+2fy+c-\frac{\Delta}{ab-h^2}=0 .......(3)\)
আবার, \(c-\frac{\Delta}{ab-h^2}=c-\frac{abc+2fgh-af^2-bg^2-ch^2}{ab-h^2}\) ➜ \(\because \Delta=abc+2fgh-af^2-bg^2-ch^2\)
\(=\frac{abc-ch^2-abc-2fgh+af^2+bg^2+ch^2}{ab-h^2}\)
\(=\frac{af^2+bg^2-2fgh}{ab-h^2}\)
\(\therefore c-\frac{\Delta}{ab-h^2}=\frac{af^2+bg^2-2fgh}{ab-h^2} .....(4)\)
আবার, \((1)\) নং কণিকের কেন্দ্র \(\alpha, \beta\) হলে,
\(\alpha=\frac{hf-bg}{ab-h^2}, \ \beta=\frac{gh-af}{ab-h^2}\)
\(\therefore g\alpha+f\beta=g\frac{hf-bg}{ab-h^2}+f\frac{gh-af}{ab-h^2}\)
\(=\frac{fgh-bg^2}{ab-h^2}+\frac{fgh-af^2}{ab-h^2}\)
\(=\frac{fgh-bg^2+fgh-af^2}{ab-h^2}\)
\(=\frac{2fgh-bg^2-af^2}{ab-h^2}\)
\(\therefore g\alpha+f\beta=-\frac{af^2+bg^2-2fgh}{ab-h^2}\)
\(\Rightarrow -(g\alpha+f\beta)=\frac{af^2+bg^2-2fgh}{ab-h^2} ......(5)\)
\((4)\) ও \((5)\) হতে,
\(c-\frac{\Delta}{ab-h^2}=-(g\alpha+f\beta)\)
\((3)\) হতে,
\(ax^2+2hxy+by^2+2gx+2fy+c-(g\alpha+f\beta)=0\) ➜ \(\because c-\frac{\Delta}{ab-h^2}=-(g\alpha+f\beta)\)
\(\therefore ax^2+2hxy+by^2+2gx+2fy+c-g\alpha-f\beta=0\)
ইহাই নির্ণেয় অসীমতটের সমীকরণ।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .......(1)\)
যেহেতু অসীমতটদ্বয়ের সমীকরণ ও কণিকের সমীকরণের মধ্যে কেবলমাত্র একটি ধ্রুবকের পার্থক্য সুতরাং অসীমতটদ্বয়ের সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c+\lambda=0 .......(2)\)
যেখানে, \(\lambda\) একটি ধ্রুবক
\(\lambda\) এর সকল মানের জন্য \((2)\) নং সমীকরণ একজোড়া সরলরেখা সূচিত করবে।
\(\left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c+\lambda\end{array}\right|=0\)
\(\Rightarrow \left|\begin{array}{c}a & h & g\\ h & b & f\\ g & f & c\end{array}\right|+\left|\begin{array}{c}a & h & 0\\ h & b & 0\\ g & f & \lambda\end{array}\right|=0\)
\(\Rightarrow \Delta+\lambda(ab-h^2)=0\)
\(\Rightarrow \lambda(ab-h^2)=-\Delta\)
\(\therefore \lambda=-\frac{\Delta}{ab-h^2}\)
এখন, \(\lambda\) এর মাণ \((2)\) এ বসিয়ে,
\(ax^2+2hxy+by^2+2gx+2fy+c-\frac{\Delta}{ab-h^2}=0 .......(3)\)
আবার, \(c-\frac{\Delta}{ab-h^2}=c-\frac{abc+2fgh-af^2-bg^2-ch^2}{ab-h^2}\) ➜ \(\because \Delta=abc+2fgh-af^2-bg^2-ch^2\)
\(=\frac{abc-ch^2-abc-2fgh+af^2+bg^2+ch^2}{ab-h^2}\)
\(=\frac{af^2+bg^2-2fgh}{ab-h^2}\)
\(\therefore c-\frac{\Delta}{ab-h^2}=\frac{af^2+bg^2-2fgh}{ab-h^2} .....(4)\)
আবার, \((1)\) নং কণিকের কেন্দ্র \(\alpha, \beta\) হলে,
\(\alpha=\frac{hf-bg}{ab-h^2}, \ \beta=\frac{gh-af}{ab-h^2}\)
\(\therefore g\alpha+f\beta=g\frac{hf-bg}{ab-h^2}+f\frac{gh-af}{ab-h^2}\)
\(=\frac{fgh-bg^2}{ab-h^2}+\frac{fgh-af^2}{ab-h^2}\)
\(=\frac{fgh-bg^2+fgh-af^2}{ab-h^2}\)
\(=\frac{2fgh-bg^2-af^2}{ab-h^2}\)
\(\therefore g\alpha+f\beta=-\frac{af^2+bg^2-2fgh}{ab-h^2}\)
\(\Rightarrow -(g\alpha+f\beta)=\frac{af^2+bg^2-2fgh}{ab-h^2} ......(5)\)
\((4)\) ও \((5)\) হতে,
\(c-\frac{\Delta}{ab-h^2}=-(g\alpha+f\beta)\)
\((3)\) হতে,
\(ax^2+2hxy+by^2+2gx+2fy+c-(g\alpha+f\beta)=0\) ➜ \(\because c-\frac{\Delta}{ab-h^2}=-(g\alpha+f\beta)\)
\(\therefore ax^2+2hxy+by^2+2gx+2fy+c-g\alpha-f\beta=0\)
ইহাই নির্ণেয় অসীমতটের সমীকরণ।
×
দুইটি সমউপকেন্দ্রিক কনিক পরস্পরকে সমকোণে ছেদ করে।
প্রমাণঃ
ধরি,
সমউপকেন্দ্রিক কনিকদ্বয়
\(\frac{x^2}{a^2+k_{1}}+\frac{y^2}{b^2+k_{1}}=1 ..........(1)\)
\(\frac{x^2}{a^2+k_{2}}+\frac{y^2}{b^2+k_{2}}=1 ..........(2)\)
মনে করি, এরা পরস্পরকে \((x_{1}, y_{1})\) বিন্দুতে ছেদ করে।
\((x_{1}, y_{1})\) বিন্দুতে \((1)\) ও \((2)\) নং কণিকের স্পর্শকের সমীকরণ,
\(\frac{xx_{1}}{a^2+k_{1}}+\frac{yy_{1}}{b^2+k_{1}}=1 ..........(3)\)
\(\frac{xx_{1}}{a^2+k_{2}}+\frac{yy_{1}}{b^2+k_{2}}=1 ..........(4)\)
\((1)\) ও \((2)\) নং কনিকদ্বয় পরস্পর \((x_{1}, y_{1})\) বিন্দুতে সমকোণে ছেদ করবে যদি \((3)\) ও \((4)\) নং স্পর্শকদ্বয় পরস্পর লম্ব হয়।
\((3)\) ও \((4)\) নং স্পর্শকদ্বয়ের পরস্পর লম্ব হওয়ার শর্ত,
\(\frac{x_{1}}{a^2+k_{1}}\times{\frac{x_{1}}{a^2+k_{2}}}+\frac{y_{1}}{b^2+k_{1}}\times{\frac{y_{1}}{b^2+k_{2}}}=0\) ➜ \(\because a_{1}x+b_{1}y+c_{1}=0\)
এবং \(a_{2}x+b_{2}y+c_{2}=0\)
সরলরেখাদ্বয়ের পরস্পর লম্ব হওয়ার শর্ত
\(a_{1}a_{2}+b_{1}b_{2}=0\)
\(\therefore \frac{x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0 .........(5)\)
আবার, \((1)\) ও \((2)\) নং কনিকদ্বয় উভয় \((x_{1}, y_{1})\) বিন্দুগামী
\(\therefore \frac{x_{1}^2}{a^2+k_{1}}+\frac{y_{1}^2}{b^2+k_{1}}=1 ..........(6)\)
এবং \(\frac{x_{1}^2}{a^2+k_{2}}+\frac{y_{1}^2}{b^2+k_{2}}=1 ..........(7)\)
\((6)-(7)\) এর সাহায্যে
\(\frac{x_{1}^2}{a^2+k_{1}}-\frac{x_{1}^2}{a^2+k_{2}}+\frac{y_{1}^2}{b^2+k_{1}}-\frac{y_{1}^2}{b^2+k_{2}}=0\)
\(\Rightarrow \frac{a^2x_{1}^2+k_{2}x_{1}^2-a^2x_{1}^2-k_{1}x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{b^2y_{1}^2+k_{2}y_{1}^2-b^2y_{1}^2-k_{1}y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0\)
\(\Rightarrow \frac{k_{2}x_{1}^2-k_{1}x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{k_{2}y_{1}^2-k_{1}y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0\)
\(\Rightarrow \frac{(k_{2}-k_{1})x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{(k_{2}-k_{1})y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0\)
\(\Rightarrow (k_{2}-k_{1})\left\{\frac{x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}\right\}=0\)
\(\Rightarrow \frac{x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0, \ \because (k_{2}-k_{1})\ne{0}\)
\(\therefore \frac{x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0\) যা \((5)\) নং শর্তের অনুরূপ
সুতরাং, \((1)\) ও \((2)\) নং কনিকদ্বয় পরস্পর সমকোণে ছেদ করে।
( প্রমাণিত )
সমউপকেন্দ্রিক কনিকদ্বয়
\(\frac{x^2}{a^2+k_{1}}+\frac{y^2}{b^2+k_{1}}=1 ..........(1)\)
\(\frac{x^2}{a^2+k_{2}}+\frac{y^2}{b^2+k_{2}}=1 ..........(2)\)
মনে করি, এরা পরস্পরকে \((x_{1}, y_{1})\) বিন্দুতে ছেদ করে।
\((x_{1}, y_{1})\) বিন্দুতে \((1)\) ও \((2)\) নং কণিকের স্পর্শকের সমীকরণ,
\(\frac{xx_{1}}{a^2+k_{1}}+\frac{yy_{1}}{b^2+k_{1}}=1 ..........(3)\)
\(\frac{xx_{1}}{a^2+k_{2}}+\frac{yy_{1}}{b^2+k_{2}}=1 ..........(4)\)
\((1)\) ও \((2)\) নং কনিকদ্বয় পরস্পর \((x_{1}, y_{1})\) বিন্দুতে সমকোণে ছেদ করবে যদি \((3)\) ও \((4)\) নং স্পর্শকদ্বয় পরস্পর লম্ব হয়।
\((3)\) ও \((4)\) নং স্পর্শকদ্বয়ের পরস্পর লম্ব হওয়ার শর্ত,
\(\frac{x_{1}}{a^2+k_{1}}\times{\frac{x_{1}}{a^2+k_{2}}}+\frac{y_{1}}{b^2+k_{1}}\times{\frac{y_{1}}{b^2+k_{2}}}=0\) ➜ \(\because a_{1}x+b_{1}y+c_{1}=0\)
এবং \(a_{2}x+b_{2}y+c_{2}=0\)
সরলরেখাদ্বয়ের পরস্পর লম্ব হওয়ার শর্ত
\(a_{1}a_{2}+b_{1}b_{2}=0\)
\(\therefore \frac{x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0 .........(5)\)
আবার, \((1)\) ও \((2)\) নং কনিকদ্বয় উভয় \((x_{1}, y_{1})\) বিন্দুগামী
\(\therefore \frac{x_{1}^2}{a^2+k_{1}}+\frac{y_{1}^2}{b^2+k_{1}}=1 ..........(6)\)
এবং \(\frac{x_{1}^2}{a^2+k_{2}}+\frac{y_{1}^2}{b^2+k_{2}}=1 ..........(7)\)
\((6)-(7)\) এর সাহায্যে
\(\frac{x_{1}^2}{a^2+k_{1}}-\frac{x_{1}^2}{a^2+k_{2}}+\frac{y_{1}^2}{b^2+k_{1}}-\frac{y_{1}^2}{b^2+k_{2}}=0\)
\(\Rightarrow \frac{a^2x_{1}^2+k_{2}x_{1}^2-a^2x_{1}^2-k_{1}x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{b^2y_{1}^2+k_{2}y_{1}^2-b^2y_{1}^2-k_{1}y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0\)
\(\Rightarrow \frac{k_{2}x_{1}^2-k_{1}x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{k_{2}y_{1}^2-k_{1}y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0\)
\(\Rightarrow \frac{(k_{2}-k_{1})x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{(k_{2}-k_{1})y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0\)
\(\Rightarrow (k_{2}-k_{1})\left\{\frac{x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}\right\}=0\)
\(\Rightarrow \frac{x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0, \ \because (k_{2}-k_{1})\ne{0}\)
\(\therefore \frac{x_{1}^2}{(a^2+k_{1})(a^2+k_{2})}+\frac{y_{1}^2}{(b^2+k_{1})(b^2+k_{2})}=0\) যা \((5)\) নং শর্তের অনুরূপ
সুতরাং, \((1)\) ও \((2)\) নং কনিকদ্বয় পরস্পর সমকোণে ছেদ করে।
( প্রমাণিত )
×
কোনো কণিকের উপকেন্দ্র পোল হলে কণিকটির পোলার সমীকরণ ও দিকাক্ষের পোলার সমীকরণঃ
কণিকের পোলার সমীকরণঃ \(\frac{l}{r}=1-e\cos{\theta}\)দিকাক্ষের পোলার সমীকরণঃ \(\frac{l}{r}=e\cos{\theta}\)
সমাধানঃ
ধরি, 
একটি কণিকের ফোকাস \(S\) নিয়ামক \(ZM\) এবং শীর্ষ বিন্দু \(A\) । \(ZM\) এর ওপর লম্ব \(ZS\) টানা হলো এবং তা \(X\) অক্ষ পর্যন্ত বর্ধিত করা হলো। \(S\) কে পোল এবং \(ZX\) কে মূলরেখা ধরা হলো।
মনে করি,
\(P\) কণিকের ওপর যেকোনো একটি বিন্দু এবং এর পোলার স্থানাঙ্ক \((r, \theta)\)
তাহলে, \(SP=r\)
এবং \(\angle{XSP}=\theta\)
মূলরেখার ওপর \(PN\) লম্ব এবং নিয়ামকের ওপর \(PM\) লম্ব টানা হলো।
ধরি, ফোকাস লম্বার্ধ \(SL=l\)
যেহেতু \(e.SZ=SL\)
\(\Rightarrow e.SZ=l\)
\(\therefore SZ=\frac{l}{e} .....(1)\)
এখন, \(r=SP\)
\(\Rightarrow r=\frac{SP}{PM}\times{PM}\)
\(\Rightarrow r=e.PM\) ➜ \(\because \frac{SP}{PM}=e\)
\(\Rightarrow r=e.ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow r=e.(ZS+SN)\)
\(\Rightarrow r=e.\left(\frac{l}{e}+SP\times{\frac{SN}{SP}}\right)\) ➜ \((1)\) হতে,
\(\because SZ=\frac{l}{e}\)
\(\Rightarrow r=e.\left(\frac{l}{e}+r\cos{\theta}\right)\) ➜ \(\because SP=r\)
\(\frac{SN}{SP}=\cos{\theta}\)
\(\Rightarrow r=l+er\cos{\theta}\)
\(\Rightarrow l+er\cos{\theta}=r\)
\(\Rightarrow l=r-er\cos{\theta}\)
\(\Rightarrow l=r(1-e\cos{\theta})\)
\(\therefore \frac{l}{r}=1-e\cos{\theta}\)
ইহাই নির্ণেয় পোলার সমীকরণ।
চিত্র হতে,
\(SZ=SP\cos{\theta}\)
\(\Rightarrow SZ=r\cos{\theta} \because SP=r\)
\(\Rightarrow \frac{l}{e}=r\cos{\theta}\) ➜ \((1)\) হতে,
\(\because SZ=\frac{l}{e}\)
\(\therefore \frac{l}{r}=e\cos{\theta}\)
ইহাই নির্ণেয় নিয়ামক বা দিকাক্ষের পোলার সমীকরণ।

একটি কণিকের ফোকাস \(S\) নিয়ামক \(ZM\) এবং শীর্ষ বিন্দু \(A\) । \(ZM\) এর ওপর লম্ব \(ZS\) টানা হলো এবং তা \(X\) অক্ষ পর্যন্ত বর্ধিত করা হলো। \(S\) কে পোল এবং \(ZX\) কে মূলরেখা ধরা হলো।
মনে করি,
\(P\) কণিকের ওপর যেকোনো একটি বিন্দু এবং এর পোলার স্থানাঙ্ক \((r, \theta)\)
তাহলে, \(SP=r\)
এবং \(\angle{XSP}=\theta\)
মূলরেখার ওপর \(PN\) লম্ব এবং নিয়ামকের ওপর \(PM\) লম্ব টানা হলো।
ধরি, ফোকাস লম্বার্ধ \(SL=l\)
যেহেতু \(e.SZ=SL\)
\(\Rightarrow e.SZ=l\)
\(\therefore SZ=\frac{l}{e} .....(1)\)
এখন, \(r=SP\)
\(\Rightarrow r=\frac{SP}{PM}\times{PM}\)
\(\Rightarrow r=e.PM\) ➜ \(\because \frac{SP}{PM}=e\)
\(\Rightarrow r=e.ZN\) ➜ \(\because PM=ZN\)
\(\Rightarrow r=e.(ZS+SN)\)
\(\Rightarrow r=e.\left(\frac{l}{e}+SP\times{\frac{SN}{SP}}\right)\) ➜ \((1)\) হতে,
\(\because SZ=\frac{l}{e}\)
\(\Rightarrow r=e.\left(\frac{l}{e}+r\cos{\theta}\right)\) ➜ \(\because SP=r\)
\(\frac{SN}{SP}=\cos{\theta}\)
\(\Rightarrow r=l+er\cos{\theta}\)
\(\Rightarrow l+er\cos{\theta}=r\)
\(\Rightarrow l=r-er\cos{\theta}\)
\(\Rightarrow l=r(1-e\cos{\theta})\)
\(\therefore \frac{l}{r}=1-e\cos{\theta}\)
ইহাই নির্ণেয় পোলার সমীকরণ।
চিত্র হতে,
\(SZ=SP\cos{\theta}\)
\(\Rightarrow SZ=r\cos{\theta} \because SP=r\)
\(\Rightarrow \frac{l}{e}=r\cos{\theta}\) ➜ \((1)\) হতে,
\(\because SZ=\frac{l}{e}\)
\(\therefore \frac{l}{r}=e\cos{\theta}\)
ইহাই নির্ণেয় নিয়ামক বা দিকাক্ষের পোলার সমীকরণ।
×
কোনো কণিকের অক্ষরেখা আদি রেখার সহিত \(\alpha\) কোণ উৎপন্ন করলে এবং এটির উপকেন্দ্র পোল হলে কণিকটির পোলার সমীকরণ ও দিকাক্ষের পোলার সমীকরণঃ
কণিকের পোলার সমীকরণঃ \(\frac{l}{r}=1-e\cos{(\theta-\alpha)}\)দিকাক্ষের পোলার সমীকরণঃ \(\frac{l}{r}=e\cos{(\theta-\alpha)}\)
সমাধানঃ
ধরি,
\(SZ\) অক্ষরেখা আদি রেখার সাথে \(\alpha\) কোণে আনত। \(P\) কণিকের ওপর যেকোনো একটি বিন্দু এবং আদি রেখার সাপেক্ষে এর পোলার স্থানাঙ্ক \((r, \theta)\)
তাহলে, \(SP=r\)
\(\angle{XSP}=\theta\)
\(\angle{XSZ}=\alpha\)
এবং \(\angle{PSZ}=\theta-\alpha\)
সংজ্ঞানুসারে,
\(SP=e.PM\)
\(\Rightarrow SP=e.NZ\) ➜ \(\because PM=ZN\)
\(\Rightarrow r=e.(ZS+SN)\)
\(\Rightarrow r=e.\left(\frac{l}{e}+SP\times{\frac{SN}{SP}}\right)\) ➜ \((1)\) হতে,
\(\because SZ=\frac{l}{e}\)
\(\Rightarrow r=e.\left\{\frac{l}{e}+r\cos{(\theta-\alpha)}\right\}\) ➜ \(\because SP=r\)
\(\frac{SN}{SP}=\cos{(\theta-\alpha)}\)
\(\Rightarrow r=l+er\cos{(\theta-\alpha)}\)
\(\Rightarrow l+er\cos{(\theta-\alpha)}=r\)
\(\Rightarrow l=r-er\cos{(\theta-\alpha)}\)
\(\Rightarrow l=r(1-e\cos{(\theta-\alpha)})\)
\(\therefore \frac{l}{r}=1-e\cos{(\theta-\alpha)}\)
ইহাই নির্ণেয় পোলার সমীকরণ।
চিত্র হতে,
\(SZ=SP\cos{(\theta-\alpha)}\)
\(\Rightarrow SZ=r\cos{(\theta-\alpha)} \because SP=r\)
\(\Rightarrow \frac{l}{e}=r\cos{(\theta-\alpha)}\) ➜ \((1)\) হতে,
\(\because SZ=\frac{l}{e}\)
\(\therefore \frac{l}{r}=e\cos{(\theta-\alpha)}\)
ইহাই নির্ণেয় নিয়ামক বা দিকাক্ষের পোলার সমীকরণ।
\(SZ\) অক্ষরেখা আদি রেখার সাথে \(\alpha\) কোণে আনত। \(P\) কণিকের ওপর যেকোনো একটি বিন্দু এবং আদি রেখার সাপেক্ষে এর পোলার স্থানাঙ্ক \((r, \theta)\)
তাহলে, \(SP=r\)
\(\angle{XSP}=\theta\)
\(\angle{XSZ}=\alpha\)
এবং \(\angle{PSZ}=\theta-\alpha\)
সংজ্ঞানুসারে,
\(SP=e.PM\)
\(\Rightarrow SP=e.NZ\) ➜ \(\because PM=ZN\)
\(\Rightarrow r=e.(ZS+SN)\)
\(\Rightarrow r=e.\left(\frac{l}{e}+SP\times{\frac{SN}{SP}}\right)\) ➜ \((1)\) হতে,
\(\because SZ=\frac{l}{e}\)
\(\Rightarrow r=e.\left\{\frac{l}{e}+r\cos{(\theta-\alpha)}\right\}\) ➜ \(\because SP=r\)
\(\frac{SN}{SP}=\cos{(\theta-\alpha)}\)
\(\Rightarrow r=l+er\cos{(\theta-\alpha)}\)
\(\Rightarrow l+er\cos{(\theta-\alpha)}=r\)
\(\Rightarrow l=r-er\cos{(\theta-\alpha)}\)
\(\Rightarrow l=r(1-e\cos{(\theta-\alpha)})\)
\(\therefore \frac{l}{r}=1-e\cos{(\theta-\alpha)}\)
ইহাই নির্ণেয় পোলার সমীকরণ।
চিত্র হতে,
\(SZ=SP\cos{(\theta-\alpha)}\)
\(\Rightarrow SZ=r\cos{(\theta-\alpha)} \because SP=r\)
\(\Rightarrow \frac{l}{e}=r\cos{(\theta-\alpha)}\) ➜ \((1)\) হতে,
\(\because SZ=\frac{l}{e}\)
\(\therefore \frac{l}{r}=e\cos{(\theta-\alpha)}\)
ইহাই নির্ণেয় নিয়ামক বা দিকাক্ষের পোলার সমীকরণ।
×
\(\frac{l}{r}=1-e\cos{\theta}\) কণিকের ক্ষেত্রেঃ
জ্যা এর সমীকরণঃ \(\frac{l}{r}=\sec{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}-e\cos{\theta}\)যেখানে, \(\alpha\) এবং \(\beta\) জ্যা এর প্রান্ত বিন্দুর ভেক্টর কোণ।
\(\alpha\) বিন্দুতে স্পর্শকের সমীকরণঃ \(\frac{l}{r}=\cos{(\theta-\alpha)}-e\cos{\theta}\)
সমাধানঃ
প্রদত্ত কণিকের সমীকরণ, \(\frac{l}{r}=1-e\cos{\theta} ........(1)\)
ধরি,
জ্যাটির প্রান্ত বিন্দুদ্বয় যথাক্রমে \(P(r_{1}, \alpha)\) এবং \(Q(r_{2}, \beta)\)
এরা \((1)\) নং কনিককে সিদ্ধ করে কাজেই
\(\frac{l}{r_{1}}=1-e\cos{\alpha} ........(2)\)
\(\frac{l}{r_{2}}=1-e\cos{\beta} ........(3)\)
\(PQ\) সরলরেখার পোলার সমীকরণ,
\(\frac{\sin{(\beta-\alpha)}}{r}=\frac{\sin{(\theta-\alpha)}}{r_{2}}+\frac{\sin{(\beta-\theta)}}{r_{1}}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=\frac{l}{r_{2}}\sin{(\theta-\alpha)}+\frac{l}{r_{1}}\sin{(\beta-\theta)}\) ➜ উভয় পার্শে \(l\) গুণ করে।
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=(1-e\cos{\beta})\sin{(\theta-\alpha)}+(1-e\cos{\alpha})\sin{(\beta-\theta)}\) ➜ \((2)\) ও \((3)\) এর সাহায্যে
\(\frac{l}{r_{1}}=1-e\cos{\alpha}\)
\(\frac{l}{r_{2}}=1-e\cos{\beta}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=\sin{(\theta-\alpha)}-e\cos{\beta}\sin{(\theta-\alpha)}+\sin{(\beta-\theta)}-e\cos{\alpha}\sin{(\beta-\theta)}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=\sin{(\theta-\alpha)}+\sin{(\beta-\theta)}-e\{\cos{\beta}\sin{(\theta-\alpha)}+\cos{\alpha}\sin{(\beta-\theta)}\}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=2\sin{\frac{\theta-\alpha+\beta-\theta}{2}}\cos{\frac{\theta-\alpha-\beta+\theta}{2}}\)\(-e\{\cos{\beta}\sin{\theta}\cos{\alpha}-\cos{\beta}\cos{\theta}\sin{\alpha}+\cos{\alpha}\sin{\beta}\cos{\theta}-\cos{\alpha}\cos{\beta}\sin{\theta}\}\) ➜ \(\because \sin{C}+\sin{D}=2\sin{\frac{C+D}{2}}\cos{\frac{C-D}{2}}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{2\theta-(\alpha+\beta)}{2}}\)\(-e\{-\cos{\beta}\cos{\theta}\sin{\alpha}+\cos{\alpha}\sin{\beta}\cos{\theta}\}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=2\sin{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}\)\(-e\cos{\theta}\{\cos{\alpha}\sin{\beta}-\sin{\alpha}\cos{\beta}\}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=2\sin{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}-e\cos{\theta}\sin{(\beta-\alpha)}\)
\(\Rightarrow \frac{l}{r}.2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{\beta-\alpha}{2}}=2\sin{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}\)\(-e\cos{\theta}.2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{\beta-\alpha}{2}}\) ➜ \(\because \sin{A}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
\(\Rightarrow \frac{l}{r}2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{\beta-\alpha}{2}}=2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{\beta-\alpha}{2}}\left\{\sec{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}-e\cos{\theta}\right\}\)
\(\therefore \frac{l}{r}=\sec{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}-e\cos{\theta} ........(4)\)
ইহাই নির্ণেয় জ্যা এর সমীকরণ।
\((4)\) নং সমীকরণে \(\beta=\alpha\) বসিয়ে,
\(\frac{l}{r}=\sec{\frac{\alpha-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\alpha}{2}\right)}-e\cos{\theta}\)
\(\Rightarrow \frac{l}{r}=\sec{\frac{0}{2}}\cos{\left(\theta-\frac{2\alpha}{2}\right)}-e\cos{\theta}\)
\(\Rightarrow \frac{l}{r}=\sec{0}\cos{(\theta-\alpha)}-e\cos{\theta}\)
\(\Rightarrow \frac{l}{r}=1.\cos{(\theta-\alpha)}-e\cos{\theta}\)
\(\therefore \frac{l}{r}=\cos{(\theta-\alpha)}-e\cos{\theta}\)
ইহাই \(\alpha\) বিন্দুতে নির্ণেয় স্পর্শকের সমীকরণ।
ধরি,
জ্যাটির প্রান্ত বিন্দুদ্বয় যথাক্রমে \(P(r_{1}, \alpha)\) এবং \(Q(r_{2}, \beta)\)
এরা \((1)\) নং কনিককে সিদ্ধ করে কাজেই
\(\frac{l}{r_{1}}=1-e\cos{\alpha} ........(2)\)
\(\frac{l}{r_{2}}=1-e\cos{\beta} ........(3)\)
\(PQ\) সরলরেখার পোলার সমীকরণ,
\(\frac{\sin{(\beta-\alpha)}}{r}=\frac{\sin{(\theta-\alpha)}}{r_{2}}+\frac{\sin{(\beta-\theta)}}{r_{1}}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=\frac{l}{r_{2}}\sin{(\theta-\alpha)}+\frac{l}{r_{1}}\sin{(\beta-\theta)}\) ➜ উভয় পার্শে \(l\) গুণ করে।
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=(1-e\cos{\beta})\sin{(\theta-\alpha)}+(1-e\cos{\alpha})\sin{(\beta-\theta)}\) ➜ \((2)\) ও \((3)\) এর সাহায্যে
\(\frac{l}{r_{1}}=1-e\cos{\alpha}\)
\(\frac{l}{r_{2}}=1-e\cos{\beta}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=\sin{(\theta-\alpha)}-e\cos{\beta}\sin{(\theta-\alpha)}+\sin{(\beta-\theta)}-e\cos{\alpha}\sin{(\beta-\theta)}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=\sin{(\theta-\alpha)}+\sin{(\beta-\theta)}-e\{\cos{\beta}\sin{(\theta-\alpha)}+\cos{\alpha}\sin{(\beta-\theta)}\}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=2\sin{\frac{\theta-\alpha+\beta-\theta}{2}}\cos{\frac{\theta-\alpha-\beta+\theta}{2}}\)\(-e\{\cos{\beta}\sin{\theta}\cos{\alpha}-\cos{\beta}\cos{\theta}\sin{\alpha}+\cos{\alpha}\sin{\beta}\cos{\theta}-\cos{\alpha}\cos{\beta}\sin{\theta}\}\) ➜ \(\because \sin{C}+\sin{D}=2\sin{\frac{C+D}{2}}\cos{\frac{C-D}{2}}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{2\theta-(\alpha+\beta)}{2}}\)\(-e\{-\cos{\beta}\cos{\theta}\sin{\alpha}+\cos{\alpha}\sin{\beta}\cos{\theta}\}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=2\sin{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}\)\(-e\cos{\theta}\{\cos{\alpha}\sin{\beta}-\sin{\alpha}\cos{\beta}\}\)
\(\Rightarrow \frac{l\sin{(\beta-\alpha)}}{r}=2\sin{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}-e\cos{\theta}\sin{(\beta-\alpha)}\)
\(\Rightarrow \frac{l}{r}.2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{\beta-\alpha}{2}}=2\sin{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}\)\(-e\cos{\theta}.2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{\beta-\alpha}{2}}\) ➜ \(\because \sin{A}=2\sin{\frac{A}{2}}\cos{\frac{A}{2}}\)
\(\Rightarrow \frac{l}{r}2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{\beta-\alpha}{2}}=2\sin{\frac{\beta-\alpha}{2}}\cos{\frac{\beta-\alpha}{2}}\left\{\sec{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}-e\cos{\theta}\right\}\)
\(\therefore \frac{l}{r}=\sec{\frac{\beta-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\beta}{2}\right)}-e\cos{\theta} ........(4)\)
ইহাই নির্ণেয় জ্যা এর সমীকরণ।
\((4)\) নং সমীকরণে \(\beta=\alpha\) বসিয়ে,
\(\frac{l}{r}=\sec{\frac{\alpha-\alpha}{2}}\cos{\left(\theta-\frac{\alpha+\alpha}{2}\right)}-e\cos{\theta}\)
\(\Rightarrow \frac{l}{r}=\sec{\frac{0}{2}}\cos{\left(\theta-\frac{2\alpha}{2}\right)}-e\cos{\theta}\)
\(\Rightarrow \frac{l}{r}=\sec{0}\cos{(\theta-\alpha)}-e\cos{\theta}\)
\(\Rightarrow \frac{l}{r}=1.\cos{(\theta-\alpha)}-e\cos{\theta}\)
\(\therefore \frac{l}{r}=\cos{(\theta-\alpha)}-e\cos{\theta}\)
ইহাই \(\alpha\) বিন্দুতে নির্ণেয় স্পর্শকের সমীকরণ।
×
কেন্দ্রীয় কনিক \(ax^2+2hxy+by^2+2gx+2fy+c=0\) এর বিকেন্দ্রিকতা \(e\) হলে,
\(e^4+\frac{(a-b)^2+4h^2}{ab-h^2}(e^2-1)=0\)
প্রমাণঃ
প্রদত্ত কণিকের সমীকরণ, \(ax^2+2hxy+by^2+2gx+2fy+c=0 ........(1)\)
মূলবিন্দুকে কণিকটির কেন্দ্রে স্থানান্তরিত করলে, \((1)\) নং সমীকরণের রূপান্তরিত রূপ হবে
\(ax^2+2hxy+by^2+k=0 .......(2)\)
যেখানে, \(k=\frac{\Delta}{ab-h^2}\)
আবার, \((2)\) নং সমীকরণ থেকে \(xy\) যুক্ত পদ অপসারণ করা হলে সমীকরণের রূপান্তরিত রূপ হবে
\(a^{\prime}x^2+b^{\prime}y^2+k=0 .......(3)\)
যেখানে, \(a^{\prime}+b^{\prime}=a+b ......(4)\)
এবং \(a^{\prime}b^{\prime}=ab-h^2 ......(5)\)
\((3)\) হতে,
\(a^{\prime}x^2+b^{\prime}y^2=-k\)
\(\Rightarrow \frac{a^{\prime}}{-k}x^2+\frac{b^{\prime}}{-k}y^2=1\)
\(\therefore \frac{x^2}{\frac{-k}{a^{\prime}}}+\frac{y^2}{\frac{-k}{b^{\prime}}}=1 .....(6)\)
এখন কণিকটির বিকেন্দ্রিকতা \(e\) এর জন্য পাই
\(e^2=1-\frac{\frac{-k}{a^{\prime}}}{\frac{-k}{b^{\prime}}}\) ➜ \(\because e^2=1-\frac{a^2}{b^2}\)
\(\Rightarrow e^2=1-\frac{b^{\prime}}{a^{\prime}}\)
\(\Rightarrow \frac{b^{\prime}}{a^{\prime}}=1-e^2 .......(7)\)
\(\Rightarrow e^2=\frac{a^{\prime}-b^{\prime}}{a^{\prime}}\)
\(\Rightarrow e^4=\frac{(a^{\prime}-b^{\prime})^2}{(a^{\prime})^2}\)
\(\Rightarrow e^4=\frac{b^{\prime}(a^{\prime}-b^{\prime})^2}{(a^{\prime})^2b^{\prime}}\)
\(\Rightarrow e^4=\frac{b^{\prime}}{a^{\prime}}\times{\frac{(a^{\prime}-b^{\prime})^2}{a^{\prime}b^{\prime}}}\)
\(\Rightarrow e^4=\frac{b^{\prime}}{a^{\prime}}\times{\frac{(a^{\prime}+b^{\prime})^2-4a^{\prime}b^{\prime}}{a^{\prime}b^{\prime}}}\)
\(\Rightarrow e^4=(1-e^2)\frac{(a+b)^2-4(ab-h^2)}{ab-h^2}\) ➜ \(\because \frac{b^{\prime}}{a^{\prime}}=1-e^2, \ a^{\prime}+b^{\prime}=a+b, \ a^{\prime}b^{\prime}=ab-h^2\)
\(\Rightarrow e^4=(1-e^2)\frac{(a+b)^2-4(ab-h^2)}{ab-h^2}\)
\(\Rightarrow e^4=(1-e^2)\frac{(a+b)^2-4ab+4h^2}{ab-h^2}\)
\(\Rightarrow e^4=(1-e^2)\frac{(a-b)^2+4h^2}{ab-h^2}\)
\(\Rightarrow e^4=-\frac{(a-b)^2+4h^2}{ab-h^2}(e^2-1)\)
\(\therefore e^4+\frac{(a-b)^2+4h^2}{ab-h^2}(e^2-1)=0\)
মূলবিন্দুকে কণিকটির কেন্দ্রে স্থানান্তরিত করলে, \((1)\) নং সমীকরণের রূপান্তরিত রূপ হবে
\(ax^2+2hxy+by^2+k=0 .......(2)\)
যেখানে, \(k=\frac{\Delta}{ab-h^2}\)
আবার, \((2)\) নং সমীকরণ থেকে \(xy\) যুক্ত পদ অপসারণ করা হলে সমীকরণের রূপান্তরিত রূপ হবে
\(a^{\prime}x^2+b^{\prime}y^2+k=0 .......(3)\)
যেখানে, \(a^{\prime}+b^{\prime}=a+b ......(4)\)
এবং \(a^{\prime}b^{\prime}=ab-h^2 ......(5)\)
\((3)\) হতে,
\(a^{\prime}x^2+b^{\prime}y^2=-k\)
\(\Rightarrow \frac{a^{\prime}}{-k}x^2+\frac{b^{\prime}}{-k}y^2=1\)
\(\therefore \frac{x^2}{\frac{-k}{a^{\prime}}}+\frac{y^2}{\frac{-k}{b^{\prime}}}=1 .....(6)\)
এখন কণিকটির বিকেন্দ্রিকতা \(e\) এর জন্য পাই
\(e^2=1-\frac{\frac{-k}{a^{\prime}}}{\frac{-k}{b^{\prime}}}\) ➜ \(\because e^2=1-\frac{a^2}{b^2}\)
\(\Rightarrow e^2=1-\frac{b^{\prime}}{a^{\prime}}\)
\(\Rightarrow \frac{b^{\prime}}{a^{\prime}}=1-e^2 .......(7)\)
\(\Rightarrow e^2=\frac{a^{\prime}-b^{\prime}}{a^{\prime}}\)
\(\Rightarrow e^4=\frac{(a^{\prime}-b^{\prime})^2}{(a^{\prime})^2}\)
\(\Rightarrow e^4=\frac{b^{\prime}(a^{\prime}-b^{\prime})^2}{(a^{\prime})^2b^{\prime}}\)
\(\Rightarrow e^4=\frac{b^{\prime}}{a^{\prime}}\times{\frac{(a^{\prime}-b^{\prime})^2}{a^{\prime}b^{\prime}}}\)
\(\Rightarrow e^4=\frac{b^{\prime}}{a^{\prime}}\times{\frac{(a^{\prime}+b^{\prime})^2-4a^{\prime}b^{\prime}}{a^{\prime}b^{\prime}}}\)
\(\Rightarrow e^4=(1-e^2)\frac{(a+b)^2-4(ab-h^2)}{ab-h^2}\) ➜ \(\because \frac{b^{\prime}}{a^{\prime}}=1-e^2, \ a^{\prime}+b^{\prime}=a+b, \ a^{\prime}b^{\prime}=ab-h^2\)
\(\Rightarrow e^4=(1-e^2)\frac{(a+b)^2-4(ab-h^2)}{ab-h^2}\)
\(\Rightarrow e^4=(1-e^2)\frac{(a+b)^2-4ab+4h^2}{ab-h^2}\)
\(\Rightarrow e^4=(1-e^2)\frac{(a-b)^2+4h^2}{ab-h^2}\)
\(\Rightarrow e^4=-\frac{(a-b)^2+4h^2}{ab-h^2}(e^2-1)\)
\(\therefore e^4+\frac{(a-b)^2+4h^2}{ab-h^2}(e^2-1)=0\)

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000001