শিক্ষা বোর্ড যশোর - 2018
উচ্চতর গণিত ( বহুনির্বাচনি )
[2018 সালের সিলেবাস অনুযায়ী ]
দ্বিতীয় পত্র বহুনির্বাচনি
বিষয় কোডঃ 266
সময়-২৫ মিনিট
পূর্ণমান-২৫
[ দ্রষ্টব্যঃ সরবরাহকৃত বহুনির্বাচনি অভীক্ষার উত্তরপত্রে প্রশ্নের ক্রমিক নম্বরের বিপরীতে প্রদত্ত বর্ণসংবলিত বৃত্তসমুহ হতে সিঠিক/সর্বোৎকৃষ্ট উত্তরের বৃত্তটি বল পয়ন্ট কলম দ্বারা সম্পুর্ণ ভরাট কর। প্রতিটি প্রশ্নের মাণ ১। প্রশ্নপত্রে কোন প্রকার দাগ/ চিহ্ন দেওয়া যাবে না। ]
উচ্চতর গণিত ( বহুনির্বাচনি )
[2018 সালের সিলেবাস অনুযায়ী ]
দ্বিতীয় পত্র বহুনির্বাচনি
বিষয় কোডঃ 266
সময়-২৫ মিনিট
পূর্ণমান-২৫
[ দ্রষ্টব্যঃ সরবরাহকৃত বহুনির্বাচনি অভীক্ষার উত্তরপত্রে প্রশ্নের ক্রমিক নম্বরের বিপরীতে প্রদত্ত বর্ণসংবলিত বৃত্তসমুহ হতে সিঠিক/সর্বোৎকৃষ্ট উত্তরের বৃত্তটি বল পয়ন্ট কলম দ্বারা সম্পুর্ণ ভরাট কর। প্রতিটি প্রশ্নের মাণ ১। প্রশ্নপত্রে কোন প্রকার দাগ/ চিহ্ন দেওয়া যাবে না। ]
১। বাস্তব সংখ্যার স্বীকার্যের ক্ষেত্রে সংযোগ বিধির উদাহরণ কোনটি?
\((i) (a+b)+c=a+(b+c)\) ইহা যোগের সংযোগ বিধি।
\((i) (a.b).c=a.(b.c)\) ইহা গুণের সংযোগ বিধি।
উত্তরঃ ( খ )
ক \(2+3=3+2\)
গ \(2+0=2\)
গ \(2+0=2\)
খ \((2+3)+4=2+(3+4)\)
ঘ \(2(3+4)=2.3+2.4\)
সংযোগ বিধিঃ বাস্তব সংখ্যার জন্য সংযোগ বিধি প্রযোজ্য। যদি \(a, b,
c\in{}\mathbb{R}\) হয়, তবে ঘ \(2(3+4)=2.3+2.4\)
\((i) (a+b)+c=a+(b+c)\) ইহা যোগের সংযোগ বিধি।
\((i) (a.b).c=a.(b.c)\) ইহা গুণের সংযোগ বিধি।
উত্তরঃ ( খ )
২। কাল্পনিক সংখ্যা \(i\) এবং \(n\in \mathbb{N}\) -এর জন্য
\(i^{4n}-i+i^{4n+1}-1\)-এর মাণ কত?
\(=i^{4n}-i+i^{4n}.i-1\)
\(=(i^{2})^{2n}-i+(i^{2})^{2n}.i-1\)
\(=(-1)^{2n}-i+(-1)^{2n}.i-1, \because i^2=-1\)
\(=1-i+1.i-1, \because 2n\) জোড় সংখ্যা।
\(=-i+i\)
\(=0\)
উত্তরঃ ( গ )
ক \(-i\)
গ \(0\)
গ \(0\)
খ \(i\)
ঘ \(1\)
\(i^{4n}-i+i^{4n+1}-1\) ঘ \(1\)
\(=i^{4n}-i+i^{4n}.i-1\)
\(=(i^{2})^{2n}-i+(i^{2})^{2n}.i-1\)
\(=(-1)^{2n}-i+(-1)^{2n}.i-1, \because i^2=-1\)
\(=1-i+1.i-1, \because 2n\) জোড় সংখ্যা।
\(=-i+i\)
\(=0\)
উত্তরঃ ( গ )
৩। \(\sec^2{(\cot^{-1}{\sqrt{2}})}-\sin^2{(\cos^{-1}{1})}\)-এর মাণ
কোনটি?
\(=\sec^2{\left(\tan^{-1}{\frac{1}{\sqrt{2}}}\right)}-\sin^2{(\cos^{-1} 1)},\) \(\because \cot^{-1}{x}=\tan^{-1}{\frac{1}{x}}\)
\(=1+\tan^2{\left(\tan^{-1}{\frac{1}{\sqrt{2}}}\right)}-\{1-\cos^2{(\cos^{-1} 1)}\},\) \(\because \sec^2{A}=1+\tan^{2}{A}, \sin^2{A}=1-\cos^{2}{A}\)
\(=1+\tan^2{\left(\tan^{-1}{\frac{1}{\sqrt{2}}}\right)}-1+\cos^2{(\cos^{-1} 1)}\)
\(=\left(\frac{1}{\sqrt{2}}\right)^2+(1)^2\)
\(=\frac{1}{2}+1\)
\(=\frac{1+2}{2}\)
\(=\frac{3}{2}\)
উত্তরঃ ( গ )
ক \(\frac{1}{2}\)
গ \(\frac{3}{2}\)
গ \(\frac{3}{2}\)
খ \(1\)
ঘ \(3\)
\(\sec^2{(\cot^{-1}{\sqrt{2}})}-\sin^2{(\cos^{-1}{1})}\)ঘ \(3\)
\(=\sec^2{\left(\tan^{-1}{\frac{1}{\sqrt{2}}}\right)}-\sin^2{(\cos^{-1} 1)},\) \(\because \cot^{-1}{x}=\tan^{-1}{\frac{1}{x}}\)
\(=1+\tan^2{\left(\tan^{-1}{\frac{1}{\sqrt{2}}}\right)}-\{1-\cos^2{(\cos^{-1} 1)}\},\) \(\because \sec^2{A}=1+\tan^{2}{A}, \sin^2{A}=1-\cos^{2}{A}\)
\(=1+\tan^2{\left(\tan^{-1}{\frac{1}{\sqrt{2}}}\right)}-1+\cos^2{(\cos^{-1} 1)}\)
\(=\left(\frac{1}{\sqrt{2}}\right)^2+(1)^2\)
\(=\frac{1}{2}+1\)
\(=\frac{1+2}{2}\)
\(=\frac{3}{2}\)
উত্তরঃ ( গ )
৪।
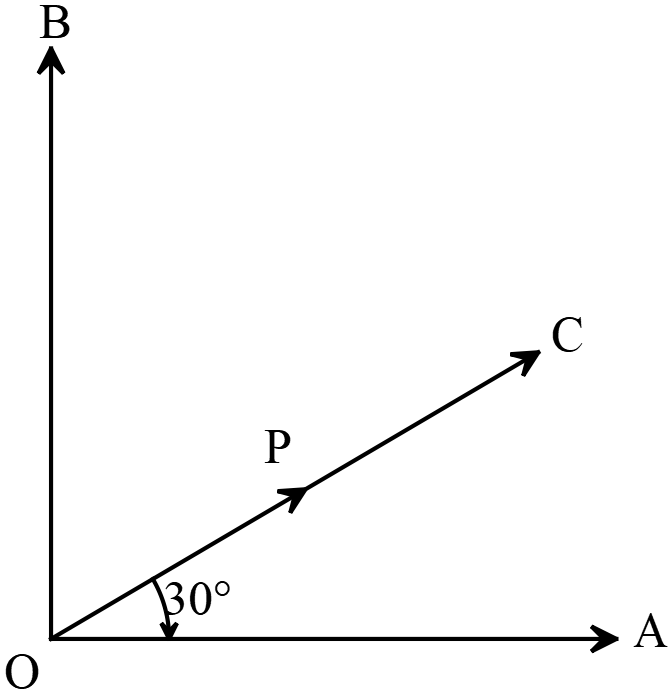উদ্দীপকে-
\(i.\) \(OA\) বরাবর \(P\) বলের লম্বাংশ \(=\frac{\sqrt{3}P}{2}\)
\(ii.\) \(OB\) বরাবর \(P\) বলের লম্বাংশ \(=\frac{P}{2}\)
\(iii.\) \(OC\) বরাবর \(P\) বলের লম্বাংশ \(=P\)
নিচের কোনটি সঠীক?
\(OA\) বরাবর \(P\) বলের লম্বাংশ \(=P\cos{30^{o}}\)
\(=P\frac{\sqrt{3}}{2}, \because \cos{30^{o}}=\frac{\sqrt{3}}{2}\)
\(=\frac{\sqrt{3}P}{2}\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
\(OB\) বরাবর \(P\) বলের লম্বাংশ \(=P\sin{30^{o}}\)
\(=P\frac{1}{2}, \because \sin{30^{o}}=\frac{1}{2}\)
\(=\frac{P}{2}\)
\(\therefore (ii.)\) নং বাক্যটি সত্য।
\(OC\) বরাবর \(P\) বলের লম্বাংশ \(=P\cos{0^{o}}\)
\(=P\times{1}, \because \cos{0^{o}}=1\)
\(=P\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( ঘ )
উদ্দীপকে-\(i.\) \(OA\) বরাবর \(P\) বলের লম্বাংশ \(=\frac{\sqrt{3}P}{2}\)
\(ii.\) \(OB\) বরাবর \(P\) বলের লম্বাংশ \(=\frac{P}{2}\)
\(iii.\) \(OC\) বরাবর \(P\) বলের লম্বাংশ \(=P\)
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
\(OA\) বরাবর \(P\) বলের লম্বাংশ \(=P\cos{30^{o}}\)
\(=P\frac{\sqrt{3}}{2}, \because \cos{30^{o}}=\frac{\sqrt{3}}{2}\)
\(=\frac{\sqrt{3}P}{2}\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
\(OB\) বরাবর \(P\) বলের লম্বাংশ \(=P\sin{30^{o}}\)
\(=P\frac{1}{2}, \because \sin{30^{o}}=\frac{1}{2}\)
\(=\frac{P}{2}\)
\(\therefore (ii.)\) নং বাক্যটি সত্য।
\(OC\) বরাবর \(P\) বলের লম্বাংশ \(=P\cos{0^{o}}\)
\(=P\times{1}, \because \cos{0^{o}}=1\)
\(=P\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( ঘ )
৫। বিস্তার পরিমাপে অনপেক্ষ (Absolute) পরিমাপ কোনটি?
\((1)\) পরিসর
\((2)\) গড় ব্যবধান
\((3)\) পরিমিত ব্যবধান
\((4)\) চতুর্থক ব্যবধান
উত্তরঃ ( খ )
ক বিভেদাংক
গ পরিসরাংক
গ পরিসরাংক
খ চতুর্থক ব্যবধান
ঘ গড় ব্যবধাংক
পরম বা অনপেক্ষ বিস্তার পরিমাপঃ কোনো নিবেশনের কেন্দ্রীয় মাণ হতে
অন্যান্য মানসমূহের ব্যবধানের গড় যা নিবেশনের মানসমূহের মূল এককে
প্রকাশিত হয়, ইহাই পরম বা অনপেক্ষ বিস্তার পরিমাপ। পরম বা অনপেক্ষ
বিস্তার পরিমাপ চার প্রকার। যথাঃ ঘ গড় ব্যবধাংক
\((1)\) পরিসর
\((2)\) গড় ব্যবধান
\((3)\) পরিমিত ব্যবধান
\((4)\) চতুর্থক ব্যবধান
উত্তরঃ ( খ )
৬। \(\sin{\left(x-\frac{\pi}{2}\right)}=0, \ n\in{\mathbb{Z}}\)
সমীকরণের সমাধান কোনটি?
\(\Rightarrow x-\frac{\pi}{2}=n\pi, \because \sin{\theta}=0\) হলে, \(\theta=n\pi\)
\(\therefore x=n\pi+\frac{\pi}{2}\)
উত্তরঃ ( ক )
ক \(n\pi+\frac{\pi}{2}\)
গ \(n\pi-\frac{\pi}{2}\)
গ \(n\pi-\frac{\pi}{2}\)
খ \(2n\pi+\frac{\pi}{2}\)
ঘ \(2n\pi-\frac{\pi}{2}\)
\(\sin{\left(x-\frac{\pi}{2}\right)}=0, \ n\in{\mathbb{Z}}\)
ঘ \(2n\pi-\frac{\pi}{2}\)
\(\Rightarrow x-\frac{\pi}{2}=n\pi, \because \sin{\theta}=0\) হলে, \(\theta=n\pi\)
\(\therefore x=n\pi+\frac{\pi}{2}\)
উত্তরঃ ( ক )
৭। \(y^2=-2x\) পরাবৃত্তের-
\(i.\) উপকেন্দ্রিক লম্বের সমীকরণ \(2x=1\)
\(ii.\) উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(2\) একক
\(iii.\) উপকেন্দ্রের স্থানাঙ্ক \(\left(-\frac{1}{2}, 0\right)\)
নিচের কোনটি সঠীক?
এখানে, \(4a=-2, \because y^2=4ax \) পরাবৃত্তের সহিত তুলুনা করে।
\(\Rightarrow a=-\frac{2}{4}\)
\(\therefore a=-\frac{1}{2}\)
উপকেন্দ্রিক লম্বের সমীকরণ \(x=a, \because y^2=4ax\) পরাবৃত্তের উপকেন্দ্রিক লম্বের সমীকরণ \(x=a\)
\(\Rightarrow x=-\frac{1}{2}\)
\(\therefore 2x=-1\)
\(\therefore (i.)\) নং বাক্যটি সত্য নয়।
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|, \because y^2=4ax\) পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
\(=|4\times{-\frac{1}{2}}|\)
\(=|-2|\)
\(=2\)
\(\therefore (ii.)\) নং বাক্যটি সত্য।
উপকেন্দ্রের স্থানাঙ্ক \((a, 0), \because y^2=4ax\) পরাবৃত্তের উপকেন্দ্রের স্থানাঙ্ক \((a, 0)\)
\(\therefore \left(-\frac{1}{2}, 0\right)\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( গ )
\(i.\) উপকেন্দ্রিক লম্বের সমীকরণ \(2x=1\)
\(ii.\) উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(2\) একক
\(iii.\) উপকেন্দ্রের স্থানাঙ্ক \(\left(-\frac{1}{2}, 0\right)\)
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
\(y^2=-2x\) পরাবৃত্তের-ঘ \(i.\), \(ii.\) ও \(iii.\)
এখানে, \(4a=-2, \because y^2=4ax \) পরাবৃত্তের সহিত তুলুনা করে।
\(\Rightarrow a=-\frac{2}{4}\)
\(\therefore a=-\frac{1}{2}\)
উপকেন্দ্রিক লম্বের সমীকরণ \(x=a, \because y^2=4ax\) পরাবৃত্তের উপকেন্দ্রিক লম্বের সমীকরণ \(x=a\)
\(\Rightarrow x=-\frac{1}{2}\)
\(\therefore 2x=-1\)
\(\therefore (i.)\) নং বাক্যটি সত্য নয়।
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|, \because y^2=4ax\) পরাবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=|4a|\)
\(=|4\times{-\frac{1}{2}}|\)
\(=|-2|\)
\(=2\)
\(\therefore (ii.)\) নং বাক্যটি সত্য।
উপকেন্দ্রের স্থানাঙ্ক \((a, 0), \because y^2=4ax\) পরাবৃত্তের উপকেন্দ্রের স্থানাঙ্ক \((a, 0)\)
\(\therefore \left(-\frac{1}{2}, 0\right)\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( গ )
৮। সম্ভাব্যতায় \(A\) ঘটনা এবং এর পূরক ঘটনা \(A^{c}\)-এর ক্ষেত্রে কোনটি
সত্য?
অর্থাৎ \(S\) সসীম নমুনাক্ষেত্রের একটি ঘটনা \(A\) এবং ঐ ঘটনা না ঘটা \(A^{c}\) হলে, \(P(A)+P(A^{c})=1\)
ইহা স্পষ্ট যে ঘটনাটি একবার ঘটতে পারে অথবা তা ঘটবে না। অর্থাৎ \(P(A)\) ও \(P(A^{c})\) এর মাণ ভগ্নাংশ হতে পারে না।
যদি ঘটনাটি ঘটে তবে, \(P(A)=1, P(A^{c})=0 \)
আবার,
যদি ঘটনাটি না ঘটে তবে, \(P(A)=0, P(A^{c})=1\)
তাহলে,
\(1\ge P(A)\ge 0\)
উত্তরঃ ( ঘ )
ক \(1\gt{P(A)}\gt{0}\)
গ \(1\gt{P(A^{c})}\gt{0}\)
গ \(1\gt{P(A^{c})}\gt{0}\)
খ \(1\gt{P(A^{c})}\ge{0}\)
ঘ \(1\ge{P(A)}\ge{0}\)
সম্ভাবনার পূরক সূত্রঃ যে কোনো দৈব্য পরীক্ষণে একটি ঘটনা ঘটা ও না
ঘটার সমষ্টি \(1\) (এক)।ঘ \(1\ge{P(A)}\ge{0}\)
অর্থাৎ \(S\) সসীম নমুনাক্ষেত্রের একটি ঘটনা \(A\) এবং ঐ ঘটনা না ঘটা \(A^{c}\) হলে, \(P(A)+P(A^{c})=1\)
ইহা স্পষ্ট যে ঘটনাটি একবার ঘটতে পারে অথবা তা ঘটবে না। অর্থাৎ \(P(A)\) ও \(P(A^{c})\) এর মাণ ভগ্নাংশ হতে পারে না।
যদি ঘটনাটি ঘটে তবে, \(P(A)=1, P(A^{c})=0 \)
আবার,
যদি ঘটনাটি না ঘটে তবে, \(P(A)=0, P(A^{c})=1\)
তাহলে,
\(1\ge P(A)\ge 0\)
উত্তরঃ ( ঘ )
৯। \(\triangle{ABC}\) এ \(A=\sin^{-1}{\frac{1}{2}}, \
B=\cos^{-1}{\frac{1}{2}}\) এবং \(C\) কোণের বহিঃস্থ কোণ \(\theta \) হলে
\(2\sin{\theta}-\sin{C}\)-এর মাণ কোনটি?
\(\Rightarrow A=\sin^{-1}{\sin{30^{o}}}, \ B=\cos^{-1}{\cos{60^{o}}}\)
\(\Rightarrow A=30^{o}, \ B=60^{o}\)
\(\triangle{ABC}\) এ
\(A+B+C=180^{o}\)
\(\Rightarrow C=180^{o}-(A+B)\)
\(\Rightarrow C=180^{o}-(30^{o}+60^{o}), \because A=30^{o}, \ B=60^{o}\)
\(\Rightarrow C=180^{o}-90^{o}\)
\(\therefore C=90^{o}\)
\(C\) কোণের বহিঃস্থ কোণ \(\theta \)
\(\therefore \theta+C=180^{0}\)
\(\Rightarrow \theta=180^{0}-C\)
\(\Rightarrow \theta=180^{0}-90^{o}, \because C=90^{o}\)
\(\therefore \theta=90^{o}\)
এখন,
\(2\sin{\theta}-\sin{C}\)
\(=2\sin{90^{o}}-\sin{90^{o}}, \because \theta=90^{o}, C=90^{o} \)
\(=2\times{1}-1, \because \sin{90^{o}}=1\)
\(=2-1\)
\(=1\)
উত্তরঃ ( খ )
ক \(0\)
গ \(2\)
গ \(2\)
খ \(1\)
ঘ \(3\)
\(\triangle{ABC}\) এ \(A=\sin^{-1}{\frac{1}{2}}, \
B=\cos^{-1}{\frac{1}{2}}\) এবং \(C\) কোণের বহিঃস্থ কোণ \(\theta
\)ঘ \(3\)
\(\Rightarrow A=\sin^{-1}{\sin{30^{o}}}, \ B=\cos^{-1}{\cos{60^{o}}}\)
\(\Rightarrow A=30^{o}, \ B=60^{o}\)
\(\triangle{ABC}\) এ
\(A+B+C=180^{o}\)
\(\Rightarrow C=180^{o}-(A+B)\)
\(\Rightarrow C=180^{o}-(30^{o}+60^{o}), \because A=30^{o}, \ B=60^{o}\)
\(\Rightarrow C=180^{o}-90^{o}\)
\(\therefore C=90^{o}\)
\(C\) কোণের বহিঃস্থ কোণ \(\theta \)
\(\therefore \theta+C=180^{0}\)
\(\Rightarrow \theta=180^{0}-C\)
\(\Rightarrow \theta=180^{0}-90^{o}, \because C=90^{o}\)
\(\therefore \theta=90^{o}\)
এখন,
\(2\sin{\theta}-\sin{C}\)
\(=2\sin{90^{o}}-\sin{90^{o}}, \because \theta=90^{o}, C=90^{o} \)
\(=2\times{1}-1, \because \sin{90^{o}}=1\)
\(=2-1\)
\(=1\)
উত্তরঃ ( খ )
উদ্দীপকটি লক্ষ কর এবং ১০ এবং ১১ নং
প্রশ্নের উত্তর দাওঃ-
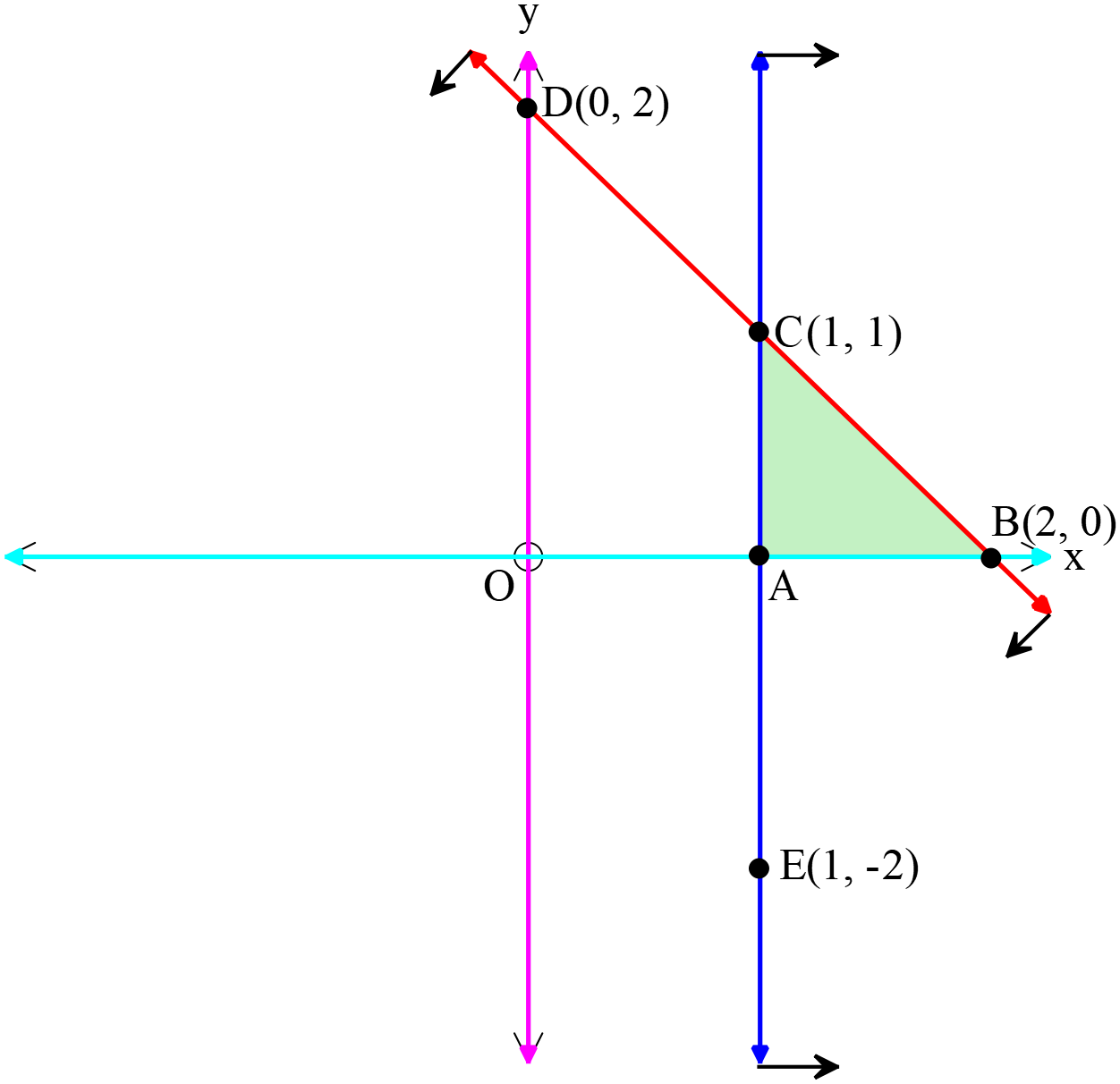যেখানে \(x\ge 0, \ y\ge 0\)
১০। \(AC\) রেখা সংশ্লিষ্ট অসমতা কোনটি?
যেখানে \(x\ge 0, \ y\ge 0\)
ক \(x\gt{1}\)
গ \(y\ge{-2}\)
গ \(y\ge{-2}\)
খ \(x\ge{1}\)
ঘ \(y\gt{1}\)
চিত্র হতে,ঘ \(y\gt{1}\)
\(AC\) এর সমীকরণ \(x-1=0\)
চিত্রে, \(AC\) রেখাস্থ এবং এর যে পার্শে মূলবিন্দু আছে তার বিপরীত পার্শের এলাকা বুঝানো হয়েছে।
\(\therefore\) অসমতাটি হবে \(x-1\ge{0}\)
\(\Rightarrow x\ge{1}\)
উত্তরঃ ( খ )
১১। অভিষ্ট এলাকায় \(z=x-y\)-এর সর্বনিম্ন মাণ কত?
চিত্রে হতে প্রাপ্ত বিন্দুগুলির মধ্যে \((1, 1)\) বিন্দুতে \(x\) এর মাণ সর্বনিম্ন এবং \(y\) এর মাণ সর্বোচ্চ।
অভীষ্ট ফাংশনের সর্বনিম্ন মাণ \(z=1-1\)
\(\Rightarrow z=0\)
উত্তরঃ ( খ )
ক \(-2\)
গ \(1\)
গ \(1\)
খ \(0\)
ঘ \(2\)
\(z=x-y\)-এর মাণ সর্বনিম্ন হবে, যখন \(x\) এর মাণ সর্বনিম্ন এবং
\(y\) এর মাণ সর্বোচ্চ হবে।ঘ \(2\)
চিত্রে হতে প্রাপ্ত বিন্দুগুলির মধ্যে \((1, 1)\) বিন্দুতে \(x\) এর মাণ সর্বনিম্ন এবং \(y\) এর মাণ সর্বোচ্চ।
অভীষ্ট ফাংশনের সর্বনিম্ন মাণ \(z=1-1\)
\(\Rightarrow z=0\)
উত্তরঃ ( খ )
১২। \(|x-1|\le{1}\) অসমতার সমাধান সেট কোনটি?
\(\Rightarrow -1\le{x-1}\le{1}, \because |a|\le{\alpha}\) হলে, \(-\alpha\le{a}\le{\alpha}\)
\(\Rightarrow -1+1\le{x-1+1}\le{1+1}\)
\(\Rightarrow 0\le{x}\le{2}\)
\(\therefore 0\le{x}\le{2}\)
\(\therefore\) সমাধান সেট \([0, 2]\)
উত্তরঃ ( খ )
ক \([-1, 1]\)
গ \((0, 2]\)
গ \((0, 2]\)
খ \([0, 2]\)
ঘ \((-1, 1]\)
\(|x-1|\le 1\)ঘ \((-1, 1]\)
\(\Rightarrow -1\le{x-1}\le{1}, \because |a|\le{\alpha}\) হলে, \(-\alpha\le{a}\le{\alpha}\)
\(\Rightarrow -1+1\le{x-1+1}\le{1+1}\)
\(\Rightarrow 0\le{x}\le{2}\)
\(\therefore 0\le{x}\le{2}\)
\(\therefore\) সমাধান সেট \([0, 2]\)
উত্তরঃ ( খ )
১৩। কোনো বিন্দুতে ভারসাম্য সৃষ্টিকারী \(1N, \ 1N\) এবং \(2N\) মানের
তিনটি বলের ১ম দুইটির অন্তর্ভুক্ত কোণ কোনটি?
এখন, \(1N, \ 1N\) বলদ্বয়ের অন্তর্গত কোণ \(\alpha\) হলে,
\(2^2=1^2+1^2+2.1.1.\cos{\alpha}\)
\(\Rightarrow 4=1+1+2\cos{\alpha}\)
\(\Rightarrow 4=2+2\cos{\alpha}\)
\(\Rightarrow 4=2(1+\cos{\alpha})\)
\(\Rightarrow 2=1+\cos{\alpha}\)
\(\Rightarrow 1+\cos{\alpha}=2\)
\(\Rightarrow \cos{\alpha}=2-1\)
\(\Rightarrow \cos{\alpha}=1\)
\(\Rightarrow \cos{\alpha}=\cos{0^{o}}\)
\(\therefore \alpha=0^{o}\)
উত্তরঃ ( ক )
ক \(0^{o}\)
গ \(120^{o}\)
গ \(120^{o}\)
খ \(90^{o}\)
ঘ \(180^{o}\)
\(1N, \ 1N\) এবং \(2N\) মানের বল তিনটি ভারসাম্য সৃষ্টি করলে \(1N,
\ 1N\) বল দুইটির লব্ধি হবে \(2N\) বলটির সমান এবং লব্ধি বল \(2N\)
বলটির বিপরীত দিকে ক্রিয়া করবে।ঘ \(180^{o}\)
এখন, \(1N, \ 1N\) বলদ্বয়ের অন্তর্গত কোণ \(\alpha\) হলে,
\(2^2=1^2+1^2+2.1.1.\cos{\alpha}\)
\(\Rightarrow 4=1+1+2\cos{\alpha}\)
\(\Rightarrow 4=2+2\cos{\alpha}\)
\(\Rightarrow 4=2(1+\cos{\alpha})\)
\(\Rightarrow 2=1+\cos{\alpha}\)
\(\Rightarrow 1+\cos{\alpha}=2\)
\(\Rightarrow \cos{\alpha}=2-1\)
\(\Rightarrow \cos{\alpha}=1\)
\(\Rightarrow \cos{\alpha}=\cos{0^{o}}\)
\(\therefore \alpha=0^{o}\)
উত্তরঃ ( ক )
১৪। যোগাশ্রয়ী প্রোগ্রামে প্রয়োজন হয়-
\(i.\) দ্বিঘাত সমীকরণ
\(ii.\) অঋণাত্মক চলক
\(iii.\) একঘাতবিশিষ্ট অসমতা
নিচের কোনটি সঠীক?
দ্বিঘাত সমীকরণ প্রয়োজন হয় না।
\(\therefore (i.)\) নং বাক্যটি সত্য নয়।
অঋণাত্মক চলক প্রয়োজন হয়। যেমনঃ \(x\ge{0}, y\ge{0}\)
\(\therefore (ii.)\) নং বাক্যটি সত্য।
একঘাতবিশিষ্ট অসমতা প্রয়োজন হয়।
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( গ )
\(i.\) দ্বিঘাত সমীকরণ
\(ii.\) অঋণাত্মক চলক
\(iii.\) একঘাতবিশিষ্ট অসমতা
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
যোগাশ্রয়ী প্রোগ্রামেঃঘ \(i.\), \(ii.\) ও \(iii.\)
দ্বিঘাত সমীকরণ প্রয়োজন হয় না।
\(\therefore (i.)\) নং বাক্যটি সত্য নয়।
অঋণাত্মক চলক প্রয়োজন হয়। যেমনঃ \(x\ge{0}, y\ge{0}\)
\(\therefore (ii.)\) নং বাক্যটি সত্য।
একঘাতবিশিষ্ট অসমতা প্রয়োজন হয়।
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( গ )
১৫। ভূমি হতে \(v\) বেগে খাড়া উপরের দিকে নিক্ষিপ্ত বস্তুর সর্বাধিক
উচ্চতা নিচের কোনটি?
\(\frac{v^2}{2g}\)
উত্তরঃ ( ঘ )
ক \(\frac{v}{g}\)
গ \(\frac{v^2}{g}\)
গ \(\frac{v^2}{g}\)
খ \(\frac{v}{2g}\)
ঘ \(\frac{v^2}{2g}\)
ভূমি হতে \(v\) বেগে খাড়া উপরের দিকে নিক্ষিপ্ত বস্তুর সর্বাধিক
উচ্চতাঃ ঘ \(\frac{v^2}{2g}\)
\(\frac{v^2}{2g}\)
উত্তরঃ ( ঘ )
১৬। দ্বিঘাত সমীকরণের একটি মূল \(\frac{1}{2-\sqrt{5}}\) হলে অপর মূল
কোনটি?
\(\frac{1}{2+\sqrt{5}}\)
\(\Rightarrow \frac{2-\sqrt{5}}{(2+\sqrt{5})(2-\sqrt{5})}\)
\(\Rightarrow \frac{2-\sqrt{5}}{2^2-(\sqrt{5})^2}\)
\(\Rightarrow \frac{2-\sqrt{5}}{4-5}\)
\(\Rightarrow \frac{2-\sqrt{5}}{-1}\)
\(\therefore -2+\sqrt{5}\)
উত্তরঃ ( গ )
ক \(-2-\sqrt{5}\)
গ \(-2+\sqrt{5}\)
গ \(-2+\sqrt{5}\)
খ \(2-\sqrt{5}\)
ঘ \(2+\sqrt{5}\)
দ্বিঘাত সমীকরণের একটি মূল \(\frac{1}{2-\sqrt{5}}\) হলে অপর মূল,
ঘ \(2+\sqrt{5}\)
\(\frac{1}{2+\sqrt{5}}\)
\(\Rightarrow \frac{2-\sqrt{5}}{(2+\sqrt{5})(2-\sqrt{5})}\)
\(\Rightarrow \frac{2-\sqrt{5}}{2^2-(\sqrt{5})^2}\)
\(\Rightarrow \frac{2-\sqrt{5}}{4-5}\)
\(\Rightarrow \frac{2-\sqrt{5}}{-1}\)
\(\therefore -2+\sqrt{5}\)
উত্তরঃ ( গ )
১৭। \(\frac{u}{\sqrt{3}}\) বেগে \(30^{o}\) কোণে প্রক্ষিপ্ত কণার
সর্বোচ্চ উচ্চতায় বেগ কত একক/সেঃ?
সর্বোচ্চ উচ্চতায় আনুভূমিক উপাংশ \(=\frac{u}{\sqrt{3}}\cos{30^{o}}\)
\(=\frac{u}{\sqrt{3}}\times{\frac{\sqrt{3}}{2}}\)
\(=\frac{u}{2}\)
সর্বোচ্চ উচ্চতায় বেগ \(=v\) হলে,
\(v^2=\left(\frac{u}{2}\right)^2+0^2\)
\(\therefore v=\sqrt{\left(\frac{u}{2}\right)^2+0}\)
\(=\sqrt{\left(\frac{u}{2}\right)^2}\)
\(=\frac{u}{2}\)
উত্তরঃ ( গ )
ক \(\frac{2u}{\sqrt{3}}\)
গ \(\frac{u}{2}\)
গ \(\frac{u}{2}\)
খ \(\frac{2u}{\sqrt{3}}\)
ঘ \(\frac{u}{2\sqrt{2}}\)
সর্বোচ্চ উচ্চতায় কণাটির বেগের আনুভূমিক উপাংশ ক্রিয়া করবে এবং
উল্লম্ব উপাংশ হবে শূন্য। ঘ \(\frac{u}{2\sqrt{2}}\)
সর্বোচ্চ উচ্চতায় আনুভূমিক উপাংশ \(=\frac{u}{\sqrt{3}}\cos{30^{o}}\)
\(=\frac{u}{\sqrt{3}}\times{\frac{\sqrt{3}}{2}}\)
\(=\frac{u}{2}\)
সর্বোচ্চ উচ্চতায় বেগ \(=v\) হলে,
\(v^2=\left(\frac{u}{2}\right)^2+0^2\)
\(\therefore v=\sqrt{\left(\frac{u}{2}\right)^2+0}\)
\(=\sqrt{\left(\frac{u}{2}\right)^2}\)
\(=\frac{u}{2}\)
উত্তরঃ ( গ )
১৮। কোন ফাংশনটি বহুপদী?
বহুপদী হওয়ার শর্তঃ
\((1)\) চলকের ঘাত অঋণাত্মক পূর্ণসংখ্যা হবে।
\((2)\) পদসংখ্যা হবে সসীম।
উপরোক্ত সকল শর্ত সিদ্ধ করে \(2x^2-x+1\)
উত্তরঃ ( ঘ )
ক \(2x^2-5\sqrt{x}+1\)
গ \(x^3+2x^2-3x+x^{-1}\)
গ \(x^3+2x^2-3x+x^{-1}\)
খ \(x^3-\frac{3}{x^2}+4x+1\)
ঘ \(2x^2-x+1\)
বহুপদীঃ যে বীজগাণিতিক রাশি এক বা একাধিক পদবিশিষ্ট এবং পদগুলি এক বা
একাধিক চলকের শুধুমাত্র অঋণাত্মক পূর্ণসাংখিক ঘাত ও ধ্রুবকের গুনফল
হয় সেটিকেই বহুপদী বলে। ঘ \(2x^2-x+1\)
বহুপদী হওয়ার শর্তঃ
\((1)\) চলকের ঘাত অঋণাত্মক পূর্ণসংখ্যা হবে।
\((2)\) পদসংখ্যা হবে সসীম।
উপরোক্ত সকল শর্ত সিদ্ধ করে \(2x^2-x+1\)
উত্তরঃ ( ঘ )
নিচের উদ্দীপকের আলোকে ১৯ এবং ২০ নং
প্রশ্নের উত্তর দাওঃ
\(\frac{x^2}{3}-\frac{y^2}{2}=1\)একটি কনিকের সমীকরণ।
১৯। কণিকটির উৎকেন্দ্রিকতা নিচের কোনটি?\(\frac{x^2}{3}-\frac{y^2}{2}=1\)একটি কনিকের সমীকরণ।
ক \(\frac{\sqrt{13}}{2}\)
গ \(\frac{\sqrt{5}}{\sqrt{2}}\)
গ \(\frac{\sqrt{5}}{\sqrt{2}}\)
খ \(\frac{\sqrt{13}}{3}\)
ঘ \(\frac{\sqrt{5}}{\sqrt{3}}\)
\(\frac{x^2}{3}-\frac{y^2}{2}=1\) একটি অধিবৃত্ত।ঘ \(\frac{\sqrt{5}}{\sqrt{3}}\)
এখানে, \(a^2=3, b^2=2; \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) সমীকরণের সহিত তুলুনা করে।
অধিবৃত্তটির উৎকেন্দ্রিকতা, \(e=\sqrt{1+\frac{b^2}{a^2}}; \because \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) অধিবৃত্তের উৎকেন্দ্রিকতা, \(e=\sqrt{1+\frac{b^2}{a^2}}\)
\(=\sqrt{1+\frac{2}{3}}, \because a^2=3, b^2=2\)
\(=\sqrt{\frac{3+2}{3}}\)
\(=\sqrt{\frac{5}{3}}\)
\(=\frac{\sqrt{5}}{\sqrt{3}}\)
উত্তরঃ ( ঘ )
২০। কণিকটির উপকেন্দ্রিক লম্বের দৈর্ঘ্য নিচের কোনটি?
এখানে, \(a^2=3, b^2=2; \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) সমীকরণের সহিত তুলুনা করে।
অধিবৃত্তটির উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2b^2}{a}\right|; \because \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) অধিবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2b^2}{a}\right|\)
\(=\left|\frac{2\times{2}}{\sqrt{3}}\right|, \because a^2=3\Rightarrow a=\sqrt{3}, b^2=2\)
\(=\frac{4}{\sqrt{3}}\)
উত্তরঃ ( ঘ )
ক \(9\)
গ \(\frac{8}{3}\)
গ \(\frac{8}{3}\)
খ \(2\sqrt{3}\)
ঘ \(\frac{4}{\sqrt{3}}\)
\(\frac{x^2}{3}-\frac{y^2}{2}=1\) একটি অধিবৃত্ত।ঘ \(\frac{4}{\sqrt{3}}\)
এখানে, \(a^2=3, b^2=2; \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) সমীকরণের সহিত তুলুনা করে।
অধিবৃত্তটির উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2b^2}{a}\right|; \because \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) অধিবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2b^2}{a}\right|\)
\(=\left|\frac{2\times{2}}{\sqrt{3}}\right|, \because a^2=3\Rightarrow a=\sqrt{3}, b^2=2\)
\(=\frac{4}{\sqrt{3}}\)
উত্তরঃ ( ঘ )
২১। \(0, 1, 2, 4, 5, 10\) সংখ্যাগুলো হতে দৈব্যভাবে একটি নিলে তার মৌলিক
ও জোড় হওয়ার সম্ভাবনা কত?
মোট সংখ্যা \(6\) টি।
দৈব্যভাবে একটি নিলে তার মৌলিক ও জোড় হওয়ার সম্ভাবনা \(=\frac{1}{6}\)
উত্তরঃ ( ক )
ক \(\frac{1}{6}\)
গ \(\frac{1}{3}\)
গ \(\frac{1}{3}\)
খ \(\frac{2}{3}\)
ঘ \(\frac{5}{6}\)
\(0, 1, 2, 4, 5, 10\) সংখ্যাগুলোর মধ্যে মৌলিক ও জোড় সংখ্যা আছে
একটি \(2\) ঘ \(\frac{5}{6}\)
মোট সংখ্যা \(6\) টি।
দৈব্যভাবে একটি নিলে তার মৌলিক ও জোড় হওয়ার সম্ভাবনা \(=\frac{1}{6}\)
উত্তরঃ ( ক )
২২। \((x-1)^2=-4y\) কণিকটির জন্য কোনটি সত্য?
\(\Rightarrow X^2=-4Y\) ইহা একটি অধিবৃত্তের সমীকরণ যেখানে, \(X=x-1, Y=y\)
অধিবৃত্তের শীর্ষবিন্দু \(A(0, 0), \because x^2=4ay \) অধিবৃত্তের শীর্ষবিন্দু \(A(0, 0)\)
\(\therefore X=0, Y=0\)
\(\Rightarrow x-1=0, y=0, \because X=x-1, Y=y\)
\(\Rightarrow x=1, y=0\)
\(\therefore\) শীর্ষবিন্দু \((1, 0) \) যা অপশন 'ক' এর চিত্রের সহিত মিলে যায়।
উত্তরঃ ( ক )
ক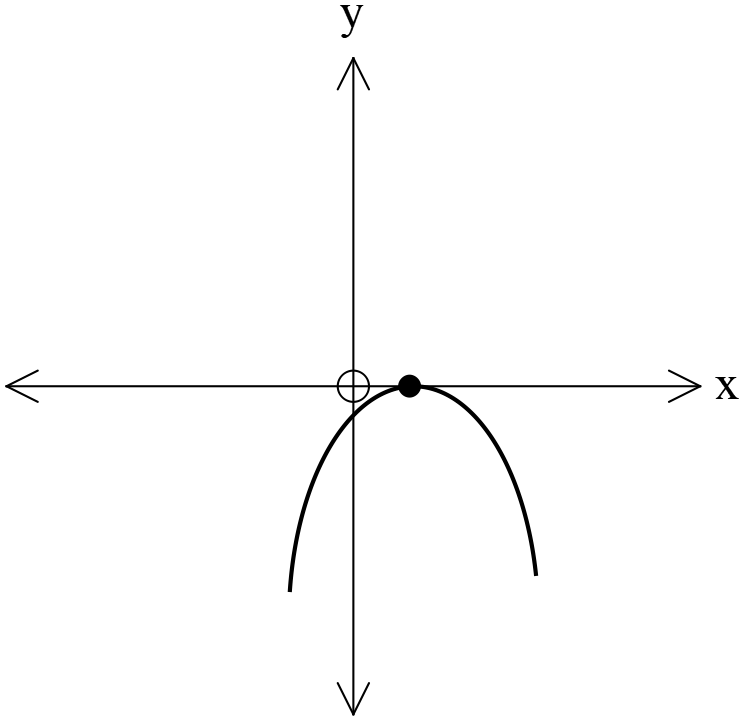 
গ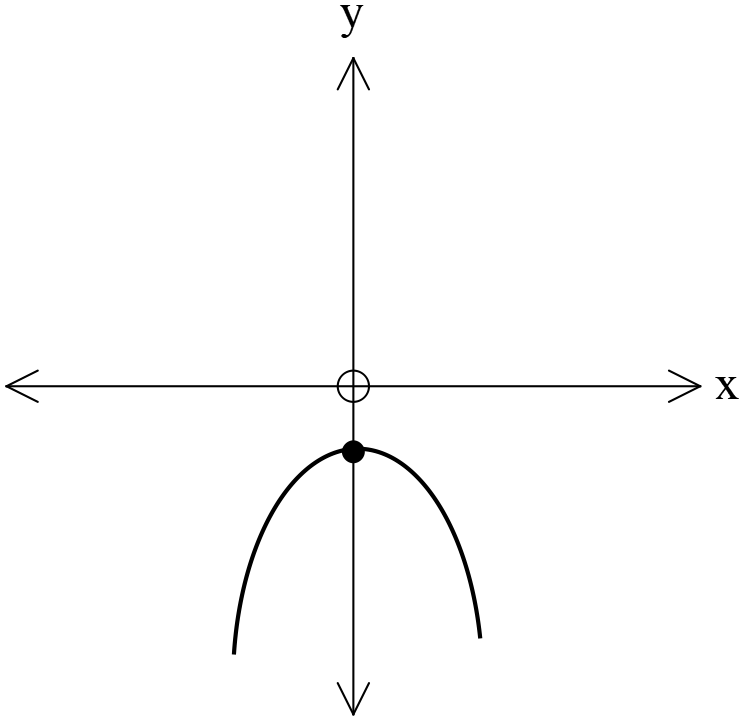
গ
খ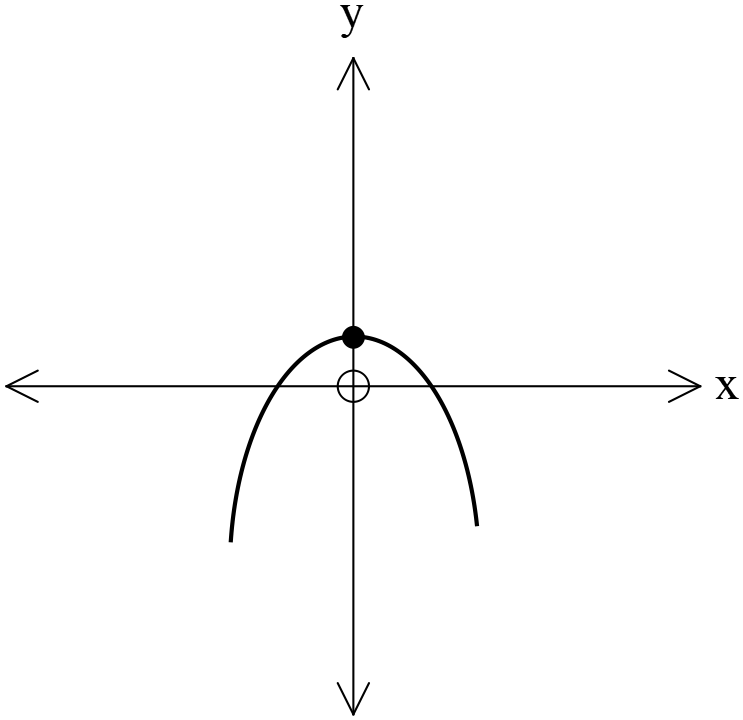 
ঘ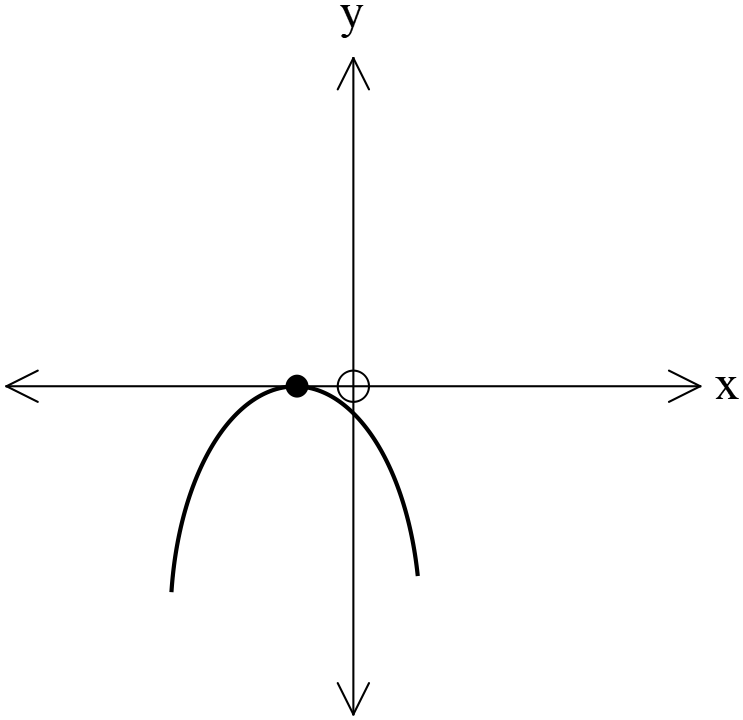
\((x-1)^2=-4y\)ঘ
\(\Rightarrow X^2=-4Y\) ইহা একটি অধিবৃত্তের সমীকরণ যেখানে, \(X=x-1, Y=y\)
অধিবৃত্তের শীর্ষবিন্দু \(A(0, 0), \because x^2=4ay \) অধিবৃত্তের শীর্ষবিন্দু \(A(0, 0)\)
\(\therefore X=0, Y=0\)
\(\Rightarrow x-1=0, y=0, \because X=x-1, Y=y\)
\(\Rightarrow x=1, y=0\)
\(\therefore\) শীর্ষবিন্দু \((1, 0) \) যা অপশন 'ক' এর চিত্রের সহিত মিলে যায়।
উত্তরঃ ( ক )
২৩। \(1-\sqrt{3}i\)-এর সাধারণ আর্গুমেন্ট কত?
এখানে, \(x=1, y=-\sqrt{3}, x+iy\) এর সহিত তুলুনা করে।
জটিল রাশিটির সাধারণ আর্গুমেন্ট \(=2n\pi\pm{\tan^{-1}\left(\frac{y}{x}\right)}, \because x+iy\) এর সাধারণ আর্গুমেন্ট \(=2n\pi\pm{\tan^{-1}\left(\frac{y}{x}\right)}\)
\(=2n\pi-\tan^{-1}\left(\frac{\sqrt{3}}{1}\right), \because x=1, y=-\sqrt{3}\) এবং ইহা চতুর্থ চৌকোণে অবস্থিত।
\(=2n\pi-\tan^{-1}{\tan{\frac{\pi}{3}}}\)
\(=2n\pi-\frac{\pi}{3}\)
উত্তরঃ ( ক )
ক \(2n\pi-\frac{\pi}{3}; \ n\in
\mathbb{Z}\)
গ \(2n\pi-\frac{5\pi}{3}; \ n\in \mathbb{Z}\)
গ \(2n\pi-\frac{5\pi}{3}; \ n\in \mathbb{Z}\)
খ \(2n\pi+\frac{\pi}{3}; \ n\in
\mathbb{Z}\)
ঘ \(2n\pi+\frac{5\pi}{3}; \ n\in \mathbb{Z}\)
\(1-\sqrt{3}i\) ইহা একটি জটিল রাশি। ঘ \(2n\pi+\frac{5\pi}{3}; \ n\in \mathbb{Z}\)
এখানে, \(x=1, y=-\sqrt{3}, x+iy\) এর সহিত তুলুনা করে।
জটিল রাশিটির সাধারণ আর্গুমেন্ট \(=2n\pi\pm{\tan^{-1}\left(\frac{y}{x}\right)}, \because x+iy\) এর সাধারণ আর্গুমেন্ট \(=2n\pi\pm{\tan^{-1}\left(\frac{y}{x}\right)}\)
\(=2n\pi-\tan^{-1}\left(\frac{\sqrt{3}}{1}\right), \because x=1, y=-\sqrt{3}\) এবং ইহা চতুর্থ চৌকোণে অবস্থিত।
\(=2n\pi-\tan^{-1}{\tan{\frac{\pi}{3}}}\)
\(=2n\pi-\frac{\pi}{3}\)
উত্তরঃ ( ক )
২৪। \(-x(1+x)^{-1}\) এর বিস্তৃতিতে ১ম তিনটি পদের সহগের সমষ্টি কত?
\(=-x(1-x+x^2-x^3+ ......),\) \(\because (1+x)^{-1}=1-x+x^2-x^3+ ......\)
\(=-x+x^2-x^3+x^4- ......\)
১ম তিনটি পদের সহগের সমষ্টি \(=-1+1-1\)
\(=-1\)
উত্তরঃ ( খ )
ক \(-3\)
গ \(1\)
গ \(1\)
খ \(-1\)
ঘ \(3\)
\(-x(1+x)^{-1}\) ঘ \(3\)
\(=-x(1-x+x^2-x^3+ ......),\) \(\because (1+x)^{-1}=1-x+x^2-x^3+ ......\)
\(=-x+x^2-x^3+x^4- ......\)
১ম তিনটি পদের সহগের সমষ্টি \(=-1+1-1\)
\(=-1\)
উত্তরঃ ( খ )
২৫। \(\alpha=\frac{-1+\sqrt{3}i}{2}\) এবং এর অনুবন্ধী
\(\overline{\alpha}\) হলে কোনটি সত্য?
\(\therefore \alpha=-\frac{1}{2}+\frac{\sqrt{3}}{2}i\)
আবার,
\(\overline{\alpha}=-\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
এখন,
\(\alpha +\overline{\alpha}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i-\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
\(=-2\times{\frac{1}{2}}\)
\(=-1\)
উত্তরঃ ( গ )
ক \(\alpha
\overline{\alpha}=\alpha^2\)
গ \(\alpha +\overline{\alpha}=-1\)
গ \(\alpha +\overline{\alpha}=-1\)
খ \(\alpha+
\overline{\alpha}=2\alpha\)
ঘ \(\overline{\alpha}+\alpha^2=-1\)
\(\alpha=\frac{-1+\sqrt{3}i}{2}\)ঘ \(\overline{\alpha}+\alpha^2=-1\)
\(\therefore \alpha=-\frac{1}{2}+\frac{\sqrt{3}}{2}i\)
আবার,
\(\overline{\alpha}=-\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
এখন,
\(\alpha +\overline{\alpha}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i-\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
\(=-2\times{\frac{1}{2}}\)
\(=-1\)
উত্তরঃ ( গ )
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000005