এ অধ্যায়ের পাঠ্যসূচী
- ঐতিহাসিক পটভূমি (Historical Background)
- ত্রিকোণমিতিক কোণ (Trigonomeriic angle)
- কোণের পরিমাপ (Measurement of angle)
- ষাটমূলক পদ্ধতি (Sexagesimal System)
- বৃত্তীয় পদ্ধতি (Circular System)
- বৃত্তের পরিধি ও ব্যাসের অনুপাত (The ratio of the circumference to the diameter of a circle)
- রেডিয়ান একটি ধ্রুবক কোণ (Radian is a constant angle)
- শতমূলক পদ্ধতি (Centesimal System)
- ডিগ্রি, রেডিয়ান ও গ্রাড এর মধ্যে সম্পর্ক (Relation between degree, radian and grad)
- বৃত্তচাপের দৈর্ঘ্য (The length of the arc)
- বৃত্তকলার ক্ষেত্রফল (Area of the sector)
- ঘড়ির ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ (The angle between the hour hand and the minute hand)
- অধ্যায় \(vi.A\)-এর উদাহরণসমুহ
- অধ্যায় \(vi.A\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(vi.A\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(vi.A\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(vi.A\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
ঐতিহাসিক পটভূমি
Historical Background

হিপার্কাস (১৯০ খ্রিষ্টপূর্ব-১২০ খ্রিষ্টপূর্ব )
গণিত, জ্যোতির্বিদা ও ভূগোলে তাঁর অবদান অপরিসীম। তিনিই প্রথম ত্রিকোণমিতক সারণি প্রণয়ন করে 'arc' ও 'chord' সিরিজের মাণ নির্ণয় করেন। এজন্য তাঁকে ত্রিকোণমিতির জনক বলা হয়।
ইংরেজী শব্দ 'Trigonometry' শব্দটি দুইটি গ্রিক শব্দ 'Trigon' যার অর্থ তিন কোণ এবং 'Metron' যার অর্থ পরিমাপ, এর সমন্বয়ে গঠিত। ত্রিকোণমিতি গণিত শাস্ত্রের একটি অত্যান্ত গুরুত্বপূর্ণ শাখা। গ্রিক গণিতবিদ ও জ্যোতির্বিদ হিপার্কাস (Hipparchus) এই শাখার আবিষ্কার করেন। এই গুরুত্বপূর্ণ শাখার বহুবিধ ব্যবহার বিজ্ঞানের বহু শাখার উন্নয়নে সহায়ক হয়েছে। প্রাথমিকভাবে ত্রিকোণমিতি ত্রিভুজে পরিমাপের জন্য ব্যবহৃত হয়েছে। অন্যভাবে বলা যায়, ত্রিভুজের বাহু, কোণ ও ক্ষেত্রফলের মধ্যে সম্পর্ক স্থাপনের জন্য ত্রিকোণমিতি ব্যবহৃত হয়। পরবর্তীতে ধনাত্মক কোণ, ঋণাত্মক কোণ তথা অন্য অনেক শাখায় বহুল সমস্যা সমাধানের জন্য এর ব্যবহার উল্লেখযোগ্য।
বিজ্ঞান ও প্রকৌশলীর বিভিন্ন শাখা ছাড়াও বিশ্লেষণী জ্যামিতি ও বিশ্লেষণী গণিত ত্রিকোণমিতির ভিত্তির ওপর প্রতিষ্ঠিত। বায়োটেকনোলজি, ভিডিও গেমস ও কম্পিউটার গ্রাফিক্সে ব্যাপক আকারে ত্রিকোণমিতিক ব্যবহার রয়েছে। কোণের ব্যবহারিক প্রয়োগ ছয়টি ত্রিকোণমিতিক ফাংশন দ্বারা সীমাবদ্ধ। একটি সমকোণী ত্রিভুজের ভূমি সংলগ্ন কোণকে তাদের বাহুদ্বয়ের অনুপাতের মাধ্যমে প্রকাশ করার জন্য ছয়টি অপারেটর ব্যবহার করা হয়।
যথাঃ Sine, Cosine, Tangent, Cotangent, Secant এবং Cosecant. জ্যোতির্বিদ্যা নিয়ে গবেষণার সূত্র ধরেই ত্রিকোণমিতিক তত্ত্বের উদ্ভব ঘটে। পিথাগোরাসের উপপাদ্য এর উৎকৃষ্ট উদাহরণ।
ভারতবর্ষে ৪র্থ - ৫ম শতাব্দীতে সিদ্ধার্থ ও আর্জভট্ট  প্রাচীন ভারতীয় গণিতের ইতিহাসে আর্যভট্টের (৪৭৬ – ৫৫০ খ্রিষ্টপূর্ব ) হাত ধরেই ক্লাসিকাল যুগ (কিংবা স্বর্ণযুগ) শুরু হয়। গণিত এবং জ্যোতির্বিদ্যা সংক্রান্ত আর্যভট্টের বিভিন্ন কাজ মূলত দুটি গ্রন্থে সংকলিত হয়েছে বলে জানা গেছে। এর মাঝে ‘আর্যভট্টীয়’ একটি, যেটি উদ্ধার করা গিয়েছে। এটি রচিত চার খণ্ডে, মোট ১১৮টি স্তোত্রে। অন্য যে কাজটি সম্পর্কে জানা যায় সেটি হল ‘আর্য-সিদ্ধান্ত’। আর্য-সিদ্ধান্তের কোন পাণ্ডুলিপি খুঁজে পাওয়া যায়নি, তবে বরাহমিহির, ব্রহ্মগুপ্ত এবং প্রথম ভাস্করের কাজে এটির উল্লেখ মেলে। আর্যভট্ট গ্রন্থ রচনা করেছেন পদবাচ্যের আকারে। , ৭ম শতাব্দীতে ভাষ্করা-১ ও ব্রহ্মগুপ্ত বিপরীত ত্রিকোণমিতিক সমীকরণ নিয়ে প্রচুর তত্ত্ব লিপিবদ্ধ করেন। মধ্যযুগে মুসলমানরা ত্রিকোণমিতির অন্তর্নিহিত তত্ত্ব উদ্ঘাটন করেন। মূসা-আল খোয়ারিজমী নির্ভুলভাবে সাইন, কোসাইন ও ট্যানজেন্ট এর সারণী প্রণয়ন করেন।
সপ্তদশ শতাব্দীতে স্যার আইজ্যাক নিউটন
প্রাচীন ভারতীয় গণিতের ইতিহাসে আর্যভট্টের (৪৭৬ – ৫৫০ খ্রিষ্টপূর্ব ) হাত ধরেই ক্লাসিকাল যুগ (কিংবা স্বর্ণযুগ) শুরু হয়। গণিত এবং জ্যোতির্বিদ্যা সংক্রান্ত আর্যভট্টের বিভিন্ন কাজ মূলত দুটি গ্রন্থে সংকলিত হয়েছে বলে জানা গেছে। এর মাঝে ‘আর্যভট্টীয়’ একটি, যেটি উদ্ধার করা গিয়েছে। এটি রচিত চার খণ্ডে, মোট ১১৮টি স্তোত্রে। অন্য যে কাজটি সম্পর্কে জানা যায় সেটি হল ‘আর্য-সিদ্ধান্ত’। আর্য-সিদ্ধান্তের কোন পাণ্ডুলিপি খুঁজে পাওয়া যায়নি, তবে বরাহমিহির, ব্রহ্মগুপ্ত এবং প্রথম ভাস্করের কাজে এটির উল্লেখ মেলে। আর্যভট্ট গ্রন্থ রচনা করেছেন পদবাচ্যের আকারে। , ৭ম শতাব্দীতে ভাষ্করা-১ ও ব্রহ্মগুপ্ত বিপরীত ত্রিকোণমিতিক সমীকরণ নিয়ে প্রচুর তত্ত্ব লিপিবদ্ধ করেন। মধ্যযুগে মুসলমানরা ত্রিকোণমিতির অন্তর্নিহিত তত্ত্ব উদ্ঘাটন করেন। মূসা-আল খোয়ারিজমী নির্ভুলভাবে সাইন, কোসাইন ও ট্যানজেন্ট এর সারণী প্রণয়ন করেন।
সপ্তদশ শতাব্দীতে স্যার আইজ্যাক নিউটন  ১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। ও জেমস স্টার্লিং
১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। ও জেমস স্টার্লিং  স্টার্লিং (11/05/1692-5/12/1770) ছিলেন আর্চিবাল্ড স্টার্লিং অফ গার্ডেনের তৃতীয় পুত্র। ১৮ বছর বয়সে তিনি বলিওল কলেজ, অক্সফোর্ডে গিয়েছিলেন, যেখানে প্রধানত আর্ল অফ মারের প্রভাবে তিনি ব্যালিওলের বিশপ ওয়ার্নারের প্রদর্শনীকারীদের (বা স্নেল প্রদর্শনী) মনোনীত হন। লন্ডনে তিনি দশ বছর অবস্থান করেন, বেশিরভাগ সময় টাওয়ার স্ট্রিটের একটি একাডেমির সাথে যুক্ত ছিলেন এবং তাঁর অবসরকে গণিত এবং খ্যাতিমান গণিতবিদদের সাথে যোগাযোগের জন্য উৎসর্গ করেছিলেন। ত্রিকোণমিতিক সিরিজের বিস্তার নির্ণয় করেন এবং ত্রিকোণমিতি আধুনিক গণিতের গুরুত্বপূর্ন শাখা হিসেবে প্রতিষ্ঠা লাভ করে। বর্তমানে ব্যবহৃত sin, cos, tan, cosec, sec এবং cot প্রতীকগুলি বৈজ্ঞানিক লেওনার্ড অয়লারের
স্টার্লিং (11/05/1692-5/12/1770) ছিলেন আর্চিবাল্ড স্টার্লিং অফ গার্ডেনের তৃতীয় পুত্র। ১৮ বছর বয়সে তিনি বলিওল কলেজ, অক্সফোর্ডে গিয়েছিলেন, যেখানে প্রধানত আর্ল অফ মারের প্রভাবে তিনি ব্যালিওলের বিশপ ওয়ার্নারের প্রদর্শনীকারীদের (বা স্নেল প্রদর্শনী) মনোনীত হন। লন্ডনে তিনি দশ বছর অবস্থান করেন, বেশিরভাগ সময় টাওয়ার স্ট্রিটের একটি একাডেমির সাথে যুক্ত ছিলেন এবং তাঁর অবসরকে গণিত এবং খ্যাতিমান গণিতবিদদের সাথে যোগাযোগের জন্য উৎসর্গ করেছিলেন। ত্রিকোণমিতিক সিরিজের বিস্তার নির্ণয় করেন এবং ত্রিকোণমিতি আধুনিক গণিতের গুরুত্বপূর্ন শাখা হিসেবে প্রতিষ্ঠা লাভ করে। বর্তমানে ব্যবহৃত sin, cos, tan, cosec, sec এবং cot প্রতীকগুলি বৈজ্ঞানিক লেওনার্ড অয়লারের  অয়লার (15 /04/1707 - 18/09/1783 ) একজন সুইস গণিতবিদ এবং পদার্থবিজ্ঞানী (বাসেল, সুইজারল্যান্ড )। তিনি ক্যালকুলাস, সংখ্যাতত্ত্ব, অন্তরক সমীকরণ, গ্রাফ তত্ত্ব ও টপোগণিতে অনেক গুরুত্বপূর্ণ অবদান রাখেন। আধুনিক গণিতে ব্যবহৃত অনেক পরিভাষা ও ধারণা তার অবদান। গাণিতিক বিশ্লেষণে ব্যবহৃত গাণিতিক ফাংশন-এর ধারণা তারই আবিষ্কার।[১] অয়লার e , পাই এর জন্য π , যোগের জন্য Σ চিহ্নের প্রবর্তন করেন। তিনি বলবিজ্ঞান, আলোকবিজ্ঞান ও জ্যোতির্বিজ্ঞানেও অবদান রাখেন। সমসাময়িককালে তার মত প্রকাশনা সম্পন্ন কোনো গণিতবিদ ছিলেন না। এমনকি মুদ্রণ ব্যবস্থার উন্নতি হওয়ার পরও তার সমপরিমাণ প্রকাশনা সম্পন্ন বিজ্ঞানীর সংখ্যা খুবই কম। অনস্বীকার্য অবদান। তিনি এগুলিকে অসীম সিরিজ আকারে বর্ণনা করেন।
অয়লার (15 /04/1707 - 18/09/1783 ) একজন সুইস গণিতবিদ এবং পদার্থবিজ্ঞানী (বাসেল, সুইজারল্যান্ড )। তিনি ক্যালকুলাস, সংখ্যাতত্ত্ব, অন্তরক সমীকরণ, গ্রাফ তত্ত্ব ও টপোগণিতে অনেক গুরুত্বপূর্ণ অবদান রাখেন। আধুনিক গণিতে ব্যবহৃত অনেক পরিভাষা ও ধারণা তার অবদান। গাণিতিক বিশ্লেষণে ব্যবহৃত গাণিতিক ফাংশন-এর ধারণা তারই আবিষ্কার।[১] অয়লার e , পাই এর জন্য π , যোগের জন্য Σ চিহ্নের প্রবর্তন করেন। তিনি বলবিজ্ঞান, আলোকবিজ্ঞান ও জ্যোতির্বিজ্ঞানেও অবদান রাখেন। সমসাময়িককালে তার মত প্রকাশনা সম্পন্ন কোনো গণিতবিদ ছিলেন না। এমনকি মুদ্রণ ব্যবস্থার উন্নতি হওয়ার পরও তার সমপরিমাণ প্রকাশনা সম্পন্ন বিজ্ঞানীর সংখ্যা খুবই কম। অনস্বীকার্য অবদান। তিনি এগুলিকে অসীম সিরিজ আকারে বর্ণনা করেন।
 প্রাচীন ভারতীয় গণিতের ইতিহাসে আর্যভট্টের (৪৭৬ – ৫৫০ খ্রিষ্টপূর্ব ) হাত ধরেই ক্লাসিকাল যুগ (কিংবা স্বর্ণযুগ) শুরু হয়। গণিত এবং জ্যোতির্বিদ্যা সংক্রান্ত আর্যভট্টের বিভিন্ন কাজ মূলত দুটি গ্রন্থে সংকলিত হয়েছে বলে জানা গেছে। এর মাঝে ‘আর্যভট্টীয়’ একটি, যেটি উদ্ধার করা গিয়েছে। এটি রচিত চার খণ্ডে, মোট ১১৮টি স্তোত্রে। অন্য যে কাজটি সম্পর্কে জানা যায় সেটি হল ‘আর্য-সিদ্ধান্ত’। আর্য-সিদ্ধান্তের কোন পাণ্ডুলিপি খুঁজে পাওয়া যায়নি, তবে বরাহমিহির, ব্রহ্মগুপ্ত এবং প্রথম ভাস্করের কাজে এটির উল্লেখ মেলে। আর্যভট্ট গ্রন্থ রচনা করেছেন পদবাচ্যের আকারে। , ৭ম শতাব্দীতে ভাষ্করা-১ ও ব্রহ্মগুপ্ত বিপরীত ত্রিকোণমিতিক সমীকরণ নিয়ে প্রচুর তত্ত্ব লিপিবদ্ধ করেন। মধ্যযুগে মুসলমানরা ত্রিকোণমিতির অন্তর্নিহিত তত্ত্ব উদ্ঘাটন করেন। মূসা-আল খোয়ারিজমী নির্ভুলভাবে সাইন, কোসাইন ও ট্যানজেন্ট এর সারণী প্রণয়ন করেন।
সপ্তদশ শতাব্দীতে স্যার আইজ্যাক নিউটন
প্রাচীন ভারতীয় গণিতের ইতিহাসে আর্যভট্টের (৪৭৬ – ৫৫০ খ্রিষ্টপূর্ব ) হাত ধরেই ক্লাসিকাল যুগ (কিংবা স্বর্ণযুগ) শুরু হয়। গণিত এবং জ্যোতির্বিদ্যা সংক্রান্ত আর্যভট্টের বিভিন্ন কাজ মূলত দুটি গ্রন্থে সংকলিত হয়েছে বলে জানা গেছে। এর মাঝে ‘আর্যভট্টীয়’ একটি, যেটি উদ্ধার করা গিয়েছে। এটি রচিত চার খণ্ডে, মোট ১১৮টি স্তোত্রে। অন্য যে কাজটি সম্পর্কে জানা যায় সেটি হল ‘আর্য-সিদ্ধান্ত’। আর্য-সিদ্ধান্তের কোন পাণ্ডুলিপি খুঁজে পাওয়া যায়নি, তবে বরাহমিহির, ব্রহ্মগুপ্ত এবং প্রথম ভাস্করের কাজে এটির উল্লেখ মেলে। আর্যভট্ট গ্রন্থ রচনা করেছেন পদবাচ্যের আকারে। , ৭ম শতাব্দীতে ভাষ্করা-১ ও ব্রহ্মগুপ্ত বিপরীত ত্রিকোণমিতিক সমীকরণ নিয়ে প্রচুর তত্ত্ব লিপিবদ্ধ করেন। মধ্যযুগে মুসলমানরা ত্রিকোণমিতির অন্তর্নিহিত তত্ত্ব উদ্ঘাটন করেন। মূসা-আল খোয়ারিজমী নির্ভুলভাবে সাইন, কোসাইন ও ট্যানজেন্ট এর সারণী প্রণয়ন করেন।
সপ্তদশ শতাব্দীতে স্যার আইজ্যাক নিউটন  ১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। ও জেমস স্টার্লিং
১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। ও জেমস স্টার্লিং  স্টার্লিং (11/05/1692-5/12/1770) ছিলেন আর্চিবাল্ড স্টার্লিং অফ গার্ডেনের তৃতীয় পুত্র। ১৮ বছর বয়সে তিনি বলিওল কলেজ, অক্সফোর্ডে গিয়েছিলেন, যেখানে প্রধানত আর্ল অফ মারের প্রভাবে তিনি ব্যালিওলের বিশপ ওয়ার্নারের প্রদর্শনীকারীদের (বা স্নেল প্রদর্শনী) মনোনীত হন। লন্ডনে তিনি দশ বছর অবস্থান করেন, বেশিরভাগ সময় টাওয়ার স্ট্রিটের একটি একাডেমির সাথে যুক্ত ছিলেন এবং তাঁর অবসরকে গণিত এবং খ্যাতিমান গণিতবিদদের সাথে যোগাযোগের জন্য উৎসর্গ করেছিলেন। ত্রিকোণমিতিক সিরিজের বিস্তার নির্ণয় করেন এবং ত্রিকোণমিতি আধুনিক গণিতের গুরুত্বপূর্ন শাখা হিসেবে প্রতিষ্ঠা লাভ করে। বর্তমানে ব্যবহৃত sin, cos, tan, cosec, sec এবং cot প্রতীকগুলি বৈজ্ঞানিক লেওনার্ড অয়লারের
স্টার্লিং (11/05/1692-5/12/1770) ছিলেন আর্চিবাল্ড স্টার্লিং অফ গার্ডেনের তৃতীয় পুত্র। ১৮ বছর বয়সে তিনি বলিওল কলেজ, অক্সফোর্ডে গিয়েছিলেন, যেখানে প্রধানত আর্ল অফ মারের প্রভাবে তিনি ব্যালিওলের বিশপ ওয়ার্নারের প্রদর্শনীকারীদের (বা স্নেল প্রদর্শনী) মনোনীত হন। লন্ডনে তিনি দশ বছর অবস্থান করেন, বেশিরভাগ সময় টাওয়ার স্ট্রিটের একটি একাডেমির সাথে যুক্ত ছিলেন এবং তাঁর অবসরকে গণিত এবং খ্যাতিমান গণিতবিদদের সাথে যোগাযোগের জন্য উৎসর্গ করেছিলেন। ত্রিকোণমিতিক সিরিজের বিস্তার নির্ণয় করেন এবং ত্রিকোণমিতি আধুনিক গণিতের গুরুত্বপূর্ন শাখা হিসেবে প্রতিষ্ঠা লাভ করে। বর্তমানে ব্যবহৃত sin, cos, tan, cosec, sec এবং cot প্রতীকগুলি বৈজ্ঞানিক লেওনার্ড অয়লারের  অয়লার (15 /04/1707 - 18/09/1783 ) একজন সুইস গণিতবিদ এবং পদার্থবিজ্ঞানী (বাসেল, সুইজারল্যান্ড )। তিনি ক্যালকুলাস, সংখ্যাতত্ত্ব, অন্তরক সমীকরণ, গ্রাফ তত্ত্ব ও টপোগণিতে অনেক গুরুত্বপূর্ণ অবদান রাখেন। আধুনিক গণিতে ব্যবহৃত অনেক পরিভাষা ও ধারণা তার অবদান। গাণিতিক বিশ্লেষণে ব্যবহৃত গাণিতিক ফাংশন-এর ধারণা তারই আবিষ্কার।[১] অয়লার e , পাই এর জন্য π , যোগের জন্য Σ চিহ্নের প্রবর্তন করেন। তিনি বলবিজ্ঞান, আলোকবিজ্ঞান ও জ্যোতির্বিজ্ঞানেও অবদান রাখেন। সমসাময়িককালে তার মত প্রকাশনা সম্পন্ন কোনো গণিতবিদ ছিলেন না। এমনকি মুদ্রণ ব্যবস্থার উন্নতি হওয়ার পরও তার সমপরিমাণ প্রকাশনা সম্পন্ন বিজ্ঞানীর সংখ্যা খুবই কম। অনস্বীকার্য অবদান। তিনি এগুলিকে অসীম সিরিজ আকারে বর্ণনা করেন।
অয়লার (15 /04/1707 - 18/09/1783 ) একজন সুইস গণিতবিদ এবং পদার্থবিজ্ঞানী (বাসেল, সুইজারল্যান্ড )। তিনি ক্যালকুলাস, সংখ্যাতত্ত্ব, অন্তরক সমীকরণ, গ্রাফ তত্ত্ব ও টপোগণিতে অনেক গুরুত্বপূর্ণ অবদান রাখেন। আধুনিক গণিতে ব্যবহৃত অনেক পরিভাষা ও ধারণা তার অবদান। গাণিতিক বিশ্লেষণে ব্যবহৃত গাণিতিক ফাংশন-এর ধারণা তারই আবিষ্কার।[১] অয়লার e , পাই এর জন্য π , যোগের জন্য Σ চিহ্নের প্রবর্তন করেন। তিনি বলবিজ্ঞান, আলোকবিজ্ঞান ও জ্যোতির্বিজ্ঞানেও অবদান রাখেন। সমসাময়িককালে তার মত প্রকাশনা সম্পন্ন কোনো গণিতবিদ ছিলেন না। এমনকি মুদ্রণ ব্যবস্থার উন্নতি হওয়ার পরও তার সমপরিমাণ প্রকাশনা সম্পন্ন বিজ্ঞানীর সংখ্যা খুবই কম। অনস্বীকার্য অবদান। তিনি এগুলিকে অসীম সিরিজ আকারে বর্ণনা করেন।
ত্রিকোণমিতিক কোণ
Trigonomeriic angle
 দুইটি সরলরেখা পরস্পরকে ছেদ করলে যে কোণ উৎপন্ন হয়, তাঁকে জ্যামিতিক কোণ বলে। জ্যামিতিক কোণ কখনো ঋণাত্মক হতে পারে না এবং \(0^{o}\) ও \(360^{o}\) এর মধ্যে সীমাবদ্ধ থাকে।
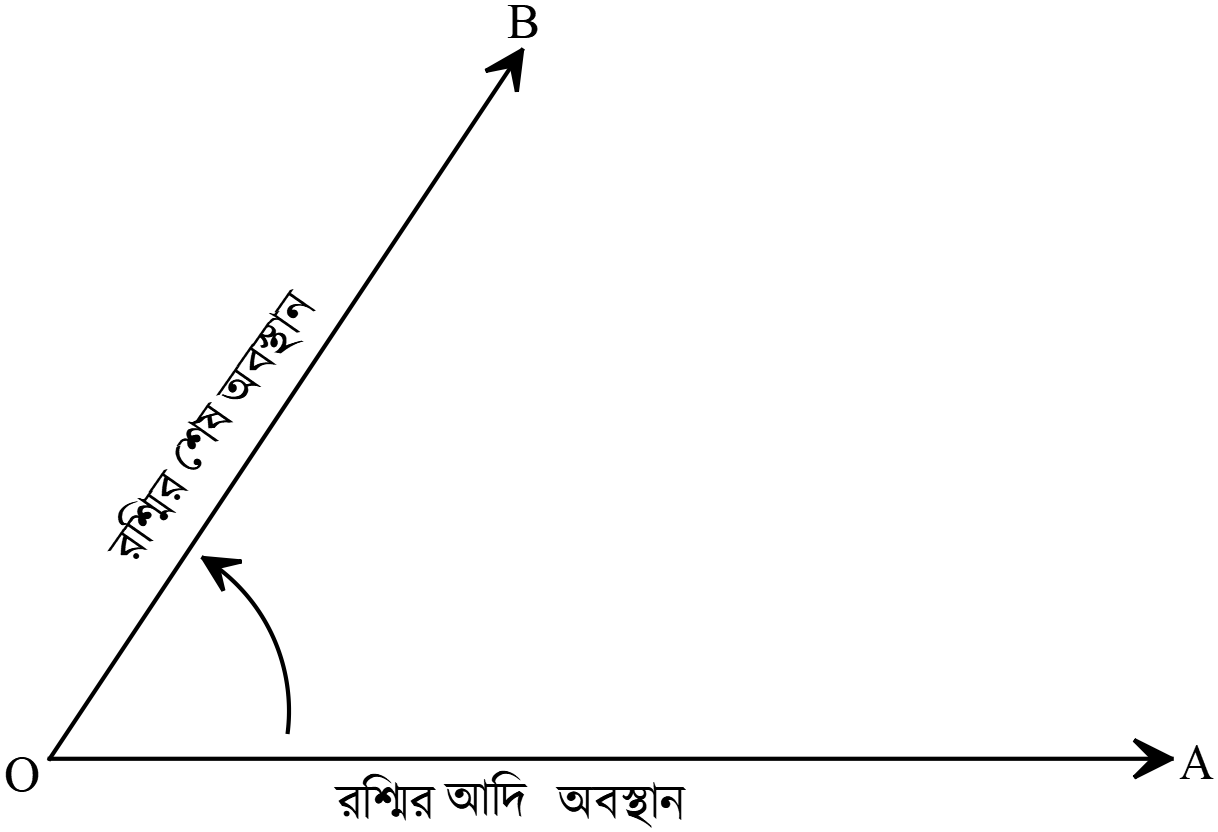
ত্রিকোণমিতিতে কোণ উৎপন্ন হয় একটি রশ্মির ঘূর্ণনের ফলে। একটি রশ্মি তাঁর প্রান্ত বিন্দুকে কেন্দ্র করে একটি নির্দিষ্ট পরিমাণ ঘুরে তাঁর আদি অবস্থানের সাথে যদি কোণ উৎপন্ন করে তবে তাকে ত্রিকোণমিতক কোণ বলা হয়। ঘূর্ণায়মান রশ্মিটি ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে যে কোণ উৎপন্ন করে তাকে ধনাত্মক কোণ এবং ঘড়ির কাঁটার ঘূর্ণনের দিকে ঘুরে যে কোণ উৎপন্ন করে তাকে ঋণাত্মক কোণ বলে।
দুইটি সরলরেখা পরস্পরকে ছেদ করলে যে কোণ উৎপন্ন হয়, তাঁকে জ্যামিতিক কোণ বলে। জ্যামিতিক কোণ কখনো ঋণাত্মক হতে পারে না এবং \(0^{o}\) ও \(360^{o}\) এর মধ্যে সীমাবদ্ধ থাকে।
ত্রিকোণমিতিতে কোণ উৎপন্ন হয় একটি রশ্মির ঘূর্ণনের ফলে। একটি রশ্মি তাঁর প্রান্ত বিন্দুকে কেন্দ্র করে একটি নির্দিষ্ট পরিমাণ ঘুরে তাঁর আদি অবস্থানের সাথে যদি কোণ উৎপন্ন করে তবে তাকে ত্রিকোণমিতক কোণ বলা হয়। ঘূর্ণায়মান রশ্মিটি ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে যে কোণ উৎপন্ন করে তাকে ধনাত্মক কোণ এবং ঘড়ির কাঁটার ঘূর্ণনের দিকে ঘুরে যে কোণ উৎপন্ন করে তাকে ঋণাত্মক কোণ বলে।
কোণের পরিমাপ
Measurement of angle
কোণ পরিমাপের পদ্ধতিঃ
\((1)\) ষাটমূলক পদ্ধতি (Sexagesimal System)
\((2)\) বৃত্তীয় পদ্ধতি (Circular System)
\((3)\) শতমূলক পদ্ধতি (Centesimal System)
\((2)\) বৃত্তীয় পদ্ধতি (Circular System)
\((3)\) শতমূলক পদ্ধতি (Centesimal System)
ষাটমূলক পদ্ধতি
Sexagesimal System
 ষাটমূলক পদ্ধতিঃ এই পদ্ধতিতে এক সমকোণকে সমান নব্বইভাগে ভাগ করা হয় এবং প্রত্যেক ভাগকে এক ডিগ্রি \((1^{o})\) বলা হয়। এক ডিগ্রিকে সমান ষাট ভাগে ভাগ করে প্রতি ভাগকে মিনিট \((1^{\prime})\) বলা হয় এবং এক মিনিটকে সমান ষাট ভাগে ভাগ করে প্রতি ভাগকে এক সেকেন্ড \((1^{\prime\prime})\) বলা হয়।
ষাটমূলক পদ্ধতিঃ এই পদ্ধতিতে এক সমকোণকে সমান নব্বইভাগে ভাগ করা হয় এবং প্রত্যেক ভাগকে এক ডিগ্রি \((1^{o})\) বলা হয়। এক ডিগ্রিকে সমান ষাট ভাগে ভাগ করে প্রতি ভাগকে মিনিট \((1^{\prime})\) বলা হয় এবং এক মিনিটকে সমান ষাট ভাগে ভাগ করে প্রতি ভাগকে এক সেকেন্ড \((1^{\prime\prime})\) বলা হয়। অর্থাৎ \(1\) সমকোণ \(=90\) ডিগ্রি \(90^{o}\)
\(1\) ডিগ্রি \(=60\) মিনিট \(60^{\prime}\)
\(1\) মিনিট \(=60\) সেকেন্ড \(60^{\prime\prime}\)
এই পদ্ধতিকে ব্রিটিশ পদ্ধতি বা ইংলিশ পদ্ধতিও বলা হয়ে থাকে।
বৃত্তীয় পদ্ধতি
Circular System
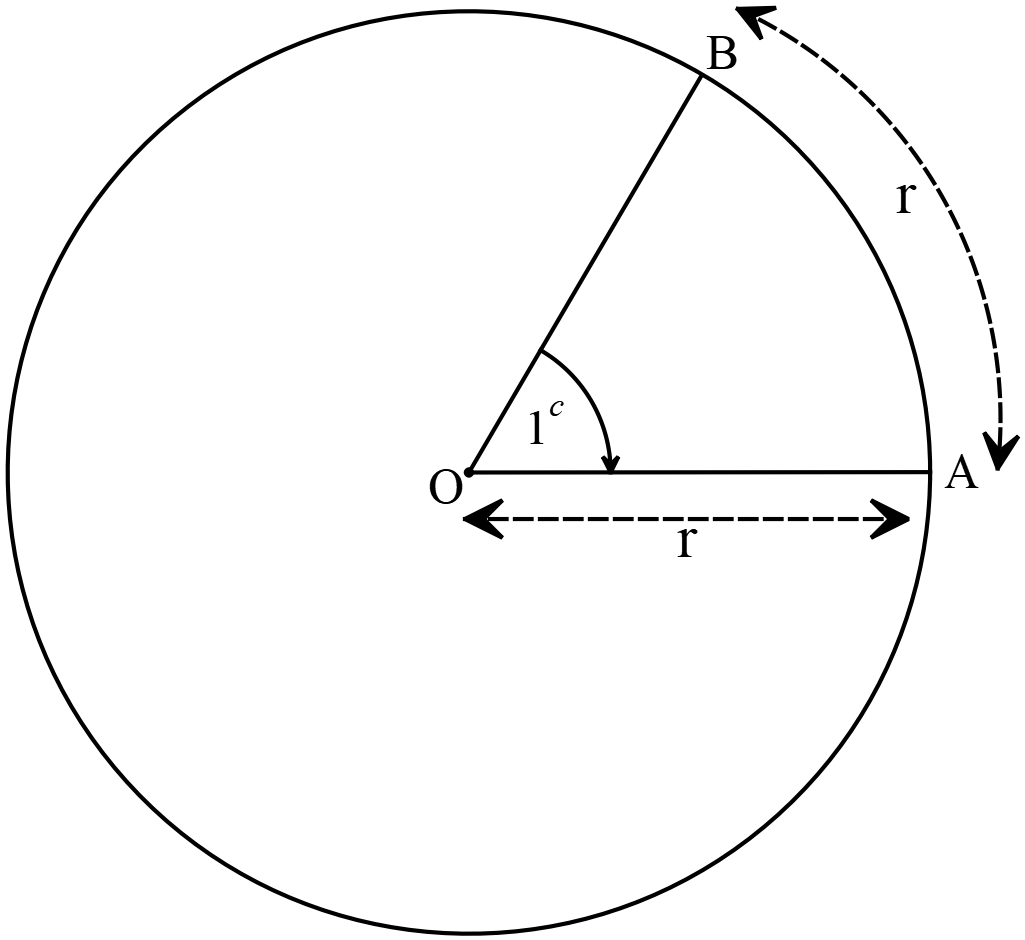 বৃত্তীয় পদ্ধতিঃ এই পদ্ধতিতে মূল একক হচ্ছে রেডিয়ান। কোনো বৃত্তের ব্যাসার্ধের সমান চাপ কেন্দ্রে যে কোণ উৎপন্ন করে তাকে এক রেডিয়ান \((1^{c})\) কোণ বলা হয়। রেডিয়ান একটি ধ্রুবক কোণ। এই কোণ পরিমাপের একককে বৃত্তীয় একক বলে। সকল তত্ত্বীয় কাজে কোণ পরিমাপের জন্য রেডিয়ানকে ব্যবহার করা হয়।
বৃত্তীয় পদ্ধতিঃ এই পদ্ধতিতে মূল একক হচ্ছে রেডিয়ান। কোনো বৃত্তের ব্যাসার্ধের সমান চাপ কেন্দ্রে যে কোণ উৎপন্ন করে তাকে এক রেডিয়ান \((1^{c})\) কোণ বলা হয়। রেডিয়ান একটি ধ্রুবক কোণ। এই কোণ পরিমাপের একককে বৃত্তীয় একক বলে। সকল তত্ত্বীয় কাজে কোণ পরিমাপের জন্য রেডিয়ানকে ব্যবহার করা হয়।
বৃত্তের পরিধি ও ব্যাসের অনুপাত
The ratio of the circumference to the diameter of a circle
বৃত্তের পরিধি ও ব্যাসের অনুপাত ধ্রুব সংখ্যা
The ratio of the circumference to the diameter of a circle is a constant number
 মনে করি,
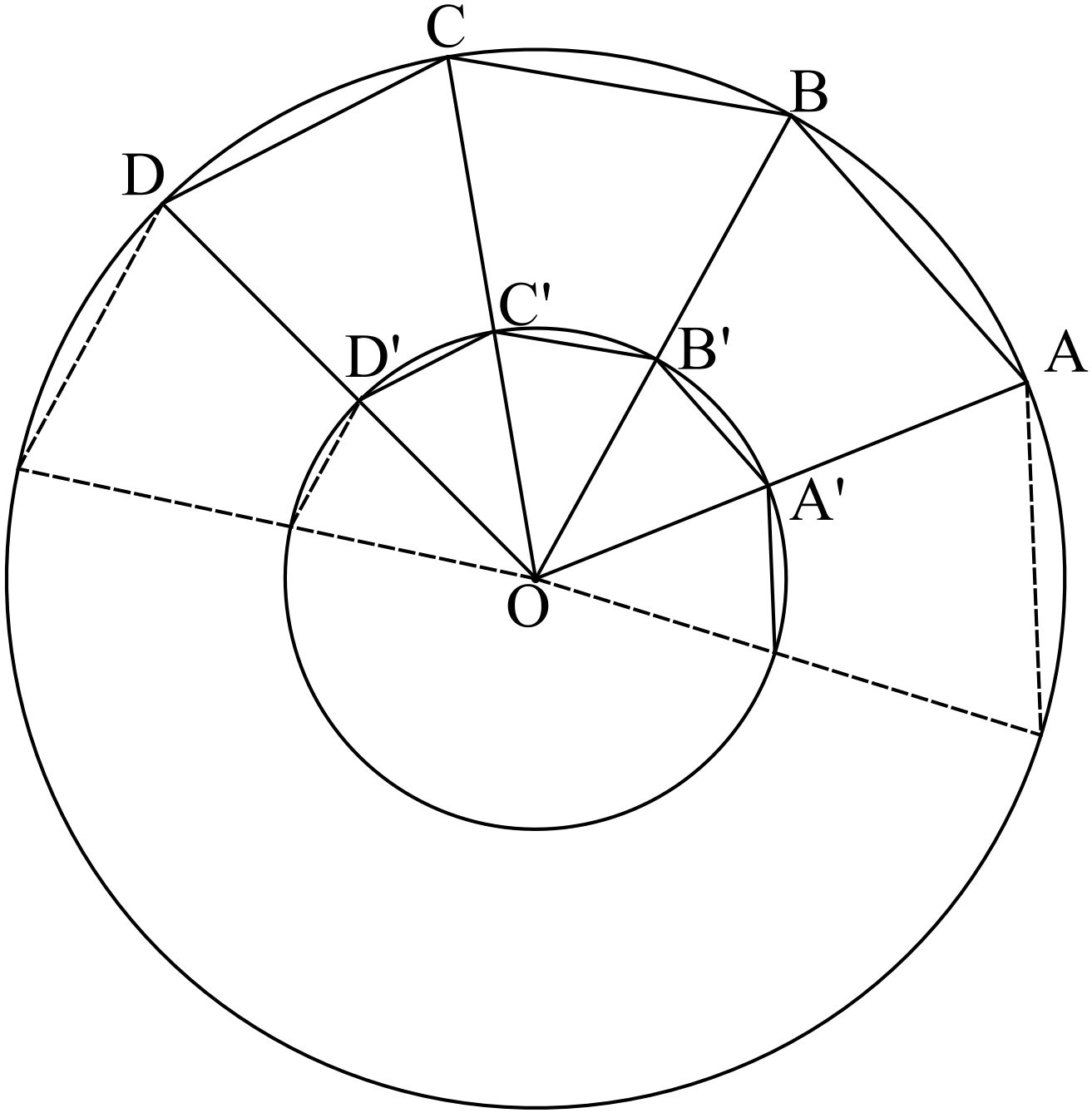
মনে করি, দুইটি বৃত্তে কেন্দ্র \(O\)
এখন, বহিঃস্থ বৃত্তটিকে \(n\) সংখ্যক \(n>1\) সমান ভাগে বিভক্ত করি। কেন্দ্র \(O\) এর সহিত বিভক্ত বিন্দুগুলি যোগ করায় অন্তঃস্থ বৃত্তটিও \(n\) সংখ্যক সমান ভাগে বিভক্ত হলো। উভয় বৃত্তে বিভক্ত বিন্দুগুলো পরস্পর যুক্ত করি। ফলে বহিঃস্থ ও অন্তঃস্থ বৃত্তে \(n\) সংখ্যক বাহুবিশিষ্ট একটি করে সুষম বহুভুজ অন্তর্লিখিত হলো।
এখন, \(OA=OB ....(1)\) (উভয়ে বহিঃস্থ বৃত্তের ব্যাসার্ধ)
এবং \(OA^{\prime}=OB^{\prime} .....(2)\) (উভয়ে অন্তঃস্থ বৃত্তের ব্যাসার্ধ)
\((1)\) কে \((2)\) দ্বারা ভাগ করে।
\(\frac{OA}{OA^{\prime}}=\frac{OB}{OB^{\prime}} .......(3)\)
\(\triangle{AOB}\) এবং \(\triangle{A^{\prime}OB^{\prime}}\) এর সাধারণ কোণ \(O\) বিন্দুতে,
অর্থাৎ ত্রিভুজদ্বয় সদৃশ
\(\therefore \frac{AB}{A^{\prime}B^{\prime}}=\frac{OB}{OB^{\prime}}\) ➜ \(\because \) সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
\(\Rightarrow \frac{n\times AB}{n\times A^{\prime}B^{\prime}}=\frac{OB}{OB^{\prime}}\) ➜ বাম পার্শে লব ও হরের সহিত \(n\) গুণ করে।
\(\Rightarrow \frac{n\times AB}{OB}=\frac{n\times A^{\prime}B^{\prime}}{OB^{\prime}}\)
অর্থাৎ \(\frac{\text{বহিঃস্থ বহুভুজের পরিসীমা}}{\text{বহিঃস্থ বৃত্তের ব্যাসার্ধ}}=\frac{\text{অন্তঃস্থ বহুভুজের পরিসীমা}}{\text{অন্তঃস্থ বৃত্তের ব্যাসার্ধ}} .........(4)\)
বহুভুজের যে কোনো সংখ্যক বাহুর জন্য \((4)\) নং সম্পর্কটি সত্য। \(n\) এর মাণ যথেষ্ট বড় হলে \((n\rightarrow{\infty})\) বহুভুজের বাহুগুলো ছোট হয় এবং বাহুগুলো বৃত্তের ছোট ছোট চাপে পরিণত হয়। তখন বহিঃস্থ এবং অন্তঃস্থ বহুভুজের পরিসীমা যথাক্রমে এদের পরিধিতে পরিগণিত হয়।
\((4)\) নং হতে,
\(\frac{\text{বহিঃস্থ বৃত্তের পরিধি}}{\text{বহিঃস্থ বৃত্তের ব্যাসার্ধ}}=\frac{\text{অন্তঃস্থ বৃত্তের পরিধি}}{\text{অন্তঃস্থ বৃত্তের ব্যাসার্ধ}} \)
অর্থাৎ বৃত্তের পরিধি ও ব্যাসার্ধের অনুপাত সমান।
অর্থাৎ \(\frac{\text{ বৃত্তের পরিধি}}{\text{ বৃত্তের ব্যাসার্ধ}}=\text{ধ্রুব সংখ্যা }\)
\(\Rightarrow \frac{\text{ বৃত্তের পরিধি}}{2\times\text{বৃত্তের ব্যাসার্ধ}}=\frac{\text{ধ্রুব সংখ্যা }}{2}\) ➜ উভয় পার্শে \(2 \) ভাগ করে।
\(\therefore \frac{\text{ বৃত্তের পরিধি}}{\text{বৃত্তের ব্যাস}}=\text{ধ্রুব সংখ্যা } ........(5)\) ➜ \(\because \) ব্যাস \(=2\times\) ব্যাসার্ধ
এবং \(\frac{\text{ধ্রুব সংখ্যা }}{2}=\text{ধ্রুব সংখ্যা }\)
এই ধ্রুব সংখ্যাটিকে গ্রিক অক্ষর \(\pi\) (পাই) দ্বারা প্রকাশ করা হয়। \(\pi\) একটি অমূলদ সংখ্যা দশমিকে প্রকাশ করলে এটি একটি অন্তহীন অপৌনঃপুনিক সংখ্যা \((\pi=3.1459265358.......)\) হয়।
\((5)\) নং হতে,
\(\frac{\text{ বৃত্তের পরিধি}}{\text{ব্যাস}}= \pi \ (\text{ধ্রুব সংখ্যা })\)
\(\Rightarrow \text{ বৃত্তের পরিধি}= \pi\times\text{ব্যাস}\)
\(\Rightarrow \text{ বৃত্তের পরিধি}= \pi\times2r\) যেখানে, \(r=\) ব্যাসার্ধ
\(\therefore \text{পরিধি}= 2\pi r\)
\(\text{পরিধি}= 2\pi r\)
রেডিয়ান একটি ধ্রুবক কোণ
Radian is a constant angle
\(1^{c}=\frac{2}{\pi}\) সমকোণ।
যেখানে, \(\pi=\frac{22}{7}\) ধ্রুবক
কেননা \(r\) ব্যাসার্ধবিশিষ্ট বৃত্তের পরিধি \(=2\pi r\) এবং ব্যাস \(=2r\)
সুতরাং \(\frac{\text{পরিধি}}{\text{ব্যাস}}=\frac{2\pi r}{2r}\)
\(=\pi\) যা একটি ধ্রুবক।
এই ধ্রুবক একটি অমূলদ সংখ্যা \(\frac{22}{7}\) ইহা অমূলদ সংখ্যা হওয়া স্বত্বেও দুই দশমিক স্থান পর্যন্ত মিল থাকায় কখনও কখনও বিশেষ সুবিধার্থে \(\pi=\frac{22}{7}\) ধরা হয়।
আবার,
\(1^{c}=\frac{2}{\pi}\) সমকোণ।
\(\Rightarrow \pi^{c}=2\) সমকোণ।
\(\therefore \pi^{c}=180^{o}\)
আবার,
\(1^{c}=\frac{2}{\pi}\) সমকোণ।
\(\Rightarrow 1^{c}=\frac{1}{\pi}\times 2\) সমকোণ।
\(\Rightarrow 1^{c}=\frac{1}{3.1416}\times 180^{o}\) যেখানে, \(\pi=3.1416\)
\(\Rightarrow 1^{c}=\frac{180^{o}}{3.1416}\)
\(\therefore 1^{c}=57.2956455\) ডিগ্রি।
যেখানে, \(\pi=\frac{22}{7}\) ধ্রুবক
প্রমাণঃ
ধরি,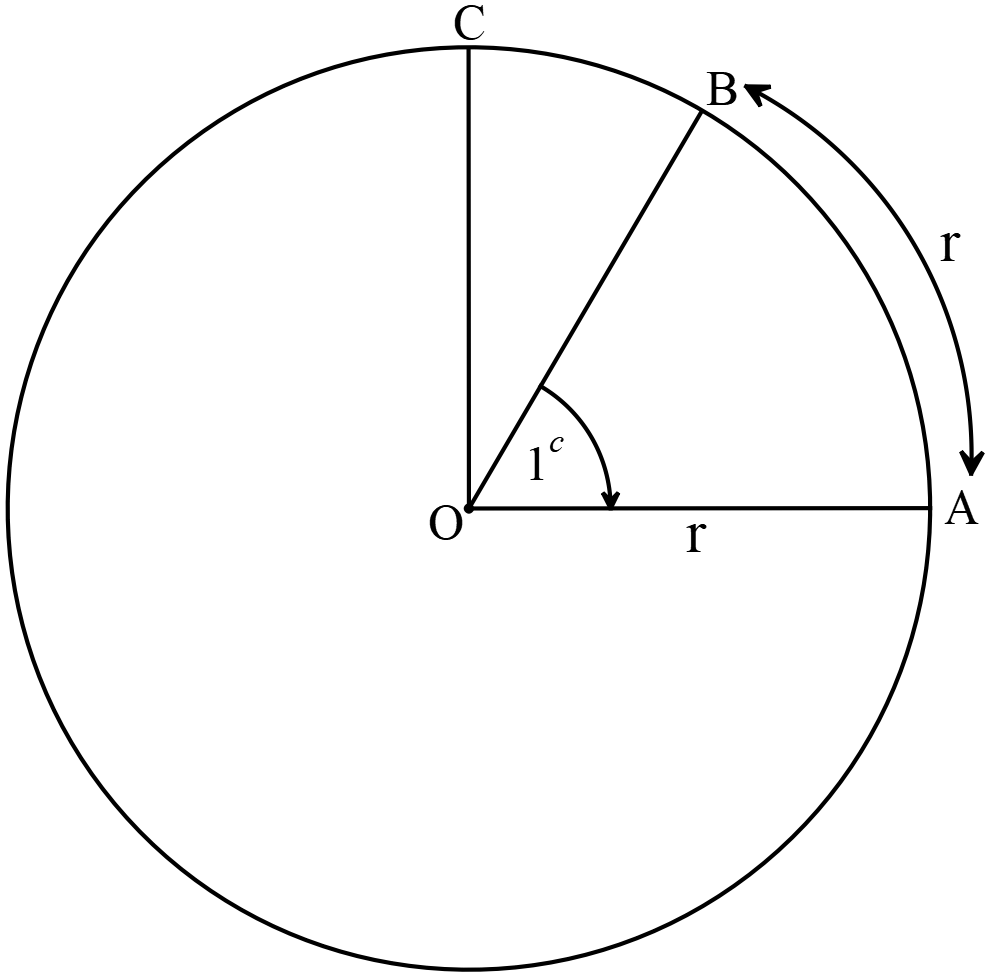
\(O\) কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ \(r\) এবং ব্যাসার্ধের সমান চাপ \(AB\)।
অর্থাৎ \(AB=r\)।
এবং \(\angle{AOB}=1\) রেডিয়ান।
কেন্দ্র \(O\) বিন্দুতে \(OA\) এর উপর \(OC\) লম্ব আঁকি।
\(\therefore \angle{AOC}=1 \) সমকোণ \(=90^{o}\)।
এবং চাপ \(AC=\frac{1}{4}\times\) পরিধি ।
\(\Rightarrow AC=\frac{1}{4}\times 2\pi r\) ➜ \(\because \) পরিধি \(=2\pi r\)
\(\therefore AC=\frac{\pi r}{2}\)
আমরা জানি,
বৃত্তচাপ দ্বারা কেন্দ্রে ধারণকৃত কোণ বৃত্তচাপটির দৈর্ঘ্যের সমানুপাতিক।
\(\therefore \frac{\angle{AOB}}{\text{চাপ} AB}=\frac{\angle{AOC}}{\text{চাপ} AC}\)
\(\Rightarrow \frac{1^{c}}{r}=\frac{90^{o}}{\frac{\pi r}{2}}\) ➜ \(\because \angle{AOB}=1\) রেডিয়ান।
\(AB=r\)।
\(\angle{AOC}=1 \) সমকোণ \(=90^{o}\)।
এবং \(AC=\frac{\pi r}{2}\)
\(\Rightarrow \frac{1^{c}}{r}=\frac{2\times 90^{o}}{\pi r}\)
\(\Rightarrow 1^{c}=\frac{2}{\pi}\times 90^{o}\)
\(\therefore 1^{c}=\frac{2}{\pi}\) সমকোণ।
এখন, \(\pi\) একটি স্থির রাশি বা ধ্রুবক।
\(\therefore \) রেডিয়ান একটি ধ্রুবক কোণ
( প্রমাণিত )
দ্রষ্টব্যঃ আমরা জানি, বৃত্তের পরিধি এবং ব্যাসের অনুপাত নিত্য বা ধ্রুবক। এই ধ্রুবকটি হচ্ছে \(\pi\) (গ্রিক অক্ষর,) ধরি,

\(O\) কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ \(r\) এবং ব্যাসার্ধের সমান চাপ \(AB\)।
অর্থাৎ \(AB=r\)।
এবং \(\angle{AOB}=1\) রেডিয়ান।
কেন্দ্র \(O\) বিন্দুতে \(OA\) এর উপর \(OC\) লম্ব আঁকি।
\(\therefore \angle{AOC}=1 \) সমকোণ \(=90^{o}\)।
এবং চাপ \(AC=\frac{1}{4}\times\) পরিধি ।
\(\Rightarrow AC=\frac{1}{4}\times 2\pi r\) ➜ \(\because \) পরিধি \(=2\pi r\)
\(\therefore AC=\frac{\pi r}{2}\)
আমরা জানি,
বৃত্তচাপ দ্বারা কেন্দ্রে ধারণকৃত কোণ বৃত্তচাপটির দৈর্ঘ্যের সমানুপাতিক।
\(\therefore \frac{\angle{AOB}}{\text{চাপ} AB}=\frac{\angle{AOC}}{\text{চাপ} AC}\)
\(\Rightarrow \frac{1^{c}}{r}=\frac{90^{o}}{\frac{\pi r}{2}}\) ➜ \(\because \angle{AOB}=1\) রেডিয়ান।
\(AB=r\)।
\(\angle{AOC}=1 \) সমকোণ \(=90^{o}\)।
এবং \(AC=\frac{\pi r}{2}\)
\(\Rightarrow \frac{1^{c}}{r}=\frac{2\times 90^{o}}{\pi r}\)
\(\Rightarrow 1^{c}=\frac{2}{\pi}\times 90^{o}\)
\(\therefore 1^{c}=\frac{2}{\pi}\) সমকোণ।
এখন, \(\pi\) একটি স্থির রাশি বা ধ্রুবক।
\(\therefore \) রেডিয়ান একটি ধ্রুবক কোণ
( প্রমাণিত )
কেননা \(r\) ব্যাসার্ধবিশিষ্ট বৃত্তের পরিধি \(=2\pi r\) এবং ব্যাস \(=2r\)
সুতরাং \(\frac{\text{পরিধি}}{\text{ব্যাস}}=\frac{2\pi r}{2r}\)
\(=\pi\) যা একটি ধ্রুবক।
এই ধ্রুবক একটি অমূলদ সংখ্যা \(\frac{22}{7}\) ইহা অমূলদ সংখ্যা হওয়া স্বত্বেও দুই দশমিক স্থান পর্যন্ত মিল থাকায় কখনও কখনও বিশেষ সুবিধার্থে \(\pi=\frac{22}{7}\) ধরা হয়।
আবার,
\(1^{c}=\frac{2}{\pi}\) সমকোণ।
\(\Rightarrow \pi^{c}=2\) সমকোণ।
\(\therefore \pi^{c}=180^{o}\)
আবার,
\(1^{c}=\frac{2}{\pi}\) সমকোণ।
\(\Rightarrow 1^{c}=\frac{1}{\pi}\times 2\) সমকোণ।
\(\Rightarrow 1^{c}=\frac{1}{3.1416}\times 180^{o}\) যেখানে, \(\pi=3.1416\)
\(\Rightarrow 1^{c}=\frac{180^{o}}{3.1416}\)
\(\therefore 1^{c}=57.2956455\) ডিগ্রি।
শতমূলক পদ্ধতি
Centesimal System
শতমূলক পদ্ধতিঃ এই পদ্ধতিতে এক সমকোণকে সমান একশত ভাগে ভাগ করা হয় এবং প্রত্যেক ভাগকে এক গ্রেড \((1^{g})\) বলা হয়। এক গ্রেডকে সমান একশত ভাগে ভাগ করে প্রতি ভাগকে মিনিট \((1^{\prime})\) বলা হয় এবং এক মিনিটকে সমান একশত ভাগে ভাগ করে প্রতি ভাগকে এক সেকেন্ড \((1^{\prime\prime})\) বলা হয়।
অর্থাৎ \(1\) সমকোণ \(=100\) গ্রেড \(100^{g}\)
\(1\) গ্রেড \(=100\) মিনিট \(100^{\prime}\)
\(1\) মিনিট \(=100\) সেকেন্ড \(100^{\prime\prime}\)
এই পদ্ধতিকে ফরাসি পদ্ধতিও বলা হয়।
আবার,
\(1\) সমকোণ \(=90^{o}=100^{g}\)
\(\Rightarrow 1^{o}=\frac{100^{g}}{90}\)
\(\therefore 1^{o}=\left(\frac{10}{9}\right)^{g}\)
আবার,
\(1\) সমকোণ \(=90^{o}=100^{g}\)
\(\Rightarrow 100^{g}=90^{o}\)
\(\Rightarrow 1^{g}=\frac{90^{0}}{100}\)
\(\therefore 1^{g}=\left(\frac{9}{10}\right)^{o}\)
অর্থাৎ \(1\) সমকোণ \(=100\) গ্রেড \(100^{g}\)
\(1\) গ্রেড \(=100\) মিনিট \(100^{\prime}\)
\(1\) মিনিট \(=100\) সেকেন্ড \(100^{\prime\prime}\)
এই পদ্ধতিকে ফরাসি পদ্ধতিও বলা হয়।
আবার,
\(1\) সমকোণ \(=90^{o}=100^{g}\)
\(\Rightarrow 1^{o}=\frac{100^{g}}{90}\)
\(\therefore 1^{o}=\left(\frac{10}{9}\right)^{g}\)
আবার,
\(1\) সমকোণ \(=90^{o}=100^{g}\)
\(\Rightarrow 100^{g}=90^{o}\)
\(\Rightarrow 1^{g}=\frac{90^{0}}{100}\)
\(\therefore 1^{g}=\left(\frac{9}{10}\right)^{o}\)
ডিগ্রি, রেডিয়ান ও গ্রাড এর মধ্যে সম্পর্ক
Relation between degree, radian and grad
\(\frac{D}{180}=\frac{R}{\pi}=\frac{G}{200}\)
প্রমাণঃ
ধরি,
একটি কোণের পরিমাণ ষাটমূলক পদ্ধতিতে \(=D^{o}\)
বৃত্তীয় পদ্ধতিতে \(=R^{c}\)
শতমূলক পদ্ধতিতে \(=G^{g}\)
\(\therefore D^{o}=R^{c}=G^{g}\)
আমরা জানি,
\(1\) সমকোণ \(=90^{o}=100^{g}\)
\(\therefore 2\) সমকোণ \(=180^{o}=200^{g}\)
\(\Rightarrow 200^{g}=180^{o}\)
\(\Rightarrow 1^{g}=\frac{180^{o}}{200}\)
\(\Rightarrow G^{g}=\left(\frac{180\times G}{200}\right)^{o}\)
\(\Rightarrow D^{o}=\left(\frac{180\times G}{200}\right)^{o}\) ➜ \(\because D^{o}=G^{g}\)
\(\Rightarrow D=\frac{180\times G}{200}\)
\(\therefore \frac{D}{180}=\frac{G}{200} ......(1)\)
আবার,
\(2\) সমকোণ \(=180^{o}=\pi^{c}\)
\(\Rightarrow \pi^{c}=180^{o}\)
\(\Rightarrow 1^{c}=\frac{180^{o}}{\pi}\)
\(\Rightarrow R^{c}=\left(\frac{180\times R}{\pi}\right)^{o}\)
\(\Rightarrow D^{o}=\left(\frac{180\times R}{\pi}\right)^{o}\) ➜ \(\because D^{o}=R^{c}\)
\(\Rightarrow D=\frac{180\times R}{\pi}\)
\(\therefore \frac{D}{180}=\frac{R}{\pi} ......(2)\)
\((1)\) ও \((2)\) হতে,
\(\frac{D}{180}=\frac{R}{\pi}=\frac{G}{200}\)
( প্রমাণিত )
ধরি,
একটি কোণের পরিমাণ ষাটমূলক পদ্ধতিতে \(=D^{o}\)
বৃত্তীয় পদ্ধতিতে \(=R^{c}\)
শতমূলক পদ্ধতিতে \(=G^{g}\)
\(\therefore D^{o}=R^{c}=G^{g}\)
আমরা জানি,
\(1\) সমকোণ \(=90^{o}=100^{g}\)
\(\therefore 2\) সমকোণ \(=180^{o}=200^{g}\)
\(\Rightarrow 200^{g}=180^{o}\)
\(\Rightarrow 1^{g}=\frac{180^{o}}{200}\)
\(\Rightarrow G^{g}=\left(\frac{180\times G}{200}\right)^{o}\)
\(\Rightarrow D^{o}=\left(\frac{180\times G}{200}\right)^{o}\) ➜ \(\because D^{o}=G^{g}\)
\(\Rightarrow D=\frac{180\times G}{200}\)
\(\therefore \frac{D}{180}=\frac{G}{200} ......(1)\)
আবার,
\(2\) সমকোণ \(=180^{o}=\pi^{c}\)
\(\Rightarrow \pi^{c}=180^{o}\)
\(\Rightarrow 1^{c}=\frac{180^{o}}{\pi}\)
\(\Rightarrow R^{c}=\left(\frac{180\times R}{\pi}\right)^{o}\)
\(\Rightarrow D^{o}=\left(\frac{180\times R}{\pi}\right)^{o}\) ➜ \(\because D^{o}=R^{c}\)
\(\Rightarrow D=\frac{180\times R}{\pi}\)
\(\therefore \frac{D}{180}=\frac{R}{\pi} ......(2)\)
\((1)\) ও \((2)\) হতে,
\(\frac{D}{180}=\frac{R}{\pi}=\frac{G}{200}\)
( প্রমাণিত )
বৃত্তচাপের দৈর্ঘ্য
The length of the arc
\(s=r\theta\)
যেখানে, \(s=\) চাপ
\(r=\) ব্যাসার্ধ
এবং \(\theta=\) কোণের বৃত্তীয় মাণ
যেখানে, \(s=\) চাপ
\(r=\) ব্যাসার্ধ
এবং \(\theta=\) কোণের বৃত্তীয় মাণ
প্রমাণঃ
ধরি,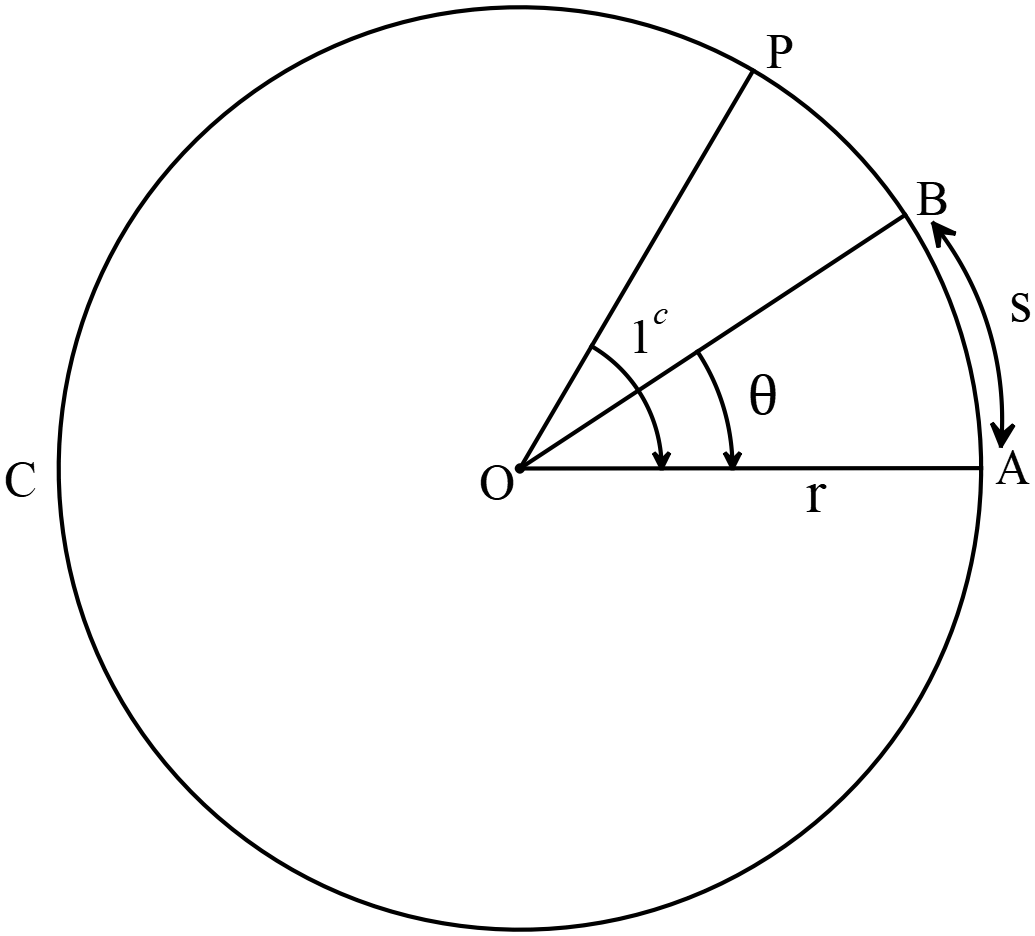
\(ABC\) বৃত্তের কেন্দ্র \(O,\) ব্যাসার্ধ \(OA=r\) একক, চাপ \(AB=s\) একক, এবং \(AB\) চাপ দ্বারা কেন্দ্রে উৎপন্ন কোণ \(\angle{AOB}=\theta\) রেডিয়ান।
প্রমাণ করতে হবে যে, \(s=r\theta\)
বৃত্তের কেন্দ্র \(O\) হতে \(OA\) সমান ব্যসার্ধ নিয়ে \(AP\) বৃত্তচাপ আঁকি যেন পরিধিকে \(P\) বিন্দুতে ছেদ করে।
\(\therefore AP=r\)
এবং \(\angle{AOP}=1\) রেডিয়ান।
কোনো বৃত্তচাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণ, বৃত্তচাপটির দৈর্ঘ্যের সমানুপাতিক।
সুতরাং, \(\frac{\angle{AOB}}{AB}=\frac{\angle{AOP}}{AP}\)
\(\Rightarrow \frac{\angle{AOB}}{\angle{AOP}}=\frac{AB}{AP}\)
\(\Rightarrow \frac{\theta}{1}=\frac{s}{r}\) ➜ \(\because \angle{AOB}=\theta\)
\(\angle{AOP}=1\) রেডিয়ান।
\(AB=s\)
এবং \(AP=r\)
\(\therefore s=r\theta\)
\(s=r\theta\)
( প্রমাণিত )
ধরি,

\(ABC\) বৃত্তের কেন্দ্র \(O,\) ব্যাসার্ধ \(OA=r\) একক, চাপ \(AB=s\) একক, এবং \(AB\) চাপ দ্বারা কেন্দ্রে উৎপন্ন কোণ \(\angle{AOB}=\theta\) রেডিয়ান।
প্রমাণ করতে হবে যে, \(s=r\theta\)
বৃত্তের কেন্দ্র \(O\) হতে \(OA\) সমান ব্যসার্ধ নিয়ে \(AP\) বৃত্তচাপ আঁকি যেন পরিধিকে \(P\) বিন্দুতে ছেদ করে।
\(\therefore AP=r\)
এবং \(\angle{AOP}=1\) রেডিয়ান।
কোনো বৃত্তচাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণ, বৃত্তচাপটির দৈর্ঘ্যের সমানুপাতিক।
সুতরাং, \(\frac{\angle{AOB}}{AB}=\frac{\angle{AOP}}{AP}\)
\(\Rightarrow \frac{\angle{AOB}}{\angle{AOP}}=\frac{AB}{AP}\)
\(\Rightarrow \frac{\theta}{1}=\frac{s}{r}\) ➜ \(\because \angle{AOB}=\theta\)
\(\angle{AOP}=1\) রেডিয়ান।
\(AB=s\)
এবং \(AP=r\)
\(\therefore s=r\theta\)
\(s=r\theta\)
( প্রমাণিত )
বৃত্তকলার ক্ষেত্রফল
Area of the sector
\(A=\frac{1}{2}r^2\theta\)
যেখানে, \(A=\) বৃত্তকলার ক্ষেত্রফল
\(r=\) ব্যাসার্ধ
এবং \(\theta=\) চাপ দ্বারা উৎপন্ন কেন্দ্রস্ত কোণের বৃত্তীয় মাণ
অথবা,
\(A=\frac{\theta}{360^{o}}\pi r^2\)
যেখানে, \(A=\) বৃত্তকলার ক্ষেত্রফল
\(r=\) ব্যাসার্ধ
এবং \(\theta=\) চাপ দ্বারা উৎপন্ন কেন্দ্রস্ত কোণ
যেখানে, \(A=\) বৃত্তকলার ক্ষেত্রফল
\(r=\) ব্যাসার্ধ
এবং \(\theta=\) চাপ দ্বারা উৎপন্ন কেন্দ্রস্ত কোণের বৃত্তীয় মাণ
অথবা,
\(A=\frac{\theta}{360^{o}}\pi r^2\)
যেখানে, \(A=\) বৃত্তকলার ক্ষেত্রফল
\(r=\) ব্যাসার্ধ
এবং \(\theta=\) চাপ দ্বারা উৎপন্ন কেন্দ্রস্ত কোণ
প্রমাণঃ
ধরি,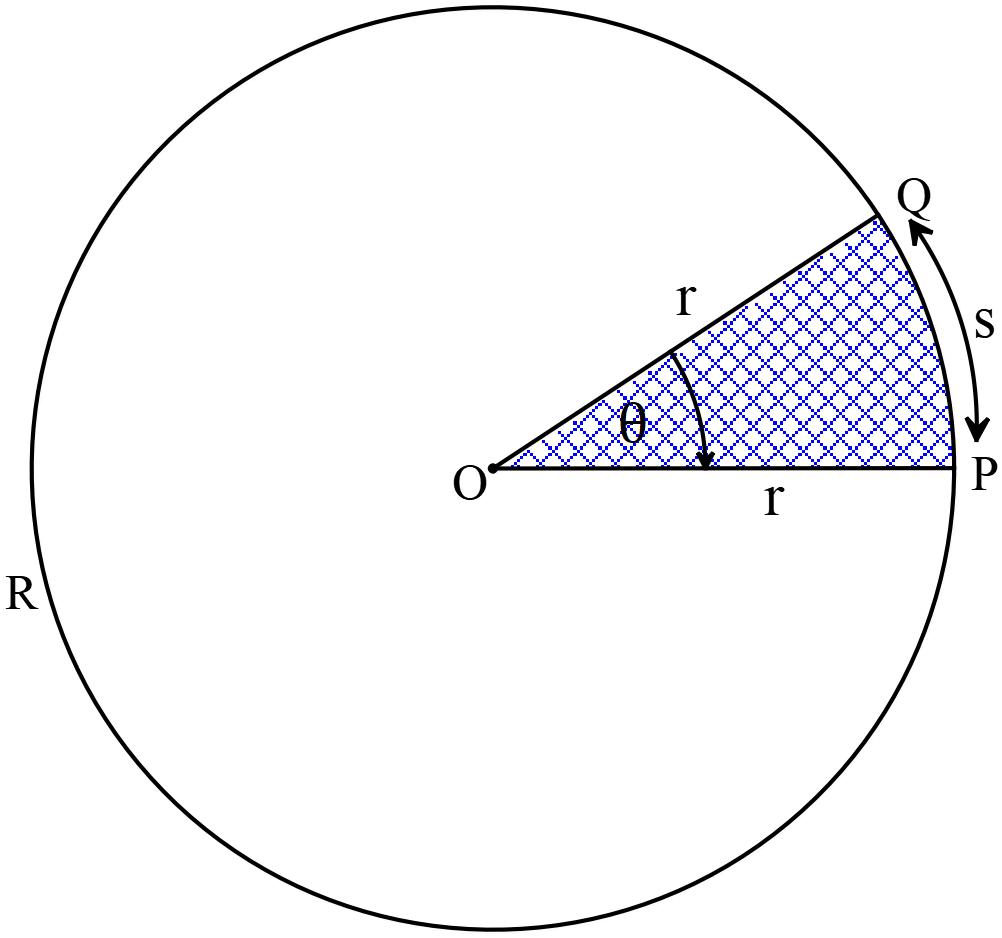
\(PQR\) বৃত্তের কেন্দ্র \(O,\) ব্যাসার্ধ \(OP=r\) একক, চাপ \(PQ=s\) একক, এবং \(PQ\) চাপ দ্বারা কেন্দ্রে উৎপন্ন কোণ \(\angle{POQ}=\theta\) রেডিয়ান।
প্রমাণ করতে হবে যে, \(A=\frac{1}{2}r^2\theta\)
বৃত্তের কেন্দ্র \(O\) হতে \(OP\) সমান ব্যসার্ধ নিয়ে \(PQ\) বৃত্তচাপ আঁকি যেন পরিধিকে \(Q\) বিন্দুতে ছেদ করে।
\(\therefore OP=r\)
কোনো বৃত্তচাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণ, বৃত্তচাপটির দ্বারা উৎপন্ন বৃত্তকলার ক্ষেত্রফলের সমানুপাতিক।
সুতরাং, \(\frac{POQ \ \text{ক্ষেত্র}}{\angle{POQ}}=\frac{\text{সম্পূর্ণ বৃত্ত}}{2\pi}\)
\(\Rightarrow \frac{A}{\theta}=\frac{\pi r^2 }{2\pi}\) ➜ \(\because A=POQ\) ক্ষেত্র
\(\angle{POQ}=\theta\) রেডিয়ান।
এবং বৃত্তের ক্ষেত্রফল \(=\pi r^2 \)
\(\Rightarrow \frac{A}{\theta}=\frac{r^2 }{2}\)
\(\therefore A=\frac{1}{2}r^2\theta\)
\(A=\frac{1}{2}r^2\theta\)
আবার,
\(180^{o}=\pi\)
\(\Rightarrow 1=\frac{\pi}{180^{o}}\)
\(\therefore \theta=\frac{\theta\pi}{180^{o}}\)
এখন, উপরোক্ত সম্পর্ক হতে,
\(A=\frac{1}{2}r^2\times\frac{\theta\pi}{180}\) ➜ \(\because \theta=\frac{\theta\pi}{180^{o}}\)
\(=\frac{\theta}{360^{o}}\pi r^2\)
\(A=\frac{\theta}{360^{o}}\pi r^2\)
( প্রমাণিত )
ধরি,

\(PQR\) বৃত্তের কেন্দ্র \(O,\) ব্যাসার্ধ \(OP=r\) একক, চাপ \(PQ=s\) একক, এবং \(PQ\) চাপ দ্বারা কেন্দ্রে উৎপন্ন কোণ \(\angle{POQ}=\theta\) রেডিয়ান।
প্রমাণ করতে হবে যে, \(A=\frac{1}{2}r^2\theta\)
বৃত্তের কেন্দ্র \(O\) হতে \(OP\) সমান ব্যসার্ধ নিয়ে \(PQ\) বৃত্তচাপ আঁকি যেন পরিধিকে \(Q\) বিন্দুতে ছেদ করে।
\(\therefore OP=r\)
কোনো বৃত্তচাপ দ্বারা উৎপন্ন কেন্দ্রস্থ কোণ, বৃত্তচাপটির দ্বারা উৎপন্ন বৃত্তকলার ক্ষেত্রফলের সমানুপাতিক।
সুতরাং, \(\frac{POQ \ \text{ক্ষেত্র}}{\angle{POQ}}=\frac{\text{সম্পূর্ণ বৃত্ত}}{2\pi}\)
\(\Rightarrow \frac{A}{\theta}=\frac{\pi r^2 }{2\pi}\) ➜ \(\because A=POQ\) ক্ষেত্র
\(\angle{POQ}=\theta\) রেডিয়ান।
এবং বৃত্তের ক্ষেত্রফল \(=\pi r^2 \)
\(\Rightarrow \frac{A}{\theta}=\frac{r^2 }{2}\)
\(\therefore A=\frac{1}{2}r^2\theta\)
\(A=\frac{1}{2}r^2\theta\)
আবার,
\(180^{o}=\pi\)
\(\Rightarrow 1=\frac{\pi}{180^{o}}\)
\(\therefore \theta=\frac{\theta\pi}{180^{o}}\)
এখন, উপরোক্ত সম্পর্ক হতে,
\(A=\frac{1}{2}r^2\times\frac{\theta\pi}{180}\) ➜ \(\because \theta=\frac{\theta\pi}{180^{o}}\)
\(=\frac{\theta}{360^{o}}\pi r^2\)
\(A=\frac{\theta}{360^{o}}\pi r^2\)
( প্রমাণিত )
ঘড়ির ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ
The angle between the hour hand and the minute hand
ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ \(\left|\frac{60H-11M}{2}\right|^{o}\)
যদি, \(\left|\frac{60H-11M}{2}\right|^{o}>180^{o}\)
ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ \(360^{o}-\left|\frac{60H-11M}{2}\right|^{o}\)
যেখানে, \(H=\) ঘন্টা
এবং \(M=\) মিনিট
যদি, \(\left|\frac{60H-11M}{2}\right|^{o}>180^{o}\)
ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ \(360^{o}-\left|\frac{60H-11M}{2}\right|^{o}\)
যেখানে, \(H=\) ঘন্টা
এবং \(M=\) মিনিট
প্রমাণঃ
ঘন্টার কাঁটা \(12\) ঘন্টা বা \(12\times 60\) মিনিটে ঘোরে \(360^{o}\)
\(1\) মিনিটে ঘোরে \(\frac{360^{o}}{12\times 60}\)
\(=\frac{1^{o}}{2}\)
আবার,
মিনিটের কাঁটা \(60\) মিনিটে ঘোরে \(360^{o}\)
\(1\) মিনিটে ঘোরে \(\frac{360^{o}}{60}\)
\(M\) মিনিটে ঘোরে \(\frac{360^{o}\times M}{60}\)
\(=6M^{o}\)
\(\therefore H\) ঘন্টা \( M\) মিনিট \(=(60H+M)\) মিনিট
ঘন্টার কাঁটা \(1\) মিনিটে ঘোরে \(=\frac{1^{o}}{2}\)
\((60H+M)\) মিনিটে ঘোরে \(=\frac{(60H+M)^{o}}{2}\)
\(\therefore \) ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ \(=\frac{(60H+M)^{o}}{2}-6M^{o}\)
\(=\frac{(60H+M)^{o}-12M^{o}}{2}\)
\(=\frac{(60H+M-12M)^{o}}{2}\)
\(=\frac{(60H-11M)^{o}}{2}\)
\(=\left|\frac{60H-11M}{2}\right|^{o}\)
ঘড়ির ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ \(\left|\frac{60H-11M}{2}\right|^{o}\)
যদি, \(\left|\frac{60H-11M}{2}\right|^{o}>180^{o}\) হয়, তবে
ঘড়ির ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ \(360^{o}-\left|\frac{60H-11M}{2}\right|^{o}\)
( প্রমাণিত )
ঘন্টার কাঁটা \(12\) ঘন্টা বা \(12\times 60\) মিনিটে ঘোরে \(360^{o}\)
\(1\) মিনিটে ঘোরে \(\frac{360^{o}}{12\times 60}\)
\(=\frac{1^{o}}{2}\)
আবার,
মিনিটের কাঁটা \(60\) মিনিটে ঘোরে \(360^{o}\)
\(1\) মিনিটে ঘোরে \(\frac{360^{o}}{60}\)
\(M\) মিনিটে ঘোরে \(\frac{360^{o}\times M}{60}\)
\(=6M^{o}\)
\(\therefore H\) ঘন্টা \( M\) মিনিট \(=(60H+M)\) মিনিট
ঘন্টার কাঁটা \(1\) মিনিটে ঘোরে \(=\frac{1^{o}}{2}\)
\((60H+M)\) মিনিটে ঘোরে \(=\frac{(60H+M)^{o}}{2}\)
\(\therefore \) ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ \(=\frac{(60H+M)^{o}}{2}-6M^{o}\)
\(=\frac{(60H+M)^{o}-12M^{o}}{2}\)
\(=\frac{(60H+M-12M)^{o}}{2}\)
\(=\frac{(60H-11M)^{o}}{2}\)
\(=\left|\frac{60H-11M}{2}\right|^{o}\)
ঘড়ির ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ \(\left|\frac{60H-11M}{2}\right|^{o}\)
যদি, \(\left|\frac{60H-11M}{2}\right|^{o}>180^{o}\) হয়, তবে
ঘড়ির ঘন্টার কাঁটা ও মিনিটের কাঁটার মধ্যবর্তী কোণ \(360^{o}-\left|\frac{60H-11M}{2}\right|^{o}\)
( প্রমাণিত )

.png)
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004