যৌগিক কোণের ত্রিকোণমিতিক অনুপাত-Trigonometric ratio of compound angles

যৌগিক কোণের ত্রিকোণমিতিক অনুপাত

Trigonometric ratio of compound angles

Posted on August 20, 2023, 4:33 am By admin

এ অধ্যায়ের পাঠ্যসূচী

যৌগিক কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of compound angles)
\(\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
\(\cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)
\(\sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
\(\cos{(A-B)}=\cos{A}\cos{B}+\sin{A}\sin{B}\)
\(\tan{(A+B)}=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\)
\(\tan{(A-B)}=\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\)
\(\cot{(A+B)}=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\)
\(\cot{(A-B)}=\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\)
\(\sin{(A+B)}\sin{(A-B)}=\sin^2{A}-\sin^2{B}\)\(=\cos^2{B}-\cos^2{A}\)
\(\cos{(A+B)}\cos{(A-B)}=\cos^2{A}-\sin^2{B}\)\(=\cos^2{B}-\sin^2{A}\)
\(\tan{(A+B)}\tan{(A-B)}=\frac{\tan^2{A}-\tan^2{B}}{1-\tan^2{A}\tan^2{B}}\)
\(\cot{(A+B)}\cot{(A-B)}=\frac{\cot^2{A}\cot^2{B}-1}{\cot^2{B}-\cot^2{A}}\)
\(\sin{(A+B+C)}=\cos{A}\cos{B}\cos{C}(\tan{A}\)\(+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C})\)
\(\cos{(A+B+C)}=\cos{A}\cos{B}\cos{C}(1-\)\(\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A})\)
\(\tan{(A+B+C)}=\frac{\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C}}{1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A}}\)
\(\cot{(A+B+C)}=\frac{\cot{A}\cot{B}\cot{C}-\cot{A}-\cot{B}-\cot{C}}{\cot{B}\cot{C}+\cot{C}\cot{A}+\cot{A}\cot{B}-1}\)
অধ্যায় \(vii.B\)-এর উদাহরণসমুহ
অধ্যায় \(vii.B\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
অধ্যায় \(vii.B\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
অধ্যায় \(vii.B\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
অধ্যায় \(vii.B\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ

যৌগিক কোণের ত্রিকোণমিতিক অনুপাত

Trigonometric ratio of compound angles

যৌগিক কোণঃ দুই বা ততোধিক কোণের বীজগাণিতিক সমষ্টিকে যৌগিক কোণ বলে।
যেমনঃ \(A+B, \ A-B, \ A+B-C, \ A-B+C\) ইত্যাদি।

\(\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)

\(\cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)

\(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B)\lt90^{o}\)

\(\sin{(A+B)}=\sin{A}\cos{B}\)\(+\cos{A}\sin{B}\)
\(\cos{(A+B)}=\cos{A}\cos{B}\)\(-\sin{A}\sin{B}\)

প্রমাণঃ
মনে করি, কোনো ঘূর্ণায়মান রশ্মি আদি অবস্থান \(OX\) হতে \(O\) বিন্দুর সাপেক্ষে ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে \(\angle{XOY}=A, \ (A\lt90^{o})\) এবং একই দিকে আরো ঘুরে
\(\angle{YOZ}=B, \ (B\lt90^{o})\) কোণ উৎপন্ন করে।
\(\therefore \angle{XOZ}=\angle{XOY}+\angle{YOZ}\)
\(=A+B\)
ঘূর্ণায়মান রেখার শেষ অবস্থান \(OZ\) এর উপর \(P\) যে কোনো বিন্দু নিয়ে \(OX\) এবং \(OY\) রেখার উপর যথাক্রমে \(PQ\) এবং \(PR\) লম্ব অংকন করি। আবার \(R\) বিন্দু হতে \(OX\) এবং \(PQ\) রেখার উপর যথাক্রমে \(RS\) এবং \(RT\) লম্ব অংকন করি।
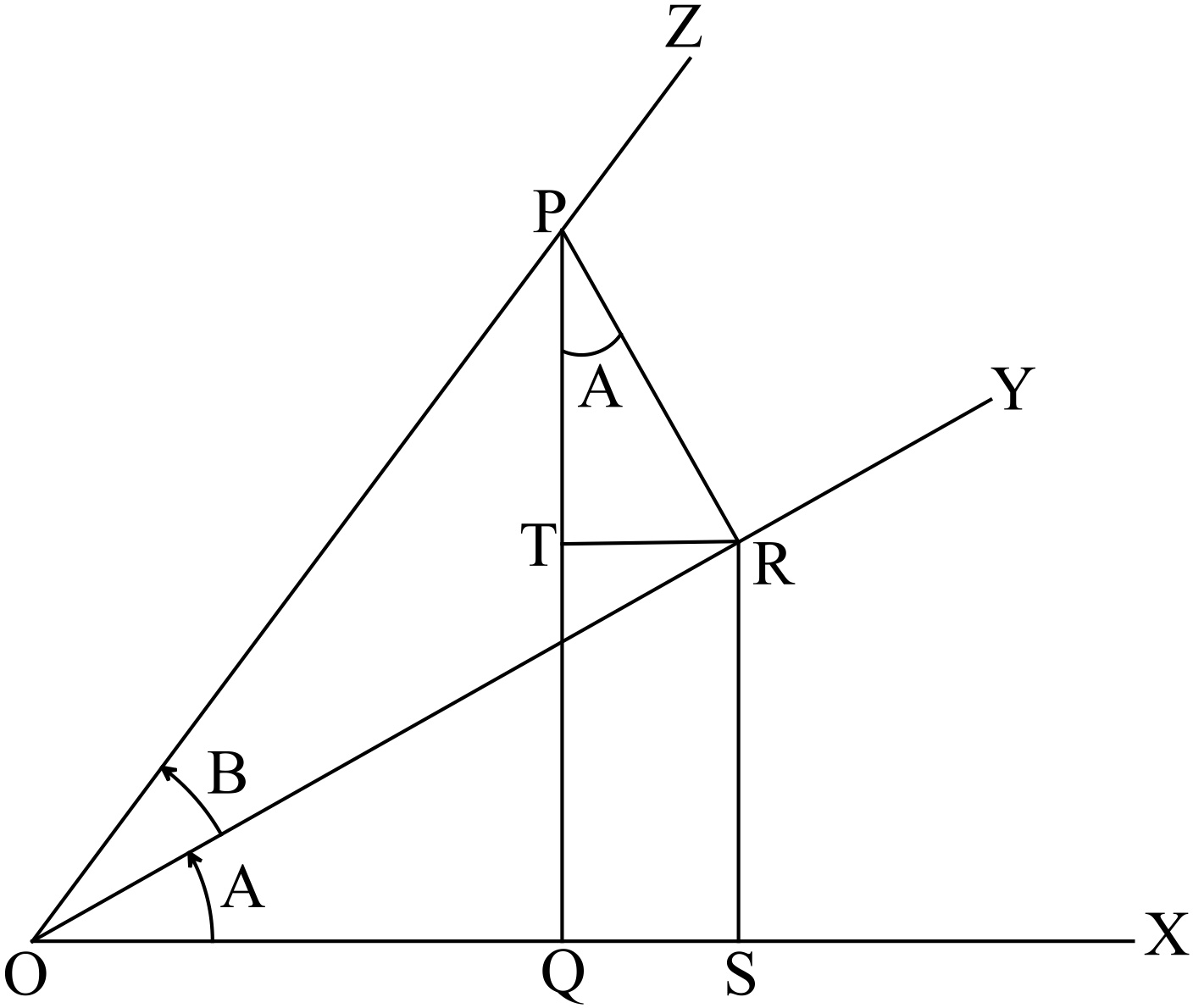
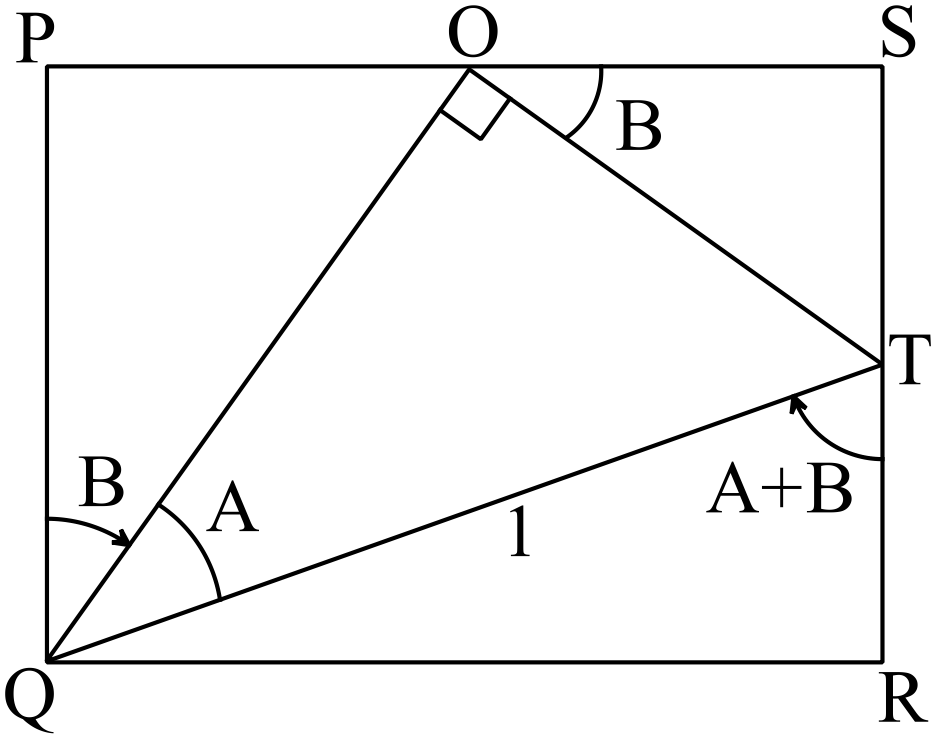
তাহলে \(QSRT\) একটি আয়তক্ষেত্র, straight3

যার \(RT=QS\) ও \(RS=TQ\)
আবার, \(TR||OX\)
\(OR\) উহাদের ছেদক।
\(\therefore \angle{TRO}=\text{একান্তর }\angle{XOY}=A\)
এখন \(\triangle{PTR}\) ত্রিভুজে
\(\angle{TPR}=90^{o}-\angle{PRT} \) ➜
\(=\angle{TRO} \)
\(=A\)
\(\therefore \angle{TPR}=A\)
\(\triangle{ROS} \)-এ
\(\sin{A}=\frac{RS}{OR}, \ \cos{A}=\frac{OS}{OR}\)
\(\triangle{POR} \)-এ
\(\sin{B}=\frac{PR}{OP}, \ \cos{B}=\frac{OR}{OP}\)
এবং \(\triangle{PTR}\)-এ
\(\sin{A}=\frac{TR}{PR}, \ \cos{A}=\frac{PT}{PR}\)
\(POQ \) সমকোণী ত্রিভুজ থেকে,
\(\angle{POQ}=A+B\)
\(\sin{(A+B)}=\frac{PQ}{OP}\)
\(=\frac{QT+TP}{OP}\)
\(=\frac{RS+TP}{OP}\) ➜
\(=\frac{RS}{OP}+\frac{TP}{OP}\)
\(=\frac{RS}{OR}\times\frac{OR}{OP}+\frac{TP}{PR}\times\frac{PR}{OP}\)
\(=\sin{A}\cos{B}+\cos{A}\sin{B}\) ➜
\(\therefore \sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
\(\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
আবার, \(\cos{(A+B)}=\frac{OQ}{OP}\)
\(=\frac{OS-QS}{OP}\)
\(=\frac{OS-TR}{OP}\) ➜
\(=\frac{OS}{OP}-\frac{TR}{OP}\)
\(=\frac{OS}{OR}\times\frac{OR}{OP}-\frac{TR}{PR}\times\frac{PR}{OP}\)
\(=\cos{A}\cos{B}-\sin{A}\sin{B}\) ➜
\(\therefore \cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)
\(\cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)

বিকল্প পদ্ধতিঃ

মনে করি, \(PQRS\) আয়তক্ষেত্রে \(TOQ\) সমকোণী ত্রিভুজ অবস্থিত,
যেখানে \(\angle{TOQ}=90^{o}\) straight3

\(\angle{OQT}=A, \ \angle{OQP}=B\)
এবং \(QT=1\) একক।
\(PQ=SR\) ও \(PS=QR\)
তাহলে, \(\angle{POQ}=90^{o}-B\)
\(\angle{SOT}=90^{o}-\angle{POQ}\)
\(=90^{o}-(90^{o}-B)\)
\(=90^{o}-90^{o}+B\)
\(=B\)
\(\therefore \angle{SOT}=B\)
\(\angle{TQR}=90^{o}-(A+B)\)
\(\angle{QTR}=90^{o}-\angle{TQR}\)
\(=90^{o}-\{90^{o}-(A+B)\}\)
\(=90^{o}-90^{o}+(A+B)\)
\(\therefore \angle{QTR}=A+B\)
এখন \(\sin{A}=\frac{OT}{QT}\)
\(\Rightarrow \sin{A}=\frac{OT}{1}\) ➜
\(\therefore OT=\sin{A}\)
আবার, \(\cos{A}=\frac{OQ}{QT}\)
\(\Rightarrow \cos{A}=\frac{OQ}{1}\) ➜
\(\therefore OQ=\cos{A}\)
\(OPQ\) সমকোণী ত্রিভুজ হতে,
\(\sin{B}=\frac{OP}{OQ}\)
\(\Rightarrow OP=OQ\sin{B}\)
\(\therefore OP=\cos{A}\sin{B}\) ➜
আবার, \(\cos{B}=\frac{PQ}{OQ}\)
\(\Rightarrow PQ=OQ\cos{B}\)
\(\therefore PQ=\cos{A}\cos{B}\) ➜
অনুরূপভাবে, \(OST\) সমকোণী ত্রিভুজ হতে,
\(OS=\sin{A}\cos{B}\)
এবং \(ST=\sin{A}\sin{B}\)
এখন \(TQR\) সমকোণী ত্রিভুজ হতে,
\(\sin{(A+B)}=\sin{QTR}\)
\(=\frac{QR}{QT}\)
\(=\frac{PS}{1}\) ➜
\(=PS\)
\(=OS+OP\)
\(=\sin{A}\cos{B}+\cos{A}\sin{B}\) ➜
\(\therefore \sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
\(\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
আবার, \(\cos{(A+B)}=\cos{QTR}\)
\(=\frac{TR}{QT}\)
\(=\frac{TR}{1}\) ➜
\(=TR\)
\(=RS-ST\)
\(=PQ-ST\) ➜
\(=\cos{A}\cos{B}-\sin{A}\sin{B}\) ➜
\(\therefore \cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)
\(\cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)

\(\sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)

\(\cos{(A-B)}=\cos{A}\cos{B}+\sin{A}\sin{B}\)

\(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B)\lt90^{o}\) ও \(A\gt B\)

\(\sin{(A-B)}=\sin{A}\cos{B}\)\(-\cos{A}\sin{B}\)
\(\cos{(A-B)}=\cos{A}\cos{B}\)\(+\sin{A}\sin{B}\)

প্রমাণঃ
মনে করি, কোনো ঘূর্ণায়মান রশ্মি আদি অবস্থান \(OX\) হতে \(O\) বিন্দুর সাপেক্ষে ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে \(\angle{XOY}=A, \ (A\lt90^{o})\) এবং \(OY\) অবস্থান থেকে ঘড়ির কাঁটার ঘূর্ণনের দিকে ঘুরে \(\angle{YOZ}=B, \ (B\lt90^{o})\) কোণ উৎপন্ন করে।
\(\therefore \angle{XOZ}=\angle{XOY}-\angle{YOZ}\)
\(=A-B\)
ঘূর্ণায়মান রেখার শেষ অবস্থান \(OZ\) এর উপর \(P\) যে কোনো বিন্দু নিয়ে \(OX\) এবং \(OY\) রেখার উপর যথাক্রমে \(PQ\) এবং \(PR\) লম্ব অংকন করি। আবার \(R\) বিন্দু হতে \(OX\) এবং \(PQ\) রেখার বর্ধিতাংশের উপর যথাক্রমে \(RS\) এবং \(RT\) লম্ব অংকন করি।
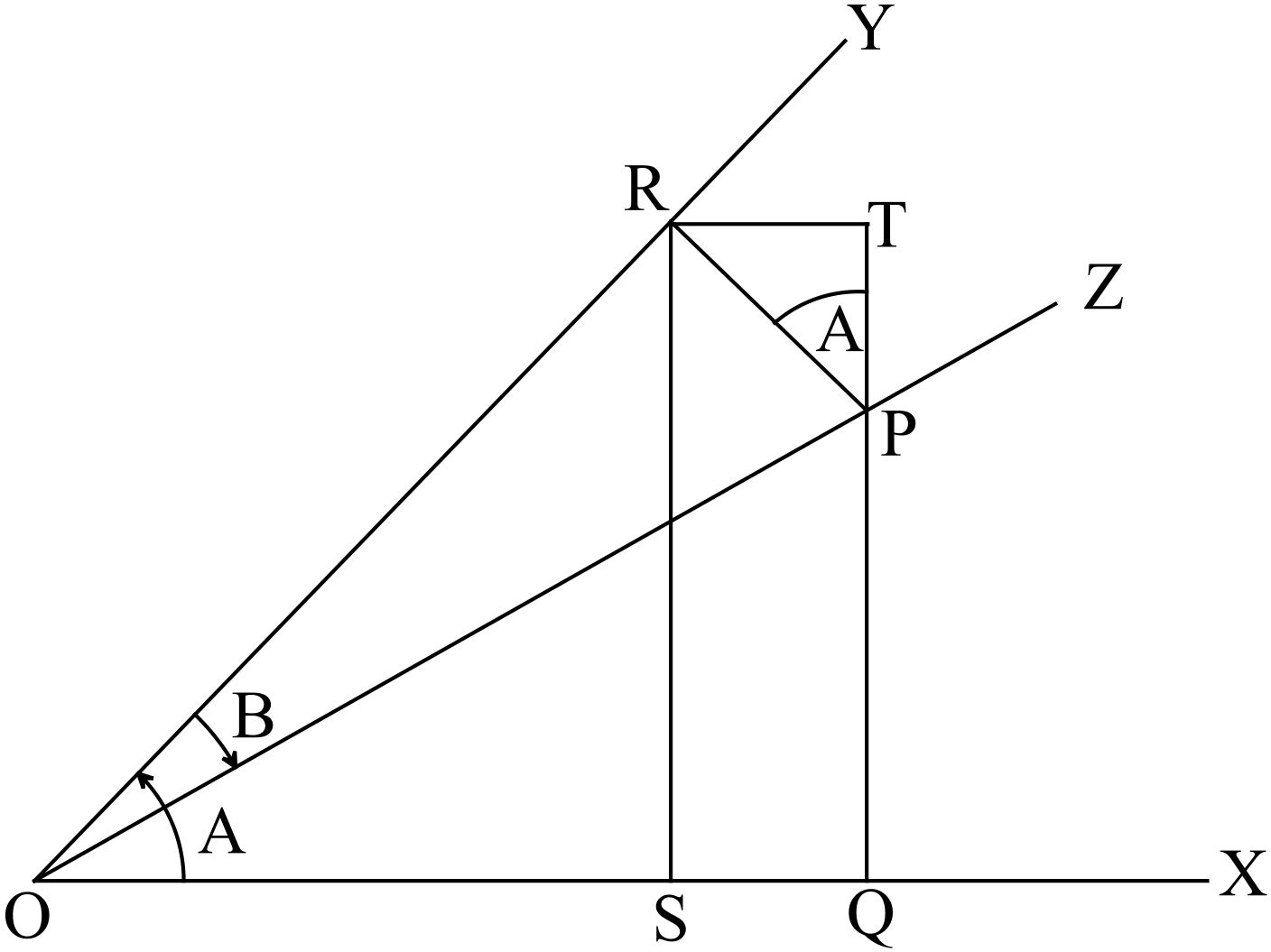
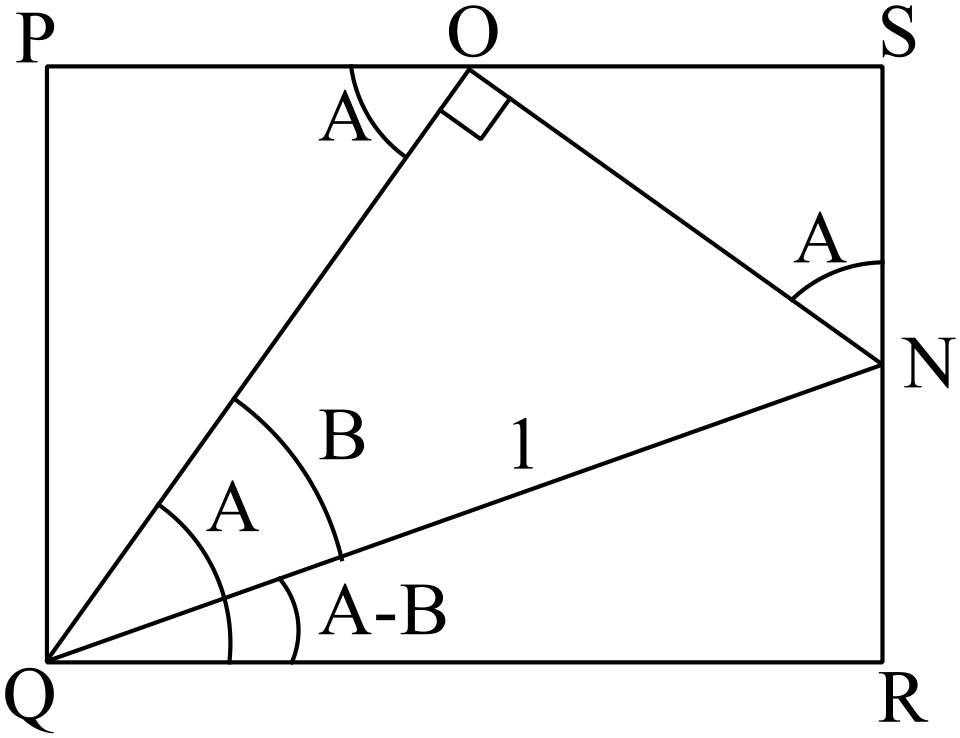
তাহলে \(QSRT\) একটি আয়তক্ষেত্র, straight3

যার \(RT=QS\) ও \(RS=TQ\)
আবার, \(TR||OX\)
\(OY\) উহাদের ছেদক।
\(\therefore \angle{YRT}=\text{অনুরূপ }\angle{XOY}=A\)
এখন \(\triangle{PTR}\) ত্রিভুজে
\(\angle{TPR}=90^{o}-\angle{PRT} \) ➜
\(=\angle{YRT} \)
\(=A\)
\(\therefore \angle{TPR}=A\)
\(\triangle{ROS} \)-এ
\(\sin{A}=\frac{RS}{OR}, \ \cos{A}=\frac{OS}{OR}\)
\(\triangle{POR} \)-এ
\(\sin{B}=\frac{PR}{OP}, \ \cos{B}=\frac{OR}{OP}\)
এবং \(\triangle{PTR}\)-এ
\(\sin{A}=\frac{TR}{PR}, \ \cos{A}=\frac{PT}{PR}\)
\(POQ \) সমকোণী ত্রিভুজ থেকে,
\(\angle{POQ}=A-B\)
\(\sin{(A-B)}=\frac{PQ}{OP}\)
\(=\frac{TQ-PT}{OP}\)
\(=\frac{RS-PT}{OP}\) ➜
\(=\frac{RS}{OP}-\frac{PT}{OP}\)
\(=\frac{RS}{OR}\times\frac{OR}{OP}-\frac{PT}{PR}\times\frac{PR}{OP}\)
\(=\sin{A}\cos{B}-\cos{A}\sin{B}\) ➜
\(\therefore \sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
\(\sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
আবার, \(\cos{(A-B)}=\frac{OQ}{OP}\)
\(=\frac{OS+QS}{OP}\)
\(=\frac{OS+TR}{OP}\) ➜
\(=\frac{OS}{OP}+\frac{TR}{OP}\)
\(=\frac{OS}{OR}\times\frac{OR}{OP}+\frac{TR}{PR}\times\frac{PR}{OP}\)
\(=\cos{A}\cos{B}+\sin{A}\sin{B}\) ➜
\(\therefore \cos{(A-B)}=\cos{A}\cos{B}+\sin{A}\sin{B}\)
\(\cos{(A-B)}=\cos{A}\cos{B}+\sin{A}\sin{B}\)

বিকল্প পদ্ধতিঃ

মনে করি, \(PQRS\) আয়তক্ষেত্রে \(NOQ\) সমকোণী ত্রিভুজ অবস্থিত,
যেখানে \(\angle{NOQ}=90^{o}\) straight3

\(\angle{OQN}=B, \ \angle{OQR}=A\)
\(\angle{POQ}=\text{একান্তর }\angle{OQR}=A\)
\(\therefore \angle{POQ}=A\)
\(\angle{ONS}=90^{o}-(90^{o}-A)\)
\(=90^{o}-90^{o}+A\)
\(\therefore \angle{ONS}=A\)
এবং \(QN=1\) একক।
\(PQ=SR\) ও \(PS=QR\)
\(\therefore \angle{NQR}=A-B\)
এখন \(\sin{B}=\frac{ON}{QN}\)
\(\Rightarrow \sin{A}=\frac{ON}{1}\) ➜
\(\therefore ON=\sin{B}\)
আবার, \(\cos{B}=\frac{OQ}{QN}\)
\(\Rightarrow \cos{B}=\frac{OQ}{1}\) ➜
\(\therefore OQ=\cos{B}\)
\(OPQ\) সমকোণী ত্রিভুজ হতে,
\(\cos{A}=\frac{OP}{OQ}\)
\(\Rightarrow OP=OQ\cos{A}\)
\(\therefore OP=\cos{A}\cos{B}\) ➜
আবার, \(\sin{A}=\frac{PQ}{OQ}\)
\(\Rightarrow PQ=OQ\sin{A}\)
\(\therefore PQ=\sin{A}\cos{B}\) ➜
\(\therefore SR=PQ=\sin{A}\cos{B}\)
অনুরূপভাবে, \(OSN\) সমকোণী ত্রিভুজ হতে,
\(OS=\sin{A}\sin{B}\)
এবং \(SN=\cos{A}\sin{B}\)
এখন \(NQR\) সমকোণী ত্রিভুজ হতে,
\(\sin{(A-B)}=\sin{NQR}\)
\(=\frac{NR}{NQ}\)
\(=\frac{NR}{1}\) ➜
\(=NR\)
\(=SR-SN\)
\(=\sin{A}\cos{B}-\cos{A}\sin{B}\) ➜
\(\therefore \sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
\(\sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
আবার, \(\cos{(A-B)}=\cos{NQR}\)
\(=\frac{QR}{QN}\)
\(=\frac{PS}{1}\) ➜
\(=PS\)
\(=OP+OS\)
\(=\cos{A}\cos{B}+\sin{A}\sin{B}\) ➜
\(\therefore \cos{(A-B)}=\cos{A}\cos{B}+\sin{A}\sin{B}\)
\(\cos{(A-B)}=\cos{A}\cos{B}+\sin{A}\sin{B}\)

\(\tan{(A+B)}=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\)

\(\tan{(A-B)}=\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\)

\(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B)\lt90^{o}\) ও \(A\gt B\)

\(\tan{(A+B)}=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\)
\(\tan{(A-B)}=\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\)

প্রমাণঃ
আমরা জানি,
\(\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
\(\cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)
এখন, \(\tan{(A+B)}=\frac{\sin{(A+B)}}{\cos{(A+B)}}\)
\(=\frac{\sin{A}\cos{B}+\cos{A}\sin{B}}{\cos{A}\cos{B}-\sin{A}\sin{B}}\) ➜
\(=\frac{\frac{\sin{A}\cos{B}}{\cos{A}\cos{B}}+\frac{\cos{A}\sin{B}}{\cos{A}\cos{B}}}{\frac{\cos{A}\cos{B}}{\cos{A}\cos{B}}-\frac{\sin{A}\sin{B}}{\cos{A}\cos{B}}}\) ➜
\(=\frac{\frac{\sin{A}}{\cos{A}}+\frac{\sin{B}}{\cos{B}}}{1-\frac{\sin{A}\sin{B}}{\cos{A}\cos{B}}}\)
\(=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\) ➜
\(\therefore \tan{(A+B)}=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\)
\(\tan{(A+B)}=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\)
আবার,
আমরা জানি,
\(\sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
\(\cos{(A-B)}=\cos{A}\cos{B}+\sin{A}\sin{B}\)
এখন, \(\tan{(A-B)}=\frac{\sin{(A-B)}}{\cos{(A-B)}}\)
\(=\frac{\sin{A}\cos{B}-\cos{A}\sin{B}}{\cos{A}\cos{B}+\sin{A}\sin{B}}\) ➜
\(=\frac{\frac{\sin{A}\cos{B}}{\cos{A}\cos{B}}-\frac{\cos{A}\sin{B}}{\cos{A}\cos{B}}}{\frac{\cos{A}\cos{B}}{\cos{A}\cos{B}}+\frac{\sin{A}\sin{B}}{\cos{A}\cos{B}}}\) ➜
\(=\frac{\frac{\sin{A}}{\cos{A}}-\frac{\sin{B}}{\cos{B}}}{1+\frac{\sin{A}\sin{B}}{\cos{A}\cos{B}}}\)
\(=\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\) ➜
\(\therefore \tan{(A-B)}=\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\)
\(\tan{(A-B)}=\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\)

\(\cot{(A+B)}=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\)

\(\cot{(A-B)}=\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\)

\(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B)\lt90^{o}\) ও \(A\gt B\)

\(\cot{(A+B)}=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\)
\(\cot{(A-B)}=\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\)

প্রমাণঃ
আমরা জানি,
\(\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
\(\cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)
এখন, \(\cot{(A+B)}=\frac{\cos{(A+B)}}{\sin{(A+B)}}\)
\(=\frac{\cos{A}\cos{B}-\sin{A}\sin{B}}{\sin{A}\cos{B}+\cos{A}\sin{B}}\) ➜
\(=\frac{\frac{\cos{A}\cos{B}}{\sin{A}\sin{B}}-\frac{\sin{A}\sin{B}}{\sin{A}\sin{B}}}{\frac{\sin{A}\cos{B}}{\sin{A}\sin{B}}+\frac{\cos{A}\sin{B}}{\sin{A}\sin{B}}}\) ➜
\(=\frac{\frac{\cos{A}\cos{B}}{\sin{A}\sin{B}}-1}{\frac{\cos{B}}{\sin{B}}+\frac{\cos{A}}{\sin{A}}}\)
\(=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\) ➜
\(\therefore \cot{(A+B)}=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\)
\(\cot{(A+B)}=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\)
আবার,
আমরা জানি,
\(\sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
\(\cos{(A-B)}=\cos{A}\cos{B}+\sin{A}\sin{B}\)
এখন, \(\cot{(A-B)}=\frac{\cos{(A-B)}}{\sin{(A-B)}}\)
\(=\frac{\cos{A}\cos{B}+\sin{A}\sin{B}}{\sin{A}\cos{B}-\cos{A}\sin{B}}\) ➜
\(=\frac{\frac{\cos{A}\cos{B}}{\sin{A}\sin{B}}+\frac{\sin{A}\sin{B}}{\sin{A}\sin{B}}}{\frac{\sin{A}\cos{B}}{\sin{A}\sin{B}}-\frac{\cos{A}\sin{B}}{\sin{A}\sin{B}}}\) ➜
\(=\frac{\frac{\cos{A}\cos{B}}{\sin{A}\sin{B}}+1}{\frac{\cos{B}}{\sin{B}}-\frac{\cos{A}}{\sin{A}}}\)
\(=\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\) ➜
\(\therefore \cot{(A-B)}=\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\)
\(\cot{(A-B)}=\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\)

\(\sin{(A+B)}\sin{(A-B)}\)\(=\sin^2{A}-\sin^2{B}=\cos^2{B}-\cos^2{A}\)

\(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B)\lt90^{o}\) ও \(A\gt B\)

\(\sin{(A+B)}\sin{(A-B)}\)\(=\sin^2{A}-\sin^2{B}=\cos^2{B}-\cos^2{A}\)

প্রমাণঃ
আমরা জানি,
\(\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
\(\sin{(A-B)}=\sin{A}\cos{B}-\cos{A}\sin{B}\)
এখন, \(\sin{(A+B)}\sin{(A-B)}=(\sin{A}\cos{B}+\cos{A}\sin{B})(\sin{A}\cos{B}-\cos{A}\sin{B})\)
\(=\sin^2{A}\cos^2{B}-\cos^2{A}\sin^2{B}\) ➜
\(=\sin^2{A}(1-\sin^2{B})-(1-\sin^2{A})\sin^2{B}\) ➜
\(=\sin^2{A}-\sin^2{A}\sin^2{B}-\sin^2{B}+\sin^2{A}\sin^2{B}\)
\(=\sin^2{A}-\sin^2{B}\)
\(\therefore \sin{(A+B)}\sin{(A-B)}=\sin^2{A}-\sin^2{B}\)
\(=1-\cos^2{A}-1+\cos^2{B}\) ➜
\(=-\cos^2{A}+\cos^2{B}\)
\(=\cos^2{B}-\cos^2{A}\)
\(\therefore \sin{(A+B)}\sin{(A-B)}=\cos^2{B}-\cos^2{A}\)
\(\sin{(A+B)}\sin{(A-B)}=\sin^2{A}-\sin^2{B}=\cos^2{B}-\cos^2{A}\)

\(\cos{(A+B)}\cos{(A-B)}\)\(=\cos^2{A}-\sin^2{B}=\cos^2{B}-\sin^2{A}\)

\(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B)\lt90^{o}\) ও \(A\gt B\)

\(\cos{(A+B)}\cos{(A-B)}\)\(=\cos^2{A}-\sin^2{B}=\cos^2{B}-\sin^2{A}\)

প্রমাণঃ
আমরা জানি,
\(\cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)
\(\cos{(A-B)}=\cos{A}\cos{B}+\sin{A}\sin{B}\)
এখন, \(\cos{(A+B)}\cos{(A-B)}=(\cos{A}\cos{B}-\sin{A}\sin{B})(\cos{A}\cos{B}+\sin{A}\sin{B})\)
\(=\cos^2{A}\cos^2{B}-\sin^2{A}\sin^2{B}\) ➜
\(=\cos^2{A}\cos^2{B}-(1-\cos^2{A})(1-\cos^2{B})\) ➜
\(=\cos^2{A}\cos^2{B}-(1-\cos^2{A}-\cos^2{B}+\cos^2{A}\cos^2{B})\)
\(=\cos^2{A}\cos^2{B}-1+\cos^2{A}+\cos^2{B}-\cos^2{A}\cos^2{B}\)
\(=-1+\cos^2{A}+\cos^2{B}\)
\(=\cos^2{A}-(1-\cos^2{B})\)
\(=\cos^2{A}-\sin^2{B}\) ➜
\(\therefore \cos{(A+B)}\cos{(A-B)}=\cos^2{A}-\sin^2{B}\)
\(=1-\sin^2{A}-(1-\cos^2{B})\) ➜
\(=1-\sin^2{A}-1+\cos^2{B}\)
\(=-\sin^2{A}+\cos^2{B}\)
\(=\cos^2{B}-\sin^2{A}\)
\(\therefore \cos{(A+B)}\cos{(A-B)}=\cos^2{B}-\sin^2{A}\)
\(\cos{(A+B)}\cos{(A-B)}=\cos^2{A}-\sin^2{B}=\cos^2{B}-\sin^2{A}\)

\(\tan{(A+B)}\tan{(A-B)}=\frac{\tan^2{A}-\tan^2{B}}{1-\tan^2{A}\tan^2{B}}\)

\(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B)\lt90^{o}\) ও \(A\gt B\)

\(\tan{(A+B)}\tan{(A-B)}=\frac{\tan^2{A}-\tan^2{B}}{1-\tan^2{A}\tan^2{B}}\)

প্রমাণঃ
আমরা জানি,
\(\tan{(A+B)}=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\)
\(\tan{(A-B)}=\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\)
এখন, \(\tan{(A+B)}\tan{(A-B)}=\frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}}\times\frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}}\)
\(=\frac{(\tan{A}+\tan{B})(\tan{A}-\tan{B})}{(1-\tan{A}\tan{B})(1+\tan{A}\tan{B})}\)
\(=\frac{\tan^2{A}-\tan^2{B}}{1-\tan^2{A}\tan^2{B}}\) ➜
\(\therefore \tan{(A+B)}\tan{(A-B)}=\frac{\tan^2{A}-\tan^2{B}}{1-\tan^2{A}\tan^2{B}}\)
\(\tan{(A+B)}\tan{(A-B)}=\frac{\tan^2{A}-\tan^2{B}}{1-\tan^2{A}\tan^2{B}}\)

\(\cot{(A+B)}\cot{(A-B)}=\frac{\cot^2{A}\cot^2{B}-1}{\cot^2{B}-\cot^2{A}}\)

\(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B)\lt90^{o}\) ও \(A\gt B\)

\(\cot{(A+B)}\cot{(A-B)}=\frac{\cot^2{A}\cot^2{B}-1}{\cot^2{B}-\cot^2{A}}\)

প্রমাণঃ
আমরা জানি,
\(\cot{(A+B)}=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\)
\(\cot{(A-B)}=\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\)
এখন, \(\cot{(A+B)}\cot{(A-B)}=\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\times\frac{\cot{A}\cot{B}+1}{\cot{B}-\cot{A}}\)
\(=\frac{(\cot{A}\cot{B}-1)(\cot{A}\cot{B}+1)}{(\cot{B}+\cot{A})(\cot{B}-\cot{A})}\)
\(=\frac{\cot^2{A}\cot^2{B}-1}{\cot^2{B}-\cot^2{A}}\) ➜
\(\therefore \cot{(A+B)}\cot{(A-B)}=\frac{\cot^2{A}\cot^2{B}-1}{\cot^2{B}-\cot^2{A}}\)
\(\cot{(A+B)}\cot{(A-B)}=\frac{\cot^2{A}\cot^2{B}-1}{\cot^2{B}-\cot^2{A}}\)

\(\sin{(A+B+C)}=\cos{A}\cos{B}\cos{C}(\tan{A}\)\(+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C})\)

\(A, \ B\) ও \(C\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B+C)\lt90^{o}\)

\(\sin{(A+B+C)}=\cos{A}\cos{B}\cos{C}(\tan{A}\)\(+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C})\)

প্রমাণঃ
আমরা জানি,
\(\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
\(\cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)
এখন, \(\sin{(A+B+C)}=\sin{\{(A+B)+C\}}\)
\(=\sin{(A+B)}\cos{C}+\cos{(A+B)}\sin{C}\)
\(=(\sin{A}\cos{B}+\cos{A}\sin{B})\cos{C}+(\cos{A}\cos{B}-\sin{A}\sin{B})\sin{C}\) ➜
\(=\sin{A}\cos{B}\cos{C}+\cos{A}\sin{B}\cos{C}+\cos{A}\cos{B}\sin{C}-\sin{A}\sin{B}\sin{C}\)
\(=\cos{A}\cos{B}\cos{C}\left(\frac{\sin{A}}{\cos{A}}+\frac{\sin{B}}{\cos{B}}+\frac{\sin{C}}{\cos{C}}-\frac{\sin{A}\sin{B}\sin{C}}{\cos{A}\cos{B}\cos{C}}\right)\)
\(=\cos{A}\cos{B}\cos{C}(\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C})\) ➜
\(\therefore \sin{(A+B+C)}=\cos{A}\cos{B}\cos{C}(\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C})\)
\(\sin{(A+B+C)}=\cos{A}\cos{B}\cos{C}(\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C})\)

\(\cos{(A+B+C)}=\cos{A}\cos{B}\cos{C}(1-\)\(\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A})\)

\(A, \ B\) ও \(C\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B+C)\lt90^{o}\)

\(\cos{(A+B+C)}=\cos{A}\cos{B}\cos{C}(1-\)\(\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A})\)

প্রমাণঃ
আমরা জানি,
\(\cos{(A+B)}=\cos{A}\cos{B}-\sin{A}\sin{B}\)
\(\sin{(A+B)}=\sin{A}\cos{B}+\cos{A}\sin{B}\)
এখন, \(\cos{(A+B+C)}=\cos{\{(A+B)+C\}}\)
\(=\cos{(A+B)}\cos{C}-\sin{(A+B)}\sin{C}\)
\(=(\cos{A}\cos{B}-\sin{A}\sin{B})\cos{C}+(\sin{A}\cos{B}+\cos{A}\sin{B})\sin{C}\) ➜
\(=\cos{A}\cos{B}\cos{C}-\sin{A}\sin{B}\cos{C}+\sin{A}\cos{B}\sin{C}+\cos{A}\sin{B}\sin{C}\)
\(=\cos{A}\cos{B}\cos{C}\left(1-\frac{\sin{A}\sin{B}}{\cos{A}\cos{B}}-\frac{\sin{B}\sin{C}}{\cos{B}\cos{C}}-\frac{\sin{C}\sin{A}}{\cos{C}\cos{A}}\right)\)
\(=\cos{A}\cos{B}\cos{C}(1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A})\) ➜
\(\therefore \cos{(A+B+C)}=\cos{A}\cos{B}\cos{C}(1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A})\)
\(\cos{(A+B+C)}=\cos{A}\cos{B}\cos{C}(1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A})\)

\(\tan{(A+B+C)}=\frac{\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C}}{1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A}}\)

\(A, \ B\) ও \(C\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B+C)\lt90^{o}\)

\(\tan{(A+B+C)}=\frac{\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C}}{1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A}}\)

প্রমাণঃ
আমরা জানি,
\(\sin{(A+B+C)}=\cos{A}\cos{B}\cos{C}(\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C})\)
\(\cos{(A+B+C)}=\cos{A}\cos{B}\cos{C}(1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A})\)
এখন, \(\tan{(A+B+C)}=\frac{\sin{(A+B+C)}}{\cos{(A+B+C)}}\)
\(=\frac{\cos{A}\cos{B}\cos{C}(\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C})}{\cos{A}\cos{B}\cos{C}(1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A})}\)
\(=\frac{\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C}}{1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A}}\)
\(\therefore \tan{(A+B+C)}=\frac{\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C}}{1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A}}\)
\(\tan{(A+B+C)}=\frac{\tan{A}+\tan{B}+\tan{C}-\tan{A}\tan{B}\tan{C}}{1-\tan{A}\tan{B}-\tan{B}\tan{C}-\tan{C}\tan{A}}\)

\(\cot{(A+B+C)}=\frac{\cot{A}\cot{B}\cot{C}-\cot{A}-\cot{B}-\cot{C}}{\cot{B}\cot{C}+\cot{C}\cot{A}+\cot{A}\cot{B}-1}\)

\(A, \ B\) ও \(C\) ধনাত্মক সূক্ষ্ণকোণ এবং \((A+B+C)\lt90^{o}\)

\(\cot{(A+B+C)}=\frac{\cot{A}\cot{B}\cot{C}-\cot{A}-\cot{B}-\cot{C}}{\cot{B}\cot{C}+\cot{C}\cot{A}+\cot{A}\cot{B}-1}\)

প্রমাণঃ
লেখা যায়,
\(\cot{(A+B+C)}=\cot{\{(A+B)+C\}}\)
\(=\frac{\cot{(A+B)}\cot{C}-1}{\cot{C}+\cot{(A+B)}}\) ➜ \(\because \cot{(P+Q)}=\frac{\cot{P}\cot{Q}-1}{\cot{Q}+\cot{P}}\)

\(=\frac{\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}\cot{C}-1}{\cot{C}+\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}}\) ➜ \(\because \cot{(P+Q)}=\frac{\cot{P}\cot{Q}-1}{\cot{Q}+\cot{P}}\)

\(=\frac{\frac{\cot{A}\cot{B}\cot{C}-\cot{C}}{\cot{B}+\cot{A}}-1}{\cot{C}+\frac{\cot{A}\cot{B}-1}{\cot{B}+\cot{A}}}\)
\(=\frac{\cot{A}\cot{B}\cot{C}-\cot{C}-\cot{B}-\cot{A}}{\cot{B}\cot{C}+\cot{C}\cot{A}+\cot{A}\cot{B}-1}\) ➜ লব ও হরকে \((\cot{B}+\cot{A})\) দ্বারা গুণ করে।

\(\therefore \cot{(A+B+C)}=\frac{\cot{A}\cot{B}\cot{C}-\cot{A}-\cot{B}-\cot{C}}{\cot{B}\cot{C}+\cot{C}\cot{A}+\cot{A}\cot{B}-1}\)

\(\cot{(A+B+C)}=\frac{\cot{A}\cot{B}\cot{C}-\cot{A}-\cot{B}-\cot{C}}{\cot{B}\cot{C}+\cot{C}\cot{A}+\cot{A}\cot{B}-1}\)

উদাহরণসমুহ

\(Ex.1.\) মান নির্ণয় করঃ
\(\sin{28^{o}32^{\prime}}\sin{88^{o}32^{\prime}}+\sin{61^{o}28^{\prime}}\sin{1^{o}28^{\prime}}\)
উত্তরঃ \(\frac{1}{2}\)

\(Ex.2.\) দেখাও যে, \(\tan{36^{o}}+\tan{9^{o}}+\tan{36^{o}}\tan{9^{o}}=1\)
কুয়েটঃ২০০৪-২০০৫; বঃ২০০৪ ।

\(Ex.3.\) মান নির্ণয় কর, \(\sin{15^{o}}\)
উত্তরঃ \(\frac{\sqrt{3}-1}{2\sqrt{2}}\)
কুঃ ২০০৫ ।

\(Ex.4.\) যদি \(A+B+C=\pi\) এবং \(\cos{A}=\cos{B}\cos{C}\) হয়, তবে প্রমাণ কর যে,
\((a)\) \(\tan{A}=\tan{B}+\tan{C};\)
কুঃ২০১৭, ২০১৩; রাঃ২০১৪; বঃ২০১৩; দিঃ২০১৩ ।
\((b)\) \(\tan{B}\tan{C}=2;\)
যঃ২০০৯, ২০০৩; বঃ২০০৫ ।

\(Ex.5.\) মান নির্ণয় কর, \(\sin{75^{o}}\)
উত্তরঃ \(\frac{1}{4}(\sqrt{6}+\sqrt{2})\)

\(Ex.6.\) \(A=\frac{a\cos{x}-b\cos{y}}{a\sin{x}+b\sin{y}}\) এবং \(B=\tan{54^{o}}\)
\((a)\) প্রমাণ কর যে, \(cosec \ {(x-y)}=\frac{\sec{x}\sec{y}}{\tan{x}-\tan{y}}.\)
বিআইটিঃ ১৯৯৫-১৯৯৬ ।
\((b)\) প্রমাণ কর যে, \(B=\tan{36^{o}}+2\tan{18^{o}}.\)
চুয়েটঃ ২০০৪-২০০৫ ।
\((c)\) \(\cot{\theta}=A\) হলে দেখাও যে, \(\frac{\sin{(\theta-x)}}{\sin{(\theta+y)}}=\frac{b}{a}.\)
ঢাঃ ২০০৫ ।

\(Ex.7.\) প্রমাণ কর যে, \(\cos{A}\sin{(B-C)}+\cos{B}\sin{(C-A)}\)\(+\cos{C}\sin{(A-B)}=0\)

\(Ex.8.\) দেখাও যে, \(\cot{\theta}-\cot{2\theta}=cosec \ {2\theta}\)

Read Example

Q.1-এর সংক্ষিপ্ত প্রশ্নসমূহ

মান নির্ণয় কর

\(Q.1.(a)\) \(\cos{15^{o}}\)
উত্তরঃ \(\frac{\sqrt{3}+1}{2\sqrt{2}}\)

মান নির্ণয় কর

\(Q.1.(b)\) \(\sin{105^{o}}\)
উত্তরঃ \(\frac{\sqrt{6}+\sqrt{2}}{4}\)

\(Q.1.(c)\) \(cosec \ {375^{o}}\)
উত্তরঃ \(\sqrt{6}+\sqrt{2}\)

\(Q.1.(d)\) \(\cos{75^{o}};\)
উত্তরঃ \(\frac{\sqrt{3}-1}{2\sqrt{2}}\)
রাঃ ২০১৯ ।

\(Q.1.(e)\) \(\tan{15^{o}}\)
উত্তরঃ \(2-\sqrt{3}\)

\(Q.1.(f)\) \(\sec{165^{o}}\)
উত্তরঃ \(-\frac{4}{\sqrt{6}+\sqrt{2}}\)

\(Q.1.(g)\) \(\tan{105^{o}}\)
উত্তরঃ \(-(2+\sqrt{3})\)

\(Q.1.(h)\) \(cosec \ {165^{o}}\)
উত্তরঃ \(\sqrt{6}+\sqrt{3}\)

\(Q.1.(i)\) \(\cot{165^{o}}\)
উত্তরঃ \(-(2+\sqrt{3})\)

মান নির্ণয় কর

\(Q.1.(ii)\) \(\cos{17^{o}40^{\prime}}\sin{77^{o}40^{\prime}}+\cos{107^{o}40^{\prime}}\sin{12^{o}20^{\prime}}\)
উত্তরঃ \(\frac{\sqrt{3}}{2}\)

মান নির্ণয় কর

\(Q.1.(iii)\) \(\sin{78^{o}19^{\prime}}\cos{18^{o}19^{\prime}}-\sin{11^{o}41^{\prime}}\sin{18^{o}19^{\prime}}\)
উত্তরঃ \(\sqrt{\frac{3}{2}}\)
চঃ ২০১৯ ।

\(Q.1.(iv)\) \(\cos{30^{o}32^{\prime}}\cos{29^{o}28^{\prime}}-\sin{149^{o}28^{\prime}}\sin{29^{o}28^{\prime}}\)
উত্তরঃ \(\frac{1}{2}\)
যঃ ২০১৯ ।

\(Q.1.(v)\) \(\cos{74^{o}33^{\prime}}\cos{14^{o}33^{\prime}}+\cos{75^{o}27^{\prime}}\cos{15^{o}27^{\prime}}\)
উত্তরঃ \(\frac{1}{2}\)

\(Q.1.(vi)\) \(\cos{38^{o}15^{\prime}}\sin{68^{o}15^{\prime}}-\cos{51^{o}45^{\prime}}\sin{21^{o}45^{\prime}}\)
উত্তরঃ \(\frac{1}{2}\)

\(Q.1.(vii)\) \(\cos{69^{o}22^{\prime}}\cos{9^{o}22^{\prime}}+\cos{80^{o}38^{\prime}}\cos{20^{o}38^{\prime}}\)
উত্তরঃ \(\frac{1}{2}\)

\(Q.1.(viii)\) \(\sin{76^{o}40^{\prime}}\cos{16^{o}40^{\prime}}-\cos{73^{o}20^{\prime}}\sin{13^{o}20^{\prime}}\)
উত্তরঃ \(\frac{\sqrt{3}}{2}\)

\(Q.1.(ix)\) \(\cos{36^{o}25^{\prime}}\sin{66^{o}25^{\prime}}-\cos{53^{o}35^{\prime}}\sin{23^{o}35^{\prime}}\)
উত্তরঃ \(\frac{1}{2}\)

মান নির্ণয় কর

\(Q.1.(x)\) \(\frac{\tan{65^{o}35^{\prime}}-\cot{69^{o}25^{\prime}}}{1+\tan{65^{o}35^{\prime}}\cot{69^{o}25^{\prime}}}\)
উত্তরঃ \(1\)

মান নির্ণয় কর

\(Q.1.(xi)\) \(\frac{\tan{68^{o}35^{\prime}}-\cot{66^{o}25^{\prime}}}{1+\tan{68^{o}35^{\prime}}\cot{66^{o}25^{\prime}}}\)
উত্তরঃ \(1\)

\(Q.1.(xii)\) \(\frac{\tan{73^{o}23^{\prime}}-\cot{76^{o}37^{\prime}}}{1+\tan{73^{o}23^{\prime}}\cot{76^{o}37^{\prime}}}\)
উত্তরঃ \(\sqrt{3}\)

প্রমাণ কর

\(Q.1.(xiii)\) \(\tan{75^{o}}=2+\sqrt{3}\)

প্রমাণ কর

\(Q.1.(xiv)\) \(\cos{68^{o}20^{\prime}}\cos{8^{o}20^{\prime}}+\cos{18^{o}40^{\prime}}\cos{21^{o}40^{\prime}}=\frac{1}{2}\)

\(Q.1.(xv)\) \(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \(\cos{A}=\frac{4}{5},\sin{B}=\frac{5}{13}\) হলে, \(\sin{(A-B)}\) ও \(\cos{(A+B)}\) এর মান নির্ণয় কর।
উত্তরঃ \(\frac{16}{65}, \frac{33}{65}\)

\(Q.1.(xvi)\) \(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \(\tan{A}=\frac{2}{11},\tan{B}=\frac{7}{24}\) হলে, \(\cot{(A-B)}\) ও \(\tan{(A+B)}\) এর মান নির্ণয় কর।
উত্তরঃ \(-\frac{278}{29}, \frac{1}{2}\)

\(Q.1.(xvii)\) \(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \(\sin{A}=\frac{3}{5},\cos{B}=\frac{12}{13}\) হলে, \(\sin{(A-B)}\) ও \(\cos{(A+B)}\) এর মান নির্ণয় কর।
উত্তরঃ \(\frac{16}{65}, \frac{33}{65}\)

\(Q.1.(xviii)\) \(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \(\cot{A}=\frac{11}{2},\tan{B}=\frac{7}{24}\) হলে, \(\cot{(A-B)}\) ও \(\tan{(A+B)}\) এর মান নির্ণয় কর।
উত্তরঃ \(-\frac{278}{29}, \frac{1}{2}\)

\(Q.1.(xix)\) \(A\) ও \(B\) ধনাত্মক সূক্ষ্ণকোণ এবং \(\sec{A}=\frac{17}{8},\ cosec \ {B}=\frac{5}{4}\) হলে, \(\sec{(A+B)}\) এর মান নির্ণয় কর।
উত্তরঃ \(-\frac{85}{36}\)

\(Q.1.(xx)\) \(\tan{A}\tan{B}=1\) হলে, \((A+B)\) এর মান কত?
উত্তরঃ \(\frac{\pi}{2}\)

\(Q.1.(xxi)\) \(\triangle{ABC}\)-এ \(A+B=105^{o}\) হলে, \(\sin{C}\) এর মান নির্ণয় কর।
উত্তরঃ \(\frac{\sqrt{3}+1}{2\sqrt{2}}\)

\(Q.1.(xxii)\) \(\sin{(A-B-C)}\) এবং \(\cos{(A-B+C)}\) কে বিস্তৃত কর।
উত্তরঃ \(\cos{A}\cos{B}\cos{C}(\tan{A}-\tan{B}-\tan{C}\)\(-\tan{A}\tan{B}\tan{C}),\)
\(\cos{A}\cos{B}\cos{C}(1+\tan{A}\tan{B}+\tan{B}\tan{C}\)\(-\tan{C}\tan{A})\)

\(Q.1.(xxiii)\) \(\cot{(A+B+C)}\) কে \(\cot{A}, \ \cot{B}, \ \cot{C}\) পদে প্রকাশ কর।
উত্তরঃ \(\frac{\cot{A}\cot{B}\cot{C}-\cot{A}-\cot{B}-\cot{C}}{\cot{B}\cot{C}+\cot{C}\cot{A}+\cot{A}\cot{B}-1}\)

Read Short Question

Q.2-এর বর্ণনামূলক প্রশ্নসমূহ

প্রমাণ কর

\(Q.2.(i)\) \(\cos{(x-60^{o})}\cos{(x-30^{o})}\)\(-\sin{(x-60^{o})}\sin{(x+330^{o})}=\sin{2x}\)

প্রমাণ কর

\(Q.2.(ii)\) \(\sin{x}\sin{(x+30^{o})}+\cos{x}\sin{(x+120^{o})}=\frac{\sqrt{3}}{2}\)
কুয়েটঃ ২০০৭-২০০৮ ।

\(Q.2.(iii)\) \(\cos{A}+\cos{(120^{o}-A)}+\cos{(120^{o}+A)}=0\)

\(Q.2.(iv)\) \(\frac{\sin{(B-C)}}{\cos{B}\cos{C}}+\frac{\sin{(C-A)}}{\cos{C}\cos{A}}+\frac{\sin{(A-B)}}{\cos{A}\cos{B}}=0\)

\(Q.2.(v)\) \(\frac{\cos{(45^{o}+A)}+\cos{(45^{o}-A)}}{\cos{(45^{o}-A)}-\cos{(45^{o}+A)}}=\cot{A}\)

\(Q.2.(vi)\) \(\frac{\tan{\left(\frac{\pi}{4}+\theta\right)}-\tan{\left(\frac{\pi}{4}-\theta\right)}}{\tan{\left(\frac{\pi}{4}+\theta\right)}+\tan{\left(\frac{\pi}{4}-\theta\right)}}=\sin{2A}\)

\(Q.2.(vii)\) \(2\sin{\left(\frac{\pi}{4}+A\right)}\cos{\left(\frac{\pi}{4}+B\right)}=\cos{(A+B)}\)\(+\sin{(A-B)}\)

\(Q.2.(viii)\) \(\tan{\left(\alpha+\frac{\pi}{3}\right)}+\tan{\left(\alpha-\frac{\pi}{3}\right)}=\frac{4\sin{2\alpha}}{1-4\sin^2{\alpha}}\)
সিঃ ২০১৩ ।

\(Q.2.(ix)\) \(\cot{(A+B)}+\cot{(A-B)}=\frac{\sin{2A}}{\sin^2{A}-\sin^2{B}}\)

\(Q.2.(x)\) \(\tan{70^{o}}=\tan{20^{o}}+2\tan{50^{o}}\)
রাঃ,কুঃ,চঃ,বঃ ২০১৮; ঢাঃ ২০১৫,২০১০; বঃ ২০০৬; চঃ ২০০৫; বুয়েটঃ ২০০৩-২০০৪ ।

\(Q.2.(xi)\) \(\tan{54^{o}}=\tan{36^{o}}+2\tan{18^{o}}\)

\(Q.2.(xii)\) \(\tan{\frac{\pi}{20}}+\tan{\frac{\pi}{5}}+\tan{\frac{\pi}{20}}\tan{\frac{\pi}{5}}=1\)

\(Q.2.(xiii)\) \(\tan{5A}\tan{3A}\tan{2A}=\tan{5A}-\tan{3A}\)\(-\tan{2A}\)

\(Q.2.(xiv)\) \(\sin{(n+1)\theta}\sin{(n-1)\theta}\)\(+\cos{(n+1)\theta}\cos{(n-1)\theta}=\cos{2\theta}\)

\(Q.2.(xv)\) \(\tan{20^{o}}+\tan{25^{o}}+\tan{20^{o}}\tan{25^{o}}=1\)

\(Q.2.(xvi)\) \(\tan{65^{o}}=\tan{25^{o}}+2\tan{40^{o}}\)

\(Q.2.(xvii)\) \(\tan{3\theta}-\tan{2\theta}-\tan{\theta}=\tan{3\theta}\tan{2\theta}\tan{\theta}\)

\(Q.2.(xviii)\) \(\tan{(A+60^{o})}+\tan{(A-60^{o})}=\frac{4\sin{2A}}{1-4\sin^2{A}}\)

\(Q.2.(xix)\) \(\sin{(25^{o}+A)}\cos{(25^{o}-A)}\)\(+\cos{(25^{o}+A)}\cos{(115^{o}-A)}=\sin{2A}\)

\(Q.2.(xx)\) \(\sin{A}\sin{(B-C)}+\sin{B}\sin{(C-A)}\)\(+\sin{C}\sin{(A-B)}=0\)

\(Q.2.(xxi)\) \(\sin{(B+C)}\sin{(B-C)}\)\(+\sin{(C+A)}\sin{(C-A)}+\sin{(A+B)}\sin{(A-B)}=0\)

\(Q.2.(xxii)\) \(\sin{(135^{o}-A)}+\cos{(135^{o}+A)}=0\)

Read Board Question2

Q.3-এর বর্ণনামূলক প্রশ্নসমূহ

প্রমাণ কর

\(Q.3.(i)\) \(\tan{(B-C)}+\tan{(C-A)}+\tan{(A-B)}\)\(=\tan{(B-C)}\tan{(C-A)}\tan{(A-B)}\)

প্রমাণ কর

\(Q.3.(ii)\) \(\tan{(A+B)}\tan{(A-B)}=\frac{\sin^2{A}-\sin^2{B}}{\cos^2{A}-\sin^2{B}}\)

\(Q.3.(iii)\) \(\cos{(A-B)}\cos{(A-C)}\)\(+\sin{(A-B)}\sin{(A-C)}=\cos{(B-C)}\)

\(Q.3.(iv)\) \(\frac{\cot{(3A-B)}\cot{B}-1}{-\cot{B}-\cot{(3A-B)}}=-\cot{3A}\)

\(Q.3.(v)\) \(\cos{A}+\cos{\left(\frac{2\pi}{3}-A\right)}+\cos{\left(\frac{2\pi}{3}+A\right)}=0\)

\(Q.3.(vi)\) \(\tan{32^{o}}+\tan{13^{o}}+\tan{32^{o}}\tan{13^{o}}=1\)

\(Q.3.(vii)\) \(\tan{50^{o}}=\tan{40^{o}}+2\tan{10^{o}}\)

\(Q.3.(viii)\) \(\tan{(45^{o}+A)}\tan{(45^{o}-A)}=1\)

\(Q.3.(ix)\) \(\cos^2{(A-B)}-\sin^2{(A+B)}=\cos{2A}\cos{2B}\)

\(Q.3.(x)\) \(\cos{\left(\frac{\pi}{3}-\alpha\right)}\cos{\left(\frac{\pi}{6}-\beta\right)}\)\(-\sin{\left(\frac{\pi}{3}-\alpha\right)}\sin{\left(\frac{\pi}{6}-\beta\right)}=\sin{(\alpha+\beta)}\)

\(Q.3.(xi)\) \(\cos{x}\sin{(y-z)}+\cos{y}\sin{(z-x)}\)\(+\cos{z}\sin{(x-y)}=0\)

\(Q.3.(xii)\) \(\frac{\tan{(3\theta-2\phi)}+\tan{2\phi}}{1-\tan{(3\theta-2\phi)}\tan{2\phi}}=\tan{3\theta}\)

\(Q.3.(xiii)\) \(1+\tan{2A}\tan{A}=\sec{2A}\)

\(Q.3.(xiv)\) \(\sin{2\theta}\cos{\theta}+\cos{2\theta}\sin{\theta}=\sin{4\theta}\cos{\theta}\)\(-\cos{4\theta}\sin{\theta}\)

\(Q.3.(xv)\) \(\frac{\cos{8^{o}}+\sin{8^{o}}}{\cos{8^{o}}-\sin{8^{o}}}=\tan{53^{o}}\)

\(Q.3.(xvi)\) \(\frac{\cos{25^{o}}+\sin{25^{o}}}{\cos{25^{o}}-\sin{25^{o}}}=\cot{20^{o}}\)
রুয়েটঃ ২০১০-২০১১ ।

\(Q.3.(xvii)\) \(\frac{\sin{75^{o}}+\sin{15^{o}}}{\sin{75^{o}}-\sin{15^{o}}}=\sqrt{3}\)
মাঃ ২০১০ ।

\(Q.3.(xviii)\) \(\frac{\cos{75^{o}}+\cos{15^{o}}}{\cos{75^{o}}-\cos{15^{o}}}=-\sqrt{3}\)
চঃ ২০১০ ।

\(Q.3.(xix)\) \(\frac{\cos{27^{o}}-\cos{63^{o}}}{\cos{27^{o}}+\cos{63^{o}}}=\tan{18^{o}}\)

\(Q.3.(xx)\) \(\frac{\cos{10^{o}}-\sin{10^{o}}}{\cos{10^{o}}+\sin{10^{o}}}=\tan{35^{o}}\)

Read Board Question3

Q.4-এর বর্ণনামূলক প্রশ্নসমূহ

\(Q.4.(i)\) যদি \(\cot{\alpha}+\cot{\beta}=a, \ \tan{\alpha}+\tan{\beta}=b\) এবং \(\alpha+\beta=\theta\) হয়, তবে প্রমাণ কর যে, \(\tan{\theta}=\frac{ab}{a-b}\)
ঢাঃ২০১১; রাঃ২০১৫; দিঃ২০১৬; চঃ২০১৬,২০১২; বঃ২০০৮; কুয়েটঃ২০১২-২০১৩ ।

\(Q.4.(ii)\) যদি \(\tan{\alpha}-\tan{\beta}=a\) এবং \(\cot{\beta}-\cot{\alpha}=b\) হয়, তবে প্রমাণ কর যে, \(\cot{(\alpha-\beta)}=\frac{1}{a}+\frac{1}{b}\)

\(Q.4.(iii)\) যদি \(A+B=\frac{\pi}{4}\) হয়, তবে দেখাও যে, \((1+\tan{A})(1+\tan{B})=2\)
রুয়েটঃ২০১০-২০১১ ।

\(Q.4.(iv)\) যদি \(\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}=1\) হয়, তবে দেখাও যে, \(1+\cot{\alpha}\tan{\beta}=0\)
সিঃ২০১৬; যঃ২০০৭ ।

\(Q.4.(v)\) যদি \(\frac{\sin{(\alpha+\gamma)}}{\sin{\alpha}}=\frac{2\sin{(\beta+\gamma)}}{\sin{\beta}}\) হয়, তবে প্রমাণ কর যে, \(\cot{\alpha}-\cot{\gamma}=2\cot{\beta}\)
কুঃ২০১২ ।

\(Q.4.(vi)\) যদি \(\tan{\beta}=\frac{2\sin{\alpha}\sin{\gamma}}{\sin{(\alpha+\gamma)}}\) হয়, তবে প্রমাণ কর যে, \(\cot{\alpha}+\cot{\gamma}=2\cot{\beta}\)

\(Q.4.(vii)\) যদি \(a\cos{(x+\alpha)}=b\cos{(x-\alpha)}\) হয়, তবে প্রমাণ কর যে, \((a+b)\tan{x}=(a-b)\cot{\alpha}\)
ঢাঃ ২০০৫ ।

\(Q.4.(viii)\) যদি \(a\sin{(x+\theta)}=b\sin{(x-\theta)}\) হয়, তবে প্রমাণ কর যে, \((a-b)\tan{x}+(a+b)\tan{\theta}=0\)

\(Q.4.(ix)\) যদি \(a\sin{(\theta+\alpha)}=b\sin{(\theta+\beta)}\) হয়, তবে প্রমাণ কর যে, \(\cot{\theta}=\frac{a\cos{\alpha}-b\cos{\beta}}{b\sin{\beta}-a\sin{\alpha}}\)
যঃ২০০৫ ।

\(Q.4.(x)\) যদি \(\theta+\phi=\alpha\) এবং \(\tan{\theta}=k\tan{\phi}\) হয়, তবে প্রমাণ কর যে, \(\sin{(\theta-\phi)}=\frac{k-1}{k+1}\sin{\alpha}\)
কুয়েটঃ ২০০৩-২০০৪ ।

\(Q.4.(xi)\) যদি \(\tan{\beta}=\frac{n\sin{\alpha}\cos{\alpha}}{1-n\sin^2{\alpha}}\) হয়, তবে দেখাও যে, \(\tan{(\alpha-\beta)}=(1-n)\tan{\alpha}\)

\(Q.4.(xii)\) \(\cot{\theta}=\frac{a\cos{x}-b\cos{y}}{a\sin{x}+b\sin{y}}\) হলে, দেখাও যে, \(\frac{\sin{(\theta-x)}}{\sin{(\theta+y)}}=\frac{b}{a}\)

\(Q.4.(xiii)\) যদি \(\sin{\alpha}=\frac{m^2-n^2}{m^2+n^2}\) হয়, তবে দেখাও যে, \(\frac{\tan{(\alpha-\beta)}+\tan{\beta}}{1-\tan{(\alpha-\beta)}\tan{\beta}}=\frac{m^2-n^2}{2mn}\)

\(Q.4.(xiv)\) যদি \(\tan{\alpha}=\frac{b}{a}\) হয়, তবে প্রমাণ কর যে, \(a\cos{\theta}+b\sin{\theta}=\sqrt{a^2+b^2}\cos{(\theta-\alpha)}\)

\(Q.4.(xv)\) যদি \(\sqrt{2}\cos{A}=\cos{B}+\cos^3{B}\) এবং \(\sqrt{2}\sin{A}=\sin{B}-\sin^3{B}\) হয়, তবে প্রমাণ কর যে, \(cosec \ {(A-B)}=\pm{3}\)

\(Q.4.(xvi)\) \(\theta\) কোণকে \(\alpha\) ও \(\beta\) অংশে এমন ভাবে বিভক্ত করা হলো যেন \(\tan{\alpha}:\tan{\beta}=x:y\) হয়, প্রমাণ কর যে, \(\sin{(\alpha-\beta)}=\frac{x-y}{x+y}\sin{\theta}\)

\(Q.4.(xvii)\) \(\tan{\theta}=\frac{a\sin{x}+b\sin{y}}{a\cos{x}+b\cos{y}}\) হলে দেখাও যে, \(a\sin{(\theta-x)}+b\sin{(\theta-y)}=0\)

\(Q.4.(xviii)\) \(\triangle{ABC}\)-এ \(\sec{B}=\sec{C}\sec{A}\) হলে দেখাও যে, \(\tan{A}=2\cot{C}\)

\(Q.4.(xix)\) যদি \(\tan{\alpha}-\tan{\beta}=x\) এবং \(\cot{\beta}-\cot{\alpha}=y\) হয়, তবে প্রমাণ কর যে, \(\cot{(\alpha-\beta)}=\frac{1}{x}+\frac{1}{y}\)

\(Q.4.(xx)\) \(\tan{\theta}=\frac{a\sin{\alpha}+b\sin{\beta}}{a\cos{\alpha}+b\cos{\beta}}\) হলে দেখাও যে, \(a\sin{(\theta-\alpha)}+b\sin{(\theta-\beta)}=0\)

\(Q.4.(xxi)\) \(A\) কোণকে \(\alpha\) ও \(\beta\) অংশে এমন ভাবে বিভক্ত করা হলো যেন \(\frac{\tan{\alpha}}{x}=\frac{\tan{\beta}}{y}\) হয়, প্রমাণ কর যে, \(\sin{(\alpha-\beta)}=\frac{x-y}{x+y}\sin{A}\)

\(Q.4.(xxii)\) \(\sin{\theta}=k\cos{(\theta-\alpha)}\) হলে দেখাও যে, \(\cot{\theta}=\frac{1-k\sin{\alpha}}{k\cos{\alpha}}\)

\(Q.4.(xxiii)\) \(\tan{\theta}+\sec{\theta}=\frac{x}{y}\) হলে দেখাও যে, \(\sin{\theta}=\frac{x^2-y^2}{x^2+y^2}\)

\(Q.4.(xxiv)\) যদি \(\cos{(\beta-\gamma)}+\cos{(\gamma-\alpha)}+\cos{(\alpha-\beta)}=-\frac{3}{2}\) হয়, তবে প্রমাণ কর যে, \(\sum{\sin{\alpha}}=0\) এবং \(\sum{\cos{\alpha}}=0\)

\(Q.4.(xxv)\) \(\sin{(A+B)}=n\sin{(A-B)}\) এবং \(n\ne{0}\) হলে দেখাও যে, \(\cot{A}=\frac{n-1}{n+1}\cot{B}\)

\(Q.4.(xxvi)\) \(\cot{\alpha}+\cot{\beta}=a, \ \tan{\alpha}+\tan{\beta}=b\) এবং \(\alpha+\beta=\theta\) হলে দেখাও যে, \((a-b)\tan{\theta}=ab\)
ঢাঃ ২০১১; রাঃ ২০১৫; দিঃ ২০১৬; চঃ ২০১৬,২০১২; বঃ ২০০৮; কুয়েটঃ ২০১২-২০১৩ ।

\(Q.4.(xxvii)\) \(\frac{\sin{(\alpha+\theta)}}{\sin{\alpha}}=\frac{2\sin{(\beta+\theta)}}{\sin{\beta}}\) হলে দেখাও যে, \(\cot{\alpha}-\cot{\theta}=2\cot{\beta}\)
কুঃ ২০১২ ।

\(Q.4.(xxviii)\) \(\tan{\beta}=\frac{2\sin{\alpha}\sin{\gamma}}{\sin{(\alpha+\gamma)}}\) হলে দেখাও যে, \(\frac{1}{\tan{\alpha}}+\frac{1}{\tan{\gamma}}=\frac{2}{\tan{\beta}}\)

\(Q.4.(xxix)\) \(\tan{\theta}=\frac{x\sin{\phi}}{1-x\cos{\phi}}\) এবং \(\tan{\phi}=\frac{y\sin{\theta}}{1-y\cos{\\theta}}\) হলে দেখাও যে, \(\frac{\sin{\theta}}{\sin{\phi}}=\frac{x}{y}\)

\(Q.4.(xxx)\) \(\sin{x}+\sin{y}=a\) এবং \(\cos{x}+\cos{y}=b\) হলে প্রমাণ কর যে, \(\sin{\frac{1}{2}(x-y)}=\pm{\frac{1}{2}\sqrt{4-a^2-b^2}}\)

\(Q.4.(xxxi)\) \(\cos{(\alpha-\beta)}\cos{\gamma}=\cos{(\alpha-\gamma+\beta)}\) হলে দেখাও যে, \(\cot{\alpha}, \cot{\gamma}\) এবং \(\cot{\beta}\) সমান্তর প্রগমন ভুক্ত।

\(Q.4.(xxxii)\) \(\sin{\alpha}=k\sin{(\alpha+\beta)}\) হলে দেখাও যে, \(\tan{(\alpha+\beta)}=\frac{\sin{\beta}}{\cos{\beta}-k}\)

\(Q.4.(xxxiii)\) \(\cos{\alpha}+\cos{\beta}=a\) এবং \(\sin{\alpha}+\sin{\beta}=b\) হলে দেখাও যে, \(\cos{(\alpha-\beta)}=\frac{1}{2}(a^2+b^2-2)\)

\(Q.4.(xxxiv)\) \(\tan{\beta}=\frac{\sin{2\alpha}}{5+\cos{2\alpha}}\) হলে দেখাও যে, \(3\tan{(\alpha-\beta)}=2\tan{\alpha}\)

\(Q.4.(xxxv)\) \(\cos{(\alpha+\beta)}\sin{(\gamma+\theta)}=\cos{(\alpha-\beta)}\sin{(\gamma-\theta)}\) হলে দেখাও যে, \(\tan{\theta}=\tan{\alpha}\tan{\beta}\tan{\gamma}\)

\(Q.4.(xxxvi)\) \(m\sin{(\theta-\alpha)}=n\sin{(\theta+\alpha)}\) হলে দেখাও যে, \((m-n)\tan{\theta}=(m+n)\tan{\alpha}\)

\(Q.4.(xxxvii)\) \(\cos{(A+B)}\sin{(C+D)}=\cos{(A-B)}\sin{(C-D)}\) হলে দেখাও যে, \(\cot{A}\cot{B}\cot{C}=\cot{D}\)

Read Board Question4

Q.5-এর সৃজনশীল প্রশ্নসমূহ

Read Creative Question

ভর্তি পরীক্ষায় আসা প্রশ্নসমূহ

Read Admission Question