এ অধ্যায়ের পাঠ্যসূচী
- \(\overline{r}\) ভেক্টরের মাণ (Value of the vector \(\overline{r}\))
- দ্বিমাত্রিক জগতে দুইটি নির্দিষ্ট বিন্দুগামী ভেক্টর (Vector through two fixed points in two dimension)
- কার্তেসীয় ত্রিমাত্রিক জগত (Cartesian three Dimension Space)
- ত্রিমাত্রিক জগতে একক ভেক্টর (Unite Vector in three Dimension Space )
- কার্তেসীয় ত্রিমাত্রিক জগতে অবস্থান ভেক্টর (Position Vector in three Dimensional Space)
- কার্তেসীয় ত্রিমাত্রিক জগতে ভেক্টরের মাণ (Value of the Vector in three Dimensional Space)
- ত্রিমাত্রিক জগতে ভেক্টর অপারেশন (Vector operations in three-dimensional Space)
- ত্রিমাত্রিক জগতে দুইটি নির্দিষ্ট বিন্দুগামী ভেক্টর (Two fixed-point vectors in a three-dimensional Space)
- অনুসিদ্ধান্ত (Postulate)
- কার্তেসীয় ত্রিমাত্রিক জগতে ভেক্টরের অংশক (Components of a Vector in three Dimensional space)
- সরলরেখার ভেক্টর সমীকরণ (Vector Equation of a Straight line)
- শর্তসাপেক্ষে সরলরেখার ভেক্টর সমীকরণ (Conditional vector equation of straight line)
- দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ (The vector equation of a straight line through two fixed points)
- সরলরেখার ভেক্টর সমীকরণ থেকে কার্তেসীয় সমীকরণ (Cartesian equation from vector equation of straight line)
- ভেক্টরের স্কেলার গুণন বা ডট গুণন (Scalar Multiplication of Vector)
- দুইটি ভেক্টরের পরস্পর লম্ব হওয়ার শর্ত (The condition that two vectors are mutually perpendicular)
- স্কেলার গুণজের ধর্ম (Properties of Scalar Product)
- ভেক্টরের ডট গুণজকে এর অংশকের মাধ্যমে প্রকাশ (Expressing the dot product of a vector in terms of its components)
- ভেক্টরের অভিক্ষেপ (Projection of a Vector)
- ভেক্টরের লম্ব অভিক্ষেপ বা উপাংশ (The perpendicular projection or Component of a vector)
- স্কেলার বা ডট গুণনের জ্যামিতিক ব্যাখ্যা (Geometric Interpretation of Scalar Multiplication of Vector)
- দুইটি ভেক্টরের অন্তর্ভুক্ত কোণ (Angle between two vectors)
- ভেক্টরের ভেক্টর গুণন বা ক্রস গুণন (Vector Multiplication of vectors)
- দুইটি ভেক্টরের পরস্পর সমান্তরাল হওয়ার শর্ত (The condition that two vectors are parallel to each other)
- ভেক্টর গুণজের ধর্ম (Properties of Vector Product)
- ভেক্টর গুণজকে এর অংশকের মাধ্যমে প্রকাশ (Expressing vector multiplication by its components)
- ভেক্টর গুণনের জ্যামিতিক ব্যাখ্যা (Geometric interpretation of Vector product)
- তিনটি ভেক্টরের স্কেলার গুণন (Scalar multiplication of three vectors)
- তিনটি ভেক্টর সমতলীয় হওয়ার শর্ত (Condition for three vectors to be coplanar)
- নির্দিষ্ট তিনটি ভেক্টর সমতলীয় হওয়ার শর্ত (Condition for fixed three vectors to be coplanar)
- ভেক্টরের যোগাশ্রয়ী সমাবেশ (linear combination of vectors)
- ত্রিমাত্রিক জগতে ভেক্টরের মাণ (Values of vectors in a three-dimensional Space)
- দুইটি নির্দিষ্ট বিন্দুগামী ভেক্টরের মাণ (The values of two fixed-point vectors)
- তিনটি ভেক্টরের ভেক্টর গুণন বা ক্রস গুণন (Vector multiplication of three vectors)
- চারটি ভেক্টরের স্কেলার গুণন (Scalar multiplication of four vectors)
- অধ্যায় \(B\)-এর উদাহরণসমুহ
- অধ্যায় \(B\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(B\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(B\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(B\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
\(\overline{r}\) ভেক্টরের মাণ
Value of the vector \(\overline{r}\)
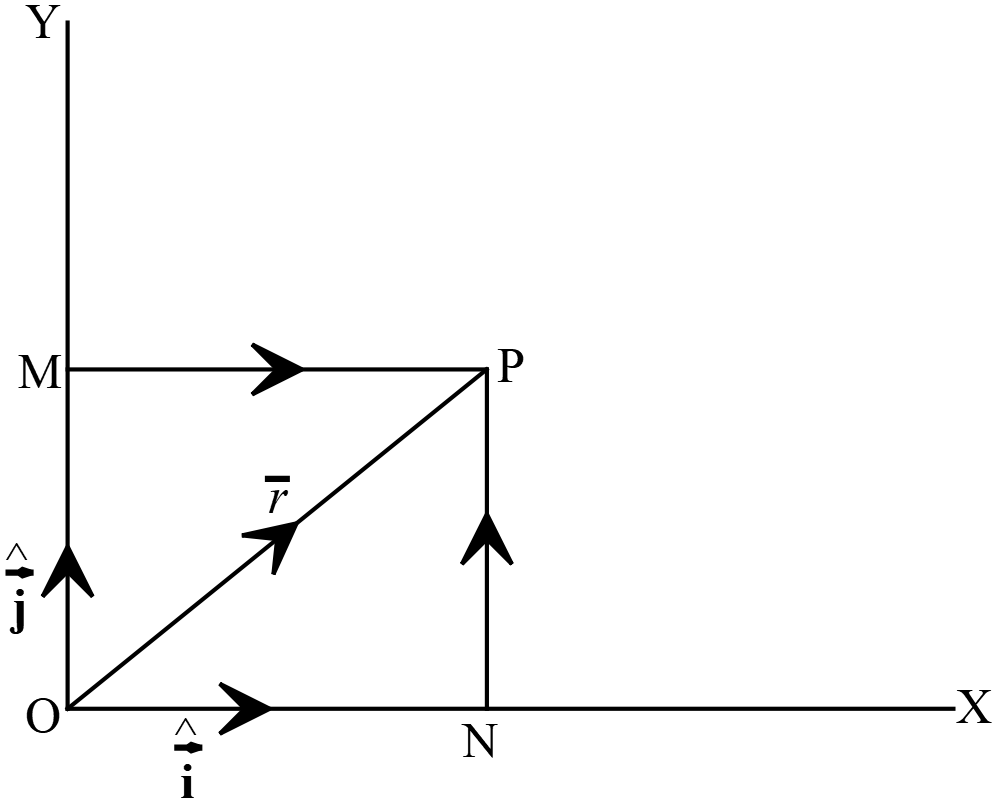ধরি,\(P(x,y), \ M(0,y), \ N(x,0), \ \overrightarrow{OP}=\overline{r}\)
এবং অক্ষরেখাগুলি বরাবর একক ভেক্টর যথাক্রমে \(\hat{i}, \ \hat{j}\)
\(\therefore \overrightarrow{ON}=x\hat{i}, \overrightarrow{NP}=\overrightarrow{OM}=y\hat{j}\)
\(\triangle{OPN}\) সমকোণী
\(\therefore OP^2=ON^2+NP^2\)
\(\Rightarrow \overrightarrow{OP}.\overrightarrow{OP}=\overrightarrow{ON}.\overrightarrow{ON}+\overrightarrow{NP}.\overrightarrow{NP}\)
\(\Rightarrow \overline{r}.\overline{r}=x\hat{i}.x\hat{i}+y\hat{j}.y\hat{j}\)
\(\Rightarrow r^2=x^2\hat{i}.\hat{i}+y^2\hat{j}.\hat{j}\) ➜ \(\because \overline{r}.\overline{r}=r^2\)
\(\Rightarrow r^2=x^2.1+y^2.1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=1\)
\(\Rightarrow r^2=x^2+y^2\)
\(\Rightarrow r=\sqrt{x^2+y^2}\) \(\therefore\) \(r=|\overline{r}|=\sqrt{x^2+y^2}\)
দ্বিমাত্রিক জগতে দুইটি নির্দিষ্ট বিন্দুগামী ভেক্টর
Vector through two fixed points in two dimension
\(P(x_{1}, y_{1})\) \(Q(x_{2}, y_{2})\) হলে,
\(\overrightarrow{PQ}=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}\)
\(\overrightarrow{PQ}=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}\)
কার্তেসীয় ত্রিমাত্রিক জগত
Cartesian three Dimension Space
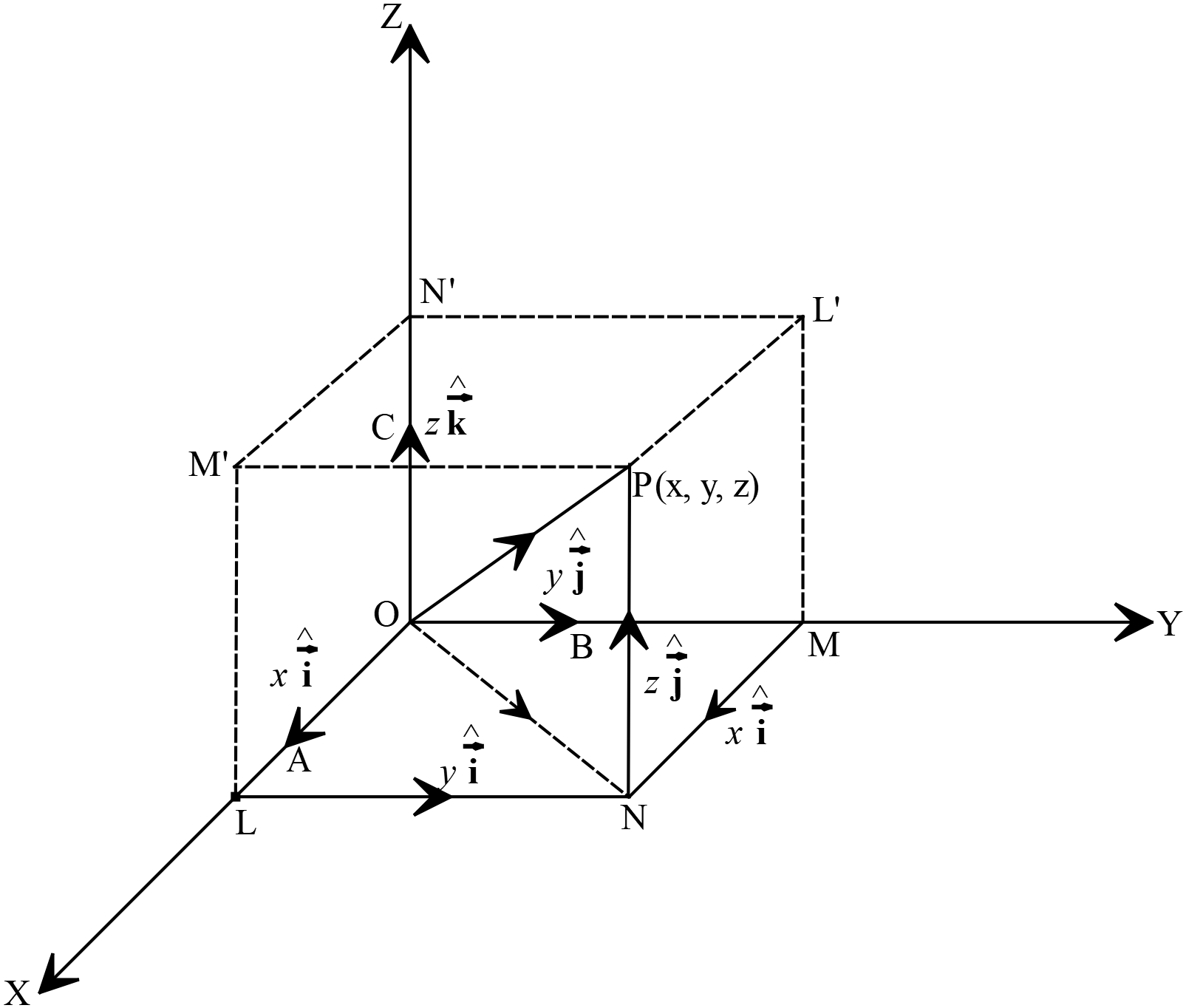ত্রিমাত্রিক কার্তেসীয় বা আয়তাকার স্থানাঙ্ক ব্যবস্থায় পরস্পর লম্ব তিনটি অক্ষ রেখা থাকে যাদের যথাক্রমে \(x, y, z\) অক্ষ বলে। এই স্থানাঙ্ক ব্যবস্থায় একটি বিন্দুর স্থানাঙ্ক \((x, y, z)\) আকারে লিখে প্রকাশ করা হয়। \(x\) স্থাংক দ্বারা \(x\) অক্ষ বরাবর দূরত্ব, \(y\) স্থাংক এবং \(z\) স্থাংক দ্বারা অনুরূপে \(y\) অক্ষ এবং \(z\) অক্ষ বরাবর মূলবিন্দু হতে দূরত্ব বুঝায়। ত্রিমাত্রিক জগতে একক ভেক্টর \(\hat{i}, \hat{j}, \hat{k}\)
Unite Vector in three Dimension Space \(\hat{i}, \hat{j}, \hat{k}\)
ত্রিমাত্রিক কার্তেসীয় বা আয়তাকার স্থানাঙ্ক ব্যবস্থায়, \(x\) অক্ষ বরাবর একক ভেক্টর \(\hat{i}\)
\(y\) অক্ষ বরাবর একক ভেক্টর \(\hat{j}\)
\(z\) অক্ষ বরাবর একক ভেক্টর \(\hat{k}\)
কার্তেসীয় ত্রিমাত্রিক জগতে অবস্থান ভেক্টর
Position Vector in three Dimensional Space
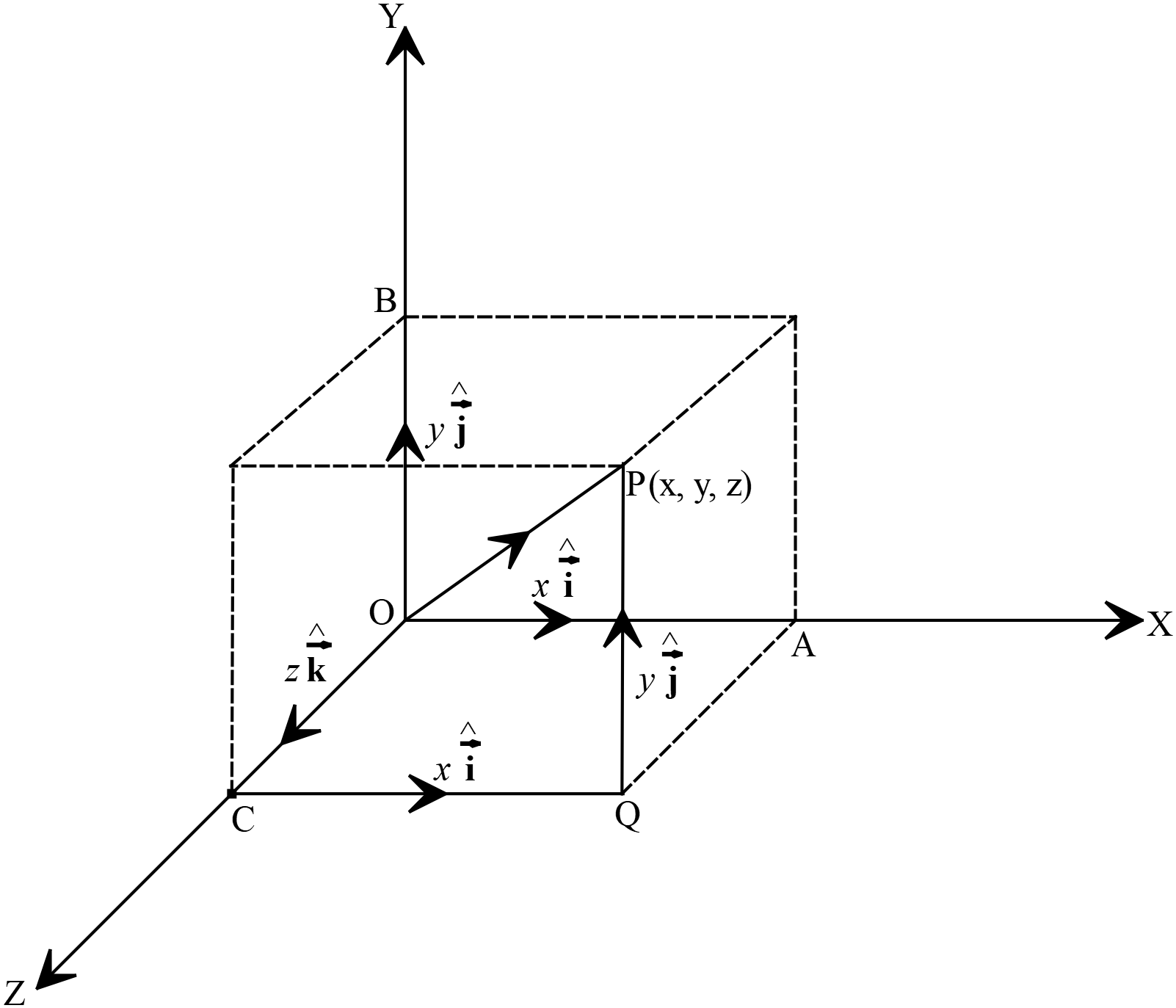কার্তেসীয় ত্রিমাত্রিক জগতে মূলবিন্দু \((0, 0, 0)\) এর সাপেক্ষে \(P(x, y, z)\) এর অবস্থান ভেক্টর \(\overline{r}\) হলে, \(P\) বিন্দুর অবস্থান ভেক্টর
\(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
কার্তেসীয় ত্রিমাত্রিক জগতে ভেক্টরের মাণ
Value of the Vector in three Dimensional Space
\(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\) এর মাণ,
\(r=|\overline{r}|=\sqrt{x^2+y^2+z^2}\)
ত্রিমাত্রিক জগতে ভেক্টর অপারেশন
Vector operations in three-dimensional Space
ধরি, \(A\) ও \(B\) ত্রিমাত্রিক জগতের দুইটি ভেক্টর যেখানে, \(\overline{A}=A_{1}\hat{i}+A_{2}\hat{j}+A_{3}\hat{k}\)
এবং \(\overline{B}=B_{1}\hat{i}+B_{2}\hat{j}+B_{3}\hat{k}\)
যোগফলঃ \(\overline{A}+\overline{B}=(A_{1}+B_{1})\hat{i}+(A_{2}+B_{2})\hat{j}+(A_{3}+B_{3})\hat{k}\)
বিয়োগফলঃ \(\overline{A}-\overline{B}=(A_{1}-B_{1})\hat{i}+(A_{2}-B_{2})\hat{j}+(A_{3}-B_{3})\hat{k}\)
ভেক্টর গুনিতকঃ \(\lambda \overline{A}=\lambda A_{1}\hat{i}+\lambda A_{2}\hat{j}+\lambda A_{3}\hat{k}\)
যখন \(\lambda\) একটি স্কেলার রাশি।
ত্রিমাত্রিক জগতে দুইটি নির্দিষ্ট বিন্দুগামী ভেক্টর
Two fixed-point vectors in a three-dimensional Space
\(P(x_{1}, y_{1}, z_{1})\) \(Q(x_{2}, y_{2}, z_{2})\) হলে, \(\overrightarrow{PQ}=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}+(z_{2}-z_{1})\hat{k}\)
অনুসিদ্ধান্ত
Postulate
যদি, \(\overrightarrow{OP}=\overline{r}\) ভেক্টর \(x, y\) ও \(z\) অক্ষের ধনাত্মক দিকের সহিত যথাক্রমে \(\alpha, \beta\) ও \(\gamma\) কোণ উৎপন্ন করে,
তখন \(\cos{\alpha}, \cos{\beta}, \cos{\gamma}\) কে \(\overline{r}\) এর দিক কোসাইন বলা হয়।
তখন \(\cos{\alpha}, \cos{\beta}, \cos{\gamma}\) কে \(\overline{r}\) এর দিক কোসাইন বলা হয়।
কার্তেসীয় ত্রিমাত্রিক জগতে ভেক্টরের অংশক
Components of a Vector in three Dimensional space
\(O\) বিন্দু থেকে তিনটি পরস্পর লম্ব সরলরেখা \(OX, OY, OZ\) আঁকা হলো।
\(\overrightarrow{OX}=\hat{i}, \overrightarrow{OY}=\hat{j}\) এবং \(\overrightarrow{OZ}=\hat{k}\) হয়, যেখানে \(\hat{i}, \hat{j}, \hat{k}\) তিনটি পরস্পর লম্ব একক ভেক্টর।
\(\overrightarrow{OP}=\overline{r}\) ভেক্টরকে তিনটি পরস্পর লম্ব একক ভেক্টর \(\hat{i}, \hat{j}, \hat{k}\) এর যোগাশ্রয়ী সমাবেশ হিসেবে প্রকাশ করা হয়েছে।
অর্থাৎ , \(\overline{r}=x\overline{i}+y\overline{j}+z\overline{k}\)
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=x\overline{i}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=y\overline{j}\)
\(OZ\) বরাবর \(\overline{r}\) এর অংশক \(=z\overline{k}\)
সরলরেখার ভেক্টর সমীকরণ
Vector Equation of a Straight line
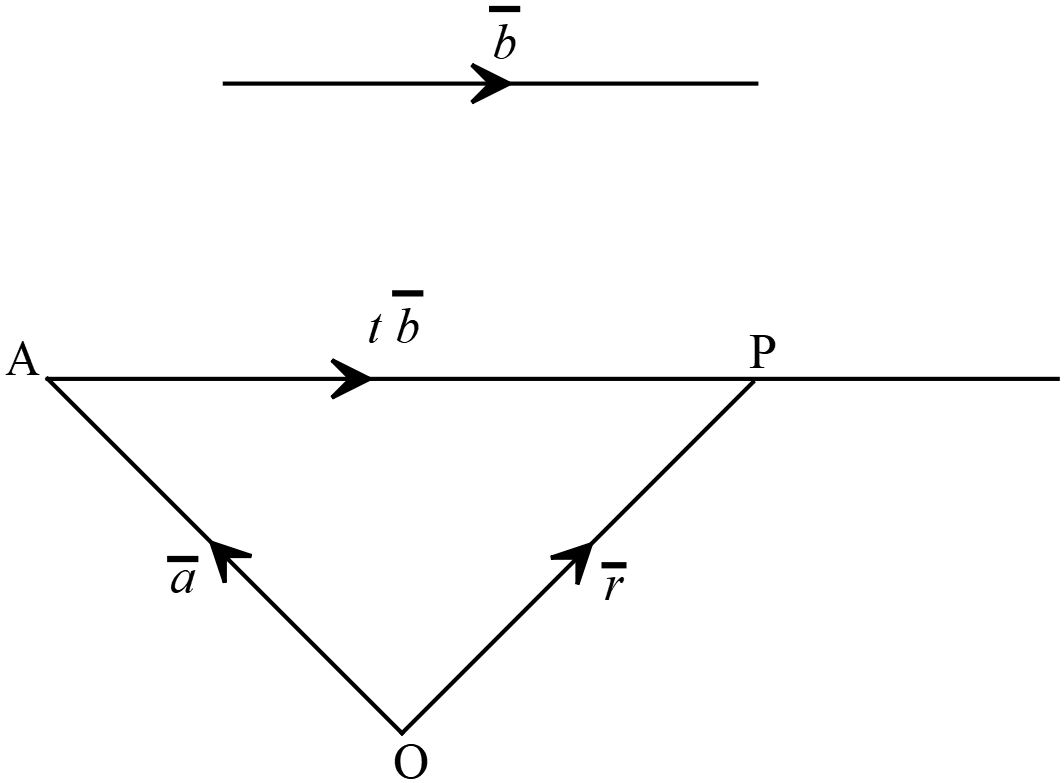\(A(\overline{a})\) বিন্দুগামী \(\overline{B}\) ভেক্টরের সমান্তরাল রেখার ভেক্টর সমীকরণঃ \(\overline{r}=\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times\overline{b}=0\)
দ্রঃ সরলরেখাটি যদি মূলবিন্দুগামী হয় তাহলে, \(\overline{a}=\overline{0}\)
সুতরাং, মূলবিন্দুগামী এবং \(\overline{b}\) ভেক্টরের সমান্তরাল সরলরেখার ভেক্টর সমীকরণঃ
\(\overline{r}=t\overline{b}\)অথবা,
\(\overline{r}\times\overline{b}=0\)
শর্তসাপেক্ষে সরলরেখার ভেক্টর সমীকরণ
Conditional vector equation of straight line
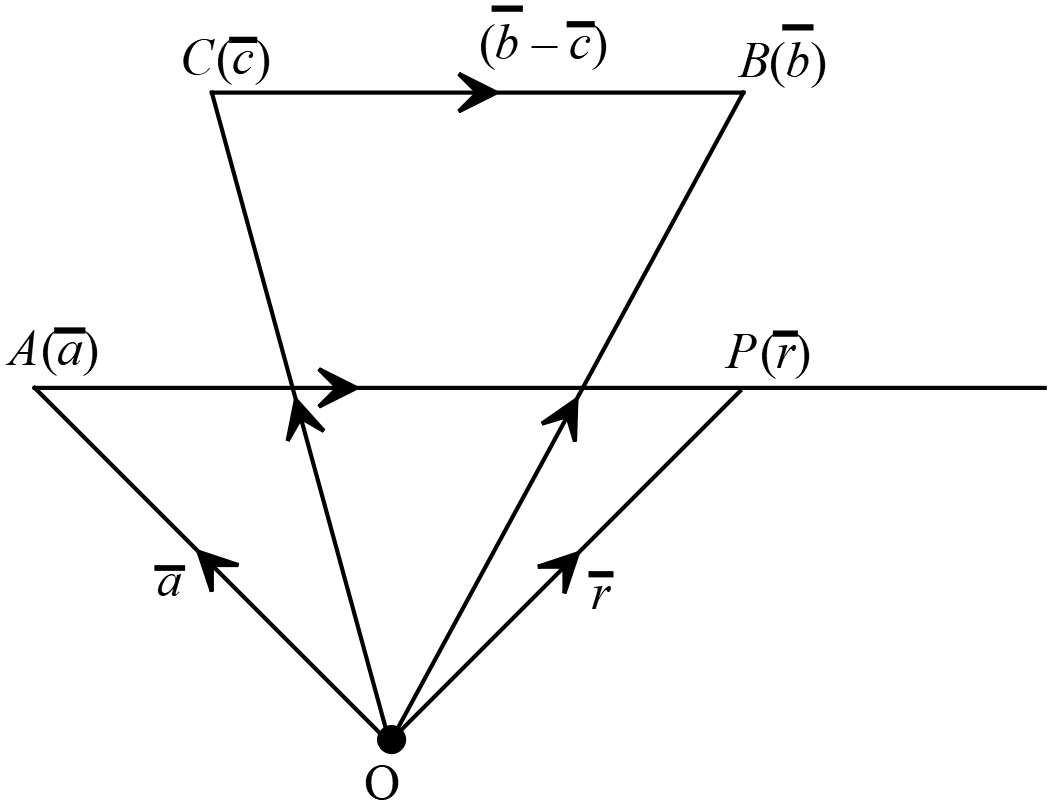\(A(\overline{a})\) বিন্দুগামী এবং \(B(\overline{b})\) ও \(C(\overline{c})\) বিন্দুদ্বয়ের সংযোগ রেখার সমান্তরাল সরলরেখার ভেক্টর সমীকরণ \(\overline{r}=\overline{a}+t(\overline{b}-\overline{c})\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{c}-\overline{b})=0\)
দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ
The vector equation of a straight line through two fixed points
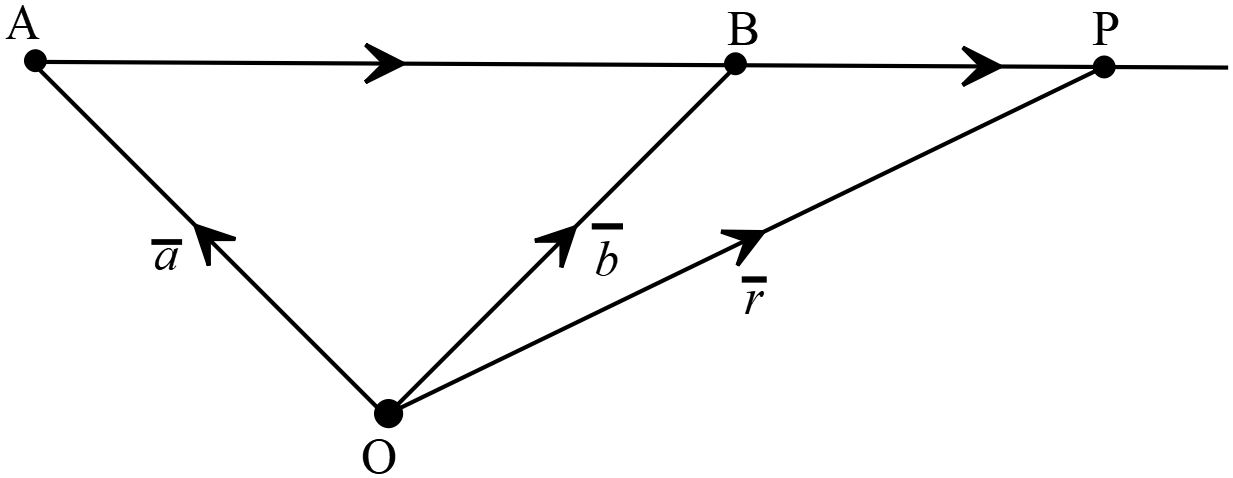\(A(\overline{a})\) এবং \(B(\overline{b})\) বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ\(\overline{r}=(1-t)\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{a})=0\)
সরলরেখার ভেক্টর সমীকরণ থেকে কার্তেসীয় সমীকরণ
Cartesian equation from vector equation of straight line
ভেক্টর সমীকরণ \(\overline{r}=\overline{a}+t\overline{b}\) এর কার্তেসীয় সমীকরণ,
\(\frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}\)
\(\frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}\)
ভেক্টরের স্কেলার গুণন বা ডট গুণন
Scalar Multiplication of Vector
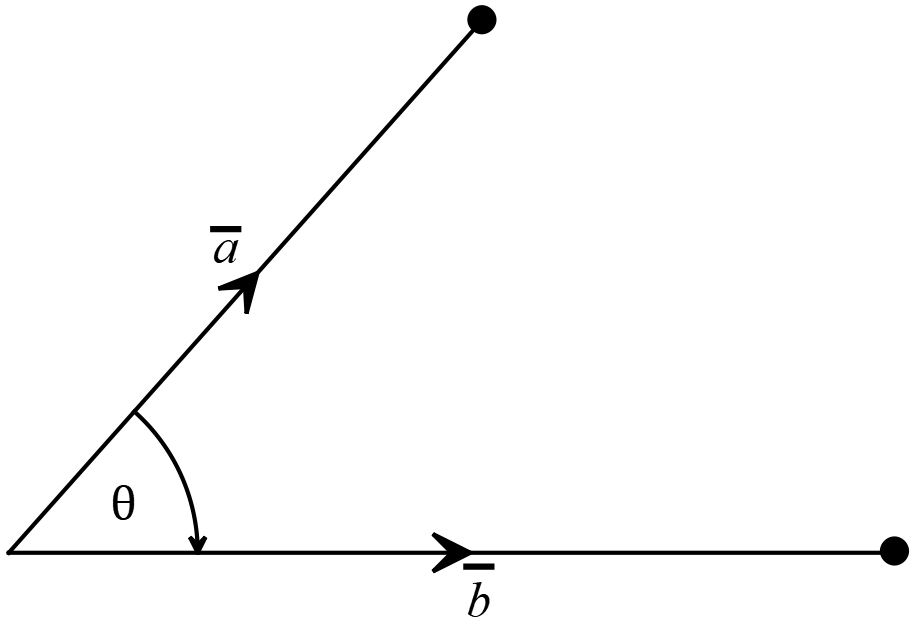দুইটি ভেক্টর রাশির গুণফল যদি একটি স্কেলার রাশি হয় তাহলে এ ধরনের গুণফলকে স্কেলার গুণন বা ডট গুণন বলা হয়। এ গুণফলের মাণ রাশি দুইটির মাণ ও এদের মধ্যবর্তী ক্ষুদ্রতর কোণের কোসাইন (cosine) এর গুণফলের সমান। \(\overline{a}\) ও \(\overline{b}\) এর স্কেলার গুণজ \(\overline{a}.\overline{b}\) দ্বারা প্রকাশ করা হয়। \(\overline{a}\) ও \(\overline{b}\) দুইটি ভেক্টর রাশির মধ্যবর্তী কোণ \(\theta\) হলে, সংজ্ঞানুসারে স্কেলার গুণফল হবে,
\(\overline{a}.\overline{b}=ab\cos{\theta}\) ভেক্টরদ্বয়ের অন্তর্ভুক্ত কোণ
\(\theta=\cos^{-1}\left(\frac{\overline{a}.\overline{b}}{ab}\right)\)
দুইটি ভেক্টরের পরস্পর লম্ব হওয়ার শর্ত
The condition that two vectors are mutually perpendicular
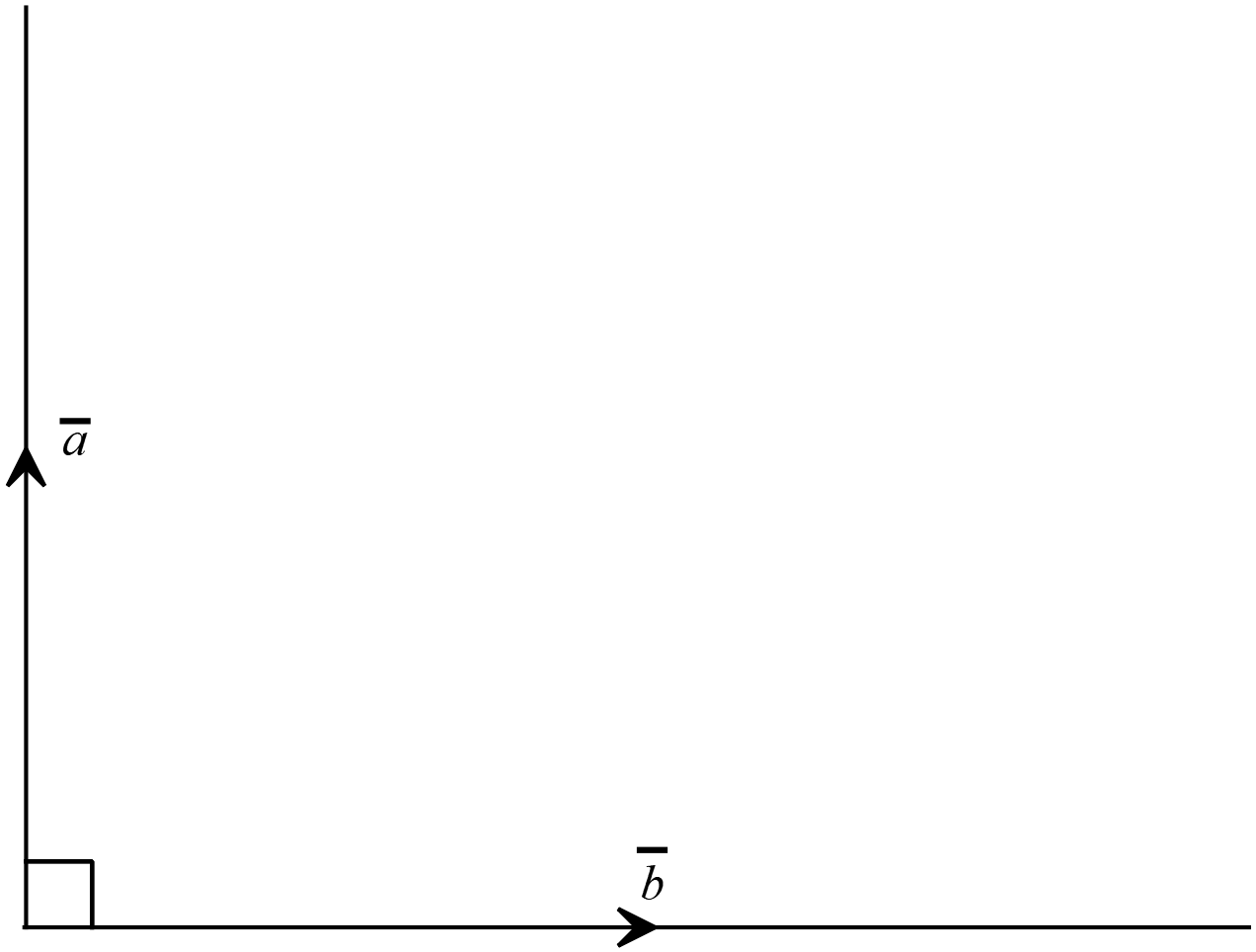\(\overline{a}\) ও \(\overline{b}\) দুইটি ভেক্টর রাশি পরস্পর লম্ব হলে,\(\overline{a}.\overline{b}=0\)
স্কেলার গুণজের ধর্ম
Properties of Scalar Product
\(\overline{a}.\overline{b}=ab\cos{\theta}=ba\cos{\theta}=\overline{b}.\overline{a}\)
\(\therefore \overline{a}.\overline{b}=\overline{b}.\overline{a}\)
অর্থাৎ স্কেলার গুণজ বিনিময় বিধি মেনে চলে।
\(\overline{a}.(-\overline{b})=-(\overline{a}.\overline{b})\)
\((-\overline{a}).(-\overline{b})=\overline{a}.\overline{b}\)
\((\overline{a}+\overline{b}).\overline{c}=\overline{a}.\overline{c}+\overline{b}.\overline{c}\)
\(\theta\) সূক্ষ্ণকোণ হলে, স্কেলার গুণন ধনাত্মক হবে
\(\theta\) স্থুলকোণ হলে, স্কেলার গুণন ঋণাত্মক হবে
\(\theta=90^{o}\) হলে, স্কেলার গুণনের মাণ শূন্য হবে
দ্রঃ দুইটি ভেক্টরের স্কেলার গুণন শূন্য হলে ভেক্টরদ্বয় পরস্পর লম্ব হয়।
\(\theta=0\) হলে, ভেক্টরদ্বয় পরস্পর সমান্তরাল হবে
\(\theta=180^{o}\) হলে, ভেক্টরদ্বয় পরস্পর অসদৃশ সমান্তরাল হবে
অনুসিদ্ধান্তঃ
\(\overline{a}.\overline{a}=a^2\)
\(\hat{i}.\hat{i}=\hat{j}.\hat{j}=\hat{k}.\hat{k}=1\)
\(\hat{i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0\)
\(\theta=\cos^{-1}\left(\frac{\overline{a}.\overline{b}}{ab}\right)\)
\(\therefore \overline{a}.\overline{b}=\overline{b}.\overline{a}\)
অর্থাৎ স্কেলার গুণজ বিনিময় বিধি মেনে চলে।
\(\overline{a}.(-\overline{b})=-(\overline{a}.\overline{b})\)
\((-\overline{a}).(-\overline{b})=\overline{a}.\overline{b}\)
\((\overline{a}+\overline{b}).\overline{c}=\overline{a}.\overline{c}+\overline{b}.\overline{c}\)
\(\theta\) সূক্ষ্ণকোণ হলে, স্কেলার গুণন ধনাত্মক হবে
\(\theta\) স্থুলকোণ হলে, স্কেলার গুণন ঋণাত্মক হবে
\(\theta=90^{o}\) হলে, স্কেলার গুণনের মাণ শূন্য হবে
দ্রঃ দুইটি ভেক্টরের স্কেলার গুণন শূন্য হলে ভেক্টরদ্বয় পরস্পর লম্ব হয়।
\(\theta=0\) হলে, ভেক্টরদ্বয় পরস্পর সমান্তরাল হবে
\(\theta=180^{o}\) হলে, ভেক্টরদ্বয় পরস্পর অসদৃশ সমান্তরাল হবে
অনুসিদ্ধান্তঃ
\(\overline{a}.\overline{a}=a^2\)
\(\hat{i}.\hat{i}=\hat{j}.\hat{j}=\hat{k}.\hat{k}=1\)
\(\hat{i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0\)
\(\theta=\cos^{-1}\left(\frac{\overline{a}.\overline{b}}{ab}\right)\)
ভেক্টরের ডট গুণজকে এর অংশকের মাধ্যমে প্রকাশ
Expressing the dot product of a vector in terms of its components
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\) এবং \(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) দুইটি অশূন্য ভেক্টর
এখন, \(\overline{a}.\overline{b}=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}).(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})\)
\(=a_{1}b_{1}\hat{i}.\hat{i}+a_{1}b_{2}\hat{i}.\hat{j}+a_{1}b_{3}\hat{i}.\hat{k}+a_{2}b_{1}\hat{j}.\hat{i}+a_{2}b_{2}\hat{j}.\hat{j}+a_{2}b_{3}\hat{j}.\hat{k}+a_{3}b_{1}\hat{k}.\hat{i}+a_{3}b_{2}\hat{k}.\hat{j}+a_{3}b_{3}\hat{k}.\hat{k}\)
\(=a_{1}b_{1}1+a_{1}b_{2}0+a_{1}b_{3}0+a_{2}b_{1}0+a_{2}b_{2}1+a_{2}b_{3}0+a_{3}b_{1}0+a_{3}b_{2}0+a_{3}b_{3}1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=\hat{k}.\hat{k}=1\)
এবং
\(\hat{i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0\)
\(=a_{1}b_{1}+0+0+0+a_{2}b_{2}+0+0+0+a_{3}b_{3}\)
\(=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\)
\(\therefore\) \(\overline{a}.\overline{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\)
এখন, \(\overline{a}.\overline{b}=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}).(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})\)
\(=a_{1}b_{1}\hat{i}.\hat{i}+a_{1}b_{2}\hat{i}.\hat{j}+a_{1}b_{3}\hat{i}.\hat{k}+a_{2}b_{1}\hat{j}.\hat{i}+a_{2}b_{2}\hat{j}.\hat{j}+a_{2}b_{3}\hat{j}.\hat{k}+a_{3}b_{1}\hat{k}.\hat{i}+a_{3}b_{2}\hat{k}.\hat{j}+a_{3}b_{3}\hat{k}.\hat{k}\)
\(=a_{1}b_{1}1+a_{1}b_{2}0+a_{1}b_{3}0+a_{2}b_{1}0+a_{2}b_{2}1+a_{2}b_{3}0+a_{3}b_{1}0+a_{3}b_{2}0+a_{3}b_{3}1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=\hat{k}.\hat{k}=1\)
এবং
\(\hat{i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0\)
\(=a_{1}b_{1}+0+0+0+a_{2}b_{2}+0+0+0+a_{3}b_{3}\)
\(=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\)
\(\therefore\) \(\overline{a}.\overline{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\)
ভেক্টরের অভিক্ষেপ
Projection of a Vector
একটি ভেক্টরের উপর অন্য একটি ভেক্টরের অভিক্ষেপ
\(\overline{a}\) বরাবর \(\overline{b}\) এর অভিক্ষেপ,
\(\frac{\overline{a}.\overline{b}}{a}\)
অথবা,
\(\hat{a}.\overline{b}\)
\(\overline{b}\) বরাবর \(\overline{a}\) এর অভিক্ষেপ,
\(\frac{\overline{a}.\overline{b}}{b}\)
অথবা,
\(\hat{b}.\overline{a}\)
\(\overline{a}\) বরাবর \(\overline{b}\) এর অভিক্ষেপ,
\(\frac{\overline{a}.\overline{b}}{a}\)
অথবা,
\(\hat{a}.\overline{b}\)
\(\overline{b}\) বরাবর \(\overline{a}\) এর অভিক্ষেপ,
\(\frac{\overline{a}.\overline{b}}{b}\)
অথবা,
\(\hat{b}.\overline{a}\)
ভেক্টরের লম্ব অভিক্ষেপ বা উপাংশ
The perpendicular projection or Component of a vector
একটি ভেক্টরের দিক বরাবর অন্য একটি ভেক্টরের ভেক্টর লম্ব অভিক্ষেপ বা অংশক
\(\overline{a}\) বরাবর \(\overline{b}\) এর ভেক্টর লম্ব অভিক্ষেপ বা উপাংশ ভেক্টর,
\((\hat{a}.\overline{b})\hat{a}\)
অথবা,
\(\frac{\overline{a}.\overline{b}}{a^2}\overline{a}\)
\(\overline{b}\) বরাবর \(\overline{a}\) এর ভেক্টর লম্ব অভিক্ষেপ বা উপাংশ ভেক্টর,
\((\overline{a}.\hat{b})\hat{b}\)
অথবা,
\(\frac{\overline{a}.\overline{b}}{b^2}\overline{b}\)
\(\overline{a}\) বরাবর \(\overline{b}\) এর ভেক্টর লম্ব অভিক্ষেপ বা উপাংশ ভেক্টর,
\((\hat{a}.\overline{b})\hat{a}\)
অথবা,
\(\frac{\overline{a}.\overline{b}}{a^2}\overline{a}\)
\(\overline{b}\) বরাবর \(\overline{a}\) এর ভেক্টর লম্ব অভিক্ষেপ বা উপাংশ ভেক্টর,
\((\overline{a}.\hat{b})\hat{b}\)
অথবা,
\(\frac{\overline{a}.\overline{b}}{b^2}\overline{b}\)
স্কেলার বা ডট গুণনের জ্যামিতিক ব্যাখ্যা
Geometric Interpretation of Scalar Multiplication of Vector
\(\overline{a}\) ও \(\overline{b}\) এর স্কেলার গুণজ,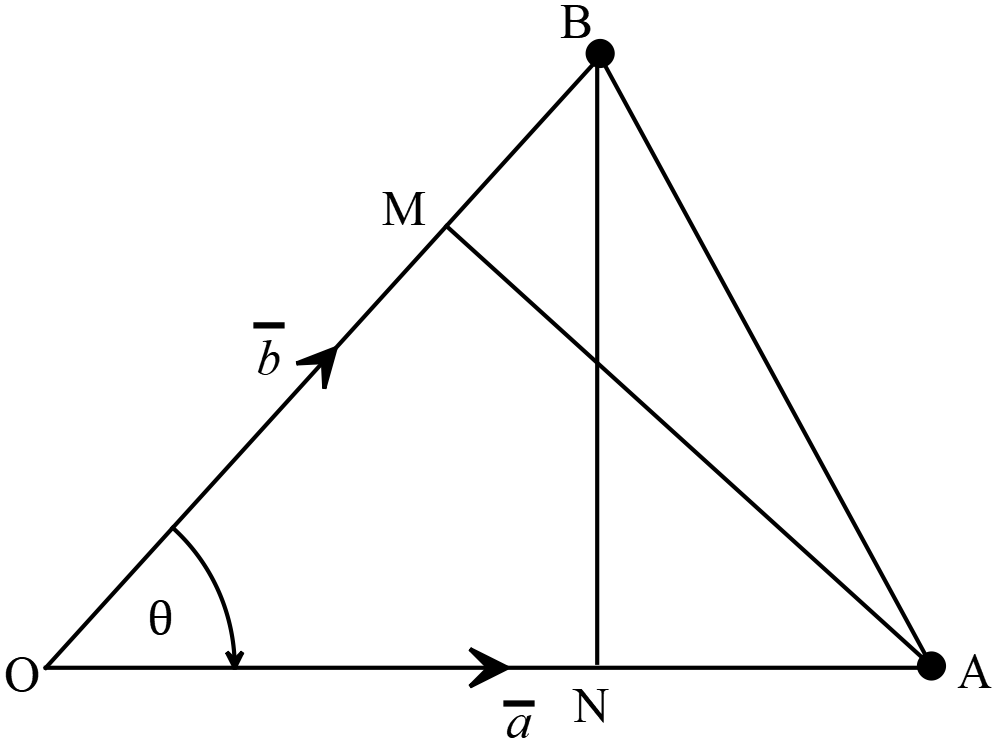
\(\overline{a}.\overline{b}=ab\cos{\theta}\)
\(=a(b\cos{\theta})\)
\(=a(OB\times{\frac{ON}{OB}})\) ➜ \(\because OB=b\)
এবং \(\cos{\theta}=\frac{ON}{OB}\)
\(=a(ON)\)
\(=a\) এর মাণ \(\times{\overline{a}}\)বরাবর \(\overline{b}\) এর অভিক্ষেপ।
\(\therefore\) \(\overline{a}.\overline{b}=a\) এর মাণ \(\times{\overline{a}}\) বরাবর \(\overline{b}\) এর অভিক্ষেপ
অনুরূপভাবে,
\(\overline{a}.\overline{b}=b\) এর মাণ \(\times{\overline{b}}\) বরাবর \(\overline{a}\) এর অভিক্ষেপ
\(\overline{a}.\overline{b}=ab\cos{\theta}\)\(=a(b\cos{\theta})\)
\(=a(OB\times{\frac{ON}{OB}})\) ➜ \(\because OB=b\)
এবং \(\cos{\theta}=\frac{ON}{OB}\)
\(=a(ON)\)
\(=a\) এর মাণ \(\times{\overline{a}}\)বরাবর \(\overline{b}\) এর অভিক্ষেপ।
\(\therefore\) \(\overline{a}.\overline{b}=a\) এর মাণ \(\times{\overline{a}}\) বরাবর \(\overline{b}\) এর অভিক্ষেপ
অনুরূপভাবে,
\(\overline{a}.\overline{b}=b\) এর মাণ \(\times{\overline{b}}\) বরাবর \(\overline{a}\) এর অভিক্ষেপ
দুইটি ভেক্টরের অন্তর্ভুক্ত কোণ
Angle between two vectors
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\) এবং \(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) দুইটি অশূন্য ভেক্টরের অন্তর্ভুক্ত কোণ \(\theta\) হলে,
\(\theta=\cos^{-1}\left(\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}}\right)\)
\(\theta=\cos^{-1}\left(\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}}\right)\)
ভেক্টরের ভেক্টর গুণন বা ক্রস গুণন
Vector Multiplication of vectors
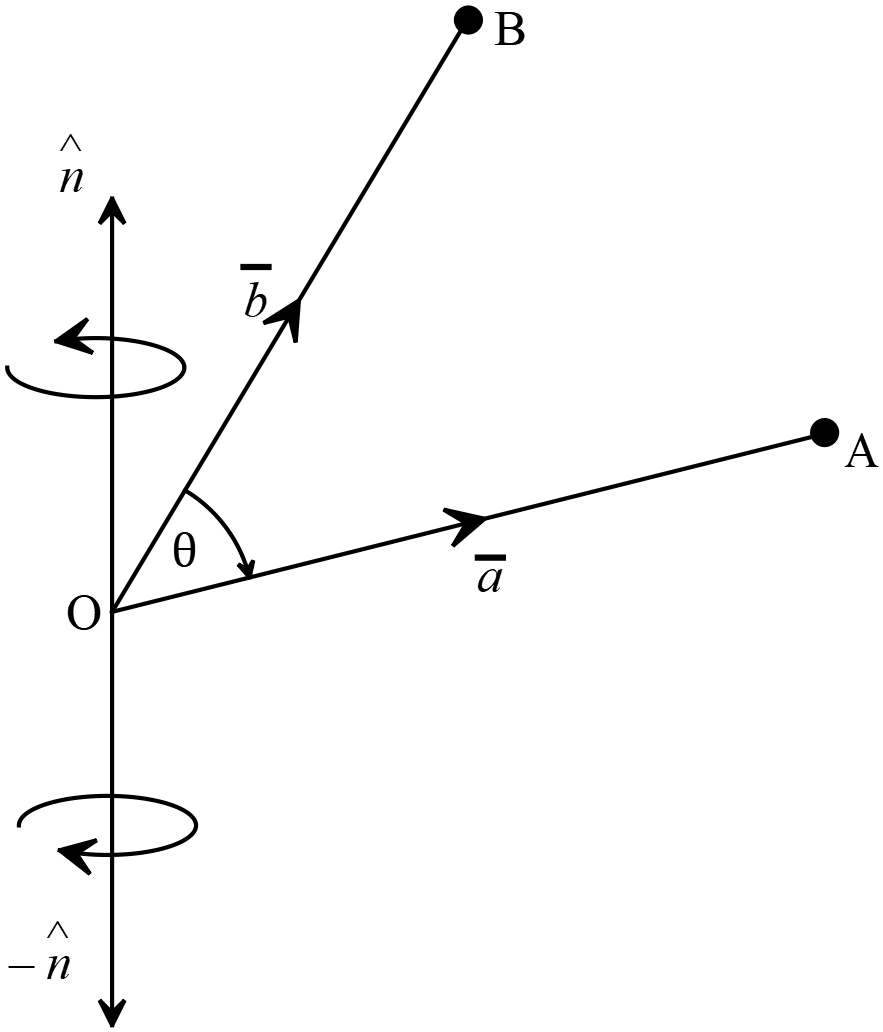দুইটি ভেক্টর রাশির গুণফল যদি একটি ভেক্টর রাশি হয় তাহলে এ ধরনের গুণফলকে ভেক্টর গুণন বা ক্রস গুণন বলা হয়। এ গুণফলের মাণ রাশি দুইটির মাণ ও এদের মধ্যবর্তী ক্ষুদ্রতর কোণের সাইন (sine) এর গুণফলের সমান। ভেক্টর গুণফলের দিক হবে প্রদত্ত ভেক্টরদ্বয়ের সমতলে লম্বভাবে স্থাপিত একটি ডানহাতি স্ক্রকে প্রথম ভেক্টর থেকে দ্বিতীয় ভেক্টরের দিকে ক্ষুদ্রতর কোণে ঘুরালে স্ক্রটি যে দিকে অগ্রসর হয় সেদিকে। \(\overline{a}\) ও \(\overline{b}\) এর ভেক্টর গুণজ \(\overline{a}\times{\overline{b}}\) দ্বারা প্রকাশ করা হয়।
\(\overline{a}\) ও \(\overline{b}\) দুইটি ভেক্টর রাশির মধ্যবর্তী কোণ \(\theta\) হলে, সংজ্ঞানুসারে ভেক্টর গুণফল হবে,
\(\overline{a}\times{\overline{b}}=ab\sin{\theta} \ \hat{n}\)
\(\hat{n}\) একটি একক ভেক্টর যা \(\overline{a}\) ও \(\overline{b}\) ভেক্টরদ্বয়ের সমতলের উপর লম্ব।
দুইটি ভেক্টরের পরস্পর সমান্তরাল হওয়ার শর্ত
The condition that two vectors are parallel to each other
\(\overline{a}\) ও \(\overline{b}\) দুইটি ভেক্টর রাশি পরস্পর সমান্তরাল হলে, \(\overline{a}\times{\overline{b}}=0\)
ভেক্টর গুণজের ধর্ম
Properties of Vector Product
\(\overline{a}\times{\overline{b}}=-\overline{b}\times{\overline{a}}\)
\(\overline{a}\times{\overline{b}}\ne{\overline{b}\times{\overline{a}}}\)
এদের মাণ ও ধারক রেখা অভিন্ন হলেও দিক ভিন্ন। সুতরাং ভেক্টরের ভেক্টর গুণন বিনিময় বিধি মেনে চলে না।
\(m(\overline{a}\times{\overline{b}})=(m\overline{a})\times{\overline{b}}=\overline{a}\times{(m\overline{b})}\)
\((m\overline{a})\times{(n\overline{b})}=(n\overline{a})\times{(m\overline{b})}=\overline{a}\times{(mn\overline{b})}=(mn\overline{a})\times{\overline{b}}=mn(\overline{a}\times{\overline{b}})\)
\(\overline{a}\times{(\overline{b}+\overline{c})}=\overline{a}\times{\overline{b}}+\overline{a}\times{\overline{c}}\)
\((\overline{a}+\overline{b})\times{\overline{c}}=\overline{a}\times{\overline{c}}+\overline{b}\times{\overline{c}}\)
\(\overline{a}\times{(\overline{b}\times{\overline{c}})}\ne{(\overline{a}\times{\overline{b}})\times{\overline{c}}}\)
\(\overline{a}\times{\overline{b}}=\overline{0}\) হলে, ভেক্টরদ্বয় পরস্পর সমান্তরাল হবে।
\(\overline{a}\times{\overline{b}}=\overline{c}\) হলে, \(\overline{c}\) ভেক্টরটি \(\overline{a}\) ও \(\overline{b}\) এর সমতলের উপর লম্ব হবে।
অনুসিদ্ধান্তঃ
\(\overline{a}\times{\overline{a}}=0\)
\(\hat{i}\times{\hat{i}}=\hat{j}\times{\hat{j}}=\hat{k}\times{\hat{k}}=0\)
\(\hat{i}\times{\hat{j}}=\hat{k}, \hat{j}\times{\hat{k}}=\hat{i}, \hat{k}\times{\hat{i}}=\hat{j}\)
\(\hat{j}\times{\hat{i}}=-\hat{k}, \hat{k}\times{\hat{j}}=-\hat{i}, \hat{i}\times{\hat{k}}=-\hat{j}\)
\(\theta=\sin^{-1}\left(\frac{|\overline{a}\times{\overline{b}}|}{ab}\right)\)
\(\overline{a}\times{\overline{b}}\ne{\overline{b}\times{\overline{a}}}\)
এদের মাণ ও ধারক রেখা অভিন্ন হলেও দিক ভিন্ন। সুতরাং ভেক্টরের ভেক্টর গুণন বিনিময় বিধি মেনে চলে না।
\(m(\overline{a}\times{\overline{b}})=(m\overline{a})\times{\overline{b}}=\overline{a}\times{(m\overline{b})}\)
\((m\overline{a})\times{(n\overline{b})}=(n\overline{a})\times{(m\overline{b})}=\overline{a}\times{(mn\overline{b})}=(mn\overline{a})\times{\overline{b}}=mn(\overline{a}\times{\overline{b}})\)
\(\overline{a}\times{(\overline{b}+\overline{c})}=\overline{a}\times{\overline{b}}+\overline{a}\times{\overline{c}}\)
\((\overline{a}+\overline{b})\times{\overline{c}}=\overline{a}\times{\overline{c}}+\overline{b}\times{\overline{c}}\)
\(\overline{a}\times{(\overline{b}\times{\overline{c}})}\ne{(\overline{a}\times{\overline{b}})\times{\overline{c}}}\)
\(\overline{a}\times{\overline{b}}=\overline{0}\) হলে, ভেক্টরদ্বয় পরস্পর সমান্তরাল হবে।
\(\overline{a}\times{\overline{b}}=\overline{c}\) হলে, \(\overline{c}\) ভেক্টরটি \(\overline{a}\) ও \(\overline{b}\) এর সমতলের উপর লম্ব হবে।
অনুসিদ্ধান্তঃ
\(\overline{a}\times{\overline{a}}=0\)
\(\hat{i}\times{\hat{i}}=\hat{j}\times{\hat{j}}=\hat{k}\times{\hat{k}}=0\)
\(\hat{i}\times{\hat{j}}=\hat{k}, \hat{j}\times{\hat{k}}=\hat{i}, \hat{k}\times{\hat{i}}=\hat{j}\)
\(\hat{j}\times{\hat{i}}=-\hat{k}, \hat{k}\times{\hat{j}}=-\hat{i}, \hat{i}\times{\hat{k}}=-\hat{j}\)
\(\theta=\sin^{-1}\left(\frac{|\overline{a}\times{\overline{b}}|}{ab}\right)\)
ভেক্টর গুণজকে এর অংশকের মাধ্যমে প্রকাশ
Expressing vector multiplication by its divisor
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\) এবং \(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) দুইটি অশূন্য ভেক্টর
এখন, \(\overline{a}\times{\overline{b}}=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times{(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})}\)
\(=a_{1}b_{1}\hat{i}\times{\hat{i}}+a_{1}b_{2}\hat{i}\times{\hat{j}}+a_{1}b_{3}\hat{i}\times{\hat{k}}+a_{2}b_{1}\hat{j}\times{\hat{i}}+a_{2}b_{2}\hat{j}\times{\hat{j}}+a_{2}b_{3}\hat{j}\times{\hat{k}}+a_{3}b_{1}\hat{k}\times{\hat{i}}+a_{3}b_{2}\hat{k}\times{\hat{j}}+a_{3}b_{3}\hat{k}\times{\hat{k}}\)
\(=a_{1}b_{1}0+a_{1}b_{2}\hat{k}+a_{1}b_{3}(-\hat{j})+a_{2}b_{1}(-\hat{k})+a_{2}b_{2}0+a_{2}b_{3}\hat{i}+a_{3}b_{1}\hat{j}+a_{3}b_{2}(-\hat{i})+a_{3}b_{3}0\) ➜ \(\because \hat{i}\times{\hat{i}}=\hat{j}\times{\hat{j}}=\hat{k}\times{\hat{k}}=0\)
\(\hat{i}\times{\hat{j}}=\hat{k}, \hat{j}\times{\hat{k}}=\hat{i}, \hat{k}\times{\hat{i}}=\hat{j}\)
এবং
\(\hat{j}\times{\hat{i}}=-\hat{k}, \hat{k}\times{\hat{j}}=-\hat{i}, \hat{i}\times{\hat{k}}=-\hat{j}\)
\(=0+a_{1}b_{2}\hat{k}-a_{1}b_{3}\hat{j}-a_{2}b_{1}\hat{k}+0+a_{2}b_{3}\hat{i}+a_{3}b_{1}\hat{j}-a_{3}b_{2}\hat{i}+0\)
\(=\hat{i}(a_{2}b_{3}-a_{3}b_{2})-\hat{j}(a_{1}b_{3}-a_{3}b_{1})+\hat{k}(a_{1}b_{2}-a_{2}b_{1})\)
\(=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\end{array}\right|\)
\(\therefore\) \(\overline{a}\times{\overline{b}}=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\end{array}\right|\)
এখন, \(\overline{a}\times{\overline{b}}=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times{(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})}\)
\(=a_{1}b_{1}\hat{i}\times{\hat{i}}+a_{1}b_{2}\hat{i}\times{\hat{j}}+a_{1}b_{3}\hat{i}\times{\hat{k}}+a_{2}b_{1}\hat{j}\times{\hat{i}}+a_{2}b_{2}\hat{j}\times{\hat{j}}+a_{2}b_{3}\hat{j}\times{\hat{k}}+a_{3}b_{1}\hat{k}\times{\hat{i}}+a_{3}b_{2}\hat{k}\times{\hat{j}}+a_{3}b_{3}\hat{k}\times{\hat{k}}\)
\(=a_{1}b_{1}0+a_{1}b_{2}\hat{k}+a_{1}b_{3}(-\hat{j})+a_{2}b_{1}(-\hat{k})+a_{2}b_{2}0+a_{2}b_{3}\hat{i}+a_{3}b_{1}\hat{j}+a_{3}b_{2}(-\hat{i})+a_{3}b_{3}0\) ➜ \(\because \hat{i}\times{\hat{i}}=\hat{j}\times{\hat{j}}=\hat{k}\times{\hat{k}}=0\)
\(\hat{i}\times{\hat{j}}=\hat{k}, \hat{j}\times{\hat{k}}=\hat{i}, \hat{k}\times{\hat{i}}=\hat{j}\)
এবং
\(\hat{j}\times{\hat{i}}=-\hat{k}, \hat{k}\times{\hat{j}}=-\hat{i}, \hat{i}\times{\hat{k}}=-\hat{j}\)
\(=0+a_{1}b_{2}\hat{k}-a_{1}b_{3}\hat{j}-a_{2}b_{1}\hat{k}+0+a_{2}b_{3}\hat{i}+a_{3}b_{1}\hat{j}-a_{3}b_{2}\hat{i}+0\)
\(=\hat{i}(a_{2}b_{3}-a_{3}b_{2})-\hat{j}(a_{1}b_{3}-a_{3}b_{1})+\hat{k}(a_{1}b_{2}-a_{2}b_{1})\)
\(=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\end{array}\right|\)
\(\therefore\) \(\overline{a}\times{\overline{b}}=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\end{array}\right|\)
ভেক্টর গুণনের জ্যামিতিক ব্যাখ্যা
Geometric interpretation of Vector product
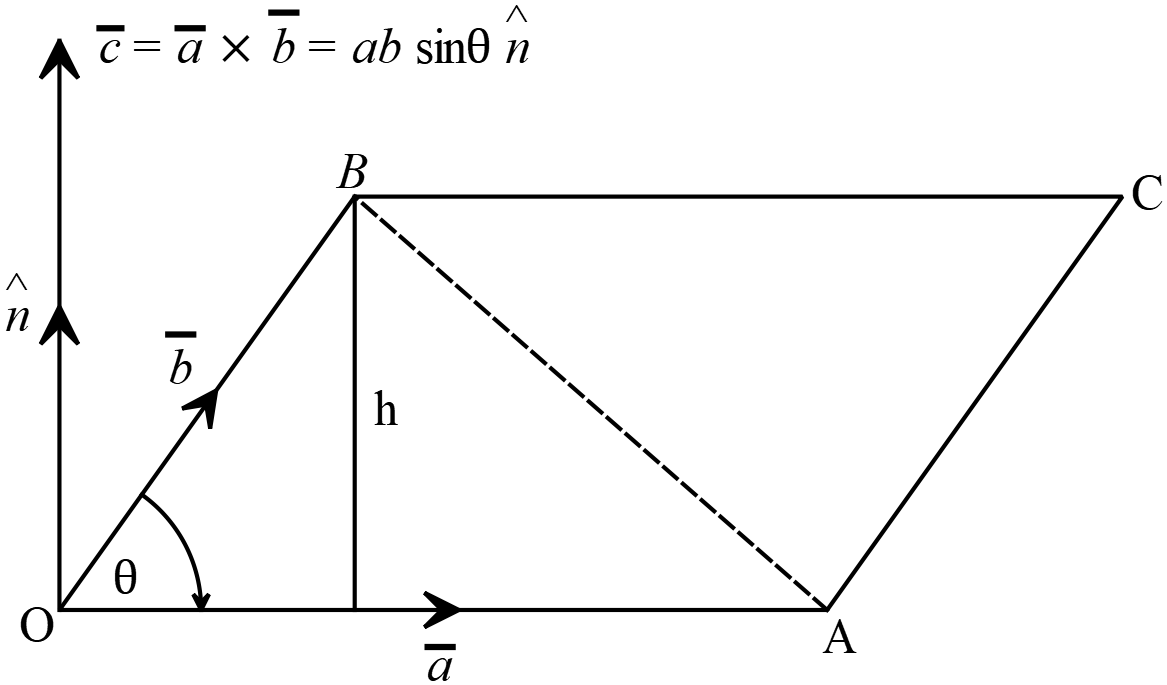\(OACB\) সামান্তরিকের \(OA\) এবং \(OB\) সন্নিহিত বাহু দুইটি দ্বারা যথাক্রমে \(\overline{a}\) এবং \(\overline{b}\) ভেক্টর দুইটি সূচীত করা হলো। যদি \(\angle{AOB}=\theta\) হয়,
তাহলে, \(\overline{a}\times{\overline{b}}=\overrightarrow{OA}\times{\overrightarrow{OB}}\)
\(=OA \ OB \sin{\theta} \ \hat{n}\)
\(=ab\sin{\theta} \ \hat{n}\)
\(=\overline{c}\)
যেখানে, \(\hat{n}\) হলো \(\overline{a}\) এবং \(\overline{b}\) ভেক্টরদ্বয়ের সমতলের উপর লম্ব একক ভেক্টর। উল্লেখ্য, ডানহাতি স্ক্র \(\overline{a}\) থেকে \(\overline{b}\) এর দিকে ক্ষুদ্রতম কোণে ঘূর্ণন হলে \(\hat{n}\) এর দিক \(OD\) বরাবর এবং \(\overline{b}\) থেকে \(\overline{a}\) এর দিকে ঘূর্ণন হলে \(\hat{n}\) এর দিক \(DO\) বরাবর হবে।
\(\overline{a}\times{\overline{b}}=OA \ OB \sin{\theta}\)
\(=OA \ h\) যখন, \(h=OB \sin{\theta}\)
\(=OACB\) সামান্তরিকের ক্ষেত্রফল।
\(\Box{OACB}=|\overline{a}\times{\overline{b}}|\)
আবার, \(\frac{1}{2}|\overline{a}\times{\overline{b}}|=\frac{1}{2}.OA.h\)
\(=\triangle{OAB}\)
\(\triangle{OAB}=\frac{1}{2}|\overline{a}\times{\overline{b}}|\)
তিনটি ভেক্টরের স্কেলার গুণন
Scalar multiplication of three vectors
\(\overline{a}, \overline{b}\) এবং \(\overline{c}\) তিনটি ভেক্টর রাশি।
তাহলে,
\(\overline{a}.(\overline{b}\times{\overline{c}})=\overline{b}.(\overline{c}\times{\overline{a}})\)\(=\overline{c}.(\overline{a}\times{\overline{b}})=\) ভেক্টর তিনটি দ্বারা গঠিত সামান্তরিক আকারের ঘনবস্তুর আয়তন।
অথবা,
\([\overline{a} \ \overline{b} \ \overline{c}]=\overline{a}.(\overline{b}\times{\overline{c}})=\overline{b}.(\overline{c}\times{\overline{a}})\)\(=\overline{c}.(\overline{a}\times{\overline{b}})=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|\)
তাহলে,
\(\overline{a}.(\overline{b}\times{\overline{c}})=\overline{b}.(\overline{c}\times{\overline{a}})\)\(=\overline{c}.(\overline{a}\times{\overline{b}})=\) ভেক্টর তিনটি দ্বারা গঠিত সামান্তরিক আকারের ঘনবস্তুর আয়তন।
অথবা,
\([\overline{a} \ \overline{b} \ \overline{c}]=\overline{a}.(\overline{b}\times{\overline{c}})=\overline{b}.(\overline{c}\times{\overline{a}})\)\(=\overline{c}.(\overline{a}\times{\overline{b}})=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|\)
তিনটি ভেক্টর সমতলীয় হওয়ার শর্ত
Condition for three vectors to be coplanar
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}, \overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) এবং \(\overline{c}=c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}\) ভেক্টর তিনটির সমতলীয় হওয়ার শর্ত
\([\overline{a} \ \overline{b} \ \overline{c}]=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|=0\)
\([\overline{a} \ \overline{b} \ \overline{c}]=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|=0\)
নির্দিষ্ট তিনটি ভেক্টর সমতলীয় হওয়ার শর্ত
Condition for fixed three vectors to be coplanar
যদি, \(\overline{a}, \ \overline{b}\) এবং \(\overline{c}\) সমতলীয় ভেক্টর হয় তবে দেখাও যে,
\(x\overline{a}+y\overline{b}+z\overline{c}=0\)
যেখানে, \(x=0, \ y=0, \ z=0\)
ভেক্টরের যোগাশ্রয়ী সমাবেশ
linear combination of vectors
দেখাও যে, ভেক্টর \(\overline{r}\) কে উহার সহিত সমতলীয় অসমরৈখিক ভেক্টর \(\overline{a}\) এবং \(\overline{b}\) এর যোগাশ্রয়ী সমাবেশ যেখানে, \(x\) এবং \(y\) স্কেলার।
\(\overline{r}=x\overline{a}+y\overline{b}\)
\(\overline{r}=x\overline{a}+y\overline{b}\)
ত্রিমাত্রিক জগতে ভেক্টরের মাণ
Values of vectors in a three-dimensional Space
দেখাও যে, \(\overline{A}=A_{1}\hat{i}+A_{2}\hat{j}+A_{3}\hat{k}\) ভেক্টরের মাণ
\(A=|\overline{A}|=\sqrt{A_{1}^2+A_{2}^2+A_{3}^2}\)
\(A=|\overline{A}|=\sqrt{A_{1}^2+A_{2}^2+A_{3}^2}\)
দুইটি নির্দিষ্ট বিন্দুগামী ভেক্টরের মাণ
The values of two fixed-point vectors
যদি, \(A(x_{1},y_{1},z_{1})\) আদি বিন্দু এবং \(B(x_{2},y_{2},z_{2})\) প্রান্তবিন্দু হয় তবে দেখাও যে, ভেক্টর \(\overrightarrow{AB}=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}+(z_{2}-z_{1})\hat{k}\) এর মাণ
\(AB=|\overrightarrow{AB}|=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2+(z_{2}-z_{1})^2}\)
\(AB=|\overrightarrow{AB}|=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2+(z_{2}-z_{1})^2}\)
তিনটি ভেক্টরের ভেক্টর গুণন বা ক্রস গুণন
Vector multiplication of three vectors
তিনটি ভেক্টর \(\overline{a}, \overline{b}\) এবং \(\overline{c}\) এর ভেক্টর গুণন
\(\overline{a}\times(\overline{b}\times{\overline{c}})=(\overline{a}.\overline{c})\overline{b}-(\overline{a}.\overline{b})\overline{c}\) \((\overline{a}\times\overline{b})\times{\overline{c}}=(\overline{a}.\overline{c})\overline{b}-(\overline{b}.\overline{c})\overline{a}\)
\(\overline{a}\times(\overline{b}\times{\overline{c}})=(\overline{a}.\overline{c})\overline{b}-(\overline{a}.\overline{b})\overline{c}\) \((\overline{a}\times\overline{b})\times{\overline{c}}=(\overline{a}.\overline{c})\overline{b}-(\overline{b}.\overline{c})\overline{a}\)
চারটি ভেক্টরের স্কেলার গুণন
Scalar multiplication of four vectors
\(\overline{a}, \overline{b}, \overline{c}\) এবং \(\overline{d}\) যে কোনো ভেক্টরের জন্য
\((\overline{a}\times\overline{b}).(\overline{c}\times\overline{d})=\left|\begin{array}{c}\overline{a}.\overline{c}&\overline{a}.\overline{d}\\\overline{b}.\overline{c}&\overline{b}.\overline{d}\end{array}\right|\)
\((\overline{a}\times\overline{b}).(\overline{c}\times\overline{d})=\left|\begin{array}{c}\overline{a}.\overline{c}&\overline{a}.\overline{d}\\\overline{b}.\overline{c}&\overline{b}.\overline{d}\end{array}\right|\)
×
কার্তেসীয় ত্রিমাত্রিক জগতে মূলবিন্দু \((0, 0, 0)\) এর সাপেক্ষে \(P(x, y, z)\) এর অবস্থান ভেক্টর \(\overline{r}\) হলে,
\(P\) বিন্দুর অবস্থান ভেক্টর \(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
\(P\) বিন্দুর অবস্থান ভেক্টর \(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
প্রমাণঃ
ধরি,
কার্তেসীয় ত্রিমাত্রিক আয়তাকার স্থাংক ব্যবস্থায় \(P\) বিন্দুর কার্তেসীয় স্থানাঙ্ক \((x, y, z)\) এবং মূলবিন্দু \((0, 0, 0), x, y\) ও \(z\) অক্ষের ধনাত্মক দিকে একক ভেক্টর যথাক্রমে \(\hat{i}, \hat{j}\) ও \(\hat{k}\)
এবং \(\overrightarrow{OP}=\overline{r}\)
এখানে, \(\overrightarrow{OA}=\overrightarrow{CQ}=x\hat{i}, \overrightarrow{OB}=\overrightarrow{QP}=y\hat{j}\) এবং \(\overrightarrow{OC}=z\hat{k}\)
এখন, \({OCQP}\)-এ ভেক্টর সংযোগের বহুভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{CQ}+\overrightarrow{QP}\)
\(\Rightarrow \overline{r}=z\overline{k}+x\overline{i}+y\overline{j}\) ➜ \(\because \overrightarrow{OC}=z\hat{k}\)
\(\overrightarrow{CQ}=x\hat{i}\)
\(\overrightarrow{QP}=y\hat{j}\)
\(\therefore\) \(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
কার্তেসীয় ত্রিমাত্রিক আয়তাকার স্থাংক ব্যবস্থায় \(P\) বিন্দুর কার্তেসীয় স্থানাঙ্ক \((x, y, z)\) এবং মূলবিন্দু \((0, 0, 0), x, y\) ও \(z\) অক্ষের ধনাত্মক দিকে একক ভেক্টর যথাক্রমে \(\hat{i}, \hat{j}\) ও \(\hat{k}\)এবং \(\overrightarrow{OP}=\overline{r}\)
এখানে, \(\overrightarrow{OA}=\overrightarrow{CQ}=x\hat{i}, \overrightarrow{OB}=\overrightarrow{QP}=y\hat{j}\) এবং \(\overrightarrow{OC}=z\hat{k}\)
এখন, \({OCQP}\)-এ ভেক্টর সংযোগের বহুভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{CQ}+\overrightarrow{QP}\)
\(\Rightarrow \overline{r}=z\overline{k}+x\overline{i}+y\overline{j}\) ➜ \(\because \overrightarrow{OC}=z\hat{k}\)
\(\overrightarrow{CQ}=x\hat{i}\)
\(\overrightarrow{QP}=y\hat{j}\)
\(\therefore\) \(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
×
\(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\) এর মাণ,
\(r=|\overline{r}|=\sqrt{x^2+y^2+z^2}\)
\(r=|\overline{r}|=\sqrt{x^2+y^2+z^2}\)
প্রমাণঃ
ধরি,\(P(x,y,z), \ L(x,0,0), \ M(0,y,0), \ N(0,0,z), \ \overrightarrow{OP}=\overline{r}\)
এবং অক্ষরেখাগুলি বরাবর একক ভেক্টর যথাক্রমে \(\hat{i}, \ \hat{j}, \ \hat{k}\)
\(\therefore \overrightarrow{OL}=\overrightarrow{MN}=x\hat{i}, \overrightarrow{OM}=y\hat{j}, \overrightarrow{ON}=\overrightarrow{NP}=z\hat{k}\)
\(\triangle{OMN}\) সমকোণী
\(\therefore ON^2=OM^2+MN^2\)
আবার, \(\triangle{OPN}\) সমকোণী
\(\therefore OP^2=ON^2+NP^2\)
\(\Rightarrow OP^2=OM^2+MN^2+NP^2\) ➜ \(\because ON^2=OM^2+MN^2\)
\(\Rightarrow OP^2=MN^2+OM^2+NP^2\)
\(\Rightarrow \overline{r}.\overline{r}=x\hat{i}.x\hat{i}+y\hat{j}.y\hat{j}+z\hat{k}.z\hat{k}\) ➜ \(\because \overrightarrow{OP}=\overline{r}, \overrightarrow{MN}=x\hat{i}, \overrightarrow{OM}=y\hat{j}, \overrightarrow{NP}=z\hat{k}\)
\(\Rightarrow r^2=x^2\hat{i}.\hat{i}+y^2\hat{j}.\hat{j}+z^2\hat{k}.\hat{k}\) ➜ \(\because \overline{r}.\overline{r}=r^2\)
\(\Rightarrow r^2=x^2.1+y^2.1+z^2.1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=\hat{k}.\hat{k}=1\)
\(\Rightarrow r^2=x^2+y^2+z^2\)
\(\Rightarrow r=\sqrt{x^2+y^2+z^2}\)
\(\therefore\) \(r=|\overline{r}|=\sqrt{x^2+y^2+z^2}\)
×
\(O\) বিন্দু থেকে তিনটি পরস্পর লম্ব সরলরেখা \(OX, OY, OZ\) আঁকা হলো।
\(\overrightarrow{OX}=\hat{i}, \overrightarrow{OY}=\hat{j}\) এবং \(\overrightarrow{OZ}=\hat{k}\) হয়, যেখানে \(\hat{i}, \hat{j}, \hat{k}\) তিনটি পরস্পর লম্ব একক ভেক্টর।
\(\overrightarrow{OP}=\overline{r}\) ভেক্টরকে তিনটি পরস্পর লম্ব একক ভেক্টর \(\hat{i}, \hat{j}, \hat{k}\) এর যোগাশ্রয়ী সমাবেশ হিসেবে প্রকাশ করা হয়েছে।
অর্থাৎ , \(\overline{r}=x\overline{i}+y\overline{j}+z\overline{k}\)
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=x\overline{i}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=y\overline{j}\)
\(OZ\) বরাবর \(\overline{r}\) এর অংশক \(=z\overline{k}\)
\(\overrightarrow{OX}=\hat{i}, \overrightarrow{OY}=\hat{j}\) এবং \(\overrightarrow{OZ}=\hat{k}\) হয়, যেখানে \(\hat{i}, \hat{j}, \hat{k}\) তিনটি পরস্পর লম্ব একক ভেক্টর।
\(\overrightarrow{OP}=\overline{r}\) ভেক্টরকে তিনটি পরস্পর লম্ব একক ভেক্টর \(\hat{i}, \hat{j}, \hat{k}\) এর যোগাশ্রয়ী সমাবেশ হিসেবে প্রকাশ করা হয়েছে।
অর্থাৎ , \(\overline{r}=x\overline{i}+y\overline{j}+z\overline{k}\)
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=x\overline{i}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=y\overline{j}\)
\(OZ\) বরাবর \(\overline{r}\) এর অংশক \(=z\overline{k}\)
প্রমাণঃ
ধরি, \(P\) যে কোনো একটি বিন্দু। \(P\) বিন্দুর মধ্য দিয়ে \(YOZ, ZOX\) এবং \(XOY\) সমতলগুলির সমান্তরাল তিনটি তল অঙ্কন করি; যারা \(OX, OY\) এবং \(OZ\) কে যথাক্রমে \(L, M\) এবং \(N^{\prime}\) বিন্দুতে ছেদ করে। এভাবে একটি আয়াতাকার ঘনক \(OLNML^{\prime}N^{\prime}M^{\prime}P\) পাওয়া যায়। যার একটি কর্ণ \(OP,\) যাকে \(\overline{r}\) দ্বারা সূচীত করা যায়।
\(\overline{r}=\overrightarrow{OP}\)
\(=\overrightarrow{ON}+\overrightarrow{NP}\) ➜ \(\triangle{OPN}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{ON}+\overrightarrow{NP}\)
\(=\overrightarrow{OM}+\overrightarrow{MN}+\overrightarrow{ON^{\prime}}\) ➜ \(\triangle{OMN}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{ON}=\overrightarrow{OM}+\overrightarrow{MN}\)
এবং \(\overrightarrow{NP}=\overrightarrow{ON^{\prime}}\)
\(=\overrightarrow{OM}+\overrightarrow{OL}+\overrightarrow{ON^{\prime}}\) ➜ \(\because \overrightarrow{MN}=\overrightarrow{OL}\)
\(=\overrightarrow{OL}+\overrightarrow{OM}+\overrightarrow{ON^{\prime}}\)
\(x, y, z\) এরূপ তিনটি স্কেলার রাশি যেখানে,
\(P\) বিন্দুর আয়াতাকার কার্তেসীয় স্থানাঙ্ক \((x, y, z)\)
এবং
\(\overrightarrow{OL}=x\overrightarrow{OA}=x\hat{i}\)
\(\overrightarrow{OM}=y\overrightarrow{OB}=y\hat{j}\)
\(\overrightarrow{ON^{\prime}}=z\overrightarrow{OC}=z\hat{k}\)
\(\therefore \overrightarrow{OP}=\overrightarrow{OL}+\overrightarrow{OM}+\overrightarrow{ON^{\prime}}\)
\(\Rightarrow \overrightarrow{OP}=x\hat{i}+y\hat{j}+z\hat{k}\)
\(\therefore \overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
ইহা স্পষ্ট যে,
\(OX\) বরাবর \(\overline{r}\) এর অংশক \(=x\overline{i}\)
\(OY\) বরাবর \(\overline{r}\) এর অংশক \(=y\overline{j}\)
\(OZ\) বরাবর \(\overline{r}\) এর অংশক \(=z\overline{k}\)
( প্রমাণিত )
×
\(A(\overline{a})\) বিন্দুগামী \(\overline{B}\) ভেক্টরের সমান্তরাল রেখার ভেক্টর সমীকরণঃ
\(\overline{r}=\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times\overline{b}=0\)
প্রমাণঃ
\(\overline{r}=\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times\overline{b}=0\)
ধরি, \(O\) মূলবিন্দু সাপেক্ষে \(A(\overline{a})\) বিন্দুর অবস্থান ভেক্টর \(\overrightarrow{OA}=\overline{a}\) এবং \(A(\overline{a})\) বিন্দুগামী সরলরেখার উপর \(P(\overline{r})\) যে কোনো একটি বিন্দু যার \(O\) মূলবিন্দু সাপেক্ষে অবস্থান ভেক্টর \(\overrightarrow{OP}=\overline{r}\)\(\triangle{OAP}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP} ........(1)\)
যেহেতু, \(\overrightarrow{AP}\) ভেক্টরটি \(\overline{b}\) ভেক্টরের সমান্তরাল।
সুতরাং, \(\overrightarrow{AP}=t\overline{b},\) যখন \(t\) একটি প্যারামিটার।
\((1)\) নং হতে,
\(\overline{r}=\overline{a}+t\overline{b}\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
এবং
\(\overrightarrow{OA}=\overline{a}\)
\(\overrightarrow{AP}=t\overline{b}\)
যা সরলরেখার ভেক্টর সমীকরণ নির্দেশ করে।
আবার,
\((1)\) নং হতে,
\(\overrightarrow{OA}+\overrightarrow{AP}=\overrightarrow{OP}\)
\(\Rightarrow \overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\)
\(\therefore \overrightarrow{AP}=\overline{r}-\overline{a}\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
এখন,
\(\overrightarrow{AP}\) এবং \(\overline{b}\) সমান্তরাল বলে,
\(\overrightarrow{AP}\times\overline{b}=0\)
\(\therefore (\overline{r}-\overline{a})\times\overline{b}=0\)➜ \(\because \overrightarrow{AP}=\overline{r}-\overline{a}\)
( প্রমাণিত )
×
\(A(\overline{a})\) বিন্দুগামী এবং \(B(\overline{b})\) ও \(C(\overline{c})\) বিন্দুদ্বয়ের সংযোগ রেখার সমান্তরাল সরলরেখার ভেক্টর সমীকরণঃ
\(\overline{r}=\overline{a}+t(\overline{b}-\overline{c})\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{c}-\overline{b})\)
প্রমাণঃ
\(\overline{r}=\overline{a}+t(\overline{b}-\overline{c})\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{c}-\overline{b})\)
ধরি, \(O\) মূলবিন্দু সাপেক্ষে \(A(\overline{a}), B(\overline{b})\) এবং \(C(\overline{c})\) বিন্দু তিনটির অবস্থান ভেক্টর \(\overrightarrow{OA}=\overline{a}, \overrightarrow{OB}=\overline{b}\) এবং \(\overrightarrow{OC}=\overline{c}\)\(\triangle{OCB}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OC}+\overrightarrow{CB}=\overrightarrow{OB}\)
\(\Rightarrow \overrightarrow{CB}=\overrightarrow{OB}-\overrightarrow{OC}\)
\(\therefore \overrightarrow{CB}=\overline{b}-\overline{c} ........(1)\)
\(A(\overline{a})\) বিন্দুগামী এবং \(CB\) রেখার সমান্তরাল সরলরেখার উপর \(P(\overline{r})\) যে কোনো একটি বিন্দু নেই যার \(O\) মূলবিন্দু সাপেক্ষে অবস্থান ভেক্টর \(\overrightarrow{OP}=\overline{r}\)
\(\triangle{OAP}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP} ........(2)\)
যেহেতু, \(\overrightarrow{AP}\) ভেক্টরটি \(\overrightarrow{CB}=\overline{b}-\overline{c}\) ভেক্টরের সমান্তরাল।
সুতরাং, \(\overrightarrow{AP}=t\overrightarrow{CB}\) যখন \(t\) একটি প্যারামিটার।
\(\therefore \overrightarrow{AP}=t(\overline{b}-\overline{c})\)
\((2)\) নং হতে,
\(\overline{r}=\overline{a}+t(\overline{b}-\overline{c})\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
\(\overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{AP}=t(\overline{b}-\overline{c})\)
যা সরলরেখার ভেক্টর সমীকরণ নির্দেশ করে।
আবার,
\((2)\) নং হতে,
\(\overrightarrow{OA}+\overrightarrow{AP}=\overrightarrow{OP}\)
\(\Rightarrow \overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\)
\(\therefore \overrightarrow{AP}=\overline{r}-\overline{a} ......(3)\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
এখন,
\(\overrightarrow{AP}\) এবং \(\overrightarrow{CB}\) সমান্তরাল বলে,
\(\overrightarrow{AP}\times\overrightarrow{CB}=0\)
\((3)\) ও \((1)\) নং হতে,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{c})=0\)
( প্রমাণিত )
×
\(A(\overline{a})\) এবং \(B(\overline{b})\) বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ,
\(\overline{r}=(1-t)\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{a})=0\)
প্রমাণঃ
\(\overline{r}=(1-t)\overline{a}+t\overline{b}\)
অথবা,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{a})=0\)
ধরি, \(O\) মূলবিন্দু , \(A(\overline{a})\) এবং \(B(\overline{b})\) বিন্দু দিয়ে যায় এবং রেখাটির উপর \(P(\overline{r})\) যে কোনো একটি বিন্দু \(O\) মূলবিন্দু সাপেক্ষে \(A, B\) এবং \(P\) বিন্দুগুলির অবস্থান ভেক্টর যথাক্রমে \(\overrightarrow{OA}=\overline{a}, \overrightarrow{OB}=\overline{b}\) এবং \(\overrightarrow{OP}=\overline{r}\)
\(\triangle{OAB}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}\)
\(\Rightarrow \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\)
\(\therefore \overrightarrow{AB}=\overline{b}-\overline{a} ........(1)\) ➜ \(\because \overrightarrow{OB}=\overline{b}\)
এবং
\(\overrightarrow{OA}=\overline{a}\)
যেহেতু, \(\overrightarrow{AP}\) এবং \(\overrightarrow{AB}\) ভেক্টরদ্বয় একই ধারক রেখার উপর অবস্থিত।
সুতরাং, \(\overrightarrow{AP}=t\overrightarrow{AB}\) যখন \(t\) একটি প্যারামিটার।
\(\therefore \overrightarrow{AP}=t(\overline{b}-\overline{a}) .......(2)\)
আবার, \(\triangle{OAP}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP} .......(3)\)
\((3)\) হতে,
\(\overline{r}=\overline{a}+t(\overline{b}-\overline{a})\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
\(\overrightarrow{OA}=\overline{a}\)
এবং \(\overrightarrow{AP}=t(\overline{b}-\overline{a})\)
\(\Rightarrow \overline{r}=\overline{a}+t\overline{b}-t\overline{a}\)
\(\therefore \overline{r}=(1-t)\overline{a}+t\overline{b}\)
যা দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার ভেক্টর সমীকরণ নির্দেশ করে।
আবার,
\((3)\) হতে,
\(\overrightarrow{OA}+\overrightarrow{AP}=\overrightarrow{OP}\)
\(\Rightarrow \overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\)
\(\Rightarrow \overrightarrow{AP}=\overline{r}-\overline{a} ......(4)\) ➜ \(\because \overrightarrow{OP}=\overline{r}\)
এবং \(\overrightarrow{OA}=\overline{a}\)
এখন,
\(\overrightarrow{AP}\) এবং \(\overrightarrow{AB}\) একই সরলরেখায় অবস্থিত বলে,
\(\overrightarrow{AP}\times\overrightarrow{AB}=0\)
\((4)\) ও \((1)\) নং হতে,
\((\overline{r}-\overline{a})\times(\overline{b}-\overline{a})=0\)
( প্রমাণিত )
×
সরলরেখার ভেক্টর সমীকরণ থেকে কার্তেসীয় সমীকরণঃ
ভেক্টর সমীকরণ \(\overline{r}=\overline{a}+t\overline{b}\) এর কার্তেসীয় সমীকরণ,
\(\frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}\)
প্রমাণঃ
ভেক্টর সমীকরণ \(\overline{r}=\overline{a}+t\overline{b}\) এর কার্তেসীয় সমীকরণ,
\(\frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}\)
ধরি, \(O\) মূলবিন্দু এবং \(A(\overline{a}), B(\overline{b}), P(\overline{r})\) বিন্দুগামী সরলরেখার ভেক্টর সমীকরণগুলি যথাক্রমে
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
\(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\)
\(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
যখন
\(\overline{r}=\overline{a}+t\overline{b}\)
\(\Rightarrow x\hat{i}+y\hat{j}+z\hat{k}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}+tb_{1}\hat{i}+tb_{2}\hat{j}+tb_{3}\hat{k}\) ➜ \(\because \overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
এবং
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
\(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\)
\(\therefore x\hat{i}+y\hat{j}+z\hat{k}=(a_{1}+tb_{1})\hat{i}+(a_{2}+tb_{2})\hat{j}+(a_{3}+tb_{3})\hat{k} ......(1)\)
\((1)\) নং সমীকরণের উভয় পার্শ হতে \(\hat{i}, \hat{j}, \hat{k}\) এর সহগগুলি সমীকৃত করে,
\(x=a_{1}+tb_{1}, y=a_{2}+tb_{2}, z=a_{3}+tb_{3}\)
\(\Rightarrow x-a_{1}=tb_{1}, y-a_{2}=tb_{2}, z-a_{3}=tb_{3}\)
\(\Rightarrow \frac{x-a_{1}}{b_{1}}=t, \frac{y-a_{2}}{b_{2}}=t, \frac{z-a_{3}}{b_{3}}=t\)
\(\Rightarrow \frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}=t\)
\(\therefore \frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}\)
ইহাই নির্ণেয় কার্তেসীয় সমীকরণ।
( প্রমাণিত )
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
\(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\)
\(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
যখন
\(\overline{r}=\overline{a}+t\overline{b}\)
\(\Rightarrow x\hat{i}+y\hat{j}+z\hat{k}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}+tb_{1}\hat{i}+tb_{2}\hat{j}+tb_{3}\hat{k}\) ➜ \(\because \overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
এবং
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
\(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\)
\(\therefore x\hat{i}+y\hat{j}+z\hat{k}=(a_{1}+tb_{1})\hat{i}+(a_{2}+tb_{2})\hat{j}+(a_{3}+tb_{3})\hat{k} ......(1)\)
\((1)\) নং সমীকরণের উভয় পার্শ হতে \(\hat{i}, \hat{j}, \hat{k}\) এর সহগগুলি সমীকৃত করে,
\(x=a_{1}+tb_{1}, y=a_{2}+tb_{2}, z=a_{3}+tb_{3}\)
\(\Rightarrow x-a_{1}=tb_{1}, y-a_{2}=tb_{2}, z-a_{3}=tb_{3}\)
\(\Rightarrow \frac{x-a_{1}}{b_{1}}=t, \frac{y-a_{2}}{b_{2}}=t, \frac{z-a_{3}}{b_{3}}=t\)
\(\Rightarrow \frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}=t\)
\(\therefore \frac{x-a_{1}}{b_{1}}=\frac{y-a_{2}}{b_{2}}=\frac{z-a_{3}}{b_{3}}\)
ইহাই নির্ণেয় কার্তেসীয় সমীকরণ।
( প্রমাণিত )
×
একটি ভেক্টরের উপর অন্য একটি ভেক্টরের অভিক্ষেপঃ
\(\overline{a}\) বরাবর \(\overline{b}\) এর অভিক্ষেপ, \(\frac{\overline{a}.\overline{b}}{a}\) অথবা, \(\hat{a}.\overline{b}\)
\(\overline{b}\) বরাবর \(\overline{a}\) এর অভিক্ষেপ, \(\frac{\overline{a}.\overline{b}}{b}\) অথবা, \(\hat{b}.\overline{a}\)
প্রমাণঃ
\(\overline{a}\) বরাবর \(\overline{b}\) এর অভিক্ষেপ, \(\frac{\overline{a}.\overline{b}}{a}\) অথবা, \(\hat{a}.\overline{b}\)
\(\overline{b}\) বরাবর \(\overline{a}\) এর অভিক্ষেপ, \(\frac{\overline{a}.\overline{b}}{b}\) অথবা, \(\hat{b}.\overline{a}\)
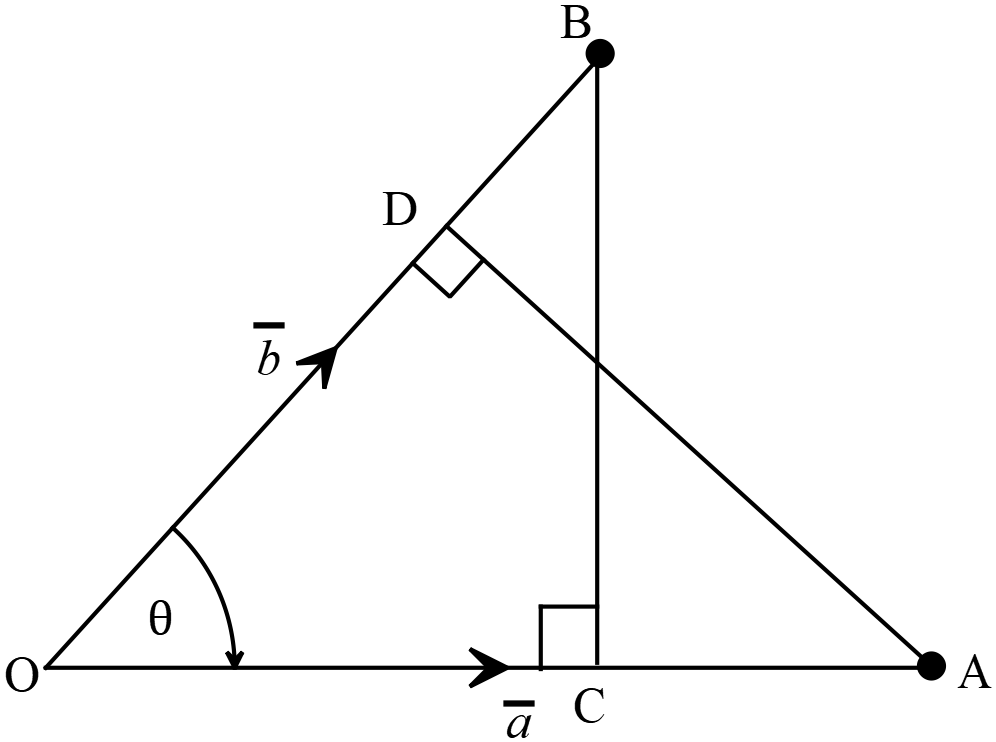ধরি, \(\overrightarrow{OA}=\overline{a}\) এবং \(\overrightarrow{OB}=\overline{b}\) এবং ভেক্টর দুইটির মধ্যবর্তী কোণ \(\theta\) \(B\) বিন্দু থেকে \(OA\) এর উপর \(BC\) এবং \(A\) বিন্দু থেকে \(OB\) এর উপর \(AD\) লম্ব অঙ্কন করি,
এখানে, \(OC=OB\times{\frac{OC}{OB}}\)
\(=b\cos{\theta}\) ➜ \(\because OB=b\)
এবং \(\frac{OC}{OB}=\cos{\theta}\)
\(\therefore OC=b\cos{\theta}\)
যা \(\overline{a}\) বরাবর \(\overline{b}\) এর অভিক্ষেপ।
আবার, \( OC=b\cos{\theta}\)
\(=\frac{\overline{a}.\overline{b}}{a}\) ➜ \(\because ab\cos{\theta}=\overline{a}.\overline{b}\)
\(\Rightarrow b\cos{\theta}=\frac{\overline{a}.\overline{b}}{a}\)
\(=\frac{\overline{a}}{a}.\overline{b}\)
\(=\hat{a}.\overline{b}\)
\(\therefore \overline{a}\) বরাবর \(\overline{b}\) এর অভিক্ষেপ, \(\frac{\overline{a}.\overline{b}}{a}\) অথবা, \(\hat{a}.\overline{b}\)
আবার, \(OD=OA\times{\frac{OD}{OA}}\)
\(=a\cos{\theta}\) ➜ \(\because OA=a\)
এবং \(\frac{OD}{OA}=\cos{\theta}\)
\(\therefore OD=a\cos{\theta}\)
যা \(\overline{b}\) বরাবর \(\overline{a}\) এর অভিক্ষেপ।
আবার, \( OD=a\cos{\theta}\)
\(=\frac{\overline{a}.\overline{b}}{b}\) ➜ \(\because ab\cos{\theta}=\overline{a}.\overline{b}\)
\(\Rightarrow a\cos{\theta}=\frac{\overline{a}.\overline{b}}{b}\)
\(=\frac{\overline{b}}{b}.\overline{a}\)
\(=\hat{b}.\overline{a}\)
\(\therefore \overline{b}\) বরাবর \(\overline{a}\) এর অভিক্ষেপ, \(\frac{\overline{a}.\overline{b}}{b}\) অথবা, \(\hat{b}.\overline{a}\)
( প্রমাণিত )
×
একটি ভেক্টরের দিক বরাবর অন্য একটি ভেক্টরের অংশকঃ
\(\overline{a}\) বরাবর \(\overline{b}\) এর উপাংশ ভেক্টর, \((\hat{a}.\overline{b})\hat{a}\) অথবা, \(\frac{\overline{a}.\overline{b}}{a^2}\overline{a}\)
\(\overline{b}\) বরাবর \(\overline{a}\) এর উপাংশ ভেক্টর, \((\overline{a}.\hat{b})\hat{b}\) অথবা, \(\frac{\overline{a}.\overline{b}}{b^2}\overline{b}\)
প্রমাণঃ
\(\overline{a}\) বরাবর \(\overline{b}\) এর উপাংশ ভেক্টর, \((\hat{a}.\overline{b})\hat{a}\) অথবা, \(\frac{\overline{a}.\overline{b}}{a^2}\overline{a}\)
\(\overline{b}\) বরাবর \(\overline{a}\) এর উপাংশ ভেক্টর, \((\overline{a}.\hat{b})\hat{b}\) অথবা, \(\frac{\overline{a}.\overline{b}}{b^2}\overline{b}\)
আমরা জানি,
\(\overline{a}\) বরাবর একক ভেক্টর \(\hat{a}=\frac{\overline{a}}{a}\) এবং \(\overline{b}\) বরাবর একক ভেক্টর \(\hat{b}=\frac{\overline{b}}{b}\)
আবার,
\(\overline{a}\) বরাবর \(\overline{b}\) এর অভিক্ষেপ \(OC=b\cos{\theta}\)
এবং \(\overline{b}\) বরাবর \(\overline{a}\) এর অভিক্ষেপ \(OD=a\cos{\theta}\)
এখন,
\(\overline{a}\) বরাবর \(\overline{b}\) এর উপাংশ ভেক্টর,
\(\overrightarrow{OC}=OC\hat{a}\)
\(=b\cos{\theta}\times{\hat{a}}\) ➜ \(\because OC=b\cos{\theta}\)
\(=b\cos{\theta}\times{\frac{\overline{a}}{a}}\) ➜ \(\because \hat{a}=\frac{\overline{a}}{a}\)
\(=\frac{\overline{a}.\overline{b}}{a}\times{\frac{\overline{a}}{a}}\) ➜ \(\because ab\cos{\theta}=\overline{a}.\overline{b}\)
\(\Rightarrow b\cos{\theta}=\frac{\overline{a}.\overline{b}}{a}\)
\(=\frac{\overline{a}.\overline{b}}{a}\times{\frac{\overline{a}}{a}}\)
\(=\frac{\overline{a}.\overline{b}}{a^2}\overline{a}\)
\(\therefore \overline{a}\) বরাবর \(\overline{b}\) এর উপাংশ ভেক্টর, \((\hat{a}.\overline{b})\hat{a}\) অথবা, \(\frac{\overline{a}.\overline{b}}{a^2}\overline{a}\)
আবার,
\(\overline{b}\) বরাবর \(\overline{a}\) এর উপাংশ ভেক্টর,
\(\overrightarrow{OD}=OD\hat{b}\)
\(=a\cos{\theta}\times{\hat{b}}\) ➜ \(\because OD=a\cos{\theta}\)
\(=a\cos{\theta}\times{\frac{\overline{b}}{b}}\) ➜ \(\because \hat{b}=\frac{\overline{b}}{b}\)
\(=\frac{\overline{a}.\overline{b}}{b}\times{\frac{\overline{b}}{b}}\) ➜ \(\because ab\cos{\theta}=\overline{a}.\overline{b}\)
\(\Rightarrow a\cos{\theta}=\frac{\overline{a}.\overline{b}}{b}\)
\(=\frac{\overline{a}.\overline{b}}{b}\times{\frac{\overline{b}}{b}}\)
\(=\frac{\overline{a}.\overline{b}}{b^2}\overline{b}\)
\(\therefore \overline{b}\) বরাবর \(\overline{a}\) এর উপাংশ ভেক্টর, \((\overline{a}.\hat{b})\hat{b}\) অথবা, \(\frac{\overline{a}.\overline{b}}{b^2}\overline{b}\)
( প্রমাণিত )
×
দুইটি ভেক্টরের অন্তর্ভুক্ত কোণ
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\) এবং \(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) দুইটি অশূন্য ভেক্টরের অন্তর্ভুক্ত কোণ \(\theta\) হলে,
\(\theta=\cos^{-1}\left(\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}}\right)\)
প্রমাণঃ
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\) এবং \(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) দুইটি অশূন্য ভেক্টরের অন্তর্ভুক্ত কোণ \(\theta\) হলে,
\(\theta=\cos^{-1}\left(\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}}\right)\)
দেওয়া আছে,
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\) এবং \(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) দুইটি অশূন্য ভেক্টরের অন্তর্ভুক্ত কোণ \(\theta\)
এখন, \(a=\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}, b=\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}\) ➜ \(\because \overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
\(\Rightarrow r=\sqrt{x^2+y^2+z^2}\)
আবার, \(\overline{a}.\overline{b}=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}).(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})\)
\(=a_{1}b_{1}\hat{i}.\hat{i}+a_{1}b_{2}\hat{i}.\hat{j}+a_{1}b_{3}\hat{i}.\hat{k}+a_{2}b_{1}\hat{j}.\hat{i}+a_{2}b_{2}\hat{j}.\hat{j}+a_{2}b_{3}\hat{j}.\hat{k}+a_{3}b_{1}\hat{k}.\hat{i}+a_{3}b_{2}\hat{k}.\hat{j}+a_{3}b_{3}\hat{k}.\hat{k}\)
\(=a_{1}b_{1}1+a_{1}b_{2}0+a_{1}b_{3}0+a_{2}b_{1}0+a_{2}b_{2}1+a_{2}b_{3}0+a_{3}b_{1}0+a_{3}b_{2}0+a_{3}b_{3}1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=\hat{k}.\hat{k}=1\)
এবং
\(\hat{i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0\)
\(=a_{1}b_{1}+0+0+0+a_{2}b_{2}+0+0+0+a_{3}b_{3}\)
\(\therefore \overline{a}.\overline{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\)
আমরা জানি,
\(\theta=\cos^{-1}\left(\frac{\overline{a}.\overline{b}}{ab}\right)\)
\(=\cos^{-1}\left(\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}}\right)\) ➜ \(\because \overline{a}.\overline{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\)
এবং
\(a=\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}, b=\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}\)
\(\therefore \) \(\theta=\cos^{-1}\left(\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}}\right)\)
( প্রমাণিত )
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\) এবং \(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) দুইটি অশূন্য ভেক্টরের অন্তর্ভুক্ত কোণ \(\theta\)
এখন, \(a=\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}, b=\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}\) ➜ \(\because \overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\)
\(\Rightarrow r=\sqrt{x^2+y^2+z^2}\)
আবার, \(\overline{a}.\overline{b}=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}).(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})\)
\(=a_{1}b_{1}\hat{i}.\hat{i}+a_{1}b_{2}\hat{i}.\hat{j}+a_{1}b_{3}\hat{i}.\hat{k}+a_{2}b_{1}\hat{j}.\hat{i}+a_{2}b_{2}\hat{j}.\hat{j}+a_{2}b_{3}\hat{j}.\hat{k}+a_{3}b_{1}\hat{k}.\hat{i}+a_{3}b_{2}\hat{k}.\hat{j}+a_{3}b_{3}\hat{k}.\hat{k}\)
\(=a_{1}b_{1}1+a_{1}b_{2}0+a_{1}b_{3}0+a_{2}b_{1}0+a_{2}b_{2}1+a_{2}b_{3}0+a_{3}b_{1}0+a_{3}b_{2}0+a_{3}b_{3}1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=\hat{k}.\hat{k}=1\)
এবং
\(\hat{i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0\)
\(=a_{1}b_{1}+0+0+0+a_{2}b_{2}+0+0+0+a_{3}b_{3}\)
\(\therefore \overline{a}.\overline{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\)
আমরা জানি,
\(\theta=\cos^{-1}\left(\frac{\overline{a}.\overline{b}}{ab}\right)\)
\(=\cos^{-1}\left(\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}}\right)\) ➜ \(\because \overline{a}.\overline{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\)
এবং
\(a=\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}, b=\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}\)
\(\therefore \) \(\theta=\cos^{-1}\left(\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^2+a_{2}^2+a_{3}^2}\sqrt{b_{1}^2+b_{2}^2+b_{3}^2}}\right)\)
( প্রমাণিত )
×
তিনটি ভেক্টরের স্কেলার গুণনঃ
\(\overline{a}, \overline{b}\) এবং \(\overline{c}\) তিনটি ভেক্টর রাশি।
তাহলে,
\(\overline{a}.(\overline{b}\times{\overline{c}})=\overline{b}.(\overline{c}\times{\overline{a}})=\overline{c}.(\overline{a}\times{\overline{b}})=\) ভেক্টর তিনটি দ্বারা গঠিত সামান্তরিক আকারের ঘনবস্তুর আয়তন।
প্রমাণঃ
\(\overline{a}, \overline{b}\) এবং \(\overline{c}\) তিনটি ভেক্টর রাশি।
তাহলে,
\(\overline{a}.(\overline{b}\times{\overline{c}})=\overline{b}.(\overline{c}\times{\overline{a}})=\overline{c}.(\overline{a}\times{\overline{b}})=\) ভেক্টর তিনটি দ্বারা গঠিত সামান্তরিক আকারের ঘনবস্তুর আয়তন।
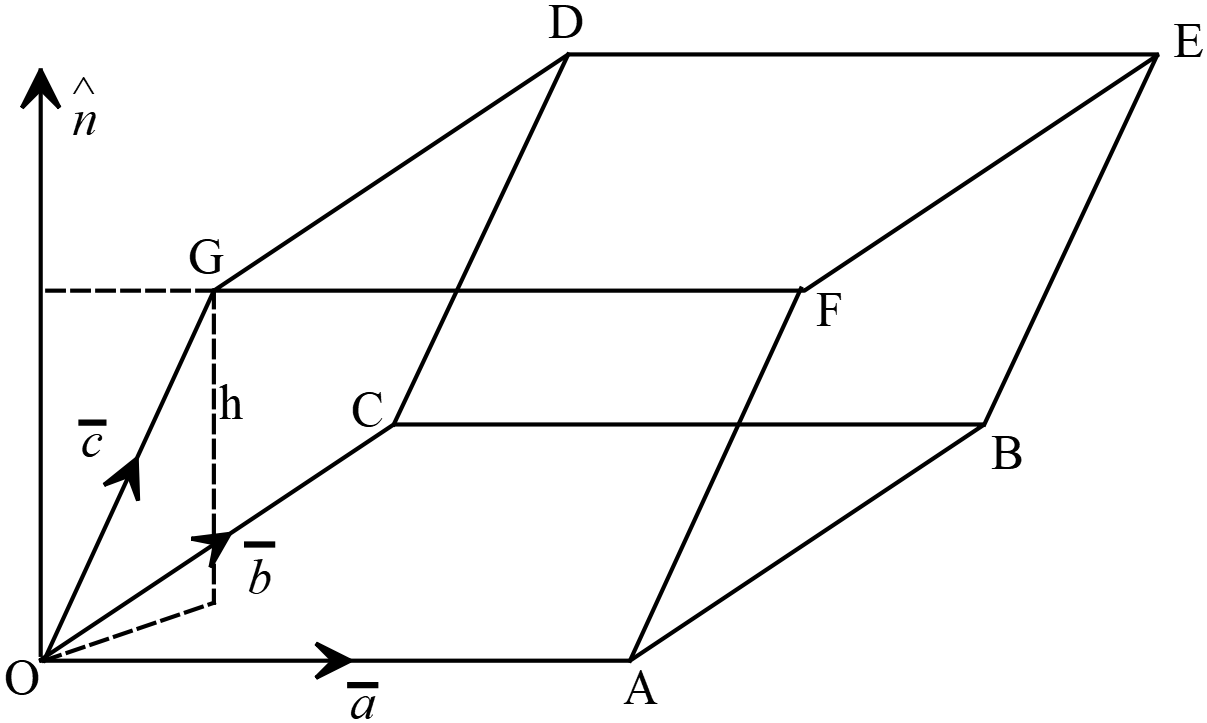দেওয়া আছে,\(\overline{a}, \overline{b}\) এবং \(\overline{c}\) তিনটি ভেক্টর রাশি।
ধরি, \(V\) আয়তন বিশিষ্ট একটি সামান্তরিক আকারের ঘনবস্তু \(OABCDEFG\) এর মূলবিন্দু \(O\) তে ছেদিত ধারগুলি \(\overrightarrow{OA}=\overline{a}, \ \overrightarrow{OC}=\overline{b}, \ \overrightarrow{OG}=\overline{c}\) এবং \(OABC\) ভূমির উপর উচ্চতা \(h.\)
এখন, \(OABC\) সামান্তরিকের ক্ষেত্রফল \(=|\overline{a}\times{\overline{b}}|\)
\(\overline{a}\) ও \(\overline{b}\) ভেক্টরদ্বয়ের উপর লম্ব একক ভেক্টর \(\hat{n}\) হলে, \(\hat{n}=\frac{\overline{a}\times{\overline{b}}}{|\overline{a}\times{\overline{b}}|}\)
আবার, \(h=\hat{n}\) এর উপর \(\overline{c}\) ভেক্টরের লম্ব অভিক্ষেপ \(=\frac{\overline{c}.\hat{n}}{|\hat{n}|}\)
\(=\overline{c}.\hat{n}\)
\(=\overline{c}.\frac{\overline{a}\times{\overline{b}}}{|\overline{a}\times{\overline{b}}|}\) ➜ \(\because \hat{n}=\frac{\overline{a}\times{\overline{b}}}{|\overline{a}\times{\overline{b}}|}\)
\(\therefore h=\overline{c}.\frac{\overline{a}\times{\overline{b}}}{|\overline{a}\times{\overline{b}}|}\)
\(\therefore OABCDEFG\) সামান্তরিক আকারের ঘনবস্তুর আয়তন \(=OABC\) সামান্তরিকের ক্ষেত্রফল \(\times \) উচ্চতা
\(=\overline{a}\times{\overline{b}}h\) ➜ \(\because OABC\) সামান্তরিকের ক্ষেত্রফল \(=|\overline{a}\times{\overline{b}}|\)
এবং উচ্চতা \(h.\)
\(=\overline{a}\times{\overline{b}} \ \overline{c}.\frac{\overline{a}\times{\overline{b}}}{|\overline{a}\times{\overline{b}}|}\) ➜ \(\because h=\overline{c}.\frac{\overline{a}\times{\overline{b}}}{|\overline{a}\times{\overline{b}}|}\)
\(=\overline{a}\times{\overline{b}} \ \overline{c}.\frac{\overline{a}\times{\overline{b}}}{|\overline{a}\times{\overline{b}}|}\)
\(=\overline{c}.(\overline{a}\times{\overline{b}})\)
\(\therefore \overline{c}.(\overline{a}\times{\overline{b}})=\) সামান্তরিক আকারের ঘনবস্তুর আয়তন
অনুরূপভাবে, \(\overline{b}.(\overline{c}\times{\overline{a}})=\) সামান্তরিক আকারের ঘনবস্তুর আয়তন
এবং \(\overline{a}.(\overline{b}\times{\overline{c}})=\) সামান্তরিক আকারের ঘনবস্তুর আয়তন
\(\therefore \overline{a}.(\overline{b}\times{\overline{c}})=\overline{b}.(\overline{c}\times{\overline{a}})=\overline{c}.(\overline{a}\times{\overline{b}})=\) সামান্তরিক আকারের ঘনবস্তুর আয়তন
( প্রমাণিত )
×
তিনটি ভেক্টর সমতলীয় হওয়ার শর্তঃ
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}, \overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) এবং \(\overline{c}=c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}\) ভেক্টর তিনটির সমতলীয় হওয়ার শর্তঃ
\([\overline{a} \ \overline{b} \ \overline{c}]=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|=0\)
প্রমাণঃ
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}, \overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) এবং \(\overline{c}=c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}\) ভেক্টর তিনটির সমতলীয় হওয়ার শর্তঃ
\([\overline{a} \ \overline{b} \ \overline{c}]=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|=0\)
দেওয়া আছে,
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
\(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\)
এবং \(\overline{c}=c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}\)
এখন, \(\overline{a}\times{\overline{b}}=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times{(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})}\)
\(=a_{1}b_{1}\hat{i}\times{\hat{i}}+a_{1}b_{2}\hat{i}\times{\hat{j}}+a_{1}b_{3}\hat{i}\times{\hat{k}}+a_{2}b_{1}\hat{j}\times{\hat{i}}+a_{2}b_{2}\hat{j}\times{\hat{j}}+a_{2}b_{3}\hat{j}\times{\hat{k}}+a_{3}b_{1}\hat{k}\times{\hat{i}}+a_{3}b_{2}\hat{k}\times{\hat{j}}+a_{3}b_{3}\hat{k}\times{\hat{k}}\)
\(=a_{1}b_{1}0+a_{1}b_{2}\hat{k}+a_{1}b_{3}(-\hat{j})+a_{2}b_{1}(-\hat{k})+a_{2}b_{2}0+a_{2}b_{3}\hat{i}+a_{3}b_{1}\hat{j}+a_{3}b_{2}(-\hat{i})+a_{3}b_{3}0\) ➜ \(\because \hat{i}\times{\hat{i}}=\hat{j}\times{\hat{j}}=\hat{k}\times{\hat{k}}=0\)
\(\hat{i}\times{\hat{j}}=\hat{k}, \ \hat{j}\times{\hat{i}}=-\hat{k}, \ \)
\(\hat{j}\times{\hat{k}}=\hat{i}, \ \hat{k}\times{\hat{j}}=-\hat{i}\)
এবং \(\hat{k}\times{\hat{i}}=\hat{j}, \ \hat{i}\times{\hat{k}}=-\hat{j}\)
\(=0+a_{1}b_{2}\hat{k}-a_{1}b_{3}\hat{j}-a_{2}b_{1}\hat{k}+0+a_{2}b_{3}\hat{i}+a_{3}b_{1}\hat{j}-a_{3}b_{2}\hat{i}+0\)
\(=a_{2}b_{3}\hat{i}-a_{3}b_{2}\hat{i}+a_{3}b_{1}\hat{j}-a_{1}b_{3}\hat{j}+a_{1}b_{2}\hat{k}-a_{2}b_{1}\hat{k}\)
\(\therefore \overline{a}\times{\overline{b}}=(a_{2}b_{3}-a_{3}b_{2})\hat{i}+(a_{3}b_{1}-a_{1}b_{3})\hat{j}+(a_{1}b_{2}-a_{2}b_{1})\hat{k}\)
আবার, \(\overline{c}.(\overline{a}\times{\overline{b}})=(c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}).\{(a_{2}b_{3}-a_{3}b_{2})\hat{i}+(a_{3}b_{1}-a_{1}b_{3})\hat{j}+(a_{1}b_{2}-a_{2}b_{1})\hat{k}\}\)
\(=c_{1}(a_{2}b_{3}-a_{3}b_{2})\hat{i}.\hat{i}+c_{1}(a_{3}b_{1}-a_{1}b_{3})\hat{i}.\hat{j}+c_{1}(a_{1}b_{2}-a_{2}b_{1})\hat{i}.\hat{k}+c_{2}(a_{2}b_{3}-a_{3}b_{2})\hat{j}.\hat{i}+c_{2}(a_{3}b_{1}-a_{1}b_{3})\hat{j}.\hat{j}\)\(+c_{2}(a_{1}b_{2}-a_{2}b_{1})\hat{j}.\hat{k}+c_{3}(a_{2}b_{3}-a_{3}b_{2})\hat{k}.\hat{i}+c_{3}(a_{3}b_{1}-a_{1}b_{3})\hat{k}.\hat{j}+c_{3}(a_{1}b_{2}-a_{2}b_{1})\hat{k}.\hat{k}\)
\(=c_{1}(a_{2}b_{3}-a_{3}b_{2})1+c_{1}(a_{3}b_{1}-a_{1}b_{3})0+c_{1}(a_{1}b_{2}-a_{2}b_{1})0+c_{2}(a_{2}b_{3}-a_{3}b_{2})0+c_{2}(a_{3}b_{1}-a_{1}b_{3})1\)\(+c_{2}(a_{1}b_{2}-a_{2}b_{1})0+c_{3}(a_{2}b_{3}-a_{3}b_{2})0+c_{3}(a_{3}b_{1}-a_{1}b_{3})0+c_{3}(a_{1}b_{2}-a_{2}b_{1})1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=\hat{k}.\hat{k}=1\)
এবং
\(\hat{i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0\)
\(=a_{2}b_{3}c_{1}-a_{3}b_{2}c_{1}+0+0+0+a_{3}b_{1}c_{2}-a_{1}b_{3}c_{2}+0+0+0+a_{1}b_{2}c_{3}-a_{2}b_{1}c_{3}\)
\(=a_{1}b_{2}c_{3}-a_{1}b_{3}c_{2}-a_{2}b_{1}c_{3}+a_{2}b_{3}c_{1}+a_{3}b_{1}c_{2}-a_{3}b_{2}c_{1}\)
\(=a_{1}(b_{2}c_{3}-b_{3}c_{2})-a_{2}(b_{1}c_{3}-b_{3}c_{1})+a_{3}(b_{1}c_{2}-b_{2}c_{1})\)
\(=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|\)
\(\therefore \overline{c}.(\overline{a}\times{\overline{b}})=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right| ....(1)\)
এখন, \(\overline{a}, \ \overline{b}, \ \overline{c} \) ভেক্টর তিনটি দ্বারা গঠিত আয়তাকার ঘনবস্তুর আয়তন \(=\overline{c}.(\overline{a}\times{\overline{b}})\)
আবার, \(\overline{a}, \ \overline{b}, \ \overline{c} \) ভেক্টর তিনটি সমতলীয় হলে, ঘনবস্তুর আয়তন \(=0\) হবে।
অর্থাৎ \(\overline{c}.(\overline{a}\times{\overline{b}})=0 ....... (2)\) হবে।
আবার
\(\overline{c}.(\overline{a}\times{\overline{b}})=[\overline{a} \ \overline{b} \ \overline{c}].... (3)\)
\((1),\) \((2)\) ও \((3)\) হতে,
\([\overline{a} \ \overline{b} \ \overline{c}]=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত
( প্রমাণিত )
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
\(\overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\)
এবং \(\overline{c}=c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}\)
এখন, \(\overline{a}\times{\overline{b}}=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times{(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})}\)
\(=a_{1}b_{1}\hat{i}\times{\hat{i}}+a_{1}b_{2}\hat{i}\times{\hat{j}}+a_{1}b_{3}\hat{i}\times{\hat{k}}+a_{2}b_{1}\hat{j}\times{\hat{i}}+a_{2}b_{2}\hat{j}\times{\hat{j}}+a_{2}b_{3}\hat{j}\times{\hat{k}}+a_{3}b_{1}\hat{k}\times{\hat{i}}+a_{3}b_{2}\hat{k}\times{\hat{j}}+a_{3}b_{3}\hat{k}\times{\hat{k}}\)
\(=a_{1}b_{1}0+a_{1}b_{2}\hat{k}+a_{1}b_{3}(-\hat{j})+a_{2}b_{1}(-\hat{k})+a_{2}b_{2}0+a_{2}b_{3}\hat{i}+a_{3}b_{1}\hat{j}+a_{3}b_{2}(-\hat{i})+a_{3}b_{3}0\) ➜ \(\because \hat{i}\times{\hat{i}}=\hat{j}\times{\hat{j}}=\hat{k}\times{\hat{k}}=0\)
\(\hat{i}\times{\hat{j}}=\hat{k}, \ \hat{j}\times{\hat{i}}=-\hat{k}, \ \)
\(\hat{j}\times{\hat{k}}=\hat{i}, \ \hat{k}\times{\hat{j}}=-\hat{i}\)
এবং \(\hat{k}\times{\hat{i}}=\hat{j}, \ \hat{i}\times{\hat{k}}=-\hat{j}\)
\(=0+a_{1}b_{2}\hat{k}-a_{1}b_{3}\hat{j}-a_{2}b_{1}\hat{k}+0+a_{2}b_{3}\hat{i}+a_{3}b_{1}\hat{j}-a_{3}b_{2}\hat{i}+0\)
\(=a_{2}b_{3}\hat{i}-a_{3}b_{2}\hat{i}+a_{3}b_{1}\hat{j}-a_{1}b_{3}\hat{j}+a_{1}b_{2}\hat{k}-a_{2}b_{1}\hat{k}\)
\(\therefore \overline{a}\times{\overline{b}}=(a_{2}b_{3}-a_{3}b_{2})\hat{i}+(a_{3}b_{1}-a_{1}b_{3})\hat{j}+(a_{1}b_{2}-a_{2}b_{1})\hat{k}\)
আবার, \(\overline{c}.(\overline{a}\times{\overline{b}})=(c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}).\{(a_{2}b_{3}-a_{3}b_{2})\hat{i}+(a_{3}b_{1}-a_{1}b_{3})\hat{j}+(a_{1}b_{2}-a_{2}b_{1})\hat{k}\}\)
\(=c_{1}(a_{2}b_{3}-a_{3}b_{2})\hat{i}.\hat{i}+c_{1}(a_{3}b_{1}-a_{1}b_{3})\hat{i}.\hat{j}+c_{1}(a_{1}b_{2}-a_{2}b_{1})\hat{i}.\hat{k}+c_{2}(a_{2}b_{3}-a_{3}b_{2})\hat{j}.\hat{i}+c_{2}(a_{3}b_{1}-a_{1}b_{3})\hat{j}.\hat{j}\)\(+c_{2}(a_{1}b_{2}-a_{2}b_{1})\hat{j}.\hat{k}+c_{3}(a_{2}b_{3}-a_{3}b_{2})\hat{k}.\hat{i}+c_{3}(a_{3}b_{1}-a_{1}b_{3})\hat{k}.\hat{j}+c_{3}(a_{1}b_{2}-a_{2}b_{1})\hat{k}.\hat{k}\)
\(=c_{1}(a_{2}b_{3}-a_{3}b_{2})1+c_{1}(a_{3}b_{1}-a_{1}b_{3})0+c_{1}(a_{1}b_{2}-a_{2}b_{1})0+c_{2}(a_{2}b_{3}-a_{3}b_{2})0+c_{2}(a_{3}b_{1}-a_{1}b_{3})1\)\(+c_{2}(a_{1}b_{2}-a_{2}b_{1})0+c_{3}(a_{2}b_{3}-a_{3}b_{2})0+c_{3}(a_{3}b_{1}-a_{1}b_{3})0+c_{3}(a_{1}b_{2}-a_{2}b_{1})1\) ➜ \(\because \hat{i}.\hat{i}=\hat{j}.\hat{j}=\hat{k}.\hat{k}=1\)
এবং
\(\hat{i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0\)
\(=a_{2}b_{3}c_{1}-a_{3}b_{2}c_{1}+0+0+0+a_{3}b_{1}c_{2}-a_{1}b_{3}c_{2}+0+0+0+a_{1}b_{2}c_{3}-a_{2}b_{1}c_{3}\)
\(=a_{1}b_{2}c_{3}-a_{1}b_{3}c_{2}-a_{2}b_{1}c_{3}+a_{2}b_{3}c_{1}+a_{3}b_{1}c_{2}-a_{3}b_{2}c_{1}\)
\(=a_{1}(b_{2}c_{3}-b_{3}c_{2})-a_{2}(b_{1}c_{3}-b_{3}c_{1})+a_{3}(b_{1}c_{2}-b_{2}c_{1})\)
\(=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|\)
\(\therefore \overline{c}.(\overline{a}\times{\overline{b}})=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right| ....(1)\)
এখন, \(\overline{a}, \ \overline{b}, \ \overline{c} \) ভেক্টর তিনটি দ্বারা গঠিত আয়তাকার ঘনবস্তুর আয়তন \(=\overline{c}.(\overline{a}\times{\overline{b}})\)
আবার, \(\overline{a}, \ \overline{b}, \ \overline{c} \) ভেক্টর তিনটি সমতলীয় হলে, ঘনবস্তুর আয়তন \(=0\) হবে।
অর্থাৎ \(\overline{c}.(\overline{a}\times{\overline{b}})=0 ....... (2)\) হবে।
আবার
\(\overline{c}.(\overline{a}\times{\overline{b}})=[\overline{a} \ \overline{b} \ \overline{c}].... (3)\)
\((1),\) \((2)\) ও \((3)\) হতে,
\([\overline{a} \ \overline{b} \ \overline{c}]=\left|\begin{array}{c}a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\\ c_{1}&c_{2}&c_{3}\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত
( প্রমাণিত )
×
যদি, \(\overline{a}, \ \overline{c}\) এবং \(\overline{c}\) সমতলীয় ভেক্টর হয় তবে দেখাও যে,
\(x\overline{a}+y\overline{b}+z\overline{c}=0\)
\(\Rightarrow x=0, \ y=0, \ z=0\)
\(x\overline{a}+y\overline{b}+z\overline{c}=0\)
\(\Rightarrow x=0, \ y=0, \ z=0\)
প্রমাণঃ
দেওয়া আছে,
\(\overline{a}, \ \overline{c}\) এবং \(\overline{c}\) সমতলীয় ভেক্টর
এবং \(x\overline{a}+y\overline{b}+z\overline{c}=0\)
\(\Rightarrow \overline{a}+\frac{y}{x}\overline{b}+\frac{z}{x}\overline{c}=0\) ➜ যদি, \(x\ne{0}\)
উভয় পার্শে \(x\) ভাগ করে।
\(\therefore \overline{a}=\left(-\frac{y}{x}\right)\overline{b}+\left(-\frac{z}{x}\right)\overline{c}\)
\(\therefore\) ইহা স্পষ্ট যে, \(\overline{a}, \ \overline{b}, \ \overline{c}\) ভেক্টরত্রয় সমতলীয়।
কিন্তু ইহা অসম্ভব কারণ \(\overline{a}, \ \overline{b}, \ \overline{c}\) ভেক্টরত্রয় অসমতলীয়।
সুতরাং, \(x=0\)
অনুরূপভাবে, প্রমাণ কর যায় \(y=0, \ z=0\)
( প্রমাণিত )
\(\overline{a}, \ \overline{c}\) এবং \(\overline{c}\) সমতলীয় ভেক্টর
এবং \(x\overline{a}+y\overline{b}+z\overline{c}=0\)
\(\Rightarrow \overline{a}+\frac{y}{x}\overline{b}+\frac{z}{x}\overline{c}=0\) ➜ যদি, \(x\ne{0}\)
উভয় পার্শে \(x\) ভাগ করে।
\(\therefore \overline{a}=\left(-\frac{y}{x}\right)\overline{b}+\left(-\frac{z}{x}\right)\overline{c}\)
\(\therefore\) ইহা স্পষ্ট যে, \(\overline{a}, \ \overline{b}, \ \overline{c}\) ভেক্টরত্রয় সমতলীয়।
কিন্তু ইহা অসম্ভব কারণ \(\overline{a}, \ \overline{b}, \ \overline{c}\) ভেক্টরত্রয় অসমতলীয়।
সুতরাং, \(x=0\)
অনুরূপভাবে, প্রমাণ কর যায় \(y=0, \ z=0\)
( প্রমাণিত )
×
দেখাও যে, ভেক্টর \(\overline{r}\) কে উহার সহিত সমতলীয় অসমরৈখিক ভেক্টর \(\overline{a}\) এবং \(\overline{b}\) এর যোগাশ্রয়ী সমাবেশ \(\overline{r}=x\overline{a}+y\overline{b}\) রূপে অনন্যভাবে প্রকাশ করা যায় যেখানে, \(x\) এবং \(y\) স্কেলার।
প্রমাণঃ
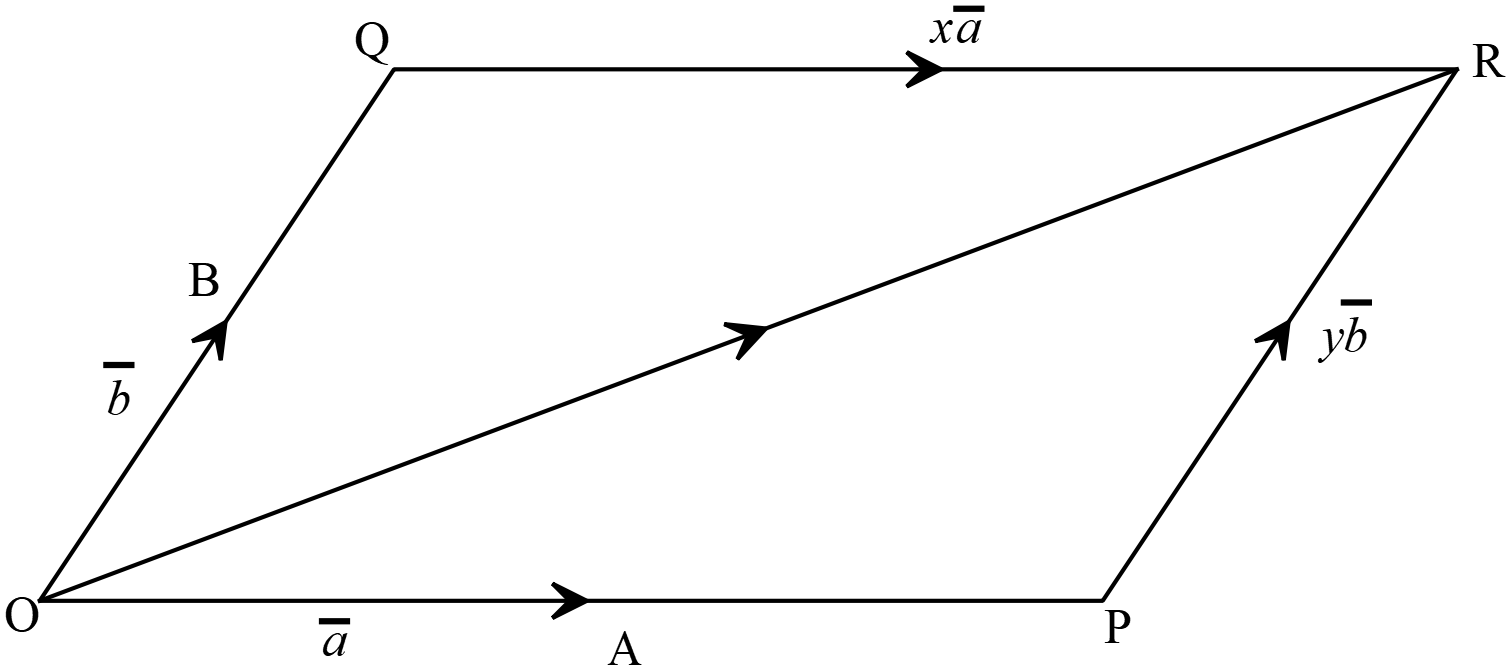দেওয়া আছে,\( \overline{r}, \ \overline{a}\) এবং \(\overline{b}\) ভেক্টরত্রয় সমতলীয় অসমরৈখিক।
ধরি,
\( \overrightarrow{OA}=\overline{a}, \ \overrightarrow{OB}=\overline{b}\) এবং \(\overrightarrow{OR}=\overline{b}\)
এখন, \( \overrightarrow{OR}\) কে কর্ণ ধরে \(OPRQ\) সামান্তরিকটি অঙ্কন করি যার \(OP\) বাহু \(OA\) বরাবর এবং \(OQ\) বাহু \(OB\) বরাবর।
এবং \( \overrightarrow{OP}=x\overrightarrow{OA}=x\overline{a}\) এবং \(\overrightarrow{OQ}=y\overrightarrow{OB}=y\overline{b}\)
যেখানে, \(x\) এবং \(y\) উভয় স্কেলার।
এখন, \( \overrightarrow{OR}=\overrightarrow{OP}+\overrightarrow{PR}\) ➜ \(\triangle{OPR}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{OR}=\overrightarrow{OP}+\overrightarrow{PR}\)
\(\Rightarrow \overrightarrow{OR}=\overrightarrow{OP}+\overrightarrow{OQ}\) ➜ \(\because \overrightarrow{PR}=\overrightarrow{OQ}\) এবং \(\overrightarrow{PR}||\overrightarrow{OQ}\)
সামান্তরিকের বিপরীত বাহু।
\(\therefore \overline{r}=x\overline{a}+y\overline{b} ....(1)\) ➜ \(\because \overrightarrow{OR}=\overline{r}\)
\(\overrightarrow{OP}=x\overline{a}\)
এবং \(\overrightarrow{OQ}=y\overline{b}\)
আবার ধরি,
\(\overline{r}=x^{\prime}\overline{a}+y^{\prime}\overline{b} ....(2)\)
\((1)\) ও \((2)\) হতে,
\(x\overline{a}+y\overline{b}=x^{\prime}\overline{a}+y^{\prime}\overline{b}\)
\(\Rightarrow x\overline{a}+y\overline{b}-x^{\prime}\overline{a}-y^{\prime}\overline{b}=0\)
\(\Rightarrow (x-x^{\prime})\overline{a}+(y-y^{\prime})\overline{b}=0\)
\(\Rightarrow x-x^{\prime}=0, \ y-y^{\prime}=0\) ➜ \(\because \overline{a}\ne{0}, \ \overline{b}\ne{0}\)
\(\therefore x=x^{\prime}, \ y=y^{\prime}\)
সুতরাং যোগাশ্রয়ী সমাবেশ \(\overline{r}=x\overline{a}+y\overline{b}\) অনন্য।
( প্রমাণিত )
×
দেখাও যে, \(\overline{A}=A_{1}\hat{i}+A_{2}\hat{j}+A_{3}\hat{k}\) ভেক্টরের মাণ \(A=|\overline{A}|=\sqrt{A_{1}^2+A_{2}^2+A_{3}^2}\)
প্রমাণঃ
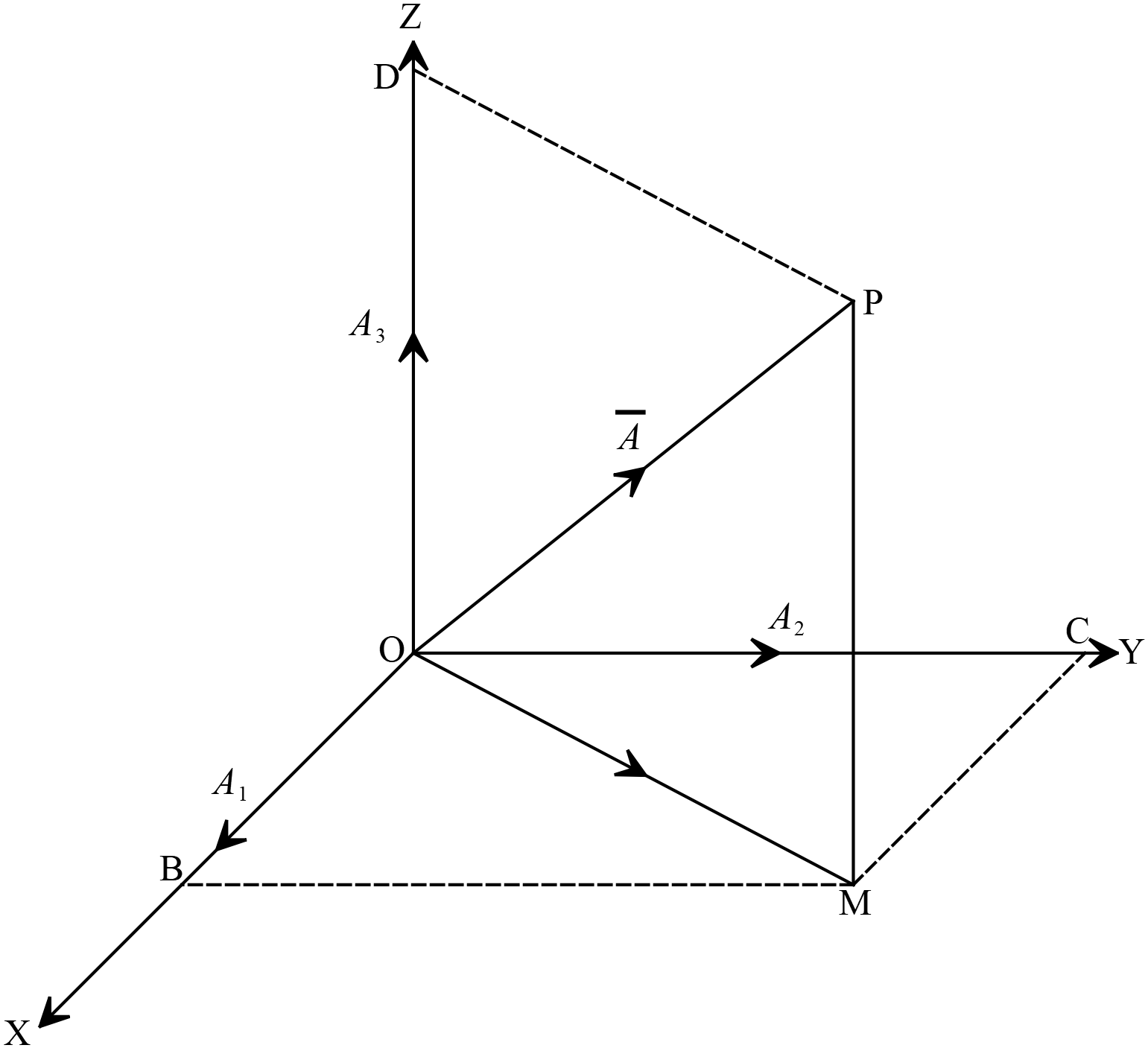দেওয়া আছে,\(\overline{A}=A_{1}\hat{i}+A_{2}\hat{j}+A_{3}\hat{k}\)
ধরি,
\(O\) মূলবিন্দু সাপেক্ষে \(P\) এর অবস্থান ভেক্টর \(\overline{A}\) এবং \(P\) বিন্দু হতে যথাক্রমে \(XY\) সমতল ও \(Z\) অক্ষের উপর \(PM\) ও \(PD\) লম্ব আঁকি।
আবার, \(M\) বিন্দু হতে \(X\) অক্ষের উপর \(MB\) লম্ব আঁকি।
\(\therefore OP=A, \ OB=A_{1}, \ OC=MB=A_{2}, \ OD=PM=A_{3}\)
\(\triangle OMB\) সমকোণী
\(\therefore OM^2=OB^2+MB^2\)
\(\therefore OM^2=A_{1}^2+A_{2}^2\) ➜ \(\because OB=A_{1}, \ OC=MB=A_{2}\)
\(\triangle OPM\) সমকোণী
\(\therefore OP^2=OM^2+PM^2\)
\(\Rightarrow A^2=A_{1}^2+A_{2}^2+A_{3}^2\) ➜ \(\because OM^2=A_{1}^2+A_{2}^2\)
এবং \(PM=A_{3}\)
\(\Rightarrow A=\sqrt{A_{1}^2+A_{2}^2+A_{3}^2}\)
\(\therefore A=|A|=\sqrt{A_{1}^2+A_{2}^2+A_{3}^2}\)
( প্রমাণিত )
×
যদি, \(A(x_{1},y_{1},z_{1})\) আদি বিন্দু এবং \(B(x_{2},y_{2},z_{2})\) প্রান্তবিন্দু হয় তবে দেখাও যে, ভেক্টর \(\overrightarrow{AB}=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}+(z_{2}-z_{1})\hat{k}\) এর মাণ \(AB=|\overrightarrow{AB}|=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2+(z_{2}-z_{1})^2}\)
প্রমাণঃ
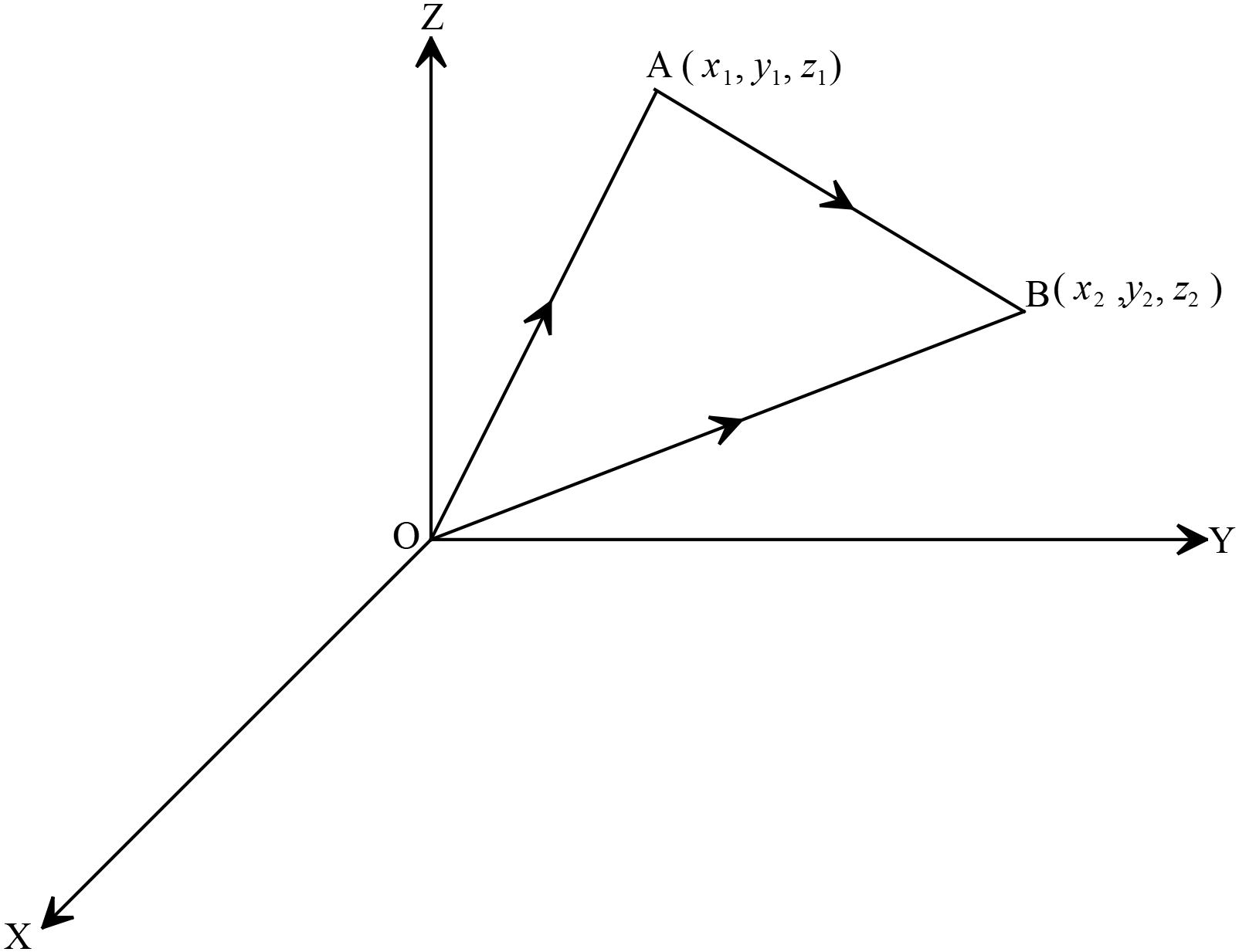দেওয়া আছে,\(A(x_{1},y_{1},z_{1})\) আদি বিন্দু এবং \(B(x_{2},y_{2},z_{2})\) প্রান্তবিন্দু
ধরি,
\(O\) মূলবিন্দু সাপেক্ষে \(A\) এবং \(B\) বিন্দুর অবস্থান ভেক্টর যথাক্রমে \(\overline{r_{1}}\) এবং \(\overline{r_{2}}\)
\(\therefore \overrightarrow{OA}=\overline{r_{1}}=x_{1}\hat{i}+y_{1}\hat{j}+z_{1}\hat{k}\)
এবং \(\overrightarrow{OB}=\overline{r_{2}}=x_{2}\hat{i}+y_{2}\hat{j}+z_{2}\hat{k}\)
এখন, \(\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}\) ➜ \(\triangle{OAB}\)-এ ভেক্টর সংযোগের ত্রিভুজ সূত্র ব্যবহার করে,
\(\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}\)
\(=-\overrightarrow{OA}+\overrightarrow{OB}\)
\(=\overrightarrow{OB}-\overrightarrow{OA}\)
\(=x_{2}\hat{i}+y_{2}\hat{j}+z_{2}\hat{k}-x_{1}\hat{i}-y_{1}\hat{j}-z_{1}\hat{k}\) ➜ \(\because \overrightarrow{OB}=x_{2}\hat{i}+y_{2}\hat{j}+z_{2}\hat{k}\)
এবং \(\overrightarrow{OA}=x_{1}\hat{i}+y_{1}\hat{j}+z_{1}\hat{k}\)
\(\therefore \overrightarrow{AB}=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}+(z_{2}-z_{1})\hat{k}\)
\(\Rightarrow AB=|\overrightarrow{AB}|=|(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}+(z_{2}-z_{1})\hat{k}|\)
\(\therefore AB=|\overrightarrow{AB}|=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2+(z_{2}-z_{1})^2}\) ➜ \(\overline{r}=x\hat{i}+y\hat{j}+z\hat{k}\) হলে,
\(r=|x\hat{i}+y\hat{j}+z\hat{k}|=\sqrt{x^2+y^2+z^2}\)
( প্রমাণিত )
×
তিনটি ভেক্টরের ভেক্টর গুণনঃ
তিনটি ভেক্টর \(\overline{a}, \overline{b}\) এবং \(\overline{c}\) এর ভেক্টর গুণন
\(\overline{a}\times(\overline{b}\times{\overline{c}})=(\overline{a}.\overline{c})\overline{b}-(\overline{a}.\overline{b})\overline{c}\)
\((\overline{a}\times\overline{b})\times{\overline{c}}=(\overline{a}.\overline{c})\overline{b}-(\overline{b}.\overline{c})\overline{a}\)
তিনটি ভেক্টর \(\overline{a}, \overline{b}\) এবং \(\overline{c}\) এর ভেক্টর গুণন
\(\overline{a}\times(\overline{b}\times{\overline{c}})=(\overline{a}.\overline{c})\overline{b}-(\overline{a}.\overline{b})\overline{c}\)
\((\overline{a}\times\overline{b})\times{\overline{c}}=(\overline{a}.\overline{c})\overline{b}-(\overline{b}.\overline{c})\overline{a}\)
প্রমাণঃ
দেওয়া আছে,
\(\overline{a}, \overline{b}\) এবং \(\overline{c}\) তিনটি ভেক্টর
ধরি,
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}, \overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) এবং \(\overline{c}=c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}\)
এখন, \(\overline{b}\times\overline{c}=(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})\times(c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k})\)
\(=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{array}\right|\) ➜ \(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
এবং \(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) হলে,
\((a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3} \end{array}\right|\)
\(\therefore (\overline{b}\times\overline{c})=\left|\begin{array}{c}b_{2}&b_{3}\\c_{2}&c_{3}\end{array}\right|\hat{i}+\left|\begin{array}{c}b_{3}&b_{1}\\c_{3}&c_{1}\end{array}\right|\hat{j}+\left|\begin{array}{c}b_{1}&b_{2}\\c_{1}&c_{2}\end{array}\right|\hat{k}\)
আবার, \(\overline{a}\times(\overline{b}\times\overline{c})=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times\left\{\left|\begin{array}{c}b_{2}&b_{3}\\c_{2}&c_{3}\end{array}\right|\hat{i}+\left|\begin{array}{c}b_{3}&b_{1}\\c_{3}&c_{1}\end{array}\right|\hat{j}+\left|\begin{array}{c}b_{1}&b_{2}\\c_{1}&c_{2}\end{array}\right|\hat{k}\right\}\)
\(=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\a_{1}&a_{2}&a_{3}\\\left|\begin{array}{c}b_{2}&b_{3}\\c_{2}&c_{3}\end{array}\right|&\left|\begin{array}{c}b_{3}&b_{1}\\c_{3}&c_{1}\end{array}\right|&\left|\begin{array}{c}b_{1}&b_{2}\\c_{1}&c_{2}\end{array}\right|\end{array}\right|\) ➜ \(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
এবং \(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) হলে,
\((a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3} \end{array}\right|\)
\(=\sum\{a_{2}(b_{1}c_{2}-b_{2}c_{1})-a_{3}(b_{3}c_{1}-b_{1}c_{3})\}\hat{i}\) ➜ \(\because \sum\{a_{2}(b_{1}c_{2}-b_{2}c_{1})-a_{3}(b_{3}c_{1}-b_{1}c_{3})\}\hat{i}=\{a_{2}(b_{1}c_{2}-b_{2}c_{1})-a_{3}(b_{3}c_{1}-b_{1}c_{3})\}\hat{i}\)\(-\{a_{1}(b_{1}c_{2}-b_{2}c_{1})-a_{3}(b_{2}c_{3}-b_{3}c_{2})\}\hat{j}+\{a_{1}(b_{3}c_{1}-b_{1}c_{3})-a_{2}(b_{2}c_{3}-b_{3}c_{2})\}\hat{k}\)
\(=\sum\{a_{2}b_{1}c_{2}-a_{2}b_{2}c_{1}-a_{3}b_{3}c_{1}+a_{3}b_{1}c_{3}\}\hat{i}\)
\(=\sum\{a_{2}b_{1}c_{2}+a_{3}b_{1}c_{3}-a_{2}b_{2}c_{1}-a_{3}b_{3}c_{1}\}\hat{i}\)
\(=\sum\{(a_{2}c_{2}+a_{3}c_{3})b_{1}-(a_{2}b_{2}+a_{3}b_{3})c_{1}\}\hat{i}\)
\(=\sum\{(a_{2}c_{2}+a_{3}c_{3})b_{1}+a_{1}b_{1}c_{1}-a_{1}b_{1}c_{1}-(a_{2}b_{2}+a_{3}b_{3})c_{1}\}\hat{i}\)
\(=\sum\{(a_{1}c_{1}+a_{2}c_{2}+a_{3}c_{3})b_{1}-(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3})c_{1}\}\hat{i}\)
\(=\sum\{(\overline{a}.\overline{c})b_{1}-(\overline{a}.\overline{b})c_{1}\}\hat{i}\) ➜ \(\because a_{1}c_{1}+a_{2}c_{2}+a_{3}c_{3}=\overline{a}.\overline{c}\)
এবং \(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}=\overline{a}.\overline{b}\)
\(=(\overline{a}.\overline{c})\sum b_{1}\hat{i}-(\overline{a}.\overline{b})\sum c_{1}\hat{i}\)
\(=(\overline{a}.\overline{c})(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})-(\overline{a}.\overline{b})(c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k})\) ➜ \(\because \sum b_{1}\hat{i}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\)
এবং \(\sum c_{1}\hat{i}=c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}\)
\(=(\overline{a}.\overline{c})\overline{b}-(\overline{a}.\overline{b})\overline{c}\) ➜ \(\because b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}=\overline{b}\)
এবং \(c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}=\overline{c}\)
\(\therefore \overline{a}\times(\overline{b}\times\overline{c})=(\overline{a}.\overline{c})\overline{b}-(\overline{a}.\overline{b})\overline{c}\)
অনুরূপভাবে দেখানো যায়,
\(\therefore (\overline{a}\times\overline{b})\times\overline{c}=(\overline{a}.\overline{c})\overline{b}-(\overline{b}.\overline{c})\overline{a}\)
( প্রমাণিত )
\(\overline{a}, \overline{b}\) এবং \(\overline{c}\) তিনটি ভেক্টর
ধরি,
\(\overline{a}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}, \overline{b}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) এবং \(\overline{c}=c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}\)
এখন, \(\overline{b}\times\overline{c}=(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})\times(c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k})\)
\(=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{array}\right|\) ➜ \(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
এবং \(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) হলে,
\((a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3} \end{array}\right|\)
\(\therefore (\overline{b}\times\overline{c})=\left|\begin{array}{c}b_{2}&b_{3}\\c_{2}&c_{3}\end{array}\right|\hat{i}+\left|\begin{array}{c}b_{3}&b_{1}\\c_{3}&c_{1}\end{array}\right|\hat{j}+\left|\begin{array}{c}b_{1}&b_{2}\\c_{1}&c_{2}\end{array}\right|\hat{k}\)
আবার, \(\overline{a}\times(\overline{b}\times\overline{c})=(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times\left\{\left|\begin{array}{c}b_{2}&b_{3}\\c_{2}&c_{3}\end{array}\right|\hat{i}+\left|\begin{array}{c}b_{3}&b_{1}\\c_{3}&c_{1}\end{array}\right|\hat{j}+\left|\begin{array}{c}b_{1}&b_{2}\\c_{1}&c_{2}\end{array}\right|\hat{k}\right\}\)
\(=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\a_{1}&a_{2}&a_{3}\\\left|\begin{array}{c}b_{2}&b_{3}\\c_{2}&c_{3}\end{array}\right|&\left|\begin{array}{c}b_{3}&b_{1}\\c_{3}&c_{1}\end{array}\right|&\left|\begin{array}{c}b_{1}&b_{2}\\c_{1}&c_{2}\end{array}\right|\end{array}\right|\) ➜ \(a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\)
এবং \(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) হলে,
\((a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k})\times(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})=\left|\begin{array}{c}\hat{i}&\hat{j}&\hat{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3} \end{array}\right|\)
\(=\sum\{a_{2}(b_{1}c_{2}-b_{2}c_{1})-a_{3}(b_{3}c_{1}-b_{1}c_{3})\}\hat{i}\) ➜ \(\because \sum\{a_{2}(b_{1}c_{2}-b_{2}c_{1})-a_{3}(b_{3}c_{1}-b_{1}c_{3})\}\hat{i}=\{a_{2}(b_{1}c_{2}-b_{2}c_{1})-a_{3}(b_{3}c_{1}-b_{1}c_{3})\}\hat{i}\)\(-\{a_{1}(b_{1}c_{2}-b_{2}c_{1})-a_{3}(b_{2}c_{3}-b_{3}c_{2})\}\hat{j}+\{a_{1}(b_{3}c_{1}-b_{1}c_{3})-a_{2}(b_{2}c_{3}-b_{3}c_{2})\}\hat{k}\)
\(=\sum\{a_{2}b_{1}c_{2}-a_{2}b_{2}c_{1}-a_{3}b_{3}c_{1}+a_{3}b_{1}c_{3}\}\hat{i}\)
\(=\sum\{a_{2}b_{1}c_{2}+a_{3}b_{1}c_{3}-a_{2}b_{2}c_{1}-a_{3}b_{3}c_{1}\}\hat{i}\)
\(=\sum\{(a_{2}c_{2}+a_{3}c_{3})b_{1}-(a_{2}b_{2}+a_{3}b_{3})c_{1}\}\hat{i}\)
\(=\sum\{(a_{2}c_{2}+a_{3}c_{3})b_{1}+a_{1}b_{1}c_{1}-a_{1}b_{1}c_{1}-(a_{2}b_{2}+a_{3}b_{3})c_{1}\}\hat{i}\)
\(=\sum\{(a_{1}c_{1}+a_{2}c_{2}+a_{3}c_{3})b_{1}-(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3})c_{1}\}\hat{i}\)
\(=\sum\{(\overline{a}.\overline{c})b_{1}-(\overline{a}.\overline{b})c_{1}\}\hat{i}\) ➜ \(\because a_{1}c_{1}+a_{2}c_{2}+a_{3}c_{3}=\overline{a}.\overline{c}\)
এবং \(a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}=\overline{a}.\overline{b}\)
\(=(\overline{a}.\overline{c})\sum b_{1}\hat{i}-(\overline{a}.\overline{b})\sum c_{1}\hat{i}\)
\(=(\overline{a}.\overline{c})(b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k})-(\overline{a}.\overline{b})(c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k})\) ➜ \(\because \sum b_{1}\hat{i}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\)
এবং \(\sum c_{1}\hat{i}=c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}\)
\(=(\overline{a}.\overline{c})\overline{b}-(\overline{a}.\overline{b})\overline{c}\) ➜ \(\because b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}=\overline{b}\)
এবং \(c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k}=\overline{c}\)
\(\therefore \overline{a}\times(\overline{b}\times\overline{c})=(\overline{a}.\overline{c})\overline{b}-(\overline{a}.\overline{b})\overline{c}\)
অনুরূপভাবে দেখানো যায়,
\(\therefore (\overline{a}\times\overline{b})\times\overline{c}=(\overline{a}.\overline{c})\overline{b}-(\overline{b}.\overline{c})\overline{a}\)
( প্রমাণিত )
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000003