এ অধ্যায়ের পাঠ্যসূচী।
- সরলরেখার (Straight line)
- সরলরেখার সাধারণ সমীকরণ (General equation of straight line)
- সরলরেখার ঢাল (Slope of a straight line)
- সরলরেখার সমীকরণ চিনবার উপায় (Identifying the equation of a straight line)
- পরামিতিক সমীকরণ (Parametric Equation):
- দুইটি বিন্দুর সংযোগ সরলরেখার ঢাল (Slope of the straight line joining two points)
- \(X\) অক্ষের সমীকরণ (Equation of the \(X\) axis)
- \(Y\) অক্ষের সমীকরণ (Equation of the \(Y\) axis)
- \(X\) অক্ষের সমান্তরাল সরলরেখার সমীকরণ (Equation of the straight line parallel to the \(X\) axis)
- \(Y\) অক্ষের সমান্তরাল সরলরেখার সমীকরণ (Equation of the straight line parallel to the \(Y\) axis)
- মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণ (General equation of a straight line through the origin)
- \(Y\) অক্ষের ছেদিতাংশ এবং ঢাল দেওয়া থাকিলে সরলরেখার সমীকরণ (Equation of the straight line given the intercept and slope of the \(Y\) axis)
- উভয় অক্ষের ছেদিতাংশ দেওয়া থাকিলে সরলরেখার সমীকরণ (Equation of straight line given intersection of both axes)
- একটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ (Equation of a straight line through a fixed point)
- দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ (Equation of a straight line through two fixed points)
- মূলবিন্দু এবং একটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ (Equation of a straight line through the origin and a fixed point)
- সরলরেখার লম্বরূপ সমীকরণ (Perpendicular type equation of straight line)
- একটি নির্দিষ্ট বিন্দুগামী এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্নকারী সরলরেখাটির সমীকরণ (Equation of a straight line through a fixed point and making an angle \(\theta \) with the positive direction of the \(X\) axis)
- তিনটি সরলরেখা দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল (Area of triangle formed by three straight lines)
- দুইটি সরলরেখার ছেদবিন্দু (Intersection of two straight lines)
- দুইটি সমীকরণ একই সরলরেখা নির্দেশ করার শর্ত (The condition that two equations point to the same straight line)
- শর্টকাট টেকনিক (Shortcut Technique)
- অধ্যায় \(3F\) -এর উদাহরণসমুহ
- অধ্যায় \(3F\) / \(Q.1\) -এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(3F\) / \(Q.2\) -এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3F\) / \(Q.3\) -এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3F\) / \(Q.4\) -এর বর্ণনামূলক প্রশ্নসমূহ
সরলরেখা
Straight line
সরলরেখাঃ
একটি বিন্দু-সেট দ্বারা সৃষ্ট সঞ্চারপথ দিক পরিবর্তন না করলে সেই সঞ্চারপথকে সরলরেখা বলে। সঞ্চারপথের সমীকরণকে সরলরেখার সমীকরণ বলে।
সরলরেখার সাধারণ সমীকরণ
General equation of straight line
সরলরেখার সাধারণ সমীকরণঃ
\(x\) এবং \(y\) এর একঘাত সমীকরণ সর্বদা সরলরেখা প্রকাশ করে। \(a, \ b, \ c\) প্রত্যেকে ধ্রুবক এবং \(a, \ b\) উভয়ে শূন্য না হলে, \(ax+by+c=0\) একটি সরলরেখা নির্দেশ করে। আবার, যে কোনো সরলরেখার সমীকরণকে উক্ত সমীকরণের আকারে প্রকাশ করা যায়। তাই \(ax+by+c=0\) কে সরলরেখার সাধারণ সমীকরণ বলা হয়।
প্রমাণঃ
মনে করি,
\(ax+by+c=0 .........(1)\)
এখানে, \(a, \ b, \ c\) ধ্রুবক।
\((1)\) নং সমীকরণের সঞ্চারপথের উপর \((x_{1}, y_{1}), \ (x_{2}, y_{2}), \ (x_{3}, y_{3})\) যে কোনো তিনটি বিন্দু।
তাহলে, \(ax_{1}+by_{1}+c=0 .........(2)\)
\(ax_{2}+by_{2}+c=0 .........(3)\)
\(ax_{3}+by_{3}+c=0 .........(4)\)
\((3)\) ও \((4)\) বজ্রগুণ করে,
\(\frac{a}{y_{2}-y_{3}}=\frac{b}{x_{3}-x_{2}}=\frac{c}{x_{2}y_{3}-x_{3}y_{2}}=k\) ( ধরি )
\(\therefore a=k(y_{2}-y_{3}), \ b=k(x_{3}-x_{2}), \ c=k(x_{2}y_{3}-x_{3}y_{2})\)
\(a, \ b, \ c\) এর মাণ \((2)\) নং সমীকরণে বসিয়ে,
\(k(y_{2}-y_{3})x_{1}+k(x_{3}-x_{2})y_{1}+k(x_{2}y_{3}-x_{3}y_{2})=0\)
\(\Rightarrow k\{(y_{2}-y_{3})x_{1}+(x_{3}-x_{2})y_{1}+(x_{2}y_{3}-x_{3}y_{2})\}=0\)
\(\Rightarrow (y_{2}-y_{3})x_{1}+(x_{3}-x_{2})y_{1}+(x_{2}y_{3}-x_{3}y_{2})=0; \ \because k\ne{0}\)
\(\Rightarrow x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})+1(x_{2}y_{3}-x_{3}y_{2})=0\)
\(\therefore \left|\begin{array}{c}x_{1}&y_{1}&1\\ x_{2}&y_{2}&1 \\ x_{3}&y_{3}&1\end{array}\right|=0\)
যা, \((x_{1}, y_{1}), \ (x_{2}, y_{2}), \ (x_{3}, y_{3})\) বিন্দু তিনটির সমরেখ হওয়ার শর্ত।
যেহেতু এই সমরেখ বিন্দুত্রয় \((1)\) নং এর সঞ্চারপথের উপর অবস্থান করে,
সুতরাং, \(ax+by+c=0\) যে কোনো সরলরেখার সাধারণ সমীকরণ।
এখানে, \(a, \ b, \ c\) ধ্রুবক।
\((1)\) নং সমীকরণের সঞ্চারপথের উপর \((x_{1}, y_{1}), \ (x_{2}, y_{2}), \ (x_{3}, y_{3})\) যে কোনো তিনটি বিন্দু।
তাহলে, \(ax_{1}+by_{1}+c=0 .........(2)\)
\(ax_{2}+by_{2}+c=0 .........(3)\)
\(ax_{3}+by_{3}+c=0 .........(4)\)
\((3)\) ও \((4)\) বজ্রগুণ করে,
\(\frac{a}{y_{2}-y_{3}}=\frac{b}{x_{3}-x_{2}}=\frac{c}{x_{2}y_{3}-x_{3}y_{2}}=k\) ( ধরি )
\(\therefore a=k(y_{2}-y_{3}), \ b=k(x_{3}-x_{2}), \ c=k(x_{2}y_{3}-x_{3}y_{2})\)
\(a, \ b, \ c\) এর মাণ \((2)\) নং সমীকরণে বসিয়ে,
\(k(y_{2}-y_{3})x_{1}+k(x_{3}-x_{2})y_{1}+k(x_{2}y_{3}-x_{3}y_{2})=0\)
\(\Rightarrow k\{(y_{2}-y_{3})x_{1}+(x_{3}-x_{2})y_{1}+(x_{2}y_{3}-x_{3}y_{2})\}=0\)
\(\Rightarrow (y_{2}-y_{3})x_{1}+(x_{3}-x_{2})y_{1}+(x_{2}y_{3}-x_{3}y_{2})=0; \ \because k\ne{0}\)
\(\Rightarrow x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})+1(x_{2}y_{3}-x_{3}y_{2})=0\)
\(\therefore \left|\begin{array}{c}x_{1}&y_{1}&1\\ x_{2}&y_{2}&1 \\ x_{3}&y_{3}&1\end{array}\right|=0\)
যা, \((x_{1}, y_{1}), \ (x_{2}, y_{2}), \ (x_{3}, y_{3})\) বিন্দু তিনটির সমরেখ হওয়ার শর্ত।
যেহেতু এই সমরেখ বিন্দুত্রয় \((1)\) নং এর সঞ্চারপথের উপর অবস্থান করে,
সুতরাং, \(ax+by+c=0\) যে কোনো সরলরেখার সাধারণ সমীকরণ।
সরলরেখার ঢাল
Slope of a straight line
সরলরেখার ঢালঃ
কোনো সরলরেখা \(X\) অক্ষের ধনাত্মক দিকের সহিত যে কোণ উৎপন্ন করে তার ত্রিকোণমিতিক ট্যানজেন্টকে রেখাটির ঢাল বলে। ঢালকে সাধারণত \(m\) দ্বারা সূচিত করা হয়। \(AB\) সরলরেখা \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্ন করলে, তার ঢাল \(m=\tan\theta\) .
সরলরেখার সমীকরণ চিহ্নিত করণ
Identifying the equation of a straight line
সরলরেখার সমীকরণ চিহ্নিত করণের উপায়ঃ
\(x\) এবং \(y\) এর একঘাত সমীকরণ সর্বদা সরলরেখা প্রকাশ করে। যেমনঃ \(ax+by+c=0\) ইহাকে সরলরেখার সাধারণ সমীকরণও বলা হয়ে থাকে।
পরামিতিক সমীকরণ
Parametric Equation
পরামিতিক সমীকরণঃ
যখন একটি সঞ্চারপথের উপর অবস্থিত কোনো বিন্দু \((x, y)\) এর স্থানাঙ্ক শুধুমাত্র একটি চলরাশি (Variable) এর মাধ্যমে প্রকাশিত হয়, তখন ঐ চলরাশিকে পরামিতি বা প্যারামিটার ( Parameter ) এবং উক্ত বিন্দুর স্থানাঙ্ককে পরামিতিক স্থানাঙ্ক বা প্যারামিটার যুক্ত স্থানাঙ্ক বলা হয়। \(x\) ও \(y\) এর মান জ্ঞাপক সমীকরণদ্বয়কে একত্রে ঐ সঞ্চারপথের পরামিতিক বা প্যারামিটারযুক্ত সমীকরণ বলে। পরামিতিকে অপসারণ করে যে সমীকরণ পাওয়া যাবে, তা কার্তেসীয় সমীকরণ হবে। সরলরেখার পরামিতিক সমীকরণকে লিখা হয়ঃ \(x=a+bt\) , \(y=c+dt\) যখন \(a, b, c, d\) ধ্রুবক এবং \(t\) পরিবর্তনশীল রাশি। এখানে \(t\) কে পরামিতি বলা হয় ।
দুইটি বিন্দুর সংযোগ সরলরেখার ঢাল
Slope of the straight line joining two points
দুইটি বিন্দুর সংযোগ সরলরেখার ঢালঃ
দুইটি নির্দিষ্ট বিন্দু \(A(x_{1}, y_{1})\) , \(B(x_{2}, y_{2})\) দিয়ে গমনকারী সরলরেখা \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্ন করলে, তার ঢাল
\(m=\tan\theta=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\) .
\(m=\tan\theta=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\) .
প্রমাণঃ
মনে করি, দুইটি নির্দিষ্ট বিন্দু \(A(x_{1}, y_{1})\) , \(B(x_{2}, y_{2})\) দিয়ে গমনকারী কোনো সরলরেখা \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্ন করে।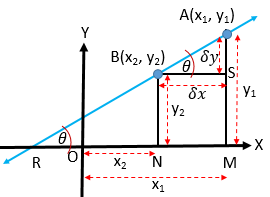
\(A\) ও \(B\) বিন্দু হতে \(OX\) এর উপর যথাক্রমে \(AM\) ও \(BN\) লম্ব আঁকি।
\(RM\parallel BS\) বলে, \(\angle ARM=\angle ABS=\theta \) .
এখানে,
\(ON=x_{2}, OM=x_{1}, BN=y_{2}, AM=y_{1} \)
আবার,
\(BS=NM=OM-ON=x_{1}-x_{2}=\delta_{x}\)
\(AS=AM-SM=AM-BN=y_{1}-y_{2}=\delta_{y} \)
সরলরেখাটির ঢাল \(=m=\tan\theta=\frac{AS}{BS}\)
\(=\frac{\delta_{y}}{\delta_{x}}\)
\(=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
\(\therefore \) ঢাল \(=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)

\(A\) ও \(B\) বিন্দু হতে \(OX\) এর উপর যথাক্রমে \(AM\) ও \(BN\) লম্ব আঁকি।
\(RM\parallel BS\) বলে, \(\angle ARM=\angle ABS=\theta \) .
এখানে,
\(ON=x_{2}, OM=x_{1}, BN=y_{2}, AM=y_{1} \)
আবার,
\(BS=NM=OM-ON=x_{1}-x_{2}=\delta_{x}\)
\(AS=AM-SM=AM-BN=y_{1}-y_{2}=\delta_{y} \)
সরলরেখাটির ঢাল \(=m=\tan\theta=\frac{AS}{BS}\)
\(=\frac{\delta_{y}}{\delta_{x}}\)
\(=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
\(\therefore \) ঢাল \(=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
\(X\) অক্ষের সমীকরণ
Equation of the \(X\) axis
\(X\) অক্ষের সমীকরণঃ
\(y=0\) .
প্রমাণঃ
\(X\) অক্ষের উপর অবস্থিত বিন্দুগুলির স্থানাঙ্ক \((x_{1}, 0)\) , \((x_{2}, 0)\) , \((x_{3}, 0)\) ......\((x_{n}, 0)\) .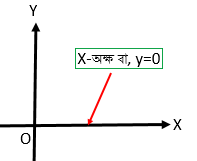
এখানে, ইহা স্পষ্ট যে, \(X\) অক্ষের উপর অবস্থিত সকল বিন্দুর \(y\) স্থানাঙ্ক \(0\) .
\(\therefore X\) অক্ষের সমীকরণ \(y=0\) .

এখানে, ইহা স্পষ্ট যে, \(X\) অক্ষের উপর অবস্থিত সকল বিন্দুর \(y\) স্থানাঙ্ক \(0\) .
\(\therefore X\) অক্ষের সমীকরণ \(y=0\) .
\(Y\) অক্ষের সমীকরণ
Equation of the \(Y\) axis
\(Y\) অক্ষের সমীকরণঃ
\(x=0\) .
প্রমাণঃ
\(Y\) অক্ষের উপর অবস্থিত বিন্দুগুলির স্থানাঙ্ক \((0, y_{1})\) , \((0, y_{2})\) , \((0, y_{3})\) .........\((0, y_{n})\) .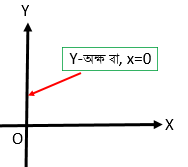
এখানে, ইহা স্পষ্ট যে, \(Y\) অক্ষের উপর অবস্থিত সকল বিন্দুর \(x\) স্থানাঙ্ক \(0\) .
\(\therefore Y\) অক্ষের সমীকরণ \(x=0\) .

এখানে, ইহা স্পষ্ট যে, \(Y\) অক্ষের উপর অবস্থিত সকল বিন্দুর \(x\) স্থানাঙ্ক \(0\) .
\(\therefore Y\) অক্ষের সমীকরণ \(x=0\) .
\(X\) অক্ষের সমান্তরাল সরলরেখার সমীকরণ
Equation of the straight line parallel to the \(X\) axis
\(X\) অক্ষের সমান্তরাল সরলরেখার সমীকরণঃ
\(y=b\) .
প্রমাণঃ
মনে করি, \(PQ\) এবং \(\acute{P}\acute{Q}\) সরলরেখাদ্বয় \(X\) অক্ষের সমান্তরাল এবং রেখাদ্বয় \(X\) অক্ষকে যথাক্রমে \(R\) ও \(\acute{R}\) বিন্দুতে ছেদ করে যেন, \(OR=b\) এবং \(O\acute{R}=\left|-b\right|=b\) হয়।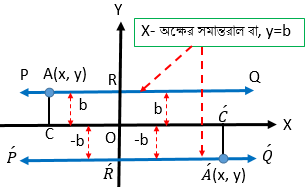
ধরি, \(PQ\) এবং \(\acute{P}\acute{Q}\) এর উপর যথাক্রমে \(A(x, y)\) ও \(\acute{A}(x, y)\) দুইটি বিন্দু ।
\(X\) অক্ষের উপর \(A(x, y)\) , \(\acute{A}(x, y)\) বিন্দু হতে যথাক্রমে \(AC\) ও \(\acute{A}\acute{C}\) লম্ব অঙ্কন করি।
\(\therefore AC=RO \Rightarrow y=b\)
আবার, \(\acute{A}\acute{C}=\acute{R}O\Rightarrow y=\left|-b\right|=b\)
\(\therefore X\) অক্ষের সমান্তরাল বা, \(Y\) অক্ষের উপর লম্ব সরলরেখার সমীকরণ \(y=b\) .

ধরি, \(PQ\) এবং \(\acute{P}\acute{Q}\) এর উপর যথাক্রমে \(A(x, y)\) ও \(\acute{A}(x, y)\) দুইটি বিন্দু ।
\(X\) অক্ষের উপর \(A(x, y)\) , \(\acute{A}(x, y)\) বিন্দু হতে যথাক্রমে \(AC\) ও \(\acute{A}\acute{C}\) লম্ব অঙ্কন করি।
\(\therefore AC=RO \Rightarrow y=b\)
আবার, \(\acute{A}\acute{C}=\acute{R}O\Rightarrow y=\left|-b\right|=b\)
\(\therefore X\) অক্ষের সমান্তরাল বা, \(Y\) অক্ষের উপর লম্ব সরলরেখার সমীকরণ \(y=b\) .
\(Y\) অক্ষের সমান্তরাল সরলরেখার সমীকরণ
Equation of the straight line parallel to the \(Y\) axis
\(Y\) অক্ষের সমান্তরাল সরলরেখার সমীকরণঃ
\(x=a\) .
প্রমাণঃ
মনে করি, \(PQ\) এবং \(\acute{P}\acute{Q}\) সরলরেখাদ্বয় \(Y\) অক্ষের সমান্তরাল এবং রেখাদ্বয় \(Y\) অক্ষকে যথাক্রমে \(R\) ও \(\acute{R}\) বিন্দুতে ছেদ করে যেন, \(OR=a\) এবং \(O\acute{R}=\left|-a\right|=a\) হয়।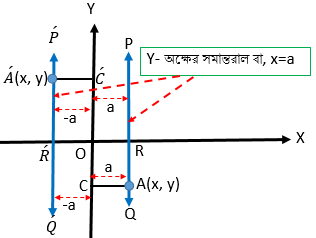
ধরি, \(PQ\) এবং \(\acute{P}\acute{Q}\) এর উপর যথাক্রমে \(A(x, y)\) ও \(\acute{A}(x, y)\) দুইটি বিন্দু ।
\(X\) অক্ষের উপর \(A(x, y)\) , \(\acute{A}(x, y)\) বিন্দু হতে যথাক্রমে \(AC\) ও \(\acute{A}\acute{C}\) লম্ব অঙ্কন করি।
\(\therefore AC=RO \Rightarrow x=a\)
আবার, \(\acute{A}\acute{C}=\acute{R}O\Rightarrow x=\left|-a\right|=a\)
\(\therefore Y\) অক্ষের সমান্তরাল বা, \(X\) অক্ষের উপর লম্ব সরলরেখার সমীকরণ \(x=a\) .

ধরি, \(PQ\) এবং \(\acute{P}\acute{Q}\) এর উপর যথাক্রমে \(A(x, y)\) ও \(\acute{A}(x, y)\) দুইটি বিন্দু ।
\(X\) অক্ষের উপর \(A(x, y)\) , \(\acute{A}(x, y)\) বিন্দু হতে যথাক্রমে \(AC\) ও \(\acute{A}\acute{C}\) লম্ব অঙ্কন করি।
\(\therefore AC=RO \Rightarrow x=a\)
আবার, \(\acute{A}\acute{C}=\acute{R}O\Rightarrow x=\left|-a\right|=a\)
\(\therefore Y\) অক্ষের সমান্তরাল বা, \(X\) অক্ষের উপর লম্ব সরলরেখার সমীকরণ \(x=a\) .
মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণ
General equation of a straight line through the origin
মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণঃ
\(y=mx\) .এখানে, \(m\) সরলরেখাটির ঢাল।
প্রমাণঃ
মনে করি, \(AB\) সরলরেখাটি মূলবিন্দু দিয়ে গমন করে এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta\) কোণ উৎপন্ন করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) হতে \(OX\) এর উপর \(PM\) লম্ব অঙ্কন করি।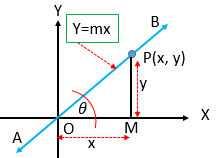
এখানে,
\(OM=x, PM=y\) এবং \(\angle POM=\theta\) .
তাহলে,
\(\tan\theta=\frac{PM}{OM}\)
\(\Rightarrow \tan\theta=\frac{y}{x}\)
\(\Rightarrow m=\frac{y}{x}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y=mx \)
\(\therefore\) মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণ \(y=mx\) .

এখানে,
\(OM=x, PM=y\) এবং \(\angle POM=\theta\) .
তাহলে,
\(\tan\theta=\frac{PM}{OM}\)
\(\Rightarrow \tan\theta=\frac{y}{x}\)
\(\Rightarrow m=\frac{y}{x}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y=mx \)
\(\therefore\) মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণ \(y=mx\) .
\(Y\) অক্ষের ছেদিতাংশ এবং ঢাল দেওয়া থাকিলে সরলরেখার সমীকরণ
Equation of the straight line given the intercept and slope of the \(Y\) axis
\(Y\) অক্ষের ছেদিতাংশ এবং ঢাল দেওয়া থাকিলে সরলরেখার সমীকরণঃ
\(y=mx+c\) .
প্রমাণঃ
মনে করি, \(AB\) সরলরেখাটি \(Y\) অক্ষকে \(Q\) বিন্দুতে ছেদ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta\) কোণ উৎপন্ন করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) হতে \(OX\) এর উপর \(PM\) এবং \(Q\) হতে \(PM\) এর উপর \(QR\) লম্ব অঙ্কন করি।
এখানে,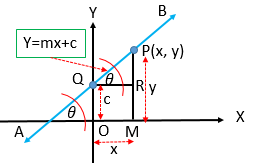
\(OQ=RM=c, OM=QR=x, PM=y.\) \(\therefore PR=PM-RM=y-c\) এবং \(\angle PQR=\theta\) .
তাহলে,
\(\tan\theta=\frac{PR}{QR}\)
\(\Rightarrow \tan\theta=\frac{y-c}{x}\)
\(\Rightarrow m=\frac{y-c}{x}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y-c=mx \)
\(\Rightarrow y=mx+c \)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y=mx+c\) .
এখানে,

\(OQ=RM=c, OM=QR=x, PM=y.\) \(\therefore PR=PM-RM=y-c\) এবং \(\angle PQR=\theta\) .
তাহলে,
\(\tan\theta=\frac{PR}{QR}\)
\(\Rightarrow \tan\theta=\frac{y-c}{x}\)
\(\Rightarrow m=\frac{y-c}{x}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y-c=mx \)
\(\Rightarrow y=mx+c \)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y=mx+c\) .
উভয় অক্ষের ছেদিতাংশ দেওয়া থাকিলে সরলরেখার সমীকরণ
Equation of straight line given intersection of both axes
উভয় অক্ষের ছেদিতাংশ দেওয়া থাকিলে সরলরেখার সমীকরণঃ
\(\frac{x}{a}+\frac{y}{b}=1\) .
প্রমাণঃ
মনে করি, \(CD\) সরলরেখাটি অক্ষদ্বয়কে যথাক্রমে \(A(a, 0)\) ও \(B(0, b)\) বিন্দুতে ছেদ করে। \(CD\) এর উপর চলমান বিন্দু \(P(x, y)\) হতে \(OX\) এবং \(OY\) এর উপর যথাক্রমে \(PM\) এবং \(PN\) লম্ব অঙ্কন করি। অতপর \(P, O\) যোগ করি।
এখানে,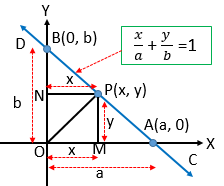
\(OA=a, OB=b, OM=PN=x, PM=y.\)
তাহলে,
\(\triangle AOB=\triangle AOP+\triangle BOP\)
\(\Rightarrow \frac{1}{2}a.b=\frac{1}{2}a.y+\frac{1}{2}b.x\) ➜ \(\because \triangle =\frac{1}{2}\times Base \times Height\)
\(\Rightarrow \frac{1}{2}ab=\frac{1}{2}(ay+bx)\)
\(\Rightarrow ab=ay+bx\) ➜ উভয় পার্শ্বে \(2\) গুণ করে।
\(\Rightarrow \frac{ab}{ab}=\frac{ay}{ab}+\frac{bx}{ab}\) ➜ উভয় পার্শ্বে \(ab\) ভাগ করে।
\(\Rightarrow 1=\frac{y}{b}+\frac{x}{a}\)
\(\Rightarrow \frac{x}{a}+\frac{y}{b}=1\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x}{a}+\frac{y}{b}=1\) .
এখানে,

\(OA=a, OB=b, OM=PN=x, PM=y.\)
তাহলে,
\(\triangle AOB=\triangle AOP+\triangle BOP\)
\(\Rightarrow \frac{1}{2}a.b=\frac{1}{2}a.y+\frac{1}{2}b.x\) ➜ \(\because \triangle =\frac{1}{2}\times Base \times Height\)
\(\Rightarrow \frac{1}{2}ab=\frac{1}{2}(ay+bx)\)
\(\Rightarrow ab=ay+bx\) ➜ উভয় পার্শ্বে \(2\) গুণ করে।
\(\Rightarrow \frac{ab}{ab}=\frac{ay}{ab}+\frac{bx}{ab}\) ➜ উভয় পার্শ্বে \(ab\) ভাগ করে।
\(\Rightarrow 1=\frac{y}{b}+\frac{x}{a}\)
\(\Rightarrow \frac{x}{a}+\frac{y}{b}=1\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x}{a}+\frac{y}{b}=1\) .
একটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ
Equation of a straight line through a fixed point
একটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণঃ
\(y-y_{1}=m(x-x_{1})\) .
প্রমাণঃ
মনে করি, \(AB\) সরলরেখাটি \(X\) অক্ষকে \(C\) বিন্দুতে ছেদ করে এবং নির্দিষ্ট \(Q(x_{1}, y_{1})\) বিন্দুদিয়ে গমন করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) এবং \(Q\) বিন্দু হতে \(OX\) এর উপর যথাক্রমে \(PM\) ও \(QN\) লম্ব আঁকি।
এখানে,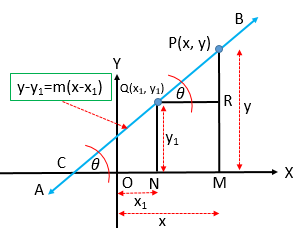
\(ON=x_{1}, OM=x, PM=y, QN=y_{1}.\)
\(QR=OM-ON=x-x_{1},\) \(PR=PM-RM=PM-QN=y-y_{1}.\)
এবং \(\angle PCM=\angle PQR=\theta.\)
তাহলে,
\(\tan\theta=\frac{PR}{QR}\)
\(\Rightarrow m=\frac{y-y_{1}}{x-x_{1}}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y-y_{1}=m(x-x_{1})\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y-y_{1}=m(x-x_{1})\) .
এখানে,

\(ON=x_{1}, OM=x, PM=y, QN=y_{1}.\)
\(QR=OM-ON=x-x_{1},\) \(PR=PM-RM=PM-QN=y-y_{1}.\)
এবং \(\angle PCM=\angle PQR=\theta.\)
তাহলে,
\(\tan\theta=\frac{PR}{QR}\)
\(\Rightarrow m=\frac{y-y_{1}}{x-x_{1}}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y-y_{1}=m(x-x_{1})\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y-y_{1}=m(x-x_{1})\) .
দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ
Equation of a straight line through two fixed points
দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণঃ
\(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\) .
প্রমাণঃ
মনে করি, \(AB\) সরলরেখাটি দুইটি নির্দিষ্ট \(Q(x_{1}, y_{1})\) , \(R(x_{2}, y_{2})\) বিন্দুদিয়ে গমন করে এবং \(X\) অক্ষকে \(E\) বিন্দুতে ছেদ করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) ।
এখন,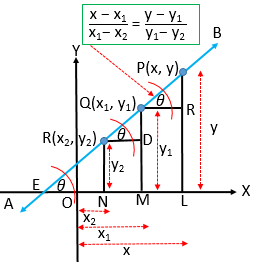
\(PQ\) এর ঢাল \(m_{1}=\frac{y-y_{1}}{x-x_{1}}\) .
\(QR\) এর ঢাল \(m_{2}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\) .
\(P, \ Q, \ R\) একই সরলরেখা \(AB\) এর উপর অবস্থিত।
তাহলে,
\(m_{1}=m_{2}\)
\(\Rightarrow \frac{y-y_{1}}{x-x_{1}}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
\(\Rightarrow \frac{y-y_{1}}{y_{1}-y_{2}}=\frac{x-x_{1}}{x_{1}-x_{2}}\)
\(\Rightarrow \frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\) .
এখন,

\(PQ\) এর ঢাল \(m_{1}=\frac{y-y_{1}}{x-x_{1}}\) .
\(QR\) এর ঢাল \(m_{2}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\) .
\(P, \ Q, \ R\) একই সরলরেখা \(AB\) এর উপর অবস্থিত।
তাহলে,
\(m_{1}=m_{2}\)
\(\Rightarrow \frac{y-y_{1}}{x-x_{1}}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
\(\Rightarrow \frac{y-y_{1}}{y_{1}-y_{2}}=\frac{x-x_{1}}{x_{1}-x_{2}}\)
\(\Rightarrow \frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\) .
মূলবিন্দু এবং একটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ
Equation of a straight line through the origin and a fixed point
মূলবিন্দু এবং একটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণঃ
\(y=\frac{y_{1}}{x_{1}}x\) .
প্রমাণঃ
মূলবিন্দু \(O(0, 0)\) এবং একটি নির্দিষ্ট বিন্দু \(P(x_{1}, y_{1})\) দিয়ে গমনকারী সরলরেখার সমীকরণ।
অর্থাৎ \(OP\) এর সমীকরণ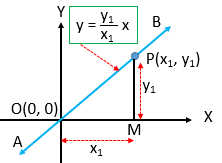
\(\frac{x-0}{0-x_{1}}=\frac{y-0}{0-y_{1}}\) ➜ \(P(x_1, y_1)\) এবং \(Q(x_2, y_2)\) , \(PQ\) -এর সমীকরণ, \(\frac{x-x_1}{x_1-x_2}=\frac{y-y_1}{y_1-y_2}\)
\(\Rightarrow \frac{x}{-x_{1}}=\frac{y}{-y_{1}}\)
\(\Rightarrow \frac{x\times -y_{1}}{-x_{1}}=y\)
\(\Rightarrow y=\frac{x\times y_{1}}{x_{1}}\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y=\frac{y_{1}}{x_{1}}x\) .
অর্থাৎ \(OP\) এর সমীকরণ

\(\frac{x-0}{0-x_{1}}=\frac{y-0}{0-y_{1}}\) ➜ \(P(x_1, y_1)\) এবং \(Q(x_2, y_2)\) , \(PQ\) -এর সমীকরণ, \(\frac{x-x_1}{x_1-x_2}=\frac{y-y_1}{y_1-y_2}\)
\(\Rightarrow \frac{x}{-x_{1}}=\frac{y}{-y_{1}}\)
\(\Rightarrow \frac{x\times -y_{1}}{-x_{1}}=y\)
\(\Rightarrow y=\frac{x\times y_{1}}{x_{1}}\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y=\frac{y_{1}}{x_{1}}x\) .
সরলরেখার লম্বরূপ সমীকরণ
Perpendicular type equation of straight line
সরলরেখার লম্বরূপ সমীকরণঃ
মূলবিন্দু হতে কোনো সরলরেখার উপর অঙ্কিত লম্বের দৈর্ঘ্য \(P\) এবং লম্বটি \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\alpha \) কোণ উৎপন্ন করলে, সরলরেখাটির সমীকরণ\(x\cos{\alpha}+y\sin{\alpha}=p\) .
প্রমাণঃ
মনে করি, \(PQ\) সরলরেখাটি অক্ষদ্বয়কে যথাক্রমে \(A\) ও \(B\) বিন্দুতে ছেদ করে। \(O\) বিন্দু হতে \(PQ\) এর উপর \(OC\) লম্ব আঁকি। \(OC\) লম্বের দৈর্ঘ্য \(p\) এবং লম্বটি \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\alpha \) কোণ উৎপন্ন করে।
এখন,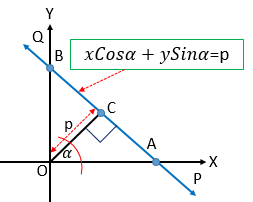
\(OA=\frac{OA}{OC}\times OC\)
\(\Rightarrow OA=\sec\alpha \times p\)
\(\Rightarrow OA=p\sec\alpha \)
আবার,
\(OB=\frac{OB}{OC}\times OC\)
\(\Rightarrow OB=\sec\angle COB \times p\)
\(\Rightarrow OB=p\sec(90^{o}-\alpha)\) ➜ \(\because \angle COB=90^{o}-\alpha \)
\(\Rightarrow OB=p\ cosec\alpha \)
\(\therefore AB\) এর সমীকরণ \(\frac{x}{OA}+\frac{y}{OB}=1\) ➜ \(\because \frac{x}{a}+\frac{y}{b}=1\)
\(\Rightarrow \frac{x}{p\sec\alpha}+\frac{y}{p\ cosec\alpha}=1\)
\(\Rightarrow \frac{x}{p}\times \frac{1}{\sec\alpha}+\frac{y}{p}\times \frac{1}{\ cosec\alpha}=1\)
\(\Rightarrow \frac{x}{p}\cos{\alpha}+\frac{y}{p}\sin{\alpha}=1\)
\(\Rightarrow x\cos{\alpha}+y\sin{\alpha}=p\) ➜ উভয় পার্শ্বে \(p\) গুণ করে।
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(x\cos{\alpha} + y\sin{\alpha}=p\) .
এখন,

\(OA=\frac{OA}{OC}\times OC\)
\(\Rightarrow OA=\sec\alpha \times p\)
\(\Rightarrow OA=p\sec\alpha \)
আবার,
\(OB=\frac{OB}{OC}\times OC\)
\(\Rightarrow OB=\sec\angle COB \times p\)
\(\Rightarrow OB=p\sec(90^{o}-\alpha)\) ➜ \(\because \angle COB=90^{o}-\alpha \)
\(\Rightarrow OB=p\ cosec\alpha \)
\(\therefore AB\) এর সমীকরণ \(\frac{x}{OA}+\frac{y}{OB}=1\) ➜ \(\because \frac{x}{a}+\frac{y}{b}=1\)
\(\Rightarrow \frac{x}{p\sec\alpha}+\frac{y}{p\ cosec\alpha}=1\)
\(\Rightarrow \frac{x}{p}\times \frac{1}{\sec\alpha}+\frac{y}{p}\times \frac{1}{\ cosec\alpha}=1\)
\(\Rightarrow \frac{x}{p}\cos{\alpha}+\frac{y}{p}\sin{\alpha}=1\)
\(\Rightarrow x\cos{\alpha}+y\sin{\alpha}=p\) ➜ উভয় পার্শ্বে \(p\) গুণ করে।
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(x\cos{\alpha} + y\sin{\alpha}=p\) .
একটি নির্দিষ্ট বিন্দুগামী এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্নকারী সরলরেখাটির সমীকরণ
Equation of a straight line through a fixed point and making an angle \(\theta \) with the positive direction of the \(X\) axis
একটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) দিয়ে গমনকারী এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্ন করলে, সরলরেখাটির সমীকরণঃ
\(\frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\) .যেখানে, \((x, y)\) বিন্দু হতে \((x_{1}, y_{1})\) বিন্দুর দূরত্ব=\(r\) .
প্রমাণঃ
\(\frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\)
মনে করি, \(AB\) সরলরেখাটি একটি নির্দিষ্ট বিন্দু \(Q(x_{1}, y_{1})\) দিয়ে গমন করে, \(X\) অক্ষকে \(C\) বিন্দুতে ছেদ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্ন করে। \(P\) ও \(Q\) হতে \(OX\) এর উপর যথাক্রমে \(PM\) , \(QN\) এবং \(Q\) হতে \(PM\) এর উপর \(QL\) লম্ব আঁকি।
এখানে,
\(OM=x, \ ON=x_{1}, \ PM=y,\)
\(QN=y_{1}, \ PQ=r,\)
\(\angle PCM=\angle PQL=\theta \)
\(QL=NM=OM-ON=x-x_{1},\)
\(PL=PM-LM=PM-QN=y-y_{1}\)
\(\sin\theta=\frac{PL}{PQ}\)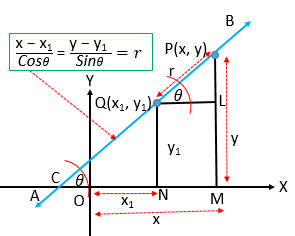
\(\Rightarrow \sin\theta=\frac{y-y_{1}}{r}\)
\(\Rightarrow r=\frac{y-y_{1}}{\sin\theta}\)
\(\Rightarrow \frac{y-y_{1}}{\sin\theta}=r ........(i)\)
আবার,
\(\cos\theta=\frac{QL}{PQ}\)
\(\Rightarrow \cos\theta=\frac{x-x_{1}}{r}\)
\(\Rightarrow r=\frac{x-x_{1}}{\cos\theta}\)
\(\Rightarrow \frac{x-x_{1}}{\cos\theta}=r ........(ii)\)
\((i)\) ও \((ii)\) হতে পাই,
\(\Rightarrow \frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\) .
এখানে,
\(OM=x, \ ON=x_{1}, \ PM=y,\)
\(QN=y_{1}, \ PQ=r,\)
\(\angle PCM=\angle PQL=\theta \)
\(QL=NM=OM-ON=x-x_{1},\)
\(PL=PM-LM=PM-QN=y-y_{1}\)
\(\sin\theta=\frac{PL}{PQ}\)

\(\Rightarrow \sin\theta=\frac{y-y_{1}}{r}\)
\(\Rightarrow r=\frac{y-y_{1}}{\sin\theta}\)
\(\Rightarrow \frac{y-y_{1}}{\sin\theta}=r ........(i)\)
আবার,
\(\cos\theta=\frac{QL}{PQ}\)
\(\Rightarrow \cos\theta=\frac{x-x_{1}}{r}\)
\(\Rightarrow r=\frac{x-x_{1}}{\cos\theta}\)
\(\Rightarrow \frac{x-x_{1}}{\cos\theta}=r ........(ii)\)
\((i)\) ও \((ii)\) হতে পাই,
\(\Rightarrow \frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\) .
\(\Rightarrow \frac{x-x_{1}}{\cos\theta}=r, \ \frac{y-y_{1}}{\sin\theta}=r\)
\(\Rightarrow x-x_{1}=r\cos\theta, \ y-y_{1}=r\sin\theta\)
\(\therefore x=x_{1}+r\cos\theta, \ y=y_{1}+r\sin\theta\)
সুতরাং, রেখাটির উপর যেকোনো বিন্দুর স্থানাংক \((x_{1}+r\cos\theta, y_{1}+r\sin\theta)\)
তিনটি সরলরেখা দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
Area of triangle formed by three straight lines
ধরি,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
উপরক্ত \((1)\) , \((2)\) এবং \((3)\) রেখাগুলি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল \(\triangle= \frac{1}{2} \frac{D^{2}}{C_{1}C_{2}C_{3}}\)
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
উপরক্ত \((1)\) , \((2)\) এবং \((3)\) রেখাগুলি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল \(\triangle= \frac{1}{2} \frac{D^{2}}{C_{1}C_{2}C_{3}}\)
যেখানে,\(D=\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\ a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|\) এবং \(C_{1}, C_{2}, C_{3}\) হচ্ছে \(D\) নির্ণায়কটির যথাক্রমে \(c_{1}, c_{2}, c_{3}\) উপাদানের সহ-গুণক।
অর্থাৎ \(C_{1}=(a_{2}b_{3}-a_{3}b_{2}),\) \(C_{2}= -(a_{1}b_{3}-a_{3}b_{1}),\) \(C_{3}=(a_{1}b_{2}-a_{2}b_{1})\)
প্রমাণঃ
মনে করি, কোনো ত্রিভুজের বাহু তিনটি যথাক্রমে
\(a_{1}x+b_{1}y+c_{1}=0 .........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 .........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 .........(3)\)
\((1)\) , \((2)\) , \((3)\) হতে \(x, y\) অপনয়ন করে পাই
\(D=\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|\)
ধরি,
\((2)\) ও \((3)\) এর ছেদবিন্দু \(A(x_{1},y_{1})\Rightarrow a_{2}x_{1}+b_{2}y_{1}+c_{2}=0 ........(4),\)
\(a_{3}x_{1}+b_{3}y_{1}+c_{3}=0 .........(5)\)
\((3)\) ও \((1)\) এর ছেদবিন্দু \(B(x_{2},y_{2})\Rightarrow a_{3}x_{2}+b_{3}y_{2}+c_{3}=0 ........(6),\)
\(a_{1}x_{2}+b_{1}y_{2}+c_{1}=0 ........(7) \)
\((1)\) ও \((2)\) এর ছেদবিন্দু \(C(x_{3},y_{3})\Rightarrow a_{1}x_{3}+b_{1}y_{3}+c_{1}=0 ........(8),\)
\(a_{2}x_{3}+b_{2}y_{3}+c_{2}=0 ........(9) \)
এখন, \(\triangle ABC\) এর ক্ষেত্রফল \(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ \ \ 1\\x_{2} \ \ y_{2} \ \ \ \ 1\\x_{3} \ \ y_{3} \ \ \ \ 1\end{array}\right| \)
\(=\frac{1}{2}\frac{\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ \ \ 1\\x_{2} \ \ y_{2} \ \ \ \ 1\\x_{3} \ \ y_{3} \ \ \ \ 1\end{array}\right|\times \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|}{\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|} \)
\(=\frac{\left|\begin{array}{c}a_{1}x_{1}+b_{1}y_{1}+c_{1} \ \ \ \ a_{2}x_{1}+b_{2}y_{1}+c_{2} \ \ \ \ a_{3}x_{1}+b_{3}y_{1}+c_{3} \\ a_{1}x_{2}+b_{1}y_{2}+c_{1} \ \ \ \ a_{2}x_{2}+b_{2}y_{2}+c_{2} \ \ \ \ a_{3}x_{2}+b_{3}y_{2}+c_{3}\\ a_{1}x_{3}+b_{1}y_{3}+c_{1} \ \ \ \ a_{2}x_{3}+b_{2}y_{3}+c_{2} \ \ \ \ a_{3}x_{3}+b_{3}y_{3}+c_{3}\end{array}\right|}{2D} \)
\(=\frac{\left|\begin{array}{c}a_{1}x_{1}+b_{1}y_{1}+c_{1} \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \\ 0 \ \ \ \ \ \ \ \ \ \ \ \ a_{2}x_{2}+b_{2}y_{2}+c_{2} \ \ \ \ \ \ \ \ \ \ \ \ 0\\ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ a_{3}x_{3}+b_{3}y_{3}+c_{3}\end{array}\right|}{2D} \) ➜ (4),(5),(6),(7),(8),(9) এর সাহায্যে
\(=\frac{(a_{1}x_{1}+b_{1}y_{1}+c_{1})(a_{2}x_{2}+b_{2}y_{2}+c_{2})(a_{3}x_{3}+b_{3}y_{3}+c_{3})}{2D} ..........(10)\)
ধরি,
\(a_{1}x_{1}+b_{1}y_{1}+c_{1}=k_{1}\)
\(\Rightarrow a_{1}x_{1}+b_{1}y_{1}+c_{1}-k_{1}=0 ............. (11)\)
\(a_{2}x_{1}+b_{2}y_{1}+c_{2}=0 ............(12)\)
\(a_{3}x_{1}+b_{3}y_{1}+c_{3}=0 ............. (13)\)
\((11), (12), (13)\) হতে \(x_{1}, y_{1}\) অপনয়ন করে পাই ,
\(\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}-k_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ \ \ \ \ c_{2} \ \ \ \ \\a_{3} \ \ \ \ b_{3} \ \ \ \ \ \ \ \ c_{3} \ \ \ \ \end{array}\right|=0\)
\(\Rightarrow \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|+\left|\begin{array}{c}a_{1} \ \ \ \ \ b_{1} \ \ \ \ -k_{1}\\a_{2} \ \ \ \ \ b_{2} \ \ \ \ \ \ \ \ 0 \ \ \ \\a_{3} \ \ \ \ \ b_{3} \ \ \ \ \ \ \ \ 0 \ \ \ \end{array}\right|=0\)
\(\Rightarrow D-k_{1}\left|\begin{array}{c}a_{2} \ \ \ \ b_{2}\\a_{3} \ \ \ \ b_{3}\end{array}\right|=0\)
\(\Rightarrow D-k_{1}(a_{2}b_{3}-a_{3}b_{2})=0\)
\(\Rightarrow D-k_{1}C_{1}=0\) ➜ \(C_{1}= D \) নির্ণায়কে \( c_{1}\) এর সহগুণক।
\(\Rightarrow D=k_{1}C_{1}\)
\(\Rightarrow k_{1}C_{1}=D\)
\(\therefore k_{1}=\frac{D}{C_{1}}\)
অনুরূপভাবে,
\(a_{2}x_{2}+b_{2}y_{2}+c_{2}=k_{2}, \ a_{3}x_{3}+b_{3}y_{3}+c_{3}=k_{3} \) কল্পনা করে পাই
\(k_{2}=-\frac{D}{C_{2}}, \ k_{3}=\frac{D}{C_{3}}\) ➜ \(C_{2}, C_{3}\) যথাক্রমে \(D \) নির্ণায়কে \( c_{2},c_{3} \) এর সহগুণক।
এখন \((10)\) হতে পাই,
ক্ষেত্রফল \(\triangle=\frac{\frac{D}{C_{1}}\times -\frac{D}{C_{2}}\times \frac{D}{C_{3}}}{2D\times C_{1}C_{2}C_{3}}\)
\(=-\frac{D^{3}}{2D\times C_{1}C_{2}C_{3}}\)
\(=\frac{D^{2}}{2C_{1}C_{2}C_{3}}\) ➜ \(\triangle \neq -ve\)
\(\therefore \triangle=\frac{1}{2}\frac{D^{2}}{C_{1}C_{2}C_{3}}\)
\(a_{1}x+b_{1}y+c_{1}=0 .........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 .........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 .........(3)\)
\((1)\) , \((2)\) , \((3)\) হতে \(x, y\) অপনয়ন করে পাই
\(D=\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|\)
ধরি,
\((2)\) ও \((3)\) এর ছেদবিন্দু \(A(x_{1},y_{1})\Rightarrow a_{2}x_{1}+b_{2}y_{1}+c_{2}=0 ........(4),\)
\(a_{3}x_{1}+b_{3}y_{1}+c_{3}=0 .........(5)\)
\((3)\) ও \((1)\) এর ছেদবিন্দু \(B(x_{2},y_{2})\Rightarrow a_{3}x_{2}+b_{3}y_{2}+c_{3}=0 ........(6),\)
\(a_{1}x_{2}+b_{1}y_{2}+c_{1}=0 ........(7) \)
\((1)\) ও \((2)\) এর ছেদবিন্দু \(C(x_{3},y_{3})\Rightarrow a_{1}x_{3}+b_{1}y_{3}+c_{1}=0 ........(8),\)
\(a_{2}x_{3}+b_{2}y_{3}+c_{2}=0 ........(9) \)
এখন, \(\triangle ABC\) এর ক্ষেত্রফল \(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ \ \ 1\\x_{2} \ \ y_{2} \ \ \ \ 1\\x_{3} \ \ y_{3} \ \ \ \ 1\end{array}\right| \)
\(=\frac{1}{2}\frac{\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ \ \ 1\\x_{2} \ \ y_{2} \ \ \ \ 1\\x_{3} \ \ y_{3} \ \ \ \ 1\end{array}\right|\times \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|}{\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|} \)
\(=\frac{\left|\begin{array}{c}a_{1}x_{1}+b_{1}y_{1}+c_{1} \ \ \ \ a_{2}x_{1}+b_{2}y_{1}+c_{2} \ \ \ \ a_{3}x_{1}+b_{3}y_{1}+c_{3} \\ a_{1}x_{2}+b_{1}y_{2}+c_{1} \ \ \ \ a_{2}x_{2}+b_{2}y_{2}+c_{2} \ \ \ \ a_{3}x_{2}+b_{3}y_{2}+c_{3}\\ a_{1}x_{3}+b_{1}y_{3}+c_{1} \ \ \ \ a_{2}x_{3}+b_{2}y_{3}+c_{2} \ \ \ \ a_{3}x_{3}+b_{3}y_{3}+c_{3}\end{array}\right|}{2D} \)
\(=\frac{\left|\begin{array}{c}a_{1}x_{1}+b_{1}y_{1}+c_{1} \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \\ 0 \ \ \ \ \ \ \ \ \ \ \ \ a_{2}x_{2}+b_{2}y_{2}+c_{2} \ \ \ \ \ \ \ \ \ \ \ \ 0\\ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ a_{3}x_{3}+b_{3}y_{3}+c_{3}\end{array}\right|}{2D} \) ➜ (4),(5),(6),(7),(8),(9) এর সাহায্যে
\(=\frac{(a_{1}x_{1}+b_{1}y_{1}+c_{1})(a_{2}x_{2}+b_{2}y_{2}+c_{2})(a_{3}x_{3}+b_{3}y_{3}+c_{3})}{2D} ..........(10)\)
ধরি,
\(a_{1}x_{1}+b_{1}y_{1}+c_{1}=k_{1}\)
\(\Rightarrow a_{1}x_{1}+b_{1}y_{1}+c_{1}-k_{1}=0 ............. (11)\)
\(a_{2}x_{1}+b_{2}y_{1}+c_{2}=0 ............(12)\)
\(a_{3}x_{1}+b_{3}y_{1}+c_{3}=0 ............. (13)\)
\((11), (12), (13)\) হতে \(x_{1}, y_{1}\) অপনয়ন করে পাই ,
\(\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}-k_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ \ \ \ \ c_{2} \ \ \ \ \\a_{3} \ \ \ \ b_{3} \ \ \ \ \ \ \ \ c_{3} \ \ \ \ \end{array}\right|=0\)
\(\Rightarrow \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|+\left|\begin{array}{c}a_{1} \ \ \ \ \ b_{1} \ \ \ \ -k_{1}\\a_{2} \ \ \ \ \ b_{2} \ \ \ \ \ \ \ \ 0 \ \ \ \\a_{3} \ \ \ \ \ b_{3} \ \ \ \ \ \ \ \ 0 \ \ \ \end{array}\right|=0\)
\(\Rightarrow D-k_{1}\left|\begin{array}{c}a_{2} \ \ \ \ b_{2}\\a_{3} \ \ \ \ b_{3}\end{array}\right|=0\)
\(\Rightarrow D-k_{1}(a_{2}b_{3}-a_{3}b_{2})=0\)
\(\Rightarrow D-k_{1}C_{1}=0\) ➜ \(C_{1}= D \) নির্ণায়কে \( c_{1}\) এর সহগুণক।
\(\Rightarrow D=k_{1}C_{1}\)
\(\Rightarrow k_{1}C_{1}=D\)
\(\therefore k_{1}=\frac{D}{C_{1}}\)
অনুরূপভাবে,
\(a_{2}x_{2}+b_{2}y_{2}+c_{2}=k_{2}, \ a_{3}x_{3}+b_{3}y_{3}+c_{3}=k_{3} \) কল্পনা করে পাই
\(k_{2}=-\frac{D}{C_{2}}, \ k_{3}=\frac{D}{C_{3}}\) ➜ \(C_{2}, C_{3}\) যথাক্রমে \(D \) নির্ণায়কে \( c_{2},c_{3} \) এর সহগুণক।
এখন \((10)\) হতে পাই,
ক্ষেত্রফল \(\triangle=\frac{\frac{D}{C_{1}}\times -\frac{D}{C_{2}}\times \frac{D}{C_{3}}}{2D\times C_{1}C_{2}C_{3}}\)
\(=-\frac{D^{3}}{2D\times C_{1}C_{2}C_{3}}\)
\(=\frac{D^{2}}{2C_{1}C_{2}C_{3}}\) ➜ \(\triangle \neq -ve\)
\(\therefore \triangle=\frac{1}{2}\frac{D^{2}}{C_{1}C_{2}C_{3}}\)
দুইটি সরলরেখার ছেদবিন্দু
Intersection of two straight lines
ধরি,\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
উপরক্ত \((1)\) এবং \((2)\) সরলরেখাদ্বয়ের ছেদবিন্দু
\(P\left(\frac{b_{1}c_{2}-b_{2}c_{1}}{a{1}b_{2}-a_{2}b_{1}}, \frac{a_{2}c_{1}-a_{1}c_{2}}{a{1}b_{2}-a_{2}b_{1}}\right)\)
প্রমাণঃ
মনে করি,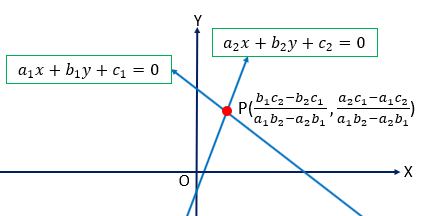
\(a_{1}x+b_{1}y+c_{1}=0 .........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 .........(2)\)
\((1)\) ও \((2)\) ( বজ্রগুণ পদ্ধতিতে ) সমাধান করি,
\(\frac{x}{b_{1}c_{2}-b_{2}c_{1}}=\frac{y}{a_{2}c_{1}-a_{1}c_{2}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow \frac{x}{b_{1}c_{2}-b_{2}c_{1}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}, \ \frac{y}{a_{2}c_{1}-a_{1}c_{2}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow x=\frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}, \ y=\frac{a_{2}c_{1}-a_{1}c_{2}}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\therefore (1)\) ও \((2)\) এর ছেদবিন্দু \(P\left(\frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}, \frac{a_{2}c_{1}-a_{1}c_{2}}{a_{1}b_{2}-a_{2}b_{1}}\right)\)

\(a_{1}x+b_{1}y+c_{1}=0 .........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 .........(2)\)
\((1)\) ও \((2)\) ( বজ্রগুণ পদ্ধতিতে ) সমাধান করি,
\(\frac{x}{b_{1}c_{2}-b_{2}c_{1}}=\frac{y}{a_{2}c_{1}-a_{1}c_{2}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow \frac{x}{b_{1}c_{2}-b_{2}c_{1}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}, \ \frac{y}{a_{2}c_{1}-a_{1}c_{2}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow x=\frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}, \ y=\frac{a_{2}c_{1}-a_{1}c_{2}}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\therefore (1)\) ও \((2)\) এর ছেদবিন্দু \(P\left(\frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}, \frac{a_{2}c_{1}-a_{1}c_{2}}{a_{1}b_{2}-a_{2}b_{1}}\right)\)
দুইটি সমীকরণ একই সরলরেখা নির্দেশ করার শর্ত
The condition that two equations point to the same straight line
ধরি,\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
উপরক্ত \((1)\) এবং \((2)\) সমীকরণদ্বয় একই সরলরেখা নির্দেশ করবে যদি,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
প্রমাণঃ
মনে করি,
\(a_{1}x+b_{1}y+c_{1}=0 .........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 .........(2)\)
\((1)\) নং সরলরেখার ঢাল \(m_{1}=-\frac{a_{1}}{b_{1}}\) ➜ \(ax+by+c=0\) সরলরেখার ঢাল \(m=-\frac{a}{b}\)
\((2)\) নং সরলরেখার ঢাল \(m_{2}=-\frac{a_{2}}{b_{2}}\) ➜ \(ax+by+c=0\) সরলরেখার ঢাল \(m=-\frac{a}{b}\)
\(\because (1)\) ও \((2)\) সমীকরণ একই সরলরেখা নির্দেশ করে,
\(\therefore m_{1}=m_{2}\)
\(\Rightarrow -\frac{a_{1}}{b_{1}}=-\frac{a_{2}}{b_{2}}\)
\(\Rightarrow \frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}\)
\(\therefore \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} ....(3)\)
আবার,
\((1)\) নং সরলরেখার দ্বারা \(Y\) অক্ষের ছেদিতাংশ \(=-\frac{c_{1}}{b_{1}}\) ➜ \(ax+by+c=0\) সরলরেখা দ্বারা \(Y\) অক্ষের ছেদিতাংশ \(=-\frac{c}{b}\)
\((2)\) নং সরলরেখার দ্বারা \(Y\) অক্ষের ছেদিতাংশ \(=-\frac{c_{2}}{b_{2}}\) ➜ \(ax+by+c=0\) সরলরেখা দ্বারা \(Y\) অক্ষের ছেদিতাংশ \(=-\frac{c}{b}\)
\(\because (1)\) ও \((2)\) সমীকরণ একই সরলরেখা নির্দেশ করে,
\(\therefore -\frac{c_{1}}{b_{1}}=-\frac{c_{2}}{b_{2}}\)
\(\Rightarrow \frac{c_{1}}{b_{1}}=\frac{c_{2}}{b_{2}}\)
\(\Rightarrow \frac{c_{2}}{b_{2}}=\frac{c_{1}}{b_{1}}\)
\(\therefore \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}} .....(4)\)
\((3)\) ও \((4)\) হতে,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
ইহাই নির্ণেয় শর্ত।

\(a_{1}x+b_{1}y+c_{1}=0 .........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 .........(2)\)
\((1)\) নং সরলরেখার ঢাল \(m_{1}=-\frac{a_{1}}{b_{1}}\) ➜ \(ax+by+c=0\) সরলরেখার ঢাল \(m=-\frac{a}{b}\)
\((2)\) নং সরলরেখার ঢাল \(m_{2}=-\frac{a_{2}}{b_{2}}\) ➜ \(ax+by+c=0\) সরলরেখার ঢাল \(m=-\frac{a}{b}\)
\(\because (1)\) ও \((2)\) সমীকরণ একই সরলরেখা নির্দেশ করে,
\(\therefore m_{1}=m_{2}\)
\(\Rightarrow -\frac{a_{1}}{b_{1}}=-\frac{a_{2}}{b_{2}}\)
\(\Rightarrow \frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}\)
\(\therefore \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} ....(3)\)
আবার,
\((1)\) নং সরলরেখার দ্বারা \(Y\) অক্ষের ছেদিতাংশ \(=-\frac{c_{1}}{b_{1}}\) ➜ \(ax+by+c=0\) সরলরেখা দ্বারা \(Y\) অক্ষের ছেদিতাংশ \(=-\frac{c}{b}\)
\((2)\) নং সরলরেখার দ্বারা \(Y\) অক্ষের ছেদিতাংশ \(=-\frac{c_{2}}{b_{2}}\) ➜ \(ax+by+c=0\) সরলরেখা দ্বারা \(Y\) অক্ষের ছেদিতাংশ \(=-\frac{c}{b}\)
\(\because (1)\) ও \((2)\) সমীকরণ একই সরলরেখা নির্দেশ করে,
\(\therefore -\frac{c_{1}}{b_{1}}=-\frac{c_{2}}{b_{2}}\)
\(\Rightarrow \frac{c_{1}}{b_{1}}=\frac{c_{2}}{b_{2}}\)
\(\Rightarrow \frac{c_{2}}{b_{2}}=\frac{c_{1}}{b_{1}}\)
\(\therefore \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}} .....(4)\)
\((3)\) ও \((4)\) হতে,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
ইহাই নির্ণেয় শর্ত।
শর্টকাট টেকনিক
Shortcut Technique
কোন সমতলে \(ax+by+c=0\) একটি সরলরেখার সমীকরণ-সরলরেখাটির ঢাল \(=-\frac{a}{b}\)
সরলরেখাটি দ্বারা \(x\) অক্ষের খন্ডিতাংশ \(=-\frac{c}{a}\)
সরলরেখাটি দ্বারা \(x\) অক্ষের খন্ডিতাংশের দৈর্ঘ্য \(=\left|-\frac{c}{a}\right|\)
সরলরেখাটি দ্বারা \(y\) অক্ষের খন্ডিতাংশ \(=-\frac{c}{b}\)
সরলরেখাটি দ্বারা \(y\) অক্ষের খন্ডিতাংশের দৈর্ঘ্য \(=\left|-\frac{c}{b}\right|\)
অক্ষদ্বয় দ্বারা সরলরেখাটি হতে খন্ডিতাংশের দৈর্ঘ্য \(=\sqrt{a^2+b^2}\)
সরলরেখাটি দ্বারা অক্ষদ্বয়ের সাথে উৎপন্ন ত্রিভুজের ক্ষেত্রফল \(=\frac{1}{2}|ab|\) বর্গ একক।
উদাহরণঃ \(3x-4y-12=0\) একটি সরলরেখার সমীকরণ-
সরলরেখাটির ঢাল \(=-\frac{3}{-4}\)
\(=\frac{3}{4}\)
সরলরেখাটি দ্বারা \(x\) অক্ষের খন্ডিতাংশ \(=-\frac{-12}{3}\)
\(=4\)
সরলরেখাটি দ্বারা \(x\) অক্ষের খন্ডিতাংশের দৈর্ঘ্য \(=\left|-\frac{-12}{3}\right|\)
\(=|4|\)
\(=4\)
সরলরেখাটি দ্বারা \(y\) অক্ষের খন্ডিতাংশ \(=-\frac{-12}{-4}\)
\(=-3\)
সরলরেখাটি দ্বারা \(y\) অক্ষের খন্ডিতাংশের দৈর্ঘ্য \(=\left|-\frac{-12}{-4}\right|\)
\(=|-3|\)
\(=3\)
অক্ষদ্বয় দ্বারা সরলরেখাটি হতে খন্ডিতাংশের দৈর্ঘ্য \(=\sqrt{3^2+(-4)^2}\)
\(=\sqrt{9+16}\)
\(=\sqrt{25}\)
\(=5\)
সরলরেখাটি দ্বারা অক্ষদ্বয়ের সাথে উৎপন্ন ত্রিভুজের ক্ষেত্রফল \(=\frac{1}{2}|3\times-4|\)
\(=\frac{1}{2}|-12|\)
\(=\frac{1}{2}\times12\)
\(=6\) বর্গ একক।
কোনো সরলরেখার অক্ষদ্বয়ের মধ্যবর্তী খন্ডিতাংশের মধ্যবিন্দু \((\alpha, \beta)\) হলে রেখাটির সমীকরণ \(\frac{x}{\alpha}+\frac{y}{\beta}=2\)
উদাহরণঃ একটি সরলরেখার অক্ষদ্বয়ের মধ্যবর্তী খন্ডিতাংশের মধ্যবিন্দু \((3, 4),\) হলে রেখাটির সমীকরণ \(\frac{x}{3}+\frac{y}{4}=2\)
\(\Rightarrow 4x+3y=24\)
\(\therefore 4x+3y-24=0\)
মূলবিন্দু এবং অক্ষদ্বয় দ্বারা \(ax+by+c=0\) সরলরেখার মধ্যবর্তী খন্ডিতাংশের মধ্যবিন্দুর সংযোজক সরলরেখার সমীকরণ \(y=\frac{b}{a}x\)
উদাহরণঃ মূলবিন্দু এবং অক্ষদ্বয় দ্বারা \(5x+7y+3=0\) সরলরেখার মধ্যবর্তী খন্ডিতাংশের মধ্যবিন্দুর সংযোজক সরলরেখার সমীকরণ \(y=\frac{7}{5}x\)
\(\Rightarrow y=\frac{7x}{5}\)
\(\Rightarrow 7x=5y \)
\(\therefore 7x-5y=0 \)
মূলবিন্দু এবং অক্ষদ্বয় দ্বারা \(ax+by+c=0\) সরলরেখার মধ্যবর্তী খন্ডিতাংশের সমত্রিখন্ডক বিন্দুদ্বয়ের সংযোজক সরলরেখাদ্বয়ের সমীকরণ \(y=\frac{2b}{a}x, \ y=\frac{b}{2a}x\)
উদাহরণঃ মূলবিন্দু এবং অক্ষদ্বয় দ্বারা \(5x+7y+3=0\) সরলরেখার মধ্যবর্তী খন্ডিতাংশের সমত্রিখন্ডক বিন্দুদ্বয়ের সংযোজক সরলরেখাদ্বয়ের সমীকরণ \(y=\frac{2\times7}{5}x, \ y=\frac{7}{2\times5}x\)
\(\Rightarrow y=\frac{14x}{5}, \ y=\frac{7x}{10}\)
\(\Rightarrow 14x=5y, \ 7x=10y\)
\(\therefore 14x-5y=0, \ 7x-10y=0 \)
\(ax+by+c=0\) সরলরেখার উপরোস্থ \((x_{1}, y_{1})\) বিন্দু হতে \(r\) একক দূরবর্তী বিন্দুর স্থানাংক \((x_{1}+r\cos{\theta}, y_{1}+r\sin{\theta})\)
যেখানে, \(\tan{\theta}=-\frac{a}{b};\) অতএব, লম্ব \(=a,\) ভূমি \(=b,\) অতিভুজ \(=\sqrt{a^2+b^2}\)
\(\therefore \cos{\theta}=\frac{b}{\sqrt{a^2+b^2}}, \ \sin{\theta}=-\frac{a}{\sqrt{a^2+b^2}}\)
অথবা, \(\cos{\theta}=-\frac{b}{\sqrt{a^2+b^2}}, \ \sin{\theta}=\frac{a}{\sqrt{a^2+b^2}}\)
বিন্দুর স্থানাংকঃ
\(a\) ও \(b\) সমচিহ্নযুক্ত হলে,
\(\left(x_{1}+\frac{r|b|}{\sqrt{a^2+b^2}}, y_{1}-\frac{r|a|}{\sqrt{a^2+b^2}}\right)\) অথবা, \(\left(x_{1}-\frac{r|b|}{\sqrt{a^2+b^2}}, y_{1}+\frac{r|a|}{\sqrt{a^2+b^2}}\right)\)
\(a\) ও \(b\) বিপরীত চিহ্নযুক্ত হলে,
\(\left(x_{1}+\frac{r|b|}{\sqrt{a^2+b^2}}, y_{1}+\frac{r|a|}{\sqrt{a^2+b^2}}\right)\) অথবা, \(\left(x_{1}-\frac{r|b|}{\sqrt{a^2+b^2}}, y_{1}-\frac{r|a|}{\sqrt{a^2+b^2}}\right)\)

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004