এ অধ্যায়ের পাঠ্যসূচী।
- কার্তেসীয় স্থানাঙ্কে দূরত্ব (Distance in Cartesian coordinates)
- পোলার স্থানাঙ্কে দূরত্ব (Distance in polar coordinates)
- দুইটি বিন্দুর মধ্যবর্তী দূরত্ব বিষয়ক অনুসিদ্ধান্ত
- সমবাহু ত্রিভুজ (Equilateral triangle)
- সমদ্বিবাহু ত্রিভুজ (Isosceles triangle)
- বিষমবাহু ত্রিভুজ (Scalene triangle)
- সমকোণী ত্রিভুজ (Right triangle)
- সমদ্বিবাহু সমকোণী ত্রিভুজ (Isosceles right triangle)
- বর্গক্ষেত্র (Square)
- রম্বস (Rhombus)
- আয়তক্ষেত্র (Rectangle)
- সামান্তরিক (Parallelogram)
- অধ্যায় \(3B\)-এর উদাহরণসমুহ
- অধ্যায় \(3B\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(3B\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3B\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3B\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
কার্তেসীয় স্থানাঙ্কে দূরত্ব
Distance in Cartesian coordinates
কোন সমতলের উপর \(P(x_{1}, y_{1})\) ও \(Q(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব হবে।
\(PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
\(PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
প্রমাণঃ
 মনে করি,
মনে করি,
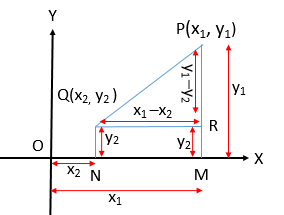
\(P(x_{1}, y_{1})\) ও \(Q(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু।
\(P\) এবং \(Q\) হতে \(OX\) এর উপর যথাক্রমে \(PM\) এবং \(QN\) লম্ব অংকন করি।
তাহলে, \(OM=x_{1}\), \(PM=y_{1}\), \(ON=x_{2}\), \(QN=y_{2}\). আবার,
\(QR=NM=OM-ON=x_{1}-x_{2}\).
\(PR=PM-RM=y_{1}-y_{2}\).
\(PQR\) সমকোণী ত্রীভুজ হতে পাই,
\(PQ^{2}=QR^{2}+PR^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}\)
\(\Rightarrow PQ^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}\)
\(\therefore PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\) ➜ \(\because\) দূরত্ব সর্বদা ধনাত্মক।
\(PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)

 মনে করি,
মনে করি,
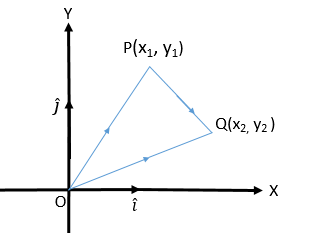
\(P(x_{1}, y_{1})\) ও \(Q(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু। মূলবিন্দু বা \(O\) বিন্দুর সাপেক্ষে বিন্দুদ্বয়ের অবস্থান ভেক্টর যথাক্রমে \(\overline{OP}=x_{1}\hat{i}+y_{1}\hat{j}\) এবং \(\overline{OQ}=x_{2}\hat{i}+y_{2}\hat{j}\)।
\(\triangle OPQ\) হতে পাই,
\(\overline{PQ}=\overline{OQ}-\overline{OP}\)
\(=x_{2}\hat{i}+y_{2}\hat{j}-x_{1}\hat{i}-y_{1}\hat{j}\)
\(=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}\)
\(P(x_{1}, y_{1})\) ও \(P(x_{2}, y_{2})\) বিন্দুর দূরত্ব \(\overline{\mid PQ \mid}\)
\(=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\)
\(=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
\(PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
উদাহরণঃ \(P(1, 2)\) ও \(Q(-2, 6)\) বিন্দু দ্বয়ের দূরত্ব
\(=\sqrt{(1+2)^{2}+(2-6)^{2}}\)
\(=\sqrt{3^{2}+4^{2}}\)
\(=\sqrt{9+19}\)
\(=\sqrt{25}\)
\(=5\)
 মনে করি,
মনে করি, \(P(x_{1}, y_{1})\) ও \(Q(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু।
\(P\) এবং \(Q\) হতে \(OX\) এর উপর যথাক্রমে \(PM\) এবং \(QN\) লম্ব অংকন করি।
তাহলে, \(OM=x_{1}\), \(PM=y_{1}\), \(ON=x_{2}\), \(QN=y_{2}\). আবার,
\(QR=NM=OM-ON=x_{1}-x_{2}\).
\(PR=PM-RM=y_{1}-y_{2}\).
\(PQR\) সমকোণী ত্রীভুজ হতে পাই,
\(PQ^{2}=QR^{2}+PR^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}\)
\(\Rightarrow PQ^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}\)
\(\therefore PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\) ➜ \(\because\) দূরত্ব সর্বদা ধনাত্মক।
\(PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)

ভেক্টর পদ্ধতিতে দূরত্ব নির্ণয়ঃ
 মনে করি,
মনে করি, \(P(x_{1}, y_{1})\) ও \(Q(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু। মূলবিন্দু বা \(O\) বিন্দুর সাপেক্ষে বিন্দুদ্বয়ের অবস্থান ভেক্টর যথাক্রমে \(\overline{OP}=x_{1}\hat{i}+y_{1}\hat{j}\) এবং \(\overline{OQ}=x_{2}\hat{i}+y_{2}\hat{j}\)।
\(\triangle OPQ\) হতে পাই,
\(\overline{PQ}=\overline{OQ}-\overline{OP}\)
\(=x_{2}\hat{i}+y_{2}\hat{j}-x_{1}\hat{i}-y_{1}\hat{j}\)
\(=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}\)
\(P(x_{1}, y_{1})\) ও \(P(x_{2}, y_{2})\) বিন্দুর দূরত্ব \(\overline{\mid PQ \mid}\)
\(=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\)
\(=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
উদাহরণঃ \(P(1, 2)\) ও \(Q(-2, 6)\) বিন্দু দ্বয়ের দূরত্ব
\(=\sqrt{(1+2)^{2}+(2-6)^{2}}\)
\(=\sqrt{3^{2}+4^{2}}\)
\(=\sqrt{9+19}\)
\(=\sqrt{25}\)
\(=5\)
পোলার স্থানাঙ্কে দূরত্ব
Distance in polar coordinates
কোন সমতলের উপর \(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব হবে।
\(PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
\(PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
প্রমাণঃ
মনে করি,
কোন সমতলের উপর \(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব নির্ণয় করতে হবে।
\(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) বিন্দুদ্বয়ের কার্তেসীয় স্থানাঙ্ক যথাক্রমে \(P(r_{1}\cos\theta_{1}, r_{1}\sin\theta_{1})\) ও \(Q(r_{2}\cos\theta_{2}, r_{2}\sin\theta_{2})\)
\(\therefore PQ=\sqrt{(r_{1}\cos\theta_{1}-r_{2}\cos\theta_{2})^{2}+(r_{1}\sin\theta_{1}-r_{2}\sin\theta_{2})^{2}}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}\cos^{2}\theta_{1}-2r_{1}r_{2}\cos\theta_{1}\cos\theta_{2}+r_{2}^{2}\cos^{2}\theta_{2}+r_{1}^{2}\sin^{2}\theta_{1}-2r_{1}r_{2}\sin\theta_{1}\sin\theta_{2}+r_{2}^{2}\sin^{2}\theta_{2}}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}(\cos^{2}\theta_{1}+\sin^{2}\theta_{1})+r_{2}^{2}(\cos^{2}\theta_{2}+\sin^{2}\theta_{2})-2r_{1}r_{2}(\cos\theta_{1}\cos\theta_{2}+\sin\theta_{1}\sin\theta_{2})}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}\times 1+r_{2}^{2}\times 1-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
কোন সমতলের উপর \(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব নির্ণয় করতে হবে।
\(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) বিন্দুদ্বয়ের কার্তেসীয় স্থানাঙ্ক যথাক্রমে \(P(r_{1}\cos\theta_{1}, r_{1}\sin\theta_{1})\) ও \(Q(r_{2}\cos\theta_{2}, r_{2}\sin\theta_{2})\)
\(\therefore PQ=\sqrt{(r_{1}\cos\theta_{1}-r_{2}\cos\theta_{2})^{2}+(r_{1}\sin\theta_{1}-r_{2}\sin\theta_{2})^{2}}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}\cos^{2}\theta_{1}-2r_{1}r_{2}\cos\theta_{1}\cos\theta_{2}+r_{2}^{2}\cos^{2}\theta_{2}+r_{1}^{2}\sin^{2}\theta_{1}-2r_{1}r_{2}\sin\theta_{1}\sin\theta_{2}+r_{2}^{2}\sin^{2}\theta_{2}}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}(\cos^{2}\theta_{1}+\sin^{2}\theta_{1})+r_{2}^{2}(\cos^{2}\theta_{2}+\sin^{2}\theta_{2})-2r_{1}r_{2}(\cos\theta_{1}\cos\theta_{2}+\sin\theta_{1}\sin\theta_{2})}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}\times 1+r_{2}^{2}\times 1-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
দুইটি বিন্দুর মধ্যবর্তী দূরত্ব বিষয়ক অনুসিদ্ধান্তঃ
\(P(x_{1}, y_{1})\) এবং মূলবিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-0)^{2}+(y_{1}-0)^{2}}\)
\(=\sqrt{x_{1}^{2}+y_{1}^{2}}\)।
\(P(x_{1}, \beta)\) ও \(P(x_{2}, \beta)\) বিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-x_{2})^{2}+(\beta-\beta)^{2}}\)
\(=\sqrt{(x_{1}-x_{2})^{2}}\)
\(=\mid x_{1}-x_{2} \mid\)।
\(P(\alpha, y_{1})\) ও \((\alpha, y_{2})\) বিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(\alpha-\alpha)^{2}+(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(y_{1}-y_{2})^{2}}\) \(= \mid y_{1}-y_{2} \mid \)।
\(=\sqrt{(x_{1}-0)^{2}+(y_{1}-0)^{2}}\)
\(=\sqrt{x_{1}^{2}+y_{1}^{2}}\)।
\(P(x_{1}, \beta)\) ও \(P(x_{2}, \beta)\) বিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-x_{2})^{2}+(\beta-\beta)^{2}}\)
\(=\sqrt{(x_{1}-x_{2})^{2}}\)
\(=\mid x_{1}-x_{2} \mid\)।
\(P(\alpha, y_{1})\) ও \((\alpha, y_{2})\) বিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(\alpha-\alpha)^{2}+(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(y_{1}-y_{2})^{2}}\) \(= \mid y_{1}-y_{2} \mid \)।
ত্রিভুজ বিষয়ক সমস্যা সমাধানের বিশেষ কৌশল
Special techniques for solving trigonometric problems
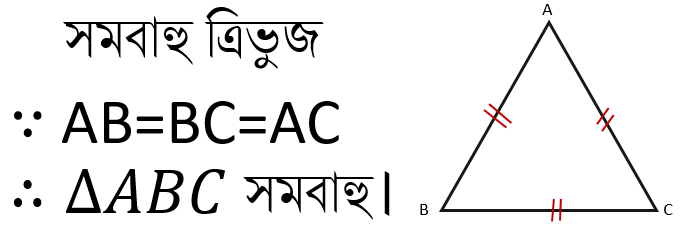
সমবাহু ত্রিভুজঃ যে ত্রিভুজের তিনটি বাহুই পরস্পর সমান তা সমবাহু ত্রিভুজ।

সমদ্বিবাহু ত্রিভুজ
Isosceles triangle
সমদ্বিবাহু ত্রিভুজঃ যে ত্রিভুজের দুইটি বাহু সমান তা সমদ্বিবাহু ত্রিভুজ।


বিষমবাহু ত্রিভুজ
Scalene triangle
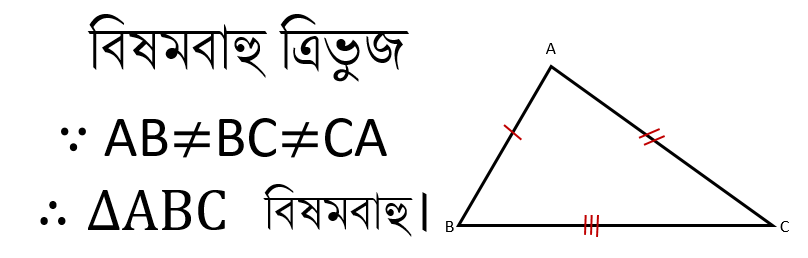
বিষমবাহু ত্রিভুজঃ যে ত্রিভুজের কোন বাহুই কোন বাহুর সমান নয় তা বিষমবাহু ত্রিভুজ।

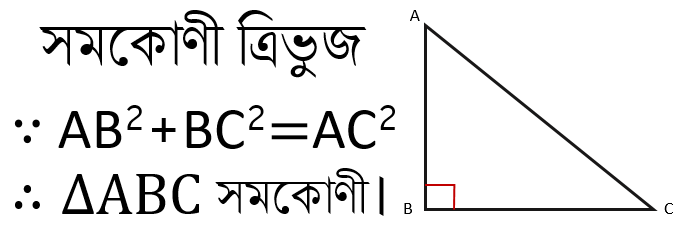
সমকোণী ত্রিভুজ
Right triangle
সমকোণী ত্রিভুজঃ যে ত্রিভুজের একটি কোণ এক সমকোণের সমান তা সমকোণী ত্রিভুজ।

সমদ্বিবাহু সমকোণী ত্রিভুজ
Isosceles right triangle

চতুর্ভুজ বিষয়ক সমস্যা সমাধানের বিশেষ কৌশল
Special techniques for solving quadratic problems
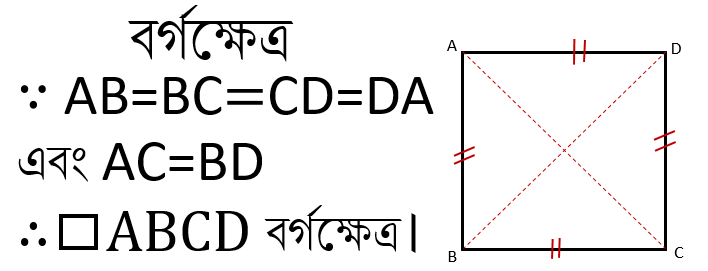
বর্গক্ষেত্রঃ যে চতুর্ভুজের চারটি বাহুই পরস্পর সমান এবং কর্ণদ্বয়ও পরস্পর সমান তাকেই বর্গক্ষেত্র বলে।

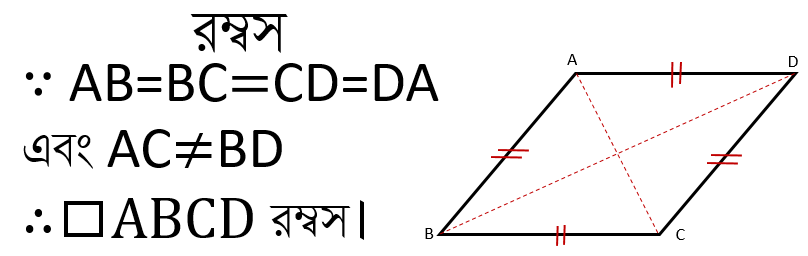
রম্বস
Rhombus
রম্বসঃ যে চতুর্ভুজের চারটি বাহুই পরস্পর সমান এবং কর্ণদ্বয়ও পরস্পর সমান নয় তাকেই রম্বস বলে।

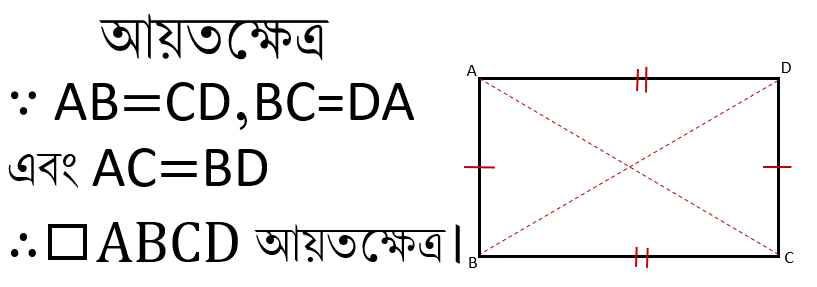
আয়তক্ষেত্র
Rectangle
আয়তক্ষেত্রঃ যে চতুর্ভুজের বিপরীত বাহুগুলি পরস্পর সমান এবং কর্ণদ্বয়ও পরস্পর সমান তাকেই আয়তক্ষেত্র বলে।

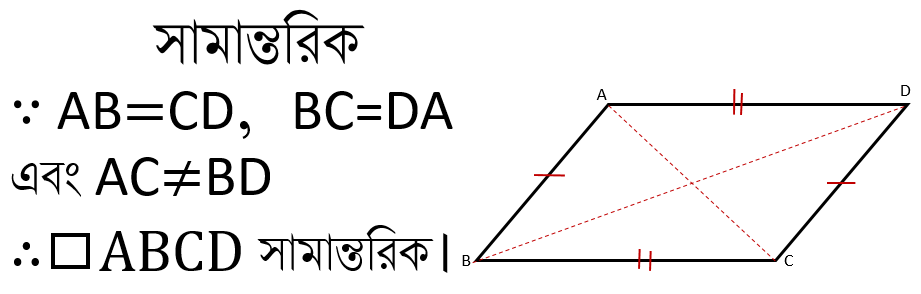
সামান্তরিক
Parallelogram
সামান্তরিকঃ যে চতুর্ভুজের বিপরীত বাহুগুলি পরস্পর সমান এবং কর্ণদ্বয়ও পরস্পর সমান নয় তাকেই সামান্তরিক বলে।

তিনটি বিন্দুর সমরেখ হওয়ার শর্ত
Condition of the three points being co-linear
কোন সমতলের উপর \((x_{1}, y_{1}), \ (x_{2}, y_{2})\) এবং \((x_{3}, y_{3})\) বিন্দু তিনটি সমরেখ হবে যদি,
\((x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})=0\)
\((x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})=0\)
প্রমাণঃ
মনে করি,
কোন সমতলের উপর তিনটি বিন্দু \(P(x_{1}, y_{1}), \ Q(x_{2}, y_{2})\) এবং \(R(x_{3}, y_{3})\)
এখন, \(\triangle{PQR}=\frac{1}{2}\left|\begin{array}{c}x_{1}&x_{2}&x_{3}&x_{1}\\ y_{1}&y_{2}&y_{3}&y_{1}\end{array}\right|\)
\(=\frac{1}{2}\{x_{1}y_{2}-x_{2}y_{1}+x_{2}y_{3}-x_{3}y_{2}+x_{3}y_{1}-x_{1}y_{3}\}\)
\(=\frac{1}{2}\{x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})+x_{2}y_{3}-x_{3}y_{2}\}\)
\(=\frac{1}{2}\{x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})-x_{2}y_{2}+x_{2}y_{3}+x_{2}y_{2}-x_{3}y_{2}\}\)
\(=\frac{1}{2}\{x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})-x_{2}(y_{2}-y_{3})+y_{2}(x_{2}-x_{3})\}\)
\(=\frac{1}{2}\{(x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})\}\)
\(\therefore \triangle{PQR}=\frac{1}{2}\{(x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})\}\)
বিন্দু তিনটি সমরেখ হবে যদি,
\(\triangle{PQR}=0\) হয়।
\(\Rightarrow \frac{1}{2}\{(x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})\}=0\)
\(\therefore (x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})=0\)
(প্রমাণিত)
কোন সমতলের উপর তিনটি বিন্দু \(P(x_{1}, y_{1}), \ Q(x_{2}, y_{2})\) এবং \(R(x_{3}, y_{3})\)
এখন, \(\triangle{PQR}=\frac{1}{2}\left|\begin{array}{c}x_{1}&x_{2}&x_{3}&x_{1}\\ y_{1}&y_{2}&y_{3}&y_{1}\end{array}\right|\)
\(=\frac{1}{2}\{x_{1}y_{2}-x_{2}y_{1}+x_{2}y_{3}-x_{3}y_{2}+x_{3}y_{1}-x_{1}y_{3}\}\)
\(=\frac{1}{2}\{x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})+x_{2}y_{3}-x_{3}y_{2}\}\)
\(=\frac{1}{2}\{x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})-x_{2}y_{2}+x_{2}y_{3}+x_{2}y_{2}-x_{3}y_{2}\}\)
\(=\frac{1}{2}\{x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})-x_{2}(y_{2}-y_{3})+y_{2}(x_{2}-x_{3})\}\)
\(=\frac{1}{2}\{(x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})\}\)
\(\therefore \triangle{PQR}=\frac{1}{2}\{(x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})\}\)
বিন্দু তিনটি সমরেখ হবে যদি,
\(\triangle{PQR}=0\) হয়।
\(\Rightarrow \frac{1}{2}\{(x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})\}=0\)
\(\therefore (x_{1}-x_{2})(y_{2}-y_{3})-(y_{1}-y_{2})(x_{2}-x_{3})=0\)
(প্রমাণিত)

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004