এ অধ্যায়ের পাঠ্যসূচী
- সূক্ষ্ণকোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratios of acute angles)
- যে কোনো কোণের ত্রিকোণমিতিক অনুপাত (The trigonometric ratio of any angle)
- চৌকোণের ভিত্তিতে কোনো বিন্দুর অবস্থান (The position of a point on the quadrant base)
- চৌকোণ বা চতুর্ভাগ অনুযায়ী ত্রিকোণমিতিক অনুপাতের চিহ্ন (Signs of trigonometric ratios according to the quadrant)
- ত্রিকোণমিতিক অনুপাতের ধ্রুব্যতা (Polarity of trigonometric ratios)
- ত্রিকোণমিতিক কোণের অনুপাতসমূহের মধ্যে সম্পর্ক (The relationship between the ratios of trigonometric angles)
- \(0^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of \(0^{o}\) angles angles)
- \(30^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of \(30^{o}\) angles angles)
- \(45^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of \(45^{o}\) angles angles)
- \(60^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of \(60^{o}\) angles angles)
- \(90^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of \(90^{o}\) angles angles)
- \(180^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of \(180^{o}\) angles angles)
- \(270^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of \(270^{o}\) angles angles)
- \(360^{o}\) কোণের ত্রিকোণমিতিক অনুপাত (Trigonometric ratio of \(360^{o}\) angles angles)
- \(0^{o}, \ 30^{o}, \ 45^{o}, \ 60^{o}, \ 90^{o}\) কোণের ত্রিকোণমিতিক অনুপাতের তালিকা (List of trigonometric ratios of \(0^{o}, \ 30^{o}, \ 45^{o}, \ 60^{o}, \ 90^{o}\) angles)
- ত্রিকোণমিতিক অনুপাত সংক্রান্ত অভেদাবলি (Differences regarding trigonometric ratios)
- ত্রিকোণমিতিক অনুপাতের সীমাবদ্ধতা (Limitations of trigonometric ratios)
- অধ্যায় \(vi.B\)-এর উদাহরণসমুহ
- অধ্যায় \(vi.B\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(vi.B\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(vi.B\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(vi.B\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
সূক্ষ্ণকোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratios of acute angles
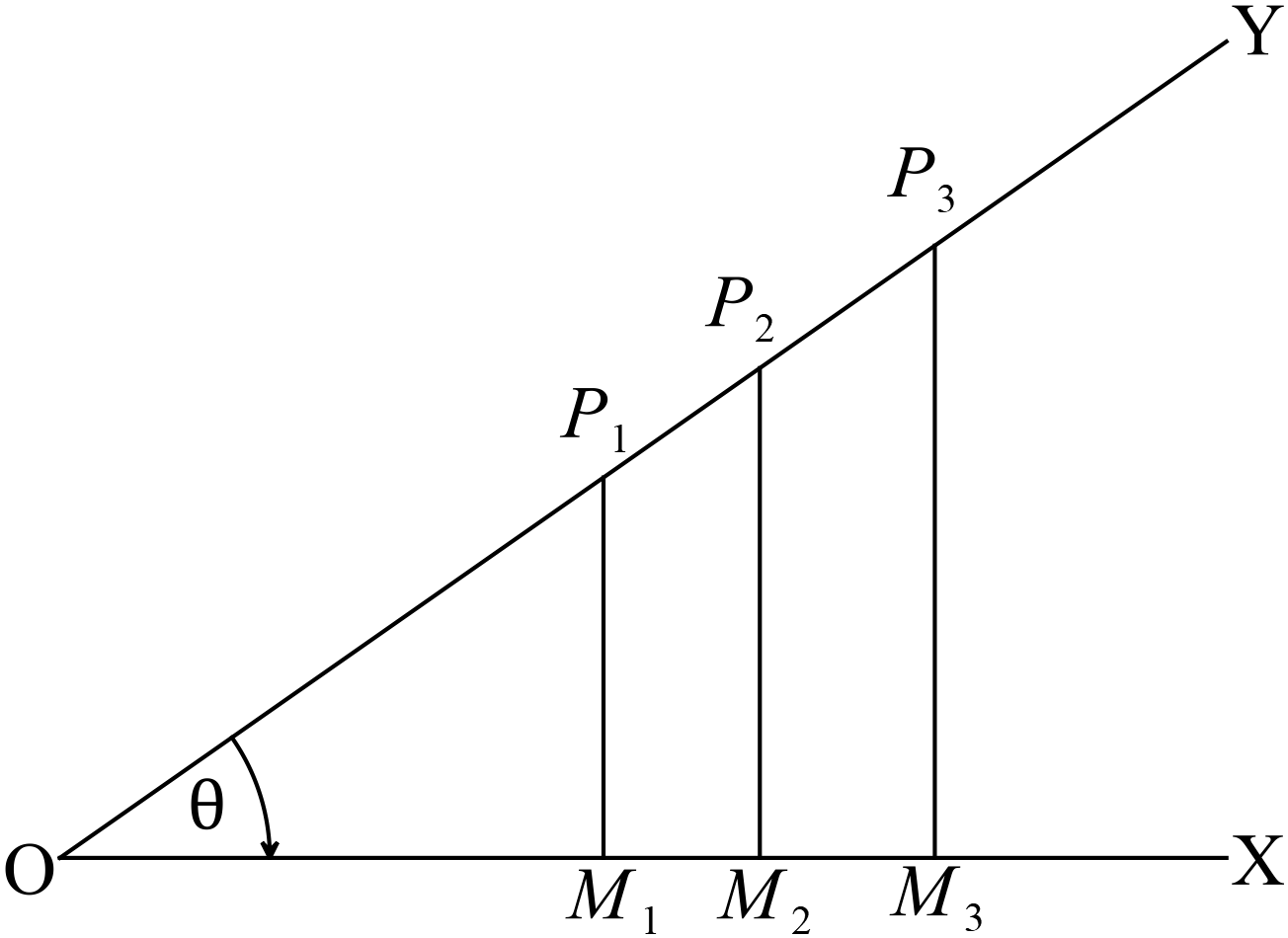ধরি, কোনো সরলরেখার আদি অবস্থান \(OX\) এবং শেষ অবস্থান \(OY\) এর উপর মূলবিন্দু ব্যতীত যে কোনো \(P_{1}, \ P_{2}, \ P_{3}, \ ... \) বিন্দুগুলি হতে \(OX\) এর উপর যথাক্রমে \(P_{1}M_{1}, \ P_{2}M_{2}, \ P_{3}M_{3}, \ ... \) লম্ব । এর ফলে, \(\triangle{P_{1}OM_{1}}, \ \triangle{P_{2}OM_{2}}, \ \triangle{P_{3}OM_{3}}, \ ... \) সদৃশকোণী ত্রিভুজগুলি উৎপন্ন হয়েছে।
\(\therefore \frac{P_{1}M_{1}}{OP_{1}}=\frac{P_{2}M_{2}}{OP_{2}}=\frac{P_{3}M_{3}}{OP_{3}}= ........=\frac{\theta \ \text{কোণের বিপরীত বাহু}}{\text{অতিভুজ}}=\frac{\text{লম্ব}}{\text{অতিভুজ}}\) ➜ \(\because \) সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
\(\frac{OM_{1}}{OP_{1}}=\frac{OM_{2}}{OP_{2}}=\frac{OM_{3}}{OP_{3}}= ........=\frac{\theta \ \text{কোণের সন্নিহিত বাহু}}{\text{অতিভুজ}}=\frac{\text{ভূমি}}{\text{অতিভুজ}}\) ➜ \(\because \) সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
\(\frac{P_{1}M_{1}}{OM_{1}}=\frac{P_{2}M_{2}}{OM_{2}}=\frac{P_{3}M_{3}}{OM_{3}}= ........=\frac{\theta \ \text{কোণের বিপরীত বাহু}}{\theta \ \text{কোণের সন্নিহিত বাহু}}=\frac{\text{লম্ব}}{\text{ভূমি}}\) ➜ \(\because \) সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
সুতরাং যে কোনো \(\triangle{OPM}\) সমকোণী ত্রিভুজের একটি সূক্ষ্ণকোণ \(\theta\) হলে তার যে কোনো দুই বাহুর অনুপাত ত্রিভুজের আকৃতির উপর নির্ভর করে না, ইহা \(\theta\) কোণের মাণের উপর নির্ভরশীল।
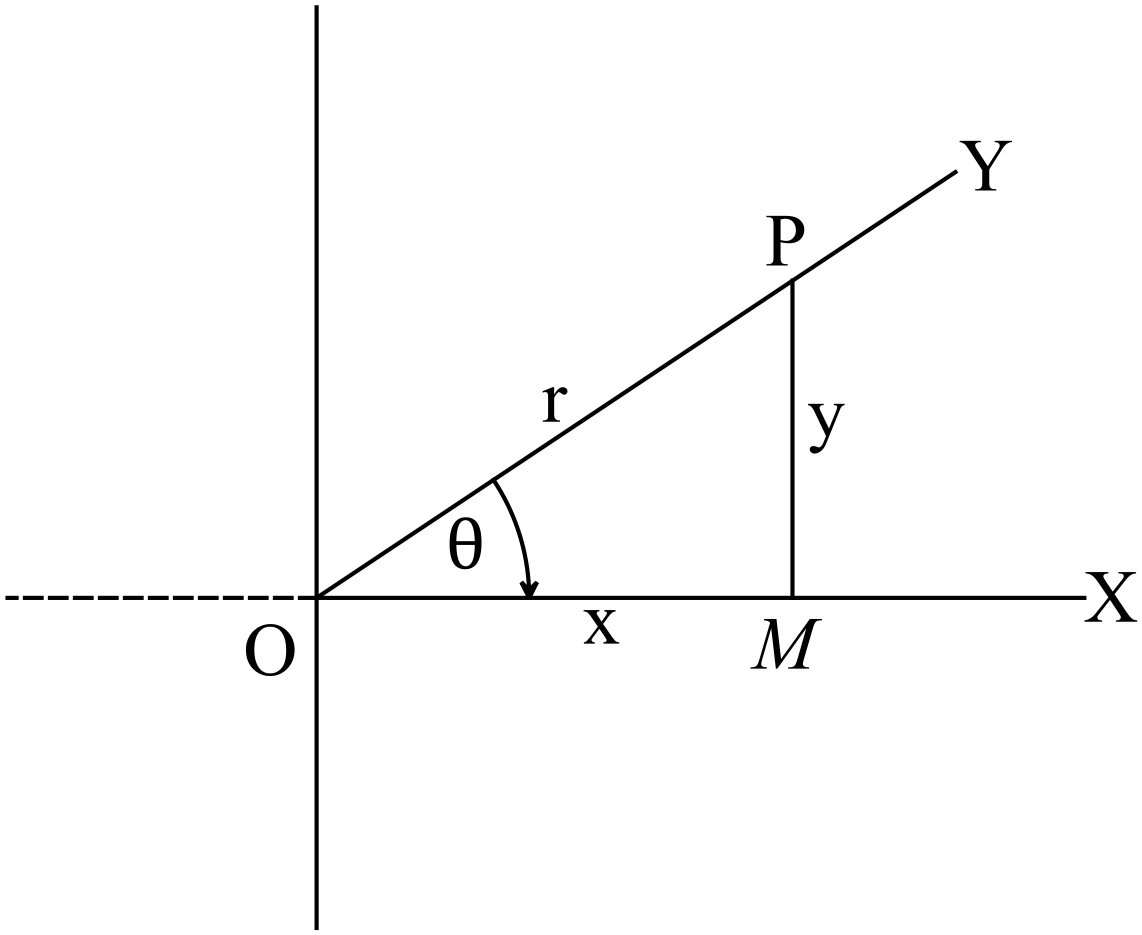
এখানে, \(\triangle{POM}\) এর \(OP\) বাহু অতিভুজ, \(PM\) বাহু লম্ব এবং \(OM\) বাহু ভূমি।
\(\therefore OP^2=OM^2+PM^2\)
\(\Rightarrow OP=\sqrt{OM^2+PM^2}\)
\(\Rightarrow OP=\sqrt{x^2+y^2}\) ➜ \(\because OM=x, \ PM=y\)
\(\therefore OP=\sqrt{x^2+y^2}=r\) ➜ \(\because OP=r\)
\(\triangle{POM}\) সমকোণী ত্রিভুজের বাহুগুলির অনুপাত,
\(\frac{PM}{OP}, \ \frac{OM}{OP}, \ \frac{PM}{OM}, \ \frac{OP}{PM}, \ \frac{OP}{OM}, \ \frac{OM}{PM}\)
এখন, \(\angle{POM}=\theta\) হলে, \(\theta\) কোণের ত্রিকোণমিতিক অনুপাত নিম্নোক্তভাবে সংজ্ঞায়িত করা হয়।
\(\theta\) কোণের \(sine\) অনুপাত সংক্ষেপে, \(\sin{\theta}=\frac{PM}{OP}=\frac{\text{লম্ব }}{\text{অতিভুজ}}=\frac{y}{r}\)
\(\theta\) কোণের \(cosine\) অনুপাত সংক্ষেপে, \(\cos{\theta}=\frac{OM}{OP}=\frac{\text{ভূমি }}{\text{অতিভুজ}}=\frac{x}{r}\)
\(\theta\) কোণের \(tangent\) অনুপাত সংক্ষেপে, \(\tan{\theta}=\frac{PM}{OM}=\frac{\text{লম্ব }}{\text{ভূমি}}=\frac{y}{x}, \ x\ne{0}\)
\(\theta\) কোণের \(cosecant\) অনুপাত সংক্ষেপে, \(cosec \ {\theta}=\frac{OP}{PM}=\frac{\text{অতিভুজ}}{\text{লম্ব }}=\frac{r}{y}, \ y\ne{0}\)
\(\theta\) কোণের \(secant\) অনুপাত সংক্ষেপে, \(\sec{\theta}=\frac{OP}{OM}=\frac{\text{অতিভুজ}}{\text{ভূমি}}=\frac{r}{x}, \ x\ne{0}\)
\(\theta\) কোণের \(cotangent\) অনুপাত সংক্ষেপে, \(\cot{\theta}=\frac{OM}{PM}=\frac{\text{ভূমি }}{\text{লম্ব}}=\frac{x}{y}, \ y\ne{0}\)
এখানে, \(\theta\) কোণ ডিগ্রি বা রেডিয়ানে পরিমাপ করা যাবে।
বিঃদ্রঃ \(\sin{\theta}, \ \cos{\theta}, \ \tan{\theta}, \ cosec \ {\theta}, \ \sec{\theta}, \ \cot{\theta}\) কে কোণের ত্রিকোণমিতক অনুপাত বা ত্রিকোণমিতক ফাংশন বলা হয়। এই ছয়টি অনুপাত ছাড়াও \(\theta\) কোণের আরও দুইটি অনুপাতের ব্যবহার ত্রিকোণমিতিতে সচরাচর দেখা যায়।
যেমনঃ \(\theta\) কোণের versed sine(vers\(\theta\)) \(=1-\cos{\theta}\)
যেমনঃ \(\theta\) কোণের coversed sine(covers\(\theta\)) \(=1-\sin{\theta}\)
\(\theta\) কোণের একটি নির্দিষ্ট একক থাকা সত্ত্বেও ত্রিকোণমিতিক অনুপাতসমূহের কোনো একক নেই। কারণ এরা দুইটি একই প্রকার রাশির অনুপাত।
যে কোনো কোণের ত্রিকোণমিতিক অনুপাত
The trigonometric ratio of any angle
ধরি, \(XOX^{\prime}\) এবং \(YOY^{\prime}\) সরলরেখা দুইটি পরস্পর \(O\) বিন্দুতে লম্বভাবে ছেদ করেছে। \(XOX^{\prime}\) কে \(x\) অক্ষ, \(YOY^{\prime}\) কে \(y\) অক্ষ এবং \(O\) বিন্দুকে মূলবিন্দু বিবেচনা করা হয়েছে। এখন কোণ উৎপন্নকারী একটি ঘূর্ণায়মান রশ্মি আদি অবস্থান \(OX\) থেকে ঘড়ির কাঁটার ঘূর্ণনের বিপরীতক্রমে ঘুরে \(\angle{XOP}=\theta\) কোণ উৎপন্ন করেছে। ঘূর্ণায়মান সরলরেখার শেষ অবস্থান \(OP\)। সুতরাং \(P\) বিন্দু চারটি চতুর্ভাগের যে কোনো একটিতে অবস্থান করবে। \(OP\) এর উপর যে কোনো বিন্দু \(P\) হতে \(YOY^{\prime}\) উপর \(PM\) লম্ব অঙ্কন করায় \(POM\) সমকোণী ত্রিভুজ গঠিত হয়। এখানে \(OP=r\) কে \(P\) বিন্দুর ব্যাসার্ধ ভেক্টর বলা হয় (যা সর্বদা ধনাত্মক এবং স্কেলার রাশি)। \(P\) বিন্দুর ভুজ \(P\)বিন্দুর \(x\) স্থানাঙ্ক, \(P\) বিন্দুর কোটি \(P\)বিন্দুর \(y\) স্থানাঙ্ক নির্দেশ করে।
চৌকোণের ভিত্তিতে কোনো বিন্দুর অবস্থান
The position of a point on the quadrant base
\(P\) এর অবস্থান প্রথম চৌকোণে বা, চতুর্ভাগে।
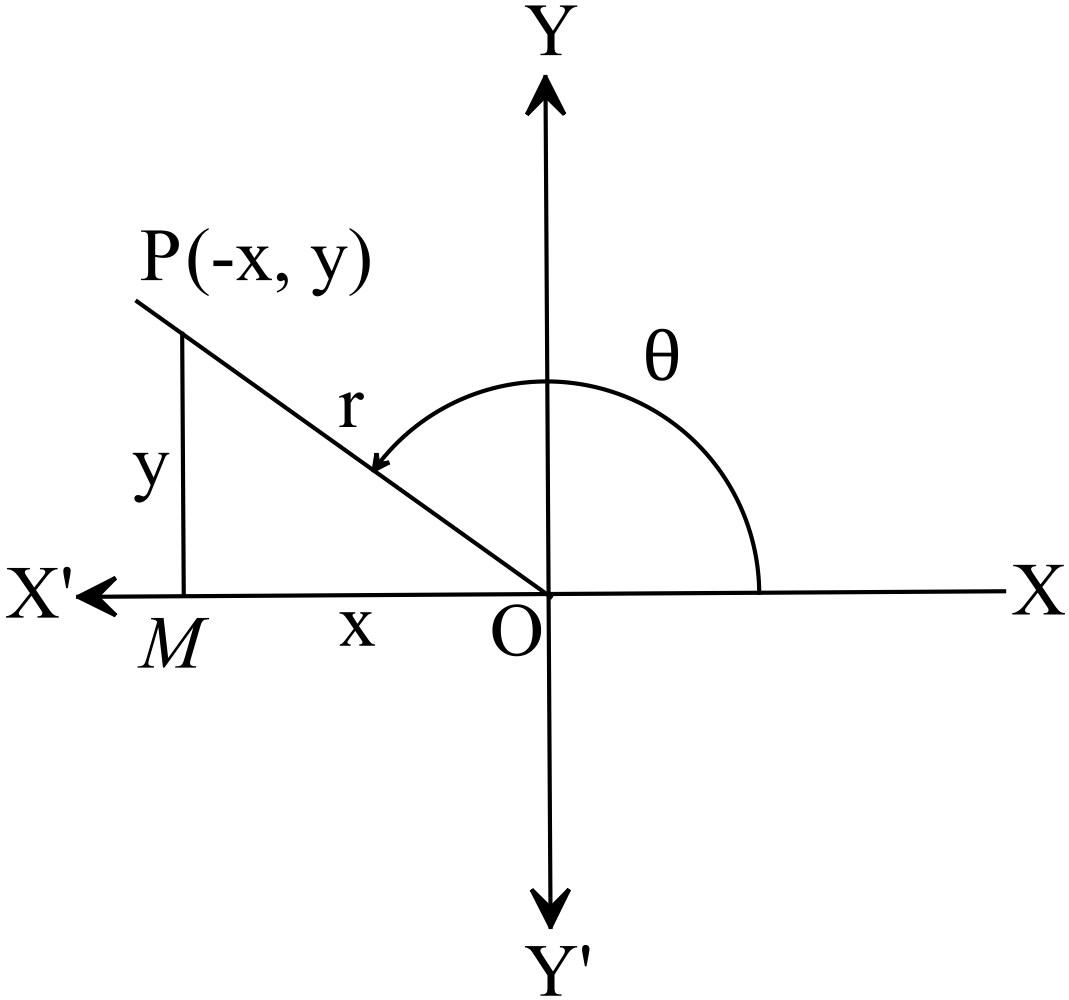\(P\) এর অবস্থান দ্বিতীয় চৌকোণে বা, চতুর্ভাগে।
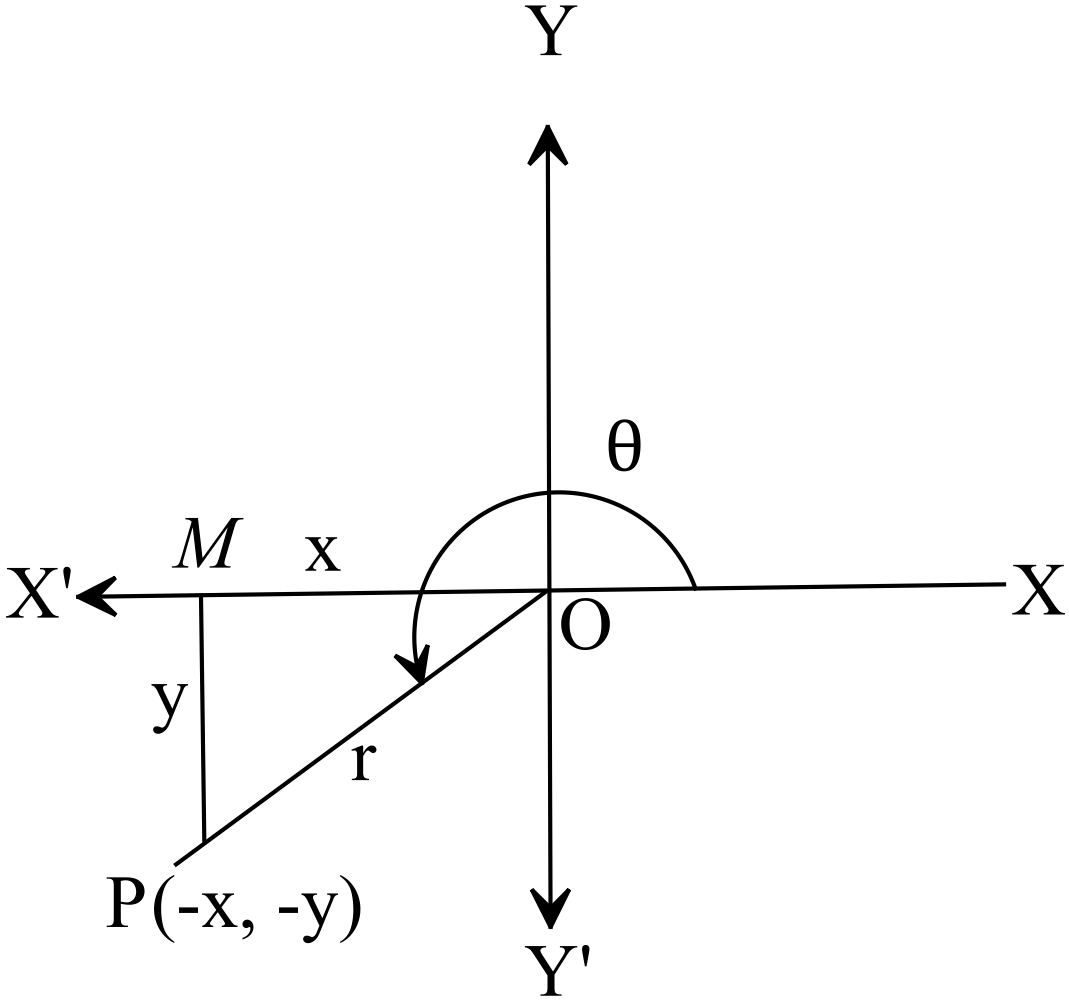\(P\) এর অবস্থান তৃতীয় চৌকোণে বা, চতুর্ভাগে।
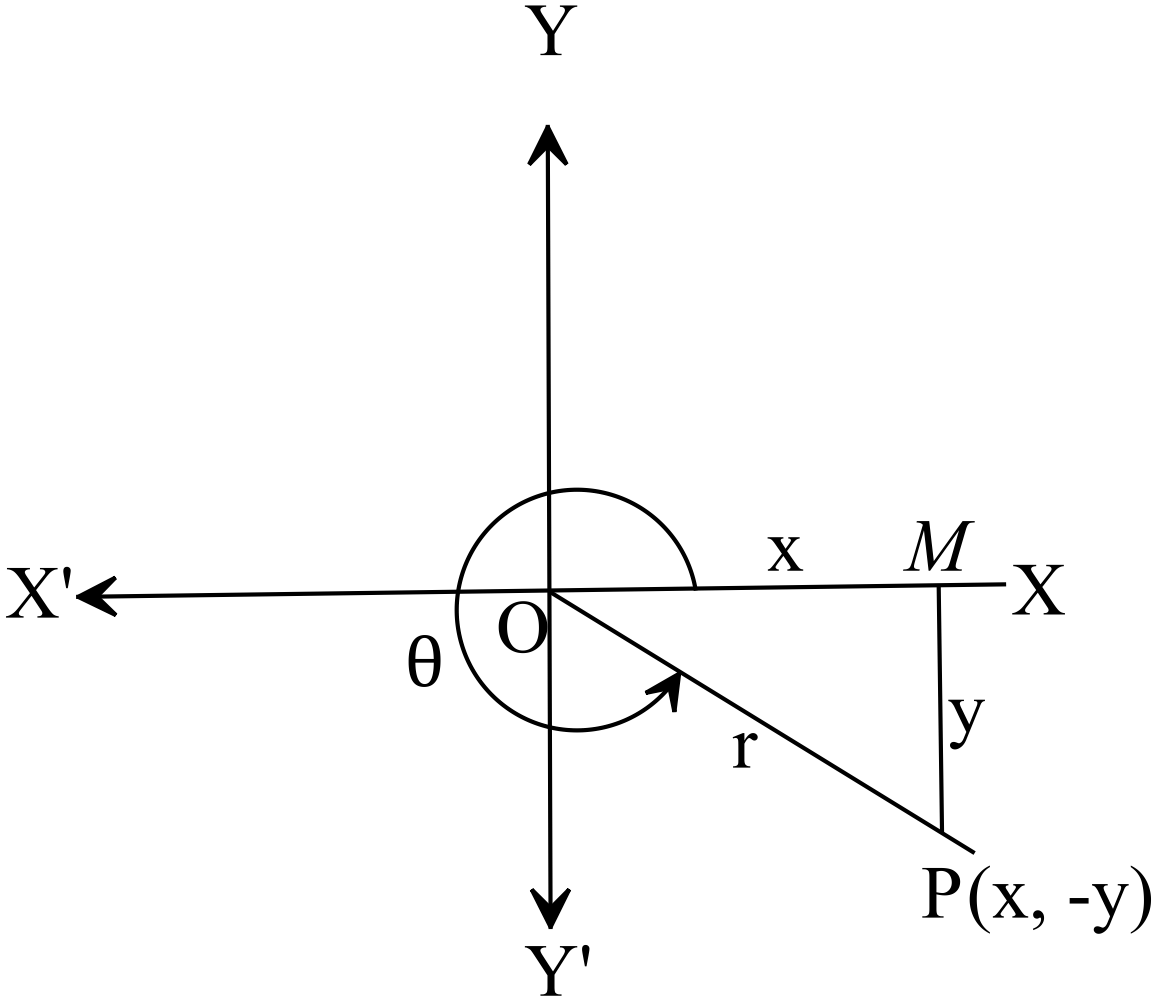\(P\) এর অবস্থান চতুর্থ চৌকোণে বা, চতুর্ভাগে।
চৌকোণ বা চতুর্ভাগ অনুযায়ী ত্রিকোণমিতিক অনুপাতের চিহ্ন
Signs of trigonometric ratios according to the quadrant
উপরোক্ত চিত্রে, \(POM\) সমকোণী ত্রিভুজ হতে ত্রিকোণমিতিক অনুপাতসমূহঃ
\(\sin{\theta}=\frac{PM}{OP}=\frac{y}{r}\) \(\cos{\theta}=\frac{OM}{OP}=\frac{x}{r}\) \(\tan{\theta}=\frac{PM}{OM}=\frac{y}{x}, \ x\ne{0}\)\(cosec \ {\theta}=\frac{OP}{PM}=\frac{r}{y}, \ y\ne{0}\) \(\sec{\theta}=\frac{OP}{OM}=\frac{r}{x}, \ x\ne{0}\) \(\cot{\theta}=\frac{OM}{PM}=\frac{x}{y}, \ y\ne{0}\)
ব্যাসার্ধ \(r\) সর্বদাই ধনাত্মক স্কেলার রাশি, তাই \(\theta\) কোণের বিভিন্ন ত্রিকোণমিতিক অনুপাতের চিহ্ন \(x\) ও \(y\) এর চিহ্নের উপর নির্ভরশীল। চিত্র থেকে আমরা সহজেই \(x\) ও \(y\) এর চিহ্ন বের করতে পারি। অর্থাৎ চারটি চতুর্ভাগে ত্রিকোণমিতিক অনুপাতগুলির চিহ্ন কি হবে তা নির্ণয় করা যায়।
নিচের ছকে ত্রিকোণমিতিক অনুপাতগুলির চিহ্ন দেখানো হলোঃ
| চতুর্ভাগ | \(x\) | \(y\) | \(r\) | \(\sin{\theta}=\frac{y}{r}\) \(cosec \ {\theta}=\frac{r}{y}\) |
\(\cos{\theta}=\frac{x}{r}\) \(\sec{\theta}=\frac{r}{x}\) |
\(\tan{\theta}=\frac{y}{x}\) \(\cot{\theta}=\frac{x}{y}\) |
মন্তব্য |
|---|---|---|---|---|---|---|---|
| প্রথম | \(+\) | \(+\) | \(+\) | \(+\) | \(+\) | \(+\) | সকল অনুপাত ধনাত্মক। |
| দ্বিতীয় | \(-\) | \(+\) | \(+\) | \(+\) | \(-\) | \(-\) | \(\sin{\theta} \ \text{এবং} \ cosec \ {\theta} \ \text{ধনাত্মক}\) |
| তৃতীয় | \(-\) | \(-\) | \(+\) | \(-\) | \(-\) | \(+\) | \(\tan{\theta} \ \text{এবং} \ \cot{\theta} \ \text{ধনাত্মক}\) |
| চতুর্থ | \(+\) | \(-\) | \(+\) | \(-\) | \(+\) | \(-\) | \(\cos{\theta} \ \text{এবং} \ \sec{\theta} \ \text{ধনাত্মক}\) |
উপরের আলোচনার সচিত্র প্রতিবেদন নিচে দেওয়া হলোঃ
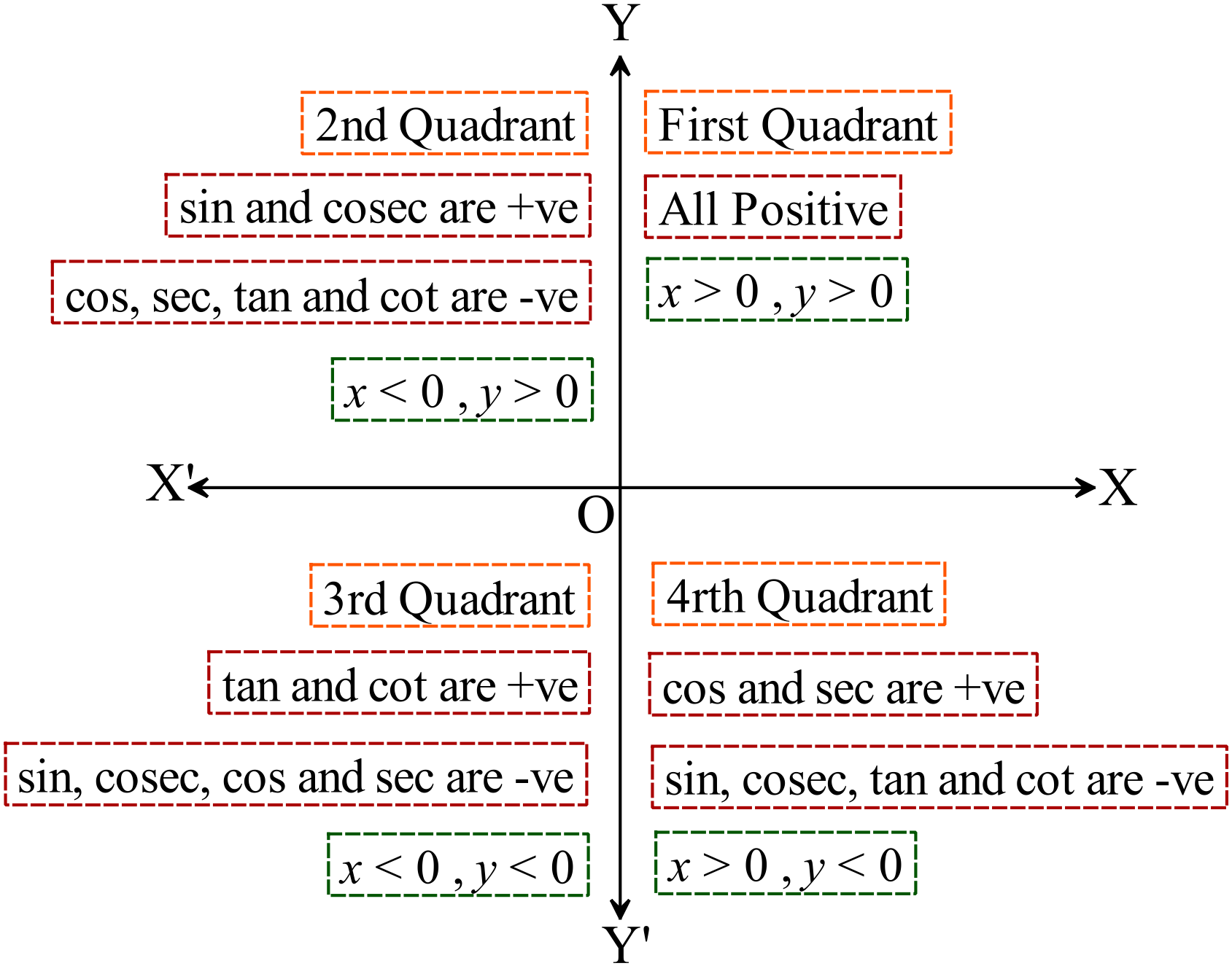যে কোনো কোণের প্রান্তিক রশ্মির অবস্থানের উপর নির্ভর করে উক্ত কোণের সকল ত্রিকোণমিতিক অনুপাতের চিহ্ন নির্ণয় সহজ হয়। নির্দিষ্ট কোণ উৎপন্ন করে ঘূর্ণায়মান রশ্মিটির শেষ অবস্থান কোণ চতুর্ভাগে তা স্থির করে পাশের চিত্রের সাহায্যে অতি সহজেই ত্রিকোণমিতিক অনুপাতের চিহ্ন নির্ণয় করা যায়।
ত্রিকোণমিতিক অনুপাতের ধ্রুব্যতা
Polarity of trigonometric ratios
একটি নির্দিষ্ট পরিমাণ কোণের জন্য ত্রিকোণমিতিক অনুপাতগুলি সবসময়ই ধ্রুব।চিত্রে \(\angle{XOP}=\theta\) একটি কোণ, যার দুইটি অবস্থান দেখানো হয়েছে। প্রথম চতুর্ভাগে এবং তৃতীয় চতুর্ভাগে \(P\) ও \(P^{\prime}\) দুইটি বিন্দু থেকে যথাক্রমে \(OX\) এবং \(OX^{\prime}\) এর উপর \(PM\) ও \(P^{\prime}M^{\prime}\) লম্ব অঙ্কন করা হয়েছে। \(\triangle{OPM}\) এবং \(\triangle{OP^{\prime}M^{\prime}}\) দুইটি ত্রিভুজের মধ্যে,
\(\angle{PMO}=\angle{P^{\prime}M^{\prime}O}=90^{o}\)
\(\angle{OPM}=\angle{OP^{\prime}M^{\prime}} \ \text{(অনুরূপ কোণ)}\)
\(\angle{POM}=\angle{P^{\prime}OM^{\prime}} \ \text{(সাধারণ কোণ)}\)
\(\therefore \) ত্রিভুজদ্বয় সদৃশ।
সুতরাং \(\frac{PM}{OP}=\frac{P^{\prime}M^{\prime}}{OP^{\prime}}\) ➜ \(\because \) সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
\(\triangle{OPM}\) থেকে, \(\sin{\theta}=\frac{PM}{OP}\)
এবং \(\triangle{OP^{\prime}M^{\prime}}\) থেকে, \(\sin{\theta}=\frac{P^{\prime}M^{\prime}}{OP^{\prime}}\)
\(\therefore \sin{\theta}=\frac{PM}{OP}=\frac{P^{\prime}M^{\prime}}{OP^{\prime}}\)
\(\sin{\theta}=\frac{PM}{OP}=\frac{P^{\prime}M^{\prime}}{OP^{\prime}}\)
উল্লেখ্য তৃতীয় চতুর্ভাগে \(PM\) এবং \(P^{\prime}M^{\prime}\) উভয়ে ঋণাত্মক। এই দুইটি ত্রিভুজ থেকে \(\sin{\theta}\) এর একই মাণ পাওয়া যাবে। অন্যান্য ত্রিকোণমিতিক অনুপাতগুলির জন্যও এই শর্ত প্রযোজ্য।
ত্রিকোণমিতিক কোণের অনুপাতসমূহের মধ্যে সম্পর্ক
The relationship between the ratios of trigonometric angles
\(\sin{\theta}=\frac{1}{cosec \ {\theta}}\) \(\cos{\theta}=\frac{1}{\sec{\theta}}\) \(\tan{\theta}=\frac{1}{\cot{\theta}}\)
\(cosec \ {\theta}=\frac{1}{\sin{\theta}}\) \(\sec{\theta}=\frac{1}{\cos{\theta}}\) \(\cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\) \(\cot{\theta}=\frac{\cos{\theta}}{\sin{\theta}}\)
\(cosec \ {\theta}=\frac{1}{\sin{\theta}}\) \(\sec{\theta}=\frac{1}{\cos{\theta}}\) \(\cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\) \(\cot{\theta}=\frac{\cos{\theta}}{\sin{\theta}}\)
প্রমাণঃ
চিত্র হতে,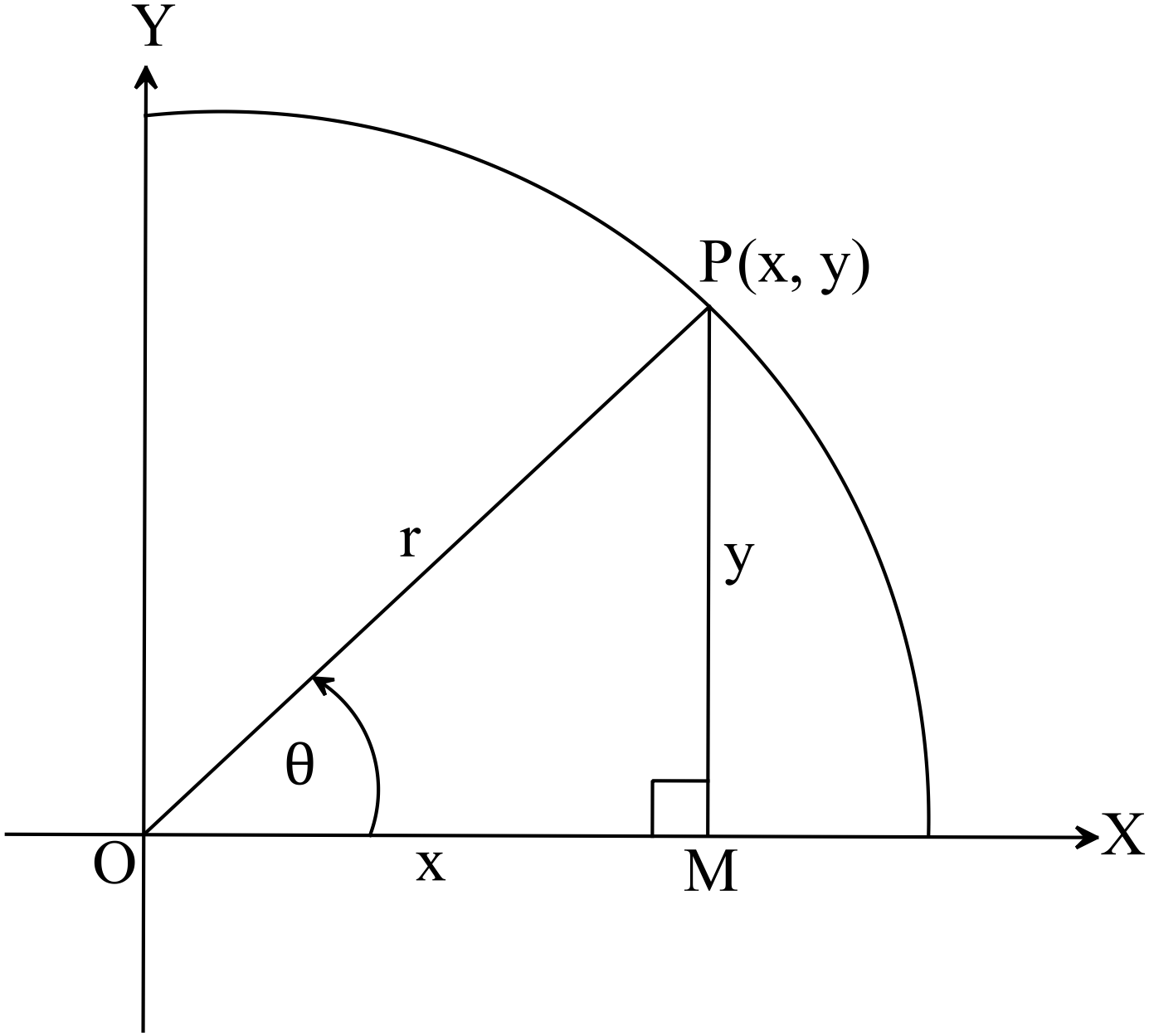
\(P(x,y)\)
\(\therefore OM=x, \ PM=y, \ OP=r\)
\(\angle{PMO}=90^{0}\) অর্থাৎ এক সমকোণ।
এবং \(\angle{POM}=\theta\)।
এখন, \(\sin{POM}=\frac{PM}{OP}\)
\(\therefore \sin{\theta}=\frac{y}{r} .....(1)\)
এবং \(cosec \ {\theta}=\frac{OP}{PM}\)
\(\therefore cosec \ {\theta}=\frac{r}{y} .....(2); \ y\ne{0}\)
\((1)\times(2)\) এর সাহায্যে
\(\sin{\theta}\times cosec \ {\theta}=\frac{y}{r}\times\frac{r}{y}\)
\(\Rightarrow \sin{\theta}\times cosec \ {\theta}=1\)
\(\therefore \sin{\theta}=\frac{1}{cosec \ {\theta}}\)
অথবা, \(cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\sin{\theta}=\frac{1}{cosec \ {\theta}}\)
অথবা,
\(cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
আবার, \(\cos{POM}=\frac{OM}{OP}\)
\(\therefore \cos{\theta}=\frac{x}{r} .....(3)\)
এবং \(\sec{\theta}=\frac{OP}{OM}\)
\(\therefore \sec{\theta}=\frac{r}{x} .....(4); \ x\ne{0}\)
\((3)\times(4)\) এর সাহায্যে
\(\cos{\theta}\times \sec{\theta}=\frac{x}{r}\times\frac{r}{x}\)
\(\Rightarrow \cos{\theta}\times \sec{\theta}=1\)
\(\therefore \cos{\theta}=\frac{1}{\sec{\theta}}\)
অথবা, \(\sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\cos{\theta}=\frac{1}{\sec{\theta}}\)
অথবা,
\(\sec{\theta}=\frac{1}{\cos{\theta}}\)
আবার, \(\tan{POM}=\frac{PM}{OM}\)
\(\therefore \tan{\theta}=\frac{y}{x} .....(5); \ x\ne{0}\)
এবং \(\cot{\theta}=\frac{OM}{PM}\)
\(\therefore \cot{\theta}=\frac{x}{y} .....(6); \ y\ne{0}\)
\((5)\times(6)\) এর সাহায্যে
\(\tan{\theta}\times \cot{\theta}=\frac{y}{x}\times\frac{x}{y}\)
\(\Rightarrow \tan{\theta}\times \cot{\theta}=1\)
\(\therefore \tan{\theta}=\frac{1}{\cot{\theta}}\)
অথবা, \(\cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\tan{\theta}=\frac{1}{\cot{\theta}}\)
অথবা,
\(\cot{\theta}=\frac{1}{\tan{\theta}}\)
\((5)\) হতে,
\(\tan{\theta}=\frac{\frac{y}{r}}{\frac{x}{r}}\) ➜ ডান পাশের লব ও হরের সহিত \(r\) ভাগ করে।
\(\therefore \tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\) ➜ \(\because \sin{\theta}=\frac{y}{r}\)
এবং \(\cos{\theta}=\frac{x}{r}\)
\(\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\)
\((6)\) হতে,
\(\cot{\theta}=\frac{\frac{x}{r}}{\frac{y}{r}}\) ➜ ডান পাশের লব ও হরের সহিত \(r\) ভাগ করে।
\(\therefore \cot{\theta}=\frac{\cos{\theta}}{\sin{\theta}}\) ➜ \(\because \cos{\theta}=\frac{x}{r}\)
এবং \(\sin{\theta}=\frac{y}{r}\)
\(\cot{\theta}=\frac{\cos{\theta}}{\sin{\theta}}\)
( প্রমাণিত )
চিত্র হতে,
\(P(x,y)\)
\(\therefore OM=x, \ PM=y, \ OP=r\)
\(\angle{PMO}=90^{0}\) অর্থাৎ এক সমকোণ।
এবং \(\angle{POM}=\theta\)।
এখন, \(\sin{POM}=\frac{PM}{OP}\)
\(\therefore \sin{\theta}=\frac{y}{r} .....(1)\)
এবং \(cosec \ {\theta}=\frac{OP}{PM}\)
\(\therefore cosec \ {\theta}=\frac{r}{y} .....(2); \ y\ne{0}\)
\((1)\times(2)\) এর সাহায্যে
\(\sin{\theta}\times cosec \ {\theta}=\frac{y}{r}\times\frac{r}{y}\)
\(\Rightarrow \sin{\theta}\times cosec \ {\theta}=1\)
\(\therefore \sin{\theta}=\frac{1}{cosec \ {\theta}}\)
অথবা, \(cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\sin{\theta}=\frac{1}{cosec \ {\theta}}\)
অথবা,
\(cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
আবার, \(\cos{POM}=\frac{OM}{OP}\)
\(\therefore \cos{\theta}=\frac{x}{r} .....(3)\)
এবং \(\sec{\theta}=\frac{OP}{OM}\)
\(\therefore \sec{\theta}=\frac{r}{x} .....(4); \ x\ne{0}\)
\((3)\times(4)\) এর সাহায্যে
\(\cos{\theta}\times \sec{\theta}=\frac{x}{r}\times\frac{r}{x}\)
\(\Rightarrow \cos{\theta}\times \sec{\theta}=1\)
\(\therefore \cos{\theta}=\frac{1}{\sec{\theta}}\)
অথবা, \(\sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\cos{\theta}=\frac{1}{\sec{\theta}}\)
অথবা,
\(\sec{\theta}=\frac{1}{\cos{\theta}}\)
আবার, \(\tan{POM}=\frac{PM}{OM}\)
\(\therefore \tan{\theta}=\frac{y}{x} .....(5); \ x\ne{0}\)
এবং \(\cot{\theta}=\frac{OM}{PM}\)
\(\therefore \cot{\theta}=\frac{x}{y} .....(6); \ y\ne{0}\)
\((5)\times(6)\) এর সাহায্যে
\(\tan{\theta}\times \cot{\theta}=\frac{y}{x}\times\frac{x}{y}\)
\(\Rightarrow \tan{\theta}\times \cot{\theta}=1\)
\(\therefore \tan{\theta}=\frac{1}{\cot{\theta}}\)
অথবা, \(\cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\tan{\theta}=\frac{1}{\cot{\theta}}\)
অথবা,
\(\cot{\theta}=\frac{1}{\tan{\theta}}\)
\((5)\) হতে,
\(\tan{\theta}=\frac{\frac{y}{r}}{\frac{x}{r}}\) ➜ ডান পাশের লব ও হরের সহিত \(r\) ভাগ করে।
\(\therefore \tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\) ➜ \(\because \sin{\theta}=\frac{y}{r}\)
এবং \(\cos{\theta}=\frac{x}{r}\)
\(\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\)
\((6)\) হতে,
\(\cot{\theta}=\frac{\frac{x}{r}}{\frac{y}{r}}\) ➜ ডান পাশের লব ও হরের সহিত \(r\) ভাগ করে।
\(\therefore \cot{\theta}=\frac{\cos{\theta}}{\sin{\theta}}\) ➜ \(\because \cos{\theta}=\frac{x}{r}\)
এবং \(\sin{\theta}=\frac{y}{r}\)
\(\cot{\theta}=\frac{\cos{\theta}}{\sin{\theta}}\)
( প্রমাণিত )
\(0^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of \(0^{o}\) angles angles
\(\sin{0^{o}}=0\) \(\cos{0^{o}}=1\) \(\tan{0^{o}}=0\)
\(cosec \ {0^{o}}=\infty\) \(\sec{0^{o}}=1\) \(\cot{0^{o}}=\infty\)
\(cosec \ {0^{o}}=\infty\) \(\sec{0^{o}}=1\) \(\cot{0^{o}}=\infty\)
প্রমাণঃ
ধরি,
\(\triangle{ABC}\) -এ \(\angle{BAC}=90^{o}\) এবং \(\angle{ABC}=\theta\)।
\(\theta\) এর মাণ ক্রমশ শূন্য হবে যদি \(C\) বিন্দুটি ক্রমশ \(A\) এর দিকে অগ্রসর হয়ে এর উপর সমপতিত হয়।
সে ক্ষেত্রে \(AC=0\) এবং \(AB=BC\) হবে।
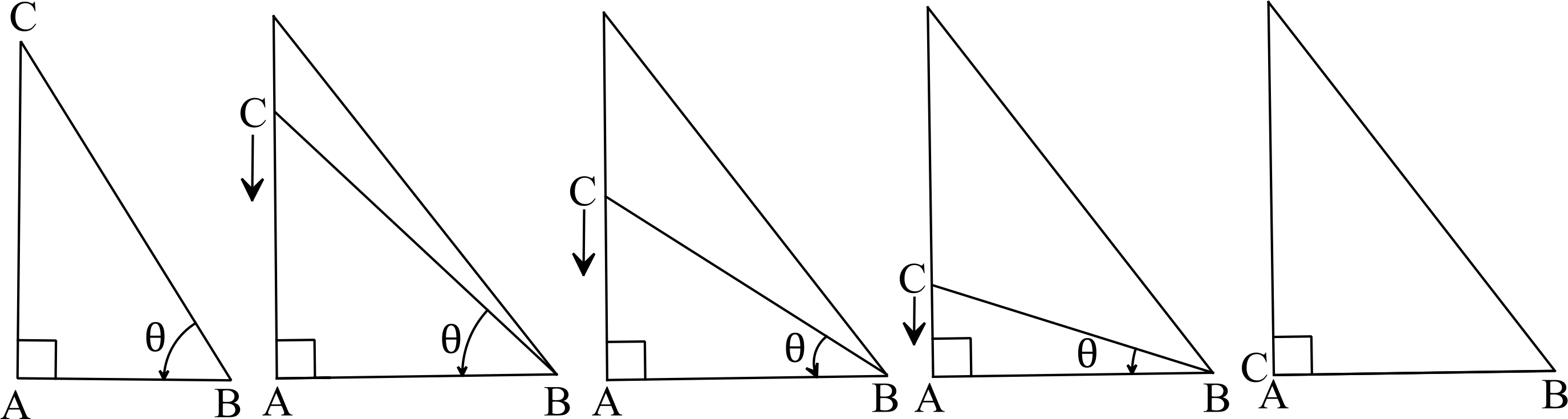
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{\theta}=\sin{\angle{ABC}}\)
\(\Rightarrow \sin{0^{o}}=\sin{\angle{ABC}}\)
\(=\frac{AC}{BC}\)
\(=\frac{0}{AB}\) ➜ \(\because AC=0, \ BC=AB\)
\(=0\)
\(\therefore \sin{0^{o}}=0\)
\(\sin{0^{o}}=0\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {0^{o}}=\frac{1}{\sin{0^{o}}}\)
\(\Rightarrow cosec \ {0^{o}}=\frac{1}{0}\) ➜ \(\because \sin{0^{o}}=0\)
\(\therefore cosec \ {0^{o}}=\infty\)
\(cosec \ {0^{o}}=\infty\)
আবার, \(\cos{\theta}=\cos{\angle{ABC}}\)
\(\Rightarrow \cos{0^{o}}=\cos{\angle{ABC}}\)
\(=\frac{AB}{BC}\)
\(=\frac{BC}{BC}\) ➜ \(\because AB=BC\)
\(=1\)
\(\therefore \cos{0^{o}}=1\)
\(\cos{0^{o}}=1\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{0^{o}}=\frac{1}{\cos{0^{o}}}\)
\(\Rightarrow \sec{0^{o}}=\frac{1}{1}\) ➜ \(\because \cos{0^{o}}=1\)
\(\therefore \sec{0^{o}}=1\)
\(\sec{0^{o}}=1\)
আবার, \(\tan{\theta}=\tan{\angle{ABC}}\)
\(\Rightarrow \tan{0^{o}}=\tan{\angle{ABC}}\)
\(=\frac{AC}{AB}\)
\(=\frac{0}{BC}\) ➜ \(\because AC=0, \ AB=BC\)
\(=0\)
\(\therefore \tan{0^{o}}=0\)
\(\tan{0^{o}}=0\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{0^{o}}=\frac{1}{\tan{0^{o}}}\)
\(\Rightarrow \cot{0^{o}}=\frac{1}{0}\) ➜ \(\because \tan{0^{o}}=0\)
\(\therefore \cot{0^{o}}=\infty\)
\(\cot{0^{o}}=\infty\)
( প্রমাণিত )
ধরি,
\(\triangle{ABC}\) -এ \(\angle{BAC}=90^{o}\) এবং \(\angle{ABC}=\theta\)।
\(\theta\) এর মাণ ক্রমশ শূন্য হবে যদি \(C\) বিন্দুটি ক্রমশ \(A\) এর দিকে অগ্রসর হয়ে এর উপর সমপতিত হয়।
সে ক্ষেত্রে \(AC=0\) এবং \(AB=BC\) হবে।
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{\theta}=\sin{\angle{ABC}}\)
\(\Rightarrow \sin{0^{o}}=\sin{\angle{ABC}}\)
\(=\frac{AC}{BC}\)
\(=\frac{0}{AB}\) ➜ \(\because AC=0, \ BC=AB\)
\(=0\)
\(\therefore \sin{0^{o}}=0\)
\(\sin{0^{o}}=0\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {0^{o}}=\frac{1}{\sin{0^{o}}}\)
\(\Rightarrow cosec \ {0^{o}}=\frac{1}{0}\) ➜ \(\because \sin{0^{o}}=0\)
\(\therefore cosec \ {0^{o}}=\infty\)
\(cosec \ {0^{o}}=\infty\)
আবার, \(\cos{\theta}=\cos{\angle{ABC}}\)
\(\Rightarrow \cos{0^{o}}=\cos{\angle{ABC}}\)
\(=\frac{AB}{BC}\)
\(=\frac{BC}{BC}\) ➜ \(\because AB=BC\)
\(=1\)
\(\therefore \cos{0^{o}}=1\)
\(\cos{0^{o}}=1\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{0^{o}}=\frac{1}{\cos{0^{o}}}\)
\(\Rightarrow \sec{0^{o}}=\frac{1}{1}\) ➜ \(\because \cos{0^{o}}=1\)
\(\therefore \sec{0^{o}}=1\)
\(\sec{0^{o}}=1\)
আবার, \(\tan{\theta}=\tan{\angle{ABC}}\)
\(\Rightarrow \tan{0^{o}}=\tan{\angle{ABC}}\)
\(=\frac{AC}{AB}\)
\(=\frac{0}{BC}\) ➜ \(\because AC=0, \ AB=BC\)
\(=0\)
\(\therefore \tan{0^{o}}=0\)
\(\tan{0^{o}}=0\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{0^{o}}=\frac{1}{\tan{0^{o}}}\)
\(\Rightarrow \cot{0^{o}}=\frac{1}{0}\) ➜ \(\because \tan{0^{o}}=0\)
\(\therefore \cot{0^{o}}=\infty\)
\(\cot{0^{o}}=\infty\)
( প্রমাণিত )
\(30^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of \(30^{o}\) angles
\(\sin{30^{o}}=\frac{1}{2}\) \(\cos{30^{o}}=\frac{\sqrt{3}}{2}\) \(\tan{30^{o}}=\frac{1}{\sqrt{3}}\)
\(cosec \ {30^{o}}=2\) \(\sec{30^{o}}=\frac{2}{\sqrt{3}}\) \(\cot{30^{o}}=\sqrt{3}\)
\(cosec \ {30^{o}}=2\) \(\sec{30^{o}}=\frac{2}{\sqrt{3}}\) \(\cot{30^{o}}=\sqrt{3}\)
প্রমাণঃ
ধরি,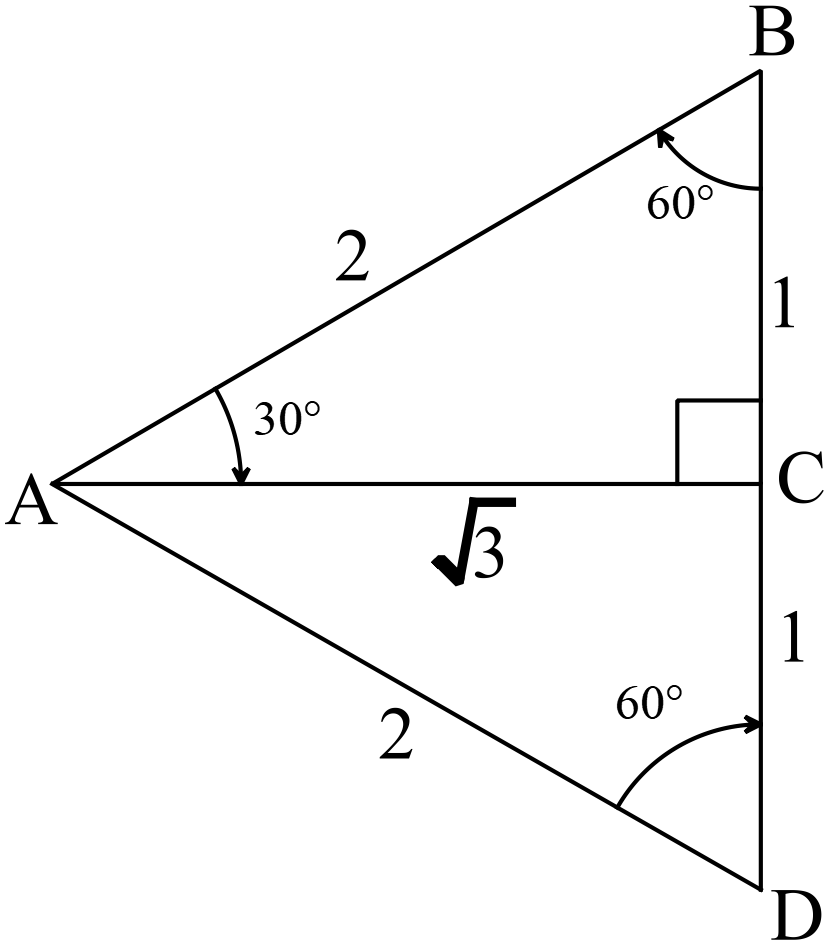
\(\triangle{ABC}\) -এ \(\angle{ACB}=90^{o},\) \(\angle{BAC}=30^{o}\) এবং \(BC=1\) ।
\(\therefore \angle{ABC}=90^{o}-30^{o}=60^{o}\)।
\(BC\) বাহুকে \(D\) পর্যন্ত এরূপভাবে বর্ধিত করি যেন, \(CD=BC=1\) হয়।
ফলে, \(\triangle{ABC}\) এবং \(\triangle{ADC}\) এর মধ্যে \(CD=BC=1, \ \angle{ACB}=\angle{ACD}=90^{o}\) এবং \(AC\) সাধারণ বাহু।
\(\therefore \triangle{ABC}\) এবং \(\triangle{ADC}\) সর্বসম।
\(\therefore \angle{ABC}=\angle{ADC}=60^{o}\)।
ফলে, \(\angle{BAD}=60^{o}\)।
\(\therefore \triangle{ABD}\) সমবাহু।
\(\therefore AB=BD=BC+CD=1+1=2\)
এখন, \(\triangle{ABC}\) সমকোণী।
\(\therefore AC^2+BC^2=AB^2\)
\(\Rightarrow AC^2=AB^2-BC^2\)
\(\Rightarrow AC=\sqrt{AB^2-BC^2}\)
\(\Rightarrow AC=\sqrt{2^2-1^2}\) ➜ \(\because AB=2, \ BC=1\)
\(\Rightarrow AC=\sqrt{4-1}\)
\(\therefore AC=\sqrt{3}\)
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{30^{o}}=\sin{\angle{BAC}}\)
\(=\frac{BC}{AB}\)
\(=\frac{1}{2}\) ➜ \(\because BC=1, \ AB=2\)
\(\therefore \sin{30^{o}}=\frac{1}{2}\)
\(\sin{30^{o}}=\frac{1}{2}\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {30^{o}}=\frac{1}{\sin{30^{o}}}\)
\(\Rightarrow cosec \ {30^{o}}=\frac{1}{\frac{1}{2}}\) ➜ \(\because \sin{30^{o}}=\frac{1}{2}\)
\(\therefore cosec \ {30^{o}}=2\)
\(cosec \ {30^{o}}=2\)
আবার, \(\cos{30^{o}}=\cos{\angle{BAC}}\)
\(=\frac{AC}{AB}\)
\(=\frac{\sqrt{3}}{2}\) ➜ \(\because AC=\sqrt{3}, \ AB=2\)
\(\therefore \cos{30^{o}}=\frac{\sqrt{3}}{2}\)
\(\cos{30^{o}}=\frac{\sqrt{3}}{2}\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{30^{o}}=\frac{1}{\cos{30^{o}}}\)
\(\Rightarrow \sec{30^{o}}=\frac{1}{\frac{\sqrt{3}}{2}}\) ➜ \(\because \cos{30^{o}}=\frac{\sqrt{3}}{2}\)
\(\therefore \sec{30^{o}}=\frac{2}{\sqrt{3}}\)
\(\sec{30^{o}}=\frac{2}{\sqrt{3}}\)
আবার, \(\tan{30^{o}}=\tan{\angle{BAC}}\)
\(=\frac{BC}{AC}\)
\(=\frac{1}{\sqrt{3}}\) ➜ \(\because BC=1, \ AC=\sqrt{3}\)
\(\therefore \tan{30^{o}}=\frac{1}{\sqrt{3}}\)
\(\tan{30^{o}}=\frac{1}{\sqrt{3}}\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{30^{o}}=\frac{1}{\tan{30^{o}}}\)
\(\Rightarrow \cot{30^{o}}=\frac{1}{\frac{1}{\sqrt{3}}}\) ➜ \(\because \tan{30^{o}}=\frac{1}{\sqrt{3}}\)
\(\therefore \cot{30^{o}}=\sqrt{3}\)
\(\cot{30^{o}}=\sqrt{3}\)
( প্রমাণিত )
ধরি,
\(\triangle{ABC}\) -এ \(\angle{ACB}=90^{o},\) \(\angle{BAC}=30^{o}\) এবং \(BC=1\) ।
\(\therefore \angle{ABC}=90^{o}-30^{o}=60^{o}\)।
\(BC\) বাহুকে \(D\) পর্যন্ত এরূপভাবে বর্ধিত করি যেন, \(CD=BC=1\) হয়।
ফলে, \(\triangle{ABC}\) এবং \(\triangle{ADC}\) এর মধ্যে \(CD=BC=1, \ \angle{ACB}=\angle{ACD}=90^{o}\) এবং \(AC\) সাধারণ বাহু।
\(\therefore \triangle{ABC}\) এবং \(\triangle{ADC}\) সর্বসম।
\(\therefore \angle{ABC}=\angle{ADC}=60^{o}\)।
ফলে, \(\angle{BAD}=60^{o}\)।
\(\therefore \triangle{ABD}\) সমবাহু।
\(\therefore AB=BD=BC+CD=1+1=2\)
এখন, \(\triangle{ABC}\) সমকোণী।
\(\therefore AC^2+BC^2=AB^2\)
\(\Rightarrow AC^2=AB^2-BC^2\)
\(\Rightarrow AC=\sqrt{AB^2-BC^2}\)
\(\Rightarrow AC=\sqrt{2^2-1^2}\) ➜ \(\because AB=2, \ BC=1\)
\(\Rightarrow AC=\sqrt{4-1}\)
\(\therefore AC=\sqrt{3}\)
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{30^{o}}=\sin{\angle{BAC}}\)
\(=\frac{BC}{AB}\)
\(=\frac{1}{2}\) ➜ \(\because BC=1, \ AB=2\)
\(\therefore \sin{30^{o}}=\frac{1}{2}\)
\(\sin{30^{o}}=\frac{1}{2}\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {30^{o}}=\frac{1}{\sin{30^{o}}}\)
\(\Rightarrow cosec \ {30^{o}}=\frac{1}{\frac{1}{2}}\) ➜ \(\because \sin{30^{o}}=\frac{1}{2}\)
\(\therefore cosec \ {30^{o}}=2\)
\(cosec \ {30^{o}}=2\)
আবার, \(\cos{30^{o}}=\cos{\angle{BAC}}\)
\(=\frac{AC}{AB}\)
\(=\frac{\sqrt{3}}{2}\) ➜ \(\because AC=\sqrt{3}, \ AB=2\)
\(\therefore \cos{30^{o}}=\frac{\sqrt{3}}{2}\)
\(\cos{30^{o}}=\frac{\sqrt{3}}{2}\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{30^{o}}=\frac{1}{\cos{30^{o}}}\)
\(\Rightarrow \sec{30^{o}}=\frac{1}{\frac{\sqrt{3}}{2}}\) ➜ \(\because \cos{30^{o}}=\frac{\sqrt{3}}{2}\)
\(\therefore \sec{30^{o}}=\frac{2}{\sqrt{3}}\)
\(\sec{30^{o}}=\frac{2}{\sqrt{3}}\)
আবার, \(\tan{30^{o}}=\tan{\angle{BAC}}\)
\(=\frac{BC}{AC}\)
\(=\frac{1}{\sqrt{3}}\) ➜ \(\because BC=1, \ AC=\sqrt{3}\)
\(\therefore \tan{30^{o}}=\frac{1}{\sqrt{3}}\)
\(\tan{30^{o}}=\frac{1}{\sqrt{3}}\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{30^{o}}=\frac{1}{\tan{30^{o}}}\)
\(\Rightarrow \cot{30^{o}}=\frac{1}{\frac{1}{\sqrt{3}}}\) ➜ \(\because \tan{30^{o}}=\frac{1}{\sqrt{3}}\)
\(\therefore \cot{30^{o}}=\sqrt{3}\)
\(\cot{30^{o}}=\sqrt{3}\)
( প্রমাণিত )
\(45^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of \(45^{o}\) angles
\(\sin{45^{o}}=\frac{1}{\sqrt{2}}\) \(\cos{45^{o}}=\frac{1}{\sqrt{2}}\) \(\tan{45^{o}}=1\)
\(cosec \ {45^{o}}=\sqrt{2}\) \(\sec{45^{o}}=\sqrt{2}\) \(\cot{45^{o}}=1\)
\(cosec \ {45^{o}}=\sqrt{2}\) \(\sec{45^{o}}=\sqrt{2}\) \(\cot{45^{o}}=1\)
প্রমাণঃ
ধরি,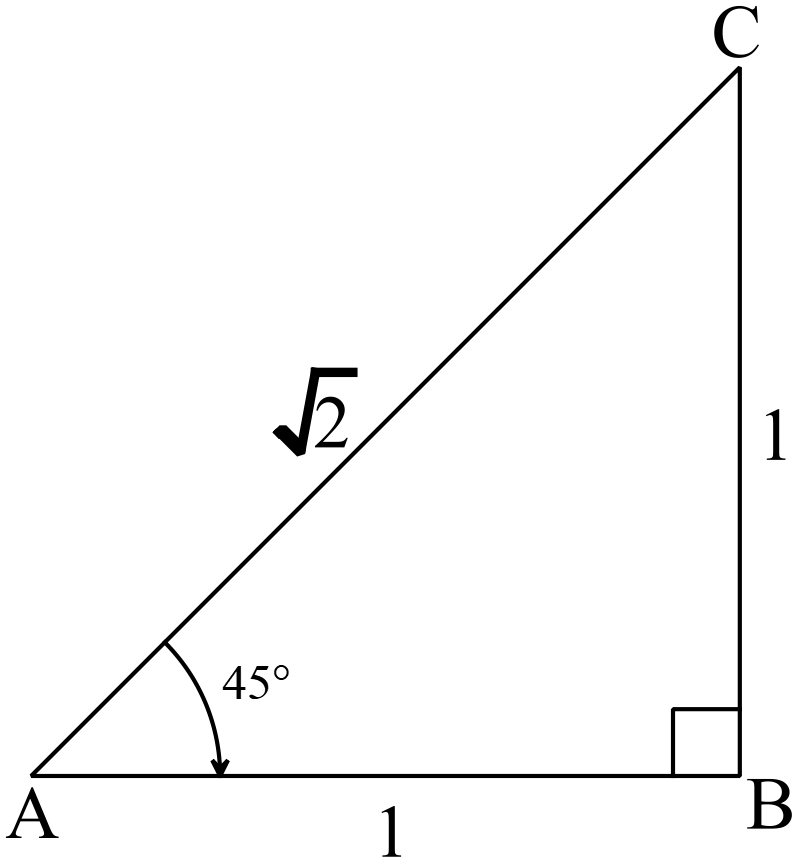
\(\triangle{ABC}\) -এ \(\angle{ABC}=90^{o},\) \(\angle{BAC}=45^{o}\) এবং \(BC=1\) ।
\(\therefore \angle{ACB}=90^{o}-45^{o}=45^{o}\)।
সুতরাং \(AB=BC=1\)
এখন, \(\triangle{ABC}\) সমকোণী।
\(\therefore AC^2=AB^2+BC^2\)
\(\therefore AC=\sqrt{AB^2+BC^2}\)
\(\Rightarrow AC=\sqrt{1^2+1^2}\) ➜ \(\because AB=BC=1\)
\(\Rightarrow AC=\sqrt{1+1}\)
\(\therefore AC=\sqrt{2}\)
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{45^{o}}=\sin{\angle{BAC}}\)
\(=\frac{BC}{AC}\)
\(=\frac{1}{\sqrt{2}}\) ➜ \(\because BC=1, \ AC=\sqrt{2}\)
\(\therefore \sin{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\sin{45^{o}}=\frac{1}{\sqrt{2}}\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {45^{o}}=\frac{1}{\sin{45^{o}}}\)
\(\Rightarrow cosec \ {45^{o}}=\frac{1}{\frac{1}{\sqrt{2}}}\) ➜ \(\because \sin{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\therefore cosec \ {45^{o}}=\sqrt{2}\)
\(cosec \ {45^{o}}=\sqrt{2}\)
আবার, \(\cos{45^{o}}=\cos{\angle{BAC}}\)
\(=\frac{AB}{AC}\)
\(=\frac{1}{\sqrt{2}}\) ➜ \(\because AB=1, \ AC=\sqrt{2}\)
\(\therefore \cos{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\cos{30^{o}}=\frac{1}{\sqrt{2}}\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{45^{o}}=\frac{1}{\cos{45^{o}}}\)
\(\Rightarrow \sec{45^{o}}=\frac{1}{\frac{1}{\sqrt{2}}}\) ➜ \(\because \cos{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\therefore \sec{45^{o}}=\sqrt{2}\)
\(\sec{45^{o}}=\sqrt{2}\)
আবার, \(\tan{45^{o}}=\tan{\angle{BAC}}\)
\(=\frac{BC}{AB}\)
\(=\frac{1}{1}\) ➜ \(\because BC=AB=1\)
\(\therefore \tan{45^{o}}=1\)
\(\tan{45^{o}}=1\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{45^{o}}=\frac{1}{\tan{45^{o}}}\)
\(\Rightarrow \cot{45^{o}}=\frac{1}{1}\) ➜ \(\because \tan{45^{o}}=1\)
\(\therefore \cot{45^{o}}=1\)
\(\cot{45^{o}}=1\)
( প্রমাণিত )
ধরি,
\(\triangle{ABC}\) -এ \(\angle{ABC}=90^{o},\) \(\angle{BAC}=45^{o}\) এবং \(BC=1\) ।
\(\therefore \angle{ACB}=90^{o}-45^{o}=45^{o}\)।
সুতরাং \(AB=BC=1\)
এখন, \(\triangle{ABC}\) সমকোণী।
\(\therefore AC^2=AB^2+BC^2\)
\(\therefore AC=\sqrt{AB^2+BC^2}\)
\(\Rightarrow AC=\sqrt{1^2+1^2}\) ➜ \(\because AB=BC=1\)
\(\Rightarrow AC=\sqrt{1+1}\)
\(\therefore AC=\sqrt{2}\)
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{45^{o}}=\sin{\angle{BAC}}\)
\(=\frac{BC}{AC}\)
\(=\frac{1}{\sqrt{2}}\) ➜ \(\because BC=1, \ AC=\sqrt{2}\)
\(\therefore \sin{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\sin{45^{o}}=\frac{1}{\sqrt{2}}\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {45^{o}}=\frac{1}{\sin{45^{o}}}\)
\(\Rightarrow cosec \ {45^{o}}=\frac{1}{\frac{1}{\sqrt{2}}}\) ➜ \(\because \sin{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\therefore cosec \ {45^{o}}=\sqrt{2}\)
\(cosec \ {45^{o}}=\sqrt{2}\)
আবার, \(\cos{45^{o}}=\cos{\angle{BAC}}\)
\(=\frac{AB}{AC}\)
\(=\frac{1}{\sqrt{2}}\) ➜ \(\because AB=1, \ AC=\sqrt{2}\)
\(\therefore \cos{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\cos{30^{o}}=\frac{1}{\sqrt{2}}\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{45^{o}}=\frac{1}{\cos{45^{o}}}\)
\(\Rightarrow \sec{45^{o}}=\frac{1}{\frac{1}{\sqrt{2}}}\) ➜ \(\because \cos{45^{o}}=\frac{1}{\sqrt{2}}\)
\(\therefore \sec{45^{o}}=\sqrt{2}\)
\(\sec{45^{o}}=\sqrt{2}\)
আবার, \(\tan{45^{o}}=\tan{\angle{BAC}}\)
\(=\frac{BC}{AB}\)
\(=\frac{1}{1}\) ➜ \(\because BC=AB=1\)
\(\therefore \tan{45^{o}}=1\)
\(\tan{45^{o}}=1\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{45^{o}}=\frac{1}{\tan{45^{o}}}\)
\(\Rightarrow \cot{45^{o}}=\frac{1}{1}\) ➜ \(\because \tan{45^{o}}=1\)
\(\therefore \cot{45^{o}}=1\)
\(\cot{45^{o}}=1\)
( প্রমাণিত )
\(60^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of \(60^{o}\) angles
\(\sin{60^{o}}=\frac{\sqrt{3}}{2}\) \(\cos{60^{o}}=\frac{1}{2}\) \(\tan{60^{o}}=\sqrt{3}\)
\(cosec \ {60^{o}}=\frac{2}{\sqrt{3}}\) \(\sec{60^{o}}=2\) \(\cot{60^{o}}=\frac{1}{\sqrt{3}}\)
\(cosec \ {60^{o}}=\frac{2}{\sqrt{3}}\) \(\sec{60^{o}}=2\) \(\cot{60^{o}}=\frac{1}{\sqrt{3}}\)
প্রমাণঃ
ধরি,
\(\triangle{ABC}\) -এ \(\angle{ACB}=90^{o},\) \(\angle{BAC}=30^{o}\) এবং \(BC=1\) ।
\(\therefore \angle{ABC}=90^{o}-30^{o}=60^{o}\)।
\(BC\) বাহুকে \(D\) পর্যন্ত এরূপভাবে বর্ধিত করি যেন, \(CD=BC=1\) হয়।
ফলে, \(\triangle{ABC}\) এবং \(\triangle{ADC}\) এর মধ্যে \(CD=BC=1, \ \angle{ACB}=\angle{ACD}=90^{o}\) এবং \(AC\) সাধারণ বাহু।
\(\therefore \triangle{ABC}\) এবং \(\triangle{ADC}\) সর্বসম।
\(\therefore \angle{ABC}=\angle{ADC}=60^{o}\)।
ফলে, \(\angle{BAD}=60^{o}\)।
\(\therefore \triangle{ABD}\) সমবাহু।
\(\therefore AB=BD=BC+CD=1+1=2\)
এখন, \(\triangle{ABC}\) সমকোণী।
\(\therefore AC^2+BC^2=AB^2\)
\(\Rightarrow AC^2=AB^2-BC^2\)
\(\Rightarrow AC=\sqrt{AB^2-BC^2}\)
\(\Rightarrow AC=\sqrt{2^2-1^2}\) ➜ \(\because AB=2, \ BC=1\)
\(\Rightarrow AC=\sqrt{4-1}\)
\(\therefore AC=\sqrt{3}\)
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{60^{o}}=\sin{\angle{ABC}}\)
\(=\frac{AC}{AB}\)
\(=\frac{\sqrt{3}}{2}\) ➜ \(\because AC=\sqrt{3}, \ AB=2\)
\(\therefore \sin{60^{o}}=\frac{\sqrt{3}}{2}\)
\(\sin{60^{o}}=\frac{\sqrt{3}}{2}\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {60^{o}}=\frac{1}{\sin{60^{o}}}\)
\(\Rightarrow cosec \ {60^{o}}=\frac{1}{\frac{\sqrt{3}}{2}}\) ➜ \(\because \sin{60^{o}}=\frac{\sqrt{3}}{2}\)
\(\therefore cosec \ {60^{o}}=\frac{2}{\sqrt{3}}\)
\(cosec \ {60^{o}}=\frac{2}{\sqrt{3}}\)
আবার, \(\cos{60^{o}}=\cos{\angle{ABC}}\)
\(=\frac{BC}{AB}\)
\(=\frac{1}{2}\) ➜ \(\because BC=1, \ AB=2\)
\(\therefore \cos{60^{o}}=\frac{1}{2}\)
\(\cos{60^{o}}=\frac{1}{2}\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{60^{o}}=\frac{1}{\cos{60^{o}}}\)
\(\Rightarrow \sec{60^{o}}=\frac{1}{\frac{1}{2}}\) ➜ \(\because \cos{60^{o}}=\frac{1}{2}\)
\(\therefore \sec{60^{o}}=2\)
\(\sec{60^{o}}=2\)
আবার, \(\tan{60^{o}}=\tan{\angle{ABC}}\)
\(=\frac{AC}{BC}\)
\(=\frac{\sqrt{3}}{1}\) ➜ \(\because AC=\sqrt{3}, \ BC=1\)
\(\therefore \tan{60^{o}}=\sqrt{3}\)
\(\tan{60^{o}}=\sqrt{3}\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{60^{o}}=\frac{1}{\tan{60^{o}}}\)
\(\Rightarrow \cot{60^{o}}=\frac{1}{\sqrt{3}}\) ➜ \(\because \tan{60^{o}}=\sqrt{3}\)
\(\therefore \cot{60^{o}}=\frac{1}{\sqrt{3}}\)
\(\cot{60^{o}}=\frac{1}{\sqrt{3}}\)
( প্রমাণিত )
ধরি,
\(\triangle{ABC}\) -এ \(\angle{ACB}=90^{o},\) \(\angle{BAC}=30^{o}\) এবং \(BC=1\) ।
\(\therefore \angle{ABC}=90^{o}-30^{o}=60^{o}\)।
\(BC\) বাহুকে \(D\) পর্যন্ত এরূপভাবে বর্ধিত করি যেন, \(CD=BC=1\) হয়।
ফলে, \(\triangle{ABC}\) এবং \(\triangle{ADC}\) এর মধ্যে \(CD=BC=1, \ \angle{ACB}=\angle{ACD}=90^{o}\) এবং \(AC\) সাধারণ বাহু।
\(\therefore \triangle{ABC}\) এবং \(\triangle{ADC}\) সর্বসম।
\(\therefore \angle{ABC}=\angle{ADC}=60^{o}\)।
ফলে, \(\angle{BAD}=60^{o}\)।
\(\therefore \triangle{ABD}\) সমবাহু।
\(\therefore AB=BD=BC+CD=1+1=2\)
এখন, \(\triangle{ABC}\) সমকোণী।
\(\therefore AC^2+BC^2=AB^2\)
\(\Rightarrow AC^2=AB^2-BC^2\)
\(\Rightarrow AC=\sqrt{AB^2-BC^2}\)
\(\Rightarrow AC=\sqrt{2^2-1^2}\) ➜ \(\because AB=2, \ BC=1\)
\(\Rightarrow AC=\sqrt{4-1}\)
\(\therefore AC=\sqrt{3}\)
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{60^{o}}=\sin{\angle{ABC}}\)
\(=\frac{AC}{AB}\)
\(=\frac{\sqrt{3}}{2}\) ➜ \(\because AC=\sqrt{3}, \ AB=2\)
\(\therefore \sin{60^{o}}=\frac{\sqrt{3}}{2}\)
\(\sin{60^{o}}=\frac{\sqrt{3}}{2}\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {60^{o}}=\frac{1}{\sin{60^{o}}}\)
\(\Rightarrow cosec \ {60^{o}}=\frac{1}{\frac{\sqrt{3}}{2}}\) ➜ \(\because \sin{60^{o}}=\frac{\sqrt{3}}{2}\)
\(\therefore cosec \ {60^{o}}=\frac{2}{\sqrt{3}}\)
\(cosec \ {60^{o}}=\frac{2}{\sqrt{3}}\)
আবার, \(\cos{60^{o}}=\cos{\angle{ABC}}\)
\(=\frac{BC}{AB}\)
\(=\frac{1}{2}\) ➜ \(\because BC=1, \ AB=2\)
\(\therefore \cos{60^{o}}=\frac{1}{2}\)
\(\cos{60^{o}}=\frac{1}{2}\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{60^{o}}=\frac{1}{\cos{60^{o}}}\)
\(\Rightarrow \sec{60^{o}}=\frac{1}{\frac{1}{2}}\) ➜ \(\because \cos{60^{o}}=\frac{1}{2}\)
\(\therefore \sec{60^{o}}=2\)
\(\sec{60^{o}}=2\)
আবার, \(\tan{60^{o}}=\tan{\angle{ABC}}\)
\(=\frac{AC}{BC}\)
\(=\frac{\sqrt{3}}{1}\) ➜ \(\because AC=\sqrt{3}, \ BC=1\)
\(\therefore \tan{60^{o}}=\sqrt{3}\)
\(\tan{60^{o}}=\sqrt{3}\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{60^{o}}=\frac{1}{\tan{60^{o}}}\)
\(\Rightarrow \cot{60^{o}}=\frac{1}{\sqrt{3}}\) ➜ \(\because \tan{60^{o}}=\sqrt{3}\)
\(\therefore \cot{60^{o}}=\frac{1}{\sqrt{3}}\)
\(\cot{60^{o}}=\frac{1}{\sqrt{3}}\)
( প্রমাণিত )
\(90^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of \(90^{o}\) angles
\(\sin{90^{o}}=1\) \(\cos{90^{o}}=0\) \(\tan{90^{o}}=\infty\)
\(cosec \ {90^{o}}=1\) \(\sec{90^{o}}=\infty\) \(\cot{90^{o}}=0\)
\(cosec \ {90^{o}}=1\) \(\sec{90^{o}}=\infty\) \(\cot{90^{o}}=0\)
প্রমাণঃ
ধরি,
\(\triangle{ABC}\) -এ \(\angle{BAC}=90^{o}\) এবং \(\angle{ABC}=\theta\)।
\(\theta\) এর মাণ ক্রমশ বড় হয়ে \(\theta=90^{o}\) হবে, যদি \(B\) বিন্দুটি ক্রমশ \(A\) এর দিকে অগ্রসর হয়ে এর উপর সমপতিত হয়।
সে ক্ষেত্রে \(AB=0\) এবং \(AC=BC\) হবে।
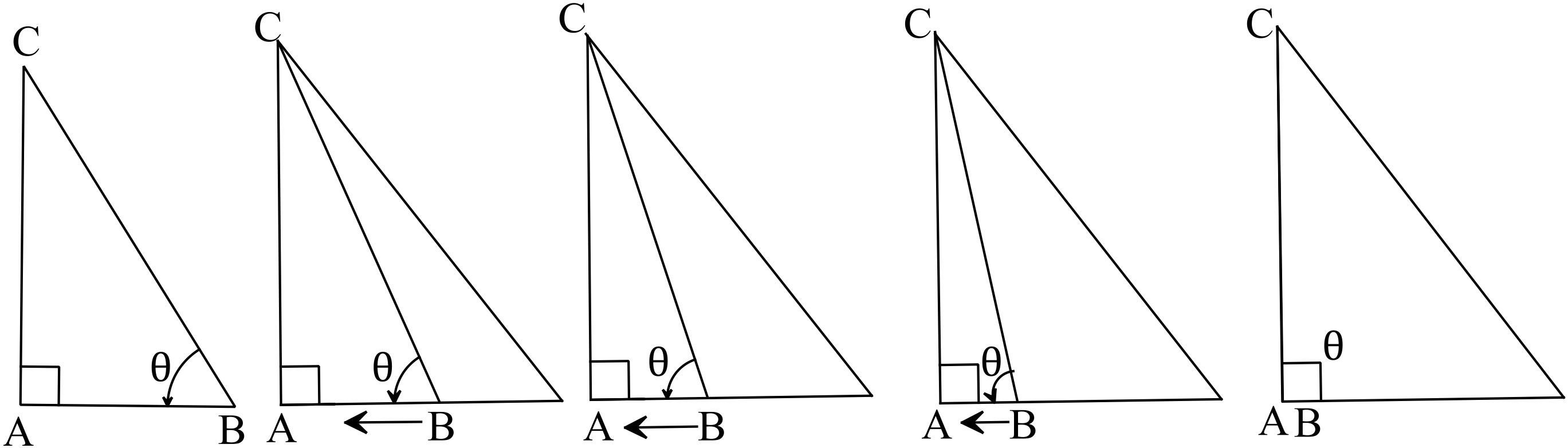
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{\theta}=\sin{\angle{ABC}}\)
\(\Rightarrow \sin{90^{o}}=\sin{\angle{ABC}}\)
\(=\frac{AC}{BC}\)
\(=\frac{BC}{BC}\) ➜ \(\because AC=BC\)
\(=1\)
\(\therefore \sin{90^{o}}=1\)
\(\sin{90^{o}}=1\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {90^{o}}=\frac{1}{\sin{90^{o}}}\)
\(\Rightarrow cosec \ {90^{o}}=\frac{1}{1}\) ➜ \(\because \sin{90^{o}}=1\)
\(\therefore cosec \ {90^{o}}=1\)
\(cosec \ {90^{o}}=1\)
আবার, \(\cos{\theta}=\cos{\angle{ABC}}\)
\(\Rightarrow \cos{90^{o}}=\cos{\angle{ABC}}\)
\(=\frac{AB}{BC}\)
\(=\frac{0}{AC}\) ➜ \(\because AB=0 , \ BC=AC\)
\(=0\)
\(\therefore \cos{90^{o}}=0\)
\(\cos{90^{o}}=0\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{90^{o}}=\frac{1}{\cos{90^{o}}}\)
\(\Rightarrow \sec{90^{o}}=\frac{1}{0}\) ➜ \(\because \cos{90^{o}}=0\)
\(\therefore \sec{0^{o}}=\infty\)
\(\sec{90^{o}}=\infty\)
আবার, \(\tan{\theta}=\tan{\angle{ABC}}\)
\(\Rightarrow \tan{90^{o}}=\tan{\angle{ABC}}\)
\(=\frac{AC}{AB}\)
\(=\frac{BC}{0}\) ➜ \(\because AB=0, \ AC=BC\)
\(=\infty\)
\(\therefore \tan{90^{o}}=\infty\)
\(\tan{90^{o}}=\infty\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{90^{o}}=\frac{1}{\tan{90^{o}}}\)
\(\Rightarrow \cot{90^{o}}=\frac{1}{\infty}\) ➜ \(\because \tan{90^{o}}=\infty\)
\(\Rightarrow \cot{90^{o}}=0\) ➜ \(\because \frac{1}{\infty}=\frac{1}{\frac{1}{0}}\)
\(=\frac{1\times 0}{1}\)
\(=\frac{0}{1}\)
\(=0\)
\(\therefore \cot{90^{o}}=0\)
\(\cot{90^{o}}=0\)
( প্রমাণিত )
ধরি,
\(\triangle{ABC}\) -এ \(\angle{BAC}=90^{o}\) এবং \(\angle{ABC}=\theta\)।
\(\theta\) এর মাণ ক্রমশ বড় হয়ে \(\theta=90^{o}\) হবে, যদি \(B\) বিন্দুটি ক্রমশ \(A\) এর দিকে অগ্রসর হয়ে এর উপর সমপতিত হয়।
সে ক্ষেত্রে \(AB=0\) এবং \(AC=BC\) হবে।
এখন, \(\triangle{ABC}\) হতে, (সমকোণী)।
\(\sin{\theta}=\sin{\angle{ABC}}\)
\(\Rightarrow \sin{90^{o}}=\sin{\angle{ABC}}\)
\(=\frac{AC}{BC}\)
\(=\frac{BC}{BC}\) ➜ \(\because AC=BC\)
\(=1\)
\(\therefore \sin{90^{o}}=1\)
\(\sin{90^{o}}=1\)
আমরা জানি, \( cosec \ {\theta}=\frac{1}{\sin{\theta}}\)
\(\Rightarrow cosec \ {90^{o}}=\frac{1}{\sin{90^{o}}}\)
\(\Rightarrow cosec \ {90^{o}}=\frac{1}{1}\) ➜ \(\because \sin{90^{o}}=1\)
\(\therefore cosec \ {90^{o}}=1\)
\(cosec \ {90^{o}}=1\)
আবার, \(\cos{\theta}=\cos{\angle{ABC}}\)
\(\Rightarrow \cos{90^{o}}=\cos{\angle{ABC}}\)
\(=\frac{AB}{BC}\)
\(=\frac{0}{AC}\) ➜ \(\because AB=0 , \ BC=AC\)
\(=0\)
\(\therefore \cos{90^{o}}=0\)
\(\cos{90^{o}}=0\)
আমরা জানি, \( \sec{\theta}=\frac{1}{\cos{\theta}}\)
\(\Rightarrow \sec{90^{o}}=\frac{1}{\cos{90^{o}}}\)
\(\Rightarrow \sec{90^{o}}=\frac{1}{0}\) ➜ \(\because \cos{90^{o}}=0\)
\(\therefore \sec{0^{o}}=\infty\)
\(\sec{90^{o}}=\infty\)
আবার, \(\tan{\theta}=\tan{\angle{ABC}}\)
\(\Rightarrow \tan{90^{o}}=\tan{\angle{ABC}}\)
\(=\frac{AC}{AB}\)
\(=\frac{BC}{0}\) ➜ \(\because AB=0, \ AC=BC\)
\(=\infty\)
\(\therefore \tan{90^{o}}=\infty\)
\(\tan{90^{o}}=\infty\)
আমরা জানি, \( \cot{\theta}=\frac{1}{\tan{\theta}}\)
\(\Rightarrow \cot{90^{o}}=\frac{1}{\tan{90^{o}}}\)
\(\Rightarrow \cot{90^{o}}=\frac{1}{\infty}\) ➜ \(\because \tan{90^{o}}=\infty\)
\(\Rightarrow \cot{90^{o}}=0\) ➜ \(\because \frac{1}{\infty}=\frac{1}{\frac{1}{0}}\)
\(=\frac{1\times 0}{1}\)
\(=\frac{0}{1}\)
\(=0\)
\(\therefore \cot{90^{o}}=0\)
\(\cot{90^{o}}=0\)
( প্রমাণিত )
\(180^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of \(180^{o}\) angles
\(\sin{180^{o}}=0\) \(\cos{180^{o}}=-1\) \(\tan{180^{o}}=0\)
\(cosec \ {180^{o}}=\infty\) \(\sec{180^{o}}=-1\) \(\cot{180^{o}}=\infty\)
\(cosec \ {180^{o}}=\infty\) \(\sec{180^{o}}=-1\) \(\cot{180^{o}}=\infty\)
প্রমাণঃ
ধরি,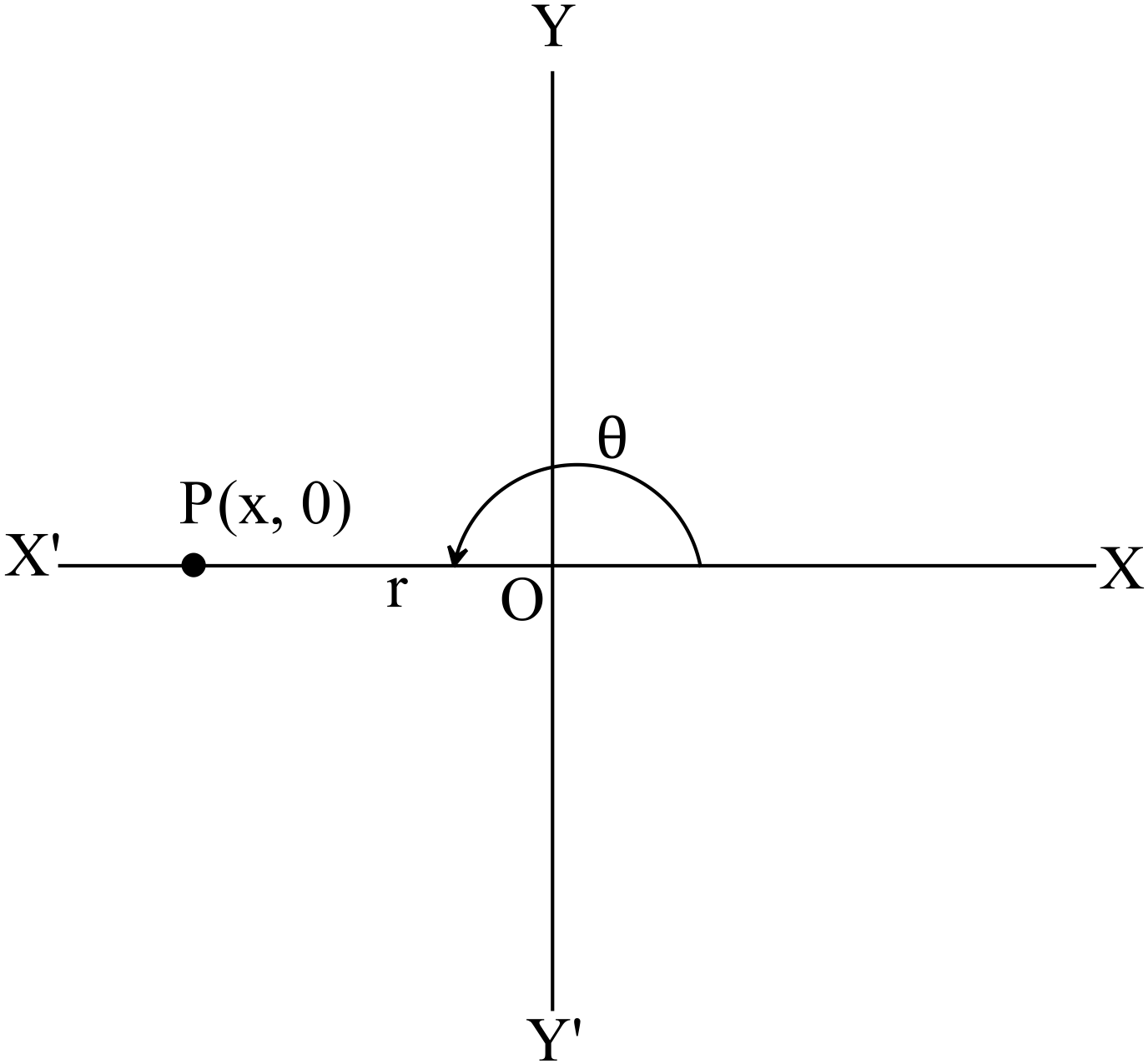
\(P(x,y)\) বিন্দুটি \(x\) অক্ষের ঋণাত্মক অংশের উপর অবস্থান করে।
ফলে, \(y=0, \ \theta=180^{o}\)
এবং \(r=-x\) ➜ \(\because x<0\)
\(\sin{180^{o}}=\frac{y}{r}\)। ➜
\(\because \sin{\theta}=\frac{y}{r}\)
\(=\frac{0}{r}\)। ➜ \(\because y=0\)
\(=0\)।
\(\therefore \sin{180^{o}}=0\)।
\(\sin{180^{o}}=0\)
এবং \(cosec \ {180^{o}}=\frac{r}{y}\)। ➜
\(\because cosec \ {\theta}=\frac{r}{y}\)
\(=\frac{r}{0}\)। ➜ \(\because y=0\)
\(=\infty\)।
\(\therefore cosec \ {180^{o}}=\infty\)।
\(cosec \ {180^{o}}=\infty\)
আবার, \(\cos{180^{o}}=\frac{x}{r}\)। ➜
\(\because \cos{\theta}=\frac{x}{r}\)
\(=\frac{x}{-x}\)। ➜ \(\because r=-x\)
\(=-1\)।
\(\therefore \cos{180^{o}}=-1\)।
\(\cos{180^{o}}=-1\)
এবং \(\sec{180^{o}}=\frac{r}{x}\)। ➜
\(\because \sec{\theta}=\frac{r}{x}\)
\(=\frac{-x}{x}\)। ➜ \(\because r=-x\)
\(=-1\)।
\(\therefore \sec{180^{o}}=-1\)।
\(\sec{180^{o}}=-1\)
আবার, \(\tan{180^{o}}=\frac{y}{x}\)। ➜
\(\because \tan{\theta}=\frac{y}{x}\)
\(=\frac{0}{x}\)। ➜ \(\because y=0\)
\(=0\)।
\(\therefore \tan{180^{o}}=0\)।
\(\tan{180^{o}}=0\)
এবং \(\cot{180^{o}}=\frac{x}{y}\)। ➜
\(\because \cot{\theta}=\frac{x}{y}\)
\(=\frac{x}{0}\)। ➜ \(\because y=0\)
\(=\infty\)।
\(\therefore \cot{180^{o}}=\infty\)।
\(\cot{180^{o}}=\infty\)
( প্রমাণিত )
ধরি,
\(P(x,y)\) বিন্দুটি \(x\) অক্ষের ঋণাত্মক অংশের উপর অবস্থান করে।
ফলে, \(y=0, \ \theta=180^{o}\)
এবং \(r=-x\) ➜ \(\because x<0\)
\(\sin{180^{o}}=\frac{y}{r}\)। ➜
\(\because \sin{\theta}=\frac{y}{r}\)\(=\frac{0}{r}\)। ➜ \(\because y=0\)
\(=0\)।
\(\therefore \sin{180^{o}}=0\)।
\(\sin{180^{o}}=0\)
এবং \(cosec \ {180^{o}}=\frac{r}{y}\)। ➜
\(\because cosec \ {\theta}=\frac{r}{y}\)\(=\frac{r}{0}\)। ➜ \(\because y=0\)
\(=\infty\)।
\(\therefore cosec \ {180^{o}}=\infty\)।
\(cosec \ {180^{o}}=\infty\)
আবার, \(\cos{180^{o}}=\frac{x}{r}\)। ➜
\(\because \cos{\theta}=\frac{x}{r}\)\(=\frac{x}{-x}\)। ➜ \(\because r=-x\)
\(=-1\)।
\(\therefore \cos{180^{o}}=-1\)।
\(\cos{180^{o}}=-1\)
এবং \(\sec{180^{o}}=\frac{r}{x}\)। ➜
\(\because \sec{\theta}=\frac{r}{x}\)\(=\frac{-x}{x}\)। ➜ \(\because r=-x\)
\(=-1\)।
\(\therefore \sec{180^{o}}=-1\)।
\(\sec{180^{o}}=-1\)
আবার, \(\tan{180^{o}}=\frac{y}{x}\)। ➜
\(\because \tan{\theta}=\frac{y}{x}\)\(=\frac{0}{x}\)। ➜ \(\because y=0\)
\(=0\)।
\(\therefore \tan{180^{o}}=0\)।
\(\tan{180^{o}}=0\)
এবং \(\cot{180^{o}}=\frac{x}{y}\)। ➜
\(\because \cot{\theta}=\frac{x}{y}\)\(=\frac{x}{0}\)। ➜ \(\because y=0\)
\(=\infty\)।
\(\therefore \cot{180^{o}}=\infty\)।
\(\cot{180^{o}}=\infty\)
( প্রমাণিত )
\(270^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of \(270^{o}\) angles
\(\sin{270^{o}}=-1\) \(\cos{270^{o}}=0\) \(\tan{270^{o}}=\infty\)
\(cosec \ {270^{o}}=-1\) \(\sec{270^{o}}=\infty\) \(\cot{270^{o}}=0\)
\(cosec \ {270^{o}}=-1\) \(\sec{270^{o}}=\infty\) \(\cot{270^{o}}=0\)
প্রমাণঃ
ধরি,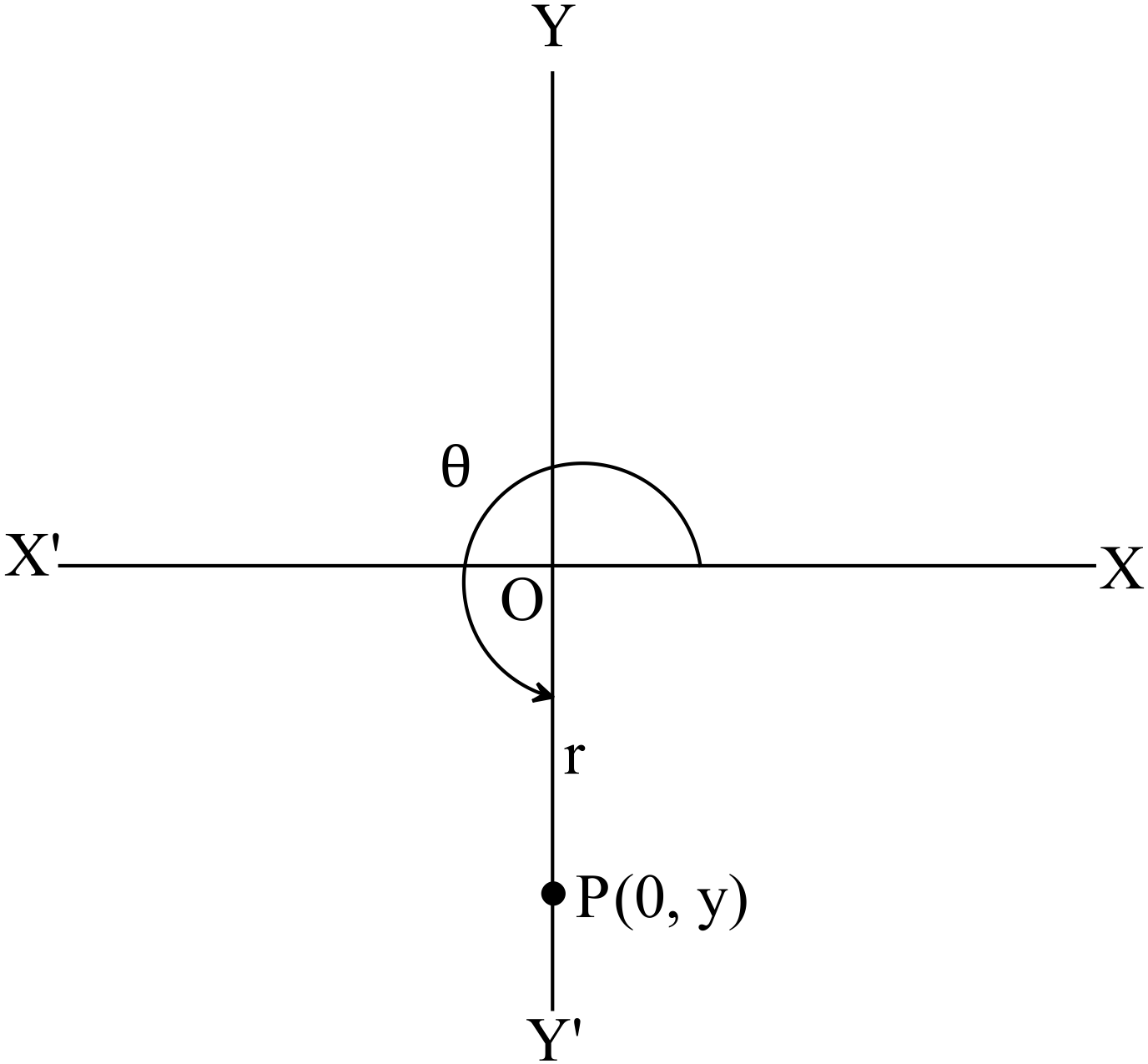
\(P(x,y)\) বিন্দুটি \(y\) অক্ষের ঋণাত্মক অংশের উপর অবস্থান করে।
ফলে, \(x=0, \ \theta=270^{o}\)
এবং \(r=-y\) ➜ \(\because y<0\)
\(\sin{270^{o}}=\frac{y}{r}\)। ➜
\(\because \sin{\theta}=\frac{y}{r}\)
\(=\frac{y}{-y}\)। ➜ \(\because r=-y\)
\(=-1\)।
\(\therefore \sin{270^{o}}=-1\)।
\(\sin{270^{o}}=-1\)
এবং \(cosec \ {270^{o}}=\frac{r}{y}\)। ➜
\(\because cosec \ {\theta}=\frac{r}{y}\)
\(=\frac{-y}{y}\)। ➜ \(\because r=-y\)
\(=-1\)।
\(\therefore cosec \ {270^{o}}=-1\)।
\(cosec \ {270^{o}}=-1\)
আবার, \(\cos{270^{o}}=\frac{x}{r}\)। ➜
\(\because \cos{\theta}=\frac{x}{r}\)
\(=\frac{0}{r}\)। ➜ \(\because x=0\)
\(=0\)।
\(\therefore \cos{270^{o}}=0\)।
\(\cos{270^{o}}=0\)
এবং \(\sec{270^{o}}=\frac{r}{x}\)। ➜
\(\because \sec{\theta}=\frac{r}{x}\)
\(=\frac{r}{0}\)। ➜ \(\because x=0\)
\(=\infty\)।
\(\therefore \sec{270^{o}}=\infty\)।
\(\sec{270^{o}}=\infty\)
আবার, \(\tan{270^{o}}=\frac{y}{x}\)। ➜
\(\because \tan{\theta}=\frac{y}{x}\)
\(=\frac{y}{0}\)। ➜ \(\because x=0\)
\(=\infty\)।
\(\therefore \tan{270^{o}}=\infty\)।
\(\tan{270^{o}}=\infty\)
এবং \(\cot{270^{o}}=\frac{x}{y}\)। ➜
\(\because \cot{\theta}=\frac{x}{y}\)
\(=\frac{0}{y}\)। ➜ \(\because x=0\)
\(=0\)।
\(\therefore \cot{270^{o}}=0\)।
\(\cot{270^{o}}=0\)
( প্রমাণিত )
ধরি,
\(P(x,y)\) বিন্দুটি \(y\) অক্ষের ঋণাত্মক অংশের উপর অবস্থান করে।
ফলে, \(x=0, \ \theta=270^{o}\)
এবং \(r=-y\) ➜ \(\because y<0\)
\(\sin{270^{o}}=\frac{y}{r}\)। ➜
\(\because \sin{\theta}=\frac{y}{r}\)\(=\frac{y}{-y}\)। ➜ \(\because r=-y\)
\(=-1\)।
\(\therefore \sin{270^{o}}=-1\)।
\(\sin{270^{o}}=-1\)
এবং \(cosec \ {270^{o}}=\frac{r}{y}\)। ➜
\(\because cosec \ {\theta}=\frac{r}{y}\)\(=\frac{-y}{y}\)। ➜ \(\because r=-y\)
\(=-1\)।
\(\therefore cosec \ {270^{o}}=-1\)।
\(cosec \ {270^{o}}=-1\)
আবার, \(\cos{270^{o}}=\frac{x}{r}\)। ➜
\(\because \cos{\theta}=\frac{x}{r}\)\(=\frac{0}{r}\)। ➜ \(\because x=0\)
\(=0\)।
\(\therefore \cos{270^{o}}=0\)।
\(\cos{270^{o}}=0\)
এবং \(\sec{270^{o}}=\frac{r}{x}\)। ➜
\(\because \sec{\theta}=\frac{r}{x}\)\(=\frac{r}{0}\)। ➜ \(\because x=0\)
\(=\infty\)।
\(\therefore \sec{270^{o}}=\infty\)।
\(\sec{270^{o}}=\infty\)
আবার, \(\tan{270^{o}}=\frac{y}{x}\)। ➜
\(\because \tan{\theta}=\frac{y}{x}\)\(=\frac{y}{0}\)। ➜ \(\because x=0\)
\(=\infty\)।
\(\therefore \tan{270^{o}}=\infty\)।
\(\tan{270^{o}}=\infty\)
এবং \(\cot{270^{o}}=\frac{x}{y}\)। ➜
\(\because \cot{\theta}=\frac{x}{y}\)\(=\frac{0}{y}\)। ➜ \(\because x=0\)
\(=0\)।
\(\therefore \cot{270^{o}}=0\)।
\(\cot{270^{o}}=0\)
( প্রমাণিত )
\(360^{o}\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric ratio of \(360^{o}\) angles
\(\sin{360^{o}}=0\) \(\cos{360^{o}}=1\) \(\tan{360^{o}}=0\)
\(cosec \ {360^{o}}=\infty\) \(\sec{180^{o}}=1\) \(\cot{360^{o}}=\infty\)
\(cosec \ {360^{o}}=\infty\) \(\sec{180^{o}}=1\) \(\cot{360^{o}}=\infty\)
প্রমাণঃ
ধরি,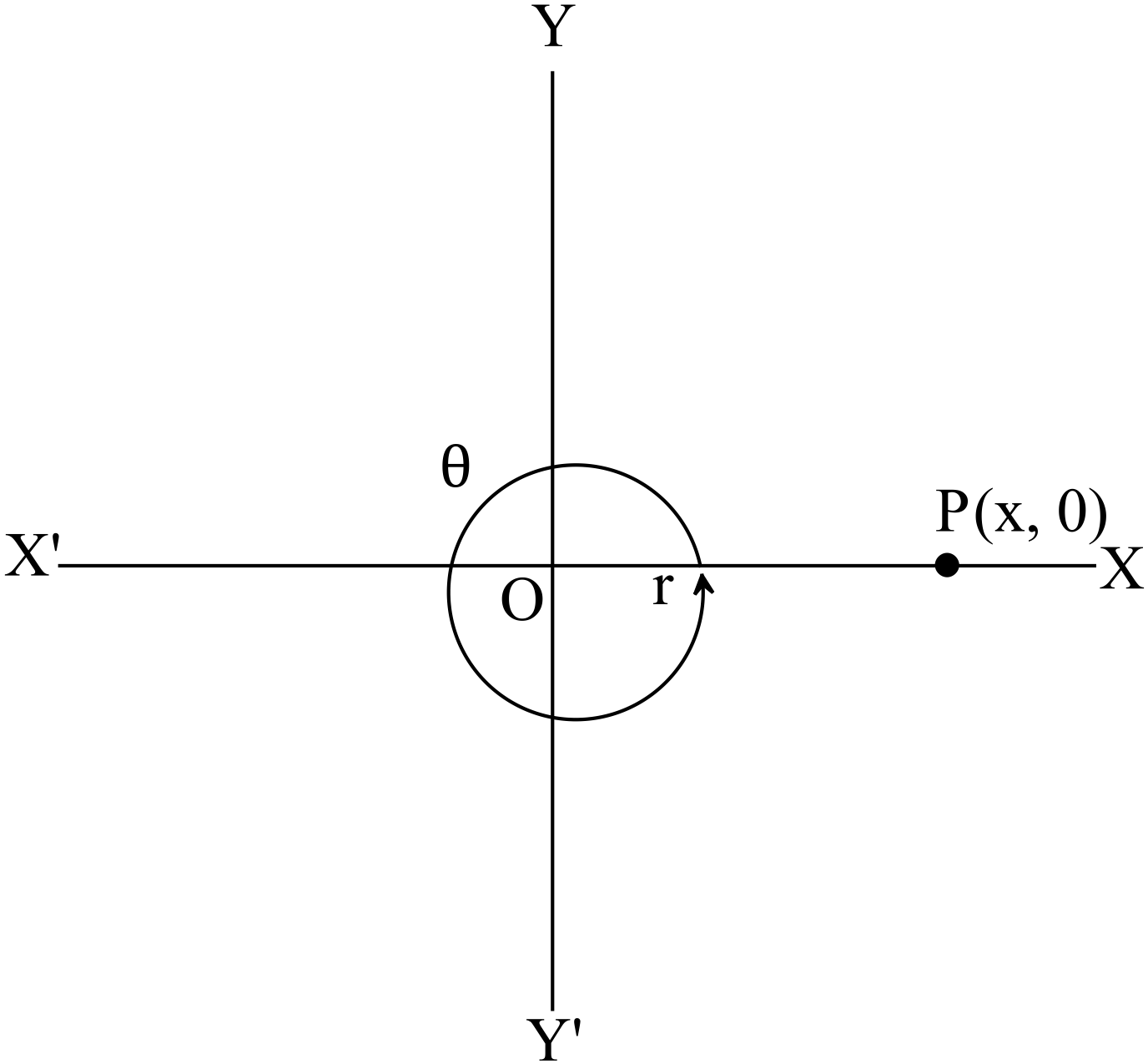
\(OP,\) কোণ উৎপন্নকারী রেখাটি ঘড়ির কাঁটা ঘূর্ণনের বিপরীতক্রমে একবার আবর্তন করে।
অর্থাৎ \(P(x,y)\) বিন্দুটি \(x\) অক্ষের ধণাত্মক অংশের উপর অবস্থান করে।
ফলে, \(y=0, \ \theta=360^{o}\)
এবং \(r=x\) ➜ \(\because x>0\)
\(\sin{360^{o}}=\frac{y}{r}\)। ➜
\(\because \sin{\theta}=\frac{y}{r}\)
\(=\frac{0}{r}\)। ➜ \(\because y=0\)
\(=0\)।
\(\therefore \sin{360^{o}}=0\)।
\(\sin{360^{o}}=0\)
এবং \(cosec \ {360^{o}}=\frac{r}{y}\)। ➜
\(\because cosec \ {\theta}=\frac{r}{y}\)
\(=\frac{r}{0}\)। ➜ \(\because y=0\)
\(=\infty\)।
\(\therefore cosec \ {360^{o}}=\infty\)।
\(cosec \ {360^{o}}=\infty\)
আবার, \(\cos{360^{o}}=\frac{x}{r}\)। ➜
\(\because \cos{\theta}=\frac{x}{r}\)
\(=\frac{x}{x}\)। ➜ \(\because r=x\)
\(=1\)।
\(\therefore \cos{360^{o}}=1\)।
\(\cos{360^{o}}=1\)
এবং \(\sec{360^{o}}=\frac{r}{x}\)। ➜
\(\because \sec{\theta}=\frac{r}{x}\)
\(=\frac{x}{x}\)। ➜ \(\because r=x\)
\(=1\)।
\(\therefore \sec{360^{o}}=1\)।
\(\sec{360^{o}}=1\)
আবার, \(\tan{360^{o}}=\frac{y}{x}\)। ➜
\(\because \tan{\theta}=\frac{y}{x}\)
\(=\frac{0}{x}\)। ➜ \(\because y=0\)
\(=0\)।
\(\therefore \tan{360^{o}}=0\)।
\(\tan{360^{o}}=0\)
এবং \(\cot{360^{o}}=\frac{x}{y}\)। ➜
\(\because \cot{\theta}=\frac{x}{y}\)
\(=\frac{x}{0}\)। ➜ \(\because y=0\)
\(=\infty\)।
\(\therefore \cot{360^{o}}=\infty\)।
\(\cot{360^{o}}=\infty\)
( প্রমাণিত )
ধরি,
\(OP,\) কোণ উৎপন্নকারী রেখাটি ঘড়ির কাঁটা ঘূর্ণনের বিপরীতক্রমে একবার আবর্তন করে।
অর্থাৎ \(P(x,y)\) বিন্দুটি \(x\) অক্ষের ধণাত্মক অংশের উপর অবস্থান করে।
ফলে, \(y=0, \ \theta=360^{o}\)
এবং \(r=x\) ➜ \(\because x>0\)
\(\sin{360^{o}}=\frac{y}{r}\)। ➜
\(\because \sin{\theta}=\frac{y}{r}\)\(=\frac{0}{r}\)। ➜ \(\because y=0\)
\(=0\)।
\(\therefore \sin{360^{o}}=0\)।
\(\sin{360^{o}}=0\)
এবং \(cosec \ {360^{o}}=\frac{r}{y}\)। ➜
\(\because cosec \ {\theta}=\frac{r}{y}\)\(=\frac{r}{0}\)। ➜ \(\because y=0\)
\(=\infty\)।
\(\therefore cosec \ {360^{o}}=\infty\)।
\(cosec \ {360^{o}}=\infty\)
আবার, \(\cos{360^{o}}=\frac{x}{r}\)। ➜
\(\because \cos{\theta}=\frac{x}{r}\)\(=\frac{x}{x}\)। ➜ \(\because r=x\)
\(=1\)।
\(\therefore \cos{360^{o}}=1\)।
\(\cos{360^{o}}=1\)
এবং \(\sec{360^{o}}=\frac{r}{x}\)। ➜
\(\because \sec{\theta}=\frac{r}{x}\)\(=\frac{x}{x}\)। ➜ \(\because r=x\)
\(=1\)।
\(\therefore \sec{360^{o}}=1\)।
\(\sec{360^{o}}=1\)
আবার, \(\tan{360^{o}}=\frac{y}{x}\)। ➜
\(\because \tan{\theta}=\frac{y}{x}\)\(=\frac{0}{x}\)। ➜ \(\because y=0\)
\(=0\)।
\(\therefore \tan{360^{o}}=0\)।
\(\tan{360^{o}}=0\)
এবং \(\cot{360^{o}}=\frac{x}{y}\)। ➜
\(\because \cot{\theta}=\frac{x}{y}\)\(=\frac{x}{0}\)। ➜ \(\because y=0\)
\(=\infty\)।
\(\therefore \cot{360^{o}}=\infty\)।
\(\cot{360^{o}}=\infty\)
( প্রমাণিত )
\(0^{o}, \ 30^{o}, \ 45^{o}, \ 60^{o}, \ 90^{o}\) কোণের ত্রিকোণমিতিক অনুপাতের তালিকা
List of trigonometric ratios of \(0^{o}, \ 30^{o}, \ 45^{o}, \ 60^{o}, \ 90^{o}\) angles
\(\sin{0^{o}}=0\) \(\sin{30^{o}}=\frac{1}{2}\) \(\sin{45^{o}}=\frac{1}{\sqrt{2}}\) \(\sin{60^{o}}=\frac{\sqrt{3}}{2}\) \(\sin{90^{o}}=1\) \(\sin{180^{o}}=0\) \(\sin{270^{o}}=-1\) \(\sin{360^{o}}=0\)
\(\cos{0^{o}}=1\) \(\cos{30^{o}}=\frac{\sqrt{3}}{2}\) \(\cos{45^{o}}=\frac{1}{\sqrt{2}}\) \(\cos{60^{o}}=\frac{1}{2}\) \(\cos{90^{o}}=0\) \(\cos{180^{o}}=-1\) \(\cos{270^{o}}=0\) \(\cos{360^{o}}=1\)
\(\tan{0^{o}}=0\) \(\tan{30^{o}}=\frac{1}{\sqrt{3}}\) \(\tan{45^{o}}=1\) \(\tan{60^{o}}=\sqrt{3}\) \(\tan{90^{o}}=\infty\) \(\tan{180^{o}}=0\) \(\tan{270^{o}}=\infty\) \(\tan{360^{o}}=0\)
\(cosec \ {0^{o}}=\infty\) \(cosec \ {30^{o}}=2\) \(cosec \ {45^{o}}=\sqrt{2}\) \(cosec \ {60^{o}}=\frac{2}{\sqrt{3}}\) \(cosec \ {90^{o}}=1\) \(cosec \ {180^{o}}=\infty\) \(cosec \ {270^{o}}=-1\) \(cosec \ {360^{o}}=\infty\)
\(\sec{0^{o}}=1\) \(\sec{30^{o}}=\frac{2}{\sqrt{3}}\) \(\sec{45^{o}}=\sqrt{2}\) \(\sec{60^{o}}=2\) \(\sec{90^{o}}=\infty\) \(\sec{180^{o}}=-1\) \(\sec{270^{o}}=\infty\) \(\sec{360^{o}}=1\)
\(\cot{0^{o}}=\infty\) \(\cot{30^{o}}=\sqrt{3}\) \(\cot{45^{o}}=1\) \(\cot{60^{o}}=\frac{1}{\sqrt{3}}\) \(\cot{90^{o}}=0\) \(\cot{180^{o}}=\infty\) \(\cot{270^{o}}=0\) \(\cot{360^{o}}=\infty\)
\(\cos{0^{o}}=1\) \(\cos{30^{o}}=\frac{\sqrt{3}}{2}\) \(\cos{45^{o}}=\frac{1}{\sqrt{2}}\) \(\cos{60^{o}}=\frac{1}{2}\) \(\cos{90^{o}}=0\) \(\cos{180^{o}}=-1\) \(\cos{270^{o}}=0\) \(\cos{360^{o}}=1\)
\(\tan{0^{o}}=0\) \(\tan{30^{o}}=\frac{1}{\sqrt{3}}\) \(\tan{45^{o}}=1\) \(\tan{60^{o}}=\sqrt{3}\) \(\tan{90^{o}}=\infty\) \(\tan{180^{o}}=0\) \(\tan{270^{o}}=\infty\) \(\tan{360^{o}}=0\)
\(cosec \ {0^{o}}=\infty\) \(cosec \ {30^{o}}=2\) \(cosec \ {45^{o}}=\sqrt{2}\) \(cosec \ {60^{o}}=\frac{2}{\sqrt{3}}\) \(cosec \ {90^{o}}=1\) \(cosec \ {180^{o}}=\infty\) \(cosec \ {270^{o}}=-1\) \(cosec \ {360^{o}}=\infty\)
\(\sec{0^{o}}=1\) \(\sec{30^{o}}=\frac{2}{\sqrt{3}}\) \(\sec{45^{o}}=\sqrt{2}\) \(\sec{60^{o}}=2\) \(\sec{90^{o}}=\infty\) \(\sec{180^{o}}=-1\) \(\sec{270^{o}}=\infty\) \(\sec{360^{o}}=1\)
\(\cot{0^{o}}=\infty\) \(\cot{30^{o}}=\sqrt{3}\) \(\cot{45^{o}}=1\) \(\cot{60^{o}}=\frac{1}{\sqrt{3}}\) \(\cot{90^{o}}=0\) \(\cot{180^{o}}=\infty\) \(\cot{270^{o}}=0\) \(\cot{360^{o}}=\infty\)
ত্রিকোণমিতিক অনুপাত সংক্রান্ত অভেদাবলি
Differences regarding trigonometric ratios
\(\sin^2{\theta}+\cos^2{\theta}=1\) \(1+\tan^2{\theta}=\sec^2{\theta}\) \(1+\cot^2{\theta}=cosec^2{\theta}\)
\(\sin^2{\theta}=1-\cos^2{\theta}\) \(\tan^2{\theta}=\sec^2{\theta}-1\) \(\cot^2{\theta}=cosec^2{\theta}-1\)
\(\sin{\theta}=\sqrt{1-\cos^2{\theta}}\) \(\tan{\theta}=\sqrt{\sec^2{\theta}-1}\) \(\cot{\theta}=\sqrt{cosec^2{\theta}-1}\)
\(\cos^2{\theta}=1-\sin^2{\theta}\) \(\sec^2{\theta}-\tan^2{\theta}=1\) \(cosec^2{\theta}-\cot^2{\theta}=1\)
\(\cos{\theta}=\sqrt{1-\sin^2{\theta}}\) \(\sec{\theta}=\sqrt{1+\tan^2{\theta}}\) \(cosec{\theta}=\sqrt{1+\cot^2{\theta}}\)
\(\sin^2{\theta}=1-\cos^2{\theta}\) \(\tan^2{\theta}=\sec^2{\theta}-1\) \(\cot^2{\theta}=cosec^2{\theta}-1\)
\(\sin{\theta}=\sqrt{1-\cos^2{\theta}}\) \(\tan{\theta}=\sqrt{\sec^2{\theta}-1}\) \(\cot{\theta}=\sqrt{cosec^2{\theta}-1}\)
\(\cos^2{\theta}=1-\sin^2{\theta}\) \(\sec^2{\theta}-\tan^2{\theta}=1\) \(cosec^2{\theta}-\cot^2{\theta}=1\)
\(\cos{\theta}=\sqrt{1-\sin^2{\theta}}\) \(\sec{\theta}=\sqrt{1+\tan^2{\theta}}\) \(cosec{\theta}=\sqrt{1+\cot^2{\theta}}\)
প্রমাণঃ
চিত্র হতে,
\(P(x,y)\)
\(\therefore OM=x, \ PM=y, \ OP=r\)
\(\angle{PMO}=90^{0}\) অর্থাৎ এক সমকোণ।
এবং \(\angle{POM}=\theta\)।
\(\triangle{POM}\) সমকোণী।
\(\therefore OM^2+PM^2=OP^2\)
\(\Rightarrow x^2+y^2=r^2 .....(1)\)
এখন, \(\sin{\angle{POM}}=\frac{PM}{OP}\)
\(\Rightarrow \sin{\theta}=\frac{y}{r}\)
\(\therefore r\sin{\theta}=y .....(2)\)
আবার, \(\cos{\angle{POM}}=\frac{OM}{OP}\)
\(\Rightarrow \cos{\theta}=\frac{x}{r}\)
\(\therefore r\cos{\theta}=x .....(3)\)
\((2)\) ও \((3)\) বর্গ করে যোগ করি।
\(r^2\sin^2{\theta}+r^2\cos^2{\theta}=y^2+x^2\)
\(\Rightarrow r^2(\sin^2{\theta}+\cos^2{\theta})=x^2+y^2\)
\(\Rightarrow r^2(\sin^2{\theta}+\cos^2{\theta})=r^2\) ➜ \((1)\) হতে,
\(\because x^2+y^2=r^2 \)
\(\Rightarrow \sin^2{\theta}+\cos^2{\theta}=\frac{r^2}{r^2}\)
\(\therefore \sin^2{\theta}+\cos^2{\theta}=1\)
\(\sin^2{\theta}+\cos^2{\theta}=1\)
\(\sin^2{\theta}=1-\cos^2{\theta}\)
\(\sin{\theta}=\sqrt{1-\cos^2{\theta}}\)
\(\cos^2{\theta}=1-\sin^2{\theta}\)
\(\cos{\theta}=\sqrt{1-\sin^2{\theta}}\)
আবার, \(\tan{\angle{POM}}=\frac{PM}{OM}\)
\(\Rightarrow \tan{\theta}=\frac{y}{x} .....(4); \ x\ne{0}\)
এবং \(\sec{\angle{POM}}=\frac{OP}{OM}\)
\(\therefore \sec{\theta}=\frac{r}{x} .....(5); \ x\ne{0}\)
\((1)\) নং সমীকরণের উভয় পার্শে \(x^2\) ভাগ করে,
\(\frac{x^2}{x^2}+\frac{y^2}{x^2}=\frac{r^2}{x^2}\)
\(\Rightarrow 1+\left(\frac{y}{x}\right)^2=\left(\frac{r}{x}\right)^2\)
\(\Rightarrow 1+\left(\tan{\theta}\right)^2=\left(\sec{\theta}\right)^2\) ➜ \((4)\) ও \((5)\) হতে,
\(\because \tan{\theta}=\frac{y}{x}\)
এবং \(\sec{\theta}=\frac{r}{x}\)
\(\therefore 1+\tan^2{\theta}=\sec^2{\theta}\)
\(1+\tan^2{\theta}=\sec^2{\theta}\)
\(\tan^2{\theta}=\sec^2{\theta}-1\)
\(\tan{\theta}=\sqrt{\sec^2{\theta}-1}\)
\(\sec^2{\theta}-\tan^2{\theta}=1\)
\(\sec{\theta}=\sqrt{1+\tan^2{\theta}}\)
আবার, \(\cot{\angle{POM}}=\frac{OM}{PM}\)
\(\Rightarrow \cot{\theta}=\frac{x}{y} .....(6); \ y\ne{0}\)
এবং \(cosec \ {\angle{POM}}=\frac{OP}{PM}\)
\(\therefore cosec \ {\theta}=\frac{r}{y} .....(7); \ y\ne{0}\)
\((1)\) নং সমীকরণের উভয় পার্শে \(y^2\) ভাগ করে,
\(\frac{x^2}{y^2}+\frac{y^2}{y^2}=\frac{r^2}{y^2}\)
\(\Rightarrow \left(\frac{x}{y}\right)^2+1=\left(\frac{r}{y}\right)^2\)
\(\Rightarrow \left(\cot{\theta}\right)^2+1=\left(cosec \ {\theta}\right)^2\) ➜ \((6)\) ও \((7)\) হতে,
\(\because \cot{\theta}=\frac{x}{y}\)
এবং \(cosec \ {\theta}=\frac{r}{y}\)
\(\therefore 1+\cot^2{\theta}=cosec^2{\theta}\)
\(1+\cot^2{\theta}=cosec^2{\theta}\)
\(\cot^2{\theta}=cosec^2{\theta}-1\)
\(\cot{\theta}=\sqrt{cosec^2{\theta}-1}\)
\(cosec^2{\theta}-\cot^2{\theta}=1\)
\(cosec \ {\theta}=\sqrt{1+\cot^2{\theta}}\)
( প্রমাণিত )
চিত্র হতে,
\(P(x,y)\)
\(\therefore OM=x, \ PM=y, \ OP=r\)
\(\angle{PMO}=90^{0}\) অর্থাৎ এক সমকোণ।
এবং \(\angle{POM}=\theta\)।
\(\triangle{POM}\) সমকোণী।
\(\therefore OM^2+PM^2=OP^2\)
\(\Rightarrow x^2+y^2=r^2 .....(1)\)
এখন, \(\sin{\angle{POM}}=\frac{PM}{OP}\)
\(\Rightarrow \sin{\theta}=\frac{y}{r}\)
\(\therefore r\sin{\theta}=y .....(2)\)
আবার, \(\cos{\angle{POM}}=\frac{OM}{OP}\)
\(\Rightarrow \cos{\theta}=\frac{x}{r}\)
\(\therefore r\cos{\theta}=x .....(3)\)
\((2)\) ও \((3)\) বর্গ করে যোগ করি।
\(r^2\sin^2{\theta}+r^2\cos^2{\theta}=y^2+x^2\)
\(\Rightarrow r^2(\sin^2{\theta}+\cos^2{\theta})=x^2+y^2\)
\(\Rightarrow r^2(\sin^2{\theta}+\cos^2{\theta})=r^2\) ➜ \((1)\) হতে,
\(\because x^2+y^2=r^2 \)
\(\Rightarrow \sin^2{\theta}+\cos^2{\theta}=\frac{r^2}{r^2}\)
\(\therefore \sin^2{\theta}+\cos^2{\theta}=1\)
\(\sin^2{\theta}+\cos^2{\theta}=1\)
\(\sin^2{\theta}=1-\cos^2{\theta}\)
\(\sin{\theta}=\sqrt{1-\cos^2{\theta}}\)
\(\cos^2{\theta}=1-\sin^2{\theta}\)
\(\cos{\theta}=\sqrt{1-\sin^2{\theta}}\)
আবার, \(\tan{\angle{POM}}=\frac{PM}{OM}\)
\(\Rightarrow \tan{\theta}=\frac{y}{x} .....(4); \ x\ne{0}\)
এবং \(\sec{\angle{POM}}=\frac{OP}{OM}\)
\(\therefore \sec{\theta}=\frac{r}{x} .....(5); \ x\ne{0}\)
\((1)\) নং সমীকরণের উভয় পার্শে \(x^2\) ভাগ করে,
\(\frac{x^2}{x^2}+\frac{y^2}{x^2}=\frac{r^2}{x^2}\)
\(\Rightarrow 1+\left(\frac{y}{x}\right)^2=\left(\frac{r}{x}\right)^2\)
\(\Rightarrow 1+\left(\tan{\theta}\right)^2=\left(\sec{\theta}\right)^2\) ➜ \((4)\) ও \((5)\) হতে,
\(\because \tan{\theta}=\frac{y}{x}\)
এবং \(\sec{\theta}=\frac{r}{x}\)
\(\therefore 1+\tan^2{\theta}=\sec^2{\theta}\)
\(1+\tan^2{\theta}=\sec^2{\theta}\)
\(\tan^2{\theta}=\sec^2{\theta}-1\)
\(\tan{\theta}=\sqrt{\sec^2{\theta}-1}\)
\(\sec^2{\theta}-\tan^2{\theta}=1\)
\(\sec{\theta}=\sqrt{1+\tan^2{\theta}}\)
আবার, \(\cot{\angle{POM}}=\frac{OM}{PM}\)
\(\Rightarrow \cot{\theta}=\frac{x}{y} .....(6); \ y\ne{0}\)
এবং \(cosec \ {\angle{POM}}=\frac{OP}{PM}\)
\(\therefore cosec \ {\theta}=\frac{r}{y} .....(7); \ y\ne{0}\)
\((1)\) নং সমীকরণের উভয় পার্শে \(y^2\) ভাগ করে,
\(\frac{x^2}{y^2}+\frac{y^2}{y^2}=\frac{r^2}{y^2}\)
\(\Rightarrow \left(\frac{x}{y}\right)^2+1=\left(\frac{r}{y}\right)^2\)
\(\Rightarrow \left(\cot{\theta}\right)^2+1=\left(cosec \ {\theta}\right)^2\) ➜ \((6)\) ও \((7)\) হতে,
\(\because \cot{\theta}=\frac{x}{y}\)
এবং \(cosec \ {\theta}=\frac{r}{y}\)
\(\therefore 1+\cot^2{\theta}=cosec^2{\theta}\)
\(1+\cot^2{\theta}=cosec^2{\theta}\)
\(\cot^2{\theta}=cosec^2{\theta}-1\)
\(\cot{\theta}=\sqrt{cosec^2{\theta}-1}\)
\(cosec^2{\theta}-\cot^2{\theta}=1\)
\(cosec \ {\theta}=\sqrt{1+\cot^2{\theta}}\)
( প্রমাণিত )
ত্রিকোণমিতিক অনুপাতের সীমাবদ্ধতা
Limitations of trigonometric ratios
আমরা জানি, \(\sin^2{\theta}+\cos^2{\theta}=1\)
এখানে, \(\sin^2{\theta}\) এবং \(\cos^2{\theta}\) দুইটিই বাস্তব সংখ্যার বর্গ, অর্থাৎ উভয়েই অঋণাত্মক। আবার, \(\sin^2{\theta}\) এবং \(\cos^2{\theta}\) এর যোগফল \(=1\)
সুতরাং এদের কোনোটির মাণ \(1\) অপেক্ষা বড় হতে পারে না।
অর্থাৎ \(\sin{\theta}\) বা \(\cos{\theta}\) এর মাণ \(1\) অপেক্ষা বড় কিংবা \(-1\) অপেক্ষা ছোট হতে পারে না।
সুতরাং \(\theta\) এর মাণ যাই হোক না কেন \(\sin{\theta}\) এবং \(\cos{\theta}\) এর মাণ সর্বদাই \(-1\) থেকে \(+1\) এর মধ্যে থাবকে।
অর্থাৎ \(-1\leq\sin{\theta}\leq1\) এবং \(-1\leq\cos{\theta}\leq1\)
\(-1\leq\sin{\theta}\leq1\) \(-1\leq\cos{\theta}\leq1\)
যেহেতু \(cosec \ {\theta}=\frac{1}{\sin{\theta}}\) এবং \(\sec{\theta}=\frac{1}{\cos{\theta}}\)
তাই \(cosec \ {\theta}\) এবং \(\sec{\theta}\) এর মাণ \(+1\) অপেক্ষা ছোট কিংবা \(-1\) অপেক্ষা বড় হতে পারে না
অর্থাৎ \(cosec \ {\theta}\) এবং \(\sec{\theta}\) এর মাণ \(-1\) হতে \(+1\) এর মধ্যে হবে না।
সুতরাং \(cosec \ {\theta}\geq 1\) অথবা \(cosec \ {\theta}\leq -1\)
এবং \(\sec{\theta}\geq 1\) অথবা \(\sec{\theta}\leq -1\)
\(cosec \ {\theta}\geq 1\) অথবা \(cosec \ {\theta}\leq -1\) \(\sec{\theta}\geq 1\) অথবা \(\sec{\theta}\leq -1\)
যেমনঃ \(cosec \ {\theta}\) এবং \(\sec{\theta}\) এর মাণ \(\frac{1}{2},\) \(\frac{1}{3},\) \(\frac{1}{4},\) \(-\frac{1}{2},\) \(-\frac{1}{3},\) \(-\frac{1}{4} ...\) ইত্যাদি হতে পারে না।
কিন্তু \(\tan{\theta}\) ও \(\cot{\theta}\) এর মাণের কোনো সীমা নেই। যে কোনো বাস্তব সংখ্যা \(\tan{\theta}\) ও \(\cot{\theta}\) এর মাণ হতে পারে।
তাই \(-\infty<\tan{\theta}<\infty\) এবং \(-\infty<\cot{\theta}<\infty\)
\(-\infty<\tan{\theta}<\infty\) \(-\infty<\cot{\theta}<\infty\)
এখানে, \(\sin^2{\theta}\) এবং \(\cos^2{\theta}\) দুইটিই বাস্তব সংখ্যার বর্গ, অর্থাৎ উভয়েই অঋণাত্মক। আবার, \(\sin^2{\theta}\) এবং \(\cos^2{\theta}\) এর যোগফল \(=1\)
সুতরাং এদের কোনোটির মাণ \(1\) অপেক্ষা বড় হতে পারে না।
অর্থাৎ \(\sin{\theta}\) বা \(\cos{\theta}\) এর মাণ \(1\) অপেক্ষা বড় কিংবা \(-1\) অপেক্ষা ছোট হতে পারে না।
সুতরাং \(\theta\) এর মাণ যাই হোক না কেন \(\sin{\theta}\) এবং \(\cos{\theta}\) এর মাণ সর্বদাই \(-1\) থেকে \(+1\) এর মধ্যে থাবকে।
অর্থাৎ \(-1\leq\sin{\theta}\leq1\) এবং \(-1\leq\cos{\theta}\leq1\)
\(-1\leq\sin{\theta}\leq1\) \(-1\leq\cos{\theta}\leq1\)
যেহেতু \(cosec \ {\theta}=\frac{1}{\sin{\theta}}\) এবং \(\sec{\theta}=\frac{1}{\cos{\theta}}\)
তাই \(cosec \ {\theta}\) এবং \(\sec{\theta}\) এর মাণ \(+1\) অপেক্ষা ছোট কিংবা \(-1\) অপেক্ষা বড় হতে পারে না
অর্থাৎ \(cosec \ {\theta}\) এবং \(\sec{\theta}\) এর মাণ \(-1\) হতে \(+1\) এর মধ্যে হবে না।
সুতরাং \(cosec \ {\theta}\geq 1\) অথবা \(cosec \ {\theta}\leq -1\)
এবং \(\sec{\theta}\geq 1\) অথবা \(\sec{\theta}\leq -1\)
\(cosec \ {\theta}\geq 1\) অথবা \(cosec \ {\theta}\leq -1\) \(\sec{\theta}\geq 1\) অথবা \(\sec{\theta}\leq -1\)
যেমনঃ \(cosec \ {\theta}\) এবং \(\sec{\theta}\) এর মাণ \(\frac{1}{2},\) \(\frac{1}{3},\) \(\frac{1}{4},\) \(-\frac{1}{2},\) \(-\frac{1}{3},\) \(-\frac{1}{4} ...\) ইত্যাদি হতে পারে না।
কিন্তু \(\tan{\theta}\) ও \(\cot{\theta}\) এর মাণের কোনো সীমা নেই। যে কোনো বাস্তব সংখ্যা \(\tan{\theta}\) ও \(\cot{\theta}\) এর মাণ হতে পারে।
তাই \(-\infty<\tan{\theta}<\infty\) এবং \(-\infty<\cot{\theta}<\infty\)
\(-\infty<\tan{\theta}<\infty\) \(-\infty<\cot{\theta}<\infty\)
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000002