এ অধ্যায়ের পাঠ্যসূচী।
- ঐতিহাসিক পটভূমি (Historical Background)
- জটিল সংখ্যা (Complex Numbers)
- জটিল সংখ্যার শ্রেণীবিন্যাস (Classification of Complex numbers)
- জটিল সংখ্যা এবং এর জ্যামিতিক প্রতিরূপ (Complex numbers and their geometric replicas)
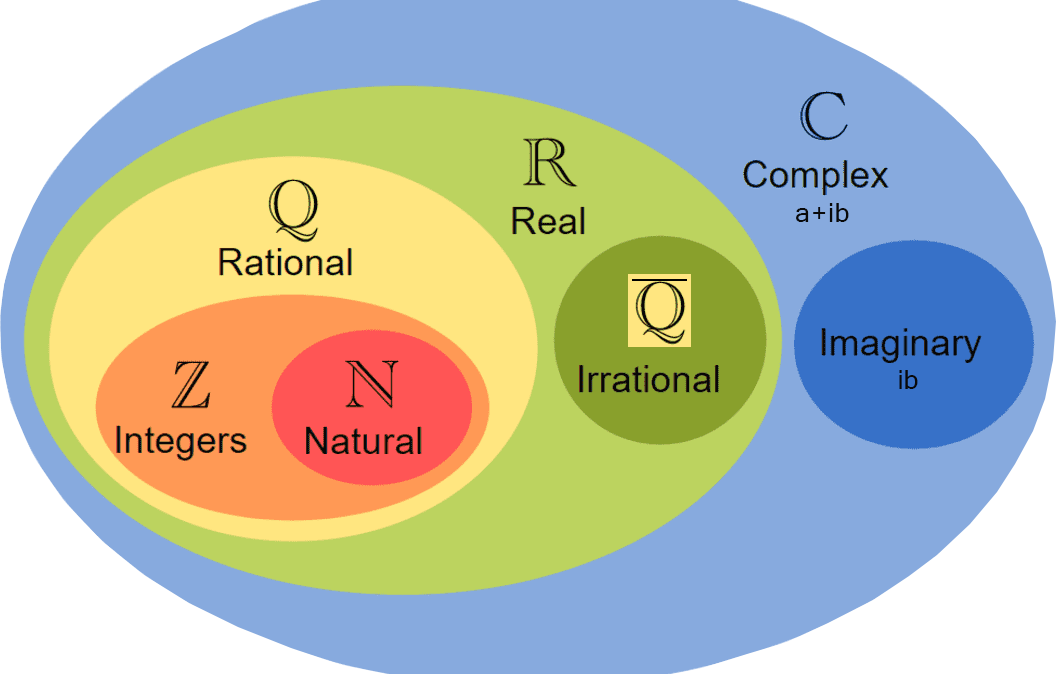
- জটিল সংখ্যার ভেনচিত্র (Venn diagram of complex numbers)
- জটিল সংখ্যার পোলার আকার (Polar size of complex numbers)
- জটিল সংখ্যার ভেক্টর আকার (Vector size of complex numbers)
- জটিল সংখ্যার মডুলাস (পরমমান) এবং আর্গুমেন্ট (নতি) (Modulus of complex numbers and argument)
- চৌকোণের ভিত্তিতে জটিল সংখ্যার আর্গুমেন্ট (নতি) (Arguments of complex numbers in quadrant)
- দুইটি জটিল সংখ্যার মধ্যবর্তী কোণ (Angle between two complex numbers)
- কাল্পনিক একক এবং এর প্রকৃতি (Imaginary unit and its nature)
- জটিল সংখ্যার যোগ এবং বিয়োগ (Addition and Subtraction of complex numbers)
- জটিল সংখ্যার গুণ এবং ভাগ (Multiplication and division of complex numbers)
- দুইটি জটিল সংখ্যার সমতা (Equality of Two complex numbers)
- অনুবন্ধী জটিল সংখ্যা (Conjugate complex numbers)
- জটিল রাশিকে A+iB আকারে প্রকাশ (Express complex numbers in the form of A+iB)
- জটিল সংখ্যার ধর্ম (Characteristics of complex numbers)
- জটিল সংখ্যার যোগ ও বিয়োগের জ্যামিতিক প্রতিরূপ (Geometrical Reprsentation of the Addition and subtraction of complex numbers)
- জটিল সংখ্যার গুণ এবং এর জ্যামিতিক প্রতিরূপ (Multiplication of complex numbers and its geometric counterpart)
- জটিল সংখ্যার ভাগ এবং এর জ্যামিতিক প্রতিরূপ (Division of complex numbers and its geometric counterpart)
- বিশেষ দ্রষ্টব্য (Special note)
- জটিল সংখ্যার বর্গমূল (Square roots of complex numbers)
- একের ঘনমূল (Cube root of one)
- একের জটিল ঘনমূল দুইটির বৈশিষ্ট্য (Properties of Complex Cube Roots of One)
- একের জটিল ঘনমূল এর প্রকৃতি (Nature of the complex cube root of one)
- অধ্যায় \(3\)-এর উদাহরণসমুহ
- অধ্যায় \(3\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.5\)-এর সৃজনশীল প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.6\)-এর ভর্তি পরীক্ষায় আসা প্রশ্নসমূহ
- বহুনির্বাচনী প্রশ্নত্তর
ঐতিহাসিক পটভূমি
Historical Background

জিরোলামো কার্দানো
Gerolamo Cardano
(১৫০১ খ্রিস্টাব্দ-১৫৭৬ খ্রিস্টাব্দ)
ইতালিয়ান গণিতবিদ
Gerolamo Cardano
(১৫০১ খ্রিস্টাব্দ-১৫৭৬ খ্রিস্টাব্দ)
ইতালিয়ান গণিতবিদ
মূলদ ও অমূলদ সংখ্যার সেট মিলে বাস্তব সংখ্যার সেট গঠিত হয়। বাস্তব সংখ্যার সবচেয়ে গুরুত্বপূর্ণ ধর্ম হলো এর বর্গ সবসময় অঋণাত্মক। কিন্তু \(\sqrt{-1}, \ \sqrt{-4}, \ \sqrt{-5}, \ .....\) প্রভৃতি এর বর্গ যথাক্রমে \(-1, \ -4, \ -5, \ .....\) প্রভৃতি যা ঋণাত্মক।
এ ধরনের সংখ্যার উদ্ভব হয়েছে \(x^2+1=0, \ x^2+4=0, \ x^2+5=0, \ ....\) প্রভৃতি সমীকরণ থেকে। এ জাতীয় সমীকরণ সমাধানের চেষ্টার ক্ষেত্রে যে সকল সংখ্যা যা বাস্তব সংখ্যা থেকে ভিন্ন তাই কাল্পনিক সংখ্যা।
জটিল সংখ্যা হচ্ছে বাস্তব সংখ্যার বর্ধিত রূপ। যা \(i, \ (i=\sqrt{-1})\) দ্বারা সূচিত একটি কাল্পনিক এককের সংযুক্তির মাধ্যমে গঠিত। খৃষ্টপূর্ব \(50\) অব্দে গ্রিক গণিতবিদ ও প্রকৌশলী আলেকজান্দ্রিয়ার হেরন জটিল সংখ্যার ধারণা দেন। জটিল সংখ্যার যোগ, বিয়োগ, গুণ এবং ভাগ সর্বপ্রথম প্রবর্তন করেন ইতালীয় গণিতবিদ Rafael Bombelli (1526-1572)। তিনি জটিল সংখ্যার আদর্শরূপ \(a+ib\) ব্যবহার করেন। রেনে দেকার্তে এবং ১৭৭৭ সালে অয়লার \(\sqrt{-1}\) এর জন্য \(i\) প্রতীক আবিষ্কার করেন। ১৮০৬ সালে রবার্ট আরগাঁ জটিল সংখ্যাকে সমতলে চিত্রের সাহায্যে উপস্থাপন করেন যা Argand Diagram নামে পরিচিত। প্রকৌশলী ও বিজ্ঞানীরা বীমের বৈশিষ্ট্য ও অনুনাদ বিশ্লেষণে \(i\) ব্যবহার করেন। প্রবাহী পদার্থ, পাইপের ভিতরের পানির প্রবাহ, ইলেক্ট্রিক সার্কিট, রেডিও তরঙ্গ প্রেরন ইত্যাদি ক্ষেত্রে জটিল সংখ্যা বিভিন্ন অভিনব সমস্যার সমাধান করে। সবচেয়ে মজার ব্যাপার হলো জটিল সংখ্যা আবিষ্কার না হলে আমরা মোবাই ফোনে কথা বলা কিংবা রেডিও শুনতে পারতাম না।
জটিল সংখ্যা হচ্ছে বাস্তব সংখ্যার বর্ধিত রূপ। যা \(i, \ (i=\sqrt{-1})\) দ্বারা সূচিত একটি কাল্পনিক এককের সংযুক্তির মাধ্যমে গঠিত। খৃষ্টপূর্ব \(50\) অব্দে গ্রিক গণিতবিদ ও প্রকৌশলী আলেকজান্দ্রিয়ার হেরন জটিল সংখ্যার ধারণা দেন। জটিল সংখ্যার যোগ, বিয়োগ, গুণ এবং ভাগ সর্বপ্রথম প্রবর্তন করেন ইতালীয় গণিতবিদ Rafael Bombelli (1526-1572)। তিনি জটিল সংখ্যার আদর্শরূপ \(a+ib\) ব্যবহার করেন। রেনে দেকার্তে এবং ১৭৭৭ সালে অয়লার \(\sqrt{-1}\) এর জন্য \(i\) প্রতীক আবিষ্কার করেন। ১৮০৬ সালে রবার্ট আরগাঁ জটিল সংখ্যাকে সমতলে চিত্রের সাহায্যে উপস্থাপন করেন যা Argand Diagram নামে পরিচিত। প্রকৌশলী ও বিজ্ঞানীরা বীমের বৈশিষ্ট্য ও অনুনাদ বিশ্লেষণে \(i\) ব্যবহার করেন। প্রবাহী পদার্থ, পাইপের ভিতরের পানির প্রবাহ, ইলেক্ট্রিক সার্কিট, রেডিও তরঙ্গ প্রেরন ইত্যাদি ক্ষেত্রে জটিল সংখ্যা বিভিন্ন অভিনব সমস্যার সমাধান করে। সবচেয়ে মজার ব্যাপার হলো জটিল সংখ্যা আবিষ্কার না হলে আমরা মোবাই ফোনে কথা বলা কিংবা রেডিও শুনতে পারতাম না।
জটিল সংখ্যা
Complex Number
যদি \(a\) ও \(b\) বাস্তব সংখ্যা হয়, তবে \(a+ib\) আকারের সংখ্যাকে জটিল সংখ্যা বা জটিল রাশি বলে যেখানে, \(i=\sqrt{-1}\) । \(a\) কে সংখ্যাটির বাস্তব অংশ এবং \(b\) কে কাল্পনিক অংশ বলা হয়। যদি \(Z=a+ib\) হয়, তবে \(Z\) এর বাস্তব অংশকে সংক্ষেপে \(Re(Z)\) এবং
কাল্পনিক অংশকে \(Im(Z)\) অর্থাৎ, \(Re(Z)=a\) ও \(Im(Z)=b\) দ্বারা প্রকাশ করা করা হয়। সংখ্যাটির বাস্তব অংশ \(a=0\) হলে, তাকে কাল্পনিক সংখ্যা বলে। আবার, কাল্পনিক অংশ \(b=0\) হলে তাকে বাস্তব সংখ্যা বলে।
জটিল সংখ্যা \(a+ib\) কে \((a, b)\) ক্রমজোড় (ordered pair) আকারে প্রকাশ করা হয়।
সুতরাং, \(1+2i=(1, 2); \ 0+i=(0, 1); 2-5i=(2, -5)\) ইত্যাদি।
অতএব, দেখা যাচ্ছে সংখ্যারেখার প্রতিটি বিন্দুই আসলে জটিল সমতলের অন্তর্ভুক্ত। এখান থেকে সহজেই দেখা যায় যে, \(\mathbb{R}\subset{\mathbb{C}}\)। যদি \((x, y)\) ক্রমজোড়টিকে আমরা \(Z\) নাম দেই তাহলে \(Z=(x, y)\) যেখানে \(Re(Z)=x\) এবং \(Im(Z)=y\) লেখা যায়।
দুইটি জটিল সংখ্যা \(Z_{1}=(x_{1}, y_{1})\) এবং \(Z_{2}=(x_{2}, y_{2})\) সমান হবে যদি তারা জটিল সমতলে একই বিন্দু নির্দেশ করে, অর্থাৎ \((x_{1}, y_{1})=(x_{2}, y_{2})\) হয়, জটিল সংখ্যা পদ্ধতি আসলে বাস্তব সংখ্যা পদ্ধতির একটা প্রাকৃতিক প্রবৃদ্ধি (Natural Extension)।
জটিল সংখ্যা \(a+ib\) কে \((a, b)\) ক্রমজোড় (ordered pair) আকারে প্রকাশ করা হয়।
সুতরাং, \(1+2i=(1, 2); \ 0+i=(0, 1); 2-5i=(2, -5)\) ইত্যাদি।
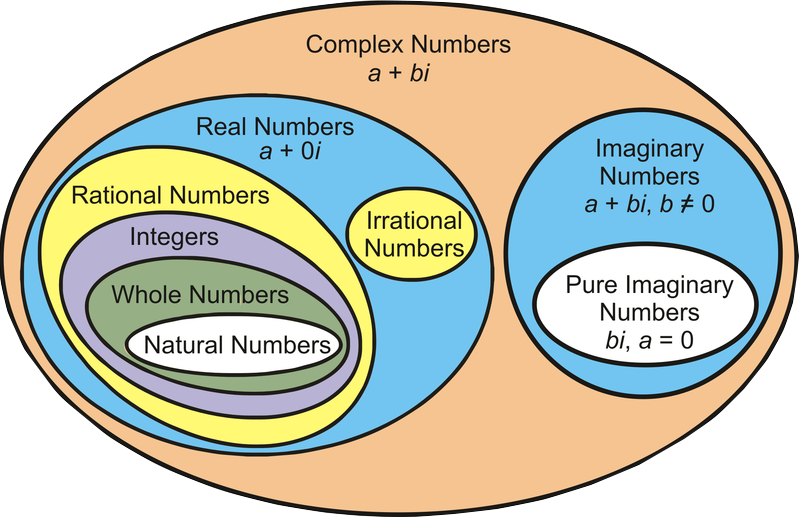
জটিল সংখ্যার সেট যে সকল সংখ্যা সেটের সুপার সেট তা চিত্রের মাধ্যমে উপস্থাপনঃ

বাস্তব সংখ্যার ক্রমজোড় হিসেবে জটিল সংখ্যাঃ
জটিল সংখ্যাকে বাস্তব সংখ্যার একটি ক্রমজোড় \((x, y)\) হিসেবে উপস্থাপন করা যেতে পারে, যেখানে সংখ্যাটি হচ্ছে জটিল সমতলে একটি বিন্দু, ঠিক যেমন বাস্তব সংখ্যাগুলিকে সংখ্যারেখার উপর একটি বিন্দু হিসেবে প্রকাশ করা যায়। জটিল সংখ্যার ক্ষেত্রে ব্যবহার করা হয় জটিল
সমতল বা জেড প্লেন। এ ক্ষেত্রে \(x\) অক্ষ বরাবর বাস্তব অংশ এবং \(y\) অক্ষ বরাবর সংখ্যাটির কাল্পনিক অংশ ধরা হয়। এখান থেকে সহজেই দেখা যায় \((x, 0)\) আকারের প্রতিটি জটিল সংখ্যাই আসলে জটিল সমতলে \(x\) অক্ষ বরাবর একেকটি বিন্দু, এবং এরা একই সাথে একেকটি বাস্তব
সংখ্যা। এভাবে জটিল সমতলে \(x\) অক্ষ বরাবর ধনাত্মক এবং ঋণাত্মক দিকে যেতে থাকলে আমরা \(\mathbb{R}\) এর প্রতিটি সংখ্যা অর্থাৎ প্রত্যেকটা বাস্তব সংখ্যাকেই খুঁজে পাব। তার মানে আমরা এই \(x\) অক্ষকে আমাদের পরিচিত সংখ্যারেখা হিসেবে ভাবতে পারি। অতএব, দেখা যাচ্ছে সংখ্যারেখার প্রতিটি বিন্দুই আসলে জটিল সমতলের অন্তর্ভুক্ত। এখান থেকে সহজেই দেখা যায় যে, \(\mathbb{R}\subset{\mathbb{C}}\)। যদি \((x, y)\) ক্রমজোড়টিকে আমরা \(Z\) নাম দেই তাহলে \(Z=(x, y)\) যেখানে \(Re(Z)=x\) এবং \(Im(Z)=y\) লেখা যায়।
দুইটি জটিল সংখ্যা \(Z_{1}=(x_{1}, y_{1})\) এবং \(Z_{2}=(x_{2}, y_{2})\) সমান হবে যদি তারা জটিল সমতলে একই বিন্দু নির্দেশ করে, অর্থাৎ \((x_{1}, y_{1})=(x_{2}, y_{2})\) হয়, জটিল সংখ্যা পদ্ধতি আসলে বাস্তব সংখ্যা পদ্ধতির একটা প্রাকৃতিক প্রবৃদ্ধি (Natural Extension)।
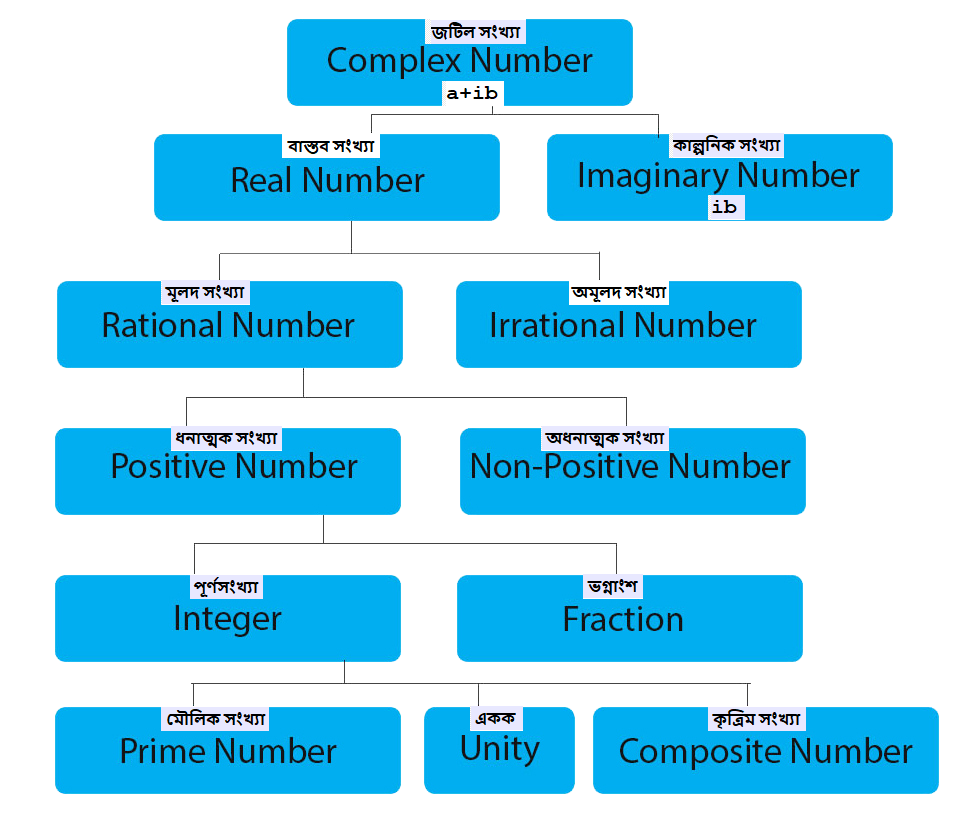
জটিল সংখ্যার শ্রেণীবিন্যাস
Classification of Complex numbers
জটিল সংখ্যা এবং এর জ্যামিতিক প্রতিরূপ (আরগাঁ চিত্র)
Complex numbers and their geometric replicas
যে কোনো জটিল সংখ্যা \(a+ib\) এর ক্রমজোড় \((a, b)\) কে বিন্দু হিসেবে বিবেচনা করে সমতলে নির্দেশ করা যায়। চিত্রের মাধ্যমে এ পদ্ধতি ১৮০৬ খৃস্টাব্দে প্রথম প্রকাশ করেন গণিতবিদ রবার্ট আরগাঁ। তার নাম অনুসারে জটিল সংখ্যা সমতলে স্থাপনের চিত্রকে আরগাঁ চিত্র (Argand
diagram) বলা হয়।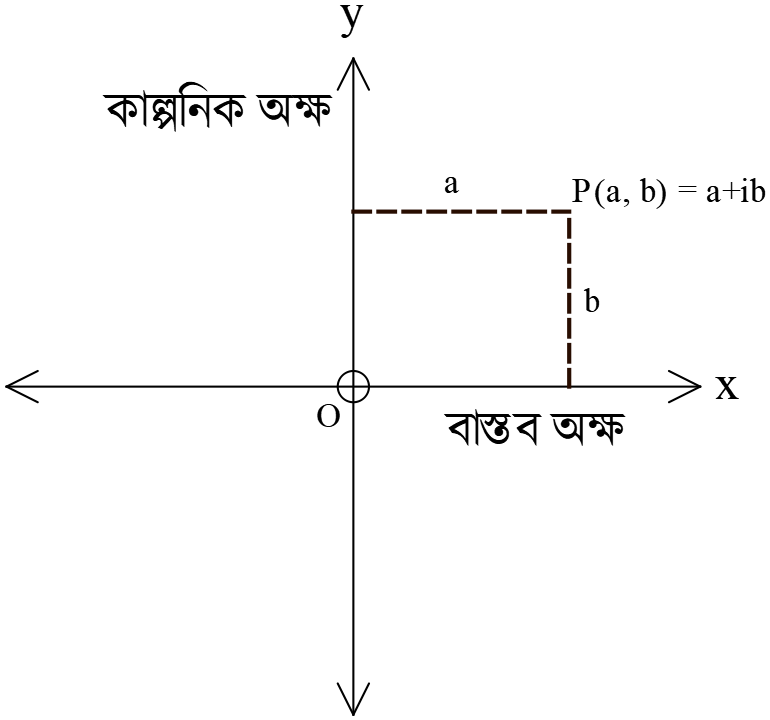
মনে করি,
\(XOX^{\prime}\) ও \(YOY^{\prime}\) সরলরেখাদ্বয় কোনো সমতলে পরস্পরকে লম্বভাবে \(O\) বিন্দুতে ছেদ করে। তাহলে, \(XOX^{\prime}\) কে \(x\) অক্ষ এবং \(YOY^{\prime}\) কে \(y\) অক্ষ বলা হয়। \(x\) অক্ষকে বাস্তব অক্ষ এবং \(y\) অক্ষকে কাল্পনিক অক্ষ ধরা হলে, \(P(a, b)\) বিন্দুটি জটিল সংখ্যা \(a+ib\) কে নির্দেশ করবে, যেখানে জটিল সংখ্যাটির বাস্তব অংশ \(a\) কে \(P\) বিন্দুটির ভুজ (বাস্তব অক্ষ বরাবর) এবং কাল্পনিক অংশ \(b\) কে \(P\) বিন্দুটির কোটি (কাল্পনিক অক্ষ বরাবর) হিসেবে বিবেচনা করা হয়।
যদি \(b=0\) হয়, তাহলে \(P\) বিন্দুটি \(x\) অক্ষের উপর মূলবিন্দু \(O\) হতে \(a\) একক দূরত্বে অবস্থান করবে।
আবার, \(a=0\) হয়, তাহলে \(P\) বিন্দুটি \(y\) অক্ষের উপর মূলবিন্দু \(O\) হতে \(b\) একক দূরত্বে অবস্থান করবে।
Example: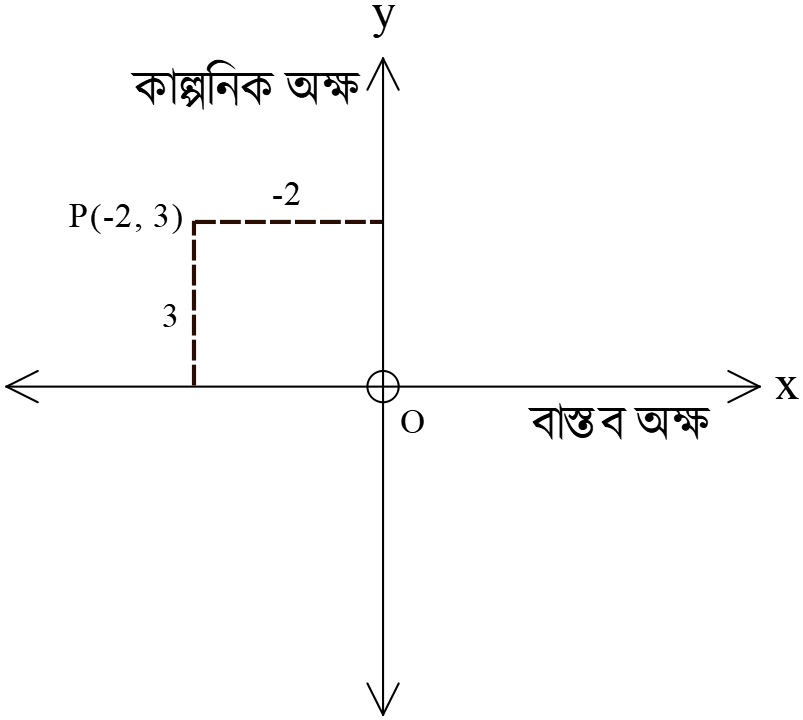
\(-2+3i\) সংখ্যাটির আরগাঁ চিত্র পাশে দেখানো হলোঃ
\(-2+3i\) সংখ্যাটির ক্রমজোড় \((-2, 3)\)
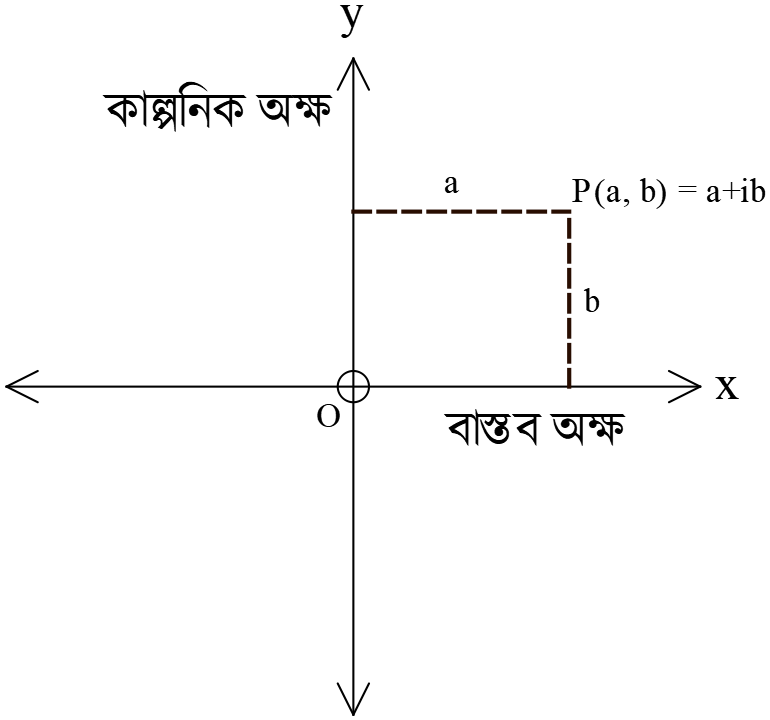
মনে করি,
\(XOX^{\prime}\) ও \(YOY^{\prime}\) সরলরেখাদ্বয় কোনো সমতলে পরস্পরকে লম্বভাবে \(O\) বিন্দুতে ছেদ করে। তাহলে, \(XOX^{\prime}\) কে \(x\) অক্ষ এবং \(YOY^{\prime}\) কে \(y\) অক্ষ বলা হয়। \(x\) অক্ষকে বাস্তব অক্ষ এবং \(y\) অক্ষকে কাল্পনিক অক্ষ ধরা হলে, \(P(a, b)\) বিন্দুটি জটিল সংখ্যা \(a+ib\) কে নির্দেশ করবে, যেখানে জটিল সংখ্যাটির বাস্তব অংশ \(a\) কে \(P\) বিন্দুটির ভুজ (বাস্তব অক্ষ বরাবর) এবং কাল্পনিক অংশ \(b\) কে \(P\) বিন্দুটির কোটি (কাল্পনিক অক্ষ বরাবর) হিসেবে বিবেচনা করা হয়।
যদি \(b=0\) হয়, তাহলে \(P\) বিন্দুটি \(x\) অক্ষের উপর মূলবিন্দু \(O\) হতে \(a\) একক দূরত্বে অবস্থান করবে।
আবার, \(a=0\) হয়, তাহলে \(P\) বিন্দুটি \(y\) অক্ষের উপর মূলবিন্দু \(O\) হতে \(b\) একক দূরত্বে অবস্থান করবে।
Example:
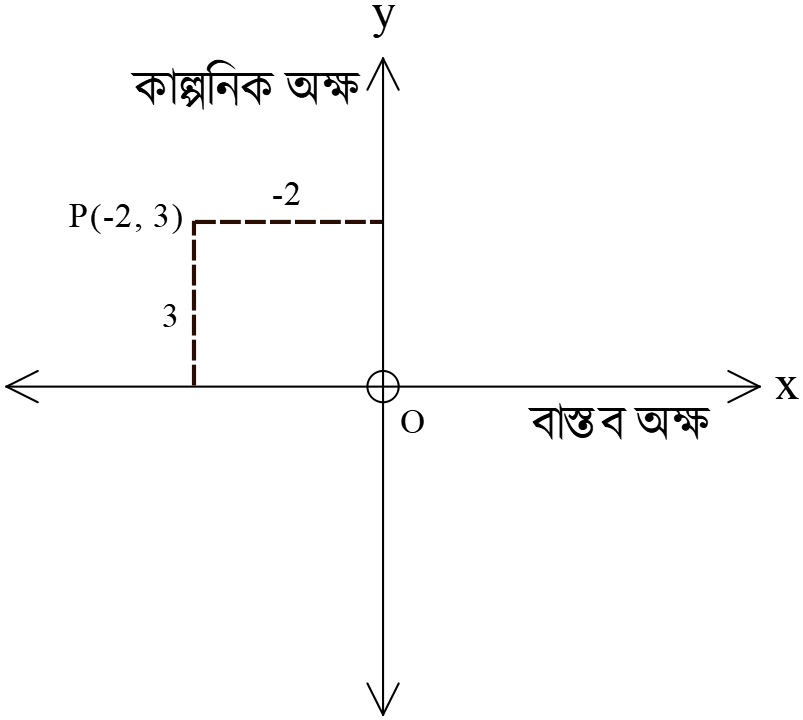
\(-2+3i\) সংখ্যাটির আরগাঁ চিত্র পাশে দেখানো হলোঃ
\(-2+3i\) সংখ্যাটির ক্রমজোড় \((-2, 3)\)
জটিল সংখ্যার ভেনচিত্র
Venn diagram of complex numbers
জটিল সংখ্যার পোলার আকার
Polar size of complex numbers
\(Z=x+iy\) হলে \(Z\) কে কার্তেসীয় আকারের জটিল সংখ্যা বলা হয়। একটি বিন্দুর কার্তেসীয় স্থানাঙ্ক \((x, y)\) ও পোলার স্থানাঙ্ক \((r, \theta)\) হলে,
\(x=r\cos{\theta}, \ y=r\sin{\theta}\)
এখন, \(Z=x+iy\)
\(\Rightarrow Z=r\cos{\theta}+ir\sin{\theta}\)
\(=r(\cos{\theta}+i\sin{\theta})\)
\(=re^{i\theta}\) ➜ \(\because \cos{\theta}+i\sin{\theta}=e^{i\theta}\)
\(re^{i\theta}\) কে \(Z\) পোলার আকার বলা হয়।
\(\therefore re^{i\theta}=x+iy\)
এক্ষেত্রে, \(r=\sqrt{x^2+y^2}\) এবং \(\theta=\tan^{-1}{\frac{y}{x}}\)
\(r\) এবং \(\theta\) যথাক্রমে \(Z\) এর মডুলাস ও আর্গুমেন্ট।
দ্রষ্টব্যঃ \(\cos{\theta}+i\sin{\theta}=re^{i\theta}\) এবং \(\cos{\theta}-i\sin{\theta}=re^{-i\theta}\) এই সূত্র অয়লারের সূত্র (Euler's formula) নামে পরিচিত।
উদাহরণঃ \(Z=3+5i\) জটিল সংখ্যার পোলার আকার \(Z=r(\cos{\theta}+i\sin{\theta})\)
যেখানে, \(r=\sqrt{3^2+5^2}=\sqrt{34}\) এবং \(\theta=\tan^{-1}{\frac{5}{3}}\)
\(x=r\cos{\theta}, \ y=r\sin{\theta}\)
এখন, \(Z=x+iy\)
\(\Rightarrow Z=r\cos{\theta}+ir\sin{\theta}\)
\(=r(\cos{\theta}+i\sin{\theta})\)
\(=re^{i\theta}\) ➜ \(\because \cos{\theta}+i\sin{\theta}=e^{i\theta}\)
\(re^{i\theta}\) কে \(Z\) পোলার আকার বলা হয়।
\(\therefore re^{i\theta}=x+iy\)
এক্ষেত্রে, \(r=\sqrt{x^2+y^2}\) এবং \(\theta=\tan^{-1}{\frac{y}{x}}\)
\(r\) এবং \(\theta\) যথাক্রমে \(Z\) এর মডুলাস ও আর্গুমেন্ট।
দ্রষ্টব্যঃ \(\cos{\theta}+i\sin{\theta}=re^{i\theta}\) এবং \(\cos{\theta}-i\sin{\theta}=re^{-i\theta}\) এই সূত্র অয়লারের সূত্র (Euler's formula) নামে পরিচিত।
উদাহরণঃ \(Z=3+5i\) জটিল সংখ্যার পোলার আকার \(Z=r(\cos{\theta}+i\sin{\theta})\)
যেখানে, \(r=\sqrt{3^2+5^2}=\sqrt{34}\) এবং \(\theta=\tan^{-1}{\frac{5}{3}}\)
জটিল সংখ্যার ভেক্টর আকার
Vector size of complex numbers
কোনো জটিল সংখ্যা \(Z=x+iy=(x, y)\) কে ভেক্টর \(\overrightarrow{OP}\) হিসেবে চিহ্নিত করা যায়।
যার \(O\) আদি বিন্দু এবং \(P\) প্রান্ত বিন্দু।
দৈর্ঘ্য \(OP\) হলো \(\overrightarrow{OP}\) বা \((Z=x+iy)\) এর পরমমান
এবং \(Z=x+iy=\overrightarrow{OP}\) কে \(P\) এর অবস্থান ভেক্টর বলা হয়।

যার \(O\) আদি বিন্দু এবং \(P\) প্রান্ত বিন্দু।
দৈর্ঘ্য \(OP\) হলো \(\overrightarrow{OP}\) বা \((Z=x+iy)\) এর পরমমান
এবং \(Z=x+iy=\overrightarrow{OP}\) কে \(P\) এর অবস্থান ভেক্টর বলা হয়।
জটিল সংখ্যার মডুলাস (পরমমান) এবং আর্গুমেন্ট (নতি)
Modulus of complex numbers and argument
\(Z=x+iy\) জটিল সংখ্যাটির আরগাঁ চিত্র \(P\) বিন্দু এবং \(P\) এর পোলার স্থানাঙ্ক \((r, \theta)\) হলে,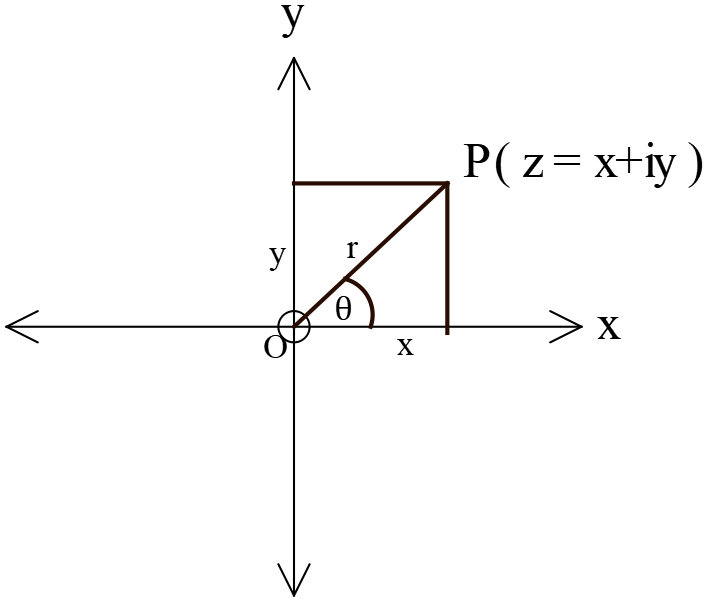
চিত্রানুযায়ী \(OP=r\) এবং \(\angle{XOP}=\theta\)
\(r=OP=\sqrt{x^2+y^2}\) কে \(Z\) এর মডুলাস (প্রকৃতমান বা পরমমান) বলা হয়
এবং একে \(|Z|\) দ্বারা প্রকাশ করা হয়।
অর্থাৎ, \(Z=x+iy\) হলে, \(|Z|=\sqrt{x^2+y^2}=\sqrt{\{Re(Z)\}^2+\{Im(Z)\}^2}\) ।
চিত্রানুযায়ী \(x=r\cos{\theta}\) এবং \(y=r\sin{\theta}\) তাহলে \(\theta=\tan^{-1}{\left(\frac{y}{x}\right)}\)
\(\theta=\tan^{-1}{\left(\frac{y}{x}\right)}\) কে \(Z\) এর আর্গুমেন্ট বলা হয়।
যদি, \(-\pi\lt{\theta}\lt{\pi}\) হয় তবে \(\theta\) কে মুখ্য আর্গুমেন্ট বলা হয়। \(Z\) এর মুখ্য আর্গুমেন্টকে \(Arg(Z)\) দ্বারা প্রকাশ করা হয়।
\(x\) এবং \(y\) এর মান নির্দিষ্ট থাকলেও ত্রিকোণমিতিক নিয়ম অনুযায়ী \(\theta\) এর অসংখ্য মান হতে পারে।
\(2n\pi+\theta\) কে সাধারণ আর্গুমেন্ট বলা হয়, যেখানে \(n\) যে কোনো স্বাভাবিক সংখ্যা এবং \(\theta\) মুখ্য আর্গুমেন্ট। ইহাকে \(arg(Z)\) দ্বারা প্রকাশ করা যায়।
অর্থাৎ, \(arg(Z)=2n\pi+\theta\)
উল্লেখ্য যে, \(-\pi\lt{\theta}\le{\pi}\) ব্যাবধিতে \(\theta\) এর কেবলমাত্র একটি মান পাওয়া যায় এবং এ মানটিই মূখ্য আর্গুমেন্ট। যদি জটিল সংখ্যার আর্গুমেন্ট নির্ণয় করতে বলা হয়, সেক্ষেত্রে মূখ্য আর্গুমেন্টকেই বোঝায়।
উদাহরণঃ \(4+3i\) এর মডলাস এবং আর্গুমেন্ট নির্ণয় কর।
সমাধানঃ
ধরি \(Z=4+3i\)
\(\Rightarrow x=4, \ y=3\) ➜ \(Z=x+iy\) এর সহিত তুলুনা করে।
\(Z\) এর মডুলাস \(|Z|=\sqrt{x^2+y^2}\)
\(=\sqrt{4^2+3^2}\)
\(=\sqrt{16+9}\)
\(=\sqrt{25}\)
\(=5\)
এবং \(Z\) এর আর্গুমেন্ট \(\theta=\tan^{-1}{\left(\frac{y}{x}\right)}\)
\(=\tan^{-1}{\left(\frac{3}{4}\right)}\)
\(\therefore \) মডুলাস \(=5\)
আর্গুমেন্ট \(=\tan^{-1}{\left(\frac{3}{4}\right)}\)
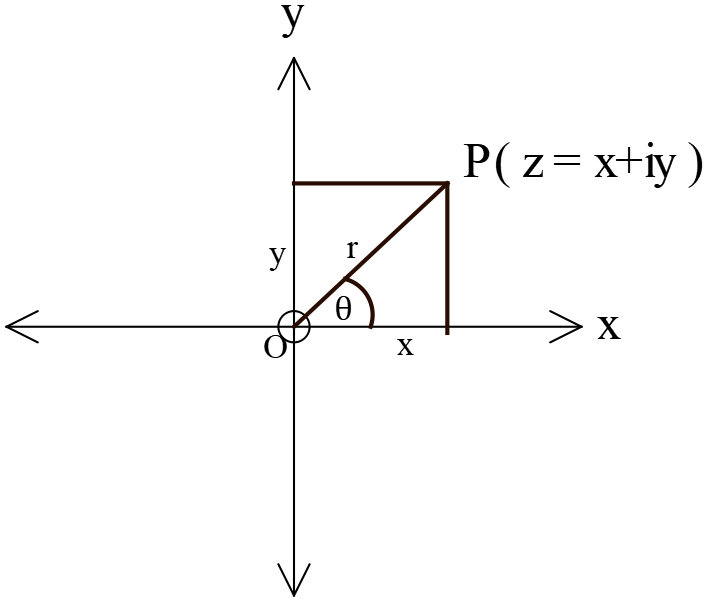
চিত্রানুযায়ী \(OP=r\) এবং \(\angle{XOP}=\theta\)
\(r=OP=\sqrt{x^2+y^2}\) কে \(Z\) এর মডুলাস (প্রকৃতমান বা পরমমান) বলা হয়
এবং একে \(|Z|\) দ্বারা প্রকাশ করা হয়।
অর্থাৎ, \(Z=x+iy\) হলে, \(|Z|=\sqrt{x^2+y^2}=\sqrt{\{Re(Z)\}^2+\{Im(Z)\}^2}\) ।
চিত্রানুযায়ী \(x=r\cos{\theta}\) এবং \(y=r\sin{\theta}\) তাহলে \(\theta=\tan^{-1}{\left(\frac{y}{x}\right)}\)
\(\theta=\tan^{-1}{\left(\frac{y}{x}\right)}\) কে \(Z\) এর আর্গুমেন্ট বলা হয়।
যদি, \(-\pi\lt{\theta}\lt{\pi}\) হয় তবে \(\theta\) কে মুখ্য আর্গুমেন্ট বলা হয়। \(Z\) এর মুখ্য আর্গুমেন্টকে \(Arg(Z)\) দ্বারা প্রকাশ করা হয়।
\(x\) এবং \(y\) এর মান নির্দিষ্ট থাকলেও ত্রিকোণমিতিক নিয়ম অনুযায়ী \(\theta\) এর অসংখ্য মান হতে পারে।
\(2n\pi+\theta\) কে সাধারণ আর্গুমেন্ট বলা হয়, যেখানে \(n\) যে কোনো স্বাভাবিক সংখ্যা এবং \(\theta\) মুখ্য আর্গুমেন্ট। ইহাকে \(arg(Z)\) দ্বারা প্রকাশ করা যায়।
অর্থাৎ, \(arg(Z)=2n\pi+\theta\)
উল্লেখ্য যে, \(-\pi\lt{\theta}\le{\pi}\) ব্যাবধিতে \(\theta\) এর কেবলমাত্র একটি মান পাওয়া যায় এবং এ মানটিই মূখ্য আর্গুমেন্ট। যদি জটিল সংখ্যার আর্গুমেন্ট নির্ণয় করতে বলা হয়, সেক্ষেত্রে মূখ্য আর্গুমেন্টকেই বোঝায়।
উদাহরণঃ \(4+3i\) এর মডলাস এবং আর্গুমেন্ট নির্ণয় কর।
সমাধানঃ
ধরি \(Z=4+3i\)
\(\Rightarrow x=4, \ y=3\) ➜ \(Z=x+iy\) এর সহিত তুলুনা করে।
\(Z\) এর মডুলাস \(|Z|=\sqrt{x^2+y^2}\)
\(=\sqrt{4^2+3^2}\)
\(=\sqrt{16+9}\)
\(=\sqrt{25}\)
\(=5\)
এবং \(Z\) এর আর্গুমেন্ট \(\theta=\tan^{-1}{\left(\frac{y}{x}\right)}\)
\(=\tan^{-1}{\left(\frac{3}{4}\right)}\)
\(\therefore \) মডুলাস \(=5\)
আর্গুমেন্ট \(=\tan^{-1}{\left(\frac{3}{4}\right)}\)
চৌকোণের ভিত্তিতে জটিল সংখ্যার আর্গুমেন্ট (নতি)
Arguments of complex numbers in quadrant
\(x\gt{0}\) এবং \(y\gt{0}\) হলে, জটিল সংখ্যা \(x+iy, \ -x+iy, \ -x-iy\) ও \(x-iy\) কে যথাক্রমে \(P(x, y), \ Q(-x, y), \ R(-x, -y)\) ও \(S(x, -y)\) দ্বারা প্রকাশ করা যায়।
\((x, y), \ (-x, y), \ (-x, -y)\) ও \((x, -y)\) বিন্দুর অবস্থান যথাক্রমে প্রথম , দ্বিতীয়, তৃতীয় ও চতুর্থ চতুর্ভাগে। জটিল সংখ্যার আর্গুমেন্ট \(]-\pi, \pi]\) সীমার মধ্যে থাকে। 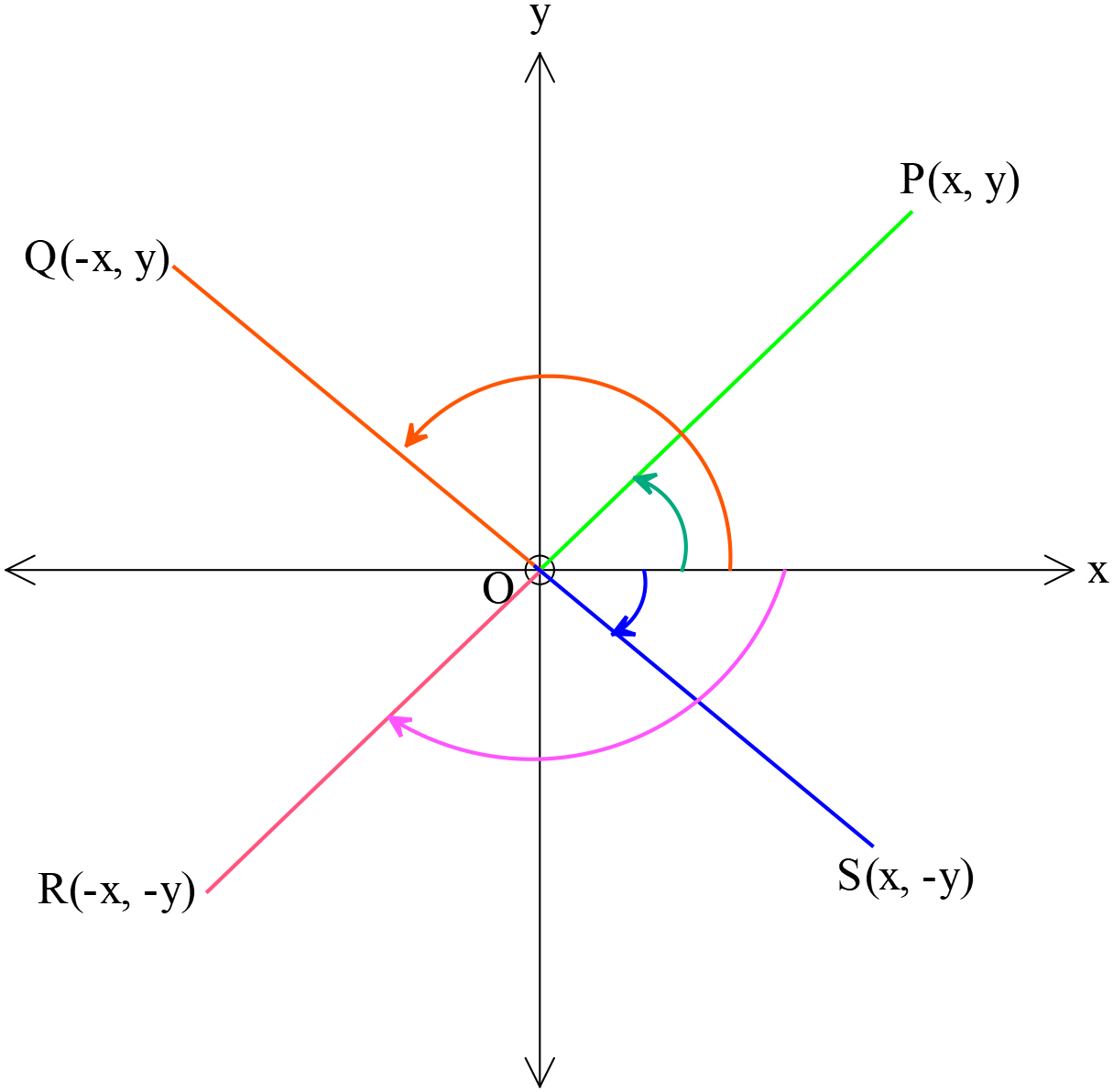
সুতরাং \(x\gt{0}, \ y\gt{0}\) হলে,
জটিল সংখ্যা \(x+iy\) এর আর্গুমেন্ট \(=\tan^{-1}{\left(\frac{y}{x}\right)}\)
জটিল সংখ্যা \(-x+iy\) এর আর্গুমেন্ট \(=\tan^{-1}{\left(\frac{y}{-x}\right)}=\pi-\tan^{-1}{\left(\frac{y}{x}\right)}\)
জটিল সংখ্যা \(-x-iy\) এর আর্গুমেন্ট \(=\tan^{-1}{\left(\frac{-y}{-x}\right)}=\pi+\tan^{-1}{\left(\frac{y}{x}\right)}=\tan^{-1}{\left(\frac{y}{x}\right)}-\pi\)
জটিল সংখ্যা \(x-iy\) এর আর্গুমেন্ট \(=-\tan^{-1}{\left(\frac{y}{x}\right)}=2\pi-\tan^{-1}{\left(\frac{y}{x}\right)}\)
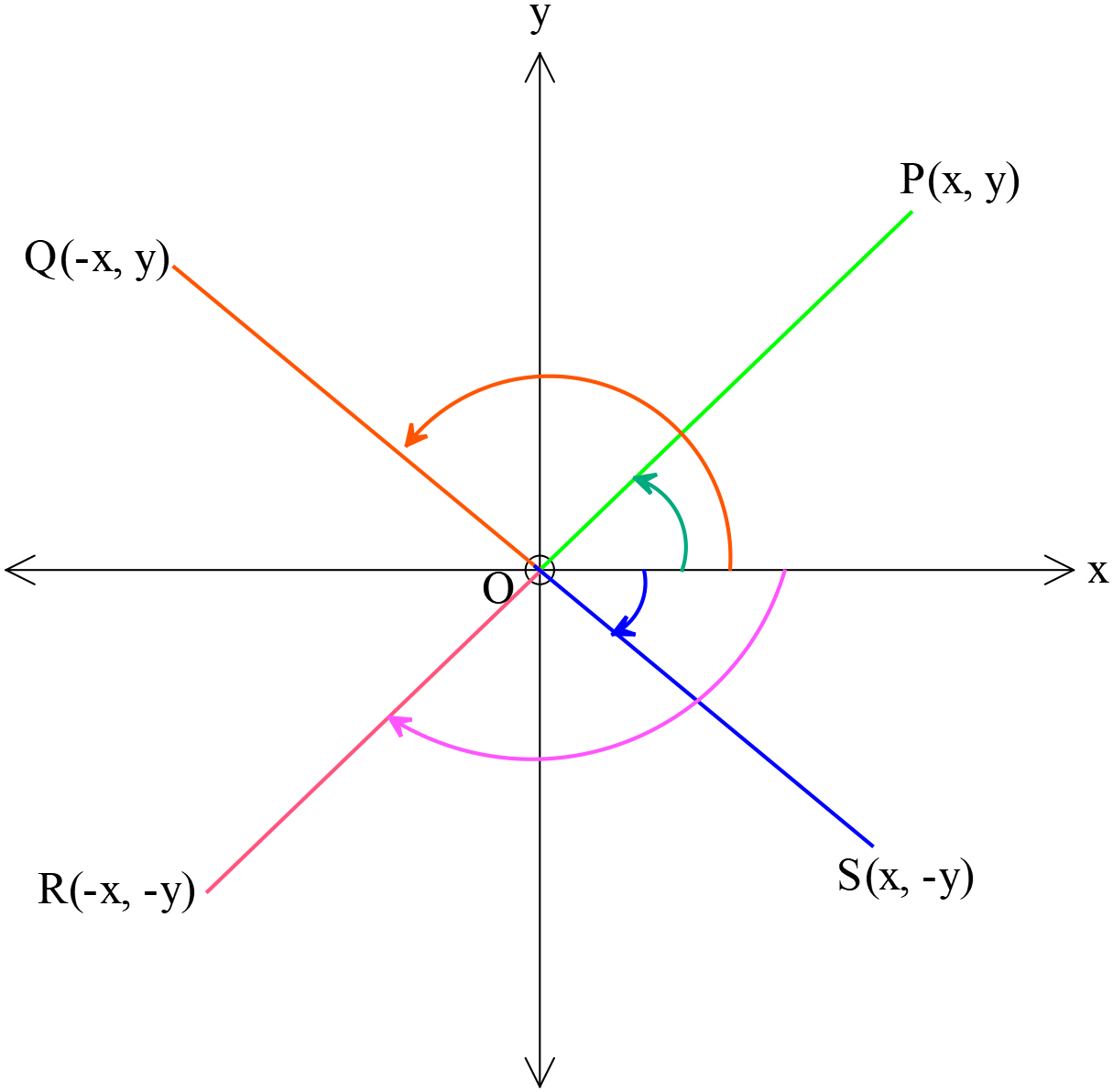
সুতরাং \(x\gt{0}, \ y\gt{0}\) হলে,
জটিল সংখ্যা \(x+iy\) এর আর্গুমেন্ট \(=\tan^{-1}{\left(\frac{y}{x}\right)}\)
জটিল সংখ্যা \(-x+iy\) এর আর্গুমেন্ট \(=\tan^{-1}{\left(\frac{y}{-x}\right)}=\pi-\tan^{-1}{\left(\frac{y}{x}\right)}\)
জটিল সংখ্যা \(-x-iy\) এর আর্গুমেন্ট \(=\tan^{-1}{\left(\frac{-y}{-x}\right)}=\pi+\tan^{-1}{\left(\frac{y}{x}\right)}=\tan^{-1}{\left(\frac{y}{x}\right)}-\pi\)
জটিল সংখ্যা \(x-iy\) এর আর্গুমেন্ট \(=-\tan^{-1}{\left(\frac{y}{x}\right)}=2\pi-\tan^{-1}{\left(\frac{y}{x}\right)}\)
দুইটি জটিল সংখ্যার মধ্যবর্তী কোণ
Angle between two complex numbers
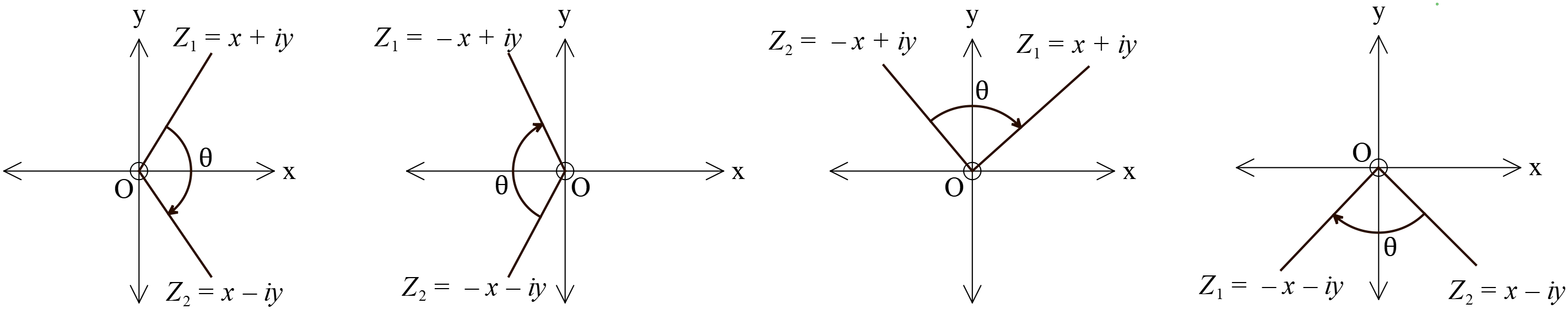
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা, \(\theta\) সংখ্যাদ্বয়ের মধ্যবর্তী কোণ।
তাহলে,
\(\theta=|arg(Z_{1})-arg(Z_{2})|\)
\(\theta\gt{\pi}\) হলে, জটিল সংখ্যাদ্বয়ের মধ্যবর্তী কোণ হবে, \(=2\pi-\theta\)
কাল্পনিক একক এবং এর প্রকৃতি
Imaginary unit and its nature
\(\sqrt{-1}\) কে কাল্পনিক একক বলা হয় এবং একে \(i\) দ্বারা প্রকাশ করা হয়।
সুতরাং, \(i=\sqrt{-1}\)
\(\therefore i^2=-1\)
\(i^3=i^2.i=-i\)
\(i^4=i^2\times{i^2}=-1\times-1=1\)
\(i^5=i^2\times{i^2}\times{i}=-1\times-1\times{i}=i\) ইত্যাদি।
\(n\) যে কোনো পূর্ণসংখ্যা হলে সাধারণভাবে,
\(i^{4n+1}=i^{4n}.i=(i^{2})^{2n}.i=(-1)^{2n}.i=\{(-1)^{2}\}^n.i\)\(=1^n.i=1.i=i\)
\(i^{4n+2}=i^{4n}.i^2=(i^{2})^{2n}\times-1=(-1)^{2n}\times-1\)\(=\{(-1)^{2}\}^n\times-1=1^n\times-1=1\times-1=-1\)
\(i^{4n+3}=i^{4n}.i^2.i=(i^{2})^{2n}\times-1\times{i}=(-1)^{2n}\times-i\)\(=\{(-1)^{2}\}^n\times-i=1^n\times-i=1\times-i=-i\)
\(i^{4n+4}=i^{4n}.i^4=(i^{2})^{2n}.(i^2)^2=(-1)^{2n}.(-1)^2\)\(=\{(-1)^{2}\}^n.1=1^n=1\) ইত্যাদি।
আবার,
\(i^{-1}=\frac{1}{i}=\frac{i}{i^2}=\frac{i}{-1}=-i\)
\(i^{-2}=\frac{1}{i^2}=\frac{1}{-1}=\frac{1}{-1}=-1\)
\(i^{-3}=\frac{1}{i^3}=\frac{1}{i^2.i}=\frac{1}{-1.i}\)\(=\frac{1}{-i}=\frac{i}{-i^2}=\frac{i}{-(-1)}=\frac{i}{1}=i\)
\(i^{-4}=\frac{1}{i^4}=\frac{1}{i^2.i^2}=\frac{1}{(-1)(-1)}\)\(=\frac{1}{1}=1\) ইত্যাদি।
সুতরাং, \(i=\sqrt{-1}\)
\(\therefore i^2=-1\)
\(i^3=i^2.i=-i\)
\(i^4=i^2\times{i^2}=-1\times-1=1\)
\(i^5=i^2\times{i^2}\times{i}=-1\times-1\times{i}=i\) ইত্যাদি।
\(n\) যে কোনো পূর্ণসংখ্যা হলে সাধারণভাবে,
\(i^{4n+1}=i^{4n}.i=(i^{2})^{2n}.i=(-1)^{2n}.i=\{(-1)^{2}\}^n.i\)\(=1^n.i=1.i=i\)
\(i^{4n+2}=i^{4n}.i^2=(i^{2})^{2n}\times-1=(-1)^{2n}\times-1\)\(=\{(-1)^{2}\}^n\times-1=1^n\times-1=1\times-1=-1\)
\(i^{4n+3}=i^{4n}.i^2.i=(i^{2})^{2n}\times-1\times{i}=(-1)^{2n}\times-i\)\(=\{(-1)^{2}\}^n\times-i=1^n\times-i=1\times-i=-i\)
\(i^{4n+4}=i^{4n}.i^4=(i^{2})^{2n}.(i^2)^2=(-1)^{2n}.(-1)^2\)\(=\{(-1)^{2}\}^n.1=1^n=1\) ইত্যাদি।
আবার,
\(i^{-1}=\frac{1}{i}=\frac{i}{i^2}=\frac{i}{-1}=-i\)
\(i^{-2}=\frac{1}{i^2}=\frac{1}{-1}=\frac{1}{-1}=-1\)
\(i^{-3}=\frac{1}{i^3}=\frac{1}{i^2.i}=\frac{1}{-1.i}\)\(=\frac{1}{-i}=\frac{i}{-i^2}=\frac{i}{-(-1)}=\frac{i}{1}=i\)
\(i^{-4}=\frac{1}{i^4}=\frac{1}{i^2.i^2}=\frac{1}{(-1)(-1)}\)\(=\frac{1}{1}=1\) ইত্যাদি।
জটিল সংখ্যার যোগ এবং বিয়োগ
Addition and Subtraction of complex numbers
জটিল সংখ্যার যোগঃ দুইটি জটিল সংখ্যা \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) এর যোগফল \(Z_{1}+Z_{2}\) কে নিম্নলিখিতভাবে সংজ্ঞায়িত করা যায়।
\(Z_{1}+Z_{2}=x_{1}+iy_{1}+x_{2}+iy_{2}\)
\(=x_{1}+x_{2}+iy_{1}+iy_{2}\)
\(=(x_{1}+x_{2})+i(y_{1}+y_{2})\)
উদাহরণঃ \(4-3i\) ও \(-2+5i\) এর যোগফল \(=(4-2)+i(-3+5)\)
\(=2+2i\)
জটিল সংখ্যার বিয়োগঃ দুইটি জটিল সংখ্যা \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) এর বিয়োগফল \(Z_{1}-Z_{2}\) কে নিম্নলিখিতভাবে সংজ্ঞায়িত করা যায়।
\(Z_{1}-Z_{2}=x_{1}+iy_{1}-x_{2}-iy_{2}\)
\(=x_{1}-x_{2}+iy_{1}-iy_{2}\)
\(=(x_{1}-x_{2})+i(y_{1}-y_{2})\)
উদাহরণঃ \(4-3i\) ও \(-2+5i\) এর যোগফল \(=(4+2)+i(-3-5)\)
\(=6-8i\)
\(Z_{1}+Z_{2}=x_{1}+iy_{1}+x_{2}+iy_{2}\)
\(=x_{1}+x_{2}+iy_{1}+iy_{2}\)
\(=(x_{1}+x_{2})+i(y_{1}+y_{2})\)
উদাহরণঃ \(4-3i\) ও \(-2+5i\) এর যোগফল \(=(4-2)+i(-3+5)\)
\(=2+2i\)
জটিল সংখ্যার বিয়োগঃ দুইটি জটিল সংখ্যা \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) এর বিয়োগফল \(Z_{1}-Z_{2}\) কে নিম্নলিখিতভাবে সংজ্ঞায়িত করা যায়।
\(Z_{1}-Z_{2}=x_{1}+iy_{1}-x_{2}-iy_{2}\)
\(=x_{1}-x_{2}+iy_{1}-iy_{2}\)
\(=(x_{1}-x_{2})+i(y_{1}-y_{2})\)
উদাহরণঃ \(4-3i\) ও \(-2+5i\) এর যোগফল \(=(4+2)+i(-3-5)\)
\(=6-8i\)
জটিল সংখ্যার গুণ এবং ভাগ
Multiplication and division of complex numbers
জটিল সংখ্যার গুণঃ দুইটি জটিল সংখ্যা \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) এর গুণফল \(Z_{1}Z_{2}\) কে নিম্নলিখিতভাবে সংজ্ঞায়িত করা যায়।
\(Z_{1}Z_{2}=(x_{1}+iy_{1})(x_{2}+iy_{2})\)
\(=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}+i^2y_{1}y_{2}\)
\(=x_{1}x_{2}+i(x_{1}y_{2}+x_{2}y_{1})-y_{1}y_{2}\) ➜ \(\because i^2=-1\)
\(=(x_{1}x_{2}-y_{1}y_{2})+i(x_{1}y_{2}+x_{2}y_{1})\)
উদাহরণঃ \(4-3i\) ও \(-2+5i\) এর গুণফল \(=\{4\times-2-(-3)\times5\}+i\{4\times5+(-2)\times-3\}\)
\(=\{-8+15\}+i\{20+6\}\)
\(=7+26i\)
জটিল সংখ্যার ভাগঃ দুইটি জটিল সংখ্যা \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) এর ভাফল \(\frac{Z_{1}}{Z_{2}}\) কে নিম্নলিখিতভাবে সংজ্ঞায়িত করা যায়।
\(\frac{Z_{1}}{Z_{2}}=\frac{x_{1}+iy_{1}}{x_{2}+iy_{2}}\)
\(=\frac{(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}\) ➜ লব ও হরের সাথে \((x_{2}-iy_{2})\) গুণ করে।
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})-i(x_{1}y_{2}-x_{2}y_{1})}{x_{2}^2-i^2y_{2}^2}\)
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})-i(x_{1}y_{2}-x_{2}y_{1})}{x_{2}^2+y_{2}^2}\) ➜ \(\because i^2=-1\)
উদাহরণঃ \(4-3i\) ও \(-2+5i\) এর ভাফল \(=\frac{\{4\times-2+(-3)\times5\}-i\{4\times5-(-2)\times-3\}}{(-2)^2+5^2}\)
\(=\frac{\{-8-15\}-i\{20-6\}}{4+25}\)
\(=\frac{-23-14i}{29}\)
\(=-\frac{23}{29}-\frac{14}{29}i\)
\(Z_{1}Z_{2}=(x_{1}+iy_{1})(x_{2}+iy_{2})\)
\(=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}+i^2y_{1}y_{2}\)
\(=x_{1}x_{2}+i(x_{1}y_{2}+x_{2}y_{1})-y_{1}y_{2}\) ➜ \(\because i^2=-1\)
\(=(x_{1}x_{2}-y_{1}y_{2})+i(x_{1}y_{2}+x_{2}y_{1})\)
উদাহরণঃ \(4-3i\) ও \(-2+5i\) এর গুণফল \(=\{4\times-2-(-3)\times5\}+i\{4\times5+(-2)\times-3\}\)
\(=\{-8+15\}+i\{20+6\}\)
\(=7+26i\)
জটিল সংখ্যার ভাগঃ দুইটি জটিল সংখ্যা \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) এর ভাফল \(\frac{Z_{1}}{Z_{2}}\) কে নিম্নলিখিতভাবে সংজ্ঞায়িত করা যায়।
\(\frac{Z_{1}}{Z_{2}}=\frac{x_{1}+iy_{1}}{x_{2}+iy_{2}}\)
\(=\frac{(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}\) ➜ লব ও হরের সাথে \((x_{2}-iy_{2})\) গুণ করে।
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})-i(x_{1}y_{2}-x_{2}y_{1})}{x_{2}^2-i^2y_{2}^2}\)
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})-i(x_{1}y_{2}-x_{2}y_{1})}{x_{2}^2+y_{2}^2}\) ➜ \(\because i^2=-1\)
উদাহরণঃ \(4-3i\) ও \(-2+5i\) এর ভাফল \(=\frac{\{4\times-2+(-3)\times5\}-i\{4\times5-(-2)\times-3\}}{(-2)^2+5^2}\)
\(=\frac{\{-8-15\}-i\{20-6\}}{4+25}\)
\(=\frac{-23-14i}{29}\)
\(=-\frac{23}{29}-\frac{14}{29}i\)
দুইটি জটিল সংখ্যার সমতা
Equality of Two complex numbers
\(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) জটিল সংখ্যা দুইটি সমান হবে অর্থাৎ, \(Z_{1}=Z_{2}\) হবে যদি এবং কেবল যদি \(x_{1}=x_{2}\) এবং \(y_{1}=y_{2}\) হয়।
\(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা।
এবং \(Z_{1}=Z_{2}\)
\(\Rightarrow x_{1}+iy_{1}=x_{2}+iy_{2}\)
\(\Rightarrow x_{1}-x_{2}=iy_{2}-iy_{1}\)
\(\Rightarrow x_{1}-x_{2}=-i(y_{1}-y_{2})\)
\(\Rightarrow (x_{1}-x_{2})^2=i^2(y_{1}-y_{2})^2\) ➜ উভয় পার্শে বর্গ করে,
\(\Rightarrow (x_{1}-x_{2})^2=-(y_{1}-y_{2})^2\) ➜ \(\because i^2=-1\)
\(\Rightarrow (x_{1}-x_{2})^2+(y_{1}-y_{2})^2=0\)
\(\Rightarrow x_{1}-x_{2}=0, \ y_{1}-y_{2}=0\) ➜ একাধিক রাশির বর্গের যোগফল শূন্য হলে, রাশিগুলি পৃথকভাবে শূন্য হয়।
\(\therefore x_{1}=x_{2}, \ y_{1}=y_{2}\)
\(\therefore Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) জটিল সংখ্যা দুইটি সমান হবে অর্থাৎ, \(Z_{1}=Z_{2}\) হবে যদি এবং কেবল যদি \(x_{1}=x_{2}\) এবং \(y_{1}=y_{2}\) হয়।
অর্থাৎ, একটি জটিল সংখ্যার বাস্তব ও কাল্পনিক অংশ যথাক্রমে অপর একটি জটিল সংখ্যার বাস্তব ও কাল্পনিক অংশের সমান হলে জটিল সংখ্যা দুইটি সমান হবে।
\(Z_{1}=3+5i\) এবং \(Z_{2}=3+5i\) হলে, \(Z_{1}=Z_{2}\) হবে।
\(Z_{1}=5+3i\) এবং \(Z_{2}=3+5i\) হলে, \(Z_{1}\ne{Z_{2}}\) হবে কারণ, \(Re(Z_{1})\ne{Re(Z_{1})}\) এবং \(Im(Z_{1})\ne{Im(Z_{1})}\)।
প্রমাণঃ
দেওয়া আছে,\(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা।
এবং \(Z_{1}=Z_{2}\)
\(\Rightarrow x_{1}+iy_{1}=x_{2}+iy_{2}\)
\(\Rightarrow x_{1}-x_{2}=iy_{2}-iy_{1}\)
\(\Rightarrow x_{1}-x_{2}=-i(y_{1}-y_{2})\)
\(\Rightarrow (x_{1}-x_{2})^2=i^2(y_{1}-y_{2})^2\) ➜ উভয় পার্শে বর্গ করে,
\(\Rightarrow (x_{1}-x_{2})^2=-(y_{1}-y_{2})^2\) ➜ \(\because i^2=-1\)
\(\Rightarrow (x_{1}-x_{2})^2+(y_{1}-y_{2})^2=0\)
\(\Rightarrow x_{1}-x_{2}=0, \ y_{1}-y_{2}=0\) ➜ একাধিক রাশির বর্গের যোগফল শূন্য হলে, রাশিগুলি পৃথকভাবে শূন্য হয়।
\(\therefore x_{1}=x_{2}, \ y_{1}=y_{2}\)
\(\therefore Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) জটিল সংখ্যা দুইটি সমান হবে অর্থাৎ, \(Z_{1}=Z_{2}\) হবে যদি এবং কেবল যদি \(x_{1}=x_{2}\) এবং \(y_{1}=y_{2}\) হয়।
অর্থাৎ, একটি জটিল সংখ্যার বাস্তব ও কাল্পনিক অংশ যথাক্রমে অপর একটি জটিল সংখ্যার বাস্তব ও কাল্পনিক অংশের সমান হলে জটিল সংখ্যা দুইটি সমান হবে।
\(Z_{1}=5+3i\) এবং \(Z_{2}=3+5i\) হলে, \(Z_{1}\ne{Z_{2}}\) হবে কারণ, \(Re(Z_{1})\ne{Re(Z_{1})}\) এবং \(Im(Z_{1})\ne{Im(Z_{1})}\)।
অনুবন্ধী জটিল সংখ্যা
Conjugate complex numbers
জটিল সংখ্যার গুণের ক্ষেত্রে একটি বিশেষ অবস্থা লক্ষ করি, \(a+ib\) এর সাথে \(a-ib\) গুণ করলে পাই, \(a^2-i^2b^2=a^2+b^2\in{\mathbb{R}}\) যা একটি বাস্তব সংখ্যা। সুতরাং কোনো জটিল সংখ্যাকে যে জটিল সংখ্যা দ্বারা গুণ করলে ফলাফল বাস্তব সংখ্যা হয় তাদের পরস্পর অনুবন্ধী
জটিল সংখ্যা বলা হয়।
\(a+ib\) এবং \(a-ib\) জটিল সংখ্যা দুইটির একটিকে অপরটির অনুবন্ধী জটিল সংখ্যা বলা হয়। কোনো জটিল সংখ্যার অনুবন্ধী জটিল সংখ্যা নির্ণয় করেতে শুধুমাত্র কাল্পনিক একক \(i\) এর চিহ্নের পরিবর্তন করতে হয়।
কোনো জটিল সংখ্যাকে \(Z\) দ্বারা প্রকাশ করলে, তার অনুবন্ধী জটিল সংখ্যাকে \(\overline{Z}\) অথবা \(Z^{\star}\) দ্বারা প্রকাশ করা হয়।
সুতরাং \(Z=a-ib\) হলে, \(\overline{Z}=a+ib\) বা \(Z^{\star}=a+ib\)
ফরাসি গণিতবিদ অগাস্টিন কসি (1789-1857) ১৮২১ খ্রিস্টাব্দে অনুবন্ধী শব্দটি প্রবর্তন করেন।
\(2+3i, \ 2-3i\) ও \(3i\) জটিল সংখ্যাগুলির অনুবন্ধী জটিল সংখ্যা যথাক্রমে \(2-3i, \ 2+3i\) ও \(-3i\)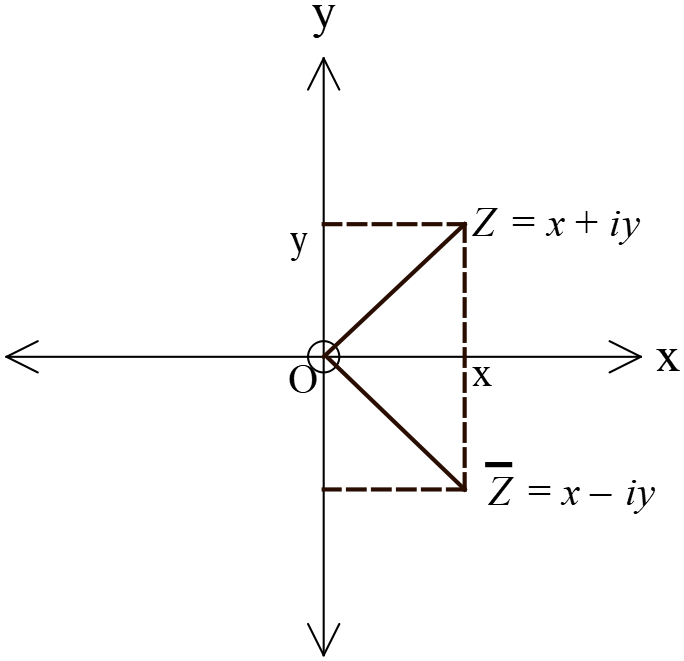
উল্লেখ্য জটিল সংখ্যার অনুবন্ধী সংখ্যাটিতে বাস্তব অংশের কোনো পরিবর্তন হয় না, কিন্তু কাল্পনিক অংশের চিহ্নের পরিবর্তন হয়।
যদি \(x\) কোনো বাস্তব সংখ্যা হয় তবে একে \(x+i.0\) লেখা যায় এবং সংখ্যাটির অনুবন্ধী সংখ্যা \(x-i.0=x\) হয়। অর্থাৎ কোনো জটিল সংখ্যার কাল্পনিক অংশ শূন্য (0) হলে তার অনুবন্ধী সংখ্যা ও ঐ সংখ্যাটি একই।
জটিল সমতলে কোনো জটিল সংখ্যা \(Z=x+iy\) এবং তার অনুবন্ধী জটিল সংখ্যা \(\overline{Z}=x-iy\) পাশের চিত্রে দেখানো হলো।
\(a+ib\) এবং \(a-ib\) জটিল সংখ্যা দুইটির একটিকে অপরটির অনুবন্ধী জটিল সংখ্যা বলা হয়। কোনো জটিল সংখ্যার অনুবন্ধী জটিল সংখ্যা নির্ণয় করেতে শুধুমাত্র কাল্পনিক একক \(i\) এর চিহ্নের পরিবর্তন করতে হয়।
কোনো জটিল সংখ্যাকে \(Z\) দ্বারা প্রকাশ করলে, তার অনুবন্ধী জটিল সংখ্যাকে \(\overline{Z}\) অথবা \(Z^{\star}\) দ্বারা প্রকাশ করা হয়।
সুতরাং \(Z=a-ib\) হলে, \(\overline{Z}=a+ib\) বা \(Z^{\star}=a+ib\)
ফরাসি গণিতবিদ অগাস্টিন কসি (1789-1857) ১৮২১ খ্রিস্টাব্দে অনুবন্ধী শব্দটি প্রবর্তন করেন।
\(2+3i, \ 2-3i\) ও \(3i\) জটিল সংখ্যাগুলির অনুবন্ধী জটিল সংখ্যা যথাক্রমে \(2-3i, \ 2+3i\) ও \(-3i\)
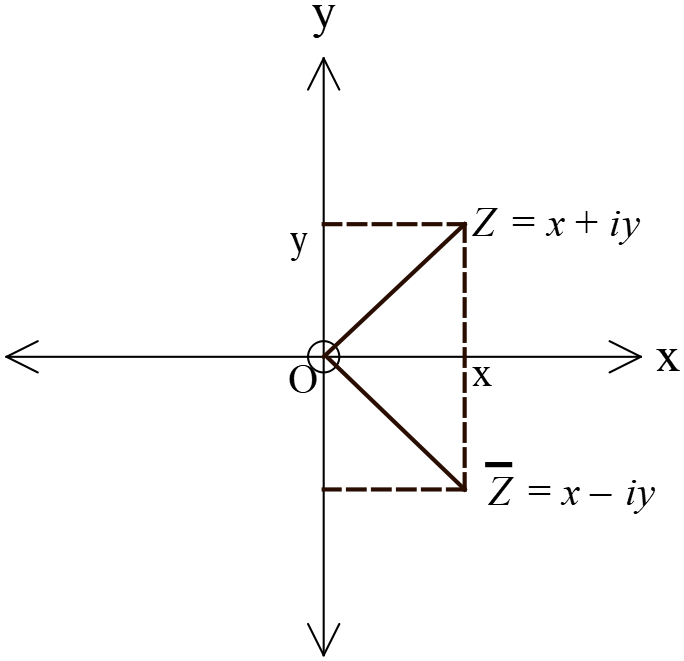
উল্লেখ্য জটিল সংখ্যার অনুবন্ধী সংখ্যাটিতে বাস্তব অংশের কোনো পরিবর্তন হয় না, কিন্তু কাল্পনিক অংশের চিহ্নের পরিবর্তন হয়।
যদি \(x\) কোনো বাস্তব সংখ্যা হয় তবে একে \(x+i.0\) লেখা যায় এবং সংখ্যাটির অনুবন্ধী সংখ্যা \(x-i.0=x\) হয়। অর্থাৎ কোনো জটিল সংখ্যার কাল্পনিক অংশ শূন্য (0) হলে তার অনুবন্ধী সংখ্যা ও ঐ সংখ্যাটি একই।
জটিল সমতলে কোনো জটিল সংখ্যা \(Z=x+iy\) এবং তার অনুবন্ধী জটিল সংখ্যা \(\overline{Z}=x-iy\) পাশের চিত্রে দেখানো হলো।
জটিল রাশিকে A+iB আকারে প্রকাশ
Express complex numbers in the form of A+iB
কোনো জটিল সংখ্যা \(Z_{2}=x_{2}+iy_{2}\ne{0}\) দ্বারা \(Z_{1}=x_{1}+iy_{1}\) কে ভাগ করলে তা, \(\frac{Z_{1}}{Z_{2}}=\frac{x_{1}+iy_{1}}{x_{2}+iy_{2}}\) হয়।
এ রাশিটিকে \(A+iB\) আকারে পরিণত করার পদ্ধতি নিম্নরূপঃ
\(\frac{x_{1}+iy_{1}}{x_{2}+iy_{2}}\)
\(=\frac{(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}\)
\(=\frac{x_{1}x_{2}-ix_{1}y_{2}+ix_{2}y_{1}-i^2y_{1}y_{2}}{x_{2}^2-i^2y_{2}^2}\)
\(=\frac{x_{1}x_{2}+i(x_{2}y_{1}-x_{1}y_{2})+y_{1}y_{2}}{x_{2}^2+y_{2}^2}\) ➜ \(\because i^2=-1\)
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})+i(x_{2}y_{1}-x_{1}y_{2})}{x_{2}^2+y_{2}^2}\)
\(=\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}+i\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}\) যা \(A+iB\) আকারের।
অর্থাৎ, ভাগ আকৃতির জটিল রাশিকে, রাশিটির হরের অনুবন্ধী সংখ্যা দ্বারা লব ও হরকে গুণ করে সরল করলে অপর একটি জটিল রাশি আকারে পরিণত করা যায়।
উদাহরণঃ \(\frac{-1+2i}{3+4i}\) কে \(A+iB\) আকারে প্রকাশ কর।
সমাধানঃ
প্রদত্ত রাশি
\(\frac{-1+2i}{3+4i}\)
\(=\frac{(-1+2i)(3-4i)}{(3+4i)(3-4i)}\) ➜ লব ও হরের সাথে \((3-4i)\) গুণ করে।
\(=\frac{-3+4i+6i-8i^2}{3^2-4^2i^2}\)
\(=\frac{-3+10i+8}{9+16}\) ➜ \(\because i^2=-1\)
\(=\frac{5+10i}{25}\)
\(=\frac{5}{25}+\frac{10}{25}i\)
\(=\frac{1}{5}+i\frac{2}{5}\)
\(A+iB\) আকারে প্রকাশ করঃ
\((1)\) \((a+ib)(c+id)\)
\((2)\) \(\frac{(1+i)^3}{4+3i}\)
\((3)\) \(\frac{5+2i}{4-3i}\)
দেওয়া আছে,
\((a+ib)(c+id)\)
\(=ac+iad+ibc+i^2bd\)
\(=ac+iad+ibc-bd\) ➜ \(\because i^2=-1\)
\(=(ac-bd)+i(ad+bc)\) যা \(A+iB\) আকারের।
\((2)\)
দেওয়া আছে,
\(\frac{(1+i)^3}{4+3i}\)
\(=\frac{1^3+3.1^2.i+3.1.i^2+i^3}{4+3i}\) ➜ \(\because (a+b)^3=a^3+3a^2b+3ab^2+b^3\)
\(=\frac{1+3i-3-i}{4+3i}\) ➜ \(\because i^2=-1, \ i^3=-i\)
\(=\frac{-2+2i}{4+3i}\)
\(=\frac{(-2+2i)(4-3i)}{(4+3i)(4-3i)}\) ➜ লব ও হরের সাথে \((4-3i)\) গুণ করে।
\(=\frac{-8+6i+8i-6i^2}{4^2-3^2i^2}\)
\(=\frac{-8+14i+6}{16+9}\) ➜ \(\because i^2=-1\)
\(=\frac{-2+14i}{25}\)
\(=-\frac{2}{25}+i\frac{14}{25}\) যা \(A+iB\) আকারের।
\((3)\)
দেওয়া আছে,
\(\frac{5+2i}{4-3i}\)
\(=\frac{(5+2i)(4+3i)}{(4-3i)(4+3i)}\) ➜ লব ও হরের সাথে \((4+3i)\) গুণ করে।
\(=\frac{20+15i+8i+6i^2}{4^2-3^2i^2}\)
\(=\frac{20+23i-6}{16+9}\) ➜ \(\because i^2=-1\)
\(=\frac{14+23i}{25}\)
\(=\frac{14}{25}+i\frac{23}{25}\) যা \(A+iB\) আকারের।
এ রাশিটিকে \(A+iB\) আকারে পরিণত করার পদ্ধতি নিম্নরূপঃ
\(\frac{x_{1}+iy_{1}}{x_{2}+iy_{2}}\)
\(=\frac{(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}\)
\(=\frac{x_{1}x_{2}-ix_{1}y_{2}+ix_{2}y_{1}-i^2y_{1}y_{2}}{x_{2}^2-i^2y_{2}^2}\)
\(=\frac{x_{1}x_{2}+i(x_{2}y_{1}-x_{1}y_{2})+y_{1}y_{2}}{x_{2}^2+y_{2}^2}\) ➜ \(\because i^2=-1\)
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})+i(x_{2}y_{1}-x_{1}y_{2})}{x_{2}^2+y_{2}^2}\)
\(=\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}+i\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}\) যা \(A+iB\) আকারের।
অর্থাৎ, ভাগ আকৃতির জটিল রাশিকে, রাশিটির হরের অনুবন্ধী সংখ্যা দ্বারা লব ও হরকে গুণ করে সরল করলে অপর একটি জটিল রাশি আকারে পরিণত করা যায়।
উদাহরণঃ \(\frac{-1+2i}{3+4i}\) কে \(A+iB\) আকারে প্রকাশ কর।
সমাধানঃ
প্রদত্ত রাশি
\(\frac{-1+2i}{3+4i}\)
\(=\frac{(-1+2i)(3-4i)}{(3+4i)(3-4i)}\) ➜ লব ও হরের সাথে \((3-4i)\) গুণ করে।
\(=\frac{-3+4i+6i-8i^2}{3^2-4^2i^2}\)
\(=\frac{-3+10i+8}{9+16}\) ➜ \(\because i^2=-1\)
\(=\frac{5+10i}{25}\)
\(=\frac{5}{25}+\frac{10}{25}i\)
\(=\frac{1}{5}+i\frac{2}{5}\)
\(A+iB\) আকারে প্রকাশ করঃ
\((1)\) \((a+ib)(c+id)\)
\((2)\) \(\frac{(1+i)^3}{4+3i}\)
\((3)\) \(\frac{5+2i}{4-3i}\)
সমাধানঃ
\((1)\) দেওয়া আছে,
\((a+ib)(c+id)\)
\(=ac+iad+ibc+i^2bd\)
\(=ac+iad+ibc-bd\) ➜ \(\because i^2=-1\)
\(=(ac-bd)+i(ad+bc)\) যা \(A+iB\) আকারের।
\((2)\)
দেওয়া আছে,
\(\frac{(1+i)^3}{4+3i}\)
\(=\frac{1^3+3.1^2.i+3.1.i^2+i^3}{4+3i}\) ➜ \(\because (a+b)^3=a^3+3a^2b+3ab^2+b^3\)
\(=\frac{1+3i-3-i}{4+3i}\) ➜ \(\because i^2=-1, \ i^3=-i\)
\(=\frac{-2+2i}{4+3i}\)
\(=\frac{(-2+2i)(4-3i)}{(4+3i)(4-3i)}\) ➜ লব ও হরের সাথে \((4-3i)\) গুণ করে।
\(=\frac{-8+6i+8i-6i^2}{4^2-3^2i^2}\)
\(=\frac{-8+14i+6}{16+9}\) ➜ \(\because i^2=-1\)
\(=\frac{-2+14i}{25}\)
\(=-\frac{2}{25}+i\frac{14}{25}\) যা \(A+iB\) আকারের।
\((3)\)
দেওয়া আছে,
\(\frac{5+2i}{4-3i}\)
\(=\frac{(5+2i)(4+3i)}{(4-3i)(4+3i)}\) ➜ লব ও হরের সাথে \((4+3i)\) গুণ করে।
\(=\frac{20+15i+8i+6i^2}{4^2-3^2i^2}\)
\(=\frac{20+23i-6}{16+9}\) ➜ \(\because i^2=-1\)
\(=\frac{14+23i}{25}\)
\(=\frac{14}{25}+i\frac{23}{25}\) যা \(A+iB\) আকারের।
জটিল সংখ্যার ধর্ম
Characteristics of complex numbers
কোনো জটিল সংখ্যা \(x+iy=0\) হবে, যদি \(x=0\) এবং \(y=0\) হয়।
প্রমাণঃ
\(x+iy=0,\) যেখানে \(x,y\in{\mathbb{R}}\)
\(\therefore x=-iy\)
\(\Rightarrow x^2=i^2y^2\)
\(\Rightarrow x^2=-y^2\) ➜ \(\because i^2=-1\)
\(\Rightarrow x^2+y^2=0\)
\(\therefore x=0, \ y=0\) ➜ একাধিক রাশির বর্গের যোগফল শূন্য হলে, রাশিগুলি পৃথকভাবে শূন্য হয়।
দুইটি জটিল সংখ্যা \(x_{1}+iy_{1}\) এবং \(x_{2}+iy_{2}\) সমান হবে যদি প্রথমটির বাস্তব অংশ \((x_{1})=\) দ্বিতীয়টির বাস্তব অংশ \((x_{2})\) এবং প্রথমটির কাল্পনিক অংশ \((y_{1})=\) দ্বিতীয়টির কাল্পনিক অংশ \((y_{2})\) হয়।
\(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা।
এবং \(Z_{1}=Z_{2}\)
\(\Rightarrow x_{1}+iy_{1}=x_{2}+iy_{2}\)
\(\Rightarrow x_{1}-x_{2}=iy_{2}-iy_{1}\)
\(\Rightarrow x_{1}-x_{2}=-i(y_{1}-y_{2})\)
\(\Rightarrow (x_{1}-x_{2})^2=i^2(y_{1}-y_{2})^2\) ➜ উভয় পার্শে বর্গ করে,
\(\Rightarrow (x_{1}-x_{2})^2=-(y_{1}-y_{2})^2\) ➜ \(\because i^2=-1\)
\(\Rightarrow (x_{1}-x_{2})^2+(y_{1}-y_{2})^2=0\)
\(\Rightarrow x_{1}-x_{2}=0, \ y_{1}-y_{2}=0\) ➜ একাধিক রাশির বর্গের যোগফল শূন্য হলে, রাশিগুলি পৃথকভাবে শূন্য হয়।
\(\therefore x_{1}=x_{2}, \ y_{1}=y_{2}\)
\(\therefore Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) জটিল সংখ্যা দুইটি সমান হবে অর্থাৎ, \(Z_{1}=Z_{2}\) হবে যদি এবং কেবল যদি \(x_{1}=x_{2}\) এবং \(y_{1}=y_{2}\) হয়।
অর্থাৎ, একটি জটিল সংখ্যার বাস্তব ও কাল্পনিক অংশ যথাক্রমে অপর একটি জটিল সংখ্যার বাস্তব ও কাল্পনিক অংশের সমান হলে জটিল সংখ্যা দুইটি সমান হবে।
কোনো জটিল সংখ্যার অনুবন্ধীর অনুবন্ধী ঐ জটিল সংখ্যাই অর্থাৎ \(\overline{\overline{Z}}=Z\)
প্রমাণঃ
ধরি, \(Z=x+iy\) তাহলে, \(\overline{Z}=x-iy\)
\(\Rightarrow \overline{\overline{Z}}=\overline{x-iy}\)
\(\Rightarrow \overline{\overline{Z}}=x+iy\) ➜ \(\because \overline{x-iy}=x+iy\)
\(\therefore \overline{\overline{Z}}=Z\)
দুইটি জটিল সংখ্যা \(Z\) এবং \(\overline{Z}\) এর সমষ্টি \(Z+\overline{Z}\) এবং গুণফল \(Z\overline{Z}\) উভয়ে বাস্তব সংখ্যা।
প্রমাণঃ
ধরি, \(Z=x+iy\) তাহলে, \(\overline{Z}=x-iy\)
এখন, \(Z+\overline{Z}\)
\(=x+iy+x-iy\)
\(=2x\) যা বাস্তব।
আবার,
\(Z\overline{Z}\)
\(=(x+iy)(x-iy)\)
\(=x^2-i^2y^2\)
\(=x^2+y^2\) যা বাস্তব। ➜ \(\because i^2=-1\)
দুইটি অনুবন্ধী জটিল সংখ্যা \(Z\) এবং \(\overline{Z}\) এর বিয়োগফল \(Z-\overline{Z}\) একটি কাল্পনিক সংখ্যা এবং ভাগফল \(\frac{Z}{\overline{Z}}\) একটি জটিল সংখ্যা।
প্রমাণঃ
ধরি, \(\sqrt[n]{a+ib}=x\)
তাহলে, \(a+ib=x^n\)
যদি \(x\) বাস্তব সংখ্যা হয় তবে \(x^n\) ও একটি বাস্তব সংখ্যা। সুতরাং একটি জটিল সংখ্যা \((a+ib)\) একটি বাস্তব সংখ্যা \((x^n)\) এর সমান হয়ে যায়, যা অসম্ভব। অতএব, \(x\) একটি জটিল সংখ্যা হবে। অর্থাৎ একটি জটিল সংখ্যার \(n-\)তম (যে কোনো সসীমতম) মূলও জটিল সংখ্যা হবে। সুতরাং একটি জটিল সংখ্যার মূল একটি জটিল সংখ্যা।
কোনো জটিল সংখ্যা \(Z=x+iy\) এর শক্তির সূচক ধনাত্মক পূর্ণসংখ্যা হলে শক্তিবিশিষ্ট জটিল সংখ্যাটিও একটি জটিল সংখ্যা।
(a) \(|Z|=|\overline{Z}|=|-Z|=|-\overline{Z}|\)
(b) \(|Z|^2=|\overline{Z}|^2=|-Z|^2=|-\overline{Z}|^2=Z\overline{Z}\)
\(|Z_{1}+Z_{2}+Z_{3}|\le{|Z_{1}|+|Z_{2}|+|Z_{3}|}\)
\(|Z_{1}+Z_{2}+....+Z_{n}|\le{|Z_{1}|+|Z_{2}|+....+|Z_{n}|}\)
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা হলে, \(|Z_{1}-Z_{2}|\le{|Z_{1}|+|Z_{2}|}\)
প্রমাণঃ
আমরা জানি, \(Z\times\frac{1}{Z}=1\)
\(\Rightarrow \left|Z\times\frac{1}{Z}\right|=|1|\)
\(\Rightarrow |Z|\times\left|\frac{1}{Z}\right|=1\) ➜ \(\because |ab|=|a||b|\)
\(\therefore \left|\frac{1}{Z}\right|=\frac{1}{|Z|}\)
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা এবং \(Z_{2}\ne{0}\) হলে, \(\left|\frac{Z_{1}}{Z_{2}}\right|=\frac{|Z_{1}|}{|Z_{2}|}\)
প্রমাণঃ
\(x+iy=0,\) যেখানে \(x,y\in{\mathbb{R}}\)
\(\therefore x=-iy\)
\(\Rightarrow x^2=i^2y^2\)
\(\Rightarrow x^2=-y^2\) ➜ \(\because i^2=-1\)
\(\Rightarrow x^2+y^2=0\)
\(\therefore x=0, \ y=0\) ➜ একাধিক রাশির বর্গের যোগফল শূন্য হলে, রাশিগুলি পৃথকভাবে শূন্য হয়।
দুইটি জটিল সংখ্যা \(x_{1}+iy_{1}\) এবং \(x_{2}+iy_{2}\) সমান হবে যদি প্রথমটির বাস্তব অংশ \((x_{1})=\) দ্বিতীয়টির বাস্তব অংশ \((x_{2})\) এবং প্রথমটির কাল্পনিক অংশ \((y_{1})=\) দ্বিতীয়টির কাল্পনিক অংশ \((y_{2})\) হয়।
প্রমাণঃ
দেওয়া আছে,\(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা।
এবং \(Z_{1}=Z_{2}\)
\(\Rightarrow x_{1}+iy_{1}=x_{2}+iy_{2}\)
\(\Rightarrow x_{1}-x_{2}=iy_{2}-iy_{1}\)
\(\Rightarrow x_{1}-x_{2}=-i(y_{1}-y_{2})\)
\(\Rightarrow (x_{1}-x_{2})^2=i^2(y_{1}-y_{2})^2\) ➜ উভয় পার্শে বর্গ করে,
\(\Rightarrow (x_{1}-x_{2})^2=-(y_{1}-y_{2})^2\) ➜ \(\because i^2=-1\)
\(\Rightarrow (x_{1}-x_{2})^2+(y_{1}-y_{2})^2=0\)
\(\Rightarrow x_{1}-x_{2}=0, \ y_{1}-y_{2}=0\) ➜ একাধিক রাশির বর্গের যোগফল শূন্য হলে, রাশিগুলি পৃথকভাবে শূন্য হয়।
\(\therefore x_{1}=x_{2}, \ y_{1}=y_{2}\)
\(\therefore Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) জটিল সংখ্যা দুইটি সমান হবে অর্থাৎ, \(Z_{1}=Z_{2}\) হবে যদি এবং কেবল যদি \(x_{1}=x_{2}\) এবং \(y_{1}=y_{2}\) হয়।
অর্থাৎ, একটি জটিল সংখ্যার বাস্তব ও কাল্পনিক অংশ যথাক্রমে অপর একটি জটিল সংখ্যার বাস্তব ও কাল্পনিক অংশের সমান হলে জটিল সংখ্যা দুইটি সমান হবে।
প্রমাণঃ
ধরি, \(Z=x+iy\) তাহলে, \(\overline{Z}=x-iy\)
\(\Rightarrow \overline{\overline{Z}}=\overline{x-iy}\)
\(\Rightarrow \overline{\overline{Z}}=x+iy\) ➜ \(\because \overline{x-iy}=x+iy\)
\(\therefore \overline{\overline{Z}}=Z\)
দুইটি জটিল সংখ্যা \(Z\) এবং \(\overline{Z}\) এর সমষ্টি \(Z+\overline{Z}\) এবং গুণফল \(Z\overline{Z}\) উভয়ে বাস্তব সংখ্যা।
প্রমাণঃ
ধরি, \(Z=x+iy\) তাহলে, \(\overline{Z}=x-iy\)
এখন, \(Z+\overline{Z}\)
\(=x+iy+x-iy\)
\(=2x\) যা বাস্তব।
আবার,
\(Z\overline{Z}\)
\(=(x+iy)(x-iy)\)
\(=x^2-i^2y^2\)
\(=x^2+y^2\) যা বাস্তব। ➜ \(\because i^2=-1\)
দুইটি অনুবন্ধী জটিল সংখ্যা \(Z\) এবং \(\overline{Z}\) এর বিয়োগফল \(Z-\overline{Z}\) একটি কাল্পনিক সংখ্যা এবং ভাগফল \(\frac{Z}{\overline{Z}}\) একটি জটিল সংখ্যা।
প্রমাণঃ
ধরি, \(Z=x+iy\) তাহলে, \(\overline{Z}=x-iy\)
এখন, \(Z-\overline{Z}\)
\(=x+iy-x+iy\)
\(=2iy\) যা কাল্পনিক সংখ্যা।
আবার,
\(\frac{Z}{\overline{Z}}\)
\(=\frac{x+iy}{x-iy}\)
\(=\frac{(x+iy)^2}{(x+iy)(x-iy)}\) ➜ লব ও হরের সাথে \((x+iy)\) গুণ করে।
\(=\frac{x^2+2xiy+i^2y^2}{x^2-i^2y^2}\)
\(=\frac{x^2+2xiy-y^2}{x^2+y^2}\) ➜ \(\because i^2=-1\)
\(=\frac{x^2-y^2+i2xy}{x^2+y^2}\)
\(=\frac{x^2-y^2}{x^2+y^2}+i\frac{2xy}{x^2+y^2}\) যা জটিল সংখ্যা।
অনুবন্ধী নয় এরূপ দুইটি জটিল সংখ্যা \(Z_{1}\) এবং \(Z_{2}\) এর যোগফল \((Z_{1}+Z_{2}),\) বিয়োগফল \((Z_{1}-Z_{2}),\) গুণফল \((Z_{1}Z_{2})\) এবং ভাগফল \(\frac{Z_{1}}{Z_{2}}\) প্রতিটিই এক একটি জটিল সংখ্যা।ধরি, \(Z=x+iy\) তাহলে, \(\overline{Z}=x-iy\)
এখন, \(Z-\overline{Z}\)
\(=x+iy-x+iy\)
\(=2iy\) যা কাল্পনিক সংখ্যা।
আবার,
\(\frac{Z}{\overline{Z}}\)
\(=\frac{x+iy}{x-iy}\)
\(=\frac{(x+iy)^2}{(x+iy)(x-iy)}\) ➜ লব ও হরের সাথে \((x+iy)\) গুণ করে।
\(=\frac{x^2+2xiy+i^2y^2}{x^2-i^2y^2}\)
\(=\frac{x^2+2xiy-y^2}{x^2+y^2}\) ➜ \(\because i^2=-1\)
\(=\frac{x^2-y^2+i2xy}{x^2+y^2}\)
\(=\frac{x^2-y^2}{x^2+y^2}+i\frac{2xy}{x^2+y^2}\) যা জটিল সংখ্যা।
প্রমাণঃ
ধরি, \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\)
এখন, \(Z_{1}+Z_{2}\)
\(=x_{1}+iy_{1}+x_{2}+iy_{2}\)
\(=(x_{1}+x_{2})+i(y_{1}+y_{2})\) যা জটিল সংখ্যা।
আবার, \(Z_{1}-Z_{2}\)
\(=x_{1}+iy_{1}-x_{2}-iy_{2}\)
\(=(x_{1}-x_{2})+i(y_{1}-y_{2})\) যা জটিল সংখ্যা।
আবার, \(Z_{1}Z_{2}\)
\(=(x_{1}+iy_{1})(x_{2}+iy_{2})\)
\(=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}+i^2y_{1}y_{2}\)
\(=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}-y_{1}y_{2}\) ➜ \(\because i^2=-1\)
\(=(x_{1}x_{2}-y_{1}y_{2})+i(x_{1}y_{2}+x_{2}y_{1})\) যা জটিল সংখ্যা।
আবার, \(\frac{Z_{1}}{Z_{2}}\)
\(=\frac{x_{1}+iy_{1}}{x_{2}+iy_{2}}\)
\(=\frac{(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}\) ➜ লব ও হরের সাথে \((x_{2}-iy_{2})\) গুণ করে।
\(=\frac{x_{1}x_{2}-ix_{1}y_{2}+ix_{2}y_{1}-i^2y_{1}y_{2}}{x_{2}^2-i^2y_{2}^2}\)
\(=\frac{x_{1}x_{2}+i(x_{2}y_{1}-x_{1}y_{2})+y_{1}y_{2}}{x_{2}^2+y_{2}^2}\) ➜ \(\because i^2=-1\)
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})+i(x_{2}y_{1}-x_{1}y_{2})}{x_{2}^2+y_{2}^2}\)
\(=\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}+i\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}\) যা জটিল সংখ্যা।
কোনো জটিল সংখ্যা \(Z=x+iy\) এর মূলও একটি জটিল সংখ্যা।ধরি, \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\)
এখন, \(Z_{1}+Z_{2}\)
\(=x_{1}+iy_{1}+x_{2}+iy_{2}\)
\(=(x_{1}+x_{2})+i(y_{1}+y_{2})\) যা জটিল সংখ্যা।
আবার, \(Z_{1}-Z_{2}\)
\(=x_{1}+iy_{1}-x_{2}-iy_{2}\)
\(=(x_{1}-x_{2})+i(y_{1}-y_{2})\) যা জটিল সংখ্যা।
আবার, \(Z_{1}Z_{2}\)
\(=(x_{1}+iy_{1})(x_{2}+iy_{2})\)
\(=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}+i^2y_{1}y_{2}\)
\(=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}-y_{1}y_{2}\) ➜ \(\because i^2=-1\)
\(=(x_{1}x_{2}-y_{1}y_{2})+i(x_{1}y_{2}+x_{2}y_{1})\) যা জটিল সংখ্যা।
আবার, \(\frac{Z_{1}}{Z_{2}}\)
\(=\frac{x_{1}+iy_{1}}{x_{2}+iy_{2}}\)
\(=\frac{(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}\) ➜ লব ও হরের সাথে \((x_{2}-iy_{2})\) গুণ করে।
\(=\frac{x_{1}x_{2}-ix_{1}y_{2}+ix_{2}y_{1}-i^2y_{1}y_{2}}{x_{2}^2-i^2y_{2}^2}\)
\(=\frac{x_{1}x_{2}+i(x_{2}y_{1}-x_{1}y_{2})+y_{1}y_{2}}{x_{2}^2+y_{2}^2}\) ➜ \(\because i^2=-1\)
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})+i(x_{2}y_{1}-x_{1}y_{2})}{x_{2}^2+y_{2}^2}\)
\(=\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}+i\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}\) যা জটিল সংখ্যা।
প্রমাণঃ
ধরি, \(\sqrt[n]{a+ib}=x\)
তাহলে, \(a+ib=x^n\)
যদি \(x\) বাস্তব সংখ্যা হয় তবে \(x^n\) ও একটি বাস্তব সংখ্যা। সুতরাং একটি জটিল সংখ্যা \((a+ib)\) একটি বাস্তব সংখ্যা \((x^n)\) এর সমান হয়ে যায়, যা অসম্ভব। অতএব, \(x\) একটি জটিল সংখ্যা হবে। অর্থাৎ একটি জটিল সংখ্যার \(n-\)তম (যে কোনো সসীমতম) মূলও জটিল সংখ্যা হবে। সুতরাং একটি জটিল সংখ্যার মূল একটি জটিল সংখ্যা।
কোনো জটিল সংখ্যা \(Z=x+iy\) এর শক্তির সূচক ধনাত্মক পূর্ণসংখ্যা হলে শক্তিবিশিষ্ট জটিল সংখ্যাটিও একটি জটিল সংখ্যা।
প্রমাণঃ
ধরি, \(Z=x+iy\)
তাহলে, \(Z^2=(x+iy)^2\)
\(=x^2+2xiy+i^2y^2\)
\(=x^2+2xiy-y^2\) ➜ \(\because i^2=-1\)
\(=(x^2-y^2)+i2xy\) যা জটিল সংখ্যা।
আবার, \(Z^3=(x+iy)^3\)
\(=x^3+3x^2iy+3xi^2y^2+i^3y^3\)
\(=x^3+3x^2iy-3xy^2-iy^3\) ➜ \(\because i^2=-1, \ i^3=-i\)
\(=(x^3-3xy^2)+i(3x^2y-y^3\) যা জটিল সংখ্যা।
অনুরূপভাবে অগ্রসর হলে \(Z^n\) একটি জটিল সংখ্যা দেখানো যাবে। এখানে \(n\) যে কোনো ধনাত্মক পূর্ণসংখ্যা।
ধরি, \(Z=x+iy\)
তাহলে, \(Z^2=(x+iy)^2\)
\(=x^2+2xiy+i^2y^2\)
\(=x^2+2xiy-y^2\) ➜ \(\because i^2=-1\)
\(=(x^2-y^2)+i2xy\) যা জটিল সংখ্যা।
আবার, \(Z^3=(x+iy)^3\)
\(=x^3+3x^2iy+3xi^2y^2+i^3y^3\)
\(=x^3+3x^2iy-3xy^2-iy^3\) ➜ \(\because i^2=-1, \ i^3=-i\)
\(=(x^3-3xy^2)+i(3x^2y-y^3\) যা জটিল সংখ্যা।
অনুরূপভাবে অগ্রসর হলে \(Z^n\) একটি জটিল সংখ্যা দেখানো যাবে। এখানে \(n\) যে কোনো ধনাত্মক পূর্ণসংখ্যা।
জটিল সংখ্যার মডুলাস (পরমমান) এবং আর্গুমেন্ট (নতি) সংক্রান্ত ধর্ম
কোনো জটিল সংখ্যা \(Z=x+iy\) হলে (a) \(|Z|=|\overline{Z}|=|-Z|=|-\overline{Z}|\)
(b) \(|Z|^2=|\overline{Z}|^2=|-Z|^2=|-\overline{Z}|^2=Z\overline{Z}\)
প্রমাণঃ
(a) ধরি, \(Z=x+iy\)
তাহলে, \(\overline{Z}=x-iy\)
\(-Z=-x-iy\)
এবং \(-\overline{Z}=-x+iy\)
এখন, \(|Z|=\sqrt{x^2+y^2}\)
\(|\overline{Z}|=\sqrt{x^2+(-y)^2}=\sqrt{x^2+y^2}\)
\(|-Z|=\sqrt{(-x)^2+(-y)^2}=\sqrt{x^2+y^2}\)
\(|-\overline{Z}|=\sqrt{(-x)^2+y^2}=\sqrt{x^2+y^2}\)
সুতরাং,\(|Z|=|\overline{Z}|=|-Z|=|-\overline{Z}|\)
(b) ধরি, \(Z=x+iy\)
তাহলে, \(\overline{Z}=x-iy\)
\(-Z=-x-iy\)
এবং \(-\overline{Z}=-x+iy\)
এখন, \(|Z|=\sqrt{x^2+y^2} \Rightarrow |Z|^2=x^2+y^2\)
\(\Rightarrow |Z|^2=x^2+y^2\)
\(|\overline{Z}|=\sqrt{x^2+(-y)^2}=\sqrt{x^2+y^2}\)
\(\Rightarrow |\overline{Z}|^2=x^2+y^2\)
\(|-Z|=\sqrt{(-x)^2+(-y)^2}=\sqrt{x^2+y^2}\)
\(\Rightarrow |-Z|^2=x^2+y^2\)
\(|-\overline{Z}|=\sqrt{(-x)^2+y^2}=\sqrt{x^2+y^2}\)
\(\Rightarrow |-\overline{Z}|^2=x^2+y^2\)
এবং \(Z\overline{Z}=(x+iy)(x-iy)=x^2-i^2y^2=x^2+y^2\)
সুতরাং,\(|Z|^2=|\overline{Z}|^2=|-Z|^2=|-\overline{Z}|^2=Z\overline{Z}\)
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা হলে, \(|Z_{1}+Z_{2}|\le{|Z_{1}|+|Z_{2}|}\) (a) ধরি, \(Z=x+iy\)
তাহলে, \(\overline{Z}=x-iy\)
\(-Z=-x-iy\)
এবং \(-\overline{Z}=-x+iy\)
এখন, \(|Z|=\sqrt{x^2+y^2}\)
\(|\overline{Z}|=\sqrt{x^2+(-y)^2}=\sqrt{x^2+y^2}\)
\(|-Z|=\sqrt{(-x)^2+(-y)^2}=\sqrt{x^2+y^2}\)
\(|-\overline{Z}|=\sqrt{(-x)^2+y^2}=\sqrt{x^2+y^2}\)
সুতরাং,\(|Z|=|\overline{Z}|=|-Z|=|-\overline{Z}|\)
(b) ধরি, \(Z=x+iy\)
তাহলে, \(\overline{Z}=x-iy\)
\(-Z=-x-iy\)
এবং \(-\overline{Z}=-x+iy\)
এখন, \(|Z|=\sqrt{x^2+y^2} \Rightarrow |Z|^2=x^2+y^2\)
\(\Rightarrow |Z|^2=x^2+y^2\)
\(|\overline{Z}|=\sqrt{x^2+(-y)^2}=\sqrt{x^2+y^2}\)
\(\Rightarrow |\overline{Z}|^2=x^2+y^2\)
\(|-Z|=\sqrt{(-x)^2+(-y)^2}=\sqrt{x^2+y^2}\)
\(\Rightarrow |-Z|^2=x^2+y^2\)
\(|-\overline{Z}|=\sqrt{(-x)^2+y^2}=\sqrt{x^2+y^2}\)
\(\Rightarrow |-\overline{Z}|^2=x^2+y^2\)
এবং \(Z\overline{Z}=(x+iy)(x-iy)=x^2-i^2y^2=x^2+y^2\)
সুতরাং,\(|Z|^2=|\overline{Z}|^2=|-Z|^2=|-\overline{Z}|^2=Z\overline{Z}\)
প্রমাণঃ
দেওয়া আছে, \(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(|Z_{1}+Z_{2}|^2=(Z_{1}+Z_{2})(\overline{Z_{1}+Z_{2}})\) ➜ \(\because |Z|^2=Z\overline{Z}\)
\(=(Z_{1}+Z_{2})(\overline{Z_{1}}+\overline{Z_{2}})\) ➜ \(\because \overline{Z_{1}+Z_{2}}=\overline{Z_{1}}+\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}+Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}}+Z_{2}\overline{Z_{2}}\)
\(=|Z_{1}|^2+2Re(Z_{1}\overline{Z_{2}})+|Z_{2}|^2\) ➜ \(\because Z\overline{Z}=|Z|^2, \ Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}}=2Re(Z_{1}\overline{Z_{2}})\)
\(\therefore |Z_{1}+Z_{2}|^2\le{|Z_{1}|^2+2|Z_{1}\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because Re(Z)\le{|Z|}\)
\(\Rightarrow |Z_{1}+Z_{2}|^2\le{|Z_{1}|^2+2|Z_{1}||\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
\(\Rightarrow |Z_{1}+Z_{2}|^2\le{(|Z_{1}|+|Z_{2}|)^2}\)
\(\therefore |Z_{1}+Z_{2}|\le{|Z_{1}|+|Z_{2}|}\)
অনুসিদ্ধান্তঃদেওয়া আছে, \(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(|Z_{1}+Z_{2}|^2=(Z_{1}+Z_{2})(\overline{Z_{1}+Z_{2}})\) ➜ \(\because |Z|^2=Z\overline{Z}\)
\(=(Z_{1}+Z_{2})(\overline{Z_{1}}+\overline{Z_{2}})\) ➜ \(\because \overline{Z_{1}+Z_{2}}=\overline{Z_{1}}+\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}+Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}}+Z_{2}\overline{Z_{2}}\)
\(=|Z_{1}|^2+2Re(Z_{1}\overline{Z_{2}})+|Z_{2}|^2\) ➜ \(\because Z\overline{Z}=|Z|^2, \ Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}}=2Re(Z_{1}\overline{Z_{2}})\)
\(\therefore |Z_{1}+Z_{2}|^2\le{|Z_{1}|^2+2|Z_{1}\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because Re(Z)\le{|Z|}\)
\(\Rightarrow |Z_{1}+Z_{2}|^2\le{|Z_{1}|^2+2|Z_{1}||\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
\(\Rightarrow |Z_{1}+Z_{2}|^2\le{(|Z_{1}|+|Z_{2}|)^2}\)
\(\therefore |Z_{1}+Z_{2}|\le{|Z_{1}|+|Z_{2}|}\)
\(|Z_{1}+Z_{2}+Z_{3}|\le{|Z_{1}|+|Z_{2}|+|Z_{3}|}\)
\(|Z_{1}+Z_{2}+....+Z_{n}|\le{|Z_{1}|+|Z_{2}|+....+|Z_{n}|}\)
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা হলে, \(|Z_{1}-Z_{2}|\le{|Z_{1}|+|Z_{2}|}\)
প্রমাণঃ
দেওয়া আছে, \(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(|Z_{1}-Z_{2}|^2=(Z_{1}-Z_{2})(\overline{Z_{1}-Z_{2}})\) ➜ \(\because |Z|^2=Z\overline{Z}\)
\(=(Z_{1}-Z_{2})(\overline{Z_{1}}-\overline{Z_{2}})\) ➜ \(\because \overline{Z_{1}-Z_{2}}=\overline{Z_{1}}-\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}-Z_{1}\overline{Z_{2}}-Z_{2}\overline{Z_{1}}+Z_{2}\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}-(Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}})+Z_{2}\overline{Z_{2}}\)
\(=|Z_{1}|^2-2Re(Z_{1}\overline{Z_{2}})+|Z_{2}|^2\) ➜ \(\because Z\overline{Z}=|Z|^2, \ Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}}=2Re(Z_{1}\overline{Z_{2}})\)
\(\therefore |Z_{1}-Z_{2}|^2\le{|Z_{1}|^2+2|Z_{1}\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because Re(Z)\le{|Z|}\)
\(\Rightarrow |Z_{1}-Z_{2}|^2\le{|Z_{1}|^2+2|Z_{1}||\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
\(\Rightarrow |Z_{1}-Z_{2}|^2\le{(|Z_{1}|+|Z_{2}|)^2}\)
\(\therefore |Z_{1}-Z_{2}|\le{|Z_{1}|+|Z_{2}|}\)
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা হলে, \(|Z_{1}-Z_{2}|\ge{|Z_{1}|-|Z_{2}|}\) দেওয়া আছে, \(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(|Z_{1}-Z_{2}|^2=(Z_{1}-Z_{2})(\overline{Z_{1}-Z_{2}})\) ➜ \(\because |Z|^2=Z\overline{Z}\)
\(=(Z_{1}-Z_{2})(\overline{Z_{1}}-\overline{Z_{2}})\) ➜ \(\because \overline{Z_{1}-Z_{2}}=\overline{Z_{1}}-\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}-Z_{1}\overline{Z_{2}}-Z_{2}\overline{Z_{1}}+Z_{2}\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}-(Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}})+Z_{2}\overline{Z_{2}}\)
\(=|Z_{1}|^2-2Re(Z_{1}\overline{Z_{2}})+|Z_{2}|^2\) ➜ \(\because Z\overline{Z}=|Z|^2, \ Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}}=2Re(Z_{1}\overline{Z_{2}})\)
\(\therefore |Z_{1}-Z_{2}|^2\le{|Z_{1}|^2+2|Z_{1}\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because Re(Z)\le{|Z|}\)
\(\Rightarrow |Z_{1}-Z_{2}|^2\le{|Z_{1}|^2+2|Z_{1}||\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
\(\Rightarrow |Z_{1}-Z_{2}|^2\le{(|Z_{1}|+|Z_{2}|)^2}\)
\(\therefore |Z_{1}-Z_{2}|\le{|Z_{1}|+|Z_{2}|}\)
প্রমাণঃ
দেওয়া আছে, \(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(|Z_{1}-Z_{2}|^2=(Z_{1}-Z_{2})(\overline{Z_{1}-Z_{2}})\) ➜ \(\because |Z|^2=Z\overline{Z}\)
\(=(Z_{1}-Z_{2})(\overline{Z_{1}}-\overline{Z_{2}})\) ➜ \(\because \overline{Z_{1}-Z_{2}}=\overline{Z_{1}}-\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}-Z_{1}\overline{Z_{2}}-Z_{2}\overline{Z_{1}}+Z_{2}\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}-(Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}})+Z_{2}\overline{Z_{2}}\)
\(=|Z_{1}|^2-2Re(Z_{1}\overline{Z_{2}})+|Z_{2}|^2\) ➜ \(\because Z\overline{Z}=|Z|^2, \ Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}}=2Re(Z_{1}\overline{Z_{2}})\)
\(\therefore |Z_{1}-Z_{2}|^2\ge{|Z_{1}|^2-2|Z_{1}\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because Re(Z)\le{|Z|}\)
\(\Rightarrow |Z_{1}-Z_{2}|^2\ge{|Z_{1}|^2-2|Z_{1}||\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
\(\Rightarrow |Z_{1}-Z_{2}|^2\ge{(|Z_{1}|-|Z_{2}|)^2}\)
\(\therefore |Z_{1}-Z_{2}|\ge{|Z_{1}|-|Z_{2}|}\)
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা হলে, \(|Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\) দেওয়া আছে, \(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(|Z_{1}-Z_{2}|^2=(Z_{1}-Z_{2})(\overline{Z_{1}-Z_{2}})\) ➜ \(\because |Z|^2=Z\overline{Z}\)
\(=(Z_{1}-Z_{2})(\overline{Z_{1}}-\overline{Z_{2}})\) ➜ \(\because \overline{Z_{1}-Z_{2}}=\overline{Z_{1}}-\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}-Z_{1}\overline{Z_{2}}-Z_{2}\overline{Z_{1}}+Z_{2}\overline{Z_{2}}\)
\(=Z_{1}\overline{Z_{1}}-(Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}})+Z_{2}\overline{Z_{2}}\)
\(=|Z_{1}|^2-2Re(Z_{1}\overline{Z_{2}})+|Z_{2}|^2\) ➜ \(\because Z\overline{Z}=|Z|^2, \ Z_{1}\overline{Z_{2}}+Z_{2}\overline{Z_{1}}=2Re(Z_{1}\overline{Z_{2}})\)
\(\therefore |Z_{1}-Z_{2}|^2\ge{|Z_{1}|^2-2|Z_{1}\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because Re(Z)\le{|Z|}\)
\(\Rightarrow |Z_{1}-Z_{2}|^2\ge{|Z_{1}|^2-2|Z_{1}||\overline{Z_{2}}|+|Z_{2}|^2}\) ➜ \(\because |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
\(\Rightarrow |Z_{1}-Z_{2}|^2\ge{(|Z_{1}|-|Z_{2}|)^2}\)
\(\therefore |Z_{1}-Z_{2}|\ge{|Z_{1}|-|Z_{2}|}\)
প্রমাণঃ
ধরি, \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(Z_{1}Z_{2}=(x_{1}+iy_{1})(x_{2}+iy_{2})\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}+i^2y_{1}y_{2}\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}-y_{1}y_{2}\) ➜ \(\because i^2=-1\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}-y_{1}y_{2}+i(x_{1}y_{2}+x_{2}y_{1})\)
\(\Rightarrow |Z_{1}Z_{2}|=|x_{1}x_{2}-y_{1}y_{2}+i(x_{1}y_{2}+x_{2}y_{1})|\)
\(\Rightarrow |Z_{1}Z_{2}|=\sqrt{(x_{1}x_{2}-y_{1}y_{2})^2+(x_{1}y_{2}+x_{2}y_{1})^2}\) ➜ \(\because |x+iy|=\sqrt{x^2+y^2}\)
\(\Rightarrow |Z_{1}Z_{2}|^2=(x_{1}x_{2}-y_{1}y_{2})^2+(x_{1}y_{2}+x_{2}y_{1})^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow |Z_{1}Z_{2}|^2=(x_{1}^2+y_{1}^2)(x_{2}^2+y_{2}^2)\) ➜ \(\because (ac-bd)^2+(ad+bc)^2=(a^2+b^2)(c^2+d^2)\)
\(\Rightarrow |Z_{1}Z_{2}|^2=|x_{1}+iy_{1}|^2|x_{2}+iy_{2}|^2\)
\(\Rightarrow |Z_{1}Z_{2}|^2=|Z_{1}|^2|Z_{2}|^2\)
\(\Rightarrow |Z_{1}Z_{2}|^2=(|Z_{1}||Z_{2}|)^2\)
\(\therefore |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
অর্থাৎ, দুইটি জটিল সংখ্যার গুণফলের মডুলাস তাদের মডুলাসের গুণফলের সমান।
কোনো জটিল সংখ্যা \(Z\ne{0}\) হলে, \(\left|\frac{1}{Z}\right|=\frac{1}{|Z|}\) ধরি, \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(Z_{1}Z_{2}=(x_{1}+iy_{1})(x_{2}+iy_{2})\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}+i^2y_{1}y_{2}\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}-y_{1}y_{2}\) ➜ \(\because i^2=-1\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}-y_{1}y_{2}+i(x_{1}y_{2}+x_{2}y_{1})\)
\(\Rightarrow |Z_{1}Z_{2}|=|x_{1}x_{2}-y_{1}y_{2}+i(x_{1}y_{2}+x_{2}y_{1})|\)
\(\Rightarrow |Z_{1}Z_{2}|=\sqrt{(x_{1}x_{2}-y_{1}y_{2})^2+(x_{1}y_{2}+x_{2}y_{1})^2}\) ➜ \(\because |x+iy|=\sqrt{x^2+y^2}\)
\(\Rightarrow |Z_{1}Z_{2}|^2=(x_{1}x_{2}-y_{1}y_{2})^2+(x_{1}y_{2}+x_{2}y_{1})^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow |Z_{1}Z_{2}|^2=(x_{1}^2+y_{1}^2)(x_{2}^2+y_{2}^2)\) ➜ \(\because (ac-bd)^2+(ad+bc)^2=(a^2+b^2)(c^2+d^2)\)
\(\Rightarrow |Z_{1}Z_{2}|^2=|x_{1}+iy_{1}|^2|x_{2}+iy_{2}|^2\)
\(\Rightarrow |Z_{1}Z_{2}|^2=|Z_{1}|^2|Z_{2}|^2\)
\(\Rightarrow |Z_{1}Z_{2}|^2=(|Z_{1}||Z_{2}|)^2\)
\(\therefore |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
অর্থাৎ, দুইটি জটিল সংখ্যার গুণফলের মডুলাস তাদের মডুলাসের গুণফলের সমান।
প্রমাণঃ
আমরা জানি, \(Z\times\frac{1}{Z}=1\)
\(\Rightarrow \left|Z\times\frac{1}{Z}\right|=|1|\)
\(\Rightarrow |Z|\times\left|\frac{1}{Z}\right|=1\) ➜ \(\because |ab|=|a||b|\)
\(\therefore \left|\frac{1}{Z}\right|=\frac{1}{|Z|}\)
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা এবং \(Z_{2}\ne{0}\) হলে, \(\left|\frac{Z_{1}}{Z_{2}}\right|=\frac{|Z_{1}|}{|Z_{2}|}\)
প্রমাণঃ
দেওয়া আছে, \(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা এবং \(Z_{2}\ne{0}\)
তাহলে, \(\left|\frac{Z_{1}}{Z_{2}}\right|=\left|Z_{1}\times\frac{1}{Z_{2}}\right|\)
\(=|Z_{1}|\times\left|\frac{1}{Z_{2}}\right|\) ➜ \(\because |ab|=|a||b|\)
\(=|Z_{1}|\times\frac{1}{|Z_{2}|}\)
\(=\frac{|Z_{1}|}{|Z_{2}|}\)
\(\therefore \left|\frac{Z_{1}}{Z_{2}}\right|=\frac{|Z_{1}|}{|Z_{2}|}\)
অর্থাৎ, দুইটি জটিল সংখ্যার ভাগফলের মডুলাস তাদের মডুলাসের ভাগফলের সমান।
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা হলে, \(arg(Z_{1}Z_{2})=arg(Z_{1})+arg(Z_{2})\) দেওয়া আছে, \(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা এবং \(Z_{2}\ne{0}\)
তাহলে, \(\left|\frac{Z_{1}}{Z_{2}}\right|=\left|Z_{1}\times\frac{1}{Z_{2}}\right|\)
\(=|Z_{1}|\times\left|\frac{1}{Z_{2}}\right|\) ➜ \(\because |ab|=|a||b|\)
\(=|Z_{1}|\times\frac{1}{|Z_{2}|}\)
\(=\frac{|Z_{1}|}{|Z_{2}|}\)
\(\therefore \left|\frac{Z_{1}}{Z_{2}}\right|=\frac{|Z_{1}|}{|Z_{2}|}\)
অর্থাৎ, দুইটি জটিল সংখ্যার ভাগফলের মডুলাস তাদের মডুলাসের ভাগফলের সমান।
প্রমাণঃ
ধরি, \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(Z_{1}Z_{2}=(x_{1}+iy_{1})(x_{2}+iy_{2})\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}+i^2y_{1}y_{2}\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}-y_{1}y_{2}\) ➜ \(\because i^2=-1\)
\(\Rightarrow Z_{1}Z_{2}=(x_{1}x_{2}-y_{1}y_{2})+i(x_{1}y_{2}+x_{2}y_{1})\)
\(\Rightarrow arg(Z_{1}Z_{2})=\tan^{-1}{\left\{\frac{x_{1}y_{2}+x_{2}y_{1}}{x_{1}x_{2}-y_{1}y_{2}}\right\}}\)
\(=\tan^{-1}{\left\{\frac{\frac{x_{1}y_{2}+x_{2}y_{1}}{x_{1}x_{2}}}{\frac{x_{1}x_{2}-y_{1}y_{2}}{x_{1}x_{2}}}\right\}}\) ➜ লব ও হরের সাথে \((x_{1}x_{2})\) ভাগ করে।
\(=\tan^{-1}{\left\{\frac{\frac{y_{2}}{x_{2}}+\frac{y_{1}}{x_{1}}}{1-\frac{y_{1}}{x_{1}}.\frac{y_{2}}{x_{2}}}\right\}}\)
\(=\tan^{-1}{\left\{\frac{\frac{y_{1}}{x_{1}}+\frac{y_{2}}{x_{2}}}{1-\frac{y_{1}}{x_{1}}.\frac{y_{2}}{x_{2}}}\right\}}\)
\(=\tan^{-1}{\frac{y_{1}}{x_{1}}}+\tan^{-1}{\frac{y_{2}}{x_{2}}}\) ➜ \(\because \tan^{-1}{\left(\frac{a+b}{1-ab}\right)}=\tan^{-1}{a}+\tan^{-1}{b}\)
\(=arg(Z_{1})+arg(Z_{2})\)
\(\therefore arg(Z_{1}Z_{2})=arg(Z_{1})+arg(Z_{2})\)
\(Z_{1}\) এবং \(Z_{2}\) দুইটি জটিল সংখ্যা হলে, \(arg\left(\frac{Z_{1}}{Z_{2}}\right)=arg(Z_{1})-arg(Z_{2})\) ধরি, \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(Z_{1}Z_{2}=(x_{1}+iy_{1})(x_{2}+iy_{2})\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}+i^2y_{1}y_{2}\)
\(\Rightarrow Z_{1}Z_{2}=x_{1}x_{2}+ix_{1}y_{2}+ix_{2}y_{1}-y_{1}y_{2}\) ➜ \(\because i^2=-1\)
\(\Rightarrow Z_{1}Z_{2}=(x_{1}x_{2}-y_{1}y_{2})+i(x_{1}y_{2}+x_{2}y_{1})\)
\(\Rightarrow arg(Z_{1}Z_{2})=\tan^{-1}{\left\{\frac{x_{1}y_{2}+x_{2}y_{1}}{x_{1}x_{2}-y_{1}y_{2}}\right\}}\)
\(=\tan^{-1}{\left\{\frac{\frac{x_{1}y_{2}+x_{2}y_{1}}{x_{1}x_{2}}}{\frac{x_{1}x_{2}-y_{1}y_{2}}{x_{1}x_{2}}}\right\}}\) ➜ লব ও হরের সাথে \((x_{1}x_{2})\) ভাগ করে।
\(=\tan^{-1}{\left\{\frac{\frac{y_{2}}{x_{2}}+\frac{y_{1}}{x_{1}}}{1-\frac{y_{1}}{x_{1}}.\frac{y_{2}}{x_{2}}}\right\}}\)
\(=\tan^{-1}{\left\{\frac{\frac{y_{1}}{x_{1}}+\frac{y_{2}}{x_{2}}}{1-\frac{y_{1}}{x_{1}}.\frac{y_{2}}{x_{2}}}\right\}}\)
\(=\tan^{-1}{\frac{y_{1}}{x_{1}}}+\tan^{-1}{\frac{y_{2}}{x_{2}}}\) ➜ \(\because \tan^{-1}{\left(\frac{a+b}{1-ab}\right)}=\tan^{-1}{a}+\tan^{-1}{b}\)
\(=arg(Z_{1})+arg(Z_{2})\)
\(\therefore arg(Z_{1}Z_{2})=arg(Z_{1})+arg(Z_{2})\)
প্রমাণঃ
ধরি, \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(\frac{Z_{1}}{Z_{2}}=\frac{x_{1}+iy_{1}}{x_{2}+iy_{2}}\)
\(=\frac{(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}\) ➜ লব ও হরের সাথে \((x_{2}-iy_{2})\) গুণ করে।
\(=\frac{x_{1}x_{2}-ix_{1}y_{2}+ix_{2}y_{1}-i^2y_{1}y_{2}}{x_{2}^2-i^2y_{2}^2}\)
\(=\frac{x_{1}x_{2}+ix_{2}y_{1}-ix_{1}y_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}\) ➜ \(\because i^2=-1\)
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})+i(x_{2}y_{1}-x_{1}y_{2})}{x_{2}^2+y_{2}^2}\)
\(=\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}+i\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}\)
\(\therefore \frac{Z_{1}}{Z_{2}}=\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}+i\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}\)
\(\therefore arg\left(\frac{Z_{1}}{Z_{2}}\right)=\tan^{-1}{\left(\frac{\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}}{\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}}\right)}\)
\(=\tan^{-1}{\left(\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{1}x_{2}+y_{1}y_{2}}\right)}\) ➜ লব ও হরের সাথে \((x_{2}^2+y_{2}^2)\) গুণ করে।
\(=\tan^{-1}{\left(\frac{\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{1}x_{2}}}{\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{1}x_{2}}}\right)}\) ➜ লব ও হরের সাথে \((x_{1}x_{2})\) ভাগ করে।
\(=\tan^{-1}{\left\{\frac{\frac{y_{1}}{x_{1}}-\frac{y_{2}}{x_{2}}}{1+\frac{y_{1}}{x_{1}}.\frac{y_{2}}{x_{2}}}\right\}}\)
\(=\tan^{-1}{\frac{y_{1}}{x_{1}}}-\tan^{-1}{\frac{y_{2}}{x_{2}}}\) ➜ \(\because \tan^{-1}{\left(\frac{a-b}{1+ab}\right)}=\tan^{-1}{a}-\tan^{-1}{b}\)
\(=arg(Z_{1})-arg(Z_{2})\)
\(\therefore arg\left(\frac{Z_{1}}{Z_{2}}\right)=arg(Z_{1})-arg(Z_{2})\)
ধরি, \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) দুইটি জটিল সংখ্যা
তাহলে, \(\frac{Z_{1}}{Z_{2}}=\frac{x_{1}+iy_{1}}{x_{2}+iy_{2}}\)
\(=\frac{(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}\) ➜ লব ও হরের সাথে \((x_{2}-iy_{2})\) গুণ করে।
\(=\frac{x_{1}x_{2}-ix_{1}y_{2}+ix_{2}y_{1}-i^2y_{1}y_{2}}{x_{2}^2-i^2y_{2}^2}\)
\(=\frac{x_{1}x_{2}+ix_{2}y_{1}-ix_{1}y_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}\) ➜ \(\because i^2=-1\)
\(=\frac{(x_{1}x_{2}+y_{1}y_{2})+i(x_{2}y_{1}-x_{1}y_{2})}{x_{2}^2+y_{2}^2}\)
\(=\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}+i\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}\)
\(\therefore \frac{Z_{1}}{Z_{2}}=\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}+i\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}\)
\(\therefore arg\left(\frac{Z_{1}}{Z_{2}}\right)=\tan^{-1}{\left(\frac{\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}^2+y_{2}^2}}{\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{2}^2+y_{2}^2}}\right)}\)
\(=\tan^{-1}{\left(\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{1}x_{2}+y_{1}y_{2}}\right)}\) ➜ লব ও হরের সাথে \((x_{2}^2+y_{2}^2)\) গুণ করে।
\(=\tan^{-1}{\left(\frac{\frac{x_{2}y_{1}-x_{1}y_{2}}{x_{1}x_{2}}}{\frac{x_{1}x_{2}+y_{1}y_{2}}{x_{1}x_{2}}}\right)}\) ➜ লব ও হরের সাথে \((x_{1}x_{2})\) ভাগ করে।
\(=\tan^{-1}{\left\{\frac{\frac{y_{1}}{x_{1}}-\frac{y_{2}}{x_{2}}}{1+\frac{y_{1}}{x_{1}}.\frac{y_{2}}{x_{2}}}\right\}}\)
\(=\tan^{-1}{\frac{y_{1}}{x_{1}}}-\tan^{-1}{\frac{y_{2}}{x_{2}}}\) ➜ \(\because \tan^{-1}{\left(\frac{a-b}{1+ab}\right)}=\tan^{-1}{a}-\tan^{-1}{b}\)
\(=arg(Z_{1})-arg(Z_{2})\)
\(\therefore arg\left(\frac{Z_{1}}{Z_{2}}\right)=arg(Z_{1})-arg(Z_{2})\)
জটিল সংখ্যার যোগ ও বিয়োগের জ্যামিতিক প্রতিরূপ
Geometrical Representation of the Addition and subtraction of complex numbers
ধরি, জটিল সমতলে \(Z_{1}=x_{1}+iy_{1}\) এবং \(Z_{2}=x_{2}+iy_{2}\) জটিল সংখ্যাদ্বয় যথাক্রমে \(P\) ও \(Q\) বিন্দু দ্বারা সূচিত। । \(OPRQ\) একটি সামান্তরিক অঙ্কন করি, যেখানে \(OP\) এবং \(OQ\) সামান্তরিকের সন্নিহিত বাহু নির্দেশ করে। 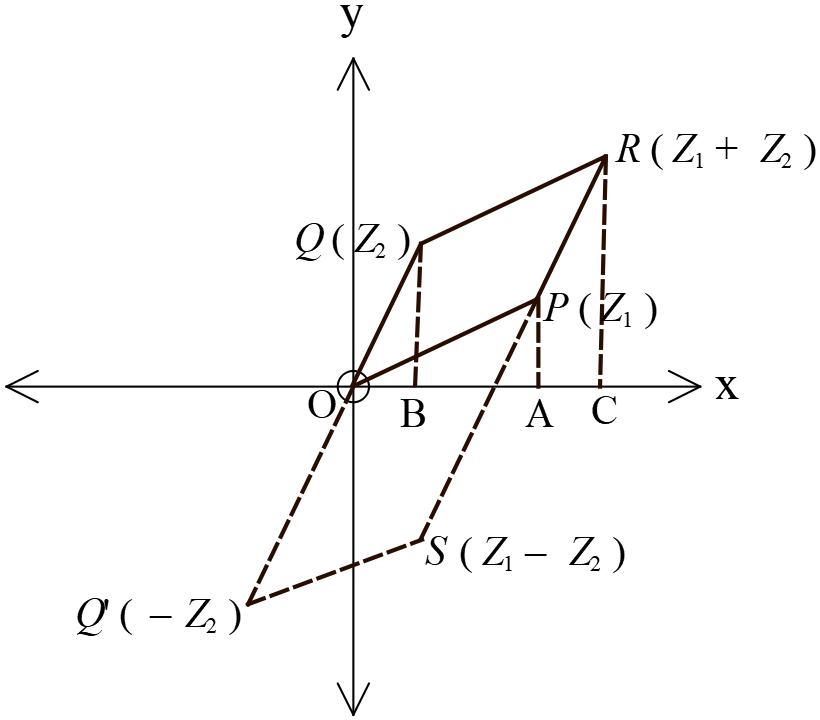
\(P, \ Q\) ও \(R\) বিন্দু হতে \(x\) অক্ষের উপর যথাক্রমে \(PA, \ QB\) ও \(RC\) লম্ব অঙ্কন করি। তাহলে \(A\) ও \(B\) এর কার্তেসীয় স্থানাঙ্ক যথাক্রমে \((x_{1}, 0)\) ও \((x_{2}, 0)\)।
এখানে, \(OC=OX\) এর উপর, \(OR\) এর লম্ব অভিক্ষেপ।
\(=OX\) এর উপর, \((OP \ \text{এর লম্ব অভিক্ষেপ})+(PR \ \text{এর লম্ব অভিক্ষেপ})\) ।
\(=OX\) এর উপর, \((OP \ \text{এর লম্ব অভিক্ষেপ})+(OQ \ \text{এর লম্ব অভিক্ষেপ})\) ➜ \(\because OQ\parallel{PR}\)
এবং \(OQ=PR\)
\(=OA+OB\)
\(=x_{1}+x_{2}\)
আবার, \(OY\) এর উপর লম্ব অভিক্ষেপ অঙ্কন করে এভাবে দেখানো যায়, \(RC=y_{1}+y_{2}\)
সুতরাং, \(R\) বিন্দুর ভুজ \(x_{1}+x_{2}\) এবং কোটি \(y_{1}+y_{2}\)
অর্থাৎ, \(R\) বিন্দুর স্থানাংক \((x_{1}+x_{2}, y_{1}+y_{2})\)
বিন্দুটির জটিল আকার \((x_{1}+x_{2})+i(y_{1}+y_{2})\)
\(=x_{1}+x_{2}+iy_{1}+iy_{2}\)
\(=(x_{1}+iy_{1})+(x_{2}+iy_{2})\)
\(=Z_{1}+Z_{2}\) ➜ \(\because x_{1}+iy_{1}=Z_{1}, \ Z_{2}=x_{2}+iy_{2}\)
সুতরাং, জটিল সমতলে \(R\) বিন্দুটি, \(P\) ও \(Q\) বিন্দুদ্বয় দ্বারা সূচিত জটিল সংখ্যাদ্বয়ের যোগফল প্রকাশ করে।
অনুরূপভাবে, \(OQ^{\prime}SP\) সামান্তরিক অঙ্কন করি যার সন্নিহিত বাহুদ্বয় যথাক্রমে \(OQ^{\prime}\) ও \(OP\)
এখানে, \(-Z_{2}=-x_{2}-iy_{2}\) জটিল সংখ্যাটি \(Q^{\prime}\) বিন্দু সূচিত করে। পূর্বের ন্যায় অগ্রসর হয়ে দেখানো যায় যে, জটিল সমতলে \(S\) বিন্দুটিই \(P\) ও \(Q\) বিন্দুদ্বয় দ্বারা সূচিত সংখ্যাদ্বয়ের বিয়োগফল প্রকাশ করে এবং \(S\) এর কার্তেসীয় স্থানাঙ্ক \((x_{1}-x_{2}, y_{1}-y_{2})\)।
বিন্দুটির জটিল আকার \((x_{1}-x_{2})+i(y_{1}-y_{2})\)
\(=x_{1}-x_{2}+iy_{1}-iy_{2}\)
\(=(x_{1}+iy_{1})-(x_{2}+iy_{2})\)
\(=Z_{1}-Z_{2}\) ➜ \(\because x_{1}+iy_{1}=Z_{1}, \ Z_{2}=x_{2}+iy_{2}\)
সতরাং, জটিল সমতলে \(S\) বিন্দুটি, \(P\) ও \(Q\) বিন্দুদ্বয় দ্বারা সূচিত সংখ্যাদ্বয়ের বিয়োগফল প্রকাশ করে।
চিত্র হতে,
\(OR\le{OP+PR}\)
\(\Rightarrow OR\le{OP+OQ}\)
\(\therefore |Z_{1}+Z_{2}|\le{|Z_{1}|+|Z_{2}|}\)
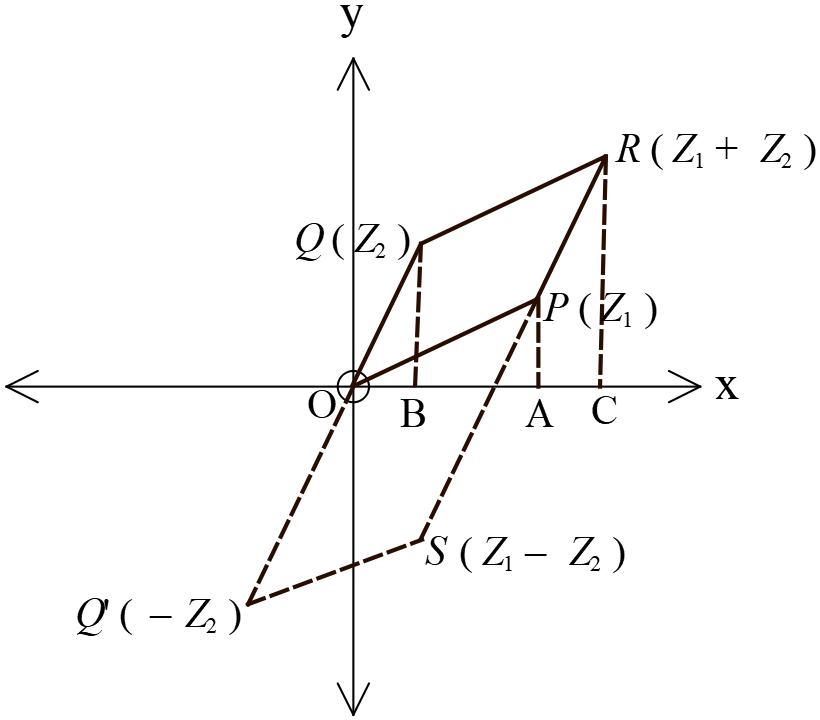
\(P, \ Q\) ও \(R\) বিন্দু হতে \(x\) অক্ষের উপর যথাক্রমে \(PA, \ QB\) ও \(RC\) লম্ব অঙ্কন করি। তাহলে \(A\) ও \(B\) এর কার্তেসীয় স্থানাঙ্ক যথাক্রমে \((x_{1}, 0)\) ও \((x_{2}, 0)\)।
এখানে, \(OC=OX\) এর উপর, \(OR\) এর লম্ব অভিক্ষেপ।
\(=OX\) এর উপর, \((OP \ \text{এর লম্ব অভিক্ষেপ})+(PR \ \text{এর লম্ব অভিক্ষেপ})\) ।
\(=OX\) এর উপর, \((OP \ \text{এর লম্ব অভিক্ষেপ})+(OQ \ \text{এর লম্ব অভিক্ষেপ})\) ➜ \(\because OQ\parallel{PR}\)
এবং \(OQ=PR\)
\(=OA+OB\)
\(=x_{1}+x_{2}\)
আবার, \(OY\) এর উপর লম্ব অভিক্ষেপ অঙ্কন করে এভাবে দেখানো যায়, \(RC=y_{1}+y_{2}\)
সুতরাং, \(R\) বিন্দুর ভুজ \(x_{1}+x_{2}\) এবং কোটি \(y_{1}+y_{2}\)
অর্থাৎ, \(R\) বিন্দুর স্থানাংক \((x_{1}+x_{2}, y_{1}+y_{2})\)
বিন্দুটির জটিল আকার \((x_{1}+x_{2})+i(y_{1}+y_{2})\)
\(=x_{1}+x_{2}+iy_{1}+iy_{2}\)
\(=(x_{1}+iy_{1})+(x_{2}+iy_{2})\)
\(=Z_{1}+Z_{2}\) ➜ \(\because x_{1}+iy_{1}=Z_{1}, \ Z_{2}=x_{2}+iy_{2}\)
সুতরাং, জটিল সমতলে \(R\) বিন্দুটি, \(P\) ও \(Q\) বিন্দুদ্বয় দ্বারা সূচিত জটিল সংখ্যাদ্বয়ের যোগফল প্রকাশ করে।
অনুরূপভাবে, \(OQ^{\prime}SP\) সামান্তরিক অঙ্কন করি যার সন্নিহিত বাহুদ্বয় যথাক্রমে \(OQ^{\prime}\) ও \(OP\)
এখানে, \(-Z_{2}=-x_{2}-iy_{2}\) জটিল সংখ্যাটি \(Q^{\prime}\) বিন্দু সূচিত করে। পূর্বের ন্যায় অগ্রসর হয়ে দেখানো যায় যে, জটিল সমতলে \(S\) বিন্দুটিই \(P\) ও \(Q\) বিন্দুদ্বয় দ্বারা সূচিত সংখ্যাদ্বয়ের বিয়োগফল প্রকাশ করে এবং \(S\) এর কার্তেসীয় স্থানাঙ্ক \((x_{1}-x_{2}, y_{1}-y_{2})\)।
বিন্দুটির জটিল আকার \((x_{1}-x_{2})+i(y_{1}-y_{2})\)
\(=x_{1}-x_{2}+iy_{1}-iy_{2}\)
\(=(x_{1}+iy_{1})-(x_{2}+iy_{2})\)
\(=Z_{1}-Z_{2}\) ➜ \(\because x_{1}+iy_{1}=Z_{1}, \ Z_{2}=x_{2}+iy_{2}\)
সতরাং, জটিল সমতলে \(S\) বিন্দুটি, \(P\) ও \(Q\) বিন্দুদ্বয় দ্বারা সূচিত সংখ্যাদ্বয়ের বিয়োগফল প্রকাশ করে।
চিত্র হতে,
\(OR\le{OP+PR}\)
\(\Rightarrow OR\le{OP+OQ}\)
\(\therefore |Z_{1}+Z_{2}|\le{|Z_{1}|+|Z_{2}|}\)
জটিল সংখ্যার গুণ এবং এর জ্যামিতিক প্রতিরূপ
Multiplication of complex numbers and its geometric counterpart
ধরি, দুইটি জটিল সংখ্যা \(Z_{1}=r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})\) এবং \(Z_{2}=r_{2}(\cos{\theta_{2}}+i\sin{\theta_{2}})\)
তাহলে সংখ্যাদ্বয়ের গুণফল,
\(Z_{1}Z_{2}=r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})\times{r_{2}}(\cos{\theta_{2}}+i\sin{\theta_{2}})\)
\(=r_{1}r_{2}(\cos{\theta_{1}}+i\sin{\theta_{1}})(\cos{\theta_{2}}+i\sin{\theta_{2}})\)
\(=r_{1}r_{2}\{\cos{\theta_{1}}\cos{\theta_{2}}+i\cos{\theta_{1}}\sin{\theta_{2}}+i\sin{\theta_{1}}\cos{\theta_{2}}+i^2\sin{\theta_{1}}\sin{\theta_{2}}\}\)
\(=r_{1}r_{2}\{\cos{\theta_{1}}\cos{\theta_{2}}+i(\cos{\theta_{1}}\sin{\theta_{2}}+\sin{\theta_{1}}\cos{\theta_{2}})-\sin{\theta_{1}}\sin{\theta_{2}}\}\) ➜ \(\because i^2=-1\)
\(=r_{1}r_{2}\{(\cos{\theta_{1}}\cos{\theta_{2}}-\sin{\theta_{1}}\sin{\theta_{2}})+i(\sin{\theta_{1}}\cos{\theta_{2}}+\cos{\theta_{1}}\sin{\theta_{2}})\}\)
\(=r_{1}r_{2}\{\cos{(\theta_{1}+\theta_{2})}+i\sin{(\theta_{1}+\theta_{2})}\}\) ➜ \(\because \cos{A}\cos{B}-\sin{A}\sin{B}=\cos{(A+B)}\)
এবং \(\sin{A}\cos{B}+\cos{A}\sin{B}=\sin{(A+B)}\)
\(\therefore Z_{1}Z_{2}=r_{1}r_{2}\{\cos{(\theta_{1}+\theta_{2})}+i\sin{(\theta_{1}+\theta_{2})}\}\)
এটি অপর একটি জটিল সংখ্যা প্রকাশ করে।
এখন, \(|Z_{1}Z_{2}|=|r_{1}r_{2}\{\cos{(\theta_{1}+\theta_{2})}+i\sin{(\theta_{1}+\theta_{2})}\}|\)
\(=r_{1}r_{2}|\cos{(\theta_{1}+\theta_{2})}+i\sin{(\theta_{1}+\theta_{2})}|\)
\(=r_{1}r_{2}\sqrt{\cos^2{(\theta_{1}+\theta_{2})}+\sin^2{(\theta_{1}+\theta_{2})}}\)
\(=r_{1}r_{2}\sqrt{1}\) ➜ \(\because \cos^2{A}+\sin^2{A}=1\)
\(=r_{1}r_{2}\)
\(\therefore |Z_{1}Z_{2}|=r_{1}r_{2}\)
\(\Rightarrow |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
আবার,
\(Arg(Z_{1}Z_{2})=\tan^{-1}{\left\{\frac{r_{1}r_{2}\sin{(\theta_{1}+\theta_{2})}}{r_{1}r_{2}\cos{(\theta_{1}+\theta_{2})}}\right\}}\)
\(=\tan^{-1}{\left\{\frac{\sin{(\theta_{1}+\theta_{2})}}{\cos{(\theta_{1}+\theta_{2})}}\right\}}\)
\(=\tan^{-1}{\tan{(\theta_{1}+\theta_{2})}}\)
\(=\theta_{1}+\theta_{2}\)
\(\therefore Arg(Z_{1}Z_{2})=\theta_{1}+\theta_{2}\)
\(\Rightarrow Arg(Z_{1}Z_{2})=Arg(Z_{1})+Arg(Z_{2})\)
সুতরাং এখানে দুইটি বিষয় স্পষ্ট
\(|Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
অর্থাৎ দুইটি জটিল সংখ্যার গুণফলের মডুলাস তাদের পৃথক পৃথক ভাবে মডুলাসের গুণফলের সমান।
\(Arg(Z_{1}Z_{2})=Arg(Z_{1})+Arg(Z_{2})\)
অর্থাৎ দুইটি জটিল সংখ্যার গুণফলের আর্গুমেন্ট তাদের পৃথক পৃথক ভাবে আর্গুমেন্টের যোগফলের সমান।
জ্যামিতিক ব্যাখ্যাঃ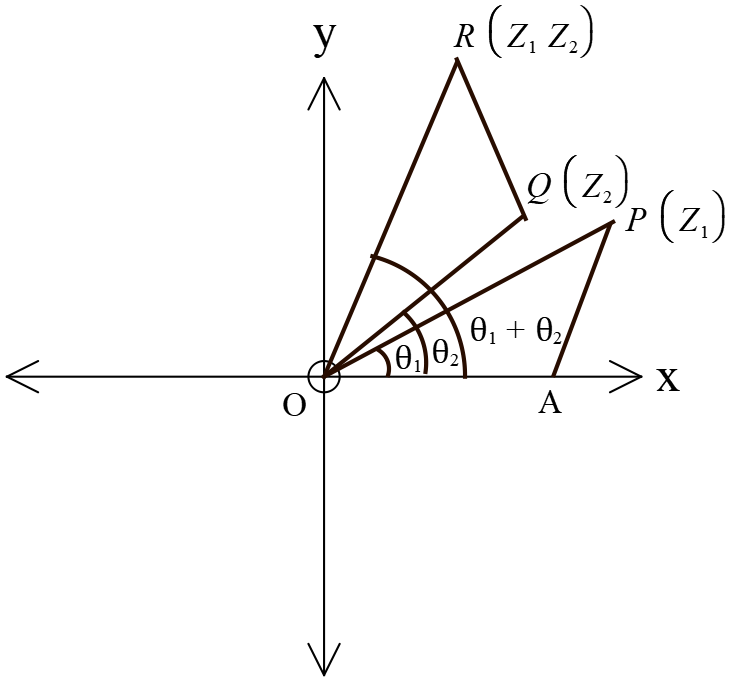
ধরি, আরগাঁ চিত্রে \(P\) ও \(Q\) বিন্দুদ্বয় যথাক্রমে \(Z_{1}=r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})\) এবং \(Z_{2}=r_{2}(\cos{\theta_{2}}+i\sin{\theta_{2}})\) জটিল সংখ্যা প্রকাশ করে এবং \(Z_{1}\) ও \(Z_{2}\) এর গুণফল \(Z\) দ্বারা প্রকাশিত বিন্দু \(R.\)
তাহলে, \(OP=r_{1}=|Z_{1}|\)
\(OQ=r_{2}=|Z_{2}|\)
\(OR=r_{1}r_{2}=|Z_{1}||Z_{2}|=OP.OQ\)
\(\angle{POX}=\theta_{1}, \ \angle{QOX}=\theta_{2}, \ \angle{ROX}=\theta_{1}+\theta_{2}\)
\(OX\) বরাবর, \(OA=1\) বিবেচনা করি এবং \(OQ\) এর যে পাশে \(OP\) আছে, তার বিপরীত পাশে \(\angle{POA}\) এর সমান \(\angle{QOR}\) অঙ্কন করি যেন \(OR=\frac{OP.OQ}{OA}\) হয়।
তাহলে, \(R\) বিন্দুই \(Z_{1}\) ও \(Z_{2}\) জটিল সংখ্যাদ্বয়ের গুণফল প্রকাশ করে।
\(P, A\) এবং \(R, Q\) যোগ করি। উৎপন্ন ত্রিভুজদ্বয় \(POA\) এবং \(ROQ\) হতে \(\angle{POA}=\angle{ROQ}\) এবং \(\frac{OR}{OQ}=\frac{OP}{OA}\) পাওয়া যায়। সুতরাং \(POA\) এবং \(ROQ\) ত্রিভুজদ্বয় সদৃশ।
অতএব আরগাঁ চিত্রে \(P(Z_{1})\) ও \(Q(Z_{2})\) বিন্দুদ্বয়ের গুণফল নির্ণয়ের জন্য \(OX\) হতে নির্বাচিত স্কেলে \(OA=1\) অংশ কেটে নিয়ে অঙ্কিত \(POA\) ত্রিভুজের সদৃশ \(ROQ\) ত্রিভুজ আঁকতে হবে, যেখানে \(OQ\) এর যে পাশে \(OP\) অবস্থিত তার বিপরীত পাশে \(OR\) অবস্থিত। তাহলে \(P(Z_{1})\) ও \(Q(Z_{2})\) বিন্দুদ্বয়ের গুণফল \(R\) দ্বারা প্রকাশিত হবে।
তাহলে সংখ্যাদ্বয়ের গুণফল,
\(Z_{1}Z_{2}=r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})\times{r_{2}}(\cos{\theta_{2}}+i\sin{\theta_{2}})\)
\(=r_{1}r_{2}(\cos{\theta_{1}}+i\sin{\theta_{1}})(\cos{\theta_{2}}+i\sin{\theta_{2}})\)
\(=r_{1}r_{2}\{\cos{\theta_{1}}\cos{\theta_{2}}+i\cos{\theta_{1}}\sin{\theta_{2}}+i\sin{\theta_{1}}\cos{\theta_{2}}+i^2\sin{\theta_{1}}\sin{\theta_{2}}\}\)
\(=r_{1}r_{2}\{\cos{\theta_{1}}\cos{\theta_{2}}+i(\cos{\theta_{1}}\sin{\theta_{2}}+\sin{\theta_{1}}\cos{\theta_{2}})-\sin{\theta_{1}}\sin{\theta_{2}}\}\) ➜ \(\because i^2=-1\)
\(=r_{1}r_{2}\{(\cos{\theta_{1}}\cos{\theta_{2}}-\sin{\theta_{1}}\sin{\theta_{2}})+i(\sin{\theta_{1}}\cos{\theta_{2}}+\cos{\theta_{1}}\sin{\theta_{2}})\}\)
\(=r_{1}r_{2}\{\cos{(\theta_{1}+\theta_{2})}+i\sin{(\theta_{1}+\theta_{2})}\}\) ➜ \(\because \cos{A}\cos{B}-\sin{A}\sin{B}=\cos{(A+B)}\)
এবং \(\sin{A}\cos{B}+\cos{A}\sin{B}=\sin{(A+B)}\)
\(\therefore Z_{1}Z_{2}=r_{1}r_{2}\{\cos{(\theta_{1}+\theta_{2})}+i\sin{(\theta_{1}+\theta_{2})}\}\)
এটি অপর একটি জটিল সংখ্যা প্রকাশ করে।
এখন, \(|Z_{1}Z_{2}|=|r_{1}r_{2}\{\cos{(\theta_{1}+\theta_{2})}+i\sin{(\theta_{1}+\theta_{2})}\}|\)
\(=r_{1}r_{2}|\cos{(\theta_{1}+\theta_{2})}+i\sin{(\theta_{1}+\theta_{2})}|\)
\(=r_{1}r_{2}\sqrt{\cos^2{(\theta_{1}+\theta_{2})}+\sin^2{(\theta_{1}+\theta_{2})}}\)
\(=r_{1}r_{2}\sqrt{1}\) ➜ \(\because \cos^2{A}+\sin^2{A}=1\)
\(=r_{1}r_{2}\)
\(\therefore |Z_{1}Z_{2}|=r_{1}r_{2}\)
\(\Rightarrow |Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
আবার,
\(Arg(Z_{1}Z_{2})=\tan^{-1}{\left\{\frac{r_{1}r_{2}\sin{(\theta_{1}+\theta_{2})}}{r_{1}r_{2}\cos{(\theta_{1}+\theta_{2})}}\right\}}\)
\(=\tan^{-1}{\left\{\frac{\sin{(\theta_{1}+\theta_{2})}}{\cos{(\theta_{1}+\theta_{2})}}\right\}}\)
\(=\tan^{-1}{\tan{(\theta_{1}+\theta_{2})}}\)
\(=\theta_{1}+\theta_{2}\)
\(\therefore Arg(Z_{1}Z_{2})=\theta_{1}+\theta_{2}\)
\(\Rightarrow Arg(Z_{1}Z_{2})=Arg(Z_{1})+Arg(Z_{2})\)
সুতরাং এখানে দুইটি বিষয় স্পষ্ট
\(|Z_{1}Z_{2}|=|Z_{1}||Z_{2}|\)
অর্থাৎ দুইটি জটিল সংখ্যার গুণফলের মডুলাস তাদের পৃথক পৃথক ভাবে মডুলাসের গুণফলের সমান।
\(Arg(Z_{1}Z_{2})=Arg(Z_{1})+Arg(Z_{2})\)
অর্থাৎ দুইটি জটিল সংখ্যার গুণফলের আর্গুমেন্ট তাদের পৃথক পৃথক ভাবে আর্গুমেন্টের যোগফলের সমান।
জ্যামিতিক ব্যাখ্যাঃ
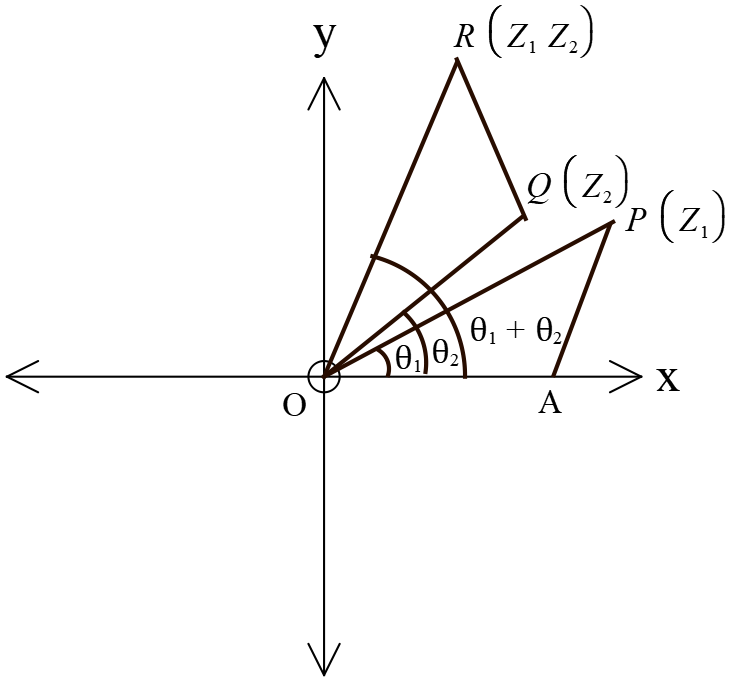
ধরি, আরগাঁ চিত্রে \(P\) ও \(Q\) বিন্দুদ্বয় যথাক্রমে \(Z_{1}=r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})\) এবং \(Z_{2}=r_{2}(\cos{\theta_{2}}+i\sin{\theta_{2}})\) জটিল সংখ্যা প্রকাশ করে এবং \(Z_{1}\) ও \(Z_{2}\) এর গুণফল \(Z\) দ্বারা প্রকাশিত বিন্দু \(R.\)
তাহলে, \(OP=r_{1}=|Z_{1}|\)
\(OQ=r_{2}=|Z_{2}|\)
\(OR=r_{1}r_{2}=|Z_{1}||Z_{2}|=OP.OQ\)
\(\angle{POX}=\theta_{1}, \ \angle{QOX}=\theta_{2}, \ \angle{ROX}=\theta_{1}+\theta_{2}\)
\(OX\) বরাবর, \(OA=1\) বিবেচনা করি এবং \(OQ\) এর যে পাশে \(OP\) আছে, তার বিপরীত পাশে \(\angle{POA}\) এর সমান \(\angle{QOR}\) অঙ্কন করি যেন \(OR=\frac{OP.OQ}{OA}\) হয়।
তাহলে, \(R\) বিন্দুই \(Z_{1}\) ও \(Z_{2}\) জটিল সংখ্যাদ্বয়ের গুণফল প্রকাশ করে।
\(P, A\) এবং \(R, Q\) যোগ করি। উৎপন্ন ত্রিভুজদ্বয় \(POA\) এবং \(ROQ\) হতে \(\angle{POA}=\angle{ROQ}\) এবং \(\frac{OR}{OQ}=\frac{OP}{OA}\) পাওয়া যায়। সুতরাং \(POA\) এবং \(ROQ\) ত্রিভুজদ্বয় সদৃশ।
অতএব আরগাঁ চিত্রে \(P(Z_{1})\) ও \(Q(Z_{2})\) বিন্দুদ্বয়ের গুণফল নির্ণয়ের জন্য \(OX\) হতে নির্বাচিত স্কেলে \(OA=1\) অংশ কেটে নিয়ে অঙ্কিত \(POA\) ত্রিভুজের সদৃশ \(ROQ\) ত্রিভুজ আঁকতে হবে, যেখানে \(OQ\) এর যে পাশে \(OP\) অবস্থিত তার বিপরীত পাশে \(OR\) অবস্থিত। তাহলে \(P(Z_{1})\) ও \(Q(Z_{2})\) বিন্দুদ্বয়ের গুণফল \(R\) দ্বারা প্রকাশিত হবে।
জটিল সংখ্যার ভাগ এবং এর জ্যামিতিক প্রতিরূপ
Division of complex numbers and its geometric counterpart
ধরি, দুইটি জটিল সংখ্যা \(Z_{1}=r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})\) এবং \(Z_{2}=r_{2}(\cos{\theta_{2}}+i\sin{\theta_{2}})\)
তাহলে সংখ্যাদ্বয়ের ভাগফল,
\(\frac{Z_{1}}{Z_{2}}=\frac{r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})}{{r_{2}}(\cos{\theta_{2}}+i\sin{\theta_{2}})}\)
\(=\frac{r_{1}}{r_{2}}\times\frac{(\cos{\theta_{1}}+i\sin{\theta_{1}})}{(\cos{\theta_{2}}+i\sin{\theta_{2}})}\)
\(=\frac{r_{1}}{r_{2}}\times\frac{(\cos{\theta_{1}}+i\sin{\theta_{1}})(\cos{\theta_{2}}-i\sin{\theta_{2}})}{(\cos{\theta_{2}}+i\sin{\theta_{2}})(\cos{\theta_{2}}-i\sin{\theta_{2}})}\) ➜ লব ও হরের সাথে \((\cos{\theta_{2}}-i\sin{\theta_{2}})\) গুণ করে।
\(=\frac{r_{1}}{r_{2}}\times\frac{\cos{\theta_{1}}\cos{\theta_{2}}-i\cos{\theta_{1}}\sin{\theta_{2}}+i\sin{\theta_{1}}\cos{\theta_{2}}-i^2\sin{\theta_{1}}\sin{\theta_{2}}}{\cos^2{\theta_{2}}-i^2\sin^2{\theta_{2}}}\)
\(=\frac{r_{1}}{r_{2}}\times\frac{\cos{\theta_{1}}\cos{\theta_{2}}+i\sin{\theta_{1}}\cos{\theta_{2}}-i\cos{\theta_{1}}\sin{\theta_{2}}+\sin{\theta_{1}}\sin{\theta_{2}}}{\cos^2{\theta_{2}}+\sin^2{\theta_{2}}}\) ➜ \(\because i^2=-1\)
\(=\frac{r_{1}}{r_{2}}\times\frac{(\cos{\theta_{1}}\cos{\theta_{2}}+\sin{\theta_{1}}\sin{\theta_{2}})+i(\sin{\theta_{1}}\cos{\theta_{2}}-\cos{\theta_{1}}\sin{\theta_{2}})}{1}\) ➜ \(\because \cos^2{A}+\sin^2{A}=1\)
\(=\frac{r_{1}}{r_{2}}\times\{\cos{(\theta_{1}-\theta_{2})}+i\sin{(\theta_{1}-\theta_{2})}\}\) ➜ \(\because \cos{A}\cos{B}+\sin{A}\sin{B}=\cos{(A-B)}\)
এবং \(\sin{A}\cos{B}-\cos{A}\sin{B}=\sin{(A-B)}\)
\(\therefore \frac{Z_{1}}{Z_{2}}=\frac{r_{1}}{r_{2}}\times\{\cos{(\theta_{1}-\theta_{2})}+i\sin{(\theta_{1}-\theta_{2})}\}\)
এটি অপর একটি জটিল সংখ্যা প্রকাশ করে।
এখন, \(\left|\frac{Z_{1}}{Z_{2}}\right|=\left|\frac{r_{1}}{r_{2}}\times\{\cos{(\theta_{1}-\theta_{2})}+i\sin{(\theta_{1}-\theta_{2})}\}\right|\)
\(=\left|\frac{r_{1}}{r_{2}}\right|\times|\{\cos{(\theta_{1}-\theta_{2})}+i\sin{(\theta_{1}-\theta_{2})}\}|\)
\(=\frac{r_{1}}{r_{2}}\sqrt{\cos^2{(\theta_{1}-\theta_{2})}+\sin^2{(\theta_{1}-\theta_{2})}}\)
\(=\frac{r_{1}}{r_{2}}\sqrt{1}\) ➜ \(\because \cos^2{A}+\sin^2{A}=1\)
\(=\frac{r_{1}}{r_{2}}\)
\(\therefore \left|\frac{Z_{1}}{Z_{2}}\right|=\frac{r_{1}}{r_{2}}\)
\(\Rightarrow \left|\frac{Z_{1}}{Z_{2}}\right|=\frac{|Z_{1}|}{|Z_{2}|}\)
আবার,
\(Arg\left(\frac{Z_{1}}{Z_{2}}\right)=\tan^{-1}{\left\{\frac{\frac{r_{1}}{r_{2}}\sin{(\theta_{1}-\theta_{2})}}{\frac{r_{1}}{r_{2}}\cos{(\theta_{1}-\theta_{2})}}\right\}}\)
\(=\tan^{-1}{\left\{\frac{\sin{(\theta_{1}-\theta_{2})}}{\cos{(\theta_{1}-\theta_{2})}}\right\}}\)
\(=\tan^{-1}{\tan{(\theta_{1}-\theta_{2})}}\)
\(=\theta_{1}-\theta_{2}\)
\(\therefore Arg\left(\frac{Z_{1}}{Z_{2}}\right)=\theta_{1}-\theta_{2}\)
\(\Rightarrow Arg\left(\frac{Z_{1}}{Z_{2}}\right)=Arg(Z_{1})-Arg(Z_{2})\)
সুতরাং এখানে দুইটি বিষয় স্পষ্ট
\(\left|\frac{Z_{1}}{Z_{2}}\right|=\frac{|Z_{1}|}{|Z_{2}|}\)
অর্থাৎ দুইটি জটিল সংখ্যার ভাগফলের মডুলাস তাদের পৃথক পৃথক ভাবে মডুলাসের ভাগফলের সমান।
\(Arg\left(\frac{Z_{1}}{Z_{2}}\right)=Arg(Z_{1})-Arg(Z_{2})\)
অর্থাৎ দুইটি জটিল সংখ্যার ভাগফলের আর্গুমেন্ট তাদের পৃথক পৃথক ভাবে আর্গুমেন্টের বিয়োগফলের সমান।
জ্যামিতিক ব্যাখ্যাঃ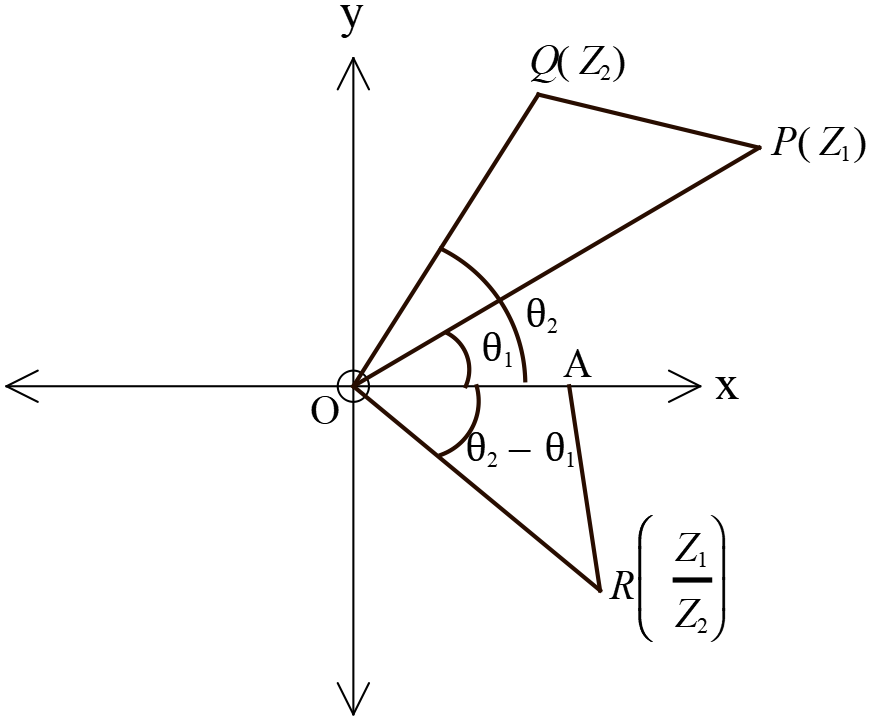
ধরি, আরগাঁ চিত্রে \(P\) ও \(Q\) বিন্দুদ্বয় যথাক্রমে \(Z_{1}=r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})\) এবং \(Z_{2}=r_{2}(\cos{\theta_{2}}+i\sin{\theta_{2}})\) জটিল সংখ্যা প্রকাশ করে এবং \(Z_{1}\) ও \(Z_{2}\) এর ভাগফল \(\frac{Z_{1}}{Z_{2}}=Z\) দ্বারা প্রকাশিত বিন্দু \(R.\)
তাহলে, \(OP=r_{1}=|Z_{1}|\)
\(OQ=r_{2}=|Z_{2}|\)
\(OR=\frac{r_{1}}{r_{2}}=\frac{|Z_{1}|}{|Z_{2}|}=\frac{OP}{OQ}\)
\(\angle{POX}=\theta_{1}, \ \angle{QOX}=\theta_{2}, \ \angle{ROX}=\theta_{2}-\theta_{1}\)
\(OX\) বরাবর, \(OA=1\) বিবেচনা করি এবং \(OP\) এর যে পাশে \(OQ\) আছে, তার বিপরীত পাশে \(\angle{QOX}\) এর সমান \(\angle{POR}\) অঙ্কন করি যেন \(\angle{OQP}\) এর সমান \(\angle{OAR}\) হয়।
তাহলে চিত্রানুযায়ী, \(\angle{QOX}=\theta_{2}=\angle{POR}\)
\(\Rightarrow \angle{QOP}+\angle{POX}=\angle{POX}+\angle{XOR}\)
\(\Rightarrow \angle{QOP}=\angle{XOR}=\angle{AOR}\)
আবার, \(\angle{OQP}=\angle{OAR}\)
সুতরাং, \(OPQ\) এবং \(OAR\) ত্রিভুজদ্বয় সদৃশ।
তাহলে, \(\frac{OR}{OP}=\frac{AR}{PQ}=\frac{OA}{OQ}\)
\(\Rightarrow \frac{OR}{OP}=\frac{OA}{OQ}\)
\(\Rightarrow \frac{OR}{OP}=\frac{1}{OQ}\) ➜ \(\because OA=1\)
\(\therefore OR=\frac{OP}{OQ}\)
আবার, \(\angle{XOR}=\angle{POR}-\angle{POX}=\theta_{2}-\theta_{1}\)
অতএব, \(R\) বিন্দুই দুইটি জটিল সংখ্যা \(Z_{1}\) ও \(Z_{2}\) এর ভাগফল \(\frac{Z_{1}}{Z_{2}}\) প্রকাশ করে।
\(Question.\) \(Z_{1}=2+3i, \ Z_{2}=2-2i\) হলে, জ্যামিতিক প্রতিরূপ দেখাওঃ
\((a) \ Z_{1}+Z_{2}\)
\((b) \ Z_{2}-Z_{1}\)
\((c) \ Z_{1}Z_{2}\)
\((d) \ \frac{Z_{1}}{Z_{2}}\)
তাহলে সংখ্যাদ্বয়ের ভাগফল,
\(\frac{Z_{1}}{Z_{2}}=\frac{r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})}{{r_{2}}(\cos{\theta_{2}}+i\sin{\theta_{2}})}\)
\(=\frac{r_{1}}{r_{2}}\times\frac{(\cos{\theta_{1}}+i\sin{\theta_{1}})}{(\cos{\theta_{2}}+i\sin{\theta_{2}})}\)
\(=\frac{r_{1}}{r_{2}}\times\frac{(\cos{\theta_{1}}+i\sin{\theta_{1}})(\cos{\theta_{2}}-i\sin{\theta_{2}})}{(\cos{\theta_{2}}+i\sin{\theta_{2}})(\cos{\theta_{2}}-i\sin{\theta_{2}})}\) ➜ লব ও হরের সাথে \((\cos{\theta_{2}}-i\sin{\theta_{2}})\) গুণ করে।
\(=\frac{r_{1}}{r_{2}}\times\frac{\cos{\theta_{1}}\cos{\theta_{2}}-i\cos{\theta_{1}}\sin{\theta_{2}}+i\sin{\theta_{1}}\cos{\theta_{2}}-i^2\sin{\theta_{1}}\sin{\theta_{2}}}{\cos^2{\theta_{2}}-i^2\sin^2{\theta_{2}}}\)
\(=\frac{r_{1}}{r_{2}}\times\frac{\cos{\theta_{1}}\cos{\theta_{2}}+i\sin{\theta_{1}}\cos{\theta_{2}}-i\cos{\theta_{1}}\sin{\theta_{2}}+\sin{\theta_{1}}\sin{\theta_{2}}}{\cos^2{\theta_{2}}+\sin^2{\theta_{2}}}\) ➜ \(\because i^2=-1\)
\(=\frac{r_{1}}{r_{2}}\times\frac{(\cos{\theta_{1}}\cos{\theta_{2}}+\sin{\theta_{1}}\sin{\theta_{2}})+i(\sin{\theta_{1}}\cos{\theta_{2}}-\cos{\theta_{1}}\sin{\theta_{2}})}{1}\) ➜ \(\because \cos^2{A}+\sin^2{A}=1\)
\(=\frac{r_{1}}{r_{2}}\times\{\cos{(\theta_{1}-\theta_{2})}+i\sin{(\theta_{1}-\theta_{2})}\}\) ➜ \(\because \cos{A}\cos{B}+\sin{A}\sin{B}=\cos{(A-B)}\)
এবং \(\sin{A}\cos{B}-\cos{A}\sin{B}=\sin{(A-B)}\)
\(\therefore \frac{Z_{1}}{Z_{2}}=\frac{r_{1}}{r_{2}}\times\{\cos{(\theta_{1}-\theta_{2})}+i\sin{(\theta_{1}-\theta_{2})}\}\)
এটি অপর একটি জটিল সংখ্যা প্রকাশ করে।
এখন, \(\left|\frac{Z_{1}}{Z_{2}}\right|=\left|\frac{r_{1}}{r_{2}}\times\{\cos{(\theta_{1}-\theta_{2})}+i\sin{(\theta_{1}-\theta_{2})}\}\right|\)
\(=\left|\frac{r_{1}}{r_{2}}\right|\times|\{\cos{(\theta_{1}-\theta_{2})}+i\sin{(\theta_{1}-\theta_{2})}\}|\)
\(=\frac{r_{1}}{r_{2}}\sqrt{\cos^2{(\theta_{1}-\theta_{2})}+\sin^2{(\theta_{1}-\theta_{2})}}\)
\(=\frac{r_{1}}{r_{2}}\sqrt{1}\) ➜ \(\because \cos^2{A}+\sin^2{A}=1\)
\(=\frac{r_{1}}{r_{2}}\)
\(\therefore \left|\frac{Z_{1}}{Z_{2}}\right|=\frac{r_{1}}{r_{2}}\)
\(\Rightarrow \left|\frac{Z_{1}}{Z_{2}}\right|=\frac{|Z_{1}|}{|Z_{2}|}\)
আবার,
\(Arg\left(\frac{Z_{1}}{Z_{2}}\right)=\tan^{-1}{\left\{\frac{\frac{r_{1}}{r_{2}}\sin{(\theta_{1}-\theta_{2})}}{\frac{r_{1}}{r_{2}}\cos{(\theta_{1}-\theta_{2})}}\right\}}\)
\(=\tan^{-1}{\left\{\frac{\sin{(\theta_{1}-\theta_{2})}}{\cos{(\theta_{1}-\theta_{2})}}\right\}}\)
\(=\tan^{-1}{\tan{(\theta_{1}-\theta_{2})}}\)
\(=\theta_{1}-\theta_{2}\)
\(\therefore Arg\left(\frac{Z_{1}}{Z_{2}}\right)=\theta_{1}-\theta_{2}\)
\(\Rightarrow Arg\left(\frac{Z_{1}}{Z_{2}}\right)=Arg(Z_{1})-Arg(Z_{2})\)
সুতরাং এখানে দুইটি বিষয় স্পষ্ট
\(\left|\frac{Z_{1}}{Z_{2}}\right|=\frac{|Z_{1}|}{|Z_{2}|}\)
অর্থাৎ দুইটি জটিল সংখ্যার ভাগফলের মডুলাস তাদের পৃথক পৃথক ভাবে মডুলাসের ভাগফলের সমান।
\(Arg\left(\frac{Z_{1}}{Z_{2}}\right)=Arg(Z_{1})-Arg(Z_{2})\)
অর্থাৎ দুইটি জটিল সংখ্যার ভাগফলের আর্গুমেন্ট তাদের পৃথক পৃথক ভাবে আর্গুমেন্টের বিয়োগফলের সমান।
জ্যামিতিক ব্যাখ্যাঃ
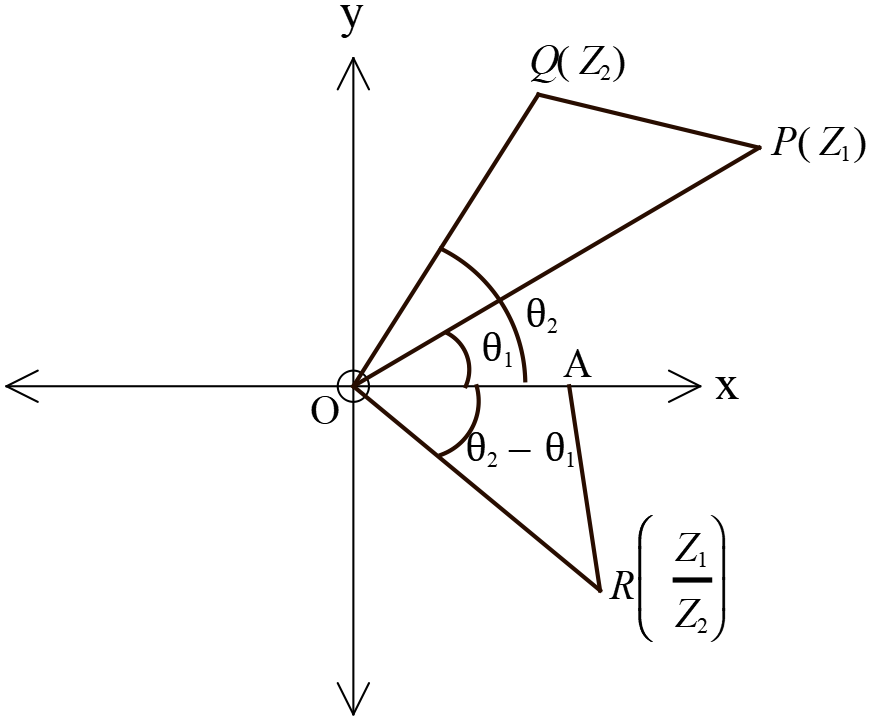
ধরি, আরগাঁ চিত্রে \(P\) ও \(Q\) বিন্দুদ্বয় যথাক্রমে \(Z_{1}=r_{1}(\cos{\theta_{1}}+i\sin{\theta_{1}})\) এবং \(Z_{2}=r_{2}(\cos{\theta_{2}}+i\sin{\theta_{2}})\) জটিল সংখ্যা প্রকাশ করে এবং \(Z_{1}\) ও \(Z_{2}\) এর ভাগফল \(\frac{Z_{1}}{Z_{2}}=Z\) দ্বারা প্রকাশিত বিন্দু \(R.\)
তাহলে, \(OP=r_{1}=|Z_{1}|\)
\(OQ=r_{2}=|Z_{2}|\)
\(OR=\frac{r_{1}}{r_{2}}=\frac{|Z_{1}|}{|Z_{2}|}=\frac{OP}{OQ}\)
\(\angle{POX}=\theta_{1}, \ \angle{QOX}=\theta_{2}, \ \angle{ROX}=\theta_{2}-\theta_{1}\)
\(OX\) বরাবর, \(OA=1\) বিবেচনা করি এবং \(OP\) এর যে পাশে \(OQ\) আছে, তার বিপরীত পাশে \(\angle{QOX}\) এর সমান \(\angle{POR}\) অঙ্কন করি যেন \(\angle{OQP}\) এর সমান \(\angle{OAR}\) হয়।
তাহলে চিত্রানুযায়ী, \(\angle{QOX}=\theta_{2}=\angle{POR}\)
\(\Rightarrow \angle{QOP}+\angle{POX}=\angle{POX}+\angle{XOR}\)
\(\Rightarrow \angle{QOP}=\angle{XOR}=\angle{AOR}\)
আবার, \(\angle{OQP}=\angle{OAR}\)
সুতরাং, \(OPQ\) এবং \(OAR\) ত্রিভুজদ্বয় সদৃশ।
তাহলে, \(\frac{OR}{OP}=\frac{AR}{PQ}=\frac{OA}{OQ}\)
\(\Rightarrow \frac{OR}{OP}=\frac{OA}{OQ}\)
\(\Rightarrow \frac{OR}{OP}=\frac{1}{OQ}\) ➜ \(\because OA=1\)
\(\therefore OR=\frac{OP}{OQ}\)
আবার, \(\angle{XOR}=\angle{POR}-\angle{POX}=\theta_{2}-\theta_{1}\)
অতএব, \(R\) বিন্দুই দুইটি জটিল সংখ্যা \(Z_{1}\) ও \(Z_{2}\) এর ভাগফল \(\frac{Z_{1}}{Z_{2}}\) প্রকাশ করে।
\(Question.\) \(Z_{1}=2+3i, \ Z_{2}=2-2i\) হলে, জ্যামিতিক প্রতিরূপ দেখাওঃ
\((a) \ Z_{1}+Z_{2}\)
\((b) \ Z_{2}-Z_{1}\)
\((c) \ Z_{1}Z_{2}\)
\((d) \ \frac{Z_{1}}{Z_{2}}\)
বিশেষ দ্রষ্টব্যঃ
Special note:
\(|Z-k_{1}|=k_{2}\) সমীকরণটি একটি বৃত্ত নির্দেশ করে যার কেন্দ্র \((k_{1}, 0)\) এবং ব্যাসার্ধ \(=k_{2}\)
\(|Z|=k\) সমীকরণটি একটি বৃত্ত নির্দেশ করে যার কেন্দ্র \((0, 0)\) এবং ব্যাসার্ধ \(=k\)
\(|aZ+k_{1}|=|aZ+k_{2}|\) সমীকরণটি একটি সরলরেখা নির্দেশ করে।
\(|aZ+k_{1}|=|bZ+k_{2}|\) সমীকরণটি একটি বৃত্ত নির্দেশ করে।
\(Z\overline{Z}=a^2\) সমীকরণটি একটি বৃত্ত নির্দেশ করে যার কেন্দ্র \((0, 0)\) এবং ব্যাসার্ধ \(=a\)
\(|Z+k|=x\) বা, \(|Z+k|=y\) সমীকরণটি একটি পরাবৃত্ত নির্দেশ করে।
\(|Z+k|+|Z-k|=r\) সমীকরণটি একটি উপবৃত্ত নির্দেশ করে।
\(Question.1\) \(Z_{1}, \ Z_{2}, \ Z_{3}\) ও \(Z_{4}\) জটিল সংখ্যা হলে প্রমাণ কর যে,
\((a) \ \left|\frac{Z_{1}}{Z_{2}+Z_{3}}\right|=\frac{|Z_{1}|}{||Z_{2}|-|Z_{3}||}\) যখন \(|Z_{2}|\ne{|Z_{3}|}\)
\((b) \ \left|\frac{Z_{1}+Z_{2}}{Z_{3}+Z_{4}}\right|=\frac{|Z_{1}|+|Z_{2}|}{||Z_{3}|-|Z_{4}||}\) যখন \(|Z_{3}|\ne{|Z_{4}|}\)
উদাহরণের যাহায্যে \((1)\) ও \((2)\) এর সত্যতা যাচাই কর।
\((2) \ Z=x+iy\) হলে \(|Z-2|=3\) দ্বারা নির্দেশিত সঞ্চারপথের সমীকরণ নির্ণয় কর। এটি কিসের সমীকরণ নির্দেশ করে?
\((3) \ Z=x+iy\) হলে \(|Z+2i|\gt{3}\) দ্বারা নির্দেশিত জ্যামিতিক অঞ্চল চিত্রের সাহায্যে দেখাও।
\(|Z|=k\) সমীকরণটি একটি বৃত্ত নির্দেশ করে যার কেন্দ্র \((0, 0)\) এবং ব্যাসার্ধ \(=k\)
\(|aZ+k_{1}|=|aZ+k_{2}|\) সমীকরণটি একটি সরলরেখা নির্দেশ করে।
\(|aZ+k_{1}|=|bZ+k_{2}|\) সমীকরণটি একটি বৃত্ত নির্দেশ করে।
\(Z\overline{Z}=a^2\) সমীকরণটি একটি বৃত্ত নির্দেশ করে যার কেন্দ্র \((0, 0)\) এবং ব্যাসার্ধ \(=a\)
\(|Z+k|=x\) বা, \(|Z+k|=y\) সমীকরণটি একটি পরাবৃত্ত নির্দেশ করে।
\(|Z+k|+|Z-k|=r\) সমীকরণটি একটি উপবৃত্ত নির্দেশ করে।
\(Question.1\) \(Z_{1}, \ Z_{2}, \ Z_{3}\) ও \(Z_{4}\) জটিল সংখ্যা হলে প্রমাণ কর যে,
\((a) \ \left|\frac{Z_{1}}{Z_{2}+Z_{3}}\right|=\frac{|Z_{1}|}{||Z_{2}|-|Z_{3}||}\) যখন \(|Z_{2}|\ne{|Z_{3}|}\)
\((b) \ \left|\frac{Z_{1}+Z_{2}}{Z_{3}+Z_{4}}\right|=\frac{|Z_{1}|+|Z_{2}|}{||Z_{3}|-|Z_{4}||}\) যখন \(|Z_{3}|\ne{|Z_{4}|}\)
উদাহরণের যাহায্যে \((1)\) ও \((2)\) এর সত্যতা যাচাই কর।
\((2) \ Z=x+iy\) হলে \(|Z-2|=3\) দ্বারা নির্দেশিত সঞ্চারপথের সমীকরণ নির্ণয় কর। এটি কিসের সমীকরণ নির্দেশ করে?
\((3) \ Z=x+iy\) হলে \(|Z+2i|\gt{3}\) দ্বারা নির্দেশিত জ্যামিতিক অঞ্চল চিত্রের সাহায্যে দেখাও।
জটিল সংখ্যার বর্গমূলঃ
Square roots of complex numbers:
\(a+ib, \ (a,b\in{\mathbb{R}}, \ b\gt{0})\) এর বর্গমূলঃ
অর্থাৎ, \(\sqrt{a+ib}=\pm{\frac{1}{\sqrt{2}}\left\{\left(\sqrt{a^2+b^2}+a\right)^{\frac{1}{2}}+i\left(\sqrt{a^2+b^2}-a\right)^{\frac{1}{2}}\right\}}\)
\(a-ib, \ (a,b\in{\mathbb{R}})\) এর বর্গমূলঃ
অর্থাৎ, \(\sqrt{a-ib}=\pm{\frac{1}{\sqrt{2}}\left\{\left(\sqrt{a^2+b^2}+a\right)^{\frac{1}{2}}-i\left(\sqrt{a^2+b^2}-a\right)^{\frac{1}{2}}\right\}}\)
অর্থাৎ, \(\sqrt{a+ib}=\pm{\frac{1}{\sqrt{2}}\left\{\left(\sqrt{a^2+b^2}+a\right)^{\frac{1}{2}}+i\left(\sqrt{a^2+b^2}-a\right)^{\frac{1}{2}}\right\}}\)
প্রমাণঃ
ধরি, \(\sqrt{a+ib}=x+iy .........(1)\)
\(\Rightarrow a+ib=(x+iy)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow a+ib=x^2+2xiy+i^2y^2\)
\(\Rightarrow a+ib=x^2+2xyi-y^2\) ➜ \(\because i^2=-1\)
\(\Rightarrow a+ib=x^2-y^2+2xyi\)
\(\Rightarrow x^2-y^2=a ........(2)\) ➜ বাস্তব ও কাল্পনিক অংশ সমীকৃত করে।
এবং \(2xy=b ........(3)\)
এখন, \(x^2+y^2=\sqrt{(x^2-y^2)^2+4x^2y^2}\) ➜ \(\because a+b=\sqrt{(a-b)^2+4ab}\)
\(=\sqrt{(x^2-y^2)^2+(2xy)^2}\)
\(=\sqrt{(a)^2+(b)^2}\) ➜ \(\because x^2-y^2=a, \ 2xy=b\)
\(\therefore x^2+y^2=\sqrt{a^2+b^2} .......(4)\)
\((4)+(2)\) এর সাহায্যে,
\(x^2+y^2+x^2-y^2=\sqrt{a^2+b^2}+a\)
\(\Rightarrow 2x^2=\sqrt{a^2+b^2}+a\)
\(\Rightarrow x^2=\frac{1}{2}\sqrt{a^2+b^2}+a\)
\(\Rightarrow x=\pm{\sqrt{\frac{1}{2}\sqrt{a^2+b^2}+a}}\)
\(\therefore x=\pm{\frac{1}{\sqrt{2}}\left(\sqrt{a^2+b^2}+a\right)^{\frac{1}{2}}}\)
আবার, \((4)-(2)\) এর সাহায্যে,
\(x^2+y^2-x^2+y^2=\sqrt{a^2+b^2}-a\)
\(\Rightarrow 2y^2=\sqrt{a^2+b^2}-a\)
\(\Rightarrow y^2=\frac{1}{2}\sqrt{a^2+b^2}-a\)
\(\Rightarrow y=\pm{\sqrt{\frac{1}{2}\sqrt{a^2+b^2}-a}}\)
\(\therefore y=\pm{\frac{1}{\sqrt{2}}\left(\sqrt{a^2+b^2}-a\right)^{\frac{1}{2}}}\)
\(x, \ y\) এর মান \((1)\) এ বসিয়ে,
\(\sqrt{a+ib}=\pm{\frac{1}{\sqrt{2}}\left\{\left(\sqrt{a^2+b^2}+a\right)^{\frac{1}{2}}+i\left(\sqrt{a^2+b^2}-a\right)^{\frac{1}{2}}\right\}}\)
(প্রমাণিত)
আবার, \(b\lt{0}\) হলে,ধরি, \(\sqrt{a+ib}=x+iy .........(1)\)
\(\Rightarrow a+ib=(x+iy)^2\) ➜ উভয় পার্শে বর্গ করে।
\(\Rightarrow a+ib=x^2+2xiy+i^2y^2\)
\(\Rightarrow a+ib=x^2+2xyi-y^2\) ➜ \(\because i^2=-1\)
\(\Rightarrow a+ib=x^2-y^2+2xyi\)
\(\Rightarrow x^2-y^2=a ........(2)\) ➜ বাস্তব ও কাল্পনিক অংশ সমীকৃত করে।
এবং \(2xy=b ........(3)\)
এখন, \(x^2+y^2=\sqrt{(x^2-y^2)^2+4x^2y^2}\) ➜ \(\because a+b=\sqrt{(a-b)^2+4ab}\)
\(=\sqrt{(x^2-y^2)^2+(2xy)^2}\)
\(=\sqrt{(a)^2+(b)^2}\) ➜ \(\because x^2-y^2=a, \ 2xy=b\)
\(\therefore x^2+y^2=\sqrt{a^2+b^2} .......(4)\)
\((4)+(2)\) এর সাহায্যে,
\(x^2+y^2+x^2-y^2=\sqrt{a^2+b^2}+a\)
\(\Rightarrow 2x^2=\sqrt{a^2+b^2}+a\)
\(\Rightarrow x^2=\frac{1}{2}\sqrt{a^2+b^2}+a\)
\(\Rightarrow x=\pm{\sqrt{\frac{1}{2}\sqrt{a^2+b^2}+a}}\)
\(\therefore x=\pm{\frac{1}{\sqrt{2}}\left(\sqrt{a^2+b^2}+a\right)^{\frac{1}{2}}}\)
আবার, \((4)-(2)\) এর সাহায্যে,
\(x^2+y^2-x^2+y^2=\sqrt{a^2+b^2}-a\)
\(\Rightarrow 2y^2=\sqrt{a^2+b^2}-a\)
\(\Rightarrow y^2=\frac{1}{2}\sqrt{a^2+b^2}-a\)
\(\Rightarrow y=\pm{\sqrt{\frac{1}{2}\sqrt{a^2+b^2}-a}}\)
\(\therefore y=\pm{\frac{1}{\sqrt{2}}\left(\sqrt{a^2+b^2}-a\right)^{\frac{1}{2}}}\)
\(x, \ y\) এর মান \((1)\) এ বসিয়ে,
\(\sqrt{a+ib}=\pm{\frac{1}{\sqrt{2}}\left\{\left(\sqrt{a^2+b^2}+a\right)^{\frac{1}{2}}+i\left(\sqrt{a^2+b^2}-a\right)^{\frac{1}{2}}\right\}}\)
(প্রমাণিত)
\(a-ib, \ (a,b\in{\mathbb{R}})\) এর বর্গমূলঃ
অর্থাৎ, \(\sqrt{a-ib}=\pm{\frac{1}{\sqrt{2}}\left\{\left(\sqrt{a^2+b^2}+a\right)^{\frac{1}{2}}-i\left(\sqrt{a^2+b^2}-a\right)^{\frac{1}{2}}\right\}}\)
একের ঘনমূলঃ
Cube root of one:
\(1\) এর ঘনমূলঃ
অর্থাৎ, \(\sqrt[3]{1}=1, \ \frac{1}{2}\left(-1+\sqrt{-3}\right), \ \frac{1}{2}\left(-1-\sqrt{-3}\right)\)
বিষেশ দ্রষ্টব্যঃ যে কোনো বাস্তব সংখ্যা \(a^3\) এর তিনটি ঘনমূল হচ্ছে \(a, \ a\omega, \ a\omega^2.\)
অর্থাৎ, \(\sqrt[3]{1}=1, \ \frac{1}{2}\left(-1+\sqrt{-3}\right), \ \frac{1}{2}\left(-1-\sqrt{-3}\right)\)
প্রমাণঃ
ধরি, \(\sqrt[3]{1}=x\)
\(\Rightarrow 1=x^3\) ➜ উভয় পার্শে ঘন করে।
\(\Rightarrow x^3=1\)
\(\Rightarrow x^3-1=0\)
\(\Rightarrow (x-1)(x^2+x+1)=0\) ➜ \(\because a^3-b^3=(a-b)(a^2+ab+b^2)\)
\(\Rightarrow x-1=0, \ x^2+x+1=0\)
\(\Rightarrow x=1, \ x=\frac{-1\pm{\sqrt{1^2-4.1.1}}}{2.1}\) ➜ \(\because ax^2+bx+c=0\)
\(\Rightarrow x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\Rightarrow x=1, \ x=\frac{-1\pm{\sqrt{1-4}}}{2}\)
\(\Rightarrow x=1, \ x=\frac{-1\pm{\sqrt{-3}}}{2}\)
\(\therefore x=1, \ \frac{1}{2}\left(-1+\sqrt{-3}\right), \ \frac{1}{2}\left(-1-\sqrt{-3}\right)\)
\(\therefore \sqrt[3]{1}=1, \ \frac{1}{2}\left(-1+\sqrt{-3}\right), \ \frac{1}{2}\left(-1-\sqrt{-3}\right)\)
(প্রমাণিত)
একের তিনটি ঘনমূল \(1, \ \frac{1}{2}\left(-1+\sqrt{-3}\right), \ \frac{1}{2}\left(-1-\sqrt{-3}\right)\)। এদের মধ্যে \(1\) বাস্তব এবং অপর দুইটি \(\left\{\frac{1}{2}\left(-1+\sqrt{-3}\right), \ \frac{1}{2}\left(-1-\sqrt{-3}\right)\right\}\) জটিল।ধরি, \(\sqrt[3]{1}=x\)
\(\Rightarrow 1=x^3\) ➜ উভয় পার্শে ঘন করে।
\(\Rightarrow x^3=1\)
\(\Rightarrow x^3-1=0\)
\(\Rightarrow (x-1)(x^2+x+1)=0\) ➜ \(\because a^3-b^3=(a-b)(a^2+ab+b^2)\)
\(\Rightarrow x-1=0, \ x^2+x+1=0\)
\(\Rightarrow x=1, \ x=\frac{-1\pm{\sqrt{1^2-4.1.1}}}{2.1}\) ➜ \(\because ax^2+bx+c=0\)
\(\Rightarrow x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\Rightarrow x=1, \ x=\frac{-1\pm{\sqrt{1-4}}}{2}\)
\(\Rightarrow x=1, \ x=\frac{-1\pm{\sqrt{-3}}}{2}\)
\(\therefore x=1, \ \frac{1}{2}\left(-1+\sqrt{-3}\right), \ \frac{1}{2}\left(-1-\sqrt{-3}\right)\)
\(\therefore \sqrt[3]{1}=1, \ \frac{1}{2}\left(-1+\sqrt{-3}\right), \ \frac{1}{2}\left(-1-\sqrt{-3}\right)\)
(প্রমাণিত)
বিষেশ দ্রষ্টব্যঃ যে কোনো বাস্তব সংখ্যা \(a^3\) এর তিনটি ঘনমূল হচ্ছে \(a, \ a\omega, \ a\omega^2.\)
একের জটিল ঘনমূল দুইটির বৈশিষ্ট্যঃ
Properties of Complex Cube Roots of One:
একের জটিল ঘনমূল দুইটির গুণফল \(1\) অর্থাৎ একটি অপরটির বিপরীত।
অতএব, \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\) হলে,
\(\frac{1}{\omega}=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
আবার, \(\omega\times\omega^3=1\) ➜ যেহেতু জটিল মূল দ্বয়ের গুণফল \(1\)।
\(\therefore \omega^3=1\)।
একের জটিল ঘনমূল দুইটি একটি অপরটির বর্গ।
অর্থাৎ, \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\) হলে,
\(\omega^2=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
একের ঘনমূল তিনটির যোগফল শূন্য \((0)\)।
অর্থাৎ, \(\omega^2+\omega+1=0\)
\(\omega^3=1\) \(\omega^2+\omega+1=0\) \(\omega^{n+2}+\omega^{n+1}+1=0\) যেখানে, \(n\in{\mathbb{N}}\)
অতএব, \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\) হলে,
\(\frac{1}{\omega}=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
প্রমাণঃ
ধরি, \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\)
\(\Rightarrow \frac{1}{\omega}=\frac{1}{\frac{1}{2}\left(-1+\sqrt{-3}\right)}\) ➜ ব্যাস্তকরণ করে।
\(=\frac{2}{\left(-1+\sqrt{-3}\right)}\)
\(=\frac{2\left(-1-\sqrt{-3}\right)}{\left(-1+\sqrt{-3}\right)\left(-1-\sqrt{-3}\right)}\) ➜ লব ও হরের সাথে \(\left(-1-\sqrt{-3}\right)\) গুণ করে।
\(=\frac{2\left(-1-\sqrt{-3}\right)}{(-1)^2-\left(\sqrt{-3}\right)^2}\)
\(=\frac{2\left(-1-\sqrt{-3}\right)}{1+3}\)
\(=\frac{2\left(-1-\sqrt{-3}\right)}{4}\)
\(=\frac{2}{4}\left(-1-\sqrt{-3}\right)\)
\(=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
\(\therefore \frac{1}{\omega}=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
(প্রমাণিত)
তাহলে একের ঘনমূল তিনটি \(1, \ \omega, \ \frac{1}{\omega}\)।ধরি, \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\)
\(\Rightarrow \frac{1}{\omega}=\frac{1}{\frac{1}{2}\left(-1+\sqrt{-3}\right)}\) ➜ ব্যাস্তকরণ করে।
\(=\frac{2}{\left(-1+\sqrt{-3}\right)}\)
\(=\frac{2\left(-1-\sqrt{-3}\right)}{\left(-1+\sqrt{-3}\right)\left(-1-\sqrt{-3}\right)}\) ➜ লব ও হরের সাথে \(\left(-1-\sqrt{-3}\right)\) গুণ করে।
\(=\frac{2\left(-1-\sqrt{-3}\right)}{(-1)^2-\left(\sqrt{-3}\right)^2}\)
\(=\frac{2\left(-1-\sqrt{-3}\right)}{1+3}\)
\(=\frac{2\left(-1-\sqrt{-3}\right)}{4}\)
\(=\frac{2}{4}\left(-1-\sqrt{-3}\right)\)
\(=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
\(\therefore \frac{1}{\omega}=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
(প্রমাণিত)
আবার, \(\omega\times\omega^3=1\) ➜ যেহেতু জটিল মূল দ্বয়ের গুণফল \(1\)।
\(\therefore \omega^3=1\)।
একের জটিল ঘনমূল দুইটি একটি অপরটির বর্গ।
অর্থাৎ, \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\) হলে,
\(\omega^2=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
প্রমাণঃ
ধরি, \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\)
\(\Rightarrow \omega^2=\frac{1}{4}\left(-1+\sqrt{-3}\right)^2\) ➜ উভয় পার্শে বর্গ করে।
\(=\frac{1}{4}\left\{(-1)^2+2(-1)\sqrt{-3}+(\sqrt{-3})^2\right\}\) ➜ \(\because (a+b)^2=a^2+2ab+b^2\)
\(=\frac{1}{4}\left\{1-2\sqrt{-3}-3\right\}\)
\(=\frac{1}{4}\left(-2-2\sqrt{-3}\right)\)
\(=\frac{1}{4}\times2\left(-1-\sqrt{-3}\right)\)
\(=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
\(\therefore \omega^2=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
(প্রমাণিত)
তাহলে একের ঘনমূল তিনটি \(1, \ \omega, \ \omega^2\)।ধরি, \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\)
\(\Rightarrow \omega^2=\frac{1}{4}\left(-1+\sqrt{-3}\right)^2\) ➜ উভয় পার্শে বর্গ করে।
\(=\frac{1}{4}\left\{(-1)^2+2(-1)\sqrt{-3}+(\sqrt{-3})^2\right\}\) ➜ \(\because (a+b)^2=a^2+2ab+b^2\)
\(=\frac{1}{4}\left\{1-2\sqrt{-3}-3\right\}\)
\(=\frac{1}{4}\left(-2-2\sqrt{-3}\right)\)
\(=\frac{1}{4}\times2\left(-1-\sqrt{-3}\right)\)
\(=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
\(\therefore \omega^2=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
(প্রমাণিত)
একের ঘনমূল তিনটির যোগফল শূন্য \((0)\)।
অর্থাৎ, \(\omega^2+\omega+1=0\)
প্রমাণঃ
\(L.S=\omega^2+\omega+1\)
\(=\frac{1}{2}\left(-1-\sqrt{-3}\right)+\frac{1}{2}\left(-1+\sqrt{-3}\right)+1\) ➜ \(\because \omega^2=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
এবং \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\)
\(=\frac{1}{2}\left(-1-\sqrt{-3}-1+\sqrt{-3}\right)+1\)
\(=\frac{1}{2}(-2)+1\)
\(=-1+1\)
\(=0\)
\(=R.S\)
\(\therefore \omega^2+\omega+1=0\)
(প্রমাণিত)
দ্রষ্টব্যঃ \(L.S=\omega^2+\omega+1\)
\(=\frac{1}{2}\left(-1-\sqrt{-3}\right)+\frac{1}{2}\left(-1+\sqrt{-3}\right)+1\) ➜ \(\because \omega^2=\frac{1}{2}\left(-1-\sqrt{-3}\right)\)
এবং \(\omega=\frac{1}{2}\left(-1+\sqrt{-3}\right)\)
\(=\frac{1}{2}\left(-1-\sqrt{-3}-1+\sqrt{-3}\right)+1\)
\(=\frac{1}{2}(-2)+1\)
\(=-1+1\)
\(=0\)
\(=R.S\)
\(\therefore \omega^2+\omega+1=0\)
(প্রমাণিত)
\(\omega^3=1\) \(\omega^2+\omega+1=0\) \(\omega^{n+2}+\omega^{n+1}+1=0\) যেখানে, \(n\in{\mathbb{N}}\)
একের জটিল ঘনমূল এর প্রকৃতি
Nature of the complex cube root of one
\(\omega\) একের জটিল ঘনমূলের একটি হলে,
অপর জটিল ঘনমূলটি হয় \(\omega^2\)
সে ক্ষেত্রে \(\omega^3=1\)
তাহলে, \(\omega^4=\omega^3\times\omega=1\times\omega=\omega\) ➜ \(\because \omega^3=1\)
\(\omega^5=\omega^3\times\omega^2=1\times\omega^2=\omega^2\) ➜ \(\because \omega^3=1\)
\(\omega^6=(\omega^3)^2=1^2=1\) ➜ \(\because \omega^3=1\)
অতএব, \(n\in{\mathbb{N}}\) এর জন্য,
\(\omega^{3n}=(\omega^3)^n=1^n=1\) ➜ \(\because \omega^3=1\)
\(\omega^{3n+1}=\omega^{3n}\times\omega=(\omega^3)^n\times\omega=1^n\times\omega=\omega\) ➜ \(\because \omega^3=1\)
\(\omega^{3n+2}=\omega^{3n}\times\omega^2=(\omega^3)^n\times\omega^2=1^n\times\omega^2=\omega^2\) ➜ \(\because \omega^3=1\)
অর্থাৎ, \(\omega^{n}=1, \ \omega, \ \omega^2\) হবে যদি \(n\) কে \(3\) দ্বারা ভাগ করলে ভাগশেষ যথাক্রমে \(0, \ 1, \ 2\) হয়।
অপর জটিল ঘনমূলটি হয় \(\omega^2\)
সে ক্ষেত্রে \(\omega^3=1\)
তাহলে, \(\omega^4=\omega^3\times\omega=1\times\omega=\omega\) ➜ \(\because \omega^3=1\)
\(\omega^5=\omega^3\times\omega^2=1\times\omega^2=\omega^2\) ➜ \(\because \omega^3=1\)
\(\omega^6=(\omega^3)^2=1^2=1\) ➜ \(\because \omega^3=1\)
অতএব, \(n\in{\mathbb{N}}\) এর জন্য,
\(\omega^{3n}=(\omega^3)^n=1^n=1\) ➜ \(\because \omega^3=1\)
\(\omega^{3n+1}=\omega^{3n}\times\omega=(\omega^3)^n\times\omega=1^n\times\omega=\omega\) ➜ \(\because \omega^3=1\)
\(\omega^{3n+2}=\omega^{3n}\times\omega^2=(\omega^3)^n\times\omega^2=1^n\times\omega^2=\omega^2\) ➜ \(\because \omega^3=1\)
অর্থাৎ, \(\omega^{n}=1, \ \omega, \ \omega^2\) হবে যদি \(n\) কে \(3\) দ্বারা ভাগ করলে ভাগশেষ যথাক্রমে \(0, \ 1, \ 2\) হয়।

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004