এ অধ্যায়ের পাঠ্যসূচী
- সীমা ( Limit )
- চলক (Variable )
- ধ্রূবক (Constant )
- চলকের লিমিট (Limit of Variable )
- চলকের বাম লিমিট (Left hand Limit of variable)
- চলকের ডান লিমিট (Right hand Limit of variable)
- ফাংশনের লিমিট (Limit of Functions)
- এক দিকবর্তী লিমিট (One sided Limit )
- ফাংশনের বাম লিমিট (Left hand Limit of function)
- ফাংশনের ডান লিমিট (Right hand Limit of function)
- চলকের অসীম লিমিট (Infinite Limit of Variables)
- ফাংশনের অসীম লিমিট (Infinite Limit of Functions)
- লিমিটের মৌলিক ধর্ম ( Fundamental properties of limit )
- বিচ্ছিন্ন ফাংশন ( Discontinuous Function )
- অবিচ্ছিন্ন ফাংশন ( Continuous Function )
- স্যান্ডউইচ উপপাদ্য ( The Sandwich theorem )
- ল্যাগ্রাঞ্জের গড় মধ্যমান উপপাদ্য ( Lagrange's Mean Value Theorem )
- ল্যাগ্রাঞ্জের গড় মধ্যমান উপপাদ্যের জ্যামিতিক ব্যাখ্যা ( Geometrical interpretation of Lagrange's Mean Value Theorem )
- সমস্যা সমাধানের ক্ষেত্রে প্রয়োজনীয় এবং স্মরণীয় সূত্রসমূহ ( Necessary and memorable formulas for solving problems )
- প্রয়োজনীয় এবং স্মরণীয় কতিপয় বিশেষ লিমিট ( Necessary and memorable Some special limit )
- অধ্যায় \(ix.A\)-এর উদাহরণসমুহ
- অধ্যায় \(ix.A\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(ix.A\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(ix.A\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(ix.A\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
সীমা
Limit
আমরা প্রায়শই বলে থাকি সীমা (limit) ফাংশনের লিমিটঃ চলমান রাশি \(x\)-এর মান উভয় দিক হতে একটি নির্দিষ্ট সংখ্যা \(a\)-এর দিকে অগ্রসর হয়ে \(a\)-এর সন্নিকটবর্তী হওয়ায় যদি ফাংশন \(f(x)\), একটি নির্দিষ্ট সংখ্যা \(l\)-এর যথেচ্ছ সন্নিকটবর্তী হয়, তাহলে \(l\) কে \(f(x)\) ফাংশনের সীমাস্থ মাণ বা সীমা বলা হয়। একে \[\lim_{x \rightarrow a}f(x)=l\] দ্বারা প্রকাশ করা হয়। অতিক্রম কর না, ফাজলামোর একটা সীমা (limit) আছে। এখানে ফাংশনের সীমা (limit) সম্পর্কে বলা হচ্ছে অর্থাৎ ফাংশনেরও সীমা (limit) আছে। একটি ফাংশনে দুই বা ততোধীক চলক ব্যবহৃত হয়। উচ্চমাধ্যমিক গণিতে দুই চলক বিশিষ্ট ফাংশন আলোচনা করা হয়েছে। এই দুইটি চলকের একটি স্বাধীন চলক এবং অপরটি অধীন। \(y=f(x)\) ফাংশনে \(x\) স্বাধীন চলক এবং \(y\) অধীন। চলকের ও সীমা (limit) আছে। স্বাধীন চলক \(x\)-এর সীমা (limit) \(x\rightarrow a\) এবং অধীন চলক \(y\)-এর সীমা (limit) \(y\rightarrow b\)। তেমনিভাবে স্বাধীন চলকের সীমার (limit) সাপেক্ষে \(f(x)\)-এর সীমা (limit) \[\lim_{x \rightarrow a}f(x)=l\] দ্বারা প্রকাশ করা হয়। কোনো ফাংশনের মূল নিয়মে অন্তরজ নির্ণয় করতে সীমার (limit) ভুমিকা অপরিহার্য। একটি ফাংশনের বিচ্ছিন্নতা ও অবিচ্ছিন্নতা দেখাতে সীমা (limit) ব্যবহার করা হয়। গণিত বিশ্লেষণে লিমিট বা সীমা (limit) একটি মৌলিক ধারণা। বিশেষ করে কোনো ফাংশনের অন্তরকলন বিদ্যার ভিত্তি হচ্ছে লিমিট বা সীমা (limit)।
চলক
Variable
চলকঃ অজ্ঞ্যাত কোনো সংখ্যা বা বস্তুকে কোনো প্রতীকের মাধ্যমে প্রকাশ করা হলে ঐ প্রতীককে চলক ( Variable ) বলা হয়।
যেমনঃ \(x, y, z, u, v, w\) ইত্যাদি অক্ষরগুলিকে চলকের প্রতীক হিসাবে ব্যবহার করা হয়।
যেমনঃ \(x, y, z, u, v, w\) ইত্যাদি অক্ষরগুলিকে চলকের প্রতীক হিসাবে ব্যবহার করা হয়।
ধ্রূবক
Constant
ধ্রূবকঃ যে প্রতীক কোনো গাণিতিক প্রক্রিয়ায় একই মানে অবস্থান করে অর্থাৎ এর মানে কোনো পরিবর্তন হয় না তাকে ধ্রূবক (Constant) বলে।
যেমনঃ \(1, 2, 3, 4, \pi\) ইত্যাদি অক্ষরগুলিকে ধ্রূবক হিসাবে ব্যবহার করা হয়। \(a, b, c, d ..... \alpha, \beta, \gamma\) ইত্যাদি প্রতীকসমূহ দ্বারা সাধারণত ইচ্ছামূলক ধ্রূবক প্রকাশ করা হয়।
যেমনঃ \(1, 2, 3, 4, \pi\) ইত্যাদি অক্ষরগুলিকে ধ্রূবক হিসাবে ব্যবহার করা হয়। \(a, b, c, d ..... \alpha, \beta, \gamma\) ইত্যাদি প্রতীকসমূহ দ্বারা সাধারণত ইচ্ছামূলক ধ্রূবক প্রকাশ করা হয়।
চলকের লিমিট
Limit of Variable
চলকের লিমিটঃ যদি \(x\) চলকের মাণ একটি ধ্রূবক \(a\) অপেক্ষা উভয় দিক হতে অর্থাৎ ছোট অথবা বড় হয়ে ক্রমশ \(a\)-এর দিকে অগ্রসর হয়ে এত নিকটবর্তী হয় যে, \(x\) ও \(a\)-এর পার্থক্য অর্থাৎ \(|x-a|\) যে কোনো ক্ষুদ্র ধনাত্মক সংখ্যা \(\delta\) হতে ক্ষুদ্রতর অর্থাৎ \(\delta>|x-a|\) হয়, তবে \(a\) কে \(x\)-এর লিমিট বা সীমা বলা হয় এবং \(x\)-এর মাণ কে \(x\rightarrow a\) প্রতীক দ্বারা প্রকাশ করা হয়।
চলকের বাম লিমিট
Left limit of variable
চলকের বাম লিমিটঃ যদি \(x\) চলকের মাণ একটি ধ্রূবক \(a\) অপেক্ষা ছোট হয়ে বামদিক হতে ক্রমশ \(a\)-এর দিকে অগ্রসর হয়ে এত নিকটবর্তী হয় যে, \(x\) ও \(a\)-এর পার্থক্য অর্থাৎ \(|x-a|\) যে কোনো ক্ষুদ্র ধনাত্মক সংখ্যা \(\delta\) হতে ক্ষুদ্রতর অর্থাৎ \(\delta>|x-a|\) হয়, তবে \(a\) কে \(x\)-এর বামদিকবর্তী লিমিট বা সীমা বলা হয় এবং \(x\)-এর মাণ কে \(x\rightarrow a^{-}\) প্রতীক দ্বারা প্রকাশ করা হয়।
যেমনঃ মনে করি চলমান রাশি \(x\)-এর মাণগুলি ক্রমান্বয়ে \(2.9, 2.99, 2.999, 2.9999 ...... \) এ ক্ষেত্রে \(3\) অপেক্ষা ক্ষুদ্রতর থেকে বা বামদিকবর্তী থেকে \(x\)-এর মাণ \(3\)-এর নিকটবর্তী হয়। এটি প্রকাশ করা হয় \(x\rightarrow 3^{-}\) সঙ্কেত দ্বারা।
যেমনঃ মনে করি চলমান রাশি \(x\)-এর মাণগুলি ক্রমান্বয়ে \(2.9, 2.99, 2.999, 2.9999 ...... \) এ ক্ষেত্রে \(3\) অপেক্ষা ক্ষুদ্রতর থেকে বা বামদিকবর্তী থেকে \(x\)-এর মাণ \(3\)-এর নিকটবর্তী হয়। এটি প্রকাশ করা হয় \(x\rightarrow 3^{-}\) সঙ্কেত দ্বারা।
চলকের ডান লিমিট
Right limit of variable
চলকের ডান লিমিটঃ যদি \(x\) চলকের মাণ একটি ধ্রূবক \(a\) অপেক্ষা বড় হয়ে ডানদিক হতে ক্রমশ \(a\)-এর দিকে অগ্রসর হয়ে এত নিকটবর্তী হয় যে, \(x\) ও \(a\)-এর পার্থক্য অর্থাৎ \(|x-a|\) যে কোনো ক্ষুদ্র ধনাত্মক সংখ্যা \(\delta\) হতে ক্ষুদ্রতর অর্থাৎ \(\delta>|x-a|\) হয়, তবে \(a\) কে \(x\)-এর ডানদিকবর্তী লিমিট বা সীমা বলা হয় এবং \(x\)-এর মাণ কে \(x\rightarrow a^{+}\) প্রতীক দ্বারা প্রকাশ করা হয়।
যেমনঃ মনে করি চলমান রাশি \(x\)-এর মাণগুলি ক্রমান্বয়ে \(3.1, 3.01, 3.001,3.0001 ...... \) এ ক্ষেত্রে \(3\) অপেক্ষা বৃহত্তর থেকে বা ডানদিকবর্তী থেকে \(x\)-এর মাণ \(3\)-এর নিকটবর্তী হয়। এটি প্রকাশ করা হয় \(x\rightarrow 3^{+}\) সঙ্কেত দ্বারা।
যেমনঃ মনে করি চলমান রাশি \(x\)-এর মাণগুলি ক্রমান্বয়ে \(3.1, 3.01, 3.001,3.0001 ...... \) এ ক্ষেত্রে \(3\) অপেক্ষা বৃহত্তর থেকে বা ডানদিকবর্তী থেকে \(x\)-এর মাণ \(3\)-এর নিকটবর্তী হয়। এটি প্রকাশ করা হয় \(x\rightarrow 3^{+}\) সঙ্কেত দ্বারা।
ফাংশনের লিমিট
Limit of Functions
ফাংশনের লিমিটঃ চলমান রাশি \(x\)-এর মান উভয় দিক হতে একটি নির্দিষ্ট সংখ্যা \(a\)-এর দিকে অগ্রসর হয়ে \(a\)-এর সন্নিকটবর্তী হওয়ায় যদি ফাংশন \(f(x)\), একটি নির্দিষ্ট সংখ্যা \(l\)-এর যথেচ্ছ সন্নিকটবর্তী হয়, তাহলে \(l\) কে \(f(x)\) ফাংশনের সীমাস্থ মাণ বা সীমা বলা হয়। একে \[\lim_{x \rightarrow a}f(x)=l\] দ্বারা প্রকাশ করা হয়।
এক দিকবর্তী লিমিট
One sided Limit
একদিকবর্তী লিমিটঃ কখনও কখনও \(f(x)\) কে একাধিক সূত্র দ্বারা সূচিত করাহয়। ঐ সব ক্ষেত্রে ফাংশনের বামদিকের এবং ডানদিকের লিমিট সম্পর্কিত ধারণা থাকা অবশ্যক। ফাংশনের এই বামদিকের লিমিট এবং ডানদিকের লিমিটকে পৃথকভাবে একদিকবর্তী লিমিট বলা হয়।
ফাংশনের বাম লিমিট
Left limit of function
ফাংশনের বাম লিমিটঃ \(x\) চলক \(a\) অপেক্ষা ক্ষুদ্র মাণগুলি গ্রহণ করে বামদিক হতে ক্রমশ \(a\)-এর খুব নিকটবর্তী হওয়ায় যদি \(f(x)\) ফাংশনের মাণ একটি স্থির রাশি \(l_{1}\)-এর নিকটবর্তী হয়, তবে \(l_{1}\) কে \(f(x)\) ফাংশনের বামদিকবর্তী লিমিট বলা হয় এবং তা \[\lim_{x \rightarrow a^{-}}f(x)=l_{1}\] বা, \[\lim_{h \rightarrow 0}f(a-h)=l_{1}, h>0\] দ্বারা প্রকাশ করা হয়।
ফাংশনের ডান লিমিট
Right Limit of function
ফাংশনের ডান লিমিটঃ \(x\) চলক \(a\) অপেক্ষা বৃহত্তর মাণগুলি গ্রহণ করে ডানদিক হতে ক্রমশ \(a\)-এর খুব নিকটবর্তী হওয়ায় যদি \(f(x)\) ফাংশনের মাণ একটি স্থির রাশি \(l_{2}\)-এর নিকটবর্তী হয়, তবে \(l_{2}\) কে \(f(x)\) ফাংশনের ডানদিকবর্তী লিমিট বলা হয় এবং তা \[\lim_{x \rightarrow a^{+}}f(x)=l_{2}\] বা, \[\lim_{h \rightarrow 0}f(a+h)=l_{2}, h>0\] দ্বারা প্রকাশ করা হয়।
চলকের অসীম লিমিট
Infinite Limit of Variables
চলকের অসীম লিমিটঃ \(x\) চলক \(0\) অপেক্ষা বৃহত্তর মাণগুলি গ্রহণ করে ডানদিকে ক্রমশ \(\infty\) অথবা, \(0\) অপেক্ষা ক্ষুদ্রত্তর মাণগুলি গ্রহণ করে বামদিকে ক্রমশ \(-\infty\) পর্যন্ত বিস্তার লাভ করলে, \(x\) চলকের অসীম লিমিট হয়। যা \[x \rightarrow \infty\] এবং \[x \rightarrow -\infty\] দ্বারা প্রকাশ করা হয়।
ফাংশনের অসীম লিমিট
Infinite Limit of Functions
ফাংশনের অসীম লিমিটঃ চলরাশি \(x\) নির্দিষ্ট সংখ্যা \(a\) অপেক্ষা ক্ষুদ্রতর বা বৃহত্তর মাণ গ্রহণপূর্বক \(a\)-এর দিকে অগ্রসর হয়ে \(a\)-এর সন্নিকটবর্তী হলেঃ
\(f(x)\)-এর মাণ সীমাহীনভাবে বৃদ্ধি পেলে একে \[\lim_{x \rightarrow a}f(x)=\infty\] দ্বারা প্রকাশ করা হয়।
\(f(x)\)-এর মাণ সীমাহীনভাবে হ্রাস পেলে একে \[\lim_{x \rightarrow a}f(x)=-\infty\] দ্বারা প্রকাশ করা হয়।
\(f(x)\)-এর মাণ সীমাহীনভাবে বৃদ্ধি পেলে একে \[\lim_{x \rightarrow a}f(x)=\infty\] দ্বারা প্রকাশ করা হয়।
\(f(x)\)-এর মাণ সীমাহীনভাবে হ্রাস পেলে একে \[\lim_{x \rightarrow a}f(x)=-\infty\] দ্বারা প্রকাশ করা হয়।
উদাহরণঃ
\[\lim_{x \rightarrow \infty}7x=\infty\]
\[\lim_{x \rightarrow -\infty}2x^2=\infty\]
\[\lim_{x \rightarrow 0^{+}}\frac{5}{x}=\infty\]
\[\lim_{x \rightarrow 0^{-}}\frac{7}{x}=-\infty\]
\[\lim_{x \rightarrow -\infty}2x^2=\infty\]
\[\lim_{x \rightarrow 0^{+}}\frac{5}{x}=\infty\]
\[\lim_{x \rightarrow 0^{-}}\frac{7}{x}=-\infty\]
\[\lim_{x \rightarrow 2^{+}}\frac{6}{x-2}=\infty\]
\[\lim_{x \rightarrow 2^{-}}\frac{6}{x-2}=-\infty\]
\[\lim_{x \rightarrow 5^{+}}\frac{6x}{x-5}=\infty\]
\[\lim_{x \rightarrow 7^{-}}\frac{2x^2}{x-7}=-\infty\]
বিশেষভাবে লক্ষনীয়ঃ
\[\lim_{x \rightarrow a}f(x)=\infty\] বা, \[\lim_{x \rightarrow a}f(x)=-\infty\] হলে, \(x=a\) বিন্দুতে লিমিট বিদ্যমান হবে না। কারণ, \(\infty\) ও \(-\infty\) কোনো সংখ্যা নয় শুধু প্রতীক মাত্র।
\[\lim_{x \rightarrow 2^{-}}\frac{6}{x-2}=-\infty\]
\[\lim_{x \rightarrow 5^{+}}\frac{6x}{x-5}=\infty\]
\[\lim_{x \rightarrow 7^{-}}\frac{2x^2}{x-7}=-\infty\]
লিমিটের মৌলিক ধর্ম
Fundamental properties of limit
যদি \[\lim_{x \rightarrow a}f(x)=l\] এবং \[\lim_{x \rightarrow a}g(x)=m\] হয় তবে
\[\lim_{x \rightarrow a}\{f(x)\pm g(x)\}=\lim_{x \rightarrow a}f(x)\pm \lim_{x \rightarrow a}g(x)=l\pm m\]
\[\lim_{x \rightarrow a}\{f(x)\times g(x)\}=\lim_{x \rightarrow a}f(x)\times \lim_{x \rightarrow a}g(x)=l\times m=lm\]
\[\lim_{x \rightarrow a}\left\{\frac{f(x)}{g(x)}\right\}=\frac{\lim_{x \rightarrow a}f(x)}{\lim_{x \rightarrow a}g(x)}=\frac{l}{m}\] যখন \(m\ne 0\)
\[\lim_{x \rightarrow a}\{f(x)\pm g(x)\}=\lim_{x \rightarrow a}f(x)\pm \lim_{x \rightarrow a}g(x)=l\pm m\]
\[\lim_{x \rightarrow a}\{f(x)\times g(x)\}=\lim_{x \rightarrow a}f(x)\times \lim_{x \rightarrow a}g(x)=l\times m=lm\]
\[\lim_{x \rightarrow a}\left\{\frac{f(x)}{g(x)}\right\}=\frac{\lim_{x \rightarrow a}f(x)}{\lim_{x \rightarrow a}g(x)}=\frac{l}{m}\] যখন \(m\ne 0\)
বিচ্ছিন্ন ফাংশন
Discontinuous Function
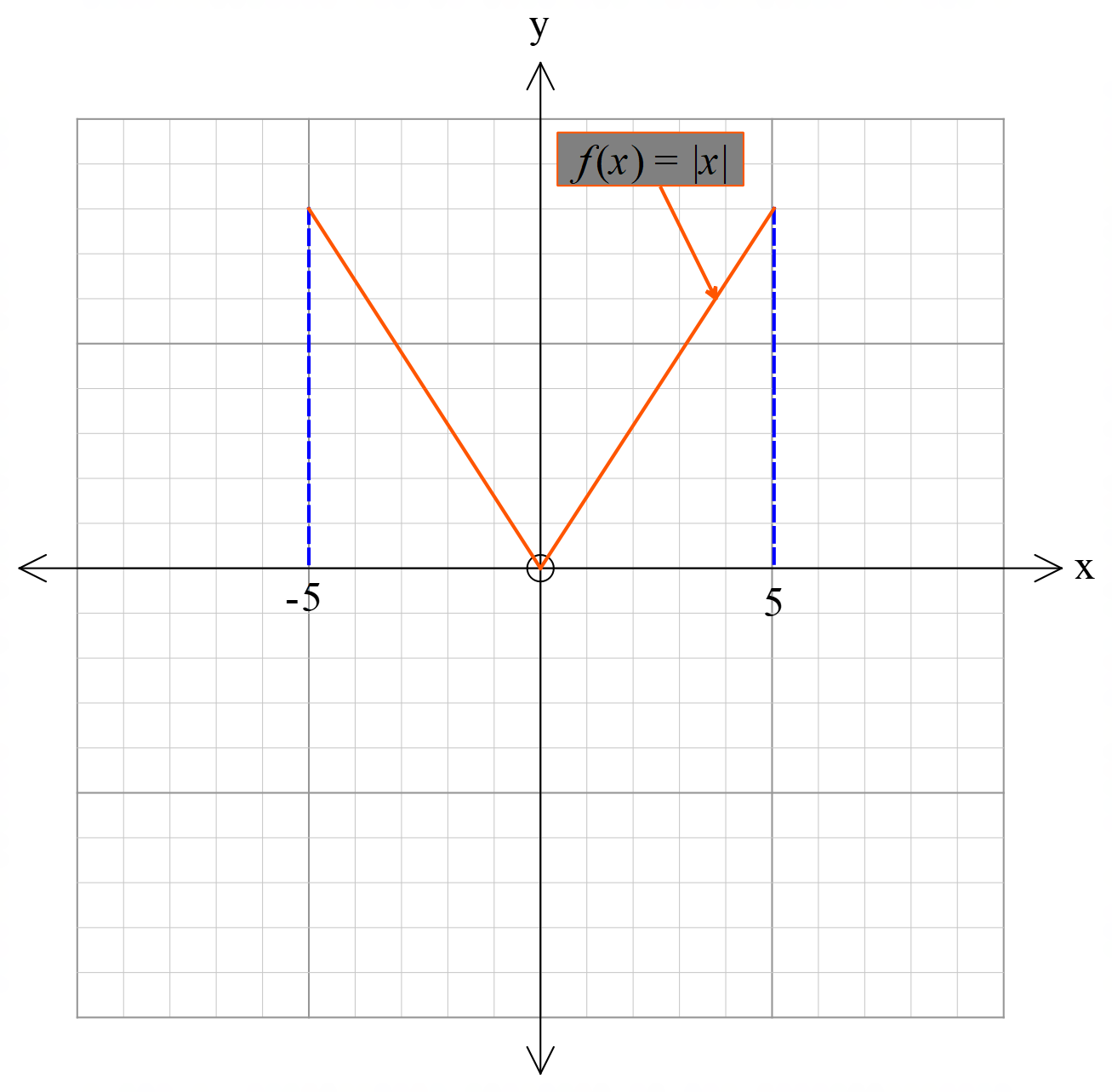
বিচ্ছিন্ন ফাংশনঃ কোনো নির্দিষ্ট ব্যাবধিতে যদি কোনো ফাংশন একাধিক অংশে বিভক্ত হয়ে বিচ্ছিন্নভাবে চলে তবে উক্ত ব্যবধিতে ফাংশনটিকে বিচ্ছিন্ন ফাংশন বলা হয়। নিম্নে বিচ্ছিন্ন ফাংশনের চিত্র দেওয়া হলো।
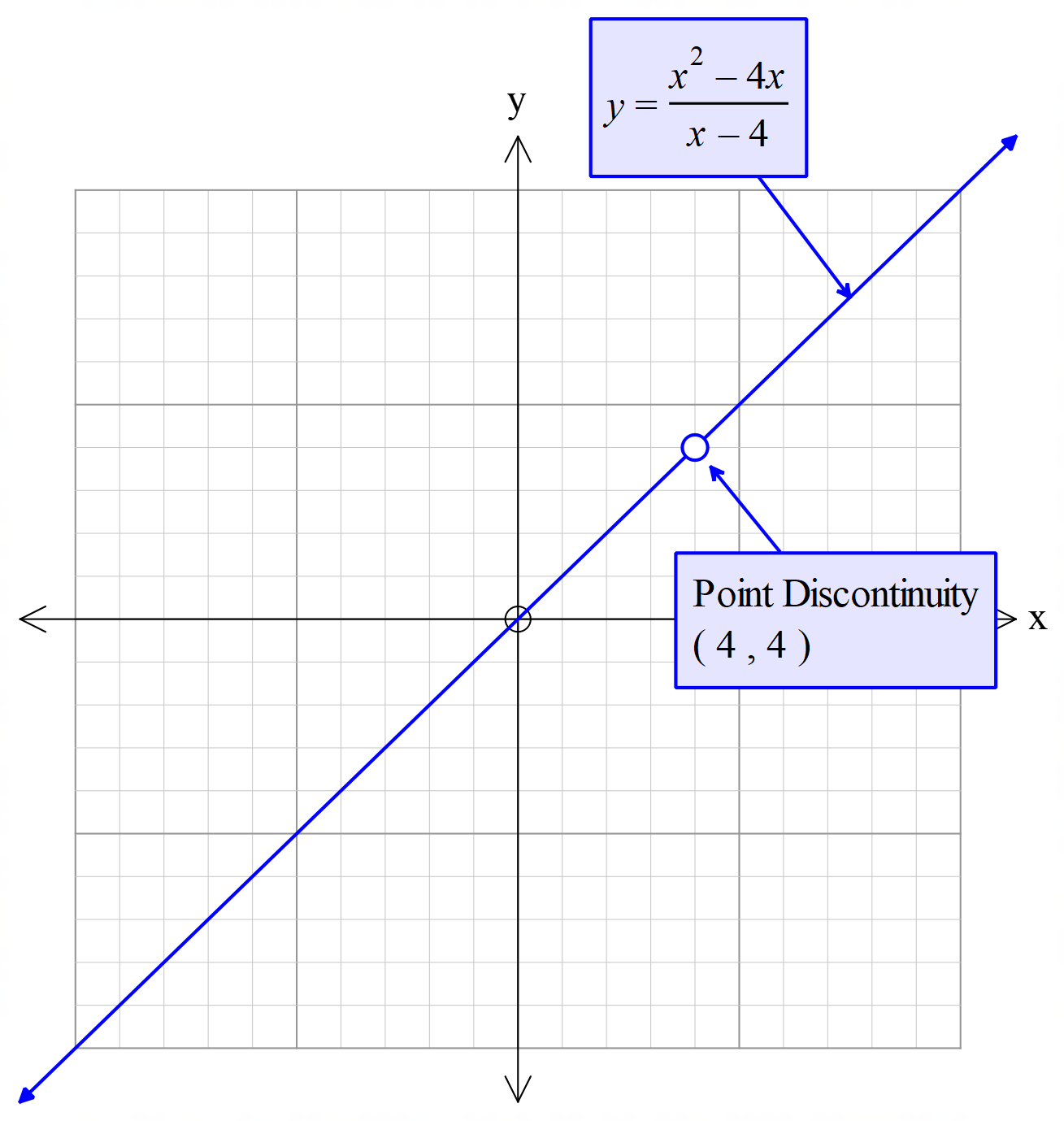
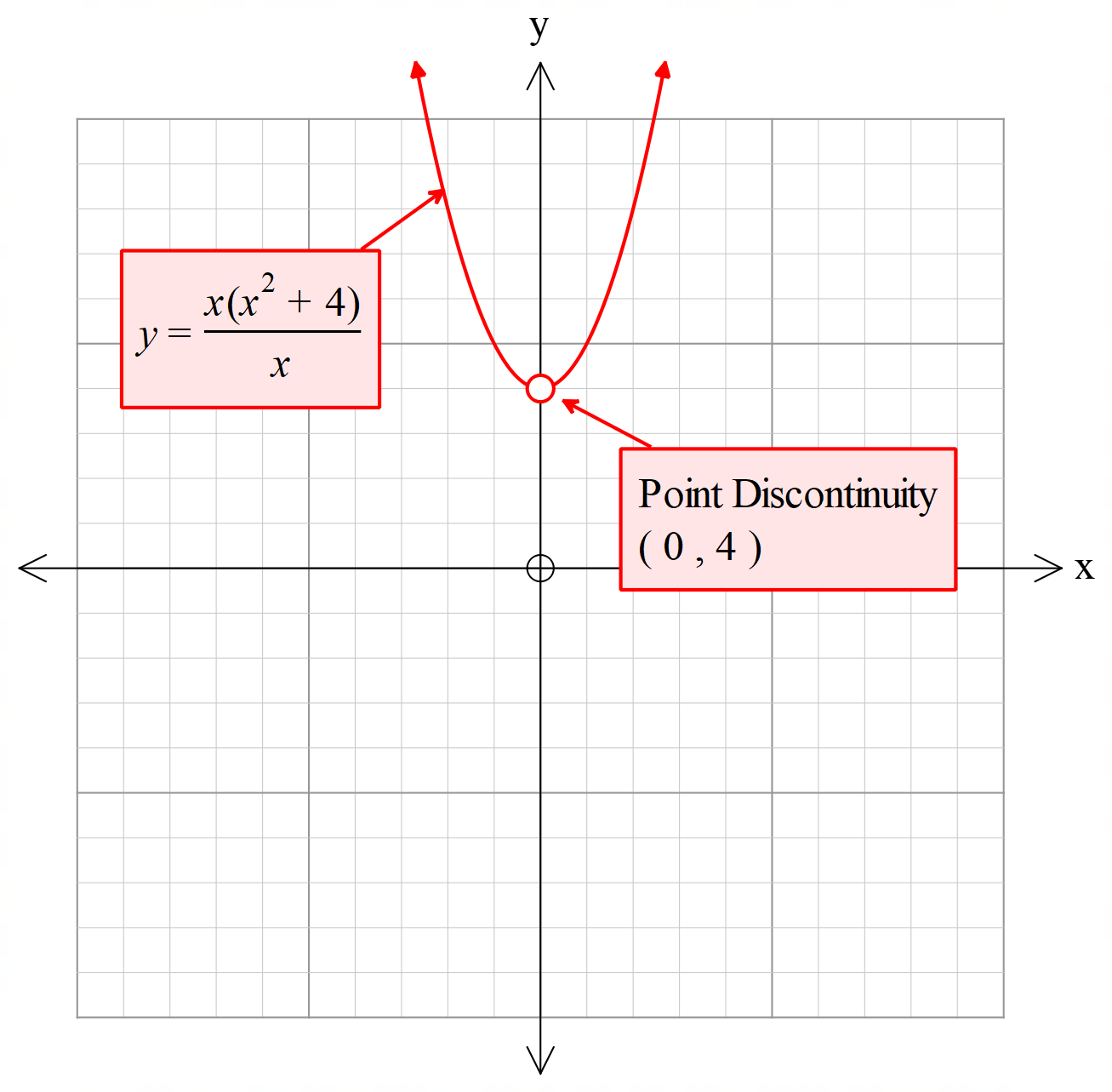
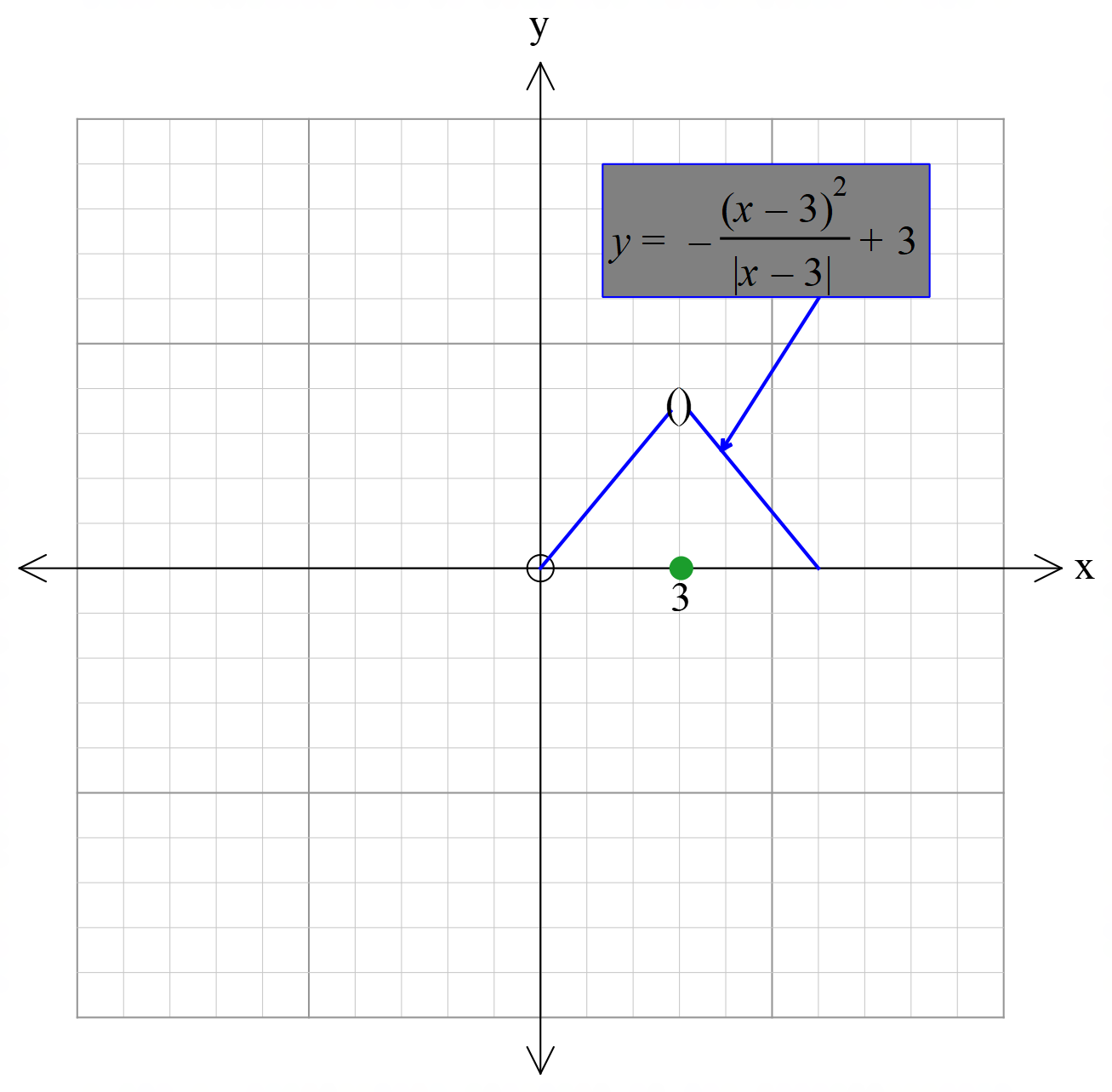



অবিচ্ছিন্ন ফাংশন
Continuous Function
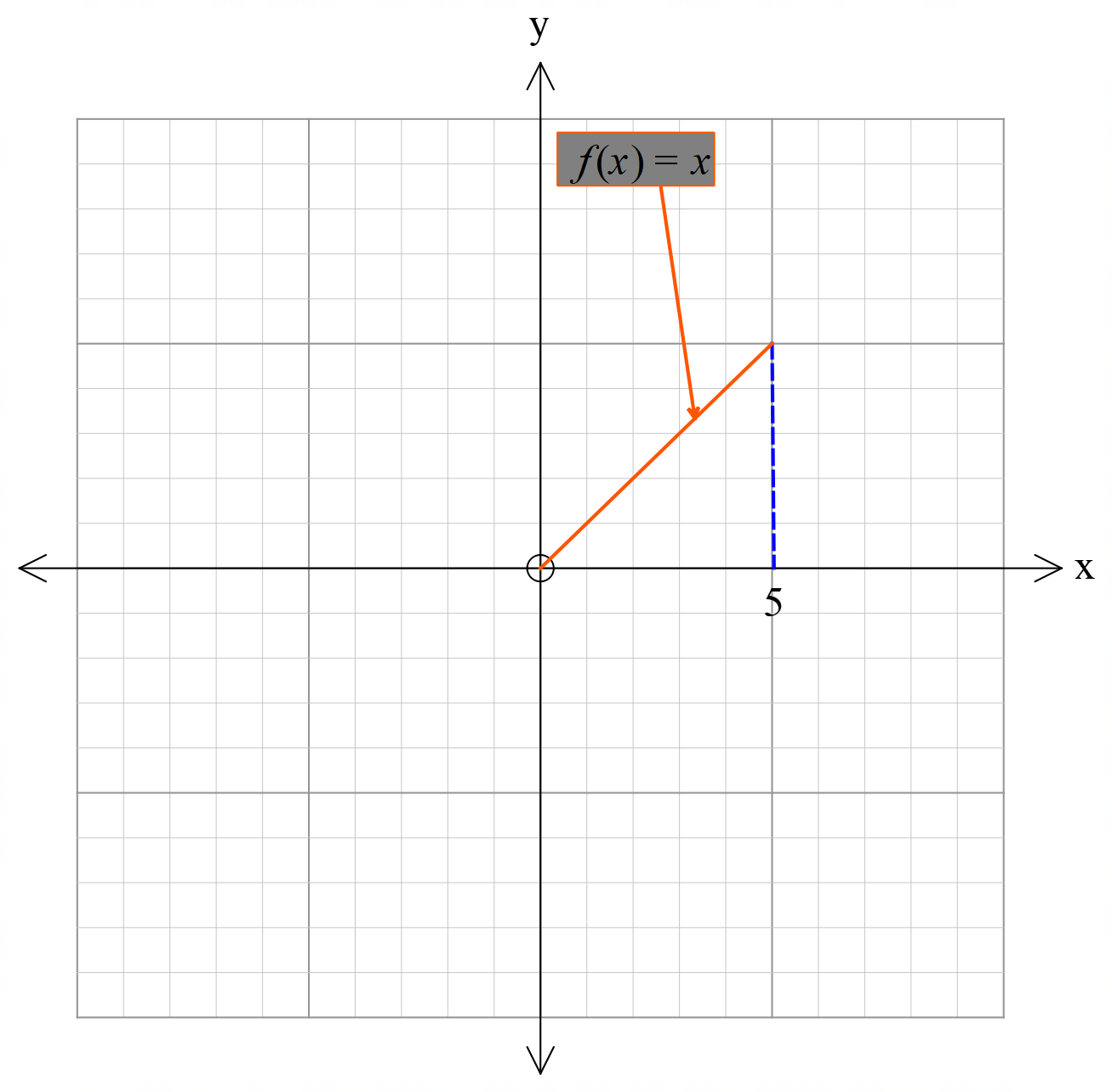
অবিচ্ছিন্ন ফাংশনঃ কোনো নির্দিষ্ট ব্যাবধিতে যদি কোনো ফাংশন একাধিক অংশে বিভক্ত না হয়ে নিরবিচ্ছিন্নভাবে চলে তবে উক্ত ব্যবধিতে ফাংশনটিকে অবিচ্ছিন্ন ফাংশন বলা হয়।
\(f(x)\) ফাংশনটি যদি একটি ব্যবধির মধ্যে সংজ্ঞায়িত হয় এবং \(x=a\) যদি ঐ ব্যবধির মধ্যে থাকে, তবে, \(x=a\) বিন্দুতে ফাংশনটি অবিচ্ছিন্ন হবে
যদি, \[\lim_{x \rightarrow a^{+}}f(x)=\lim_{x \rightarrow a^{-}}f(x)=f(a)\] হয়।
নিম্নে অবিচ্ছিন্ন ফাংশনের চিত্র দেওয়া হলো।
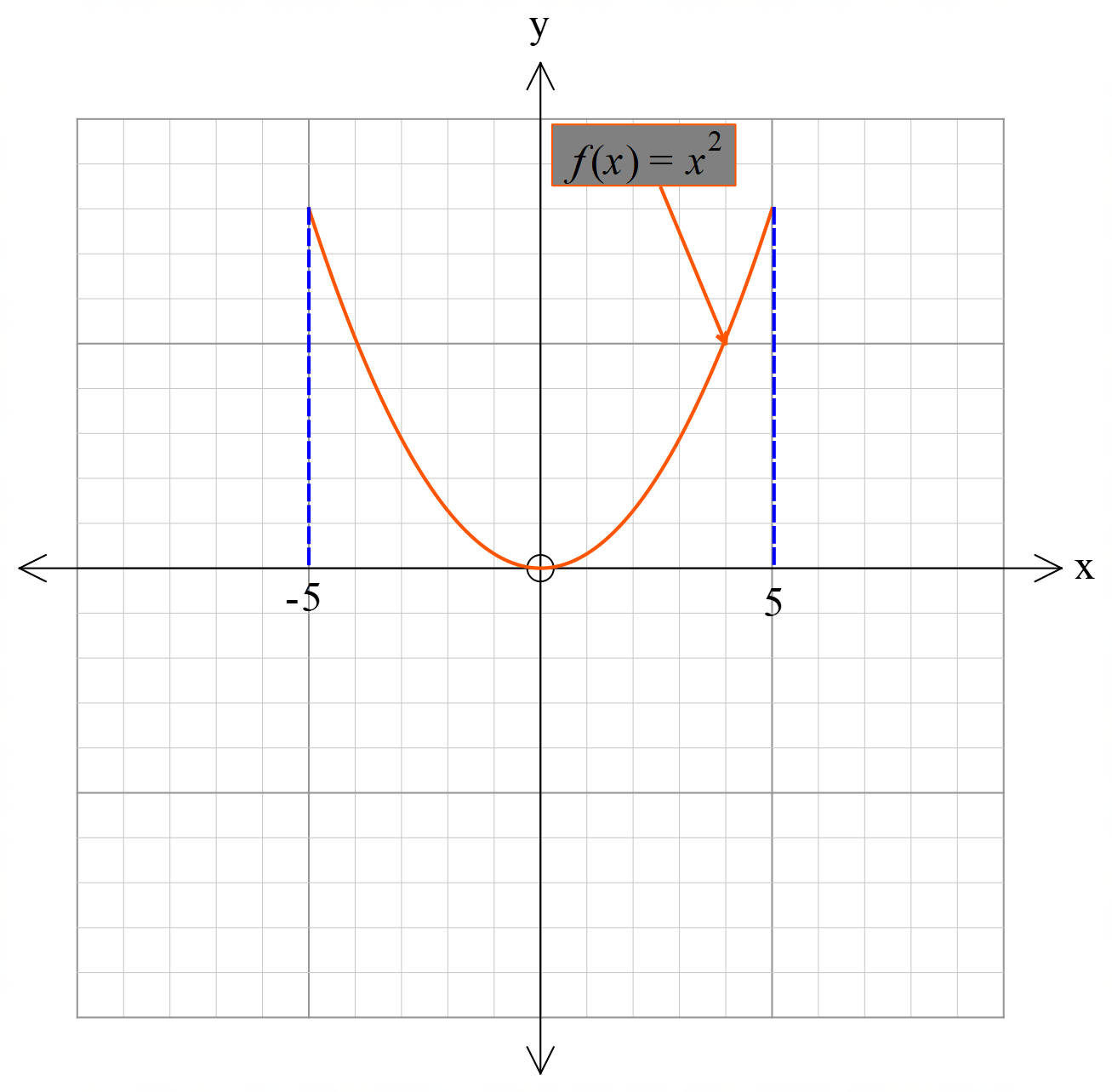
 বিশেষভাবে লক্ষনীয়ঃ
বিশেষভাবে লক্ষনীয়ঃ
যদি, \[\lim_{x \rightarrow a^{+}}f(x)=\lim_{x \rightarrow a^{-}}f(x)\ne f(a)\] হয় তবে ফাংশনটি \(x=a\) বিন্দুতে বিচ্ছিন্ন কিন্তু সীমা বিদ্যমান।
যদি, \[\lim_{x \rightarrow a^{+}}f(x)\ne \lim_{x \rightarrow a^{-}}f(x)\ne f(a)\] হয় তবে ফাংশনটি \(x=a\) বিন্দুতে বিচ্ছিন্ন এবং সীমা বিদ্যমান নেই।
যদি, \[\lim_{x \rightarrow a^{+}}f(x)\ne \lim_{x \rightarrow a^{-}}f(x)= f(a)\] হয় তবে ফাংশনটি \(x=a\) বিন্দুতে বিচ্ছিন্ন এবং সীমা বিদ্যমান নেই।
\(f(x)\) ফাংশনটি যদি একটি ব্যবধির মধ্যে সংজ্ঞায়িত হয় এবং \(x=a\) যদি ঐ ব্যবধির মধ্যে থাকে, তবে, \(x=a\) বিন্দুতে ফাংশনটি অবিচ্ছিন্ন হবে
যদি, \[\lim_{x \rightarrow a^{+}}f(x)=\lim_{x \rightarrow a^{-}}f(x)=f(a)\] হয়।
নিম্নে অবিচ্ছিন্ন ফাংশনের চিত্র দেওয়া হলো।



যদি, \[\lim_{x \rightarrow a^{+}}f(x)=\lim_{x \rightarrow a^{-}}f(x)\ne f(a)\] হয় তবে ফাংশনটি \(x=a\) বিন্দুতে বিচ্ছিন্ন কিন্তু সীমা বিদ্যমান।
যদি, \[\lim_{x \rightarrow a^{+}}f(x)\ne \lim_{x \rightarrow a^{-}}f(x)\ne f(a)\] হয় তবে ফাংশনটি \(x=a\) বিন্দুতে বিচ্ছিন্ন এবং সীমা বিদ্যমান নেই।
যদি, \[\lim_{x \rightarrow a^{+}}f(x)\ne \lim_{x \rightarrow a^{-}}f(x)= f(a)\] হয় তবে ফাংশনটি \(x=a\) বিন্দুতে বিচ্ছিন্ন এবং সীমা বিদ্যমান নেই।
স্যান্ডউইচ উপপাদ্য
The Sandwich theorem
স্যান্ডউইচ উপপাদ্যঃ যদি \(\delta >|x-a|> 0\) ব্যবধির অন্তর্গত \(x\)-এর সকল মানের জন্য \(f(x)\leq g(x)\leq h(x)\) এবং \[\lim_{x \rightarrow a}f(x)=l=\lim_{x \rightarrow a}h(x)\] হয় তবে, \[\lim_{x \rightarrow a}g(x)=l\] স্যান্ডউইচ এর উপপাদ্য বা স্কুইজিং ( Squeezing ) বা পিনচিং ( Pinching ) উপপাদ্য নামেও পরিচিত।
উদাহরণঃ \[\lim_{x \rightarrow \infty}\frac{\sin x}{x}=0\] প্রমান কর।
\[-1\leq \sin x\leq 1\]
\[\Rightarrow \frac{-1}{x}\leq \frac{\sin x}{x}\leq \frac{1}{x}\] ➜ প্রতিটি পদে \(x\) ভাগ করে।
\[\Rightarrow \lim_{x \rightarrow \infty}\frac{-1}{x}\leq \lim_{x \rightarrow \infty}\frac{\sin x}{x}\leq \lim_{x \rightarrow \infty}\frac{1}{x}\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow 0\leq \lim_{x \rightarrow \infty}\frac{\sin x}{x}\leq 0\]
\[\therefore \lim_{x \rightarrow \infty}\frac{\sin x}{x}=0\]
উদাহরণঃ \[\lim_{x \rightarrow \infty}\frac{\sin x}{x}=0\] প্রমান কর।
সমাধানঃ
আমরা জানি,\[-1\leq \sin x\leq 1\]
\[\Rightarrow \frac{-1}{x}\leq \frac{\sin x}{x}\leq \frac{1}{x}\] ➜ প্রতিটি পদে \(x\) ভাগ করে।
\[\Rightarrow \lim_{x \rightarrow \infty}\frac{-1}{x}\leq \lim_{x \rightarrow \infty}\frac{\sin x}{x}\leq \lim_{x \rightarrow \infty}\frac{1}{x}\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow 0\leq \lim_{x \rightarrow \infty}\frac{\sin x}{x}\leq 0\]
\[\therefore \lim_{x \rightarrow \infty}\frac{\sin x}{x}=0\]
ল্যাগ্রাঞ্জের গড় মধ্যমান উপপাদ্য
Lagrange's Mean Value Theorem
ল্যাগ্রাঞ্জের গড় মধ্যমান উপপাদ্যঃ
যদি \(f(x)\) ফাংশন
\((1)\) \[b\ge x\ge a\] বদ্ধ ব্যবধিতে অবিচ্ছিন্ন এবং
\((2)\) \[b > x > a\] খোলা ব্যবধিতে \[\acute{f}(x)\] বিদ্যমান অর্থাৎ অন্তরীকরণযোগ্য হয় তবে \[a\] এবং \[b\]-এর মধ্যে অন্ততপক্ষে \[x\]-এর এমন একটি মাণ \[c\] পাওয়া যাবে যেখানে, \[f(b)-f(a)=(b-a)\acute{f}(c)\] হয়।
যদি \(f(x)\) ফাংশন
\((1)\) \[b\ge x\ge a\] বদ্ধ ব্যবধিতে অবিচ্ছিন্ন এবং
\((2)\) \[b > x > a\] খোলা ব্যবধিতে \[\acute{f}(x)\] বিদ্যমান অর্থাৎ অন্তরীকরণযোগ্য হয় তবে \[a\] এবং \[b\]-এর মধ্যে অন্ততপক্ষে \[x\]-এর এমন একটি মাণ \[c\] পাওয়া যাবে যেখানে, \[f(b)-f(a)=(b-a)\acute{f}(c)\] হয়।
ল্যাগ্রাঞ্জের গড় মধ্যমান উপপাদ্যের জ্যামিতিক ব্যাখ্যা
Geometrical interpretation of Lagrange's Mean Value Theorem
ল্যাগ্রাঞ্জের গড় মধ্যমান উপপাদ্যের জ্যামিতিক ব্যাখ্যাঃ
মনে করি, \(y=f(x)\) বক্ররেখার উপর \[P, Q, R\] তিনটি বিন্দু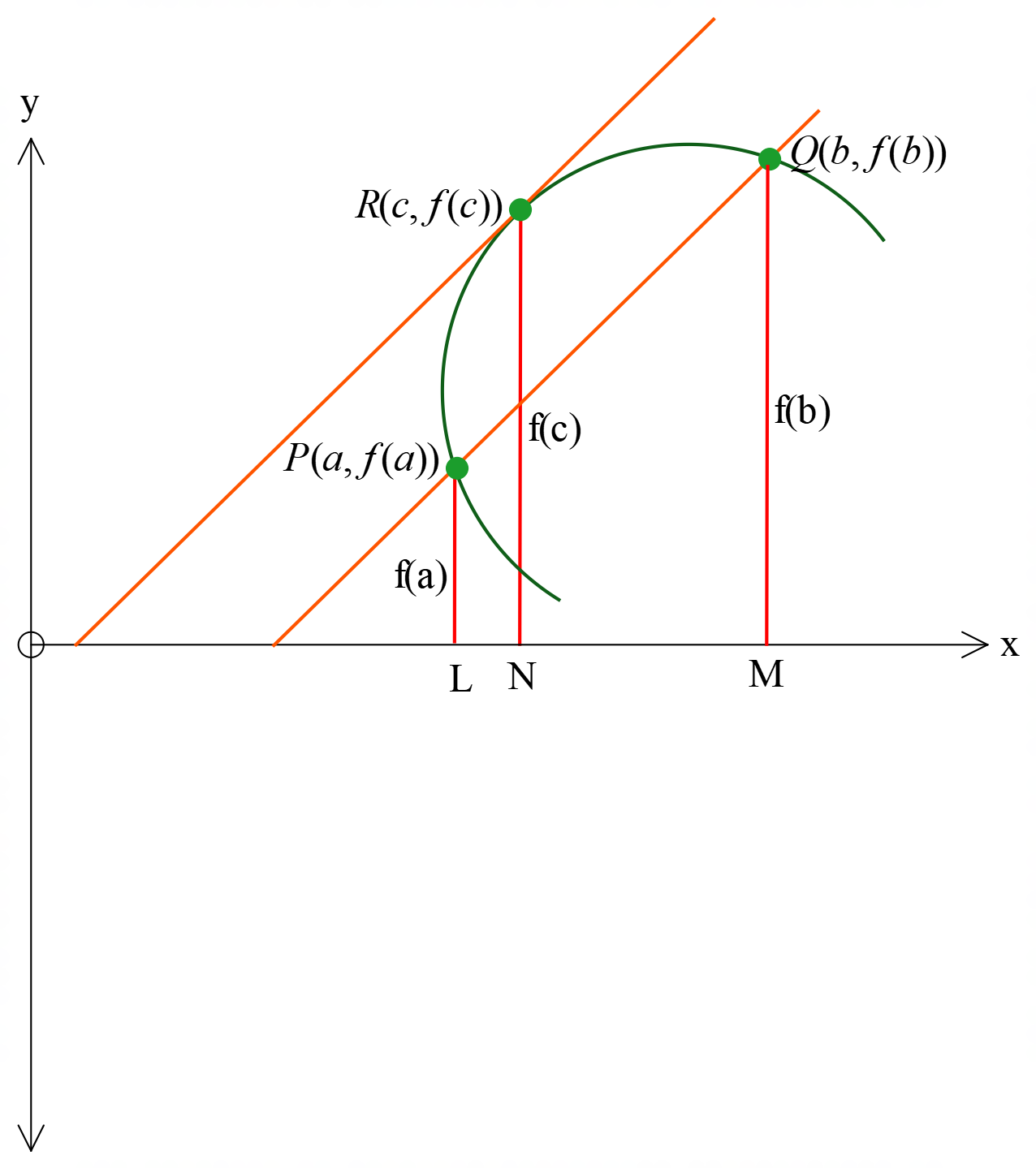
এখন \[P, Q, R\] হতে \[X\] অক্ষের উপর যথাক্রমে \[PL, QM, RN\] লম্ব অঙ্কন করি।
ধরি,
\[OL=a, OM=b\] এবং \[ON=c\]
তাহলে,
\[PL=f(a), QM=f(b)\] এবং \[RN=f(c)\]
\[\therefore P\] ও \[Q\] বিন্দুর স্থানাঙ্ক যথাক্রমে \[P(a, f(a))\] এবং \[Q(b, f(b))\]
\[\therefore PQ\] সরলরেখার ঢাল \[=\frac{f(b)-f(a)}{b-a} ........(1)\]
\[R\] বিন্দুতে স্পর্শকের ঢাল \[=\acute{f}(c) .....(2)\]
যেহেতু \[f(x)\] ফাংশন \[b\ge x\ge a\] বদ্ধ ব্যবধিতে অবিচ্ছিন্ন এবং \[b > x > a\] খোলা ব্যবধিতে অন্তরীকরণযোগ্য, কাজেই \[PQ\]-এর মধ্যবর্তী অংশে এমন একটি বিন্দু \[R\] পাওয়া যাবে যার ভুজ হবে \[c\] এবং \[R\] বিন্দুতে স্পর্শক \[PQ\] ছেদকের সমান্তরাল হবে।
\[R\] বিন্দুতে স্পর্শকের ঢাল \[PQ\]-এর ঢাল
\[\acute{f}(c)=\frac{f(b)-f(a)}{b-a} \] ➜ \((1)\) ও \((2)\)-এর সাহায্যে।
\[\therefore f(b)-f(a)=(b-a)\acute{f}(c)\]
মনে করি, \(y=f(x)\) বক্ররেখার উপর \[P, Q, R\] তিনটি বিন্দু

এখন \[P, Q, R\] হতে \[X\] অক্ষের উপর যথাক্রমে \[PL, QM, RN\] লম্ব অঙ্কন করি।
ধরি,
\[OL=a, OM=b\] এবং \[ON=c\]
তাহলে,
\[PL=f(a), QM=f(b)\] এবং \[RN=f(c)\]
\[\therefore P\] ও \[Q\] বিন্দুর স্থানাঙ্ক যথাক্রমে \[P(a, f(a))\] এবং \[Q(b, f(b))\]
\[\therefore PQ\] সরলরেখার ঢাল \[=\frac{f(b)-f(a)}{b-a} ........(1)\]
\[R\] বিন্দুতে স্পর্শকের ঢাল \[=\acute{f}(c) .....(2)\]
যেহেতু \[f(x)\] ফাংশন \[b\ge x\ge a\] বদ্ধ ব্যবধিতে অবিচ্ছিন্ন এবং \[b > x > a\] খোলা ব্যবধিতে অন্তরীকরণযোগ্য, কাজেই \[PQ\]-এর মধ্যবর্তী অংশে এমন একটি বিন্দু \[R\] পাওয়া যাবে যার ভুজ হবে \[c\] এবং \[R\] বিন্দুতে স্পর্শক \[PQ\] ছেদকের সমান্তরাল হবে।
\[R\] বিন্দুতে স্পর্শকের ঢাল \[PQ\]-এর ঢাল
\[\acute{f}(c)=\frac{f(b)-f(a)}{b-a} \] ➜ \((1)\) ও \((2)\)-এর সাহায্যে।
\[\therefore f(b)-f(a)=(b-a)\acute{f}(c)\]
প্রয়োজনীয় এবং স্মরণীয় সূত্রসমূহ
Necessary and memorable formulas
\[e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ .......... \infty\]
\[e^{x}=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+ .......... \infty\]
\[e^{-x}=1-\frac{x}{1!}+\frac{x^2}{2!}-\frac{x^3}{3!}+ .......... \infty\]
\[e^{x}+e^{-x}=2\left(1+\frac{x^2}{2!}+\frac{x^4}{4!}+ .......... \infty \right)\]
\[e^{x}-e^{-x}=2\left(\frac{x}{1!}+\frac{x^3}{3!}+\frac{x^5}{5!}+ .......... \infty \right)\]
\[a^{x}=1+\frac{x}{1!}\ln a+\frac{x^2}{2!}(\ln a)^2+\frac{x^3}{3!}(\ln a)^3+ .......... \infty \]
\[a^{-x}=1-\frac{x}{1!}\ln a+\frac{x^2}{2!}(\ln a)^2-\frac{x^3}{3!}(\ln a)^3+ .......... \infty \]
\[\ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^5}{5}+ .......... \infty \]
\[\ln(1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-\frac{x^5}{5}- .......... \infty \]
\[\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}- .......... \infty \]
\[\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}- .......... \infty \]
\[\tan x=x+\frac{x^3}{3}+\frac{2x^5}{15}+\frac{17x^7}{315}+ .......... \infty \]
\[e^{x}=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+ .......... \infty\]
\[e^{-x}=1-\frac{x}{1!}+\frac{x^2}{2!}-\frac{x^3}{3!}+ .......... \infty\]
\[e^{x}+e^{-x}=2\left(1+\frac{x^2}{2!}+\frac{x^4}{4!}+ .......... \infty \right)\]
\[e^{x}-e^{-x}=2\left(\frac{x}{1!}+\frac{x^3}{3!}+\frac{x^5}{5!}+ .......... \infty \right)\]
\[a^{x}=1+\frac{x}{1!}\ln a+\frac{x^2}{2!}(\ln a)^2+\frac{x^3}{3!}(\ln a)^3+ .......... \infty \]
\[a^{-x}=1-\frac{x}{1!}\ln a+\frac{x^2}{2!}(\ln a)^2-\frac{x^3}{3!}(\ln a)^3+ .......... \infty \]
\[\ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^5}{5}+ .......... \infty \]
\[\ln(1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-\frac{x^5}{5}- .......... \infty \]
\[\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}- .......... \infty \]
\[\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}- .......... \infty \]
\[\tan x=x+\frac{x^3}{3}+\frac{2x^5}{15}+\frac{17x^7}{315}+ .......... \infty \]
প্রয়োজনীয় এবং স্মরণীয় কতিপয় বিশেষ লিমিট
Necessary and memorable Some special limit
\[\lim_{x \rightarrow 0}\frac{\sin x}{x}=1\]
\[\lim_{x \rightarrow 0}\frac{x}{\sin x}=1\]
\[\lim_{x \rightarrow 0}\frac{\tan x}{x}=1\]
\[\lim_{x \rightarrow 0}\frac{x}{\tan x}=1\]
\[\lim_{x \rightarrow 0}\frac{e^x-1}{x}=1\]
\[\lim_{x \rightarrow 0}\frac{x}{\sin x}=1\]
\[\lim_{x \rightarrow 0}\frac{\tan x}{x}=1\]
\[\lim_{x \rightarrow 0}\frac{x}{\tan x}=1\]
\[\lim_{x \rightarrow 0}\frac{e^x-1}{x}=1\]
\[\lim_{x \rightarrow 0}\frac{\ln(1+x)}{x}=1\]
\[\lim_{x \rightarrow 0}\frac{(1+x)^n-1}{x}=n\]
\[\lim_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^n=e\]
\[\lim_{n \rightarrow 0}(1+n)^{\frac{1}{n}}=e\]
\[\lim_{x \rightarrow a}\frac{x^n-a^n}{x-a}=n.a^{n-1}\]
\[\lim_{x \rightarrow 0}\frac{(1+x)^n-1}{x}=n\]
\[\lim_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^n=e\]
\[\lim_{n \rightarrow 0}(1+n)^{\frac{1}{n}}=e\]
\[\lim_{x \rightarrow a}\frac{x^n-a^n}{x-a}=n.a^{n-1}\]
×
ল্যাগ্রাঞ্জের গড় মধ্যমান উপপাদ্যঃ
যদি \(f(x)\) ফাংশন
\((1)\) \[b\ge x\ge a\] বদ্ধ ব্যবধিতে অবিচ্ছিন্ন এবং
\((2)\) \[b > x > a\] খোলা ব্যবধিতে \[\acute{f}(x)\] বিদ্যমান অর্থাৎ অন্তরীকরণযোগ্য হয় তবে \[a\] এবং \[b\]-এর মধ্যে অন্ততপক্ষে \[x\]-এর এমন একটি মাণ \[c\] পাওয়া যাবে যেখানে, \[f(b)-f(a)=(b-a)\acute{f}(c)\] হয়।
যদি \(f(x)\) ফাংশন
\((1)\) \[b\ge x\ge a\] বদ্ধ ব্যবধিতে অবিচ্ছিন্ন এবং
\((2)\) \[b > x > a\] খোলা ব্যবধিতে \[\acute{f}(x)\] বিদ্যমান অর্থাৎ অন্তরীকরণযোগ্য হয় তবে \[a\] এবং \[b\]-এর মধ্যে অন্ততপক্ষে \[x\]-এর এমন একটি মাণ \[c\] পাওয়া যাবে যেখানে, \[f(b)-f(a)=(b-a)\acute{f}(c)\] হয়।
প্রমাণঃ
মনে করি,
\[F(x)=f(x)-Ax ......(1)\]
একটি সহায়ক ফাংশন এবং \[A\] কে এমনভাবে নির্ধারণ করা হয়েছে যেন, \[F(a)=F(b)\] হয়।
এখন \[(1)\]-এ \[x=a\] এবং \[x=b\] বসালে,
\[F(a)=f(a)-Aa ......(2)\]
\[F(b)=f(b)-Ab ......(3)\]
যেহেতু \[F(a)=F(b)\]
\[\therefore f(a)-Aa=f(b)-Ab\] ➜ \((2)\) ও \((3)\)-এর সাহায্যে।
\[\Rightarrow f(b)-Ab=f(a)-Aa\]
\[\Rightarrow f(b)-f(a)=Ab-Aa\]
\[\Rightarrow f(b)-f(a)=A(b-a)\]
\[\Rightarrow \frac{f(b)-f(a)}{b-a}=A\]
\[\therefore A=\frac{f(b)-f(a)}{b-a}\]
উক্ত \[A\]-এর মাণ \[(1)\]-এ বসিয়ে,
\[F(x)=f(x)-\left(\frac{f(b)-f(a)}{b-a}\right)x \]
\[\acute{F}(x)=\acute{f}(x)-\left(\frac{f(b)-f(a)}{b-a}\right) .......(4)\] ➜ উভয় পার্শে \((x)\)-এর সাপেক্ষে অন্তরীকরণ করে।
যেহেতু \(f(x)\) ফাংশন \[b\ge x\ge a\] বদ্ধ ব্যবধিতে অবিচ্ছিন্ন এবং \[b > x > a\] খোলা ব্যবধিতে অন্তরীকরণযোগ্য এবং \[F(a)=F(b)\].
অর্থাৎ \[F(x)\] ফাংশন রোলের উপপাদ্যের সকল শর্ত মেনে চলে।
অতএব, \[b > c > a\]-এর জন্য , \[\acute{F}(c)=0 ....(5)\]
এখন \[(4)\]-এ \[x=c\] বসিয়ে,
\[\acute{F}(c)=\acute{f}(c)-\left(\frac{f(b)-f(a)}{b-a}\right)\]
\[\Rightarrow 0=\acute{f}(c)-\left(\frac{f(b)-f(a)}{b-a}\right)\] ➜ \(\because \acute{F}(c)=0 \) অর্থাৎ \[(5)\]-এর সাহায্যে।
\[\Rightarrow \left(\frac{f(b)-f(a)}{b-a}\right)=\acute{f}(c)\]
\[\therefore f(b)-f(a)=(b-a)\acute{f}(c)\]
(proved)
\[F(x)=f(x)-Ax ......(1)\]
একটি সহায়ক ফাংশন এবং \[A\] কে এমনভাবে নির্ধারণ করা হয়েছে যেন, \[F(a)=F(b)\] হয়।
এখন \[(1)\]-এ \[x=a\] এবং \[x=b\] বসালে,
\[F(a)=f(a)-Aa ......(2)\]
\[F(b)=f(b)-Ab ......(3)\]
যেহেতু \[F(a)=F(b)\]
\[\therefore f(a)-Aa=f(b)-Ab\] ➜ \((2)\) ও \((3)\)-এর সাহায্যে।
\[\Rightarrow f(b)-Ab=f(a)-Aa\]
\[\Rightarrow f(b)-f(a)=Ab-Aa\]
\[\Rightarrow f(b)-f(a)=A(b-a)\]
\[\Rightarrow \frac{f(b)-f(a)}{b-a}=A\]
\[\therefore A=\frac{f(b)-f(a)}{b-a}\]
উক্ত \[A\]-এর মাণ \[(1)\]-এ বসিয়ে,
\[F(x)=f(x)-\left(\frac{f(b)-f(a)}{b-a}\right)x \]
\[\acute{F}(x)=\acute{f}(x)-\left(\frac{f(b)-f(a)}{b-a}\right) .......(4)\] ➜ উভয় পার্শে \((x)\)-এর সাপেক্ষে অন্তরীকরণ করে।
যেহেতু \(f(x)\) ফাংশন \[b\ge x\ge a\] বদ্ধ ব্যবধিতে অবিচ্ছিন্ন এবং \[b > x > a\] খোলা ব্যবধিতে অন্তরীকরণযোগ্য এবং \[F(a)=F(b)\].
অর্থাৎ \[F(x)\] ফাংশন রোলের উপপাদ্যের সকল শর্ত মেনে চলে।
অতএব, \[b > c > a\]-এর জন্য , \[\acute{F}(c)=0 ....(5)\]
এখন \[(4)\]-এ \[x=c\] বসিয়ে,
\[\acute{F}(c)=\acute{f}(c)-\left(\frac{f(b)-f(a)}{b-a}\right)\]
\[\Rightarrow 0=\acute{f}(c)-\left(\frac{f(b)-f(a)}{b-a}\right)\] ➜ \(\because \acute{F}(c)=0 \) অর্থাৎ \[(5)\]-এর সাহায্যে।
\[\Rightarrow \left(\frac{f(b)-f(a)}{b-a}\right)=\acute{f}(c)\]
\[\therefore f(b)-f(a)=(b-a)\acute{f}(c)\]
(proved)
×
\[\lim_{x \rightarrow 0}\frac{\sin x}{x}=1\]
Proof:
মনে করি,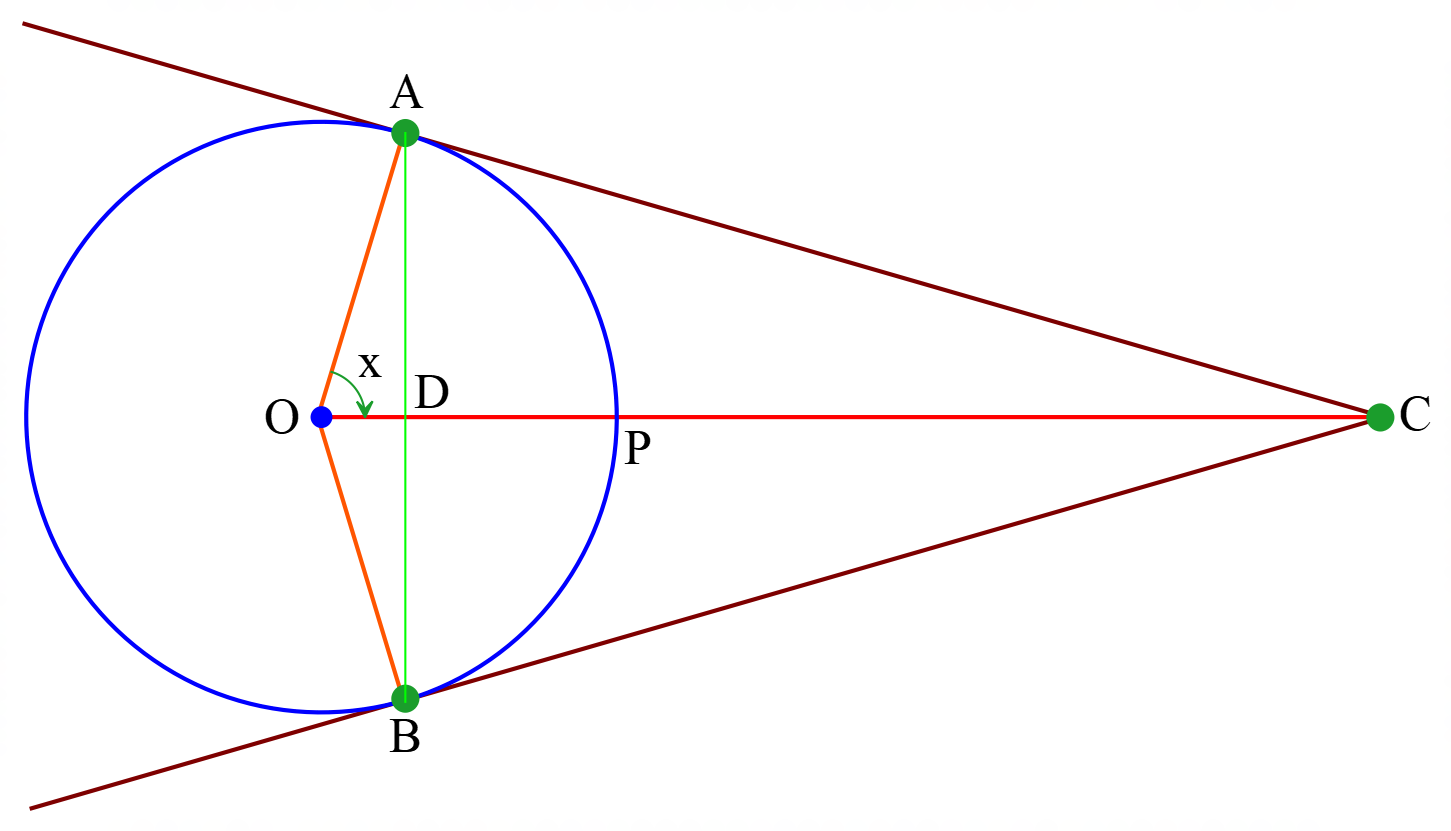
\(O\) কেন্দ্রবিশিষ্ট বৃত্তে \(APB\) একটি চাপ। \(OP\) ব্যাসার্ধ \(AB\) জ্যা কে \(D\) বিন্দুতে সমদ্বিখন্ডিত করে। তাহলে \(OP\) দ্বারা চাপ \(APB\) সমদ্বিখন্ডিত হয়। \(A\) ও \(B\) বিন্দুতে অঙ্কিত স্পর্শকদ্বয় \(AC\) ও \(BC\) বর্ধিত \(OP\)-এর সহিত \(C\) বিন্দুতে মিলিত হয়েছে।
ধরি,
\(\angle POA=x\) রেডিয়ান এবং \(\frac{\pi}{2}>x>0\)
এখন,
\(AC+BC>APB\) চাপ \(>AB\) জ্যা
\(\Rightarrow 2AC>2\) চাপ \(AP>2AD\) ➜ \(\because BC=AC, BP=AP, AB=2AD\)
\(\Rightarrow AC>\) চাপ \(AP>AD\) ➜ \(2\) দ্বারা ভাগ করে।
\(\Rightarrow \frac{AC}{OA}>\) চাপ \(\frac{AP}{OA}>\frac{AD}{OA}\) ➜ \(\because OA>0, OA\) দ্বারা ভাগ করে।
\(\Rightarrow \tan x > x >\sin x\) ➜ \(\because \tan \angle AOC=\tan x=\frac{AC}{OA}, \sin \angle AOD=\sin x=\frac{AD}{OA}\)
\(\Rightarrow \frac{\sin x}{\cos x} > x >\sin x \)
\(\Rightarrow \frac{1}{\cos x} > \frac{x}{\sin x} >1\) ➜ \(\because \sin x>0, \sin x\) দ্বারা ভাগ করে।
\(\Rightarrow 1 > \frac{x}{\sin x} > \cos x\) ➜ ব্যস্তকরণ করে।
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{\sin x}{x} >\lim_{x \rightarrow 0}\cos x\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{\sin x}{x} >1\]
এখানে, স্পষ্ট যে, \[\lim_{x \rightarrow 0}\frac{\sin x}{x}\] রাশিটি দুইটি বাস্তব সংখ্যার মধ্যে অবস্থিত, উভয় সংখ্যার মাণ \(1\)
\[\therefore \lim_{x \rightarrow 0}\frac{\sin x}{x} =1\]
(proved)

\(O\) কেন্দ্রবিশিষ্ট বৃত্তে \(APB\) একটি চাপ। \(OP\) ব্যাসার্ধ \(AB\) জ্যা কে \(D\) বিন্দুতে সমদ্বিখন্ডিত করে। তাহলে \(OP\) দ্বারা চাপ \(APB\) সমদ্বিখন্ডিত হয়। \(A\) ও \(B\) বিন্দুতে অঙ্কিত স্পর্শকদ্বয় \(AC\) ও \(BC\) বর্ধিত \(OP\)-এর সহিত \(C\) বিন্দুতে মিলিত হয়েছে।
ধরি,
\(\angle POA=x\) রেডিয়ান এবং \(\frac{\pi}{2}>x>0\)
এখন,
\(AC+BC>APB\) চাপ \(>AB\) জ্যা
\(\Rightarrow 2AC>2\) চাপ \(AP>2AD\) ➜ \(\because BC=AC, BP=AP, AB=2AD\)
\(\Rightarrow AC>\) চাপ \(AP>AD\) ➜ \(2\) দ্বারা ভাগ করে।
\(\Rightarrow \frac{AC}{OA}>\) চাপ \(\frac{AP}{OA}>\frac{AD}{OA}\) ➜ \(\because OA>0, OA\) দ্বারা ভাগ করে।
\(\Rightarrow \tan x > x >\sin x\) ➜ \(\because \tan \angle AOC=\tan x=\frac{AC}{OA}, \sin \angle AOD=\sin x=\frac{AD}{OA}\)
\(\Rightarrow \frac{\sin x}{\cos x} > x >\sin x \)
\(\Rightarrow \frac{1}{\cos x} > \frac{x}{\sin x} >1\) ➜ \(\because \sin x>0, \sin x\) দ্বারা ভাগ করে।
\(\Rightarrow 1 > \frac{x}{\sin x} > \cos x\) ➜ ব্যস্তকরণ করে।
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{\sin x}{x} >\lim_{x \rightarrow 0}\cos x\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{\sin x}{x} >1\]
এখানে, স্পষ্ট যে, \[\lim_{x \rightarrow 0}\frac{\sin x}{x}\] রাশিটি দুইটি বাস্তব সংখ্যার মধ্যে অবস্থিত, উভয় সংখ্যার মাণ \(1\)
\[\therefore \lim_{x \rightarrow 0}\frac{\sin x}{x} =1\]
(proved)
×
\[\lim_{x \rightarrow 0}\frac{x}{\sin x}=1\]
Proof:
মনে করি,
\(O\) কেন্দ্রবিশিষ্ট বৃত্তে \(APB\) একটি চাপ। \(OP\) ব্যাসার্ধ \(AB\) জ্যা কে \(D\) বিন্দুতে সমদ্বিখন্ডিত করে। তাহলে \(OP\) দ্বারা চাপ \(APB\) সমদ্বিখন্ডিত হয়। \(A\) ও \(B\) বিন্দুতে অঙ্কিত স্পর্শকদ্বয় \(AC\) ও \(BC\) বর্ধিত \(OP\)-এর সহিত \(C\) বিন্দুতে মিলিত হয়েছে।
ধরি,
\(\angle POA=x\) রেডিয়ান এবং \(\frac{\pi}{2}>x>0\)
এখন,
\(AC+BC>APB\) চাপ \(>AB\) জ্যা
\(\Rightarrow 2AC>2\) চাপ \(AP>2AD\) ➜ \(\because BC=AC, BP=AP, AB=2AD\)
\(\Rightarrow AC>\) চাপ \(AP>AD\) ➜ \(2\) দ্বারা ভাগ করে।
\(\Rightarrow \frac{AC}{OA}>\) চাপ \(\frac{AP}{OA}>\frac{AD}{OA}\) ➜ \(\because OA>0, OA\) দ্বারা ভাগ করে।
\(\Rightarrow \tan x > x >\sin x\) ➜ \(\because \tan \angle AOC=\tan x=\frac{AC}{OA}, \sin \angle AOD=\sin x=\frac{AD}{OA}\)
\(\Rightarrow \frac{\sin x}{\cos x} > x >\sin x \)
\(\Rightarrow \frac{1}{\cos x} > \frac{x}{\sin x} >1\) ➜ \(\because \sin x>0, \sin x\) দ্বারা ভাগ করে।
\[\Rightarrow \lim_{x \rightarrow 0}\frac{1}{\cos x}> \lim_{x \rightarrow 0}\frac{x}{\sin x} >1\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow \frac{1}{1}> \lim_{x \rightarrow 0}\frac{x}{\sin x} >1\]
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{x}{\sin x} >1\]
এখানে, স্পষ্ট যে, \[\lim_{x \rightarrow 0}\frac{x}{\sin x}\] রাশিটি দুইটি বাস্তব সংখ্যার মধ্যে অবস্থিত, উভয় সংখ্যার মাণ \(1\)
\[\therefore \lim_{x \rightarrow 0}\frac{x}{\sin x} =1\]
(proved)

\(O\) কেন্দ্রবিশিষ্ট বৃত্তে \(APB\) একটি চাপ। \(OP\) ব্যাসার্ধ \(AB\) জ্যা কে \(D\) বিন্দুতে সমদ্বিখন্ডিত করে। তাহলে \(OP\) দ্বারা চাপ \(APB\) সমদ্বিখন্ডিত হয়। \(A\) ও \(B\) বিন্দুতে অঙ্কিত স্পর্শকদ্বয় \(AC\) ও \(BC\) বর্ধিত \(OP\)-এর সহিত \(C\) বিন্দুতে মিলিত হয়েছে।
ধরি,
\(\angle POA=x\) রেডিয়ান এবং \(\frac{\pi}{2}>x>0\)
এখন,
\(AC+BC>APB\) চাপ \(>AB\) জ্যা
\(\Rightarrow 2AC>2\) চাপ \(AP>2AD\) ➜ \(\because BC=AC, BP=AP, AB=2AD\)
\(\Rightarrow AC>\) চাপ \(AP>AD\) ➜ \(2\) দ্বারা ভাগ করে।
\(\Rightarrow \frac{AC}{OA}>\) চাপ \(\frac{AP}{OA}>\frac{AD}{OA}\) ➜ \(\because OA>0, OA\) দ্বারা ভাগ করে।
\(\Rightarrow \tan x > x >\sin x\) ➜ \(\because \tan \angle AOC=\tan x=\frac{AC}{OA}, \sin \angle AOD=\sin x=\frac{AD}{OA}\)
\(\Rightarrow \frac{\sin x}{\cos x} > x >\sin x \)
\(\Rightarrow \frac{1}{\cos x} > \frac{x}{\sin x} >1\) ➜ \(\because \sin x>0, \sin x\) দ্বারা ভাগ করে।
\[\Rightarrow \lim_{x \rightarrow 0}\frac{1}{\cos x}> \lim_{x \rightarrow 0}\frac{x}{\sin x} >1\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow \frac{1}{1}> \lim_{x \rightarrow 0}\frac{x}{\sin x} >1\]
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{x}{\sin x} >1\]
এখানে, স্পষ্ট যে, \[\lim_{x \rightarrow 0}\frac{x}{\sin x}\] রাশিটি দুইটি বাস্তব সংখ্যার মধ্যে অবস্থিত, উভয় সংখ্যার মাণ \(1\)
\[\therefore \lim_{x \rightarrow 0}\frac{x}{\sin x} =1\]
(proved)
×
\[\lim_{x \rightarrow 0}\frac{\tan x}{x}=1\]
Proof:
মনে করি,
\(O\) কেন্দ্রবিশিষ্ট বৃত্তে \(APB\) একটি চাপ। \(OP\) ব্যাসার্ধ \(AB\) জ্যা কে \(D\) বিন্দুতে সমদ্বিখন্ডিত করে। তাহলে \(OP\) দ্বারা চাপ \(APB\) সমদ্বিখন্ডিত হয়। \(A\) ও \(B\) বিন্দুতে অঙ্কিত স্পর্শকদ্বয় \(AC\) ও \(BC\) বর্ধিত \(OP\)-এর সহিত \(C\) বিন্দুতে মিলিত হয়েছে।
ধরি,
\(\angle POA=x\) রেডিয়ান এবং \(\frac{\pi}{2}>x>0\)
এখন,
\(AC+BC>APB\) চাপ \(>AB\) জ্যা
\(\Rightarrow 2AC>2\) চাপ \(AP>2AD\) ➜ \(\because BC=AC, BP=AP, AB=2AD\)
\(\Rightarrow AC>\) চাপ \(AP>AD\) ➜ \(2\) দ্বারা ভাগ করে।
\(\Rightarrow \frac{AC}{OA}>\) চাপ \(\frac{AP}{OA}>\frac{AD}{OA}\) ➜ \(\because OA>0, OA\) দ্বারা ভাগ করে।
\(\Rightarrow \tan x > x >\sin x\) ➜ \(\because \tan \angle AOC=\tan x=\frac{AC}{OA}, \sin \angle AOD=\sin x=\frac{AD}{OA}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x}{\tan x}\) ➜ \(\because \tan x>0, \tan x\) দ্বারা ভাগ করে।
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x}{\frac{\sin x}{\cos x}}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x\times \cos x}{\sin x}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\cos x\)
\(\Rightarrow \frac{1}{\cos x} > \frac{\tan x}{x} >1\) ➜ ব্যস্তকরণ করে।
\[\Rightarrow \lim_{x \rightarrow 0}\frac{1}{\cos x}> \lim_{x \rightarrow 0}\frac{\tan x}{x} >1\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow \frac{1}{1}> \lim_{x \rightarrow 0}\frac{\tan x}{x} >1\]
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{\tan x}{x} >1\]
এখানে, স্পষ্ট যে, \[\lim_{x \rightarrow 0}\frac{\tan x}{x}\] রাশিটি দুইটি বাস্তব সংখ্যার মধ্যে অবস্থিত, উভয় সংখ্যার মাণ \(1\)
\[\therefore \lim_{x \rightarrow 0}\frac{\tan x}{x} =1\]
(proved)

\(O\) কেন্দ্রবিশিষ্ট বৃত্তে \(APB\) একটি চাপ। \(OP\) ব্যাসার্ধ \(AB\) জ্যা কে \(D\) বিন্দুতে সমদ্বিখন্ডিত করে। তাহলে \(OP\) দ্বারা চাপ \(APB\) সমদ্বিখন্ডিত হয়। \(A\) ও \(B\) বিন্দুতে অঙ্কিত স্পর্শকদ্বয় \(AC\) ও \(BC\) বর্ধিত \(OP\)-এর সহিত \(C\) বিন্দুতে মিলিত হয়েছে।
ধরি,
\(\angle POA=x\) রেডিয়ান এবং \(\frac{\pi}{2}>x>0\)
এখন,
\(AC+BC>APB\) চাপ \(>AB\) জ্যা
\(\Rightarrow 2AC>2\) চাপ \(AP>2AD\) ➜ \(\because BC=AC, BP=AP, AB=2AD\)
\(\Rightarrow AC>\) চাপ \(AP>AD\) ➜ \(2\) দ্বারা ভাগ করে।
\(\Rightarrow \frac{AC}{OA}>\) চাপ \(\frac{AP}{OA}>\frac{AD}{OA}\) ➜ \(\because OA>0, OA\) দ্বারা ভাগ করে।
\(\Rightarrow \tan x > x >\sin x\) ➜ \(\because \tan \angle AOC=\tan x=\frac{AC}{OA}, \sin \angle AOD=\sin x=\frac{AD}{OA}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x}{\tan x}\) ➜ \(\because \tan x>0, \tan x\) দ্বারা ভাগ করে।
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x}{\frac{\sin x}{\cos x}}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x\times \cos x}{\sin x}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\cos x\)
\(\Rightarrow \frac{1}{\cos x} > \frac{\tan x}{x} >1\) ➜ ব্যস্তকরণ করে।
\[\Rightarrow \lim_{x \rightarrow 0}\frac{1}{\cos x}> \lim_{x \rightarrow 0}\frac{\tan x}{x} >1\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow \frac{1}{1}> \lim_{x \rightarrow 0}\frac{\tan x}{x} >1\]
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{\tan x}{x} >1\]
এখানে, স্পষ্ট যে, \[\lim_{x \rightarrow 0}\frac{\tan x}{x}\] রাশিটি দুইটি বাস্তব সংখ্যার মধ্যে অবস্থিত, উভয় সংখ্যার মাণ \(1\)
\[\therefore \lim_{x \rightarrow 0}\frac{\tan x}{x} =1\]
(proved)
×
\[\lim_{x \rightarrow 0}\frac{x}{\tan x}=1\]
Proof:
মনে করি,
\(O\) কেন্দ্রবিশিষ্ট বৃত্তে \(APB\) একটি চাপ। \(OP\) ব্যাসার্ধ \(AB\) জ্যা কে \(D\) বিন্দুতে সমদ্বিখন্ডিত করে। তাহলে \(OP\) দ্বারা চাপ \(APB\) সমদ্বিখন্ডিত হয়। \(A\) ও \(B\) বিন্দুতে অঙ্কিত স্পর্শকদ্বয় \(AC\) ও \(BC\) বর্ধিত \(OP\)-এর সহিত \(C\) বিন্দুতে মিলিত হয়েছে।
ধরি,
\(\angle POA=x\) রেডিয়ান এবং \(\frac{\pi}{2}>x>0\)
এখন,
\(AC+BC>APB\) চাপ \(>AB\) জ্যা
\(\Rightarrow 2AC>2\) চাপ \(AP>2AD\) ➜ \(\because BC=AC, BP=AP, AB=2AD\)
\(\Rightarrow AC>\) চাপ \(AP>AD\) ➜ \(2\) দ্বারা ভাগ করে।
\(\Rightarrow \frac{AC}{OA}>\) চাপ \(\frac{AP}{OA}>\frac{AD}{OA}\) ➜ \(\because OA>0, OA\) দ্বারা ভাগ করে।
\(\Rightarrow \tan x > x >\sin x\) ➜ \(\because \tan \angle AOC=\tan x=\frac{AC}{OA}, \sin \angle AOD=\sin x=\frac{AD}{OA}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x}{\tan x}\) ➜ \(\because \tan x>0, \tan x\) দ্বারা ভাগ করে।
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x}{\frac{\sin x}{\cos x}}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x\times \cos x}{\sin x}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\cos x\)
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{x}{\tan x} >\lim_{x \rightarrow 0}\cos x\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{x}{\tan x} >1\]
এখানে, স্পষ্ট যে, \[\lim_{x \rightarrow 0}\frac{x}{\tan x}\] রাশিটি দুইটি বাস্তব সংখ্যার মধ্যে অবস্থিত, উভয় সংখ্যার মাণ \(1\)
\[\therefore \lim_{x \rightarrow 0}\frac{x}{\tan x} =1\]
(proved)

\(O\) কেন্দ্রবিশিষ্ট বৃত্তে \(APB\) একটি চাপ। \(OP\) ব্যাসার্ধ \(AB\) জ্যা কে \(D\) বিন্দুতে সমদ্বিখন্ডিত করে। তাহলে \(OP\) দ্বারা চাপ \(APB\) সমদ্বিখন্ডিত হয়। \(A\) ও \(B\) বিন্দুতে অঙ্কিত স্পর্শকদ্বয় \(AC\) ও \(BC\) বর্ধিত \(OP\)-এর সহিত \(C\) বিন্দুতে মিলিত হয়েছে।
ধরি,
\(\angle POA=x\) রেডিয়ান এবং \(\frac{\pi}{2}>x>0\)
এখন,
\(AC+BC>APB\) চাপ \(>AB\) জ্যা
\(\Rightarrow 2AC>2\) চাপ \(AP>2AD\) ➜ \(\because BC=AC, BP=AP, AB=2AD\)
\(\Rightarrow AC>\) চাপ \(AP>AD\) ➜ \(2\) দ্বারা ভাগ করে।
\(\Rightarrow \frac{AC}{OA}>\) চাপ \(\frac{AP}{OA}>\frac{AD}{OA}\) ➜ \(\because OA>0, OA\) দ্বারা ভাগ করে।
\(\Rightarrow \tan x > x >\sin x\) ➜ \(\because \tan \angle AOC=\tan x=\frac{AC}{OA}, \sin \angle AOD=\sin x=\frac{AD}{OA}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x}{\tan x}\) ➜ \(\because \tan x>0, \tan x\) দ্বারা ভাগ করে।
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x}{\frac{\sin x}{\cos x}}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\frac{\sin x\times \cos x}{\sin x}\)
\(\Rightarrow 1 > \frac{x}{\tan x} >\cos x\)
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{x}{\tan x} >\lim_{x \rightarrow 0}\cos x\] ➜ লিমিট ব্যবহার করে।
\[\Rightarrow 1> \lim_{x \rightarrow 0}\frac{x}{\tan x} >1\]
এখানে, স্পষ্ট যে, \[\lim_{x \rightarrow 0}\frac{x}{\tan x}\] রাশিটি দুইটি বাস্তব সংখ্যার মধ্যে অবস্থিত, উভয় সংখ্যার মাণ \(1\)
\[\therefore \lim_{x \rightarrow 0}\frac{x}{\tan x} =1\]
(proved)
×
\[\lim_{x \rightarrow 0}\frac{e^x-1}{x}=1\]
Proof:
\[L.S=\lim_{x \rightarrow 0}\frac{e^x-1}{x}\]
\[=\lim_{x \rightarrow 0}\frac{\left(1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+ ... +\infty \right)-1}{x}\] ➜ \(\because e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+ .... +\infty \)
\[=\lim_{x \rightarrow 0}\frac{\left(\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+ ..... +\infty \right)}{x}\]
\[=\lim_{x \rightarrow 0}\frac{x\left(\frac{1}{1!}+\frac{x}{2!}+\frac{x^2}{3!}+ ..... +\infty \right)}{x}\]
\[=\lim_{x \rightarrow 0}\left(\frac{1}{1}+\frac{x}{2!}+\frac{x^2}{3!}+ ...... \right)\] ➜ \(\because 1!=1 \)
\[=1+\frac{0}{2!}+\frac{0}{3!}+ ..... \]
\[=1+0+0+ .... \]
\[=1\]
\[=R.S\]
\[\therefore L.S=R.S\]
(proved)
\[=\lim_{x \rightarrow 0}\frac{\left(1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+ ... +\infty \right)-1}{x}\] ➜ \(\because e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+ .... +\infty \)
\[=\lim_{x \rightarrow 0}\frac{\left(\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+ ..... +\infty \right)}{x}\]
\[=\lim_{x \rightarrow 0}\frac{x\left(\frac{1}{1!}+\frac{x}{2!}+\frac{x^2}{3!}+ ..... +\infty \right)}{x}\]
\[=\lim_{x \rightarrow 0}\left(\frac{1}{1}+\frac{x}{2!}+\frac{x^2}{3!}+ ...... \right)\] ➜ \(\because 1!=1 \)
\[=1+\frac{0}{2!}+\frac{0}{3!}+ ..... \]
\[=1+0+0+ .... \]
\[=1\]
\[=R.S\]
\[\therefore L.S=R.S\]
(proved)
×
\[\lim_{x \rightarrow 0}\frac{\ln(1+x)}{x}=1\]
Proof:
\[L.S=\lim_{x \rightarrow 0}\frac{\ln(1+x)}{x}\]
\[=\lim_{x \rightarrow 0}\frac{\left(x+\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+ .... +\infty \right)}{x}\] ➜ \(\because \ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+ ..... \infty\)
\[=\lim_{x \rightarrow 0}\frac{x\left(1+\frac{x}{2}+\frac{x^2}{3}+\frac{x^3}{4}+ .... +\infty \right)}{x}\]
\[=\lim_{x \rightarrow 0}\left(1+\frac{x}{2}+\frac{x^2}{3}+\frac{x^3}{4}+ .... +\infty \right)\]
\[=\lim_{x \rightarrow 0} \left(1+\frac{x}{2}+\frac{x^2}{3}+\frac{x^3}{4}+ ... \right)\]
\[=1+\frac{0}{2}+\frac{0}{3}+\frac{0}{4}+ ... \]
\[=1+0+0+ ...... \]
\[=1\]
\[=R.S\]
\[\therefore L.S=R.S\]
(proved)
\[=\lim_{x \rightarrow 0}\frac{\left(x+\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+ .... +\infty \right)}{x}\] ➜ \(\because \ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+ ..... \infty\)
\[=\lim_{x \rightarrow 0}\frac{x\left(1+\frac{x}{2}+\frac{x^2}{3}+\frac{x^3}{4}+ .... +\infty \right)}{x}\]
\[=\lim_{x \rightarrow 0}\left(1+\frac{x}{2}+\frac{x^2}{3}+\frac{x^3}{4}+ .... +\infty \right)\]
\[=\lim_{x \rightarrow 0} \left(1+\frac{x}{2}+\frac{x^2}{3}+\frac{x^3}{4}+ ... \right)\]
\[=1+\frac{0}{2}+\frac{0}{3}+\frac{0}{4}+ ... \]
\[=1+0+0+ ...... \]
\[=1\]
\[=R.S\]
\[\therefore L.S=R.S\]
(proved)
×
\[\lim_{x \rightarrow 0}\frac{(1+x)^n-1}{x}=n\]
Proof:
\[L.S=\lim_{x \rightarrow 0}\frac{(1+x)^n-1}{x}\]
\[=\lim_{x \rightarrow 0}\frac{\left(1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ ... \right)-1}{x}\] ➜ \(\because (1+x)^n=1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ ...\)
\[=\lim_{x \rightarrow 0}\frac{x\left(\frac{n}{1}+\frac{n(n-1)x}{2!}+\frac{n(n-1)(n-2)x^2}{3!}+ ... \right)}{x}\]
\[=\lim_{x \rightarrow 0}\left(\frac{n}{1}+\frac{n(n-1)x}{2!}+\frac{n(n-1)(n-2)x^2}{3!}+ .... \right)\]
\[=\lim_{x \rightarrow 0} \left(n+\frac{n(n-1)x}{2!}+\frac{n(n-1)(n-2)x^2}{3!}+ .... \right)\]
\[=n+\frac{n(n-1).0}{2!}+\frac{n(n-1)(n-2).0}{3!}+ .... \]
\[=1+0+0+ .....\]
\[=1\]
\[=R.S\]
\[\therefore L.S=R.S\]
(proved)
\[=\lim_{x \rightarrow 0}\frac{\left(1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ ... \right)-1}{x}\] ➜ \(\because (1+x)^n=1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ ...\)
\[=\lim_{x \rightarrow 0}\frac{x\left(\frac{n}{1}+\frac{n(n-1)x}{2!}+\frac{n(n-1)(n-2)x^2}{3!}+ ... \right)}{x}\]
\[=\lim_{x \rightarrow 0}\left(\frac{n}{1}+\frac{n(n-1)x}{2!}+\frac{n(n-1)(n-2)x^2}{3!}+ .... \right)\]
\[=\lim_{x \rightarrow 0} \left(n+\frac{n(n-1)x}{2!}+\frac{n(n-1)(n-2)x^2}{3!}+ .... \right)\]
\[=n+\frac{n(n-1).0}{2!}+\frac{n(n-1)(n-2).0}{3!}+ .... \]
\[=1+0+0+ .....\]
\[=1\]
\[=R.S\]
\[\therefore L.S=R.S\]
(proved)
×
\[\lim_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^n=e\]
Proof:
\[L.S=\lim_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^n\]
\[=\lim_{n \rightarrow \infty}\left(1+\frac{n\times \frac{1}{n}}{1!}+\frac{n(n-1)\times \frac{1}{n^2}}{2!}+\frac{n(n-1)(n-2)\times \frac{1}{n^3}}{3!}+ ... \infty \right)\] ➜ \(\because (1+x)^n=1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ .... \infty\)
\[=\lim_{n \rightarrow \infty}\left(1+\frac{1}{1!}+\frac{n^2(1-\frac{1}{n})\times \frac{1}{n^2}}{2!}+\frac{n^3(1-\frac{1}{n})(1-\frac{2}{n})\times \frac{1}{n^3}}{3!}+ ... \infty \right)\]
\[=\lim_{n \rightarrow \infty}\left(1+\frac{1}{1!}+\frac{(1-\frac{1}{n})}{2!}+\frac{(1-\frac{1}{n})(1-\frac{2}{n})}{3!}+ ... \infty \right)\]
\[=1+\frac{1}{1!}+\frac{(1-0)}{2!}+\frac{(1-0)(1-0)}{3!}+ ... \infty \] ➜ \[\because \lim_{n \rightarrow \infty}\frac{1}{n}=0, \lim_{n \rightarrow \infty}\frac{2}{n}=0 \]
\[=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ .... \infty\]
\[=e \] ➜ \[\because e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ ... \infty\]
\[=R.S \]
\[\therefore L.S=R.S\]
(proved)
\[=\lim_{n \rightarrow \infty}\left(1+\frac{n\times \frac{1}{n}}{1!}+\frac{n(n-1)\times \frac{1}{n^2}}{2!}+\frac{n(n-1)(n-2)\times \frac{1}{n^3}}{3!}+ ... \infty \right)\] ➜ \(\because (1+x)^n=1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ .... \infty\)
\[=\lim_{n \rightarrow \infty}\left(1+\frac{1}{1!}+\frac{n^2(1-\frac{1}{n})\times \frac{1}{n^2}}{2!}+\frac{n^3(1-\frac{1}{n})(1-\frac{2}{n})\times \frac{1}{n^3}}{3!}+ ... \infty \right)\]
\[=\lim_{n \rightarrow \infty}\left(1+\frac{1}{1!}+\frac{(1-\frac{1}{n})}{2!}+\frac{(1-\frac{1}{n})(1-\frac{2}{n})}{3!}+ ... \infty \right)\]
\[=1+\frac{1}{1!}+\frac{(1-0)}{2!}+\frac{(1-0)(1-0)}{3!}+ ... \infty \] ➜ \[\because \lim_{n \rightarrow \infty}\frac{1}{n}=0, \lim_{n \rightarrow \infty}\frac{2}{n}=0 \]
\[=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ .... \infty\]
\[=e \] ➜ \[\because e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ ... \infty\]
\[=R.S \]
\[\therefore L.S=R.S\]
(proved)
×
\[\lim_{n \rightarrow 0}(1+n)^{\frac{1}{n}}=e\]
Proof:
\[L.S=\lim_{n \rightarrow 0}(1+n)^{\frac{1}{n}}\]
\[=\lim_{n \rightarrow 0}\{1+\frac{\frac{1}{n}\times n}{1!}+\frac{\frac{1}{n}\left(\frac{1}{n}-1\right)\times n^2}{2!}+\frac{\frac{1}{n}\left(\frac{1}{n}-1\right)\left(\frac{1}{n}-2\right)\times n^3}{3!}+ ... \infty \}\] ➜ \(\because (1+x)^n=1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ ... \infty\)
\[=\lim_{n \rightarrow 0}\{1+\frac{1}{1!}+\frac{\frac{1}{n^2}(1-n)\times n^2}{2!}+\frac{\frac{1}{n^3}(1-n)(1-2n)\times n^3}{3!}+ ...\infty \}\]
\[=\lim_{n \rightarrow 0}\{1+\frac{1}{1!}+\frac{(1-n)}{2!}+\frac{(1-n)(1-2n)}{3!}+ ... \infty \}\]
\[=\{1+\frac{1}{1!}+\frac{(1-0)}{2!}+\frac{(1-0)(1-0)}{3!}+ .... \infty \}\] ➜ লিমিট ব্যবহার করে।
\[=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ .... \infty \]
\[=e \] ➜ \[\because e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ ..... \infty\]
\[=R.S \]
\[\therefore L.S=R.S\]
(proved)
\[=\lim_{n \rightarrow 0}\{1+\frac{\frac{1}{n}\times n}{1!}+\frac{\frac{1}{n}\left(\frac{1}{n}-1\right)\times n^2}{2!}+\frac{\frac{1}{n}\left(\frac{1}{n}-1\right)\left(\frac{1}{n}-2\right)\times n^3}{3!}+ ... \infty \}\] ➜ \(\because (1+x)^n=1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ ... \infty\)
\[=\lim_{n \rightarrow 0}\{1+\frac{1}{1!}+\frac{\frac{1}{n^2}(1-n)\times n^2}{2!}+\frac{\frac{1}{n^3}(1-n)(1-2n)\times n^3}{3!}+ ...\infty \}\]
\[=\lim_{n \rightarrow 0}\{1+\frac{1}{1!}+\frac{(1-n)}{2!}+\frac{(1-n)(1-2n)}{3!}+ ... \infty \}\]
\[=\{1+\frac{1}{1!}+\frac{(1-0)}{2!}+\frac{(1-0)(1-0)}{3!}+ .... \infty \}\] ➜ লিমিট ব্যবহার করে।
\[=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ .... \infty \]
\[=e \] ➜ \[\because e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+ ..... \infty\]
\[=R.S \]
\[\therefore L.S=R.S\]
(proved)
×
\[\lim_{x \rightarrow a}\frac{x^n-a^n}{x-a}=n.a^{n-1}\]
Proof:
\[L.S=\lim_{x \rightarrow a}\frac{x^n-a^n}{x-a}\]
\[=\lim_{x \rightarrow a}\frac{(x-a)(x^{n-1}+x^{n-2}a+x^{n-3}a^2+.......+a^{n-1})}{x-a}\] ➜ \(\because x^n-a^n=(x-a)(x^{n-1}+x^{n-2}a+x^{n-3}a^2+.......+a^{n-1})\)
\[=\lim_{x \rightarrow a}(x^{n-1}+x^{n-2}a+x^{n-3}a^2+.......+a^{n-1})\]
\[=a^{n-1}+a^{n-2}a+a^{n-3}a^2+.......+a^{n-1}\] ➜ লিমিট ব্যবহার করে।
\[=a^{n-1}+a^{n-2+1}+a^{n-3+2}+.......+a^{n-1}\]
\[=a^{n-1}+a^{n-1}+a^{n-1}+.......+a^{n-1}\]
\[=n.a^{n-1}\] ➜ \(n\) পদের যোগফল।
\[=R.S \]
\[\therefore L.S=R.S\]
(proved)
\[=\lim_{x \rightarrow a}\frac{(x-a)(x^{n-1}+x^{n-2}a+x^{n-3}a^2+.......+a^{n-1})}{x-a}\] ➜ \(\because x^n-a^n=(x-a)(x^{n-1}+x^{n-2}a+x^{n-3}a^2+.......+a^{n-1})\)
\[=\lim_{x \rightarrow a}(x^{n-1}+x^{n-2}a+x^{n-3}a^2+.......+a^{n-1})\]
\[=a^{n-1}+a^{n-2}a+a^{n-3}a^2+.......+a^{n-1}\] ➜ লিমিট ব্যবহার করে।
\[=a^{n-1}+a^{n-2+1}+a^{n-3+2}+.......+a^{n-1}\]
\[=a^{n-1}+a^{n-1}+a^{n-1}+.......+a^{n-1}\]
\[=n.a^{n-1}\] ➜ \(n\) পদের যোগফল।
\[=R.S \]
\[\therefore L.S=R.S\]
(proved)
বিকল্প পদ্ধতিঃ
Proof:
\[L.S=\lim_{x \rightarrow a}\frac{x^n-a^n}{x-a}\]
ধরি,
\(x=a+h \therefore x\rightarrow a\) হলে, \(h\rightarrow 0\)
\[=\lim_{h \rightarrow 0}\frac{(a+h)^n-a^n}{a+h-a}\]
\[=\lim_{h \rightarrow 0}\frac{a^n\left(1+\frac{h}{a}\right)^n-a^n}{h}\]
\[=a^n\lim_{h \rightarrow 0}\frac{\left(1+\frac{h}{a}\right)^n-1}{h}\]
\[=a^n\lim_{h \rightarrow 0}\frac{\left(1+\frac{n}{1!}.\frac{h}{a}+\frac{n(n-1)}{2!}.\frac{h^2}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{h^3}{a^3}+...\right)-1}{h}\] ➜ \(\because (1+x)^n=1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ ...\infty\)
\[=a^n\lim_{h \rightarrow 0}\frac{\left(\frac{n}{1!}.\frac{h}{a}+\frac{n(n-1)}{2!}.\frac{h^2}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{h^3}{a^3}+...\right)}{h}\]
\[=a^n\lim_{h \rightarrow 0}\frac{h\left(\frac{n}{1!}.\frac{1}{a}+\frac{n(n-1)}{2!}.\frac{h}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{h^2}{a^3}+...\right)}{h}\]
\[=a^n\lim_{h \rightarrow 0}\left(\frac{n}{1!}.\frac{1}{a}+\frac{n(n-1)}{2!}.\frac{h}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{h^2}{a^3}+.... \right)\]
\[=a^n\left(\frac{n}{1!}.\frac{1}{a}+\frac{n(n-1)}{2!}.\frac{0}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{0}{a^3}+.... \right)\] ➜ লিমিট ব্যবহার করে।
\[=a^n\left(\frac{n}{1}.\frac{1}{a}+0+0+... \right)\] ➜ \(\because 1!=1\)
\[=a^n\left(\frac{n}{a}\right)\]
\[=n.a^{n-1}\]
\[=R.S \]
\[\therefore L.S=R.S\]
(proved)
ধরি,
\(x=a+h \therefore x\rightarrow a\) হলে, \(h\rightarrow 0\)
\[=\lim_{h \rightarrow 0}\frac{(a+h)^n-a^n}{a+h-a}\]
\[=\lim_{h \rightarrow 0}\frac{a^n\left(1+\frac{h}{a}\right)^n-a^n}{h}\]
\[=a^n\lim_{h \rightarrow 0}\frac{\left(1+\frac{h}{a}\right)^n-1}{h}\]
\[=a^n\lim_{h \rightarrow 0}\frac{\left(1+\frac{n}{1!}.\frac{h}{a}+\frac{n(n-1)}{2!}.\frac{h^2}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{h^3}{a^3}+...\right)-1}{h}\] ➜ \(\because (1+x)^n=1+\frac{nx}{1!}+\frac{n(n-1)x^2}{2!}+\frac{n(n-1)(n-2)x^3}{3!}+ ...\infty\)
\[=a^n\lim_{h \rightarrow 0}\frac{\left(\frac{n}{1!}.\frac{h}{a}+\frac{n(n-1)}{2!}.\frac{h^2}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{h^3}{a^3}+...\right)}{h}\]
\[=a^n\lim_{h \rightarrow 0}\frac{h\left(\frac{n}{1!}.\frac{1}{a}+\frac{n(n-1)}{2!}.\frac{h}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{h^2}{a^3}+...\right)}{h}\]
\[=a^n\lim_{h \rightarrow 0}\left(\frac{n}{1!}.\frac{1}{a}+\frac{n(n-1)}{2!}.\frac{h}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{h^2}{a^3}+.... \right)\]
\[=a^n\left(\frac{n}{1!}.\frac{1}{a}+\frac{n(n-1)}{2!}.\frac{0}{a^2}+\frac{n(n-1)(n-2)}{3!}.\frac{0}{a^3}+.... \right)\] ➜ লিমিট ব্যবহার করে।
\[=a^n\left(\frac{n}{1}.\frac{1}{a}+0+0+... \right)\] ➜ \(\because 1!=1\)
\[=a^n\left(\frac{n}{a}\right)\]
\[=n.a^{n-1}\]
\[=R.S \]
\[\therefore L.S=R.S\]
(proved)

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000003