সংযুক্ত কোণের কোণমিতিক অনুপাত
The angular ratio of the connected angles
Posted on August 18, 2023, 12:53 pm By admin
barcode
এ অধ্যায়ের পাঠ্যসূচী
ঐতিহাসিক পটভূমি
Historical Background
straight3
বার্থোলোমিয়াস পিটিসকাস (১৫৬১-১৬১৩)
পিটিসকাস লাতিন ভাষায় তাঁর প্রভাবশালী রচনার মাধ্যমে খ্যাতি অর্জন করেছিলেন, যাকে ট্রাইগনোমেট্রিয়া বলা হয়: সিভ ডি সলিউশন ট্রাইঙ্গুলোরাম ট্র্যাক্যাটাস ব্রাভিস এট পার্সপিকিউস (১৫৯৫, হাইডেলবার্গে প্রথম সংস্করণে ছাপা হয়েছিল), যা ইংরেজী এবং ফরাসি ভাষায় ত্রিকোণমিতি শব্দটি চালু করেছিলেন, অনুবাদ করেছিলেন।
\(-\theta, \ 90^{o}\pm\theta, \ 180^{o}\pm\theta, .........\) এরূপ কোণকে \(\theta\) কোণের সংযুক্ত কোণ বলা হয়। সংযুক্ত কোণের ত্রিকোণমিতিক অনুপাত নির্ণয়ের সময় স্থানাঙ্কের যথাযথ চিহ্ন অবশ্যই বিবেচনা করতে হবে এবং স্মরণ রাখতে হবে যে ব্যাসার্ধ ভেক্টর সব সময়ই ধনাত্মক। এরূপ কোণের সকল ত্রিকোণমিতিক অনুপাতকে \(\theta\) কোণের ত্রিকোণমিতিক অনুপাতের মাধ্যমে প্রকাশ করা যায়। দুই বা ততোধিক কোণের সমষ্টি অথবা অন্তরফলকে যৌগিক কোণ বলে।
\(A+B, \ A-B, \ A+B-C, \ A-B-C \) প্রভৃতি যৌগিক কোণের উদাহরণ। এরূপ কোণের সকল ত্রিকোণমিতিক সরল অনুপাতকে \(A\) ও \(B\) কোণের ত্রিকোণমিতিক অনুপাতের মাধ্যমে প্রকাশ করা যায়। এ সকল সূত্র প্রতিষ্ঠা ও এদের প্রয়োগ ত্রিকোণমিতিতে বিশেষ গুরুত্বপূর্ণ।
ত্রিভুজের বাহুর দৈর্ঘ্য ও কোণের মধ্যকার সম্পর্কের বিষয়টি ত্রিকোণমিতিতে আলোচনা করা হয়। সংযুক্ত কোণের ত্রিকোণমিতিক অনুপাত; ত্রিকোণমিতিক অনুপাতগুলোর পারস্পারিক সম্পর্ক, গুণিতক, উপগুণিতক কোণের ত্রিকোণমিতিক অনুপাত, ত্রিকোণমিতিক অভেদাবলি, ত্রিভুজের বাহু ও কোণ সম্পর্কিত সূত্রাবলির ব্যাখ্যা প্রদান করে। সুমেরীয় জ্যোতির্বিদ্গণ বৃত্তকে \(\text{৩৬০}^{o}\) তে ভাগ করেন, তাদের উত্তরসূরী ব্যবিলনীয়রা দুইটি সদৃশ ত্রিভুজের বাহুর অনুপাতের ধর্মাবলী নির্ণয় করেছিলেন, তবে এর মাধ্যমে ত্রিভুজের বাহু ও কোণের সম্পর্ক নির্ণয় করা সম্ভব হয়নি। প্রাচীন গ্রীক বিজ্ঞানীগণ ত্রিকোণমিতিক বৈজ্ঞানিকরূপ প্রদান করেন।
জ্যোতির্বিদ ও ধর্মতত্ত্ববিদ বার্থোলোমিয়াস পিটিসকাস straight3 বার্থোলোমিয়াস পিটিসকাস (১৫৬১-১৬১৩) পিটিসকাস লাতিন ভাষায় তাঁর প্রভাবশালী রচনার মাধ্যমে খ্যাতি অর্জন করেছিলেন, যাকে ট্রাইগনোমেট্রিয়া বলা হয়: সিভ ডি সলিউশন ট্রাইঙ্গুলোরাম ট্র্যাক্যাটাস ব্রাভিস এট পার্সপিকিউস (১৫৯৫, হাইডেলবার্গে প্রথম সংস্করণে ছাপা হয়েছিল), যা ইংরেজী এবং ফরাসি ভাষায় ত্রিকোণমিতি শব্দটি চালু করেছিলেন, অনুবাদ করেছিলেন। (১৫৬১-১৬১৩) তাঁর বিখ্যাত গ্রন্থ "ট্রাইগনোমেট্রিয়াঃ সিভ ডি সলিউশন ট্রাইঙ্গুলোরাম ট্র্যাক্যাটাস ব্রাভিস এট পার্সপিকিউস" এ "Trigonometry" শব্দটি প্রথম ব্যবহার করেন। তিনি হেটিকাস এর ত্রিকোণমিতিক টেবিলের উন্নতি সাধন করেন।
ত্রিকোণমিতি ও ত্রিকোণমিতিক ফাংশন ব্যবহার করে এক গ্রহ থেকে অন্য গ্রহের দূরত্ব, ভৌগোলিকভাবে অবস্থিত দুইটি বিন্দুর দূরত্ব ও কৃত্রিম উপগ্রহের ঘূর্ণন গতি নির্ণয় করা যায়। শব্দ ও আলোক তরঙ্গের মত পর্যায়বৃত্ত ফাংশনের মূলভিত্তি সাইন ও কোসাইন ফাংশন। এছাড়াও জ্যোতির্বিদ্যা, সঙ্গিত তত্ত্ব, আলোক বিজ্ঞান, আবহাওয়া বিজ্ঞান, অর্থনীতি, প্রকৌশল বিদ্যা, কম্পিউটার গ্রাফিক্স ইত্যাদিতে ত্রিকোণমিতিক ফাংশন ব্যবহৃত হয়।
সংযুক্ত কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of associated Angles
\(-\theta, \ 90^{o}\pm\theta, \ 180^{o}\pm\theta, .........\) এরূপ কোণকে \(\theta\) কোণের সংযুক্ত কোণ বলা হয়। সংযুক্ত কোণের ত্রিকোণমিতিক অনুপাত নির্ণয়ের সময় স্থানাঙ্কের যথাযথ চিহ্ন অবশ্যই বিবেচনা করতে হবে এবং স্মরণ রাখতে হবে যে ব্যাসার্ধ ভেক্টর সব সময়ই ধনাত্মক।
আলোচনার এই অংশে প্রথমে ঋণাত্মক কোণ \(-\theta\) এর অনুপাত নির্ণয় করা হবে। এর ওপর ভিত্তি করে \(90^{o}-\theta, \ 90^{o}+\theta,\)\(180^{o}-\theta, \ 180^{o}+\theta,\)\(270^{o}-\theta, \ 270^{o}+\theta,\)\(360^{o}-\theta, \ 360^{o}+\theta\) এবং \(n\times90^{o}+\theta, \ n\times90^{o}-\theta \ (\text{যেখানে } \ n\in{\mathbb{Z}})\) এবং \(0\lt\theta\lt\frac{\pi}{2}\) কোণসমুহের ত্রিকোণমিতিক অনুপাত সম্পর্কে আলোচনা করব।
\((-\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of \((-\theta)\) Angle
\(\sin{(-\theta)}=-\sin{\theta}\)
\(\cos{(-\theta)}=\cos{\theta}\)
\(\tan{(-\theta)}=-\tan{\theta}\)
\(cosec \ {(-\theta)}=-cosec \ {\theta}\)
\(\sec{(-\theta)}=\sec{\theta}\)
\(\cot{(-\theta)}=-\cot{\theta}\)

প্রমাণঃ
মনে করি, কোনো ঘূর্ণায়মান রশ্মি আদি অবস্থান \(OX\) হতে \(O\) বিন্দুর সাপেক্ষে ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে \(\angle{POX}=\theta, \ (\theta\lt90^{o})\) কোণ উৎপন্ন করে। অপর কোনো ঘূর্ণায়মান রশ্মি ঐ একই অবস্থান \(OX\) হতে ঘড়ির কাঁটার ঘূর্ণনের দিকে ঘুরে \(\theta\) কোণের সমপরিমানে \(\angle{QOX}\) কোণ উৎপন্ন করে।
\(\therefore \angle{QOX}=\theta\)
\(OP\) রেখার উপর যে কোনো বিন্দু \(P\) থেকে \(XOX^{\prime}\) এর উপর \(PN\) লম্ব অঙ্কন করি। \(PN\) কে এমনভাবে বর্ধিত করি যেন \(OQ\) কে \(Q\) বিন্দুতে ছেদ করে।
\(\triangle{OPN}\) ও \(\triangle{OQN}\) এ
\(\angle{PON}=\angle{QON}=\theta\)
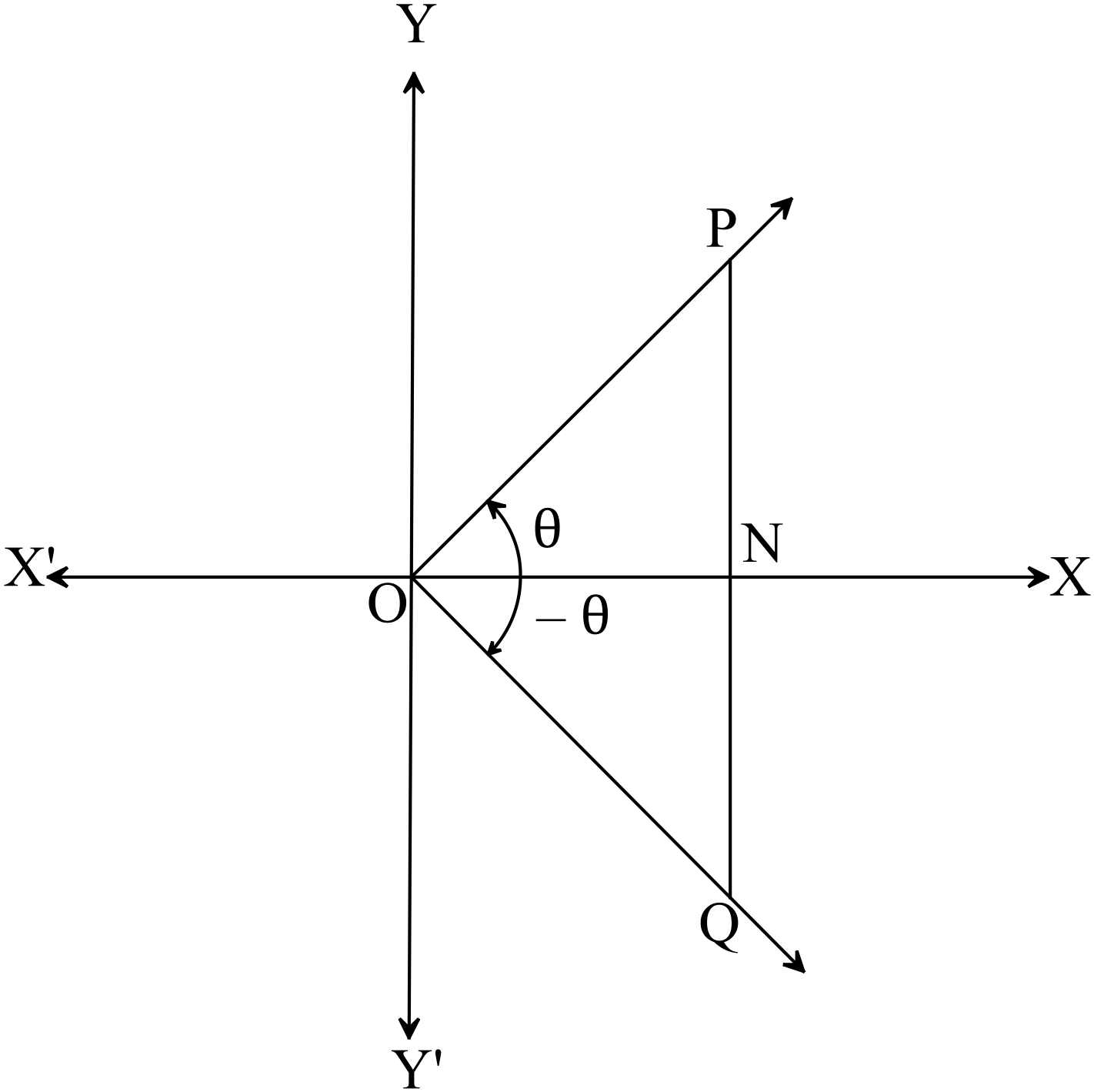straight3 \(\angle{ONP}=\angle{ONQ}=90^{o}\)
এবং \(ON\) উভয় ত্রিভুজের সাধারণ বাহু।
\(\therefore \triangle{OPN}\cong\triangle{OQN}\)
সুতরাং \(OP=OQ\)
\(PN=NQ\) যেখানে, \(NQ\) ঋণাত্মক।

এখন \(\sin{(-\theta)}=\frac{-NQ}{OQ}\)
\(=-\frac{NQ}{OP}\) ➜ \(\because OQ=OP\)

\(=-\frac{PN}{OP}\) ➜ \(\because NQ=PN\)

\(=-\sin{\theta}\)
\(\sin{(-\theta)}=-\sin{\theta}\)
\(\cos{(-\theta)}=\frac{ON}{OQ}\)
\(=\frac{ON}{OP}\) ➜ \(\because OQ=OP\)

\(=\cos{\theta}\)
\(\cos{(-\theta)}=\cos{\theta}\)
\(\tan{(-\theta)}=\frac{-NQ}{ON}\)
\(=-\frac{NQ}{ON}\)
\(=-\frac{PN}{ON}\) ➜ \(\because NQ=PN\)

\(=-\tan{\theta}\)
\(\tan{(-\theta)}=-\tan{\theta}\)
অনুরূপভাবে প্রমাণ করা যায়,
\(cosec \ {(-\theta)}=-cosec \ {\theta}\) \(\sec{(-\theta)}=\sec{\theta}\) \(\cot{(-\theta)}=-\cot{\theta}\)
\((90^{o}-\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of \((90^{o}-\theta)\) Angle
\(\sin{(90^{o}-\theta)}=\cos{\theta}\)
\(\cos{(90^{o}-\theta)}=\sin{\theta}\)
\(\tan{(90^{o}-\theta)}=\cot{\theta}\)
\(cosec \ {(90^{o}-\theta)}=\sec {\theta}\)
\(\sec{(90^{o}-\theta)}=cosec \ {\theta}\)
\(\cot{(90^{o}-\theta)}=\tan{\theta}\)

প্রমাণঃ
মনে করি, কোনো ঘূর্ণায়মান রশ্মি আদি অবস্থান \(OX\) হতে \(O\) বিন্দুর সাপেক্ষে ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে \(\angle{POM}=\theta, \ (\theta\lt90^{o})\) এবং আরও ঘুরে \(\angle{XOY}=90^{o}\) কোণ উৎপন্ন করে। এর পর রশ্মিটি আবার ঘড়ির কাঁটার ঘূর্ণনের দিকে ঘুরে \(\angle{YOP^{\prime}}=\theta\) কোণ উৎপন্ন করে।
সুতরাং \(\angle{XOP^{\prime}}=\angle{XOY}-\angle{YOP^{\prime}}\)
\(\therefore \angle{XOP^{\prime}}=90^{o}-\theta\)
\(OP\) রেখার উপর \(P\) এবং \(OP^{\prime}\) এর উপর যে কোনো বিন্দু \(P^{\prime}\) নেয়া হলো যেন \(OP=OP^{\prime}\) হয়। \(P\) এবং \(P^{\prime}\) বিন্দু থেকে \(XOX^{\prime}\) রেখার উপর যথাক্রমে \(PM\) এবং \(P^{\prime}M^{\prime}\) লম্ব অঙ্কন করি।
এখন \(\triangle{OPM}\) ও \(\triangle{OP^{\prime}M^{\prime}}\) এ
\(\angle{OMP}=\angle{OM^{\prime}P^{\prime}}=90^{o}\)
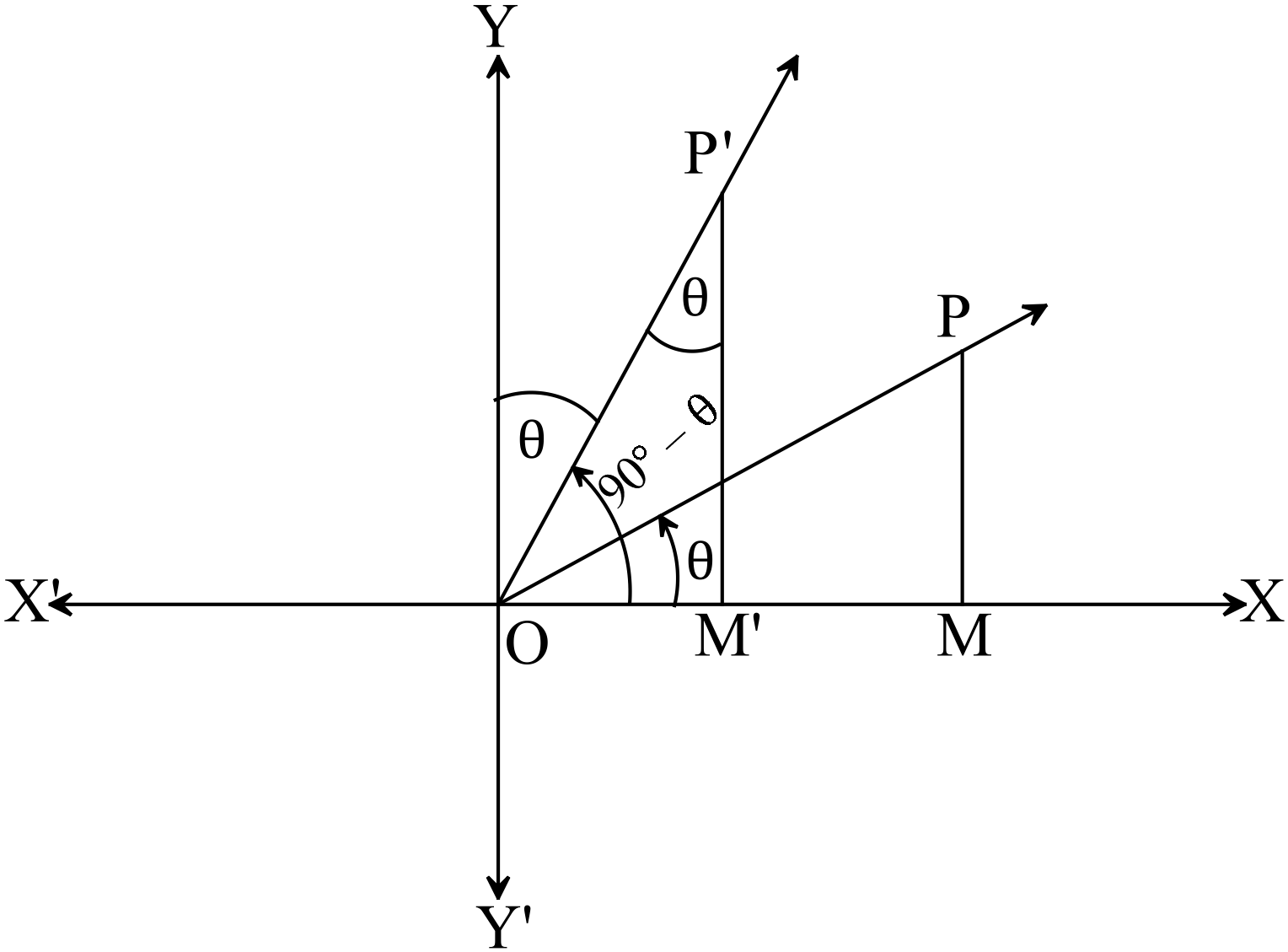straight3 \(\angle{POM}=\angle{YOP^{\prime}}=\text{একান্তর }\angle{OP^{\prime}M^{\prime}}=\theta\)
এবং \(OP=OP^{\prime}\)
\(\therefore \triangle{OPM}\cong\triangle{OP^{\prime}M^{\prime}}\)
\(\therefore OM=P^{\prime}M^{\prime}\)
এবং \(PM=OM^{\prime}\)
এখন \(\sin{(90^{o}-\theta)}=\sin{P^{\prime}OM^{\prime}}\)
\(=\frac{P^{\prime}M^{\prime}}{OP^{\prime}}\)
\(=\frac{OM}{OP}\) ➜ \(\because P^{\prime}M^{\prime}=OM\)
এবং \(OP^{\prime}=OP\)

\(=\cos{POM}\)
\(=\cos{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\sin{(90^{o}-\theta)}=\cos{\theta}\)
\(\cos{(90^{o}-\theta)}=\cos{P^{\prime}OM^{\prime}}\)
\(=\frac{OM^{\prime}}{OP^{\prime}}\)
\(=\frac{PM}{OP}\) ➜ \(\because OM^{\prime}=PM\)
এবং \(OP^{\prime}=OP\)

\(=\sin{POM}\)
\(=\sin{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\cos{(90^{o}-\theta)}=\sin{\theta}\)
\(\tan{(90^{o}-\theta)}=\tan{P^{\prime}OM^{\prime}}\)
\(=\frac{P^{\prime}M^{\prime}}{OM^{\prime}}\)
\(=\frac{OM}{PM}\) ➜ \(\because P^{\prime}M^{\prime}=OM\)
এবং \(OM^{\prime}=PM\)

\(=\cot{POM}\)
\(=\cot{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\tan{(90^{o}-\theta)}=\cot{\theta}\)
অনুরূপভাবে প্রমাণ করা যায়,
\(cosec \ {(90^{o}-\theta)}=\sec{\theta}\) \(\sec{(90^{o}-\theta)}=cosec \ {\theta}\) \(\cot{(90^{o}-\theta)}=\tan{\theta}\)
দ্রষ্টব্যঃ \((90^{o}-\theta)\) এবং \(\theta\) পরস্পরের পূরক কোণ। দুইটি পূরক কোণের একটি কোণের সাইন অপরটির কোসাইন, একটি কোণের ট্যানজেণ্ট অপরটির কোট্যানজেণ্ট এবং একটি কোণের কোসেকেন্ট অপরটির সেকেন্ট এর সমান। এই সম্পর্কগুলি সূক্ষ্ণকোণের জন্য সত্য।
\((90^{o}+\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of \((90^{o}+\theta)\) Angle
\(\sin{(90^{o}+\theta)}=\cos{\theta}\)
\(\cos{(90^{o}+\theta)}=-\sin{\theta}\)
\(\tan{(90^{o}+\theta)}=-\cot{\theta}\)
\(cosec \ {(90^{o}+\theta)}=\sec {\theta}\)
\(\sec{(90^{o}+\theta)}=-cosec \ {\theta}\)
\(\cot{(90^{o}+\theta)}=-\tan{\theta}\)

প্রমাণঃ
মনে করি, কোনো ঘূর্ণায়মান রশ্মি আদি অবস্থান \(OX\) হতে \(O\) বিন্দুর সাপেক্ষে ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে \(\angle{POM}=\theta, \ (\theta\lt90^{o})\) এবং আরও ঘুরে \(\angle{POP^{\prime}}=90^{o}\) কোণ উৎপন্ন করে। সুতরাং \(\angle{XOP^{\prime}}=\angle{POP^{\prime}}+\angle{POM}=90^{o}+\theta\)
\(\therefore \angle{XOP^{\prime}}=90^{o}+\theta\)
\(\Rightarrow \angle{XOY}+\angle{YOP^{\prime}}=90^{o}+\theta\) ➜ \(\because \angle{XOP^{\prime}}=\angle{XOY}+\angle{YOP^{\prime}}\)

\(\Rightarrow 90^{o}+\angle{YOP^{\prime}}=90^{o}+\theta\) ➜ \(\because \angle{XOY}=90^{o}\)

\(\Rightarrow \angle{YOP^{\prime}}=90^{o}+\theta-90^{o}\)
\(\therefore \angle{YOP^{\prime}}=\theta\)
আবার, \(\angle{OP^{\prime}M^{\prime}}=\text{একান্তর } \angle{YOP^{\prime}}=\theta\)
\(\therefore \angle{OP^{\prime}M^{\prime}}=\theta\)
\(OP\) রেখার উপর \(P\) এবং \(OP^{\prime}\) এর উপর যে কোনো বিন্দু \(P^{\prime}\) নেয়া হলো যেন \(OP=OP^{\prime}\) হয়। \(P\) এবং \(P^{\prime}\) বিন্দু থেকে \(XOX^{\prime}\) রেখার উপর যথাক্রমে \(PM\) এবং \(P^{\prime}M^{\prime}\) লম্ব অঙ্কন করি।
এখন \(\triangle{OPM}\) ও \(\triangle{OP^{\prime}M^{\prime}}\) এ
\(\angle{OMP}=\angle{OM^{\prime}P^{\prime}}=90^{o}\)
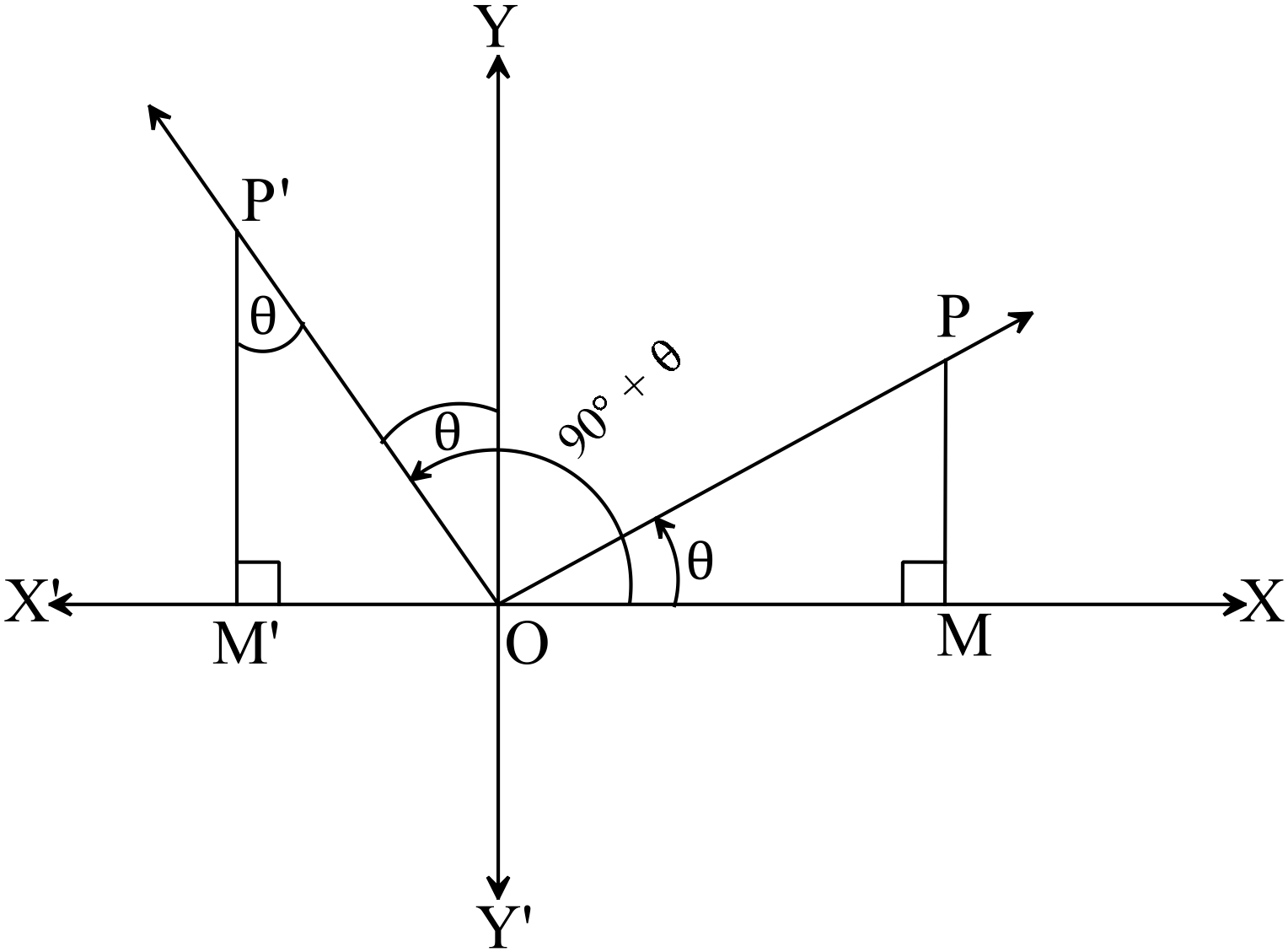straight3 \(\angle{POM}=\angle{YOP^{\prime}}=\text{একান্তর }\angle{OP^{\prime}M^{\prime}}=\theta\)
এবং \(OP=OP^{\prime}\)
\(\therefore \triangle{OPM}\cong\triangle{OP^{\prime}M^{\prime}}\)
\(\therefore OM=P^{\prime}M^{\prime}\)
এবং \(PM=OM^{\prime}\) যেখানে, \(OM^{\prime}\) ঋণাত্মক।
এখন \(\sin{(90^{o}+\theta)}=\sin{MOP^{\prime}}=\sin{P^{\prime}OM^{\prime}}\) ➜ \(\because \angle{MOP^{\prime}}=\text{সম্পূরক } \angle{P^{\prime}OM^{\prime}}\)

\(=\frac{P^{\prime}M^{\prime}}{OP^{\prime}}\)
\(=\frac{OM}{OP}\) ➜ \(\because P^{\prime}M^{\prime}=OM\)
এবং \(OP^{\prime}=OP\)

\(=\cos{POM}\)
\(=\cos{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\sin{(90^{o}+\theta)}=\cos{\theta}\)
\(\cos{(90^{o}+\theta)}=\cos{MOP^{\prime}}=\cos{P^{\prime}OM^{\prime}}\) ➜ \(\because \angle{MOP^{\prime}}=\text{সম্পূরক } \angle{P^{\prime}OM^{\prime}}\)

\(=\frac{-OM^{\prime}}{OP^{\prime}}\)
\(=\frac{-PM}{OP}\) ➜ \(\because OM^{\prime}=PM\)
এবং \(OP^{\prime}=OP\)

\(=-\frac{PM}{OP}\)
\(=-\sin{POM}\)
\(=-\sin{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\cos{(90^{o}+\theta)}=-\sin{\theta}\)
\(\tan{(90^{o}+\theta)}=\tan{MOP^{\prime}}=\tan{P^{\prime}OM^{\prime}}\) ➜ \(\because \angle{MOP^{\prime}}=\text{সম্পূরক } \angle{P^{\prime}OM^{\prime}}\)

\(=\frac{P^{\prime}M^{\prime}}{-OM^{\prime}}\)
\(=\frac{OM}{-PM}\) ➜ \(\because P^{\prime}M^{\prime}=OM\)
এবং \(OM^{\prime}=PM\)

\(=-\frac{OM}{PM}\)
\(=-\cot{POM}\)
\(=-\cot{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\tan{(90^{o}+\theta)}=-\cot{\theta}\)
অনুরূপভাবে প্রমাণ করা যায়,
\(cosec \ {(90^{o}+\theta)}=\sec{\theta}\) \(\sec{(90^{o}+\theta)}=-cosec \ {\theta}\) \(\cot{(90^{o}+\theta)}=-\tan{\theta}\)
\((180^{o}-\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of \((180^{o}-\theta)\) Angle
\(\sin{(180^{o}-\theta)}=\sin{\theta}\)
\(\cos{(180^{o}-\theta)}=-\cos{\theta}\)
\(\tan{(180^{o}-\theta)}=-\tan{\theta}\)
\(cosec \ {(180^{o}-\theta)}=cosec \ {\theta}\)
\(\sec{(180^{o}-\theta)}=-\sec {\theta}\)
\(\cot{(180^{o}-\theta)}=-\cot{\theta}\)

প্রমাণঃ
মনে করি, কোনো ঘূর্ণায়মান রশ্মি আদি অবস্থান \(OX\) হতে \(O\) বিন্দুর সাপেক্ষে ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে \(\angle{POM}=\theta, \ (\theta\lt90^{o})\) কোণ উৎপন্ন করে। অপর কোণ রশ্মি একই আদি অবস্থান \(OX\) হতে \(O\) বিন্দুর সাপেক্ষে ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে \(\angle{MOM^{\prime}}=180^{o})\) কোণ উৎপন্ন করে অতঃপর তা ঘড়ির কাঁটার দিকে ঘুরে \(\angle{M^{\prime}OP^{\prime}}=\theta\) কোণ উৎপন্ন করে।
সুতরাং \(\angle{MOP^{\prime}}=\angle{MOM^{\prime}}-\angle{M^{\prime}OP^{\prime}}=180^{o}-\theta\)
তাহলে, \(\angle{MOP}=\angle{M^{\prime}OP^{\prime}}=\theta\)
\(OP\) রেখার উপর \(P\) এবং \(OP^{\prime}\) এর উপর যে কোনো বিন্দু \(P^{\prime}\) নেয়া হলো যেন \(OP=OP^{\prime}\) হয়। \(P\) এবং \(P^{\prime}\) বিন্দু থেকে \(XOX^{\prime}\) রেখার উপর যথাক্রমে \(PM\) এবং \(P^{\prime}M^{\prime}\) লম্ব অঙ্কন করি।
এখন \(\triangle{OPM}\) ও \(\triangle{OP^{\prime}M^{\prime}}\) এ
\(\angle{MOP}=\angle{M^{\prime}OP^{\prime}}=\theta\)
\(\angle{OMP}=\angle{OM^{\prime}P^{\prime}}=90^{o}\)
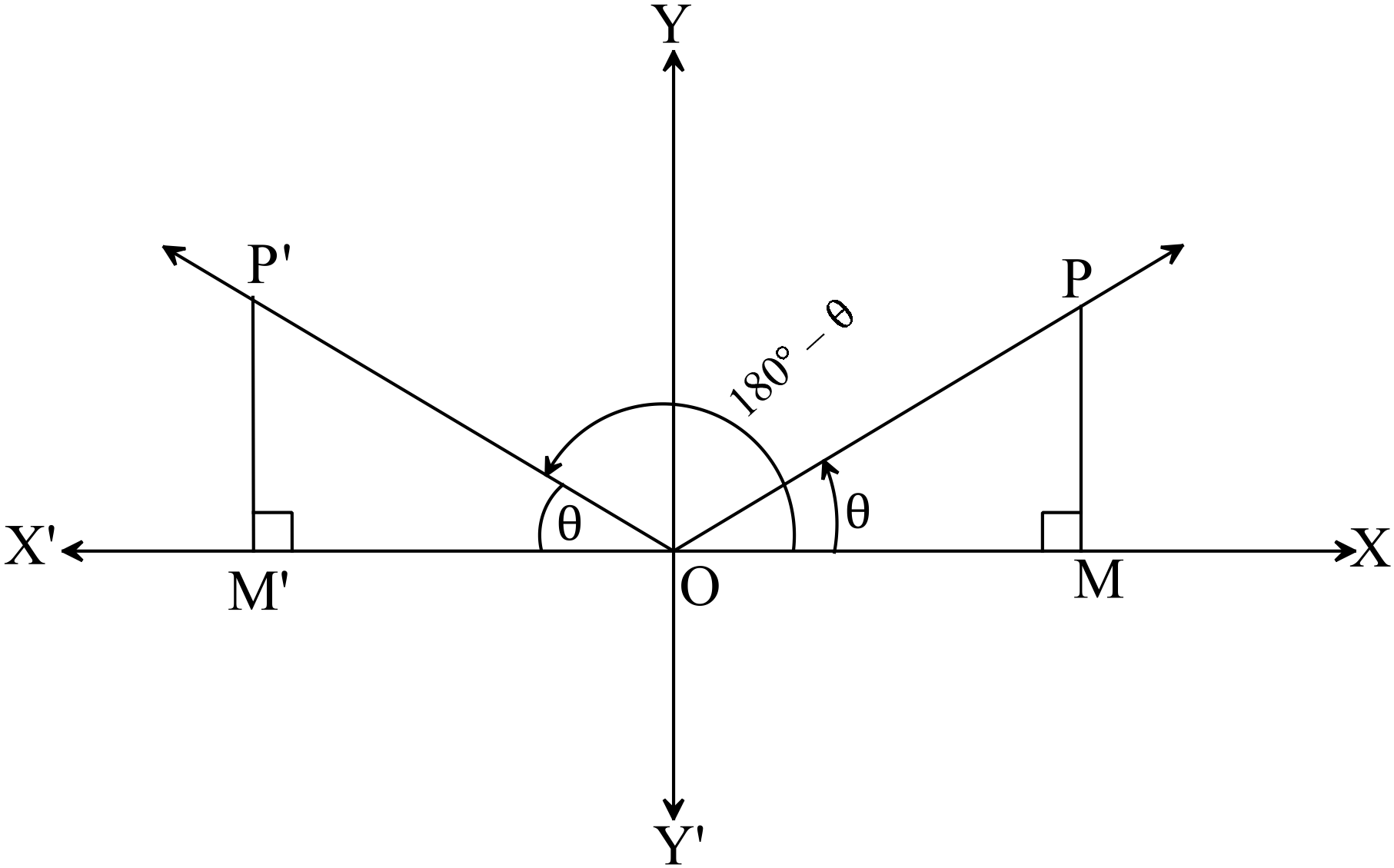straight3 এবং \(OP=OP^{\prime}\)
\(\therefore \triangle{OPM}\cong\triangle{OP^{\prime}M^{\prime}}\)
\(\therefore PM=P^{\prime}M^{\prime}\)
এবং \(OM=OM^{\prime}\) যেখানে, \(OM^{\prime}\) ঋণাত্মক।
এখন \(\sin{(180^{o}-\theta)}=\sin{MOP^{\prime}}=\sin{P^{\prime}OM^{\prime}}\) ➜ \(\because \angle{MOP^{\prime}}=\text{সম্পূরক } \angle{P^{\prime}OM^{\prime}}\)

\(=\frac{P^{\prime}M^{\prime}}{OP^{\prime}}\)
\(=\frac{PM}{OP}\) ➜ \(\because P^{\prime}M^{\prime}=PM\)
এবং \(OP^{\prime}=OP\)

\(=\sin{POM}\)
\(=\sin{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\sin{(180^{o}-\theta)}=\sin{\theta}\)
\(\cos{(180^{o}-\theta)}=\cos{MOP^{\prime}}=\cos{P^{\prime}OM^{\prime}}\) ➜ \(\because \angle{MOP^{\prime}}=\text{সম্পূরক } \angle{P^{\prime}OM^{\prime}}\)

\(=\frac{-OM^{\prime}}{OP^{\prime}}\)
\(=\frac{-OM}{OP}\) ➜ \(\because OM^{\prime}=OM\)
এবং \(OP^{\prime}=OP\)

\(=-\frac{OM}{OP}\)
\(=-\cos{POM}\)
\(=-\cos{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\cos{(180^{o}-\theta)}=-\cos{\theta}\)
\(\tan{(180^{o}-\theta)}=\tan{MOP^{\prime}}=\tan{P^{\prime}OM^{\prime}}\) ➜ \(\because \angle{MOP^{\prime}}=\text{সম্পূরক } \angle{P^{\prime}OM^{\prime}}\)

\(=\frac{P^{\prime}M^{\prime}}{-OM^{\prime}}\)
\(=\frac{PM}{-OM}\) ➜ \(\because P^{\prime}M^{\prime}=PM\)
এবং \(OM^{\prime}=OM\)

\(=-\frac{PM}{OM}\)
\(=-\tan{POM}\)
\(=-\tan{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\tan{(180^{o}-\theta)}=-\tan{\theta}\)
অনুরূপভাবে প্রমাণ করা যায়,
\(cosec \ {(180^{o}-\theta)}=cosec \ {\theta}\) \(\sec{(180^{o}-\theta)}=-\sec {\theta}\) \(\cot{(180^{o}-\theta)}=-\cot{\theta}\)
\((180^{o}+\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of \((180^{o}+\theta)\) Angle
\(\sin{(180^{o}+\theta)}=-\sin{\theta}\)
\(\cos{(180^{o}+\theta)}=-\cos{\theta}\)
\(\tan{(180^{o}+\theta)}=\tan{\theta}\)
\(cosec \ {(180^{o}+\theta)}=-cosec \ {\theta}\)
\(\sec{(180^{o}+\theta)}=-\sec {\theta}\)
\(\cot{(180^{o}+\theta)}=\cot{\theta}\)

প্রমাণঃ
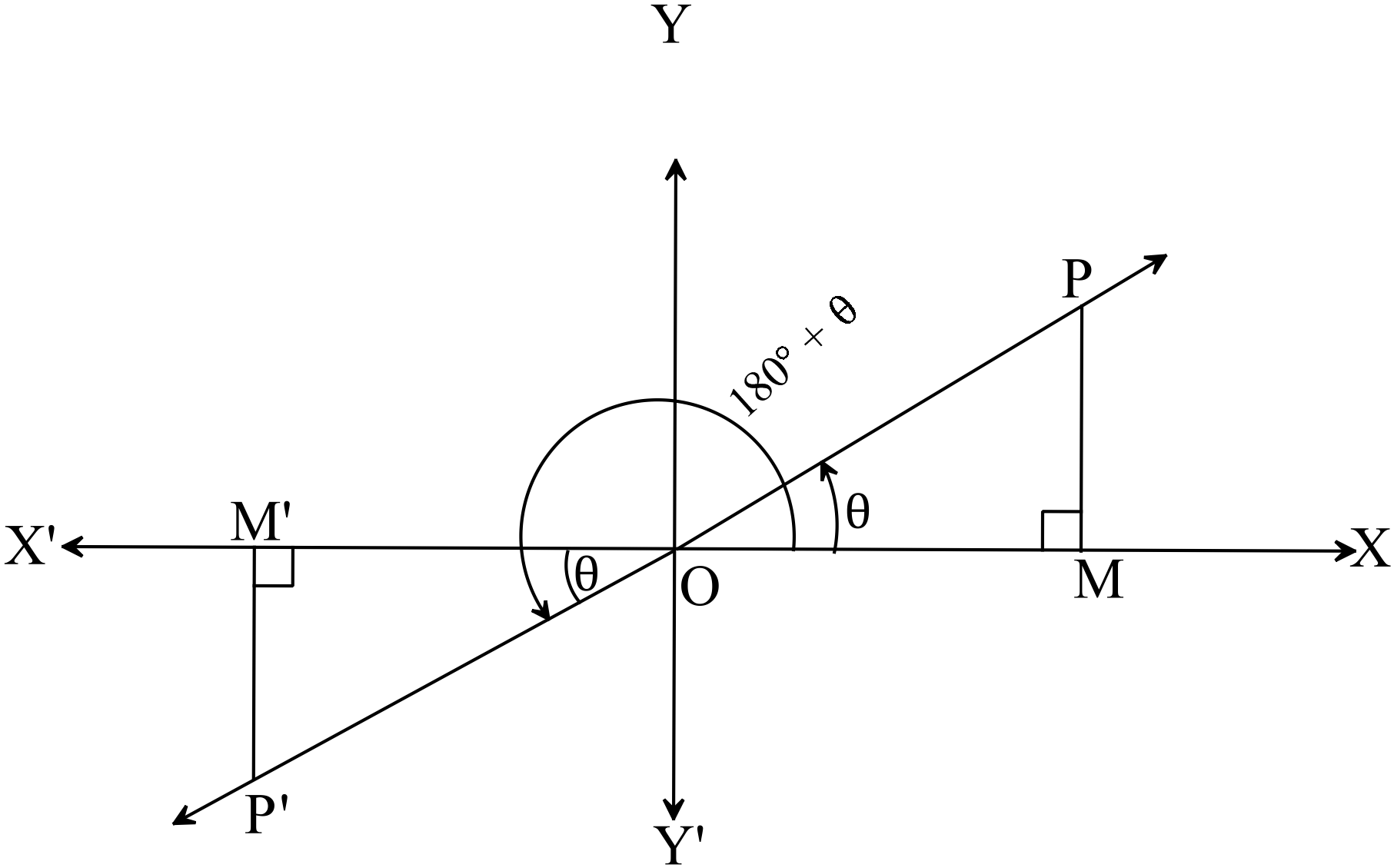
মনে করি, কোনো ঘূর্ণায়মান রশ্মি আদি অবস্থান \(OX\) হতে \(O\) বিন্দুর সাপেক্ষে ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিকে ঘুরে \(\angle{POM}=\theta, \ (\theta\lt90^{o})\) কোণ উৎপন্ন করে এবং আরও ঘুরে \(\angle{POP^{\prime}}=180^{o})\) কোণ উৎপন্ন করে।
সুতরাং \(\angle{MOP^{\prime}}=\angle{MOM^{\prime}}+\angle{M^{\prime}OP^{\prime}}=180^{o}+\theta\)
তাহলে, \(\angle{MOP}=\angle{M^{\prime}OP^{\prime}}=\theta\)
\(OP\) রেখার উপর \(P\) এবং \(OP^{\prime}\) এর উপর যে কোনো বিন্দু \(P^{\prime}\) নেয়া হলো যেন \(OP=OP^{\prime}\) হয়। \(P\) এবং \(P^{\prime}\) বিন্দু থেকে \(XOX^{\prime}\) রেখার উপর যথাক্রমে \(PM\) এবং \(P^{\prime}M^{\prime}\) লম্ব অঙ্কন করি।
এখন \(\triangle{OPM}\) ও \(\triangle{OP^{\prime}M^{\prime}}\) এ
\(\angle{MOP}=\angle{M^{\prime}OP^{\prime}}=\theta\)
\(\angle{OMP}=\angle{OM^{\prime}P^{\prime}}=90^{o}\)
straight3 এবং \(OP=OP^{\prime}\)
\(\therefore \triangle{OPM}\cong\triangle{OP^{\prime}M^{\prime}}\)
\(\therefore PM=P^{\prime}M^{\prime}\) যেখানে, \(P^{\prime}M^{\prime}\) ঋণাত্মক।
এবং \(OM=OM^{\prime}\) যেখানে, \(OM^{\prime}\) ঋণাত্মক।
এখন \(\sin{(180^{o}+\theta)}=\sin{MOP^{\prime}}=\sin{P^{\prime}OM^{\prime}}\) ➜ \(\because \angle{MOP^{\prime}}=\text{ঋণাত্মক সম্পূরক } \angle{P^{\prime}OM^{\prime}}\)

\(=\frac{-P^{\prime}M^{\prime}}{OP^{\prime}}\)
\(=\frac{-PM}{OP}\) ➜ \(\because P^{\prime}M^{\prime}=PM\)
এবং \(OP^{\prime}=OP\)

\(=-\frac{PM}{OP}\)
\(=-\sin{POM}\)
\(=-\sin{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\sin{(180^{o}+\theta)}=-\sin{\theta}\)
\(\cos{(180^{o}+\theta)}=\cos{MOP^{\prime}}=\cos{P^{\prime}OM^{\prime}}\) ➜ \(\because \angle{MOP^{\prime}}=\text{ঋণাত্মক সম্পূরক } \angle{P^{\prime}OM^{\prime}}\)

\(=\frac{-OM^{\prime}}{OP^{\prime}}\)
\(=\frac{-OM}{OP}\) ➜ \(\because OM^{\prime}=OM\)
এবং \(OP^{\prime}=OP\)

\(=-\frac{OM}{OP}\)
\(=-\cos{POM}\)
\(=-\cos{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\cos{(180^{o}+\theta)}=-\cos{\theta}\)
\(\tan{(180^{o}+\theta)}=\tan{MOP^{\prime}}=\tan{P^{\prime}OM^{\prime}}\) ➜ \(\because \angle{MOP^{\prime}}=\text{ঋণাত্মক সম্পূরক } \angle{P^{\prime}OM^{\prime}}\)

\(=\frac{-P^{\prime}M^{\prime}}{-OM^{\prime}}\)
\(=\frac{PM}{OM}\) ➜ \(\because P^{\prime}M^{\prime}=PM\)
এবং \(OM^{\prime}=OM\)

\(=-\tan{POM}\)
\(=-\tan{\theta}\) ➜ \(\because \angle{POM}=\theta\)

\(\tan{(180^{o}+\theta)}=-\tan{\theta}\)
অনুরূপভাবে প্রমাণ করা যায়,
\(cosec \ {(180^{o}+\theta)}=-cosec \ {\theta}\) \(\sec{(180^{o}+\theta)}=-\sec {\theta}\) \(\cot{(180^{o}+\theta)}=\cot{\theta}\)
\((270^{o}-\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of \((270^{o}-\theta)\) Angle
\(\sin{(270^{o}-\theta)}=-\cos{\theta}\)
\(\cos{(270^{o}-\theta)}=-\sin{\theta}\)
\(\tan{(270^{o}-\theta)}=\cot{\theta}\)
\(cosec \ {(270^{o}-\theta)}=-\sec{\theta}\)
\(\sec{(270^{o}-\theta)}=-cosec \ {\theta}\)
\(\cot{(270^{o}-\theta)}=\tan{\theta}\)

প্রমাণঃ
পূর্বের অভিজ্ঞতা ব্যবহার করে \((270^{o}-\theta)\) কোণের ত্রিকোণমিতিক অনুপাত প্রমাণ করা হলো।
\(\sin{(270^{o}-\theta)}=\sin{\{180^{o}+(90^{o}-\theta)\}}\)
\(=-\sin{(90^{o}-\theta)}\) ➜ \(\because \sin{(180^{o}+A)}=-\sin{A}\)

\(=-\cos{\theta}\) ➜ \(\because \sin{(90^{o}-A)}=\cos{A}\)

\(\sin{(270^{o}-\theta)}=-\cos{\theta}\)
\(\cos{(270^{o}-\theta)}=\cos{\{180^{o}+(90^{o}-\theta)\}}\)
\(=-\cos{(90^{o}-\theta)}\) ➜ \(\because \cos{(180^{o}+A)}=-\cos{A}\)

\(=-\sin{\theta}\) ➜ \(\because \cos{(90^{o}-A)}=\sin{A}\)

\(\cos{(270^{o}-\theta)}=-\sin{\theta}\)
\(\tan{(270^{o}-\theta)}=\tan{\{180^{o}+(90^{o}-\theta)\}}\)
\(=\tan{(90^{o}-\theta)}\) ➜ \(\because \tan{(180^{o}+A)}=\tan{A}\)

\(=\cot{\theta}\) ➜ \(\because \tan{(90^{o}-A)}=\cot{A}\)

\(\tan{(270^{o}-\theta)}=\cot{\theta}\)
অনুরূপভাবে প্রমাণ করা যায়,
\(cosec \ {(270^{o}-\theta)}=-\sec{\theta}\) \(\sec{(270^{o}-\theta)}=-cosec \ {\theta}\) \(\cot{(270^{o}-\theta)}=\tan{\theta}\)
\((270^{o}+\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of \((270^{o}+\theta)\) Angle
\(\sin{(270^{o}+\theta)}=-\cos{\theta}\)
\(\cos{(270^{o}+\theta)}=\sin{\theta}\)
\(\tan{(270^{o}+\theta)}=-\cot{\theta}\)
\(cosec \ {(270^{o}+\theta)}=-\sec{\theta}\)
\(\sec{(270^{o}+\theta)}=cosec \ {\theta}\)
\(\cot{(270^{o}+\theta)}=-\tan{\theta}\)

প্রমাণঃ
পূর্বের অভিজ্ঞতা ব্যবহার করে \((270^{o}+\theta)\) কোণের ত্রিকোণমিতিক অনুপাত প্রমাণ করা হলো।
\(\sin{(270^{o}+\theta)}=\sin{\{180^{o}+(90^{o}+\theta)\}}\)
\(=-\sin{(90^{o}+\theta)}\) ➜ \(\because \sin{(180^{o}+A)}=-\sin{A}\)

\(=-\cos{\theta}\) ➜ \(\because \sin{(90^{o}+A)}=\cos{A}\)

\(\sin{(270^{o}+\theta)}=-\cos{\theta}\)
\(\cos{(270^{o}+\theta)}=\cos{\{180^{o}+(90^{o}+\theta)\}}\)
\(=-\cos{(90^{o}+\theta)}\) ➜ \(\because \cos{(180^{o}+A)}=-\cos{A}\)

\(=-(-\sin{\theta})\) ➜ \(\because \cos{(90^{o}+A)}=-\sin{A}\)

\(=\sin{\theta}\)
\(\cos{(270^{o}+\theta)}=\sin{\theta}\)
\(\tan{(270^{o}+\theta)}=\tan{\{180^{o}+(90^{o}+\theta)\}}\)
\(=\tan{(90^{o}+\theta)}\) ➜ \(\because \tan{(180^{o}+A)}=\tan{A}\)

\(=-\cot{\theta}\) ➜ \(\because \tan{(90^{o}+A)}=-\cot{A}\)

\(\tan{(270^{o}+\theta)}=-\cot{\theta}\)
অনুরূপভাবে প্রমাণ করা যায়,
\(cosec \ {(270^{o}+\theta)}=-\sec{\theta}\) \(\sec{(270^{o}+\theta)}=cosec \ {\theta}\) \(\cot{(270^{o}+\theta)}=-\tan{\theta}\)
\((360^{o}-\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of \((360^{o}-\theta)\) Angle
\(\sin{(360^{o}-\theta)}=-\sin{\theta}\)
\(\cos{(360^{o}-\theta)}=\cos{\theta}\)
\(\tan{(360^{o}-\theta)}=-\tan{\theta}\)
\(cosec \ {(360^{o}-\theta)}=-cosec \ {\theta}\)
\(\sec{(360^{o}-\theta)}=\sec {\theta}\)
\(\cot{(360^{o}-\theta)}=-\cot{\theta}\)

প্রমাণঃ
পূর্বের অভিজ্ঞতা ব্যবহার করে \((360^{o}-\theta)\) কোণের ত্রিকোণমিতিক অনুপাত প্রমাণ করা হলো।
\(\sin{(360^{o}-\theta)}=\sin{\{270^{o}+(90^{o}-\theta)\}}\)
\(=-\cos{(90^{o}-\theta)}\) ➜ \(\because \sin{(270^{o}+A)}=-\cos{A}\)

\(=-\sin{\theta}\) ➜ \(\because \cos{(90^{o}-A)}=\sin{A}\)

\(\sin{(360^{o}-\theta)}=-\sin{\theta}\)
\(\cos{(360^{o}-\theta)}=\cos{\{270^{o}+(90^{o}-\theta)\}}\)
\(=\sin{(90^{o}-\theta)}\) ➜ \(\because \cos{(270^{o}+A)}=\sin{A}\)

\(=\cos{\theta}\) ➜ \(\because \sin{(90^{o}-A)}=\cos{A}\)

\(\cos{(360^{o}-\theta)}=\cos{\theta}\)
\(\tan{(360^{o}-\theta)}=\tan{\{270^{o}+(90^{o}-\theta)\}}\)
\(=-\cot{(90^{o}-\theta)}\) ➜ \(\because \tan{(270^{o}+A)}=-\cot{A}\)

\(=-\tan{\theta}\) ➜ \(\because \cot{(90^{o}-A)}=\tan{A}\)

\(\tan{(360^{o}-\theta)}=-\tan{\theta}\)
অনুরূপভাবে প্রমাণ করা যায়,
\(cosec \ {(360^{o}-\theta)}=-cosec \ {\theta}\) \(\sec{(360^{o}-\theta)}=\sec {\theta}\) \(\cot{(360^{o}-\theta)}=-\cot{\theta}\)
\((360^{o}+\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
Trigonometric Ratios of \((360^{o}+\theta)\) Angle
\(\sin{(360^{o}+\theta)}=\sin{\theta}\)
\(\cos{(360^{o}+\theta)}=\cos{\theta}\)
\(\tan{(360^{o}+\theta)}=\tan{\theta}\)
\(cosec \ {(360^{o}+\theta)}=cosec \ {\theta}\)
\(\sec{(360^{o}+\theta)}=\sec {\theta}\)
\(\cot{(360^{o}+\theta)}=\cot{\theta}\)

প্রমাণঃ
পূর্বের অভিজ্ঞতা ব্যবহার করে \((360^{o}-\theta)\) কোণের ত্রিকোণমিতিক অনুপাত প্রমাণ করা হলো।
\(\sin{(360^{o}+\theta)}=\sin{\{270^{o}+(90^{o}+\theta)\}}\)
\(=-\cos{(90^{o}+\theta)}\) ➜ \(\because \sin{(270^{o}+A)}=-\cos{A}\)

\(=-(-\sin{\theta})\) ➜ \(\because \cos{(90^{o}+A)}=-\sin{A}\)

\(=\sin{\theta}\)
\(\sin{(360^{o}+\theta)}=\sin{\theta}\)
\(\cos{(360^{o}+\theta)}=\cos{\{270^{o}+(90^{o}+\theta)\}}\)
\(=\sin{(90^{o}+\theta)}\) ➜ \(\because \cos{(270^{o}+A)}=\sin{A}\)

\(=\cos{\theta}\) ➜ \(\because \sin{(90^{o}+A)}=\cos{A}\)

\(\cos{(360^{o}+\theta)}=\cos{\theta}\)
\(\tan{(360^{o}+\theta)}=\tan{\{270^{o}+(90^{o}+\theta)\}}\)
\(=-\cot{(90^{o}+\theta)}\) ➜ \(\because \tan{(270^{o}+A)}=-\cot{A}\)

\(=-(-\tan{\theta})\) ➜ \(\because \cot{(90^{o}+A)}=-\tan{A}\)

\(=\tan{\theta}\)
\(\tan{(360^{o}+\theta)}=\tan{\theta}\)
অনুরূপভাবে প্রমাণ করা যায়,
\(cosec \ {(360^{o}+\theta)}=cosec \ {\theta}\) \(\sec{(360^{o}+\theta)}=\sec {\theta}\) \(\cot{(360^{o}+\theta)}=\cot{\theta}\)
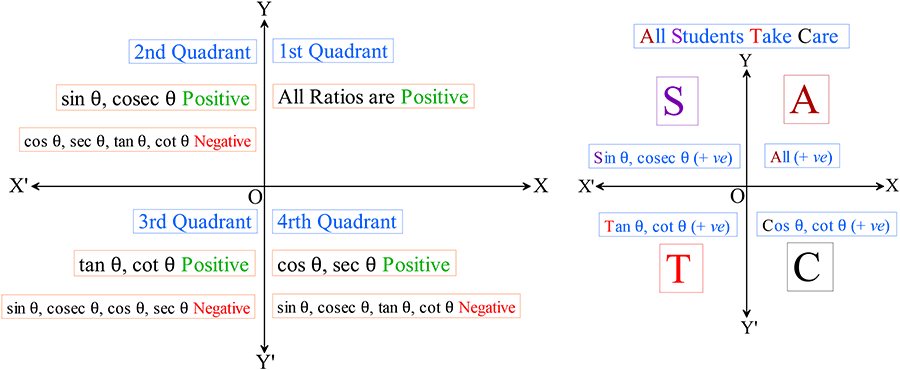
সংযুক্ত কোণের ত্রিকোণমিতিক অনুপাত নির্ণয়ের নিয়ম চিত্রের সাহায্যে প্রদর্শন
The rules for determining the trigonometric ratio of associated angles
straight3
\((90^{o}\times{n}\pm\theta)\) কোণের ত্রিকোণমিতিক অনুপাত নির্ণয়
Determining the trigonometric ratio of \((90^{o}\times{n}\pm\theta)\) angles
\((90^{o}\times{n}\pm\theta)\) কোণের ত্রিকোণমিতিক অনুপাত
\(\alpha\) কোণকে দুই ভাগে ভাগ করতে হবে যার একটি অংশ \(90^{o}\) এর \(n\) গুণিতক এবং অপরটি সূক্ষ্ণকোণ \((\theta)\) । অর্থাৎ \(\alpha\) কোণকে \((90^{o}\times{n}\pm\theta)\) আকারে প্রকাশ করতে হবে।
\((90^{o}\times{n}\pm\theta) \text{ যেখানে, } n\in{\mathbb{Z}}\)
\((90^{o}\times{n}\pm\theta) \text{ যেখানে, } n\in{\mathbb{Z}}\) কোণের ত্রিকোণমিতিক অনুপাত নির্ণয়ের ক্ষেত্রে নিম্নলিখিত পদক্ষেপগুলি অনুস্মরণ করতে হবে।
\((1)\) \(n\) জোড় সংখ্যা হলে,
অনুপাতের কোনো পরিবর্তন হবে না, অনুপাতের সামনের চিহ্ন চতুর্ভাগের অবস্থান দেখে বসাতে হবে।
\((2)\) \(n\) বিজোড় সংখ্যা হলে,
অনুপাতের পরিবর্তন হবে , অনুপাতের সামনের চিহ্ন চতুর্ভাগের অবস্থান দেখে বসাতে হবে।
অনুপাতের পরিবর্তনসমূহ নিম্নে দেখানো হলো।
\(\sin \rightleftharpoons \cos\)
\(cosec \rightleftharpoons \sec\)
\(\tan \rightleftharpoons \cot\)
উদাহরণসমুহ
মান নির্ণয় কর
\(Ex.1.(a)\) \(\sec{(-1050^{o})}\)
উত্তরঃ \(\frac{2}{\sqrt{3}}\)

মান নির্ণয় কর
\(Ex.1.(b)\) \(\cot{(765^{o})}\)
উত্তরঃ \(1\)

\(Ex.1.(c)\) \(cosec \ {(-1125^{o})}\)
উত্তরঃ \(-\sqrt{2}\)

\(Ex.1.(d)\) \(\tan{\left(\frac{5\pi}{2}-\frac{19\pi}{3}\right)}\)
উত্তরঃ \(\frac{1}{\sqrt{3}}\)

\(Ex.1.(e)\) \(cosec \ {\left\{\frac{n\pi}{2}+(-1)^{n}\frac{\pi}{6}\right\}}; \ n\in{\mathbb Z}\)
উত্তরঃ \(\pm2, \ \pm\frac{2}{\sqrt{3}}\)

\(Ex.1.(f)\) \(\sin{\left(-\frac{11\pi}{4}\right)}\)
উত্তরঃ \(-\frac{1}{\sqrt{2}}.\)

\(Ex.2.\) যদি \(\alpha=\frac{11\pi}{4}\) হয়, তবে \(\sin^2{\alpha}-\cos^2{\alpha}-2\tan{\alpha}-\sec^2{\alpha}\) এর মান নির্ণয় কর।
উত্তরঃ \(0\)

\(Ex.3.\) মান নির্ণয় করঃ \(\sin^2{\frac{\pi}{7}}+\sin^2{\frac{5\pi}{14}}+\sin^2{\frac{8\pi}{7}}+\sin^2{\frac{9\pi}{14}}\)
উত্তরঃ \(2\)
কুঃ ২০১৬; রাঃ ২০১৩; যঃ ২০১১; বঃ ২০১০; মাঃ ২০০৯,২০০১; সিঃ ২০০৯, ঢাঃ ২০০২; চঃ ২০০০ ।

\(Ex.4.\) \(A=\frac{\pi}{12}\) \(B=\frac{\cot{\theta}+cosec \ ({-\theta})}{\cos{\theta}+\sin{(-\theta)}}\)
\((a)\) মান নির্ণয় করঃ \(\sin{480^{o}}\cos{750^{o}}+\cos{(-660^{o})}\sin{(-870^{o})}\)
\((b)\) \(\cos^2{A}+\cos^2{3A}+\cos^2{5A}+\cos^2{7A}+\cos^2{9A}+\cos^2{11A}\) এর মান কত?
\((c)\) \(\tan{\theta}=\frac{4}{3}\) এবং \(\cos{\theta}\) ঋণাত্মক হলে, \(B\) এর মান কত?
উত্তরঃ \((a) \ \frac{1}{2},\) \((b) \ 3,\) \((c) \ 10.\)

\(Ex.5.\) মান নির্ণয় কর \(\cos^2{\frac{\pi}{7}}+\cos^2{\frac{5\pi}{14}}+\cos^2{\frac{8\pi}{7}}+\cos^2{\frac{9\pi}{14}}\)
উত্তরঃ \(\)
কুঃ ২০১৬; মাঃ ২০০৯; সিঃ ২০০৫ ।

\(Ex.6.\) মান নির্ণয় কর \(\cos{18^{o}}+\cos{162^{o}}+\cos{234^{o}}+\cos{1386^{o}}\)
উত্তরঃ \(0\)

\(Ex.7.\) মান নির্ণয় কর \(\cos^2{\frac{\pi}{12}}+\cos^2{\frac{3\pi}{12}}+\cos^2{\frac{5\pi}{12}}+\cos^2{\frac{7\pi}{12}}+\cos^2{\frac{9\pi}{12}}+\cos^2{\frac{11\pi}{12}}\)
উত্তরঃ \(3\)

\(Ex.8.\) যদি \(\sin{\theta}=\frac{5}{13}\) এবং \(\frac{\pi}{2}\lt \theta\lt \pi\) হয় তবে প্রমাণ কর যে, \(\frac{\tan{\theta}+\sec{(-\theta)}}{\cot{\theta}+cosec \ {(-\theta)}}=\frac{3}{10}\)

\(Ex.9.\) যোগফল নির্ণয় কর \(\cot{\theta}+\cot{(\pi+\theta)}+\cot{(2\pi+\theta)}+..........+\cot{(n\pi+\theta)}\)
উত্তরঃ \((n+1)\cot{\theta}\)

\(Ex.10.\) \(n\) পূর্ণ সংখ্যা হলে দেখাও যে,
\((a)\) \(\sin{\{(2n+1)\pi+\alpha\}}=-\sin{\alpha}\)
\((b)\) \(\tan{\{(2n+1)\pi+\alpha\}}+\tan{\{(2n+1)\pi-\alpha\}}=0\)

\(Ex.11.\) সমাধান করঃ
\(2(\sin{\theta}\cos{\theta}+\sqrt{3})=\sqrt{3}\cos{\theta}+4\sin{\theta},\) যখন \(0\lt \theta\lt 360^{o}\)
উত্তরঃ \(\theta=60^{o}; \ 120^{o}\)

Read Example
Q.1-এর সংক্ষিপ্ত প্রশ্নসমূহ
মান নির্ণয় কর
\(Q.1.(i).(a)\) \(\sin{(405^{o})}\)
উত্তরঃ \(\frac{1}{\sqrt{2}}\)

মান নির্ণয় কর
\(Q.1.(i).(b)\) \(\sin{(-750^{o})}\)
উত্তরঃ \(-\frac{1}{2}\)

\(Q.1.(i).(c)\) \(\cos{(570^{o})}\)
উত্তরঃ \(-\frac{\sqrt{3}}{2}\)

\(Q.1.(i).(d)\) \(\cos{(-570^{o})}\)
উত্তরঃ \(\frac{\sqrt{3}}{2}\)

\(Q.1.(i).(e)\) \(\sec{(510^{o})}\)
উত্তরঃ \(-\frac{2}{\sqrt{3}}\)

\(Q.1.(i).(f)\) \(\sec{(-2580^{o})}\)
উত্তরঃ \(2\)

\(Q.1.(i).(g)\) \(\cot{(-1500^{o})}\)
উত্তরঃ \(-\frac{1}{\sqrt{3}}\)

\(Q.1.(i).(h)\) \(\tan{(-1590^{o})}\)
উত্তরঃ \(\frac{1}{\sqrt{3}}\)

\(Q.1.(i).(i)\) \(\cot{\left(\frac{11\pi}{6}\right)}\)
উত্তরঃ \(-\sqrt{3}\)

\(Q.1.(i).(j)\) \(\sin{\left(-\frac{29\pi}{4}\right)}\)
উত্তরঃ \(\frac{1}{\sqrt{2}}\)

\(Q.1.(i).(k)\) \(\tan{\left(\frac{11\pi}{6}\right)}\)
উত্তরঃ \(-\frac{1}{\sqrt{3}}\)

\(Q.1.(i).(l)\) \(cosec \ {\left(\frac{16\pi}{3}\right)}\)
উত্তরঃ \(-\frac{2}{\sqrt{3}}\)

\(Q.1.(i).(m)\) \(\cot{(765^{o})}\)
উত্তরঃ \(1\)
চুয়েটঃ ২০০৫-২০০৬ ।

\(Q.1.(i).(n)\) \(\sin{(210^{o})}+\cot{225^{o}}\)
উত্তরঃ \(\frac{1}{2}\)
বুটেক্সঃ ২০১০-২০১১ ।

\(Q.1.(i).(o)\) \(\sec{(3630^{o})}\)
উত্তরঃ \(\frac{2}{\sqrt{3}}\)

\(Q.1.(i).(p)\) \(\cot{(-1575^{o})}\)
উত্তরঃ \(1\)

\(Q.1.(i).(q)\) \(\cos{\left(\frac{5\pi}{2}-\frac{19\pi}{3}\right)}\)
উত্তরঃ \(\frac{\sqrt{3}}{2}\)

\(Q.1.(i).(r)\) \(\sin{(675^{o})}\)
উত্তরঃ \(-\frac{1}{\sqrt{2}}\)

\(Q.1.(i).(s)\) \(\tan{(1305^{o})}\)
উত্তরঃ \(1\)

\(Q.1.(i).(t)\) \(cosec \ {(765^{o})}\)
উত্তরঃ \(\sqrt{2}\)

\(Q.1.(i).(u)\) \(\cot{(3750^{o})}\)
উত্তরঃ \(-\sqrt{3}\)

\(Q.1.(i).(v)\) \(\sin{(1395^{o})}\)
উত্তরঃ \(\frac{1}{\sqrt{2}}\)

\(Q.1.(i).(w)\) \(\cot{(-1530^{o})}\)
উত্তরঃ \(0\)

\(Q.1.(i).(x)\) \(\cot{\left(\frac{3\pi}{2}+\frac{\pi}{3}\right)}\)
উত্তরঃ \(-\sqrt{3}\)

\(Q.1.(i).(y)\) \(\cos{\left(\frac{49\pi}{6}\right)}\)
উত্তরঃ \(\frac{\sqrt{3}}{2}\)

\(Q.1.(i).(z)\) \(\tan{(-1230^{o})}\)
উত্তরঃ \(\frac{1}{\sqrt{3}}\)

\(n\) যে কোনো পূর্ণ সংখ্যা হলে, মান নির্ণয় কর
\(Q.1.(ii).(a)\) \(\sin{\left\{n\pi+(-1)^n\frac{\pi}{4}\right\}}\)
উত্তরঃ \(\frac{1}{\sqrt{2}}\)

\(n\) যে কোনো পূর্ণ সংখ্যা হলে, মান নির্ণয় কর
\(Q.1.(ii).(b)\) \(\cos{\left\{(2n+1)\pi+\frac{\pi}{3}\right\}}\)
উত্তরঃ \(-\frac{1}{2}\)

\(Q.1.(ii).(c)\) \(\sin{\left\{n\pi+(-1)^n\frac{\pi}{6}\right\}}\)
উত্তরঃ \(\frac{1}{2}\)

\(Q.1.(ii).(d)\) \(\cos{\left\{2n\pi\pm\frac{\pi}{4}\right\}}\)
উত্তরঃ \(\frac{1}{\sqrt{2}}\)

\(Q.1.(ii).(e)\) \(\sin{\left\{n\pi+(-1)^n\frac{\pi}{3}\right\}}\)
উত্তরঃ \(\frac{\sqrt{3}}{2}\)

\(Q.1.(ii).(f)\) \(\sin{(-1230^{o})}-\cos{\left\{(2n+1)\pi+\frac{\pi}{3}\right\}}; \ n\in{\mathbb{Z}}\)
উত্তরঃ \(0\)

\(Q.1.(ii).(g)\) \(\tan{\left\{\frac{n\pi}{2}+(-1)^{n}\frac{\pi}{4}\right\}}\)
উত্তরঃ \(1\)

মান নির্ণয় কর
\(Q.1.(iii).(a)\) \(\cos{558^{o}}+\sin{792^{o}}+\tan{168^{o}}+\tan{12^{o}}\)
উত্তরঃ \(0\)

মান নির্ণয় কর
\(Q.1.(iii).(b)\) \(\tan{18^{o}}+\cos{102^{o}}+\tan{162^{o}}+\cos{438^{o}}\)
উত্তরঃ \(0\)
সিঃ ২০০৬ ।

\(Q.1.(iii).(c)\) \(\sin{780^{o}}\cos{390^{o}}+\sin{(-300^{o})}\cos{(-300^{o})}\)
উত্তরঃ \(1\)
চঃ ২০০১ ।

\(Q.1.(iii).(d)\) \(\frac{\cos{(540^{o}-A)}\sin{(1080^{o}-A)}\cot{(105^{o}+A)}}{\tan{(195^{o}+A)}\cos{(-A)}\tan{(630^{o}-A)}}\)
উত্তরঃ \(-\sin{A}\tan{A}\)

\(Q.1.(iii).(e)\) \(\frac{\sin^3{(\pi+\theta)}\tan{(2\pi-\theta)}\sec^2{(\pi-\theta)}}{\cos^2{\left(\frac{1}{2}\pi-\theta\right)} \ cosec^2{\theta}\sin{(\pi-\theta)}}\)
উত্তরঃ \(\tan^3{\theta}\)

\(Q.1.(iii).(f)\) \(\tan{\frac{17\pi}{4}}\cos{\left(-\frac{11\pi}{4}\right)}+\sec{\left(-\frac{34\pi}{3}\right)} \ cosec \ {\left(\frac{25\pi}{6}\right)}\)
উত্তরঃ \(-\left(4+\frac{1}{\sqrt{2}}\right)\)

\(Q.1.(iii).(g)\) \(\cos{198^{o}}+\sin{432^{o}}+\tan{168^{o}}+\tan{12^{o}}\)
উত্তরঃ \(0\)

\(Q.1.(iii).(h)\) \(\cos{420^{o}}\sin{(-300^{o})}-\sin{870^{o}}\cos{570^{o}}\)
উত্তরঃ \(\frac{\sqrt{3}}{2}\)

\(Q.1.(iii).(i)\) \(\sin{480^{o}}\cos{(750^{o})}+\cos{(-660^{o})}\sin{(-870^{o})}\)
উত্তরঃ \(\frac{1}{2}\)

\(Q.1.(iii).(j)\) \(\frac{\cos{(360^{o}-\theta)}\tan{(180^{o}-\theta)}\sec{(90^{o}-\theta)}}{cosec \ {(360^{o}+\theta)}\cot{(270^{o}+\theta)}\cos{(180^{o}+\theta)}}\)
উত্তরঃ \(1\)

Read Short Question
Q.2-এর বর্ণনামূলক প্রশ্নসমূহ
\(Q.2.(i)\) \(\tan{x}=\frac{3}{4}, \ \cos{x}\) ধনাত্মক হলে, \(\sin{x}\) এর মান নির্ণয় কর।
উত্তরঃ \(\frac{3}{5}\)
রাঃ ২০১৯ ।

\(Q.2.(ii)\) \(\sec{x}=-2\) এবং \(\pi\lt x\lt\frac{3\pi}{2}\) হলে প্রমাণ কর যে, \(\cos{x}+\tan{x}=\frac{2\sqrt{3}-1}{2}.\)
চঃ ২০১৯ ।

\(Q.2.(iii)\) \(\tan{\theta}=\frac{5}{12}, \ \pi\lt \theta\lt\frac{3\pi}{2}\) হলে, \(\sin{(-\theta)}+\cos{\theta}\) এর মান নির্ণয় কর।
উত্তরঃ \(-\frac{7}{13}\)
যঃ ২০১৯ ।

\(Q.2.(iv)\) \(\cos{\theta}=\frac{1}{2}\) এবং \(180^{o}\lt \theta\lt 360^{o}\) হলে, \(\theta=\) কত?
উত্তরঃ \(300^{o}\)

\(Q.2.(v)\) \(\tan{\theta}=\frac{3}{4}\) এবং \(180^{o}\lt \theta\lt 270^{o}\) হলে, \(\sin{\theta}\) এর মান কত?
উত্তরঃ \(-\frac{3}{5}\)

\(Q.2.(vi)\) যদি \(\frac{\pi}{2}\lt \alpha\lt \pi\) এবং \(\sin{\alpha}=\frac{4}{5}\) হয়, তবে \(\tan{\alpha}\) এর মান নির্ণয় কর।
উত্তরঃ \(-\frac{4}{3}\)
কুঃ ২০১৬ ।

\(Q.2.(vii)\) যদি \(x=r\sin{(\theta+45^{o})}\) এবং \(y=r\sin{(\theta-45^{o})}\) হয়, তবে প্রমাণ কর যে, \(x^2+y^2=r^2\)

\(Q.2.(viii)\) যদি \(ABCD\) চতুর্ভুজের কোণগুলি যথাক্রমে \(A, \ B, \ C, \ D \) হয়, তবে দেখাও যে,
\((a)\) \(\cos{\frac{1}{2}(A+C)}+\cos{\frac{1}{2}(B+D)}=0\)
\((b)\) \(\sin{(A+B+C)}+\sin{(A+B+C+2D)}=0\)

\(Q.2.(ix)\) যদি \(\sin{\theta}=\frac{5}{13}\) এবং \(\frac{\pi}{2}\lt \theta\lt \pi\) হয়, তবে \(\frac{\tan{\theta}+\sec{(-\theta)}}{\cot{\theta}+cosec \ {(-\theta)}}\) এর মান নির্ণয় কর।
উত্তরঃ \(\frac{3}{10}\)
দিঃ ২০১৪; যঃ২০১২; চঃ ২০০৯ ।

\(Q.2.(x)\) \(\tan{\theta}=\frac{5}{12}\) এবং \(\sin{\theta}\) ঋণাত্মক হলে, প্রমাণ কর যে, \(\frac{\sin{\theta}+\cos{(-\theta)}}{\sec{(-\theta)}+\tan{\theta}}=\frac{51}{26}\)
ঢাঃ ২০০৫; বঃ ২০০৫, ২০০০ ।

\(Q.2.(xi)\) যদি \(\tan{\theta}=\frac{5}{12}\) এবং \(\cos{\theta}\) ধণাত্মক হয়, তবে \(\frac{\sin{\theta}+\cos{(-\theta)}}{\sec{(-\theta)}+\tan{\theta}}\) এর মান নির্ণয় কর।
উত্তরঃ \(\frac{34}{39}\)
বুয়েটঃ ২০১১-২০১২ ।

\(Q.2.(xii)\) যদি \(n\) এর মান যে কোনো পূর্ণ সংখ্যা হয়, তবে দেখাও যে, \(\cos{\left(2n\pi+\frac{\pi}{4}\right)}\) এর মান সব সময় \(\frac{1}{\sqrt{2}}\)

\(Q.2.(xiii)\) \(\tan{\theta}=\frac{b}{a}\) হলে, \(\frac{a\cos{\theta}+b\sin{\theta}}{a\cos{\theta}-b\sin{\theta}}\) এর মান নির্ণয় কর।
উত্তরঃ \(\frac{a^2-b^2}{a^2+b^2}\)

\(Q.2.(xiv)\) দেখাও যে, \(\cos{A}+\sin{\left(\frac{23\pi}{2}+A\right)}-\sin{\left(\frac{23\pi}{2}-A\right)}+\cos{(17\pi+A)}=0\)

\(Q.2.(xv)\) যদি \(\sin{\theta}=\frac{12}{13}\) এবং \(90^{o}\lt \theta\lt 180^{o}\) হয়, তবে দেখাও যে, \(\frac{\tan{\theta}+\sec{(-\theta)}}{\cot{\theta}+cosec \ {(-\theta)}}=\frac{10}{3}\)

\(Q.2.(xvi)\) যদি \(\cot{\theta}=\frac{3}{4}\) এবং \(\cos{\theta}\) ঋণাত্মক হয়, তবে দেখাও যে, \(\frac{\cot{(-\theta)}+cosec \ {\theta}}{\cos{\theta}+\sin{(-\theta)}}=-10\)

\(Q.2.(xvii)\) \(n\) পূর্ণ সংখ্যা হলে দেখাও যে,
\((a)\) \(\sin{(n\pi+\alpha)}=(-1)^n\sin{\alpha}\)
\((b)\) \(\cos{(n\pi+\alpha)}=(-1)^n\cos{\alpha}\)

\(Q.2.(xviii)\) দেখাও যে,
\((a)\) \(\sin{\left(\frac{\pi}{2}+\theta\right)}\cot{\left(\frac{3\pi}{2}+\theta\right)}\cos{(\pi-\theta)}=\)\(\sin{\left(\frac{\pi}{2}-\theta\right)}\sin{\left(\frac{3\pi}{2}-\theta\right)}\cot{\left(\frac{\pi}{2}+\theta\right)}\)
\((b)\) \(\sin{\left(\frac{5\pi}{2}+\theta\right)}\cos{(3\pi-\theta)}\cot{\left(\frac{7\pi}{2}+\theta\right)}=\)\(\sin{\left(\frac{\pi}{2}-\theta\right)}\sin{\left(\frac{3\pi}{2}-\theta\right)}\cot{\left(\frac{5\pi}{2}+\theta\right)}\)

Read Board Question2
Q.3-এর বর্ণনামূলক প্রশ্নসমূহ
মান নির্ণয় কর
\(Q.3.(i)\) \(\sin^2{\frac{17\pi}{18}}+\sin^2{\frac{5\pi}{8}}+\cos^2{\frac{37\pi}{18}}+\cos^2{\frac{3\pi}{8}}\)
উত্তরঃ \(2\)

মান নির্ণয় কর
\(Q.3.(ii)\) \(\cos^2{\frac{\pi}{8}}+\cos^2{\frac{3\pi}{8}}+\cos^2{\frac{5\pi}{8}}+\cos^2{\frac{7\pi}{8}}\)
উত্তরঃ \(2\)
ঢাঃ ২০১৩, ২০০০; সিঃ,চঃ ২০০২; যঃ ২০০০; মাঃ ২০০৫

\(Q.3.(iii)\) \(\sec^2{\frac{14\pi}{17}}-\sec^2{\frac{39\pi}{17}}+\cot^2{\frac{41\pi}{34}}-\cot^2{\frac{23\pi}{34}}\)
উত্তরঃ \(0\)
সিঃ, যঃ ২০০৬ ।

\(Q.3.(iv)\) \(\cot{\frac{\pi}{20}}\cot{\frac{3\pi}{20}}\cot{\frac{5\pi}{20}}\cot{\frac{7\pi}{20}}\cot{\frac{9\pi}{20}}\)
উত্তরঃ \(1\)
ঢাঃ, বঃ ২০০৩

\(Q.3.(v)\) সমকোণী \(\triangle{ABC}\) এ \(\angle{B}=90^{o}\) হলে প্রমাণ কর যে, \(\sin^2{A}-\sin^2{B}+\sin^2{C}=0\)
রাঃ ২০১৯

\(Q.3.(vi)\) \(\tan{\frac{\pi}{12}}\tan{\frac{5\pi}{12}}\tan{\frac{7\pi}{12}}\tan{\frac{11\pi}{12}}\)
উত্তরঃ \(1\)

\(Q.3.(vii)\) \(\sin^2{\frac{\pi}{4}}+\sin^2{\frac{3\pi}{4}}+\sin^2{\frac{5\pi}{4}}+\sin^2{\frac{7\pi}{4}}\)
উত্তরঃ \(2\)

\(Q.3.(viii)\) \(\cos^2{\frac{\pi}{24}}+\cos^2{\frac{19\pi}{24}}+\cos^2{\frac{31\pi}{24}}+\cos^2{\frac{37\pi}{24}}\)
উত্তরঃ \(2\)

\(Q.3.(ix)\) \(\sin^2{\frac{\pi}{12}}+\sin^2{\frac{3\pi}{12}}+\sin^2{\frac{5\pi}{12}}+\sin^2{\frac{7\pi}{12}}+\) \(\sin^2{\frac{9\pi}{12}}+\sin^2{\frac{11\pi}{12}}\)
উত্তরঃ \(3\)

\(Q.3.(x)\) \(\cos^2{25^{o}}+\cos^2{35^{o}}+\cos^2{45^{o}}+\cos^2{55^{o}}+\cos^2{65^{o}}\)
উত্তরঃ \(\frac{5}{2}\)

\(Q.3.(xi)\) প্রমান কর যে, \(\tan{\frac{\pi}{12}}\tan{\frac{5\pi}{12}}\tan{\frac{7\pi}{12}}\tan{\frac{11\pi}{12}}=1\)

Read Board Question3
Q.4-এর বর্ণনামূলক প্রশ্নসমূহ
মান নির্ণয় কর
\(Q.4.(i)\) \(\sin^2{10^{o}}+\sin^2{20^{o}}+\sin^2{30^{o}}+..........+\sin^2{80^{o}}\)
উত্তরঃ \(4\)

মান নির্ণয় কর।
\(Q.4.(ii)\) \(\cos^2{15^{o}}+\cos^2{25^{o}}+\cos^2{35^{o}}+.....\)\(+\cos^2{75^{o}}\)
উত্তরঃ \(\frac{7}{2}\)

\(Q.4.(iii)\) যদি \(\theta=\frac{\pi}{36}\) হয়, তবে \(\sin^2{3\theta}+\sin^2{4\theta}+\sin^2{5\theta}+........+\sin^2{15\theta}\) এর মান নির্ণয় কর।
উত্তরঃ \(\frac{13}{2}\)
বুয়েটঃ ২০১৩-২০১৪ ।

\(Q.4.(iv)\) \(\theta=\frac{\pi}{20}\) হলে দেখাও যে, \(\cot{\theta}\cot{3\theta}\cot{5\theta}........\cot{19\theta}=-1\)
বুয়েটঃ ২০১১-২০১২ ।

\(Q.4.(v)\) \(\theta=\frac{\pi}{28}\) হলে দেখাও যে, \(\tan{\theta}\tan{3\theta}\tan{5\theta}........\cot{13\theta}=1\)

\(Q.4.(vi)\) \(\cos{x}+\cos{(\pi+x)}+\cos{(2\pi+x)}+....\)\(+\cos{(n\pi+x)}\)
উত্তরঃ \(\cos{x}\) বা \(0\) যখন \(n\) যথাক্রমে জোড় ও বিজোড় সংখ্যা।

\(Q.4.(vii)\) \(\sin{\theta}+\sin{(\pi+\theta)}+\sin{(2\pi+\theta)}+....\)\(+\sin{(n\pi+\theta)}\)
উত্তরঃ \(\sin{\theta}\) বা \(0\) যখন \(n\) যথাক্রমে জোড় ও বিজোড় সংখ্যা।

\(Q.4.(viii)\) \(\tan{\theta}+\tan{(\pi+\theta)}+\tan{(2\pi+\theta)}+....\)\(+\tan{(n\pi+\theta)}\)
উত্তরঃ \((n+1)\tan{\theta}\)

দেখাও যে,
\(Q.4.(ix)\) \(\sin^2{15^{o}}+\sin^2{20^{o}}+\sin^2{25^{o}}+....+\sin^2{75^{o}}=\frac{13}{2}\)

দেখাও যে,
\(Q.4.(x)\) \(\cos^2{3^{o}}+\cos^2{9^{o}}+\cos^2{15^{o}}+....+\cos^2{177^{o}}=15\)

\(Q.4.(xi)\) \(\cos^2{10^{o}}+\cos^2{20^{o}}+\cos^2{30^{o}}+....+\cos^2{80^{o}}=4\)

\(Q.4.(xii)\) \(\tan{\frac{\pi}{28}}\tan{\frac{3\pi}{28}}\tan{\frac{5\pi}{28}}....\tan{\frac{13\pi}{28}}=1\)

\(Q.4.(xiii)\) \(\tan{15^{o}}+\tan{45^{o}}+\tan{75^{o}}+....+\tan{165^{o}}=0\)

\(Q.4.(xiv)\) \(\cos{\left(\frac{\pi}{11}\right)}\cos{\left(\frac{2\pi}{11}\right)}\cos{\left(\frac{3\pi}{11}\right)}....\cos{\left(\frac{10\pi}{11}\right)}=-2^{n}\) হলে \(n\) এর মান নির্ণয় কর।
উত্তরঃ \(n=-10\)

\(Q.4.(xv)\) \(\theta\) কোণের মান \(180^{o}\) এবং \(270^{o}\) এর মধ্যবর্তী এবং \(cosec \ {\theta}=-\frac{7}{3}\) হলে, \(\cot{\theta}\) এর মান নির্ণয় কর।
উত্তরঃ \(\frac{\sqrt{40}}{3}\)

Read Board Question4
Q.5-এর সৃজনশীল প্রশ্নসমূহ
Read Creative Question
ভর্তি পরীক্ষায় আসা প্রশ্নসমূহ
Read Admission Question

Read More

Post List

Mathematics

Geometry 11 and 12 standard
Algebra 11 and 12 standard
Trigonometry 11 and 12 standard
Diff. Calculus 11 and 12 standard
Int. Calculus 11 and 12 standard
Geometry Honours course standard
Vector 11 and 12 standard
Vector Honours course standard
Algebra 9 and 10 standard
    Coming Soon !

Chemistry

Physical chemistry 11 and 12 standard

Post List

Multiple Choise

Ctagory

Copyright © Mathgr All Right Reserved. 2024