এ অধ্যায়ের পাঠ্যসূচী।
- ঐতিহাসিক পটভূমি
- সার সংক্ষেপ
- ম্যাট্রিক্স (Matrix)
- ম্যাট্রিক্সের সারি ও কলাম (Row and Column of Matrix)
- ম্যাট্রিক্সের ক্রম (Order of Matrix)
- ম্যাটিক্সের সাধারণ আকার (General shape of matrices)
- ম্যাটিক্সের প্রকারভেদ (Types of Matics)
- সারি ম্যাট্রিক্স (Row Matrix)
- কলাম ম্যাট্রিক্স (Column Matrix)
- বর্গ ম্যাট্রিক্স (Square Matrix)
- ম্যাট্রিক্সের প্রধান কর্ণ (Principal or main diagonal)
- উর্ধ ত্রিভুজাকার ম্যাট্রিক্স (Upper Triangular Matrix)
- নিম্ন ত্রিভুজাকার ম্যাট্রিক্স (Lower Triangular Matrix)
- কর্ণ ম্যাট্রিক্স (Diagonal Matrix)
- স্কেলার ম্যাট্রিক্স (Scalar Matrix)
- একক বা অভেদক ম্যাট্রিক্স (Unit or Identity Matrix)
- শুন্য ম্যাট্রিক্স (Zero or Null Matrix)
- সমঘাতি ম্যাট্রিক্স (Idempotent Matrix)
- শুন্যঘাতি ম্যাট্রিক্স (Nilpotent Matrix)
- অভেদঘাতি ম্যাট্রিক্স (Involutory Matrix)
- বিম্ব ম্যাট্রিক্স (Transpose of a Matrix)
- প্রতিসম ম্যাট্রিক্স (Symmetric Matrix)
- বিপ্রতিসম ম্যাট্রিক্স ( Skew Symmetric Matrix)
- উপ-ম্যাট্রিক্স ( Sub Matrix)
- উল্লম্ব ম্যাট্রিক্স ( Orthogonal Matrix)
- ম্যাট্রিক্সের ট্রেস ( Trace of Matrix)
- পর্যায়বৃত্ত ম্যাট্রিক্স ( Periodic Matrix)
- অনুবন্ধী ম্যাট্রিক্স ( Conjugate Matrix)
- হারমিসিয়ান ম্যাট্রিক্স ( Hermitian Matrix)
- বিহারমিসিয়ান ম্যাট্রিক্স (Skew Hermitian Matrix)
- ম্যাটিক্সের সমতা, যোগ, বিয়োগ ও গুণ
- ম্যাট্রিক্সের সমতা (Equality of Matrices)
- ম্যাট্রিক্সের যোগ ও বিয়োগ (Addition and Subtraction of Matrices)
- ম্যাট্রিক্সের স্কেলার গুণন (Scalar Multiplication of a Matrix)
- ম্যাট্রিক্সের গুণন (Multiplication of Matrices)
- ম্যাট্রিক্সের গুণন যোগ্যতা (Competence of multiplication of matrix)
- অধ্যায় \(1A\)-এর উদাহরণসমুহ
- অধ্যায় \(1A\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(1A\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(1A\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(1A\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
ঐতিহাসিক পটভূমি
Historical Background

আর্থার ক্যালি (১৮২১ খ্রিষ্টাব্দ-১৮৯৫ খ্রিষ্টাব্দ)
ম্যাট্রিক্স ও নির্ণায়কের সূচনা হয় খ্রিস্টপূর্ব দ্বিতীয় শতকের পূর্বে। প্রাচীন ব্যাবিলন ও চীন থেকেই ম্যাট্রিক্স সম্পর্কিত ধারনা পাওয়া যায়। ইংরেজ গণিতবিদ জেমস জোসেফ সিলভেস্টার  সিলভেস্টার (১৮১৪ খ্রিষ্টাব্দ-১৮৯৭ খ্রিষ্টাব্দ)
সিলভেস্টার (১৮১৪ খ্রিষ্টাব্দ-১৮৯৭ খ্রিষ্টাব্দ)
ইংরেজ গণিতবিদ জেমস জোসেফ সিলভেস্টার (১৮১৪ খ্রিষ্টাব্দ-১৮৯৭ খ্রিষ্টাব্দ) ১৮৫০ খ্রিস্টাব্দে সর্বপ্রথম ম্যাট্রিক্স সম্পর্কে ধারনা ব্যাক্ত করেন। ১৮৫০ খ্রিস্টাব্দে সর্বপ্রথম ম্যাট্রিক্স সম্পর্কে ধারনা ব্যাক্ত করেন। তারই সহকারী আর্থার ক্যালি (Arthur Cayley) বিপরীত ম্যাট্রিক্সের ধারনাসহ ম্যাট্রিক্সের তাৎপর্য তুলে ধরেন। এটি তিনি ১৮৫৩ খ্রিস্টাব্দে প্রকাশ করেন। পরবর্তিতে তিনি ১৮৫৮ খ্রিস্টাব্দে তাঁর পত্রিকা 'A memoir on the theory of matrices' এ প্রথমে বিশ্লেষণমূলকভাবে ম্যাট্রিক্সকে প্রকাশ করেন। এ কারনে আর্থার ক্যালিকে 'ম্যাট্রিক্স' এর জনক বলা হয়। বিখ্যাত পদার্থবিজ্ঞানী হেইজেনবার্গ হেইজেনবার্গ (১৯০১ খ্রিষ্টাব্দ-১৯৭৬ খ্রিষ্টাব্দ)
হেইজেনবার্গ (১৯০১ খ্রিষ্টাব্দ-১৯৭৬ খ্রিষ্টাব্দ)
ভার্নার কার্ল হেইজেনবার্গ ছিলেন জার্মান গবেষণা কাউন্সিলের সভাপতি, পারমাণবিক পদার্থবিজ্ঞান কমিশনের চেয়ারম্যান, পারমাণবিক পদার্থবিজ্ঞান ওয়ার্কিং গ্রুপের চেয়ারম্যান এবং আলেকজান্ডার ভন হাম্বোল্ট ফাউন্ডেশনের সভাপতি। ১৯২৫ খ্রিস্টাব্দে কোয়ান্টাম বলবিদ্যায় প্রথম ম্যাট্রিক্সের ব্যবহার শুরু করেন। গণিতে সমীকরণ জোটের সমাধান, পরিসংখ্যানের সম্ভাবনা তত্ত্বে, উচ্চতর অর্থনীতিতে, ব্যবসায় গণিতে আয়-ব্যয় হিসাব ইত্যাদিতে ম্যাট্রিক্স বহুলভাবে ব্যবহৃত হয়। শেয়ারের ক্রয়-বিক্রয় হিসাব, কোন প্রকার ট্রেজারি বন্ডে কী পরিমান অর্থ বিনিয়োগ করতে হবে তা বিপরীত ম্যাট্রিক্সের সাহায্যে সহজে নির্ণয় করা যায়।
১৬৮৩ খ্রিস্টাব্দে প্রথম জাপানি গনিতবিদ সেকি তাকাকাজু (Seki Takakazu) সেকি (১৬৪২ খ্রিষ্টাব্দ-১৭০৮ খ্রিষ্টাব্দ)
সেকি (১৬৪২ খ্রিষ্টাব্দ-১৭০৮ খ্রিষ্টাব্দ)
সেকি তাকাকাজু একটি নতুন বীজগণিত স্বরলিপি ব্যবস্থা তৈরি করেছিলেন এবং জ্যোতির্বিদ্যার গণনা দ্বারা অনুপ্রাণিত হয়ে ইনফিনাইটিমাল ক্যালকুলাস এবং ডায়োফ্যান্টাইন সমীকরণ নিয়ে কাজ করেছিলেন। তিনি জার্মান পলিম্যাথ গণিতবিদ এবং দার্শনিক গটফ্রিড লাইবনিজ এবং ব্রিটিশ গণিতবিদ আইজাক নিউটনের সমসাময়িক হলেও সেকির কাজটি স্বাধীন ছিল। তার উত্তরসূরীরা পরবর্তীতে এডো পিরিয়ডের শেষ অবধি জাপানি গণিতে বিদ্যালয়ের প্রভাবশালী হয়ে ওঠে। নির্ণায়ক বিষয়ক প্রাথমিক ধারনা প্রকাশ করেন। তিনি \(2\times2, \ 3\times3, \ 4\times4\) এবং \(5\times5\) ম্যাট্রিক্সের নির্ণায়ক নিরূপন করেন এবং সমীকরণের সমাধান নির্ণয়ে নির্ণায়কের ব্যবহার প্রসঙ্গে ধারনা দেন। একই বছরে জার্মান গণিতবিদ লিবনিজ অনুরূপ ধারনা ও প্রয়োজনিয়তা উল্লেখ করেন।
১৯৫০ সালে সুইস গণিতবিদ গ্যাব্রিয়েল ক্রেমার (Gabriel Cramer) ক্রেমার (১৭০৪ খ্রিষ্টাব্দ-১৭৫২ খ্রিষ্টাব্দ)
ক্রেমার (১৭০৪ খ্রিষ্টাব্দ-১৭৫২ খ্রিষ্টাব্দ)
গ্যাব্রিয়েল ক্রেমার ছিলেন জেনেভান গণিতবিদ। তিনি চিকিত্সক জিন ক্র্যামার এবং অ্যান মাললেট ক্র্যামারের পুত্র ছিলেন। নির্ণায়কের সাহায্যে একঘাতিক সমীকরণ জোটের সমাধান করেন। স্থানাংক জ্যামিতিতে বহুভুজের ক্ষেত্রফল নির্ণয়, একঘাত সমীকরণ জোটের সমাধান ও ভেক্টর জ্যামিতিতে নির্ণায়ক ব্যবহৃত হয়।
বিভিন্ন ধরনের তথ্য সংগ্রহ ও সংরক্ষণের জন্য আমরা সর্বদা বিভিন্ন উপায় অবলম্বন করে থাকি। আর এই সংগৃহীত তথ্য ম্যাট্রিক্সের মাধ্যমে এমনভাবে সাজানো হয় যেন পরবর্তিতে ঐ তথ্য বোঝা ও বিশ্লেষণ করা সহজতর হয়।
 সিলভেস্টার (১৮১৪ খ্রিষ্টাব্দ-১৮৯৭ খ্রিষ্টাব্দ)
সিলভেস্টার (১৮১৪ খ্রিষ্টাব্দ-১৮৯৭ খ্রিষ্টাব্দ) ইংরেজ গণিতবিদ জেমস জোসেফ সিলভেস্টার (১৮১৪ খ্রিষ্টাব্দ-১৮৯৭ খ্রিষ্টাব্দ) ১৮৫০ খ্রিস্টাব্দে সর্বপ্রথম ম্যাট্রিক্স সম্পর্কে ধারনা ব্যাক্ত করেন। ১৮৫০ খ্রিস্টাব্দে সর্বপ্রথম ম্যাট্রিক্স সম্পর্কে ধারনা ব্যাক্ত করেন। তারই সহকারী আর্থার ক্যালি (Arthur Cayley) বিপরীত ম্যাট্রিক্সের ধারনাসহ ম্যাট্রিক্সের তাৎপর্য তুলে ধরেন। এটি তিনি ১৮৫৩ খ্রিস্টাব্দে প্রকাশ করেন। পরবর্তিতে তিনি ১৮৫৮ খ্রিস্টাব্দে তাঁর পত্রিকা 'A memoir on the theory of matrices' এ প্রথমে বিশ্লেষণমূলকভাবে ম্যাট্রিক্সকে প্রকাশ করেন। এ কারনে আর্থার ক্যালিকে 'ম্যাট্রিক্স' এর জনক বলা হয়। বিখ্যাত পদার্থবিজ্ঞানী হেইজেনবার্গ
 হেইজেনবার্গ (১৯০১ খ্রিষ্টাব্দ-১৯৭৬ খ্রিষ্টাব্দ)
হেইজেনবার্গ (১৯০১ খ্রিষ্টাব্দ-১৯৭৬ খ্রিষ্টাব্দ) ভার্নার কার্ল হেইজেনবার্গ ছিলেন জার্মান গবেষণা কাউন্সিলের সভাপতি, পারমাণবিক পদার্থবিজ্ঞান কমিশনের চেয়ারম্যান, পারমাণবিক পদার্থবিজ্ঞান ওয়ার্কিং গ্রুপের চেয়ারম্যান এবং আলেকজান্ডার ভন হাম্বোল্ট ফাউন্ডেশনের সভাপতি। ১৯২৫ খ্রিস্টাব্দে কোয়ান্টাম বলবিদ্যায় প্রথম ম্যাট্রিক্সের ব্যবহার শুরু করেন। গণিতে সমীকরণ জোটের সমাধান, পরিসংখ্যানের সম্ভাবনা তত্ত্বে, উচ্চতর অর্থনীতিতে, ব্যবসায় গণিতে আয়-ব্যয় হিসাব ইত্যাদিতে ম্যাট্রিক্স বহুলভাবে ব্যবহৃত হয়। শেয়ারের ক্রয়-বিক্রয় হিসাব, কোন প্রকার ট্রেজারি বন্ডে কী পরিমান অর্থ বিনিয়োগ করতে হবে তা বিপরীত ম্যাট্রিক্সের সাহায্যে সহজে নির্ণয় করা যায়।
১৬৮৩ খ্রিস্টাব্দে প্রথম জাপানি গনিতবিদ সেকি তাকাকাজু (Seki Takakazu)
 সেকি (১৬৪২ খ্রিষ্টাব্দ-১৭০৮ খ্রিষ্টাব্দ)
সেকি (১৬৪২ খ্রিষ্টাব্দ-১৭০৮ খ্রিষ্টাব্দ) সেকি তাকাকাজু একটি নতুন বীজগণিত স্বরলিপি ব্যবস্থা তৈরি করেছিলেন এবং জ্যোতির্বিদ্যার গণনা দ্বারা অনুপ্রাণিত হয়ে ইনফিনাইটিমাল ক্যালকুলাস এবং ডায়োফ্যান্টাইন সমীকরণ নিয়ে কাজ করেছিলেন। তিনি জার্মান পলিম্যাথ গণিতবিদ এবং দার্শনিক গটফ্রিড লাইবনিজ এবং ব্রিটিশ গণিতবিদ আইজাক নিউটনের সমসাময়িক হলেও সেকির কাজটি স্বাধীন ছিল। তার উত্তরসূরীরা পরবর্তীতে এডো পিরিয়ডের শেষ অবধি জাপানি গণিতে বিদ্যালয়ের প্রভাবশালী হয়ে ওঠে। নির্ণায়ক বিষয়ক প্রাথমিক ধারনা প্রকাশ করেন। তিনি \(2\times2, \ 3\times3, \ 4\times4\) এবং \(5\times5\) ম্যাট্রিক্সের নির্ণায়ক নিরূপন করেন এবং সমীকরণের সমাধান নির্ণয়ে নির্ণায়কের ব্যবহার প্রসঙ্গে ধারনা দেন। একই বছরে জার্মান গণিতবিদ লিবনিজ অনুরূপ ধারনা ও প্রয়োজনিয়তা উল্লেখ করেন।
১৯৫০ সালে সুইস গণিতবিদ গ্যাব্রিয়েল ক্রেমার (Gabriel Cramer)
 ক্রেমার (১৭০৪ খ্রিষ্টাব্দ-১৭৫২ খ্রিষ্টাব্দ)
ক্রেমার (১৭০৪ খ্রিষ্টাব্দ-১৭৫২ খ্রিষ্টাব্দ) গ্যাব্রিয়েল ক্রেমার ছিলেন জেনেভান গণিতবিদ। তিনি চিকিত্সক জিন ক্র্যামার এবং অ্যান মাললেট ক্র্যামারের পুত্র ছিলেন। নির্ণায়কের সাহায্যে একঘাতিক সমীকরণ জোটের সমাধান করেন। স্থানাংক জ্যামিতিতে বহুভুজের ক্ষেত্রফল নির্ণয়, একঘাত সমীকরণ জোটের সমাধান ও ভেক্টর জ্যামিতিতে নির্ণায়ক ব্যবহৃত হয়।
বিভিন্ন ধরনের তথ্য সংগ্রহ ও সংরক্ষণের জন্য আমরা সর্বদা বিভিন্ন উপায় অবলম্বন করে থাকি। আর এই সংগৃহীত তথ্য ম্যাট্রিক্সের মাধ্যমে এমনভাবে সাজানো হয় যেন পরবর্তিতে ঐ তথ্য বোঝা ও বিশ্লেষণ করা সহজতর হয়।
ম্যাট্রিক্স ও ম্যাটিক্সের প্রকারভেদ
Matrix and Types of Matrices
বিজ্ঞান ও গণিতের বিভিন্ন তথ্য আয়তাকারে সারি (আনুভূমিক রেখা) ও কলাম (উল্লম্ব রেখা) বরাবর সাজালে যে আয়তাকার বিন্যাস পাওয়া যায় একে ম্যাট্রিক্স বলে। এই বিন্যাস শুধুমাত্র তথ্য সংরক্ষণেই সীমাবদ্ধ নয়। গণিতের বিভিন্ন সমস্যা সমাধানেও ম্যাট্রিক্সের ভূমিকা অপরিসীম।
যেমনঃ একজন ছাত্র একটি নির্দিষ্ট সপ্তাহে, কোন দিনে কত সময় গণিত, পদার্থ ও রসায়ন অধ্যয়ন করেছে তা আয়তাকারে সাজালে তিনটি সারি ও সাতটি কলামবিশিষ্ট একটি বিন্যাস পাওয়া যায়। যা নিম্নে দেখানো হলো।
| Sub\Day | Sat Sun Mon Tues Wed Thus Fri | ||||||
|---|---|---|---|---|---|---|---|
| Math. Physics Chemistry |
5 | 3 | 2 | 4 | 1 | 6 | 0 |
| 1 | 0 | 2 | 4 | 6 | 2 | 3 | |
| 4 | 6 | 5 | 3 | 1 | 2 | 0 | |
\(\begin{bmatrix}5 & 3 & 2 & 4 & 1 & 6 & 0 \\1 & 0 & 2 & 4 & 6 & 2 & 3 \\4 & 6 & 5 & 3 & 1 & 2 & 0 \end{bmatrix}\) অথবা, \(\left(\begin{array}{c}5 & 3 & 2 & 4 & 1 & 6 & 0 \\1 & 0 & 2 & 4 & 6 & 2 & 3 \\4 & 6 & 5 & 3 & 1 & 2 & 0 \end{array}\right)\) অথবা, \(\left|\left|\begin{array}{c}5 & 3 & 2 & 4 & 1 & 6 & 0 \\1 & 0 & 2 & 4 & 6 & 2 & 3 \\4 & 6 & 5 & 3 & 1 & 2 & 0 \end{array}\right|\right|\)
\(\left\{\begin{array}{c}2x+5y=-2\\ 3x-2y=7\end{array}\right\}\) সমীকরণ জোটের সমাধান করার জন্য যে সকল তথ্য প্রয়োজন এর সবকিছুই \(\begin{bmatrix}2 & \ \ 5 & -2 \\3 & -2 & \ \ 7 \end{bmatrix}\) ম্যাট্রিক্স হতে পাওয়া যায়।
ম্যাট্রিক্সের মাধ্যমেই উপরোক্ত সমীকরণ জোটের সমাধান নির্ণয় করা যায়। বর্তমানে গাণিতিক সমস্যা কম্পিউটারের মাধ্যমে অল্প সময়ে সমাধান করা হয়ে থাকে। কম্পিউটারের মাধ্যমে সমাধানের ক্ষেত্রে, সংখ্যার এই আয়তাকার বিন্যাসের ভূমিকা তথা ম্যাট্রিক্সের ভূমিকা অপরিসীম।
https://www.youtube.com/embed/mrXJnBow9OU?si=EiJE92PrAlq4BaPl
ম্যাট্রিক্সের সারি ও কলাম
Rows and Column Matrices
ম্যাট্রিক্সের সারি ও কলামঃ ম্যাট্রিক্সে সংখ্যার আয়তাকার বিন্যাসকে দুই প্রকারে বিশ্লেষণ করা হয়।
যথাঃ আনুভূমিক রেখা বরাবর এবং উল্লম্ব রেখা বরাবর। সংখাগুলির আনুভূমিক রেখাগুলিকে সারি (row) এবং উল্লম্ব রেখাগুলিকে কলাম (column) বলা হয়।
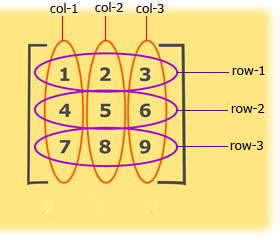
যথাঃ আনুভূমিক রেখা বরাবর এবং উল্লম্ব রেখা বরাবর। সংখাগুলির আনুভূমিক রেখাগুলিকে সারি (row) এবং উল্লম্ব রেখাগুলিকে কলাম (column) বলা হয়।

ম্যাট্রিক্সের ক্রম
Order of Matrices
ম্যাট্রিক্সের ক্রমঃ \(m\) সংখ্যক সারি ও \(n\) সংখ্যক কলামবিশিষ্ট কোনো ম্যাট্রিক্সকে \(m\times{n}\) (পড়তে হবে \(m\) বাই \(n\)) ক্রমের ম্যাট্রিক্স বলা হয়।
যেমনঃ \(\begin{bmatrix}1 & \ \ 4 & -3 \\2 & -6 & \ \ 7 \end{bmatrix}\) কে \(2\times3\) ক্রমের ম্যাট্রিক্স বলা হয়।
কোনো ম্যাট্রিক্সের মোট ভুক্তি সংখ্যা, এর সারি ও কলাম সংখ্যার গুনফলের সমান হয়। উপরের ম্যাট্রিক্সটিতে মোট ছয়টি ভুক্তি আছে এবং ম্যাট্রিক্সটির সারি ও কলাম সংখ্যার গুণফলও (\(2\times3=6\)) ছয়।
যেমনঃ \(\begin{bmatrix}1 & \ \ 4 & -3 \\2 & -6 & \ \ 7 \end{bmatrix}\) কে \(2\times3\) ক্রমের ম্যাট্রিক্স বলা হয়।
কোনো ম্যাট্রিক্সের মোট ভুক্তি সংখ্যা, এর সারি ও কলাম সংখ্যার গুনফলের সমান হয়। উপরের ম্যাট্রিক্সটিতে মোট ছয়টি ভুক্তি আছে এবং ম্যাট্রিক্সটির সারি ও কলাম সংখ্যার গুণফলও (\(2\times3=6\)) ছয়।
ম্যাটিক্সের সাধারণ আকার
General form of Matrix
\(2\times2\) ক্রমের যে কোনো ম্যাট্রিক্স \(A\) হলে, \(A=\left[a_{ij}\right]_{2\times2}=\begin{bmatrix}a_{11} & a_{12} \\a_{21} & a_{22} \end{bmatrix}\)
\(3\times3\) ক্রমের যে কোনো ম্যাট্রিক্স \(A\) হলে, \(A=\left[a_{ij}\right]_{3\times3}=\begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{bmatrix}\)
\(m\times{n}\) ক্রমের যে কোনো ম্যাট্রিক্স \(A\) হলে, \(A=\left[a_{ij}\right]_{m\times{n}}=\begin{bmatrix}a_{11} & a_{12} & ... & a_{1n} \\a_{21} & a_{22} & ... & a_{2n} \\... & ... & ... & ... \\a_{m1} & a_{m2} & ... & a_{mn} \end{bmatrix}\)
\(3\times3\) ক্রমের যে কোনো ম্যাট্রিক্স \(A\) হলে, \(A=\left[a_{ij}\right]_{3\times3}=\begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{bmatrix}\)
\(m\times{n}\) ক্রমের যে কোনো ম্যাট্রিক্স \(A\) হলে, \(A=\left[a_{ij}\right]_{m\times{n}}=\begin{bmatrix}a_{11} & a_{12} & ... & a_{1n} \\a_{21} & a_{22} & ... & a_{2n} \\... & ... & ... & ... \\a_{m1} & a_{m2} & ... & a_{mn} \end{bmatrix}\)
https://www.youtube.com/embed/Zz7btctR4IM?si=BuRCX_0gHePkjXMB
ম্যাটিক্সের প্রকারভেদ
Classification of Matrices
সারি ম্যাট্রিক্স (Row Matrix): যে ম্যাটিরক্সের কেবল একটি সারি বিদ্যমান তাকে সারি ম্যাট্রিক্স বলা হয়।
যেমনঃ \(A=\begin{bmatrix}3 & -2 & 4 \end{bmatrix}\) একটি সারি ম্যাট্রিক্স এবং এর ক্রম \(1\times3\)
যেমনঃ \(A=\begin{bmatrix}3 & -2 & 4 \end{bmatrix}\) একটি সারি ম্যাট্রিক্স এবং এর ক্রম \(1\times3\)
কলাম ম্যাট্রিক্স
Column Matrix
কলাম ম্যাট্রিক্স (Column Matrix): যে ম্যাটিরক্সের কেবল একটি কলাম বিদ্যমান তাকে কলাম ম্যাট্রিক্স বলা হয়।
যেমনঃ \(B=\begin{bmatrix}-4 \\ \ \ 5 \\ \ \ 4 \end{bmatrix}\) একটি কলাম ম্যাট্রিক্স এবং এর ক্রম \(3\times1\)
যেমনঃ \(B=\begin{bmatrix}-4 \\ \ \ 5 \\ \ \ 4 \end{bmatrix}\) একটি কলাম ম্যাট্রিক্স এবং এর ক্রম \(3\times1\)
বর্গ ম্যাট্রিক্স
Square Matrix
বর্গ ম্যাট্রিক্স (Square Matrix): যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\) একটি \(3\times3\) ক্রমের বা সংক্ষেপে \(3\) ক্রমের বর্গ ম্যাট্রিক্স বলে।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\) একটি \(3\times3\) ক্রমের বা সংক্ষেপে \(3\) ক্রমের বর্গ ম্যাট্রিক্স বলে।
ম্যাট্রিক্সের প্রধান কর্ণ
Principal or main diagonal
ম্যাট্রিক্সের প্রধান কর্ণ (Principal or main diagonal): মনে করি \(A=\left[a_{ij}\right]_{n\times{n}}\) একটি \(n\) ক্রমের বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। ।
এখানে, \(a_{11}, \ a_{22}, \ ..., \ a_{nn}\) ভুক্তিগুলি নিয়ে যে কর্ণ গঠিত তাকে মূখ্য বা প্রধান কর্ণ বলা হয়।
যেমনঃ
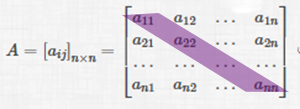
একটি কর্ণ ম্যাট্রিক্স যার ছায়াঘেরা কর্ণটি মূখ্য বা প্রধান কর্ণ ।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। ।
এখানে, \(a_{11}, \ a_{22}, \ ..., \ a_{nn}\) ভুক্তিগুলি নিয়ে যে কর্ণ গঠিত তাকে মূখ্য বা প্রধান কর্ণ বলা হয়।
যেমনঃ

একটি কর্ণ ম্যাট্রিক্স যার ছায়াঘেরা কর্ণটি মূখ্য বা প্রধান কর্ণ ।
উর্ধ ত্রিভুজাকার ম্যাট্রিক্স
Upper Triangular Matrix
উর্ধ ত্রিভুজাকার ম্যাট্রিক্স (Upper Triangular Matrix): কোনো বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left[a_{ij}\right]_{n\times{n}}\) এর মূখ্য বা প্রধান কর্ণের নিম্নস্থ সবগুলি ভুক্তি শুন্য \((0)\) হলে ( অর্থাৎ \(a_{ij}=0\) যখন \(i\gt{j}\)) তাকে উর্ধ ত্রিভুজাকার ম্যাট্রিক্স বলা হয়।
যেমনঃ

একটি \(3\) ক্রমের উর্ধ ত্রিভুজাকার ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left[a_{ij}\right]_{n\times{n}}\) এর মূখ্য বা প্রধান কর্ণের নিম্নস্থ সবগুলি ভুক্তি শুন্য \((0)\) হলে ( অর্থাৎ \(a_{ij}=0\) যখন \(i\gt{j}\)) তাকে উর্ধ ত্রিভুজাকার ম্যাট্রিক্স বলা হয়।
যেমনঃ

একটি \(3\) ক্রমের উর্ধ ত্রিভুজাকার ম্যাট্রিক্স।
নিম্ন ত্রিভুজাকার ম্যাট্রিক্স
Lower Triangular Matrix
নিম্ন ত্রিভুজাকার ম্যাট্রিক্স (Lower Triangular Matrix): কোনো বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left[a_{ij}\right]_{n\times{n}}\) এর মূখ্য বা প্রধান কর্ণের উপরোস্থ সবগুলি ভুক্তি শুন্য \((0)\) হলে ( অর্থাৎ \(a_{ij}=0\) যখন \(i\lt{j}\)) তাকে নিম্ন ত্রিভুজাকার ম্যাট্রিক্স বলা হয়।
যেমনঃ
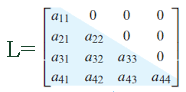
একটি \(3\) ক্রমের নিম্ন ত্রিভুজাকার ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left[a_{ij}\right]_{n\times{n}}\) এর মূখ্য বা প্রধান কর্ণের উপরোস্থ সবগুলি ভুক্তি শুন্য \((0)\) হলে ( অর্থাৎ \(a_{ij}=0\) যখন \(i\lt{j}\)) তাকে নিম্ন ত্রিভুজাকার ম্যাট্রিক্স বলা হয়।
যেমনঃ
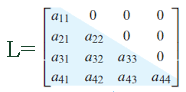
একটি \(3\) ক্রমের নিম্ন ত্রিভুজাকার ম্যাট্রিক্স।
https://www.youtube.com/embed/opOeyij68SA?si=EgBRHTSpE7h0zwvX
কর্ণ ম্যাট্রিক্স
Diagonal Matrix
কর্ণ ম্যাট্রিক্স (Diagonal Matrix): কোনো বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left[a_{ij}\right]_{n\times{n}}\) কে \(n\) ক্রমের কর্ণ ম্যাট্রিক্স বলা হবে যদি \(a_{ij}=0\) হয়, যখন \(i\ne{j};\) অর্থাৎ মূখ্য বা প্রধান কর্ণের ভুক্তি ব্যতীত অপর সকল ভুক্তি শুন্য \((0)\) হবে।
যেমনঃ

একটি কর্ণ ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left[a_{ij}\right]_{n\times{n}}\) কে \(n\) ক্রমের কর্ণ ম্যাট্রিক্স বলা হবে যদি \(a_{ij}=0\) হয়, যখন \(i\ne{j};\) অর্থাৎ মূখ্য বা প্রধান কর্ণের ভুক্তি ব্যতীত অপর সকল ভুক্তি শুন্য \((0)\) হবে।
যেমনঃ

একটি কর্ণ ম্যাট্রিক্স।
https://www.youtube.com/embed/-wtWRK0iJTQ?si=2jEJnZxEoIOKc3S9
স্কেলার ম্যাট্রিক্স
Scalar Matrix
স্কেলার ম্যাট্রিক্স (Scalar Matrix): কোনো কর্ণ ম্যাট্রিক্স কোনো বর্গ ম্যাট্রিক্স \(A=\left[a_{ij}\right]_{n\times{n}}\) কে \(n\) ক্রমের কর্ণ ম্যাট্রিক্স বলা হবে যদি \(a_{ij}=0\) হয়, যখন \(i\ne{j};\)
অর্থাৎ কোনো বর্গ ম্যাট্রিক্সের মূখ্য বা প্রধান কর্ণের ভুক্তি ব্যতীত অপর সকল ভুক্তি শুন্য \((0)\) হলে তাকে কর্ণ ম্যাট্রিক্স বলা হবে। এর অশুন্য ভুক্তিগুলি সমান হলে, ঐ কর্ণ ম্যাট্রিক্সকে স্কেলার ম্যাট্রিক্স বলা হয়।
যেমনঃ
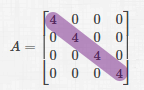
একটি স্কেলার ম্যাট্রিক্স।
অর্থাৎ কোনো বর্গ ম্যাট্রিক্সের মূখ্য বা প্রধান কর্ণের ভুক্তি ব্যতীত অপর সকল ভুক্তি শুন্য \((0)\) হলে তাকে কর্ণ ম্যাট্রিক্স বলা হবে। এর অশুন্য ভুক্তিগুলি সমান হলে, ঐ কর্ণ ম্যাট্রিক্সকে স্কেলার ম্যাট্রিক্স বলা হয়।
যেমনঃ

একটি স্কেলার ম্যাট্রিক্স।
একক বা অভেদক ম্যাট্রিক্স
Unit or Identity Matrix
একক বা অভেদক ম্যাট্রিক্স (Unit or Identity Matrix): কোনো বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left[a_{ij}\right]_{n\times{n}}\) কে \(n\) ক্রমের একক বা অভেদক ম্যাট্রিক্স যদি \(a_{ij}=0\) হয়, যখন \(i\ne{j};\) এবং \(a_{ij}=1\) যখন \(i=j\) হয়।
অর্থাৎ কোনো বর্গ ম্যাট্রিক্সের মূখ্য বা প্রধান কর্ণের ভুক্তি ব্যতীত অপর সকল ভুক্তি শুন্য \((0)\) এবং প্রধান কর্ণের প্রত্যেক ভুক্তি এক \((1)\) হলে তাকে একক বা অভেদক ম্যাট্রিক্স বলা হয়। অভেদক ম্যাট্রিক্সকে \(I_{n}\) দ্বারা সূচিত করা হয়।
যেমনঃ \(I_{n}=\begin{bmatrix}1 & 0 & 0 & ... & 0 \\0 & 1 & 0 &... & 0 \\0 & 0 & 1 &... & 0 \\... & ... & ... & ... & ... \\0 & 0 & 0 & ... & 1 \end{bmatrix}_{n\times{n}}\) একটি \(n\) ক্রমের একক বা অভেদক ম্যাট্রিক্স।
যেমনঃ \(I_{3}=\begin{bmatrix}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1 \end{bmatrix}_{3\times{3}}\) একটি \(3\) ক্রমের একক বা অভেদক ম্যাট্রিক্স।
যেমনঃ \(I_{2}=\begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix}_{2\times{2}}\) একটি \(2\) ক্রমের একক বা অভেদক ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left[a_{ij}\right]_{n\times{n}}\) কে \(n\) ক্রমের একক বা অভেদক ম্যাট্রিক্স যদি \(a_{ij}=0\) হয়, যখন \(i\ne{j};\) এবং \(a_{ij}=1\) যখন \(i=j\) হয়।
অর্থাৎ কোনো বর্গ ম্যাট্রিক্সের মূখ্য বা প্রধান কর্ণের ভুক্তি ব্যতীত অপর সকল ভুক্তি শুন্য \((0)\) এবং প্রধান কর্ণের প্রত্যেক ভুক্তি এক \((1)\) হলে তাকে একক বা অভেদক ম্যাট্রিক্স বলা হয়। অভেদক ম্যাট্রিক্সকে \(I_{n}\) দ্বারা সূচিত করা হয়।
যেমনঃ \(I_{n}=\begin{bmatrix}1 & 0 & 0 & ... & 0 \\0 & 1 & 0 &... & 0 \\0 & 0 & 1 &... & 0 \\... & ... & ... & ... & ... \\0 & 0 & 0 & ... & 1 \end{bmatrix}_{n\times{n}}\) একটি \(n\) ক্রমের একক বা অভেদক ম্যাট্রিক্স।
যেমনঃ \(I_{3}=\begin{bmatrix}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1 \end{bmatrix}_{3\times{3}}\) একটি \(3\) ক্রমের একক বা অভেদক ম্যাট্রিক্স।
যেমনঃ \(I_{2}=\begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix}_{2\times{2}}\) একটি \(2\) ক্রমের একক বা অভেদক ম্যাট্রিক্স।
https://www.youtube.com/embed/_U5DU4UUWaU?si=539fFpIUURvli_C-
শুন্য ম্যাট্রিক্স
Zero or Null Matrix
শুন্য ম্যাট্রিক্স (Zero or Null Matrix): কোনো ম্যাট্রিক্সের সকল ভুক্তি শুন্য \((0)\) হলে তাকে শুন্য ম্যাট্রিক্স বলে।
যেমনঃ \(A=\begin{bmatrix}0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}\) একটি \(3\times4\) ক্রমের শুন্য ম্যাট্রিক্স।
যেমনঃ \(A=\begin{bmatrix}0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}\) একটি \(3\times4\) ক্রমের শুন্য ম্যাট্রিক্স।
সমঘাতি ম্যাট্রিক্স
Idempotent Matrix
সমঘাতি ম্যাট্রিক্স (Idempotent Matrix): বর্গাকার কোনো ম্যাট্রিক্স \(A\) কে সমঘাতি ম্যাট্রিক্স বলা হবে যদি \(A^2=A\) হয়।
যেমনঃ \(A=\begin{bmatrix}4 & -1 \\12 & -3 \end{bmatrix}\) এখানে \(A^2=A\) সুতরাং \(A\) একটি সমঘাতি ম্যাট্রিক্স।
যেমনঃ \(A=\begin{bmatrix}4 & -1 \\12 & -3 \end{bmatrix}\) এখানে \(A^2=A\) সুতরাং \(A\) একটি সমঘাতি ম্যাট্রিক্স।
https://www.youtube.com/embed/8nW3bzF6VHY?si=XQudBN-XltFze6cI
শুন্যঘাতি ম্যাট্রিক্স
Nilpotent Matrix
শুন্যঘাতি ম্যাট্রিক্স (Nilpotent Matrix): একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে শুন্যঘাতি ম্যাট্রিক্স বলা হবে যদি \(A^n=0\) হয়, যেখানে \(n\in{\mathbb{N}}\) যদি \(1\) ব্যাতিত র্বনিম্ন ধনাত্মক পূর্ণ সংখ্যা \(n\) এর জন্য \(A^n=0\) হয়, তবে ম্যাট্রিক্স \(A\) কে সূচক (index) \(n\) এর শুন্যঘাতি ম্যাট্রিক্স বলা হয়।
যেমনঃ \(A=\begin{bmatrix} \ \ 4 & \ \ 4 \\-4 & -4 \end{bmatrix},\) এখানে \(A^2=\begin{bmatrix}0 & 0 \\0 & 0 \end{bmatrix}=0\) সুতরাং \(A\) একটি শুন্যঘাতি ম্যাট্রিক্স।
একইভাবে \(A^3=0, \ A^4=0\) ইত্যাদি। সুতরাং \(A\) হলো সূচক \(2\) এর শুন্যঘাতি ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে শুন্যঘাতি ম্যাট্রিক্স বলা হবে যদি \(A^n=0\) হয়, যেখানে \(n\in{\mathbb{N}}\) যদি \(1\) ব্যাতিত র্বনিম্ন ধনাত্মক পূর্ণ সংখ্যা \(n\) এর জন্য \(A^n=0\) হয়, তবে ম্যাট্রিক্স \(A\) কে সূচক (index) \(n\) এর শুন্যঘাতি ম্যাট্রিক্স বলা হয়।
যেমনঃ \(A=\begin{bmatrix} \ \ 4 & \ \ 4 \\-4 & -4 \end{bmatrix},\) এখানে \(A^2=\begin{bmatrix}0 & 0 \\0 & 0 \end{bmatrix}=0\) সুতরাং \(A\) একটি শুন্যঘাতি ম্যাট্রিক্স।
একইভাবে \(A^3=0, \ A^4=0\) ইত্যাদি। সুতরাং \(A\) হলো সূচক \(2\) এর শুন্যঘাতি ম্যাট্রিক্স।
অভেদঘাতি ম্যাট্রিক্স
Involutory Matrix
অভেদঘাতি ম্যাট্রিক্স (Involutory Matrix): একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে অভেদঘাতি ম্যাট্রিক্স বলা হবে যদি \(A^2=I\) হয়।
যেমনঃ \(A=\begin{bmatrix}2 & -3 \\1 & -2 \end{bmatrix},\) এখানে \(A^2=\begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix}=I\) সুতরাং \(A\) একটি অভেদঘাতি ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে অভেদঘাতি ম্যাট্রিক্স বলা হবে যদি \(A^2=I\) হয়।
যেমনঃ \(A=\begin{bmatrix}2 & -3 \\1 & -2 \end{bmatrix},\) এখানে \(A^2=\begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix}=I\) সুতরাং \(A\) একটি অভেদঘাতি ম্যাট্রিক্স।
https://www.youtube.com/embed/encfs3dR_Yc?si=4nOGqoVnaseaDQgm
বিম্ব ম্যাট্রিক্স
Transpose of a Matrix
বিম্ব ম্যাট্রিক্স (Transpose of a Matrix): কোনো ম্যাট্রিক্স \(A\) এর যথাযথ সারি এবং কলাম বিনিময় করলে যে নতুন ম্যাট্রিক্স পাওয়া যায় তাকে \(A\) ম্যাট্রিক্সের ট্রান্সপোজ ম্যাট্রিক্স অথবা বিম্ব ম্যাট্রিক্স বলা হয়। \(A\) ম্যাট্রিক্সের ট্রান্সপোজ ম্যাট্রিক্সকে \(A^{t}\) বা \(A^{\prime}\) দ্বারা প্রকাশ করা হয়।
যেমনঃ \(A=\begin{bmatrix}4 & 3 \\1 & 2 \\5 & 9 \end{bmatrix}\) হলে, \(A^{t}=\begin{bmatrix}4 & 1 & 5 \\3 & 2 & 9 \end{bmatrix}\) হলো \(A\) এর ট্রান্সপোজ ম্যাট্রিক্স।
যেমনঃ \(A=\begin{bmatrix}4 & 3 \\1 & 2 \\5 & 9 \end{bmatrix}\) হলে, \(A^{t}=\begin{bmatrix}4 & 1 & 5 \\3 & 2 & 9 \end{bmatrix}\) হলো \(A\) এর ট্রান্সপোজ ম্যাট্রিক্স।
https://www.youtube.com/embed/Zhn_P4GCEOg?si=uRr1oY3ZUMwOly55
প্রতিসম ম্যাট্রিক্স
Symmetric Matrix
প্রতিসম ম্যাট্রিক্স (Symmetric Matrix): একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left(a_{ij}\right)_{n\times{n}}\) কে প্রতিসম ম্যাট্রিক্স বলা হবে যদি \(A^{t}=A\) হয়, অর্থাৎ \(a_{ij}=a_{ji}\) হয়।
যেমনঃ \(A=\begin{bmatrix}-2 & 3 & -1 \\ \ \ 3 & 4 & \ \ 6 \\-1 & 6 & -5 \end{bmatrix}\) হলে, \(A^{t}=\begin{bmatrix}-2 & 3 & -1 \\ \ \ 3 & 4 & \ \ 6 \\-1 & 6 & -5 \end{bmatrix}\)
অর্থাৎ \(A=A^{t}\) সুতরাং \(A\) হলো একটি প্রতিসম ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left(a_{ij}\right)_{n\times{n}}\) কে প্রতিসম ম্যাট্রিক্স বলা হবে যদি \(A^{t}=A\) হয়, অর্থাৎ \(a_{ij}=a_{ji}\) হয়।
যেমনঃ \(A=\begin{bmatrix}-2 & 3 & -1 \\ \ \ 3 & 4 & \ \ 6 \\-1 & 6 & -5 \end{bmatrix}\) হলে, \(A^{t}=\begin{bmatrix}-2 & 3 & -1 \\ \ \ 3 & 4 & \ \ 6 \\-1 & 6 & -5 \end{bmatrix}\)
অর্থাৎ \(A=A^{t}\) সুতরাং \(A\) হলো একটি প্রতিসম ম্যাট্রিক্স।
https://www.youtube.com/embed/k8yHXQLQSC4?si=5lqxu2sgRqB2Ihwr
বিপ্রতিসম ম্যাট্রিক্স
Skew Symmetric Matrix
বিপ্রতিসম ম্যাট্রিক্স ( Skew Symmetric Matrix): একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left(a_{ij}\right)_{n\times{n}}\) কে বিপ্রতিসম ম্যাট্রিক্স বলা হবে যদি \(A^{t}=-A\) হয়, অর্থাৎ \(a_{ij}=-a_{ji}\) হয়।
যেমনঃ \(A=\begin{bmatrix} \ \ 0 & \ \ 3 & 4 \\-3 & \ \ 0 & 7 \\-4 & -7 & 0 \end{bmatrix}\) হলে, \(A^{t}=\begin{bmatrix}0 & -3 & -4 \\3 & \ \ 0 & -7 \\4 & \ \ 7 & \ \ 0 \end{bmatrix}=-\begin{bmatrix} \ \ 0 & \ \ 3 & 4 \\-3 & \ \ 0 & 7 \\-4 & -7 & 0 \end{bmatrix}=-A\)
অর্থাৎ \(A^{t}=-A\) সুতরাং \(A\) হলো একটি বিপ্রতিসম ম্যাট্রিক্স।
উল্লেখ্য যে, প্রত্যেক বিপ্রতিসম ম্যাট্রিক্সের প্রধান কর্ণের ভুক্তিসমূহ শুন্য, অর্থাৎ \(a_{ij}=0\) যখন \(i=j\)
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A=\left(a_{ij}\right)_{n\times{n}}\) কে বিপ্রতিসম ম্যাট্রিক্স বলা হবে যদি \(A^{t}=-A\) হয়, অর্থাৎ \(a_{ij}=-a_{ji}\) হয়।
যেমনঃ \(A=\begin{bmatrix} \ \ 0 & \ \ 3 & 4 \\-3 & \ \ 0 & 7 \\-4 & -7 & 0 \end{bmatrix}\) হলে, \(A^{t}=\begin{bmatrix}0 & -3 & -4 \\3 & \ \ 0 & -7 \\4 & \ \ 7 & \ \ 0 \end{bmatrix}=-\begin{bmatrix} \ \ 0 & \ \ 3 & 4 \\-3 & \ \ 0 & 7 \\-4 & -7 & 0 \end{bmatrix}=-A\)
অর্থাৎ \(A^{t}=-A\) সুতরাং \(A\) হলো একটি বিপ্রতিসম ম্যাট্রিক্স।
উল্লেখ্য যে, প্রত্যেক বিপ্রতিসম ম্যাট্রিক্সের প্রধান কর্ণের ভুক্তিসমূহ শুন্য, অর্থাৎ \(a_{ij}=0\) যখন \(i=j\)
https://www.youtube.com/embed/YovEUBFKelc?si=nfXdhW-6RlUmouZZ
উপ-ম্যাট্রিক্স
Sub Matrix
উপ-ম্যাট্রিক্স ( Sub Matrix): কোনো একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। এর যেকোনো সংখ্যক কলাম ও যেকোনো সংখ্যক সারির ভুক্তি বাদ দিয়ে গঠিত অপর একটি ম্যাট্রিক্সকে মূল ম্যাট্রিক্সের উপ-ম্যাট্রিক্স বলা হয়।
যেমনঃ \(A=\begin{bmatrix}1 & \ \ 2 & 3 \\4 & \ \ 5 & 6 \\7 & \ \ 8 & 9 \\3 & -1 & 4 \end{bmatrix}\) ম্যাট্রিক্সের উপ-ম্যাট্রিক্সগুলি \(\begin{bmatrix}1 & 2 \\4 & 5 \end{bmatrix}, \ \begin{bmatrix}2 & 3 \\5 & 6 \end{bmatrix}, \ \begin{bmatrix}4 & 5 \\7 & 8 \end{bmatrix}, \ \begin{bmatrix}4 & \ \ 5 \\7 & \ \ 8 \\3 & -1 \end{bmatrix}\) ইত্যাদি।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। এর যেকোনো সংখ্যক কলাম ও যেকোনো সংখ্যক সারির ভুক্তি বাদ দিয়ে গঠিত অপর একটি ম্যাট্রিক্সকে মূল ম্যাট্রিক্সের উপ-ম্যাট্রিক্স বলা হয়।
যেমনঃ \(A=\begin{bmatrix}1 & \ \ 2 & 3 \\4 & \ \ 5 & 6 \\7 & \ \ 8 & 9 \\3 & -1 & 4 \end{bmatrix}\) ম্যাট্রিক্সের উপ-ম্যাট্রিক্সগুলি \(\begin{bmatrix}1 & 2 \\4 & 5 \end{bmatrix}, \ \begin{bmatrix}2 & 3 \\5 & 6 \end{bmatrix}, \ \begin{bmatrix}4 & 5 \\7 & 8 \end{bmatrix}, \ \begin{bmatrix}4 & \ \ 5 \\7 & \ \ 8 \\3 & -1 \end{bmatrix}\) ইত্যাদি।
https://www.youtube.com/embed/W31dL7gcSQc?si=CNr_WWKqY5BeNkvs
উল্লম্ব ম্যাট্রিক্স
Orthogonal Matrix
উল্লম্ব ম্যাট্রিক্স ( Orthogonal Matrix): একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে উল্লম্ব ম্যাট্রিক্স বলা হবে যদি \(AA^{t}=A^{t}A=I\) হয়।
যেমনঃ \(A=\begin{bmatrix}\cos{x} & \sin{x} \\-\sin{x} & \cos{x} \end{bmatrix}\) একটি উল্লম্ব ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে উল্লম্ব ম্যাট্রিক্স বলা হবে যদি \(AA^{t}=A^{t}A=I\) হয়।
যেমনঃ \(A=\begin{bmatrix}\cos{x} & \sin{x} \\-\sin{x} & \cos{x} \end{bmatrix}\) একটি উল্লম্ব ম্যাট্রিক্স।
https://www.youtube.com/embed/-fIznamRBCE?si=i2mELAFE_26k3hxp
ম্যাট্রিক্সের ট্রেস
Trace of Matrix
ম্যাট্রিক্সের ট্রেস ( Trace of Matrix): কোনো একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। এর মূখ্য বা প্রধান কর্ণের ভুক্তি সমূহের যোগফলকে ম্যাট্রিক্সের ট্রেস (Trace) বলা হয়।
যেমনঃ
একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স।
যার ট্রেস \(=-4+9+1\)
\(=-4+10\)
\(=6\)
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। এর মূখ্য বা প্রধান কর্ণের ভুক্তি সমূহের যোগফলকে ম্যাট্রিক্সের ট্রেস (Trace) বলা হয়।
যেমনঃ
| \(-4\) | \(6\) | \(3\) | ||
| \( \ \ \ 5\) | \(9\) | \(7\) | ||
| \(-3\) | \(7\) | \(1\) |
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স।
যার ট্রেস \(=-4+9+1\)
\(=-4+10\)
\(=6\)
https://www.youtube.com/embed/Y9OH4UQNj-s?si=9DiaNkSTIRVoyrVj
পর্যায়বৃত্ত ম্যাট্রিক্স
Periodic Matrix
পর্যায়বৃত্ত ম্যাট্রিক্স ( Periodic Matrix): যদি \(A\) যেকোনো একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। ও \(A^{k+1}=A, \ k\in{\mathbb{N}}\) হয়, তবে \(A\) কে পর্যায়বৃত্ত ম্যাট্রিক্স ও \(k\) কে পর্যায়কাল বলা হয়।
যেমনঃ \(A=\begin{bmatrix} \ \ 2 & -3 & -5 \\-1 & \ \ 4 & \ \ 5 \\ \ \ 1 & -3 & -4 \end{bmatrix}\) একটি পর্যায়বৃত্ত ম্যাট্রিক্স যার পর্যায়কাল \(2\) । কারণ এখানে, \(A^{3}=A^{2+1}=A\)
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। ও \(A^{k+1}=A, \ k\in{\mathbb{N}}\) হয়, তবে \(A\) কে পর্যায়বৃত্ত ম্যাট্রিক্স ও \(k\) কে পর্যায়কাল বলা হয়।
যেমনঃ \(A=\begin{bmatrix} \ \ 2 & -3 & -5 \\-1 & \ \ 4 & \ \ 5 \\ \ \ 1 & -3 & -4 \end{bmatrix}\) একটি পর্যায়বৃত্ত ম্যাট্রিক্স যার পর্যায়কাল \(2\) । কারণ এখানে, \(A^{3}=A^{2+1}=A\)
https://www.youtube.com/embed/TLUpEyMokyk?si=T0LJ0rRsgucn1LQ0
অনুবন্ধী ম্যাট্রিক্স
Conjugate Matrix
অনুবন্ধী ম্যাট্রিক্স ( Conjugate Matrix): কোনো \(A\) ম্যাট্রিক্সের ভুক্তি জটিল সংখ্যা হলে, প্রত্যেক জটিল সংখ্যার স্থলে তার অনুবন্ধী জটিল সংখ্যা বসিয়ে প্রাপ্ত ম্যাট্রিক্সকে \(A\) এর অনুবন্ধী ম্যাট্রিক্স বলা হয় এবং এটিকে \(\overline{A}\) প্রতীক দ্বারা সূচিত করা হয়।
যেমনঃ \(A=\begin{bmatrix} \ \ 2 & 3-2i \\1+2i & i-2 \end{bmatrix}\) এর অনুবন্ধী ম্যাট্রিক্স, \(\overline{A}=\begin{bmatrix} \ \ 2 & 3+2i \\1+2i & -i-2 \end{bmatrix}\)
যেমনঃ \(A=\begin{bmatrix} \ \ 2 & 3-2i \\1+2i & i-2 \end{bmatrix}\) এর অনুবন্ধী ম্যাট্রিক্স, \(\overline{A}=\begin{bmatrix} \ \ 2 & 3+2i \\1+2i & -i-2 \end{bmatrix}\)
https://www.youtube.com/embed/_-T427xp3nA?si=Zrt0BvtbHsFWXjrz
হারমিসিয়ান ম্যাট্রিক্স
Hermitian Matrix
হারমিসিয়ান ম্যাট্রিক্স ( Hermitian Matrix): একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে হারমিসিয়ান ম্যাট্রিক্স বলা হবে যদি \(\left(\overline{A}\right)^{t}=A\) হয় অর্থাৎ \(i, \ j\) এর সকল মানের জন্য \(\overline{a_{ij}}=a_{ji}\) হয়। এরূপ ক্ষেত্রে ম্যাট্রিক্সের কর্ণের ভুক্তিসমূহ বাস্তব সংখ্যা এবং কর্ণ ব্যতীত অন্য সকল ভুক্তি বাস্তব সংখ্যা ও জটিল সংখ্যা উভয়ই হতে পারে।
যেমনঃ \(A=\begin{bmatrix} \ \ 2 & 3-i \\3+i & 3 \end{bmatrix}\)
\(\Rightarrow \overline{A}=\begin{bmatrix} \ \ 2 & 3+i \\3-i & 3 \end{bmatrix}\)
\(\Rightarrow \left(\overline{A}\right)^{t}=\begin{bmatrix} \ \ 2 & 3-i \\3+i & 3 \end{bmatrix}\)
\(\therefore \left(\overline{A}\right)^{t}=A\)
\(\therefore A\) একটি হারমিসিয়ান ম্যাট্রিক্স।
আবার,
\(B=\begin{bmatrix} \ \ 2 & 3-i & 4 \\3+i & \ \ 5 & i \\ \ \ 4 & -i & 0 \end{bmatrix}\) ও একটি হারমিসিয়ান ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে হারমিসিয়ান ম্যাট্রিক্স বলা হবে যদি \(\left(\overline{A}\right)^{t}=A\) হয় অর্থাৎ \(i, \ j\) এর সকল মানের জন্য \(\overline{a_{ij}}=a_{ji}\) হয়। এরূপ ক্ষেত্রে ম্যাট্রিক্সের কর্ণের ভুক্তিসমূহ বাস্তব সংখ্যা এবং কর্ণ ব্যতীত অন্য সকল ভুক্তি বাস্তব সংখ্যা ও জটিল সংখ্যা উভয়ই হতে পারে।
যেমনঃ \(A=\begin{bmatrix} \ \ 2 & 3-i \\3+i & 3 \end{bmatrix}\)
\(\Rightarrow \overline{A}=\begin{bmatrix} \ \ 2 & 3+i \\3-i & 3 \end{bmatrix}\)
\(\Rightarrow \left(\overline{A}\right)^{t}=\begin{bmatrix} \ \ 2 & 3-i \\3+i & 3 \end{bmatrix}\)
\(\therefore \left(\overline{A}\right)^{t}=A\)
\(\therefore A\) একটি হারমিসিয়ান ম্যাট্রিক্স।
আবার,
\(B=\begin{bmatrix} \ \ 2 & 3-i & 4 \\3+i & \ \ 5 & i \\ \ \ 4 & -i & 0 \end{bmatrix}\) ও একটি হারমিসিয়ান ম্যাট্রিক্স।
https://www.youtube.com/embed/W1iTq11b2Oc?si=9A6AfX76g-AhThY4
বিহারমিসিয়ান ম্যাট্রিক্স
Skew Hermitian Matrix
বিহারমিসিয়ান ম্যাট্রিক্স (Skew Hermitian Matrix): একটি বর্গ ম্যাট্রিক্স যে ম্যাটিরক্সের সারি ও কলাম সংখ্যা সমান তাকে বর্গ ম্যাট্রিক্স বলা হয়।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে বিহারমিসিয়ান ম্যাট্রিক্স বলা হবে যদি \(\left(\overline{A}\right)^{t}=-A\) হয় অর্থাৎ \(i, \ j\) এর সকল মানের জন্য \(\overline{a_{ij}}=-a_{ji}\) হয়।
যেমনঃ \(A=\begin{bmatrix}0 & i \\i & 0 \end{bmatrix}\)
\(\Rightarrow \overline{A}=\begin{bmatrix} \ \ 0 & -i \\-i & \ \ 0 \end{bmatrix}\)
\(\Rightarrow \left(\overline{A}\right)^{t}=\begin{bmatrix} \ \ 0 & -i \\-i & \ \ 0 \end{bmatrix}\)
\(\Rightarrow \left(\overline{A}\right)^{t}=-\begin{bmatrix}0 & i \\i & 0 \end{bmatrix}\)
\(\therefore \left(\overline{A}\right)^{t}=-A\)
\(\therefore A\) একটি বিহারমিসিয়ান ম্যাট্রিক্স।
অর্থাৎ, \(C=\left[c_{ij}\right]_{m\times{n}}\) ম্যাট্রিক্সকে বর্গ ম্যাট্রিক্স বলা হবে যদি \(m=n\) হয়। তখন \(C\) কে \(m\) অথবা \(n\) ক্রমের একটি বর্গ ম্যাট্রিক্স বলা হয়।
যেমনঃ \(C=\begin{bmatrix}-4 & 4 & 5 \\ \ \ 5 & 7 & 1\\ \ \ 6 & 3 & 1 \end{bmatrix}\)
একটি বর্গ ম্যাট্রিক্স। \(A\) কে বিহারমিসিয়ান ম্যাট্রিক্স বলা হবে যদি \(\left(\overline{A}\right)^{t}=-A\) হয় অর্থাৎ \(i, \ j\) এর সকল মানের জন্য \(\overline{a_{ij}}=-a_{ji}\) হয়।
যেমনঃ \(A=\begin{bmatrix}0 & i \\i & 0 \end{bmatrix}\)
\(\Rightarrow \overline{A}=\begin{bmatrix} \ \ 0 & -i \\-i & \ \ 0 \end{bmatrix}\)
\(\Rightarrow \left(\overline{A}\right)^{t}=\begin{bmatrix} \ \ 0 & -i \\-i & \ \ 0 \end{bmatrix}\)
\(\Rightarrow \left(\overline{A}\right)^{t}=-\begin{bmatrix}0 & i \\i & 0 \end{bmatrix}\)
\(\therefore \left(\overline{A}\right)^{t}=-A\)
\(\therefore A\) একটি বিহারমিসিয়ান ম্যাট্রিক্স।
https://www.youtube.com/embed/ggf5pv9-_0I?si=raZRaGcPM7lkGkfR
ম্যাটিক্সের সমতা, যোগ, বিয়োগ ও গুণ
ম্যাট্রিক্সের সমতা
Equality of Matrices
ম্যাট্রিক্সের সমতা (Equality of Matrices): দুইটি ম্যাট্রিক্স \(A=\left[a_{ij}\right]\) এবং \(B=\left[b_{ij}\right]\) কে সমান ম্যাট্রিক্স (Equal Matrix) বলা হবে যদি এবং কেবল যদি তাদের মাত্রা একই হয় এবং প্রথমটির প্রতিটি ভুক্তি অপরটির অনুরূপ ভুক্তির সমান হয়।
দুইটি সমান ম্যাট্রিক্সের জন্য -
প্রতীকে \(\left[a_{ij}\right]=\left[b_{ij}\right]\) হবে যদি \(a_{ij}=b_{ij} \ (i=1, \ 2, \ 3, \ ... \ ... m, \ j=1, \ 2, \ 3, \ ... \ ... n)\) হয়।
যেমনঃ \(A=\begin{bmatrix}2 & 3 & \ \ 5 \\1 & 0 & -9 \\9 & 2 & \ \ 7 \end{bmatrix}\) এবং \(B=\begin{bmatrix}2 & 3 & \ \ 5 \\1 & 0 & -9 \\9 & 2 & \ \ 7 \end{bmatrix}\) দুইটি সমান ম্যাট্রিক্স
অর্থাৎ \(A=B\)
দুইটি সমান ম্যাট্রিক্সের জন্য -
প্রতীকে \(\left[a_{ij}\right]=\left[b_{ij}\right]\) হবে যদি \(a_{ij}=b_{ij} \ (i=1, \ 2, \ 3, \ ... \ ... m, \ j=1, \ 2, \ 3, \ ... \ ... n)\) হয়।
যেমনঃ \(A=\begin{bmatrix}2 & 3 & \ \ 5 \\1 & 0 & -9 \\9 & 2 & \ \ 7 \end{bmatrix}\) এবং \(B=\begin{bmatrix}2 & 3 & \ \ 5 \\1 & 0 & -9 \\9 & 2 & \ \ 7 \end{bmatrix}\) দুইটি সমান ম্যাট্রিক্স
অর্থাৎ \(A=B\)
https://www.youtube.com/embed/qGJxm6mHq7w?si=9lx3Yw9VO7ePV3Q-
ম্যাট্রিক্সের যোগ ও বিয়োগ
Addition and Subtraction of Matrices
ম্যাট্রিক্সের যোগ ও বিয়োগ (Addition and Subtraction of Matrices): দুইটি ম্যাট্রিক্সের যোগফল ও বিয়োগফল নির্ণয় করা যাবে যদি ম্যাট্রিক্স দুইটির ক্রম (Order) একই হয়। দুইটি ম্যাট্রিক্সের যোগফল বা বিয়োগফল একটি ম্যাট্রিক্স হবে যার প্রতিটি ভুক্তি ম্যাট্রিক্স দুইটির অনুরূপ ভুক্তির যোগফল বা বিয়োগফল হবে।
যেমনঃ \(A=\begin{bmatrix}2 & 3 \\1 & 0 \end{bmatrix}\) এবং \(B=\begin{bmatrix}1 & 6 \\9 & 2 \end{bmatrix}\) দুইটি ম্যাট্রিক্স
এখন,
\(A+B=\begin{bmatrix}2 & 3 \\1 & 0 \end{bmatrix}+\begin{bmatrix}1 & 6 \\9 & 2 \end{bmatrix}\)
\(=\begin{bmatrix}2+1 & 3+6 \\1+9 & 0+2 \end{bmatrix}\)
\(\therefore A+B=\begin{bmatrix}3 & 9 \\10 & 2 \end{bmatrix}\)
এবং
\(A-B=\begin{bmatrix}2 & 3 \\1 & 0 \end{bmatrix}-\begin{bmatrix}1 & 6 \\9 & 2 \end{bmatrix}\)
\(=\begin{bmatrix}2-1 & 3-6 \\1-9 & 0-2 \end{bmatrix}\)
\(\therefore A-B=\begin{bmatrix} \ \ 1 & -3 \\-8 & -2 \end{bmatrix}\)
\(A+B\) নির্ণয়ের পদ্ধতিঃ
\(A-B\) নির্ণয়ের পদ্ধতিঃ
যেমনঃ \(A=\begin{bmatrix}2 & 3 \\1 & 0 \end{bmatrix}\) এবং \(B=\begin{bmatrix}1 & 6 \\9 & 2 \end{bmatrix}\) দুইটি ম্যাট্রিক্স
এখন,
\(A+B=\begin{bmatrix}2 & 3 \\1 & 0 \end{bmatrix}+\begin{bmatrix}1 & 6 \\9 & 2 \end{bmatrix}\)
\(=\begin{bmatrix}2+1 & 3+6 \\1+9 & 0+2 \end{bmatrix}\)
\(\therefore A+B=\begin{bmatrix}3 & 9 \\10 & 2 \end{bmatrix}\)
এবং
\(A-B=\begin{bmatrix}2 & 3 \\1 & 0 \end{bmatrix}-\begin{bmatrix}1 & 6 \\9 & 2 \end{bmatrix}\)
\(=\begin{bmatrix}2-1 & 3-6 \\1-9 & 0-2 \end{bmatrix}\)
\(\therefore A-B=\begin{bmatrix} \ \ 1 & -3 \\-8 & -2 \end{bmatrix}\)
\(A+B\) নির্ণয়ের পদ্ধতিঃ
| A+B= | \(-1\) | \( \ \ \ 3\) | \(1\) | \(6\) | \(+\) | ||
| \(-4\) | \(-3\) | \(4\) | \(0\) | ||||
| \( \ \ \ 7\) | \( \ \ \ 2\) | \(8\) | \(5\) | ||||
| \( \ \ \ 9\) | \( \ \ \ 10\) | \(11\) | \(12\) |
| \(13\) | \(14\) | \( \ \ \ 3\) | \(1\) | ||
| \(15\) | \(1\) | \( \ \ \ 16\) | \(10\) | ||
| \(4\) | \(7\) | \( \ \ \ 8\) | \(2\) | ||
| \(9\) | \(10\) | \(-3\) | \(3\) |
| = | \(-1+13\) | \( \ \ \ 3+14\) | \(1+3\) | \(6+1\) | ||
| \(-4+15\) | \(-3+1\) | \(4+16\) | \(0+10\) | |||
| \( \ \ \ 7+4\) | \( \ \ \ 2+7\) | \(8+8\) | \(5+2\) | |||
| \( \ \ \ 9+9\) | \( \ \ \ 10+10\) | \(11+(-3)\) | \(12+3\) |
| = | \(12\) | \( \ \ \ 17\) | \(4\) | \(7\) | ||
| \(11\) | \(-2\) | \(20\) | \(10\) | |||
| \( \ \ \ 11\) | \(9\) | \(16\) | \(7\) | |||
| \(18\) | \( \ \ \ 20\) | \(8\) | \(15\) |
| A-B= | \(-1\) | \( \ \ \ 3\) | \(1\) | \(6\) | \(-\) | ||
| \(-4\) | \(-3\) | \(4\) | \(0\) | ||||
| \( \ \ \ 7\) | \( \ \ \ 2\) | \(8\) | \(5\) | ||||
| \( \ \ \ 9\) | \( \ \ \ 10\) | \(11\) | \(12\) |
| \(13\) | \(14\) | \( \ \ \ 3\) | \(1\) | ||
| \(15\) | \(1\) | \( \ \ \ 16\) | \(10\) | ||
| \(4\) | \(7\) | \( \ \ \ 8\) | \(2\) | ||
| \(9\) | \(10\) | \(-3\) | \(3\) |
| = | \(-1-13\) | \( \ \ \ 3-14\) | \(1-3\) | \(6-1\) | ||
| \(-4-15\) | \(-3-1\) | \(4-16\) | \(0-10\) | |||
| \( \ \ \ 7-4\) | \( \ \ \ 2-7\) | \(8-8\) | \(5-2\) | |||
| \( \ \ \ 9-9\) | \( \ \ \ 10-10\) | \(11-(-3)\) | \(12-3\) |
| = | \(-14\) | \( -11\) | \(-2\) | \( \ \ \ 5\) | ||
| \(-19\) | \(-4\) | \(-12\) | \(-10\) | |||
| \( \ \ \ 3\) | \(-5\) | \( \ \ \ 0\) | \( \ \ \ 3\) | |||
| \( \ \ \ 0\) | \( \ \ \ 0\) | \( \ \ \ 14\) | \( \ \ \ 9\) |
https://www.youtube.com/embed/Ur7cpa93dJk?si=dGm38vX5hH7Np91y
ম্যাট্রিক্সের স্কেলার গুণন
Scalar Multiplication of a Matrix
ম্যাট্রিক্সের স্কেলার গুণন (Scalar Multiplication of a Matrix): \(k\) একটি ধ্রুবসংখ্যা হলে \(kA\) এমন একটি ম্যাট্রিক্স যার প্রতিটি ভুক্তি \(A\) ম্যাট্রিক্সের প্রতিসঙ্গী ভুক্তির \(k\) গুণ।
যেমনঃ \(A=\begin{bmatrix}4 & 4 \\5 & 6 \end{bmatrix}\) হলে,
\(kA=\begin{bmatrix}4k & 4k \\5k & 6k \end{bmatrix}\)
এবং \(B=\begin{bmatrix}2 & 5 & 1 \\3 & 4 & 2 \\4 & 1 & 3 \end{bmatrix}\) হলে,
\(4B=\begin{bmatrix}2\times4 & 5\times4 & 1\times4 \\3\times4 & 4\times4 & 2\times4 \\4\times4 & 1\times4 & 3\times4 \end{bmatrix}\)
\(=\begin{bmatrix}8 & 20 & 4 \\12 & 16 & 8 \\16 & 4 & 12 \end{bmatrix}\)
যেমনঃ \(A=\begin{bmatrix}4 & 4 \\5 & 6 \end{bmatrix}\) হলে,
\(kA=\begin{bmatrix}4k & 4k \\5k & 6k \end{bmatrix}\)
এবং \(B=\begin{bmatrix}2 & 5 & 1 \\3 & 4 & 2 \\4 & 1 & 3 \end{bmatrix}\) হলে,
\(4B=\begin{bmatrix}2\times4 & 5\times4 & 1\times4 \\3\times4 & 4\times4 & 2\times4 \\4\times4 & 1\times4 & 3\times4 \end{bmatrix}\)
\(=\begin{bmatrix}8 & 20 & 4 \\12 & 16 & 8 \\16 & 4 & 12 \end{bmatrix}\)
https://www.youtube.com/embed/6RCeafnayq0?si=hM30e0I827U8bb2b
ম্যাট্রিক্সের গুণন
Multiplication of Matrices
গুণন যোগ্যতাঃ \(A\) ও \(B\) ম্যাট্রিক্সের গুণফল \(AB\) সংজ্ঞায়িত হবে যদি \(A\) এর কলামের সংখ্যা \(B\) এর সারি সংখ্যার সমান হয় এবং \(AB\) অসংজ্ঞায়িত হবে যদি \(A\) এর কলামের সংখ্যা \(B\) এর সারি সংখ্যার সমান না হয়।
গুণন প্রক্রিয়াঃ প্রথম ম্যাট্রিক্সের প্রতিটি সারি দ্বারা দ্বিতীয় ম্যাট্রিক্সের প্রতিটি কলামকে গুণ করতে হবে। প্রথম ম্যাট্রিক্সের \(i-\)তম সারির প্রতিটি ভুক্তির সহিত দ্বিতীয় ম্যাট্রিক্সের \(j-\)তম কলামের অনুরূপ ভুক্তিগুলি গুণ করে প্রাপ্ত গুণফলগুলির যোগফলই হবে গুণফল ম্যাট্রিক্সের \((i, \ j)\) তম ভুক্তি।
একটি \(3\times2\) ও একটি \(2\times2\) ক্রমের ম্যাট্রিক্সের গুণ প্রক্রিয়া নিম্নরূপঃ
\(\begin{bmatrix}a_{11} & a_{12} \\a_{21} & a_{22} \\a_{31} & a_{32} \end{bmatrix} \begin{bmatrix}b_{11} & b_{12} \\b_{21} & b_{22} \end{bmatrix}\)
\(=\begin{bmatrix}a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} \\a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22} \\a_{31}b_{11}+a_{32}b_{21} & a_{31}b_{12}+a_{32}b_{22} \end{bmatrix}\)
দুইটি ম্যাট্রিক্স \(A\) ও \(B\) এর গুণফল \(AB\) সংজ্ঞায়িত হলে, \(AB\) নির্ণয়ের পদ্ধতিঃ \(A\) এর প্রথম সারির ভুক্তিগুলি দ্বারা \(B\) এর প্রথম কলামের সকল অনুরূপ ভুক্তি গুণ করে গুণফলগুলি পর্যায়ক্রমে পাশাপাশি যোগ করতে হবে এবং এই যোগফল \(AB\) ম্যাট্রিক্সের প্রথম সারির প্রথম ভুক্তি হবে, যাকে \(AB\) এর \((1, \ 1)\)-তম ভুক্তি বলা হয়।
আবার, \(A\) এর প্রথম সারির ভুক্তিগুলি দ্বারা \(B\) এর দ্বিতীয় কলামের সকল অনুরূপ ভুক্তি গুণ করে গুণফলগুলি পর্যায়ক্রমে পাশাপাশি যোগ করতে হবে এবং এই যোগফল \(AB\) ম্যাট্রিক্সের প্রথম সারির দ্বিতীয় ভুক্তি হবে, যাকে \(AB\) এর \((1, \ 2)\)-তম ভুক্তি বলা হয়।
অনুরূপভাবে, \(A\) এর প্রথম সারির সাথে \(B\) এর অবশিষ্ট কলামগুলির প্রয়োগে প্রাপ্ত ফলাফলগুলি পর্যায়ক্রমে \(AB\) ম্যাট্রিক্সের প্রথম সারির ভুক্তি হবে।
পুনরায়, \(A\) এর দ্বিতীয় সারি দিয়ে \(B\) এর প্রত্যেক কলামকে একইভাবে গুণ করলে প্রাপ্ত ফলকে \(AB\) ম্যাট্রিক্সের দ্বিতীয় সারি বরাবর বসাতে হবে। এভাবে অগ্রসর হয়ে \(A\) এর সকল সারি প্রয়োগ সমাপ্ত হলে, \(AB\) ম্যাট্রিক্স পাওয়া যাবে।
যেমনঃ ধরি,
\(A\) এর ক্রম \(m\times{n}\) এবং \(B\) এর ক্রম \(n\times{p},\) সুতরাং \(AB\) নির্ণয় সম্ভব এবং \(AB\) এর ক্রম হবে \(m\times{p}\)
একইভাবে, দুইটি ম্যাট্রিক্স \(A\) এর ক্রম \(4\times4\) এবং \(B\) এর ক্রম \(4\times3,\) সুতরাং \(AB\) নির্ণয় সম্ভব এবং \(AB\) এর ক্রম হবে \(4\times3\)
অর্থাৎ, প্রথম ম্যাট্রিক্সের সারি সংখ্যা এবং দ্বিতীয় ম্যাট্রিক্সের কলাম সংখ্যা নিয়ে গুণফল ম্যাট্রিক্সের ক্রম গঠিত হয়।
\(AB\) এর \((1, \ 1)\)-তম ভুক্তি নির্ণয়ের পদ্ধতিঃ
\(AB\) এর \((1, \ 2)\)-তম ভুক্তি নির্ণয়ের পদ্ধতিঃ
\(AB\) এর \((1, \ 3)\)-তম ভুক্তি নির্ণয়ের পদ্ধতিঃ
\(AB\) এর \((2, \ 1)\)-তম ভুক্তি নির্ণয়ের পদ্ধতিঃ
\(AB\) এর \((2, \ 2)\)-তম ভুক্তি নির্ণয়ের পদ্ধতিঃ
অনুরূপভাবে, \(AB\) নির্ণয়ের পদ্ধতি নিম্নরূপঃ
গুণন প্রক্রিয়াঃ প্রথম ম্যাট্রিক্সের প্রতিটি সারি দ্বারা দ্বিতীয় ম্যাট্রিক্সের প্রতিটি কলামকে গুণ করতে হবে। প্রথম ম্যাট্রিক্সের \(i-\)তম সারির প্রতিটি ভুক্তির সহিত দ্বিতীয় ম্যাট্রিক্সের \(j-\)তম কলামের অনুরূপ ভুক্তিগুলি গুণ করে প্রাপ্ত গুণফলগুলির যোগফলই হবে গুণফল ম্যাট্রিক্সের \((i, \ j)\) তম ভুক্তি।
একটি \(3\times2\) ও একটি \(2\times2\) ক্রমের ম্যাট্রিক্সের গুণ প্রক্রিয়া নিম্নরূপঃ
\(\begin{bmatrix}a_{11} & a_{12} \\a_{21} & a_{22} \\a_{31} & a_{32} \end{bmatrix} \begin{bmatrix}b_{11} & b_{12} \\b_{21} & b_{22} \end{bmatrix}\)
\(=\begin{bmatrix}a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} \\a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22} \\a_{31}b_{11}+a_{32}b_{21} & a_{31}b_{12}+a_{32}b_{22} \end{bmatrix}\)
দুইটি ম্যাট্রিক্স \(A\) ও \(B\) এর গুণফল \(AB\) সংজ্ঞায়িত হলে, \(AB\) নির্ণয়ের পদ্ধতিঃ \(A\) এর প্রথম সারির ভুক্তিগুলি দ্বারা \(B\) এর প্রথম কলামের সকল অনুরূপ ভুক্তি গুণ করে গুণফলগুলি পর্যায়ক্রমে পাশাপাশি যোগ করতে হবে এবং এই যোগফল \(AB\) ম্যাট্রিক্সের প্রথম সারির প্রথম ভুক্তি হবে, যাকে \(AB\) এর \((1, \ 1)\)-তম ভুক্তি বলা হয়।
আবার, \(A\) এর প্রথম সারির ভুক্তিগুলি দ্বারা \(B\) এর দ্বিতীয় কলামের সকল অনুরূপ ভুক্তি গুণ করে গুণফলগুলি পর্যায়ক্রমে পাশাপাশি যোগ করতে হবে এবং এই যোগফল \(AB\) ম্যাট্রিক্সের প্রথম সারির দ্বিতীয় ভুক্তি হবে, যাকে \(AB\) এর \((1, \ 2)\)-তম ভুক্তি বলা হয়।
অনুরূপভাবে, \(A\) এর প্রথম সারির সাথে \(B\) এর অবশিষ্ট কলামগুলির প্রয়োগে প্রাপ্ত ফলাফলগুলি পর্যায়ক্রমে \(AB\) ম্যাট্রিক্সের প্রথম সারির ভুক্তি হবে।
পুনরায়, \(A\) এর দ্বিতীয় সারি দিয়ে \(B\) এর প্রত্যেক কলামকে একইভাবে গুণ করলে প্রাপ্ত ফলকে \(AB\) ম্যাট্রিক্সের দ্বিতীয় সারি বরাবর বসাতে হবে। এভাবে অগ্রসর হয়ে \(A\) এর সকল সারি প্রয়োগ সমাপ্ত হলে, \(AB\) ম্যাট্রিক্স পাওয়া যাবে।
যেমনঃ ধরি,
|
|
একইভাবে, দুইটি ম্যাট্রিক্স \(A\) এর ক্রম \(4\times4\) এবং \(B\) এর ক্রম \(4\times3,\) সুতরাং \(AB\) নির্ণয় সম্ভব এবং \(AB\) এর ক্রম হবে \(4\times3\)
অর্থাৎ, প্রথম ম্যাট্রিক্সের সারি সংখ্যা এবং দ্বিতীয় ম্যাট্রিক্সের কলাম সংখ্যা নিয়ে গুণফল ম্যাট্রিক্সের ক্রম গঠিত হয়।
\(AB\) এর \((1, \ 1)\)-তম ভুক্তি নির্ণয়ের পদ্ধতিঃ
|
|
| = | \(-1×13 + 3×15 + 1×4 + 6×9\) | \(\Box\) | \(\Box\) | ||
| \(\Box\) | \(\Box\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) |
|
|
| = | \(\Box\) | \(-1×14 + 3×1 + 1×7 + 6×10\) | \(\Box\) | ||
| \(\Box\) | \(\Box\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) |
|
|
| = | \(\Box\) | \(\Box\) | \(-1×3 + 3×16 + 1×8 + 6×-3\) | ||
| \(\Box\) | \(\Box\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) |
|
|
| = | \(\Box\) | \(\Box\) | \(\Box\) | ||
| \(-4×13 + -3×15 + 4×4 + 0×9\) | \(\Box\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) |
|
|
| = | \(\Box\) | \(\Box\) | \(\Box\) | ||
| \(\Box\) | \(-4×14 + -3×1 + 4×7 + 0×10\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) | |||
| \(\Box\) | \(\Box\) | \(\Box\) |
| AB= | \(-1\) | \( \ \ \ 3\) | \(1\) | \(6\) | \(\times\) | ||
| \(-4\) | \(-3\) | \(4\) | \(0\) | ||||
| \( \ \ \ 7\) | \( \ \ \ 2\) | \(8\) | \(5\) | ||||
| \( \ \ \ 9\) | \( \ \ \ 10\) | \(11\) | \(12\) |
| \(13\) | \(14\) | \( \ \ \ 3\) | ||
| \(15\) | \(1\) | \( \ \ \ 16\) | ||
| \(4\) | \(7\) | \( \ \ \ 8\) | ||
| \(9\) | \(10\) | \(-3\) |
| = | \(-1\times13+3\times15+1\times4+6\times9\) | \(-1\times14+3\times1+1\times7+6\times10\) | \(-1\times3+3\times16+1\times8+6\times-3\) | ||
| \(-4\times13+(-3)\times15+4\times4+0\times9\) | \(-4\times14+(-3)\times1+4\times7+0\times10\) | \(-4\times3+(-3)\times16+4\times8+0\times-3\) | |||
| \( \ \ \ 7\times13+2\times15+8\times4+5\times9\) | \( \ \ \ 7\times14+2\times1+8\times7+5\times10\) | \( \ \ \ 7\times3+2\times16+8\times8+5\times(-3)\) | |||
| \( \ \ \ 9\times13+10\times15+11\times4+12\times9\) | \( \ \ \ 9\times14+10\times1+11\times7+12\times10\) | \( \ \ \ 9\times3+10\times16+11\times8+12\times-3\) |
| = | \(-13+45+4+54\) | \(-14+3+7+60\) | \(-3+48+8-18\) | ||
| \(-52-45+16+0\) | \(-56-3+28+0\) | \(-12-48+32-0\) | |||
| \( \ \ \ 91+150+44+108\) | \( \ \ \ 98+2+56+50\) | \( \ \ \ 21+32+64-15\) | |||
| \( \ \ \ 117+150+44+108\) | \( \ \ \ 126+10+77+120\) | \( \ \ \ 27+160+88-36\) |
| = | \( \ \ \ 90\) | \( \ \ \ 56 \) | \( \ \ \ 35\) | ||
| \(-81\) | \(-31\) | \(-28\) | |||
| \( \ \ \ 198\) | \( \ \ \ 206\) | \( \ \ \ 102\) | |||
| \( \ \ \ 419\) | \( \ \ \ 333\) | \( \ \ \ 239\) |
https://www.youtube.com/embed/hgs8UyDJXP4?si=Mu2ZCkDm3yt-jI_p

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000006