এ অধ্যায়ের পাঠ্যসূচী
- স্পর্শক (Tangent)
- অভিলম্ব (Normal)
- অন্তরজের জ্যামিতিক ব্যাখ্যা (Geometric Interpretation Of Derivative)
- নির্দিষ্ট বিন্দুতে বক্ররেখার স্পর্শকের ঢাল (The slope of the tangent to the curve at a given point)
- নির্দিষ্ট বিন্দুতে বক্ররেখার স্পর্শকের সমীকরণ (The equation of the tangent to the curve at a given point)
- নির্দিষ্ট বিন্দুতে বক্ররেখার অভিলম্বের সমীকরণ (The equation of the normal to the curve at a given point)
- \(f(x,y)=0\) বক্ররেখার \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ (The equation of the tangent to the curve \(f(x,y)=0\) at a given point \((x_{1}, y_{1})\))
- পরিবর্তনের হার হিসাবে অন্তরজ (The Derivative as a rate of change)
- স্পর্শকের ভিন্ন ভিন্ন অবস্থান সাপেক্ষে এর ঢাল (Determine its slope with different positions of tangents)
- অধ্যায় \(ix.H\)-এর উদাহরণসমুহ
- অধ্যায় \(ix.H\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(ix.H\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(ix.H\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(ix.H\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
স্পর্শক
Tangent
স্পর্শকঃ মনে করি কোনো বক্ররেখার উপর \(P\) একটি বিন্দু। \(P\) বিন্দু দিয়ে একটি সরলরেখা অঙ্কন করি যা ঐ বক্ররেখাকে \(Q\) বিন্দুতে ছেদ করে। সুতরাং আমরা বলতে পারি \(PQ\) একটি ছেদক। এখন \(P\) কে কেন্দ্র করে যদি ছেদক \(PQ\) কে এমনভাবে ঘুরানো হয় যেন \(Q\) বিন্দু বক্ররেখা বরাবর \(P\) এর সমীপবর্তী হয়ে \(P\) বিন্দুর সহিত সম্পুর্ণভাবে মিলে যায়। ছেদক \(PQ\) এর এই সীমায়িত অবস্থানে \(P\) বিন্দুতে ঐ বক্ররেখার উপর \(PQ\) এর এই অবস্থানকে স্পর্শক (Tangent) বলে।
অভিলম্ব
Normal
অভিলম্বঃ কোনো বক্ররেখার স্পর্শকের স্পর্শবিন্দু দিয়ে অতিক্রান্ত এবং স্পর্শকের উপর অঙ্কিত লম্ব রেখাটিকে বক্ররেখাটির অভিলম্ব (Normal) বলে।
অন্তরজের জ্যামিতিক ব্যাখ্যা
Geometric Interpretation Of Derivative
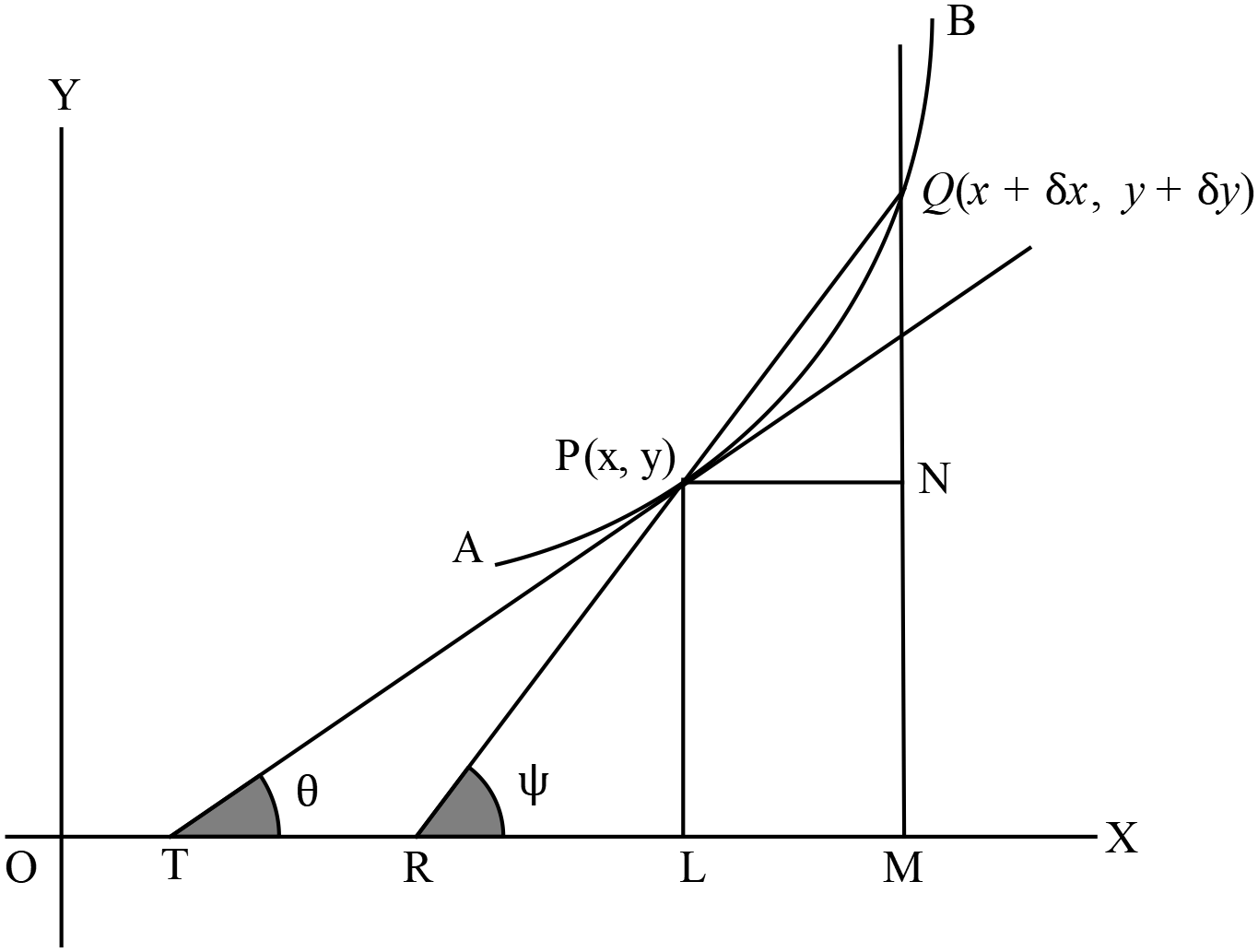মনে করি, \(y=f(x)\) একটি অবিচ্ছিন্ন ফাংশন এবং তার লেখচিত্র \(AB\) বক্ররেখা। \(P(x, y)\) ও \(Q(x+\delta{x}, y+\delta{y})\) এই বক্ররেখার উপর নিকটবর্তী দুইটি বিন্দু।
\(PQ\) সরলরেখাকে বর্ধিত করলে তা \(X\) অক্ষের সাথে \(\psi\) কোণ উৎপন্ন করে। অর্থাৎ \(\angle{XRP}=\psi\) । এখন \(P\) ও \(Q\) বিন্দু হতে \(X\) অক্ষের উপর যথাক্রমে \(PL\) ও \(QM\) লম্ব আঁকি। আবার, \(P\) বিন্দু হতে \(QM\) এর উপর \(PN\) লম্ব আঁকি।এখন,
\(PN=LM=OM-OL\)
\(=x+\delta{x}-x=\delta{x}\)
এবং
\(NQ=MQ-MN=MQ-LP\)
\(=y+\delta{y}-y=\delta{y}\).
\(\angle{NPQ}=\angle{XRP}=\psi\).
\(\therefore \tan{\psi}=\frac{NQ}{PN}=\frac{\delta{y}}{\delta{x}} .......(1)\).
এখন যদি \(AB\) বক্ররেখার উপর দিয়ে ক্রমশ \(Q\rightarrow{P}\) হয়, তবে \(PQ\) জ্যা \(PT\) স্পর্শক হবে। সেক্ষেত্রে \(\delta{x}\rightarrow{0}\) এবং \(\psi\rightarrow{\theta}\) হবে, যেখানে \(\theta=\angle{XPT}\).
এখন,
\[\lim_{\delta{x} \rightarrow{\theta}}\tan{\psi}=\lim_{\delta{x} \rightarrow{0}}\frac{\delta{y}}{\delta{x}}\] ➜ \((1)\)-এর সাহায্যে।
\[\therefore \tan{\theta}=\frac{dy}{dx}\] ➜ \[\because \lim_{\delta{x} \rightarrow{0}}\frac{\delta{y}}{\delta{x}}=\frac{dy}{dx}\]
সুতরাং \(\frac{dy}{dx}=\tan{\theta}=AB\) বক্ররেখার \(P(x, y)\) বিন্দুতে স্পর্শকের ঢাল।
নির্দিষ্ট বিন্দুতে বক্ররেখার স্পর্শকের ঢাল
The slope of the tangent to the curve at a given point
\(X\) অক্ষের ধনাত্মক দিকের সাথে \(\theta\) কোণ উৎপন্ন করে এরূপ রেখার ঢাল \(m=\tan{\theta}\).
যে স্পর্শক \(y=f(x)\) বক্ররেখাকে \((x, y)\) বিন্দুতে স্পর্শ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সাথে \(\theta\) কোণ উৎপন্ন করে তার ঢাল,
\(m=\tan{\theta}=\frac{dy}{dx}=f^{\prime}(x)\).
যে স্পর্শক \(y=f(x)\) বক্ররেখাকে \((x_{1}, y_{1})\) বিন্দুতে স্পর্শ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সাথে \(\theta\) কোণ উৎপন্ন করে তার ঢাল,
\(m=\tan{\theta}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}=f^{\prime}(x_{1})\).
যে স্পর্শক \(y=f(x)\) বক্ররেখাকে \((x, y)\) বিন্দুতে স্পর্শ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সাথে \(\theta\) কোণ উৎপন্ন করে তার ঢাল,
\(m=\tan{\theta}=\frac{dy}{dx}=f^{\prime}(x)\).
যে স্পর্শক \(y=f(x)\) বক্ররেখাকে \((x_{1}, y_{1})\) বিন্দুতে স্পর্শ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সাথে \(\theta\) কোণ উৎপন্ন করে তার ঢাল,
\(m=\tan{\theta}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}=f^{\prime}(x_{1})\).
নির্দিষ্ট বিন্দুতে বক্ররেখার স্পর্শকের সমীকরণ
The equation of the tangent to the curve at a given point
\(y=f(x)\) বক্ররেখার \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ
\(y-y_{1}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}(x-x_{1})\).
\(y-y_{1}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}(x-x_{1})\).
নির্দিষ্ট বিন্দুতে বক্ররেখার অভিলম্বের সমীকরণ
The equation of the normal to the curve at a given point
\(y=f(x)\) বক্ররেখার \((x_{1}, y_{1})\) বিন্দুতে অভিলম্বের সমীকরণ
\((y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}+(x-x_{1})=0\).
\((y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}+(x-x_{1})=0\).
\(f(x,y)=0\) বক্ররেখার \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ
The equation of the tangent to the curve \(f(x,y)=0\) at a given point \((x_{1}, y_{1})\)
\(f(x,y)=0\) বক্ররেখার \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ
\((x-x_{1})f_{(x_{1})}+(y-y_{1})f_{(y_{1})}=0\).
\((x-x_{1})f_{(x_{1})}+(y-y_{1})f_{(y_{1})}=0\).
পরিবর্তনের হার হিসাবে অন্তরজ
The Derivative as a rate of change
অন্তরীকরণের আর একটি উল্লেখযোগ্য দিক হচ্ছে, অন্তরীকরণকে পরিবর্তনের হার পরিমাপক হিসাবেও ব্যবহার করা যায়। উদাহরণস্বরূপ বলা যায়, যদি \(t\) সময়ে কোনো চলমান বিন্দুর অতিক্রান্ত দূরত্ব \(s\) হয় তবে \(s, t\) এর একটি ফাংশন অর্থাৎ, \(s=f(t)\) যদি \(t+\delta{t}\) সময়ে \(s\) এর মাণ \(s+\delta{s}\) হয়, তবে \(\delta{t}\) সময়ে অতিক্রান্ত দূরত্ব হয় \(\delta{s}\).
অতএব, \[\lim_{\delta{t} \rightarrow 0}\frac{\delta{s}}{\delta{t}}\] চলমান বিন্দু কতৃক সেই মুহূর্তে একক সময়ে অতিক্রান্ত দূরত্বকে বোঝায়। কিন্তু সংজ্ঞানুসারে \[\lim_{\delta{t} \rightarrow 0}\frac{\delta{s}}{\delta{t}}=\frac{ds}{dt}\].
সুতরাং, \(\frac{ds}{dt}\) প্রকৃতপক্ষে সময়ের সাপেক্ষে দূরত্বের পরিবর্তনের হার অর্থাৎ চলমান বিন্দুটির গতিবেগ। অর্থাৎ বেগ, \(v=\frac{ds}{dt}\) অনুরূপভাবে, \(\frac{dv}{dt}\) সময়ের সাপেক্ষে গতিবেগ পরিবর্তনের হার অর্থাৎ ত্বরণ। আবার, ত্বরণ \(=\frac{dv}{dt}=\frac{d^2s}{dt^2}\).
সাধারণভাবে, যদি \(y, x\) এর ফাংশন হয় অর্থাৎ \(y=f(x)\) হয় তবে \(\frac{dy}{dx}, x\) এর সাপাক্ষে \(y\) এর পরিবর্তনের হার।
অতএব, \[\lim_{\delta{t} \rightarrow 0}\frac{\delta{s}}{\delta{t}}\] চলমান বিন্দু কতৃক সেই মুহূর্তে একক সময়ে অতিক্রান্ত দূরত্বকে বোঝায়। কিন্তু সংজ্ঞানুসারে \[\lim_{\delta{t} \rightarrow 0}\frac{\delta{s}}{\delta{t}}=\frac{ds}{dt}\].
সুতরাং, \(\frac{ds}{dt}\) প্রকৃতপক্ষে সময়ের সাপেক্ষে দূরত্বের পরিবর্তনের হার অর্থাৎ চলমান বিন্দুটির গতিবেগ। অর্থাৎ বেগ, \(v=\frac{ds}{dt}\) অনুরূপভাবে, \(\frac{dv}{dt}\) সময়ের সাপেক্ষে গতিবেগ পরিবর্তনের হার অর্থাৎ ত্বরণ। আবার, ত্বরণ \(=\frac{dv}{dt}=\frac{d^2s}{dt^2}\).
সাধারণভাবে, যদি \(y, x\) এর ফাংশন হয় অর্থাৎ \(y=f(x)\) হয় তবে \(\frac{dy}{dx}, x\) এর সাপাক্ষে \(y\) এর পরিবর্তনের হার।
স্পর্শকের ভিন্ন ভিন্ন অবস্থান সাপেক্ষে এর ঢাল নির্ণয়
Determine its slope with different positions of tangents
\(y=f(x)\) বক্ররেখার \((x, y)\) বিন্দুতে অঙ্কিত স্পর্শক
\((a)\) \(X\) অক্ষের সাথে সমান্তরাল বা \(Y\) অক্ষের উপর লম্ব হওয়ার শর্তঃ \(\frac{dy}{dx}=0\) \((b)\) \(X\) অক্ষের উপর লম্ব বা \(Y\) অক্ষের সাথে সমান্তরাল হওয়ার শর্তঃ \(\frac{dy}{dx}=\infty\) \((c)\) \(X\) অক্ষের ধনাত্মক দিকের সাথে \(45^{o}\) কোণ উৎপন্ন করার শর্তঃ \(\frac{dy}{dx}=1\) \((d)\) অক্ষদ্বয়ের সাথে সমান সমান কোণ উৎপন্ন করার শর্তঃ \(\frac{dy}{dx}=\pm{1}\) \((e)\) \(X\) অক্ষের ধনাত্মক দিকের সাথে স্থুলকোণ উৎপন্ন করার শর্তঃ \(\frac{dy}{dx}<0\) \((f)\) \(X\) অক্ষের ধনাত্মক দিকের সাথে সূক্ষ্ণকোণ উৎপন্ন করার শর্তঃ \(\frac{dy}{dx}>0\)
\((a)\) \(X\) অক্ষের সাথে সমান্তরাল বা \(Y\) অক্ষের উপর লম্ব হওয়ার শর্তঃ \(\frac{dy}{dx}=0\) \((b)\) \(X\) অক্ষের উপর লম্ব বা \(Y\) অক্ষের সাথে সমান্তরাল হওয়ার শর্তঃ \(\frac{dy}{dx}=\infty\) \((c)\) \(X\) অক্ষের ধনাত্মক দিকের সাথে \(45^{o}\) কোণ উৎপন্ন করার শর্তঃ \(\frac{dy}{dx}=1\) \((d)\) অক্ষদ্বয়ের সাথে সমান সমান কোণ উৎপন্ন করার শর্তঃ \(\frac{dy}{dx}=\pm{1}\) \((e)\) \(X\) অক্ষের ধনাত্মক দিকের সাথে স্থুলকোণ উৎপন্ন করার শর্তঃ \(\frac{dy}{dx}<0\) \((f)\) \(X\) অক্ষের ধনাত্মক দিকের সাথে সূক্ষ্ণকোণ উৎপন্ন করার শর্তঃ \(\frac{dy}{dx}>0\)
×
\(y=f(x)\) বক্ররেখার \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণঃ
\(y-y_{1}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}(x-x_{1})\)
\(y-y_{1}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}(x-x_{1})\)
Proof:
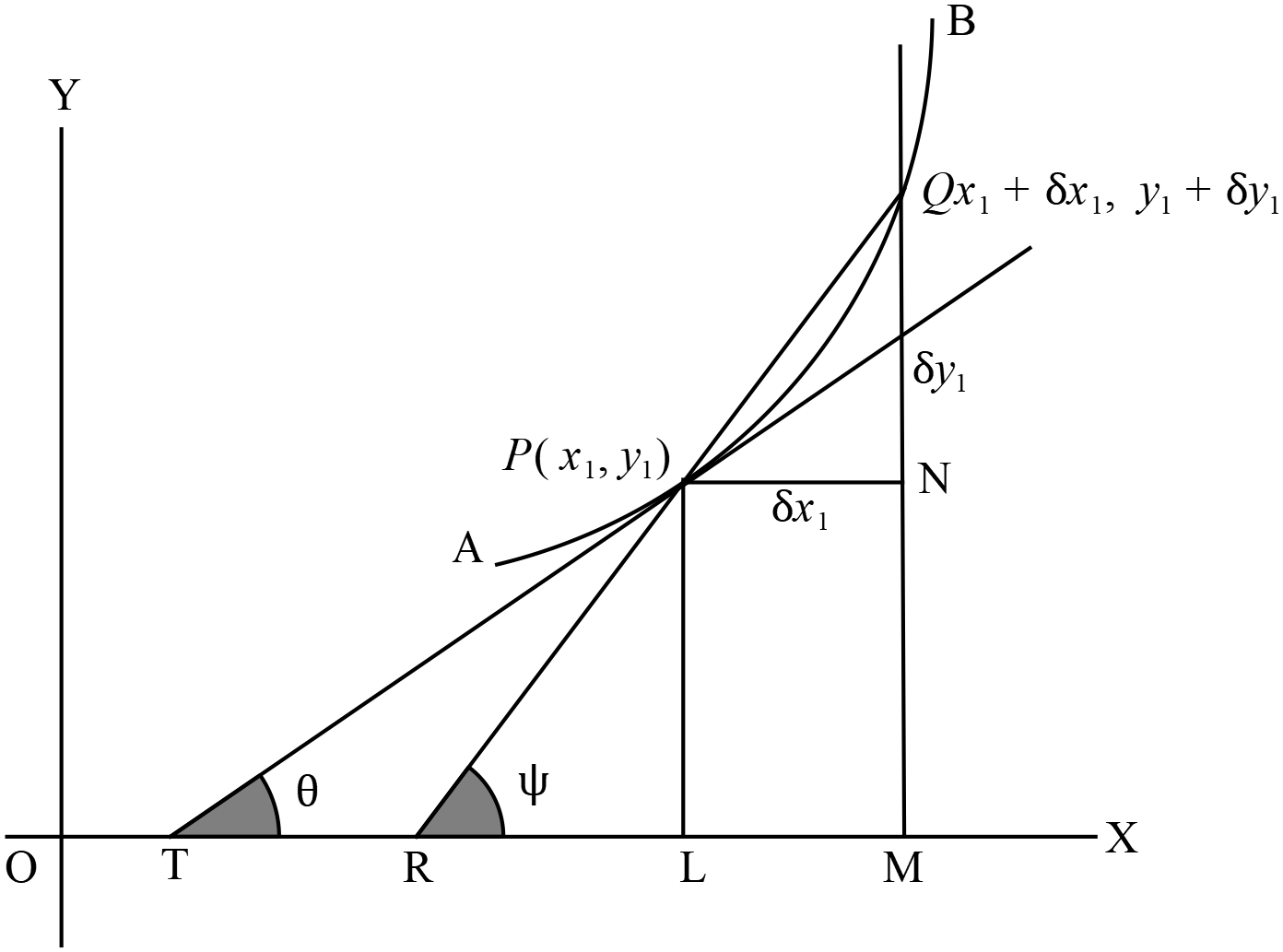মনে করি,\(y=f(x)\) বক্ররেখার উপর \(P(x_{1}, y_{1})\) একটি বিন্দু । \(P\) বিন্দু দিয়ে অতিক্রান্ত সরলরেখটি উক্ত বক্ররেখাটিকে \(Q(x_{1}+\delta{x_{1}}, y_{1}+\delta{y_{1}})\) বিন্দুতে ছেদ করেছে। সুতরাং \(PQ\) জ্যা এর সমীকরণ হবে
\(\frac{x-x_{1}}{x_{1}-x_{1}-\delta{x_{1}}}=\frac{y-y_{1}}{y_{1}-y_{1}-\delta{y_{1}}}\) ➜ যেহেতু দুইটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) দিয়ে গমনকারী সরলরেখার সমীকরণ \(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\)
এখানে, \((x, y)\) কে চলমান বিন্দু ধরা হয়েছে।
\(\Rightarrow \frac{x-x_{1}}{-\delta{x_{1}}}=\frac{y-y_{1}}{-\delta{y_{1}}}\)
\(\Rightarrow \frac{x-x_{1}}{\delta{x_{1}}}=\frac{y-y_{1}}{\delta{y_{1}}}\)
\(\Rightarrow \frac{y-y_{1}}{\delta{y_{1}}}=\frac{x-x_{1}}{\delta{x_{1}}}\)
\(\Rightarrow y-y_{1}=\frac{\delta{y_{1}}}{\delta{x_{1}}}(x-x_{1}) ......(1)\)
যদি \(P\rightarrow{Q}\) হয়, তখন \(\delta{x_{1}}\rightarrow{0}, \delta{y_{1}}\rightarrow{0}\) হবে।
\((1)\) নং হতে \(P(x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ
\[y-y_{1}=\lim_{\delta{x_{1}} \rightarrow 0}\frac{\delta{y_{1}}}{\delta{x_{1}}}(x-x_{1})\] যদি সীমার অস্তিত্ব থাকে।
\(\Rightarrow y-y_{1}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}(x-x_{1})\) ➜ \[\because \lim_{\delta{x_{1}} \rightarrow 0}\frac{\delta{y_{1}}}{\delta{x_{1}}}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}\]
অর্থাৎ \(y=f(x)\) বক্ররেখার \(P(x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ
\(y-y_{1}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}(x-x_{1})\)
এখানে, \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের ঢাল \(=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}\)
×
\(y=f(x)\) বক্ররেখার \((x_{1}, y_{1})\) বিন্দুতে অভিলম্বের সমীকরণঃ
\((y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}+(x-x_{1})=0\)
\((y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}+(x-x_{1})=0\)
Proof:
কোনো বক্ররেখার স্পর্শকের স্পর্শবিন্দু দিয়ে অতিক্রান্ত এবং স্পর্শকের উপর অঙ্কিত লম্ব রেখাটিকে বক্ররেখাটির অভিলম্ব বলে।
আমরা জানি,
\(P(x_{1}, y_{1})\) বিন্দু দিয়ে অতিক্রান্ত সরলরেখার সমীকরণ
\(y-y_{1}=m(x-x_{1}) ......(1)\) ➜ যেহেতু একটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) দিয়ে গমনকারী এবং তার ঢাল \((m)\) দেওয়া থাকিলে সরলরেখার সমীকরণ \(y-y_{1}=m(x-x_{1})\)
\(\Rightarrow (y-y_{1})\frac{1}{m}=(x-x_{1})\)
\(\Rightarrow (y-y_{1})\frac{1}{m}-(x-x_{1})=0 ......(2)\)
\((1)\) নং সরলরেখা \(P(x_{1}, y_{1})\) বিন্দুতে স্পর্শকের উপর লম্ব হবে
যদি,
\(m\times{\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}}=-1\) হয়।
\(\Rightarrow \left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}=-\frac{1}{m}\)
\(\therefore \frac{1}{m}=-\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}\)
\((2)\) নং সমীকরণ হতে,
\(\Rightarrow (y-y_{1})\times{-\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}}-(x-x_{1})=0\)
\(\Rightarrow -(y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}-(x-x_{1})=0\)
\(\therefore (y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}+(x-x_{1})=0\)
অর্থাৎ \(y=f(x)\) বক্ররেখার \(P(x_{1}, y_{1})\) বিন্দুতে অভিলম্বের সমীকরণ
\((y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}+(x-x_{1})=0\)
আমরা জানি,
\(P(x_{1}, y_{1})\) বিন্দু দিয়ে অতিক্রান্ত সরলরেখার সমীকরণ
\(y-y_{1}=m(x-x_{1}) ......(1)\) ➜ যেহেতু একটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) দিয়ে গমনকারী এবং তার ঢাল \((m)\) দেওয়া থাকিলে সরলরেখার সমীকরণ \(y-y_{1}=m(x-x_{1})\)
\(\Rightarrow (y-y_{1})\frac{1}{m}=(x-x_{1})\)
\(\Rightarrow (y-y_{1})\frac{1}{m}-(x-x_{1})=0 ......(2)\)
\((1)\) নং সরলরেখা \(P(x_{1}, y_{1})\) বিন্দুতে স্পর্শকের উপর লম্ব হবে
যদি,
\(m\times{\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}}=-1\) হয়।
\(\Rightarrow \left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}=-\frac{1}{m}\)
\(\therefore \frac{1}{m}=-\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}\)
\((2)\) নং সমীকরণ হতে,
\(\Rightarrow (y-y_{1})\times{-\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}}-(x-x_{1})=0\)
\(\Rightarrow -(y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}-(x-x_{1})=0\)
\(\therefore (y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}+(x-x_{1})=0\)
অর্থাৎ \(y=f(x)\) বক্ররেখার \(P(x_{1}, y_{1})\) বিন্দুতে অভিলম্বের সমীকরণ
\((y-y_{1})\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}+(x-x_{1})=0\)
×
\(f(x,y)=0\) বক্ররেখার \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণঃ
\((x-x_{1})f_{(x_{1})}+(y-y_{1})f_{(y_{1})}=0\)
\((x-x_{1})f_{(x_{1})}+(y-y_{1})f_{(y_{1})}=0\)
Proof:
মনে করি,\(f(x,y)=0\) বক্ররেখার উপর \(P(x_{1}, y_{1})\) একটি বিন্দু । \(P\) বিন্দু দিয়ে অতিক্রান্ত সরলরেখটি উক্ত বক্ররেখাটিকে \(Q(x_{1}+\delta{x_{1}}, y_{1}+\delta{y_{1}})\) বিন্দুতে ছেদ করেছে। সুতরাং \(PQ\) জ্যা এর সমীকরণ হবে
\(\frac{x-x_{1}}{x_{1}-x_{1}-\delta{x_{1}}}=\frac{y-y_{1}}{y_{1}-y_{1}-\delta{y_{1}}}\) ➜ যেহেতু দুইটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) দিয়ে গমনকারী সরলরেখার সমীকরণ \(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\)
এখানে, \((x, y)\) কে চলমান বিন্দু ধরা হয়েছে।
\(\Rightarrow \frac{x-x_{1}}{-\delta{x_{1}}}=\frac{y-y_{1}}{-\delta{y_{1}}}\)
\(\Rightarrow \frac{x-x_{1}}{\delta{x_{1}}}=\frac{y-y_{1}}{\delta{y_{1}}}\)
\(\Rightarrow \frac{y-y_{1}}{\delta{y_{1}}}=\frac{x-x_{1}}{\delta{x_{1}}}\)
\(\Rightarrow y-y_{1}=\frac{\delta{y_{1}}}{\delta{x_{1}}}(x-x_{1}) ......(1)\)
যদি \(P\rightarrow{Q}\) হয়, তখন \(\delta{x_{1}}\rightarrow{0}, \delta{y_{1}}\rightarrow{0}\) হবে।
\((1)\) নং হতে \(P(x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ
\[y-y_{1}=\lim_{\delta{x_{1}} \rightarrow 0}\frac{\delta{y_{1}}}{\delta{x_{1}}}(x-x_{1})\] যদি সীমার অস্তিত্ব থাকে।
\(\Rightarrow y-y_{1}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}(x-x_{1})\) ➜ \[\because \lim_{\delta{x_{1}} \rightarrow 0}\frac{\delta{y_{1}}}{\delta{x_{1}}}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}\]
অর্থাৎ \(f(x,y)=0\) বক্ররেখার \(P(x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ
\(y-y_{1}=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}(x-x_{1}) ......(2)\)
এখানে, \((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের ঢাল \(=\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}\)
এখন,
আংশিক অন্তরীকরণের পূর্ণ বৃদ্ধির হার নির্ণয়ের ক্ষেত্রে আমরা জানি,
\(\frac{dy}{dx}=-\frac{f_{x}}{f_{y}}\) যদি \(f_{y}\ne{0}\) হয়।
\((x_{1}, y_{1})\) বিন্দুতে স্পর্শকের ঢাল
\(\left(\frac{dy}{dx}\right)_{(x_{1}, y_{1})}=-\frac{f_{x_{1}}}{f_{y_{1}}} .....(3)\)
\((2)\) ও \((3)\) হতে পাই,
\(y-y_{1}=-\frac{f_{x_{1}}}{f_{y_{1}}}(x-x_{1})\)
\(\Rightarrow (y-y_{1})f_{y_{1}}=-f_{x_{1}}(x-x_{1})\)
\(\Rightarrow f_{x_{1}}(x-x_{1})+(y-y_{1})f_{y_{1}}=0\)
\(\therefore (x-x_{1})f_{x_{1}}+(y-y_{1})f_{y_{1}}=0\)
অর্থাৎ \(f(x,y)=0\) বক্ররেখার \(P(x_{1}, y_{1})\) বিন্দুতে স্পর্শকের সমীকরণ,
\((x-x_{1})f_{x_{1}}+(y-y_{1})f_{y_{1}}=0\)
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000003