এ অধ্যায়ের পাঠ্যসূচী।
- ঐতিহাসিক পটভূমি (Historical Background)
- বৃত্ত (Circle)
- বৃত্তের সমীকরণ চিহ্নিতকরণের উপায় (Methods of identifying the equation of a circle)
- কেন্দ্র মূলবিন্দু এবং নির্দিষ্ট ব্যাসার্ধবিশিষ্ট বৃত্তের সমীকরণ (Equation of circle with center origin and fixed radius)
- নির্দিষ্ট কেন্দ্র এবং ব্যাসার্ধবিশিষ্ট বৃত্তের সমীকরণ (Equation of circle with fixed center and radius)
- বৃত্তের সাধারণ সমীকরণ (General equation of circle)
- সাধারণ দ্বিঘাত সমীকরণ (General quadratic equation)
- নির্দিষ্ট বিন্দুতে কেন্দ্র এবং একটি নির্দিষ্ট বিন্দুগামী বৃত্তের সমীকরণ (Equation of a circle with center at a given point and through a given point)
- নির্দিষ্ট দুইটি বিন্দুর সংযোগ রেখাংশকে ব্যাস ধরে বৃত্তের সমীকরণ (The equation of a circle is the diameter of the line joining two given points)
- মূলবিন্দুগামী বৃত্তের সাধারণ সমীকরণ (General equation of the circle passing through the origin)
- বৃত্তের সাধারণ সমীকরণের অক্ষদ্বয়কে স্পর্শ করার শর্ত (The condition of touching two axes of the general equation of a circle)
- বৃত্তের সাধারণ সমীকরণ যখন উভয় অক্ষকে ছেদ করে (General equation of the circle when it intersects both axes)
- একটি বৃত্ত ও একটি সরলরেখার ছেদবিন্দুগামী বৃত্তের সমীকরণ (Equation of the intersection of a circle and a straight line)
- দুইটি নির্দিষ্ট বিন্দুগামী বৃত্তের সমীকরণ 'খলিফার নিয়ম' (Equation of two circles through fixed points 'Rule of the Caliph')
- বৃত্তের সাপেক্ষে কোনো বিন্দুর আপেক্ষিক অবস্থান (The relative position of a point with respect to a circle)
- দুইটি বৃত্তের পরস্পরকে স্পর্শ করার শর্ত (The condition of two circles touching each other)
- দুইটি বৃত্তের সাধারণ জ্যা এর সমীকরণ (Equation of common chord of two circles)
- দুইটি বৃত্তের ছেদবিন্দুগামী বৃত্তের সমীকরণ (Equation of the circle to the point of intersection of two circles)
- পোলার স্থানাঙ্কে বৃত্তের সমীকরণ (Equation of circle in polar coordinates)
- বৃত্তের পরামিতিক সমীকরণ (Parametric equation of circle)
- অধ্যায় \(4A\)-এর উদাহরণসমুহ
- অধ্যায় \(4A\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(4A\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(4A\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(4A\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
ঐতিহাসিক পটভূমি ( Historical Background )
বৃত্ত
The Circle
ইউক্লিড
৩০০ খ্রিষ্টপূর্বাব্দে ইউক্লিড তাঁর এলিমেন্ট গ্রন্থের তৃতীয় খন্ডে বৃত্তের বৈশিষ্ট্যসমূহের উপর আলোচনা করেন।
বক্ররেখার মধ্যে বৃত্ত সর্বাধীক পরিচিত এবং গুরুত্বপূর্ণ। স্কুল গণিতে বৃত্ত সম্পর্কিত বিভিন্ন বিষয় আলোচিত হয়েছে। কোনো সমতলে একটি চলমান বিন্দু এমনভাবে পরিভ্রমণ করে যে, চলমান বিন্দু হতে ঐ সমতলস্থ কোনো নির্দিষ্ট বিন্দুর দূরত্ব সর্বদা সমান হয়, তবে উক্ত চলমান বিন্দুর সঞ্চারপথটিই বৃত্ত। নির্দিষ্ট দূরত্বকে বৃত্তের ব্যাসার্ধ এবং নির্দিষ্ট বিন্দুকে বৃত্তের কেন্দ্র বলে। গ্রীক শব্দ 'Kirkos' থেকে বৃত্ত (Circle) শব্দটি এসেছে। 'Kirkos' শব্দটির অর্থ আংটা।
বৃত্ত সম্পর্কে মানুষের ধারণা আক্রিতিক। গ্রিক দার্শনিক ইউক্লিড 
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। , প্লেটোর 
প্লেটো (Plato) (খ্রিষ্টপূর্ব ৪২৭ - খ্রিষ্টপূর্ব ৩৪৭) বিশ্ববিখ্যাত গ্রিক দার্শনিক। তিনি দার্শনিক সক্রেটিসের ছাত্র ছিলেন এবং দার্শনিক এরিস্টটল তার ছাত্র ছিলেন। এবং আর্কিমিডিস 
আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। বৃত্তের পরিমার্জন করেন। ১৭০০ খ্রিস্টাব্দে রাইন্ড প্যাপিরাস 
The late Alexander Henry Rhind was the only surviving son of Josiah Rhind of Sibster, banker in Wick. He was born on the 26th July 1833, and during his earlier years pursued his studies at the Pulteneytown Academy, under the tuition of Mr Andrew Scott, now Professor of Oriental Languages in the University of Aberdeen. He then proceeded to the University of Edinburgh, where he became a student in the class of Natural History in the session of 1848-49, and in the class of Natural Philosophy in the session of 1849-50. ( Rhind Papyrus) বৃত্তের ক্ষেত্রফল নির্ণয়ের একটি পদ্ধতি উদ্ভাবন করেন। গাড়ীর চাকা, চন্দ্র, সূর্য এবং গাছের প্রস্তছেদ প্রভৃতি বস্তু বৃত্তাকার দেখায়। স্থানাংক জ্যামিতিতে, ক্যালকুলাসে, জ্যোতির্বিদ্যায় এবং কম্পিউটার গ্রাফিক্স ডিজাইনে বৃত্ত সম্পর্কিত অধ্যয়ন গুরুত্বপূর্ণ। প্রাচীন সভ্যতায় যোগাযোগের মাধ্যম চাকাবৃত্তের ধারণা থেকে সৃষ্ট, যা এই উত্তর আধুনিক সভ্যতায় বিস্ময় এনেছে।
উচ্চমাধ্যমিক গণিতে বৃত্তকে সমীকরণের মাধ্যমে উপস্থাপন ও সংশ্লিষ্ট কতিপয় বিষয়ের উপর আলোকপাত করা হয়েছে।
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। , প্লেটোর প্লেটো (Plato) (খ্রিষ্টপূর্ব ৪২৭ - খ্রিষ্টপূর্ব ৩৪৭) বিশ্ববিখ্যাত গ্রিক দার্শনিক। তিনি দার্শনিক সক্রেটিসের ছাত্র ছিলেন এবং দার্শনিক এরিস্টটল তার ছাত্র ছিলেন। এবং আর্কিমিডিস আর্কিমিডিস (২৮৭-২১২ খ্রিষ্টপূর্ব) একজন গ্রিক গণিতবিদ, পদার্থবিজ্ঞানী, প্রকৌশলী, জ্যোতির্বিদ ও দার্শনিক। তাঁকে গণিতের জনক বলা হয়। বৃত্তের পরিমার্জন করেন। ১৭০০ খ্রিস্টাব্দে রাইন্ড প্যাপিরাস The late Alexander Henry Rhind was the only surviving son of Josiah Rhind of Sibster, banker in Wick. He was born on the 26th July 1833, and during his earlier years pursued his studies at the Pulteneytown Academy, under the tuition of Mr Andrew Scott, now Professor of Oriental Languages in the University of Aberdeen. He then proceeded to the University of Edinburgh, where he became a student in the class of Natural History in the session of 1848-49, and in the class of Natural Philosophy in the session of 1849-50. ( Rhind Papyrus) বৃত্তের ক্ষেত্রফল নির্ণয়ের একটি পদ্ধতি উদ্ভাবন করেন। গাড়ীর চাকা, চন্দ্র, সূর্য এবং গাছের প্রস্তছেদ প্রভৃতি বস্তু বৃত্তাকার দেখায়। স্থানাংক জ্যামিতিতে, ক্যালকুলাসে, জ্যোতির্বিদ্যায় এবং কম্পিউটার গ্রাফিক্স ডিজাইনে বৃত্ত সম্পর্কিত অধ্যয়ন গুরুত্বপূর্ণ। প্রাচীন সভ্যতায় যোগাযোগের মাধ্যম চাকাবৃত্তের ধারণা থেকে সৃষ্ট, যা এই উত্তর আধুনিক সভ্যতায় বিস্ময় এনেছে।
উচ্চমাধ্যমিক গণিতে বৃত্তকে সমীকরণের মাধ্যমে উপস্থাপন ও সংশ্লিষ্ট কতিপয় বিষয়ের উপর আলোকপাত করা হয়েছে।
বৃত্ত
Circle
সমতলে একটি নির্দিষ্ট বিন্দু হতে সমান দূরত্বে অবস্থিত বিন্দুসমুহের সেট দ্বারা উৎপন্ন জ্যামিতিক চিত্রকে বৃত্ত (Circle) বলা হয়। নির্দিষ্ট বিন্দুকে বৃত্তের কেন্দ্র (Center) এবং স্থির দূরত্বকে বৃত্তের ব্যাসার্ধ (Radius) বলে।
বৃত্তের সমীকরণ চিহ্নিতকরণের উপায়
Methods of identifying the equation of a circle
\(x\) ও \(y\) এর দ্বিঘাত সমীকরণে \(x^{2}\) ও \(y^{2}\) এর সহগদ্বয় সমান এবং \(xy\) সম্বলিত পদের সহগ শুন্য \((0)\) হলে, তা বৃত্ত প্রকাশ করে।
কেন্দ্র মূলবিন্দু এবং নির্দিষ্ট ব্যাসার্ধবিশিষ্ট বৃত্তের সমীকরণ
Equation of circle with center origin and fixed radius
কেন্দ্র মূলবিন্দু তথা \(O(0, 0)\) এবং ব্যাসার্ধ \(r \ (r>0)\) বৃত্তের সমীকরণ।
\(x^{2}+y^{2}=r^{2}\)
\(x^{2}+y^{2}=r^{2}\)
প্রমাণঃ
ধরি,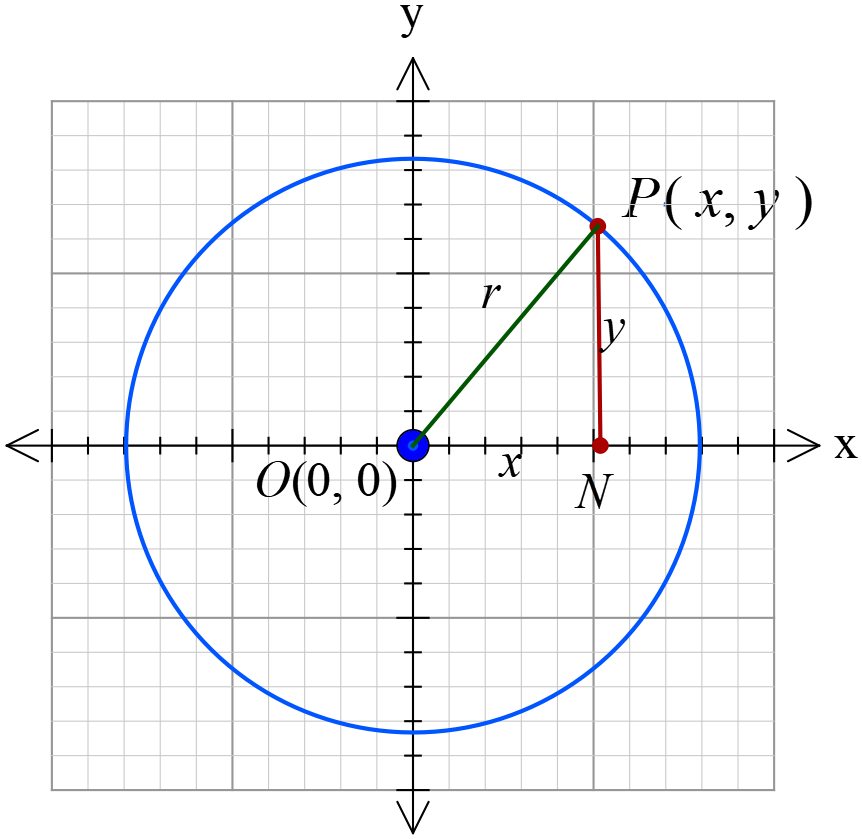
সঞ্চারপথের উপর চলমান বিন্দুটি \(P(x, y)\) ।
\(O, P\) যোগ করি। \(P\) বিন্দু হতে \(X\) অক্ষের উপর \(PN\) লম্ব টানি।
এখানে,
\(OP=r\) ➜ বৃত্তের ব্যাসার্ধ
\(ON=x, PN=y\)
\(\triangle OPN\) সমকোণী। \(OP\) ইহার অতিভুজ।
\(\therefore ON^{2}+PN^{2}=OP^{2}\)
\(\Rightarrow x^{2}+y^{2}=r^{2}\)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
ধরি,
সঞ্চারপথের উপর চলমান বিন্দুটি \(P(x, y)\) ।\(O, P\) যোগ করি। \(P\) বিন্দু হতে \(X\) অক্ষের উপর \(PN\) লম্ব টানি।
এখানে,
\(OP=r\) ➜ বৃত্তের ব্যাসার্ধ
\(ON=x, PN=y\)
\(\triangle OPN\) সমকোণী। \(OP\) ইহার অতিভুজ।
\(\therefore ON^{2}+PN^{2}=OP^{2}\)
\(\Rightarrow x^{2}+y^{2}=r^{2}\)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
নির্দিষ্ট কেন্দ্র এবং ব্যাসার্ধবিশিষ্ট বৃত্তের সমীকরণ
Equation of circle with fixed center and radius
কেন্দ্র \(P(h, k)\) এবং ব্যাসার্ধ \(r \ (r>0)\) বৃত্তের সমীকরণ।
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
প্রমাণঃ
দেওয়া আছে,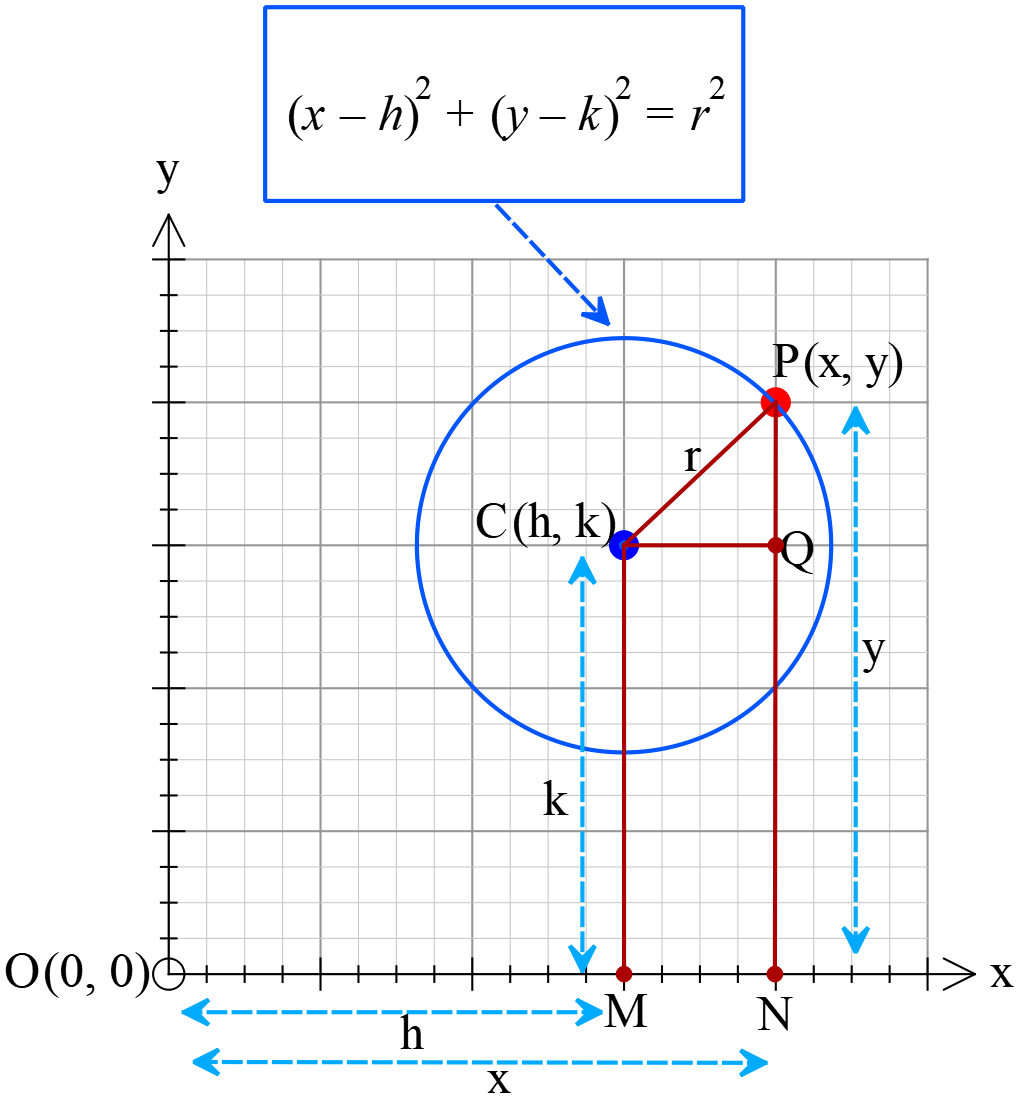
কেন্দ্র \(C(h, k)\) এবং ব্যাসার্ধ \(r \ (r>0)\)
ধরি,
সঞ্চারপথের উপর চলমান বিন্দুটি \(P(x, y)\) ।
\(C, P\) যোগ করি। \(C\) এবং \(P\) বিন্দু হতে \(X\) অক্ষের উপর যথাক্রমে \(CM\) এবং \(PN\) লম্ব টানি।
এখানে,
\(CP=r\) ➜ বৃত্তের ব্যাসার্ধ
\(ON=x, PN=y, OM=h, CM=k\)
\(CQ=MN=ON-OM=x-h\)
\(PQ=PN-QN=PN-CM=y-k\) ➜ \(\because CM=QN\)
\(\triangle CPQ\) সমকোণী। \(CP\) ইহার অতিভুজ।
\(\therefore CQ^{2}+PQ^{2}=CP^{2}\)
\(\Rightarrow (x-h)^{2}+(y-k)^{2}=r^{2}\)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
দেওয়া আছে,
কেন্দ্র \(C(h, k)\) এবং ব্যাসার্ধ \(r \ (r>0)\)
ধরি,
সঞ্চারপথের উপর চলমান বিন্দুটি \(P(x, y)\) ।
\(C, P\) যোগ করি। \(C\) এবং \(P\) বিন্দু হতে \(X\) অক্ষের উপর যথাক্রমে \(CM\) এবং \(PN\) লম্ব টানি।
এখানে,
\(CP=r\) ➜ বৃত্তের ব্যাসার্ধ
\(ON=x, PN=y, OM=h, CM=k\)
\(CQ=MN=ON-OM=x-h\)
\(PQ=PN-QN=PN-CM=y-k\) ➜ \(\because CM=QN\)
\(\triangle CPQ\) সমকোণী। \(CP\) ইহার অতিভুজ।
\(\therefore CQ^{2}+PQ^{2}=CP^{2}\)
\(\Rightarrow (x-h)^{2}+(y-k)^{2}=r^{2}\)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
বৃত্তের সাধারণ সমীকরণ
General equation of circle
বৃত্তের সাধারণ সমীকরণ।
\(x^{2}+y^{2}+2gx\)\(+2fy+c=0\)
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((a)\) এটি \(x, y\) সম্বলিত একটি দ্বিঘাত সমীকরণ।
\((b)\) \(x^{2}\) এবং \(y^{2}\) এর সহগদ্বয় সমান হবে।
\((c)\) \(xy\) সম্বলিত কোনো পদ থাকবে না।
\((d)\) \(g^{2}+f^{2}>c\) হবে।
\(x^{2}+y^{2}+2gx\)\(+2fy+c=0\)
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
প্রমাণঃ
আমরা জানি,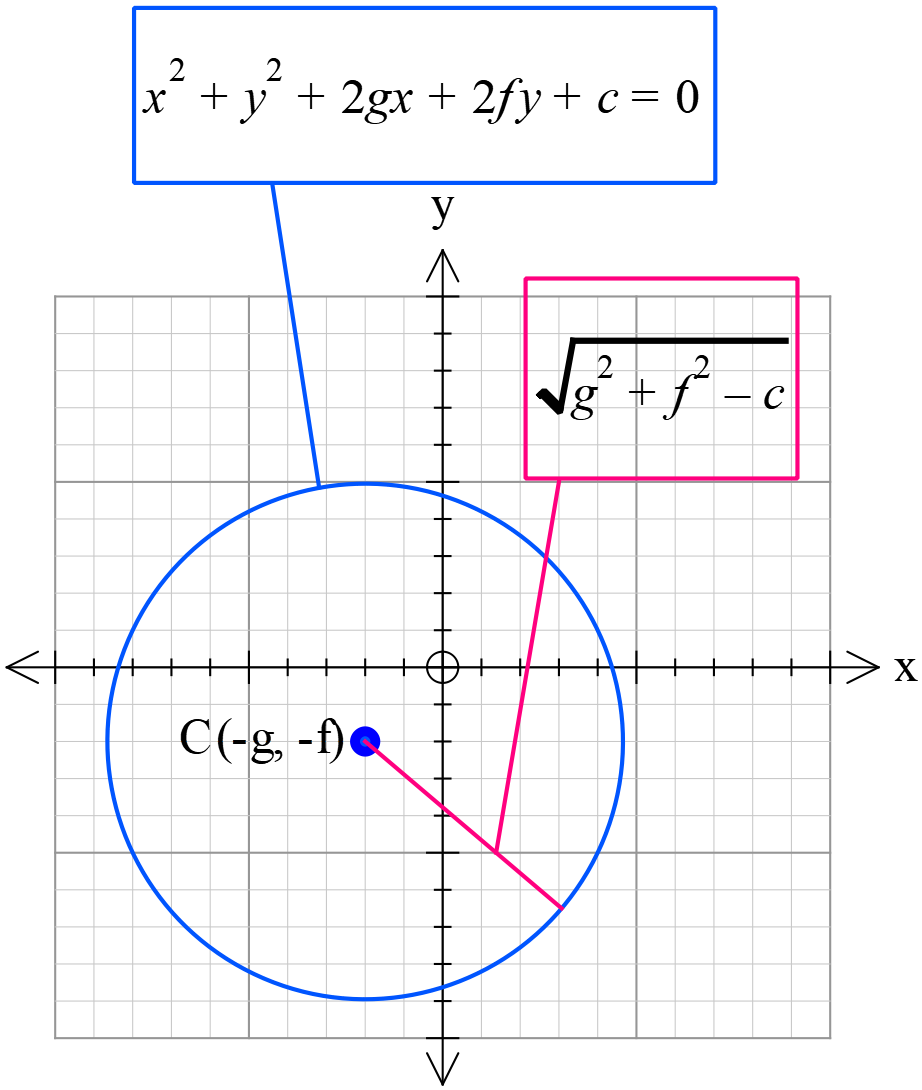
কেন্দ্র \(C(h, k)\) এবং ব্যাসার্ধ \(r \ (r>0)\) হলে,
বৃত্তের সমীকরণ হয়,
\(\Rightarrow (x-h)^{2}+(y-k)^{2}=r^{2} ..........(1)\)
এখন,
কেন্দ্র \(C(h, k)\Rightarrow c(-g, -f)\)
অর্থাৎ \(h=-g, k=-f\)
এবং ব্যাসার্ধ \(r \Rightarrow \sqrt{g^{2}+f^{2}-c}\) হলে,
\((1)\) সমীকরণ হতে পাই,
\((x+g)^{2}+(y+f)^{2}=(\sqrt{g^{2}+f^{2}-c})^{2}\)
\(\Rightarrow x^{2}+2gx+g^{2}+y^{2}+2fy+f^{2}=g^{2}+f^{2}-c\)
\(\Rightarrow x^{2}+2gx+g^{2}+y^{2}+2fy+f^{2}-g^{2}-f^{2}+c=0\)
\(\Rightarrow x^{2}+y^{2}+2gx+2fy+c=0\)
ইহাই বৃত্তের নির্ণেয় সাধারণ সমীকরণ।
বৃত্তের সাধারণ সমীকরণের বৈশিষ্ট্যঃআমরা জানি,
কেন্দ্র \(C(h, k)\) এবং ব্যাসার্ধ \(r \ (r>0)\) হলে,
বৃত্তের সমীকরণ হয়,
\(\Rightarrow (x-h)^{2}+(y-k)^{2}=r^{2} ..........(1)\)
এখন,
কেন্দ্র \(C(h, k)\Rightarrow c(-g, -f)\)
অর্থাৎ \(h=-g, k=-f\)
এবং ব্যাসার্ধ \(r \Rightarrow \sqrt{g^{2}+f^{2}-c}\) হলে,
\((1)\) সমীকরণ হতে পাই,
\((x+g)^{2}+(y+f)^{2}=(\sqrt{g^{2}+f^{2}-c})^{2}\)
\(\Rightarrow x^{2}+2gx+g^{2}+y^{2}+2fy+f^{2}=g^{2}+f^{2}-c\)
\(\Rightarrow x^{2}+2gx+g^{2}+y^{2}+2fy+f^{2}-g^{2}-f^{2}+c=0\)
\(\Rightarrow x^{2}+y^{2}+2gx+2fy+c=0\)
ইহাই বৃত্তের নির্ণেয় সাধারণ সমীকরণ।
\((a)\) এটি \(x, y\) সম্বলিত একটি দ্বিঘাত সমীকরণ।
\((b)\) \(x^{2}\) এবং \(y^{2}\) এর সহগদ্বয় সমান হবে।
\((c)\) \(xy\) সম্বলিত কোনো পদ থাকবে না।
\((d)\) \(g^{2}+f^{2}>c\) হবে।
সাধারণ দ্বিঘাত সমীকরণ
General quadratic equation
\(x, y\) সম্বলিত সধারণ দ্বিঘাত সমীকরণ।
\(ax^{2}+2hxy+by^{2}\)\(+2gx+2fy+c=0\)
\(ax^{2}+2hxy+by^{2}\)\(+2gx+2fy+c=0\)
সাধারণ দ্বিঘাত সমীকরণের বৃত্ত প্রকাশ করার শর্তাবলীঃ
\((a)\) \(x^{2}\) এবং \(y^{2}\) এর সহগদ্বয় সমান হবে, অর্থাৎ \(a=b\)।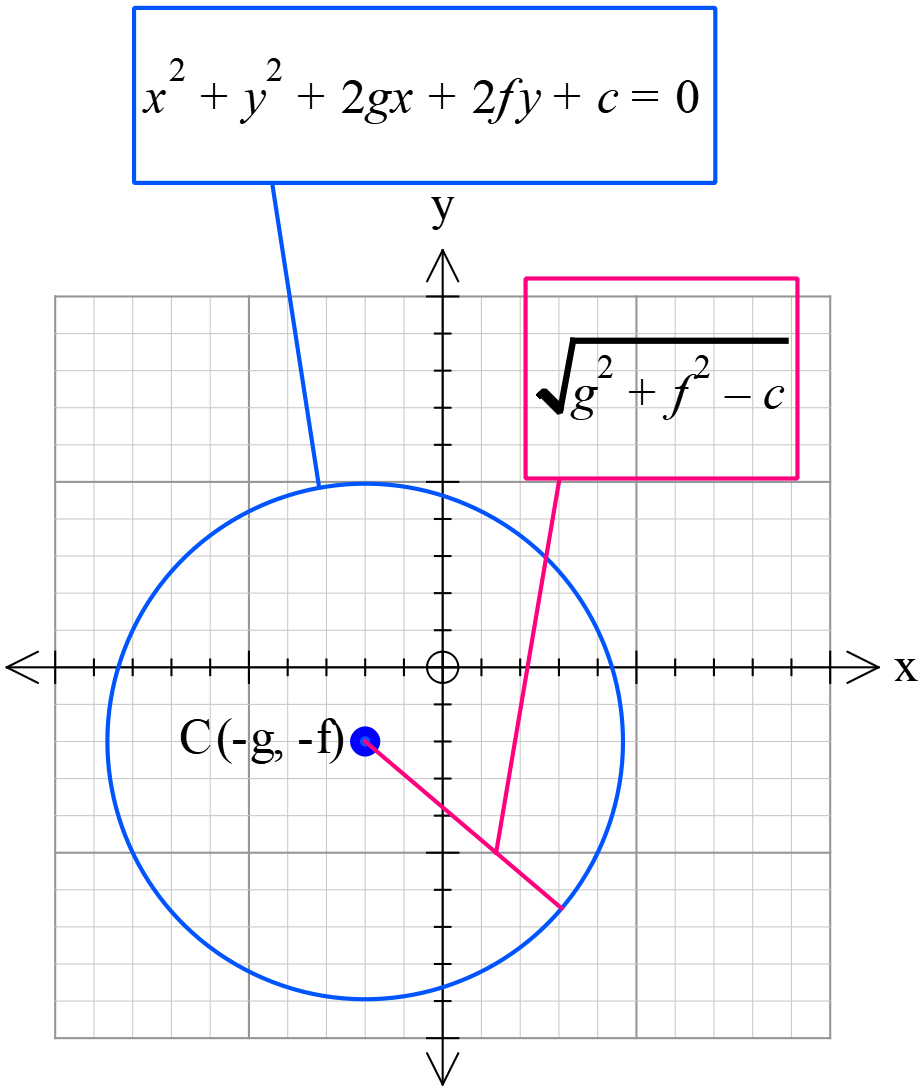
\((b)\) \(xy\) সম্বলিত কোনো পদ থাকবে না, অর্থাৎ \(h=0\)।
\((c)\) \(g^{2}+f^{2}>c\) হবে।
এই ক্ষেত্রে বৃত্তের,
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((b)\) \(xy\) সম্বলিত কোনো পদ থাকবে না, অর্থাৎ \(h=0\)।
\((c)\) \(g^{2}+f^{2}>c\) হবে।
এই ক্ষেত্রে বৃত্তের,
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
নির্দিষ্ট বিন্দুতে কেন্দ্র এবং একটি নির্দিষ্ট বিন্দুগামী বৃত্তের সমীকরণ
Equation of a circle with center at a given point and through a given point
কেন্দ্র \((h, k)\) এবং \((\alpha, \beta)\) বিন্দুগামী বৃত্তের সমীকরণ।
\((x-h)^{2}+(y-k)^{2}\)\(=(\alpha-h)^{2}+(\beta-k)^{2}\)
কেন্দ্রঃ \((h, k)\)
ব্যাসার্ধঃ \(=\sqrt{(\alpha-h)^{2}+(\beta-k)^{2}}\)
\((x-h)^{2}+(y-k)^{2}\)\(=(\alpha-h)^{2}+(\beta-k)^{2}\)
কেন্দ্রঃ \((h, k)\)
ব্যাসার্ধঃ \(=\sqrt{(\alpha-h)^{2}+(\beta-k)^{2}}\)
প্রমাণঃ
আমরা জানি,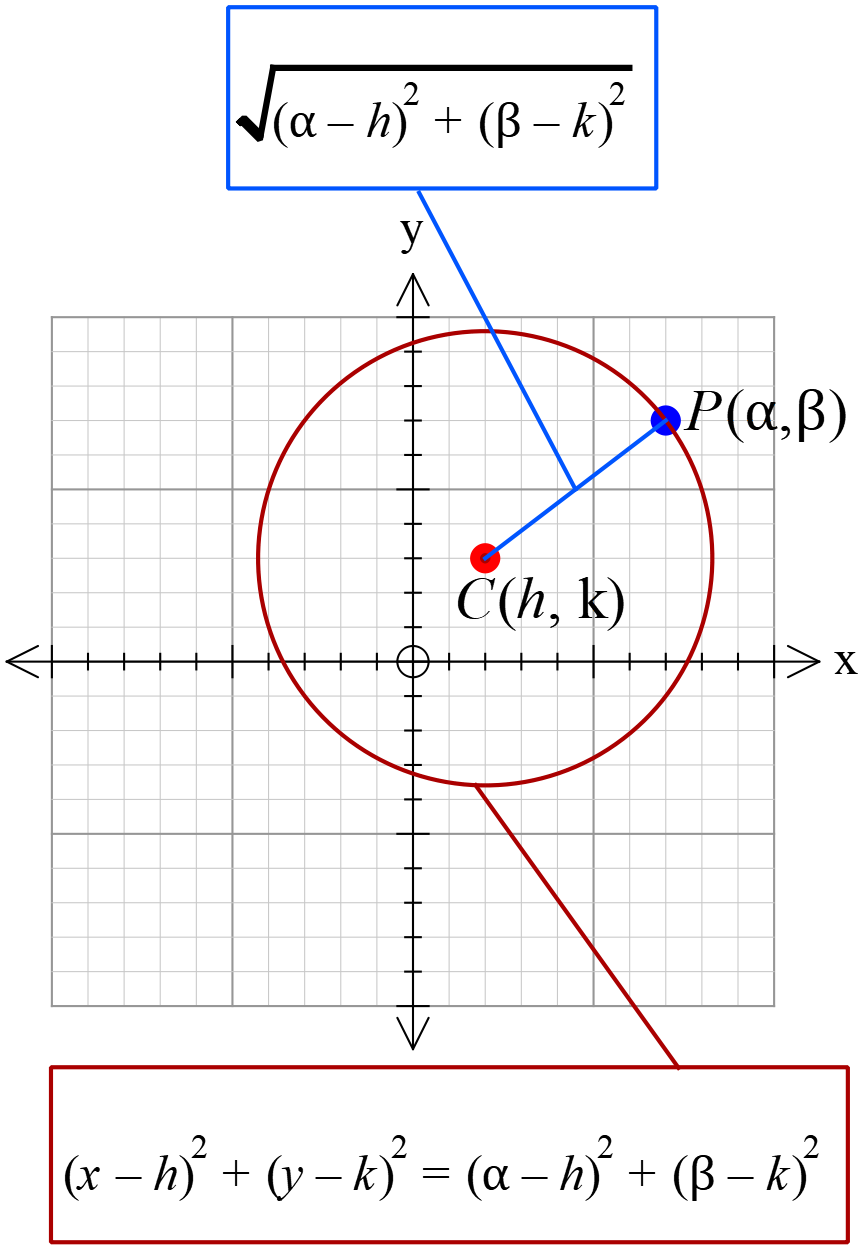
কেন্দ্র \(C(h, k)\) এবং ব্যাসার্ধ \(r \ (r>0)\) হলে,
বৃত্তের সমীকরণ হয়,
\(\Rightarrow (x-h)^{2}+(y-k)^{2}=r^{2} ..........(1)\)
\((1)\) নং বৃত্তটি \((\alpha, \beta)\) বিন্দু দিয়ে যায়,
\(\therefore (\alpha-h)^{2}+(\beta-k)^{2}=r^{2}\)
\(\Rightarrow r^{2}=(\alpha-h)^{2}+(\beta-k)^{2}\)
\(r^{2}\) এর এই মান \((1)\) এ বসিয়ে পাই,
\((x-h)^{2}+(y-k)^{2}=(\alpha-h)^{2}+(\beta-k)^{2} \)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
আমরা জানি,
কেন্দ্র \(C(h, k)\) এবং ব্যাসার্ধ \(r \ (r>0)\) হলে,
বৃত্তের সমীকরণ হয়,
\(\Rightarrow (x-h)^{2}+(y-k)^{2}=r^{2} ..........(1)\)
\((1)\) নং বৃত্তটি \((\alpha, \beta)\) বিন্দু দিয়ে যায়,
\(\therefore (\alpha-h)^{2}+(\beta-k)^{2}=r^{2}\)
\(\Rightarrow r^{2}=(\alpha-h)^{2}+(\beta-k)^{2}\)
\(r^{2}\) এর এই মান \((1)\) এ বসিয়ে পাই,
\((x-h)^{2}+(y-k)^{2}=(\alpha-h)^{2}+(\beta-k)^{2} \)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
নির্দিষ্ট দুইটি বিন্দুর সংযোগ রেখাংশকে ব্যাস ধরে বৃত্তের সমীকরণ
The equation of a circle is the diameter of the line joining two given points
\((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) বিন্দু দুইটির সংযোগ রেখাংশকে ব্যাস ধরে অঙ্কিত বৃত্তের সমীকরণ।
\((x-x_{1})(x-x_{2})+\)\((y-y_{1})(y-y_{2})=0\)
\((x-x_{1})(x-x_{2})+\)\((y-y_{1})(y-y_{2})=0\)
প্রমাণঃ
মনে করি,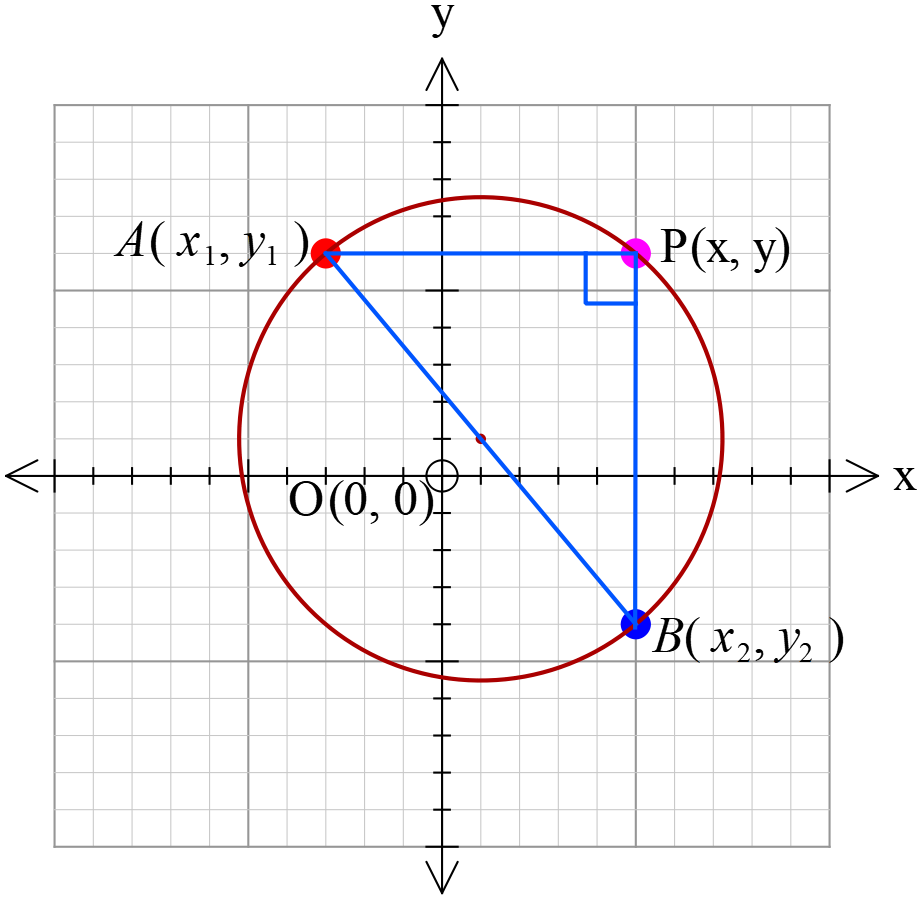
\(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\)
এবং বৃত্তের পরিধীর উপর চলমান বিন্দু \(P(x, y)\)
\(A, P\) এবং \(B, P\) যোগ করি।
এখন,
\(\angle APB\) অর্ধবৃত্তস্থ বিধায় এক সমকোণ।
\(\therefore PA\perp PB\)
\(PA\) এর ঢাল \(m_{1}=\frac{y-y_{1}}{x-x_{1}}\)
\(PB\) এর ঢাল \(m_{2}=\frac{y-y_{2}}{x-x_{2}}\)
শর্তমতে,
\(m_{1}\times m_{2}=-1\)
\(\Rightarrow \frac{y-y_{1}}{x-x_{1}}\times \frac{y-y_{2}}{x-x_{2}}=-1\)
\(\Rightarrow \frac{(y-y_{1})(y-y_{2})}{(x-x_{1})(x-x_{2})}=-1\)
\(\Rightarrow (y-y_{1})(y-y_{2})=-(x-x_{1})(x-x_{2})\)
\(\therefore (x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0\)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
মনে করি,
\(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\)
এবং বৃত্তের পরিধীর উপর চলমান বিন্দু \(P(x, y)\)
\(A, P\) এবং \(B, P\) যোগ করি।
এখন,
\(\angle APB\) অর্ধবৃত্তস্থ বিধায় এক সমকোণ।
\(\therefore PA\perp PB\)
\(PA\) এর ঢাল \(m_{1}=\frac{y-y_{1}}{x-x_{1}}\)
\(PB\) এর ঢাল \(m_{2}=\frac{y-y_{2}}{x-x_{2}}\)
শর্তমতে,
\(m_{1}\times m_{2}=-1\)
\(\Rightarrow \frac{y-y_{1}}{x-x_{1}}\times \frac{y-y_{2}}{x-x_{2}}=-1\)
\(\Rightarrow \frac{(y-y_{1})(y-y_{2})}{(x-x_{1})(x-x_{2})}=-1\)
\(\Rightarrow (y-y_{1})(y-y_{2})=-(x-x_{1})(x-x_{2})\)
\(\therefore (x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0\)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
মূলবিন্দুগামী বৃত্তের সাধারণ সমীকরণ
General equation of the circle passing through the origin
মূলবিন্দুগামী বৃত্তের সাধারণ সমীকরণ
\(x^{2}+y^{2}+2gx+2fy=0\)
\(x^{2}+y^{2}+2gx+2fy=0\)
প্রমাণঃ
আমরা জানি,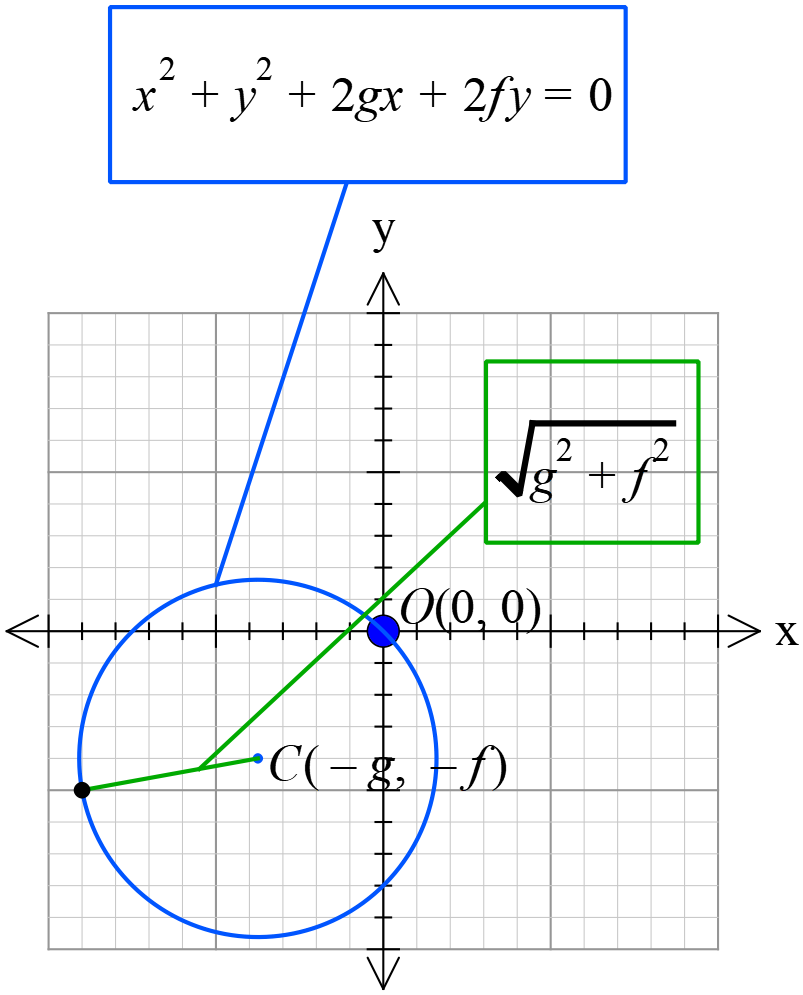
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
\((1)\) নং বৃত্ত মূলবিন্দু তথা \(O(0, 0)\) দিয়ে যায়,
\(0^{2}+0^{2}+2g.0+2f.0+c=0\)
\(\Rightarrow 0+0+0+0+c=0\)
\(\Rightarrow 0+c=0\)
\(\Rightarrow c=0\)
\(c\) এর এই মান \((1)\) এ বসিয়ে পাই,
\(x^{2}+y^{2}+2gx+2fy+0=0\)
\(\therefore x^{2}+y^{2}+2gx+2fy=0\)
ইহাই নির্ণেয় মূলবিন্দুগামী বৃত্তের সাধারণ সমীকরণ।
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
\((1)\) নং বৃত্ত মূলবিন্দু তথা \(O(0, 0)\) দিয়ে যায়,
\(0^{2}+0^{2}+2g.0+2f.0+c=0\)
\(\Rightarrow 0+0+0+0+c=0\)
\(\Rightarrow 0+c=0\)
\(\Rightarrow c=0\)
\(c\) এর এই মান \((1)\) এ বসিয়ে পাই,
\(x^{2}+y^{2}+2gx+2fy+0=0\)
\(\therefore x^{2}+y^{2}+2gx+2fy=0\)
ইহাই নির্ণেয় মূলবিন্দুগামী বৃত্তের সাধারণ সমীকরণ।
বৃত্তের সাধারণ সমীকরণের অক্ষদ্বয়কে স্পর্শ করার শর্ত
The condition of touching two axes of the general equation of a circle
বৃত্তের সাধারণ সমীকরণ \(x^{2}+y^{2}+2gx+2fy+c=0\) এর অক্ষদ্বয়কে স্পর্শ করার শর্ত
\(X\) অক্ষকে স্পর্শ করার শর্তঃ
\(g^{2}=c\)
\(Y\) অক্ষকে স্পর্শ করার শর্তঃ
\(f^{2}=c\)
উভয় অক্ষকে স্পর্শ করার শর্তঃ
\(g^{2}=f^{2}=c\)
\(X\) অক্ষকে স্পর্শ করার শর্তঃ
\(g^{2}=c\)
\(Y\) অক্ষকে স্পর্শ করার শর্তঃ
\(f^{2}=c\)
উভয় অক্ষকে স্পর্শ করার শর্তঃ
\(g^{2}=f^{2}=c\)
প্রমাণঃ
\(X\) অক্ষকে স্পর্শ করার শর্তঃ
আমরা জানি,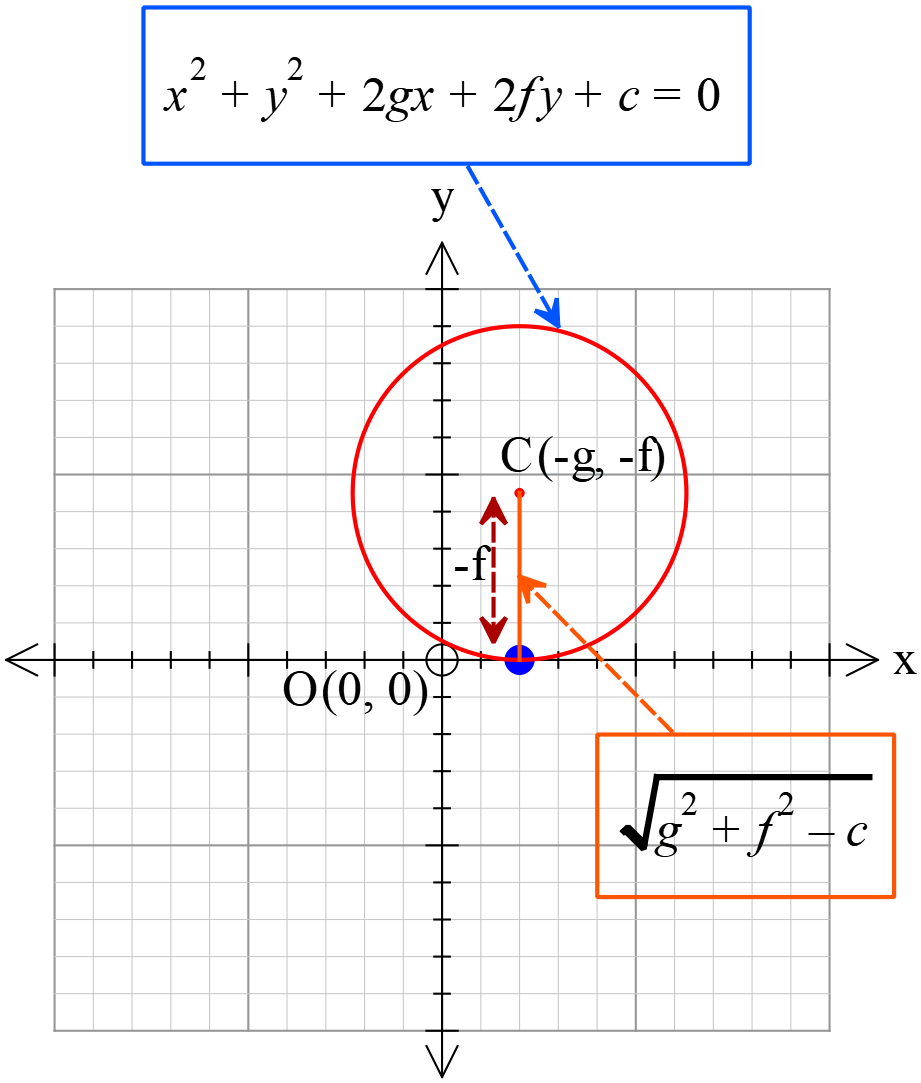
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) নং বৃত্ত , যখন \(X\) অক্ষকে স্পর্শ করে তখন কেন্দ্রের \(y\) স্থানাংক ব্যাসার্ধের সমান হয়,
\(\therefore \sqrt{g^{2}+f^{2}-c}=-f\)
\(\Rightarrow g^{2}+f^{2}-c=(-f)^{2}\)
\(\Rightarrow g^{2}+f^{2}-c=f^{2}\)
\(\Rightarrow g^{2}+f^{2}-c-f^{2}=0\)
\(\Rightarrow g^{2}-c=0\)
\(\therefore g^{2}=c\)
ইহাই নির্ণেয় শর্ত।
\(Y\) অক্ষকে স্পর্শ করার শর্তঃ
আমরা জানি,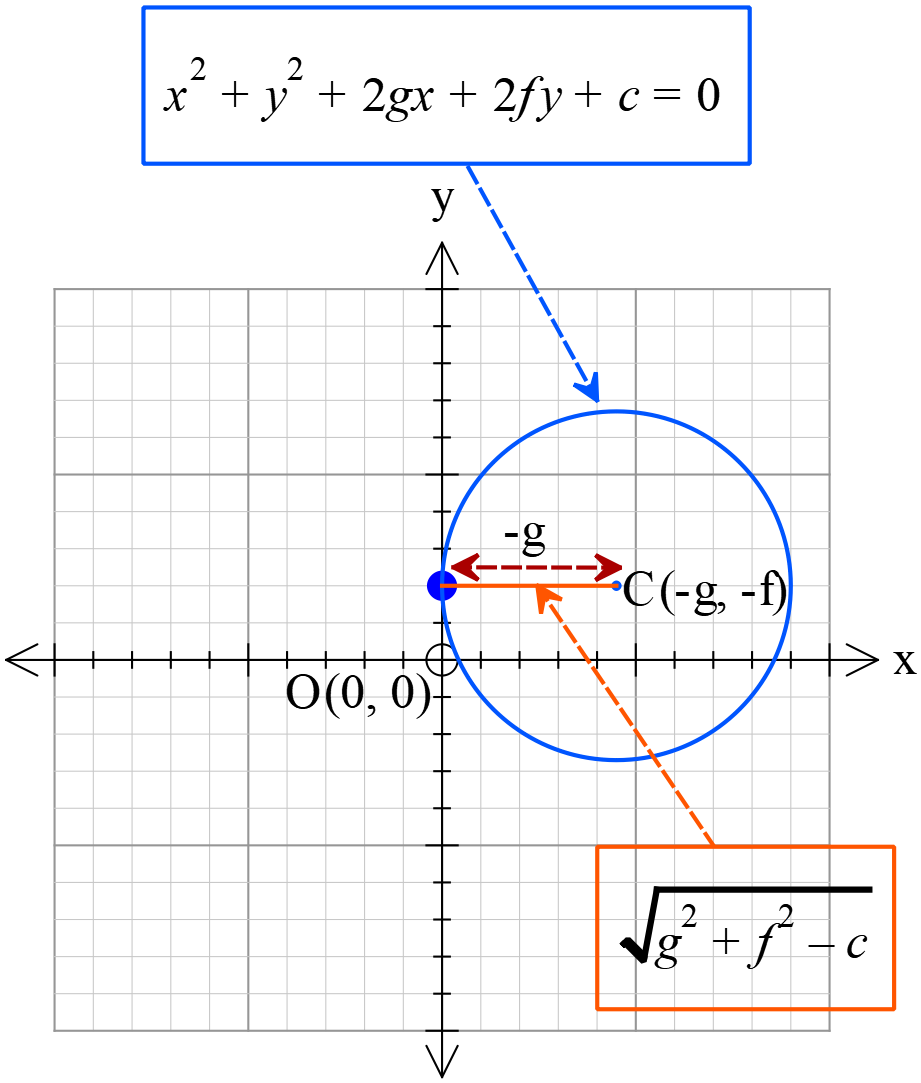
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) নং বৃত্ত , যখন \(Y\) অক্ষকে স্পর্শ করে তখন কেন্দ্রের \(x\) স্থানাংক ব্যাসার্ধের সমান হয়,
\(\therefore \sqrt{g^{2}+f^{2}-c}=-g\)
\(\Rightarrow g^{2}+f^{2}-c=(-g)^{2}\)
\(\Rightarrow g^{2}+f^{2}-c=g^{2}\)
\(\Rightarrow g^{2}+f^{2}-c-g^{2}=0\)
\(\Rightarrow f^{2}-c=0\)
\(\therefore f^{2}=c\)
ইহাই নির্ণেয় শর্ত।
উভয় অক্ষকে স্পর্শ করার শর্তঃ
আমরা জানি,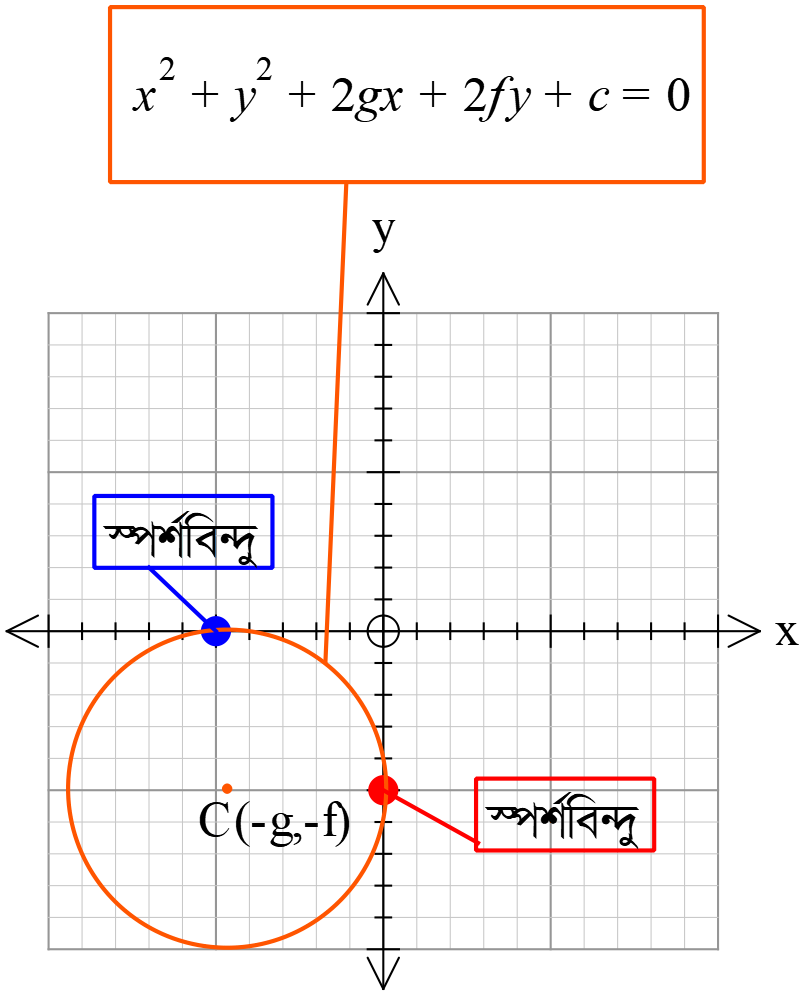
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) নং বৃত্তের উভয় অক্ষকে স্পর্শ করার শর্ত,
\((a)\) ও \((b)\) হতে প্রাপ্ত,
\(g^{2}=f^{2}=c\)
ইহাই নির্ণেয় শর্ত।
\(X\) অক্ষকে স্পর্শ করার শর্তঃ
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) নং বৃত্ত , যখন \(X\) অক্ষকে স্পর্শ করে তখন কেন্দ্রের \(y\) স্থানাংক ব্যাসার্ধের সমান হয়,
\(\therefore \sqrt{g^{2}+f^{2}-c}=-f\)
\(\Rightarrow g^{2}+f^{2}-c=(-f)^{2}\)
\(\Rightarrow g^{2}+f^{2}-c=f^{2}\)
\(\Rightarrow g^{2}+f^{2}-c-f^{2}=0\)
\(\Rightarrow g^{2}-c=0\)
\(\therefore g^{2}=c\)
ইহাই নির্ণেয় শর্ত।
\(Y\) অক্ষকে স্পর্শ করার শর্তঃ
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) নং বৃত্ত , যখন \(Y\) অক্ষকে স্পর্শ করে তখন কেন্দ্রের \(x\) স্থানাংক ব্যাসার্ধের সমান হয়,
\(\therefore \sqrt{g^{2}+f^{2}-c}=-g\)
\(\Rightarrow g^{2}+f^{2}-c=(-g)^{2}\)
\(\Rightarrow g^{2}+f^{2}-c=g^{2}\)
\(\Rightarrow g^{2}+f^{2}-c-g^{2}=0\)
\(\Rightarrow f^{2}-c=0\)
\(\therefore f^{2}=c\)
ইহাই নির্ণেয় শর্ত।
উভয় অক্ষকে স্পর্শ করার শর্তঃ
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
কেন্দ্রঃ \((-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) নং বৃত্তের উভয় অক্ষকে স্পর্শ করার শর্ত,
\((a)\) ও \((b)\) হতে প্রাপ্ত,
\(g^{2}=f^{2}=c\)
ইহাই নির্ণেয় শর্ত।
বৃত্তের সাধারণ সমীকরণ যখন উভয় অক্ষকে ছেদ করে
General equation of the circle when it intersects both axes
বৃত্তের সাধারণ সমীকরণ \(x^{2}+y^{2}+2gx+2fy+c=0\) যখন অক্ষদ্বয়কে ছেদ করে।
\(X\) অক্ষের ছেদিতাংশের পরিমাণঃ
\(=2\sqrt{g^{2}-c}\) \(Y\) অক্ষের ছেদিতাংশের পরিমাণঃ
\(=2\sqrt{f^{2}-c}\)
\(X\) অক্ষের ছেদিতাংশের পরিমাণঃ
\(=2\sqrt{g^{2}-c}\) \(Y\) অক্ষের ছেদিতাংশের পরিমাণঃ
\(=2\sqrt{f^{2}-c}\)
প্রমাণঃ
\(X\) অক্ষের ছেদিতাংশ নির্ণয়ঃ
আমরা জানি,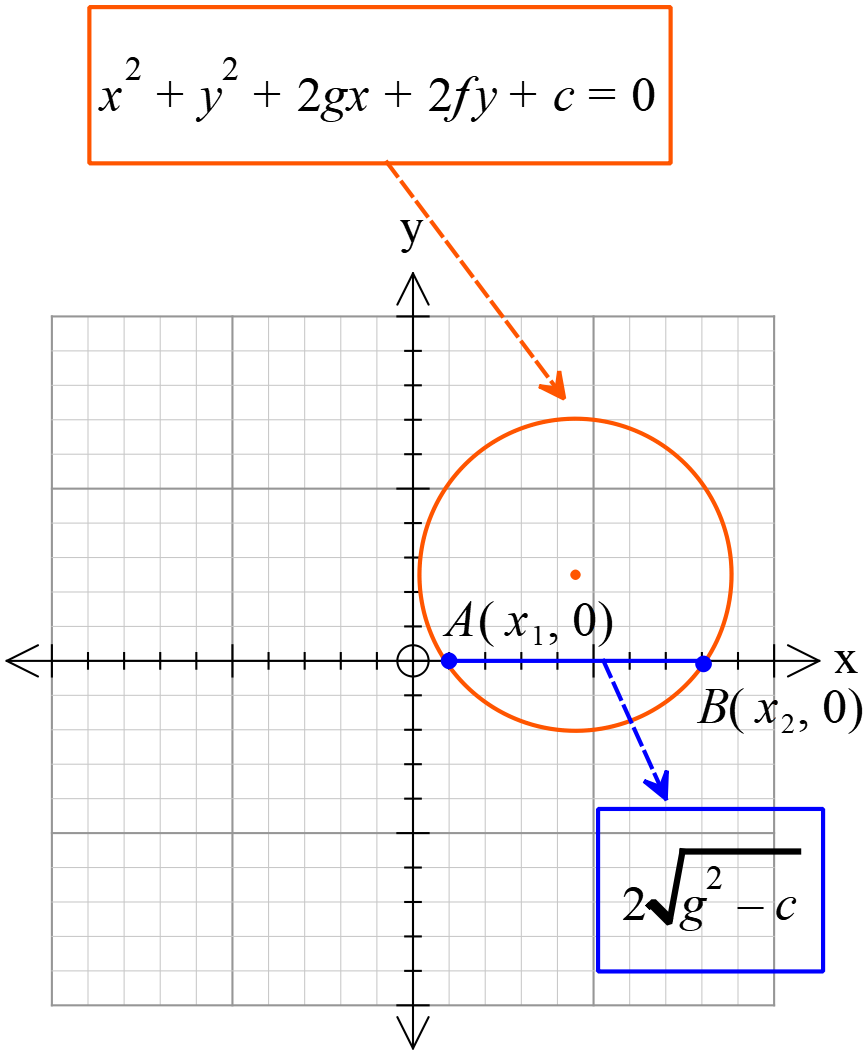
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
ধরি,
\((1)\) নং বৃত্তটি \(X\) অক্ষকে \(A(x_{1}, 0)\) ও \(B(x_{2}, 0)\) বিন্দুতে ছেদ করে,
সুতরাং, \((1)\) নং সমীকরণে \(y=0\) বসিয়ে পাই,
\(x^{2}+2gx+c=0\) যা \(x\) এর দ্বিঘাত সমীকরণ যার মূলদ্বয় \(x_{1}\) ও \(x_{2}\)।
\(\therefore\) মূলদ্বয়ের যোগফল, \(x_{1}+x_{2}=-2g\)
এবং মূলদ্বয়ের গুনফল, \(x_{1}x_{2}=c\)
সুতরাং, বৃত্তটি দ্বারা \(X\) অক্ষের ছেদিতাংশের পরিমাণ \(=|x_{1}-x_{2}|\)
\(=\sqrt{(x_{1}-x_{2})^{2}}\)
\(=\sqrt{(x_{1}+x_{2})^{2}-4x_{1}x_{2}}\)
\(=\sqrt{(-2g)^{2}-4c}\)
\(=\sqrt{4g^{2}-4c}\)
\(=\sqrt{4(g^{2}-c)}\)
\(=2\sqrt{g^{2}-c}\)
ইহাই নির্ণেয় ছেদিতাংশ ।
\(Y\) অক্ষের ছেদিতাংশ নির্ণয়ঃ
আমরা জানি,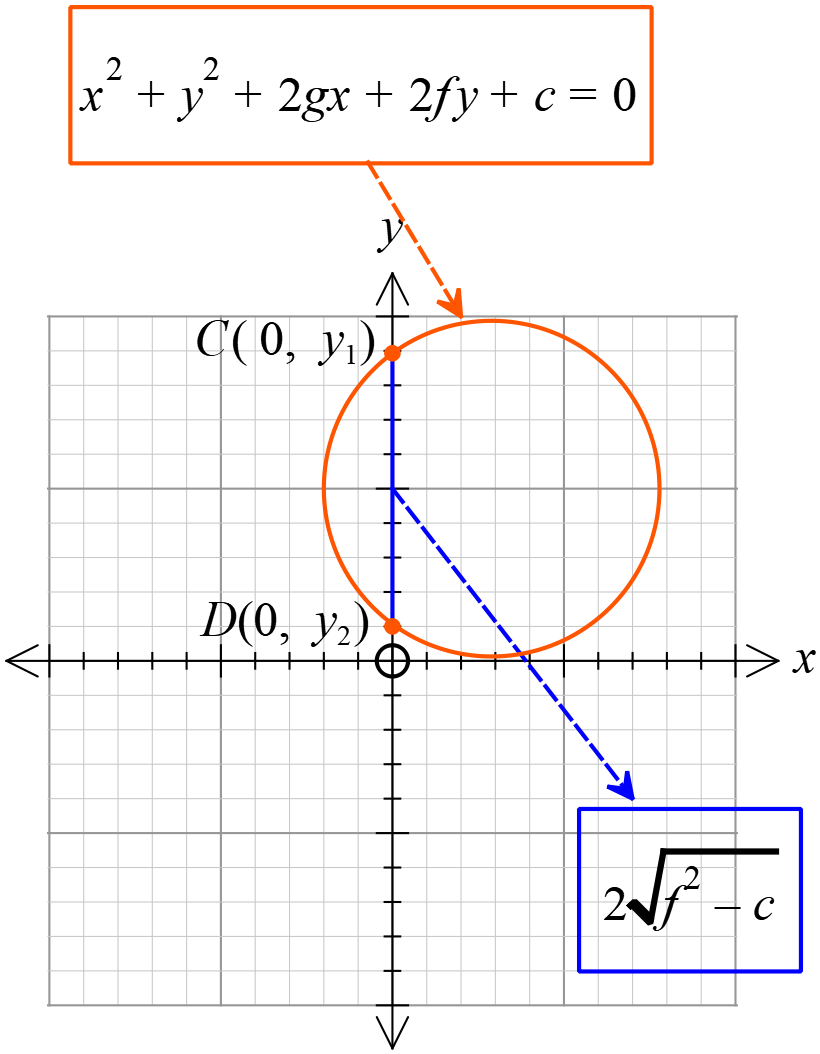
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
ধরি,
\((1)\) নং বৃত্তটি \(Y\) অক্ষকে \(C(x_{1}, 0)\) ও \(D(x_{2}, 0)\) বিন্দুতে ছেদ করে,
সুতরাং, \((1)\) নং সমীকরণে \(x=0\) বসিয়ে পাই,
\(y^{2}+2fy+c=0\) যা \(y\) এর দ্বিঘাত সমীকরণ যার মূলদ্বয় \(y_{1}\) ও \(y_{2}\)।
\(\therefore\) মূলদ্বয়ের যোগফল, \(y_{1}+y_{2}=-2f\)
এবং মূলদ্বয়ের গুনফল, \(y_{1}y_{2}=c\)
সুতরাং, বৃত্তটি দ্বারা \(Y\) অক্ষের ছেদিতাংশের পরিমাণ \(=|y_{1}-y_{2}|\)
\(=\sqrt{(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(y_{1}+y_{2})^{2}-4y_{1}y_{2}}\)
\(=\sqrt{(-2f)^{2}-4c}\)
\(=\sqrt{4f^{2}-4c}\)
\(=\sqrt{4(f^{2}-c)}\)
\(=2\sqrt{f^{2}-c}\)
ইহাই নির্ণেয় ছেদিতাংশ ।
\(X\) অক্ষের ছেদিতাংশ নির্ণয়ঃ
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
ধরি,
\((1)\) নং বৃত্তটি \(X\) অক্ষকে \(A(x_{1}, 0)\) ও \(B(x_{2}, 0)\) বিন্দুতে ছেদ করে,
সুতরাং, \((1)\) নং সমীকরণে \(y=0\) বসিয়ে পাই,
\(x^{2}+2gx+c=0\) যা \(x\) এর দ্বিঘাত সমীকরণ যার মূলদ্বয় \(x_{1}\) ও \(x_{2}\)।
\(\therefore\) মূলদ্বয়ের যোগফল, \(x_{1}+x_{2}=-2g\)
এবং মূলদ্বয়ের গুনফল, \(x_{1}x_{2}=c\)
সুতরাং, বৃত্তটি দ্বারা \(X\) অক্ষের ছেদিতাংশের পরিমাণ \(=|x_{1}-x_{2}|\)
\(=\sqrt{(x_{1}-x_{2})^{2}}\)
\(=\sqrt{(x_{1}+x_{2})^{2}-4x_{1}x_{2}}\)
\(=\sqrt{(-2g)^{2}-4c}\)
\(=\sqrt{4g^{2}-4c}\)
\(=\sqrt{4(g^{2}-c)}\)
\(=2\sqrt{g^{2}-c}\)
ইহাই নির্ণেয় ছেদিতাংশ ।
\(Y\) অক্ষের ছেদিতাংশ নির্ণয়ঃ
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ..........(1)\)
ধরি,
\((1)\) নং বৃত্তটি \(Y\) অক্ষকে \(C(x_{1}, 0)\) ও \(D(x_{2}, 0)\) বিন্দুতে ছেদ করে,
সুতরাং, \((1)\) নং সমীকরণে \(x=0\) বসিয়ে পাই,
\(y^{2}+2fy+c=0\) যা \(y\) এর দ্বিঘাত সমীকরণ যার মূলদ্বয় \(y_{1}\) ও \(y_{2}\)।
\(\therefore\) মূলদ্বয়ের যোগফল, \(y_{1}+y_{2}=-2f\)
এবং মূলদ্বয়ের গুনফল, \(y_{1}y_{2}=c\)
সুতরাং, বৃত্তটি দ্বারা \(Y\) অক্ষের ছেদিতাংশের পরিমাণ \(=|y_{1}-y_{2}|\)
\(=\sqrt{(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(y_{1}+y_{2})^{2}-4y_{1}y_{2}}\)
\(=\sqrt{(-2f)^{2}-4c}\)
\(=\sqrt{4f^{2}-4c}\)
\(=\sqrt{4(f^{2}-c)}\)
\(=2\sqrt{f^{2}-c}\)
ইহাই নির্ণেয় ছেদিতাংশ ।
একটি বৃত্ত ও একটি সরলরেখার ছেদবিন্দুগামী বৃত্তের সমীকরণ
Equation of the intersection of a circle and a straight line
\(x^{2}+y^{2}+2gx\)\(+2fy+c=0\) বৃত্ত ও \(ax+by+c_{1}=0\) সরলরেখার ছেদবিন্দুগামী বৃত্তের সমীকরণ।
\(x^{2}+y^{2}+2gx+2fy+c+k(ax+by+c_{1})=0\)
\(k\) শুন্য ব্যতীত যে কোনো বাস্তব সংখ্যা (ইচ্ছামূলক ধ্রুবক)।
\(x^{2}+y^{2}+2gx+2fy+c+k(ax+by+c_{1})=0\)
\(k\) শুন্য ব্যতীত যে কোনো বাস্তব সংখ্যা (ইচ্ছামূলক ধ্রুবক)।
দুইটি নির্দিষ্ট বিন্দুগামী বৃত্তের সমীকরণ 'খলিফার নিয়ম'
Equation of two circles through fixed points 'Rule of the Caliph'
দুইটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) দিয়ে গমনকারী বৃত্তের সমীকরণ।
(খলিফার নিয়ম)
\((x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})+\)\(k\{(x-x_{1})(y_{1}-y_{2})-(y-y_{1})(x_{1}-x_{2})\}=0\)
\((x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})+\)\(k\{(x-x_{1})(y_{1}-y_{2})-(y-y_{1})(x_{1}-x_{2})\}=0\)
প্রমাণঃ
ধরি,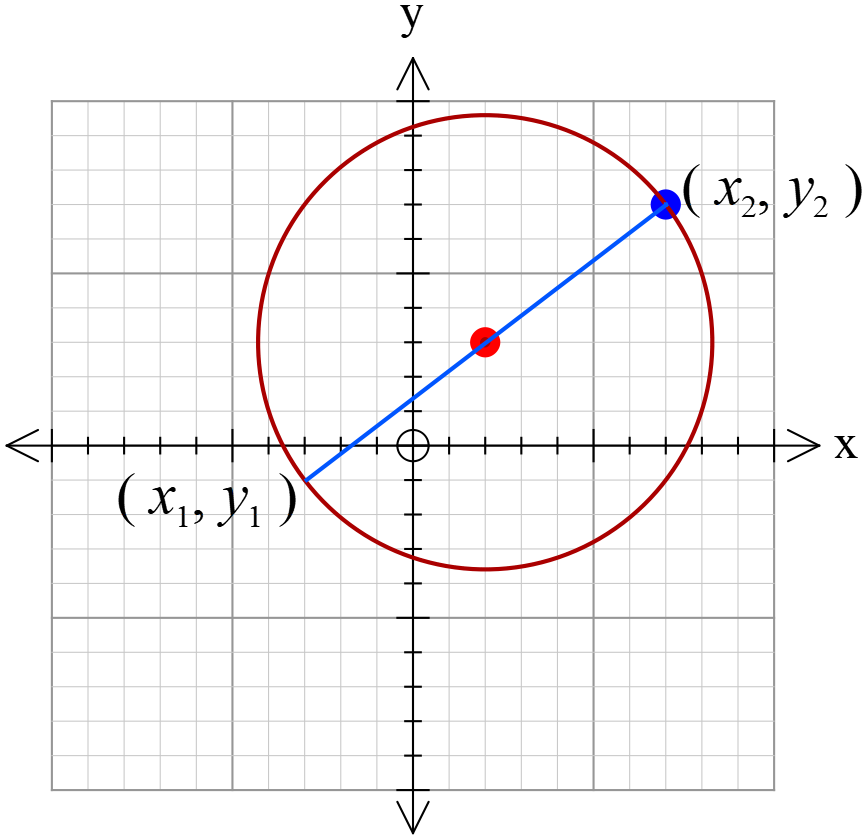
\(A(x_{1}, y_{1})\) ও \(B(x_{2}, y_{2})\)
\(AB\) কে ব্যাস ধরে বৃত্তের সমীকরণ,
\((x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0 ......(1)\)
আবার,
\(AB\) সরলরেখার সমীকরণ,
\(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\)
\(\Rightarrow (x-x_{1})(y_{1}-y_{2})=(y-y_{1})(x_{1}-x_{2})\)
\(\Rightarrow (x-x_{1})(y_{1}-y_{2})-(y-y_{1})(x_{1}-x_{2})=0 ....(2)\)
\((1)\) নং বৃত্ত ও \((2)\) নং সরলরেখার ছেদবিন্দুগামী বৃত্তের সমীকরণ,
\((x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})+\)\(k\{(x-x_{1})(y_{1}-y_{2})-(y-y_{1})(x_{1}-x_{2})\}=0\)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
ধরি,
\(A(x_{1}, y_{1})\) ও \(B(x_{2}, y_{2})\)
\(AB\) কে ব্যাস ধরে বৃত্তের সমীকরণ,
\((x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0 ......(1)\)
আবার,
\(AB\) সরলরেখার সমীকরণ,
\(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\)
\(\Rightarrow (x-x_{1})(y_{1}-y_{2})=(y-y_{1})(x_{1}-x_{2})\)
\(\Rightarrow (x-x_{1})(y_{1}-y_{2})-(y-y_{1})(x_{1}-x_{2})=0 ....(2)\)
\((1)\) নং বৃত্ত ও \((2)\) নং সরলরেখার ছেদবিন্দুগামী বৃত্তের সমীকরণ,
\((x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})+\)\(k\{(x-x_{1})(y_{1}-y_{2})-(y-y_{1})(x_{1}-x_{2})\}=0\)
ইহাই নির্ণেয় বৃত্তের সমীকরণ।
বৃত্তের সাপেক্ষে কোনো বিন্দুর আপেক্ষিক অবস্থান
The relative position of a point with respect to a circle
\((x_{1}, y_{1})\) বিন্দুটির \(f(x,y)\equiv x^{2}+y^{2}\)\(+2gx+2fy+c=0\) বৃত্তের সাপেক্ষে আপেক্ষিক অবস্থান।
বাহিরে অবস্থান করার শর্তঃ
\(f(x_{1},y_{1})>0\) পরিধীর উপরে অবস্থান করার শর্তঃ
\(f(x_{1},y_{1})=0\) ভিতরে অবস্থান করার শর্তঃ
\(f(x_{1},y_{1})<0 \)
বাহিরে অবস্থান করার শর্তঃ
\(f(x_{1},y_{1})>0\) পরিধীর উপরে অবস্থান করার শর্তঃ
\(f(x_{1},y_{1})=0\) ভিতরে অবস্থান করার শর্তঃ
\(f(x_{1},y_{1})<0 \)
প্রমাণঃ
\(A(x_{1}, y_{1})\) বিন্দু বৃত্তের বাহিরে অবস্থিত।
আমরা জানি,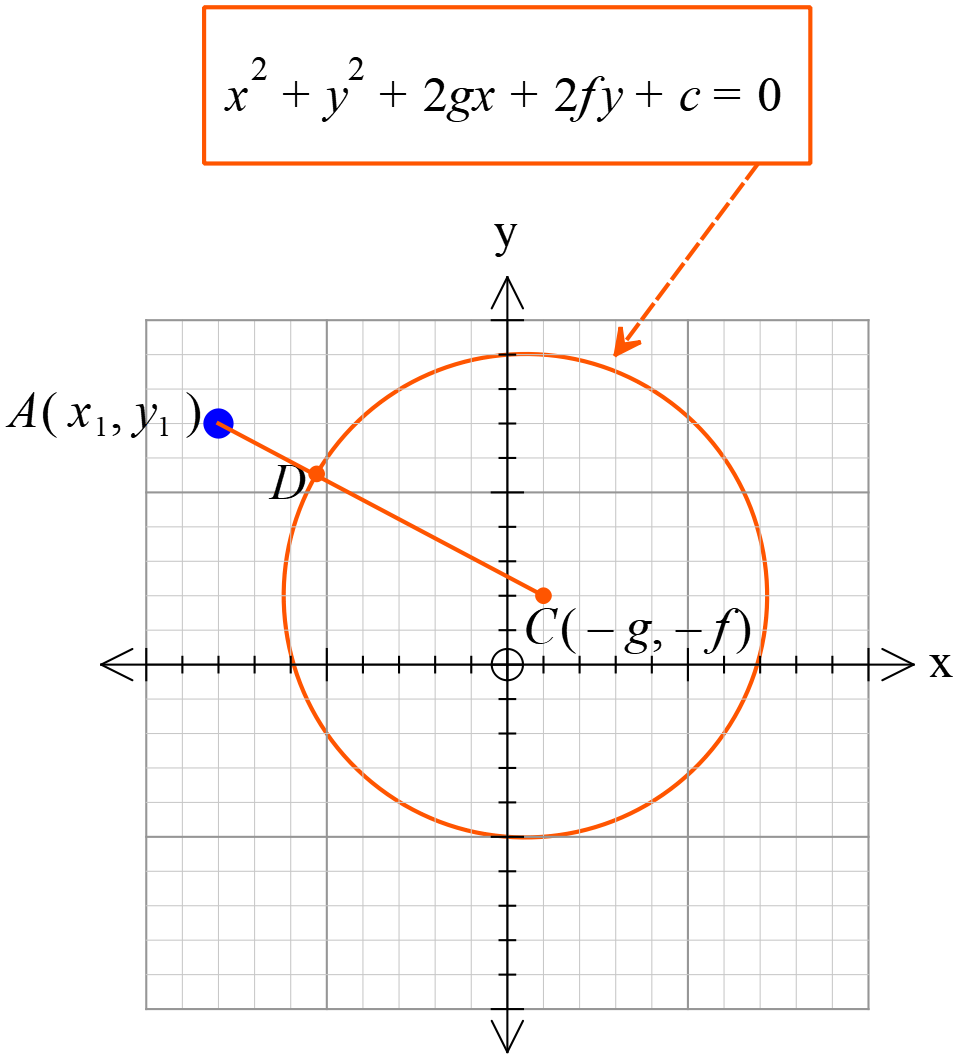
বৃত্তের সাধারণ সমীকরণ,
\(f(x,y)\equiv x^{2}+y^{2}+2gx+2fy+c=0 ...(1)\)
কেন্দ্রঃ \(C(-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) হতে \(f(x_{1},y_{1})\equiv x_{1}^{2}+y_{1}^{2}+2gx_{1}+2fy_{1}+c=0 ...(2)\)
\(A, C\) যোগ করি,
\(AC\) রেখা বৃত্তের পরিধীকে \(D\) বিন্দুতে ছেদ করে।
এখানে,
ব্যাসার্ধঃ \(CD=\sqrt{g^{2}+f^{2}-c}\)
\(\because A\) বৃত্তের বাহিরে অবস্থিত,
\(\therefore AC>CD\)
\(\Rightarrow AC^{2}>CD^{2}\)
\(\Rightarrow (x_{1}+g)^{2}+(y_{1}+f)^{2}>(\sqrt{g^{2}+f^{2}-c})^{2}\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}>g^{2}+f^{2}-c\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}-g^{2}-f^{2}+c>0\)
\(\Rightarrow x^{2}_{1}+y^{2}_{1}+2x_{1}g+2y_{1}f+c>0\)
\(\therefore f(x_{1},y_{1})>0\)
\(\therefore A(x_{1}, y_{1})\) বিন্দু বৃত্তের বাহিরে অবস্থিত হবে যদি,
\(f(x_{1},y_{1})>0\) হয়।
\(A(x_{1}, y_{1})\) বিন্দু বৃত্তের পরিধীর উপর অবস্থিত।
আমরা জানি,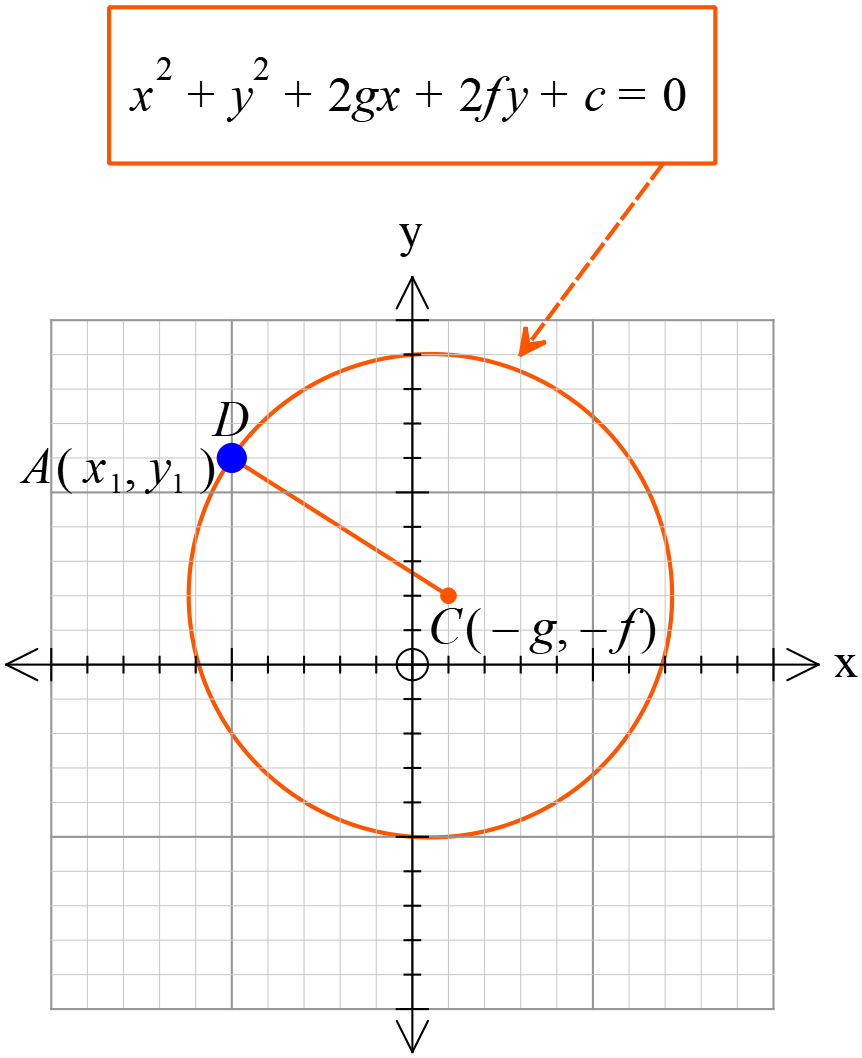
বৃত্তের সাধারণ সমীকরণ,
\(f(x,y)\equiv x^{2}+y^{2}+2gx+2fy+c=0 ...(1)\)
কেন্দ্রঃ \(C(-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) হতে \(f(x_{1},y_{1})\equiv x_{1}^{2}+y_{1}^{2}+2gx_{1}+2fy_{1}+c...(2)\)
\(A, C\) যোগ করি,
এখানে,
ব্যাসার্ধঃ \(AC=\sqrt{g^{2}+f^{2}-c}\)
\(\because A\) বৃত্তের পরিধীর উপর অবস্থিত,
\(\therefore AC=\sqrt{g^{2}+f^{2}-c}\)
\(\Rightarrow AC^{2}=\sqrt{g^{2}+f^{2}-c}^{2}\)
\(\Rightarrow (x_{1}+g)^{2}+(y_{1}+f)^{2}=(\sqrt{g^{2}+f^{2}-c})^{2}\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}=g^{2}+f^{2}-c\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}-g^{2}-f^{2}+c=0\)
\(\Rightarrow x^{2}_{1}+y^{2}_{1}+2x_{1}g+2y_{1}f+c=0\)
\(\therefore f(x_{1},y_{1})=0\)
\(\therefore A(x_{1}, y_{1})\) বিন্দু বৃত্তের পরিধীর উপর অবস্থিত হবে যদি,
\(f(x_{1},y_{1})=0\) হয়।
\(A(x_{1}, y_{1})\) বিন্দু বৃত্তের ভিতরে অবস্থিত।
আমরা জানি,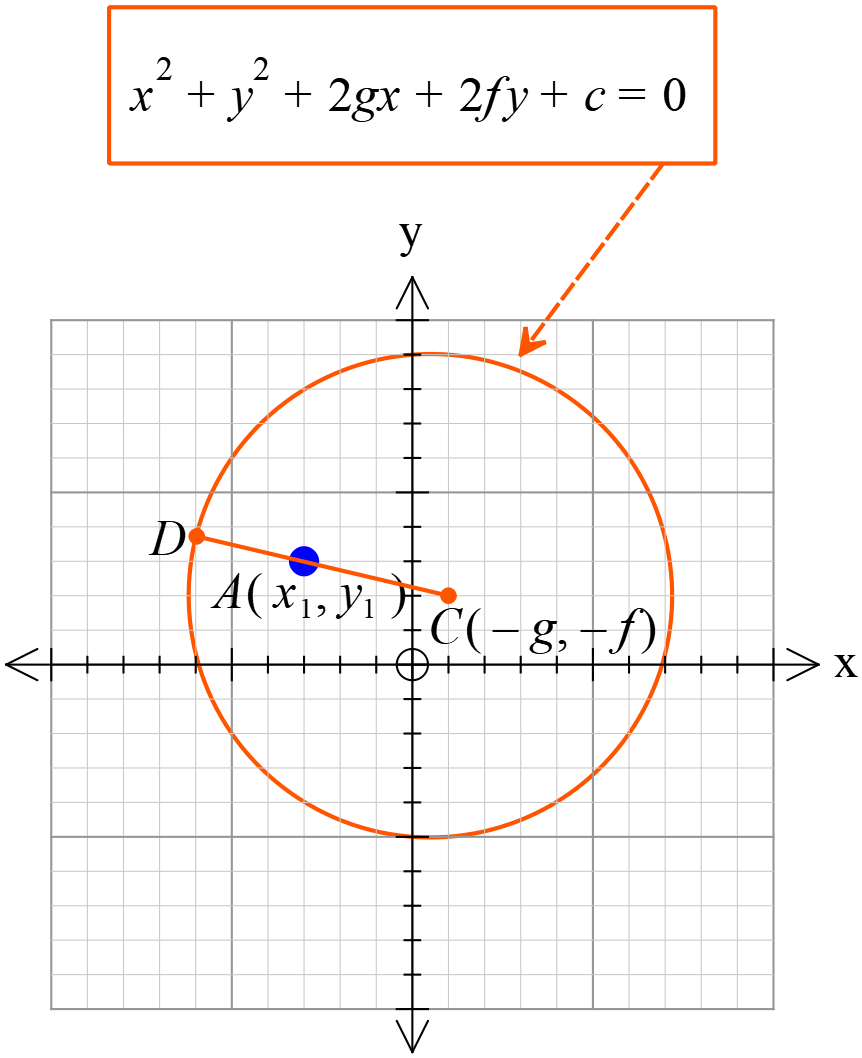
বৃত্তের সাধারণ সমীকরণ,
\(f(x,y)\equiv x^{2}+y^{2}+2gx+2fy+c=0 ...(1)\)
কেন্দ্রঃ \(C(-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) হতে \(f(x_{1},y_{1})\equiv x_{1}^{2}+y_{1}^{2}+2gx_{1}+2fy_{1}+c=0 ...(2)\)
\(A, C\) যোগ করি,
\(CA\) রেখার বর্ধিতাংশ বৃত্তের পরিধীকে \(D\) বিন্দুতে ছেদ করে।
এখানে,
ব্যাসার্ধঃ \(CD=\sqrt{g^{2}+f^{2}-c}\)
\(\because A\) বৃত্তের ভিতরে অবস্থিত,
\(\therefore CD>AC \)
\(\Rightarrow CD^{2}>AC^{2}\)
\(\Rightarrow (\sqrt{g^{2}+f^{2}-c})^{2}>(x_{1}+g)^{2}+(y_{1}+f)^{2}\)
\(\Rightarrow g^{2}+f^{2}-c>x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}-g^{2}-f^{2}+c<0\)
\(\Rightarrow x^{2}_{1}+y^{2}_{1}+2x_{1}g+2y_{1}f+c<0\)
\(\therefore f(x_{1},y_{1})<0\)
\(\therefore A(x_{1}, y_{1})\) বিন্দু বৃত্তের ভিতরে অবস্থিত হবে যদি,
\(f(x_{1},y_{1})<0\) হয়।
\(A(x_{1}, y_{1})\) বিন্দু বৃত্তের বাহিরে অবস্থিত।
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(f(x,y)\equiv x^{2}+y^{2}+2gx+2fy+c=0 ...(1)\)
কেন্দ্রঃ \(C(-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) হতে \(f(x_{1},y_{1})\equiv x_{1}^{2}+y_{1}^{2}+2gx_{1}+2fy_{1}+c=0 ...(2)\)
\(A, C\) যোগ করি,
\(AC\) রেখা বৃত্তের পরিধীকে \(D\) বিন্দুতে ছেদ করে।
এখানে,
ব্যাসার্ধঃ \(CD=\sqrt{g^{2}+f^{2}-c}\)
\(\because A\) বৃত্তের বাহিরে অবস্থিত,
\(\therefore AC>CD\)
\(\Rightarrow AC^{2}>CD^{2}\)
\(\Rightarrow (x_{1}+g)^{2}+(y_{1}+f)^{2}>(\sqrt{g^{2}+f^{2}-c})^{2}\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}>g^{2}+f^{2}-c\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}-g^{2}-f^{2}+c>0\)
\(\Rightarrow x^{2}_{1}+y^{2}_{1}+2x_{1}g+2y_{1}f+c>0\)
\(\therefore f(x_{1},y_{1})>0\)
\(\therefore A(x_{1}, y_{1})\) বিন্দু বৃত্তের বাহিরে অবস্থিত হবে যদি,
\(f(x_{1},y_{1})>0\) হয়।
\(A(x_{1}, y_{1})\) বিন্দু বৃত্তের পরিধীর উপর অবস্থিত।
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(f(x,y)\equiv x^{2}+y^{2}+2gx+2fy+c=0 ...(1)\)
কেন্দ্রঃ \(C(-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) হতে \(f(x_{1},y_{1})\equiv x_{1}^{2}+y_{1}^{2}+2gx_{1}+2fy_{1}+c...(2)\)
\(A, C\) যোগ করি,
এখানে,
ব্যাসার্ধঃ \(AC=\sqrt{g^{2}+f^{2}-c}\)
\(\because A\) বৃত্তের পরিধীর উপর অবস্থিত,
\(\therefore AC=\sqrt{g^{2}+f^{2}-c}\)
\(\Rightarrow AC^{2}=\sqrt{g^{2}+f^{2}-c}^{2}\)
\(\Rightarrow (x_{1}+g)^{2}+(y_{1}+f)^{2}=(\sqrt{g^{2}+f^{2}-c})^{2}\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}=g^{2}+f^{2}-c\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}-g^{2}-f^{2}+c=0\)
\(\Rightarrow x^{2}_{1}+y^{2}_{1}+2x_{1}g+2y_{1}f+c=0\)
\(\therefore f(x_{1},y_{1})=0\)
\(\therefore A(x_{1}, y_{1})\) বিন্দু বৃত্তের পরিধীর উপর অবস্থিত হবে যদি,
\(f(x_{1},y_{1})=0\) হয়।
\(A(x_{1}, y_{1})\) বিন্দু বৃত্তের ভিতরে অবস্থিত।
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(f(x,y)\equiv x^{2}+y^{2}+2gx+2fy+c=0 ...(1)\)
কেন্দ্রঃ \(C(-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
\((1)\) হতে \(f(x_{1},y_{1})\equiv x_{1}^{2}+y_{1}^{2}+2gx_{1}+2fy_{1}+c=0 ...(2)\)
\(A, C\) যোগ করি,
\(CA\) রেখার বর্ধিতাংশ বৃত্তের পরিধীকে \(D\) বিন্দুতে ছেদ করে।
এখানে,
ব্যাসার্ধঃ \(CD=\sqrt{g^{2}+f^{2}-c}\)
\(\because A\) বৃত্তের ভিতরে অবস্থিত,
\(\therefore CD>AC \)
\(\Rightarrow CD^{2}>AC^{2}\)
\(\Rightarrow (\sqrt{g^{2}+f^{2}-c})^{2}>(x_{1}+g)^{2}+(y_{1}+f)^{2}\)
\(\Rightarrow g^{2}+f^{2}-c>x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}\)
\(\Rightarrow x^{2}_{1}+2x_{1}g+g^{2}+y^{2}_{1}+2y_{1}f+f^{2}-g^{2}-f^{2}+c<0\)
\(\Rightarrow x^{2}_{1}+y^{2}_{1}+2x_{1}g+2y_{1}f+c<0\)
\(\therefore f(x_{1},y_{1})<0\)
\(\therefore A(x_{1}, y_{1})\) বিন্দু বৃত্তের ভিতরে অবস্থিত হবে যদি,
\(f(x_{1},y_{1})<0\) হয়।
দুইটি বৃত্তের পরস্পরকে স্পর্শ করার শর্ত
The condition of two circles touching each other
\(S_{1}\equiv x^{2}+y^{2}+2g_{1}x\)\(+2f_{1}y+c_{1}=0 ....(1)\) বৃত্তের,
কেন্দ্রঃ \(C_{1}\)
ব্যাসার্ধঃ \(r_{1}\)
\(S_{2}\equiv x^{2}+y^{2}+2g_{2}x+2f_{2}y+c_{2}=0 ....(2)\) বৃত্তের,
কেন্দ্রঃ \(C_{2}\)
ব্যাসার্ধঃ \(r_{2}\)
কেন্দ্রদ্বয়ের মধ্যবর্তী দূরত্ব \(=C_{1}C_{2}\)
বৃত্তদ্বয় পরস্পরকে বহিঃস্থভাবে স্পর্শ করার শর্তঃ
\(C_{1}C_{2}=r_{1}+r_{2}\)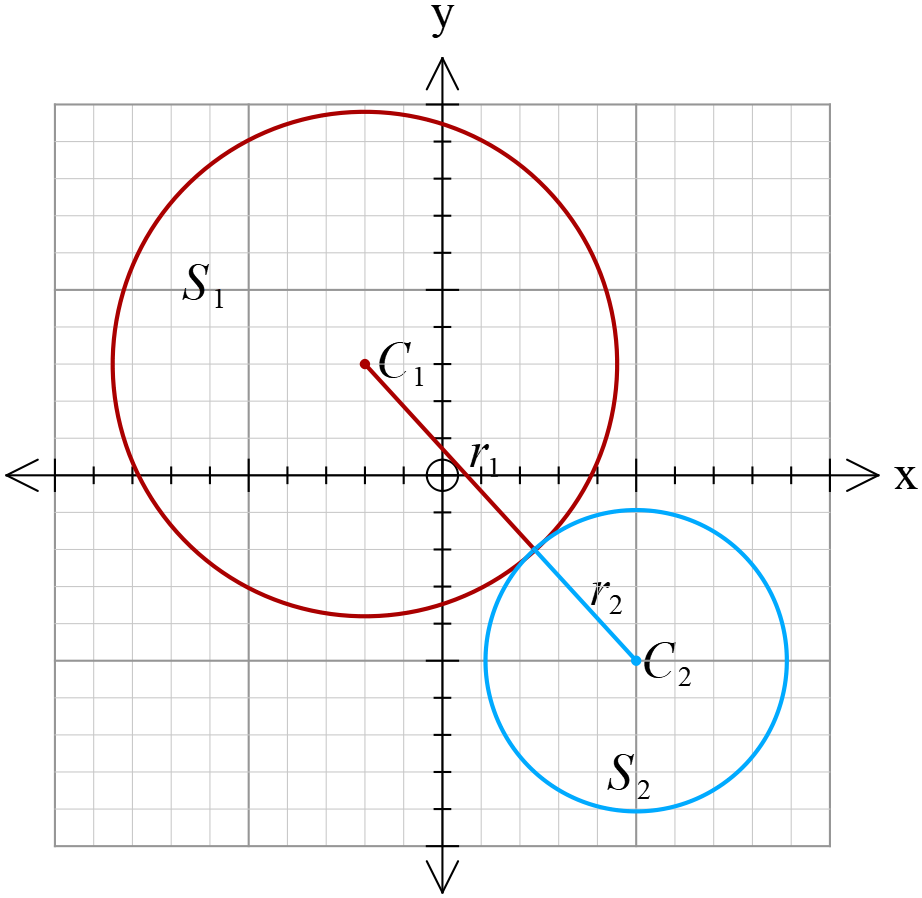
বৃত্তদ্বয় পরস্পরকে অন্তঃস্থভাবে স্পর্শ করার শর্তঃ
\(C_{1}C_{2}=|r_{1}-r_{2}|\)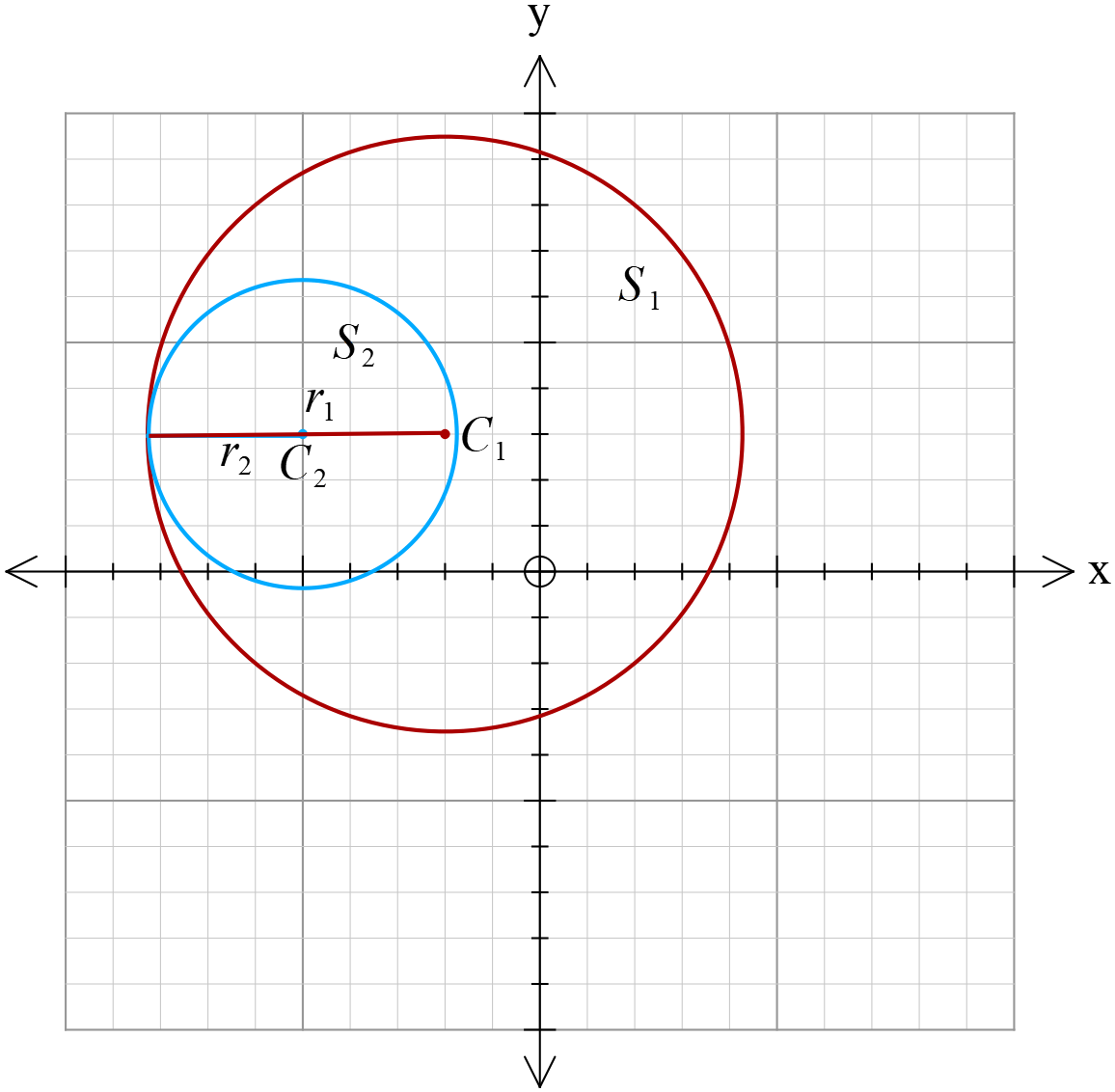
কেন্দ্রঃ \(C_{1}\)
ব্যাসার্ধঃ \(r_{1}\)
\(S_{2}\equiv x^{2}+y^{2}+2g_{2}x+2f_{2}y+c_{2}=0 ....(2)\) বৃত্তের,
কেন্দ্রঃ \(C_{2}\)
ব্যাসার্ধঃ \(r_{2}\)
কেন্দ্রদ্বয়ের মধ্যবর্তী দূরত্ব \(=C_{1}C_{2}\)
বৃত্তদ্বয় পরস্পরকে বহিঃস্থভাবে স্পর্শ করার শর্তঃ
\(C_{1}C_{2}=r_{1}+r_{2}\)
বৃত্তদ্বয় পরস্পরকে অন্তঃস্থভাবে স্পর্শ করার শর্তঃ
\(C_{1}C_{2}=|r_{1}-r_{2}|\)
দুইটি বৃত্তের সাধারণ জ্যা এর সমীকরণ
Equation of common chord of two circles
\(S_{1}\equiv x^{2}+y^{2}+2g_{1}x+2f_{1}y+c_{1}=0 ....(1)\)
\(S_{2}\equiv x^{2}+y^{2}+2g_{2}x+2f_{2}y+c_{2}=0 ....(2)\)
বৃত্তদ্বয়ের সাধারণ জ্যা এর সমীকরণ,
\(S_{1}-S_{2}=0 .....(3)\)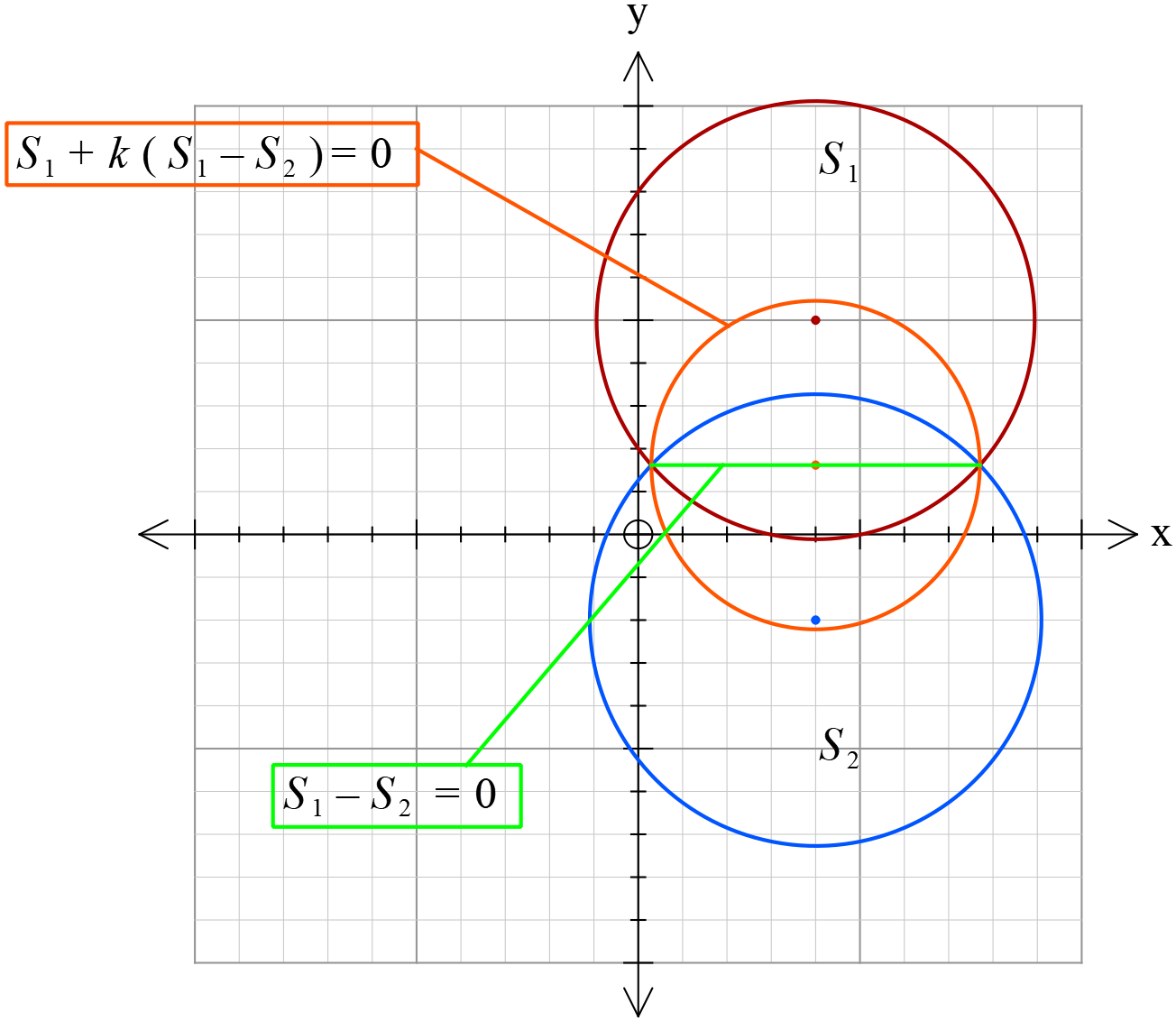
\(S_{2}\equiv x^{2}+y^{2}+2g_{2}x+2f_{2}y+c_{2}=0 ....(2)\)
বৃত্তদ্বয়ের সাধারণ জ্যা এর সমীকরণ,
\(S_{1}-S_{2}=0 .....(3)\)
দুইটি বৃত্তের ছেদবিন্দুগামী বৃত্তের সমীকরণ
Equation of the circle to the point of intersection of two circles
\(S_{1}\equiv x^{2}+y^{2}+2g_{1}x+2f_{1}y+c_{1}=0 ....(1)\)
\(S_{2}\equiv x^{2}+y^{2}+2g_{2}x+2f_{2}y+c_{2}=0 ....(2)\)
বৃত্তদ্বয়ের সাধারণ জ্যা এর সমীকরণ,
\(S_{1}-S_{2}=0 .....(3)\)
বৃত্তদ্বয়ের ছেদবিন্দুগামী বৃত্তের সমীকরণ,
\(S_{1}+k(S_{1}-S_{2})=0\)
\(k\) শুন্য ব্যতীত যে কোনো বাস্তব সংখ্যা (ইচ্ছামূলক ধ্রূবক)।
\(S_{2}\equiv x^{2}+y^{2}+2g_{2}x+2f_{2}y+c_{2}=0 ....(2)\)
বৃত্তদ্বয়ের সাধারণ জ্যা এর সমীকরণ,
\(S_{1}-S_{2}=0 .....(3)\)
বৃত্তদ্বয়ের ছেদবিন্দুগামী বৃত্তের সমীকরণ,
\(S_{1}+k(S_{1}-S_{2})=0\)
\(k\) শুন্য ব্যতীত যে কোনো বাস্তব সংখ্যা (ইচ্ছামূলক ধ্রূবক)।
পোলার স্থানাঙ্কে বৃত্তের সমীকরণ
Equation of circle in polar coordinates
\(x^{2}+y^{2}=a^{2} ....(1)\)
বৃত্ত \((1)\) এর পোলার সমীকরণ,
\(r=a\)
কেন্দ্রের পোলার স্থানাংক \((0, 0^{o})\)
ব্যাসার্ধ \(=a\)
পরিধিস্থ সাধারণ বিন্দুর পোলার স্থানাংক \((r, \theta)\)
\((x-h)^{2}+(y-k)^{2}=a^{2} ....(2)\)
বৃত্ত \((2)\) এর পোলার সমীকরণ,
\(r^{2}-2rr_{1}\cos(\theta-\theta_{1})+r^{2}_{1}=a^{2}\)
কেন্দ্রের পোলার স্থানাংক \((r_{1}, \theta_{1})\)
ব্যাসার্ধ \(=a\)
পরিধিস্থ সাধারণ বিন্দুর পোলার স্থানাংক \((r, \theta)\)
\(x^{2}+y^{2}+2gx+2fy+c=0 ....(3)\)
বৃত্ত \((3)\) এর পোলার সমীকরণ,
\(r^{2}-2rr_{1}\cos(\theta-\theta_{1})+c=0\)
বৃত্ত \((1)\) এর পোলার সমীকরণ,
\(r=a\)
কেন্দ্রের পোলার স্থানাংক \((0, 0^{o})\)
ব্যাসার্ধ \(=a\)
পরিধিস্থ সাধারণ বিন্দুর পোলার স্থানাংক \((r, \theta)\)
\((x-h)^{2}+(y-k)^{2}=a^{2} ....(2)\)
বৃত্ত \((2)\) এর পোলার সমীকরণ,
\(r^{2}-2rr_{1}\cos(\theta-\theta_{1})+r^{2}_{1}=a^{2}\)
কেন্দ্রের পোলার স্থানাংক \((r_{1}, \theta_{1})\)
ব্যাসার্ধ \(=a\)
পরিধিস্থ সাধারণ বিন্দুর পোলার স্থানাংক \((r, \theta)\)
\(x^{2}+y^{2}+2gx+2fy+c=0 ....(3)\)
বৃত্ত \((3)\) এর পোলার সমীকরণ,
\(r^{2}-2rr_{1}\cos(\theta-\theta_{1})+c=0\)
প্রমাণঃ
বৃত্তের সমীকরণ \(x^{2}+y^{2}=a^{2}\)।
আমরা জানি,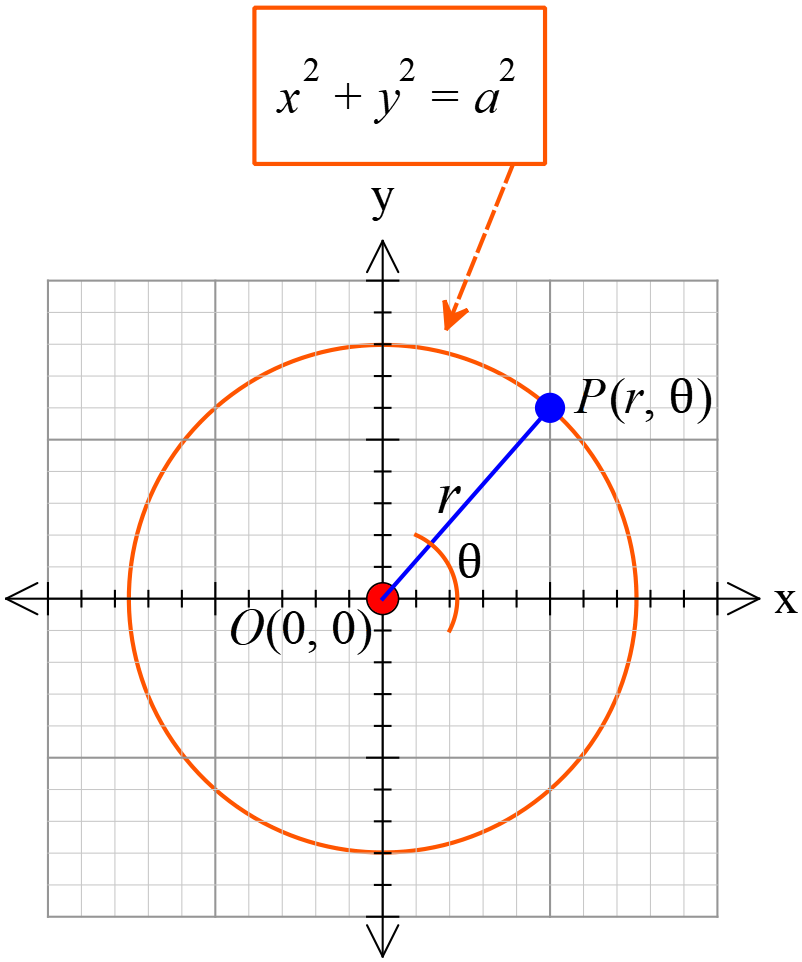
কেন্দ্র মূলবিন্দু তথা \(O(0, 0)\) এবং ব্যাসার্ধ \(a \ (a>0)\) বৃত্তের সমীকরণ
\(x^{2}+y^{2}=a^{2} ........(1)\)
বৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) এর পোলার স্থানাঙ্ক \(P(r\cos\theta, r\sin\theta)\) হলে,
\(x=r\cos\theta, \ y=r\sin\theta\)
তবে, \( (1)\) হতে পাই,
\((r\cos\theta)^{2}+(r\sin\theta)^{2}=a^{2}\)
\(\Rightarrow r^{2}\cos^{2}\theta+r^{2}\sin^{2}\theta=a^{2}\)
\(\Rightarrow r^{2}(\cos^{2}\theta+\sin^{2}\theta)=a^{2}\)
\(\Rightarrow r^{2}.1=a^{2}\) ➜ \(\because \cos^{2}\theta+\sin^{2}\theta=1\)
\(\Rightarrow r^{2}=a^{2}\)
\(\therefore r=a\)
ইহাই নির্ণেয় পোলার সমীকরণ।
বৃত্তের সমীকরণ \((x-h)^{2}+(y-k)^{2}=a^{2}\)।
আমরা জানি,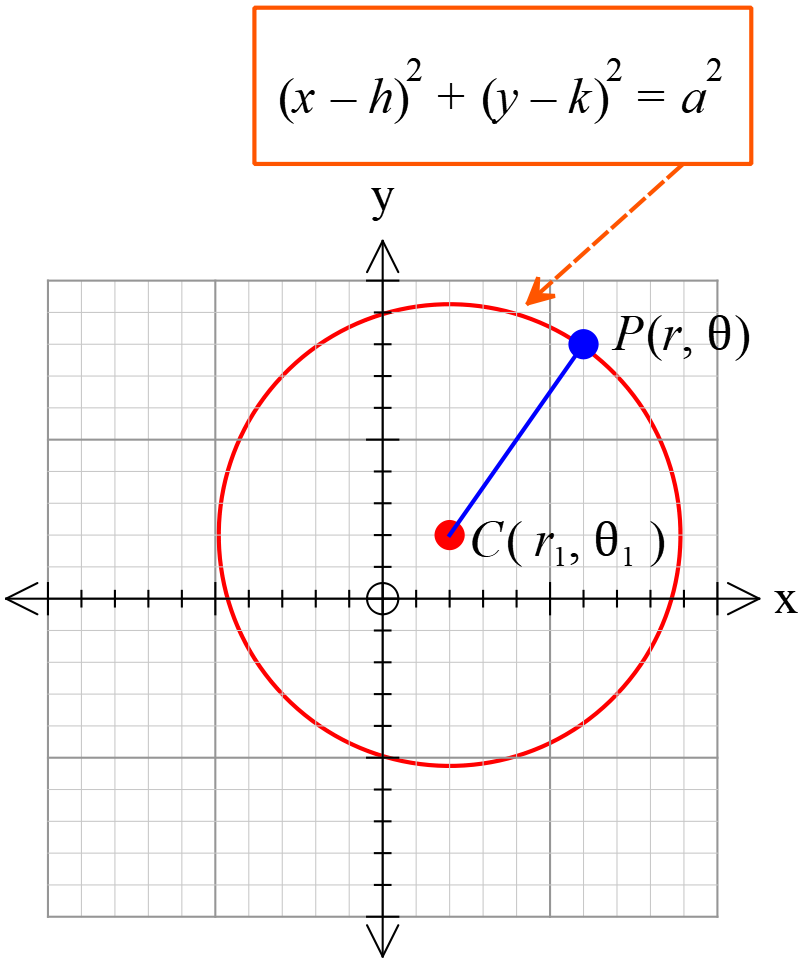
কেন্দ্র \(C(h, k)\) ব্যাসার্ধ \(a\)
বৃত্তের সমীকরণ,
\((x-h)^{2}+(y-k)^{2}=a^{2} ....(2)\)
মনে করি,
বৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) এর পোলার স্থানাঙ্ক \(P(r\cos\theta, r\sin\theta)\)
এবং কেন্দ্র \(C(h, k)\) এর পোলার স্থানাঙ্ক \(P(r_{1}\cos\theta_{1}, r_{1}\sin\theta_{1})\)
তাহলে,
\(x=r\cos\theta, y=r\sin\theta\) এবং \(h=r_{1}\cos\theta_{1}, k=r_{1}\sin\theta_{1}\)
\((2)\) হতে,
\(\Rightarrow (r\cos\theta-r_{1}\cos\theta_{1})^{2}+(r\sin\theta-r_{1}\sin\theta_{1})^{2}=a^{2}\)
\(\Rightarrow r^{2}\cos^{2}\theta+r^{2}_{1}\cos^{2}\theta_{1}-2rr_{1}\cos\theta\cos\theta_{1}+r^{2}\sin^{2}\theta+\)\(r^{2}_{1}\sin^{2}\theta_{1}-2rr_{1}\sin\theta\sin\theta_{1}=a^{2}\)
\(\Rightarrow r^{2}(\cos^{2}\theta+\sin^{2}\theta)-2rr_{1}(\cos\theta\cos\theta_{1}+\sin\theta\sin\theta_{1})\)\(+r^{2}_{1}(\cos^{2}\theta_{1}+\sin^{2}\theta_{1})=a^{2}\)
\(\Rightarrow r^{2}.1-2rr_{1}\cos(\theta-\theta_{1})+r^{2}_{1}.1=a^{2}\)
\(\therefore r^{2}-2rr_{1}\cos(\theta-\theta_{1})+r^{2}_{1}=a^{2}\)
ইহাই নির্ণেয় পোলার সমীকরণ।
বৃত্তের সমীকরণ \(x^{2}+y^{2}+2gx+2fy+c=0\)।
আমরা জানি,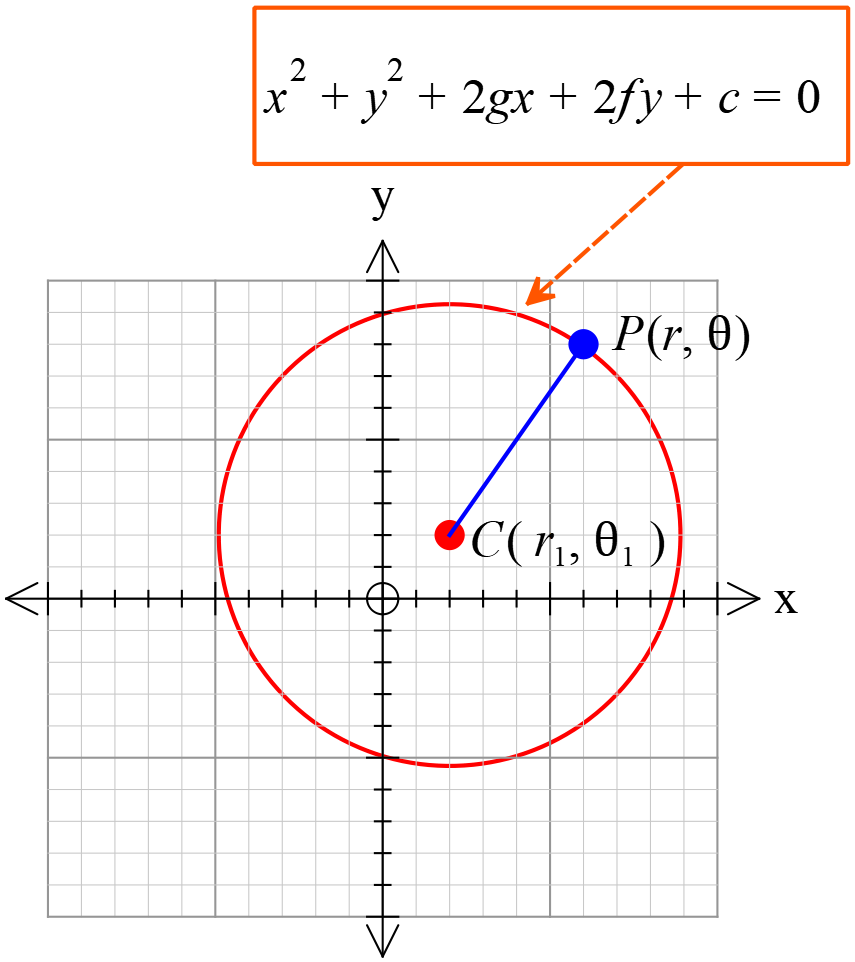
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ...(3)\)
কেন্দ্রঃ \(C(-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
মনে করি,
বৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) এর পোলার স্থানাঙ্ক \(P(r\cos\theta, r\sin\theta)\)
এবং কেন্দ্র \(C(-g, -f)\) এর পোলার স্থানাঙ্ক \(P(r_{1}\cos\theta_{1}, r_{1}\sin\theta_{1})\)
তাহলে,
\(x=r\cos\theta, y=r\sin\theta\) এবং \(-g=r_{1}\cos\theta_{1}, -f=r_{1}\sin\theta_{1}\)
\((3)\) হতে,
\(x^{2}+y^{2}+2gx+2fy+c=0\)
\(\Rightarrow x^{2}+2gx+g^{2}+y^{2}+2fy+f^{2}-g^{2}-f^{2}+c=0\)
\(\Rightarrow (x+g)^{2}+(y+f)^{2}-g^{2}-f^{2}+c=0\)
\(\Rightarrow \{x-(-g)\}^{2}+\{y-(-f)\}^{2}-(-g)^{2}-(-f)^{2}+c=0\)
\(\Rightarrow (r\cos\theta-r_{1}\cos\theta_{1})^{2}+(r\sin\theta-r_{1}\sin\theta_{1})^{2}-\)\((r_{1}\cos\theta_{1})^{2}-(r_{1}\sin\theta_{1})^{2}+c=0\)
\(\Rightarrow r^{2}\cos^{2}\theta+r^{2}_{1}\cos^{2}\theta_{1}-2rr_{1}\cos\theta\cos\theta_{1}+r^{2}\sin^{2}\theta+\)\(r^{2}_{1}\sin^{2}\theta_{1}\)\(-2rr_{1}\sin\theta\sin\theta_{1}-r^{2}_{1}\cos^{2}\theta_{1}-r^{2}_{1}\sin^{2}\theta_{1}+c=0\)
\(\Rightarrow r^{2}(\cos^{2}\theta+\sin^{2}\theta)-2rr_{1}(\cos\theta\cos\theta_{1}+\)\(\sin\theta\sin\theta_{1})+c=0\)
\(\Rightarrow r^{2}.1-2rr_{1}\cos(\theta-\theta_{1})+c=0\)
\(\therefore r^{2}-2rr_{1}\cos(\theta-\theta_{1})+c=0\)
ইহাই নির্ণেয় পোলার সমীকরণ।
বৃত্তের সমীকরণ \(x^{2}+y^{2}=a^{2}\)।
আমরা জানি,
কেন্দ্র মূলবিন্দু তথা \(O(0, 0)\) এবং ব্যাসার্ধ \(a \ (a>0)\) বৃত্তের সমীকরণ
\(x^{2}+y^{2}=a^{2} ........(1)\)
বৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) এর পোলার স্থানাঙ্ক \(P(r\cos\theta, r\sin\theta)\) হলে,
\(x=r\cos\theta, \ y=r\sin\theta\)
তবে, \( (1)\) হতে পাই,
\((r\cos\theta)^{2}+(r\sin\theta)^{2}=a^{2}\)
\(\Rightarrow r^{2}\cos^{2}\theta+r^{2}\sin^{2}\theta=a^{2}\)
\(\Rightarrow r^{2}(\cos^{2}\theta+\sin^{2}\theta)=a^{2}\)
\(\Rightarrow r^{2}.1=a^{2}\) ➜ \(\because \cos^{2}\theta+\sin^{2}\theta=1\)
\(\Rightarrow r^{2}=a^{2}\)
\(\therefore r=a\)
ইহাই নির্ণেয় পোলার সমীকরণ।
বৃত্তের সমীকরণ \((x-h)^{2}+(y-k)^{2}=a^{2}\)।
আমরা জানি,
কেন্দ্র \(C(h, k)\) ব্যাসার্ধ \(a\)
বৃত্তের সমীকরণ,
\((x-h)^{2}+(y-k)^{2}=a^{2} ....(2)\)
মনে করি,
বৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) এর পোলার স্থানাঙ্ক \(P(r\cos\theta, r\sin\theta)\)
এবং কেন্দ্র \(C(h, k)\) এর পোলার স্থানাঙ্ক \(P(r_{1}\cos\theta_{1}, r_{1}\sin\theta_{1})\)
তাহলে,
\(x=r\cos\theta, y=r\sin\theta\) এবং \(h=r_{1}\cos\theta_{1}, k=r_{1}\sin\theta_{1}\)
\((2)\) হতে,
\(\Rightarrow (r\cos\theta-r_{1}\cos\theta_{1})^{2}+(r\sin\theta-r_{1}\sin\theta_{1})^{2}=a^{2}\)
\(\Rightarrow r^{2}\cos^{2}\theta+r^{2}_{1}\cos^{2}\theta_{1}-2rr_{1}\cos\theta\cos\theta_{1}+r^{2}\sin^{2}\theta+\)\(r^{2}_{1}\sin^{2}\theta_{1}-2rr_{1}\sin\theta\sin\theta_{1}=a^{2}\)
\(\Rightarrow r^{2}(\cos^{2}\theta+\sin^{2}\theta)-2rr_{1}(\cos\theta\cos\theta_{1}+\sin\theta\sin\theta_{1})\)\(+r^{2}_{1}(\cos^{2}\theta_{1}+\sin^{2}\theta_{1})=a^{2}\)
\(\Rightarrow r^{2}.1-2rr_{1}\cos(\theta-\theta_{1})+r^{2}_{1}.1=a^{2}\)
\(\therefore r^{2}-2rr_{1}\cos(\theta-\theta_{1})+r^{2}_{1}=a^{2}\)
ইহাই নির্ণেয় পোলার সমীকরণ।
বৃত্তের সমীকরণ \(x^{2}+y^{2}+2gx+2fy+c=0\)।
আমরা জানি,
বৃত্তের সাধারণ সমীকরণ,
\(x^{2}+y^{2}+2gx+2fy+c=0 ...(3)\)
কেন্দ্রঃ \(C(-g, -f)\)
ব্যাসার্ধঃ \(=\sqrt{g^{2}+f^{2}-c}\) যখন, \((g^{2}+f^{2}>c)\)
মনে করি,
বৃত্তের উপর যে কোনো বিন্দু \(P(x, y)\) এর পোলার স্থানাঙ্ক \(P(r\cos\theta, r\sin\theta)\)
এবং কেন্দ্র \(C(-g, -f)\) এর পোলার স্থানাঙ্ক \(P(r_{1}\cos\theta_{1}, r_{1}\sin\theta_{1})\)
তাহলে,
\(x=r\cos\theta, y=r\sin\theta\) এবং \(-g=r_{1}\cos\theta_{1}, -f=r_{1}\sin\theta_{1}\)
\((3)\) হতে,
\(x^{2}+y^{2}+2gx+2fy+c=0\)
\(\Rightarrow x^{2}+2gx+g^{2}+y^{2}+2fy+f^{2}-g^{2}-f^{2}+c=0\)
\(\Rightarrow (x+g)^{2}+(y+f)^{2}-g^{2}-f^{2}+c=0\)
\(\Rightarrow \{x-(-g)\}^{2}+\{y-(-f)\}^{2}-(-g)^{2}-(-f)^{2}+c=0\)
\(\Rightarrow (r\cos\theta-r_{1}\cos\theta_{1})^{2}+(r\sin\theta-r_{1}\sin\theta_{1})^{2}-\)\((r_{1}\cos\theta_{1})^{2}-(r_{1}\sin\theta_{1})^{2}+c=0\)
\(\Rightarrow r^{2}\cos^{2}\theta+r^{2}_{1}\cos^{2}\theta_{1}-2rr_{1}\cos\theta\cos\theta_{1}+r^{2}\sin^{2}\theta+\)\(r^{2}_{1}\sin^{2}\theta_{1}\)\(-2rr_{1}\sin\theta\sin\theta_{1}-r^{2}_{1}\cos^{2}\theta_{1}-r^{2}_{1}\sin^{2}\theta_{1}+c=0\)
\(\Rightarrow r^{2}(\cos^{2}\theta+\sin^{2}\theta)-2rr_{1}(\cos\theta\cos\theta_{1}+\)\(\sin\theta\sin\theta_{1})+c=0\)
\(\Rightarrow r^{2}.1-2rr_{1}\cos(\theta-\theta_{1})+c=0\)
\(\therefore r^{2}-2rr_{1}\cos(\theta-\theta_{1})+c=0\)
ইহাই নির্ণেয় পোলার সমীকরণ।
বৃত্তের পরামিতিক সমীকরণ
Parametric equation of circle
\(x^{2}+y^{2}=a^{2} ....(1)\)
বৃত্ত \((1)\) এর পরামিতিক সমীকরণ,
\(x=a\cos{\theta}, \ y=a\sin{\theta}\)
\((x-h)^{2}+(y-k)^{2}=r^{2} ....(2)\)
বৃত্ত \((2)\) এর পরামিতিক সমীকরণ,
\(x=h+r\cos{\theta}, \ y=k+r\sin{\theta}\)
বৃত্ত \((1)\) এর পরামিতিক সমীকরণ,
\(x=a\cos{\theta}, \ y=a\sin{\theta}\)
\((x-h)^{2}+(y-k)^{2}=r^{2} ....(2)\)
বৃত্ত \((2)\) এর পরামিতিক সমীকরণ,
\(x=h+r\cos{\theta}, \ y=k+r\sin{\theta}\)
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000005