এ অধ্যায়ের পাঠ্যসূচী।
- ঐতিহাসিক পটভূমি (Historical Background)
- বহুপদী ও বহুপদী সমীকরণ (Polynomials and Polynomial Equations)
- এক চলকের বহুপদী রাশি (Polynomial expression in one variable)
- একাধিক চলকের বহুপদী রাশি (Polynomial expression in more than one variable)
- দুই, তিন ও চার ঘাতবিশিষ্ট এক চলকের বহুপদীর চিত্র (Graphs of polynomials in one variable with two, three and four terms)
- এক চলকের বীজগাণিতিক রাশি যা বহুপদী নয় (An algebraic expression in one variable that is not a polynomial)
- সমমাত্রিক ও অসমমাত্রিক বহুপদী (Homogeneous and Non-homogeneous polynomials)
- সমীকরণ (Equations)
- অভেদ (Arguments of complex numbers in quadrant)
- বহুপদী সমীকরণ (Polynomial Equations)
- বহুপদী সমীকরণের মূল (Roots of a Polynomial Equations)
- বহুপদী সমীকরণের উৎপাদক উপপাদ্য (Factor Theorem for Polynomial Equations)
- বহুপদীর ভাগশেষ উপপাদ্য (Remainder Theorem of Polynomials)
- প্রত্যেক \('n'\) ঘাত বহুপদী সমীকরণের মূলের সংখ্যা (Number of roots of every \('n'\) degree polynomial equations)
- বহুপদী সমীকরণ এবং অভেদ (Polynomial Equations and Identity)
- মূলদ সহগবিশিষ্ট বহুপদী সমীকরণের অমূলদ মূল (Irrational roots of polynomial equations with rational coefficients)
- বাস্তব সহগবিশিষ্ট বহুপদী সমীকরণের কাল্পনিক মূল (Imaginary roots of polynomial equations with real coefficients)
- দ্বিঘাত রাশি এবং দ্বিঘাত সমীকরণ (Quadratic Quantity and Quadratic Equations)
- দ্বিঘাত সমীকরণের সমাধান (Solving quadratic equations)
- দ্বিঘাত সমীকরণের মূলের সংখ্যা (Number of roots of quadratic equation)
- দ্বিঘাত সমীকরণের মূল ও সহগের মধ্যে সম্পর্ক (Relationship between roots and coefficients of quadratic equations)
- দ্বিঘাত সমীকরণের সাধারণ মূল (Common roots of quadratic equations)
- নিশ্চায়ক বা পৃথায়ক (Discriminant)
- দ্বিঘাত সমীকরণের মূলের প্রকৃতি (Nature of roots of quadratic equations)
- দ্বিঘাত সমীকরণ গঠন (Formation of quadratic equations)
- ত্রিঘাত সমীকরণের মূল ও সহগের মধ্যে সম্পর্ক (Relationship between roots and coefficients of qubic equations)
- ত্রিঘাত সমীকরণ গঠন (Formation of qubic equations)
- বিভিন্ন প্রগমনভুক্ত রাশিসমূহ (Various Sequential Quantity)
- অধ্যায় \(3\)-এর উদাহরণসমুহ
- অধ্যায় \(3\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.5\)-এর সৃজনশীল প্রশ্নসমূহ
- অধ্যায় \(3\) / \(Q.6\)-এর ভর্তি পরীক্ষায় আসা প্রশ্নসমূহ
- বহুনির্বাচনী প্রশ্নত্তর
ঐতিহাসিক পটভূমি
Historical Background

ওমর খৈয়াম
Omar Khoyyam
(১০৪৮ খ্রিস্টাব্দ-১১৩১ খ্রিস্টাব্দ)
পার্সিয়ান গণিতবিদ ও জ্যোতির্বিজ্ঞান।
Omar Khoyyam
(১০৪৮ খ্রিস্টাব্দ-১১৩১ খ্রিস্টাব্দ)
পার্সিয়ান গণিতবিদ ও জ্যোতির্বিজ্ঞান।
গণিতে যোগ, বিয়োগ এবং গুণ পদ্ধতিতে প্রকাশিত বহুপদী একটি পরিবর্তনশীল রাশি। যেমনঃ \(x^2+x+1=0\) সমীকরণটিতে তিনটি পদ বিদ্যমান। যেখানে, \(x\) পরিবর্তনশীল চলক, কিন্তু \(1\) ধ্রুবক। মূলত সমীকরণটি চলকের ঘাতকে সংজ্ঞায়িত করে, যার রূপ \(ax^n\)। বীজগণিত ও ক্যালকুলাসে
বহুপদীর পরিপুর্ণতা প্রতিষ্ঠিত হয়।
বহুপদী ও বহুপদী সমীকরণের সংজ্ঞা ও এই সম্পর্কিত বিস্তারিত আলোচনা এ অধ্যায়ে ধারাবাহিকভাবে বর্ণনা করা হয়েছে। শুরুতে আমরা একটি উদাহরণের মাধ্যমে এর প্রয়োজনীয়তা তুলে ধরেছি। "যদি কোনো আয়তক্ষেত্রের দৈর্ঘ্য, প্রস্থ অপেক্ষা \(4\) মিটার বেশি হয় এবং ক্ষেত্রটির ক্ষেত্রফল \(192\) বর্গমিটার হয়, তবে ক্ষেত্রটির দৈর্ঘ্য ও প্রস্থ কত হবে?"
উপরিউক্ত সমস্যাটিকে গাণিতিক রূপ দিলে তা নিম্নরূপঃ
মনে করি ক্ষেত্রটির প্রস্থ \(x\) মিটার। তাহলে, ক্ষেত্রটির দৈর্ঘ্য \(x+4\) মিটার এবং ক্ষেত্রটির ক্ষেত্রফল \(x(x+4)\) বর্গমিটার
অতএব, \(x(x+4)=192\)
\(\Rightarrow x^2+x-192=0\)
এ সমীকরণটি একটি বহুপদী সমীকরণ। অর্থাৎ, \(x\) এর মান নির্ণয়ের জন্য এ সমীকরণের সমাধান করা প্রয়োজন।
আধুনিক গণিতে রবার্ট রেকর্ড \((=)\) চিহ্ন প্রয়োগ করে বহুপদী সমীকরণ তৈরিকরেন।
বহুপদী মূল নির্ণয় বা "বীজগাণিতিক সমীকরণের সমাধান নির্ণয়", গণিতের অতি পুরাতন একটি সমস্যা। যদিও পনের শতক থেকে এই বিষয়ে ব্যবহারিক প্রতীকের প্রয়োগ, সুচারুভাবে উন্নতি সাধন শুরু হয়েছে। এর পূর্বে সমীকরনকে কথায় লেখা হতো।
খ্রিষ্টপূর্ব \(2000\)-এ ব্যবিলনের অধিবাসিরা সর্বপ্রথম দ্বিঘাত সমীকরণের মৌলিক সমাধান দেন।
খ্রিষ্টপূর্ব \(300\)-এ ইউক্লিড দ্বিঘাত সমীকরণকে জ্যামিতিকভাবে সমাধান করেন। \(1000\) খ্রিষ্টাব্দে আরব গণিতবিদ দ্বিঘাত সমীকরণকে \(ux^{2p}+vx^p=w\) আকারে রূপান্তর করেন।
\(1400\) খ্রিষ্টাব্দে আলকাশি ত্রিঘাত সমীকরণকে পুনরুক্তি পদ্ধতিতে সমাধান করেন। এ ছাড়া আরও যে সকল গণিতবিদ এই বিষয়ে উন্নতি সাধনে বিশেষ অবদান রেখেছেন তাদের মধ্যে রেনে দেকার্ত \(1596-1650\), সার আইজ্যাক নিউটন \(1642-1727\) মাইকেল রোল \(1652-1719\), লিওনার্দো অয়লার \(1707-1787\) ও গাউস উল্লেখযোগ্য। আধুনিককালে বহুপদী সমীকরণের অর্থিনীতির ব্যয় বিশ্লেষণ, শেয়ার বাজারের পরিবর্তন, বাজেট বিশ্লেষণ, দ্রব্যমূল্য হ্রাস-বৃদ্ধির পরিমাণ, মিসাইলের গতিপথ, ভোল্টেজের উঠানামা, বস্তুর জড়তা ইত্যাদি পরিমাপ করা যায়।
বহুপদী ও বহুপদী সমীকরণের সংজ্ঞা ও এই সম্পর্কিত বিস্তারিত আলোচনা এ অধ্যায়ে ধারাবাহিকভাবে বর্ণনা করা হয়েছে। শুরুতে আমরা একটি উদাহরণের মাধ্যমে এর প্রয়োজনীয়তা তুলে ধরেছি। "যদি কোনো আয়তক্ষেত্রের দৈর্ঘ্য, প্রস্থ অপেক্ষা \(4\) মিটার বেশি হয় এবং ক্ষেত্রটির ক্ষেত্রফল \(192\) বর্গমিটার হয়, তবে ক্ষেত্রটির দৈর্ঘ্য ও প্রস্থ কত হবে?"
উপরিউক্ত সমস্যাটিকে গাণিতিক রূপ দিলে তা নিম্নরূপঃ
মনে করি ক্ষেত্রটির প্রস্থ \(x\) মিটার। তাহলে, ক্ষেত্রটির দৈর্ঘ্য \(x+4\) মিটার এবং ক্ষেত্রটির ক্ষেত্রফল \(x(x+4)\) বর্গমিটার
অতএব, \(x(x+4)=192\)
\(\Rightarrow x^2+x-192=0\)
এ সমীকরণটি একটি বহুপদী সমীকরণ। অর্থাৎ, \(x\) এর মান নির্ণয়ের জন্য এ সমীকরণের সমাধান করা প্রয়োজন।
আধুনিক গণিতে রবার্ট রেকর্ড \((=)\) চিহ্ন প্রয়োগ করে বহুপদী সমীকরণ তৈরিকরেন।
বহুপদী মূল নির্ণয় বা "বীজগাণিতিক সমীকরণের সমাধান নির্ণয়", গণিতের অতি পুরাতন একটি সমস্যা। যদিও পনের শতক থেকে এই বিষয়ে ব্যবহারিক প্রতীকের প্রয়োগ, সুচারুভাবে উন্নতি সাধন শুরু হয়েছে। এর পূর্বে সমীকরনকে কথায় লেখা হতো।
খ্রিষ্টপূর্ব \(2000\)-এ ব্যবিলনের অধিবাসিরা সর্বপ্রথম দ্বিঘাত সমীকরণের মৌলিক সমাধান দেন।
খ্রিষ্টপূর্ব \(300\)-এ ইউক্লিড দ্বিঘাত সমীকরণকে জ্যামিতিকভাবে সমাধান করেন। \(1000\) খ্রিষ্টাব্দে আরব গণিতবিদ দ্বিঘাত সমীকরণকে \(ux^{2p}+vx^p=w\) আকারে রূপান্তর করেন।
\(1400\) খ্রিষ্টাব্দে আলকাশি ত্রিঘাত সমীকরণকে পুনরুক্তি পদ্ধতিতে সমাধান করেন। এ ছাড়া আরও যে সকল গণিতবিদ এই বিষয়ে উন্নতি সাধনে বিশেষ অবদান রেখেছেন তাদের মধ্যে রেনে দেকার্ত \(1596-1650\), সার আইজ্যাক নিউটন \(1642-1727\) মাইকেল রোল \(1652-1719\), লিওনার্দো অয়লার \(1707-1787\) ও গাউস উল্লেখযোগ্য। আধুনিককালে বহুপদী সমীকরণের অর্থিনীতির ব্যয় বিশ্লেষণ, শেয়ার বাজারের পরিবর্তন, বাজেট বিশ্লেষণ, দ্রব্যমূল্য হ্রাস-বৃদ্ধির পরিমাণ, মিসাইলের গতিপথ, ভোল্টেজের উঠানামা, বস্তুর জড়তা ইত্যাদি পরিমাপ করা যায়।
বহুপদী ও বহুপদী সমীকরণ
Polynomials and Polynomial Equations
বহপদী একটি বীজগাণিতিক রাশি যা এক বা একাধিক পদবিশিষ্ট এবং এক বা একাধিক চলকবিশিষ্ট হতে পারে। এ রাশিতে চলকের ঘাত শুন্য বা স্বাভাবিক সংখ্যা হতে হবে।
বহপদীঃ এক বা একাধিক চলকবিশিষ্ট বীজগাণিতিক রাশির চলকের ঘাত শুন্য বা স্বাভাবিক সংখ্যা হলে সেটিকে বহুপদী বলে।
বহুপদী রাশিতে বিদ্যমান পদগুলিতে চলকের সর্বোচ্চ ঘাতকে ঐ রাশির ঘাত বলা হয়।
একটি বহুপদী রাশিতে একটি মাত্র চলক বিদ্যমান থাকলে রাশিটিকে এক চলকের বহুপদী, দুইটি চলক বিদ্যমান থাকলে রাশিটিকে দুই চলকের বহুপদী, তিনটি চলক বিদ্যমান থাকলে রাশিটিকে তিন চলকের বহুপদী বলা হয়। এভাবে বহুপদী রাশিতে যে কয়টি চলক বিদ্যমান থাকে রাশিটিকে তত চলকের বহুপদী বলা হয়।
যদি কোনো বীজগাণিতিক রাশিতে কোনো চলক না থাকে অর্থাৎ, রাশিটি শুধুমাত্র একটি ধ্রুবকের রাশি হয় তবে ঐ রাশিকে শূন্য ঘাতবিশিষ্ট বহুপদী বলা হয়।
বহপদীঃ এক বা একাধিক চলকবিশিষ্ট বীজগাণিতিক রাশির চলকের ঘাত শুন্য বা স্বাভাবিক সংখ্যা হলে সেটিকে বহুপদী বলে।
বহুপদী রাশিতে বিদ্যমান পদগুলিতে চলকের সর্বোচ্চ ঘাতকে ঐ রাশির ঘাত বলা হয়।
একটি বহুপদী রাশিতে একটি মাত্র চলক বিদ্যমান থাকলে রাশিটিকে এক চলকের বহুপদী, দুইটি চলক বিদ্যমান থাকলে রাশিটিকে দুই চলকের বহুপদী, তিনটি চলক বিদ্যমান থাকলে রাশিটিকে তিন চলকের বহুপদী বলা হয়। এভাবে বহুপদী রাশিতে যে কয়টি চলক বিদ্যমান থাকে রাশিটিকে তত চলকের বহুপদী বলা হয়।
যদি কোনো বীজগাণিতিক রাশিতে কোনো চলক না থাকে অর্থাৎ, রাশিটি শুধুমাত্র একটি ধ্রুবকের রাশি হয় তবে ঐ রাশিকে শূন্য ঘাতবিশিষ্ট বহুপদী বলা হয়।
এক চলকের বহুপদী রাশি
Polynomial expression in one variable
\(a_{0}\) একটি শূন্য ঘাতবিশিষ্ট বহুপদী।
\(a_{0}x+a_{1}\) একটি এক ঘাতবিশিষ্ট এক চলকের বহুপদী।
\(10x^3+5x^2-4x+8\) একটি তিন ঘাতবিশিষ্ট এক চলকের বহুপদী।
\(a_{0}x^n+a_{1}x^{n-1}+a_{2}x^{n-2}+...+a_{n}\) একটি \(n\)ঘাতবিশিষ্ট এক চলকের বহুপদী।
এখানে \(a_{0}, \ a_{1}, \ a_{2} ...... a_{n}\) ধ্রুবক এবং \(a_{0}\ne{0}\)
\(a_{0}x+a_{1}\) একটি এক ঘাতবিশিষ্ট এক চলকের বহুপদী।
\(10x^3+5x^2-4x+8\) একটি তিন ঘাতবিশিষ্ট এক চলকের বহুপদী।
\(a_{0}x^n+a_{1}x^{n-1}+a_{2}x^{n-2}+...+a_{n}\) একটি \(n\)ঘাতবিশিষ্ট এক চলকের বহুপদী।
এখানে \(a_{0}, \ a_{1}, \ a_{2} ...... a_{n}\) ধ্রুবক এবং \(a_{0}\ne{0}\)
একাধিক চলকের বহুপদী রাশি
Polynomial expression in more than one variable
\(ax+by+c\) একটি এক ঘাতবিশিষ্ট দুই চলকের বহুপদী।
\(ax^2+2hxy+by^2+2gx+2fy+c\) একটি দুই ঘাতবিশিষ্ট দুই চলকের বহুপদী।
\(6x^3+4x^2y+3xy^2+7x^2+3y+3\) একটি তিন ঘাতবিশিষ্ট দুই চলকের বহুপদী।
\(ax^2yz+bxy^3+cz^4\) একটি চার ঘাতবিশিষ্ট তিন চলকের বহুপদী।
\(ax^2+2hxy+by^2+2gx+2fy+c\) একটি দুই ঘাতবিশিষ্ট দুই চলকের বহুপদী।
\(6x^3+4x^2y+3xy^2+7x^2+3y+3\) একটি তিন ঘাতবিশিষ্ট দুই চলকের বহুপদী।
\(ax^2yz+bxy^3+cz^4\) একটি চার ঘাতবিশিষ্ট তিন চলকের বহুপদী।
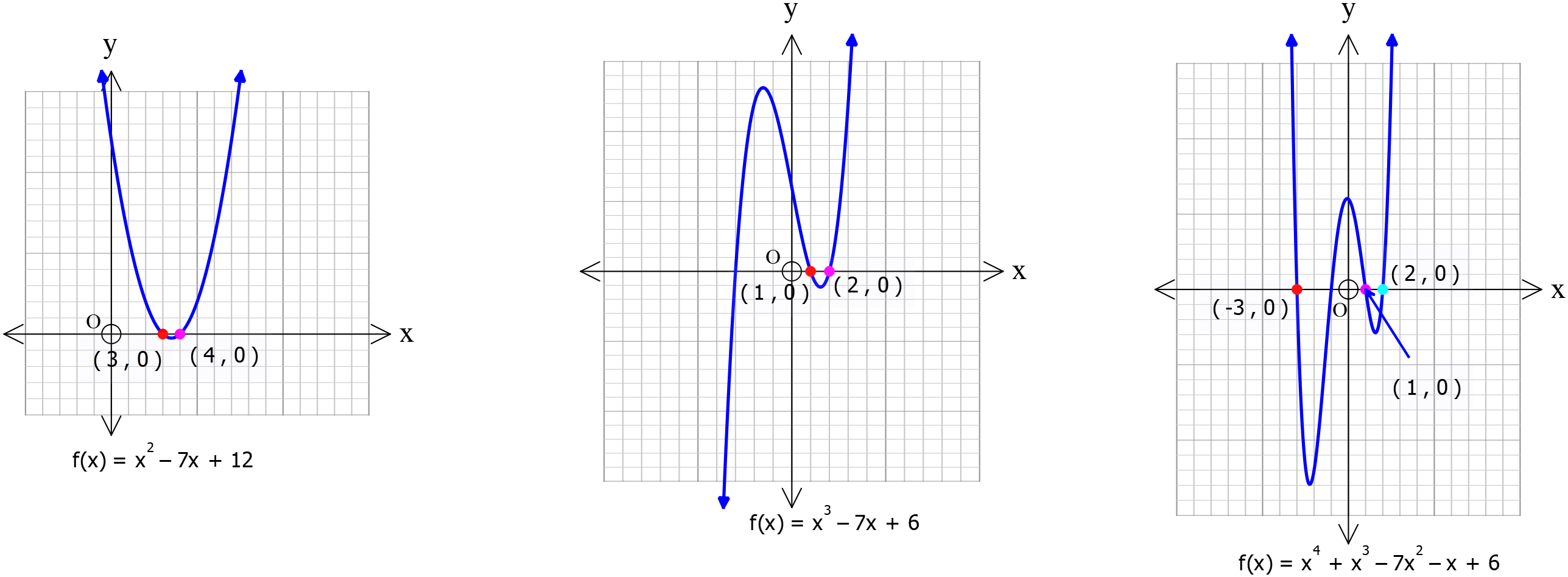
দুই, তিন ও চার ঘাতবিশিষ্ট এক চলকের বহুপদীর চিত্র
Graphs of polynomials in one variable with two, three and four terms
এক চলকের বীজগাণিতিক রাশি যা বহুপদী নয়
An algebraic expression in one variable that is not a polynomial
\(5x^2+2x^{\frac{2}{3}}+4\) রাশিটি বহুপদী নয় কেননা, দ্বিতীয় পদে \(x\) এর ঘাত \(\frac{2}{3}\) যা স্বাভাবিক সংখ্যা নয়।
\(6x^3+5x^2-7x^{-1}+4\) রাশিটি বহুপদী নয় কেননা, তৃতীয় পদে \(x\) এর ঘাত \(-1\) যা স্বাভাবিক সংখ্যা নয়।
\(6x^3+5x^2-7x^{-1}+4\) রাশিটি বহুপদী নয় কেননা, তৃতীয় পদে \(x\) এর ঘাত \(-1\) যা স্বাভাবিক সংখ্যা নয়।
সমমাত্রিক ও অসমমাত্রিক বহুপদী
Homogeneous and Non-homogeneous polynomials
কোনো বহুপদীর সকল পদের ঘাত সমান হলে ঐ বহুপদীকে সমমাত্রিক বহুপদী এবং সমান না হলে তাকে অসমমাত্রিক বহুপদী বলা হয়।
যেমনঃ \(ax^2+2hxy+by^2\) একটি \(x\) ও \(y\) চলকের দুই ঘাতবিশিষ্ট সমমাত্রিক বহুপদী।
যেমনঃ \(ax^2+bx+c\) একটি \(x\) চলকের দুই ঘাতবিশিষ্ট অসমমাত্রিক বহুপদী। কেননা,
যেমনঃ \(ax^2+2hxy+by^2\) একটি \(x\) ও \(y\) চলকের দুই ঘাতবিশিষ্ট সমমাত্রিক বহুপদী।
যেমনঃ \(ax^2+bx+c\) একটি \(x\) চলকের দুই ঘাতবিশিষ্ট অসমমাত্রিক বহুপদী। কেননা,
সমীকরণ
Equations
বীজগণিতীয় চলক সম্বলিত দুইটি রাশি \("="\) চিহ্ন দিয়ে সংযুক্ত হলে ঐ রাশিদ্বয়ের সমতাজ্ঞাপক সম্বন্ধটিকে সমীকরণ বলে।
এতে ব্যবহৃত চলককে বলে অজ্ঞাত রাশি।
সমীকরণের সমান চিহ্নের বাম দিকের রাশিকে বাম পক্ষ এবং ডান দিকের রাশিকে ডান পক্ষ বলে।
যেমনঃ \((i) \ 3x+5=2x+2\)
\((ii) \ 2x^2+5=2x\)
\((iii) \ 3x^3+5x^2=2x+8\)
\((iv) \ 4x^4+5x^2-6x+8=0\)
এতে ব্যবহৃত চলককে বলে অজ্ঞাত রাশি।
সমীকরণের সমান চিহ্নের বাম দিকের রাশিকে বাম পক্ষ এবং ডান দিকের রাশিকে ডান পক্ষ বলে।
যেমনঃ \((i) \ 3x+5=2x+2\)
\((ii) \ 2x^2+5=2x\)
\((iii) \ 3x^3+5x^2=2x+8\)
\((iv) \ 4x^4+5x^2-6x+8=0\)
অভেদ
Identity
যদি কোনো সমীকরণ এর অজ্ঞাত রাশি বা চলকের ঘাত সংখ্যার অধিক মান দ্বারা সিদ্ধ হয় তবে ঐ সমীকরণকে অভেদ বলে।
যেমনঃ \((i) \ (x+2)^2=x^2+4x+4\)
\((ii) \ (a+b)^2=a^2+2ab+b^2\)
\((iii) \ (x+1)^3=x^3+3x^2+3x+1\)
দ্রষ্টব্যঃ প্রত্যেক অভেদ একটি সমীকরণ তবে প্রত্যেক সমীকরণ অভেদ নয়।
যেমনঃ \((i) \ (x+2)^2=x^2+4x+4\)
\((ii) \ (a+b)^2=a^2+2ab+b^2\)
\((iii) \ (x+1)^3=x^3+3x^2+3x+1\)
দ্রষ্টব্যঃ প্রত্যেক অভেদ একটি সমীকরণ তবে প্রত্যেক সমীকরণ অভেদ নয়।
বহুপদী সমীকরণ
Polynomial Equations
\(f(x)=a_{0}x^n+a_{1}x^{n-1}+a_{2}x^{n-2}+ ... ... +a_{n}\) একটি \(n\) ঘাতের বহুপদী। যদি বহুপদীটি শূন্য এর সমান হয়, অর্থাৎ \(f(x)=0\) বা \(a_{0}x^n+a_{1}x^{n-1}+a_{2}x^{n-2}+ ... ... +a_{n}=0\) হয় এবং \(a_{0}\ne{0},\) তবে এই সমীকরণকে \(x\) এর \(n\) ঘাতবিশিষ্ট বহুপদী সমীকরণ বা সংক্ষেপে \(x\) এর \(n\) ঘাতের বহুপদী সমীকরণ বলা হয়।
যেখানে, \(a_{0}, \ a_{1}, \ a_{2}, .....a_{n}\) ইত্যাদি সমীকরণটির সহগ।
যেমনঃ \(ax^2+bx+c=0, \ a\ne{0}\) একটি \(x\) চলকের দুই ঘাতবিশিষ্ট বহুপদী সমীকরণ বা সংক্ষেপে দ্বিঘাত সমীকরণ বলা হয়।
একইভাবে, \(5x^3+4x^2+8x+2=0\) একটি \(x\) চলকের ত্রিঘাত সমীকরণ।
যেখানে, \(a_{0}, \ a_{1}, \ a_{2}, .....a_{n}\) ইত্যাদি সমীকরণটির সহগ।
যেমনঃ \(ax^2+bx+c=0, \ a\ne{0}\) একটি \(x\) চলকের দুই ঘাতবিশিষ্ট বহুপদী সমীকরণ বা সংক্ষেপে দ্বিঘাত সমীকরণ বলা হয়।
একইভাবে, \(5x^3+4x^2+8x+2=0\) একটি \(x\) চলকের ত্রিঘাত সমীকরণ।
বহুপদী সমীকরণের মূল
Roots of a Polynomial Equations
ধরি, \(f(x)=0\) একটি বহুপদী সমীকরণ।
যদি \(f(a)=0\) হয়, তবে \(x=a\) কে বহুপদী সমীকরণের একটি মূল বলা হয়।
যেমনঃ \(x^2-3x+2=0\)
বা, \(f(x)=0\) সমীকরণের দুইটি মূল \(1\) এবং \(2,\)
কেননা \(f(x)=x^2-3x+2\) এর জন্য \(f(1)=0\) ও \(f(2)=0\)
যদি \(f(a)=0\) হয়, তবে \(x=a\) কে বহুপদী সমীকরণের একটি মূল বলা হয়।
যেমনঃ \(x^2-3x+2=0\)
বা, \(f(x)=0\) সমীকরণের দুইটি মূল \(1\) এবং \(2,\)
কেননা \(f(x)=x^2-3x+2\) এর জন্য \(f(1)=0\) ও \(f(2)=0\)
বহুপদী সমীকরণের উৎপাদক উপপাদ্য
Factor Theorem for Polynomial Equations
বর্ণনাঃ যদি \(f(x)\) একটি বহুপদী হয় এবং \(f(a)=0\) হয়, তবে বহুপদী \(f(x)\) এর একটি উৎপাদক \(x-a\) হবে।
তাহলে সংজ্ঞানুসারে, \(f(x)=(x-a)q(x)+r .......(1)\) ➜ \(\because \text{ভাজ্য}=(\text{ভাজক}\times\text{ভাগফল})+\text{ভাগশেষ}\)
\((1)\) নং সমীকরণে \(x=a\) বসিয়ে,
\(f(a)=(a-a)q(x)+r\)
\(\Rightarrow f(a)=0.q(x)+r\)
\(\Rightarrow f(a)=r\)
\(\therefore r=f(a)\)
সে ক্ষেত্রে \((1)\) নং হতে, \(f(x)=(x-a)q(x)+f(a) .......(2)\)
যদি, \(f(x)=0\) এর একটি মূল \(a\) হয়, তবে \(f(a)=0\) হবে।
সুতরাং এ শর্তে \((2)\) নং হতে পাওয়া যায় \(f(x)=(x-a)q(x)\) যা স্পষ্ট করে যে, \(f(x)\) বহুপদী, \((x-a)\) দ্বারা নিঃশেষে বিভাজ্য।
অতএব, বহুপদী \(f(x)\) এর \((x-a)\) একটি উৎপাদক।
উদাহরণঃ ধরি, \(f(x)=x^4-2x^3-21x^2+22x+40\)
এখানে, \(f(-1)=(-1)^4-2.(-1)^3-21.(-1)^2+22.(-1)+40\)
\(=1+2-21-22+40\)
\(=-43+43\)
\(=0\)
অর্থাৎ, বহুপদী \(f(x)\) এর \(x-(-1)=x+1\) একটি উৎপাদক।
তাহলে, \(x^4-2x^3-21x^2+22x+40=(x+1)(x^3-3x^2-18x+40)\)
প্রমাণঃ
ধরি \(f(x)\) বহুপদীকে \(x-a\) দ্বারা ভাগ করলে ভাগফল \(q(x)\) এবং ভাগশেষ \(r\) পাওয়া যায়।তাহলে সংজ্ঞানুসারে, \(f(x)=(x-a)q(x)+r .......(1)\) ➜ \(\because \text{ভাজ্য}=(\text{ভাজক}\times\text{ভাগফল})+\text{ভাগশেষ}\)
\((1)\) নং সমীকরণে \(x=a\) বসিয়ে,
\(f(a)=(a-a)q(x)+r\)
\(\Rightarrow f(a)=0.q(x)+r\)
\(\Rightarrow f(a)=r\)
\(\therefore r=f(a)\)
সে ক্ষেত্রে \((1)\) নং হতে, \(f(x)=(x-a)q(x)+f(a) .......(2)\)
যদি, \(f(x)=0\) এর একটি মূল \(a\) হয়, তবে \(f(a)=0\) হবে।
সুতরাং এ শর্তে \((2)\) নং হতে পাওয়া যায় \(f(x)=(x-a)q(x)\) যা স্পষ্ট করে যে, \(f(x)\) বহুপদী, \((x-a)\) দ্বারা নিঃশেষে বিভাজ্য।
অতএব, বহুপদী \(f(x)\) এর \((x-a)\) একটি উৎপাদক।
এখানে, \(f(-1)=(-1)^4-2.(-1)^3-21.(-1)^2+22.(-1)+40\)
\(=1+2-21-22+40\)
\(=-43+43\)
\(=0\)
অর্থাৎ, বহুপদী \(f(x)\) এর \(x-(-1)=x+1\) একটি উৎপাদক।
তাহলে, \(x^4-2x^3-21x^2+22x+40=(x+1)(x^3-3x^2-18x+40)\)
বহুপদীর ভাগশেষ উপপাদ্য
Remainder Theorem of Polynomials
বর্ণনাঃ যদি \(a\) যে কোনো একটি ধ্রুবক হয় এবং \(f(x)\) বহুপদীকে \((x-a)\) দ্বারা ভাগ করা হয়, তবে ভাগশেষ \(f(a)\) হবে।
তাহলে সংজ্ঞানুসারে, \(f(x)=(x-a)q(x)+r .......(1)\) ➜ \(\because \text{ভাজ্য}=(\text{ভাজক}\times\text{ভাগফল})+\text{ভাগশেষ}\)
\((1)\) নং সমীকরণে \(x=a\) বসিয়ে,
\(f(a)=(a-a)q(x)+r\)
\(\Rightarrow f(a)=0.q(x)+r\)
\(\Rightarrow f(a)=r\)
\(\therefore r=f(a)\)
সুতরাং \(f(x)\) বহুপদীকে \((x-a)\) দ্বারা ভাগ করলে ভাগশেষ \(f(a)\) পাওয়া যায়।
উদাহরণঃ \(f(x)=x^3-3x^2+4x-10\) কে
\((x-1)\) দ্বারা ভাগ করলে ভাগশেষ, \(f(1)=1^3-3.1^2+4.1-10\)
\(=1-3+4-10\)
\(=5-13\)
\(=-8\)
\((x+2)\) দ্বারা ভাগ করলে ভাগশেষ, \(f(-2)=(-2)^3-3.(-2)^2+4.(-2)-10\)
\(=-8-12-8-10\)
\(=-38\)
দ্রষ্টব্যঃ যদি ভাগশেষ শূন্য হয় অর্থাৎ, \(f(a)=0\) হয়, তবে \((x-a)\) কে \(f(x)\) এর একটি উৎপাদক বলা হয়।
প্রমাণঃ
ধরি \(f(x)\) বহুপদীকে \(x-a\) দ্বারা ভাগ করলে ভাগফল \(q(x)\) এবং ভাগশেষ \(r\) পাওয়া যায়।তাহলে সংজ্ঞানুসারে, \(f(x)=(x-a)q(x)+r .......(1)\) ➜ \(\because \text{ভাজ্য}=(\text{ভাজক}\times\text{ভাগফল})+\text{ভাগশেষ}\)
\((1)\) নং সমীকরণে \(x=a\) বসিয়ে,
\(f(a)=(a-a)q(x)+r\)
\(\Rightarrow f(a)=0.q(x)+r\)
\(\Rightarrow f(a)=r\)
\(\therefore r=f(a)\)
সুতরাং \(f(x)\) বহুপদীকে \((x-a)\) দ্বারা ভাগ করলে ভাগশেষ \(f(a)\) পাওয়া যায়।
\((x-1)\) দ্বারা ভাগ করলে ভাগশেষ, \(f(1)=1^3-3.1^2+4.1-10\)
\(=1-3+4-10\)
\(=5-13\)
\(=-8\)
\((x+2)\) দ্বারা ভাগ করলে ভাগশেষ, \(f(-2)=(-2)^3-3.(-2)^2+4.(-2)-10\)
\(=-8-12-8-10\)
\(=-38\)
দ্রষ্টব্যঃ যদি ভাগশেষ শূন্য হয় অর্থাৎ, \(f(a)=0\) হয়, তবে \((x-a)\) কে \(f(x)\) এর একটি উৎপাদক বলা হয়।
প্রত্যেক \('n'\) ঘাত বহুপদী সমীকরণের মূলের সংখ্যা
Number of roots of every \('n'\) degree polynomial equations
বর্ণনাঃ প্রত্যেক \('n'\) ঘাত বহুপদী সমীকরণ \(f(x)=0\) এর কেবলমাত্র \('n'\) সংখ্যক মূল বিদ্যমান।
বীজগণিতীয় মৌলিক উপপাদ্য অনুসারে, প্রত্যেক \('n'\) ঘাতের বহুপদী সমীকরণ \(f(x)=0\) এর কমপক্ষে একটি বাস্তব অথবা কাল্পনিক মূল বিদ্যমান।
ধরি, সমীকরণ \(f(x)=0\) এর একটি মূল \(\alpha_{1}\)।
তাহলে উপপাদ্য অনুযায়ী \(f(x)\) এর একটি উৎপাদক \((x-\alpha_{1})\)
সুতরাং, \(f(x)=(x-\alpha_{1})\phi_{1}(x) ..... (1)\)
যেখানে, \(\phi_{1}(x)\) হলো \((n-1)\) ঘাতের বহুপদী যার প্রথম পদ \(=a_{0}x^{n-1}.\)
আবার,
বীজগণিতীয় মৌলিক উপপাদ্য অনুসারে,\(\phi_{1}(x)=0\) এর কমপক্ষে একটি মূল বিদ্যমান।
ধরি, সমীকরণ \(\phi_{1}(x)=0\) এর একটি মূল \(\alpha_{2}\)।
তাহলে উপপাদ্য অনুযায়ী \(\phi_{1}(x)\) এর একটি উৎপাদক \((x-\alpha_{2})\)
সুতরাং, \(\phi_{1}(x)=(x-\alpha_{2})\phi_{2}(x) ..... (2)\)
যেখানে, \(\phi_{2}(x)\) হলো \((n-2)\) ঘাতের বহুপদী যার প্রথম পদ \(=a_{0}x^{n-2}.\)
এখন, \((1)\) ও \((2)\) নং হতে,
\(f(x)=(x-\alpha_{1})(x-\alpha_{2})\phi_{2}(x)\)
এভাবে অগ্রসর হয়ে \(n\) ধাপের পর,
\(f(x)=(x-\alpha_{1})(x-\alpha_{2})(x-\alpha_{3}) .... (x-\alpha_{n})\phi_{n}(x) .... (3)\)
এখানে, \(\phi_{n}(x)\) হলো \((n-n)\) ঘাতের বহুপদী।
অর্থাৎ, \(\phi_{n}(x)=a_{0}x^{n-n}=a_{0}\) যা ধ্রুবক।
সুতরাং, \((3)\) নং হতে,
\(f(x)=(x-\alpha_{1})(x-\alpha_{2})(x-\alpha_{3}) .... (x-\alpha_{n})a_{0}\)
\(\therefore f(x)=a_{0}(x-\alpha_{1})(x-\alpha_{2})(x-\alpha_{3}) .... (x-\alpha_{n}) ...... (4)\)
এখন, \(\alpha_{i}\in{\{\alpha_{1}, \ \alpha_{2}, \ \alpha_{3}, ... \alpha_{n}\}}\) হলে,
\((4)\) নং হতে,
\(f(\alpha_{i})=0\) যেখানে, \(i=1, \ 2, \ 3, ....n\)
অতএব, \(f(x)=0\) বহুপদী সমীকরণের \('n'\) সংখ্যক মূল \(\alpha_{1}, \ \alpha_{2}, \ \alpha_{3}, ... \alpha_{n}\)বিদ্যমান।
এখন যদি \(\alpha_{i}\ne{\{\alpha_{1}, \ \alpha_{2}, \ \alpha_{3}, ... \alpha_{n}\}}\) হয়
তবে \(f(\alpha)=a_{0}(\alpha-\alpha_{1})(\alpha-\alpha_{2})(\alpha-\alpha_{3}) .... (\alpha-\alpha_{n})\ne{0}\)
সুতরাং, বহুপদী সমীকরণ \(f(x)=0\) এর \(\alpha_{1}, \ \alpha_{2}, \ \alpha_{3}, ... \alpha_{n}\) এ \(n\) সংখ্যক মূল ব্যতীত অন্য কোনো মূল বিদ্যমান থাকতে পারে না।
উদাহরণঃ নিচের সমীকরণগুলির মাত্রা ও মূলের সংখ্যা নির্ণয় কর।
\((i) \ 16x^2=0\)
\((ii) \ x^3+x=0\)
\((iii) \ 4x^4-12x^2+4=0\)
প্রমাণঃ
ধরি \(f(x)\equiv a_{0}x^n+a_{1}x^{n-1}+a_{2}x^{n-2}+ ... ... +a_{n}=0\) একটি \('n'\) ঘাতবিশিষ্ট বহুপদী সমীকরণ।বীজগণিতীয় মৌলিক উপপাদ্য অনুসারে, প্রত্যেক \('n'\) ঘাতের বহুপদী সমীকরণ \(f(x)=0\) এর কমপক্ষে একটি বাস্তব অথবা কাল্পনিক মূল বিদ্যমান।
ধরি, সমীকরণ \(f(x)=0\) এর একটি মূল \(\alpha_{1}\)।
তাহলে উপপাদ্য অনুযায়ী \(f(x)\) এর একটি উৎপাদক \((x-\alpha_{1})\)
সুতরাং, \(f(x)=(x-\alpha_{1})\phi_{1}(x) ..... (1)\)
যেখানে, \(\phi_{1}(x)\) হলো \((n-1)\) ঘাতের বহুপদী যার প্রথম পদ \(=a_{0}x^{n-1}.\)
আবার,
বীজগণিতীয় মৌলিক উপপাদ্য অনুসারে,\(\phi_{1}(x)=0\) এর কমপক্ষে একটি মূল বিদ্যমান।
ধরি, সমীকরণ \(\phi_{1}(x)=0\) এর একটি মূল \(\alpha_{2}\)।
তাহলে উপপাদ্য অনুযায়ী \(\phi_{1}(x)\) এর একটি উৎপাদক \((x-\alpha_{2})\)
সুতরাং, \(\phi_{1}(x)=(x-\alpha_{2})\phi_{2}(x) ..... (2)\)
যেখানে, \(\phi_{2}(x)\) হলো \((n-2)\) ঘাতের বহুপদী যার প্রথম পদ \(=a_{0}x^{n-2}.\)
এখন, \((1)\) ও \((2)\) নং হতে,
\(f(x)=(x-\alpha_{1})(x-\alpha_{2})\phi_{2}(x)\)
এভাবে অগ্রসর হয়ে \(n\) ধাপের পর,
\(f(x)=(x-\alpha_{1})(x-\alpha_{2})(x-\alpha_{3}) .... (x-\alpha_{n})\phi_{n}(x) .... (3)\)
এখানে, \(\phi_{n}(x)\) হলো \((n-n)\) ঘাতের বহুপদী।
অর্থাৎ, \(\phi_{n}(x)=a_{0}x^{n-n}=a_{0}\) যা ধ্রুবক।
সুতরাং, \((3)\) নং হতে,
\(f(x)=(x-\alpha_{1})(x-\alpha_{2})(x-\alpha_{3}) .... (x-\alpha_{n})a_{0}\)
\(\therefore f(x)=a_{0}(x-\alpha_{1})(x-\alpha_{2})(x-\alpha_{3}) .... (x-\alpha_{n}) ...... (4)\)
এখন, \(\alpha_{i}\in{\{\alpha_{1}, \ \alpha_{2}, \ \alpha_{3}, ... \alpha_{n}\}}\) হলে,
\((4)\) নং হতে,
\(f(\alpha_{i})=0\) যেখানে, \(i=1, \ 2, \ 3, ....n\)
অতএব, \(f(x)=0\) বহুপদী সমীকরণের \('n'\) সংখ্যক মূল \(\alpha_{1}, \ \alpha_{2}, \ \alpha_{3}, ... \alpha_{n}\)বিদ্যমান।
এখন যদি \(\alpha_{i}\ne{\{\alpha_{1}, \ \alpha_{2}, \ \alpha_{3}, ... \alpha_{n}\}}\) হয়
তবে \(f(\alpha)=a_{0}(\alpha-\alpha_{1})(\alpha-\alpha_{2})(\alpha-\alpha_{3}) .... (\alpha-\alpha_{n})\ne{0}\)
সুতরাং, বহুপদী সমীকরণ \(f(x)=0\) এর \(\alpha_{1}, \ \alpha_{2}, \ \alpha_{3}, ... \alpha_{n}\) এ \(n\) সংখ্যক মূল ব্যতীত অন্য কোনো মূল বিদ্যমান থাকতে পারে না।
\((i) \ 16x^2=0\)
\((ii) \ x^3+x=0\)
\((iii) \ 4x^4-12x^2+4=0\)
বহুপদী সমীকরণ এবং অভেদ
Polynomial Equations and Identity
ধরি \(n\) ঘাতের একটি বহুপদী সমীকরণ \(f(x)=0\) যদি সমীকরণটি \(x\) এর সর্বোচ্চ \(n\) সংখ্যক মান দ্বারা সিদ্ধ হয়, অর্থাৎ সমীকরণটির সর্বোচ্চ \(n\) সংখ্যক মান বিদ্যমান থাকে, তবে \(f(x)=0\) কে বহুপদী সমীকরণ বলা হয়।
যেমনঃ \((i) \ x^3-6x^2+11x-6=0\) একটি সমীকরণ কেননা, সমীকরণটির ঘাত তিন এবং এর কেবলমাত্র \(1, \ 2\) ও \(3\) এ তিনটি মূল বিদ্যমান।
আবার, যদি সমীকরণটি \(x\) এর সকল মান দ্বারা সিদ্ধ হয়, তবে \(f(x)=0\) কে বহুপদী অভেদ বলা হয়।
যেমনঃ \((i) \ (x-a)^3=x^3-3x^2a+3xa^2-a^3\) এটি একটি অভেদ কেননা, এটি \(x\) এর সকল মান দ্বারা সিদ্ধ হয়।
যেমনঃ \((i) \ x^3-6x^2+11x-6=0\) একটি সমীকরণ কেননা, সমীকরণটির ঘাত তিন এবং এর কেবলমাত্র \(1, \ 2\) ও \(3\) এ তিনটি মূল বিদ্যমান।
আবার, যদি সমীকরণটি \(x\) এর সকল মান দ্বারা সিদ্ধ হয়, তবে \(f(x)=0\) কে বহুপদী অভেদ বলা হয়।
যেমনঃ \((i) \ (x-a)^3=x^3-3x^2a+3xa^2-a^3\) এটি একটি অভেদ কেননা, এটি \(x\) এর সকল মান দ্বারা সিদ্ধ হয়।
মূলদ সহগবিশিষ্ট বহুপদী সমীকরণের অমূলদ মূল
Irrational roots of polynomial equations with rational coefficients
বর্ণনাঃ মূলদ সহগবিশিষ্ট একটি বহুপদী সমীকরণের অমূলদ মূলগুলি যুগলে থাকে।
তাহলে, \(f(p+\sqrt{q})=0 ........(1)\)
আবার,
যেহেতু বহুপদী \(f(x)=0\) এর সহগগুলি মূলদ।
সুতরাং, \(f(p+\sqrt{q})=A+\sqrt{B} ..... (2)\)
এবং \(f(p-\sqrt{q})=A-\sqrt{B} ....... (3)\)
যেখানে, \(A\in{\mathbb{Q}}\) এবং \(\sqrt{B}\in{\mathbb{Q^{\prime}}}.\)
এখন, \((1)\) ও \((2)\) নং হতে,
\(A+\sqrt{B}=0\)
\(\Rightarrow A=0, \ B=0\) ➜ \(\because\) একটি মূলদ ও একটি অমূলদ সংখ্যার যোগফল শূন্য হতে পারে না।
তাহলে, \((3)\) হতে,
\(f(p-\sqrt{q})=0\)
সুতরাং, প্রদত্ত সমীকরণের একটি মূল \(p+\sqrt{q}\) হলে অপর একটি মূল \(p-\sqrt{q}\) পাওয়া যায় এবং বিপরীতক্রমে একটি মূল \(p-\sqrt{q}\) হলে অপর একটি মূল \(p+\sqrt{q}\) পাওয়া যাবে।
\(\therefore\) মূলদ সহগবিশিষ্ট একটি বহুপদী সমীকরণের অমূলদ মূলগুলি যুগলে থাকে।
উদাহরণঃ \(x^3-6x^2+9x-2=0\) মূলদ সহগবিশিষ্ট একটি বহুপদী সমীকরণ।
এর অমূলদ যূগল মূল \(2+\sqrt{3}\) এবং \(2-\sqrt{3}\) বিদ্যমান।
আবার,
\(x^3-(7+\sqrt{2})x^2+(12+7\sqrt{2})x-12\sqrt{2}=0\) একটি বহুপদী সমীকরণ। যার একটি মূল \(\sqrt{2}\) কিন্তু অপর মূল \(-\sqrt{2}\) নয়। কারন, সমীকরণটি মূলদ সহগবিশিষ্ট নয়।
প্রমাণঃ
ধরি \(f(x)=0\) একটি মূলদ সহগবিশিষ্ট বহুপদী সমীকরণ এবং \(x=p+\sqrt{q}\) এর একটি মূল, যেখানে \(p\in{\mathbb{Q}}\) এবং \(\sqrt{q}\in{\mathbb{Q^{\prime}}}\) ।তাহলে, \(f(p+\sqrt{q})=0 ........(1)\)
আবার,
যেহেতু বহুপদী \(f(x)=0\) এর সহগগুলি মূলদ।
সুতরাং, \(f(p+\sqrt{q})=A+\sqrt{B} ..... (2)\)
এবং \(f(p-\sqrt{q})=A-\sqrt{B} ....... (3)\)
যেখানে, \(A\in{\mathbb{Q}}\) এবং \(\sqrt{B}\in{\mathbb{Q^{\prime}}}.\)
এখন, \((1)\) ও \((2)\) নং হতে,
\(A+\sqrt{B}=0\)
\(\Rightarrow A=0, \ B=0\) ➜ \(\because\) একটি মূলদ ও একটি অমূলদ সংখ্যার যোগফল শূন্য হতে পারে না।
তাহলে, \((3)\) হতে,
\(f(p-\sqrt{q})=0\)
সুতরাং, প্রদত্ত সমীকরণের একটি মূল \(p+\sqrt{q}\) হলে অপর একটি মূল \(p-\sqrt{q}\) পাওয়া যায় এবং বিপরীতক্রমে একটি মূল \(p-\sqrt{q}\) হলে অপর একটি মূল \(p+\sqrt{q}\) পাওয়া যাবে।
\(\therefore\) মূলদ সহগবিশিষ্ট একটি বহুপদী সমীকরণের অমূলদ মূলগুলি যুগলে থাকে।
এর অমূলদ যূগল মূল \(2+\sqrt{3}\) এবং \(2-\sqrt{3}\) বিদ্যমান।
আবার,
\(x^3-(7+\sqrt{2})x^2+(12+7\sqrt{2})x-12\sqrt{2}=0\) একটি বহুপদী সমীকরণ। যার একটি মূল \(\sqrt{2}\) কিন্তু অপর মূল \(-\sqrt{2}\) নয়। কারন, সমীকরণটি মূলদ সহগবিশিষ্ট নয়।
বাস্তব সহগবিশিষ্ট বহুপদী সমীকরণের কাল্পনিক মূল
Imaginary roots of polynomial equations with real coefficients
বর্ণনাঃ বাস্তব সহগবিশিষ্ট বহুপদী সমীকরণের কাল্পনিক মূলগুলি অনুবন্ধী যুগলে থাকে।
তাহলে, \(f(p+iq)=0 ........(1)\)
আবার,
যেহেতু বহুপদী \(f(x)=0\) এর সহগগুলি বাস্তব।
সুতরাং, \(f(p+iq)=A+iB ..... (2)\)
এবং \(f(p-iq)=A-iB ....... (3)\)
যেখানে, \(A,B\in{\mathbb{R}}\) এবং \(i=\sqrt{-1}.\)
এখন, \((1)\) ও \((2)\) নং হতে,
\(A+iB=0\)
\(\Rightarrow A+iB=0+i0\)
\(\Rightarrow A=0, \ B=0\) ➜ উভয় পার্শ হতে বাস্তব ও কাল্পনিক অংশের সমতা নিয়ে।
তাহলে, \((3)\) হতে,
\(f(p-iq)=0\)
সুতরাং, প্রদত্ত সমীকরণের একটি মূল \(p+iq\) হলে অপর একটি মূল \(p-iq\) পাওয়া যায় এবং বিপরীতক্রমে একটি মূল \(p-iq\) হলে অপর একটি মূল \(p+iq\) পাওয়া যাবে।
\(\therefore\) বাস্তব সহগবিশিষ্ট বহুপদী সমীকরণের কাল্পনিক মূলগুলি অনুবন্ধী যুগলে থাকে।
উদাহরণঃ \(2x^3-9x^2+14x-5=0\) বাস্তব সহগবিশিষ্ট বহুপদী সমীকরণের।
এর কাল্পনিক যূগল মূল \(2+i\) এবং \(2-i\) বিদ্যমান।
আবার,
\(x^3+(5-i)x^2+(6+5i)x-6i=0\) একটি বহুপদী সমীকরণ। যার একটি মূল \(i\) কিন্তু অপর মূল \(-i\) নয়। কারন, সমীকরণটি বাস্তব সহগবিশিষ্ট নয়।
প্রমাণঃ
ধরি \(f(x)=0\) একটি বাস্তব সহগবিশিষ্ট বহুপদী সমীকরণ এবং \(x=p+iq\) এর একটি মূল, যেখানে \(p,q\in{\mathbb{R}}\) এবং \(i=\sqrt{-1}\) ।তাহলে, \(f(p+iq)=0 ........(1)\)
আবার,
যেহেতু বহুপদী \(f(x)=0\) এর সহগগুলি বাস্তব।
সুতরাং, \(f(p+iq)=A+iB ..... (2)\)
এবং \(f(p-iq)=A-iB ....... (3)\)
যেখানে, \(A,B\in{\mathbb{R}}\) এবং \(i=\sqrt{-1}.\)
এখন, \((1)\) ও \((2)\) নং হতে,
\(A+iB=0\)
\(\Rightarrow A+iB=0+i0\)
\(\Rightarrow A=0, \ B=0\) ➜ উভয় পার্শ হতে বাস্তব ও কাল্পনিক অংশের সমতা নিয়ে।
তাহলে, \((3)\) হতে,
\(f(p-iq)=0\)
সুতরাং, প্রদত্ত সমীকরণের একটি মূল \(p+iq\) হলে অপর একটি মূল \(p-iq\) পাওয়া যায় এবং বিপরীতক্রমে একটি মূল \(p-iq\) হলে অপর একটি মূল \(p+iq\) পাওয়া যাবে।
\(\therefore\) বাস্তব সহগবিশিষ্ট বহুপদী সমীকরণের কাল্পনিক মূলগুলি অনুবন্ধী যুগলে থাকে।
এর কাল্পনিক যূগল মূল \(2+i\) এবং \(2-i\) বিদ্যমান।
আবার,
\(x^3+(5-i)x^2+(6+5i)x-6i=0\) একটি বহুপদী সমীকরণ। যার একটি মূল \(i\) কিন্তু অপর মূল \(-i\) নয়। কারন, সমীকরণটি বাস্তব সহগবিশিষ্ট নয়।
দ্বিঘাত রাশি এবং দ্বিঘাত সমীকরণ
Quadratic Quantity and Quadratic Equations
\(ax^2+bx+c, \ a,b,c\in{\mathbb{R}}\) এবং \(a\ne{0}\) আকারের রাশিকে এক চলকবিশিষ্ট দ্বিঘাত রাশি বলা হয়।
\(ax^2+bx+c=0, \ a,b,c\in{\mathbb{R}}\) এবং \(a\ne{0}\) আকারের সমীকরণকে এক চলকবিশিষ্ট দ্বিঘাত সমীকরণ বলা হয়। দ্বিঘাত সমীকরণের বামপক্ষে একটি দ্বিঘাত রাশি এবং ডানপক্ষে শূন্য ধরা হয়।
\(ax^2+bx+c=0, \ a,b,c\in{\mathbb{R}}\) এবং \(a\ne{0}\) আকারের সমীকরণকে এক চলকবিশিষ্ট দ্বিঘাত সমীকরণ বলা হয়। দ্বিঘাত সমীকরণের বামপক্ষে একটি দ্বিঘাত রাশি এবং ডানপক্ষে শূন্য ধরা হয়।
দ্বিঘাত সমীকরণের সমাধান
Solving quadratic equations
\(ax^2+bx+c=0, \ a,b,c\in{\mathbb{R}}\) এবং \(a\ne{0}\) কে দ্বিঘাত সমীকরণের প্রমাণ আকার বা আদর্শ আকার বলে। একাধিক উপায়ে এ সমীকরণের সমাধান করা যায়।
প্রথম পদ্ধতিঃ যদি সমীকরণের বামপক্ষ \(ax^2+bx+c\) কে দুইটি সরল একঘাতি উতপাদকে বিশ্লেষণ করা যায় তবে উতপাদকদ্বয় পৃথকভাবে শূন্য \((0)\) এর সমান ধরে দুইটি সমাধান পাওয়া যায়।
দ্বিতীয় পদ্ধতিঃ প্রদত্ত সমীকরণ \(ax^2+bx+c=0\)
\(\Rightarrow 4a^2x^2+4abx+4ac=0\) ➜ উভয় পক্ষে \(4a\) গুণ করে।
\(\Rightarrow (2ax)^2+2.2ax.b+b^2-b^2+4ac=0\)
\(\Rightarrow (2ax+b)^2-b^2+4ac=0\)
\(\Rightarrow (2ax+b)^2=b^2-4ac\)
\(\Rightarrow 2ax+b=\pm{\sqrt{b^2-4ac}}\)
\(\Rightarrow 2ax=-b\pm{\sqrt{b^2-4ac}}\)
\(\therefore x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
বহুলভাবে ব্যবহৃত এ পদ্ধতিটি বিখ্যাত ভারতীয় গণিতবিদ শ্রীধর আচার্যের \((870-930)\) পদ্ধতি নামে পরিচিত।
প্রথম পদ্ধতিঃ যদি সমীকরণের বামপক্ষ \(ax^2+bx+c\) কে দুইটি সরল একঘাতি উতপাদকে বিশ্লেষণ করা যায় তবে উতপাদকদ্বয় পৃথকভাবে শূন্য \((0)\) এর সমান ধরে দুইটি সমাধান পাওয়া যায়।
দ্বিতীয় পদ্ধতিঃ প্রদত্ত সমীকরণ \(ax^2+bx+c=0\)
\(\Rightarrow 4a^2x^2+4abx+4ac=0\) ➜ উভয় পক্ষে \(4a\) গুণ করে।
\(\Rightarrow (2ax)^2+2.2ax.b+b^2-b^2+4ac=0\)
\(\Rightarrow (2ax+b)^2-b^2+4ac=0\)
\(\Rightarrow (2ax+b)^2=b^2-4ac\)
\(\Rightarrow 2ax+b=\pm{\sqrt{b^2-4ac}}\)
\(\Rightarrow 2ax=-b\pm{\sqrt{b^2-4ac}}\)
\(\therefore x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
বহুলভাবে ব্যবহৃত এ পদ্ধতিটি বিখ্যাত ভারতীয় গণিতবিদ শ্রীধর আচার্যের \((870-930)\) পদ্ধতি নামে পরিচিত।
দ্বিঘাত সমীকরণের মূলের সংখ্যা
Number of roots of quadratic equation
বর্ণনাঃ দ্বিঘাত সমীকরণের মূলের সংখ্যা দুইয়ের অধিক হতে পারে না।
\(x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\therefore x=\frac{-b+\sqrt{b^2-4ac}}{2a}, \ \frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(x\) এর এই দুইটি মানকে প্রদত্ত সমীকরণের দুইটি মূল বলে। প্রমাণ করতে হবে যে, দ্বিঘাত সমীকরণের দুইটির বেশী মূল থাকতে পারে না।
ধরি, দ্বিঘাত সমীকরণ \(ax^2+bx+c=0, \ a\ne{0}\) এর তিনটি ভিন্ন ভিন্ন মূল বিদ্যমান এবং মূলগুলি যথাক্রমে \(\alpha, \ \beta\) ও \(\gamma\)।
তাহলে, সমীকরণটি \(\alpha, \ \beta\) ও \(\gamma\) দ্বারা সিদ্ধ হবে।
অতএব, \(a\alpha^2+b\alpha+c=0 ....... (1)\)
\(a\beta^2+b\beta+c=0 ....... (2)\)
\(a\gamma^2+b\gamma+c=0 ....... (3)\)
এখন, \((1)-(2)\) এর সাহায্যে,
\(a(\alpha^2-\beta^2)+b(\alpha-\beta)=0\)
\(\Rightarrow a(\alpha-\beta)(\alpha+\beta)+b(\alpha-\beta)=0\)
\(\Rightarrow (\alpha-\beta)\{a(\alpha+\beta)+b\}=0\)
\(\Rightarrow (\alpha-\beta)\ne{0}\)
\(\therefore a(\alpha+\beta)+b=0 ........(4)\) ➜ \(\because \alpha\ne{\beta}\)
অনুরূপভাবে, \((2)-(3)\) এর সাহায্যে,
\(a(\beta^2-\gamma^2)+b(\beta-\gamma)=0\)
\(\Rightarrow a(\beta-\gamma)(\beta+\gamma)+b(\beta-\gamma)=0\)
\(\Rightarrow (\beta-\gamma)\{a(\beta+\gamma)+b\}=0\)
\(\Rightarrow (\beta-\gamma)\ne{0}\)
\(\therefore a(\beta+\gamma)+b=0 ........(5)\) ➜ \(\because \beta\ne{\gamma}\)
এখন, \((4)-(5)\) এর সাহায্যে,
\(a(\alpha+\beta)-a(\beta+\gamma)=0\)
\(\Rightarrow a(\alpha+\beta-\beta-\gamma)=0\)
\(\Rightarrow a(\alpha-\gamma)=0\) যা অসম্ভব।
কারন, \(a\ne{0}\) এবং \(\alpha\ne{\gamma}\)
\(\therefore\) দ্বিঘাত সমীকরণের মূলের সংখ্যা দুইয়ের অধিক হতে পারে না।
উদাহরণঃ \(2x^2+13x-5=0\) সমীকরণের সর্বোচ্চ কয়টি মূল থাকতে পারে? প্রদত্ত সমীকরণের সমাধান নির্ণয় কর।
প্রমাণঃ
প্রদত্ত সমীকরণ \(ax^2+bx+c=0, \ a,b,c\in{\mathbb{R}}\) এবং \(a\ne{0}\) এর সমাধান\(x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\therefore x=\frac{-b+\sqrt{b^2-4ac}}{2a}, \ \frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(x\) এর এই দুইটি মানকে প্রদত্ত সমীকরণের দুইটি মূল বলে। প্রমাণ করতে হবে যে, দ্বিঘাত সমীকরণের দুইটির বেশী মূল থাকতে পারে না।
ধরি, দ্বিঘাত সমীকরণ \(ax^2+bx+c=0, \ a\ne{0}\) এর তিনটি ভিন্ন ভিন্ন মূল বিদ্যমান এবং মূলগুলি যথাক্রমে \(\alpha, \ \beta\) ও \(\gamma\)।
তাহলে, সমীকরণটি \(\alpha, \ \beta\) ও \(\gamma\) দ্বারা সিদ্ধ হবে।
অতএব, \(a\alpha^2+b\alpha+c=0 ....... (1)\)
\(a\beta^2+b\beta+c=0 ....... (2)\)
\(a\gamma^2+b\gamma+c=0 ....... (3)\)
এখন, \((1)-(2)\) এর সাহায্যে,
\(a(\alpha^2-\beta^2)+b(\alpha-\beta)=0\)
\(\Rightarrow a(\alpha-\beta)(\alpha+\beta)+b(\alpha-\beta)=0\)
\(\Rightarrow (\alpha-\beta)\{a(\alpha+\beta)+b\}=0\)
\(\Rightarrow (\alpha-\beta)\ne{0}\)
\(\therefore a(\alpha+\beta)+b=0 ........(4)\) ➜ \(\because \alpha\ne{\beta}\)
অনুরূপভাবে, \((2)-(3)\) এর সাহায্যে,
\(a(\beta^2-\gamma^2)+b(\beta-\gamma)=0\)
\(\Rightarrow a(\beta-\gamma)(\beta+\gamma)+b(\beta-\gamma)=0\)
\(\Rightarrow (\beta-\gamma)\{a(\beta+\gamma)+b\}=0\)
\(\Rightarrow (\beta-\gamma)\ne{0}\)
\(\therefore a(\beta+\gamma)+b=0 ........(5)\) ➜ \(\because \beta\ne{\gamma}\)
এখন, \((4)-(5)\) এর সাহায্যে,
\(a(\alpha+\beta)-a(\beta+\gamma)=0\)
\(\Rightarrow a(\alpha+\beta-\beta-\gamma)=0\)
\(\Rightarrow a(\alpha-\gamma)=0\) যা অসম্ভব।
কারন, \(a\ne{0}\) এবং \(\alpha\ne{\gamma}\)
\(\therefore\) দ্বিঘাত সমীকরণের মূলের সংখ্যা দুইয়ের অধিক হতে পারে না।
দ্বিঘাত সমীকরণের মূল ও সহগের মধ্যে সম্পর্ক
Relationship between roots and coefficients of quadratic equations
দ্বিঘাত সমীকরণ \(ax^2+bx+c=0, \ a,b,c\in{\mathbb{R}}\) এবং \(a\ne{0}\) এর সমাধান
\(x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\therefore x=\frac{-b+\sqrt{b^2-4ac}}{2a}, \ \frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(x\) এর এই দুইটি মানকে প্রদত্ত সমীকরণের দুইটি মূল বলে এবং \(a, \ b, \ c\) সমীকরণের সহগ নামে পরিচিত।
সমীকরণের মূলদ্বয়কে যথাক্রমে \(\alpha\) ও \(\beta\) দ্বারা প্রকাশ করা হলো।
অর্থাৎ, \(\alpha=\frac{-b+\sqrt{b^2-4ac}}{2a}\) এবং \(\beta=\frac{-b-\sqrt{b^2-4ac}}{2a}\)
এখন, \(\alpha\) ও \(\beta\) এর সাথে \(a, \ b, \ c\) সহগগুলির সম্পর্ক স্থাপন করতে হবে।
ধরি, \(\alpha=\frac{-b+\sqrt{b^2-4ac}}{2a} .......(1)\)
এবং \(\beta=\frac{-b-\sqrt{b^2-4ac}}{2a} .......(2)\)
\((1)+(2)\) এর সাহায্যে
\(\alpha+\beta=\frac{-b+\sqrt{b^2-4ac}}{2a}+\frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(=\frac{-b+\sqrt{b^2-4ac}-b-\sqrt{b^2-4ac}}{2a}\)
\(=\frac{-2b}{2a}\)
\(=-\frac{b}{a}\)
\(\therefore \alpha+\beta=-\frac{b}{a}\)
\((1)\times(2)\) এর সাহায্যে
\(\alpha\beta=\frac{-b+\sqrt{b^2-4ac}}{2a}\times\frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(=\frac{(-b+\sqrt{b^2-4ac})(-b-\sqrt{b^2-4ac})}{4a^2}\)
\(=\frac{(-b)^2-(\sqrt{b^2-4ac})^2}{4a^2}\)
\(=\frac{b^2-b^2+4ac}{4a^2}\)
\(=\frac{4ac}{4a^2}\)
\(=\frac{c}{a}\)
\(\therefore \alpha\beta=\frac{c}{a}\)
সুতরাং, দ্বিঘাত সমীকরণের মূল ও সহগের মধ্যে সম্পর্ক,
\(x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\therefore x=\frac{-b+\sqrt{b^2-4ac}}{2a}, \ \frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(x\) এর এই দুইটি মানকে প্রদত্ত সমীকরণের দুইটি মূল বলে এবং \(a, \ b, \ c\) সমীকরণের সহগ নামে পরিচিত।
সমীকরণের মূলদ্বয়কে যথাক্রমে \(\alpha\) ও \(\beta\) দ্বারা প্রকাশ করা হলো।
অর্থাৎ, \(\alpha=\frac{-b+\sqrt{b^2-4ac}}{2a}\) এবং \(\beta=\frac{-b-\sqrt{b^2-4ac}}{2a}\)
এখন, \(\alpha\) ও \(\beta\) এর সাথে \(a, \ b, \ c\) সহগগুলির সম্পর্ক স্থাপন করতে হবে।
ধরি, \(\alpha=\frac{-b+\sqrt{b^2-4ac}}{2a} .......(1)\)
এবং \(\beta=\frac{-b-\sqrt{b^2-4ac}}{2a} .......(2)\)
\((1)+(2)\) এর সাহায্যে
\(\alpha+\beta=\frac{-b+\sqrt{b^2-4ac}}{2a}+\frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(=\frac{-b+\sqrt{b^2-4ac}-b-\sqrt{b^2-4ac}}{2a}\)
\(=\frac{-2b}{2a}\)
\(=-\frac{b}{a}\)
\(\therefore \alpha+\beta=-\frac{b}{a}\)
\((1)\times(2)\) এর সাহায্যে
\(\alpha\beta=\frac{-b+\sqrt{b^2-4ac}}{2a}\times\frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(=\frac{(-b+\sqrt{b^2-4ac})(-b-\sqrt{b^2-4ac})}{4a^2}\)
\(=\frac{(-b)^2-(\sqrt{b^2-4ac})^2}{4a^2}\)
\(=\frac{b^2-b^2+4ac}{4a^2}\)
\(=\frac{4ac}{4a^2}\)
\(=\frac{c}{a}\)
\(\therefore \alpha\beta=\frac{c}{a}\)
সুতরাং, দ্বিঘাত সমীকরণের মূল ও সহগের মধ্যে সম্পর্ক,
দ্বিঘাত সমীকরণের সাধারণ মূল
Common roots of quadratic equations
দুইটি দ্বিঘাত সমীকরণের একটি সাধারণ মূল থাকতে পারে অথবা, উভয় মূলই সাধারণ হতে পারে।
বর্ণনাঃ দুইটি দ্বিঘাত সমীকরণের একটি সাধারণ মূল থাকার শর্ত নির্ণয় কর।
\(a_{1}x^2+b_{1}x+c_{1}=0 .......(1)\)
\(a_{2}x^2+b_{2}x+c_{2}=0 .......(2)\)
\(\alpha,\) সমীকরণদ্বয়ের সাধারণ মূল।
তাহলে, \(\alpha,\) উভয় সমীকরণকে সিদ্ধ করবে।
\(\therefore a_{1}\alpha^2+b_{1}\alpha+c_{1}=0 .......(3)\)
\(a_{2}\alpha^2+b_{2}\alpha+c_{2}=0 .......(4)\)
\((3)\) ও \((4)\) নং সমীকরণ বজ্রগুণ করে,
\(\frac{\alpha^2}{b_{1}c_{2}-b_{2}c_{1}}=\frac{\alpha}{c_{1}a_{2}-c_{2}a_{1}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow \frac{\alpha^2}{b_{1}c_{2}-b_{2}c_{1}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}, \ \frac{\alpha}{c_{1}a_{2}-c_{2}a_{1}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow \alpha^2=\frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}, \ \alpha=\frac{c_{1}a_{2}-c_{2}a_{1}}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow \frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}=\left(\frac{c_{1}a_{2}-c_{2}a_{1}}{a_{1}b_{2}-a_{2}b_{1}}\right)^2\)
\(\Rightarrow \frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}=\frac{(c_{1}a_{2}-c_{2}a_{1})^2}{(a_{1}b_{2}-a_{2}b_{1})^2}\)
\(\Rightarrow b_{1}c_{2}-b_{2}c_{1}=\frac{(c_{1}a_{2}-c_{2}a_{1})^2}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\therefore (b_{1}c_{2}-b_{2}c_{1})(a_{1}b_{2}-a_{2}b_{1})=(c_{1}a_{2}-c_{2}a_{1})^2\)
ইহাই নির্ণেয় শর্ত।
বর্ণনাঃ দুইটি দ্বিঘাত সমীকরণের উভয় মূলই সাধারণ হওয়ার শর্ত নির্ণয় কর।
\(a_{1}x^2+b_{1}x+c_{1}=0 .......(1)\)
\(a_{2}x^2+b_{2}x+c_{2}=0 .......(2)\)
\(\alpha, \ \beta\) উভয় সমীকরণের সাধারণ মূল।
\(\alpha, \ \beta\) যখন, \((1)\) নং সমীকরণের মূল হবে।
\(\alpha+\beta=-\frac{b_{1}}{a_{1}} .......(3)\)
\(\alpha\beta=\frac{c_{1}}{a_{1}} .......(4)\)
\(\alpha, \ \beta\) যখন, \((2)\) নং সমীকরণের মূল হবে।
\(\alpha+\beta=-\frac{b_{2}}{a_{2}} .......(5)\)
\(\alpha\beta=\frac{c_{2}}{a_{2}} .......(6)\)
\((3)\) ও \((5)\) নং সমীকরণ হতে,
\(-\frac{b_{2}}{a_{2}}=-\frac{b_{1}}{a_{1}}\)
\(\Rightarrow \frac{b_{2}}{a_{2}}=\frac{b_{1}}{a_{1}}\)
\(\therefore \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} ...... (7)\)
আবার, \((4)\) ও \((6)\) নং সমীকরণ হতে,
\(\frac{c_{2}}{a_{2}}=\frac{c_{1}}{a_{1}}\)
\(\therefore \frac{a_{1}}{a_{2}}=\frac{c_{1}}{c_{2}} ...... (8)\)
আবার, \((7)\) ও \((8)\) নং সমীকরণ হতে,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
ইহাই নির্ণেয় শর্ত।
বর্ণনাঃ দুইটি দ্বিঘাত সমীকরণের একটি সাধারণ মূল থাকার শর্ত নির্ণয় কর।
প্রমাণঃ
ধরি, দুইটি দ্বিঘাত সমীকরণ যথাক্রমে\(a_{1}x^2+b_{1}x+c_{1}=0 .......(1)\)
\(a_{2}x^2+b_{2}x+c_{2}=0 .......(2)\)
\(\alpha,\) সমীকরণদ্বয়ের সাধারণ মূল।
তাহলে, \(\alpha,\) উভয় সমীকরণকে সিদ্ধ করবে।
\(\therefore a_{1}\alpha^2+b_{1}\alpha+c_{1}=0 .......(3)\)
\(a_{2}\alpha^2+b_{2}\alpha+c_{2}=0 .......(4)\)
\((3)\) ও \((4)\) নং সমীকরণ বজ্রগুণ করে,
\(\frac{\alpha^2}{b_{1}c_{2}-b_{2}c_{1}}=\frac{\alpha}{c_{1}a_{2}-c_{2}a_{1}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow \frac{\alpha^2}{b_{1}c_{2}-b_{2}c_{1}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}, \ \frac{\alpha}{c_{1}a_{2}-c_{2}a_{1}}=\frac{1}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow \alpha^2=\frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}, \ \alpha=\frac{c_{1}a_{2}-c_{2}a_{1}}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\Rightarrow \frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}=\left(\frac{c_{1}a_{2}-c_{2}a_{1}}{a_{1}b_{2}-a_{2}b_{1}}\right)^2\)
\(\Rightarrow \frac{b_{1}c_{2}-b_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}=\frac{(c_{1}a_{2}-c_{2}a_{1})^2}{(a_{1}b_{2}-a_{2}b_{1})^2}\)
\(\Rightarrow b_{1}c_{2}-b_{2}c_{1}=\frac{(c_{1}a_{2}-c_{2}a_{1})^2}{a_{1}b_{2}-a_{2}b_{1}}\)
\(\therefore (b_{1}c_{2}-b_{2}c_{1})(a_{1}b_{2}-a_{2}b_{1})=(c_{1}a_{2}-c_{2}a_{1})^2\)
ইহাই নির্ণেয় শর্ত।
প্রমাণঃ
ধরি, দুইটি দ্বিঘাত সমীকরণ যথাক্রমে\(a_{1}x^2+b_{1}x+c_{1}=0 .......(1)\)
\(a_{2}x^2+b_{2}x+c_{2}=0 .......(2)\)
\(\alpha, \ \beta\) উভয় সমীকরণের সাধারণ মূল।
\(\alpha, \ \beta\) যখন, \((1)\) নং সমীকরণের মূল হবে।
\(\alpha+\beta=-\frac{b_{1}}{a_{1}} .......(3)\)
\(\alpha\beta=\frac{c_{1}}{a_{1}} .......(4)\)
\(\alpha, \ \beta\) যখন, \((2)\) নং সমীকরণের মূল হবে।
\(\alpha+\beta=-\frac{b_{2}}{a_{2}} .......(5)\)
\(\alpha\beta=\frac{c_{2}}{a_{2}} .......(6)\)
\((3)\) ও \((5)\) নং সমীকরণ হতে,
\(-\frac{b_{2}}{a_{2}}=-\frac{b_{1}}{a_{1}}\)
\(\Rightarrow \frac{b_{2}}{a_{2}}=\frac{b_{1}}{a_{1}}\)
\(\therefore \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} ...... (7)\)
আবার, \((4)\) ও \((6)\) নং সমীকরণ হতে,
\(\frac{c_{2}}{a_{2}}=\frac{c_{1}}{a_{1}}\)
\(\therefore \frac{a_{1}}{a_{2}}=\frac{c_{1}}{c_{2}} ...... (8)\)
আবার, \((7)\) ও \((8)\) নং সমীকরণ হতে,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
ইহাই নির্ণেয় শর্ত।
নিশ্চায়ক বা পৃথায়ক
Discriminant
দ্বিঘাত সমীকরণ \(ax^2+bx+c=0, \ a,b,c\in{\mathbb{R}}\) এবং \(a\ne{0}\) এর সমাধান
\(x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\therefore x=\frac{-b+\sqrt{b^2-4ac}}{2a}, \ \frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(x\) এর এই দুইটি মানকে প্রদত্ত সমীকরণের দুইটি মূল বলে এবং \(a, \ b, \ c\) সমীকরণের সহগ নামে পরিচিত।
\(a, \ b, \ c\) সহগগুলি বাস্তব সংখ্যা হলে, সমীকরণের মূলদ্বয়ে বিদ্যমান \(b^2-4ac\) রাশিটি মূলদ্বয়ের প্রকৃতি নিশ্চিত করে। তাই \(b^2-4ac\) রাশিটিকে সমীকরণের নিশ্চায়ক বা পৃথায়ক বলে।
নিশ্চায়ককে (Discriminant) শব্দের প্রথম অক্ষর (D) দ্বারা প্রকাশ করা হয়।
অর্থাৎ নিশ্চায়ক,
\(x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
\(\therefore x=\frac{-b+\sqrt{b^2-4ac}}{2a}, \ \frac{-b-\sqrt{b^2-4ac}}{2a}\)
\(x\) এর এই দুইটি মানকে প্রদত্ত সমীকরণের দুইটি মূল বলে এবং \(a, \ b, \ c\) সমীকরণের সহগ নামে পরিচিত।
\(a, \ b, \ c\) সহগগুলি বাস্তব সংখ্যা হলে, সমীকরণের মূলদ্বয়ে বিদ্যমান \(b^2-4ac\) রাশিটি মূলদ্বয়ের প্রকৃতি নিশ্চিত করে। তাই \(b^2-4ac\) রাশিটিকে সমীকরণের নিশ্চায়ক বা পৃথায়ক বলে।
নিশ্চায়ককে (Discriminant) শব্দের প্রথম অক্ষর (D) দ্বারা প্রকাশ করা হয়।
অর্থাৎ নিশ্চায়ক,
দ্বিঘাত সমীকরণের মূলের প্রকৃতি
Nature of roots of quadratic equations
দ্বিঘাত সমীকরণ \(ax^2+bx+c=0, \ a,b,c\in{\mathbb{R}}\) এবং \(a\ne{0}\) এর সমাধান
\(x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
যদি \(b^2-4ac=0\) হয়, তবে মূলদ্বয় বাস্তব ও সমান হয়।
যদি \(b^2-4ac\gt{0}\) হয়, তবে মূলদ্বয় বাস্তব ও অসমান হয়।
যদি \(b^2-4ac\lt{0}\) হয়, তবে মূলদ্বয় জটিল ও অসমান হবে। জটিল মূলদ্বয় একটি অপরটির অনুবন্ধী হয়।
যদি \(b^2-4ac\gt{0}\) এবং পূর্ণবর্গ সংখ্যা এবং \(a, \ b, \ c\) মূলদ সংখ্যা হয়, তবে মূলদ্বয় মূলদ ও অসমান হয়।
\(x=\frac{-b\pm{\sqrt{b^2-4ac}}}{2a}\)
যদি \(b^2-4ac=0\) হয়, তবে মূলদ্বয় বাস্তব ও সমান হয়।
যদি \(b^2-4ac\gt{0}\) হয়, তবে মূলদ্বয় বাস্তব ও অসমান হয়।
যদি \(b^2-4ac\lt{0}\) হয়, তবে মূলদ্বয় জটিল ও অসমান হবে। জটিল মূলদ্বয় একটি অপরটির অনুবন্ধী হয়।
যদি \(b^2-4ac\gt{0}\) এবং পূর্ণবর্গ সংখ্যা এবং \(a, \ b, \ c\) মূলদ সংখ্যা হয়, তবে মূলদ্বয় মূলদ ও অসমান হয়।
দ্বিঘাত সমীকরণ গঠন
Formation of quadratic equations
ধরি, কোনো দ্বিঘাত সমীকরণের মূলদ্বয় \(\alpha, \ \beta\)
তাহলে, \((x-\alpha), \ (x-\beta)\) উক্ত সমীকরণের বাম পক্ষের দুইটি উৎপাদক হবে।
যেহেতু, দ্বিঘাত সমীকরণের কেবলমাত্র দুইটি মূল বিদ্যমান;
সুতরাং, \(\alpha, \ \beta\) মূলবিশিষ্ট সমীকরণ \((x-\alpha)(x-\beta)=0\)
\(\Rightarrow x^2-(\alpha+\beta)x+\alpha\beta=0\)
\(\therefore\) কোনো দ্বিঘাত সমীকরণের মূলদ্বয় জানা থাকলে, সমীকরণটি
তাহলে, \((x-\alpha), \ (x-\beta)\) উক্ত সমীকরণের বাম পক্ষের দুইটি উৎপাদক হবে।
যেহেতু, দ্বিঘাত সমীকরণের কেবলমাত্র দুইটি মূল বিদ্যমান;
সুতরাং, \(\alpha, \ \beta\) মূলবিশিষ্ট সমীকরণ \((x-\alpha)(x-\beta)=0\)
\(\Rightarrow x^2-(\alpha+\beta)x+\alpha\beta=0\)
\(\therefore\) কোনো দ্বিঘাত সমীকরণের মূলদ্বয় জানা থাকলে, সমীকরণটি
ত্রিঘাত সমীকরণের মূল ও সহগের মধ্যে সম্পর্ক
Relationship between roots and coefficients of cubic equations
ধরি, ত্রিঘাত সমীকরণ \(ax^3+bx^2+cx+d=0\)
\(\therefore x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}=0\) ➜ উভয় পার্শে \(a\) ভাগ করে,
ত্রিঘাত সমীকরণের মূলত্রয় \(\alpha, \ \beta, \ \gamma\) হলে,
\(x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}\equiv(x-\alpha)(x-\beta)(x-\gamma)\) হবে।
\(\Rightarrow x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}\equiv x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\alpha\gamma)x-\alpha\beta\gamma\)
\(\Rightarrow x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\alpha\gamma)x-\alpha\beta\gamma\equiv x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}\)
\(\Rightarrow -(\alpha+\beta+\gamma)=\frac{b}{a}, \ \alpha\beta+\beta\gamma+\alpha\gamma=\frac{c}{a}, \ -\alpha\beta\gamma=\frac{d}{a}\) ➜ উভয় পার্শ হতে \(x^3, \ x^2, \ x\) এর সহগ ও ধ্রুবক রাশির সমতা নিয়ে,
\(\therefore \alpha+\beta+\gamma=-\frac{b}{a}, \ \alpha\beta+\beta\gamma+\alpha\gamma=\frac{c}{a}, \ \alpha\beta\gamma=-\frac{d}{a}\)
\(\therefore\) ত্রিঘাত সমীকরণের মূল ও সহগের মধ্যে সম্পর্কগুলি,
\(\therefore x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}=0\) ➜ উভয় পার্শে \(a\) ভাগ করে,
ত্রিঘাত সমীকরণের মূলত্রয় \(\alpha, \ \beta, \ \gamma\) হলে,
\(x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}\equiv(x-\alpha)(x-\beta)(x-\gamma)\) হবে।
\(\Rightarrow x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}\equiv x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\alpha\gamma)x-\alpha\beta\gamma\)
\(\Rightarrow x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\alpha\gamma)x-\alpha\beta\gamma\equiv x^3+\frac{b}{a}x^2+\frac{c}{a}x+\frac{d}{a}\)
\(\Rightarrow -(\alpha+\beta+\gamma)=\frac{b}{a}, \ \alpha\beta+\beta\gamma+\alpha\gamma=\frac{c}{a}, \ -\alpha\beta\gamma=\frac{d}{a}\) ➜ উভয় পার্শ হতে \(x^3, \ x^2, \ x\) এর সহগ ও ধ্রুবক রাশির সমতা নিয়ে,
\(\therefore \alpha+\beta+\gamma=-\frac{b}{a}, \ \alpha\beta+\beta\gamma+\alpha\gamma=\frac{c}{a}, \ \alpha\beta\gamma=-\frac{d}{a}\)
\(\therefore\) ত্রিঘাত সমীকরণের মূল ও সহগের মধ্যে সম্পর্কগুলি,
ত্রিঘাত সমীকরণ গঠন
Formation of cubic equations
ধরি, ত্রিঘাত সমীকরণের মূলত্রয় \(\alpha, \ \beta, \ \gamma\) হলে,
তাহলে, \((x-\alpha), \ (x-\beta), \ (x-\gamma)\) উক্ত সমীকরণের বাম পক্ষের তিনটি উৎপাদক হবে।
যেহেতু, ত্রিঘাত সমীকরণের কেবলমাত্র তিনটি মূল বিদ্যমান;
সুতরাং, \(\alpha, \ \beta, \ \gamma\) মূলবিশিষ্ট সমীকরণ \((x-\alpha)(x-\beta)(x-\gamma)=0\)
\(\Rightarrow x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\alpha\gamma)x-\alpha\beta\gamma=0\)
\(\therefore\) কোনো ত্রিঘাত সমীকরণের মূলত্রয় জানা থাকলে, সমীকরণটি
তাহলে, \((x-\alpha), \ (x-\beta), \ (x-\gamma)\) উক্ত সমীকরণের বাম পক্ষের তিনটি উৎপাদক হবে।
যেহেতু, ত্রিঘাত সমীকরণের কেবলমাত্র তিনটি মূল বিদ্যমান;
সুতরাং, \(\alpha, \ \beta, \ \gamma\) মূলবিশিষ্ট সমীকরণ \((x-\alpha)(x-\beta)(x-\gamma)=0\)
\(\Rightarrow x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\alpha\gamma)x-\alpha\beta\gamma=0\)
\(\therefore\) কোনো ত্রিঘাত সমীকরণের মূলত্রয় জানা থাকলে, সমীকরণটি
বিভিন্ন প্রগমনভুক্ত রাশিসমূহ
Various Sequential Quantity
তিনটি সমান্তর প্রগমনভুক্ত রাশি \(a-d, \ a, \ a+d\)
তিনটি সমানুপাতিক (গুণোত্তর) প্রগমনভুক্ত রাশি \(\frac{a}{d}, \ a, \ ad\)
তিনটি ভাজিত (Harmonic) প্রগমনভুক্ত রাশি \(\frac{1}{a-d}, \ \frac{1}{a}, \ \frac{1}{a+d}\)
চারটি সমান্তর প্রগমনভুক্ত রাশি \(a-3d, \ a-d, \ a+d, \ a+3d\)
চারটি সমানুপাতিক (গুণোত্তর) প্রগমনভুক্ত রাশি \(\frac{a}{d^3}, \ \frac{a}{d}, \ ad, \ ad^3\)
চারটি ভাজিত (Harmonic) প্রগমনভুক্ত রাশি \(\frac{1}{a-3d}, \ \frac{1}{a-d}, \ \frac{1}{a+d}, \ \frac{1}{a+3d}\)
তিনটি সমানুপাতিক (গুণোত্তর) প্রগমনভুক্ত রাশি \(\frac{a}{d}, \ a, \ ad\)
তিনটি ভাজিত (Harmonic) প্রগমনভুক্ত রাশি \(\frac{1}{a-d}, \ \frac{1}{a}, \ \frac{1}{a+d}\)
চারটি সমান্তর প্রগমনভুক্ত রাশি \(a-3d, \ a-d, \ a+d, \ a+3d\)
চারটি সমানুপাতিক (গুণোত্তর) প্রগমনভুক্ত রাশি \(\frac{a}{d^3}, \ \frac{a}{d}, \ ad, \ ad^3\)
চারটি ভাজিত (Harmonic) প্রগমনভুক্ত রাশি \(\frac{1}{a-3d}, \ \frac{1}{a-d}, \ \frac{1}{a+d}, \ \frac{1}{a+3d}\)

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000002