এ অধ্যায়ের পাঠ্যসূচী
- ঐতিহাসিক পটভূমি
- স্থানাঙ্ক (Coordinates)
- স্থানাঙ্কের রূপান্তর (Transformation of coordinates)
- পোলার স্থানাঙ্ক এবং কার্তেসীয় স্থানাঙ্ক (Cartesian and Polar Coordinates)
- পোলার ও কার্তেসীয় স্থানাঙ্কের মধ্যে সম্পর্ক (Relation between Cartesian and Polar Coordinates)
- দূরত্ব (Distance)
- বিভক্তিকরণ সূত্র (Section Formulae)
- মধ্যবিন্দুর সূত্র (Midpoint Formulae)
- ত্রিভুজের ভরকেন্দ্র (Center of mass of triangle)
- ত্রিভুজের ক্ষেত্রফল (Area of triangle)
- চতুর্ভুজের ক্ষেত্রফল (Area of Quadrilateral)
- বহুভুজের ক্ষেত্রফল (Area of Polygon)
- মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণ (General equation of the St. line through the Origin)
- \(Y\) অক্ষের ছেদিতাংশ এবং ঢাল দেওয়া থাকিলে সরলরেখার সমীকরণ (Equation of the straight line given the intercept and slope of the \(Y\) axis)
- তীর্যক অক্ষের প্রেক্ষিতে \(y=mx+c\) এর আকার (Form of \(y=mx+c\) with respect to the oblique axis)
- উভয় অক্ষের ছেদিতাংশ দেওয়া থাকিলে সরলরেখার সমীকরণ (Equation of straight line given intersection of both axes)
- একটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ (Equation of a straight line through a fixed point)
- দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ (Equation of a straight line through two fixed points)
- সরলরেখার লম্বরূপ সমীকরণ (Perpendicular type equation of straight line)
- একটি নির্দিষ্ট বিন্দুগামী এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta\) কোণ উৎপন্নকারী সরলরেখাটির সমীকরণ (Equation of a straight line through a fixed point and making an angle \(\theta\) with the positive direction of the \(X\) axis)
- দুইটি অসমান্তরাল সরলরেখার মধ্যবর্তী কোণ (Angle between two non-parallel straight lines)
- তীর্যক অক্ষের সাপেক্ষে দুইটি অসমান্তরাল সরলরেখার মধ্যবর্তী কোণ (Angle between two non-parallel straight lines to oblique axis)
- তিনটি সরলরেখার সমবিন্দু তথা এক বিন্দুতে মিলিত হওয়ার শর্ত (The condition of three straight lines meeting at a point)
- তিনটি সরলরেখা দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল (Area of triangle formed by three straight lines)
- লম্ব দূরত্ব (Perpendicular Distance)
- মূলবিন্দু হতে একটি সরলরেখার লম্ব দূরত্ব (Perpendicular distance of a straight line from the origin)
- দুইটি সমান্তরাল সরলরেখার মধ্যবর্তী লম্ব দূরত্ব (Perpendicular distance between two parallel straight lines)
- দুইটি পরস্পরছেদী সরলরেখার অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ (Equation of the bisector of the angle included by two intersecting straight lines)
- ত্রিভুজের অন্তঃকেন্দ্র নির্ণয় (Finding incenter of a triangle)
- কোনো সরলরেখার সমান্তরাল এবং নির্দিষ্ট একক দূরবর্তী সরলরেখার সমীকরণ (Equation of a straight line parallel to and a given unit distance from a straight line)
- অক্ষের দিক অপরিবর্তিত রেখে মূলবিন্দুর পরিবর্তন (Changing the origin while keeping the direction of the axis unchanged)
- মূলবিন্দুর অবস্থান অপরিবর্তিত রেখে অক্ষদ্বয়কে নির্দিষ্ট কোণে আবর্তন (Rotate the two axes through a specified angle, keeping the position of the origin unchanged)
- মূলবিন্দুর অবস্থান পরিবর্তিত করে অক্ষদ্বয়কে নির্দিষ্ট কোণে আবর্তন (Rotate the axis by a certain angle by changing the position of the origin)
- দুই জোড়া অক্ষ সাপেক্ষে কোনো বিন্দুর রূপান্তরিত স্থানাঙ্ক (The transformed coordinates of a point with respect to two pairs of axes)
- মূলবিন্দু ও \(x\) অক্ষকে স্থির রেখে তীর্যক অক্ষদ্বয়কে আয়তাকার অক্ষদ্বয়ে রূপান্তর করলে (By keeping the origin and \(x\) axis fixed, the oblique axes are converted to rectangular axes)
- মূলবিন্দুকে স্থির রেখে প্রদত্ত কোনো তীর্যক অক্ষদ্বয়কে অন্য তীর্যক অক্ষদ্বয়ে রূপান্তর (Transform any given oblique axis to another oblique axis while keeping the origin fixed)
- সাধারণ দ্বিঘাত সমীকরণ হতে এক ঘাত পদগুলো অপসারণ (Eliminating the linear terms from the general quadratic equation)
- সাধারণ দ্বিঘাত সমীকরণ হতে \(xy\) সম্বলিত পদ অপসারণ (Eliminating \(xy\) terms from the general quadratic equation)
- মূলবিন্দু অপরিবর্তিত রেখে আয়তাকার অক্ষদ্বয়কে নির্দিষ্ট কোণে আবর্তন (Rotate the rectangular axis through a specified angle, keeping the origin unchanged)
- মূলবিন্দু অপরিবর্তিত রেখে আয়তাকার অক্ষদ্বয়কে আবর্তন (Rotate the rectangular axis keeping the origin unchanged)
- অধ্যায় \(A\)-এর উদাহরণসমুহ
- অধ্যায় \(A\) / \(Q.1\)-এর সংক্ষিপ্ত প্রশ্নসমূহ
- অধ্যায় \(A\) / \(Q.2\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(A\) / \(Q.3\)-এর বর্ণনামূলক প্রশ্নসমূহ
- অধ্যায় \(A\) / \(Q.4\)-এর বর্ণনামূলক প্রশ্নসমূহ
ঐতিহাসিক পটভূমি
Historical Background

স্যার আইজ্যাক নিউটন
( ১৬৪২-১৭২৭ )
১৬৬৯ সালে তিনি ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন।
গ্রীক শব্দ Geo এবং Metria এর সমন্বিত রূপ হলো জ্যামিতি (Geometry)। মূলতঃ স্থানিক সম্পর্ক সংক্রান্ত আলোচনাই জ্যামিতির জন্ম দেয়। গণিতশাস্ত্রের দুটি প্রাক আধুনিক শাখার মধ্যে জ্যামিতি অন্যতম। সনাতন জ্যামিতি মূলতঃ রুলার কম্পাস নির্মিত চিত্র নির্ভর। ইউক্লিড  ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। (৩০০-২৫০ খ্রিষ্টপূর্ব) গাণিতিক যথাযথতা এবং স্বীকার্যভিত্তিক পদ্ধতি প্রবর্তন করলে জ্যামিতিশাস্ত্রে বৈপ্লবিক পরিবর্তন সাধিত হয়। ইউক্লিডের এই ধারণাসমূহ অদ্যাবধি জ্যামিতিতে ব্যবহৃত হয়। খ্রীষ্টপূর্ব ৩০০ অব্দে তার রচিত The Element গ্রন্থটি অদ্যাবধি সর্বকালের সবচেয়ে প্রভাবশালী পাঠ্যপুস্তক হিসেবে পরিগণিত হয়। যা বিংশ শতাব্দীর মধ্যভাগ পর্যন্ত পাশ্চাত্যের সকল শিক্ষিতজনের নিকট এক নামে পরিচিত ছিল। আধুনিক যুগে জ্যামিতিক ধারণা সাধারণীকরণ এর ফলে আরও বেশি বিমূর্ততা ও জটিলতায় পরিপূর্ণ এটি উচ্চ-পর্যায়ে উন্নিত হয়েছে। ক্যালকুলাসের মত গণিতের অন্যান্য অনেক শাখাই জ্যামিতিক ধারণার উপর প্রতিষ্ঠিত। তাই বর্তমানকালের গণিতশাস্ত্রের বহু শাখাকে জ্যামিতিশাস্ত্রের উত্তরসূরী বলে বিবেচনা করা হয়।
গ্রীক দার্শনিক ম্যানিসমিউস
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। (৩০০-২৫০ খ্রিষ্টপূর্ব) গাণিতিক যথাযথতা এবং স্বীকার্যভিত্তিক পদ্ধতি প্রবর্তন করলে জ্যামিতিশাস্ত্রে বৈপ্লবিক পরিবর্তন সাধিত হয়। ইউক্লিডের এই ধারণাসমূহ অদ্যাবধি জ্যামিতিতে ব্যবহৃত হয়। খ্রীষ্টপূর্ব ৩০০ অব্দে তার রচিত The Element গ্রন্থটি অদ্যাবধি সর্বকালের সবচেয়ে প্রভাবশালী পাঠ্যপুস্তক হিসেবে পরিগণিত হয়। যা বিংশ শতাব্দীর মধ্যভাগ পর্যন্ত পাশ্চাত্যের সকল শিক্ষিতজনের নিকট এক নামে পরিচিত ছিল। আধুনিক যুগে জ্যামিতিক ধারণা সাধারণীকরণ এর ফলে আরও বেশি বিমূর্ততা ও জটিলতায় পরিপূর্ণ এটি উচ্চ-পর্যায়ে উন্নিত হয়েছে। ক্যালকুলাসের মত গণিতের অন্যান্য অনেক শাখাই জ্যামিতিক ধারণার উপর প্রতিষ্ঠিত। তাই বর্তমানকালের গণিতশাস্ত্রের বহু শাখাকে জ্যামিতিশাস্ত্রের উত্তরসূরী বলে বিবেচনা করা হয়।
গ্রীক দার্শনিক ম্যানিসমিউস  ম্যানিসমিউস (৩৮০-৩২০ খ্রিষ্টপূর্ব) কোণক দ্বারা সমতলে বক্ররেখার ছেদাংশের বিভিন্ন অংশকে পরাবৃত্ত, উপবৃত্ত ও অধিবৃত্ত নামকরণ করেন। (৩০০-২৫০ খ্রিষ্টপূর্ব) এমন কিছু গাণিতিক সমস্যা সমাধান করেন। এই সমস্যাগুলো সমাধানের ক্ষেত্রে তিনি এমন একটি পদ্ধতি ব্যবহার করেন যা বর্তমান সময়ের স্থানাঙ্ক ব্যবস্থার অনুরূপ। স্থানাঙ্কের অনুরূপ এই পদ্ধতিটি ব্যবহার করে তিনি কয়েকটি উপপাদ্যেরও প্রমাণ করেন। তাই ম্যানিসমিউসকে প্রায়শঃই স্থানাঙ্ক ব্যবস্থার প্রবর্তক হিসেবে বিবেচনা করা হয়। কোনো সরলরেখার অন্তর্গত কোনো বিন্দুর অবস্থান নির্ণয় করতে যেয়ে অ্যাপোলোনিয়াস
ম্যানিসমিউস (৩৮০-৩২০ খ্রিষ্টপূর্ব) কোণক দ্বারা সমতলে বক্ররেখার ছেদাংশের বিভিন্ন অংশকে পরাবৃত্ত, উপবৃত্ত ও অধিবৃত্ত নামকরণ করেন। (৩০০-২৫০ খ্রিষ্টপূর্ব) এমন কিছু গাণিতিক সমস্যা সমাধান করেন। এই সমস্যাগুলো সমাধানের ক্ষেত্রে তিনি এমন একটি পদ্ধতি ব্যবহার করেন যা বর্তমান সময়ের স্থানাঙ্ক ব্যবস্থার অনুরূপ। স্থানাঙ্কের অনুরূপ এই পদ্ধতিটি ব্যবহার করে তিনি কয়েকটি উপপাদ্যেরও প্রমাণ করেন। তাই ম্যানিসমিউসকে প্রায়শঃই স্থানাঙ্ক ব্যবস্থার প্রবর্তক হিসেবে বিবেচনা করা হয়। কোনো সরলরেখার অন্তর্গত কোনো বিন্দুর অবস্থান নির্ণয় করতে যেয়ে অ্যাপোলোনিয়াস  পের্গার অ্যাপোলোনিয়াস ছিলেন গ্রীক জিওমিটার এবং জ্যোতির্বিজ্ঞানী, যেটি শঙ্কু বিভাগের বিষয়ে তত্ত্বগুলির জন্য পরিচিত ছিল। এই বিষয়ে ইউক্লিড এবং আর্কিমিডিসের তত্ত্বগুলি থেকে শুরু করে, তিনি বিশ্লেষণাত্মক জ্যামিতির আবিষ্কারের ঠিক আগে তারা তাদের সেই অবস্থায় নিয়ে এসেছিলেন। একটি অনুপাত-নির্ভর স্থানাঙ্ক পদ্ধতি বর্ণনা করেন। এই পদ্ধতিটির মাধ্যমেই এক-মাত্রিক স্থানাঙ্ক পদ্ধতির সূত্রপাত ঘটে। একাদশ শতাব্দীতে পারস্যের গণিতবিদ ওমর খৈয়াম বীজগণিত ও জ্যামিতির মধ্যে যোগসূত্র স্থাপন করেন। বৈশ্লেষিক জ্যামিতির বিকাসে মূল অবদানটি রেনে দেকার্তে
পের্গার অ্যাপোলোনিয়াস ছিলেন গ্রীক জিওমিটার এবং জ্যোতির্বিজ্ঞানী, যেটি শঙ্কু বিভাগের বিষয়ে তত্ত্বগুলির জন্য পরিচিত ছিল। এই বিষয়ে ইউক্লিড এবং আর্কিমিডিসের তত্ত্বগুলি থেকে শুরু করে, তিনি বিশ্লেষণাত্মক জ্যামিতির আবিষ্কারের ঠিক আগে তারা তাদের সেই অবস্থায় নিয়ে এসেছিলেন। একটি অনুপাত-নির্ভর স্থানাঙ্ক পদ্ধতি বর্ণনা করেন। এই পদ্ধতিটির মাধ্যমেই এক-মাত্রিক স্থানাঙ্ক পদ্ধতির সূত্রপাত ঘটে। একাদশ শতাব্দীতে পারস্যের গণিতবিদ ওমর খৈয়াম বীজগণিত ও জ্যামিতির মধ্যে যোগসূত্র স্থাপন করেন। বৈশ্লেষিক জ্যামিতির বিকাসে মূল অবদানটি রেনে দেকার্তে  প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে আধুনিক ফাংশনের ধারণা দেন । (Rene Descartes) (১৫৯৬-১৬৫০) এর। ১৬৩৭ সালে তার প্রকাশিত তিনটি রচনা হতেই মূলতঃ আধুনিক বৈশ্লেষিক জ্যামিতির সূচনা লাভ করে। যদিও ফরাসী ভাষায় লেখা এই রচনাগুলো যুক্তির কমতি ও জটিল সমীকরণের ব্যবহারের কারণে তৎকালীন সময়ে সাদরে গৃহীত হয়নি। পরবর্তীতে এই রচনাগুলো ল্যাটিন ভাষায় অনুবাদ করা হলে এবং ১৬৪৯ সাল হতে পরবর্তী কয়েকটি লেখায় ভ্যান স্কুটেন
প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে আধুনিক ফাংশনের ধারণা দেন । (Rene Descartes) (১৫৯৬-১৬৫০) এর। ১৬৩৭ সালে তার প্রকাশিত তিনটি রচনা হতেই মূলতঃ আধুনিক বৈশ্লেষিক জ্যামিতির সূচনা লাভ করে। যদিও ফরাসী ভাষায় লেখা এই রচনাগুলো যুক্তির কমতি ও জটিল সমীকরণের ব্যবহারের কারণে তৎকালীন সময়ে সাদরে গৃহীত হয়নি। পরবর্তীতে এই রচনাগুলো ল্যাটিন ভাষায় অনুবাদ করা হলে এবং ১৬৪৯ সাল হতে পরবর্তী কয়েকটি লেখায় ভ্যান স্কুটেন  ফ্রান্সিস্কাস ভ্যান শুটেন ছিলেন একজন ডাচ গণিতবিদ যিনি রেনা ডেসকার্টসের বিশ্লেষণাত্মক জ্যামিতি জনপ্রিয় করার জন্য সবচেয়ে বেশি পরিচিত। (Van Schooten) (১৬১৫-১৬৬০) কতৃক ব্যাখ্যা সংযোজনের ফলে সেগুলো সর্বজনস্বীকৃত হয়।
ফ্রান্সিস্কাস ভ্যান শুটেন ছিলেন একজন ডাচ গণিতবিদ যিনি রেনা ডেসকার্টসের বিশ্লেষণাত্মক জ্যামিতি জনপ্রিয় করার জন্য সবচেয়ে বেশি পরিচিত। (Van Schooten) (১৬১৫-১৬৬০) কতৃক ব্যাখ্যা সংযোজনের ফলে সেগুলো সর্বজনস্বীকৃত হয়।
স্যার আইজ্যাক নিউটন ১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। (Sir Isaac Newton) ( ১৬৪২-১৭২৭ ) দ্বিমাত্রিক কার্তেসীয় সমতলকে বর্তমানে বহুল প্রচলিত চারটি চতুর্ভাগে বিভক্ত করেন।
১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। (Sir Isaac Newton) ( ১৬৪২-১৭২৭ ) দ্বিমাত্রিক কার্তেসীয় সমতলকে বর্তমানে বহুল প্রচলিত চারটি চতুর্ভাগে বিভক্ত করেন।
 ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। (৩০০-২৫০ খ্রিষ্টপূর্ব) গাণিতিক যথাযথতা এবং স্বীকার্যভিত্তিক পদ্ধতি প্রবর্তন করলে জ্যামিতিশাস্ত্রে বৈপ্লবিক পরিবর্তন সাধিত হয়। ইউক্লিডের এই ধারণাসমূহ অদ্যাবধি জ্যামিতিতে ব্যবহৃত হয়। খ্রীষ্টপূর্ব ৩০০ অব্দে তার রচিত The Element গ্রন্থটি অদ্যাবধি সর্বকালের সবচেয়ে প্রভাবশালী পাঠ্যপুস্তক হিসেবে পরিগণিত হয়। যা বিংশ শতাব্দীর মধ্যভাগ পর্যন্ত পাশ্চাত্যের সকল শিক্ষিতজনের নিকট এক নামে পরিচিত ছিল। আধুনিক যুগে জ্যামিতিক ধারণা সাধারণীকরণ এর ফলে আরও বেশি বিমূর্ততা ও জটিলতায় পরিপূর্ণ এটি উচ্চ-পর্যায়ে উন্নিত হয়েছে। ক্যালকুলাসের মত গণিতের অন্যান্য অনেক শাখাই জ্যামিতিক ধারণার উপর প্রতিষ্ঠিত। তাই বর্তমানকালের গণিতশাস্ত্রের বহু শাখাকে জ্যামিতিশাস্ত্রের উত্তরসূরী বলে বিবেচনা করা হয়।
গ্রীক দার্শনিক ম্যানিসমিউস
ইউক্লিড (৩০০-২৫০ খ্রিষ্টপূর্ব) বিখ্যাত গ্রিক গণিতজ্ঞ। তার লেখা গ্রন্থগুলির মধ্যে মাত্র তিনটির সন্ধান পাওয়া গিয়েছে এগুলো, ডাটা, অপটিক্স ও এলিমেন্টস। এলিমেন্টস বইটি মোট ১৩ খণ্ডে প্রকাশিত হয়েছিল। (৩০০-২৫০ খ্রিষ্টপূর্ব) গাণিতিক যথাযথতা এবং স্বীকার্যভিত্তিক পদ্ধতি প্রবর্তন করলে জ্যামিতিশাস্ত্রে বৈপ্লবিক পরিবর্তন সাধিত হয়। ইউক্লিডের এই ধারণাসমূহ অদ্যাবধি জ্যামিতিতে ব্যবহৃত হয়। খ্রীষ্টপূর্ব ৩০০ অব্দে তার রচিত The Element গ্রন্থটি অদ্যাবধি সর্বকালের সবচেয়ে প্রভাবশালী পাঠ্যপুস্তক হিসেবে পরিগণিত হয়। যা বিংশ শতাব্দীর মধ্যভাগ পর্যন্ত পাশ্চাত্যের সকল শিক্ষিতজনের নিকট এক নামে পরিচিত ছিল। আধুনিক যুগে জ্যামিতিক ধারণা সাধারণীকরণ এর ফলে আরও বেশি বিমূর্ততা ও জটিলতায় পরিপূর্ণ এটি উচ্চ-পর্যায়ে উন্নিত হয়েছে। ক্যালকুলাসের মত গণিতের অন্যান্য অনেক শাখাই জ্যামিতিক ধারণার উপর প্রতিষ্ঠিত। তাই বর্তমানকালের গণিতশাস্ত্রের বহু শাখাকে জ্যামিতিশাস্ত্রের উত্তরসূরী বলে বিবেচনা করা হয়।
গ্রীক দার্শনিক ম্যানিসমিউস  ম্যানিসমিউস (৩৮০-৩২০ খ্রিষ্টপূর্ব) কোণক দ্বারা সমতলে বক্ররেখার ছেদাংশের বিভিন্ন অংশকে পরাবৃত্ত, উপবৃত্ত ও অধিবৃত্ত নামকরণ করেন। (৩০০-২৫০ খ্রিষ্টপূর্ব) এমন কিছু গাণিতিক সমস্যা সমাধান করেন। এই সমস্যাগুলো সমাধানের ক্ষেত্রে তিনি এমন একটি পদ্ধতি ব্যবহার করেন যা বর্তমান সময়ের স্থানাঙ্ক ব্যবস্থার অনুরূপ। স্থানাঙ্কের অনুরূপ এই পদ্ধতিটি ব্যবহার করে তিনি কয়েকটি উপপাদ্যেরও প্রমাণ করেন। তাই ম্যানিসমিউসকে প্রায়শঃই স্থানাঙ্ক ব্যবস্থার প্রবর্তক হিসেবে বিবেচনা করা হয়। কোনো সরলরেখার অন্তর্গত কোনো বিন্দুর অবস্থান নির্ণয় করতে যেয়ে অ্যাপোলোনিয়াস
ম্যানিসমিউস (৩৮০-৩২০ খ্রিষ্টপূর্ব) কোণক দ্বারা সমতলে বক্ররেখার ছেদাংশের বিভিন্ন অংশকে পরাবৃত্ত, উপবৃত্ত ও অধিবৃত্ত নামকরণ করেন। (৩০০-২৫০ খ্রিষ্টপূর্ব) এমন কিছু গাণিতিক সমস্যা সমাধান করেন। এই সমস্যাগুলো সমাধানের ক্ষেত্রে তিনি এমন একটি পদ্ধতি ব্যবহার করেন যা বর্তমান সময়ের স্থানাঙ্ক ব্যবস্থার অনুরূপ। স্থানাঙ্কের অনুরূপ এই পদ্ধতিটি ব্যবহার করে তিনি কয়েকটি উপপাদ্যেরও প্রমাণ করেন। তাই ম্যানিসমিউসকে প্রায়শঃই স্থানাঙ্ক ব্যবস্থার প্রবর্তক হিসেবে বিবেচনা করা হয়। কোনো সরলরেখার অন্তর্গত কোনো বিন্দুর অবস্থান নির্ণয় করতে যেয়ে অ্যাপোলোনিয়াস  পের্গার অ্যাপোলোনিয়াস ছিলেন গ্রীক জিওমিটার এবং জ্যোতির্বিজ্ঞানী, যেটি শঙ্কু বিভাগের বিষয়ে তত্ত্বগুলির জন্য পরিচিত ছিল। এই বিষয়ে ইউক্লিড এবং আর্কিমিডিসের তত্ত্বগুলি থেকে শুরু করে, তিনি বিশ্লেষণাত্মক জ্যামিতির আবিষ্কারের ঠিক আগে তারা তাদের সেই অবস্থায় নিয়ে এসেছিলেন। একটি অনুপাত-নির্ভর স্থানাঙ্ক পদ্ধতি বর্ণনা করেন। এই পদ্ধতিটির মাধ্যমেই এক-মাত্রিক স্থানাঙ্ক পদ্ধতির সূত্রপাত ঘটে। একাদশ শতাব্দীতে পারস্যের গণিতবিদ ওমর খৈয়াম বীজগণিত ও জ্যামিতির মধ্যে যোগসূত্র স্থাপন করেন। বৈশ্লেষিক জ্যামিতির বিকাসে মূল অবদানটি রেনে দেকার্তে
পের্গার অ্যাপোলোনিয়াস ছিলেন গ্রীক জিওমিটার এবং জ্যোতির্বিজ্ঞানী, যেটি শঙ্কু বিভাগের বিষয়ে তত্ত্বগুলির জন্য পরিচিত ছিল। এই বিষয়ে ইউক্লিড এবং আর্কিমিডিসের তত্ত্বগুলি থেকে শুরু করে, তিনি বিশ্লেষণাত্মক জ্যামিতির আবিষ্কারের ঠিক আগে তারা তাদের সেই অবস্থায় নিয়ে এসেছিলেন। একটি অনুপাত-নির্ভর স্থানাঙ্ক পদ্ধতি বর্ণনা করেন। এই পদ্ধতিটির মাধ্যমেই এক-মাত্রিক স্থানাঙ্ক পদ্ধতির সূত্রপাত ঘটে। একাদশ শতাব্দীতে পারস্যের গণিতবিদ ওমর খৈয়াম বীজগণিত ও জ্যামিতির মধ্যে যোগসূত্র স্থাপন করেন। বৈশ্লেষিক জ্যামিতির বিকাসে মূল অবদানটি রেনে দেকার্তে  প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে আধুনিক ফাংশনের ধারণা দেন । (Rene Descartes) (১৫৯৬-১৬৫০) এর। ১৬৩৭ সালে তার প্রকাশিত তিনটি রচনা হতেই মূলতঃ আধুনিক বৈশ্লেষিক জ্যামিতির সূচনা লাভ করে। যদিও ফরাসী ভাষায় লেখা এই রচনাগুলো যুক্তির কমতি ও জটিল সমীকরণের ব্যবহারের কারণে তৎকালীন সময়ে সাদরে গৃহীত হয়নি। পরবর্তীতে এই রচনাগুলো ল্যাটিন ভাষায় অনুবাদ করা হলে এবং ১৬৪৯ সাল হতে পরবর্তী কয়েকটি লেখায় ভ্যান স্কুটেন
প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে আধুনিক ফাংশনের ধারণা দেন । (Rene Descartes) (১৫৯৬-১৬৫০) এর। ১৬৩৭ সালে তার প্রকাশিত তিনটি রচনা হতেই মূলতঃ আধুনিক বৈশ্লেষিক জ্যামিতির সূচনা লাভ করে। যদিও ফরাসী ভাষায় লেখা এই রচনাগুলো যুক্তির কমতি ও জটিল সমীকরণের ব্যবহারের কারণে তৎকালীন সময়ে সাদরে গৃহীত হয়নি। পরবর্তীতে এই রচনাগুলো ল্যাটিন ভাষায় অনুবাদ করা হলে এবং ১৬৪৯ সাল হতে পরবর্তী কয়েকটি লেখায় ভ্যান স্কুটেন  ফ্রান্সিস্কাস ভ্যান শুটেন ছিলেন একজন ডাচ গণিতবিদ যিনি রেনা ডেসকার্টসের বিশ্লেষণাত্মক জ্যামিতি জনপ্রিয় করার জন্য সবচেয়ে বেশি পরিচিত। (Van Schooten) (১৬১৫-১৬৬০) কতৃক ব্যাখ্যা সংযোজনের ফলে সেগুলো সর্বজনস্বীকৃত হয়।
ফ্রান্সিস্কাস ভ্যান শুটেন ছিলেন একজন ডাচ গণিতবিদ যিনি রেনা ডেসকার্টসের বিশ্লেষণাত্মক জ্যামিতি জনপ্রিয় করার জন্য সবচেয়ে বেশি পরিচিত। (Van Schooten) (১৬১৫-১৬৬০) কতৃক ব্যাখ্যা সংযোজনের ফলে সেগুলো সর্বজনস্বীকৃত হয়। স্যার আইজ্যাক নিউটন
 ১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। (Sir Isaac Newton) ( ১৬৪২-১৭২৭ ) দ্বিমাত্রিক কার্তেসীয় সমতলকে বর্তমানে বহুল প্রচলিত চারটি চতুর্ভাগে বিভক্ত করেন।
১৬৮৭ সালে স্যার আইজ্যাক নিউটনের বিশ্ব নন্দিত গ্রন্থ প্রকাশিত হয়, যেখানে তিনি সর্বজনীন মহাকর্ষ সূত্র সহ গতির তিনটি সূত্র প্রদান করেন। তিনি বলবিজ্ঞানের ভিত্তি স্থাপন করেন। আলোকবিজ্ঞান, শব্দবিজ্ঞান, তাপবিজ্ঞানসহ পদার্থবিজ্ঞানের সকল মৌলিক শাখায় তাঁর অবদান অনস্বীকার্য। বৈজ্ঞানিক পর্যবেক্ষন ও পরীক্ষণের তিনি উদ্ভাবিত তত্ত্বকে যাচাই ও পরীক্ষা নিরীক্ষার জন্য পরীক্ষণের ব্যবস্থা করতেন। ১৬৬৯ সালে নিউটন ক্যামব্রিজ বিশ্ববিদ্যালয়ে গণিতের লুকাসিয়ান প্রফেসর হিসাবে যোগদান করেন। (Sir Isaac Newton) ( ১৬৪২-১৭২৭ ) দ্বিমাত্রিক কার্তেসীয় সমতলকে বর্তমানে বহুল প্রচলিত চারটি চতুর্ভাগে বিভক্ত করেন।

রেনে দেকার্তে
(১৫৯৬-১৬৫০)
প্রখ্যাত ফরাসি দার্শনিক, গণিতবিদ রেনে দেকার্তে আধুনিক ফাংশনের ধারণা দেন ।
বৈশ্লেষিক জ্যামিতির ক্রমবিকাশের অপর একজন অগ্রদূত পিয়ারে ফার্মা  পিয়েরে ডি ফার্মাট ছিলেন ফ্রান্সের টালুউজের পার্লামেন্টে ফরাসী আইনজীবী এবং একজন গণিতবিদ যিনি প্রাথমিক পর্যায়ে বিকাশের জন্য কৃতিত্ব লাভ করেছিলেন যার ফলে তার যথেষ্ট যোগ্যতার কৌশল সহ অনন্য ক্যালকুলাসের জন্ম হয়েছিল। (Pierre Fermat) (১৬০৭-১৬৬৫) । ১৬৩৭ সালে রেনে দেকার্তের রচনাগুলো প্রকাশের কিছুদিন পূর্বে এবং ফার্মার মৃত্যুর কিছুদিন পর ফার্মার রচিত Introductiion to Plane and Solid Loci শিরোনামের একটি অপ্রকাশিত পাণ্ডুলিপির কথা সমগ্র প্যারিস জুড়ে প্রচারিত হতে থাকে। যা অত্যান্ত সুলিখিত এবং সহজবোধ্য। দেকার্তে এবং ফার্মার গবেষণাকর্মের পার্থক্য মূলতঃ দৃষ্টিভঙ্গিগত। দেকার্তে জ্যামিতিক চিত্র হতে তার বীজগাণিতিক সমীকরণসহ অন্যান্য ধর্ম নির্ণয় করেন, পক্ষান্তরে ফার্মা কোনো বক্ররেখার বীজগাণিতিক সমীকরণ হতে তার চিত্র অঙ্কন করেন। পোলার স্থানাঙ্কের ইতিহাস অতি সুপ্রাচীন। আদিযুগ হতেই কোণ ও ব্যাসার্ধের ধারণা প্রচলিত ছিল। গ্রীক জোতির্বিদ হিপ্পার্কাস
পিয়েরে ডি ফার্মাট ছিলেন ফ্রান্সের টালুউজের পার্লামেন্টে ফরাসী আইনজীবী এবং একজন গণিতবিদ যিনি প্রাথমিক পর্যায়ে বিকাশের জন্য কৃতিত্ব লাভ করেছিলেন যার ফলে তার যথেষ্ট যোগ্যতার কৌশল সহ অনন্য ক্যালকুলাসের জন্ম হয়েছিল। (Pierre Fermat) (১৬০৭-১৬৬৫) । ১৬৩৭ সালে রেনে দেকার্তের রচনাগুলো প্রকাশের কিছুদিন পূর্বে এবং ফার্মার মৃত্যুর কিছুদিন পর ফার্মার রচিত Introductiion to Plane and Solid Loci শিরোনামের একটি অপ্রকাশিত পাণ্ডুলিপির কথা সমগ্র প্যারিস জুড়ে প্রচারিত হতে থাকে। যা অত্যান্ত সুলিখিত এবং সহজবোধ্য। দেকার্তে এবং ফার্মার গবেষণাকর্মের পার্থক্য মূলতঃ দৃষ্টিভঙ্গিগত। দেকার্তে জ্যামিতিক চিত্র হতে তার বীজগাণিতিক সমীকরণসহ অন্যান্য ধর্ম নির্ণয় করেন, পক্ষান্তরে ফার্মা কোনো বক্ররেখার বীজগাণিতিক সমীকরণ হতে তার চিত্র অঙ্কন করেন। পোলার স্থানাঙ্কের ইতিহাস অতি সুপ্রাচীন। আদিযুগ হতেই কোণ ও ব্যাসার্ধের ধারণা প্রচলিত ছিল। গ্রীক জোতির্বিদ হিপ্পার্কাস  নিকিয়ার হিপ্পার্কাস ছিলেন একজন গ্রীক জ্যোতির্বিদ, ভূগোলবিদ এবং গণিতবিদ। তাকে ত্রিকোণমিতির প্রতিষ্ঠাতা হিসাবে বিবেচনা করা হয় তবে তিনি বিষুবোধগুলির প্রিভিসেশন সম্পর্কিত ঘটনাগত আবিষ্কারের জন্য সবচেয়ে বিখ্যাত। হিপ্পার্কাসের জন্ম বিথিনিয়ার নাইসিয়ায় হয়েছিল এবং সম্ভবত তিনি গ্রিসের রোডস দ্বীপে মারা গেছেন। (Hipparchus) (১৯০-১২০ খ্রিষ্টপূর্ব) বিভিন্ন পরিমাপের কোণের বিপরীতে বৃত্তচাপের দৈর্ঘ্য নির্ণয়ের একটি সারণী প্রস্তুত করেন। আর্কিমিডিস তার On Spirals নামক গ্রন্থে এক ধরণের শঙ্খবৃত্ত (Spiral) এর কথা উল্লেখ করেন যার ব্যসার্ধ কোণ বৃদ্ধির সাথে সাথে পরিবর্তিত হয়। এই শঙ্খবৃত্তটি আর্কিমিডিয়ান শঙ্খবৃত্ত (Archimedean Spiral) নামেও পরিচিত। অষ্টম শতাব্দীতে পৃথিবীর বিভিন্ন স্থান হতে কাবা শরীফের দিক এবং দূরত্ব নির্ণয়ের একটি পদ্ধতি আবিষ্কার করেন। অনেক গণিতবিদের মতে তাদের এই পদ্ধতির মধ্যেই পোলার স্থানাঙ্কের ধারণা লুকায়িত ছিল। জ্যাকব বার্নোলীই
নিকিয়ার হিপ্পার্কাস ছিলেন একজন গ্রীক জ্যোতির্বিদ, ভূগোলবিদ এবং গণিতবিদ। তাকে ত্রিকোণমিতির প্রতিষ্ঠাতা হিসাবে বিবেচনা করা হয় তবে তিনি বিষুবোধগুলির প্রিভিসেশন সম্পর্কিত ঘটনাগত আবিষ্কারের জন্য সবচেয়ে বিখ্যাত। হিপ্পার্কাসের জন্ম বিথিনিয়ার নাইসিয়ায় হয়েছিল এবং সম্ভবত তিনি গ্রিসের রোডস দ্বীপে মারা গেছেন। (Hipparchus) (১৯০-১২০ খ্রিষ্টপূর্ব) বিভিন্ন পরিমাপের কোণের বিপরীতে বৃত্তচাপের দৈর্ঘ্য নির্ণয়ের একটি সারণী প্রস্তুত করেন। আর্কিমিডিস তার On Spirals নামক গ্রন্থে এক ধরণের শঙ্খবৃত্ত (Spiral) এর কথা উল্লেখ করেন যার ব্যসার্ধ কোণ বৃদ্ধির সাথে সাথে পরিবর্তিত হয়। এই শঙ্খবৃত্তটি আর্কিমিডিয়ান শঙ্খবৃত্ত (Archimedean Spiral) নামেও পরিচিত। অষ্টম শতাব্দীতে পৃথিবীর বিভিন্ন স্থান হতে কাবা শরীফের দিক এবং দূরত্ব নির্ণয়ের একটি পদ্ধতি আবিষ্কার করেন। অনেক গণিতবিদের মতে তাদের এই পদ্ধতির মধ্যেই পোলার স্থানাঙ্কের ধারণা লুকায়িত ছিল। জ্যাকব বার্নোলীই  জেকব বার্নৌল্লি ছিলেন বার্নৌল্লি পরিবারের অনেক বিশিষ্ট গণিতবিদদের মধ্যে একজন। তিনি লাইবনিজিয়ান ক্যালকুলাসের প্রারম্ভিক প্রবক্তা ছিলেন এবং লাইবনিজ-নিউটনের ক্যালকুলাস বিতর্কের সময় গটফ্রাইড উইলহেলাম লাইবনিজের পক্ষে ছিলেন। (Jacob Bernoulli) (1655–1705) সম্ভবত প্রথম গণিতবিদ যিনি বিভিন্ন ফাংশনের লেখচিত্র অঙ্কনের জন্য পোলার স্থানাঙ্ক পদ্ধতি ব্যবহার করেন।
স্থনাংক পদ্ধতি সংক্রান্ত বিভিন্ন আলোচনায় জন ওয়ালিস
জেকব বার্নৌল্লি ছিলেন বার্নৌল্লি পরিবারের অনেক বিশিষ্ট গণিতবিদদের মধ্যে একজন। তিনি লাইবনিজিয়ান ক্যালকুলাসের প্রারম্ভিক প্রবক্তা ছিলেন এবং লাইবনিজ-নিউটনের ক্যালকুলাস বিতর্কের সময় গটফ্রাইড উইলহেলাম লাইবনিজের পক্ষে ছিলেন। (Jacob Bernoulli) (1655–1705) সম্ভবত প্রথম গণিতবিদ যিনি বিভিন্ন ফাংশনের লেখচিত্র অঙ্কনের জন্য পোলার স্থানাঙ্ক পদ্ধতি ব্যবহার করেন।
স্থনাংক পদ্ধতি সংক্রান্ত বিভিন্ন আলোচনায় জন ওয়ালিস  জন ওয়ালিস ছিলেন একজন ইংরেজ ধর্মযাজক এবং গণিতবিদ যিনি অনন্য ক্যালকুলাসের বিকাশের জন্য আংশিক কৃতিত্ব দেওয়া হয়। ১৬৪৩ থেকে ১৬৮৯ এর মধ্যে তিনি সংসদের প্রধান ক্রিপ্টোগ্রাফার এবং পরে রাজদরবারের দায়িত্ব পালন করেন। অনন্তের ধারণাকে উপস্থাপন করার জন্য \(\infty\) প্রতীকটি পরিচয় করিয়ে দেওয়ার কৃতিত্ব তাঁর। (John Wallis) (১৬১৬-১৭০৩), জেমস গ্রেগরি
জন ওয়ালিস ছিলেন একজন ইংরেজ ধর্মযাজক এবং গণিতবিদ যিনি অনন্য ক্যালকুলাসের বিকাশের জন্য আংশিক কৃতিত্ব দেওয়া হয়। ১৬৪৩ থেকে ১৬৮৯ এর মধ্যে তিনি সংসদের প্রধান ক্রিপ্টোগ্রাফার এবং পরে রাজদরবারের দায়িত্ব পালন করেন। অনন্তের ধারণাকে উপস্থাপন করার জন্য \(\infty\) প্রতীকটি পরিচয় করিয়ে দেওয়ার কৃতিত্ব তাঁর। (John Wallis) (১৬১৬-১৭০৩), জেমস গ্রেগরি  জেমস গ্রেগরি এফ আরএস ছিলেন একজন স্কটিশ গণিতবিদ এবং জ্যোতির্বিদ। তাঁর উপনামটি কখনও কখনও গ্রেগরি হিসাবে বানান হয়, মূল স্কটিশ বানান। (James Gregory) (১৬৩৮-১৬৭৫), আইজ্যাক ব্যারো
জেমস গ্রেগরি এফ আরএস ছিলেন একজন স্কটিশ গণিতবিদ এবং জ্যোতির্বিদ। তাঁর উপনামটি কখনও কখনও গ্রেগরি হিসাবে বানান হয়, মূল স্কটিশ বানান। (James Gregory) (১৬৩৮-১৬৭৫), আইজ্যাক ব্যারো  আইজাক ব্যারো ছিলেন একজন ইংরেজ খ্রিস্টান ধর্মতত্ত্ববিদ এবং গণিতবিদ যিনি সাধারণত অনন্য ক্যালকুলাসের বিকাশে তাঁর প্রাথমিক ভূমিকার জন্য কৃতিত্ব লাভ করেন; বিশেষত, ক্যালকুলাসের মৌলিক উপপাদ্য আবিষ্কারের জন্য। (Isaac Barrow) (1630-1677) প্রমূখের নাম বিশেষ উল্লেখযোগ্য।
আইজাক ব্যারো ছিলেন একজন ইংরেজ খ্রিস্টান ধর্মতত্ত্ববিদ এবং গণিতবিদ যিনি সাধারণত অনন্য ক্যালকুলাসের বিকাশে তাঁর প্রাথমিক ভূমিকার জন্য কৃতিত্ব লাভ করেন; বিশেষত, ক্যালকুলাসের মৌলিক উপপাদ্য আবিষ্কারের জন্য। (Isaac Barrow) (1630-1677) প্রমূখের নাম বিশেষ উল্লেখযোগ্য।
 পিয়েরে ডি ফার্মাট ছিলেন ফ্রান্সের টালুউজের পার্লামেন্টে ফরাসী আইনজীবী এবং একজন গণিতবিদ যিনি প্রাথমিক পর্যায়ে বিকাশের জন্য কৃতিত্ব লাভ করেছিলেন যার ফলে তার যথেষ্ট যোগ্যতার কৌশল সহ অনন্য ক্যালকুলাসের জন্ম হয়েছিল। (Pierre Fermat) (১৬০৭-১৬৬৫) । ১৬৩৭ সালে রেনে দেকার্তের রচনাগুলো প্রকাশের কিছুদিন পূর্বে এবং ফার্মার মৃত্যুর কিছুদিন পর ফার্মার রচিত Introductiion to Plane and Solid Loci শিরোনামের একটি অপ্রকাশিত পাণ্ডুলিপির কথা সমগ্র প্যারিস জুড়ে প্রচারিত হতে থাকে। যা অত্যান্ত সুলিখিত এবং সহজবোধ্য। দেকার্তে এবং ফার্মার গবেষণাকর্মের পার্থক্য মূলতঃ দৃষ্টিভঙ্গিগত। দেকার্তে জ্যামিতিক চিত্র হতে তার বীজগাণিতিক সমীকরণসহ অন্যান্য ধর্ম নির্ণয় করেন, পক্ষান্তরে ফার্মা কোনো বক্ররেখার বীজগাণিতিক সমীকরণ হতে তার চিত্র অঙ্কন করেন। পোলার স্থানাঙ্কের ইতিহাস অতি সুপ্রাচীন। আদিযুগ হতেই কোণ ও ব্যাসার্ধের ধারণা প্রচলিত ছিল। গ্রীক জোতির্বিদ হিপ্পার্কাস
পিয়েরে ডি ফার্মাট ছিলেন ফ্রান্সের টালুউজের পার্লামেন্টে ফরাসী আইনজীবী এবং একজন গণিতবিদ যিনি প্রাথমিক পর্যায়ে বিকাশের জন্য কৃতিত্ব লাভ করেছিলেন যার ফলে তার যথেষ্ট যোগ্যতার কৌশল সহ অনন্য ক্যালকুলাসের জন্ম হয়েছিল। (Pierre Fermat) (১৬০৭-১৬৬৫) । ১৬৩৭ সালে রেনে দেকার্তের রচনাগুলো প্রকাশের কিছুদিন পূর্বে এবং ফার্মার মৃত্যুর কিছুদিন পর ফার্মার রচিত Introductiion to Plane and Solid Loci শিরোনামের একটি অপ্রকাশিত পাণ্ডুলিপির কথা সমগ্র প্যারিস জুড়ে প্রচারিত হতে থাকে। যা অত্যান্ত সুলিখিত এবং সহজবোধ্য। দেকার্তে এবং ফার্মার গবেষণাকর্মের পার্থক্য মূলতঃ দৃষ্টিভঙ্গিগত। দেকার্তে জ্যামিতিক চিত্র হতে তার বীজগাণিতিক সমীকরণসহ অন্যান্য ধর্ম নির্ণয় করেন, পক্ষান্তরে ফার্মা কোনো বক্ররেখার বীজগাণিতিক সমীকরণ হতে তার চিত্র অঙ্কন করেন। পোলার স্থানাঙ্কের ইতিহাস অতি সুপ্রাচীন। আদিযুগ হতেই কোণ ও ব্যাসার্ধের ধারণা প্রচলিত ছিল। গ্রীক জোতির্বিদ হিপ্পার্কাস  নিকিয়ার হিপ্পার্কাস ছিলেন একজন গ্রীক জ্যোতির্বিদ, ভূগোলবিদ এবং গণিতবিদ। তাকে ত্রিকোণমিতির প্রতিষ্ঠাতা হিসাবে বিবেচনা করা হয় তবে তিনি বিষুবোধগুলির প্রিভিসেশন সম্পর্কিত ঘটনাগত আবিষ্কারের জন্য সবচেয়ে বিখ্যাত। হিপ্পার্কাসের জন্ম বিথিনিয়ার নাইসিয়ায় হয়েছিল এবং সম্ভবত তিনি গ্রিসের রোডস দ্বীপে মারা গেছেন। (Hipparchus) (১৯০-১২০ খ্রিষ্টপূর্ব) বিভিন্ন পরিমাপের কোণের বিপরীতে বৃত্তচাপের দৈর্ঘ্য নির্ণয়ের একটি সারণী প্রস্তুত করেন। আর্কিমিডিস তার On Spirals নামক গ্রন্থে এক ধরণের শঙ্খবৃত্ত (Spiral) এর কথা উল্লেখ করেন যার ব্যসার্ধ কোণ বৃদ্ধির সাথে সাথে পরিবর্তিত হয়। এই শঙ্খবৃত্তটি আর্কিমিডিয়ান শঙ্খবৃত্ত (Archimedean Spiral) নামেও পরিচিত। অষ্টম শতাব্দীতে পৃথিবীর বিভিন্ন স্থান হতে কাবা শরীফের দিক এবং দূরত্ব নির্ণয়ের একটি পদ্ধতি আবিষ্কার করেন। অনেক গণিতবিদের মতে তাদের এই পদ্ধতির মধ্যেই পোলার স্থানাঙ্কের ধারণা লুকায়িত ছিল। জ্যাকব বার্নোলীই
নিকিয়ার হিপ্পার্কাস ছিলেন একজন গ্রীক জ্যোতির্বিদ, ভূগোলবিদ এবং গণিতবিদ। তাকে ত্রিকোণমিতির প্রতিষ্ঠাতা হিসাবে বিবেচনা করা হয় তবে তিনি বিষুবোধগুলির প্রিভিসেশন সম্পর্কিত ঘটনাগত আবিষ্কারের জন্য সবচেয়ে বিখ্যাত। হিপ্পার্কাসের জন্ম বিথিনিয়ার নাইসিয়ায় হয়েছিল এবং সম্ভবত তিনি গ্রিসের রোডস দ্বীপে মারা গেছেন। (Hipparchus) (১৯০-১২০ খ্রিষ্টপূর্ব) বিভিন্ন পরিমাপের কোণের বিপরীতে বৃত্তচাপের দৈর্ঘ্য নির্ণয়ের একটি সারণী প্রস্তুত করেন। আর্কিমিডিস তার On Spirals নামক গ্রন্থে এক ধরণের শঙ্খবৃত্ত (Spiral) এর কথা উল্লেখ করেন যার ব্যসার্ধ কোণ বৃদ্ধির সাথে সাথে পরিবর্তিত হয়। এই শঙ্খবৃত্তটি আর্কিমিডিয়ান শঙ্খবৃত্ত (Archimedean Spiral) নামেও পরিচিত। অষ্টম শতাব্দীতে পৃথিবীর বিভিন্ন স্থান হতে কাবা শরীফের দিক এবং দূরত্ব নির্ণয়ের একটি পদ্ধতি আবিষ্কার করেন। অনেক গণিতবিদের মতে তাদের এই পদ্ধতির মধ্যেই পোলার স্থানাঙ্কের ধারণা লুকায়িত ছিল। জ্যাকব বার্নোলীই  জেকব বার্নৌল্লি ছিলেন বার্নৌল্লি পরিবারের অনেক বিশিষ্ট গণিতবিদদের মধ্যে একজন। তিনি লাইবনিজিয়ান ক্যালকুলাসের প্রারম্ভিক প্রবক্তা ছিলেন এবং লাইবনিজ-নিউটনের ক্যালকুলাস বিতর্কের সময় গটফ্রাইড উইলহেলাম লাইবনিজের পক্ষে ছিলেন। (Jacob Bernoulli) (1655–1705) সম্ভবত প্রথম গণিতবিদ যিনি বিভিন্ন ফাংশনের লেখচিত্র অঙ্কনের জন্য পোলার স্থানাঙ্ক পদ্ধতি ব্যবহার করেন।
স্থনাংক পদ্ধতি সংক্রান্ত বিভিন্ন আলোচনায় জন ওয়ালিস
জেকব বার্নৌল্লি ছিলেন বার্নৌল্লি পরিবারের অনেক বিশিষ্ট গণিতবিদদের মধ্যে একজন। তিনি লাইবনিজিয়ান ক্যালকুলাসের প্রারম্ভিক প্রবক্তা ছিলেন এবং লাইবনিজ-নিউটনের ক্যালকুলাস বিতর্কের সময় গটফ্রাইড উইলহেলাম লাইবনিজের পক্ষে ছিলেন। (Jacob Bernoulli) (1655–1705) সম্ভবত প্রথম গণিতবিদ যিনি বিভিন্ন ফাংশনের লেখচিত্র অঙ্কনের জন্য পোলার স্থানাঙ্ক পদ্ধতি ব্যবহার করেন।
স্থনাংক পদ্ধতি সংক্রান্ত বিভিন্ন আলোচনায় জন ওয়ালিস  জন ওয়ালিস ছিলেন একজন ইংরেজ ধর্মযাজক এবং গণিতবিদ যিনি অনন্য ক্যালকুলাসের বিকাশের জন্য আংশিক কৃতিত্ব দেওয়া হয়। ১৬৪৩ থেকে ১৬৮৯ এর মধ্যে তিনি সংসদের প্রধান ক্রিপ্টোগ্রাফার এবং পরে রাজদরবারের দায়িত্ব পালন করেন। অনন্তের ধারণাকে উপস্থাপন করার জন্য \(\infty\) প্রতীকটি পরিচয় করিয়ে দেওয়ার কৃতিত্ব তাঁর। (John Wallis) (১৬১৬-১৭০৩), জেমস গ্রেগরি
জন ওয়ালিস ছিলেন একজন ইংরেজ ধর্মযাজক এবং গণিতবিদ যিনি অনন্য ক্যালকুলাসের বিকাশের জন্য আংশিক কৃতিত্ব দেওয়া হয়। ১৬৪৩ থেকে ১৬৮৯ এর মধ্যে তিনি সংসদের প্রধান ক্রিপ্টোগ্রাফার এবং পরে রাজদরবারের দায়িত্ব পালন করেন। অনন্তের ধারণাকে উপস্থাপন করার জন্য \(\infty\) প্রতীকটি পরিচয় করিয়ে দেওয়ার কৃতিত্ব তাঁর। (John Wallis) (১৬১৬-১৭০৩), জেমস গ্রেগরি  জেমস গ্রেগরি এফ আরএস ছিলেন একজন স্কটিশ গণিতবিদ এবং জ্যোতির্বিদ। তাঁর উপনামটি কখনও কখনও গ্রেগরি হিসাবে বানান হয়, মূল স্কটিশ বানান। (James Gregory) (১৬৩৮-১৬৭৫), আইজ্যাক ব্যারো
জেমস গ্রেগরি এফ আরএস ছিলেন একজন স্কটিশ গণিতবিদ এবং জ্যোতির্বিদ। তাঁর উপনামটি কখনও কখনও গ্রেগরি হিসাবে বানান হয়, মূল স্কটিশ বানান। (James Gregory) (১৬৩৮-১৬৭৫), আইজ্যাক ব্যারো  আইজাক ব্যারো ছিলেন একজন ইংরেজ খ্রিস্টান ধর্মতত্ত্ববিদ এবং গণিতবিদ যিনি সাধারণত অনন্য ক্যালকুলাসের বিকাশে তাঁর প্রাথমিক ভূমিকার জন্য কৃতিত্ব লাভ করেন; বিশেষত, ক্যালকুলাসের মৌলিক উপপাদ্য আবিষ্কারের জন্য। (Isaac Barrow) (1630-1677) প্রমূখের নাম বিশেষ উল্লেখযোগ্য।
আইজাক ব্যারো ছিলেন একজন ইংরেজ খ্রিস্টান ধর্মতত্ত্ববিদ এবং গণিতবিদ যিনি সাধারণত অনন্য ক্যালকুলাসের বিকাশে তাঁর প্রাথমিক ভূমিকার জন্য কৃতিত্ব লাভ করেন; বিশেষত, ক্যালকুলাসের মৌলিক উপপাদ্য আবিষ্কারের জন্য। (Isaac Barrow) (1630-1677) প্রমূখের নাম বিশেষ উল্লেখযোগ্য।
স্থানাংক
Coordinates
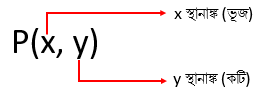
বিন্দুর অবস্থান অঙ্কের সাহায্যে প্রকাশ করা হলে, ঐ অংকগুলিকে বিন্দুর স্থানাঙ্ক বলে। যেমনঃ \(A(3, -7)\), \(B(3, 2)\)...........\(P(x, y)\). এখানে \(x\) এবং \(y\) যে কোন বাস্তব সংখ্যা।

স্থানাঙ্কের রূপান্তর
Transformation of coordinates
জ্যামিতিক সমস্যার সরলীকরণ ও সহজ সমাধানের জন্য অনেক সময়েই স্থানাংকের অক্ষদ্বয়ের অবস্থান পরিবর্তন করা আবশ্যক হয়ে দাঁড়ায়। অক্ষ দুইটির অবস্থান পরিবর্তনের কাজটি নিম্নলিখিত তিনটি উপায়ে হতে পারে,
অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুর পরিবর্তন।
মূলবিন্দু অপরিবর্তিত রেখে অক্ষের দিক পরিবর্তন।
মূলবিন্দুর পরিবর্তিনসহ অক্ষের দিক পরিবর্তন।
স্পষ্টতই শেষোক্ত উপায়টি প্রথম ও দ্বিতীয় উপায়ের সংজোগ ফল।
ধরি, প্রদত্ত দুইটি অক্ষের সাপেক্ষে সমতলে কোনো বিন্দু \(P\) এর স্থানাংক \((x, y)\)। অক্ষ দুইটির অবস্থান পরিবর্তন করে প্রাপ্ত নতুন অক্ষদ্বয়ের সাপেক্ষে যদি \(P\) বিন্দুর স্থানাংক \((x^{\prime}, y^{\prime})\) হয় তবে \((x^{\prime}, y^{\prime})\) কে \((x, y)\) এর রূপান্তরিত স্থানাংক বলা হয়। \(P\) এর আদি স্থানাংক \((x, y)\) এবং নতুন স্থানাংক \((x^{\prime}, y^{\prime})\) এর মধ্যে সম্পর্ক নির্ণয় করা যায় এবং আমরা দেখব যে, \(x\) ও \(y\) এর প্রত্যেককে \(x^{\prime}\) ও \(y^{\prime}\) এর একঘাত ফাংশন অর্থাৎ \(x=l_1x^{\prime}+m_1y^{\prime}+n_1, \ y=l_2x^{\prime}+m_2y^{\prime}+n_2\) যেখানে, \(l_1, \ m_1, \ n_1\) ধ্রুবক। ধরি, আদি অক্ষদ্বয়ের সাপেক্ষে কোনো সঞ্চারপথের সমীকরণ \(f(x,y)=0\) এতে \(x=l_1x^{\prime}+m_1y^{\prime}+n_1\) এবং \(y=l_2x^{\prime}+m_2y^{\prime}+n_2\) বসালে আমরা \(x^{\prime}, \ y^{\prime}\) এর মাধ্যমে প্রকাশিত একটি সমীকরণ \(F(x^{\prime}, y^{\prime})=0\) পাব; যা নতুন অক্ষদ্বয়ের সাপেক্ষে সঞ্চার পথটিকে প্রকাশ করবে। \(F(x^{\prime}, y^{\prime})=0\) কে \(f(x,y)=0\) এর রূপান্তরিত সমীকরণ বলা হয়। আবার \(x^{\prime}, \ y^{\prime}\) এর প্রত্যেককে \(x\) ও \(y\) এর একঘাত ফাংশন হিসেবে পাওয়া যাবে এবং \(F(x^{\prime}, y^{\prime})=0\) এ \(x^{\prime}, \ y^{\prime}\) এর মান বসিয়ে আমরা \(f(x,y)=0\) সমীকরণটি ফিরে পাব।
অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুর পরিবর্তন।
মূলবিন্দু অপরিবর্তিত রেখে অক্ষের দিক পরিবর্তন।
মূলবিন্দুর পরিবর্তিনসহ অক্ষের দিক পরিবর্তন।
স্পষ্টতই শেষোক্ত উপায়টি প্রথম ও দ্বিতীয় উপায়ের সংজোগ ফল।
ধরি, প্রদত্ত দুইটি অক্ষের সাপেক্ষে সমতলে কোনো বিন্দু \(P\) এর স্থানাংক \((x, y)\)। অক্ষ দুইটির অবস্থান পরিবর্তন করে প্রাপ্ত নতুন অক্ষদ্বয়ের সাপেক্ষে যদি \(P\) বিন্দুর স্থানাংক \((x^{\prime}, y^{\prime})\) হয় তবে \((x^{\prime}, y^{\prime})\) কে \((x, y)\) এর রূপান্তরিত স্থানাংক বলা হয়। \(P\) এর আদি স্থানাংক \((x, y)\) এবং নতুন স্থানাংক \((x^{\prime}, y^{\prime})\) এর মধ্যে সম্পর্ক নির্ণয় করা যায় এবং আমরা দেখব যে, \(x\) ও \(y\) এর প্রত্যেককে \(x^{\prime}\) ও \(y^{\prime}\) এর একঘাত ফাংশন অর্থাৎ \(x=l_1x^{\prime}+m_1y^{\prime}+n_1, \ y=l_2x^{\prime}+m_2y^{\prime}+n_2\) যেখানে, \(l_1, \ m_1, \ n_1\) ধ্রুবক। ধরি, আদি অক্ষদ্বয়ের সাপেক্ষে কোনো সঞ্চারপথের সমীকরণ \(f(x,y)=0\) এতে \(x=l_1x^{\prime}+m_1y^{\prime}+n_1\) এবং \(y=l_2x^{\prime}+m_2y^{\prime}+n_2\) বসালে আমরা \(x^{\prime}, \ y^{\prime}\) এর মাধ্যমে প্রকাশিত একটি সমীকরণ \(F(x^{\prime}, y^{\prime})=0\) পাব; যা নতুন অক্ষদ্বয়ের সাপেক্ষে সঞ্চার পথটিকে প্রকাশ করবে। \(F(x^{\prime}, y^{\prime})=0\) কে \(f(x,y)=0\) এর রূপান্তরিত সমীকরণ বলা হয়। আবার \(x^{\prime}, \ y^{\prime}\) এর প্রত্যেককে \(x\) ও \(y\) এর একঘাত ফাংশন হিসেবে পাওয়া যাবে এবং \(F(x^{\prime}, y^{\prime})=0\) এ \(x^{\prime}, \ y^{\prime}\) এর মান বসিয়ে আমরা \(f(x,y)=0\) সমীকরণটি ফিরে পাব।
কার্তেসীয় স্থানাংক এবং পোলার স্থানাংক
Cartesian and Polar Coordinates
এখানে, দ্বিমাত্রিক জ্যামিতিতে বিন্দুর দুই প্রকারের স্থানাংক আলোচনা করা হয়েছে। যেমনঃ কার্তেসীয় স্থানাংক এবং পোলার স্থানাংক।
কার্তেসীয় স্থানাংকঃ পরস্পর সমকোণে ছেদকৃত একজোড়া সরলরেখার সাপেক্ষে কোন বিন্দুর স্থানাঙ্ককে আয়তাকার কার্তেসীয় স্থানাঙ্ক বলাহয়। সরলরেখাদ্বয়কে অক্ষরেখা যাদের একটি X-অক্ষ অপরটি Y-অক্ষ এবং তাদের ছেদবিন্দুকে মূল বিন্দু বলা হয়।
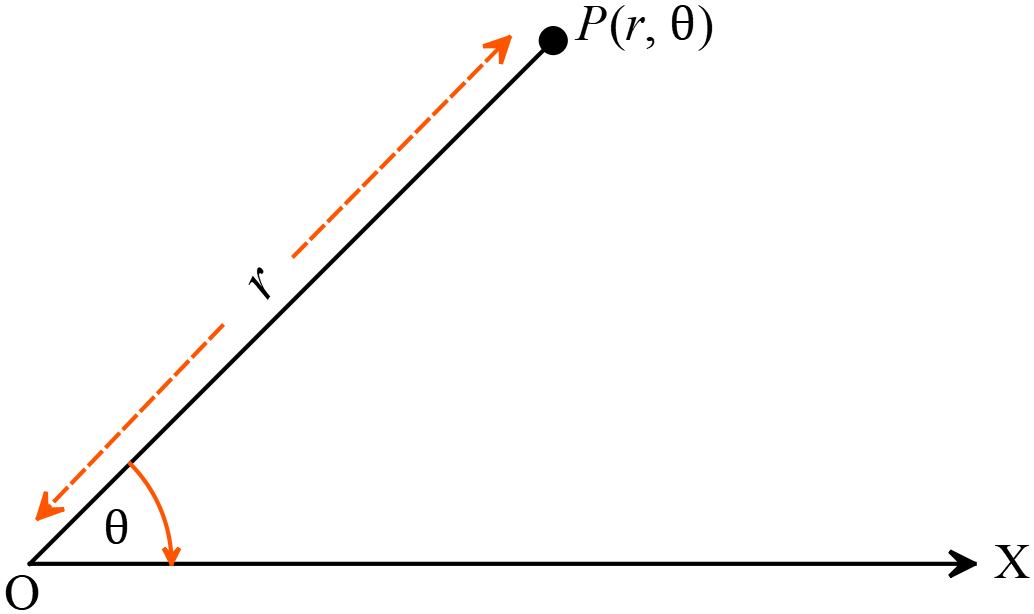
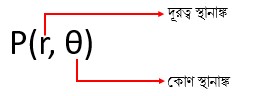
 পোলার স্থানাংকঃ কার্তেসীয় স্থানাঙ্কের মূল বিন্দু হতে সরাসরি দূরত্ব এবং ঐ দূরত্ব রেখা X- অক্ষের ধনাত্মক দিকের সহিত যে কোণ উৎপন্ন করে এই দুইয়ের সমন্বয়ে কোন বিন্দুর অবস্থান প্রকাশ করার পদ্ধতিকে পোলার স্থানাঙ্ক বলে।
পোলার স্থানাংকঃ কার্তেসীয় স্থানাঙ্কের মূল বিন্দু হতে সরাসরি দূরত্ব এবং ঐ দূরত্ব রেখা X- অক্ষের ধনাত্মক দিকের সহিত যে কোণ উৎপন্ন করে এই দুইয়ের সমন্বয়ে কোন বিন্দুর অবস্থান প্রকাশ করার পদ্ধতিকে পোলার স্থানাঙ্ক বলে।
কার্তেসীয় স্থানাংকঃ পরস্পর সমকোণে ছেদকৃত একজোড়া সরলরেখার সাপেক্ষে কোন বিন্দুর স্থানাঙ্ককে আয়তাকার কার্তেসীয় স্থানাঙ্ক বলাহয়। সরলরেখাদ্বয়কে অক্ষরেখা যাদের একটি X-অক্ষ অপরটি Y-অক্ষ এবং তাদের ছেদবিন্দুকে মূল বিন্দু বলা হয়।




পোলার ও কার্তেসীয় স্থানাঙ্কের মধ্যে সম্পর্ক
Relation between Cartesian and Polar Coordinates
পোলার স্থানাঙ্ক হতে কার্তেসীয় স্থানাঙ্কে রূপান্তরঃ
কার্তেসীয় স্থানাঙ্ক হতে পোলার স্থানাঙ্কে রূপান্তরঃ
\(x=r\cos\theta\)
\(y=r\sin\theta\)
\(y=r\sin\theta\)
কার্তেসীয় স্থানাঙ্ক হতে পোলার স্থানাঙ্কে রূপান্তরঃ
\(r=\sqrt{x^{2}+y^{2}}\)
\(\theta=tan^{-1}\frac{y}{x}\)
\(\theta=tan^{-1}\frac{y}{x}\)
দূরত্ব
Distance
কার্তেসীয় স্থানাঙ্কে দূরত্ব
কোন সমতলের উপর \(P(x_{1}, y_{1})\) ও \(P(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব হবে।
কোন সমতলের উপর \(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব হবে।
কোন সমতলের উপর \(P(x_{1}, y_{1})\) ও \(P(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব হবে।
\(PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
পোলার স্থানাঙ্কে দূরত্বকোন সমতলের উপর \(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব হবে।
\(PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
অনুসিদ্ধান্তঃ
\(P(x_{1}, y_{1})\) এবং মূলবিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-0)^{2}+(y_{1}-0)^{2}}\)
\(=\sqrt{x_{1}^{2}+y_{1}^{2}}\)।
\(P(x_{1}, \beta)\) ও \(P(x_{2}, \beta)\) বিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-x_{2})^{2}+(\beta-\beta)^{2}}\)
\(=\sqrt{(x_{1}-x_{2})^{2}}\)
\(=|(x_{1}-x_{2})|\)।
\(P(\alpha, y_{1})\) ও \((\alpha, y_{2})\) বিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(\alpha-\alpha)^{2}+(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(y_{1}-y_{2})^{2}}\)
\(=|(y_{1}-y_{2})|\)।
\(=\sqrt{(x_{1}-0)^{2}+(y_{1}-0)^{2}}\)
\(=\sqrt{x_{1}^{2}+y_{1}^{2}}\)।
\(P(x_{1}, \beta)\) ও \(P(x_{2}, \beta)\) বিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(x_{1}-x_{2})^{2}+(\beta-\beta)^{2}}\)
\(=\sqrt{(x_{1}-x_{2})^{2}}\)
\(=|(x_{1}-x_{2})|\)।
\(P(\alpha, y_{1})\) ও \((\alpha, y_{2})\) বিন্দুর মধ্যবর্তী দূরত্ব
\(=\sqrt{(\alpha-\alpha)^{2}+(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(y_{1}-y_{2})^{2}}\)
\(=|(y_{1}-y_{2})|\)।
বিভক্তিকরণ সূত্র
Section Formulae
অন্তর্বিভক্তিকরণ সূত্র
কোন সমতলে \(P(x_{1}, y_{1})\) এবং \(Q(x_{2}, y_{2})\) দুইটি নির্দিষ্ট বিন্দু \(R(x, y)\) বিন্দু \(PQ\) কে \(m:n\) অনুপাতে অন্তর্বিভক্ত করে। তবে, এর স্থানাঙ্ক হবে,
\(R\left(\frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n}\right)\)
বহির্বিভক্তিকরণ সূত্র\(R\left(\frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n}\right)\)
কোন সমতলে \(P(x_{1}, y_{1})\) এবং \(Q(x_{2}, y_{2})\) দুইটি নির্দিষ্ট বিন্দু \(R(x, y)\) বিন্দু \(PQ\) কে \(m:n\) অনুপাতে বহির্বিভক্ত করে। তবে, এর স্থানাঙ্ক হবে,
\(R\left(\frac{mx_{2}-nx_{1}}{m-n}, \frac{my_{2}-ny_{1}}{m-n}\right)\)
\(R\left(\frac{mx_{2}-nx_{1}}{m-n}, \frac{my_{2}-ny_{1}}{m-n}\right)\)
মধ্যবিন্দুর সূত্র
Midpoint Formulae
কোন সমতলে \(P(x_{1}, y_{1})\) এবং \(Q(x_{2}, y_{2})\) দুইটি নির্দিষ্ট বিন্দু \(R(x, y)\) বিন্দু \(PQ\) এর মধ্যবিন্দু হলে, এর স্থানাঙ্ক হবে,
\(R\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
\(R\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
ত্রিভুজের ভরকেন্দ্র
Center of mass of triangle
কোন সমতলে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\) এবং \(C(x_{3}, y_{3})\) কোন ত্রিভুজের তিনটি শীর্ষবিন্দু হলে, \(\triangle ABC\) এর ভরকেন্দ্রের স্থনাংক হবে,
\(G\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
\(G\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
ত্রিভুজের ক্ষেত্রফল
Area of triangle
কোন সমতলে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\) এবং \(C(x_{3}, y_{3})\) বিন্দুতিনটি \(\triangle ABC\) এর শীর্ষবিন্দু হলে,
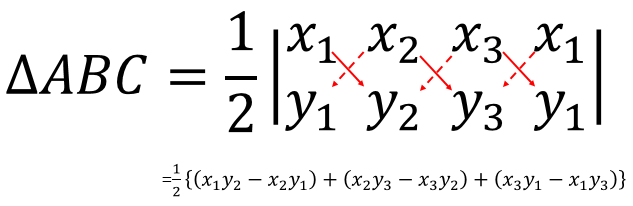
\(\triangle ABC=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ 1\\x_{2} \ \ y_{2} \ \ 1\\x_{3} \ \ y_{3} \ \ 1\end{array}\right|\) \(\triangle ABC=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)
\(\triangle ABC=\frac{1}{2}\sin{\omega}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ 1\\x_{2} \ \ y_{2} \ \ 1\\x_{3} \ \ y_{3} \ \ 1\end{array}\right|\)
\(\triangle ABC=\frac{1}{2}\sin{\omega}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
কোন সমতলে \(A(r_{1}, \theta_{1})\), \(B(r_{2}, \theta_{2})\) এবং \(C(r_{3}, \theta_{3})\) বিন্দু তিনটি \(\triangle ABC\) এর শীর্ষবিন্দু হলে,
\(\triangle ABC=\frac{1}{2}\{r_{1}r_{2}\sin{(\theta_{2}-\theta_{1})}+r_{2}r_{3}\sin{(\theta_{3}-\theta_{2})}+r_{3}r_{1}\sin{(\theta_{1}-\theta_{3})}\}\)
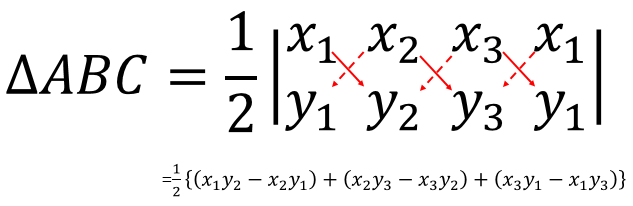
\(\triangle ABC=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ 1\\x_{2} \ \ y_{2} \ \ 1\\x_{3} \ \ y_{3} \ \ 1\end{array}\right|\) \(\triangle ABC=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)
অনুসিদ্ধান্তঃ
তীর্যক অক্ষের সাপেক্ষে কোন সমতলে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\) এবং \(C(x_{3}, y_{3})\) বিন্দুতিনটি \(\triangle ABC\) এর শীর্ষবিন্দু হলে,\(\triangle ABC=\frac{1}{2}\sin{\omega}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ 1\\x_{2} \ \ y_{2} \ \ 1\\x_{3} \ \ y_{3} \ \ 1\end{array}\right|\)
\(\triangle ABC=\frac{1}{2}\sin{\omega}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
কোন সমতলে \(A(r_{1}, \theta_{1})\), \(B(r_{2}, \theta_{2})\) এবং \(C(r_{3}, \theta_{3})\) বিন্দু তিনটি \(\triangle ABC\) এর শীর্ষবিন্দু হলে,
\(\triangle ABC=\frac{1}{2}\{r_{1}r_{2}\sin{(\theta_{2}-\theta_{1})}+r_{2}r_{3}\sin{(\theta_{3}-\theta_{2})}+r_{3}r_{1}\sin{(\theta_{1}-\theta_{3})}\}\)
চতুর্ভুজের ক্ষেত্রফল
Area of Quadrilateral
কোন সমতলে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\), \(C(x_{3}, y_{3})\) এবং \(D(x_{4}, y_{4})\) বিন্দুচারটি \(\Box ABCD\) এর শীর্ষবিন্দু হলে,
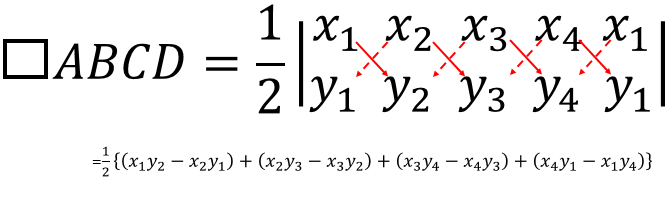
\(\Box ABCD=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{4}+y_{4}x_{1})\}\)
\(\Box ABCD=\frac{1}{2}\sin{\omega}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{4}+y_{4}x_{1})\}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
কোন সমতলে \(A(r_{1}, \theta_{1})\), \(B(r_{2}, \theta_{2})\), \(C(r_{3}, \theta_{3})\) এবং \(D(r_{4}, \theta_{4})\) বিন্দু চারটি \(\Box ABCD\) এর শীর্ষবিন্দু হলে,
\(\Box ABCD=\frac{1}{2}\{r_{1}r_{2}\sin{(\theta_{2}-\theta_{1})}+r_{2}r_{3}\sin{(\theta_{3}-\theta_{2})}+r_{3}r_{4}\sin{(\theta_{4}-\theta_{3})}+r_{4}r_{1}\sin{(\theta_{1}-\theta_{4})}\}\)
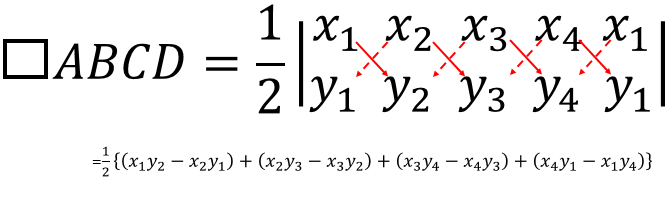
\(\Box ABCD=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{4}+y_{4}x_{1})\}\)
অনুসিদ্ধান্তঃ
তীর্যক অক্ষের সাপেক্ষে কোন সমতলে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\), \(C(x_{3}, y_{3})\) এবং \(D(x_{4}, y_{4})\) বিন্দুচারটি \(\Box ABCD\) এর শীর্ষবিন্দু হলে,\(\Box ABCD=\frac{1}{2}\sin{\omega}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{4}+y_{4}x_{1})\}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
কোন সমতলে \(A(r_{1}, \theta_{1})\), \(B(r_{2}, \theta_{2})\), \(C(r_{3}, \theta_{3})\) এবং \(D(r_{4}, \theta_{4})\) বিন্দু চারটি \(\Box ABCD\) এর শীর্ষবিন্দু হলে,
\(\Box ABCD=\frac{1}{2}\{r_{1}r_{2}\sin{(\theta_{2}-\theta_{1})}+r_{2}r_{3}\sin{(\theta_{3}-\theta_{2})}+r_{3}r_{4}\sin{(\theta_{4}-\theta_{3})}+r_{4}r_{1}\sin{(\theta_{1}-\theta_{4})}\}\)
বহুভুজের ক্ষেত্রফল
Area of Polygon
অনুরূপভাবে যে কোন সংখ্যক বাহু বিশিষ্ট বহুভুজের ক্ষেত্রফল নির্ণয় করা সম্ভব।
কোন সমতলে \((x_{1}, y_{1})\), \((x_{2}, y_{2})\), \((x_{3}, y_{3})\)...... \((x_{n}, y_{n})\) বিন্দুগুলি কোন বহুভুজের শীর্ষবিন্দু হলে,
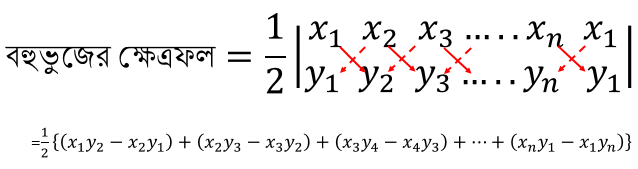
বহুভুজের ক্ষেত্রফল \(=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+...+x_{n}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+...+y_{n}x_{1})\}\)
বহুভুজের ক্ষেত্রফল \(=\frac{1}{2}\sin{\omega}\{(x_{1}y_{2}+x_{2}y_{3}+...+x_{n}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+...+y_{n}x_{1})\}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
কোন সমতলে \(P_{1}(r_{1}, \theta_{1})\), \(P_{2}(r_{2}, \theta_{2})\), \(P_{3}(r_{3}, \theta_{3})\)....\(P_{n}(r_{n}, \theta_{n})\) বিন্দু গুলি কোনো বহুভুজের শীর্ষবিন্দু হলে,
বহুভুজের ক্ষেত্রফল \(=\frac{1}{2}\{r_{1}r_{2}\sin{(\theta_{2}-\theta_{1})}+r_{2}r_{3}\sin{(\theta_{3}-\theta_{2})}+....+r_{n}r_{1}\sin{(\theta_{1}-\theta_{n})}\}\)
কোন সমতলে \((x_{1}, y_{1})\), \((x_{2}, y_{2})\), \((x_{3}, y_{3})\)...... \((x_{n}, y_{n})\) বিন্দুগুলি কোন বহুভুজের শীর্ষবিন্দু হলে,
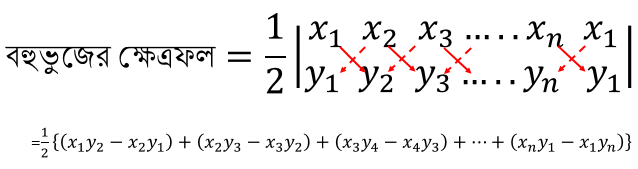
বহুভুজের ক্ষেত্রফল \(=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+...+x_{n}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+...+y_{n}x_{1})\}\)
অনুসিদ্ধান্তঃ
তীর্যক অক্ষের সাপেক্ষে কোন সমতলে \((x_{1}, y_{1})\), \((x_{2}, y_{2})\), \((x_{3}, y_{3})\)...... \((x_{n}, y_{n})\) বিন্দুগুলি কোন বহুভুজের শীর্ষবিন্দু হলে,বহুভুজের ক্ষেত্রফল \(=\frac{1}{2}\sin{\omega}\{(x_{1}y_{2}+x_{2}y_{3}+...+x_{n}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+...+y_{n}x_{1})\}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
কোন সমতলে \(P_{1}(r_{1}, \theta_{1})\), \(P_{2}(r_{2}, \theta_{2})\), \(P_{3}(r_{3}, \theta_{3})\)....\(P_{n}(r_{n}, \theta_{n})\) বিন্দু গুলি কোনো বহুভুজের শীর্ষবিন্দু হলে,
বহুভুজের ক্ষেত্রফল \(=\frac{1}{2}\{r_{1}r_{2}\sin{(\theta_{2}-\theta_{1})}+r_{2}r_{3}\sin{(\theta_{3}-\theta_{2})}+....+r_{n}r_{1}\sin{(\theta_{1}-\theta_{n})}\}\)
মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণ
General equation of the St. line through the Origin
\(y=mx\).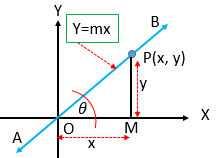
এখানে, \(m\) সরলরেখাটির ঢাল।

এখানে, \(m\) সরলরেখাটির ঢাল।
\(Y\) অক্ষের ছেদিতাংশ এবং ঢাল দেওয়া থাকিলে সরলরেখার সমীকরণ
Equation of the straight line given the intercept and slope of the \(Y\) axis
\(Y\) অক্ষের ছেদিতাংশ \((c)\) এবং ঢাল \((m)\) দেওয়া থাকিলে সরলরেখার সমীকরণ,
\(y=mx+c\).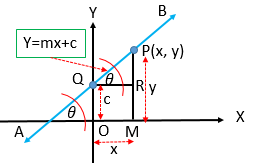
\(y=mx+c\).

তীর্যক অক্ষের প্রেক্ষিতে \(y=mx+c\) এর আকার
Form of \(y=mx+c\) with respect to the oblique axis
\(y=\frac{\sin{\theta}}{\sin{(\omega-\theta)}}x+c\).
যেখানে,
\(\theta\) রেখাটির নতি
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ

যেখানে,
\(\theta\) রেখাটির নতি
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
উভয় অক্ষের ছেদিতাংশ দেওয়া থাকিলে সরলরেখার সমীকরণ
Equation of straight line given intersection of both axes
উভয় অক্ষের ছেদিতাংশ \(a\) ও \(b\) দেওয়া থাকিলে সরলরেখার সমীকরণ
\(\frac{x}{a}+\frac{y}{b}=1\).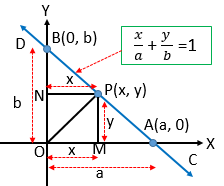
\(\frac{x}{a}+\frac{y}{b}=1\).

একটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ
Equation of a straight line through a fixed point
একটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) দিয়ে গমনকারী এবং তার ঢাল \((m)\) দেওয়া থাকিলে সরলরেখার সমীকরণ
\(y-y_{1}=m(x-x_{1})\).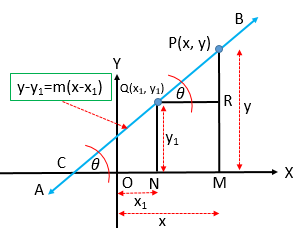
\(y-y_{1}=m(x-x_{1})\).

দুইটি নির্দিষ্ট বিন্দুগামী সরলরেখার সমীকরণ
Equation of a straight line through two fixed points
দুইটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) দিয়ে গমনকারী সরলরেখার সমীকরণ
\(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\).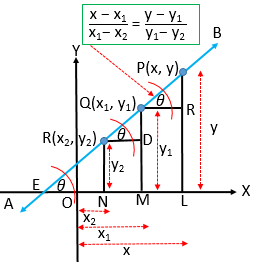
\(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\).

সরলরেখার লম্বরূপ সমীকরণ
Perpendicular type equation of straight line
মূলবিন্দু হতে কোনো সরলরেখার উপর অঙ্কিত লম্বের দৈর্ঘ্য \(P\) এবং লম্বটি \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\alpha \) কোণ উৎপন্ন করলে, সরলরেখাটির সমীকরণ
\(x\cos\alpha+y\sin\alpha=p\).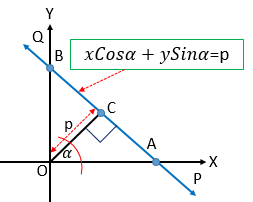
\(x\cos\alpha+y\sin\alpha=p\).

একটি নির্দিষ্ট বিন্দুগামী এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta\) কোণ উৎপন্নকারী সরলরেখাটির সমীকরণ
Equation of a straight line through a fixed point and making an angle \(\theta\) with the positive direction of the \(X\) axis
একটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) দিয়ে গমনকারী এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta\) কোণ উৎপন্ন করলে, সরলরেখাটির সমীকরণ
\(\frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\).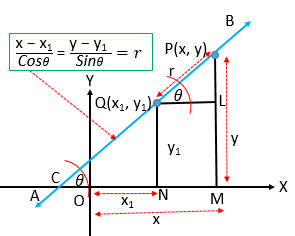
যেখানে, \((x, y)\) বিন্দু হতে \((x_{1}, y_{1})\) বিন্দুর দূরত্ব=\(r\)
\(\frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\).

যেখানে, \((x, y)\) বিন্দু হতে \((x_{1}, y_{1})\) বিন্দুর দূরত্ব=\(r\)
দুইটি অসমান্তরাল সরলরেখার মধ্যবর্তী কোণ
Angle between two non-parallel straight lines
দুইটি অসমান্তরাল সরলরেখা উভয়ই \(Y\) অক্ষের অসমান্তরাল হলে, তাদের মধ্যবর্তী কোণঃ
ধরি,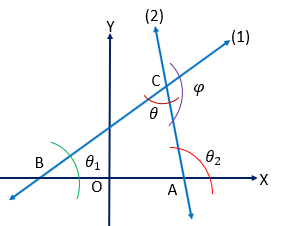
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণঃ
\(\theta=tan^{-1}\left(\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\right)\).
এখানে,
\((1)\) নং সরলরেখার ঢাল \(=m_{1}\)
\((2)\) নং সরলরেখার ঢাল \(=m_{2}\)

\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণঃ
\(\theta=tan^{-1}\left(\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\right)\).
এখানে,
\((1)\) নং সরলরেখার ঢাল \(=m_{1}\)
\((2)\) নং সরলরেখার ঢাল \(=m_{2}\)
সরলরেখাদ্বয়ের আকার সাধারণ হলে
অর্থাৎ রেখাদ্বয়,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণঃ
\(\theta=tan^{-1}\left(\pm \frac{a_{1}b_{2}-a_{2}b_{1}}{a_{1}a_{2}+b_{1}b_{2}}\right)\).
এখানে,
\((1)\) নং সরলরেখার ঢাল \(=-\frac{a_{1}}{b_{1}}\)
\((2)\) নং সরলরেখার ঢাল \(=-\frac{a_{2}}{b_{2}}\)
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণঃ
\(\theta=tan^{-1}\left(\pm \frac{a_{1}b_{2}-a_{2}b_{1}}{a_{1}a_{2}+b_{1}b_{2}}\right)\).
এখানে,
\((1)\) নং সরলরেখার ঢাল \(=-\frac{a_{1}}{b_{1}}\)
\((2)\) নং সরলরেখার ঢাল \(=-\frac{a_{2}}{b_{2}}\)
তীর্যক অক্ষের সাপেক্ষে দুইটি অসমান্তরাল সরলরেখার মধ্যবর্তী কোণ
Angle between two non-parallel straight lines to oblique axis
ধরি,
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণঃ
\(\theta=tan^{-1}\left\{\pm \frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\sin{\omega}+m_{1}m_{2}}\right\}\).
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
\((1)\) নং সরলরেখার ঢাল \(=m_{1}\)
\((2)\) নং সরলরেখার ঢাল \(=m_{2}\)
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণঃ
\(\theta=tan^{-1}\left\{\pm \frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\sin{\omega}+m_{1}m_{2}}\right\}\).
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
\((1)\) নং সরলরেখার ঢাল \(=m_{1}\)
\((2)\) নং সরলরেখার ঢাল \(=m_{2}\)
অনুসিদ্ধান্তঃ
সরলরেখাদ্বয়ের আকার সাধারণ হলে
অর্থাৎ রেখাদ্বয়,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণঃ
\(\theta=tan^{-1}\left(\pm \frac{(a_{1}b_{2}-a_{2}b_{1})\sin{\omega}}{a_{1}a_{2}+b_{1}b_{2}-(a_{1}b_{2}+a_{2}b_{1})\cos{\omega}}\right)\).
এখানে,
\((1)\) নং সরলরেখার ঢাল \(=-\frac{a_{1}}{b_{1}}\)
\((2)\) নং সরলরেখার ঢাল \(=-\frac{a_{2}}{b_{2}}\)
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণঃ
\(\theta=tan^{-1}\left(\pm \frac{(a_{1}b_{2}-a_{2}b_{1})\sin{\omega}}{a_{1}a_{2}+b_{1}b_{2}-(a_{1}b_{2}+a_{2}b_{1})\cos{\omega}}\right)\).
এখানে,
\((1)\) নং সরলরেখার ঢাল \(=-\frac{a_{1}}{b_{1}}\)
\((2)\) নং সরলরেখার ঢাল \(=-\frac{a_{2}}{b_{2}}\)
অনুসিদ্ধান্তঃ
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের পরস্পর সমান্তরাল হওয়ার শর্তঃ \(a_{1}b_{2}-a_{2}b_{1}=0\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের পরস্পর লম্ব হওয়ার শর্তঃ
\(a_{1}a_{2}+b_{1}b_{2}-(a_{1}b_{2}+a_{2}b_{1})\cos{\omega}=0\)
তিনটি সরলরেখার সমবিন্দু তথা এক বিন্দুতে মিলিত হওয়ার শর্ত
The condition of three straight lines meeting at a point
ধরি, সরলরেখা তিনটি ,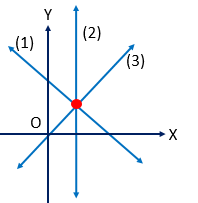
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
\((1)\) , \((2)\) , \((3)\) নং সরলরেখাত্রয় সমবিন্দু হবে যদি , \(\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|=0\) হয় ।

\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
\((1)\) , \((2)\) , \((3)\) নং সরলরেখাত্রয় সমবিন্দু হবে যদি , \(\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|=0\) হয় ।
তিনটি সরলরেখা দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
Area of triangle formed by three straight lines
ধরি,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
উপরক্ত \((1)\), \((2)\) এবং \((3)\) রেখাগুলি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
= \(\frac{1}{2} \frac{\Delta^{2}}{C_{1}C_{2}C_{3}}\)\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
উপরক্ত \((1)\), \((2)\) এবং \((3)\) রেখাগুলি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
যেখানে, \(\Delta=\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\ a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|\) এবং \(C_{1}, C_{2}, C_{3}\) হচ্ছে \(\Delta\) নির্ণায়কটির যথাক্রমে \(c_{1}, c_{2}, c_{3}\) উপাদানের সহ-গুণক।
অর্থাৎ \(C_{1}=(a_{2}b_{3}-a_{3}b_{2}),\) \(C_{2}= -(a_{1}b_{3}-a_{3}b_{1}),\) \(C_{3}=(a_{1}b_{2}-a_{2}b_{1})\)
অনুসিদ্ধান্তঃ
যদি অক্ষদ্বয় তীর্যক হয় তবে \((1)\), \((2)\) এবং \((3)\) রেখাগুলি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল= \(\frac{1}{2}\frac{\Delta^{2}\sin{\omega}}{C_{1}C_{2}C_{3}}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
লম্ব দূরত্ব
Perpendicular Distance
একটি বিন্দু হতে একটি সরলরেখার লম্ব দূরত্ব।
\((x_{1}, y_{1})\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব,
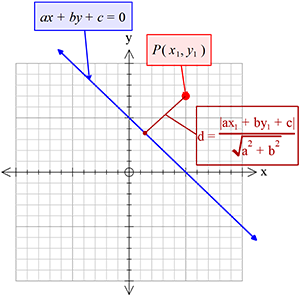
\(d=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
অনুসিদ্ধান্তঃ
তীর্যক অক্ষের সাপেক্ষে \((x_{1}, y_{1})\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব,
\(d=\frac{\left|(ax_{1}+by_{1}+c)\sin{\omega}\right|}{\sqrt{a^{2}+b^{2}-2ab\cos{\omega}}}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
\((x_{1}, y_{1})\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব,

\(d=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
অনুসিদ্ধান্তঃ
তীর্যক অক্ষের সাপেক্ষে \((x_{1}, y_{1})\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব,
\(d=\frac{\left|(ax_{1}+by_{1}+c)\sin{\omega}\right|}{\sqrt{a^{2}+b^{2}-2ab\cos{\omega}}}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
মূলবিন্দু হতে একটি সরলরেখার লম্ব দূরত্ব
Perpendicular distance of a straight line from the origin
মূলবিন্দু তথা \(O(0, 0)\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব,
\(d=\frac{\left|c \right|}{\sqrt{a^{2}+b^{2}}}\)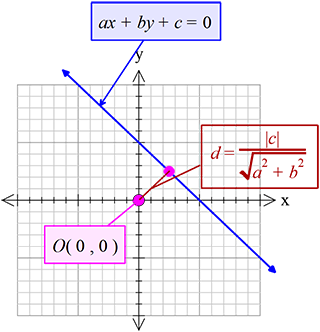
অনুসিদ্ধান্তঃ
তীর্যক অক্ষের সাপেক্ষে মূলবিন্দু তথা \(O(0, 0)\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব,
\(d=\frac{\left|c\sin{\omega}\right|}{\sqrt{a^{2}+b^{2}-2ab\cos{\omega}}}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
অনুসিদ্ধান্তঃ
মূলবিন্দু তথা \(O(0, 0)\) বিন্দু থেকে \(ax+by+c=0; \ (b>0)\) সরলরেখার ওপর অংকিত লম্বের বীজগাণিতিক দৈর্ঘ্য \(d=-\frac{c}{\sqrt{a^{2}+b^{2}}}\)
\(0>c\) হলে \(d>0;\)
অতএব লম্বটি প্রথম অথবা দ্বিতীয় চতুর্ভাগে অবস্থিত হবে যদি \(x\) এর সহগ \(a\) ধনাত্মক অথবা ঋনাত্মক হয়।
\(c>0\) হলে \(0>d;\)
কাজেই লম্বটি তৃতীয় অথবা চতুর্থ চতুর্ভাগে থাকবে যদি \(a\) ধনাত্মক অথবা ঋনাত্মক হয়।
\(d=\frac{\left|c \right|}{\sqrt{a^{2}+b^{2}}}\)

অনুসিদ্ধান্তঃ
তীর্যক অক্ষের সাপেক্ষে মূলবিন্দু তথা \(O(0, 0)\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব,
\(d=\frac{\left|c\sin{\omega}\right|}{\sqrt{a^{2}+b^{2}-2ab\cos{\omega}}}\)
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
অনুসিদ্ধান্তঃ
মূলবিন্দু তথা \(O(0, 0)\) বিন্দু থেকে \(ax+by+c=0; \ (b>0)\) সরলরেখার ওপর অংকিত লম্বের বীজগাণিতিক দৈর্ঘ্য \(d=-\frac{c}{\sqrt{a^{2}+b^{2}}}\)
\(0>c\) হলে \(d>0;\)
অতএব লম্বটি প্রথম অথবা দ্বিতীয় চতুর্ভাগে অবস্থিত হবে যদি \(x\) এর সহগ \(a\) ধনাত্মক অথবা ঋনাত্মক হয়।
\(c>0\) হলে \(0>d;\)
কাজেই লম্বটি তৃতীয় অথবা চতুর্থ চতুর্ভাগে থাকবে যদি \(a\) ধনাত্মক অথবা ঋনাত্মক হয়।
দুইটি সমান্তরাল সরলরেখার মধ্যবর্তী লম্ব দূরত্ব
Perpendicular distance between two parallel straight lines
\(ax+by+c_{1}=0\) ও \(ax+by+c_{2}=0\) সরলরেখাদ্বয়ের মধ্যবর্তী লম্ব দূরত্ব,
\(d=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)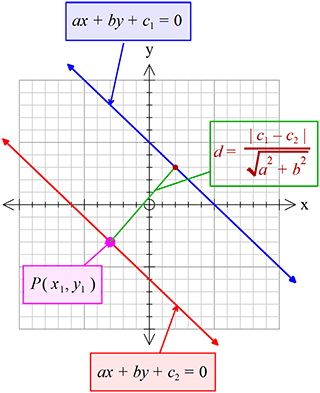
\(d=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)

দুইটি পরস্পরছেদী সরলরেখার অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ
Equation of the bisector of the angle included by two intersecting straight lines
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
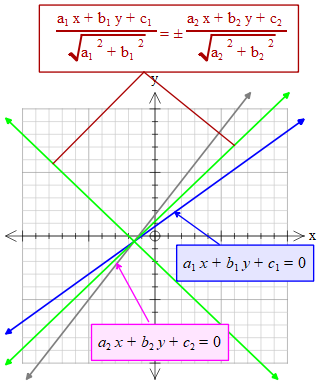
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ,
\(\frac{a_{1}x+b_{1}y+c_{1}}{\sqrt{a_1^{2}+b_1^{2}}}=\pm \frac{a_{2}x+b_{2}y+c_{2}}{\sqrt{a_2^{2}+b_2^{2}}}\).\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ,
ত্রিভুজের অন্তঃকেন্দ্র নির্ণয়
Finding incenter of a triangle
একটি ত্রিভুজের শীর্ষবিন্দু তিনটি এবং বাহুগুলির মাধ্যমে ত্রিভুজটির অন্তঃকেন্দ্র নির্ণয়।
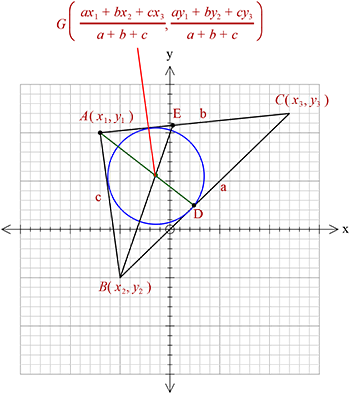
\(\triangle ABC\) এর শীর্ষবিন্দু তিনটি \((x_{1}, y_{1})\), \((x_{2}, y_{2})\) এবং \((x_{3}, y_{3})\) এবং বাহুগুলি \(BC=a, \ CA=b, \ AB=c \) হলে, এর অন্তঃকেন্দ্র,
\(I(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c})\).
কোনো সরলরেখার সমান্তরাল এবং নির্দিষ্ট একক দূরবর্তী সরলরেখার সমীকরণ
Equation of a straight line parallel to and a given unit distance from a straight line
\(ax+by+c=0\) সরলরেখার সমান্তরাল এবং \(d\) একক দূরবর্তী সরলরেখার সমীকরণ,
\(ax+by+c\pm d\sqrt{a^{2}+b^{2}}=0\).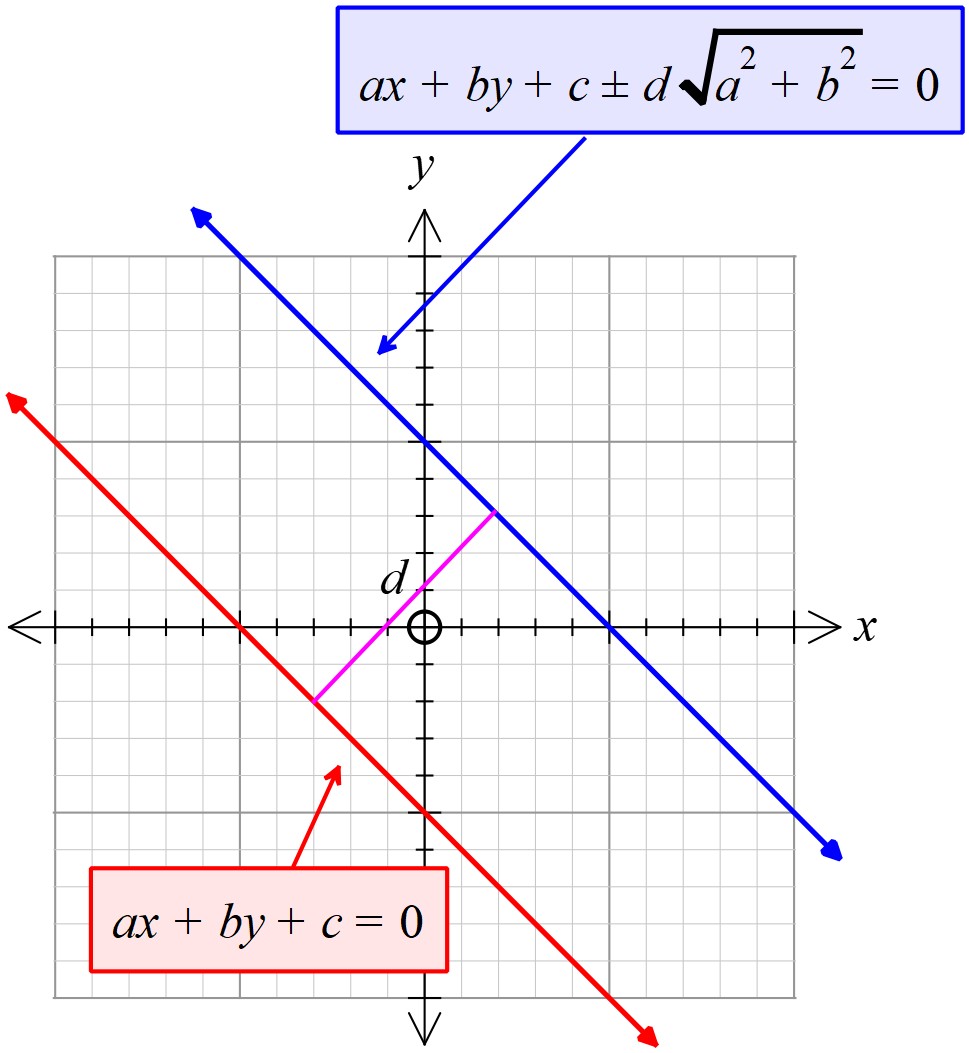
\(ax+by+c\pm d\sqrt{a^{2}+b^{2}}=0\).

অক্ষের দিক অপরিবর্তিত রেখে মূলবিন্দুর পরিবর্তন
Changing the origin while keeping the direction of the axis unchanged
অক্ষের দিক অপরিবর্তিত রেখে মূলবিন্দু \(O(0,0)\) কে \(O^{\prime}(\alpha, \beta)\) বিন্দুতে স্থানান্তর করলে, নুতন অক্ষের সাপেক্ষে
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক,
\((x^{\prime}, y^{\prime})\Rightarrow (x-\alpha, y-\beta)\) \((x, y)\Rightarrow (x^{\prime}+\alpha, y^{\prime}+\beta)\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f(x^{\prime}+\alpha, y^{\prime}+\beta)=0\)
\((x^{\prime}, y^{\prime})\Rightarrow (x-\alpha, y-\beta)\) \((x, y)\Rightarrow (x^{\prime}+\alpha, y^{\prime}+\beta)\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f(x^{\prime}+\alpha, y^{\prime}+\beta)=0\)
মূলবিন্দুর অবস্থান অপরিবর্তিত রেখে অক্ষদ্বয়কে নির্দিষ্ট কোণে আবর্তন
Rotate the two axes through a specified angle, keeping the position of the origin unchanged
মূলবিন্দুর অবস্থান অপরিবর্তিত রেখে অক্ষদ্বয়কে \(\theta\) কোণে আবর্তন করলে, নুতন অক্ষের সাপেক্ষে
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক,
\((x^{\prime}, y^{\prime})\Rightarrow (x\cos{\theta}+y\sin{\theta}, -x\sin{\theta}+y\cos{\theta})\) \((x, y)\Rightarrow (x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ,
\(f(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
\((x^{\prime}, y^{\prime})\Rightarrow (x\cos{\theta}+y\sin{\theta}, -x\sin{\theta}+y\cos{\theta})\) \((x, y)\Rightarrow (x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ,
\(f(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
মূলবিন্দুর অবস্থান পরিবর্তিত করে অক্ষদ্বয়কে নির্দিষ্ট কোণে আবর্তন
Rotate the axis by a certain angle by changing the position of the origin
অক্ষদ্বয়কে \(\theta\) কোণে আবর্তন করলে এবং মূলবিন্দু \(O(0,0)\) কে \(O^{\prime}(\alpha, \beta)\) বিন্দুতে স্থানান্তর করলে, নুতন অক্ষের সাপেক্ষে
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক,
\((x^{\prime}, y^{\prime})\Rightarrow \{(x-\alpha)\cos{\theta}+(y-\beta)\sin{\theta}, -(x-\alpha)\sin{\theta}+(y-\beta)\cos{\theta}\}\)
\((x, y)\Rightarrow \{\alpha+x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, \beta+x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\}\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ,
\(f(\alpha+x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, \beta+x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
\((x^{\prime}, y^{\prime})\Rightarrow \{(x-\alpha)\cos{\theta}+(y-\beta)\sin{\theta}, -(x-\alpha)\sin{\theta}+(y-\beta)\cos{\theta}\}\)
\((x, y)\Rightarrow \{\alpha+x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, \beta+x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\}\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ,
\(f(\alpha+x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, \beta+x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
দুই জোড়া অক্ষ সাপেক্ষে কোনো বিন্দুর রূপান্তরিত স্থানাঙ্ক
The transformed coordinates of a point with respect to two pairs of axes
যদি \(OX, \ OY\) এবং \(O^{\prime}X^{\prime}, \ O^{\prime}Y^{\prime}\) দুইজোড়া ভিন্ন ভিন্ন অক্ষ হয় এবং \(OX, \ OY\) অক্ষ সাপেক্ষে \(O^{\prime}X^{\prime},\) এবং \(O^{\prime}Y^{\prime}\) এর সমীকরণদ্বয় যথাক্রমে \(ax+by+c=0\) ও \(bx-ay+d=0\) হয় তবে, নুতন অক্ষের সাপেক্ষে
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক,
\((x^{\prime}, y^{\prime})\Rightarrow \left(\frac{bx-ay+d}{\sqrt{a^2+b^2}}, \frac{ax+by+c}{\sqrt{a^2+a^2}}\right)\) \((x, y)\Rightarrow \left(\frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}-\frac{ac+bd}{a^2+b^2}, -\frac{ax^{\prime}-by^{\prime}}{\sqrt{a^2+b^2}}-\frac{bc-ad}{a^2+b^2}\right)\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ,
\(f\left(\frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}-\frac{ac+bd}{a^2+b^2}, -\frac{ax^{\prime}-by^{\prime}}{\sqrt{a^2+b^2}}-\frac{bc-ad}{a^2+b^2}\right)=0\)
\((x^{\prime}, y^{\prime})\Rightarrow \left(\frac{bx-ay+d}{\sqrt{a^2+b^2}}, \frac{ax+by+c}{\sqrt{a^2+a^2}}\right)\) \((x, y)\Rightarrow \left(\frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}-\frac{ac+bd}{a^2+b^2}, -\frac{ax^{\prime}-by^{\prime}}{\sqrt{a^2+b^2}}-\frac{bc-ad}{a^2+b^2}\right)\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ,
\(f\left(\frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}-\frac{ac+bd}{a^2+b^2}, -\frac{ax^{\prime}-by^{\prime}}{\sqrt{a^2+b^2}}-\frac{bc-ad}{a^2+b^2}\right)=0\)
মূলবিন্দু ও \(x\) অক্ষকে স্থির রেখে তীর্যক অক্ষদ্বয়কে আয়তাকার অক্ষদ্বয়ে রূপান্তর করলে
By keeping the origin and \(x\) axis fixed, the oblique axes are converted to rectangular axes
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক,
\((x^{\prime}, y^{\prime})\Rightarrow (x+y\cos{\omega}, y\sin{\omega})\) \((x, y)\Rightarrow (x^{\prime}-y^{\prime}\cot{\omega}, y^{\prime} \ cosec \ {\omega})\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ,
\(f(x^{\prime}-y^{\prime}\cot{\omega}, y^{\prime} \ cosec{\omega})=0\)
যেখানে, \(\omega\) তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
\((x^{\prime}, y^{\prime})\Rightarrow (x+y\cos{\omega}, y\sin{\omega})\) \((x, y)\Rightarrow (x^{\prime}-y^{\prime}\cot{\omega}, y^{\prime} \ cosec \ {\omega})\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ,
\(f(x^{\prime}-y^{\prime}\cot{\omega}, y^{\prime} \ cosec{\omega})=0\)
যেখানে, \(\omega\) তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
মূলবিন্দুকে স্থির রেখে প্রদত্ত কোনো তীর্যক অক্ষদ্বয়কে অন্য তীর্যক অক্ষদ্বয়ে রূপান্তর
Transform any given oblique axis to another oblique axis while keeping the origin fixed
রূপান্তর সূত্র,
\(x=\frac{x^{\prime}\sin{(\omega-\theta)}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega-\omega^{\prime}-\theta)}}{\sin{\omega}}\) \(y=\frac{x^{\prime}\sin{\theta}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega^{\prime}+\theta)}}{\sin{\omega}}\)
যেখানে, \(\omega\) আদি তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
\(\omega^{\prime}\) নুতন তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
\(x=\frac{x^{\prime}\sin{(\omega-\theta)}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega-\omega^{\prime}-\theta)}}{\sin{\omega}}\) \(y=\frac{x^{\prime}\sin{\theta}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega^{\prime}+\theta)}}{\sin{\omega}}\)
যেখানে, \(\omega\) আদি তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
\(\omega^{\prime}\) নুতন তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
সাধারণ দ্বিঘাত সমীকরণ হতে এক ঘাত পদগুলো অপসারণ
Eliminating the linear terms from the general quadratic equation
সাধারণ দ্বিঘাত সমীকরণ হতে এক ঘাত পদগুলো অর্থাৎ \(x\) ও \(y\) সম্বলিত পদ অপসারণ
দ্রষ্টব্যঃ সমীকরণ \((1)\) থেকে এটা স্পষ্ট যে অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুকে ওপর কোনো বিন্দুতে স্থানান্তরিত করলে সাধারণ দ্বিঘাত সমীকরণের \(x^2, \ y^2, \ xy\) এর সহগগুলি অর্থাৎ \(a, \ b, \ h\) সহগগুলি অপরিবর্তিত থাকে কিন্তু \(x, \ y\) এর সহগ \(g, \ f\) এবং ধ্রুবক পদ \(c\) এরা বদলিয়ে যায়। সুতরাং রূপান্তরিত দ্বিঘাত সমীকরণটি দাঁড়ায়
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
অথবা,
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) সমীকরণ হতে এক ঘাত পদগুলো অর্থাৎ \(x\) ও \(y\) সম্বলিত পদ অপসারণ
রূপান্তরিত সমীকরণ,
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\) নুতন মূলবিন্দু
\(c^{\prime}=g\alpha+f\beta+c\) নুতন ধ্রুবক
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\) নুতন মূলবিন্দু
\(c^{\prime}=g\alpha+f\beta+c\) নুতন ধ্রুবক
অথবা
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+\frac{\Delta}{ab-h^2}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\) নুতন মূলবিন্দু
\(c^{\prime}=\frac{\Delta}{ab-h^2}\) নুতন ধ্রুবক
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+\frac{\Delta}{ab-h^2}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\) নুতন মূলবিন্দু
\(c^{\prime}=\frac{\Delta}{ab-h^2}\) নুতন ধ্রুবক
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
সাধারণ দ্বিঘাত সমীকরণ হতে \(xy\) সম্বলিত পদ অপসারণ
Eliminating \(xy\) terms from the general quadratic equation
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) সমীকরণ হতে \(xy\) সম্বলিত পদ অপসারণ
দ্রষ্টব্যঃ মূল সমীকরণ এবং রূপান্তরিত সমীকরণ উভয়ের একই ধ্রুবক পদ। অতএব, মূলবিন্দুতে আয়তাকার অক্ষদ্বয়কে কোনো কোণে ঘুরালে সমীকরণের ধ্রুবক পদ অপরিবর্তিত থেকে যায়।
রূপান্তরিত সমীকরণ,
\(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0\)
যেখানে,
\(a^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}\)
\(b^{\prime}=a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}\)
\(g^{\prime}=g\cos{\theta}+f\sin{\theta}\)
\(f^{\prime}=f\cos{\theta}-g\sin{\theta}\)
\(\theta=\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)}\)
\(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0\)
যেখানে,
\(a^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}\)
\(b^{\prime}=a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}\)
\(g^{\prime}=g\cos{\theta}+f\sin{\theta}\)
\(f^{\prime}=f\cos{\theta}-g\sin{\theta}\)
\(\theta=\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)}\)
দ্রষ্টব্যঃ মূল সমীকরণ এবং রূপান্তরিত সমীকরণ উভয়ের একই ধ্রুবক পদ। অতএব, মূলবিন্দুতে আয়তাকার অক্ষদ্বয়কে কোনো কোণে ঘুরালে সমীকরণের ধ্রুবক পদ অপরিবর্তিত থেকে যায়।
মূলবিন্দু অপরিবর্তিত রেখে আয়তাকার অক্ষদ্বয়কে নির্দিষ্ট কোণে আবর্তন
Rotate the rectangular axis through a specified angle, keeping the origin unchanged
মূলবিন্দু অপরিবর্তিত রেখে আয়তাকার অক্ষদ্বয়কে \(\frac{1}{2}\tan^{-1}\frac{2h}{a-b}\) কোণে আবর্তন করায় \(ax^2+2hxy+by^2+c=0\) সমীকরণের পরিবর্তিত রূপ \(a^{\prime}x^2+b^{\prime}y^2+c=0\) হওয়ার শর্ত,
\(a^{\prime}+b^{\prime}=a+b\)
\(a^{\prime}b^{\prime}=ab-h^2\)
মূলবিন্দু অপরিবর্তিত রেখে আয়তাকার অক্ষদ্বয়কে আবর্তন
Rotate the rectangular axis keeping the origin unchanged
মূলবিন্দু অপরিবর্তিত রেখে আয়তাকার অক্ষদ্বয়কে আবর্তন করায় \(ax^2+2hxy+by^2=0\) সমীকরণের পরিবর্তিত রূপ \(a^{\prime}x^2+2h^{\prime}xy+b^{\prime}y^2=0\) হওয়ার শর্ত,
দ্রষ্টব্যঃ এখানে, \(a+b\) এবং \(ab-h^2\) কে অপরিবর্তক বলা হয়।
\(a^{\prime}+b^{\prime}=a+b\)
\(a^{\prime}b^{\prime}-{h^{\prime}}^2=ab-h^2\)
দ্রষ্টব্যঃ এখানে, \(a+b\) এবং \(ab-h^2\) কে অপরিবর্তক বলা হয়।
×

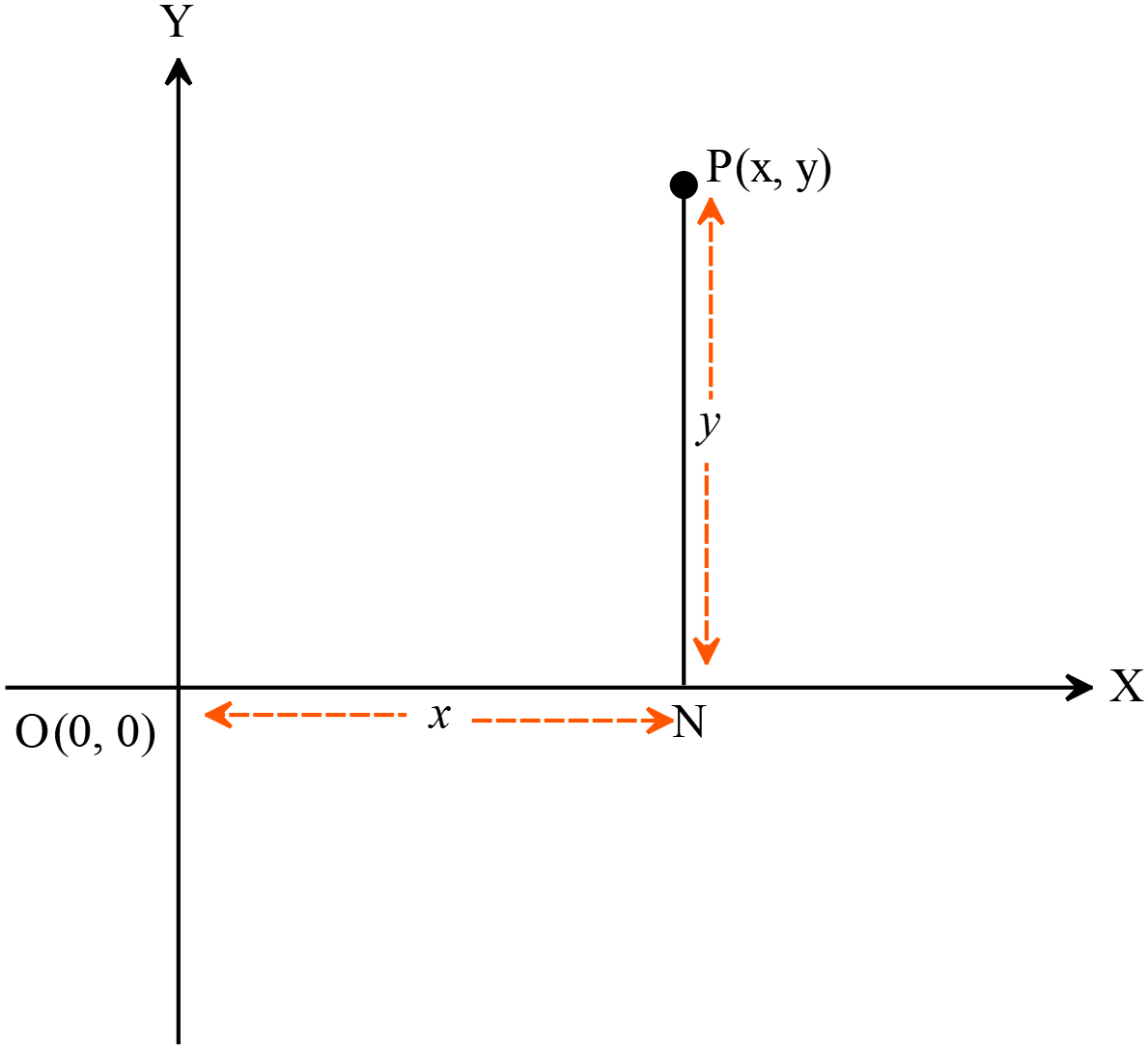
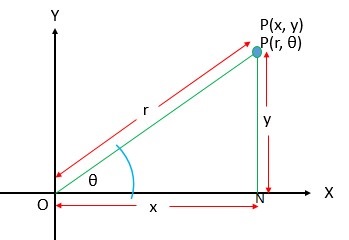
মনেকরি কোন সমতলে \(X^{\prime}OX\) ও \(Y^{\prime}OY\) সরলরেখা দুইটি পরস্পরকে O বিন্দুতে সমকোণে ছেদ করে। P বিন্দুর কার্তেসীয় স্থানাঙ্ক \((x, y)\) এবং পোলার স্থানাঙ্ক (r, \(\theta\)) যখন O মেরু ( মূলবিন্দু ) এবং \(OX\) মেরু অক্ষ (অক্ষের ধনাত্মক দিক )। O, P যোগ করি এবং \(OX\) এর উপর \(PN\) লম্ব টানি। তাহলে,
\(ON = x\), \(PN = y\), \(OP = r\) এবং \(\angle PON=\theta\). এখন,
\(x = ON\)
\(\Rightarrow x = OP\times\frac{ON}{OP}\)
\(\Rightarrow x = r\cos\theta\)
\(\therefore x = r\cos\theta\)
আবার,
\(y = PN\)
\(\Rightarrow y = OP\times\frac{PN}{OP}\)
\(\Rightarrow y = r\sin\theta\)
\(\therefore y = r\sin\theta\)
\(y = r\sin\theta\)
×

আমরা জানি,
\(x = r\cos\theta........(i)\)
\(y = r\sin\theta........(ii)\)
এখন, \((i)\) ও \((ii)\) বর্গ করে যোগ করি,
\(x^{2}+y^{2}=r^{2}\cos^{2}\theta+r^{2}\sin^{2}\theta\)\(=r^{2}(\cos^{2}\theta+\sin^{2}\theta)\)\(=r^{2}\times{1}\)\(=r^{2}\)

\(\Rightarrow x^{2}+y^{2}=r^{2}\)
\(\Rightarrow r^{2}= x^{2}+y^{2}\)
\(\therefore r=\sqrt{x^{2}+y^{2}}\)
আবার, \((ii) \div (i)\) এর সাহায্যে,
\(\frac{y}{x}=\frac{r\sin\theta}{r\cos\theta}\)
\(=\frac{\sin\theta}{\cos\theta}\)
\(=\tan\theta\)
\(\Rightarrow \tan\theta=\frac{y}{x}\)
\(\therefore \theta=tan^{-1}\frac{y}{x}\)
\(r=\sqrt{x^{2}+y^{2}}\)
\(\theta=tan^{-1}\frac{y}{x}\)
×
কার্তেসীয় স্থানাঙ্কে দূরত্ব নির্ণয়
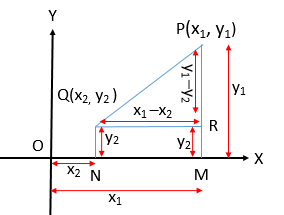
মনে করি,
\(P(x_{1}, y_{1})\) ও \(Q(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু।
\(P\) এবং \(Q\) হতে \(OX\) এর উপর যথাক্রমে \(PM\) এবং \(QN\) লম্ব অংকন করি।
তাহলে, \(OM=x_{1}\), \(PM=y_{1}\), \(ON=x_{2}\), \(QN=y_{2}\). আবার,
\(QR=NM=OM-ON=x_{1}-x_{2}\).
\(PR=PM-RM=y_{1}-y_{2}\).
\(PQR\) সমকোণী ত্রীভুজ হতে পাই,
\(PQ^{2}=QR^{2}+PR^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}\)
\(\Rightarrow PQ^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}\)
\(\therefore PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\) ➜ \(\because\) দূরত্ব সর্বদা ধনাত্মক।


মনে করি,
\(P(x_{1}, y_{1})\) ও \(Q(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু।
\(P\) এবং \(Q\) হতে \(OX\) এর উপর যথাক্রমে \(PM\) এবং \(QN\) লম্ব অংকন করি।
তাহলে, \(OM=x_{1}\), \(PM=y_{1}\), \(ON=x_{2}\), \(QN=y_{2}\). আবার,
\(QR=NM=OM-ON=x_{1}-x_{2}\).
\(PR=PM-RM=y_{1}-y_{2}\).
\(PQR\) সমকোণী ত্রীভুজ হতে পাই,
\(PQ^{2}=QR^{2}+PR^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}\)
\(\Rightarrow PQ^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}\)
\(\therefore PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\) ➜ \(\because\) দূরত্ব সর্বদা ধনাত্মক।

ভেক্টর পদ্ধতিতে দূরত্ব নির্ণয়
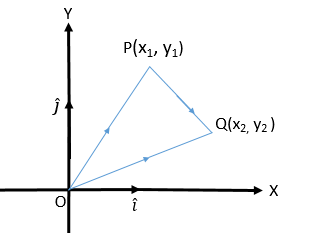
মনে করি,
\(P(x_{1}, y_{1})\) ও \(Q(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু। মূলবিন্দু বা \(O\) বিন্দুর সাপেক্ষে বিন্দুদ্বয়ের অবস্থান ভেক্টর যথাক্রমে \(\overline{OP}=x_{1}\hat{i}+y_{1}\hat{j}\) এবং \(\overline{OQ}=x_{2}\hat{i}+y_{2}\hat{j}\)।
\(\triangle OPQ\) হতে পাই,
\(\overline{PQ}=\overline{OQ}-\overline{OP}\)
\(=x_{2}\hat{i}+y_{2}\hat{j}-x_{1}\hat{i}-y_{1}\hat{j}\)
\(=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}\)
\(P(x_{1}, y_{1})\) ও \(P(x_{2}, y_{2})\) বিন্দুর দূরত্ব \(\overline{\mid PQ \mid}\)
\(=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\)
\(=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
উদাহরণঃ \(P(1, 2)\) ও \(Q(-2, 6)\) বিন্দু দ্বয়ের দূরত্ব
\(=\sqrt{(1+2)^{2}+(2-6)^{2}}\)
\(=\sqrt{3^{2}+4^{2}}\) \(=\sqrt{9+19}\)
\(=\sqrt{25}\)
\(=5\)।

মনে করি,
\(P(x_{1}, y_{1})\) ও \(Q(x_{2}, y_{2})\) যে কোন দুইটি বিন্দু। মূলবিন্দু বা \(O\) বিন্দুর সাপেক্ষে বিন্দুদ্বয়ের অবস্থান ভেক্টর যথাক্রমে \(\overline{OP}=x_{1}\hat{i}+y_{1}\hat{j}\) এবং \(\overline{OQ}=x_{2}\hat{i}+y_{2}\hat{j}\)।
\(\triangle OPQ\) হতে পাই,
\(\overline{PQ}=\overline{OQ}-\overline{OP}\)
\(=x_{2}\hat{i}+y_{2}\hat{j}-x_{1}\hat{i}-y_{1}\hat{j}\)
\(=(x_{2}-x_{1})\hat{i}+(y_{2}-y_{1})\hat{j}\)
\(P(x_{1}, y_{1})\) ও \(P(x_{2}, y_{2})\) বিন্দুর দূরত্ব \(\overline{\mid PQ \mid}\)
\(=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\)
\(=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
উদাহরণঃ \(P(1, 2)\) ও \(Q(-2, 6)\) বিন্দু দ্বয়ের দূরত্ব
\(=\sqrt{(1+2)^{2}+(2-6)^{2}}\)
\(=\sqrt{3^{2}+4^{2}}\) \(=\sqrt{9+19}\)
\(=\sqrt{25}\)
\(=5\)।
×
পোলার স্থানাঙ্কে দূরত্ব নির্ণয়
মনে করি,
কোন সমতলের উপর \(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব নির্ণয় করতে হবে।
\(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) বিন্দুদ্বয়ের কার্তেসীয় স্থানাঙ্ক যথাক্রমে \(P(r_{1}\cos\theta_{1}, r_{1}\sin\theta_{1})\) ও \(Q(r_{2}\cos\theta_{2}, r_{2}\sin\theta_{2})\)
\(\therefore PQ=\sqrt{(r_{1}\cos\theta_{1}-r_{2}\cos\theta_{2})^{2}+(r_{1}\sin\theta_{1}-r_{2}\sin\theta_{2})^{2}}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}\cos^{2}\theta_{1}-2r_{1}r_{2}\cos\theta_{1}\cos\theta_{2}+r_{2}^{2}\cos^{2}\theta_{2}+r_{1}^{2}\sin^{2}\theta_{1}-2r_{1}r_{2}\sin\theta_{1}\sin\theta_{2}+r_{2}^{2}\sin^{2}\theta_{2}}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}(\cos^{2}\theta_{1}+\sin^{2}\theta_{1})+r_{2}^{2}(\cos^{2}\theta_{2}+\sin^{2}\theta_{2})-2r_{1}r_{2}(\cos\theta_{1}\cos\theta_{2}+\sin\theta_{1}\sin\theta_{2})}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}\times 1+r_{2}^{2}\times 1-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
পোলার স্থানাঙ্কে দূরত্বঃ \(PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)মনে করি,
কোন সমতলের উপর \(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) যে কোন দুইটি বিন্দু এদের মধ্যবর্তী দূরত্ব নির্ণয় করতে হবে।
\(P(r_{1}, \theta_{1})\) ও \(Q(r_{2}, \theta_{2})\) বিন্দুদ্বয়ের কার্তেসীয় স্থানাঙ্ক যথাক্রমে \(P(r_{1}\cos\theta_{1}, r_{1}\sin\theta_{1})\) ও \(Q(r_{2}\cos\theta_{2}, r_{2}\sin\theta_{2})\)
\(\therefore PQ=\sqrt{(r_{1}\cos\theta_{1}-r_{2}\cos\theta_{2})^{2}+(r_{1}\sin\theta_{1}-r_{2}\sin\theta_{2})^{2}}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}\cos^{2}\theta_{1}-2r_{1}r_{2}\cos\theta_{1}\cos\theta_{2}+r_{2}^{2}\cos^{2}\theta_{2}+r_{1}^{2}\sin^{2}\theta_{1}-2r_{1}r_{2}\sin\theta_{1}\sin\theta_{2}+r_{2}^{2}\sin^{2}\theta_{2}}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}(\cos^{2}\theta_{1}+\sin^{2}\theta_{1})+r_{2}^{2}(\cos^{2}\theta_{2}+\sin^{2}\theta_{2})-2r_{1}r_{2}(\cos\theta_{1}\cos\theta_{2}+\sin\theta_{1}\sin\theta_{2})}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}\times 1+r_{2}^{2}\times 1-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
\(\Rightarrow PQ=\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos(\theta_{1}-\theta_{2})}\)
×
অন্তর্বিভক্তিকরণ সূত্র নির্ণয়
মনে করি, \(XY\) সমতলে \(P(x_{1}, y_{1})\) এবং \(Q(x_{2}, y_{2})\) দুইটি নির্দিষ্ট বিন্দু। \(P\), \(Q\) যোগ করি। \(R(x, y)\) বিন্দু \(PQ\) রেখাংশকে এরূপভাবে অন্তর্বিভক্ত করেছে যে, \(PR:RQ=m:n\).
\(P, Q, R\) হতে \(OX\) এর উপর যথাক্রমে \(PM\), \(QN\) ও \(RS\) লম্ব টানি। আবার \(P\) হতে \(RS\) এর উপর \(PL\) এবং \(R\) হতে \(QN\) এর উপর \(RT\) লম্ব টানি।
স্পষ্টতঃ \(\ OM=x_{1}, \ OS=x, \ ON=x_{2}\) এবং \( \ PM=y_{1}, \ RS=y, \ QN=y_{2}, \ PR=m, \ RQ=n\)
এখন,
\(\ PL=MS=OS-OM=x-x_{1}\)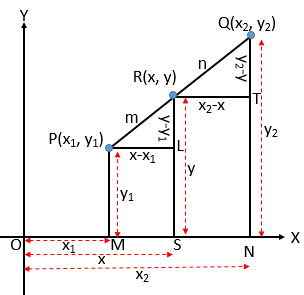
\(\ RT=SN=ON-OS=x_{2}-x\)
\(\ RL=RS-SL=RS-PM=y-y_{1}\) ➜ \(\because SL=PM\)
\(\ QT=QN-TN=QN-RS=y_{2}-y\) ➜ \(\because TN=RS\)
এখন, \(QTR\) ও \(RLP\) সদৃশ ত্রিভুজ সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক। হতে পাই,
\(\frac{PL}{RT}=\frac{RL}{QT}=\frac{PR}{RQ}=\frac{m}{n}\)
\(\Rightarrow \frac{PL}{RT}=\frac{m}{n}\)
\(\Rightarrow \frac{x-x_{1}}{x_{2}-x}=\frac{m}{n}\)
\(\Rightarrow nx-nx_{1}=mx_{2}-mx\)
\(\Rightarrow mx+nx=mx_{2}+nx_{1}\)
\(\Rightarrow x(m+n)=mx_{2}+nx_{1}\)
\(\therefore x=\frac{mx_{2}+nx_{1}}{(m+n)}\)
আবার,
\(\Rightarrow \frac{RL}{QT}=\frac{m}{n}\)
\(\Rightarrow \frac{y-y_{1}}{y_{2}-y}=\frac{m}{n}\)
\(\Rightarrow ny-ny_{1}=my_{2}-my\)
\(\Rightarrow my+ny=my_{2}+ny_{1}\)
\(\Rightarrow y(m+n)=my_{2}+ny_{1}\)
\(\therefore y=\frac{my_{2}+ny_{1}}{(m+n)}\)
\(\therefore R\) বিন্দুর স্থানাঙ্ক,\((\frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n})\)
মনে করি, \(XY\) সমতলে \(P(x_{1}, y_{1})\) এবং \(Q(x_{2}, y_{2})\) দুইটি নির্দিষ্ট বিন্দু। \(P\), \(Q\) যোগ করি। \(R(x, y)\) বিন্দু \(PQ\) রেখাংশকে এরূপভাবে অন্তর্বিভক্ত করেছে যে, \(PR:RQ=m:n\).
\(P, Q, R\) হতে \(OX\) এর উপর যথাক্রমে \(PM\), \(QN\) ও \(RS\) লম্ব টানি। আবার \(P\) হতে \(RS\) এর উপর \(PL\) এবং \(R\) হতে \(QN\) এর উপর \(RT\) লম্ব টানি।
স্পষ্টতঃ \(\ OM=x_{1}, \ OS=x, \ ON=x_{2}\) এবং \( \ PM=y_{1}, \ RS=y, \ QN=y_{2}, \ PR=m, \ RQ=n\)
এখন,
\(\ PL=MS=OS-OM=x-x_{1}\)

\(\ RT=SN=ON-OS=x_{2}-x\)
\(\ RL=RS-SL=RS-PM=y-y_{1}\) ➜ \(\because SL=PM\)
\(\ QT=QN-TN=QN-RS=y_{2}-y\) ➜ \(\because TN=RS\)
এখন, \(QTR\) ও \(RLP\) সদৃশ ত্রিভুজ সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক। হতে পাই,
\(\frac{PL}{RT}=\frac{RL}{QT}=\frac{PR}{RQ}=\frac{m}{n}\)
\(\Rightarrow \frac{PL}{RT}=\frac{m}{n}\)
\(\Rightarrow \frac{x-x_{1}}{x_{2}-x}=\frac{m}{n}\)
\(\Rightarrow nx-nx_{1}=mx_{2}-mx\)
\(\Rightarrow mx+nx=mx_{2}+nx_{1}\)
\(\Rightarrow x(m+n)=mx_{2}+nx_{1}\)
\(\therefore x=\frac{mx_{2}+nx_{1}}{(m+n)}\)
আবার,
\(\Rightarrow \frac{RL}{QT}=\frac{m}{n}\)
\(\Rightarrow \frac{y-y_{1}}{y_{2}-y}=\frac{m}{n}\)
\(\Rightarrow ny-ny_{1}=my_{2}-my\)
\(\Rightarrow my+ny=my_{2}+ny_{1}\)
\(\Rightarrow y(m+n)=my_{2}+ny_{1}\)
\(\therefore y=\frac{my_{2}+ny_{1}}{(m+n)}\)
\(\therefore R\) বিন্দুর স্থানাঙ্ক,\((\frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n})\)
×
বহির্বিভক্তিকরণ সূত্র নির্ণয়
মনে করি, \(XY\) সমতলে \(P(x_{1}, y_{1})\) এবং \(Q(x_{2}, y_{2})\) দুইটি নির্দিষ্ট বিন্দু। \(P\), \(Q\) যোগ করে বর্ধিত করি। ধরি, \(PQ\) এর বর্ধিতাংশের উপর \(R(x, y)\) এমন একটি বিন্দু যেন, \(PR:RQ=m:n\).
অর্থাৎ \(R(x, y)\) বিন্দু \(PQ\) কে \(m:n\) অনুপাতে বহির্বিভক্ত করে।
\(P, Q, R\) হতে \(OX\) এর উপর যথাক্রমে \(PM\), \(QN\) ও \(RS\) লম্ব টানি। আবার \(P\) হতে \(RS\) এর উপর \(PL\) এবং \(Q\) হতে \(RS\) এর উপর \(QT\) লম্ব টানি।
স্পষ্টতঃ \(\ OM=x_{1}, \ OS=x, \ ON=x_{2}\) এবং \( \ PM=y_{1}, \ RS=y, \ QN=y_{2}, \ PR=m, \ RQ=n\)
\(\ PL=MS=OS-OM=x-x_{1}\)
\(\ QT=NS=OS-ON=x-x_{2}\)
\(\ RL=RS-LS=RS-PM=y-y_{1}\) ➜ \(\because SL=PM\)
\(\ RT=RS-TS=RS-QN=y-y_{2}\) ➜ \(\because TS=QN\)
এখন, \(RLP\) ও \(RTQ\) সদৃশ ত্রিভুজ সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক। হতে পাই,
\(\frac{PL}{QT}=\frac{RL}{RT}=\frac{PR}{RQ}=\frac{m}{n}\)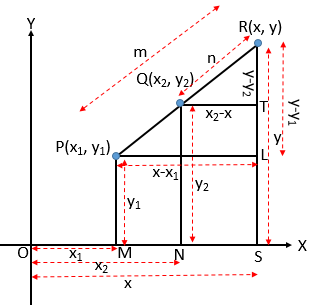
\(\Rightarrow \frac{PL}{QT}=\frac{m}{n}\)
\(\Rightarrow \frac{x-x_{1}}{x-x_{2}}=\frac{m}{n}\)
\(\Rightarrow nx-nx_{1}=mx-mx_{2}\)
\(\Rightarrow mx-mx_{2}=nx-nx_{1}\)
\(\Rightarrow mx-nx=mx_{2}-nx_{1}\)
\(\Rightarrow x(m-n)=mx_{2}-nx_{1}\)
\(\therefore x=\frac{mx_{2}-nx_{1}}{(m-n)}\)
আবার,
\(\Rightarrow \frac{RL}{RT}=\frac{m}{n}\)
\(\Rightarrow \frac{y-y_{1}}{y-y_{2}}=\frac{m}{n}\)
\(\Rightarrow ny-ny_{1}=my-my_{2}\)
\(\Rightarrow my-my_{2}=ny-ny_{1}\)
\(\Rightarrow my-ny=my_{2}-ny_{1}\)
\(\Rightarrow y(m-n)=my_{2}-ny_{1}\)
\(\therefore y=\frac{my_{2}-ny_{1}}{(m-n)}\)
\(\therefore R\) বিন্দুর স্থানাঙ্ক,\((\frac{mx_{2}-nx_{1}}{m-n}, \frac{my_{2}-ny_{1}}{m-n})\)
মনে করি, \(XY\) সমতলে \(P(x_{1}, y_{1})\) এবং \(Q(x_{2}, y_{2})\) দুইটি নির্দিষ্ট বিন্দু। \(P\), \(Q\) যোগ করে বর্ধিত করি। ধরি, \(PQ\) এর বর্ধিতাংশের উপর \(R(x, y)\) এমন একটি বিন্দু যেন, \(PR:RQ=m:n\).
অর্থাৎ \(R(x, y)\) বিন্দু \(PQ\) কে \(m:n\) অনুপাতে বহির্বিভক্ত করে।
\(P, Q, R\) হতে \(OX\) এর উপর যথাক্রমে \(PM\), \(QN\) ও \(RS\) লম্ব টানি। আবার \(P\) হতে \(RS\) এর উপর \(PL\) এবং \(Q\) হতে \(RS\) এর উপর \(QT\) লম্ব টানি।
স্পষ্টতঃ \(\ OM=x_{1}, \ OS=x, \ ON=x_{2}\) এবং \( \ PM=y_{1}, \ RS=y, \ QN=y_{2}, \ PR=m, \ RQ=n\)
\(\ PL=MS=OS-OM=x-x_{1}\)
\(\ QT=NS=OS-ON=x-x_{2}\)
\(\ RL=RS-LS=RS-PM=y-y_{1}\) ➜ \(\because SL=PM\)
\(\ RT=RS-TS=RS-QN=y-y_{2}\) ➜ \(\because TS=QN\)
এখন, \(RLP\) ও \(RTQ\) সদৃশ ত্রিভুজ সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক। হতে পাই,
\(\frac{PL}{QT}=\frac{RL}{RT}=\frac{PR}{RQ}=\frac{m}{n}\)

\(\Rightarrow \frac{PL}{QT}=\frac{m}{n}\)
\(\Rightarrow \frac{x-x_{1}}{x-x_{2}}=\frac{m}{n}\)
\(\Rightarrow nx-nx_{1}=mx-mx_{2}\)
\(\Rightarrow mx-mx_{2}=nx-nx_{1}\)
\(\Rightarrow mx-nx=mx_{2}-nx_{1}\)
\(\Rightarrow x(m-n)=mx_{2}-nx_{1}\)
\(\therefore x=\frac{mx_{2}-nx_{1}}{(m-n)}\)
আবার,
\(\Rightarrow \frac{RL}{RT}=\frac{m}{n}\)
\(\Rightarrow \frac{y-y_{1}}{y-y_{2}}=\frac{m}{n}\)
\(\Rightarrow ny-ny_{1}=my-my_{2}\)
\(\Rightarrow my-my_{2}=ny-ny_{1}\)
\(\Rightarrow my-ny=my_{2}-ny_{1}\)
\(\Rightarrow y(m-n)=my_{2}-ny_{1}\)
\(\therefore y=\frac{my_{2}-ny_{1}}{(m-n)}\)
\(\therefore R\) বিন্দুর স্থানাঙ্ক,\((\frac{mx_{2}-nx_{1}}{m-n}, \frac{my_{2}-ny_{1}}{m-n})\)
×
মধ্যবিন্দুর সূত্র নির্ণয়
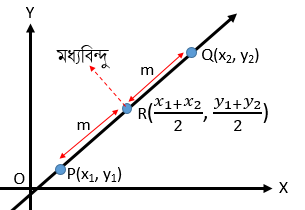
মনে করি,
\(XY\) সমতলে \(P(x_{1}, y_{1})\) এবং \(Q(x_{2}, y_{2})\) দুইটি নির্দিষ্ট বিন্দু \(R(x, y)\) বিন্দু \(PQ\) এর মধ্যবিন্দু হলে, \(m=n\) হবে। সে ক্ষেত্রে \(R\) বিন্দুর স্থানাঙ্ক, \(R(\frac{mx_{2}+mx_{1}}{m+m}, \frac{my_{2}+my_{1}}{m+m})\)
\(\Rightarrow R(\frac{m(x_{2}+x_{1})}{2m}, \frac{m(y_{2}+y_{1})}{2m})\)
\(\Rightarrow R(\frac{x_{2}+x_{1}}{2}, \frac{y_{2}+y_{1}}{2})\)
\(\Rightarrow R(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2})\)
\(\therefore \) মধ্যবিন্দুর স্থানাঙ্ক \(R(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2})\)

মনে করি,
\(XY\) সমতলে \(P(x_{1}, y_{1})\) এবং \(Q(x_{2}, y_{2})\) দুইটি নির্দিষ্ট বিন্দু \(R(x, y)\) বিন্দু \(PQ\) এর মধ্যবিন্দু হলে, \(m=n\) হবে। সে ক্ষেত্রে \(R\) বিন্দুর স্থানাঙ্ক, \(R(\frac{mx_{2}+mx_{1}}{m+m}, \frac{my_{2}+my_{1}}{m+m})\)
\(\Rightarrow R(\frac{m(x_{2}+x_{1})}{2m}, \frac{m(y_{2}+y_{1})}{2m})\)
\(\Rightarrow R(\frac{x_{2}+x_{1}}{2}, \frac{y_{2}+y_{1}}{2})\)
\(\Rightarrow R(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2})\)
\(\therefore \) মধ্যবিন্দুর স্থানাঙ্ক \(R(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2})\)
×
ত্রিভুজের ভরকেন্দ্র নির্ণয়
মনে করি, কোন সমতলে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\) এবং \(C(x_{3}, y_{3})\) কোন ত্রিভুজের তিনটি শীর্ষবিন্দু, \(\triangle ABC\) এর ভরকেন্দ্রের \(G\).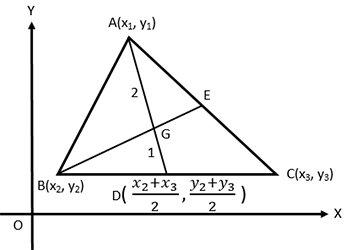
\(BC\) এর মধ্যবিন্দু \(D\), তাহলে \(AD\) হবে একটি মধ্যমা। \(AD\) এর উপর ভরকেন্দ্র \(G\) অবস্থান করবে। অর্থাৎ মধ্যমাগুলির ছেদবিন্দুই হবে ত্রিভুজের ভরকেন্দ্র।
ধরি, \(G(x, y)\).
এখন,
\(D\), \(BC\) এর মধ্যবিন্দু \(\therefore D(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2})\).
আবার,
\(AG:GD=2:1\) ➜ ত্রিভুজের মধ্যমাগুলি পরস্পরকে \(2:1\) অনপাতে অন্তর্বিভক্ত করে।
\(\therefore G(\frac{2\times \frac{x_{2}+x_{3}}{2}+1\times x_{1}}{2+1}, \frac{2\times \frac{y_{2}+y_{3}}{2}+1\times y_{1}}{2+1})\).
\(\Rightarrow G(\frac{x_{2}+x_{3}+x_{1}}{3}, \frac{y_{2}+y_{3}+y_{1}}{3})\).
\(\therefore G(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3})\).
\(\therefore \) \(\triangle ABC\) এর ভরকেন্দ্রের স্থানাঙ্ক \((\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3})\).
মনে করি, কোন সমতলে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\) এবং \(C(x_{3}, y_{3})\) কোন ত্রিভুজের তিনটি শীর্ষবিন্দু, \(\triangle ABC\) এর ভরকেন্দ্রের \(G\).

\(BC\) এর মধ্যবিন্দু \(D\), তাহলে \(AD\) হবে একটি মধ্যমা। \(AD\) এর উপর ভরকেন্দ্র \(G\) অবস্থান করবে। অর্থাৎ মধ্যমাগুলির ছেদবিন্দুই হবে ত্রিভুজের ভরকেন্দ্র।
ধরি, \(G(x, y)\).
এখন,
\(D\), \(BC\) এর মধ্যবিন্দু \(\therefore D(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2})\).
আবার,
\(AG:GD=2:1\) ➜ ত্রিভুজের মধ্যমাগুলি পরস্পরকে \(2:1\) অনপাতে অন্তর্বিভক্ত করে।
\(\therefore G(\frac{2\times \frac{x_{2}+x_{3}}{2}+1\times x_{1}}{2+1}, \frac{2\times \frac{y_{2}+y_{3}}{2}+1\times y_{1}}{2+1})\).
\(\Rightarrow G(\frac{x_{2}+x_{3}+x_{1}}{3}, \frac{y_{2}+y_{3}+y_{1}}{3})\).
\(\therefore G(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3})\).
\(\therefore \) \(\triangle ABC\) এর ভরকেন্দ্রের স্থানাঙ্ক \((\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3})\).
×
ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র নির্ণয়
মনে করি, কোন সমতলে \(\) ত্রিভুজের শীর্ষত্রয় যথক্রমে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\) এবং \(C(x_{3}, y_{3})\)। \(A, B, C\) বিন্দু হতে \(X\) অক্ষের উপর যথাক্রমে \(AL\), \(BM\) এবং \(CN\) লম্ব আঁকি।
তাহলে, \(OL=x_{1}\)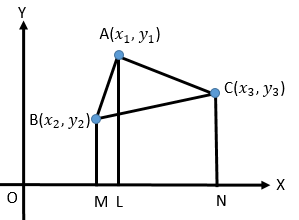
\(OM=x_{2}\)
\(ON=x_{3}\)
\(AL=y_{1}\)
\(BM=y_{2}\)
\(CN=y_{3}\).
আবার,
\(ML=OL-OM=x_{1}-x_{2}\)
\(LN=ON-OL=x_{3}-x_{1}\)
\(MN=ON-OM=x_{3}-x_{2}\).
এখন,
\(\triangle ABC=\) ট্রাপিজিয়াম \(ABML\) এর ক্ষেত্রফল + ট্রাপিজিয়াম \(ALNC\) এর ক্ষেত্রফল -ট্রাপিজিয়াম \(MBNC\) এর ক্ষেত্রফল।
\(=\frac{1}{2}(AL+BM)\times ML+\frac{1}{2}(AL+CN)\times LN-\frac{1}{2}(BM+CN)\times MN\)
\(=\frac{1}{2}(y_{1}+y_{2})\times (x_{1}-x_{2})+\frac{1}{2}(y_{1}+y_{3})\times (x_{3}-x_{1})-\frac{1}{2}(y_{2}+y_{3})\times (x_{3}-x_{2})\)
\(=\frac{1}{2}\{(y_{1}+y_{2})(x_{1}-x_{2})+(y_{1}+y_{3})(x_{3}-x_{1})-(y_{2}+y_{3})(x_{3}-x_{2})\}\)
\(=\frac{1}{2}\{x_{1}y_{1}+x_{1}y_{2}-x_{2}y_{1}-x_{2}y_{2}+x_{3}y_{1}+x_{3}y_{3}-x_{1}y_{1}-x_{1}y_{3}-(x_{3}y_{2}+x_{3}y_{3}-x_{2}y_{2}-x_{2}y_{3})\}\)
\(=\frac{1}{2}\{x_{1}y_{1}+x_{1}y_{2}-x_{2}y_{1}-x_{2}y_{2}+x_{3}y_{1}+x_{3}y_{3}-x_{1}y_{1}-x_{1}y_{3}-x_{3}y_{2}-x_{3}y_{3}+x_{2}y_{2}+x_{2}y_{3}\}\)
\(=\frac{1}{2}\{x_{1}y_{2}-x_{2}y_{1}+x_{3}y_{1}-x_{1}y_{3}-x_{3}y_{2}+x_{2}y_{3}\}\)
\(=\frac{1}{2}\{(x_{1}y_{2}-x_{2}y_{1})+(x_{2}y_{3}-x_{3}y_{2})+(x_{3}y_{1}-x_{1}y_{3})\}\)
\(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{1}\\ y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{1}\end{array}\right|\)
আবার,
\(\triangle ABC=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{1}\\ y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{1}\end{array}\right|\)
\(=\frac{1}{2}\{(x_{1}y_{2}-x_{2}y_{1})+(x_{2}y_{3}-x_{3}y_{2})+(x_{3}y_{1}-x_{1}y_{3})\}\)
\(=\frac{1}{2}\{x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})+1(x_{2}y_{3}-x_{3}y_{2})\}\)
\(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ 1\\x_{2} \ \ y_{2} \ \ 1\\x_{3} \ \ y_{3} \ \ 1\end{array}\right|\)
\(\therefore \triangle ABC=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ 1\\x_{2} \ \ y_{2} \ \ 1\\x_{3} \ \ y_{3} \ \ 1\end{array}\right|\)
আবার,
\(\triangle ABC=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{1}\\ y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{1}\end{array}\right|\)
\(=\frac{1}{2}\{(x_{1}y_{2}-x_{2}y_{1})+(x_{2}y_{3}-x_{3}y_{2})+(x_{3}y_{1}-x_{1}y_{3})\}\)
\(=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)
\(\therefore \triangle ABC=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)
মনে করি, কোন সমতলে \(\) ত্রিভুজের শীর্ষত্রয় যথক্রমে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\) এবং \(C(x_{3}, y_{3})\)। \(A, B, C\) বিন্দু হতে \(X\) অক্ষের উপর যথাক্রমে \(AL\), \(BM\) এবং \(CN\) লম্ব আঁকি।
তাহলে, \(OL=x_{1}\)

\(OM=x_{2}\)
\(ON=x_{3}\)
\(AL=y_{1}\)
\(BM=y_{2}\)
\(CN=y_{3}\).
আবার,
\(ML=OL-OM=x_{1}-x_{2}\)
\(LN=ON-OL=x_{3}-x_{1}\)
\(MN=ON-OM=x_{3}-x_{2}\).
এখন,
\(\triangle ABC=\) ট্রাপিজিয়াম \(ABML\) এর ক্ষেত্রফল + ট্রাপিজিয়াম \(ALNC\) এর ক্ষেত্রফল -ট্রাপিজিয়াম \(MBNC\) এর ক্ষেত্রফল।
\(=\frac{1}{2}(AL+BM)\times ML+\frac{1}{2}(AL+CN)\times LN-\frac{1}{2}(BM+CN)\times MN\)
\(=\frac{1}{2}(y_{1}+y_{2})\times (x_{1}-x_{2})+\frac{1}{2}(y_{1}+y_{3})\times (x_{3}-x_{1})-\frac{1}{2}(y_{2}+y_{3})\times (x_{3}-x_{2})\)
\(=\frac{1}{2}\{(y_{1}+y_{2})(x_{1}-x_{2})+(y_{1}+y_{3})(x_{3}-x_{1})-(y_{2}+y_{3})(x_{3}-x_{2})\}\)
\(=\frac{1}{2}\{x_{1}y_{1}+x_{1}y_{2}-x_{2}y_{1}-x_{2}y_{2}+x_{3}y_{1}+x_{3}y_{3}-x_{1}y_{1}-x_{1}y_{3}-(x_{3}y_{2}+x_{3}y_{3}-x_{2}y_{2}-x_{2}y_{3})\}\)
\(=\frac{1}{2}\{x_{1}y_{1}+x_{1}y_{2}-x_{2}y_{1}-x_{2}y_{2}+x_{3}y_{1}+x_{3}y_{3}-x_{1}y_{1}-x_{1}y_{3}-x_{3}y_{2}-x_{3}y_{3}+x_{2}y_{2}+x_{2}y_{3}\}\)
\(=\frac{1}{2}\{x_{1}y_{2}-x_{2}y_{1}+x_{3}y_{1}-x_{1}y_{3}-x_{3}y_{2}+x_{2}y_{3}\}\)
\(=\frac{1}{2}\{(x_{1}y_{2}-x_{2}y_{1})+(x_{2}y_{3}-x_{3}y_{2})+(x_{3}y_{1}-x_{1}y_{3})\}\)
\(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{1}\\ y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{1}\end{array}\right|\)
আবার,
\(\triangle ABC=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{1}\\ y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{1}\end{array}\right|\)
\(=\frac{1}{2}\{(x_{1}y_{2}-x_{2}y_{1})+(x_{2}y_{3}-x_{3}y_{2})+(x_{3}y_{1}-x_{1}y_{3})\}\)
\(=\frac{1}{2}\{x_{1}(y_{2}-y_{3})-y_{1}(x_{2}-x_{3})+1(x_{2}y_{3}-x_{3}y_{2})\}\)
\(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ 1\\x_{2} \ \ y_{2} \ \ 1\\x_{3} \ \ y_{3} \ \ 1\end{array}\right|\)
\(\therefore \triangle ABC=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ 1\\x_{2} \ \ y_{2} \ \ 1\\x_{3} \ \ y_{3} \ \ 1\end{array}\right|\)
আবার,
\(\triangle ABC=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{1}\\ y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{1}\end{array}\right|\)
\(=\frac{1}{2}\{(x_{1}y_{2}-x_{2}y_{1})+(x_{2}y_{3}-x_{3}y_{2})+(x_{3}y_{1}-x_{1}y_{3})\}\)
\(=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)
\(\therefore \triangle ABC=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)
×
চতুর্ভুজের ক্ষেত্রফল নির্ণয়ের সূত্র নির্ণয়
মনে করি, কোন সমতলে \(ABCD\) চতুর্ভুজের শীর্ষচতুষ্টয় যথক্রমে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\), \(C(x_{3}, y_{3})\) এবং \(D(x_{3}, y_{3})\)। ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র ব্যাবহার করে।
\(\Box ABCD=\triangle ABC+\triangle ACD\)
\(=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)+\(\frac{1}{2}\{(x_{1}y_{3}+x_{3}y_{4}+x_{4}y_{1})-(y_{1}x_{3}+y_{3}x_{4}+y_{4}x_{1})\}\)
\(=\frac{1}{2}\{x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-y_{1}x_{2}-y_{2}x_{3}-y_{3}x_{1}+x_{1}y_{3}+x_{3}y_{4}+x_{4}y_{1}-y_{1}x_{3}-y_{3}x_{4}-y_{4}x_{1}\}\)
\(=\frac{1}{2}\{x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1}-y_{1}x_{2}-y_{2}x_{3}-y_{3}x_{4}-y_{4}x_{1}\}\)
\(=\frac{1}{2}\{(x_{1}y_{2}-y_{1}x_{2})+(x_{2}y_{3}-y_{2}x_{3})+(x_{3}y_{4}-y_{3}x_{4})+(x_{4}y_{1}-y_{4}x_{1})\}\)
\(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{4}\\y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{4}\end{array}\right|\)
\(\therefore \Box ABCD=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{4}\\y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{4}\end{array}\right|\)
মনে করি, কোন সমতলে \(ABCD\) চতুর্ভুজের শীর্ষচতুষ্টয় যথক্রমে \(A(x_{1}, y_{1})\), \(B(x_{2}, y_{2})\), \(C(x_{3}, y_{3})\) এবং \(D(x_{3}, y_{3})\)। ত্রিভুজের ক্ষেত্রফল নির্ণয়ের সূত্র ব্যাবহার করে।
\(\Box ABCD=\triangle ABC+\triangle ACD\)
\(=\frac{1}{2}\{(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(y_{1}x_{2}+y_{2}x_{3}+y_{3}x_{1})\}\)+\(\frac{1}{2}\{(x_{1}y_{3}+x_{3}y_{4}+x_{4}y_{1})-(y_{1}x_{3}+y_{3}x_{4}+y_{4}x_{1})\}\)
\(=\frac{1}{2}\{x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-y_{1}x_{2}-y_{2}x_{3}-y_{3}x_{1}+x_{1}y_{3}+x_{3}y_{4}+x_{4}y_{1}-y_{1}x_{3}-y_{3}x_{4}-y_{4}x_{1}\}\)
\(=\frac{1}{2}\{x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1}-y_{1}x_{2}-y_{2}x_{3}-y_{3}x_{4}-y_{4}x_{1}\}\)
\(=\frac{1}{2}\{(x_{1}y_{2}-y_{1}x_{2})+(x_{2}y_{3}-y_{2}x_{3})+(x_{3}y_{4}-y_{3}x_{4})+(x_{4}y_{1}-y_{4}x_{1})\}\)
\(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{4}\\y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{4}\end{array}\right|\)
\(\therefore \Box ABCD=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ x_{2} \ \ x_{3} \ \ x_{4}\\y_{1} \ \ y_{2} \ \ y_{3} \ \ y_{4}\end{array}\right|\)
×
মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণ নির্ণয়
মনে করি, \(AB\) সরলরেখাটি মূলবিন্দু দিয়ে গমন করে এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta\) কোণ উৎপন্ন করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) হতে \(OX\) এর উপর \(PM\) লম্ব অঙ্কন করি।
এখানে,
\(OM=x, PM=y\) এবং \(\angle POM=\theta\).
তাহলে,
\(\tan\theta=\frac{PM}{OM}\)
\(\Rightarrow \tan\theta=\frac{y}{x}\)
\(\Rightarrow m=\frac{y}{x}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y=mx \)
\(\therefore\) মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণ \(y=mx\).
মনে করি, \(AB\) সরলরেখাটি মূলবিন্দু দিয়ে গমন করে এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta\) কোণ উৎপন্ন করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) হতে \(OX\) এর উপর \(PM\) লম্ব অঙ্কন করি।

এখানে,
\(OM=x, PM=y\) এবং \(\angle POM=\theta\).
তাহলে,
\(\tan\theta=\frac{PM}{OM}\)
\(\Rightarrow \tan\theta=\frac{y}{x}\)
\(\Rightarrow m=\frac{y}{x}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y=mx \)
\(\therefore\) মূলবিন্দুগামী সরলরেখার সাধারণ সমীকরণ \(y=mx\).
×
\(Y\) অক্ষের ছেদিতাংশ \((c)\) এবং ঢাল \((m)\) দেওয়া থাকিলে সরলরেখার সমীকরণ নির্ণয়
মনে করি, \(AB\) সরলরেখাটি \(Y\) অক্ষকে \(Q\) বিন্দুতে ছেদ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta\) কোণ উৎপন্ন করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) হতে \(OX\) এর উপর \(PM\) এবং \(Q\) হতে \(PM\) এর উপর \(QR\) লম্ব অঙ্কন করি।
এখানে,
\(OQ=RM=c, OM=QR=x, PM=y.\) \(\therefore PR=PM-RM=y-c\) এবং \(\angle PQR=\theta\).
তাহলে,
\(\tan\theta=\frac{PR}{QR}\)
\(\Rightarrow \tan\theta=\frac{y-c}{x}\)
\(\Rightarrow m=\frac{y-c}{x}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y-c=mx \)
\(\Rightarrow y=mx+c \)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y=mx+c\).
মনে করি, \(AB\) সরলরেখাটি \(Y\) অক্ষকে \(Q\) বিন্দুতে ছেদ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta\) কোণ উৎপন্ন করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) হতে \(OX\) এর উপর \(PM\) এবং \(Q\) হতে \(PM\) এর উপর \(QR\) লম্ব অঙ্কন করি।
এখানে,

\(OQ=RM=c, OM=QR=x, PM=y.\) \(\therefore PR=PM-RM=y-c\) এবং \(\angle PQR=\theta\).
তাহলে,
\(\tan\theta=\frac{PR}{QR}\)
\(\Rightarrow \tan\theta=\frac{y-c}{x}\)
\(\Rightarrow m=\frac{y-c}{x}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y-c=mx \)
\(\Rightarrow y=mx+c \)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y=mx+c\).
×
তীর্যক অক্ষের প্রেক্ষিতে \(Y\) অক্ষের ছেদিতাংশ \(c\) এবং ঢাল \(m\) দেওয়া থাকিলে সরলরেখার সমীকরণ
\(y=\frac{\sin{\theta}}{\sin{(\omega-\theta)}}x+c\).
যেখানে,
\(\theta\) রেখাটির নতি
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
\(y=\frac{\sin{\theta}}{\sin{(\omega-\theta)}}x+c\).
যেখানে,
\(\theta\) রেখাটির নতি
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
আমরা দেখেছি আয়তাকার অক্ষের প্রেক্ষিতে ঢাল \(= m =\tan{\theta}\) যেখানে \(\theta\) রেখাটির নতি কোণ এবং \(c=y\) অক্ষের ছেদিতাংশ।
কিন্তু তীর্যক অক্ষের প্রেক্ষিতে \(m\) কে এই অর্থে পাওয়া যাবে না যদিও \(c\) কে \(y\) অক্ষের ছেদিতাংশ হিসেবেই পাওয়া যাবে।
চিত্রে,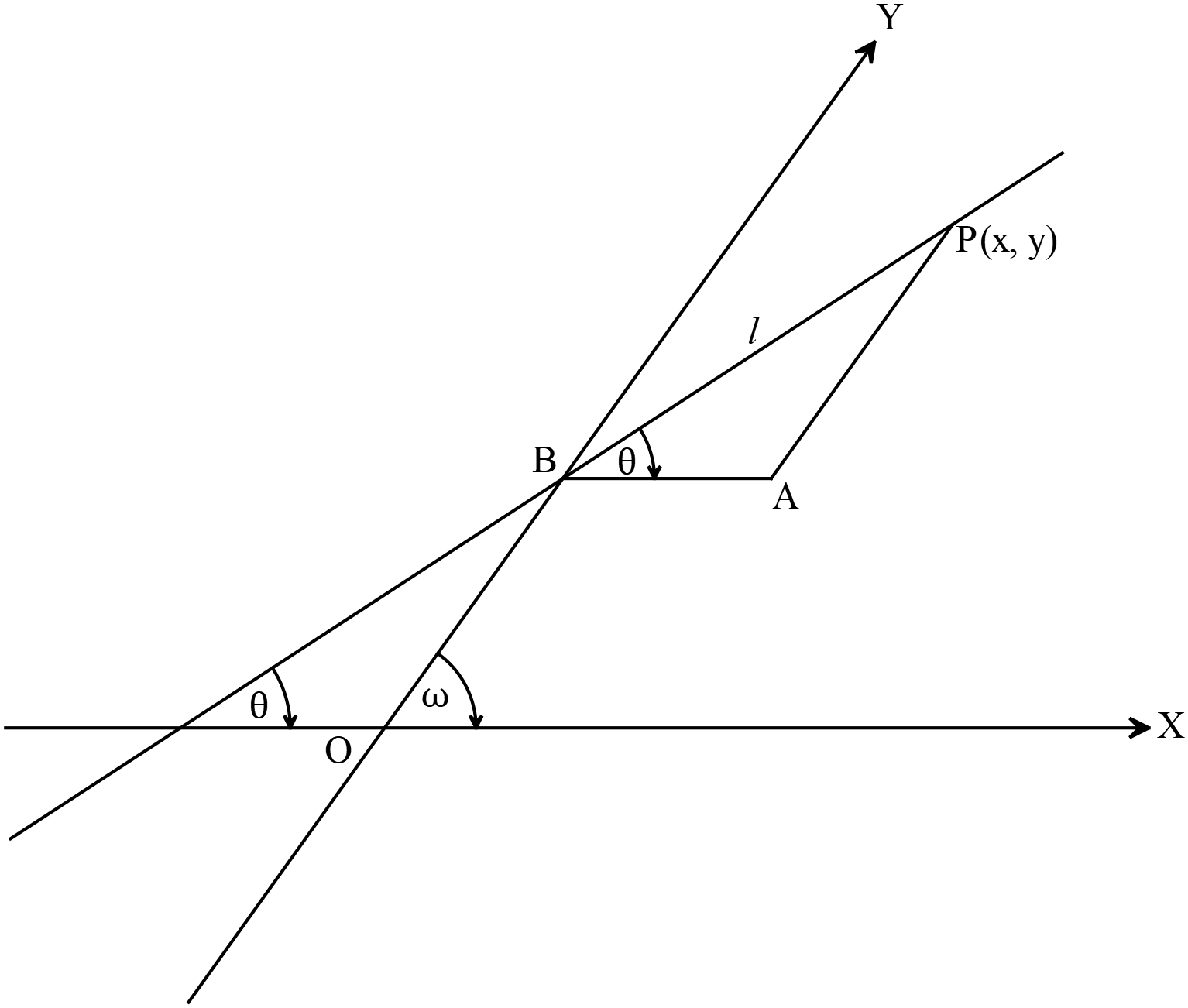
\(l\) রেখটির নতিকোণ \(\theta\) এবং এটা \(y\) অক্ষকে \(B\) বিন্দুতে ছেদ করেছে।
অতএব \(y\) অক্ষের ছেদিতাংশ \(OB=c\)
\(P(x, y),\) রেখাটির ওপর যেকোন বিন্দু। \(P\) ও \(B\) দিয়ে যথাক্রমে \(y\) অক্ষ ও \(x\) অক্ষের সমান্তরালে টানা রেখাদ্বয় \(A\) বিন্দুতে মিলিত হয়েছে।
কাজেই \(BA=x\) এবং \(AP=y-c\)
এখন \(APB\) ত্রিভুজ হতে পাই,
\(\frac{AP}{\sin{\angle{ABP}}}=\frac{BA}{\sin{\angle{APB}}}\)
\(\Rightarrow \frac{y-c}{\sin{\theta}}=\frac{x}{\sin{(\omega-\theta)}}\)
\(\Rightarrow y-c=\frac{x\sin{\theta}}{\sin{(\omega-\theta)}}\)
\(\therefore y=\frac{\sin{\theta}}{\sin{(\omega-\theta)}}x+c\)
যেখানে,
\(\theta\) রেখাটির নতি
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
দ্রষ্টব্যঃ তীর্যক অক্ষের প্রেক্ষিতে, \(y=mx+c\) সমীকরণে \(m=\frac{\sin{\theta}}{\sin{(90^{o}-\theta)}}, \ c=y\) অক্ষের ছেদিতাংশ। \(\theta\) হলো রেখাটির নতি; \(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ। যদি \(\omega=90^{o}\) হয় তবে,
\(m=\frac{\sin{\theta}}{\sin{(90^{o}-\theta)}}\)
\(=\frac{\sin{\theta}}{\cos{\theta}}\)
\(=\tan{\theta}\)
কিন্তু তীর্যক অক্ষের প্রেক্ষিতে \(m\) কে এই অর্থে পাওয়া যাবে না যদিও \(c\) কে \(y\) অক্ষের ছেদিতাংশ হিসেবেই পাওয়া যাবে।
চিত্রে,

\(l\) রেখটির নতিকোণ \(\theta\) এবং এটা \(y\) অক্ষকে \(B\) বিন্দুতে ছেদ করেছে।
অতএব \(y\) অক্ষের ছেদিতাংশ \(OB=c\)
\(P(x, y),\) রেখাটির ওপর যেকোন বিন্দু। \(P\) ও \(B\) দিয়ে যথাক্রমে \(y\) অক্ষ ও \(x\) অক্ষের সমান্তরালে টানা রেখাদ্বয় \(A\) বিন্দুতে মিলিত হয়েছে।
কাজেই \(BA=x\) এবং \(AP=y-c\)
এখন \(APB\) ত্রিভুজ হতে পাই,
\(\frac{AP}{\sin{\angle{ABP}}}=\frac{BA}{\sin{\angle{APB}}}\)
\(\Rightarrow \frac{y-c}{\sin{\theta}}=\frac{x}{\sin{(\omega-\theta)}}\)
\(\Rightarrow y-c=\frac{x\sin{\theta}}{\sin{(\omega-\theta)}}\)
\(\therefore y=\frac{\sin{\theta}}{\sin{(\omega-\theta)}}x+c\)
যেখানে,
\(\theta\) রেখাটির নতি
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
দ্রষ্টব্যঃ তীর্যক অক্ষের প্রেক্ষিতে, \(y=mx+c\) সমীকরণে \(m=\frac{\sin{\theta}}{\sin{(90^{o}-\theta)}}, \ c=y\) অক্ষের ছেদিতাংশ। \(\theta\) হলো রেখাটির নতি; \(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ। যদি \(\omega=90^{o}\) হয় তবে,
\(m=\frac{\sin{\theta}}{\sin{(90^{o}-\theta)}}\)
\(=\frac{\sin{\theta}}{\cos{\theta}}\)
\(=\tan{\theta}\)
×
উভয় অক্ষের ছেদিতাংশ \(a, b\) দেওয়া থাকিলে সরলরেখার সমীকরণ নির্ণয়
মনে করি, \(CD\) সরলরেখাটি অক্ষদ্বয়কে যথাক্রমে \(A(a, 0)\) ও \(B(0, b)\) বিন্দুতে ছেদ করে। \(CD\) এর উপর চলমান বিন্দু \(P(x, y)\) হতে \(OX\) এবং \(OY\) এর উপর যথাক্রমে \(PM\) এবং \(PN\) লম্ব অঙ্কন করি। অতপর \(P, O\) যোগ করি।
এখানে,
\(OA=a, OB=b, OM=PN=x, PM=y.\)
তাহলে,
\(\triangle AOB=\triangle AOP+\triangle BOP\)
\(\Rightarrow \frac{1}{2}a.b=\frac{1}{2}a.y+\frac{1}{2}b.x\) ➜ \(\because \triangle =\frac{1}{2}\times Base \times Height\)
\(\Rightarrow \frac{1}{2}ab=\frac{1}{2}(ay+bx)\)
\(\Rightarrow ab=ay+bx\) ➜ উভয় পার্শে \(2\) গুণ করে।
\(\Rightarrow \frac{ab}{ab}=\frac{ay}{ab}+\frac{bx}{ab}\) ➜ উভয় পার্শে \(ab\) ভাগ করে।
\(\Rightarrow 1=\frac{y}{b}+\frac{x}{a}\)
\(\Rightarrow \frac{x}{a}+\frac{y}{b}=1\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x}{a}+\frac{y}{b}=1\).
মনে করি, \(CD\) সরলরেখাটি অক্ষদ্বয়কে যথাক্রমে \(A(a, 0)\) ও \(B(0, b)\) বিন্দুতে ছেদ করে। \(CD\) এর উপর চলমান বিন্দু \(P(x, y)\) হতে \(OX\) এবং \(OY\) এর উপর যথাক্রমে \(PM\) এবং \(PN\) লম্ব অঙ্কন করি। অতপর \(P, O\) যোগ করি।
এখানে,

\(OA=a, OB=b, OM=PN=x, PM=y.\)
তাহলে,
\(\triangle AOB=\triangle AOP+\triangle BOP\)
\(\Rightarrow \frac{1}{2}a.b=\frac{1}{2}a.y+\frac{1}{2}b.x\) ➜ \(\because \triangle =\frac{1}{2}\times Base \times Height\)
\(\Rightarrow \frac{1}{2}ab=\frac{1}{2}(ay+bx)\)
\(\Rightarrow ab=ay+bx\) ➜ উভয় পার্শে \(2\) গুণ করে।
\(\Rightarrow \frac{ab}{ab}=\frac{ay}{ab}+\frac{bx}{ab}\) ➜ উভয় পার্শে \(ab\) ভাগ করে।
\(\Rightarrow 1=\frac{y}{b}+\frac{x}{a}\)
\(\Rightarrow \frac{x}{a}+\frac{y}{b}=1\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x}{a}+\frac{y}{b}=1\).
×
একটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) দিয়ে গমনকারী এবং তার ঢাল \((m)\) দেওয়া থাকিলে সরলরেখার সমীকরণ নির্ণয়
মনে করি, \(AB\) সরলরেখাটি \(X\) অক্ষকে \(C\) বিন্দুতে ছেদ করে এবং নির্দিষ্ট \(Q(x_{1}, y_{1})\) বিন্দুদিয়ে গমন করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) এবং \(Q\) বিন্দু হতে \(OX\) এর উপর যথাক্রমে \(PM\) ও \(QN\) লম্ব আঁকি।
এখানে,
\(ON=x_{1}, OM=x, PM=y, QN=y_{1}.\)
\(QR=OM-ON=x-x_{1},\) \(PR=PM-RM=PM-QN=y-y_{1}.\)
এবং \(\angle PCM=\angle PQR=\theta.\)
তাহলে,
\(\tan\theta=\frac{PR}{QR}\)
\(\Rightarrow m=\frac{y-y_{1}}{x-x_{1}}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y-y_{1}=m(x-x_{1})\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y-y_{1}=m(x-x_{1})\).
মনে করি, \(AB\) সরলরেখাটি \(X\) অক্ষকে \(C\) বিন্দুতে ছেদ করে এবং নির্দিষ্ট \(Q(x_{1}, y_{1})\) বিন্দুদিয়ে গমন করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\) এবং \(Q\) বিন্দু হতে \(OX\) এর উপর যথাক্রমে \(PM\) ও \(QN\) লম্ব আঁকি।
এখানে,

\(ON=x_{1}, OM=x, PM=y, QN=y_{1}.\)
\(QR=OM-ON=x-x_{1},\) \(PR=PM-RM=PM-QN=y-y_{1}.\)
এবং \(\angle PCM=\angle PQR=\theta.\)
তাহলে,
\(\tan\theta=\frac{PR}{QR}\)
\(\Rightarrow m=\frac{y-y_{1}}{x-x_{1}}\) ➜ \(\because m=\tan\theta\)
\(\Rightarrow y-y_{1}=m(x-x_{1})\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(y-y_{1}=m(x-x_{1})\).
×
দুইটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) এবং \((x_{2}, y_{2})\) দিয়ে গমনকারী সরলরেখার সমীকরণ নির্ণয়
মনে করি, \(AB\) সরলরেখাটি দুইটি নির্দিষ্ট \(Q(x_{1}, y_{1})\), \(R(x_{2}, y_{2})\) বিন্দুদিয়ে গমন করে এবং \(X\) অক্ষকে \(E\) বিন্দুতে ছেদ করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\)।
এখন,
\(PQ\) এর ঢাল \(m_{1}=\frac{y-y_{1}}{x-x_{1}}\).
\(QR\) এর ঢাল \(m_{2}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\).
\(P, \ Q, \ R\) একই সরলরেখা \(AB\) এর উপর অবস্থিত।
তাহলে,
\(m_{1}=m_{2}\)
\(\Rightarrow \frac{y-y_{1}}{x-x_{1}}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
\(\Rightarrow \frac{y-y_{1}}{y_{1}-y_{2}}=\frac{x-x_{1}}{x_{1}-x_{2}}\)
\(\Rightarrow \frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\).
মনে করি, \(AB\) সরলরেখাটি দুইটি নির্দিষ্ট \(Q(x_{1}, y_{1})\), \(R(x_{2}, y_{2})\) বিন্দুদিয়ে গমন করে এবং \(X\) অক্ষকে \(E\) বিন্দুতে ছেদ করে। \(AB\) এর উপর চলমান বিন্দু \(P(x, y)\)।
এখন,

\(PQ\) এর ঢাল \(m_{1}=\frac{y-y_{1}}{x-x_{1}}\).
\(QR\) এর ঢাল \(m_{2}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\).
\(P, \ Q, \ R\) একই সরলরেখা \(AB\) এর উপর অবস্থিত।
তাহলে,
\(m_{1}=m_{2}\)
\(\Rightarrow \frac{y-y_{1}}{x-x_{1}}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
\(\Rightarrow \frac{y-y_{1}}{y_{1}-y_{2}}=\frac{x-x_{1}}{x_{1}-x_{2}}\)
\(\Rightarrow \frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x-x_{1}}{x_{1}-x_{2}}=\frac{y-y_{1}}{y_{1}-y_{2}}\).
×
মূলবিন্দু হতে কোনো সরলরেখার উপর অঙ্কিত লম্বের দৈর্ঘ্য \(P\) এবং লম্বটি \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\alpha \) কোণ উৎপন্ন করলে, সরলরেখাটির সমীকরণ নির্ণয়
মনে করি, \(PQ\) সরলরেখাটি অক্ষদ্বয়কে যথাক্রমে \(A\) ও \(B\) বিন্দুতে ছেদ করে। \(O\) বিন্দু হতে \(PQ\) এর উপর \(OC\) লম্ব আঁকি। \(OC\) লম্বের দৈর্ঘ্য \(p\) এবং লম্বটি \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\alpha \) কোণ উৎপন্ন করে।
এখন,
\(OA=\frac{OA}{OC}\times OC\)
\(\Rightarrow OA=\sec\alpha \times p\)
\(\Rightarrow OA=p\sec\alpha \)
আবার,
\(OB=\frac{OB}{OC}\times OC\)
\(\Rightarrow OB=\sec\angle COB \times p\)
\(\Rightarrow OB=p\sec(90^{o}-\alpha)\) ➜ \(\because \angle COB=90^{o}-\alpha \)
\(\Rightarrow OB=p\ cosec\alpha \)
\(\therefore AB\) এর সমীকরণ \(\frac{x}{OA}+\frac{y}{OB}=1\) ➜ \(\because \frac{x}{a}+\frac{y}{b}=1\)
\(\Rightarrow \frac{x}{p\sec\alpha}+\frac{y}{p\ cosec\alpha}=1\)
\(\Rightarrow \frac{x}{p}\times \frac{1}{\sec\alpha}+\frac{y}{p}\times \frac{1}{\ cosec\alpha}=1\)
\(\Rightarrow \frac{x}{p}\cos\alpha+\frac{y}{p}\sin\alpha=1\)
\(\Rightarrow x\cos\alpha+y\sin\alpha=p\) ➜ উভয় পার্শে \(p\) গুণ করে।
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(x\cos\alpha + y\sin\alpha=p\).
মনে করি, \(PQ\) সরলরেখাটি অক্ষদ্বয়কে যথাক্রমে \(A\) ও \(B\) বিন্দুতে ছেদ করে। \(O\) বিন্দু হতে \(PQ\) এর উপর \(OC\) লম্ব আঁকি। \(OC\) লম্বের দৈর্ঘ্য \(p\) এবং লম্বটি \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\alpha \) কোণ উৎপন্ন করে।
এখন,

\(OA=\frac{OA}{OC}\times OC\)
\(\Rightarrow OA=\sec\alpha \times p\)
\(\Rightarrow OA=p\sec\alpha \)
আবার,
\(OB=\frac{OB}{OC}\times OC\)
\(\Rightarrow OB=\sec\angle COB \times p\)
\(\Rightarrow OB=p\sec(90^{o}-\alpha)\) ➜ \(\because \angle COB=90^{o}-\alpha \)
\(\Rightarrow OB=p\ cosec\alpha \)
\(\therefore AB\) এর সমীকরণ \(\frac{x}{OA}+\frac{y}{OB}=1\) ➜ \(\because \frac{x}{a}+\frac{y}{b}=1\)
\(\Rightarrow \frac{x}{p\sec\alpha}+\frac{y}{p\ cosec\alpha}=1\)
\(\Rightarrow \frac{x}{p}\times \frac{1}{\sec\alpha}+\frac{y}{p}\times \frac{1}{\ cosec\alpha}=1\)
\(\Rightarrow \frac{x}{p}\cos\alpha+\frac{y}{p}\sin\alpha=1\)
\(\Rightarrow x\cos\alpha+y\sin\alpha=p\) ➜ উভয় পার্শে \(p\) গুণ করে।
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(x\cos\alpha + y\sin\alpha=p\).
×
একটি নির্দিষ্ট বিন্দু \((x_{1}, y_{1})\) দিয়ে গমনকারী এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্ন করলে, সরলরেখাটির সমীকরণ নির্ণয়
মনে করি, \(AB\) সরলরেখাটি একটি নির্দিষ্ট বিন্দু \(Q(x_{1}, y_{1})\) দিয়ে গমন করে, \(X\) অক্ষকে \(C\) বিন্দুতে ছেদ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্ন করে। \(P\) ও \(Q\) হতে \(OX\) এর উপর যথাক্রমে \(PM\), \(QN\) এবং \(Q\) হতে \(PM\) এর উপর \(QL\) লম্ব আঁকি।
এখানে,
\(OM=x, \ ON=x_{1}, \ PM=y,\)
\(QN=y_{1}, \ PQ=r,\)
\(\angle PCM=\angle PQL=\theta \)
\(QL=NM=OM-ON=x-x_{1},\)
\(PL=PM-LM=PM-QN=y-y_{1}\)
\(\sin\theta=\frac{PL}{PQ}\)
\(\Rightarrow \sin\theta=\frac{y-y_{1}}{r}\)
\(\Rightarrow r=\frac{y-y_{1}}{\sin\theta}\)
\(\Rightarrow \frac{y-y_{1}}{\sin\theta}=r ........(i)\)
আবার,
\(\cos\theta=\frac{QL}{PQ}\)
\(\Rightarrow \cos\theta=\frac{x-x_{1}}{r}\)
\(\Rightarrow r=\frac{x-x_{1}}{\cos\theta}\)
\(\Rightarrow \frac{x-x_{1}}{\cos\theta}=r ........(ii)\)
\((i)\) ও \((ii)\) হতে পাই,
\(\Rightarrow \frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\).
মনে করি, \(AB\) সরলরেখাটি একটি নির্দিষ্ট বিন্দু \(Q(x_{1}, y_{1})\) দিয়ে গমন করে, \(X\) অক্ষকে \(C\) বিন্দুতে ছেদ করে এবং \(X\) অক্ষের ধনাত্মক দিকের সহিত \(\theta \) কোণ উৎপন্ন করে। \(P\) ও \(Q\) হতে \(OX\) এর উপর যথাক্রমে \(PM\), \(QN\) এবং \(Q\) হতে \(PM\) এর উপর \(QL\) লম্ব আঁকি।
এখানে,
\(OM=x, \ ON=x_{1}, \ PM=y,\)
\(QN=y_{1}, \ PQ=r,\)
\(\angle PCM=\angle PQL=\theta \)
\(QL=NM=OM-ON=x-x_{1},\)
\(PL=PM-LM=PM-QN=y-y_{1}\)
\(\sin\theta=\frac{PL}{PQ}\)

\(\Rightarrow \sin\theta=\frac{y-y_{1}}{r}\)
\(\Rightarrow r=\frac{y-y_{1}}{\sin\theta}\)
\(\Rightarrow \frac{y-y_{1}}{\sin\theta}=r ........(i)\)
আবার,
\(\cos\theta=\frac{QL}{PQ}\)
\(\Rightarrow \cos\theta=\frac{x-x_{1}}{r}\)
\(\Rightarrow r=\frac{x-x_{1}}{\cos\theta}\)
\(\Rightarrow \frac{x-x_{1}}{\cos\theta}=r ........(ii)\)
\((i)\) ও \((ii)\) হতে পাই,
\(\Rightarrow \frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\)
\(\therefore\) নির্ণেয় সরলরেখার সমীকরণ \(\frac{x-x_{1}}{\cos\theta}=\frac{y-y_{1}}{\sin\theta}=r\).
×
দুইটি অসমান্তরাল সরলরেখা উভয়ই \(Y\) অক্ষের অসমান্তরাল হলে, তাদের মধ্যবর্তী কোণ নির্ণয়
ধরি,
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণ \(\theta\).
\(BC\Rightarrow (1)\) ও \(AC\Rightarrow (2)\) রেখাদ্বয় পরস্পর \(C\) বিন্দুতে এবং অক্ষদ্বয়কে যথাক্রমে \(B\) ও \(A\) ছেদ করে ।
\((1)\) ও \((2)\) সরলরেখাদ্বয় অক্ষদ্বয়ের সহিত যথাক্রমে \(\theta_{1}\) ও \(\theta_{2}\) কোণ উৎপন্ন করে।
\(\therefore m_{1}=\tan\theta_{1}, \ m_{2}=\tan\theta_{2}\)
এখানে,
\(\angle ACB=\theta, \ \angle CBA=\theta_{1}, \ \angle CAX=\theta_{2},\)
\(\angle ACB+\angle CBA=\angle CAX\) ➜ ত্রিভুজের একবাহু বর্ধিত করায় উৎপন্ন বহিঃ কোণ, অন্তস্ত অপর দুই কোণের যোগফলের সমান।
\(\Rightarrow \theta+\theta_{1}=\theta_{2}\)
\(\Rightarrow \theta=\theta_{2}-\theta_{1}\)
\(\therefore \theta=-(\theta_{1}-\theta_{2}) ........(3)\)
আবার বিপরীতক্রমে,
\(BC\Rightarrow (2)\) ও \(AC\Rightarrow (1)\) বিবেচনা করে ।
\(\angle ACB+\angle CBA=\angle CAX\)
\(\Rightarrow \theta+\theta_{2}=\theta_{1}\)
\(\Rightarrow \theta=\theta_{1}-\theta_{2}\)
\(\therefore \theta=\theta_{1}-\theta_{2} ...........(4)\)
\((3)\) ও \((4)\) সমন্বয় করে,
\(\theta=\pm (\theta_{1}-\theta_{2}) ...........(5)\)
\(\Rightarrow \tan\theta=\tan\pm (\theta_{1}-\theta_{2})\) ➜ উভয় পার্শে \(\tan\) অনুপাত নিয়ে।
\(\Rightarrow \tan\theta=\pm \tan(\theta_{1}-\theta_{2})\)
\(\Rightarrow \tan\theta=\pm \frac{\tan\theta_{1}-\tan\theta_{2}}{1+\tan\theta_{1}\tan\theta_{2}}\)
\(\Rightarrow \tan\theta=\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\) ➜ \(\because m_{1}=\tan\theta_{1}, \ m_{2}=\tan\theta_{2}\)
\(\therefore \theta=\tan^{-1}\left(\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\right)\)
ধরি,

\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী কোণ \(\theta\).
\(BC\Rightarrow (1)\) ও \(AC\Rightarrow (2)\) রেখাদ্বয় পরস্পর \(C\) বিন্দুতে এবং অক্ষদ্বয়কে যথাক্রমে \(B\) ও \(A\) ছেদ করে ।
\((1)\) ও \((2)\) সরলরেখাদ্বয় অক্ষদ্বয়ের সহিত যথাক্রমে \(\theta_{1}\) ও \(\theta_{2}\) কোণ উৎপন্ন করে।
\(\therefore m_{1}=\tan\theta_{1}, \ m_{2}=\tan\theta_{2}\)
এখানে,
\(\angle ACB=\theta, \ \angle CBA=\theta_{1}, \ \angle CAX=\theta_{2},\)
\(\angle ACB+\angle CBA=\angle CAX\) ➜ ত্রিভুজের একবাহু বর্ধিত করায় উৎপন্ন বহিঃ কোণ, অন্তস্ত অপর দুই কোণের যোগফলের সমান।
\(\Rightarrow \theta+\theta_{1}=\theta_{2}\)
\(\Rightarrow \theta=\theta_{2}-\theta_{1}\)
\(\therefore \theta=-(\theta_{1}-\theta_{2}) ........(3)\)
আবার বিপরীতক্রমে,
\(BC\Rightarrow (2)\) ও \(AC\Rightarrow (1)\) বিবেচনা করে ।
\(\angle ACB+\angle CBA=\angle CAX\)
\(\Rightarrow \theta+\theta_{2}=\theta_{1}\)
\(\Rightarrow \theta=\theta_{1}-\theta_{2}\)
\(\therefore \theta=\theta_{1}-\theta_{2} ...........(4)\)
\((3)\) ও \((4)\) সমন্বয় করে,
\(\theta=\pm (\theta_{1}-\theta_{2}) ...........(5)\)
\(\Rightarrow \tan\theta=\tan\pm (\theta_{1}-\theta_{2})\) ➜ উভয় পার্শে \(\tan\) অনুপাত নিয়ে।
\(\Rightarrow \tan\theta=\pm \tan(\theta_{1}-\theta_{2})\)
\(\Rightarrow \tan\theta=\pm \frac{\tan\theta_{1}-\tan\theta_{2}}{1+\tan\theta_{1}\tan\theta_{2}}\)
\(\Rightarrow \tan\theta=\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\) ➜ \(\because m_{1}=\tan\theta_{1}, \ m_{2}=\tan\theta_{2}\)
\(\therefore \theta=\tan^{-1}\left(\pm \frac{m_{1}-m_{2}}{1+m_{1}m_{2}}\right)\)
×
তীর্যক অক্ষের সাপেক্ষে দুইটি অসমান্তরাল সরলরেখার মধ্যবর্তী কোণ
\(\theta=tan^{-1}\left\{\pm \frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\sin{\omega}+m_{1}m_{2}}\right\}\).
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
\((1)\) নং সরলরেখার ঢাল \(=m_{1}\)
\((2)\) নং সরলরেখার ঢাল \(=m_{2}\)
\(\theta=tan^{-1}\left\{\pm \frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\sin{\omega}+m_{1}m_{2}}\right\}\).
যেখানে,
\(\omega\) অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ
\((1)\) নং সরলরেখার ঢাল \(=m_{1}\)
\((2)\) নং সরলরেখার ঢাল \(=m_{2}\)
Proof:
ধরি,রেখা দুইটির সমীকরণ,
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
এবং এদের নতি কোণ যথাক্রমে \(\theta_{1}, \ \theta_{2}\)
যদি তীর্যক অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ \(\omega\) হয় তবে,
\(m_{1}=\frac{\sin{\theta_{1}}}{\sin{(\omega-\theta_{1})}} .......(3)\)
\(m_{2}=\frac{\sin{\theta_{2}}}{\sin{(\omega-\theta_{2})}} .......(4)\)
\((3)\) হতে,
\(m_{1}=\frac{\sin{\theta_{1}}}{\sin{\omega}\cos{\theta_{1}}-\cos{\omega}\sin{\theta_{1}}}\)
\(\Rightarrow \sin{\theta_{1}}=m_{1}\sin{\omega}\cos{\theta_{1}}-m_{1}\cos{\omega}\sin{\theta_{1}}\)
\(\Rightarrow \sin{\theta_{1}}+m_{1}\cos{\omega}\sin{\theta_{1}}=m_{1}\sin{\omega}\cos{\theta_{1}}\)
\(\Rightarrow \sin{\theta_{1}}(1+m_{1}\cos{\omega})=m_{1}\sin{\omega}\cos{\theta_{1}}\)
\(\Rightarrow \frac{\sin{\theta_{1}}}{\cos{\theta_{1}}}=\frac{m_{1}\sin{\omega}}{1+m_{1}\cos{\omega}}\)
\(\therefore \tan{\theta_{1}}=\frac{m_{1}\sin{\omega}}{1+m_{1}\cos{\omega}} .......(5)\)
\((4)\) হতে,
\(m_{2}=\frac{\sin{\theta_{2}}}{\sin{\omega}\cos{\theta_{2}}-\cos{\omega}\sin{\theta_{2}}}\)
\(\Rightarrow \sin{\theta_{2}}=m_{2}\sin{\omega}\cos{\theta_{2}}-m_{2}\cos{\omega}\sin{\theta_{2}}\)
\(\Rightarrow \sin{\theta_{2}}+m_{2}\cos{\omega}\sin{\theta_{2}}=m_{2}\sin{\omega}\cos{\theta_{2}}\)
\(\Rightarrow \sin{\theta_{2}}(1+m_{2}\cos{\omega})=m_{2}\sin{\omega}\cos{\theta_{2}}\)
\(\Rightarrow \frac{\sin{\theta_{2}}}{\cos{\theta_{2}}}=\frac{m_{2}\sin{\omega}}{1+m_{2}\cos{\omega}}\)
\(\therefore \tan{\theta_{2}}=\frac{m_{2}\sin{\omega}}{1+m_{2}\cos{\omega}} .......(6)\)
এখন রেখা দুইটির অন্তর্ভুক্ত কোণ \(\theta\) এর জন্য পাই,
\(\tan{\theta}=\pm{\tan{(\theta_{1}-\theta_{2})}}\)
\(=\pm{\frac{\tan{\theta_{1}}-\tan{\theta_{2}}}{1+\tan{\theta_{1}}\tan{\theta_{2}}}}\)
\(=\pm{\frac{\frac{m_{1}\sin{\omega}}{1+m_{1}\cos{\omega}}-\frac{m_{2}\sin{\omega}}{1+m_{2}\cos{\omega}}}{1+\frac{m_{1}\sin{\omega}}{1+m_{1}\cos{\omega}}\frac{m_{2}\sin{\omega}}{1+m_{2}\cos{\omega}}}}\)
\(=\pm{\frac{m_{1}\sin{\omega}+m_{1}m_{2}\sin{\omega}\cos{\omega}-m_{2}\sin{\omega}-m_{1}m_{2}\sin{\omega}\cos{\omega}}{(1+m_{1}\cos{\omega})(1+m_{2}\cos{\omega})+m_{1}m_{2}\sin^2{\omega}}}\)
\(=\pm{\frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\cos{\omega}+m_{1}m_{2}\cos^2{\omega}+m_{1}m_{2}\sin^2{\omega}}}\)
\(=\pm{\frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\cos{\omega}+m_{1}m_{2}(\sin^2{\omega}+\cos^2{\omega})}}\)
\(\Rightarrow \tan{\theta}=\pm{\frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\cos{\omega}+m_{1}m_{2}}}\)
\(\therefore \theta=tan^{-1}\left\{\pm \frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\sin{\omega}+m_{1}m_{2}}\right\}\)
\(y=m_{1}x+c_{1} ........(1)\)
\(y=m_{2}x+c_{2} ........(2)\)
এবং এদের নতি কোণ যথাক্রমে \(\theta_{1}, \ \theta_{2}\)
যদি তীর্যক অক্ষদ্বয়ের অন্তর্ভুক্ত কোণ \(\omega\) হয় তবে,
\(m_{1}=\frac{\sin{\theta_{1}}}{\sin{(\omega-\theta_{1})}} .......(3)\)
\(m_{2}=\frac{\sin{\theta_{2}}}{\sin{(\omega-\theta_{2})}} .......(4)\)
\((3)\) হতে,
\(m_{1}=\frac{\sin{\theta_{1}}}{\sin{\omega}\cos{\theta_{1}}-\cos{\omega}\sin{\theta_{1}}}\)
\(\Rightarrow \sin{\theta_{1}}=m_{1}\sin{\omega}\cos{\theta_{1}}-m_{1}\cos{\omega}\sin{\theta_{1}}\)
\(\Rightarrow \sin{\theta_{1}}+m_{1}\cos{\omega}\sin{\theta_{1}}=m_{1}\sin{\omega}\cos{\theta_{1}}\)
\(\Rightarrow \sin{\theta_{1}}(1+m_{1}\cos{\omega})=m_{1}\sin{\omega}\cos{\theta_{1}}\)
\(\Rightarrow \frac{\sin{\theta_{1}}}{\cos{\theta_{1}}}=\frac{m_{1}\sin{\omega}}{1+m_{1}\cos{\omega}}\)
\(\therefore \tan{\theta_{1}}=\frac{m_{1}\sin{\omega}}{1+m_{1}\cos{\omega}} .......(5)\)
\((4)\) হতে,
\(m_{2}=\frac{\sin{\theta_{2}}}{\sin{\omega}\cos{\theta_{2}}-\cos{\omega}\sin{\theta_{2}}}\)
\(\Rightarrow \sin{\theta_{2}}=m_{2}\sin{\omega}\cos{\theta_{2}}-m_{2}\cos{\omega}\sin{\theta_{2}}\)
\(\Rightarrow \sin{\theta_{2}}+m_{2}\cos{\omega}\sin{\theta_{2}}=m_{2}\sin{\omega}\cos{\theta_{2}}\)
\(\Rightarrow \sin{\theta_{2}}(1+m_{2}\cos{\omega})=m_{2}\sin{\omega}\cos{\theta_{2}}\)
\(\Rightarrow \frac{\sin{\theta_{2}}}{\cos{\theta_{2}}}=\frac{m_{2}\sin{\omega}}{1+m_{2}\cos{\omega}}\)
\(\therefore \tan{\theta_{2}}=\frac{m_{2}\sin{\omega}}{1+m_{2}\cos{\omega}} .......(6)\)
এখন রেখা দুইটির অন্তর্ভুক্ত কোণ \(\theta\) এর জন্য পাই,
\(\tan{\theta}=\pm{\tan{(\theta_{1}-\theta_{2})}}\)
\(=\pm{\frac{\tan{\theta_{1}}-\tan{\theta_{2}}}{1+\tan{\theta_{1}}\tan{\theta_{2}}}}\)
\(=\pm{\frac{\frac{m_{1}\sin{\omega}}{1+m_{1}\cos{\omega}}-\frac{m_{2}\sin{\omega}}{1+m_{2}\cos{\omega}}}{1+\frac{m_{1}\sin{\omega}}{1+m_{1}\cos{\omega}}\frac{m_{2}\sin{\omega}}{1+m_{2}\cos{\omega}}}}\)
\(=\pm{\frac{m_{1}\sin{\omega}+m_{1}m_{2}\sin{\omega}\cos{\omega}-m_{2}\sin{\omega}-m_{1}m_{2}\sin{\omega}\cos{\omega}}{(1+m_{1}\cos{\omega})(1+m_{2}\cos{\omega})+m_{1}m_{2}\sin^2{\omega}}}\)
\(=\pm{\frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\cos{\omega}+m_{1}m_{2}\cos^2{\omega}+m_{1}m_{2}\sin^2{\omega}}}\)
\(=\pm{\frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\cos{\omega}+m_{1}m_{2}(\sin^2{\omega}+\cos^2{\omega})}}\)
\(\Rightarrow \tan{\theta}=\pm{\frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\cos{\omega}+m_{1}m_{2}}}\)
\(\therefore \theta=tan^{-1}\left\{\pm \frac{(m_{1}-m_{2})\sin{\omega}}{1+(m_{1}+m_{2})\sin{\omega}+m_{1}m_{2}}\right\}\)
×
তিনটি সরলরেখার সমবিন্দু তথা এক বিন্দুতে মিলিত হওয়ার শর্ত নির্ণয়

ধরি, সরলরেখা তিনটি ,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
\((2)\) ও \((3)\) ( বজ্রগুণ পদ্ধতিতে ) সমাধান করি,
\(\frac{x}{b_{2}c_{3}-b_{3}c_{2}}=\frac{y}{a_{3}c_{2}-a_{2}c_{3}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\Rightarrow \frac{x}{b_{2}c_{3}-b_{3}c_{2}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}, \ \frac{y}{a_{3}c_{2}-a_{2}c_{3}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\Rightarrow x=\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}, \ y=\frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\therefore (2)\) ও \((3)\) এর ছেদবিন্দু \(P(\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}, \frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}})\)
শর্তমতে ,\(P\) বিন্দুটি \(\) নং সমীকরণকে সিদ্ধ করবে।
\(a_{1}\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}+b_{1}\frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}}+c_{1}=0\)
\(\Rightarrow \frac{a_{1}(b_{2}c_{3}-b_{3}c_{2})}{a_{2}b_{3}-a_{3}b_{2}}+\frac{b_{1}(a_{3}c_{2}-a_{2}c_{3})}{a_{2}b_{3}-a_{3}b_{2}}+c_{1}=0\)
\(\Rightarrow a_{1}(b_{2}c_{3}-b_{3}c_{2})+b_{1}(a_{3}c_{2}-a_{2}c_{3})+c_{1}(a_{2}b_{3}-a_{3}b_{2})=0\) ➜ উভয় পার্শে \(a_{2}b_{3}-a_{3}b_{2}\) গুণ করে
\(\Rightarrow \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত।

ধরি, সরলরেখা তিনটি ,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 ........(3)\)
\((2)\) ও \((3)\) ( বজ্রগুণ পদ্ধতিতে ) সমাধান করি,
\(\frac{x}{b_{2}c_{3}-b_{3}c_{2}}=\frac{y}{a_{3}c_{2}-a_{2}c_{3}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\Rightarrow \frac{x}{b_{2}c_{3}-b_{3}c_{2}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}, \ \frac{y}{a_{3}c_{2}-a_{2}c_{3}}=\frac{1}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\Rightarrow x=\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}, \ y=\frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}}\)
\(\therefore (2)\) ও \((3)\) এর ছেদবিন্দু \(P(\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}, \frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}})\)
শর্তমতে ,\(P\) বিন্দুটি \(\) নং সমীকরণকে সিদ্ধ করবে।
\(a_{1}\frac{b_{2}c_{3}-b_{3}c_{2}}{a_{2}b_{3}-a_{3}b_{2}}+b_{1}\frac{a_{3}c_{2}-a_{2}c_{3}}{a_{2}b_{3}-a_{3}b_{2}}+c_{1}=0\)
\(\Rightarrow \frac{a_{1}(b_{2}c_{3}-b_{3}c_{2})}{a_{2}b_{3}-a_{3}b_{2}}+\frac{b_{1}(a_{3}c_{2}-a_{2}c_{3})}{a_{2}b_{3}-a_{3}b_{2}}+c_{1}=0\)
\(\Rightarrow a_{1}(b_{2}c_{3}-b_{3}c_{2})+b_{1}(a_{3}c_{2}-a_{2}c_{3})+c_{1}(a_{2}b_{3}-a_{3}b_{2})=0\) ➜ উভয় পার্শে \(a_{2}b_{3}-a_{3}b_{2}\) গুণ করে
\(\Rightarrow \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|=0\)
ইহাই নির্ণেয় শর্ত।
×
একটি ত্রিভুজের বাহুগুলির সমীকরণ দেওয়া আছে । ত্রিভুজটির ক্ষেত্রফল নির্ণয়
\(a_{1}x+b_{1}y+c_{1}=0 .........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 .........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 .........(3)\)
\((1)\), \((2)\), \((3)\) হতে \(x, y\) অপনয়ন করে পাই
\(\Delta=\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|\)
ধরি,
\((2)\) ও \((3)\) এর ছেদবিন্দু \(A(x_{1},y_{1})\Rightarrow a_{2}x_{1}+b_{2}y_{1}+c_{2}=0 ........(4),\)
\(a_{3}x_{1}+b_{3}y_{1}+c_{3}=0 .........(5)\)
\((3)\) ও \((1)\) এর ছেদবিন্দু \(B(x_{2},y_{2})\Rightarrow a_{3}x_{2}+b_{3}y_{2}+c_{3}=0 ........(6),\)
\(a_{1}x_{2}+b_{1}y_{2}+c_{1}=0 ........(7) \)
\((1)\) ও \((2)\) এর ছেদবিন্দু \(C(x_{3},y_{3})\Rightarrow a_{1}x_{3}+b_{1}y_{3}+c_{1}=0 ........(8),\)
\(a_{2}x_{3}+b_{2}y_{3}+c_{2}=0 ........(9) \)
এখন, \(\triangle ABC\) এর ক্ষেত্রফল \(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ \ \ 1\\x_{2} \ \ y_{2} \ \ \ \ 1\\x_{3} \ \ y_{3} \ \ \ \ 1\end{array}\right| \)
\(=\frac{1}{2}\frac{\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ \ \ 1\\x_{2} \ \ y_{2} \ \ \ \ 1\\x_{3} \ \ y_{3} \ \ \ \ 1\end{array}\right|\times \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|}{\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|} \)
\(=\frac{\left|\begin{array}{c}a_{1}x_{1}+b_{1}y_{1}+c_{1} \ \ \ \ a_{2}x_{1}+b_{2}y_{1}+c_{2} \ \ \ \ a_{3}x_{1}+b_{3}y_{1}+c_{3} \\ a_{1}x_{2}+b_{1}y_{2}+c_{1} \ \ \ \ a_{2}x_{2}+b_{2}y_{2}+c_{2} \ \ \ \ a_{3}x_{2}+b_{3}y_{2}+c_{3}\\ a_{1}x_{3}+b_{1}y_{3}+c_{1} \ \ \ \ a_{2}x_{3}+b_{2}y_{3}+c_{2} \ \ \ \ a_{3}x_{3}+b_{3}y_{3}+c_{3}\end{array}\right|}{2\Delta} \)
\(=\frac{\left|\begin{array}{c}a_{1}x_{1}+b_{1}y_{1}+c_{1} \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \\ 0 \ \ \ \ \ \ \ \ \ \ \ \ a_{2}x_{2}+b_{2}y_{2}+c_{2} \ \ \ \ \ \ \ \ \ \ \ \ 0\\ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ a_{3}x_{3}+b_{3}y_{3}+c_{3}\end{array}\right|}{2\Delta} \) ➜ (4),(5),(6),(7),(8),(9) এর সাহায্যে
\(=\frac{(a_{1}x_{1}+b_{1}y_{1}+c_{1})(a_{2}x_{2}+b_{2}y_{2}+c_{2})(a_{3}x_{3}+b_{3}y_{3}+c_{3})}{2\Delta} ..........(10)\)
ধরি,
\(a_{1}x_{1}+b_{1}y_{1}+c_{1}=k_{1}\)
\(\Rightarrow a_{1}x_{1}+b_{1}y_{1}+c_{1}-k_{1}=0 ............. (11)\)
\(a_{2}x_{1}+b_{2}y_{1}+c_{2}=0 ............(12)\)
\(a_{3}x_{1}+b_{3}y_{1}+c_{3}=0 ............. (13)\)
\((11), (12), (13)\) হতে \(x_{1}, y_{1}\) অপনয়ন করে পাই ,
\(\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}-k_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ \ \ \ \ c_{2} \ \ \ \ \\a_{3} \ \ \ \ b_{3} \ \ \ \ \ \ \ \ c_{3} \ \ \ \ \end{array}\right|=0\)
\(\Rightarrow \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|+\left|\begin{array}{c}a_{1} \ \ \ \ \ b_{1} \ \ \ \ -k_{1}\\a_{2} \ \ \ \ \ b_{2} \ \ \ \ \ \ \ \ 0 \ \ \ \\a_{3} \ \ \ \ \ b_{3} \ \ \ \ \ \ \ \ 0 \ \ \ \end{array}\right|=0\)
\(\Rightarrow \Delta-k_{1}\left|\begin{array}{c}a_{2} \ \ \ \ b_{2}\\a_{3} \ \ \ \ b_{3}\end{array}\right|=0\)
\(\Rightarrow \Delta-k_{1}(a_{2}b_{3}-a_{3}b_{2})=0\)
\(\Rightarrow \Delta-k_{1}C_{1}=0\) ➜ \(C_{1}= \Delta \) নির্ণায়কে \( c_{1}\) এর সহগুণক।
\(\Rightarrow \Delta=k_{1}C_{1}\)
\(\Rightarrow k_{1}C_{1}=\Delta\)
\(\therefore k_{1}=\frac{\Delta}{C_{1}}\)
অনুরূপভাবে,
\(a_{2}x_{2}+b_{2}y_{2}+c_{2}=k_{2}, \ a_{3}x_{3}+b_{3}y_{3}+c_{3}=k_{3} \) কল্পনা করে পাই
\(k_{2}=-\frac{\Delta}{C_{2}}, \ k_{3}=\frac{\Delta}{C_{3}}\) ➜ \(C_{2}, C_{3}\) যথাক্রমে \(\Delta \) নির্ণায়কে \( c_{2},c_{3} \) এর সহগুণক।
এখন \((10)\) হতে পাই,
\(\triangle ABC\) এর ক্ষেত্রফল \(=\frac{\frac{\Delta}{C_{1}}\times -\frac{\Delta}{C_{2}}\times \frac{\Delta}{C_{3}}}{2\Delta\times C_{1}C_{2}C_{3}}\)
\(=-\frac{\Delta^{3}}{2\Delta\times C_{1}C_{2}C_{3}}\)
\(=\frac{\Delta^{2}}{2C_{1}C_{2}C_{3}}\) ➜ \(\because \triangle \neq -ve\)
Proof:
মনে করি, কোনো ত্রিভুজের বাহু তিনটি যথাক্রমে\(a_{1}x+b_{1}y+c_{1}=0 .........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 .........(2)\)
\(a_{3}x+b_{3}y+c_{3}=0 .........(3)\)
\((1)\), \((2)\), \((3)\) হতে \(x, y\) অপনয়ন করে পাই
\(\Delta=\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|\)
ধরি,
\((2)\) ও \((3)\) এর ছেদবিন্দু \(A(x_{1},y_{1})\Rightarrow a_{2}x_{1}+b_{2}y_{1}+c_{2}=0 ........(4),\)
\(a_{3}x_{1}+b_{3}y_{1}+c_{3}=0 .........(5)\)
\((3)\) ও \((1)\) এর ছেদবিন্দু \(B(x_{2},y_{2})\Rightarrow a_{3}x_{2}+b_{3}y_{2}+c_{3}=0 ........(6),\)
\(a_{1}x_{2}+b_{1}y_{2}+c_{1}=0 ........(7) \)
\((1)\) ও \((2)\) এর ছেদবিন্দু \(C(x_{3},y_{3})\Rightarrow a_{1}x_{3}+b_{1}y_{3}+c_{1}=0 ........(8),\)
\(a_{2}x_{3}+b_{2}y_{3}+c_{2}=0 ........(9) \)
এখন, \(\triangle ABC\) এর ক্ষেত্রফল \(=\frac{1}{2}\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ \ \ 1\\x_{2} \ \ y_{2} \ \ \ \ 1\\x_{3} \ \ y_{3} \ \ \ \ 1\end{array}\right| \)
\(=\frac{1}{2}\frac{\left|\begin{array}{c}x_{1} \ \ y_{1} \ \ \ \ 1\\x_{2} \ \ y_{2} \ \ \ \ 1\\x_{3} \ \ y_{3} \ \ \ \ 1\end{array}\right|\times \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|}{\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|} \)
\(=\frac{\left|\begin{array}{c}a_{1}x_{1}+b_{1}y_{1}+c_{1} \ \ \ \ a_{2}x_{1}+b_{2}y_{1}+c_{2} \ \ \ \ a_{3}x_{1}+b_{3}y_{1}+c_{3} \\ a_{1}x_{2}+b_{1}y_{2}+c_{1} \ \ \ \ a_{2}x_{2}+b_{2}y_{2}+c_{2} \ \ \ \ a_{3}x_{2}+b_{3}y_{2}+c_{3}\\ a_{1}x_{3}+b_{1}y_{3}+c_{1} \ \ \ \ a_{2}x_{3}+b_{2}y_{3}+c_{2} \ \ \ \ a_{3}x_{3}+b_{3}y_{3}+c_{3}\end{array}\right|}{2\Delta} \)
\(=\frac{\left|\begin{array}{c}a_{1}x_{1}+b_{1}y_{1}+c_{1} \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \\ 0 \ \ \ \ \ \ \ \ \ \ \ \ a_{2}x_{2}+b_{2}y_{2}+c_{2} \ \ \ \ \ \ \ \ \ \ \ \ 0\\ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \ \ \ \ \ \ \ \ \ \ \ \ a_{3}x_{3}+b_{3}y_{3}+c_{3}\end{array}\right|}{2\Delta} \) ➜ (4),(5),(6),(7),(8),(9) এর সাহায্যে
\(=\frac{(a_{1}x_{1}+b_{1}y_{1}+c_{1})(a_{2}x_{2}+b_{2}y_{2}+c_{2})(a_{3}x_{3}+b_{3}y_{3}+c_{3})}{2\Delta} ..........(10)\)
ধরি,
\(a_{1}x_{1}+b_{1}y_{1}+c_{1}=k_{1}\)
\(\Rightarrow a_{1}x_{1}+b_{1}y_{1}+c_{1}-k_{1}=0 ............. (11)\)
\(a_{2}x_{1}+b_{2}y_{1}+c_{2}=0 ............(12)\)
\(a_{3}x_{1}+b_{3}y_{1}+c_{3}=0 ............. (13)\)
\((11), (12), (13)\) হতে \(x_{1}, y_{1}\) অপনয়ন করে পাই ,
\(\left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}-k_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ \ \ \ \ c_{2} \ \ \ \ \\a_{3} \ \ \ \ b_{3} \ \ \ \ \ \ \ \ c_{3} \ \ \ \ \end{array}\right|=0\)
\(\Rightarrow \left|\begin{array}{c}a_{1} \ \ \ \ b_{1} \ \ \ \ c_{1}\\a_{2} \ \ \ \ b_{2} \ \ \ \ c_{2}\\a_{3} \ \ \ \ b_{3} \ \ \ \ c_{3}\end{array}\right|+\left|\begin{array}{c}a_{1} \ \ \ \ \ b_{1} \ \ \ \ -k_{1}\\a_{2} \ \ \ \ \ b_{2} \ \ \ \ \ \ \ \ 0 \ \ \ \\a_{3} \ \ \ \ \ b_{3} \ \ \ \ \ \ \ \ 0 \ \ \ \end{array}\right|=0\)
\(\Rightarrow \Delta-k_{1}\left|\begin{array}{c}a_{2} \ \ \ \ b_{2}\\a_{3} \ \ \ \ b_{3}\end{array}\right|=0\)
\(\Rightarrow \Delta-k_{1}(a_{2}b_{3}-a_{3}b_{2})=0\)
\(\Rightarrow \Delta-k_{1}C_{1}=0\) ➜ \(C_{1}= \Delta \) নির্ণায়কে \( c_{1}\) এর সহগুণক।
\(\Rightarrow \Delta=k_{1}C_{1}\)
\(\Rightarrow k_{1}C_{1}=\Delta\)
\(\therefore k_{1}=\frac{\Delta}{C_{1}}\)
অনুরূপভাবে,
\(a_{2}x_{2}+b_{2}y_{2}+c_{2}=k_{2}, \ a_{3}x_{3}+b_{3}y_{3}+c_{3}=k_{3} \) কল্পনা করে পাই
\(k_{2}=-\frac{\Delta}{C_{2}}, \ k_{3}=\frac{\Delta}{C_{3}}\) ➜ \(C_{2}, C_{3}\) যথাক্রমে \(\Delta \) নির্ণায়কে \( c_{2},c_{3} \) এর সহগুণক।
এখন \((10)\) হতে পাই,
\(\triangle ABC\) এর ক্ষেত্রফল \(=\frac{\frac{\Delta}{C_{1}}\times -\frac{\Delta}{C_{2}}\times \frac{\Delta}{C_{3}}}{2\Delta\times C_{1}C_{2}C_{3}}\)
\(=-\frac{\Delta^{3}}{2\Delta\times C_{1}C_{2}C_{3}}\)
\(=\frac{\Delta^{2}}{2C_{1}C_{2}C_{3}}\) ➜ \(\because \triangle \neq -ve\)
×
\((x_{1}, y_{1})\) বিন্দু থেকে \(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব নির্ণয়
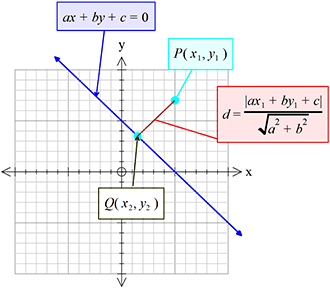
ধরি,
\(P(x_{1}, y_{1})\)
\(ax+by+c=0 ..............(1)\)
\((1)\) এর উপর যে কোনো বিন্দু \(Q(x_{2}, y_{2})\)
\((1)\) এর ঢাল \(m_{1}=-\frac{a}{b}\)
\(PQ\) এর ঢাল \(m_{2}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
শর্তমতে,
\((1)\) সরলরেখা এবং \(PQ\) রেখাংশ পরস্পর লম্ব।
\(\therefore m_{1}\times m_{2}=-1\)
\(\Rightarrow -\frac{a}{b}\times \frac{y_{1}-y_{2}}{x_{1}-x_{2}}=-1\)
\(\Rightarrow \frac{ay_{1}-ay_{2}}{bx_{1}-bx_{2}}=1\)
\(\Rightarrow ay_{1}-ay_{2}=bx_{1}-bx_{2}\)
\(\Rightarrow ay_{1}-ay_{2}-bx_{1}+bx_{2}=0\)
\(\Rightarrow bx_{2}-bx_{1}+ay_{1}-ay_{2}=0 ...........(2)\)
আবার,
\(Q\) বিন্দুটি \((1)\) এর উপর অবস্থিত।
\(\therefore ax_{2}+by_{2}+c=0 ......(3)\)
\((2)\) ও \((3)\) সমাধান করে \(x_{2}\) ও \(y_{2}\) এর মান নির্ণয় করি।
\((2)\times b+(3)\times a\) এর সাহায্যে,
\(b^{2}x_{2}-b^{2}x_{1}+aby_{1}-aby_{2}+a^{2}x_{2}+aby_{2}+ac=0\)
\(\Rightarrow b^{2}x_{2}-b^{2}x_{1}+aby_{1}+a^{2}x_{2}+ac=0\)
\(\Rightarrow x_{2}(b^{2}+a^{2})=b^{2}x_{1}-aby_{1}-ac\)
\(\therefore x_{2}=\frac{b^{2}x_{1}-aby_{1}-ac}{b^{2}+a^{2}}\)
\((2)\times a-(3)\times b\) এর সাহায্যে,
\(ab^{2}x_{2}-abx_{1}+a^{2}y_{1}-a^{2}y_{2}-abx_{2}-b^{2}y_{2}-bc=0\)
\(\Rightarrow -abx_{1}+a^{2}y_{1}-a^{2}y_{2}-b^{2}y_{2}-bc=0\)
\(\Rightarrow -y_{2}(a^{2}+b^{2})=abx_{1}-a^{2}y_{1}+bc\)
\(\therefore y_{2}=-\frac{abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}}\)
এখন,
লম্ব দূরত্ব
\(d=PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(x_{1}-\frac{b^{2}x_{1}-aby_{1}-ac}{b^{2}+a^{2}})^{2}+(y_{1}+\frac{abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}})^{2}}\)
\(=\sqrt{(\frac{b^{2}x_{1}+a^{2}x_{1}-b^{2}x_{1}+aby_{1}+ac}{a^{2}+b^{2}})^{2}+(\frac{a^{2}y_{1}+b^{2}y_{1}+abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}})^{2}}\)
\(=\sqrt{\frac{(a^{2}x_{1}+aby_{1}+ac)^{2}}{(a^{2}+b^{2})^{2}}+\frac{(b^{2}y_{1}+abx_{1}+bc)^{2}}{(a^{2}+b^{2})^{2}}}\)
\(=\sqrt{\frac{a^{2}(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}+\frac{b^{2}(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}}\)
\(=\sqrt{\frac{(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}\times (a^{2}+b^{2})}\)
\(=\sqrt{\frac{(ax_{1}+by_{1}+c)^{2}}{a^{2}+b^{2}}}\)
\(=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore \) লম্ব দূরত্ব \(d=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)

ধরি,
\(P(x_{1}, y_{1})\)
\(ax+by+c=0 ..............(1)\)
\((1)\) এর উপর যে কোনো বিন্দু \(Q(x_{2}, y_{2})\)
\((1)\) এর ঢাল \(m_{1}=-\frac{a}{b}\)
\(PQ\) এর ঢাল \(m_{2}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}\)
শর্তমতে,
\((1)\) সরলরেখা এবং \(PQ\) রেখাংশ পরস্পর লম্ব।
\(\therefore m_{1}\times m_{2}=-1\)
\(\Rightarrow -\frac{a}{b}\times \frac{y_{1}-y_{2}}{x_{1}-x_{2}}=-1\)
\(\Rightarrow \frac{ay_{1}-ay_{2}}{bx_{1}-bx_{2}}=1\)
\(\Rightarrow ay_{1}-ay_{2}=bx_{1}-bx_{2}\)
\(\Rightarrow ay_{1}-ay_{2}-bx_{1}+bx_{2}=0\)
\(\Rightarrow bx_{2}-bx_{1}+ay_{1}-ay_{2}=0 ...........(2)\)
আবার,
\(Q\) বিন্দুটি \((1)\) এর উপর অবস্থিত।
\(\therefore ax_{2}+by_{2}+c=0 ......(3)\)
\((2)\) ও \((3)\) সমাধান করে \(x_{2}\) ও \(y_{2}\) এর মান নির্ণয় করি।
\((2)\times b+(3)\times a\) এর সাহায্যে,
\(b^{2}x_{2}-b^{2}x_{1}+aby_{1}-aby_{2}+a^{2}x_{2}+aby_{2}+ac=0\)
\(\Rightarrow b^{2}x_{2}-b^{2}x_{1}+aby_{1}+a^{2}x_{2}+ac=0\)
\(\Rightarrow x_{2}(b^{2}+a^{2})=b^{2}x_{1}-aby_{1}-ac\)
\(\therefore x_{2}=\frac{b^{2}x_{1}-aby_{1}-ac}{b^{2}+a^{2}}\)
\((2)\times a-(3)\times b\) এর সাহায্যে,
\(ab^{2}x_{2}-abx_{1}+a^{2}y_{1}-a^{2}y_{2}-abx_{2}-b^{2}y_{2}-bc=0\)
\(\Rightarrow -abx_{1}+a^{2}y_{1}-a^{2}y_{2}-b^{2}y_{2}-bc=0\)
\(\Rightarrow -y_{2}(a^{2}+b^{2})=abx_{1}-a^{2}y_{1}+bc\)
\(\therefore y_{2}=-\frac{abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}}\)
এখন,
লম্ব দূরত্ব
\(d=PQ=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\)
\(=\sqrt{(x_{1}-\frac{b^{2}x_{1}-aby_{1}-ac}{b^{2}+a^{2}})^{2}+(y_{1}+\frac{abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}})^{2}}\)
\(=\sqrt{(\frac{b^{2}x_{1}+a^{2}x_{1}-b^{2}x_{1}+aby_{1}+ac}{a^{2}+b^{2}})^{2}+(\frac{a^{2}y_{1}+b^{2}y_{1}+abx_{1}-a^{2}y_{1}+bc}{a^{2}+b^{2}})^{2}}\)
\(=\sqrt{\frac{(a^{2}x_{1}+aby_{1}+ac)^{2}}{(a^{2}+b^{2})^{2}}+\frac{(b^{2}y_{1}+abx_{1}+bc)^{2}}{(a^{2}+b^{2})^{2}}}\)
\(=\sqrt{\frac{a^{2}(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}+\frac{b^{2}(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}}\)
\(=\sqrt{\frac{(ax_{1}+by_{1}+c)^{2}}{(a^{2}+b^{2})^{2}}\times (a^{2}+b^{2})}\)
\(=\sqrt{\frac{(ax_{1}+by_{1}+c)^{2}}{a^{2}+b^{2}}}\)
\(=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore \) লম্ব দূরত্ব \(d=\frac{\left|ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
বিকল্প পদ্ধতিঃ
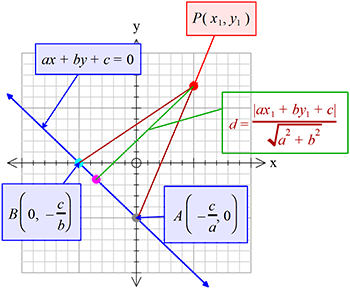
ধরি,
\(P(x_{1}, y_{1})\)
\(ax+by+c=0 .........(1)\)
\(P\) হতে \((1)\) এর লম্ব দূরত্ব \(d\).
\((1)\) হতে,
\(ax+by=-c\)
\(\Rightarrow \frac{ax}{-c}+\frac{by}{-c}=\frac{-c}{-c}\) ➜ উভয় পার্শে \(-c\) ভাগ করে
\(\Rightarrow \frac{x}{\frac{-c}{a}}+\frac{y}{\frac{-c}{b}}=1\)
\(\therefore (1)\) নং সরলরেখা অক্ষদ্বয়কে যথাক্রমে \(A(-\frac{c}{a}, 0)\) ও \(B(0, -\frac{c}{b})\) বিন্দুতে ছেদ করে।
এখন,
\(\triangle ABP=\frac{1}{2}\left|\begin{array}{c}-\frac{c}{a} \ \ \ \ 0 \ \ \ \ \ x_{1} \ \ \ -\frac{c}{a}\\ 0 \ -\frac{c}{b} \ \ \ \ \ y_{1} \ \ \ \ \ \ \ \ 0\end{array}\right|\)
\(=\frac{1}{2}\{(\frac{c^{2}}{ab}-0)+(0+\frac{cx_{1}}{b})+(0+\frac{cy_{1}}{a})\}\)
\(=\frac{1}{2}\{\frac{c^{2}}{ab}+\frac{cx_{1}}{b}+\frac{cy_{1}}{a}\}\)
\(=\frac{1}{2}\times \frac{c}{ab}\{c+ax_{1}+by_{1}\}\)
\(=\frac{c}{2ab}(ax_{1}+by_{1}+c)\)
\(AB=\sqrt{(-\frac{c}{a}-0)^{2}+(0+\frac{c}{b})^{2}}\)
\(=\sqrt{\frac{c^{2}}{a^{2}}+\frac{c^{2}}{b^{2}}}\)
\(=\sqrt{\frac{c^{2}(a^{2}+b^{2})}{a^{2}b^{2}}}\)
\(=\frac{c}{ab}\sqrt{a^{2}+b^{2}}\)
কিন্তু,
\(\frac{1}{2}\times AB\times d=\triangle ABP\)
\(\Rightarrow \frac{1}{2}\times \frac{c}{ab}\sqrt{a^{2}+b^{2}}\times d=\frac{c}{2ab}(ax_{1}+by_{1}+c)\)
\(\Rightarrow d=\frac{c}{2ab}(ax_{1}+by_{1}+c)\times 2\times \frac{ab}{c\sqrt{a^{2}+b^{2}}}\)
\(\Rightarrow d=\frac{\left| ax_{1}+by_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
×
মূলবিন্দু হতে একটি সরলরেখার লম্ব দূরত্ব নির্ণয়

ধরি,
মূলবিন্দু তথা \(O(0, 0)\)
\(ax+by+c=0 ...........(1)\)
\(O(0, 0)\) হতে \((1)\) এর লম্ব দূরত্ব \(d=\frac{\left|a.0+b.0+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\Rightarrow d=\frac{\left|0+0+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore d=\frac{\left|c\right|}{\sqrt{a^{2}+b^{2}}}\)

ধরি,
মূলবিন্দু তথা \(O(0, 0)\)
\(ax+by+c=0 ...........(1)\)
\(O(0, 0)\) হতে \((1)\) এর লম্ব দূরত্ব \(d=\frac{\left|a.0+b.0+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\Rightarrow d=\frac{\left|0+0+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore d=\frac{\left|c\right|}{\sqrt{a^{2}+b^{2}}}\)
×
দুইটি সমান্তরাল সরলরেখার মধ্যবর্তী লম্ব দূরত্ব নির্ণয়

ধরি,
\(ax+by+c_{1}=0 ......(1)\)
\(ax+by+c_{2}=0 ......(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী লম্ব দূরত্ব \(d\)
\(p(x_{1}, y_{1})\) বিন্দুটি \((2)\) এর উপর অবস্থিত,
\(\therefore ax_{1}+by_{1}+c_{2}=0\)
\(\Rightarrow ax_{1}+by_{1}=-c_{2}...........(3)\)
আবার,
\(p(x_{1}, y_{1})\) বিন্দু হতে \((1)\) এর লম্ব দূরত্ব,
\(d=\frac{\left|ax_{1}+bx_{1}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}\)
\(=\frac{\left|-c_{2}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}\) ➜ \((3)\) এর সাহায্যে
\(=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore d=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)

ধরি,
\(ax+by+c_{1}=0 ......(1)\)
\(ax+by+c_{2}=0 ......(2)\)
\((1)\) ও \((2)\) সরলরেখাদ্বয়ের মধ্যবর্তী লম্ব দূরত্ব \(d\)
\(p(x_{1}, y_{1})\) বিন্দুটি \((2)\) এর উপর অবস্থিত,
\(\therefore ax_{1}+by_{1}+c_{2}=0\)
\(\Rightarrow ax_{1}+by_{1}=-c_{2}...........(3)\)
আবার,
\(p(x_{1}, y_{1})\) বিন্দু হতে \((1)\) এর লম্ব দূরত্ব,
\(d=\frac{\left|ax_{1}+bx_{1}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}\)
\(=\frac{\left|-c_{2}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}\) ➜ \((3)\) এর সাহায্যে
\(=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
\(\therefore d=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
×
দুইটি পরস্পরছেদী সরলরেখার অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ নির্ণয়
ধরি,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের উপর যে কোনো বিন্দু \(P(x, y)\)।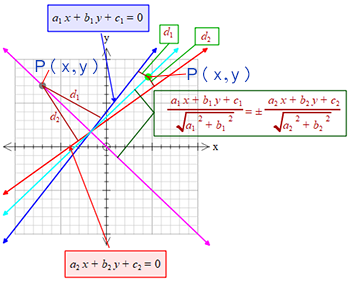
\(P(x, y)\) হতে \((1)\) এর লম্ব দূরত্ব \(d_{1}=\frac{\left| a_{1}x+b_{1}y+c_{1} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}\)
\(P(x, y)\) হতে \((2)\) এর লম্ব দূরত্ব \(d_{2}=\frac{\left| a_{2}x+b_{2}y+c_{2} \right|}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
শর্তমতে,
\(d_{1}=d_{2}\)
\(\Rightarrow \frac{\left| a_{1}x+b_{1}y+c_{1} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\frac{\left| a_{2}x+b_{2}y+c_{2} \right|}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
\(\Rightarrow \frac{ a_{1}x+b_{1}y+c_{1} }{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\pm \frac{ a_{2}x+b_{2}y+c_{2} }{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
ইহাই নির্ণেয় সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ।
ধরি,
\(a_{1}x+b_{1}y+c_{1}=0 ........(1)\)
\(a_{2}x+b_{2}y+c_{2}=0 ........(2)\)
\((1)\) ও \((2)\) এর অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক সরলরেখাদ্বয়ের উপর যে কোনো বিন্দু \(P(x, y)\)।

\(P(x, y)\) হতে \((1)\) এর লম্ব দূরত্ব \(d_{1}=\frac{\left| a_{1}x+b_{1}y+c_{1} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}\)
\(P(x, y)\) হতে \((2)\) এর লম্ব দূরত্ব \(d_{2}=\frac{\left| a_{2}x+b_{2}y+c_{2} \right|}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
শর্তমতে,
\(d_{1}=d_{2}\)
\(\Rightarrow \frac{\left| a_{1}x+b_{1}y+c_{1} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\frac{\left| a_{2}x+b_{2}y+c_{2} \right|}{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
\(\Rightarrow \frac{ a_{1}x+b_{1}y+c_{1} }{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\pm \frac{ a_{2}x+b_{2}y+c_{2} }{\sqrt{a_{2}^{2}+b_{2}^{2}}}\)
ইহাই নির্ণেয় সমদ্বিখন্ডক সরলরেখাদ্বয়ের সমীকরণ।
×
\(\triangle ABC\) এর শীর্ষবিন্দু তিনটি \((x_{1}, y_{1})\), \((x_{2}, y_{2})\) এবং \((x_{3}, y_{3})\)। বাহুগুলি \(BC=a, \ CA=b, \ AB=c \) হলে, এর অন্তঃকেন্দ্র নির্ণয়

ধরি,
\(\triangle ABC\) এর \(\angle A\), \(\angle B\) কোণ দুইটির সমদ্বিখন্ডক \(AD\) ও \(BE\) পরস্পর \(I\) বিন্দুতে ছেদ করে যা ত্রিভুজের অন্তঃকেন্দ্র।
শর্তমতে,
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{c}{b}\)
\(\Rightarrow \frac{BD}{DC}=\frac{c}{b}\)
\(\Rightarrow BD:DC=c:b\)
\(\therefore D(\frac{bx_{2}+cx_{3}}{b+c}, \frac{by_{2}+cy_{3}}{b+c})\)
আবার,
\(\frac{AI}{ID}=\frac{AB}{BD}=\frac{AC}{CD}=\frac{AB+AC}{BD+CD}\)
\(\Rightarrow \frac{AI}{ID}=\frac{c+b}{BC}\)
\(\Rightarrow \frac{AI}{ID}=\frac{c+b}{a}\)
\(\Rightarrow AI:ID=(c+b):a\)
\(\therefore I(\frac{(b+c).\frac{bx_{2}+cx_{3}}{b+c}+a.x_{1}}{a+b+c}, \frac{(b+c).\frac{by_{2}+cy_{3}}{b+c}+a.y_{1}}{a+b+c})\)
\(\Rightarrow I(\frac{bx_{2}+cx_{3}+ax_{1}}{a+b+c}, \frac{by_{2}+cy_{3}+ay_{1}}{a+b+c})\)
\(\Rightarrow I(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c})\).
\(\therefore \triangle ABC \) এর অন্তঃকেন্দ্র \(I(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c})\).

ধরি,
\(\triangle ABC\) এর \(\angle A\), \(\angle B\) কোণ দুইটির সমদ্বিখন্ডক \(AD\) ও \(BE\) পরস্পর \(I\) বিন্দুতে ছেদ করে যা ত্রিভুজের অন্তঃকেন্দ্র।
শর্তমতে,
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{c}{b}\)
\(\Rightarrow \frac{BD}{DC}=\frac{c}{b}\)
\(\Rightarrow BD:DC=c:b\)
\(\therefore D(\frac{bx_{2}+cx_{3}}{b+c}, \frac{by_{2}+cy_{3}}{b+c})\)
আবার,
\(\frac{AI}{ID}=\frac{AB}{BD}=\frac{AC}{CD}=\frac{AB+AC}{BD+CD}\)
\(\Rightarrow \frac{AI}{ID}=\frac{c+b}{BC}\)
\(\Rightarrow \frac{AI}{ID}=\frac{c+b}{a}\)
\(\Rightarrow AI:ID=(c+b):a\)
\(\therefore I(\frac{(b+c).\frac{bx_{2}+cx_{3}}{b+c}+a.x_{1}}{a+b+c}, \frac{(b+c).\frac{by_{2}+cy_{3}}{b+c}+a.y_{1}}{a+b+c})\)
\(\Rightarrow I(\frac{bx_{2}+cx_{3}+ax_{1}}{a+b+c}, \frac{by_{2}+cy_{3}+ay_{1}}{a+b+c})\)
\(\Rightarrow I(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c})\).
\(\therefore \triangle ABC \) এর অন্তঃকেন্দ্র \(I(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c}, \frac{ay_{1}+by_{2}+cy_{3}}{a+b+c})\).
×
\(ax+by+c=0\) সরলরেখার সমান্তরাল এবং \(d\) একক দূরবর্তী সরলরেখার সমীকরণ নির্ণয়
ধরি,
\(ax+by+c=0 ............(1)\)
\((1)\) এর সমান্তরাল যে কোনো সরলরেখার সমীকরণ,
\(ax+by+k=0 ............(2)\) ➜ \(k\) যে কোন বাস্তব সংখ্যা।
\((1)\) ও \((2)\) এর মধ্যবর্তী দূরত্ব \(=\frac{|k-c|}{\sqrt{a^{2}+b^{2}}}\)
শর্তমতে,
\(\frac{|k-c|}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow \pm \frac{k-c}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow \frac{k-c}{\sqrt{a^{2}+b^{2}}}=\pm d\)
\(\Rightarrow k-c=\pm d \sqrt{a^{2}+b^{2}}\)
\(\therefore k=c\pm d \sqrt{a^{2}+b^{2}}\)
\(k\) এর মান \((2)\) এ বসিয়ে,
\(ax+by+c\pm d \sqrt{a^{2}+b^{2}}=0\)
ইহাই নির্ণেয় সরলরেখার সমীকরণ।
ধরি,
\(ax+by+c=0 ............(1)\)
\((1)\) এর সমান্তরাল যে কোনো সরলরেখার সমীকরণ,

\(ax+by+k=0 ............(2)\) ➜ \(k\) যে কোন বাস্তব সংখ্যা।
\((1)\) ও \((2)\) এর মধ্যবর্তী দূরত্ব \(=\frac{|k-c|}{\sqrt{a^{2}+b^{2}}}\)
শর্তমতে,
\(\frac{|k-c|}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow \pm \frac{k-c}{\sqrt{a^{2}+b^{2}}}=d\)
\(\Rightarrow \frac{k-c}{\sqrt{a^{2}+b^{2}}}=\pm d\)
\(\Rightarrow k-c=\pm d \sqrt{a^{2}+b^{2}}\)
\(\therefore k=c\pm d \sqrt{a^{2}+b^{2}}\)
\(k\) এর মান \((2)\) এ বসিয়ে,
\(ax+by+c\pm d \sqrt{a^{2}+b^{2}}=0\)
ইহাই নির্ণেয় সরলরেখার সমীকরণ।
×
অক্ষের দিক অপরিবর্তিত রেখে মূলবিন্দু \(O(0,0)\) কে \(O^{\prime}(\alpha, \beta)\) বিন্দুতে স্থানান্তর করলে, নুতন অক্ষের সাপেক্ষে
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow (x-\alpha, y-\beta)\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f(x^{\prime}+\alpha, y^{\prime}+\beta)=0\)
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow (x-\alpha, y-\beta)\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f(x^{\prime}+\alpha, y^{\prime}+\beta)=0\)
Proof:
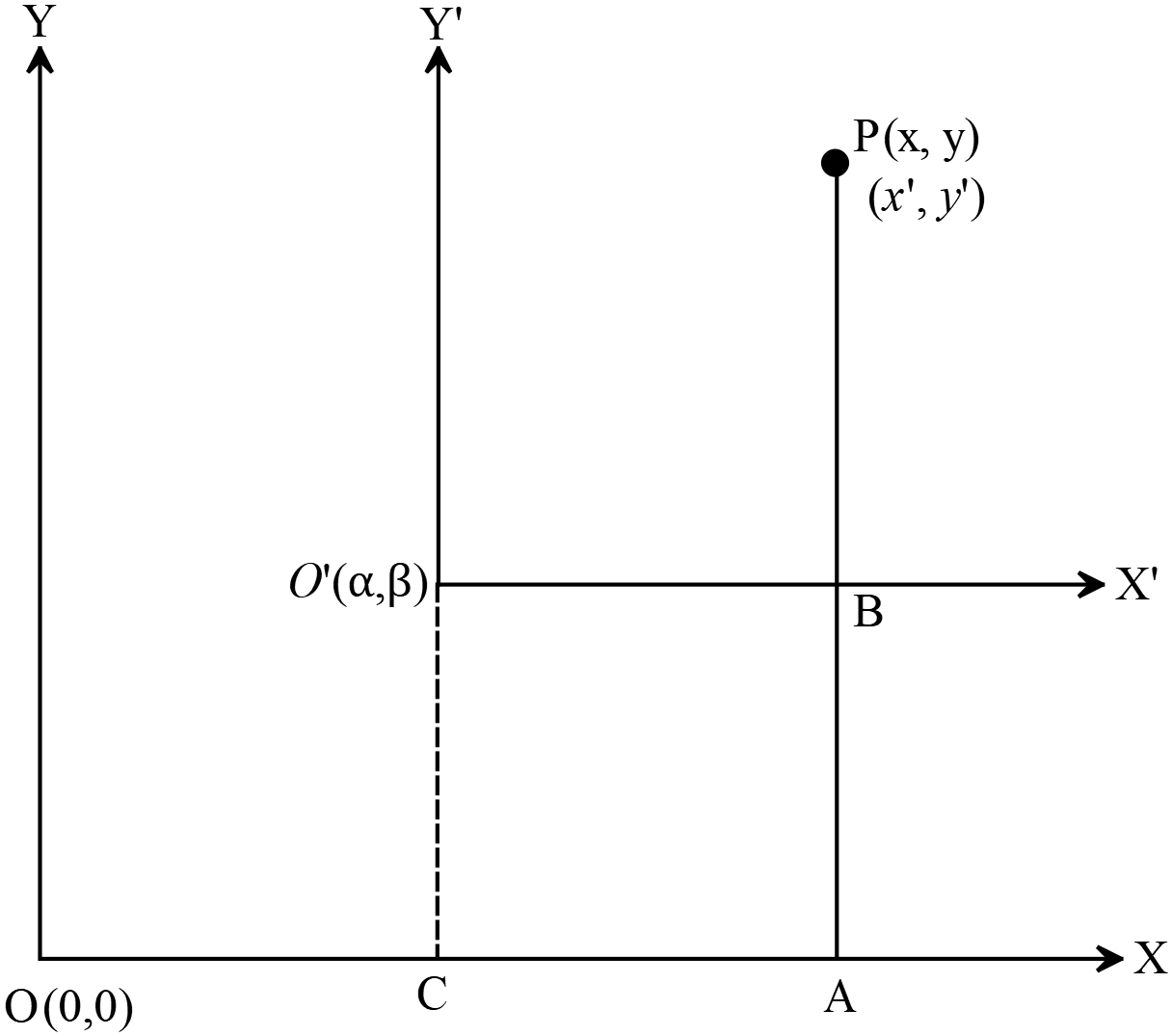
মনে করি,
আদি অক্ষদ্বয় \(OX\) এবং \(OY\) এর সাপেক্ষে কোনো একটি বিন্দু \(P\) এর স্থানাঙ্ক \((x, y)\) এবং নুতন অক্ষদ্বয় \(OX^{\prime}\) এবং \(OY^{\prime}\) এর সাপেক্ষে স্থানাঙ্ক \((x^{\prime}, y^{\prime})\)
যেখানে, \(O^{\prime}X^{\prime}\parallel{OX}, \ O^{\prime}Y^{\prime}\parallel{OY}\) এবং \(O^{\prime}\) এর স্থানাংক \((\alpha, \beta)\)
\(P\) বিন্দু থেকে \(OX\) অক্ষের উপর \(PA\) লম্ব আঁকি যা \(O^{\prime}X^{\prime}\) অক্ষেকে \(B\) বিন্দুতে ছেদ করে।
আবার \( O^{\prime}\) বিন্দু থেকে \(OX\) এর উপর \( O^{\prime}C\) লম্ব অঙ্কন করি।
এখানে, \(x=OA, \ x^{\prime}=O^{\prime}B, \ y=AP, \ y^{\prime}=BP, \ \alpha=OC, \ \beta=O^{\prime}C=AB\)
তাহলে \(x=OA\)
\(=OC+CA\)
\(=OC+O^{\prime}B\)
\(\therefore x=\alpha+x^{\prime}\)
\(\Rightarrow x-\alpha=x^{\prime}\)
\(\therefore x^{\prime}=x-\alpha\)
এবং \(y=AP\)
\(=AB+BP\)
\(=\beta+y^{\prime}\)
\(\therefore y=\beta+y^{\prime}\)
\(\Rightarrow y-\beta=y^{\prime}\)
\(\therefore y^{\prime}=y-\beta\)
\(\therefore \) নুতন অক্ষ সাপেক্ষে \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক \((x^{\prime}, y^{\prime})\Rightarrow (x-\alpha, y-\beta)\)
\((b)\) এখানে, \(x=x^{\prime}+\alpha, \ y=y^{\prime}+\beta\)
নুতন অক্ষ সাপেক্ষে \(f(x,y)=0\) সমীকরণের রূপান্তরিত সমীকরণ \(f(x^{\prime}+\alpha,y^{\prime}+\beta)=0\)
( প্রমাণিত )
×
মূলবিন্দুর অবস্থান অপরিবর্তিত রেখে অক্ষদ্বয়কে \(\theta\) কোণে আবর্তন করলে, নুতন অক্ষের সাপেক্ষে
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow (x\cos{\theta}+y\sin{\theta}, -x\sin{\theta}+y\cos{\theta})\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow (x\cos{\theta}+y\sin{\theta}, -x\sin{\theta}+y\cos{\theta})\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
Proof:
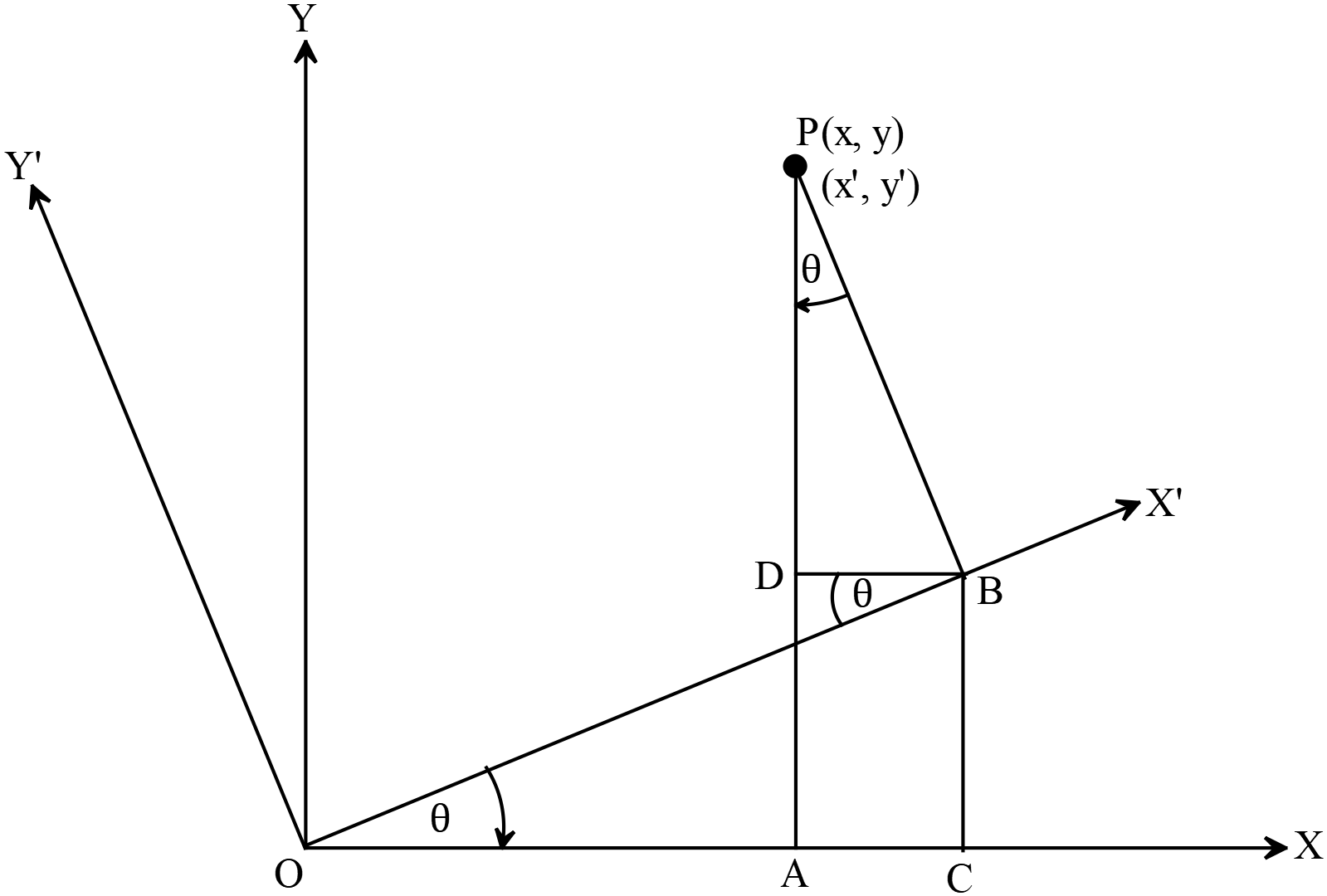
মনে করি,
আদি অক্ষদ্বয় \(OX\) এবং \(OY\) এর সাপেক্ষে কোনো একটি বিন্দু \(P\) এর স্থানাঙ্ক \((x, y)\) এবং নুতন অক্ষদ্বয় \(OX^{\prime}\) এবং \(OY^{\prime}\) এর সাপেক্ষে স্থানাঙ্ক \((x^{\prime}, y^{\prime})\)
এখানে, আদি অক্ষদ্বয় \(OX\) এবং \(OY\) কে \(\theta\) কোণে আবর্তনের ফলে উৎপন্ন নুতন অক্ষদ্বয় যথাক্রমে \(OX^{\prime}\) এবং \(OY^{\prime}, \ \angle{X^{\prime}OX}=\theta, \ \angle{Y^{\prime}OY}=\theta\)
\(P\) বিন্দু থেকে \(OX\) অক্ষের উপর \(PA\) এবং \(OX^{\prime}\) অক্ষের উপর \(PB\) লম্ব আঁকি।
আবার \(B\) বিন্দু থেকে \(OX\) এর উপর \( BC\) এবং \(PA\) এর উপর \(BD\) লম্ব অঙ্কন করি।
তাহলে \(OB=x^{\prime}, \ PB=y^{\prime}, \ \angle{OBD}=\theta\)
\(\Rightarrow \angle{PBD}=90^{o}-\theta\)
\(\therefore \angle{P}=\theta\)
\(\triangle{PBD}\) হতে,
\(\cos{\theta}=\frac{PD}{PB}\)
\(\Rightarrow \cos{\theta}=\frac{PD}{y^{\prime}}\)
\(\therefore PD=y^{\prime}\cos{\theta}\)
এবং \(\sin{\theta}=\frac{BD}{PB}\)
\(\Rightarrow \sin{\theta}=\frac{BD}{y^{\prime}}\)
\(\therefore BD=y^{\prime}\sin{\theta}\)
\(\triangle{OBC}\) হতে,
\(\cos{\theta}=\frac{OC}{OB}\)
\(\Rightarrow \cos{\theta}=\frac{OC}{x^{\prime}}\)
\(\therefore OC=x^{\prime}\cos{\theta}\)
এবং \(\sin{\theta}=\frac{BC}{OB}\)
\(\Rightarrow \sin{\theta}=\frac{BC}{x^{\prime}}\)
\(\therefore BC=x^{\prime}\sin{\theta}\)
এখন, \(x=OA\)
\(\Rightarrow x=OC-AC\)
\(\Rightarrow x=OC-BD, \ \because AC=BD\)
\(\therefore x=x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta} .......(1)\)
এবং \(y=PA\)
\(\Rightarrow y=AD+PD\)
\(\Rightarrow y=BC+PD, \ \because AD=BC\)
\(\therefore y=x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta} .....(2)\)
\((1)\times{\cos{\theta}}+(2)\times{\sin{\theta}}\) এর সাহায্যে
\(x^{\prime}=x\cos{\theta}+y\sin{\theta}\)
\((2)\times{\cos{\theta}}-(1)\times{\sin{\theta}}\) এর সাহায্যে
\(y^{\prime}=y\cos{\theta}-x\sin{\theta}\)
\(\therefore \) নুতন অক্ষ সাপেক্ষে \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক \((x^{\prime}, y^{\prime})\Rightarrow (x\cos{\theta}+y\sin{\theta}, -x\sin{\theta}+y\cos{\theta})\)
\((b)\) এখানে, \(x=x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, \ y=x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\)
নুতন অক্ষ সাপেক্ষে \(f(x,y)=0\) সমীকরণের রূপান্তরিত সমীকরণ \(f(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta},x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
( প্রমাণিত )
×
অক্ষদ্বয়কে \(\theta\) কোণে আবর্তন করলে এবং মূলবিন্দু \(O(0,0)\) কে \(O^{\prime}(\alpha, \beta)\) বিন্দুতে স্থানান্তর করলে,, নুতন অক্ষের সাপেক্ষে
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow \{(x-\alpha)\cos{\theta}+(y-\beta)\sin{\theta}, -(x-\alpha)\sin{\theta}+(y-\beta)\cos{\theta}\}\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f(\alpha+x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, \beta+x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow \{(x-\alpha)\cos{\theta}+(y-\beta)\sin{\theta}, -(x-\alpha)\sin{\theta}+(y-\beta)\cos{\theta}\}\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f(\alpha+x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}, \beta+x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
Proof:
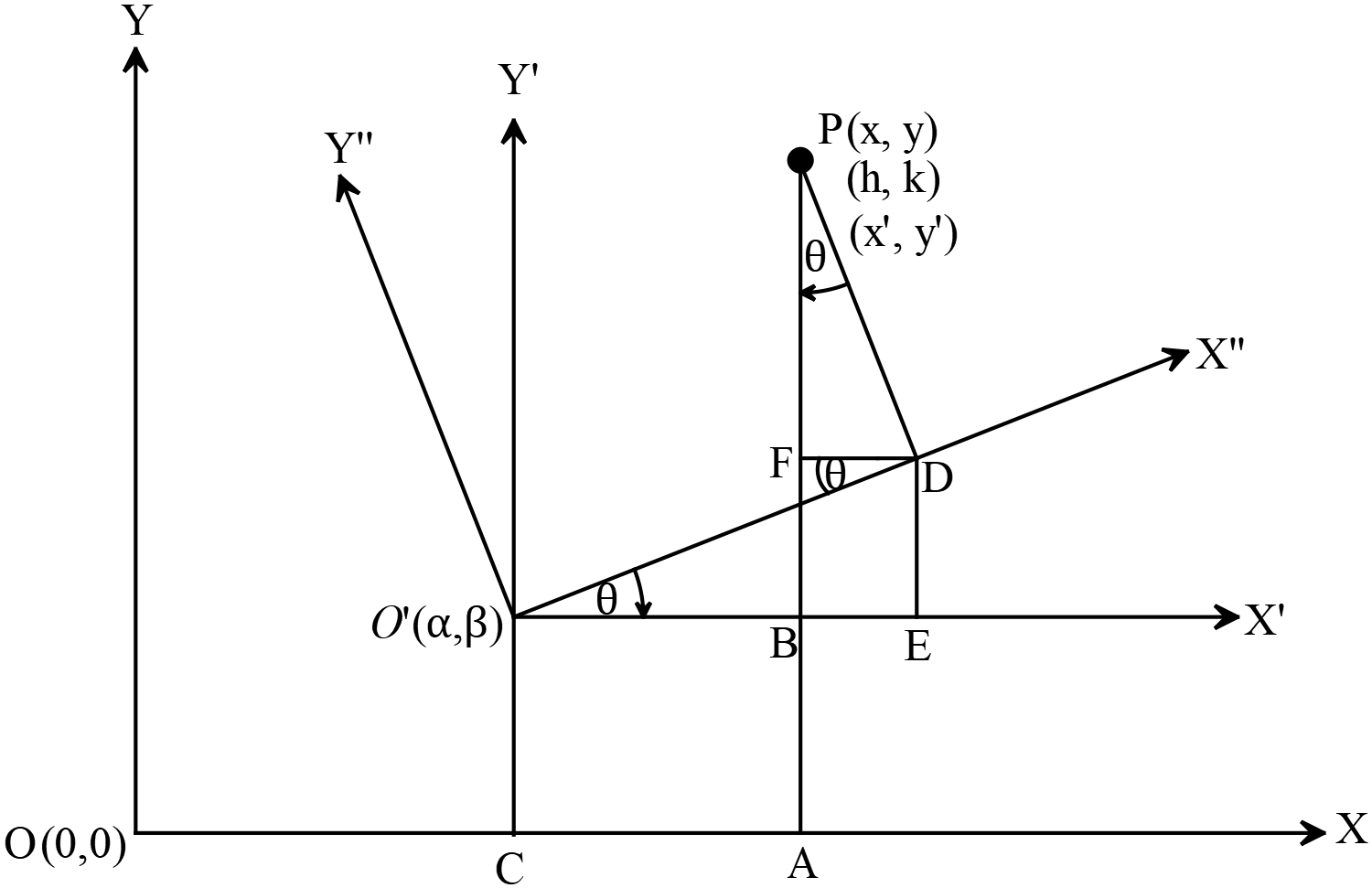
মনে করি,
আদি অক্ষদ্বয় \(OX\) এবং \(OY\) এর সাপেক্ষে কোনো একটি বিন্দু \(P\) এর স্থানাঙ্ক \((x, y)\) এবং নুতন অক্ষদ্বয় \(OX^{\prime}\) এবং \(OY^{\prime}\) এর সাপেক্ষে স্থানাঙ্ক \((h, k)\)
যেখানে, \(O^{\prime}X^{\prime}\parallel{OX}, \ O^{\prime}Y^{\prime}\parallel{OY}\) এবং \(O^{\prime}\) এর স্থানাংক \((\alpha, \beta)\)
এখন, \(P\) বিন্দু থেকে \(OX\) অক্ষের উপর \(PA\) লম্ব অঙ্কন করি যা \(O^{\prime}X^{\prime}\) কে \(B\) বিন্দুতে ছেদ করে।
আবার, \(O^{\prime}\) বিন্দু থেকে \(OX\) অক্ষের উপর \(O^{\prime}C\) লম্ব অঙ্কন করি ।
তাহলে \(OC=\alpha, \ O^{\prime}B=h, \ O^{\prime}C=\beta, \ PB=k\)
এখন, \(x=OA\)
\(=OC+CA\)
\(=OC+O^{\prime}B; \ \because CA=O^{\prime}B\)
\(\therefore x=\alpha+h\)
\(\Rightarrow x-\alpha=h\)
\(\therefore h=x-\alpha\)
এবং \(y=PA\)
\(=PB+BA\)
\(=PB+O^{\prime}C; \ \because BA=O^{\prime}C\)
\(\therefore y=k+\beta\)
\(\Rightarrow y-\beta=k\)
\(\therefore k=y-\beta\)
আবার ধরি, \(O^{\prime}\) বিন্দুকে স্থির রেখে \(O^{\prime}X^{\prime}\) এবং \(O^{\prime}Y^{\prime}\) অক্ষদ্বয়কে \(\theta\) আবর্তন করলে \((h, k)\) বিন্দুর নুতন স্থানাঙ্ক \((x^{\prime}, y^{\prime})\) হয়।
এবং \(O^{\prime}X^{\prime}\) এবং \(O^{\prime}Y^{\prime}\) অক্ষদ্বয়ের রূপান্তরিত অক্ষদ্বয় যথাক্রমে \(O^{\prime}X^{\prime\prime}\) এবং \(O^{\prime}Y^{\prime\prime}\) হয়।
যদি \(PB\perp{O^{\prime}X^{\prime}}, \ PD\perp{O^{\prime}X^{\prime\prime}}, DE\perp{O^{\prime}X^{\prime}}\) এবং \(DF\perp{PB}\) হয়।
তবে, \(O^{\prime}B=h, \ PB=k, \ O^{\prime}D=x^{\prime}, \ PD=y^{\prime}\)
এবং \(\angle{X^{\prime\prime}O^{\prime}X^{\prime}}=\theta\)
\(\Rightarrow \angle{O^{\prime}DF}=\theta\)
\(\therefore \angle{DPE}=\theta\)
\(\triangle{DPF}\) হতে,
\(\cos{\theta}=\frac{PF}{PD}\)
\(\Rightarrow \cos{\theta}=\frac{PF}{y^{\prime}}\)
\(\therefore PF=y^{\prime}\cos{\theta}\)
এবং \(\sin{\theta}=\frac{FD}{PD}\)
\(\Rightarrow \sin{\theta}=\frac{FD}{y^{\prime}}\)
\(\therefore FD=y^{\prime}\sin{\theta}\)
আবার, \(\triangle{O^{\prime}DE}\) হতে,
\(\sin{\theta}=\frac{DE}{O^{\prime}D}\)
\(\Rightarrow \sin{\theta}=\frac{DE}{x^{\prime}}\)
\(\therefore DE=x^{\prime}\sin{\theta}\)
এবং \(\cos{\theta}=\frac{O^{\prime}E}{O^{\prime}D}\)
\(\Rightarrow \cos{\theta}=\frac{O^{\prime}E}{x^{\prime}}\)
\(\therefore O^{\prime}E=x^{\prime}\cos{\theta}\)
এখন, \(h=O^{\prime}B\)
\(\Rightarrow h=O^{\prime}E-BE\)
\(\Rightarrow h=O^{\prime}E-FD, \ \because BE=FD\)
\(\therefore h=x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta} .......(1)\)
এবং \(k=PB\)
\(\Rightarrow k=PF+FB\)
\(\Rightarrow k=PF+DE, \ \because FB=DE\)
\(\Rightarrow k=y^{\prime}\cos{\theta}+x^{\prime}\sin{\theta}\)
\(\therefore k=x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta} .......(2)\)
\((1)\times{\cos{\theta}}+(2)\times{\sin{\theta}}\) এর সাহায্যে
\(x^{\prime}=h\cos{\theta}+k\sin{\theta}\)
\(\therefore x^{\prime}=(x-\alpha)\cos{\theta}+(y-\beta)\sin{\theta}, \ \because h=(x-\alpha), \ k=(y-\beta)\)
\((2)\times{\cos{\theta}}-(1)\times{\sin{\theta}}\) এর সাহায্যে
\(y^{\prime}=k\cos{\theta}-h\sin{\theta}\)
\(\Rightarrow y^{\prime}=(y-\beta)\cos{\theta}-(x-\alpha)\sin{\theta}, \ \because h=(x-\alpha), \ k=(y-\beta)\)
\(\therefore y^{\prime}=-(x-\alpha)\sin{\theta}+(y-\beta)\cos{\theta}\)
\(\therefore \) নুতন অক্ষ সাপেক্ষে \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক \((x^{\prime}, y^{\prime})\Rightarrow \{(x-\alpha)\cos{\theta}+(y-\beta)\sin{\theta}, -(x-\alpha)\sin{\theta}+(y-\beta)\cos{\theta}\}\)
\((b)\) এখানে, \(x=\alpha+h\)
\(\Rightarrow x=\alpha+x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}\)
এবং \(y=\beta+k\)
\(\Rightarrow y=\beta+x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\)
নুতন অক্ষ সাপেক্ষে \(f(x,y)=0\) সমীকরণের রূপান্তরিত সমীকরণ \(f(\alpha+x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta},\beta+x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})=0\)
( প্রমাণিত )
×
যদি \(OX, \ OY\) এবং \(O^{\prime}X^{\prime}, \ O^{\prime}Y^{\prime}\) দুইজোড়া ভিন্ন ভিন্ন অক্ষ হয় এবং \(OX, \ OY\) অক্ষ সাপেক্ষে \(O^{\prime}X^{\prime},\) এবং \( O^{\prime}Y^{\prime}\) এর সমীকরণদ্বয় যথাক্রমে \(ax+by+c=0\) ও \(bx-ay+d=0\) হয় তবে, নুতন অক্ষের সাপেক্ষে
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow \left\{\frac{bx-ay+d}{\sqrt{a^2+b^2}}, \frac{ax+by+c}{\sqrt{a^2+a^2}}\right\}\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f\left(\frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}-\frac{ac+bd}{a^2+b^2}, -\frac{ax^{\prime}-by^{\prime}}{\sqrt{a^2+b^2}}-\frac{bc-ad}{a^2+b^2}\right)=0\)
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow \left\{\frac{bx-ay+d}{\sqrt{a^2+b^2}}, \frac{ax+by+c}{\sqrt{a^2+a^2}}\right\}\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণ
\(f\left(\frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}-\frac{ac+bd}{a^2+b^2}, -\frac{ax^{\prime}-by^{\prime}}{\sqrt{a^2+b^2}}-\frac{bc-ad}{a^2+b^2}\right)=0\)
Proof:
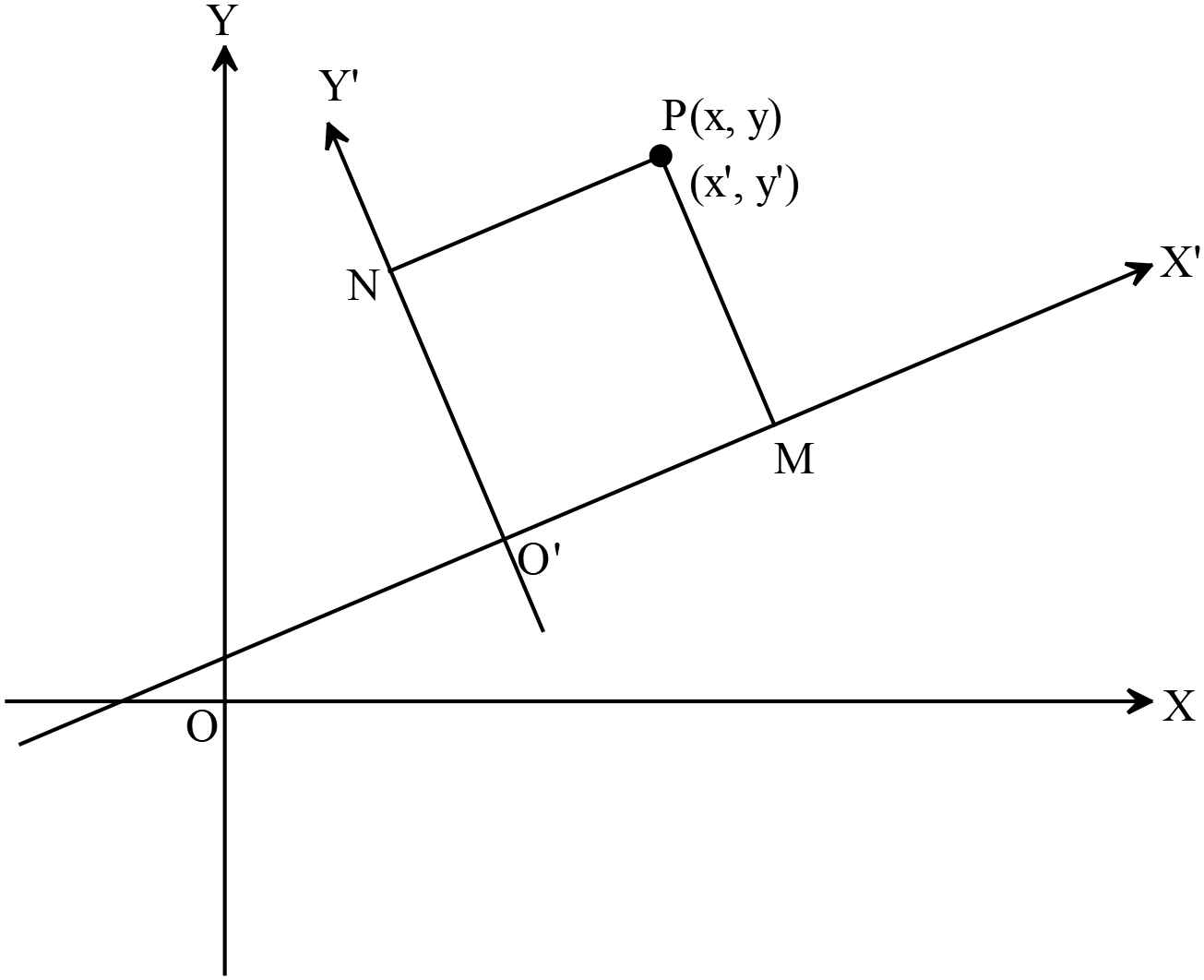
মনে করি,
\(OX\) এবং \(OY\) মূল আয়াতাকার অক্ষ এবং \(O^{\prime}X^{\prime},\) \(O^{\prime}Y^{\prime}\) নুতন আয়াতাকার অক্ষ ।
\(OX, \ OY\) অক্ষ সাপেক্ষে \(O^{\prime}X^{\prime},\) এবং \( O^{\prime}Y^{\prime}\) এর সমীকরণদ্বয় যথাক্রমে \(ax+by+c=0\) ও \(bx-ay+d=0\)
\(ax+by+c=0 ........(1)\)
\(bx-ay+d=0 ........(2)\)
অতএব \((1)\) ও \((2)\) যথাক্রমে নুতন \(x\) ও \(y\) অক্ষদ্বয় প্রকাশ করে।
ধরি, \(P\) একটি বিন্দু যার স্থানাঙ্ক মূল অক্ষদ্বয় অনুসারে \((x, y)\) এবং নুতন অক্ষদ্বয় অনুসারে \((x^{\prime}, y^{\prime})\)
\(O^{\prime}X^{\prime},\) \(O^{\prime}Y^{\prime}\) এর উপর যথাক্রমে \(PM,\) \(PN\) লম্ব অঙ্কন করি
এখন, \(x^{\prime}=O^{\prime}M\)
\(=NP\)
\(=P(x, y)\) হতে \((2)\) এর উপর লম্বের দৈর্ঘ্য
\(\therefore x^{\prime}=\frac{bx-ay+d}{\sqrt{b^2+a^2}}\) ➜ \(\because (x_{1}, y_{1})\) বিন্দু হতে,
\(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব
\(=\frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\)
\(\therefore x^{\prime}=\frac{bx-ay+d}{\sqrt{a^2+b^2}} .......(3)\)
এবং \(y^{\prime}=O^{\prime}N\)
\(=MP\)
\(=P(x, y)\) হতে \((1)\) এর উপর লম্বের দৈর্ঘ্য
\(\therefore y^{\prime}=\frac{ax+by+c}{\sqrt{a^2+b^2}} .......(4)\)➜ \(\because (x_{1}, y_{1})\) বিন্দু হতে,
\(ax+by+c=0\) সরলরেখার লম্ব দূরত্ব
\(=\frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\)
\((x, y)\) এর রূপান্তরিত স্থানাঙ্কঃ
\((x^{\prime}, y^{\prime})\Rightarrow \left\{\frac{bx-ay+d}{\sqrt{a^2+b^2}}, \frac{ax+by+c}{\sqrt{a^2+a^2}}\right\}\)
এখন,
\((3)\times{\frac{b}{\sqrt{a^2+b^2}}}+(4)\times{\frac{a}{\sqrt{a^2+b^2}}}\) এর সাহায্যে
\(\therefore \frac{bx^{\prime}}{\sqrt{a^2+b^2}}+\frac{ay^{\prime}}{\sqrt{a^2+b^2}}=\frac{b^2x-aby+bd}{a^2+b^2}+\frac{a^2x-aby+ac}{a^2+b^2}\)
\(\Rightarrow \frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}=\frac{b^2x-aby+bd+a^2x-aby+ac}{a^2+b^2}\)
\(\Rightarrow \frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}=\frac{b^2x+bd+a^2x+ac}{a^2+b^2}\)
\(\Rightarrow \frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}=\frac{x(a^2+b^2)+bd+ac}{a^2+b^2}\)
\(\Rightarrow \frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}=x+\frac{bd+ac}{a^2+b^2}\)
\(\Rightarrow x+\frac{ac+bd}{a^2+b^2}=\frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}\)
\(\therefore x=\frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}-\frac{ac+bd}{a^2+b^2}\)
আবার, \((4)\times{\frac{b}{\sqrt{a^2+b^2}}}-(3)\times{\frac{a}{\sqrt{a^2+b^2}}}\) এর সাহায্যে
\(\therefore \frac{by^{\prime}}{\sqrt{a^2+b^2}}-\frac{ax^{\prime}}{\sqrt{a^2+b^2}}=\frac{abx+b^2y+bc}{a^2+b^2}-\frac{abx-a^2y+ad}{a^2+b^2}\)
\(\Rightarrow \frac{by^{\prime}-ax^{\prime}}{\sqrt{a^2+b^2}}=\frac{abx+b^2y+bc-abx+a^2y-ad}{a^2+b^2}\)
\(\Rightarrow \frac{by^{\prime}-ax^{\prime}}{\sqrt{a^2+b^2}}=\frac{b^2y+bc+a^2y-ad}{a^2+b^2}\)
\(\Rightarrow \frac{by^{\prime}-ax^{\prime}}{\sqrt{a^2+b^2}}=\frac{y(a^2+b^2)+bc-ad}{a^2+b^2}\)
\(\Rightarrow \frac{by^{\prime}-ax^{\prime}}{\sqrt{a^2+b^2}}=y+\frac{bc-ad}{a^2+b^2}\)
\(\Rightarrow y+\frac{bc-ad}{a^2+b^2}=\frac{by^{\prime}-ax^{\prime}}{\sqrt{a^2+b^2}}\)
\(\therefore y=-\frac{ax^{\prime}-by^{\prime}}{\sqrt{a^2+b^2}}-\frac{bc-ad}{a^2+b^2}\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণঃ
\(f\left(\frac{bx^{\prime}+ay^{\prime}}{\sqrt{a^2+b^2}}-\frac{ac+bd}{a^2+b^2}, -\frac{ax^{\prime}-by^{\prime}}{\sqrt{a^2+b^2}}-\frac{bc-ad}{a^2+b^2}\right)=0\)
( প্রমাণিত )
×
মূলবিন্দু ও \(x\) অক্ষকে স্থির রেখে তীর্যক অক্ষদ্বয়কে আয়তাকার অক্ষদবয়ে রূপান্তর করলে,
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow (x+y\cos{\omega}, y\sin{\omega})\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণঃ
\(f(x^{\prime}-y^{\prime}\cot{\omega}, y^{\prime} \ cosec{\omega})=0\)
যেখানে, \(\omega\) তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
কোনো বিন্দু \((x, y)\) এর রূপান্তরিত স্থানাঙ্ক
\((x^{\prime}, y^{\prime})\Rightarrow (x+y\cos{\omega}, y\sin{\omega})\)
\(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণঃ
\(f(x^{\prime}-y^{\prime}\cot{\omega}, y^{\prime} \ cosec{\omega})=0\)
যেখানে, \(\omega\) তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
Proof:
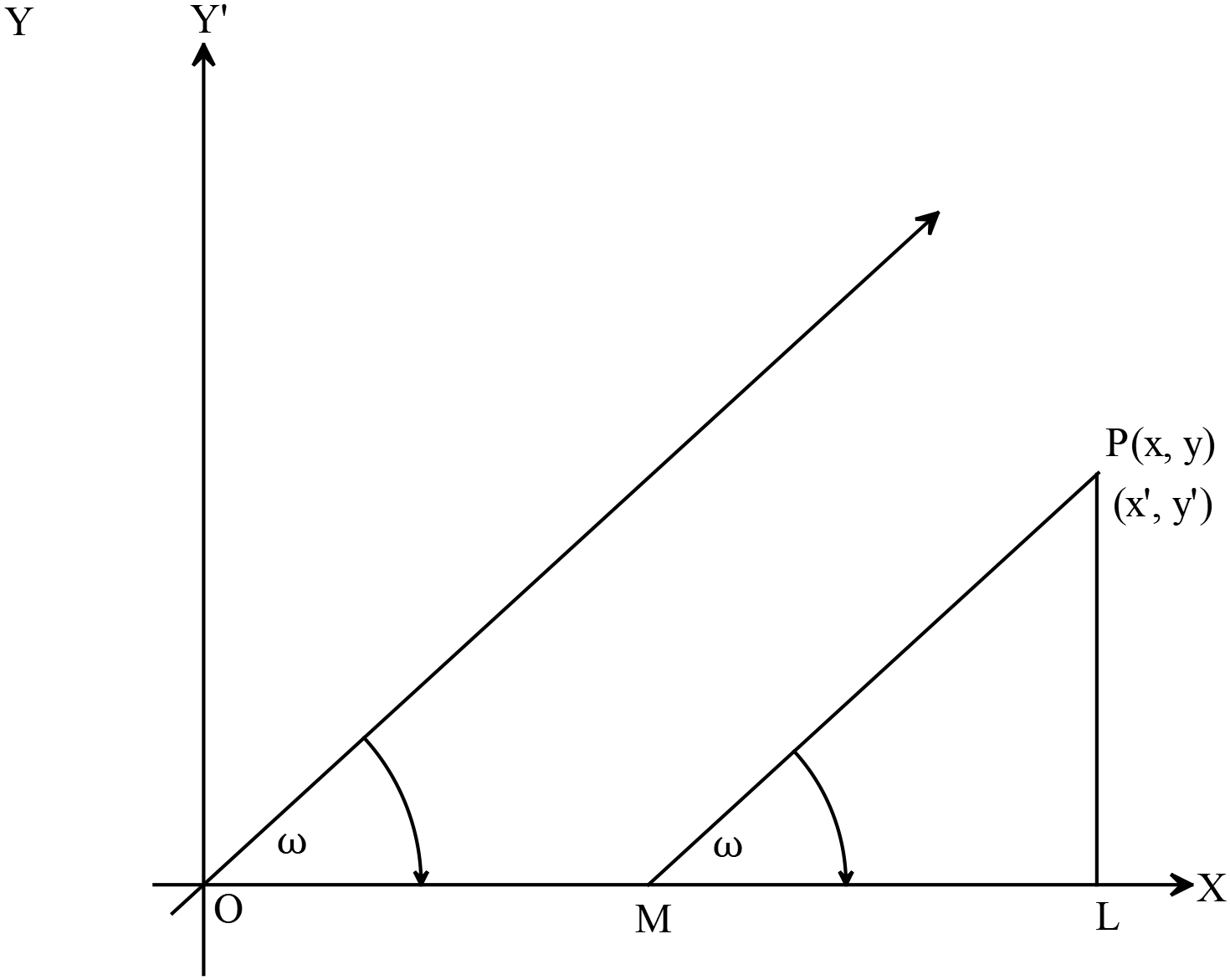
চিত্রে,
তীর্যক অক্ষ দুইটি \(OX\) এবং \(OY\)
যেখানে, \(\angle{XOY}=\omega\) এবং রূপান্তরিত আয়তাকার অক্ষ দুইটি হলো \(OX, \ OY^{\prime}\)
\(P\) যে কোনো বিন্দু যার স্থানাঙ্ক \(OX, \ OY\) এর সাপেক্ষে \((x, y)\) এবং \(OX, \ OY^{\prime}\) এর সাপেক্ষে \((x^{\prime}, y^{\prime})\)
\(OY\) এর সমান্তরাল \(PM\) এবং \(OX\) এর ওপর লম্ব \(PL\) অঙ্কন করা হলো।
এখন, \(OM=x\)
\(MP=y\)
\(OL=x^{\prime}\)
\(LP=y^{\prime}\)
\(\therefore x=OM\)
\(=OL-ML\)
\(=OL-LP\times{\frac{ML}{LP}}\)
\(=OL-LP\cos{\omega}\)
\(\therefore x=x^{\prime}-y^{\prime}\cot{\omega} ......(1)\)
আবার, \(y=MP\)
\(=LP\times{\frac{MP}{LP}}\)
\(\therefore y=y^{\prime} \ cosec \ {\omega} ....(2)\)
\((2)\) হতে,
\(y=\frac{y^{\prime}}{\sin{\omega}}\)
\(\Rightarrow y\sin{\omega}=y^{\prime}\)
\(\therefore y^{\prime}=y\sin{\omega}\)
\(y^{\prime}\) এর এই মান \((1)\) এ বসিয়ে,
\(x=x^{\prime}-y\sin{\omega}\times{\cot{\omega}} \)
\(\Rightarrow x=x^{\prime}-y\sin{\omega}\times{\frac{\cos{\omega}}{\sin{\omega}}}\)
\(\Rightarrow x=x^{\prime}-y\sin{\omega}\times{\frac{\cos{\omega}}{\sin{\omega}}}\)
\(\Rightarrow x+y\cos{\omega}=x^{\prime}\)
\(\therefore x^{\prime}=x+y\cos{\omega} ...(3)\)
এবং \(y^{\prime}=y\sin{\omega} .......(4)\)
\((x, y)\) এর রূপান্তরিত স্থানাঙ্কঃ
\((x^{\prime}, y^{\prime})\Rightarrow (x+y\cos{\omega}, \ y\sin{\omega})\)
আবার, \(f(x, y)=0\) সমীকরণের রূপান্তরিত সমীকরণঃ
\(f(x^{\prime}-y^{\prime}\cot{\omega}, y^{\prime} \ cosec{\omega})=0\)
( প্রমাণিত )
×
মূলবিন্দুকে স্থির রেখে প্রদত্ত কোনো তীর্যক অক্ষদ্বয়কে অন্য কোনো তীর্যক অক্ষদ্বয়ে রূপান্তর করলে
রূপান্তর সূত্র
\(x=\frac{x^{\prime}\sin{(\omega-\theta)}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega-\omega^{\prime}-\theta)}}{\sin{\omega}}\) \(y=\frac{x^{\prime}\sin{\theta}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega^{\prime}+\theta)}}{\sin{\omega}}\)
যেখানে, \(\omega\) আদি তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
\(\omega^{\prime}\) নুতন তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
রূপান্তর সূত্র
\(x=\frac{x^{\prime}\sin{(\omega-\theta)}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega-\omega^{\prime}-\theta)}}{\sin{\omega}}\) \(y=\frac{x^{\prime}\sin{\theta}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega^{\prime}+\theta)}}{\sin{\omega}}\)
যেখানে, \(\omega\) আদি তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
\(\omega^{\prime}\) নুতন তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
Proof:
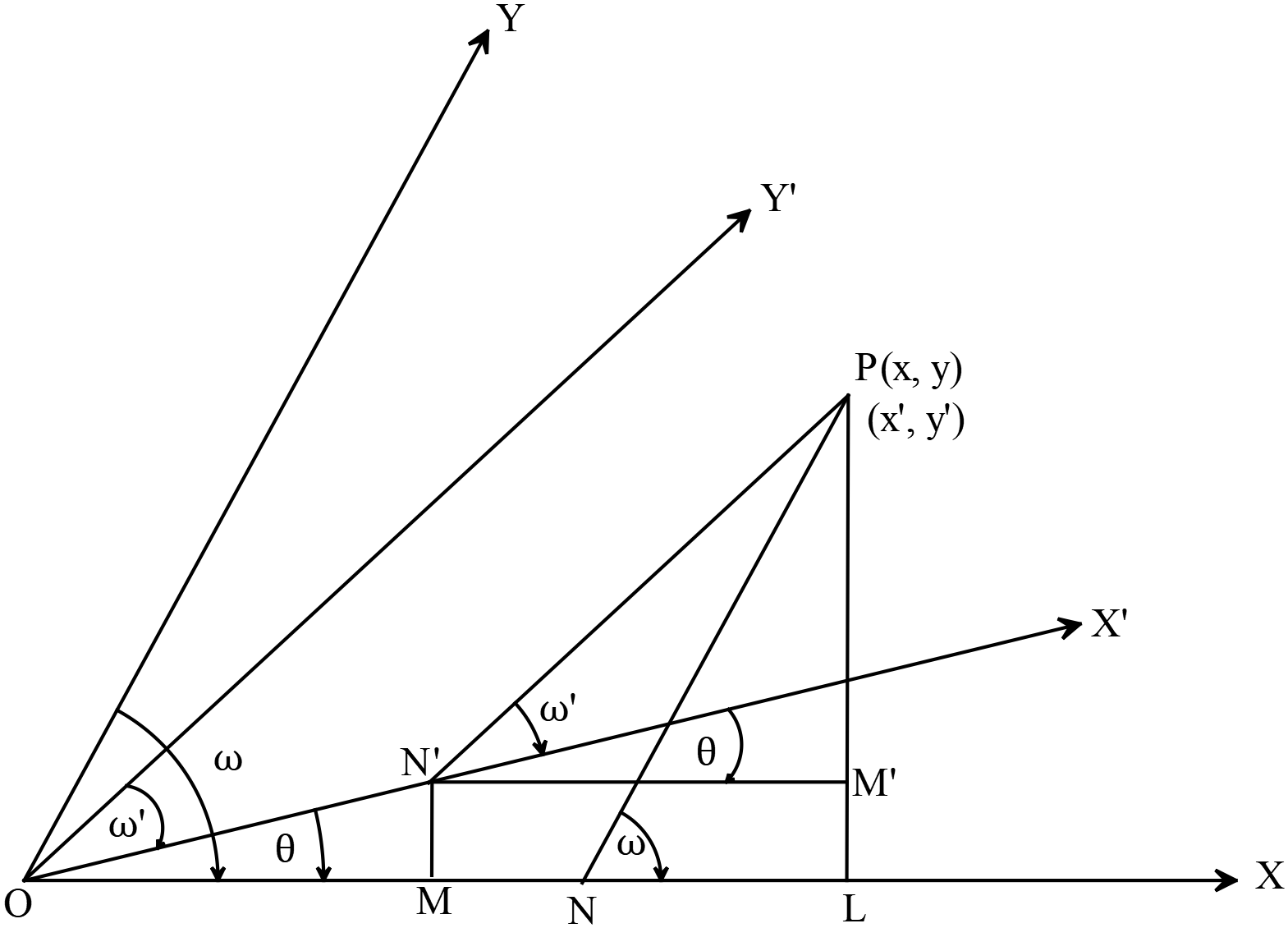
চিত্রে,
\(\omega\) কোণ ধারণকারী তীর্যক অক্ষ দুইটি \(OX\) এবং \(OY\)
এবং \(\omega^{\prime}\) কোণ ধারণকারী তীর্যক অক্ষ দুইটি \(OX^{\prime}\) এবং \(OY^{\prime}\)
মনে করি, \(\angle{XOX^{\prime}}=\theta\) কোণ ধারণকারী তীর্যক অক্ষ দুইটি \(OX^{\prime}\) এবং \(OY^{\prime}\)
\(P\) যে কোনো বিন্দু যার স্থানাঙ্ক \(OX, \ OY\) এর সাপেক্ষে \((x, y)\) এবং \(OX^{\prime}, \ OY^{\prime}\) এর সাপেক্ষে \((x^{\prime}, y^{\prime})\)
\(OY\) ও \(OY^{\prime}\) এর সমান্তরালে যথাক্রমে \(PN\) ও \(PN^{\prime}\) অঙ্কন করা হলো।
\(OX\) এর ওপর \(N^{\prime}M\) এবং \(PL\) লম্ব এবং \(PL\) ওপর \(N^{\prime}M^{\prime}\) লম্ব অঙ্কন করা হলো।
এখন, \(ON=x\)
\(NP=y\)
\(ON^{\prime}=x^{\prime}\)
\(N^{\prime}P=y^{\prime}\)
এবং \(\angle{PNL}=\angle{YOX}\)
\(=\omega\)
\(\angle{PN^{\prime}M^{\prime}}=\angle{Y^{\prime}OX}\)
\(=\omega^{\prime}+\theta\)
\(\therefore x=ON\)
\(=OM+MN\)
\(=OM+N^{\prime}M^{\prime}-NL\)
\(=ON^{\prime}\frac{OM}{ON^{\prime}}+N^{\prime}P\frac{N^{\prime}M^{\prime}}{N^{\prime}P}-NP\frac{NL}{NP}\)
\(=ON^{\prime}\cos{\theta}+N^{\prime}P\cos{\angle{PN^{\prime}M^{\prime}}}-NP\cos{\angle{PNL}}\)
\(\therefore x=x^{\prime}\cos{\theta}+y^{\prime}\cos{(\omega^{\prime}+\theta)}-y\cos{\omega}\)
\(\Rightarrow x+y\cos{\omega}=x^{\prime}\cos{\theta}+y^{\prime}\cos{(\omega^{\prime}+\theta)} .......(1)\)
আবার, \(y=NP\)
\(=LP\times{\frac{NP}{LP}}\)
\(=LP \ cosec \ {\omega}\)
\(=LP\frac{1}{\sin{\omega}}\)
\(\therefore y=LP\frac{1}{\sin{\omega}}\)
\(\Rightarrow y\sin{\omega}=LP\)
\(\Rightarrow y\sin{\omega}=MN^{\prime}+M^{\prime}P\)
\(\Rightarrow y\sin{\omega}=ON^{\prime}\frac{MN^{\prime}}{ON^{\prime}}+N^{\prime}P\frac{M^{\prime}P}{N^{\prime}P}\)
\(\therefore y\sin{\omega}=x^{\prime}\sin{\theta}+y^{\prime}\sin{(\omega^{\prime}+\theta)} .......(2)\)
\((1)\times{\sin{\omega}}-(2)\times{\cos{\omega}}\) এর সাহায্যে
\(x\sin{\omega}+y\sin{\omega}\cos{\omega}-y\sin{\omega}\cos{\omega}=x^{\prime}\sin{\omega}\cos{\theta}+y^{\prime}\sin{\omega}\cos{(\omega^{\prime}+\theta)}-x^{\prime}\sin{\theta}\cos{\omega}-y^{\prime}\sin{(\omega^{\prime}+\theta)}\cos{\omega}\)
\(\Rightarrow x\sin{\omega}=x^{\prime}(\sin{\omega}\cos{\theta}-\cos{\omega}\sin{\theta})+y^{\prime}\{\sin{\omega}\cos{(\omega^{\prime}+\theta)}-\cos{\omega}\sin{(\omega^{\prime}+\theta)}\}\)
\(\Rightarrow x\sin{\omega}=x^{\prime}\sin{(\omega-\theta)}+y^{\prime}\sin{(\omega-\omega^{\prime}-\theta)}\)
\(\therefore x=\frac{x^{\prime}\sin{(\omega-\theta)}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega-\omega^{\prime}-\theta)}}{\sin{\omega}}\)
\((2)\) হতে,
\(y=\frac{x^{\prime}\sin{\theta}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega^{\prime}+\theta)}}{\sin{\omega}}\)
\(\therefore \) রূপান্তর সূত্রঃ
\(x=\frac{x^{\prime}\sin{(\omega-\theta)}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega-\omega^{\prime}-\theta)}}{\sin{\omega}}\) \(y=\frac{x^{\prime}\sin{\theta}}{\sin{\omega}}+\frac{y^{\prime}\sin{(\omega^{\prime}+\theta)}}{\sin{\omega}}\)
যেখানে, \(\omega\) আদি তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
\(\omega^{\prime}\) নুতন তীর্যক অক্ষদ্বয়ের মধ্যবর্তী কোণ।
( প্রমাণিত )
×
সাধারণ দ্বিঘাত সমীকরণ হতে এক ঘাত পদগুলো অর্থাৎ \(x\) ও \(y\) সম্বলিত পদ অপসারণ
অথবা,
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) সমীকরণ হতে এক ঘাত পদগুলো অর্থাৎ \(x\) ও \(y\) সম্বলিত পদ অপসারণ
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) সমীকরণ হতে এক ঘাত পদগুলো অর্থাৎ \(x\) ও \(y\) সম্বলিত পদ অপসারণ
রূপান্তরিত সমীকরণ
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\) নুতন মূলবিন্দু
এবং \(c^{\prime}=g\alpha+f\beta+c\) নুতন ধ্রুবক
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\) নুতন মূলবিন্দু
এবং \(c^{\prime}=g\alpha+f\beta+c\) নুতন ধ্রুবক
অথবা
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+\frac{\Delta}{ab-h^2}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\) নুতন মূলবিন্দু
এবং \(c^{\prime}=\frac{\Delta}{ab-h^2}\) নুতন ধ্রুবক
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+\frac{\Delta}{ab-h^2}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\) নুতন মূলবিন্দু
এবং \(c^{\prime}=\frac{\Delta}{ab-h^2}\) নুতন ধ্রুবক
Proof:
প্রদত্ত সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুকে \((\alpha, \beta)\) বিন্দুতে স্থানান্তরিত করা হলে স্থানান্তর সূত্রঃ
\(x=x^{\prime}+\alpha\)
\(y=y^{\prime}+\beta\)
ফলে, \((1)\) সমীকরণটির পরিবর্তিত রূপ দাঁড়াবে
\(a(x^{\prime}+\alpha)^2+2h(x^{\prime}+\alpha)(y^{\prime}+\beta)+b(y^{\prime}+\beta)^2+2g(x^{\prime}+\alpha)+2f(y^{\prime}+\beta)+c=0\) ➜ \(x=x^{\prime}+\alpha\)
\(y=y^{\prime}+\beta\)
বসিয়ে
\(\therefore a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+2(a\alpha+h\beta+g)x^{\prime}+2(h\alpha+b\beta+f)y^{\prime}+\)\(a\alpha^2+2h\alpha\beta+b\beta^2+2g\alpha+2f\beta+c=0 ........(2)\)
\((1)\) নং সমীকরণ থেকে \(x^{\prime}\) ও \(y^{\prime}\) যুক্ত পদ অপসারিত হবে যদি \(x^{\prime}\) ও \(y^{\prime}\) এর সহগ দুইটি শূন্য হয়।
অর্থাৎ যদি
\(a\alpha+h\beta+g=0 .........(3)\)
এবং \(h\alpha+b\beta+f=0 .........(4)\)
পদ দুইটি অপসারণের পর \((2)\) এর রূপ দাঁড়াবে
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0 .......(5)\)
যেখানে, \(c^{\prime}=a\alpha^2+2h\alpha\beta+b\beta^2+2g\alpha+2f\beta+c\)
\(=a\alpha^2+h\alpha\beta+g\alpha+h\alpha\beta+b\beta^2+f\beta+g\alpha+f\beta+c\)
\(=\alpha(a\alpha+h\beta+g)+\beta(h\alpha+b\beta+f)+g\alpha+f\beta+c\)
\(=\alpha(0)+\beta(0)+g\alpha+f\beta+c\) ➜ \(\because a\alpha+h\beta+g=0\)
\(h\alpha+b\beta+f=0\)
\((3)\) ও \((4)\) হতে,
\(=0+0+g\alpha+f\beta+c\)
\(\therefore c^{\prime}=g\alpha+f\beta+c\)
\(\therefore (5)\) নং হতে, রূপান্তরিত সমীকরণ, \(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0 \)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
এবং \(c^{\prime}=g\alpha+f\beta+c\)
আবার
\((3)\) ও \((4)\) সমাধান করি
\(a\alpha+h\beta+g=0\)
\(h\alpha+b\beta+f=0\)
\(\frac{\alpha}{hf-bg}=\frac{\beta}{hg-af}=\frac{1}{ab-h^2}\)
\(\Rightarrow \frac{\alpha}{hf-bg}=\frac{1}{ab-h^2}, \ \frac{\beta}{hg-af}=\frac{1}{ab-h^2}\)
\(\therefore \alpha=\frac{hf-bg}{ab-h^2}, \ \beta=\frac{hg-af}{ab-h^2}\)
\(\therefore (\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
সুতরাং সাধারণ দ্বিঘাত সমীকরণ হতে একঘাত পদগুলো অপসারণ করতে হলে অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুকে \((\alpha, \beta)\) বিন্দুতে স্থানান্তরিত করতে হবে, যেন
\(c^{\prime}=g\alpha+f\beta+c\)
\(\therefore c^{\prime}=g\frac{fh-bg}{ab-h^2}+f\frac{gh-af}{ab-h^2}+c\)
\(=\frac{fgh-bg^2}{ab-h^2}+\frac{fgh-af^2}{ab-h^2}+c\)
\(=\frac{fgh-bg^2+fgh-af^2+abc-ch^2}{ab-h^2}\)
\(=\frac{abc+2fgh-af^2-bg^2-ch^2}{ab-h^2}\)
\(\therefore c^{\prime}=\frac{\Delta}{ab-h^2}\) ➜ \(\because \Delta=abc+2fgh-af^2-bg^2-ch^2\)
\(\therefore (5)\) নং হতে, রূপান্তরিত সমীকরণটি হবে,
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
এবং \(c^{\prime}=\frac{\Delta}{ab-h^2}\)
( প্রমাণিত )
দ্রষ্টব্যঃ সমীকরণ \((5)\) থেকে এটা স্পষ্ট যে অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুকে ওপর কোনো বিন্দুতে স্থানান্তরিত করলে সাধারণ দ্বিঘাত সমীকরণের \(x^2, \ y^2, \ xy\) এর সহগগুলি অর্থাৎ \(a, \ b, \ h\) সহগগুলি অপরিবর্তিত থাকে কিন্তু \(x, \ y\) এর সহগ \(g, \ f\) এবং ধ্রুবক পদ \(c\) এরা বদলিয়ে যায়। সুতরাং রূপান্তরিত দ্বিঘাত সমীকরণটি দাঁড়ায়
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুকে \((\alpha, \beta)\) বিন্দুতে স্থানান্তরিত করা হলে স্থানান্তর সূত্রঃ
\(x=x^{\prime}+\alpha\)
\(y=y^{\prime}+\beta\)
ফলে, \((1)\) সমীকরণটির পরিবর্তিত রূপ দাঁড়াবে
\(a(x^{\prime}+\alpha)^2+2h(x^{\prime}+\alpha)(y^{\prime}+\beta)+b(y^{\prime}+\beta)^2+2g(x^{\prime}+\alpha)+2f(y^{\prime}+\beta)+c=0\) ➜ \(x=x^{\prime}+\alpha\)
\(y=y^{\prime}+\beta\)
বসিয়ে
\(\therefore a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+2(a\alpha+h\beta+g)x^{\prime}+2(h\alpha+b\beta+f)y^{\prime}+\)\(a\alpha^2+2h\alpha\beta+b\beta^2+2g\alpha+2f\beta+c=0 ........(2)\)
\((1)\) নং সমীকরণ থেকে \(x^{\prime}\) ও \(y^{\prime}\) যুক্ত পদ অপসারিত হবে যদি \(x^{\prime}\) ও \(y^{\prime}\) এর সহগ দুইটি শূন্য হয়।
অর্থাৎ যদি
\(a\alpha+h\beta+g=0 .........(3)\)
এবং \(h\alpha+b\beta+f=0 .........(4)\)
পদ দুইটি অপসারণের পর \((2)\) এর রূপ দাঁড়াবে
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0 .......(5)\)
যেখানে, \(c^{\prime}=a\alpha^2+2h\alpha\beta+b\beta^2+2g\alpha+2f\beta+c\)
\(=a\alpha^2+h\alpha\beta+g\alpha+h\alpha\beta+b\beta^2+f\beta+g\alpha+f\beta+c\)
\(=\alpha(a\alpha+h\beta+g)+\beta(h\alpha+b\beta+f)+g\alpha+f\beta+c\)
\(=\alpha(0)+\beta(0)+g\alpha+f\beta+c\) ➜ \(\because a\alpha+h\beta+g=0\)
\(h\alpha+b\beta+f=0\)
\((3)\) ও \((4)\) হতে,
\(=0+0+g\alpha+f\beta+c\)
\(\therefore c^{\prime}=g\alpha+f\beta+c\)
\(\therefore (5)\) নং হতে, রূপান্তরিত সমীকরণ, \(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0 \)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
এবং \(c^{\prime}=g\alpha+f\beta+c\)
আবার
\((3)\) ও \((4)\) সমাধান করি
\(a\alpha+h\beta+g=0\)
\(h\alpha+b\beta+f=0\)
\(\frac{\alpha}{hf-bg}=\frac{\beta}{hg-af}=\frac{1}{ab-h^2}\)
\(\Rightarrow \frac{\alpha}{hf-bg}=\frac{1}{ab-h^2}, \ \frac{\beta}{hg-af}=\frac{1}{ab-h^2}\)
\(\therefore \alpha=\frac{hf-bg}{ab-h^2}, \ \beta=\frac{hg-af}{ab-h^2}\)
\(\therefore (\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
সুতরাং সাধারণ দ্বিঘাত সমীকরণ হতে একঘাত পদগুলো অপসারণ করতে হলে অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুকে \((\alpha, \beta)\) বিন্দুতে স্থানান্তরিত করতে হবে, যেন
\(c^{\prime}=g\alpha+f\beta+c\)
\(\therefore c^{\prime}=g\frac{fh-bg}{ab-h^2}+f\frac{gh-af}{ab-h^2}+c\)
\(=\frac{fgh-bg^2}{ab-h^2}+\frac{fgh-af^2}{ab-h^2}+c\)
\(=\frac{fgh-bg^2+fgh-af^2+abc-ch^2}{ab-h^2}\)
\(=\frac{abc+2fgh-af^2-bg^2-ch^2}{ab-h^2}\)
\(\therefore c^{\prime}=\frac{\Delta}{ab-h^2}\) ➜ \(\because \Delta=abc+2fgh-af^2-bg^2-ch^2\)
\(\therefore (5)\) নং হতে, রূপান্তরিত সমীকরণটি হবে,
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
যেখানে, \((\alpha,\beta)\Rightarrow \left(\frac{fh-bg}{ab-h^2}, \frac{gh-af}{ab-h^2}\right)\)
এবং \(c^{\prime}=\frac{\Delta}{ab-h^2}\)
( প্রমাণিত )
দ্রষ্টব্যঃ সমীকরণ \((5)\) থেকে এটা স্পষ্ট যে অক্ষদ্বয়ের দিক অপরিবর্তিত রেখে মূলবিন্দুকে ওপর কোনো বিন্দুতে স্থানান্তরিত করলে সাধারণ দ্বিঘাত সমীকরণের \(x^2, \ y^2, \ xy\) এর সহগগুলি অর্থাৎ \(a, \ b, \ h\) সহগগুলি অপরিবর্তিত থাকে কিন্তু \(x, \ y\) এর সহগ \(g, \ f\) এবং ধ্রুবক পদ \(c\) এরা বদলিয়ে যায়। সুতরাং রূপান্তরিত দ্বিঘাত সমীকরণটি দাঁড়ায়
\(a{x^{\prime}}^2+2hx^{\prime}y^{\prime}+b{y^{\prime}}^2+c^{\prime}=0\)
×
সাধারণ দ্বিঘাত সমীকরণ হতে \(xy\) সম্বলিত পদ অপসারণ
অথবা,
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) সমীকরণ হতে \(xy\) সম্বলিত পদ অপসারণ
রূপান্তরিত সমীকরণ
\(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0\)
যেখানে, \(\theta=\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)}\)
অথবা,
\(ax^2+2hxy+by^2+2gx+2fy+c=0\) সমীকরণ হতে \(xy\) সম্বলিত পদ অপসারণ
রূপান্তরিত সমীকরণ
\(a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0\)
যেখানে, \(\theta=\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)}\)
Proof:
প্রদত্ত সমীকরণ,
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
যদি অক্ষদ্বয়কে মূলবিন্দুতে \(\theta\) কোণে ঘুরানো হয় তবে আমরা স্থনাংকের রূপান্তরিত সূত্র পাব,
\(x=x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}\)
\(y=x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\)
প্রদত্ত \((1)\) নং সমীকরণের রূপান্তরিত রূপ হবে,
\(a(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})^2+2h(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})+b(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})^2+2g(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})+\)\(2f(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})+c=0\)
\(\therefore (a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}){x^{\prime}}^2+2\{-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}\}x^{\prime}y^{\prime}+(a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+\)\(b\cos^2{\theta}){y^{\prime}}^2+2(g\cos{\theta}+f\sin{\theta})x^{\prime}+2(f\cos{\theta}-g\sin{\theta})y^{\prime}+c=0 ........(2)\)
\((2)\) নং সমীকরণ থেকে \(x^{\prime}y^{\prime}\) যুক্ত পদ অপসারিত হবে যদি \(x^{\prime}y^{\prime}\) এর সহগটি শূন্য হয়।
অর্থাৎ যদি
\(-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}=0\)
\(-\frac{1}{2}a.2\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+\frac{1}{2}b.2\sin{\theta}\cos{\theta}=0\)
\(\Rightarrow -\frac{1}{2}a\sin{2\theta}+h\cos{2\theta}+\frac{1}{2}b\sin{2\theta}=0\) ➜ \(\because 2\sin{A}\cos{A}=\sin{2A}\)
\(\cos^2{A}-\sin^2{A}=\cos{2A}\)
\(\Rightarrow h\cos{2\theta}-\frac{1}{2}(a-b)\sin{2\theta}=0\)
\(\Rightarrow h\cos{2\theta}=\frac{1}{2}(a-b)\sin{2\theta}\)
\(\Rightarrow 2h\cos{2\theta}=(a-b)\sin{2\theta}\)
\(\Rightarrow (a-b)\sin{2\theta}=2h\cos{2\theta}\)
\(\Rightarrow \frac{\sin{2\theta}}{\cos{2\theta}}=\frac{2h}{a-b}\)
\(\Rightarrow \tan{2\theta}=\frac{2h}{a-b}\)
\(\Rightarrow 2\theta=\tan^{-1}{\left(\frac{2h}{a-b}\right)}\)
\(\therefore \theta=\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)} ......(3)\)
অর্থাৎ অক্ষদ্বয়কে \(\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)}\) কোণে ঘুরালে দ্বিঘাত সমীকরণ থেকে \(xy\) যুক্ত পদ অপসারিত হবে এবং \((2)\) নং সমীকরণটির রূপান্তরিত রূপ হবে,
\((a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}){x^{\prime}}^2+(a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+\)\(b\cos^2{\theta}){y^{\prime}}^2+2(g\cos{\theta}+f\sin{\theta})x^{\prime}+2(f\cos{\theta}-g\sin{\theta})y^{\prime}+c=0\)
\(\therefore a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0 ....(3)\)
যেখানে, \(a^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}\)
\(b^{\prime}=a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}\)
\(g^{\prime}=g\cos{\theta}+f\sin{\theta}\)
\(f^{\prime}=f\cos{\theta}-g\sin{\theta}\)
( প্রমাণিত )
দ্রষ্টব্যঃ মূল সমীকরণ এবং রূপান্তরিত সমীকরণ উভয়ের একই ধ্রুবক পদ। অতএব, মূলবিন্দুতে আয়তাকার অক্ষদ্বয়কে কোনো কোণে ঘুরালে সমীকরণের ধ্রুবক পদ অপরিবর্তিত থেকে যায়।
\(ax^2+2hxy+by^2+2gx+2fy+c=0 .........(1)\)
যদি অক্ষদ্বয়কে মূলবিন্দুতে \(\theta\) কোণে ঘুরানো হয় তবে আমরা স্থনাংকের রূপান্তরিত সূত্র পাব,
\(x=x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}\)
\(y=x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\)
প্রদত্ত \((1)\) নং সমীকরণের রূপান্তরিত রূপ হবে,
\(a(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})^2+2h(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})+b(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})^2+2g(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})+\)\(2f(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})+c=0\)
\(\therefore (a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}){x^{\prime}}^2+2\{-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}\}x^{\prime}y^{\prime}+(a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+\)\(b\cos^2{\theta}){y^{\prime}}^2+2(g\cos{\theta}+f\sin{\theta})x^{\prime}+2(f\cos{\theta}-g\sin{\theta})y^{\prime}+c=0 ........(2)\)
\((2)\) নং সমীকরণ থেকে \(x^{\prime}y^{\prime}\) যুক্ত পদ অপসারিত হবে যদি \(x^{\prime}y^{\prime}\) এর সহগটি শূন্য হয়।
অর্থাৎ যদি
\(-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}=0\)
\(-\frac{1}{2}a.2\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+\frac{1}{2}b.2\sin{\theta}\cos{\theta}=0\)
\(\Rightarrow -\frac{1}{2}a\sin{2\theta}+h\cos{2\theta}+\frac{1}{2}b\sin{2\theta}=0\) ➜ \(\because 2\sin{A}\cos{A}=\sin{2A}\)
\(\cos^2{A}-\sin^2{A}=\cos{2A}\)
\(\Rightarrow h\cos{2\theta}-\frac{1}{2}(a-b)\sin{2\theta}=0\)
\(\Rightarrow h\cos{2\theta}=\frac{1}{2}(a-b)\sin{2\theta}\)
\(\Rightarrow 2h\cos{2\theta}=(a-b)\sin{2\theta}\)
\(\Rightarrow (a-b)\sin{2\theta}=2h\cos{2\theta}\)
\(\Rightarrow \frac{\sin{2\theta}}{\cos{2\theta}}=\frac{2h}{a-b}\)
\(\Rightarrow \tan{2\theta}=\frac{2h}{a-b}\)
\(\Rightarrow 2\theta=\tan^{-1}{\left(\frac{2h}{a-b}\right)}\)
\(\therefore \theta=\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)} ......(3)\)
অর্থাৎ অক্ষদ্বয়কে \(\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)}\) কোণে ঘুরালে দ্বিঘাত সমীকরণ থেকে \(xy\) যুক্ত পদ অপসারিত হবে এবং \((2)\) নং সমীকরণটির রূপান্তরিত রূপ হবে,
\((a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}){x^{\prime}}^2+(a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+\)\(b\cos^2{\theta}){y^{\prime}}^2+2(g\cos{\theta}+f\sin{\theta})x^{\prime}+2(f\cos{\theta}-g\sin{\theta})y^{\prime}+c=0\)
\(\therefore a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+2g^{\prime}x^{\prime}+2f^{\prime}y^{\prime}+c=0 ....(3)\)
যেখানে, \(a^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}\)
\(b^{\prime}=a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}\)
\(g^{\prime}=g\cos{\theta}+f\sin{\theta}\)
\(f^{\prime}=f\cos{\theta}-g\sin{\theta}\)
( প্রমাণিত )
দ্রষ্টব্যঃ মূল সমীকরণ এবং রূপান্তরিত সমীকরণ উভয়ের একই ধ্রুবক পদ। অতএব, মূলবিন্দুতে আয়তাকার অক্ষদ্বয়কে কোনো কোণে ঘুরালে সমীকরণের ধ্রুবক পদ অপরিবর্তিত থেকে যায়।
×
মূলবিন্দু অপরিবর্তিত রেখে আয়তাকার অক্ষদ্বয়কে \(\frac{1}{2}\tan^{-1}\frac{2h}{a-b}\) কোণে আবর্তন করায় \(ax^2+2hxy+by^2+c=0\) সমীকরণের পরিবর্তিত রূপ
\(a^{\prime}x^2+b^{\prime}y^2+c=0\) হওয়ার শর্ত \(a^{\prime}+b^{\prime}=a+b\) \(a^{\prime}b^{\prime}=ab-h^2\)
\(a^{\prime}x^2+b^{\prime}y^2+c=0\) হওয়ার শর্ত \(a^{\prime}+b^{\prime}=a+b\) \(a^{\prime}b^{\prime}=ab-h^2\)
Proof:
প্রদত্ত সমীকরণ,
\(ax^2+2hxy+by^2+c=0 .........(1)\)
মূলবিন্দু ঠিক রেখে অক্ষদ্বয়কে \(\theta\) কোণে ঘুরানো হয় তবে আমরা স্থনাংকের রূপান্তরিত সূত্র পাব,
\(x=x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}\)
\(y=x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\)
প্রদত্ত \((1)\) নং সমীকরণের রূপান্তরিত রূপ হবে,
\(a(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})^2+2h(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})+b(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})^2+c=0\)
\(\therefore (a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}){x^{\prime}}^2+2\{-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}\}x^{\prime}y^{\prime}+\)\((a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}){y^{\prime}}^2+c=0 .....(2)\)
\((2)\) নং সমীকরণ থেকে \(x^{\prime}y^{\prime}\) যুক্ত পদ অপসারিত হবে যদি \(x^{\prime}y^{\prime}\) এর সহগটি শূন্য হয়।
অর্থাৎ যদি
\(-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}=0\)
\(-\frac{1}{2}a.2\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+\frac{1}{2}b.2\sin{\theta}\cos{\theta}=0\)
\(\Rightarrow -\frac{1}{2}a\sin{2\theta}+h\cos{2\theta}+\frac{1}{2}b\sin{2\theta}=0\) ➜ \(\because 2\sin{A}\cos{A}=\sin{2A}\)
\(\cos^2{A}-\sin^2{A}=\cos{2A}\)
\(\Rightarrow h\cos{2\theta}-\frac{1}{2}(a-b)\sin{2\theta}=0\)
\(\Rightarrow h\cos{2\theta}=\frac{1}{2}(a-b)\sin{2\theta}\)
\(\Rightarrow 2h\cos{2\theta}=(a-b)\sin{2\theta} ....(3)\)
\(\Rightarrow (a-b)\sin{2\theta}=2h\cos{2\theta}\)
\(\Rightarrow \frac{\sin{2\theta}}{\cos{2\theta}}=\frac{2h}{a-b}\)
\(\Rightarrow \tan{2\theta}=\frac{2h}{a-b}\)
\(\Rightarrow 2\theta=\tan^{-1}{\left(\frac{2h}{a-b}\right)}\)
\(\therefore \theta=\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)} ......(4)\)
অর্থাৎ অক্ষদ্বয়কে \(\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)}\) কোণে ঘুরালে দ্বিঘাত সমীকরণ থেকে \(xy\) যুক্ত পদ অপসারিত হবে এবং \((2)\) নং সমীকরণটির রূপান্তরিত রূপ হবে,
\(\therefore a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+c=0 .....(5)\)
যেখানে, \(a^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta} ....(6)\)
\(b^{\prime}=a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta} ....(7)\)
\((6)+(7)\) এর সাহায্যে
\(a^{\prime}+b^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}+a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}\)
\(=a\cos^2{\theta}+b\sin^2{\theta}+a\sin^2{\theta}+b\cos^2{\theta}\)
\(=a(\sin^2{\theta}+\cos^2{\theta})+b(\sin^2{\theta}+\cos^2{\theta})\)
\(=a.1+b.1\)
\(\therefore a^{\prime}+b^{\prime}=a+b\)
\((6)\) ও \((7)\) হতে
\(2a^{\prime}=a.2\cos^2{\theta}+2h.2\sin{\theta}\cos{\theta}+b.2\sin^2{\theta}\)
\(=a(1+\cos{2\theta})+2h\sin{2\theta}+b(1-\cos{2\theta})\)
\(=a+a\cos{2\theta}+2h\sin{2\theta}+b-b\cos{2\theta}\)
\(=(a+b)+(a-b)\cos{2\theta}+2h\sin{2\theta}\)
\(\therefore 2a^{\prime}=(a+b)+\{2h\sin{2\theta}+(a-b)\cos{2\theta}\} ......(8)\)
আবার,
\(2b^{\prime}=a.2\sin^2{\theta}-2h.2\sin{\theta}\cos{\theta}+b.2\cos^2{\theta}\)
\(=a(1-\cos{2\theta})-2h\sin{2\theta}+b(1+\cos{2\theta})\)
\(=a-a\cos{2\theta}-2h\sin{2\theta}+b+b\cos{2\theta}\)
\(=(a+b)-(a-b)\cos{2\theta}-2h\sin{2\theta}\)
\(\therefore 2b^{\prime}=(a+b)-\{2h\sin{2\theta}+(a-b)\cos{2\theta}\} ......(9)\)
\((8)\times{(9)}\) এর সাহায্যে
\(4a^{\prime}b^{\prime}=(a+b)^2-\{2h\sin{2\theta}+(a-b)\cos{2\theta}\}^2\)
\(=(a+b)^2-4h^2\sin^2{2\theta}-(a-b)^2\cos^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}\)
\(=(a+b)^2-4h^2+4h^2\cos^2{2\theta}-(a-b)^2\cos^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}\)
\(=(a+b)^2-4h^2+(2h\cos{2\theta})^2-(a-b)^2\cos^2{2\theta}-2(a-b)\sin{2\theta}.2h\cos{2\theta}\)
\(=(a+b)^2-4h^2+(a-b)^2\sin^2{2\theta}-(a-b)^2+(a-b)^2\sin^2{2\theta}-2(a-b)\sin{2\theta}(a-b)\sin{2\theta}\) ➜ \(\because 2h\cos{2\theta}=(a-b)\sin{2\theta}\)
\((3)\) হতে,
\(=(a+b)^2-(a-b)^2-4h^2+2(a-b)^2\sin^2{2\theta}-2(a-b)^2\sin^2{2\theta}\)
\(=4ab-4h^2\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow 4a^{\prime}b^{\prime}=4(ab-h^2)\)
\(\therefore a^{\prime}b^{\prime}=ab-h^2\)
( প্রমাণিত )
\(ax^2+2hxy+by^2+c=0 .........(1)\)
মূলবিন্দু ঠিক রেখে অক্ষদ্বয়কে \(\theta\) কোণে ঘুরানো হয় তবে আমরা স্থনাংকের রূপান্তরিত সূত্র পাব,
\(x=x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}\)
\(y=x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\)
প্রদত্ত \((1)\) নং সমীকরণের রূপান্তরিত রূপ হবে,
\(a(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})^2+2h(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})+b(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})^2+c=0\)
\(\therefore (a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}){x^{\prime}}^2+2\{-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}\}x^{\prime}y^{\prime}+\)\((a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}){y^{\prime}}^2+c=0 .....(2)\)
\((2)\) নং সমীকরণ থেকে \(x^{\prime}y^{\prime}\) যুক্ত পদ অপসারিত হবে যদি \(x^{\prime}y^{\prime}\) এর সহগটি শূন্য হয়।
অর্থাৎ যদি
\(-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}=0\)
\(-\frac{1}{2}a.2\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+\frac{1}{2}b.2\sin{\theta}\cos{\theta}=0\)
\(\Rightarrow -\frac{1}{2}a\sin{2\theta}+h\cos{2\theta}+\frac{1}{2}b\sin{2\theta}=0\) ➜ \(\because 2\sin{A}\cos{A}=\sin{2A}\)
\(\cos^2{A}-\sin^2{A}=\cos{2A}\)
\(\Rightarrow h\cos{2\theta}-\frac{1}{2}(a-b)\sin{2\theta}=0\)
\(\Rightarrow h\cos{2\theta}=\frac{1}{2}(a-b)\sin{2\theta}\)
\(\Rightarrow 2h\cos{2\theta}=(a-b)\sin{2\theta} ....(3)\)
\(\Rightarrow (a-b)\sin{2\theta}=2h\cos{2\theta}\)
\(\Rightarrow \frac{\sin{2\theta}}{\cos{2\theta}}=\frac{2h}{a-b}\)
\(\Rightarrow \tan{2\theta}=\frac{2h}{a-b}\)
\(\Rightarrow 2\theta=\tan^{-1}{\left(\frac{2h}{a-b}\right)}\)
\(\therefore \theta=\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)} ......(4)\)
অর্থাৎ অক্ষদ্বয়কে \(\frac{1}{2}\tan^{-1}{\left(\frac{2h}{a-b}\right)}\) কোণে ঘুরালে দ্বিঘাত সমীকরণ থেকে \(xy\) যুক্ত পদ অপসারিত হবে এবং \((2)\) নং সমীকরণটির রূপান্তরিত রূপ হবে,
\(\therefore a^{\prime}{x^{\prime}}^2+b^{\prime}{y^{\prime}}^2+c=0 .....(5)\)
যেখানে, \(a^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta} ....(6)\)
\(b^{\prime}=a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta} ....(7)\)
\((6)+(7)\) এর সাহায্যে
\(a^{\prime}+b^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}+a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}\)
\(=a\cos^2{\theta}+b\sin^2{\theta}+a\sin^2{\theta}+b\cos^2{\theta}\)
\(=a(\sin^2{\theta}+\cos^2{\theta})+b(\sin^2{\theta}+\cos^2{\theta})\)
\(=a.1+b.1\)
\(\therefore a^{\prime}+b^{\prime}=a+b\)
\((6)\) ও \((7)\) হতে
\(2a^{\prime}=a.2\cos^2{\theta}+2h.2\sin{\theta}\cos{\theta}+b.2\sin^2{\theta}\)
\(=a(1+\cos{2\theta})+2h\sin{2\theta}+b(1-\cos{2\theta})\)
\(=a+a\cos{2\theta}+2h\sin{2\theta}+b-b\cos{2\theta}\)
\(=(a+b)+(a-b)\cos{2\theta}+2h\sin{2\theta}\)
\(\therefore 2a^{\prime}=(a+b)+\{2h\sin{2\theta}+(a-b)\cos{2\theta}\} ......(8)\)
আবার,
\(2b^{\prime}=a.2\sin^2{\theta}-2h.2\sin{\theta}\cos{\theta}+b.2\cos^2{\theta}\)
\(=a(1-\cos{2\theta})-2h\sin{2\theta}+b(1+\cos{2\theta})\)
\(=a-a\cos{2\theta}-2h\sin{2\theta}+b+b\cos{2\theta}\)
\(=(a+b)-(a-b)\cos{2\theta}-2h\sin{2\theta}\)
\(\therefore 2b^{\prime}=(a+b)-\{2h\sin{2\theta}+(a-b)\cos{2\theta}\} ......(9)\)
\((8)\times{(9)}\) এর সাহায্যে
\(4a^{\prime}b^{\prime}=(a+b)^2-\{2h\sin{2\theta}+(a-b)\cos{2\theta}\}^2\)
\(=(a+b)^2-4h^2\sin^2{2\theta}-(a-b)^2\cos^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}\)
\(=(a+b)^2-4h^2+4h^2\cos^2{2\theta}-(a-b)^2\cos^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}\)
\(=(a+b)^2-4h^2+(2h\cos{2\theta})^2-(a-b)^2\cos^2{2\theta}-2(a-b)\sin{2\theta}.2h\cos{2\theta}\)
\(=(a+b)^2-4h^2+(a-b)^2\sin^2{2\theta}-(a-b)^2+(a-b)^2\sin^2{2\theta}-2(a-b)\sin{2\theta}(a-b)\sin{2\theta}\) ➜ \(\because 2h\cos{2\theta}=(a-b)\sin{2\theta}\)
\((3)\) হতে,
\(=(a+b)^2-(a-b)^2-4h^2+2(a-b)^2\sin^2{2\theta}-2(a-b)^2\sin^2{2\theta}\)
\(=4ab-4h^2\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(\Rightarrow 4a^{\prime}b^{\prime}=4(ab-h^2)\)
\(\therefore a^{\prime}b^{\prime}=ab-h^2\)
( প্রমাণিত )
×
মূলবিন্দু অপরিবর্তিত রেখে আয়তাকার অক্ষদ্বয়কে কোনো নির্দিষ্ট কোণে আবর্তন করায় \(ax^2+2hxy+by^2=0\) সমীকরণের পরিবর্তিত রূপ \(a^{\prime}x^2+2h^{\prime}xy+b^{\prime}y^2=0\) হওয়ার শর্ত
\(a^{\prime}+b^{\prime}=a+b\)
\(a^{\prime}b^{\prime}-{h^{\prime}}^2=ab-h^2\)
দ্রষ্টব্যঃ এখানে, \(a+b\) এবং \(ab-h^2\) কে অপরিবর্তক বলা হয়।
দ্রষ্টব্যঃ এখানে, \(a+b\) এবং \(ab-h^2\) কে অপরিবর্তক বলা হয়।
Proof:
প্রদত্ত সমীকরণ,
\(ax^2+2hxy+by^2=0 .........(1)\)
মূলবিন্দু ঠিক রেখে অক্ষদ্বয়কে \(\theta\) কোণে ঘুরানো হয় তবে আমরা স্থনাংকের রূপান্তরিত সূত্র পাব,
\(x=x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}\)
\(y=x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\)
প্রদত্ত \((1)\) নং সমীকরণের রূপান্তরিত রূপ হবে,
\(a(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})^2+2h(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})+b(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})^2+c=0\)
\(\Rightarrow (a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}){x^{\prime}}^2+2\{-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}\}x^{\prime}y^{\prime}+\)\((a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}){y^{\prime}}^2=0\)
\(\therefore a^{\prime}{x^{\prime}}^2+2h^{\prime}x^{\prime}y^{\prime}+b^{\prime}{y^{\prime}}^2=0 .....(2)\)
যেখানে, \(a^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta} ....(3)\)
\(b^{\prime}=a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta} ....(4)\)
\(h^{\prime}=-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta} ....(5)\)
\((3)+(4)\) এর সাহায্যে
\(a^{\prime}+b^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}+a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}\)
\(=a\cos^2{\theta}+b\sin^2{\theta}+a\sin^2{\theta}+b\cos^2{\theta}\)
\(=a(\sin^2{\theta}+\cos^2{\theta})+b(\sin^2{\theta}+\cos^2{\theta})\)
\(=a.1+b.1\)
\(\therefore a^{\prime}+b^{\prime}=a+b\)
\((3), \ (4)\) ও \((5)\) হতে
\(2a^{\prime}=a.2\cos^2{\theta}+2h.2\sin{\theta}\cos{\theta}+b.2\sin^2{\theta}\)
\(=a(1+\cos{2\theta})+2h\sin{2\theta}+b(1-\cos{2\theta})\)
\(=a+a\cos{2\theta}+2h\sin{2\theta}+b-b\cos{2\theta}\)
\(=(a+b)+(a-b)\cos{2\theta}+2h\sin{2\theta}\)
\(\therefore 2a^{\prime}=(a+b)+\{2h\sin{2\theta}+(a-b)\cos{2\theta}\} ......(6)\)
আবার,
\(2b^{\prime}=a.2\sin^2{\theta}-2h.2\sin{\theta}\cos{\theta}+b.2\cos^2{\theta}\)
\(=a(1-\cos{2\theta})-2h\sin{2\theta}+b(1+\cos{2\theta})\)
\(=a-a\cos{2\theta}-2h\sin{2\theta}+b+b\cos{2\theta}\)
\(=(a+b)-(a-b)\cos{2\theta}-2h\sin{2\theta}\)
\(\therefore 2b^{\prime}=(a+b)-\{2h\sin{2\theta}+(a-b)\cos{2\theta}\} ......(7)\)
আবার,
\(h^{\prime}=-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}\)
\(=-\frac{1}{2}a.2\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+\frac{1}{2}b.2\sin{\theta}\cos{\theta}\)
\(=-\frac{1}{2}a\sin{2\theta}+h\cos{2\theta}+\frac{1}{2}b\sin{2\theta}=0\) ➜ \(\because 2\sin{A}\cos{A}=\sin{2A}\)
\(\cos^2{A}-\sin^2{A}=\cos{2A}\)
\(=h\cos{2\theta}-\frac{1}{2}(a-b)\sin{2\theta}\)
\(\therefore h^{\prime}=h\cos{2\theta}-\frac{1}{2}(a-b)\sin{2\theta}\)
\(\therefore 2h^{\prime}=2h\cos{2\theta}-(a-b)\sin{2\theta} .......(8)\)
\((6)\times{(7)}\) এর সাহায্যে
\(4a^{\prime}b^{\prime}=(a+b)^2-\{2h\sin{2\theta}+(a-b)\cos{2\theta}\}^2\)
\(=(a+b)^2-4h^2\sin^2{2\theta}-(a-b)^2\cos^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}\)
\(=(a+b)^2-4h^2+4h^2\cos^2{2\theta}-(a-b)^2+(a-b)^2\sin^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}\)
\(=(a+b)^2-(a-b)^2-4h^2+4h^2\cos^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}+(a-b)^2\sin^2{2\theta}\)
\(=4ab-4h^2+\{2h\cos{2\theta}-(a-b)\sin{2\theta}\}^2\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(=4ab-4h^2+{2h^{\prime}}^2\) ➜ \(\because 2h\cos{2\theta}-(a-b)\sin{2\theta}=2h^{\prime}\)
\((8)\) হতে,
\(=4ab-4h^2+4{h^{\prime}}^2\)
\(\Rightarrow 4a^{\prime}b^{\prime}=4(ab-h^2+{h^{\prime}}^2)\)
\(\Rightarrow a^{\prime}b^{\prime}=ab-h^2+{h^{\prime}}^2\)
\(\therefore a^{\prime}b^{\prime}-{h^{\prime}}^2=ab-h^2\)
( প্রমাণিত )
দ্রষ্টব্যঃ এখানে, \(a+b\) এবং \(ab-h^2\) কে অপরিবর্তক বলা হয়।
\(ax^2+2hxy+by^2=0 .........(1)\)
মূলবিন্দু ঠিক রেখে অক্ষদ্বয়কে \(\theta\) কোণে ঘুরানো হয় তবে আমরা স্থনাংকের রূপান্তরিত সূত্র পাব,
\(x=x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta}\)
\(y=x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta}\)
প্রদত্ত \((1)\) নং সমীকরণের রূপান্তরিত রূপ হবে,
\(a(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})^2+2h(x^{\prime}\cos{\theta}-y^{\prime}\sin{\theta})(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})+b(x^{\prime}\sin{\theta}+y^{\prime}\cos{\theta})^2+c=0\)
\(\Rightarrow (a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}){x^{\prime}}^2+2\{-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}\}x^{\prime}y^{\prime}+\)\((a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}){y^{\prime}}^2=0\)
\(\therefore a^{\prime}{x^{\prime}}^2+2h^{\prime}x^{\prime}y^{\prime}+b^{\prime}{y^{\prime}}^2=0 .....(2)\)
যেখানে, \(a^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta} ....(3)\)
\(b^{\prime}=a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta} ....(4)\)
\(h^{\prime}=-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta} ....(5)\)
\((3)+(4)\) এর সাহায্যে
\(a^{\prime}+b^{\prime}=a\cos^2{\theta}+2h\sin{\theta}\cos{\theta}+b\sin^2{\theta}+a\sin^2{\theta}-2h\sin{\theta}\cos{\theta}+b\cos^2{\theta}\)
\(=a\cos^2{\theta}+b\sin^2{\theta}+a\sin^2{\theta}+b\cos^2{\theta}\)
\(=a(\sin^2{\theta}+\cos^2{\theta})+b(\sin^2{\theta}+\cos^2{\theta})\)
\(=a.1+b.1\)
\(\therefore a^{\prime}+b^{\prime}=a+b\)
\((3), \ (4)\) ও \((5)\) হতে
\(2a^{\prime}=a.2\cos^2{\theta}+2h.2\sin{\theta}\cos{\theta}+b.2\sin^2{\theta}\)
\(=a(1+\cos{2\theta})+2h\sin{2\theta}+b(1-\cos{2\theta})\)
\(=a+a\cos{2\theta}+2h\sin{2\theta}+b-b\cos{2\theta}\)
\(=(a+b)+(a-b)\cos{2\theta}+2h\sin{2\theta}\)
\(\therefore 2a^{\prime}=(a+b)+\{2h\sin{2\theta}+(a-b)\cos{2\theta}\} ......(6)\)
আবার,
\(2b^{\prime}=a.2\sin^2{\theta}-2h.2\sin{\theta}\cos{\theta}+b.2\cos^2{\theta}\)
\(=a(1-\cos{2\theta})-2h\sin{2\theta}+b(1+\cos{2\theta})\)
\(=a-a\cos{2\theta}-2h\sin{2\theta}+b+b\cos{2\theta}\)
\(=(a+b)-(a-b)\cos{2\theta}-2h\sin{2\theta}\)
\(\therefore 2b^{\prime}=(a+b)-\{2h\sin{2\theta}+(a-b)\cos{2\theta}\} ......(7)\)
আবার,
\(h^{\prime}=-a\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+b\sin{\theta}\cos{\theta}\)
\(=-\frac{1}{2}a.2\sin{\theta}\cos{\theta}+h(\cos^2{\theta}-\sin^2{\theta})+\frac{1}{2}b.2\sin{\theta}\cos{\theta}\)
\(=-\frac{1}{2}a\sin{2\theta}+h\cos{2\theta}+\frac{1}{2}b\sin{2\theta}=0\) ➜ \(\because 2\sin{A}\cos{A}=\sin{2A}\)
\(\cos^2{A}-\sin^2{A}=\cos{2A}\)
\(=h\cos{2\theta}-\frac{1}{2}(a-b)\sin{2\theta}\)
\(\therefore h^{\prime}=h\cos{2\theta}-\frac{1}{2}(a-b)\sin{2\theta}\)
\(\therefore 2h^{\prime}=2h\cos{2\theta}-(a-b)\sin{2\theta} .......(8)\)
\((6)\times{(7)}\) এর সাহায্যে
\(4a^{\prime}b^{\prime}=(a+b)^2-\{2h\sin{2\theta}+(a-b)\cos{2\theta}\}^2\)
\(=(a+b)^2-4h^2\sin^2{2\theta}-(a-b)^2\cos^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}\)
\(=(a+b)^2-4h^2+4h^2\cos^2{2\theta}-(a-b)^2+(a-b)^2\sin^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}\)
\(=(a+b)^2-(a-b)^2-4h^2+4h^2\cos^2{2\theta}-4h(a-b)\sin{2\theta}\cos{2\theta}+(a-b)^2\sin^2{2\theta}\)
\(=4ab-4h^2+\{2h\cos{2\theta}-(a-b)\sin{2\theta}\}^2\) ➜ \(\because (a+b)^2-(a-b)^2=4ab\)
\(=4ab-4h^2+{2h^{\prime}}^2\) ➜ \(\because 2h\cos{2\theta}-(a-b)\sin{2\theta}=2h^{\prime}\)
\((8)\) হতে,
\(=4ab-4h^2+4{h^{\prime}}^2\)
\(\Rightarrow 4a^{\prime}b^{\prime}=4(ab-h^2+{h^{\prime}}^2)\)
\(\Rightarrow a^{\prime}b^{\prime}=ab-h^2+{h^{\prime}}^2\)
\(\therefore a^{\prime}b^{\prime}-{h^{\prime}}^2=ab-h^2\)
( প্রমাণিত )
দ্রষ্টব্যঃ এখানে, \(a+b\) এবং \(ab-h^2\) কে অপরিবর্তক বলা হয়।

- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000010