শিক্ষা বোর্ড যশোর - 2019
উচ্চতর গণিত ( বহুনির্বাচনি )
[2019 সালের সিলেবাস অনুযায়ী ]
প্রথম পত্র বহুনির্বাচনি
বিষয় কোডঃ 265
সময়-২৫ মিনিট
পূর্ণমান-২৫
[ দ্রষ্টব্যঃ সরবরাহকৃত বহুনির্বাচনি অভীক্ষার উত্তরপত্রে প্রশ্নের ক্রমিক নম্বরের বিপরীতে প্রদত্ত বর্ণসংবলিত বৃত্তসমুহ হতে সিঠিক/সর্বোৎকৃষ্ট উত্তরের বৃত্তটি বল পয়ন্ট কলম দ্বারা সম্পুর্ণ ভরাট কর। প্রতিটি প্রশ্নের মাণ ১। প্রশ্নপত্রে কোন প্রকার দাগ/ চিহ্ন দেওয়া যাবে না। ]
উচ্চতর গণিত ( বহুনির্বাচনি )
[2019 সালের সিলেবাস অনুযায়ী ]
প্রথম পত্র বহুনির্বাচনি
বিষয় কোডঃ 265
সময়-২৫ মিনিট
পূর্ণমান-২৫
[ দ্রষ্টব্যঃ সরবরাহকৃত বহুনির্বাচনি অভীক্ষার উত্তরপত্রে প্রশ্নের ক্রমিক নম্বরের বিপরীতে প্রদত্ত বর্ণসংবলিত বৃত্তসমুহ হতে সিঠিক/সর্বোৎকৃষ্ট উত্তরের বৃত্তটি বল পয়ন্ট কলম দ্বারা সম্পুর্ণ ভরাট কর। প্রতিটি প্রশ্নের মাণ ১। প্রশ্নপত্রে কোন প্রকার দাগ/ চিহ্ন দেওয়া যাবে না। ]
১। \(A=\begin{bmatrix}2 & 3 \\4 & 1 \end{bmatrix}\) হলে, \(Adj(A)=?\)
\(Adj(P)=\begin{bmatrix} \ \ d & -b \\-c & \ \ d \end{bmatrix}\)
\(\therefore A=\begin{bmatrix}2 & 3 \\4 & 1 \end{bmatrix}\) হলে,
\(Adj(A)=\begin{bmatrix} \ \ 1 & -3 \\-4 & \ \ 2 \end{bmatrix}\)
উত্তরঃ ( গ )
ক \(\begin{bmatrix}1 & 3 \\4 & 2 \end{bmatrix}\)
গ \(\begin{bmatrix} \ \ 1 & -3 \\-4 & \ \ 2 \end{bmatrix}\)
গ \(\begin{bmatrix} \ \ 1 & -3 \\-4 & \ \ 2 \end{bmatrix}\)
খ \(\begin{bmatrix} 2 & 4 \\3 & 1 \end{bmatrix}\)
ঘ \(\begin{bmatrix} -1 & \ \ 3 \\ \ \ 4 & -2 \end{bmatrix}\)
\(P=\begin{bmatrix}a & b \\c & d \end{bmatrix}\) হলে,ঘ \(\begin{bmatrix} -1 & \ \ 3 \\ \ \ 4 & -2 \end{bmatrix}\)
\(Adj(P)=\begin{bmatrix} \ \ d & -b \\-c & \ \ d \end{bmatrix}\)
\(\therefore A=\begin{bmatrix}2 & 3 \\4 & 1 \end{bmatrix}\) হলে,
\(Adj(A)=\begin{bmatrix} \ \ 1 & -3 \\-4 & \ \ 2 \end{bmatrix}\)
উত্তরঃ ( গ )
২। \(P=\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\) ও \(Q=\begin{bmatrix} 0 \\ 1 \\ 2 \end{bmatrix}\) হলে, \(PQ\) এর মান কত?
\(PQ=\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\times\begin{bmatrix} 0 \\ 1 \\ 2 \end{bmatrix}\)
\(=\begin{bmatrix} 1\times0+2\times1+3\times2 \end{bmatrix}\)
\(=\begin{bmatrix} 0+2+6 \end{bmatrix}\)
\(=\begin{bmatrix} 8 \end{bmatrix}\)
উত্তরঃ ( ক )
ক \(\begin{bmatrix} 8 \end{bmatrix}\)
গ \(\begin{bmatrix} 0 \\ 2 \\ 6 \end{bmatrix}\)
গ \(\begin{bmatrix} 0 \\ 2 \\ 6 \end{bmatrix}\)
খ \(\begin{bmatrix} 1476 \end{bmatrix}\)
ঘ \(\begin{bmatrix} 0 & 2 & 6 \end{bmatrix}\)
\(P=\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\) ও \(Q=\begin{bmatrix} 0 \\ 1 \\ 2 \end{bmatrix}\) হলে,ঘ \(\begin{bmatrix} 0 & 2 & 6 \end{bmatrix}\)
\(PQ=\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\times\begin{bmatrix} 0 \\ 1 \\ 2 \end{bmatrix}\)
\(=\begin{bmatrix} 1\times0+2\times1+3\times2 \end{bmatrix}\)
\(=\begin{bmatrix} 0+2+6 \end{bmatrix}\)
\(=\begin{bmatrix} 8 \end{bmatrix}\)
উত্তরঃ ( ক )
৩। \(\left|\begin{array}{c}1 & \ \ \ 1 & 3\\ 0 & -1 & x\\ 1 & -3 & 3\end{array}\right|\) নির্ণায়কটির \((1, 2)\) তম অনুরাশি \(-3\) হলে, \(x\) এর মান-
\((1, 2)\) তম অনুরাশি \(=\left|\begin{array}{c}0 & x \\1 & 3\end{array}\right|\)
\(=0\times3-x\times1\)
\(=-x\)
অতএব, \(-x=-3\)
\(\Rightarrow x=3\)
উত্তরঃ ( গ )
ক \(-12\)
গ \(3\)
গ \(3\)
খ \(-3\)
ঘ \(12\)
\(\left|\begin{array}{c}1 & \ \ \ 1 & 3\\ 0 & -1 & x\\ 1 & -3 & 3\end{array}\right|\) নির্ণায়কটিরঘ \(12\)
\((1, 2)\) তম অনুরাশি \(=\left|\begin{array}{c}0 & x \\1 & 3\end{array}\right|\)
\(=0\times3-x\times1\)
\(=-x\)
অতএব, \(-x=-3\)
\(\Rightarrow x=3\)
উত্তরঃ ( গ )
৪। \(\hat{i}+\lambda\hat{j}+2\hat{k}\) এবং \(2\hat{i}+\hat{j}-2\hat{k}\) ভেক্টরদ্বয় পরস্পর লম্ব হলে, \(\lambda\) এর মান কোনটি?
\((\hat{i}+\lambda\hat{j}+2\hat{k}).(2\hat{i}+\hat{j}-2\hat{k})=0\)
\(\Rightarrow 1.2+\lambda.1+2.(-2)=0\)
\(\Rightarrow 2+\lambda-4=0\)
\(\Rightarrow \lambda-2=0\)
\(\therefore \lambda=2\)
উত্তরঃ ( ঘ )
ক \(-6\)
গ \(0\)
গ \(0\)
খ \(-2\)
ঘ \(2\)
\(\hat{i}+\lambda\hat{j}+2\hat{k}\) এবং \(2\hat{i}+\hat{j}-2\hat{k}\) ভেক্টরদ্বয় পরস্পর লম্ব হলে,ঘ \(2\)
\((\hat{i}+\lambda\hat{j}+2\hat{k}).(2\hat{i}+\hat{j}-2\hat{k})=0\)
\(\Rightarrow 1.2+\lambda.1+2.(-2)=0\)
\(\Rightarrow 2+\lambda-4=0\)
\(\Rightarrow \lambda-2=0\)
\(\therefore \lambda=2\)
উত্তরঃ ( ঘ )
৫। \(\overrightarrow{P}=\sqrt{2}\hat{i}+\alpha\hat{j}\) এবং \(\overrightarrow{Q}=\hat{i}+\sqrt{2}\hat{j}\) ভেক্টরদ্বয় পরস্পর সমান্তরাল হলে \(\alpha\) এর মান কত হবে?
এবং \(\overrightarrow{B}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) ভেক্টরদ্বয় পরস্পর সমান্তরাল হওয়ার শর্তঃ
\(\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\frac{a_{3}}{b_{3}}\)
অতএব,
\(\overrightarrow{P}=\sqrt{2}\hat{i}+\alpha\hat{j}\) এবং \(\overrightarrow{Q}=\hat{i}+\sqrt{2}\hat{j}\) ভেক্টরদ্বয় পরস্পর সমান্তরাল হল,
\(\frac{\sqrt{2}}{1}=\frac{\alpha}{\sqrt{2}}\)
\(\therefore \alpha=2\)
উত্তরঃ ( ঘ )
ক \(-2\)
গ \(-\sqrt{2}\)
গ \(-\sqrt{2}\)
খ \(-1\)
ঘ \(2\)
\(\overrightarrow{A}=a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\) ঘ \(2\)
এবং \(\overrightarrow{B}=b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\) ভেক্টরদ্বয় পরস্পর সমান্তরাল হওয়ার শর্তঃ
\(\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\frac{a_{3}}{b_{3}}\)
অতএব,
\(\overrightarrow{P}=\sqrt{2}\hat{i}+\alpha\hat{j}\) এবং \(\overrightarrow{Q}=\hat{i}+\sqrt{2}\hat{j}\) ভেক্টরদ্বয় পরস্পর সমান্তরাল হল,
\(\frac{\sqrt{2}}{1}=\frac{\alpha}{\sqrt{2}}\)
\(\therefore \alpha=2\)
উত্তরঃ ( ঘ )
৬। কোনো বিন্দুর পোলার স্থানাঙ্ক \((5, 90^{o})\) হলে কার্তেসীয় স্থানাঙ্ক হবে-
\(r=5, \ \theta=90^{o}\)
এখন, \(x=r\cos{\theta}, \ y=r\sin{\theta}\)
\(\Rightarrow x=5\cos{90^{o}}, \ y=5\sin{90^{o}}\)
\(\Rightarrow x=5\times0, \ y=5\times1\)
\(\therefore x=0, \ y=5\)
অতএব, বিন্দুটির কার্তেসীয় স্থানাঙ্ক \((0, 5)\)
উত্তরঃ ( খ )
ক \((0, 0)\)
গ \((5, 0)\)
গ \((5, 0)\)
খ \((0, 5)\)
ঘ \((5, 5)\)
কোনো বিন্দুর পোলার স্থানাঙ্ক \((5, 90^{o})\) হলে,ঘ \((5, 5)\)
\(r=5, \ \theta=90^{o}\)
এখন, \(x=r\cos{\theta}, \ y=r\sin{\theta}\)
\(\Rightarrow x=5\cos{90^{o}}, \ y=5\sin{90^{o}}\)
\(\Rightarrow x=5\times0, \ y=5\times1\)
\(\therefore x=0, \ y=5\)
অতএব, বিন্দুটির কার্তেসীয় স্থানাঙ্ক \((0, 5)\)
উত্তরঃ ( খ )
৭। \(x=0, \ x=4, \ y=2, \ y=6\) রেখাগুলো দ্বারা আবদ্ধ এলাকার ক্ষেত্রফল কত বর্গ একক?
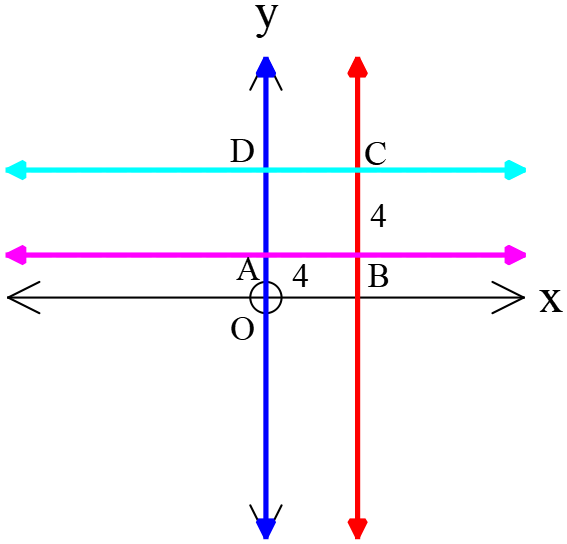
এখানে,
\(AB=4-0=4\)
\(BC=6-2=4\)
ক্ষেত্রফল,
\(AB\times{BC}=4\times4\)
\(=16\) বর্গ একক।
উত্তরঃ ( খ )
ক \(24\)
গ \(12\)
গ \(12\)
খ \(16\)
ঘ \(8\)
\(x=0, \ x=4, \ y=2, \ y=6\) রেখাগুলো দ্বারা আবদ্ধ এলাকা \(\Box{ABCD}\)ঘ \(8\)

এখানে,
\(AB=4-0=4\)
\(BC=6-2=4\)
ক্ষেত্রফল,
\(AB\times{BC}=4\times4\)
\(=16\) বর্গ একক।
উত্তরঃ ( খ )
৮। \(b\) এর মান কত হলে, \(y=bx(1-bx)\) বক্ররেখার মূলবিন্দুতে স্পর্শকটি \(x\) অক্ষের ধনাত্মক দিকের সাথে \(60^{o}\) কোণ উৎপন্ন করে?
\(\Rightarrow y=bx-b^2x^2\)
\(\Rightarrow \frac{dy}{dx}=b\frac{d}{dx}(x)-b^2\frac{d}{dx}(x^2)\)
\(\Rightarrow \frac{dy}{dx}=b-b^2.2x\)
\(\Rightarrow \frac{dy}{dx}=b-2b^2x\)
\(\therefore \left(\frac{dy}{dx}\right)_{(0, 0)}=b-2b^2\times0=b\)
অতএব, মূলবিন্দুতে স্পর্শকটির ঢাল \(\tan{\theta}=\left(\frac{dy}{dx}\right)_{(0, 0)}=b\)
\(\Rightarrow b=\tan{\theta}\)
\(=\tan{60^{o}}\)
\(=\sqrt{3}\)
উত্তরঃ ( ঘ )
ক \(-\sqrt{3}\)
গ \(\frac{1}{\sqrt{3}}\)
গ \(\frac{1}{\sqrt{3}}\)
খ \(-\frac{1}{\sqrt{3}}\)
ঘ \(\sqrt{3}\)
\(y=bx(1-bx)\)ঘ \(\sqrt{3}\)
\(\Rightarrow y=bx-b^2x^2\)
\(\Rightarrow \frac{dy}{dx}=b\frac{d}{dx}(x)-b^2\frac{d}{dx}(x^2)\)
\(\Rightarrow \frac{dy}{dx}=b-b^2.2x\)
\(\Rightarrow \frac{dy}{dx}=b-2b^2x\)
\(\therefore \left(\frac{dy}{dx}\right)_{(0, 0)}=b-2b^2\times0=b\)
অতএব, মূলবিন্দুতে স্পর্শকটির ঢাল \(\tan{\theta}=\left(\frac{dy}{dx}\right)_{(0, 0)}=b\)
\(\Rightarrow b=\tan{\theta}\)
\(=\tan{60^{o}}\)
\(=\sqrt{3}\)
উত্তরঃ ( ঘ )
নিচের উদ্দীপকের আলোকে ৯ ও ১০ নং প্রশ্নের উত্তর দাওঃ
\(x^2+y^2+2x+2y+5=0\)
এবং \(4x^2+4y^2-8x+8y+1=0\) দুইটি বৃত্তের সমীকরণ।
৯। বৃত্তদ্বয়ের সাধারণ জ্যা এর সমীকরণ হলো-\(x^2+y^2+2x+2y+5=0\)
এবং \(4x^2+4y^2-8x+8y+1=0\) দুইটি বৃত্তের সমীকরণ।
ক \(16x+19=0\)
গ \(6y-10x-4=0\)
গ \(6y-10x-4=0\)
খ \(16x+21=0\)
ঘ \(10y-6x+6=0\)
\(S_{1}=0\)ঘ \(10y-6x+6=0\)
এবং \(S_{2}=0\) বৃত্ত দুইটির সাধারণ জ্যা এর সমীকরণ,
\(S_{1}-S_{2}=0\)
এখন, \(x^2+y^2+2x+2y+5=0\)
এবং \(4x^2+4y^2-8x+8y+1=0\) দুইটি বৃত্তের সমীকরণ।
অতএব, \(x^2+y^2+2x+2y+5=0\)
এবং \(x^2+y^2-2x+2y+\frac{1}{4}=0\) বৃত্ত দুইটির সাধারণ জ্যা এর সমীকরণ,
\(x^2+y^2+2x+2y+5-x^2-y^2+2x-2y-\frac{1}{4}=0\)
\(\Rightarrow 4x+5-\frac{1}{4}=0\)
\(\Rightarrow 16x+20-1=0\)
\(\therefore 16x+19=0\)
উত্তরঃ ( ক )
১০। দ্বিতীয় বৃত্ত দ্বারা \(y\) অক্ষের ছেদাংশের পরিমাণ-
\(\Rightarrow x^2+y^2-2x+2y+\frac{1}{4}=0\)
এখানে, \(2g=-2, \ 2f=2, \ c=\frac{1}{4}\)
\(\Rightarrow g=-1, \ f=1, \ c=\frac{1}{4}\)
\(y\) অক্ষের ছেদাংশের পরিমাণ \(=2\sqrt{f^2-c}\)
\(=2\sqrt{(1)^2-\frac{1}{4}}\)
\(=2\sqrt{1-\frac{1}{4}}\)
\(=2\sqrt{\frac{4-1}{4}}\)
\(=2\sqrt{\frac{3}{4}}\)
\(=2\frac{\sqrt{3}}{2}\)
\(=\sqrt{3}\)
উত্তরঃ ( গ )
ক \(\frac{\sqrt{3}}{2}\)
গ \(\sqrt{3}\)
গ \(\sqrt{3}\)
খ \(\frac{\sqrt{5}}{2}\)
ঘ \(\sqrt{5}\)
দ্বিতীয় বৃত্ত \(4x^2+4y^2-8x+8y+1=0\)ঘ \(\sqrt{5}\)
\(\Rightarrow x^2+y^2-2x+2y+\frac{1}{4}=0\)
এখানে, \(2g=-2, \ 2f=2, \ c=\frac{1}{4}\)
\(\Rightarrow g=-1, \ f=1, \ c=\frac{1}{4}\)
\(y\) অক্ষের ছেদাংশের পরিমাণ \(=2\sqrt{f^2-c}\)
\(=2\sqrt{(1)^2-\frac{1}{4}}\)
\(=2\sqrt{1-\frac{1}{4}}\)
\(=2\sqrt{\frac{4-1}{4}}\)
\(=2\sqrt{\frac{3}{4}}\)
\(=2\frac{\sqrt{3}}{2}\)
\(=\sqrt{3}\)
উত্তরঃ ( গ )
১১। \(\frac{3n!}{4!(n-1)!}=4\) হলে, \(n\) এর মান-
\(\Rightarrow \frac{3n(n-1)!}{4.3.2.1!(n-1)!}=4\)
\(\Rightarrow \frac{n}{4.2.1!}=4\)
\(\Rightarrow \frac{n}{8}=4\)
\(\therefore n=32\)
উত্তরঃ ( ঘ )
ক \(\frac{16}{3}\)
গ \(16\)
গ \(16\)
খ \(\frac{32}{3}\)
ঘ \(32\)
\(\frac{3n!}{4!(n-1)!}=4\)ঘ \(32\)
\(\Rightarrow \frac{3n(n-1)!}{4.3.2.1!(n-1)!}=4\)
\(\Rightarrow \frac{n}{4.2.1!}=4\)
\(\Rightarrow \frac{n}{8}=4\)
\(\therefore n=32\)
উত্তরঃ ( ঘ )
১২। কোনো শর্ত ছাড়া \(0, \ 1, \ 7, \ 1, \ 1, \ 2\) অঙ্কগুলো দ্বারা ছয় অঙ্কের কতগুলো সংখ্যা গঠন করা যাবে?
\(=\frac{6!}{3!}-\frac{5!}{3!}\)
\(=\frac{6.5.4.3!}{3!}-\frac{5.4.3!}{3!}\)
\(=120-20\)
\(=100\) টি
উত্তরঃ ( ক )
ক \(100\)
গ \(300\)
গ \(300\)
খ \(120\)
ঘ \(720\)
কোনো শর্ত ছাড়া \(0, \ 1, \ 7, \ 1, \ 1, \ 2\) অঙ্কগুলো দ্বারা ছয় অঙ্কের গঠিত সংখ্যা,ঘ \(720\)
\(=\frac{6!}{3!}-\frac{5!}{3!}\)
\(=\frac{6.5.4.3!}{3!}-\frac{5.4.3!}{3!}\)
\(=120-20\)
\(=100\) টি
উত্তরঃ ( ক )
১৩। তোমার বাবাকে কল করতে গিয়ে বাবার মোবাইলের শেষ তিনটি ডিজিট ভুলে গেলে। কত প্রকারে চেষ্টা করলে অন্ততঃ একবার সংযোগ পাবে?
\(10\) টি অঙ্ক দ্বারা শেষ তিনটি ডিজিট পূরণের উপায়,
\(=10^{3}\)
উত্তরঃ ( ঘ )
ক \(10^{9}\)
গ \(3^{10}\)
গ \(3^{10}\)
খ \(9^{10}\)
ঘ \(10^{3}\)
শেষ তিনটি ডিজিট পূরণের জন্য \(0, \ 1, \ 2, 3, \ 4, \ 5, 6, \ 7, \ 8, \ 9\) মোট \(10\) টি অঙ্ক বিদ্যমান।ঘ \(10^{3}\)
\(10\) টি অঙ্ক দ্বারা শেষ তিনটি ডিজিট পূরণের উপায়,
\(=10^{3}\)
উত্তরঃ ( ঘ )
১৪। \(A=40^{o}\) ও \(B=50^{o}\) হলে-
\(i.\) \(\cos{2A}=\sin{10^{o}}\)
\(ii.\) \(\sin{(A-B)}=\sin{10^{o}}\)
\(iii.\) \(\cot{(A+B)}=\tan{0^{o}}\)
নিচের কোনটি সঠীক?
\(\therefore \cos{2A}=\cos{(2\times40^{o})}\)
\(=\cos{80^{o}}\)
\(=\cos{(90^{o}-10^{o})}\)
\(=\sin{10^{o}}\)
\(\therefore i.\) নং বাক্যটি সত্য
\(A=40^{o}\) ও \(B=50^{o}\) হলে-
\(\therefore \sin{(A-B)}=\sin{(40^{o}-50^{o})}\)
\(=\sin{(-10^{o})}\)
\(=-\sin{10^{o}}\)
\(\therefore ii.\) নং বাক্যটি সত্য নয়।
আবার,
\(A=40^{o}\) ও \(B=50^{o}\) হলে-
\(\therefore \cot{(A+B)}=\cot{(40^{o}+50^{o})}\)
\(=\cot{90^{o}}\)
\(=0\)
\(=\tan{0^{o}}\)
\(\therefore iii.\) নং বাক্যটি সত্য।
উত্তরঃ ( গ )
\(i.\) \(\cos{2A}=\sin{10^{o}}\)
\(ii.\) \(\sin{(A-B)}=\sin{10^{o}}\)
\(iii.\) \(\cot{(A+B)}=\tan{0^{o}}\)
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
\(A=40^{o}\) ও \(B=50^{o}\) হলে-ঘ \(i.\), \(ii.\) ও \(iii.\)
\(\therefore \cos{2A}=\cos{(2\times40^{o})}\)
\(=\cos{80^{o}}\)
\(=\cos{(90^{o}-10^{o})}\)
\(=\sin{10^{o}}\)
\(\therefore i.\) নং বাক্যটি সত্য
\(A=40^{o}\) ও \(B=50^{o}\) হলে-
\(\therefore \sin{(A-B)}=\sin{(40^{o}-50^{o})}\)
\(=\sin{(-10^{o})}\)
\(=-\sin{10^{o}}\)
\(\therefore ii.\) নং বাক্যটি সত্য নয়।
আবার,
\(A=40^{o}\) ও \(B=50^{o}\) হলে-
\(\therefore \cot{(A+B)}=\cot{(40^{o}+50^{o})}\)
\(=\cot{90^{o}}\)
\(=0\)
\(=\tan{0^{o}}\)
\(\therefore iii.\) নং বাক্যটি সত্য।
উত্তরঃ ( গ )
১৫। \(\frac{\pi}{2}\lt{\theta}\lt{\pi}\) এবং \(\sin{\theta}=\frac{3}{5}\) হলে-
\(i.\) \(\cos{\theta}=\frac{2}{3}\)
\(ii.\) \(\tan^2{\theta}=\frac{9}{16}\)
\(iii.\) \(\sec{\theta}\tan{\theta}=\frac{15}{16}\)
নিচের কোনটি সঠীক?
লম্ব \(=3\)
অতিভুজ \(=5\)
অতএব, ভূমি \(=-\sqrt{5^2-3^2}\) যেহেতু, \(\frac{\pi}{2}\lt{\theta}\lt{\pi}\)
\(=-\sqrt{25-9}\)
\(=-\sqrt{16}\)
\(=-4\)
\(\cos{\theta}=\frac{\text{ভূমি}}{\text{অতিভুজ}}=\frac{-4}{5}\)
\(=-\frac{4}{5}\)
\(\therefore i.\) নং বাক্যটি সত্য নয়।
\(\tan^2{\theta}\)
\(=\left(\frac{\text{লম্ব}}{\text{ভূমি}}\right)^2\)
\(=\left(\frac{3}{-4}\right)^2\)
\(=\frac{9}{16}\)
\(\therefore ii.\) নং বাক্যটি সত্য
আবার,
\(\sec{\theta}\tan{\theta}\)
\(=\frac{\text{অতিভুজ}}{\text{ভূমি}}\times\frac{\text{লম্ব}}{\text{ভূমি}}\)
\(=\frac{5}{-4}\times\frac{3}{-4}\)
\(=\frac{15}{16}\)
\(\therefore iii.\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
\(i.\) \(\cos{\theta}=\frac{2}{3}\)
\(ii.\) \(\tan^2{\theta}=\frac{9}{16}\)
\(iii.\) \(\sec{\theta}\tan{\theta}=\frac{15}{16}\)
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
\(\frac{\pi}{2}\lt{\theta}\lt{\pi}\) এবং \(\sin{\theta}=\frac{3}{5}\) হলে-ঘ \(i.\), \(ii.\) ও \(iii.\)
লম্ব \(=3\)
অতিভুজ \(=5\)
অতএব, ভূমি \(=-\sqrt{5^2-3^2}\) যেহেতু, \(\frac{\pi}{2}\lt{\theta}\lt{\pi}\)
\(=-\sqrt{25-9}\)
\(=-\sqrt{16}\)
\(=-4\)
\(\cos{\theta}=\frac{\text{ভূমি}}{\text{অতিভুজ}}=\frac{-4}{5}\)
\(=-\frac{4}{5}\)
\(\therefore i.\) নং বাক্যটি সত্য নয়।
\(\tan^2{\theta}\)
\(=\left(\frac{\text{লম্ব}}{\text{ভূমি}}\right)^2\)
\(=\left(\frac{3}{-4}\right)^2\)
\(=\frac{9}{16}\)
\(\therefore ii.\) নং বাক্যটি সত্য
আবার,
\(\sec{\theta}\tan{\theta}\)
\(=\frac{\text{অতিভুজ}}{\text{ভূমি}}\times\frac{\text{লম্ব}}{\text{ভূমি}}\)
\(=\frac{5}{-4}\times\frac{3}{-4}\)
\(=\frac{15}{16}\)
\(\therefore iii.\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
১৬। একটি ত্রিভুজের তিনটি কোণের অনুপাত \(3:4:5\) হলে, কোণ তিনটির পরিমাণ হবে-
কোণের অনুপাতগুলির যোগফল \(=3+4+5=12\)
কোণেগুলির পরিমাণ যথাক্রমে \(3\times\frac{180^{o}}{12}, \ 4\times\frac{180^{o}}{12}, \ 5\times\frac{180^{o}}{12},\)
\(\Rightarrow 3\times15^{o}, \ 4\times15^{o}, \ 5\times15^{o},\)
\(\therefore 45^{o}, \ 60^{o}, \ 75^{o},\)
উত্তরঃ ( গ )
ক \(30^{o}, \ 40^{o}, \ 50^{o}\)
গ \(45^{o}, \ 60^{o}, \ 75^{o}\)
গ \(45^{o}, \ 60^{o}, \ 75^{o}\)
খ \(40^{o}, \ 60^{o}, \ 80^{o}\)
ঘ \(50^{o}, \ 60^{o}, \ 75^{o}\)
ত্রিভুজের তিনটি কোণের যোগফল \(=180^{o}\) ঘ \(50^{o}, \ 60^{o}, \ 75^{o}\)
কোণের অনুপাতগুলির যোগফল \(=3+4+5=12\)
কোণেগুলির পরিমাণ যথাক্রমে \(3\times\frac{180^{o}}{12}, \ 4\times\frac{180^{o}}{12}, \ 5\times\frac{180^{o}}{12},\)
\(\Rightarrow 3\times15^{o}, \ 4\times15^{o}, \ 5\times15^{o},\)
\(\therefore 45^{o}, \ 60^{o}, \ 75^{o},\)
উত্তরঃ ( গ )
১৭। \(\sec{\theta}=\frac{13}{12}\) হলে, \(\tan{\left(\frac{\pi}{2}-\theta\right)}\) এর মান কোনটি?
অতিভুজ \(=13\)
অতএব, লম্ব \(=\sqrt{13^2-12^2}\)
\(=\sqrt{169-144}\)
\(=\sqrt{25}\)
\(=5\)
এখন, \(\tan{\left(\frac{\pi}{2}-\theta\right)}\)
\(=\cot{\theta}\)
\(=\frac{\text{ভূমি}}{\text{লম্ব}}\)
\(=\frac{12}{5}\)
উত্তরঃ ( ঘ )
ক \(\frac{5}{12}\)
গ \(\frac{13}{5}\)
গ \(\frac{13}{5}\)
খ \(\frac{5}{13}\)
ঘ \(\frac{12}{5}\)
\(\sec{\theta}=\frac{13}{12}\) হলে,
ভূমি \(=12\) ঘ \(\frac{12}{5}\)
অতিভুজ \(=13\)
অতএব, লম্ব \(=\sqrt{13^2-12^2}\)
\(=\sqrt{169-144}\)
\(=\sqrt{25}\)
\(=5\)
এখন, \(\tan{\left(\frac{\pi}{2}-\theta\right)}\)
\(=\cot{\theta}\)
\(=\frac{\text{ভূমি}}{\text{লম্ব}}\)
\(=\frac{12}{5}\)
উত্তরঃ ( ঘ )
১৮। \(f(x)=\frac{1}{|x-1|}\) এর ডোমেন-
\(\Rightarrow x-1\ne{0}\)
\(\therefore x\ne{1}\)
\(\therefore\) ডোমেন \(=(-\infty, 1)\cup{(1, +\infty)}\)
উত্তরঃ ( ক )
ক \((-\infty, 1)\cup{(1, +\infty)}\)
গ \((-\infty, -1]\)
গ \((-\infty, -1]\)
খ \((-\infty, 0)\cup{(0, \infty)}\)
ঘ \([1, +\infty)\)
\(f(x)=\frac{1}{|x-1|}\)ঘ \([1, +\infty)\)
\(\Rightarrow x-1\ne{0}\)
\(\therefore x\ne{1}\)
\(\therefore\) ডোমেন \(=(-\infty, 1)\cup{(1, +\infty)}\)
উত্তরঃ ( ক )
নিচের উদ্দীপকের আলোকে ১৯ ও ২০ নং প্রশ্নের উত্তর দাওঃ
\(f(x)=2\ln{(\cos{x})}, \ g(x)=x^2-3\)
১৯। \(e^{f(x)}\) এর মান নিচের কোনটি?\(f(x)=2\ln{(\cos{x})}, \ g(x)=x^2-3\)
ক \(2(1+\cos{x})\)
গ \(\frac{1}{2}(1-\cos{2x})\)
গ \(\frac{1}{2}(1-\cos{2x})\)
খ \(\frac{1}{2}(1+\cos{2x})\)
ঘ \(2(125-8\cos{x})\)
\(f(x)=2\ln{(\cos{x})}\) হলে, ঘ \(2(125-8\cos{x})\)
\(e^{f(x)}=e^{2\ln{(\cos{x})}}\)
\(=e^{\ln{(\cos^2{x})}}\) যেহেতু, \(2\ln{m}=\ln{m^2}\)
\(=\cos^2{x}\) যেহেতু, \(e^{\ln{m}}=m\)
\(=\frac{1}{2}\times2\cos^2{x}\)
\(=\frac{1}{2}(1+\cos{2x})\)
উত্তরঃ ( খ )
২০। \(gof(x)=?\)
এখন, \(gof(x)=g\{f(x)\}\)
\(=\{f(x)\}^2-3\)
\(=\{2\ln{(\cos{x})}\}^2-3\)
\(=4\{\ln{(\cos{x})}\}^2-3\)
উত্তরঃ ( খ )
ক \(8\{\ln{(\cos{x})}\}^2-3\)
গ \(2\{\ln{(\cos{x})}\}^2-3\)
গ \(2\{\ln{(\cos{x})}\}^2-3\)
খ \(4\{\ln{(\cos{x})}\}^2-3\)
ঘ \(\{\ln{(\cos{x})}\}^2-3\)
দেওয়া আছে, \(f(x)=2\ln{(\cos{x})}, \ g(x)=x^2-3\)ঘ \(\{\ln{(\cos{x})}\}^2-3\)
এখন, \(gof(x)=g\{f(x)\}\)
\(=\{f(x)\}^2-3\)
\(=\{2\ln{(\cos{x})}\}^2-3\)
\(=4\{\ln{(\cos{x})}\}^2-3\)
উত্তরঃ ( খ )
২১। \(y=\frac{1}{x}\) হলে, \(y_{2}\) এর মান-
\(\Rightarrow y_{1}=\frac{d}{dx}\left(\frac{1}{x}\right)\)
\(\Rightarrow y_{1}=-\frac{1}{x^2}\)
\(\Rightarrow y_{2}=-\frac{d}{dx}\left(\frac{1}{x^2}\right)\)
\(=-\left(-\frac{2}{x^3}\right)\)
\(=\frac{2}{x^3}\)
\(=2x^{-3}\)
উত্তরঃ ( গ )
ক \(x^{-3}\)
গ \(2x^{-3}\)
গ \(2x^{-3}\)
খ \(x^{3}\)
ঘ \(2x^{3}\)
\(y=\frac{1}{x}\) হলে, ঘ \(2x^{3}\)
\(\Rightarrow y_{1}=\frac{d}{dx}\left(\frac{1}{x}\right)\)
\(\Rightarrow y_{1}=-\frac{1}{x^2}\)
\(\Rightarrow y_{2}=-\frac{d}{dx}\left(\frac{1}{x^2}\right)\)
\(=-\left(-\frac{2}{x^3}\right)\)
\(=\frac{2}{x^3}\)
\(=2x^{-3}\)
উত্তরঃ ( গ )
২২। \[\lim_{x \rightarrow 2}\frac{x^3-8}{x^2-4}\] এর মান কোনটি?
\[\lim_{x \rightarrow 2}\frac{x^3-2^3}{x^2-2^2}\]
\[=\lim_{x \rightarrow 2}\frac{(x-2)(x^2+2x+4)}{(x-2)(x+2)}\]
\[=\lim_{x \rightarrow 2}\frac{x^2+2x+4}{x+2}\]
\[=\frac{2^2+2\times2+4}{2+2}\]
\[=\frac{4+4+4}{4}\]
\[=\frac{12}{4}\]
\[=3\]
উত্তরঃ ( ঘ )
ক \(-4\)
গ \(1\)
গ \(1\)
খ \(0\)
ঘ \(3\)
\[\lim_{x \rightarrow 2}\frac{x^3-8}{x^2-4}\]ঘ \(3\)
\[\lim_{x \rightarrow 2}\frac{x^3-2^3}{x^2-2^2}\]
\[=\lim_{x \rightarrow 2}\frac{(x-2)(x^2+2x+4)}{(x-2)(x+2)}\]
\[=\lim_{x \rightarrow 2}\frac{x^2+2x+4}{x+2}\]
\[=\frac{2^2+2\times2+4}{2+2}\]
\[=\frac{4+4+4}{4}\]
\[=\frac{12}{4}\]
\[=3\]
উত্তরঃ ( ঘ )
২৩। \(y=\sin{\sqrt{x}}\) হলে, \(\frac{dy}{dx}\) এর মান কোনটি?
\(y=\sin{\sqrt{x}}\)
\(\Rightarrow \frac{dy}{dx}=\frac{d}{dx}\left(\sin{\sqrt{x}}\right)\)
\(=\cos{\sqrt{x}}\frac{d}{dx}\left(\sqrt{x}\right)\)
\(=\cos{\sqrt{x}}\times\frac{1}{2\sqrt{x}}\)
\(=\frac{\cos{\sqrt{x}}}{2\sqrt{x}}\)
উত্তরঃ ( ক )
ক \(\frac{\cos{\sqrt{x}}}{2\sqrt{x}}\)
গ \(\frac{\cos{\sqrt{x}}}{\sqrt{x}}\)
গ \(\frac{\cos{\sqrt{x}}}{\sqrt{x}}\)
খ \(\frac{\sin{\sqrt{x}}}{2\sqrt{x}}\)
ঘ \(\frac{\sin{\sqrt{x}}}{\sqrt{x}}\)
দেওয়া আছে,ঘ \(\frac{\sin{\sqrt{x}}}{\sqrt{x}}\)
\(y=\sin{\sqrt{x}}\)
\(\Rightarrow \frac{dy}{dx}=\frac{d}{dx}\left(\sin{\sqrt{x}}\right)\)
\(=\cos{\sqrt{x}}\frac{d}{dx}\left(\sqrt{x}\right)\)
\(=\cos{\sqrt{x}}\times\frac{1}{2\sqrt{x}}\)
\(=\frac{\cos{\sqrt{x}}}{2\sqrt{x}}\)
উত্তরঃ ( ক )
২৪। \(\int{\frac{dx}{x\sqrt{x^2-1}}}=f(x)+c\) হলে, \(f(x)\) এর মান-
\(\int{\frac{dx}{x\sqrt{x^2-1}}}=f(x)+c\)
\(\Rightarrow \sec^{-1}{x}+c=f(x)+c\)
\(\Rightarrow \sec^{-1}{x}=f(x)\)
\(\therefore f(x)=\sec^{-1}{x}\)
উত্তরঃ ( খ )
ক \(\cos^{-1}{x}\)
গ \(\sin^{-1}{x}\)
গ \(\sin^{-1}{x}\)
খ \(\sec^{-1}{x}\)
ঘ \(cosec^{-1}{x}\)
দেওয়া আছে,ঘ \(cosec^{-1}{x}\)
\(\int{\frac{dx}{x\sqrt{x^2-1}}}=f(x)+c\)
\(\Rightarrow \sec^{-1}{x}+c=f(x)+c\)
\(\Rightarrow \sec^{-1}{x}=f(x)\)
\(\therefore f(x)=\sec^{-1}{x}\)
উত্তরঃ ( খ )
২৫। \(\int_{0}^{\frac{\pi}{2}}{2\sin^2{x}dx}=?\)
\(=\int_{0}^{\frac{\pi}{2}}{(1-\cos{2x})dx}\)
\(=\left[x-\frac{1}{2}\sin{2x}\right]_{0}^{\frac{\pi}{2}}\)
\(=\left[\frac{\pi}{2}-\frac{1}{2}\sin{2\times\frac{\pi}{2}}\right]-\left[0-\frac{1}{2}\sin{2\times0}\right]\)
\(=\left[\frac{\pi}{2}-\frac{1}{2}\sin{\pi}\right]-\left[-\frac{1}{2}\sin{0}\right]\)
\(=\left[\frac{\pi}{2}-\frac{1}{2}\times0\right]-0\)
\(=\frac{\pi}{2}-0\)
\(=\frac{\pi}{2}\)
উত্তরঃ ( খ )
ক \(\frac{\pi}{2}-\frac{1}{2}\)
গ \(1\)
গ \(1\)
খ \(\frac{\pi}{2}\)
ঘ \(2\)
\(\int_{0}^{\frac{\pi}{2}}{2\sin^2{x}dx}\)ঘ \(2\)
\(=\int_{0}^{\frac{\pi}{2}}{(1-\cos{2x})dx}\)
\(=\left[x-\frac{1}{2}\sin{2x}\right]_{0}^{\frac{\pi}{2}}\)
\(=\left[\frac{\pi}{2}-\frac{1}{2}\sin{2\times\frac{\pi}{2}}\right]-\left[0-\frac{1}{2}\sin{2\times0}\right]\)
\(=\left[\frac{\pi}{2}-\frac{1}{2}\sin{\pi}\right]-\left[-\frac{1}{2}\sin{0}\right]\)
\(=\left[\frac{\pi}{2}-\frac{1}{2}\times0\right]-0\)
\(=\frac{\pi}{2}-0\)
\(=\frac{\pi}{2}\)
উত্তরঃ ( খ )
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000004