শিক্ষা বোর্ড দিনাজপুর - 2019
উচ্চতর গণিত ( বহুনির্বাচনি )
[2019 সালের সিলেবাস অনুযায়ী ]
দ্বিতীয় পত্র বহুনির্বাচনি
বিষয় কোডঃ 266
সময়-২৫ মিনিট
পূর্ণমান-২৫
[ দ্রষ্টব্যঃ সরবরাহকৃত বহুনির্বাচনি অভীক্ষার উত্তরপত্রে প্রশ্নের ক্রমিক নম্বরের বিপরীতে প্রদত্ত বর্ণসংবলিত বৃত্তসমুহ হতে সিঠিক/সর্বোৎকৃষ্ট উত্তরের বৃত্তটি বল পয়ন্ট কলম দ্বারা সম্পুর্ণ ভরাট কর। প্রতিটি প্রশ্নের মাণ ১। প্রশ্নপত্রে কোন প্রকার দাগ/ চিহ্ন দেওয়া যাবে না। ]
উচ্চতর গণিত ( বহুনির্বাচনি )
[2019 সালের সিলেবাস অনুযায়ী ]
দ্বিতীয় পত্র বহুনির্বাচনি
বিষয় কোডঃ 266
সময়-২৫ মিনিট
পূর্ণমান-২৫
[ দ্রষ্টব্যঃ সরবরাহকৃত বহুনির্বাচনি অভীক্ষার উত্তরপত্রে প্রশ্নের ক্রমিক নম্বরের বিপরীতে প্রদত্ত বর্ণসংবলিত বৃত্তসমুহ হতে সিঠিক/সর্বোৎকৃষ্ট উত্তরের বৃত্তটি বল পয়ন্ট কলম দ্বারা সম্পুর্ণ ভরাট কর। প্রতিটি প্রশ্নের মাণ ১। প্রশ্নপত্রে কোন প্রকার দাগ/ চিহ্ন দেওয়া যাবে না। ]
১। \(-7\lt{x+3}\lt{5}\) কে পরম মানের সাহায্যে প্রকাশ করঃ
\(-7\lt{x+3}\lt{5}\)
এখানে, প্রান্তিক মানের গড় \(\frac{-7+5}{2}=\frac{-2}{2}=-1\)
অসমতাটির প্রত্যেক অংশের সাথে \(1\) যোগ করে,
\(\Rightarrow -7+1\lt{x+3+1}\lt{5+1}\)
\(\Rightarrow -6\lt{x+4}\lt{6}\)
\(\therefore |x+4|\lt{6}\)
উত্তরঃ ( খ )
ক \(|x+2|\lt{4}\)
গ \(|x+3|\lt{6}\)
গ \(|x+3|\lt{6}\)
খ \(|x+4|\lt{6}\)
ঘ \(|x+1|\lt{3}\)
দেওয়াআছে,ঘ \(|x+1|\lt{3}\)
\(-7\lt{x+3}\lt{5}\)
এখানে, প্রান্তিক মানের গড় \(\frac{-7+5}{2}=\frac{-2}{2}=-1\)
অসমতাটির প্রত্যেক অংশের সাথে \(1\) যোগ করে,
\(\Rightarrow -7+1\lt{x+3+1}\lt{5+1}\)
\(\Rightarrow -6\lt{x+4}\lt{6}\)
\(\therefore |x+4|\lt{6}\)
উত্তরঃ ( খ )
২। \(-\sqrt{3}+3i\) -এর আর্গুমেন্ট কোনটি?
তাহলে,
\(-\sqrt{3}+3i\) এর আর্গুমেন্ট
\(=\tan^{-1}{\frac{3}{-\sqrt{3}}}\)
\(=\tan^{-1}{\frac{\sqrt{3}.\sqrt{3}}{-\sqrt{3}}}\)
\(=\tan^{-1}{-\sqrt{3}}\)
\(=\tan^{-1}{\tan{-\frac{\pi}{3}}}\)
\(=\tan^{-1}{\tan{\left(\pi-\frac{\pi}{3}\right)}}\)
\(=\pi-\frac{\pi}{3}\)
\(=\frac{3\pi-\pi}{3}\)
\(=\frac{2\pi}{3}\)
উত্তরঃ ( ঘ )
ক \(-\frac{2\pi}{3}\)
গ \(\frac{\pi}{3}\)
গ \(\frac{\pi}{3}\)
খ \(-\frac{\pi}{3}\)
ঘ \(\frac{2\pi}{3}\)
\(x+iy\) এর আর্গুমেন্ট \(=\tan^{-1}{\frac{y}{x}}\)ঘ \(\frac{2\pi}{3}\)
তাহলে,
\(-\sqrt{3}+3i\) এর আর্গুমেন্ট
\(=\tan^{-1}{\frac{3}{-\sqrt{3}}}\)
\(=\tan^{-1}{\frac{\sqrt{3}.\sqrt{3}}{-\sqrt{3}}}\)
\(=\tan^{-1}{-\sqrt{3}}\)
\(=\tan^{-1}{\tan{-\frac{\pi}{3}}}\)
\(=\tan^{-1}{\tan{\left(\pi-\frac{\pi}{3}\right)}}\)
\(=\pi-\frac{\pi}{3}\)
\(=\frac{3\pi-\pi}{3}\)
\(=\frac{2\pi}{3}\)
উত্তরঃ ( ঘ )
৩। \(S=\left\{\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81} ....... \right\}\) এর সুপ্রিমাম কত?
\(S=\left\{\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81} ....... \right\}\)
\(\therefore S=\left\{\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81} ....... \frac{1}{3^n}\right\}\)
এখানে,
\(n\rightarrow{\infty} \Rightarrow \frac{1}{3^n}\rightarrow{0}\)
\(\therefore Sup(S)=\frac{1}{3}\)
উত্তরঃ ( গ )
ক \(0\)
গ \(\frac{1}{3}\)
গ \(\frac{1}{3}\)
খ \(\frac{1}{81}\)
ঘ \(\infty\)
দেওয়া আছে,ঘ \(\infty\)
\(S=\left\{\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81} ....... \right\}\)
\(\therefore S=\left\{\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81} ....... \frac{1}{3^n}\right\}\)
এখানে,
\(n\rightarrow{\infty} \Rightarrow \frac{1}{3^n}\rightarrow{0}\)
\(\therefore Sup(S)=\frac{1}{3}\)
উত্তরঃ ( গ )
৪। \(x+y\le{9}, \ 3x+4y\le{30}, \ x\gt{0}, \ y\gt{0}\) শর্তাধীনে-
\(i.\) সমাধান এলাকার প্রান্তিক \((0, 0), (9, 0), \left(0, \frac{15}{2}\right), (6, 3)\)
\(ii.\) \(2x+5y\) এর সর্বোচ্চ মান \(=27\)
\(iii.\) \(x-2y\) এর সর্বনিম্ন মান \(-15\)
নিচের কোনটি সঠীক?
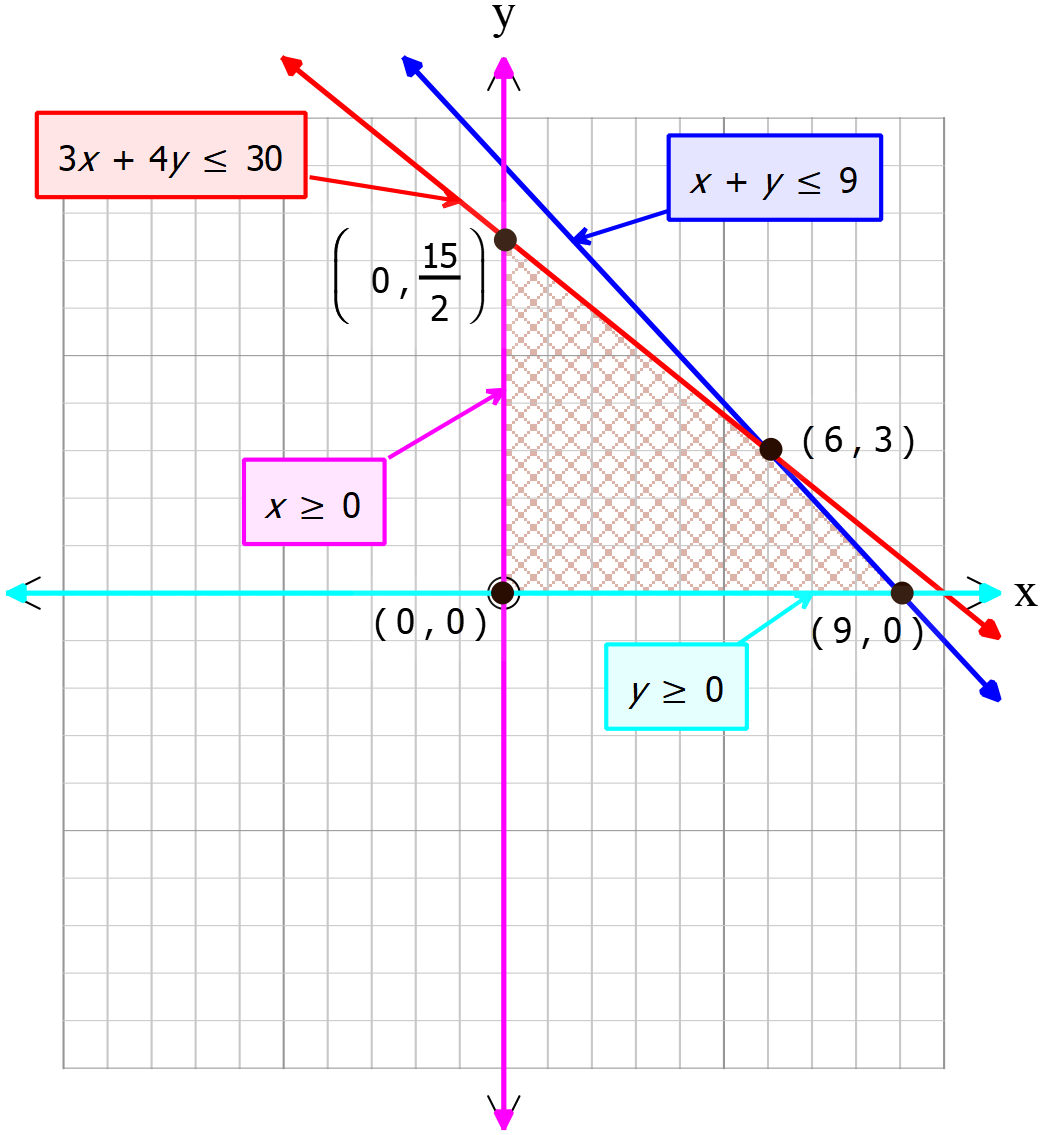
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার, \(\left(0, \frac{15}{2}\right)\) বিন্দুটি দ্বারা সর্বোচ্চ ও সর্বনিম্ন মান পাওয়া যাবে।
\(2x+5y\) এর সর্বোচ্চ মান \(=2\times0+5\times\frac{15}{2}\)
\(=\frac{75}{2}\)
\(=37\frac{1}{2}\)
\(\therefore (ii.)\) নং বাক্যটি সত্য নয়।
আবার,
\(x-2y\) এর সর্বনিম্ন মান \(=2\times0-2\times\frac{15}{2}\)
\(=-15\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
\(i.\) সমাধান এলাকার প্রান্তিক \((0, 0), (9, 0), \left(0, \frac{15}{2}\right), (6, 3)\)
\(ii.\) \(2x+5y\) এর সর্বোচ্চ মান \(=27\)
\(iii.\) \(x-2y\) এর সর্বনিম্ন মান \(-15\)
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)

\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার, \(\left(0, \frac{15}{2}\right)\) বিন্দুটি দ্বারা সর্বোচ্চ ও সর্বনিম্ন মান পাওয়া যাবে।
\(2x+5y\) এর সর্বোচ্চ মান \(=2\times0+5\times\frac{15}{2}\)
\(=\frac{75}{2}\)
\(=37\frac{1}{2}\)
\(\therefore (ii.)\) নং বাক্যটি সত্য নয়।
আবার,
\(x-2y\) এর সর্বনিম্ন মান \(=2\times0-2\times\frac{15}{2}\)
\(=-15\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
৫। \(P=x+iy\) হলে, \(|P+2|=3\) নির্দেশ করে-
\(|P+2|=3\)
\(\Rightarrow |x+iy+2|=3\)
\(\Rightarrow |x+2+iy|=3\)
\(\Rightarrow \sqrt{(x+2)^2+y^2}=3\)
\(\therefore (x+2)^2+y^2=3^2\) যা একটি বৃত্তের সমীকরণ,
যার কেন্দ্র \((-2, 0)\) ব্যাসার্ধ \(=3\)
উত্তরঃ ( ক )
ক বৃত্ত
গ প্যারাবোলা
গ প্যারাবোলা
খ সরলরেখা
ঘ উপবৃত্ত
\(P=x+iy\) হলে, ঘ উপবৃত্ত
\(|P+2|=3\)
\(\Rightarrow |x+iy+2|=3\)
\(\Rightarrow |x+2+iy|=3\)
\(\Rightarrow \sqrt{(x+2)^2+y^2}=3\)
\(\therefore (x+2)^2+y^2=3^2\) যা একটি বৃত্তের সমীকরণ,
যার কেন্দ্র \((-2, 0)\) ব্যাসার্ধ \(=3\)
উত্তরঃ ( ক )
৬। \(11-60i\) এর বর্গমূল কত?
\(=\pm{\sqrt{36-60i-25}}\)
\(=\pm{\sqrt{6^2-2.6.5i+(5i)^2}}\)
\(=\pm{\sqrt{(6-5i)^2}}\)
\(=\pm{(6-5i)}\)
উত্তরঃ ( গ )
ক \(\pm(5-6i)\)
গ \(\pm(6-5i)\)
গ \(\pm(6-5i)\)
খ \(\pm(6+5i)\)
ঘ \(\pm(6i-5)\)
\(11-60i\) এর বর্গমূল \(=\pm{\sqrt{11-60i}}\)ঘ \(\pm(6i-5)\)
\(=\pm{\sqrt{36-60i-25}}\)
\(=\pm{\sqrt{6^2-2.6.5i+(5i)^2}}\)
\(=\pm{\sqrt{(6-5i)^2}}\)
\(=\pm{(6-5i)}\)
উত্তরঃ ( গ )
৭। \(P\) এর কোন মানের জন্য \(x^2-8x+P=0\) সমীকরণের মূলদ্বয় সমান হবে?
নিশ্চায়ক \(=0\) হয়।
\(\Rightarrow (-8)^2-4.1.P=0\)
\(\Rightarrow 64-4P=0\)
\(\Rightarrow -4P=-64\)
\(\therefore P=16\)
উত্তরঃ ( খ )
ক \(8\)
গ \(32\)
গ \(32\)
খ \(16\)
ঘ \(64\)
\(x^2-8x+P=0\) সমীকরণের মূলদ্বয় সমান হবে যদি,ঘ \(64\)
নিশ্চায়ক \(=0\) হয়।
\(\Rightarrow (-8)^2-4.1.P=0\)
\(\Rightarrow 64-4P=0\)
\(\Rightarrow -4P=-64\)
\(\therefore P=16\)
উত্তরঃ ( খ )
নিচের তথ্যের আলোকে ৮ এবং ৯ নং প্রশ্নের
উত্তর দাওঃ
\(2x^2-2x+1=0\) সমীকরণের মূলদ্বয় \(\frac{1}{p}, \ \frac{1}{q}\)
৮। \(p+q\) এর মান কত?\(2x^2-2x+1=0\) সমীকরণের মূলদ্বয় \(\frac{1}{p}, \ \frac{1}{q}\)
ক \(-2\)
গ \(2\)
গ \(2\)
খ \(0\)
ঘ \(\pm2\)
দেওয়া আছে,ঘ \(\pm2\)
\(2x^2-2x+1=0\) সমীকরণের মূলদ্বয় \(\frac{1}{p}, \ \frac{1}{q}\)
মূলদ্বয়ের গুণফল \(\frac{1}{p}\times\frac{1}{q}=\frac{1}{2}\)
\(\Rightarrow \frac{1}{pq}=\frac{1}{2}\)
\(\therefore pq=2\)
মূলদ্বয়ের যোগফল \(\frac{1}{p}+\frac{1}{q}=-\frac{-2}{2}\)
\(\Rightarrow \frac{q+p}{pq}=1\)
\(\Rightarrow p+q=pq\)
\(\therefore p+q=2 \ \because pq=2\)
উত্তরঃ ( গ )
৯। \(q\) এর মান কত?
\(2x^2-2x+1=0\) সমীকরণের মূলদ্বয় \(\frac{1}{p}, \ \frac{1}{q}\)
মূলদ্বয়ের গুণফল \(\frac{1}{p}\times\frac{1}{q}=\frac{1}{2}\)
\(\Rightarrow \frac{1}{pq}=\frac{1}{2}\)
\(\therefore pq=2 ......(1)\)
মূলদ্বয়ের যোগফল \(\frac{1}{p}+\frac{1}{q}=-\frac{-2}{2}\)
\(\Rightarrow \frac{q+p}{pq}=1\)
\(\Rightarrow p+q=pq\)
\(\Rightarrow p+q=2 \ \because pq=2\)
\(\therefore p=2-q .....(2)\)
\((1)\) ও \((2)\) হতে,
\((2-q)q=2\)
\(\Rightarrow 2q-q^2-2=0\)
\(\Rightarrow -(q^2-2q+2)=0\)
\(\Rightarrow q^2-2q+2=0\)
\(\therefore q=\frac{2\pm{\sqrt{(-2)^2-4.1.2}}}{2\times1}\)
\(=\frac{2\pm{\sqrt{4-8}}}{2}\)
\(=\frac{2\pm{\sqrt{-4}}}{2}\)
\(=\frac{2\pm{2i}}{2}\)
\(=\frac{2(1\pm{i})}{2}\)
\(=1\pm{i}\)
উত্তরঃ ( খ )
ক \(-1\pm{i}\)
গ \(\frac{-1\pm{i}}{2}\)
গ \(\frac{-1\pm{i}}{2}\)
খ \(1\pm{i}\)
ঘ \(\frac{1\pm{i}}{3}\)
দেওয়া আছে,ঘ \(\frac{1\pm{i}}{3}\)
\(2x^2-2x+1=0\) সমীকরণের মূলদ্বয় \(\frac{1}{p}, \ \frac{1}{q}\)
মূলদ্বয়ের গুণফল \(\frac{1}{p}\times\frac{1}{q}=\frac{1}{2}\)
\(\Rightarrow \frac{1}{pq}=\frac{1}{2}\)
\(\therefore pq=2 ......(1)\)
মূলদ্বয়ের যোগফল \(\frac{1}{p}+\frac{1}{q}=-\frac{-2}{2}\)
\(\Rightarrow \frac{q+p}{pq}=1\)
\(\Rightarrow p+q=pq\)
\(\Rightarrow p+q=2 \ \because pq=2\)
\(\therefore p=2-q .....(2)\)
\((1)\) ও \((2)\) হতে,
\((2-q)q=2\)
\(\Rightarrow 2q-q^2-2=0\)
\(\Rightarrow -(q^2-2q+2)=0\)
\(\Rightarrow q^2-2q+2=0\)
\(\therefore q=\frac{2\pm{\sqrt{(-2)^2-4.1.2}}}{2\times1}\)
\(=\frac{2\pm{\sqrt{4-8}}}{2}\)
\(=\frac{2\pm{\sqrt{-4}}}{2}\)
\(=\frac{2\pm{2i}}{2}\)
\(=\frac{2(1\pm{i})}{2}\)
\(=1\pm{i}\)
উত্তরঃ ( খ )
১০। যদি \(x^2-4y=0\) কনিকের নিয়ামকের সমীকরণ কনটি?
\(x^2-4y=0\)
\(\therefore x^2=4y\)
এখানে, \(a=1; \ x^2=4ay\) এর সহিত তুলুনা করে,
নিয়ামকের সমীকরণ, \(y=-a\)
\(\Rightarrow y=-1 \ \because a=1\)
\(\therefore y+1=0\)
উত্তরঃ ( ক )
ক \(y+1=0\)
গ \(x+1=0\)
গ \(x+1=0\)
খ \(y-1=0\)
ঘ \(x-1=0\)
দেওয়া আছে,ঘ \(x-1=0\)
\(x^2-4y=0\)
\(\therefore x^2=4y\)
এখানে, \(a=1; \ x^2=4ay\) এর সহিত তুলুনা করে,
নিয়ামকের সমীকরণ, \(y=-a\)
\(\Rightarrow y=-1 \ \because a=1\)
\(\therefore y+1=0\)
উত্তরঃ ( ক )
১১। \((y+1)^{2n}\) এর বিস্তৃতিতে \(y^{n+1}\) এর সহগ কত?
\(=^{2n}C_{r}y^{2n-r}\)
পদটিতে \(y^{n+1}\) থাকবে যদি \(n+1=2n-r\) হয়।
\(\Rightarrow r=2n-n-1\)
\(\therefore r=n-1\)
\(\therefore (r+1)\) তম পদ \(=^{2n}C_{n-1}y^{2n-n+1}\)
\(=^{2n}C_{n+1}y^{n+1}\)
\(\therefore y^{n+1}\) এর সহগ \(=^{2n}C_{n+1}\)
উত্তরঃ ( ক )
ক \(^{2n}C_{n+1}\)
গ \(^{2n}C_{n-1}\)
গ \(^{2n}C_{n-1}\)
খ \(^{2n}C_{n}\)
ঘ \(^{2n+1}C_{n+1}\)
\((y+1)^{2n}\) এর বিস্তৃতিতে \((r+1)\) তম পদঘ \(^{2n+1}C_{n+1}\)
\(=^{2n}C_{r}y^{2n-r}\)
পদটিতে \(y^{n+1}\) থাকবে যদি \(n+1=2n-r\) হয়।
\(\Rightarrow r=2n-n-1\)
\(\therefore r=n-1\)
\(\therefore (r+1)\) তম পদ \(=^{2n}C_{n-1}y^{2n-n+1}\)
\(=^{2n}C_{n+1}y^{n+1}\)
\(\therefore y^{n+1}\) এর সহগ \(=^{2n}C_{n+1}\)
উত্তরঃ ( ক )
১২। \((x+5)^{13}\) এর বিস্তৃতিতে-
\(i.\) পদ সংখ্যা \(=14\)
\(ii.\) ৩য় পদ \(=^{13}C_{3}x^{10}5^3\)
\(iii.\) ৮ম পদ একটি মধ্যপদ
নিচের কোনটি সঠীক?
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
\((x+5)^{13}\) এর বিস্তৃতিতে \((r+1)\) তম পদ \(=^{13}C_{r}x^{13-r}5^r\)
৩য় পদ বা \((2+1)\) তম পদ \(=^{13}C_{2}x^{13-2}5^2\)
\(=^{13}C_{2}x^{11}5^2\)
\(\therefore (ii.)\) নং বাক্যটি সত্য নয়।
আবার,
\((x+5)^{13}\) এর বিস্তৃতিতে দুইটি মধ্যপদ আছে,
যেগুলি \(\frac{13-1}{2}+1\) তম ও \(\frac{13+1}{2}+1\) তম।
\(\Rightarrow \frac{12}{2}+1\) তম ও \(\frac{14}{2}+1\) তম।
\(\Rightarrow 6+1\) তম ও \(7+1\) তম।
\(\Rightarrow 7\) তম ও \(8\) তম।
\(\therefore \) ৮ম পদ একটি মধ্যপদ
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
\(i.\) পদ সংখ্যা \(=14\)
\(ii.\) ৩য় পদ \(=^{13}C_{3}x^{10}5^3\)
\(iii.\) ৮ম পদ একটি মধ্যপদ
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
\((x+5)^{13}\) এর বিস্তৃতিতে পদ সংখ্যা \(=13+1=14\)ঘ \(i.\), \(ii.\) ও \(iii.\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
\((x+5)^{13}\) এর বিস্তৃতিতে \((r+1)\) তম পদ \(=^{13}C_{r}x^{13-r}5^r\)
৩য় পদ বা \((2+1)\) তম পদ \(=^{13}C_{2}x^{13-2}5^2\)
\(=^{13}C_{2}x^{11}5^2\)
\(\therefore (ii.)\) নং বাক্যটি সত্য নয়।
আবার,
\((x+5)^{13}\) এর বিস্তৃতিতে দুইটি মধ্যপদ আছে,
যেগুলি \(\frac{13-1}{2}+1\) তম ও \(\frac{13+1}{2}+1\) তম।
\(\Rightarrow \frac{12}{2}+1\) তম ও \(\frac{14}{2}+1\) তম।
\(\Rightarrow 6+1\) তম ও \(7+1\) তম।
\(\Rightarrow 7\) তম ও \(8\) তম।
\(\therefore \) ৮ম পদ একটি মধ্যপদ
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
১৩। \(x^2+12x+3y=0\) পরাবৃত্তের শীর্ষবিদু-
\(\Rightarrow x^2+12x+36-36+3y=0\)
\(\Rightarrow (x+6)^2-36+3y=0\)
\(\Rightarrow (x+6)^2=36-3y\)
\(\Rightarrow (x+6)^2=-3(y-12)\)
\(\therefore X^2=-3Y\) যেখানে, \(x+6=X, \ y-12=Y\)
এখন, শীর্ষবিন্দুতে \(X=0, \ Y=0\)
\(\Rightarrow x+6=0, \ y-12=0\)
\(\therefore x=-6, \ y=12\)
\(\therefore\) শীর্ষবিন্দু \((-6, 12)\)
উত্তরঃ ( গ )
ক \((-6, -12)\)
গ \((-6, 12)\)
গ \((-6, 12)\)
খ \((6, 12)\)
ঘ \((6, -12)\)
\(x^2+12x+3y=0\)ঘ \((6, -12)\)
\(\Rightarrow x^2+12x+36-36+3y=0\)
\(\Rightarrow (x+6)^2-36+3y=0\)
\(\Rightarrow (x+6)^2=36-3y\)
\(\Rightarrow (x+6)^2=-3(y-12)\)
\(\therefore X^2=-3Y\) যেখানে, \(x+6=X, \ y-12=Y\)
এখন, শীর্ষবিন্দুতে \(X=0, \ Y=0\)
\(\Rightarrow x+6=0, \ y-12=0\)
\(\therefore x=-6, \ y=12\)
\(\therefore\) শীর্ষবিন্দু \((-6, 12)\)
উত্তরঃ ( গ )
নিচের তথ্যের আলোকে ১৪ এবং ১৫ নং প্রশ্নের
উত্তর দাওঃ
\(7x^2+16y^2=112\) একটি কনিক।
১৪। উপকেন্দ্রিক লম্বের দৈর্ঘ্য কত?\(7x^2+16y^2=112\) একটি কনিক।
ক \(\frac{\sqrt{7}}{8}\)
গ \(\frac{7}{2}\)
গ \(\frac{7}{2}\)
খ \(\frac{8}{7}\)
ঘ \(\frac{32}{\sqrt{7}}\)
\(7x^2+16y^2=112\) একটি কনিক।ঘ \(\frac{32}{\sqrt{7}}\)
\(\Rightarrow \frac{7x^2}{112}+\frac{16y^2}{112}=1\)
\(\Rightarrow \frac{x^2}{16}+\frac{y^2}{7}=1\)
\(\therefore \frac{x^2}{4^2}+\frac{y^2}{(\sqrt{7})^2}=1\)
এখানে, \(a=4, \ b=\sqrt{7} \therefore a\gt{b}\)
\(\therefore\) উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\frac{2b^2}{a}\)
\(=\frac{2\times7}{4}\)
\(=\frac{7}{2}\)
উত্তরঃ ( গ )
১৫। উপকেন্দ্রের স্থানাঙ্ক-
\(\Rightarrow \frac{7x^2}{112}+\frac{16y^2}{112}=1\)
\(\Rightarrow \frac{x^2}{16}+\frac{y^2}{7}=1\)
\(\therefore \frac{x^2}{4^2}+\frac{y^2}{(\sqrt{7})^2}=1\)
এখানে, \(a=4, \ b=\sqrt{7} \therefore a\gt{b}\)
\(\therefore\) উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(=\sqrt{1-\frac{7}{16}}\)
\(=\sqrt{\frac{16-7}{16}}\)
\(=\sqrt{\frac{9}{16}}\)
\(=\frac{3}{4}\)
উপকেন্দ্রের স্থানাঙ্ক \((\pm{ae}, 0)\)
\(\Rightarrow (\pm{4\times\frac{3}{4}}, 0)\)
\(\therefore (\pm{3}, 0)\)
উত্তরঃ ( ক )
ক \((\pm3, 0)\)
গ \(\left(\pm\frac{3\sqrt{7}}{4}, 0\right)\)
গ \(\left(\pm\frac{3\sqrt{7}}{4}, 0\right)\)
খ \((0 , \pm3)\)
ঘ \(\left(0, \pm\frac{3\sqrt{7}}{4}\right)\)
\(7x^2+16y^2=112\) একটি কনিক।ঘ \(\left(0, \pm\frac{3\sqrt{7}}{4}\right)\)
\(\Rightarrow \frac{7x^2}{112}+\frac{16y^2}{112}=1\)
\(\Rightarrow \frac{x^2}{16}+\frac{y^2}{7}=1\)
\(\therefore \frac{x^2}{4^2}+\frac{y^2}{(\sqrt{7})^2}=1\)
এখানে, \(a=4, \ b=\sqrt{7} \therefore a\gt{b}\)
\(\therefore\) উৎকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(=\sqrt{1-\frac{7}{16}}\)
\(=\sqrt{\frac{16-7}{16}}\)
\(=\sqrt{\frac{9}{16}}\)
\(=\frac{3}{4}\)
উপকেন্দ্রের স্থানাঙ্ক \((\pm{ae}, 0)\)
\(\Rightarrow (\pm{4\times\frac{3}{4}}, 0)\)
\(\therefore (\pm{3}, 0)\)
উত্তরঃ ( ক )
১৬। যদি \(\sin^{-1}{x}=2\theta\) হয়, তবে \(\cos{2\theta}\) এর মান কত?
\(\sin^{-1}{x}=2\theta\)
\(\Rightarrow 2\theta=\sin^{-1}{x}\)
\(\therefore \sin{2\theta}=x\)
আবার,
\(\cos{2\theta}=\sqrt{1-\sin^2{2\theta}}\)
\(=\sqrt{1-x^2}\)
উত্তরঃ ( ঘ )
ক \(1-x^2\)
গ \(1-2x^2\)
গ \(1-2x^2\)
খ \(2x^2-1\)
ঘ \(\sqrt{1-x^2}\)
দেওয়া আছে,ঘ \(\sqrt{1-x^2}\)
\(\sin^{-1}{x}=2\theta\)
\(\Rightarrow 2\theta=\sin^{-1}{x}\)
\(\therefore \sin{2\theta}=x\)
আবার,
\(\cos{2\theta}=\sqrt{1-\sin^2{2\theta}}\)
\(=\sqrt{1-x^2}\)
উত্তরঃ ( ঘ )
১৭। \(\cos{\left\{2\left(\sin^{-1}\frac{3x}{2}+\cos^{-1}\frac{3x}{2}\right)\right\}}=P\) হলে, \(P\) এর মান কত?
\(\Rightarrow P=\cos{\left\{2\left(\sin^{-1}\frac{3x}{2}+\cos^{-1}\frac{3x}{2}\right)\right\}}\)
\(\Rightarrow P=\cos{\left\{2\times\frac{\pi}{2}\right\}}\) যেহেতু \(\sin^{-1}a+\cos^{-1}a=\frac{\pi}{2}\)
\(\Rightarrow P=\cos{\pi}\)
\(\therefore P=-1\) যেহেতু \(\cos{\pi}=-1\)
উত্তরঃ ( গ )
ক \(0\)
গ \(-1\)
গ \(-1\)
খ \(1\)
ঘ \(\frac{\pi}{2}\)
\(\cos{\left\{2\left(\sin^{-1}\frac{3x}{2}+\cos^{-1}\frac{3x}{2}\right)\right\}}=P\)ঘ \(\frac{\pi}{2}\)
\(\Rightarrow P=\cos{\left\{2\left(\sin^{-1}\frac{3x}{2}+\cos^{-1}\frac{3x}{2}\right)\right\}}\)
\(\Rightarrow P=\cos{\left\{2\times\frac{\pi}{2}\right\}}\) যেহেতু \(\sin^{-1}a+\cos^{-1}a=\frac{\pi}{2}\)
\(\Rightarrow P=\cos{\pi}\)
\(\therefore P=-1\) যেহেতু \(\cos{\pi}=-1\)
উত্তরঃ ( গ )
১৮। \(P\) এবং \(Q\) বল দুইটি পরস্পর বিপরীত দিকে ক্রিয়া করলে লব্ধি হয় \(5 N\) এবং একই দিকে ক্রিয়া করলে লব্ধি হয় \(7 N.\)
\(i.\) \(P\) বলের মান \(6 N\)
\(ii.\) \(Q\) বলের মান \(1 N\)
\(iii.\) বল দুইটির মধ্যবর্তী কোণ যথাক্রমে \(180^{o}\) এবং \(0^{o}\)
নিচের কোনটি সঠীক?
\(P-Q=5 N ....(1)\)
\(P+Q=7 N ....(2)\)
\((1)+(2)\) এর সাহায্যে
\(P-Q+P+Q=5+7\)
\(\Rightarrow 2P=12\)
\(\Rightarrow P=6\)
\(\therefore P=6 N\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
\((2)-(1)\) এর সাহায্যে
\(P+Q-P+Q=7-5\)
\(\Rightarrow 2Q=2\)
\(\Rightarrow Q=1\)
\(\therefore Q=1 N\)
\(\therefore (ii.)\) নং বাক্যটি সত্য।
আবার,
যখন বলদ্বয় বিপরীত দিকে ক্রিয়া করে তখন মধ্যবর্তী কোণ \(180^{o}\)
যখন বলদ্বয় একই দিকে ক্রিয়া করে তখন মধ্যবর্তী কোণ \(0^{o}\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( ঘ )
\(i.\) \(P\) বলের মান \(6 N\)
\(ii.\) \(Q\) বলের মান \(1 N\)
\(iii.\) বল দুইটির মধ্যবর্তী কোণ যথাক্রমে \(180^{o}\) এবং \(0^{o}\)
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
শর্তমতে, \(=13+1=14\)ঘ \(i.\), \(ii.\) ও \(iii.\)
\(P-Q=5 N ....(1)\)
\(P+Q=7 N ....(2)\)
\((1)+(2)\) এর সাহায্যে
\(P-Q+P+Q=5+7\)
\(\Rightarrow 2P=12\)
\(\Rightarrow P=6\)
\(\therefore P=6 N\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
\((2)-(1)\) এর সাহায্যে
\(P+Q-P+Q=7-5\)
\(\Rightarrow 2Q=2\)
\(\Rightarrow Q=1\)
\(\therefore Q=1 N\)
\(\therefore (ii.)\) নং বাক্যটি সত্য।
আবার,
যখন বলদ্বয় বিপরীত দিকে ক্রিয়া করে তখন মধ্যবর্তী কোণ \(180^{o}\)
যখন বলদ্বয় একই দিকে ক্রিয়া করে তখন মধ্যবর্তী কোণ \(0^{o}\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( ঘ )
১৯। কোনো বিন্দুতে \(120^{o}\) কোণে ক্রিয়াশীল দুইটি বলের বৃহত্তম বলটি \(16N\) এবং ক্ষুদ্রতম বলটি লব্ধির সাথে সমকোণ উৎপন্ন করে। ক্ষুদ্রতম বলটি কত?
\(\tan{90^{o}}=\frac{16\sin{120^{o}}}{P+16\cos{120^{o}}}\)
\(\Rightarrow \frac{1}{0}=\frac{16\times\frac{\sqrt{3}}{2}}{P+16\times-\frac{1}{2}}\)
\(\Rightarrow \frac{1}{0}=\frac{8\sqrt{3}}{P-8}\)
\(\Rightarrow P-8=0\)
\(\therefore P=8 N\)
উত্তরঃ ( গ )
ক \(\sqrt{3} N\)
গ \(8 N\)
গ \(8 N\)
খ \(3 N\)
ঘ \(8\sqrt{3} N\)
ক্ষুদ্রতম বলটি \(P\) হলে,ঘ \(8\sqrt{3} N\)
\(\tan{90^{o}}=\frac{16\sin{120^{o}}}{P+16\cos{120^{o}}}\)
\(\Rightarrow \frac{1}{0}=\frac{16\times\frac{\sqrt{3}}{2}}{P+16\times-\frac{1}{2}}\)
\(\Rightarrow \frac{1}{0}=\frac{8\sqrt{3}}{P-8}\)
\(\Rightarrow P-8=0\)
\(\therefore P=8 N\)
উত্তরঃ ( গ )
২০। \(u\) গতিবেগে ও অনুভূমিকের সাথে \(\alpha\) কোণে প্রক্ষিপ্ত বস্তুর অনুভূমিক পাল্লা-
\(u\) গতিবেগে ও অনুভূমিকের সাথে \(\alpha\) কোণে প্রক্ষিপ্ত বস্তুর অনুভূমিক পাল্লা
\(\frac{u^2\sin{2\alpha}}{g}\)
উত্তরঃ ( খ )
ক \(\frac{u\sin{2\alpha}}{g}\)
গ \(\frac{u\sin{2\alpha}}{2g}\)
গ \(\frac{u\sin{2\alpha}}{2g}\)
খ \(\frac{u^2\sin{2\alpha}}{g}\)
ঘ \(\frac{u^2\sin{2\alpha}}{2g}\)
আমরা জানি,ঘ \(\frac{u^2\sin{2\alpha}}{2g}\)
\(u\) গতিবেগে ও অনুভূমিকের সাথে \(\alpha\) কোণে প্রক্ষিপ্ত বস্তুর অনুভূমিক পাল্লা
\(\frac{u^2\sin{2\alpha}}{g}\)
উত্তরঃ ( খ )
২১। একখানা গাড়ী সমত্বরণে \(25 km/hr\) আদিবেগে \(150 km\) অতিক্রম করে \(60 km/hr\) চূড়ান্ত বেগ প্রাপ্ত হয়। গাড়িটির ত্বরণ কত?
\(v=60 km/hr\)
\(S=150 km\)
ধরি, ত্বরণ \(=a km/h^2\)
আমরা জানি, \(v^2=u^2+2as\)
\(\Rightarrow (60)^2=(25)^2+2a\times150\)
\(\Rightarrow 3600=625+300a\)
\(\Rightarrow 625+300a=3600\)
\(\Rightarrow 300a=3600-625\)
\(\Rightarrow 300a=2975\)
\(\Rightarrow a=\frac{2975}{300}\)
\(\therefore a=9.92 km/h^2\)
উত্তরঃ ( ক )
ক \(9.92 km/h^2\)
গ \(19.83 km/h^2\)
গ \(19.83 km/h^2\)
খ \(14.08 km/h^2\)
ঘ \(28.16 km/h^2\)
এখানে, \(u=25 km/hr\)ঘ \(28.16 km/h^2\)
\(v=60 km/hr\)
\(S=150 km\)
ধরি, ত্বরণ \(=a km/h^2\)
আমরা জানি, \(v^2=u^2+2as\)
\(\Rightarrow (60)^2=(25)^2+2a\times150\)
\(\Rightarrow 3600=625+300a\)
\(\Rightarrow 625+300a=3600\)
\(\Rightarrow 300a=3600-625\)
\(\Rightarrow 300a=2975\)
\(\Rightarrow a=\frac{2975}{300}\)
\(\therefore a=9.92 km/h^2\)
উত্তরঃ ( ক )
২২। \(P(A)=\frac{1}{6}, P(B)=\frac{4}{5} \ A\) ও \(B\) স্বাধীন হলে, \(P(A\cup{B})=\)?
\(\therefore P(A\cap{B})=P(A)\times{P(B)}\)
\(=\frac{1}{6}\times\frac{4}{5}\)
\(=\frac{4}{30}\)
আমরা জানি, \(P(A\cup{B})=P(A)+P(B)-P(A\cap{B})\)
\(=\frac{1}{6}+\frac{4}{5}-\frac{4}{30}\)
\(=\frac{5+24-4}{30}\)
\(=\frac{25}{30}\)
উত্তরঃ ( খ )
ক \(\frac{4}{30}\)
গ \(\frac{29}{30}\)
গ \(\frac{29}{30}\)
খ \(\frac{25}{30}\)
ঘ \(\frac{33}{30}\)
\(P(A)=\frac{1}{6}, P(B)=\frac{4}{5} \ A\) ও \(B\) স্বাধীনঘ \(\frac{33}{30}\)
\(\therefore P(A\cap{B})=P(A)\times{P(B)}\)
\(=\frac{1}{6}\times\frac{4}{5}\)
\(=\frac{4}{30}\)
আমরা জানি, \(P(A\cup{B})=P(A)+P(B)-P(A\cap{B})\)
\(=\frac{1}{6}+\frac{4}{5}-\frac{4}{30}\)
\(=\frac{5+24-4}{30}\)
\(=\frac{25}{30}\)
উত্তরঃ ( খ )
২৩। একটি সমস্যা সমাধান করতে পারার ক্ষেত্রে \(A\) এর সম্ভাবনা \(\frac{5}{9}\) এবং \(B\) এর সম্ভাবনা \(\frac{7}{8}\) হলে তাদের একত্রে সমস্যাটি সমাধান করতে পারার সম্ভাবনা কত?
\(P(A)=\frac{5}{9}, P(B)=\frac{7}{8} \ A\) ও \(B\) স্বাধীন
\(\therefore P(A\cap{B})=P(A)\times{P(B)}\)
\(=\frac{5}{9}\times\frac{7}{8}\)
\(=\frac{35}{72}\)
আমরা জানি, \(P(A\cup{B})=P(A)+P(B)-P(A\cap{B})\)
\(=\frac{5}{9}+\frac{7}{8}-\frac{35}{72}\)
\(=\frac{40+63-35}{72}\)
\(=\frac{68}{72}\)
\(=\frac{17}{18}\)
উত্তরঃ ( ঘ )
ক \(\frac{1}{18}\)
গ \(\frac{37}{72}\)
গ \(\frac{37}{72}\)
খ \(\frac{35}{72}\)
ঘ \(\frac{17}{18}\)
এখানে,ঘ \(\frac{17}{18}\)
\(P(A)=\frac{5}{9}, P(B)=\frac{7}{8} \ A\) ও \(B\) স্বাধীন
\(\therefore P(A\cap{B})=P(A)\times{P(B)}\)
\(=\frac{5}{9}\times\frac{7}{8}\)
\(=\frac{35}{72}\)
আমরা জানি, \(P(A\cup{B})=P(A)+P(B)-P(A\cap{B})\)
\(=\frac{5}{9}+\frac{7}{8}-\frac{35}{72}\)
\(=\frac{40+63-35}{72}\)
\(=\frac{68}{72}\)
\(=\frac{17}{18}\)
উত্তরঃ ( ঘ )
২৪। \(5, 7, 9, 11\) সংখ্যাগুলির পরিমিত ব্যবধান কত?
\(=\frac{32}{4}\)
\(=8\)
সংখ্যাগুলির পরিমিত ব্যবধান \(\sigma=\sqrt{\frac{(5-8)^2+(7-8)^2+(9-8)^2+(11-8)^2}{4}}\)
\(=\sqrt{\frac{9+1+1+9}{4}}\)
\(=\sqrt{\frac{20}{4}}\)
\(=\sqrt{5}\)
উত্তরঃ ( ক )
ক \(\sqrt{5}\)
গ \(5 N\)
গ \(5 N\)
খ \(\sqrt{8}\)
ঘ \(8\)
সংখ্যাগুলির গাণিতিক গড় \(=\frac{5+7+9+11}{4}\)ঘ \(8\)
\(=\frac{32}{4}\)
\(=8\)
সংখ্যাগুলির পরিমিত ব্যবধান \(\sigma=\sqrt{\frac{(5-8)^2+(7-8)^2+(9-8)^2+(11-8)^2}{4}}\)
\(=\sqrt{\frac{9+1+1+9}{4}}\)
\(=\sqrt{\frac{20}{4}}\)
\(=\sqrt{5}\)
উত্তরঃ ( ক )
২৫। \(\cos{\theta}=-\frac{1}{2}\) সমীকরণের সমাধান কোনটি?
\(\Rightarrow \cos{\theta}=\cos{\frac{2\pi}{3}}\)
\(\therefore \theta=2n\pi\pm{\frac{2\pi}{3}}; \ \because \cos{x}=\cos{\alpha} \Rightarrow x=2n\pi\pm{\alpha}\)
উত্তরঃ ( ঘ )
ক \(n\pi\pm{\frac{\pi}{3}}\)
গ \(n\pi\pm{\frac{2\pi}{3}}\)
গ \(n\pi\pm{\frac{2\pi}{3}}\)
খ \(2n\pi\pm{\frac{\pi}{3}}\)
ঘ \(2n\pi\pm{\frac{2\pi}{3}}\)
\(\cos{\theta}=-\frac{1}{2}\)ঘ \(2n\pi\pm{\frac{2\pi}{3}}\)
\(\Rightarrow \cos{\theta}=\cos{\frac{2\pi}{3}}\)
\(\therefore \theta=2n\pi\pm{\frac{2\pi}{3}}; \ \because \cos{x}=\cos{\alpha} \Rightarrow x=2n\pi\pm{\alpha}\)
উত্তরঃ ( ঘ )
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000001