শিক্ষা বোর্ড দিনাজপুর - 2021
উচ্চতর গণিত ( বহুনির্বাচনি )
[2021 সালের সিলেবাস অনুযায়ী ]
দ্বিতীয় পত্র বহুনির্বাচনি
বিষয় কোডঃ 266
সময়-২৫ মিনিট
পূর্ণমান-২৫
[ দ্রষ্টব্যঃ সরবরাহকৃত বহুনির্বাচনি অভীক্ষার উত্তরপত্রে প্রশ্নের ক্রমিক নম্বরের বিপরীতে প্রদত্ত বর্ণসংবলিত বৃত্তসমুহ হতে সিঠিক/সর্বোৎকৃষ্ট উত্তরের বৃত্তটি বল পয়ন্ট কলম দ্বারা সম্পুর্ণ ভরাট কর। প্রতিটি প্রশ্নের মাণ ১। প্রশ্নপত্রে কোন প্রকার দাগ/ চিহ্ন দেওয়া যাবে না। ]
উচ্চতর গণিত ( বহুনির্বাচনি )
[2021 সালের সিলেবাস অনুযায়ী ]
দ্বিতীয় পত্র বহুনির্বাচনি
বিষয় কোডঃ 266
সময়-২৫ মিনিট
পূর্ণমান-২৫
[ দ্রষ্টব্যঃ সরবরাহকৃত বহুনির্বাচনি অভীক্ষার উত্তরপত্রে প্রশ্নের ক্রমিক নম্বরের বিপরীতে প্রদত্ত বর্ণসংবলিত বৃত্তসমুহ হতে সিঠিক/সর্বোৎকৃষ্ট উত্তরের বৃত্তটি বল পয়ন্ট কলম দ্বারা সম্পুর্ণ ভরাট কর। প্রতিটি প্রশ্নের মাণ ১। প্রশ্নপত্রে কোন প্রকার দাগ/ চিহ্ন দেওয়া যাবে না। ]
১। \(2x^3-x^2-5x-2=0\) সমীকরণের মূলত্রয়ের সমষ্টি কত?
মূলত্রয়ের সমষ্টি \(\alpha+\beta+\gamma=-\frac{-1}{2}\)
\(=\frac{1}{2}\)
উত্তরঃ ( খ )
ক \(-\frac{5}{2}\)
গ \(-2\)
গ \(-2\)
খ \(\frac{1}{2}\)
ঘ \(2\)
\(2x^3-x^2-5x-2=0\) সমীকরণের মূলত্রয় \(\alpha, \beta\) ও
\(\gamma\) হয়, তবে ঘ \(2\)
মূলত্রয়ের সমষ্টি \(\alpha+\beta+\gamma=-\frac{-1}{2}\)
\(=\frac{1}{2}\)
উত্তরঃ ( খ )
২। \(x^3-px^2+q=0\) সমীকরণের মূলত্রয় \(\alpha, \beta\) ও \(\gamma\)
হলে, \(\sum{\alpha^2}\)-এর মাণ কত?
মূলত্রয়ের সমষ্টি \(\alpha+\beta+\gamma=-\frac{-p}{1}=p\)
মূলত্রয়ের দুইটি করে গুণফলের যোগফল \(\alpha\beta+\beta\gamma+\alpha\gamma=\frac{0}{1}=0\)
এখন,
\(\sum{\alpha^2}\)
\(=\alpha^2+\beta^2+\gamma^2\)
\(=(\alpha+\beta+\gamma)^2-2(\alpha\beta+\beta\gamma+\alpha\gamma)\)
\(=p^2-2\times0\)
\(=p^2-0\)
\(=p^2\)
উত্তরঃ ( ক )
ক \(p^2\)
গ \(-p^2\)
গ \(-p^2\)
খ \(p^2-2q\)
ঘ \(-q\)
\(x^3-px^2+q=0\) সমীকরণের মূলত্রয় \(\alpha, \beta\) ও
\(\gamma\)ঘ \(-q\)
মূলত্রয়ের সমষ্টি \(\alpha+\beta+\gamma=-\frac{-p}{1}=p\)
মূলত্রয়ের দুইটি করে গুণফলের যোগফল \(\alpha\beta+\beta\gamma+\alpha\gamma=\frac{0}{1}=0\)
এখন,
\(\sum{\alpha^2}\)
\(=\alpha^2+\beta^2+\gamma^2\)
\(=(\alpha+\beta+\gamma)^2-2(\alpha\beta+\beta\gamma+\alpha\gamma)\)
\(=p^2-2\times0\)
\(=p^2-0\)
\(=p^2\)
উত্তরঃ ( ক )
নিচের তথ্যের আলোকে ৩ এবং ৪ নং প্রশ্নের
উত্তর দাওঃ
\(3x^2-4y+6x-5=0\)একটি পরাবৃত্ত।
৩। পরাবৃত্তটির ফোকাস কোনটি?\(3x^2-4y+6x-5=0\)একটি পরাবৃত্ত।
ক \(\left(-1, -\frac{5}{3}\right)\)
গ \(\left(0, \frac{1}{3}\right)\)
গ \(\left(0, \frac{1}{3}\right)\)
খ \(\left(0, -\frac{1}{3}\right)\)
ঘ \((-1, -2)\)
\(3x^2-4y+6x-5=0\)ঘ \((-1, -2)\)
\(\Rightarrow 3x^2+6x-5=4y\)
\(\Rightarrow 3(x^2+2x)-5=4y\)
\(\Rightarrow 3(x^2+2x+1-1)-5=4y\)
\(\Rightarrow 3(x^2+2x+1)-3-5=4y\)
\(\Rightarrow 3(x+1)^2-8=4y\)
\(\Rightarrow 3(x+1)^2=4y+8\)
\(\Rightarrow 3(x+1)^2=4(y+2)\)
\(\therefore (x+1)^2=4.\frac{1}{3}.(y+2)\)
\((x-\alpha)^2=4a(y-\beta)\) এর সহিত তুলুনা করে,
\(a=\frac{1}{3}, \ \alpha=-1, \ \beta=-2\)
পরাবৃত্তটির ফোকাস \(\left(\alpha, a+\beta\right)\)
\(\left(-1, \frac{1}{3}-2\right)\)
\(\Rightarrow \left(-1, \frac{1-6}{3}\right)\)
\(\therefore \left(-1, -\frac{5}{3}\right)\)
উত্তরঃ ( ক )
৪। পরাবৃত্তটির নিয়ামক রেখা কোনটি?
\(\Rightarrow 3x^2+6x-5=4y\)
\(\Rightarrow 3(x^2+2x)-5=4y\)
\(\Rightarrow 3(x^2+2x+1-1)-5=4y\)
\(\Rightarrow 3(x^2+2x+1)-3-5=4y\)
\(\Rightarrow 3(x+1)^2-8=4y\)
\(\Rightarrow 3(x+1)^2=4y+8\)
\(\Rightarrow 3(x+1)^2=4(y+2)\)
\(\Rightarrow (x+1)^2=4.\frac{1}{3}.(y+2)\)
\(\therefore X^2=4.\frac{1}{3}.Y\) যেখানে, \(X=x+1, \ Y=y+2\)
\(x^2=4ay\) এর সহিত তুলুনা করে,
\(a=\frac{1}{3}\)
নিয়ামক রেখা \(Y=-a\)
\(\Rightarrow y+2=-\frac{1}{3}\)
\(\Rightarrow 3y+6=-1\)
\(\Rightarrow 3y+6+1=0\)
\(\therefore 3y+7=0\)
উত্তরঃ ( গ )
ক \(3y+2=0\)
গ \(3y+7=0\)
গ \(3y+7=0\)
খ \(3y+5=0\)
ঘ \(3y-7=0\)
\(3x^2-4y+6x-5=0\)ঘ \(3y-7=0\)
\(\Rightarrow 3x^2+6x-5=4y\)
\(\Rightarrow 3(x^2+2x)-5=4y\)
\(\Rightarrow 3(x^2+2x+1-1)-5=4y\)
\(\Rightarrow 3(x^2+2x+1)-3-5=4y\)
\(\Rightarrow 3(x+1)^2-8=4y\)
\(\Rightarrow 3(x+1)^2=4y+8\)
\(\Rightarrow 3(x+1)^2=4(y+2)\)
\(\Rightarrow (x+1)^2=4.\frac{1}{3}.(y+2)\)
\(\therefore X^2=4.\frac{1}{3}.Y\) যেখানে, \(X=x+1, \ Y=y+2\)
\(x^2=4ay\) এর সহিত তুলুনা করে,
\(a=\frac{1}{3}\)
নিয়ামক রেখা \(Y=-a\)
\(\Rightarrow y+2=-\frac{1}{3}\)
\(\Rightarrow 3y+6=-1\)
\(\Rightarrow 3y+6+1=0\)
\(\therefore 3y+7=0\)
উত্তরঃ ( গ )
৫। \(3x^2+4y^2=1\) উপবৃত্তের-
\(i.\) উপকেন্দ্রিকতা \(=\frac{1}{2}\)
\(ii.\) উপকেন্দ্র \(\left(\pm2\sqrt{3}, 0\right)\)
\(iii.\) উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\frac{\sqrt{3}}{2}\)
নিচের কোনটি সঠীক?
\(\Rightarrow \frac{x^2}{\frac{1}{3}}+\frac{y^2}{\frac{1}{4}}=1\)
\(\therefore \frac{x^2}{\left(\frac{1}{\sqrt{3}}\right)^2}+\frac{y^2}{\left(\frac{1}{2}\right)^2}=1\)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=\frac{1}{\sqrt{3}}, \ b=\frac{1}{2} \ \therefore a\gt{b}\)
উপকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(=\sqrt{1-\frac{\frac{1}{4}}{\frac{1}{3}}}\)
\(=\sqrt{1-\frac{3}{4}}\)
\(=\sqrt{\frac{4-3}{4}}\)
\(=\sqrt{\frac{1}{4}}\)
\(=\frac{1}{2}\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
উপকেন্দ্র \(\left(\pm{ae}, 0\right)\)
\(\Rightarrow \left(\pm{\frac{1}{\sqrt{3}}\times\frac{1}{2}}, 0\right)\)
\(\therefore \left(\pm{\frac{1}{2\sqrt{3}}}, 0\right)\)
\(\therefore (ii.)\) নং বাক্যটি সত্য নয়।
আবার,
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2b^2}{a}\right|\)
\(=\left|\frac{2\times\frac{1}{4}}{\frac{1}{\sqrt{3}}}\right|\)
\(=\left|\frac{\frac{1}{2}}{\frac{1}{\sqrt{3}}}\right|\)
\(=\frac{\sqrt{3}}{2}\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
\(i.\) উপকেন্দ্রিকতা \(=\frac{1}{2}\)
\(ii.\) উপকেন্দ্র \(\left(\pm2\sqrt{3}, 0\right)\)
\(iii.\) উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\frac{\sqrt{3}}{2}\)
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
\(3x^2+4y^2=1\) ঘ \(i.\), \(ii.\) ও \(iii.\)
\(\Rightarrow \frac{x^2}{\frac{1}{3}}+\frac{y^2}{\frac{1}{4}}=1\)
\(\therefore \frac{x^2}{\left(\frac{1}{\sqrt{3}}\right)^2}+\frac{y^2}{\left(\frac{1}{2}\right)^2}=1\)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=\frac{1}{\sqrt{3}}, \ b=\frac{1}{2} \ \therefore a\gt{b}\)
উপকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(=\sqrt{1-\frac{\frac{1}{4}}{\frac{1}{3}}}\)
\(=\sqrt{1-\frac{3}{4}}\)
\(=\sqrt{\frac{4-3}{4}}\)
\(=\sqrt{\frac{1}{4}}\)
\(=\frac{1}{2}\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
উপকেন্দ্র \(\left(\pm{ae}, 0\right)\)
\(\Rightarrow \left(\pm{\frac{1}{\sqrt{3}}\times\frac{1}{2}}, 0\right)\)
\(\therefore \left(\pm{\frac{1}{2\sqrt{3}}}, 0\right)\)
\(\therefore (ii.)\) নং বাক্যটি সত্য নয়।
আবার,
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2b^2}{a}\right|\)
\(=\left|\frac{2\times\frac{1}{4}}{\frac{1}{\sqrt{3}}}\right|\)
\(=\left|\frac{\frac{1}{2}}{\frac{1}{\sqrt{3}}}\right|\)
\(=\frac{\sqrt{3}}{2}\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
৬। \(9x^2+16y^2=144\) উপবৃত্তটির নিয়ামক রেখা কোনটি?
\(\Rightarrow \frac{9x^2}{144}+\frac{16y^2}{144}=1\)
\(\Rightarrow \frac{x^2}{16}+\frac{y^2}{9}=1\)
\(\therefore \frac{x^2}{4^2}+\frac{y^2}{3^2}=1\)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=4, \ b=3 \ \therefore a\gt{b}\)
উপকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(=\sqrt{1-\frac{9}{16}}\)
\(=\sqrt{\frac{16-9}{16}}\)
\(=\sqrt{\frac{7}{16}}\)
\(=\frac{\sqrt{7}}{4}\)
উপবৃত্তটির নিয়ামক রেখা, \(x=\pm\frac{a}{e}\)
\(\Rightarrow x=\pm\frac{4}{\frac{\sqrt{7}}{4}}\)
\(\Rightarrow x=\pm\frac{16}{\sqrt{7}}\)
\(\Rightarrow \sqrt{7}x=\pm16\)
\(\therefore \sqrt{7}x\pm16=0\)
উত্তরঃ ( ক )
ক \(\sqrt{7}x\pm16\)
গ \(\sqrt{7}y\pm16\)
গ \(\sqrt{7}y\pm16\)
খ \(\sqrt{7}x\pm12\)
ঘ \(\sqrt{7}y\pm12\)
\(9x^2+16y^2=144\)ঘ \(\sqrt{7}y\pm12\)
\(\Rightarrow \frac{9x^2}{144}+\frac{16y^2}{144}=1\)
\(\Rightarrow \frac{x^2}{16}+\frac{y^2}{9}=1\)
\(\therefore \frac{x^2}{4^2}+\frac{y^2}{3^2}=1\)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=4, \ b=3 \ \therefore a\gt{b}\)
উপকেন্দ্রিকতা \(e=\sqrt{1-\frac{b^2}{a^2}}\)
\(=\sqrt{1-\frac{9}{16}}\)
\(=\sqrt{\frac{16-9}{16}}\)
\(=\sqrt{\frac{7}{16}}\)
\(=\frac{\sqrt{7}}{4}\)
উপবৃত্তটির নিয়ামক রেখা, \(x=\pm\frac{a}{e}\)
\(\Rightarrow x=\pm\frac{4}{\frac{\sqrt{7}}{4}}\)
\(\Rightarrow x=\pm\frac{16}{\sqrt{7}}\)
\(\Rightarrow \sqrt{7}x=\pm16\)
\(\therefore \sqrt{7}x\pm16=0\)
উত্তরঃ ( ক )
৭। \(y=3x+c\) রেখাটি \(3x^2+4y^2=12\) উপবৃত্তটিকে স্পর্শ করলে \(c\) এর
মান কত?
নিচের কোনটি সঠীক?
আবার,
\(3x^2+4y^2=12\)
\(\Rightarrow \frac{3x^2}{12}+\frac{4y^2}{12}=1\)
\(\Rightarrow \frac{x^2}{4}+\frac{y^2}{3}=1\)
\(\therefore \frac{x^2}{2^2}+\frac{y^2}{(\sqrt{3})^2}=1\)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=2, \ b=\sqrt{3} \ \therefore a\gt{b}\)
\(y=mx+c\) সরলরেখার \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তকে স্পর্শ করার শর্ত \(c=\pm\sqrt{a^2m^2+b^2}\)
\(c=\pm\sqrt{2^2\times3^2+(\sqrt{3})^2}\)
\(=\pm\sqrt{4\times9+3}\)
\(=\pm\sqrt{36+3}\)
\(=\pm\sqrt{39}\)
উত্তরঃ ( ঘ )
নিচের কোনটি সঠীক?
ক \(\pm5\)
গ \(\pm\sqrt{31}\)
গ \(\pm\sqrt{31}\)
খ \(\pm\sqrt{7}\)
ঘ \(\pm\sqrt{39}\)
\(y=3x+c\) রেখাটির ঢাল \(m=3\)ঘ \(\pm\sqrt{39}\)
আবার,
\(3x^2+4y^2=12\)
\(\Rightarrow \frac{3x^2}{12}+\frac{4y^2}{12}=1\)
\(\Rightarrow \frac{x^2}{4}+\frac{y^2}{3}=1\)
\(\therefore \frac{x^2}{2^2}+\frac{y^2}{(\sqrt{3})^2}=1\)
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=2, \ b=\sqrt{3} \ \therefore a\gt{b}\)
\(y=mx+c\) সরলরেখার \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) উপবৃত্তকে স্পর্শ করার শর্ত \(c=\pm\sqrt{a^2m^2+b^2}\)
\(c=\pm\sqrt{2^2\times3^2+(\sqrt{3})^2}\)
\(=\pm\sqrt{4\times9+3}\)
\(=\pm\sqrt{36+3}\)
\(=\pm\sqrt{39}\)
উত্তরঃ ( ঘ )
৮। \(x^2-8y^2=2\) অধিবৃত্তের উৎকেন্দ্রিকতা কোনটি?
\(\Rightarrow \frac{x^2}{2}-\frac{8y^2}{2}=1\)
\(\Rightarrow \frac{x^2}{2}-\frac{y^2}{\frac{2}{8}}=1\)
\(\Rightarrow \frac{x^2}{2}-\frac{y^2}{\frac{1}{4}}=1\)
\(\therefore \frac{x^2}{(\sqrt{2})^2}-\frac{y^2}{\left(\frac{1}{2}\right)^2}=1\)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=\sqrt{2}, \ b=\frac{1}{2}\)
উপকেন্দ্রিকতা \(e=\sqrt{1+\frac{b^2}{a^2}}\)
\(=\sqrt{1+\frac{\frac{1}{4}}{2}}\)
\(=\sqrt{1+\frac{1}{8}}\)
\(=\sqrt{\frac{8+1}{8}}\)
\(=\sqrt{\frac{9}{8}}\)
\(=\frac{3}{2\sqrt{2}}\)
উত্তরঃ ( খ )
ক \(\frac{3}{\sqrt{2}}\)
গ \(\frac{\sqrt{3}}{\sqrt{2}}\)
গ \(\frac{\sqrt{3}}{\sqrt{2}}\)
খ \(\frac{3}{2\sqrt{2}}\)
ঘ \(\frac{\sqrt{7}}{2\sqrt{2}}\)
\(x^2-8y^2=2\)ঘ \(\frac{\sqrt{7}}{2\sqrt{2}}\)
\(\Rightarrow \frac{x^2}{2}-\frac{8y^2}{2}=1\)
\(\Rightarrow \frac{x^2}{2}-\frac{y^2}{\frac{2}{8}}=1\)
\(\Rightarrow \frac{x^2}{2}-\frac{y^2}{\frac{1}{4}}=1\)
\(\therefore \frac{x^2}{(\sqrt{2})^2}-\frac{y^2}{\left(\frac{1}{2}\right)^2}=1\)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=\sqrt{2}, \ b=\frac{1}{2}\)
উপকেন্দ্রিকতা \(e=\sqrt{1+\frac{b^2}{a^2}}\)
\(=\sqrt{1+\frac{\frac{1}{4}}{2}}\)
\(=\sqrt{1+\frac{1}{8}}\)
\(=\sqrt{\frac{8+1}{8}}\)
\(=\sqrt{\frac{9}{8}}\)
\(=\frac{3}{2\sqrt{2}}\)
উত্তরঃ ( খ )
৯। \(4x^2-9y^2-1=0\) অধিবৃত্তের উপকেন্দ্রিক লম্বের দৈর্ঘ্য কত?
\(\Rightarrow 4x^2-9y^2=1\)
\(\Rightarrow \frac{x^2}{\frac{1}{4}}-\frac{9y^2}{\frac{1}{9}}=1\)
\(\therefore \frac{x^2}{\left(\frac{1}{2}\right)^2}-\frac{y^2}{\left(\frac{1}{3}\right)^2}=1\)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=\frac{1}{2}, \ b=\frac{1}{3}\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2b^2}{a}\right|\)
\(=\left|\frac{2\times\frac{1}{9}}{\frac{1}{2}}\right|\)
\(=\left|\frac{\frac{2}{9}}{\frac{1}{2}}\right|\)
\(=\frac{4}{9}\)
উত্তরঃ ( খ )
ক \(9\)
গ \(\frac{3}{2}\)
গ \(\frac{3}{2}\)
খ \(\frac{4}{9}\)
ঘ \(\frac{8}{3}\)
\(4x^2-9y^2-1=0\)ঘ \(\frac{8}{3}\)
\(\Rightarrow 4x^2-9y^2=1\)
\(\Rightarrow \frac{x^2}{\frac{1}{4}}-\frac{9y^2}{\frac{1}{9}}=1\)
\(\therefore \frac{x^2}{\left(\frac{1}{2}\right)^2}-\frac{y^2}{\left(\frac{1}{3}\right)^2}=1\)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) এর সহিত তুলুনা করে,
\(a=\frac{1}{2}, \ b=\frac{1}{3}\)
উপকেন্দ্রিক লম্বের দৈর্ঘ্য \(=\left|\frac{2b^2}{a}\right|\)
\(=\left|\frac{2\times\frac{1}{9}}{\frac{1}{2}}\right|\)
\(=\left|\frac{\frac{2}{9}}{\frac{1}{2}}\right|\)
\(=\frac{4}{9}\)
উত্তরঃ ( খ )
১০। যদি \(f(x)=\tan^{-1}x\) হয়-
\(i.\) \(2f(x)=\tan^{-1}\frac{2x}{1-x^2}\)
\(ii.\) \(2f(x)=\sin^{-1}\frac{2x}{1-x^2}\)
\(iii.\) \(2f(x)=\cos^{-1}\frac{1-x^2}{1+x^2}\)
নিচের কোনটি সঠীক?
\(\Rightarrow 2f(x)=2\tan^{-1}x\)
\(\therefore 2f(x)=\tan^{-1}\frac{2x}{1-x^2}\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
\(f(x)=\tan^{-1}x\)
\(\Rightarrow 2f(x)=2\tan^{-1}x\)
\(\therefore 2f(x)=\sin^{-1}\frac{2x}{1+x^2}\)
\(\therefore (ii.)\) নং বাক্যটি সত্য নয়।
আবার,
\(f(x)=\tan^{-1}x\)
\(\Rightarrow 2f(x)=2\tan^{-1}x\)
\(\therefore 2f(x)=\cos^{-1}\frac{1-x^2}{1+x^2}\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
\(i.\) \(2f(x)=\tan^{-1}\frac{2x}{1-x^2}\)
\(ii.\) \(2f(x)=\sin^{-1}\frac{2x}{1-x^2}\)
\(iii.\) \(2f(x)=\cos^{-1}\frac{1-x^2}{1+x^2}\)
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
\(f(x)=\tan^{-1}x\)ঘ \(i.\), \(ii.\) ও \(iii.\)
\(\Rightarrow 2f(x)=2\tan^{-1}x\)
\(\therefore 2f(x)=\tan^{-1}\frac{2x}{1-x^2}\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
\(f(x)=\tan^{-1}x\)
\(\Rightarrow 2f(x)=2\tan^{-1}x\)
\(\therefore 2f(x)=\sin^{-1}\frac{2x}{1+x^2}\)
\(\therefore (ii.)\) নং বাক্যটি সত্য নয়।
আবার,
\(f(x)=\tan^{-1}x\)
\(\Rightarrow 2f(x)=2\tan^{-1}x\)
\(\therefore 2f(x)=\cos^{-1}\frac{1-x^2}{1+x^2}\)
\(\therefore (iii.)\) নং বাক্যটি সত্য।
উত্তরঃ ( খ )
১১। \(\tan{\left(\tan^{-1}\frac{1}{3}+\tan^{-1}\frac{1}{5}\right)}=\)
কত?
\(=\tan{\left(\tan^{-1}\frac{\frac{1}{3}+\frac{1}{5}}{1-\frac{1}{3}\times\frac{1}{5}}\right)}\)
\(=\frac{\frac{5+3}{15}}{1-\frac{1}{15}}\)
\(=\frac{\frac{8}{15}}{\frac{15-1}{15}}\)
\(=\frac{\frac{8}{15}}{\frac{14}{15}}\)
\(=\frac{8}{15}\times\frac{15}{14}\)
\(=\frac{4}{7}\)
উত্তরঃ ( ঘ )
ক \(\frac{1}{8}\)
গ \(\frac{8}{15}\)
গ \(\frac{8}{15}\)
খ \(\frac{1}{2}\)
ঘ \(\frac{4}{7}\)
\(\tan{\left(\tan^{-1}\frac{1}{3}+\tan^{-1}\frac{1}{5}\right)}\)ঘ \(\frac{4}{7}\)
\(=\tan{\left(\tan^{-1}\frac{\frac{1}{3}+\frac{1}{5}}{1-\frac{1}{3}\times\frac{1}{5}}\right)}\)
\(=\frac{\frac{5+3}{15}}{1-\frac{1}{15}}\)
\(=\frac{\frac{8}{15}}{\frac{15-1}{15}}\)
\(=\frac{\frac{8}{15}}{\frac{14}{15}}\)
\(=\frac{8}{15}\times\frac{15}{14}\)
\(=\frac{4}{7}\)
উত্তরঃ ( ঘ )
১২। \(\sec^2{\left(\tan^{-1}2\right)}+cosec^2{\left(\cot^{-1}3\right)}=\)
কত?
\(=1+\tan^2{\left(\tan^{-1}2\right)}+1+\cot^2{\left(\cot^{-1}3\right)}\)
\(=1+\{\tan{\left(\tan^{-1}2\right)}\}^2+1+\{\cot{\left(\cot^{-1}3\right)}\}^2\)
\(=1+\{2\}^2+1+\{3\}^2\)
\(=1+4+1+9\)
\(=15\)
উত্তরঃ ( ঘ )
ক \(5\)
গ \(11\)
গ \(11\)
খ \(7\)
ঘ \(15\)
\(\sec^2{\left(\tan^{-1}2\right)}+cosec^2{\left(\cot^{-1}3\right)}\)ঘ \(15\)
\(=1+\tan^2{\left(\tan^{-1}2\right)}+1+\cot^2{\left(\cot^{-1}3\right)}\)
\(=1+\{\tan{\left(\tan^{-1}2\right)}\}^2+1+\{\cot{\left(\cot^{-1}3\right)}\}^2\)
\(=1+\{2\}^2+1+\{3\}^2\)
\(=1+4+1+9\)
\(=15\)
উত্তরঃ ( ঘ )
১৩। \(\sin^{-1}x+\cos^{-1}x=\theta\) হলে, \(\sin{\theta}\) এর মান
কত?
\(\Rightarrow \frac{\pi}{2}=\theta; \ \because \sin^{-1}x+\cos^{-1}x=\frac{\pi}{2}\)
\(\Rightarrow \theta=\frac{\pi}{2}\)
\(\Rightarrow \sin{\theta}=\sin{\frac{\pi}{2}}\)
\(\therefore \sin{\theta}=1; \ \because \sin{\frac{\pi}{2}}=1\)
উত্তরঃ ( খ )
ক \(0\)
গ \(2x\)
গ \(2x\)
খ \(1\)
ঘ \(2x\sqrt{1-x^2}\)
\(\sin^{-1}x+\cos^{-1}x=\theta\) ঘ \(2x\sqrt{1-x^2}\)
\(\Rightarrow \frac{\pi}{2}=\theta; \ \because \sin^{-1}x+\cos^{-1}x=\frac{\pi}{2}\)
\(\Rightarrow \theta=\frac{\pi}{2}\)
\(\Rightarrow \sin{\theta}=\sin{\frac{\pi}{2}}\)
\(\therefore \sin{\theta}=1; \ \because \sin{\frac{\pi}{2}}=1\)
উত্তরঃ ( খ )
১৪। \(\cos{2\theta}=\frac{1}{2}\) সমীকরণের সাধারণ সমাধান কোনটি?
\(\Rightarrow \cos{2\theta}=\cos{\frac{\pi}{3}}\)
\(\Rightarrow 2\theta=2n\pi\pm\frac{\pi}{3}; \ \because \cos{\theta}=\cos{\alpha} \Rightarrow \theta=2n\pi\pm\alpha\)
\(\therefore \theta=n\pi\pm\frac{\pi}{6}\)
উত্তরঃ ( গ )
ক \(2n\pi\pm\frac{\pi}{6}\)
গ \(n\pi\pm\frac{\pi}{6}\)
গ \(n\pi\pm\frac{\pi}{6}\)
খ \(2n\pi\pm\frac{\pi}{3}\)
ঘ \(n\pi\pm\frac{\pi}{3}\)
\(\cos{2\theta}=\frac{1}{2}\)ঘ \(n\pi\pm\frac{\pi}{3}\)
\(\Rightarrow \cos{2\theta}=\cos{\frac{\pi}{3}}\)
\(\Rightarrow 2\theta=2n\pi\pm\frac{\pi}{3}; \ \because \cos{\theta}=\cos{\alpha} \Rightarrow \theta=2n\pi\pm\alpha\)
\(\therefore \theta=n\pi\pm\frac{\pi}{6}\)
উত্তরঃ ( গ )
১৫। \(\cot{2x}\cot{x}=1\) হলে, \(x=\) কত?
\(\Rightarrow \frac{\cos{2x}\cos{x}}{\sin{2x}\sin{x}}=1\)
\(\Rightarrow \cos{2x}\cos{x}=\sin{2x}\sin{x}\)
\(\Rightarrow \cos{2x}\cos{x}-\sin{2x}\sin{x}=0\)
\(\Rightarrow \cos{(2x+x)}=0; \ \because \cos{A}\cos{B}-\sin{A}\sin{B}=\cos{(A+B)}\)
\(\Rightarrow \cos{3x}=0\)
\(\Rightarrow 3x=(2n+1)\frac{\pi}{2}; \ \because \cos{\theta}=0 \Rightarrow \theta=(2n+1)\frac{\pi}{2}\)
\(\therefore x=(2n+1)\frac{\pi}{6}\)
উত্তরঃ ( খ )
ক \((2n+1)\frac{\pi}{2}\)
গ \((2n+1)\frac{\pi}{3}\)
গ \((2n+1)\frac{\pi}{3}\)
খ \((2n+1)\frac{\pi}{6}\)
ঘ \((2n\pm1)\frac{\pi}{2}\)
\(\cot{2x}\cot{x}=1\)ঘ \((2n\pm1)\frac{\pi}{2}\)
\(\Rightarrow \frac{\cos{2x}\cos{x}}{\sin{2x}\sin{x}}=1\)
\(\Rightarrow \cos{2x}\cos{x}=\sin{2x}\sin{x}\)
\(\Rightarrow \cos{2x}\cos{x}-\sin{2x}\sin{x}=0\)
\(\Rightarrow \cos{(2x+x)}=0; \ \because \cos{A}\cos{B}-\sin{A}\sin{B}=\cos{(A+B)}\)
\(\Rightarrow \cos{3x}=0\)
\(\Rightarrow 3x=(2n+1)\frac{\pi}{2}; \ \because \cos{\theta}=0 \Rightarrow \theta=(2n+1)\frac{\pi}{2}\)
\(\therefore x=(2n+1)\frac{\pi}{6}\)
উত্তরঃ ( খ )
১৬। দুইটি সমান বল \(P\) পরস্পর \(60^{o}\) কোণে কোনো বিন্দুতে ক্রিয়া
করলে এদের লব্ধি কত হবে?
\(\therefore R=\sqrt{P^2+P^2+2P.P\cos{60^{o}}}\)
\(=\sqrt{2P^2+2P^2\times\frac{1}{2}}; \ \because \cos{60^{o}}=\frac{1}{2}\)
\(=\sqrt{2P^2+P^2}\)
\(=\sqrt{3P^2}\)
\(\therefore R=\sqrt{3}P\)
উত্তরঃ ( গ )
ক \(3P\)
গ \(\sqrt{3}P\)
গ \(\sqrt{3}P\)
খ \(2P\)
ঘ \(\sqrt{2}P\)
ধরি বলদ্বয়ের লব্ধি \(R\)ঘ \(\sqrt{2}P\)
\(\therefore R=\sqrt{P^2+P^2+2P.P\cos{60^{o}}}\)
\(=\sqrt{2P^2+2P^2\times\frac{1}{2}}; \ \because \cos{60^{o}}=\frac{1}{2}\)
\(=\sqrt{2P^2+P^2}\)
\(=\sqrt{3P^2}\)
\(\therefore R=\sqrt{3}P\)
উত্তরঃ ( গ )
১৭। \(P\) ও \(Q\) মানের দুইটি বল পরস্পর \(45^{o}\) কোণে কোনো একটি
বিন্দুতে ক্রিয়ারত। এদের লব্ধি \(16N, \ P\) বলের সাথে \(30^{o}\) কোণ
উৎপন্ন করে। \(Q\) বলের মান কত?
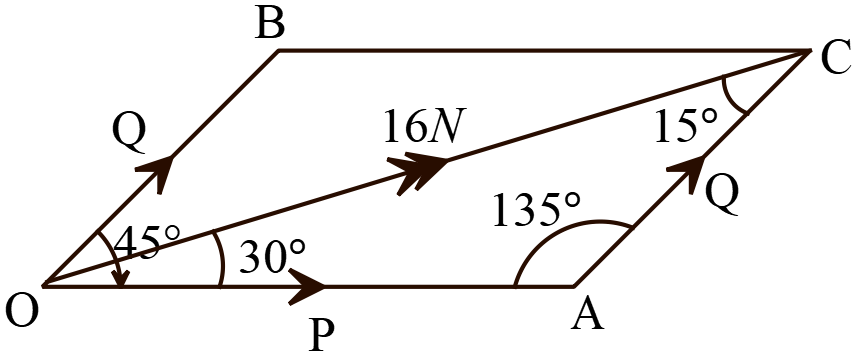
চিত্রে, \(\triangle{OAC}\) এ সাইন সূত্র ব্যবহার করে,
\(\frac{P}{\sin{15^{o}}}=\frac{Q}{\sin{30^{o}}}=\frac{16}{\sin{135^{o}}}\)
\(\Rightarrow \frac{Q}{\sin{30^{o}}}=\frac{16}{\sin{135^{o}}}\)
\(\Rightarrow \frac{Q}{\frac{1}{2}}=\frac{16}{\sin{(90^{o}\times2-45^{o})}}\)
\(\Rightarrow 2Q=\frac{16}{\sin{45^{o}}}\)
\(\Rightarrow Q=\frac{8}{\frac{1}{\sqrt{2}}}\)
\(\Rightarrow Q=8\sqrt{2}\)
\(\therefore Q=8\sqrt{2}N\)
উত্তরঃ ( ক )
ক \(8\sqrt{2}N\)
গ \(32\sqrt{2}N\)
গ \(32\sqrt{2}N\)
খ \(4\sqrt{2}N\)
ঘ \(8N\)
\(P\) ও \(Q\) মানের দুইটি বল পরস্পর \(45^{o}\) কোণে কোনো একটি
বিন্দুতে ক্রিয়ারত। এদের লব্ধি \(16N, \ P\) বলের সাথে \(30^{o}\)
কোণ উৎপন্ন করে। ঘ \(8N\)

চিত্রে, \(\triangle{OAC}\) এ সাইন সূত্র ব্যবহার করে,
\(\frac{P}{\sin{15^{o}}}=\frac{Q}{\sin{30^{o}}}=\frac{16}{\sin{135^{o}}}\)
\(\Rightarrow \frac{Q}{\sin{30^{o}}}=\frac{16}{\sin{135^{o}}}\)
\(\Rightarrow \frac{Q}{\frac{1}{2}}=\frac{16}{\sin{(90^{o}\times2-45^{o})}}\)
\(\Rightarrow 2Q=\frac{16}{\sin{45^{o}}}\)
\(\Rightarrow Q=\frac{8}{\frac{1}{\sqrt{2}}}\)
\(\Rightarrow Q=8\sqrt{2}\)
\(\therefore Q=8\sqrt{2}N\)
উত্তরঃ ( ক )
১৮। দুইটি সমান বল \(P\) এর লব্ধি \(\sqrt{2}P\) বল দুইটির মধ্যবর্তী কোণ
কত?
বল দুইটির মধ্যবর্তী কোণ \(\alpha\) হলে,
\(P^2+P^2+2P.P\cos{\alpha}=(\sqrt{2}P)^2; \ \because P^2+Q^2+2PQ\cos{\alpha}=R^2\)
\(\Rightarrow 2P^2+2P^2\cos{\alpha}=2P^2\)
\(\Rightarrow 2P^2(1+\cos{\alpha})=2P^2\)
\(\Rightarrow 1+\cos{\alpha}=1\)
\(\Rightarrow \cos{\alpha}=1-1\)
\(\Rightarrow \cos{\alpha}=0\)
\(\Rightarrow \cos{\alpha}=\cos{90^{o}}\)
\(\therefore \alpha=90^{o}\)
উত্তরঃ ( গ )
ক \(0^{o}\)
গ \(90^{o}\)
গ \(90^{o}\)
খ \(45^{o}\)
ঘ \(180^{o}\)
দুইটি সমান বল \(P\) এর লব্ধি \(\sqrt{2}P\) ঘ \(180^{o}\)
বল দুইটির মধ্যবর্তী কোণ \(\alpha\) হলে,
\(P^2+P^2+2P.P\cos{\alpha}=(\sqrt{2}P)^2; \ \because P^2+Q^2+2PQ\cos{\alpha}=R^2\)
\(\Rightarrow 2P^2+2P^2\cos{\alpha}=2P^2\)
\(\Rightarrow 2P^2(1+\cos{\alpha})=2P^2\)
\(\Rightarrow 1+\cos{\alpha}=1\)
\(\Rightarrow \cos{\alpha}=1-1\)
\(\Rightarrow \cos{\alpha}=0\)
\(\Rightarrow \cos{\alpha}=\cos{90^{o}}\)
\(\therefore \alpha=90^{o}\)
উত্তরঃ ( গ )
১৯। \(\sqrt{37}N, \ 3N\) এবং \(4N\) মানের তিনটি বল একটি বস্তুর উপর
ক্রিয়া করে ভারসাম্য সৃষ্টি করে। \(3N\) ও \(4N\) বলদ্বয়ের মধ্যবর্তী কোণ
কত?
ফলে এই তিনটি বলের যে কোনো একটি বল অপর বলদ্বয়ের লব্ধির সমান হবে।
ধরি, \(3N\) ও \(4N\) বলদ্বয়ের মধ্যবর্তী কোণ \(\alpha\)
\(\therefore (3)^2+(4)^2+2\times3\times4\cos{\alpha}=(\sqrt{37})^2; \ \because P^2+Q^2+2PQ\cos{\alpha}=R^2\)
\(\Rightarrow 9+16+24\cos{\alpha}=37\)
\(\Rightarrow 25+24\cos{\alpha}=37\)
\(\Rightarrow 24\cos{\alpha}=37-25\)
\(\Rightarrow 24\cos{\alpha}=12\)
\(\Rightarrow \cos{\alpha}=\frac{12}{24}\)
\(\Rightarrow \cos{\alpha}=\frac{1}{2}\)
\(\Rightarrow \cos{\alpha}=\cos{60^{o}}\)
\(\therefore \alpha=60^{o}\)
উত্তরঃ ( গ )
ক \(30^{o}\)
গ \(60^{o}\)
গ \(60^{o}\)
খ \(45^{o}\)
ঘ \(90^{o}\)
\(\sqrt{37}N, \ 3N\) এবং \(4N\) মানের তিনটি বল একটি বস্তুর উপর
ক্রিয়া করে ভারসাম্য সৃষ্টি করে।ঘ \(90^{o}\)
ফলে এই তিনটি বলের যে কোনো একটি বল অপর বলদ্বয়ের লব্ধির সমান হবে।
ধরি, \(3N\) ও \(4N\) বলদ্বয়ের মধ্যবর্তী কোণ \(\alpha\)
\(\therefore (3)^2+(4)^2+2\times3\times4\cos{\alpha}=(\sqrt{37})^2; \ \because P^2+Q^2+2PQ\cos{\alpha}=R^2\)
\(\Rightarrow 9+16+24\cos{\alpha}=37\)
\(\Rightarrow 25+24\cos{\alpha}=37\)
\(\Rightarrow 24\cos{\alpha}=37-25\)
\(\Rightarrow 24\cos{\alpha}=12\)
\(\Rightarrow \cos{\alpha}=\frac{12}{24}\)
\(\Rightarrow \cos{\alpha}=\frac{1}{2}\)
\(\Rightarrow \cos{\alpha}=\cos{60^{o}}\)
\(\therefore \alpha=60^{o}\)
উত্তরঃ ( গ )
নিচের উদ্দীপকের আলোকে ২০ এবং ২১ নং
প্রশ্নের উত্তর দাওঃ
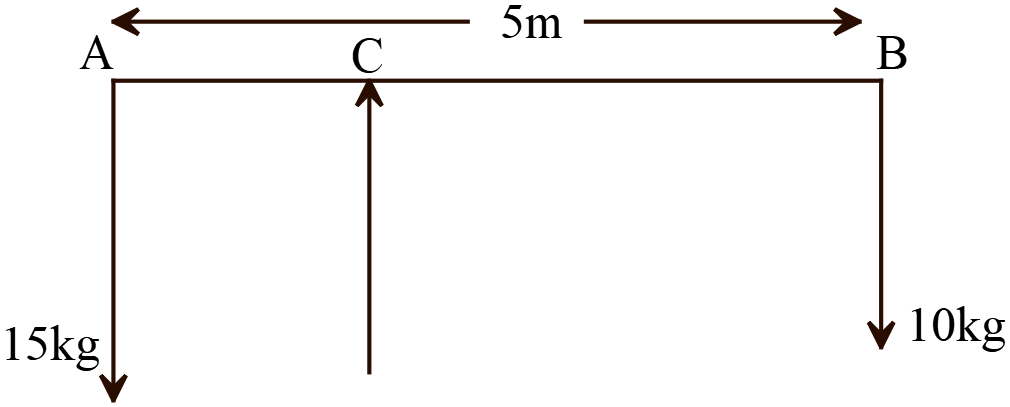
২০। \(C\) বিন্দুতে দণ্ডটি অনুভূমিকভাবে ভারসাম্যে থাকলে \(BC\) এর
দৈর্ঘ্য কত মিটার?
ক \(1\)
গ \(3\)
গ \(3\)
খ \(2\)
ঘ \(4\)
ঘ \(4\)

চিত্র হতে, \(AB=5m\)
\(A\) ও \(B\) বিন্দুতে ক্রিয়ারত সদৃশ সমান্তরাল বলদ্বয় \(15kg\) ও \(10kg\) যাদের লব্ধি \(C\) বিন্দুতে ক্রিয়ারত।
\(\therefore AC.15=BC.10\)
\(\Rightarrow \frac{AC}{BC}=\frac{10}{15}\)
\(\Rightarrow \frac{AC+BC}{BC}=\frac{10+15}{15}\)
\(\Rightarrow \frac{AB}{BC}=\frac{25}{15}\)
\(\Rightarrow \frac{5}{BC}=\frac{5}{3}\)
\(\Rightarrow \frac{1}{BC}=\frac{1}{3}\)
\(\Rightarrow BC=3\)
\(\therefore BC=3\) মিটার।
উত্তরঃ ( গ )
২১। \(A\) ও \(B\) বিন্দুতে ক্রিয়ারত বলদ্বয় বিসদৃশ হলে বলদ্বয়ের লব্ধি
\(A\) বিন্দু হতে কত দূরে ক্রিয়া করবে?

চিত্র হতে, \(AB=5m\)
\(A\) ও \(B\) বিন্দুতে ক্রিয়ারত বিসদৃশ সমান্তরাল বলদ্বয় \(15kg\) ও \(10kg\) যাদের লব্ধি \(D\) বিন্দুতে ক্রিয়ারত।
\(\therefore AD.15=BD.10\)
\(\Rightarrow \frac{AD}{BD}=\frac{10}{15}\)
\(\Rightarrow \frac{AD}{BD-AD}=\frac{10}{15-10}\)
\(\Rightarrow \frac{AD}{AB}=\frac{10}{5}\)
\(\Rightarrow \frac{AD}{5}=\frac{10}{5}\)
\(\Rightarrow AD=10\)
\(\therefore AD=10m\)
উত্তরঃ ( ঘ )
ক \(4m\)
গ \(8m\)
গ \(8m\)
খ \(5m\)
ঘ \(10m\)
ঘ \(10m\)

চিত্র হতে, \(AB=5m\)
\(A\) ও \(B\) বিন্দুতে ক্রিয়ারত বিসদৃশ সমান্তরাল বলদ্বয় \(15kg\) ও \(10kg\) যাদের লব্ধি \(D\) বিন্দুতে ক্রিয়ারত।
\(\therefore AD.15=BD.10\)
\(\Rightarrow \frac{AD}{BD}=\frac{10}{15}\)
\(\Rightarrow \frac{AD}{BD-AD}=\frac{10}{15-10}\)
\(\Rightarrow \frac{AD}{AB}=\frac{10}{5}\)
\(\Rightarrow \frac{AD}{5}=\frac{10}{5}\)
\(\Rightarrow AD=10\)
\(\therefore AD=10m\)
উত্তরঃ ( ঘ )
২২। \(\sqrt{3}-1\) মূলবিশিষ্ট দ্বিঘাত সমীকরণ কোণটি?
সমীকরণ, \(x^2-(\sqrt{3}-1-\sqrt{3}-1)x+(\sqrt{3}-1)(-\sqrt{3}-1)=0\)
\(\Rightarrow x^2-(-2)x+(-1+\sqrt{3})(-1-\sqrt{3})=0\)
\(\Rightarrow x^2+2x+(-1)^2-(\sqrt{3})^2=0\)
\(\Rightarrow x^2+2x+1-3=0\)
\(\therefore x^2+2x-2=0\)
উত্তরঃ ( খ )
ক \(x^2-2x-2=0\)
গ \(x^2-2\sqrt{3}x+2=0\)
গ \(x^2-2\sqrt{3}x+2=0\)
খ \(x^2+2x-2=0\)
ঘ \(x^2+2\sqrt{3}x+2=0\)
\(\sqrt{3}-1\) মূলবিশিষ্ট দ্বিঘাত সমীকরণের মূলদ্বয় হবে
\(\sqrt{3}-1\) ও \(-\sqrt{3}-1\) ঘ \(x^2+2\sqrt{3}x+2=0\)
সমীকরণ, \(x^2-(\sqrt{3}-1-\sqrt{3}-1)x+(\sqrt{3}-1)(-\sqrt{3}-1)=0\)
\(\Rightarrow x^2-(-2)x+(-1+\sqrt{3})(-1-\sqrt{3})=0\)
\(\Rightarrow x^2+2x+(-1)^2-(\sqrt{3})^2=0\)
\(\Rightarrow x^2+2x+1-3=0\)
\(\therefore x^2+2x-2=0\)
উত্তরঃ ( খ )
২৩। দ্বিঘাত সমীকরণের মূলগুলো বাস্তব হবে যদি-
\(i.\) পৃথায়ক শূন্য হয়
\(ii.\) পৃথায়ক ধনাত্মক হয়
\(iii.\) পৃথায়ক ঋনাত্মক হয়
নিচের কোনটি সঠীক?
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
পৃথায়ক ধনাত্মক হলে, দ্বিঘাত সমীকরণের মূলগুলো বাস্তব হবে।
\(\therefore (ii.)\) নং বাক্যটি সত্য।
আবার,
পৃথায়ক ঋনাত্মক হলে, দ্বিঘাত সমীকরণের মূলগুলো কাল্পনিক হবে।
\(\therefore (iii.)\) নং বাক্যটি সত্য নয়।
উত্তরঃ ( ক )
\(i.\) পৃথায়ক শূন্য হয়
\(ii.\) পৃথায়ক ধনাত্মক হয়
\(iii.\) পৃথায়ক ঋনাত্মক হয়
নিচের কোনটি সঠীক?
ক \(i.\) ও \(ii.\)
গ \(ii.\) ও \(iii.\)
গ \(ii.\) ও \(iii.\)
খ \(i.\) ও \(iii.\)
ঘ \(i.\), \(ii.\) ও \(iii.\)
পৃথায়ক শূন্য হলে, দ্বিঘাত সমীকরণের মূলগুলো বাস্তব হবে।ঘ \(i.\), \(ii.\) ও \(iii.\)
\(\therefore (i.)\) নং বাক্যটি সত্য।
আবার,
পৃথায়ক ধনাত্মক হলে, দ্বিঘাত সমীকরণের মূলগুলো বাস্তব হবে।
\(\therefore (ii.)\) নং বাক্যটি সত্য।
আবার,
পৃথায়ক ঋনাত্মক হলে, দ্বিঘাত সমীকরণের মূলগুলো কাল্পনিক হবে।
\(\therefore (iii.)\) নং বাক্যটি সত্য নয়।
উত্তরঃ ( ক )
২৪। \(x^2+5x-7=0\) সমীকরণের মূলগুলো-
\(D=5^2-4\times1\times-7=25+28=53\)
\(\therefore D\gt{0}\) এবং অপূর্ণ বর্গ সংখ্যা।
\(\therefore \) সমীকরণটির মূলগুলো বাস্তব ও অমূলদ হবে।
উত্তরঃ ( খ )
ক বাস্তব ও মূলদ
গ জটিল
গ জটিল
খ বাস্তব ও অমূলদ
ঘ বাস্তব ও সমান
\(x^2+5x-7=0\) সমীকরণের ক্ষেত্রে,ঘ বাস্তব ও সমান
\(D=5^2-4\times1\times-7=25+28=53\)
\(\therefore D\gt{0}\) এবং অপূর্ণ বর্গ সংখ্যা।
\(\therefore \) সমীকরণটির মূলগুলো বাস্তব ও অমূলদ হবে।
উত্তরঃ ( খ )
২৫। \(2x^2-5x+c=0\) সমীকরণের মূলদ্বয় পরস্পর গুণাত্মক বিপরীত হলে \(c\)
এর মান কত?
\(\therefore\) মূলদ্বয় \(\alpha, \ \frac{1}{\alpha}\)
তাহলে, মূলদ্বয় \(\alpha\times\frac{1}{\alpha}=\frac{c}{2}\)
\(\Rightarrow 1=\frac{c}{2}\)
\(\therefore c=2\)
উত্তরঃ ( ঘ )
ক \(\frac{1}{2}\)
গ \(-2\)
গ \(-2\)
খ \(-\frac{1}{2}\)
ঘ \(2\)
\(2x^2-5x+c=0\) সমীকরণের মূলদ্বয় পরস্পর গুণাত্মক বিপরীত ঘ \(2\)
\(\therefore\) মূলদ্বয় \(\alpha, \ \frac{1}{\alpha}\)
তাহলে, মূলদ্বয় \(\alpha\times\frac{1}{\alpha}=\frac{c}{2}\)
\(\Rightarrow 1=\frac{c}{2}\)
\(\therefore c=2\)
উত্তরঃ ( ঘ )
- About
- Author
-
Contact
Call me at +880-1715-651163Email: Golzarrahman1966@gmail.com
Visitors online: 000005